Thermodynamic-Based Perceived Predictive Power Control for Renewable Energy Penetrated Resident Microgrids
Abstract
1. Introduction
1.1. Motivation
1.2. Literature Review
1.3. Contribution
2. Thermodynamics-Based Symmetrical Power Predictive Control
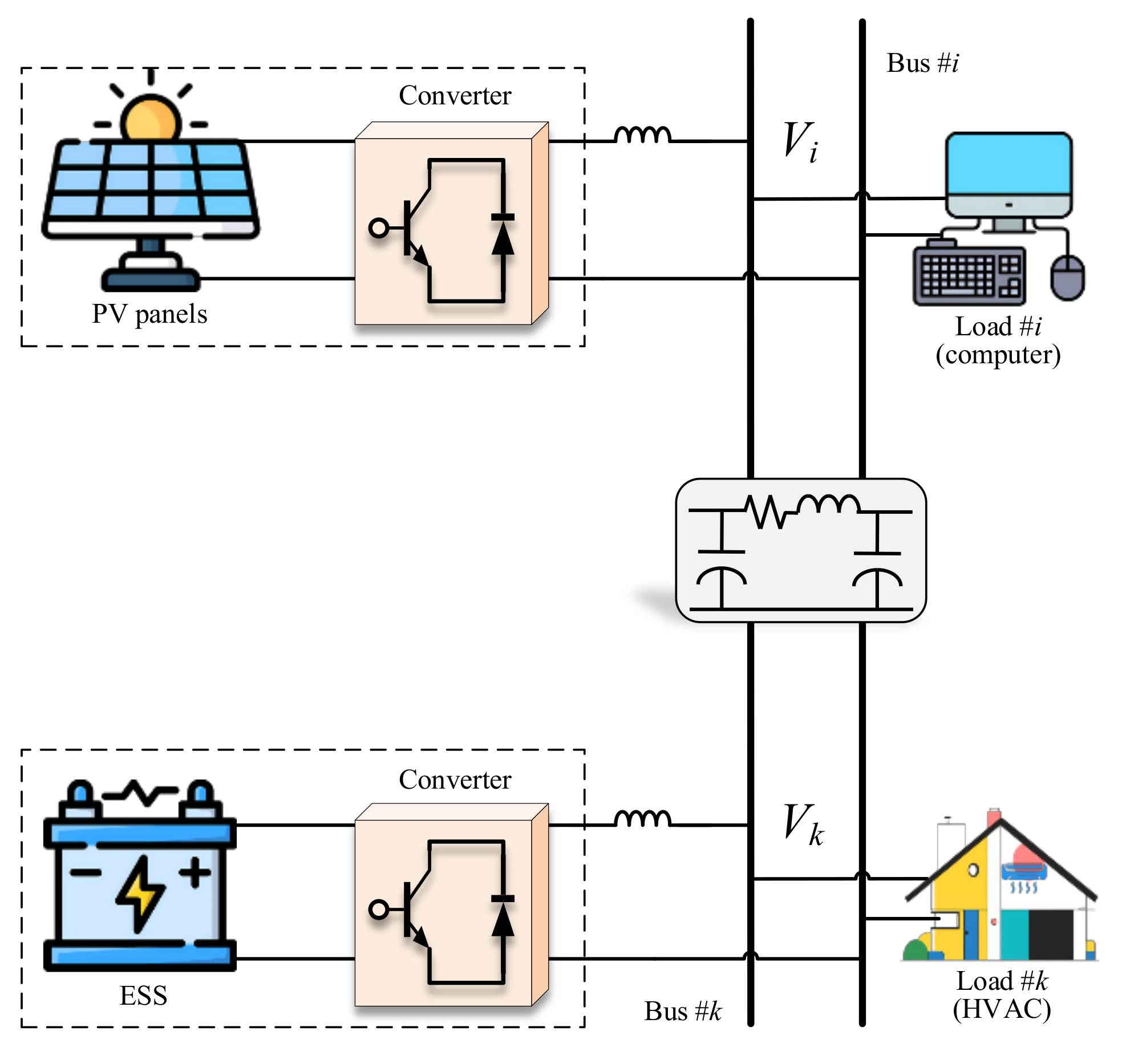
2.1. Framework Structure of Residential Microgrids with HVAC Systems
2.2. Mathematical R-C Network Model for Room Thermodynamic Analysis
2.3. Design of Robust and Symmetrical Predictive Temperature Control for HVAC
- (i)
- The dynamics constraint of the HVAC system, i.e., the nominal system of the augmented system:
- (ii)
- Initial value constraints on the invariant set defined as
- (iii)
- Essentially, it is the state constraints of x and u. In order for x and u of the original system to satisfy the sets X and U, the state constraints of the nominal system of the original system need to satisfy an indentation set, and hence equivalently, the conditions that the state constraints of the nominal system of the augmented system need to satisfy the following:for each time instant .
- (iv)
- Terminal constraints that satisfy the MOAS
2.4. Parameter Selection Guidelines for Robust and Symmetrical Predictive Temperature Control
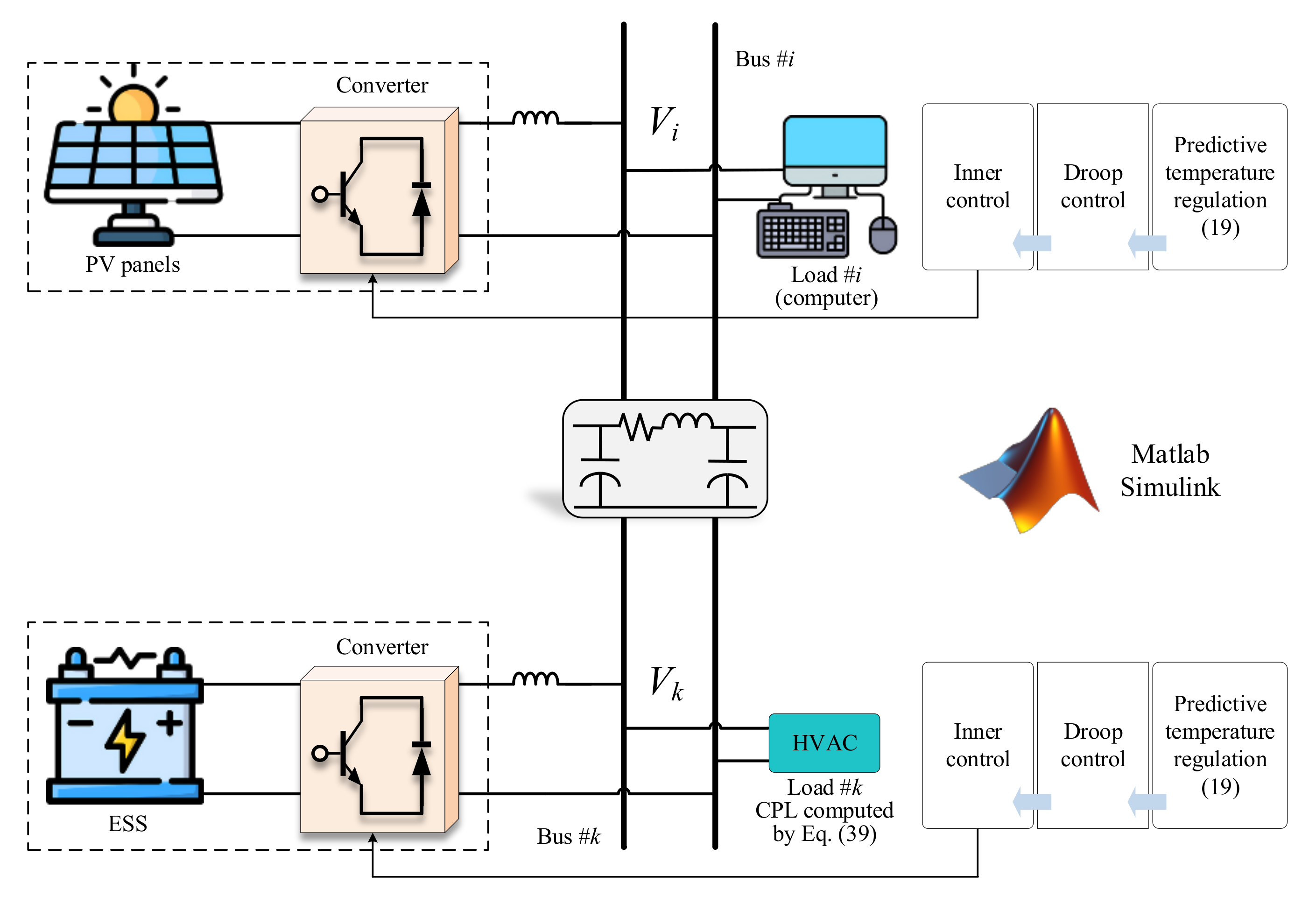
2.5. Consumption Interface Between HVAC System and Microgrid System
3. Results
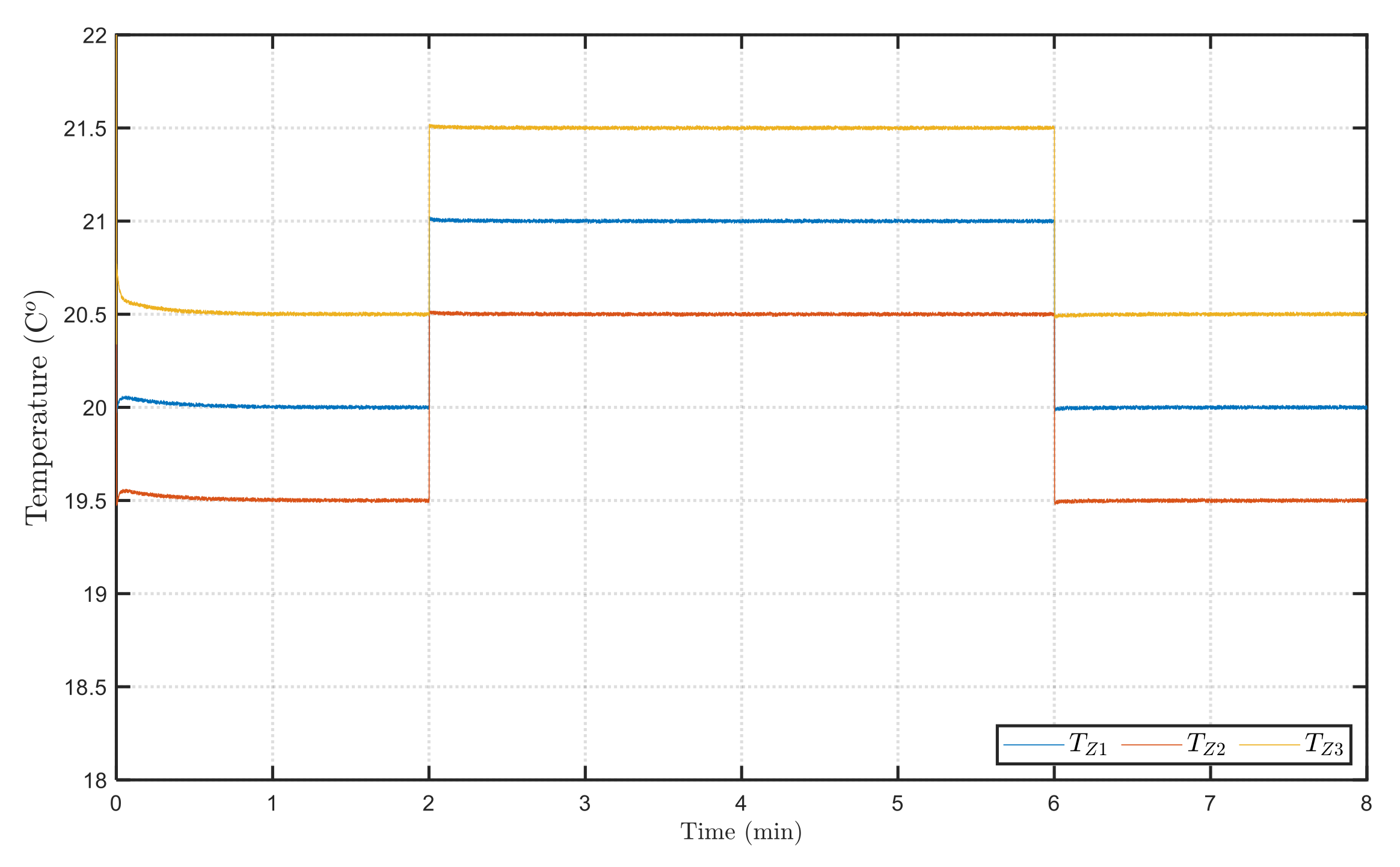
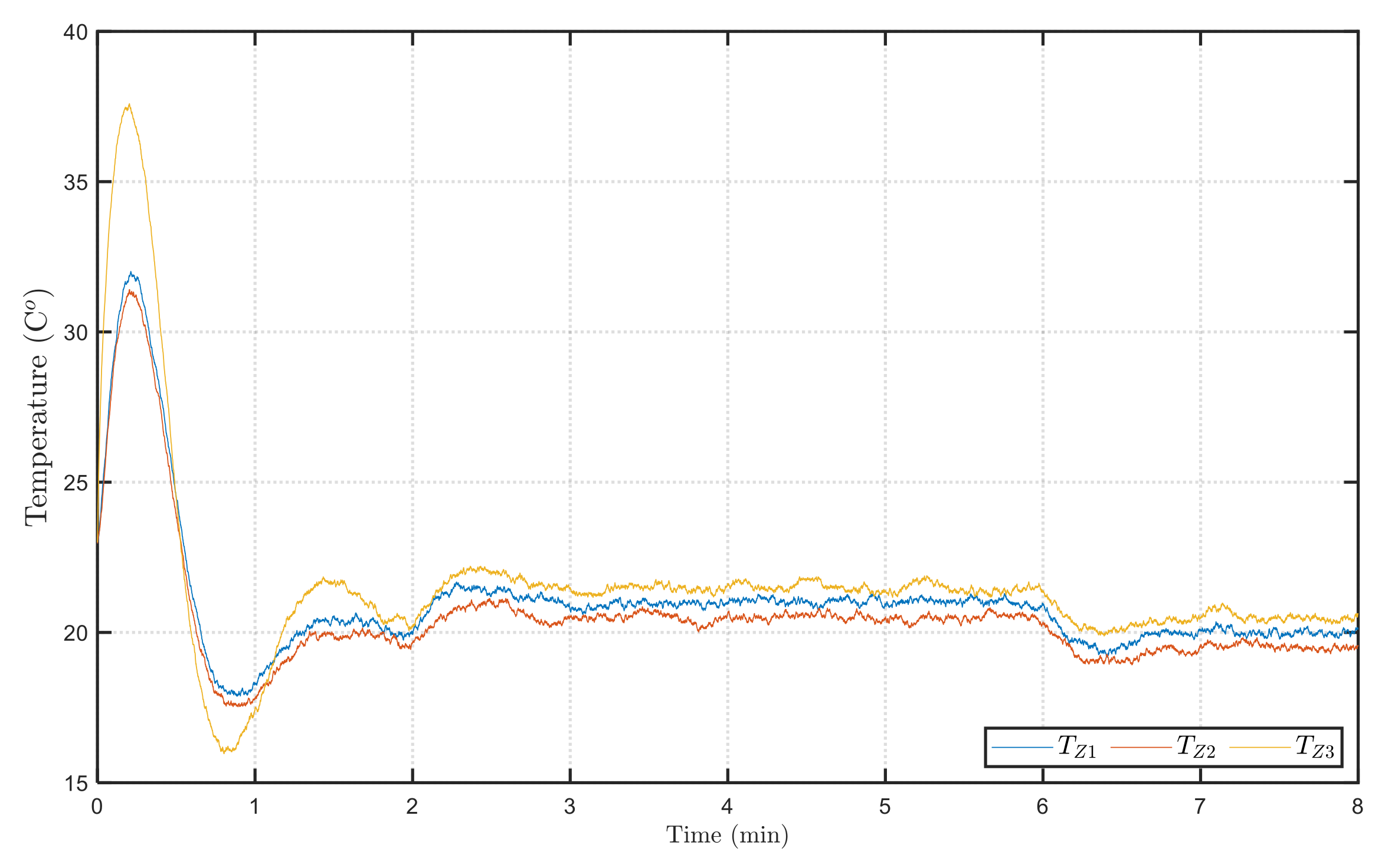
3.1. Results of Robust and Symmetrical Predictive Temperature Control for the HVAC System
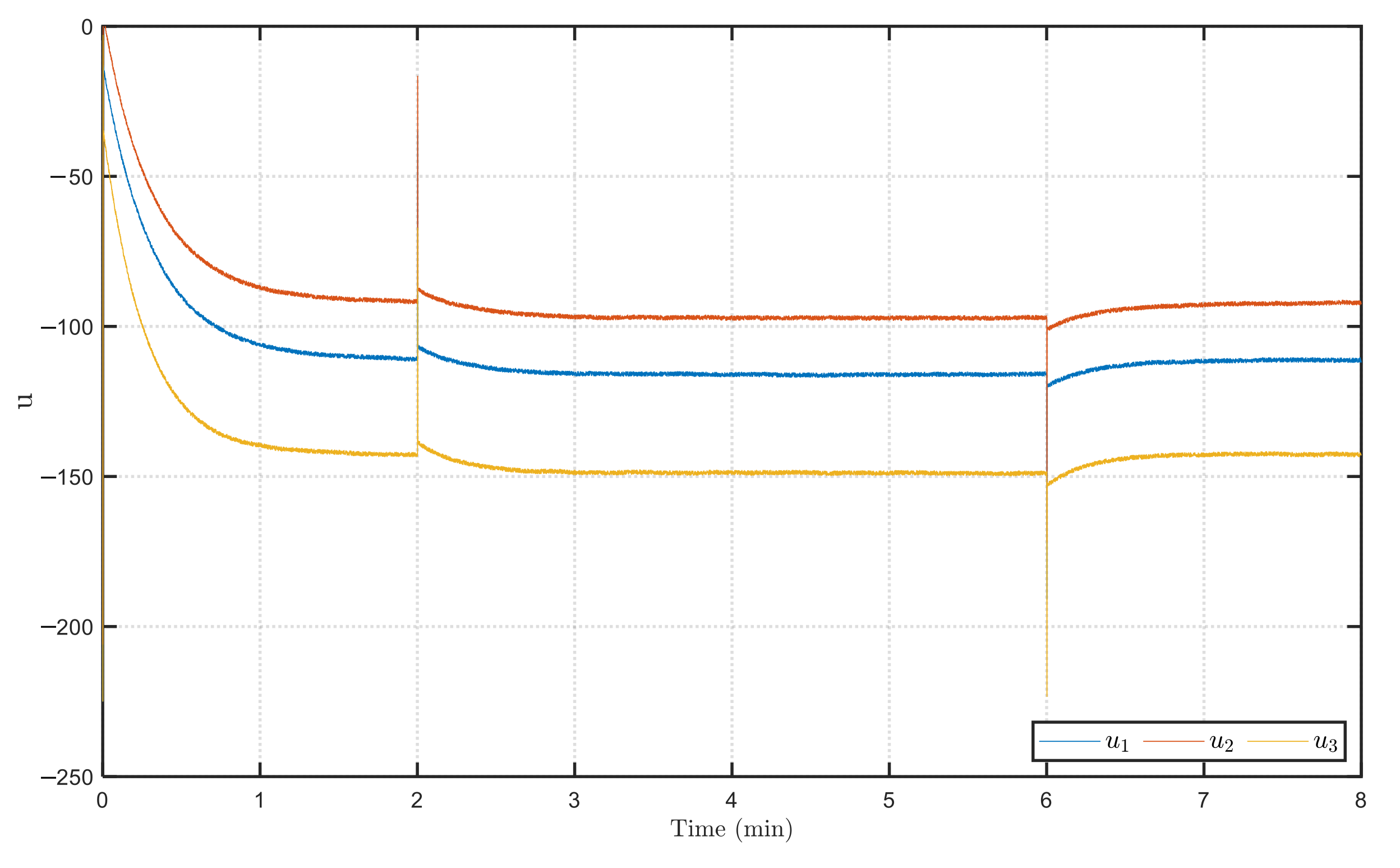
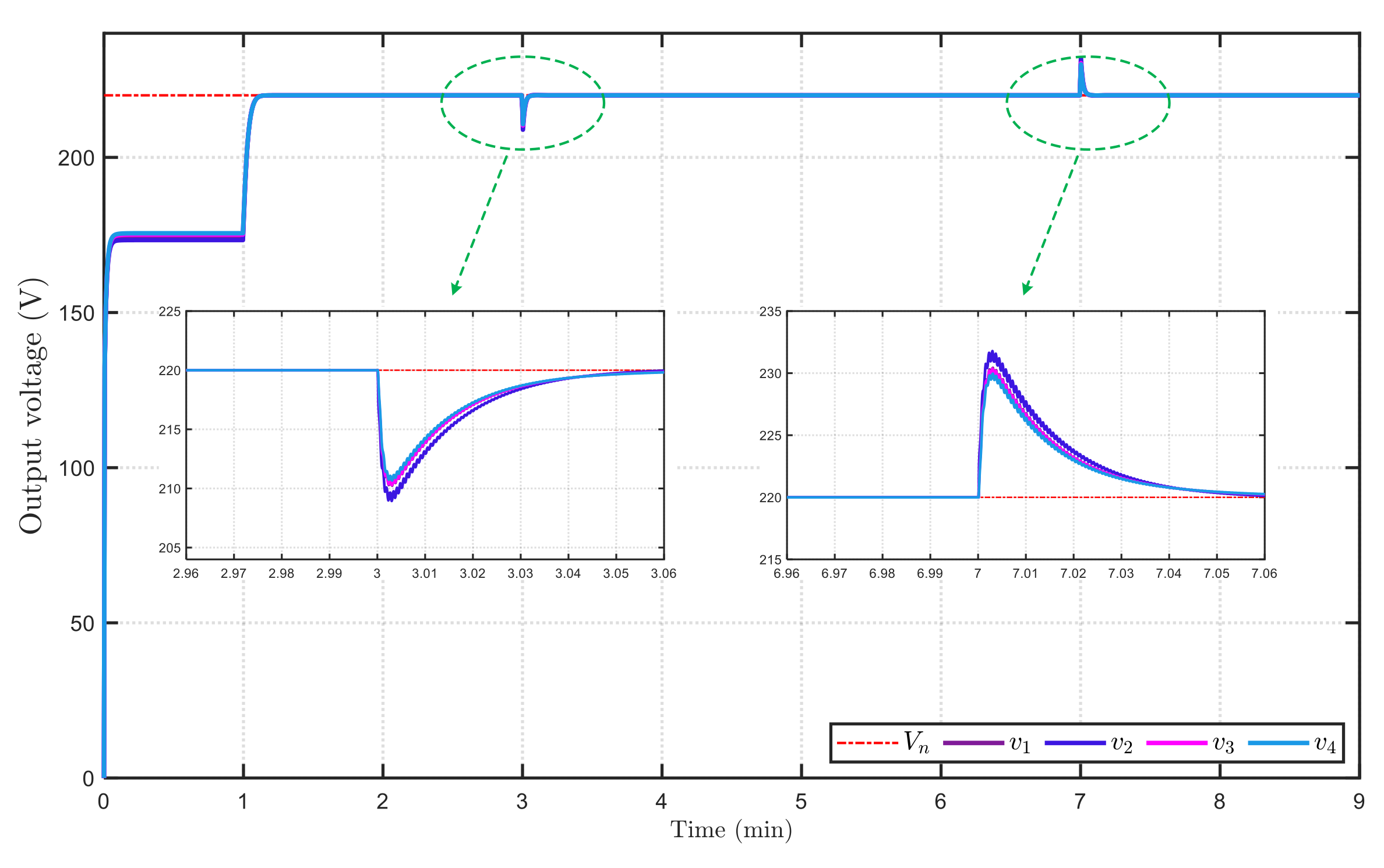
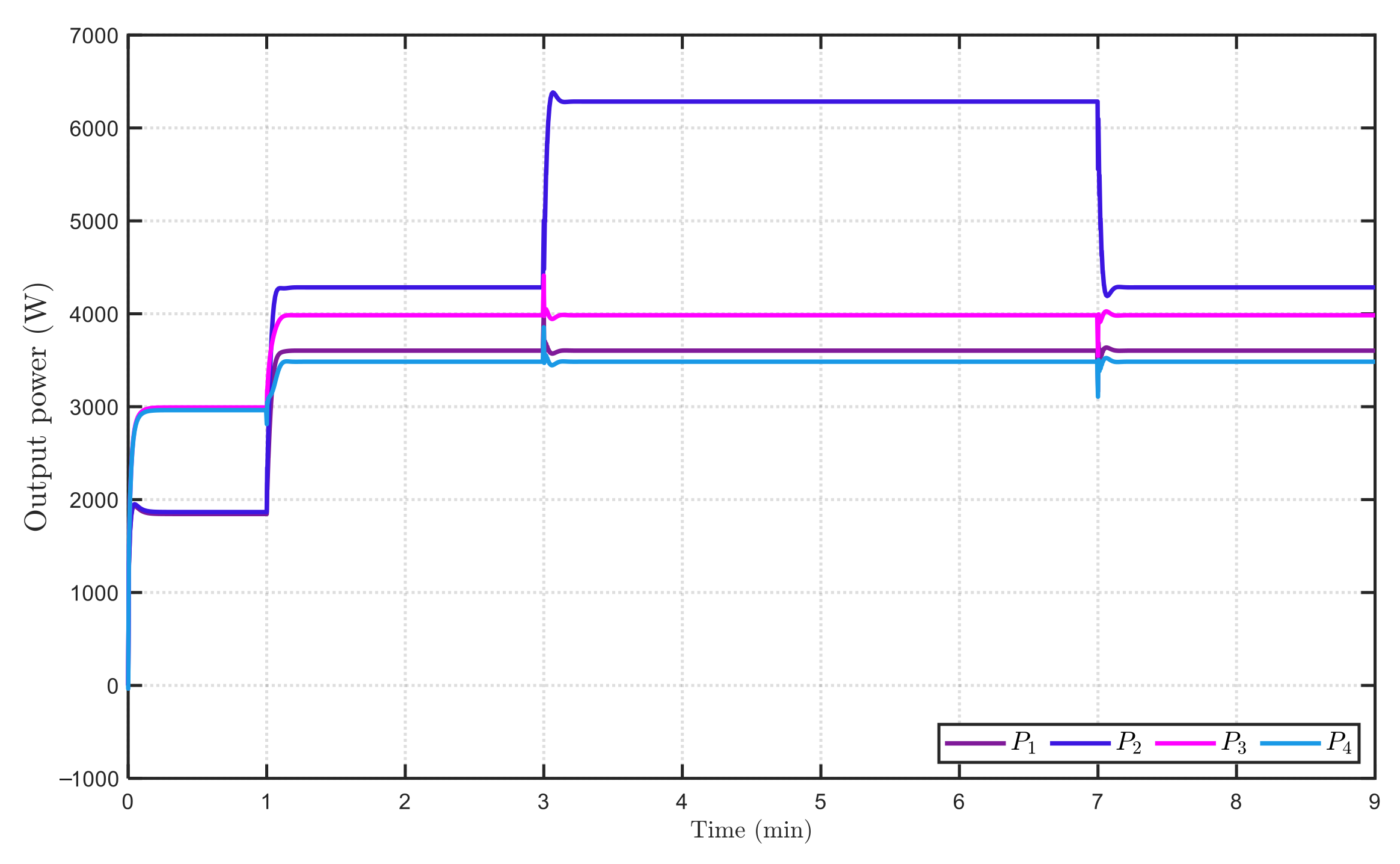
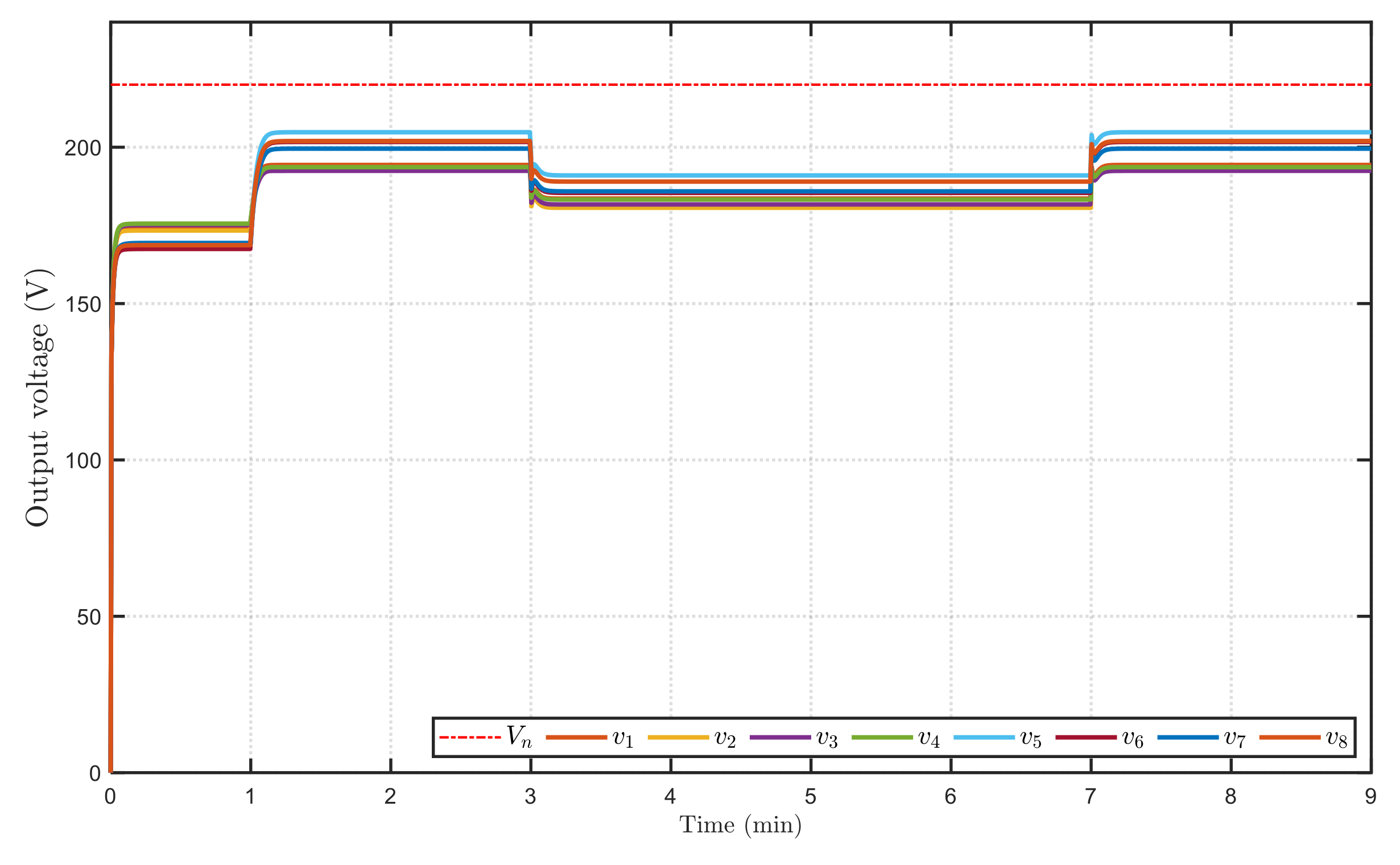
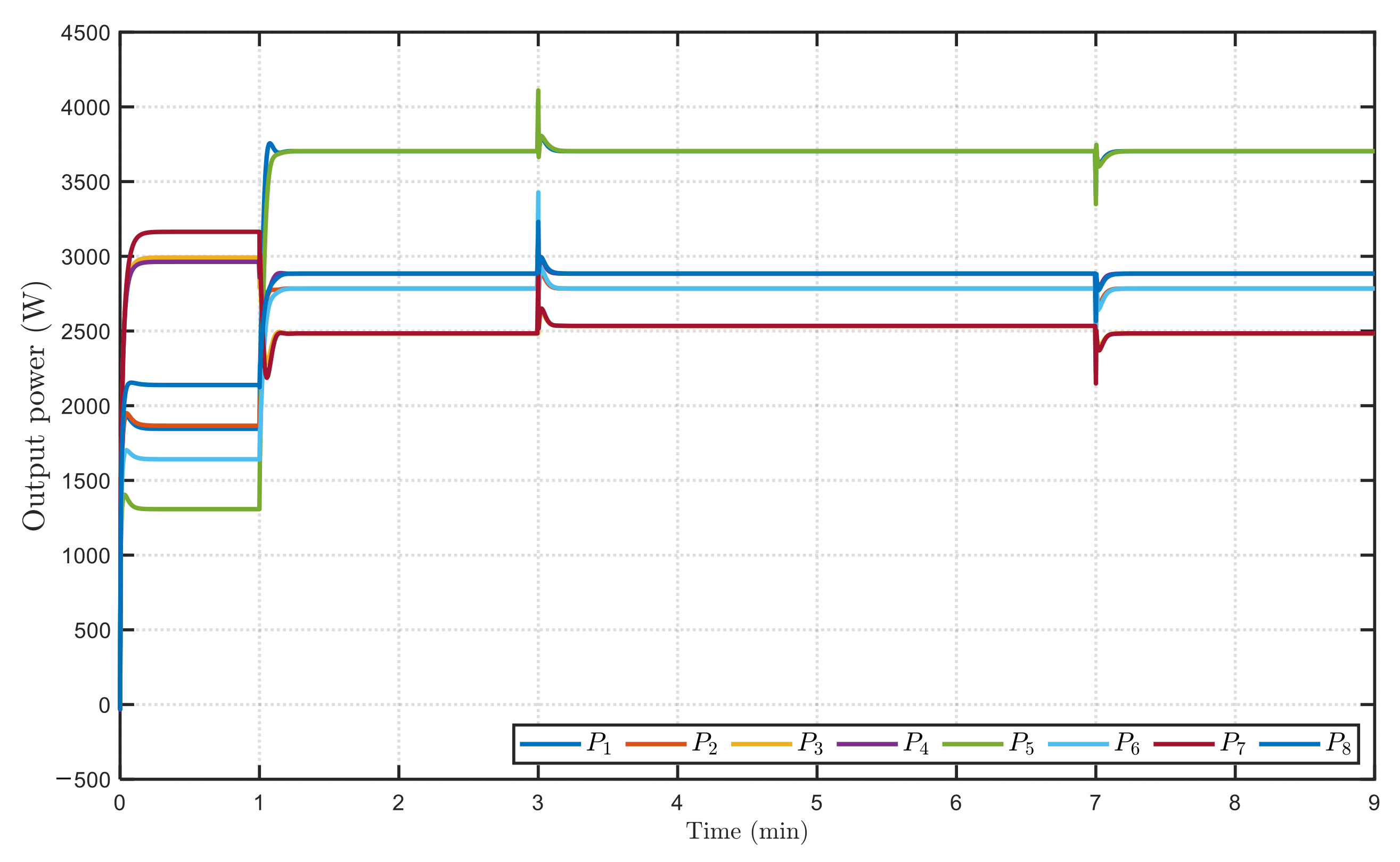
3.2. Results of Power Tracking and Voltage Balance for the Microgrid System
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ou, K.; Gao, S.; Wang, Y.; Zhai, B.; Zhang, W. Assessment of the Renewable Energy Consumption Capacity of Power Systems Considering the Uncertainty of Renewables and Symmetry of Active Power. Symmetry 2024, 16, 1184. [Google Scholar] [CrossRef]
- IEA. Renewables 2019: Analysis and Forecasts to 2024; International Energy Agency: Paris, France, 2019; pp. 1–204. [Google Scholar]
- Joshi, S.; Mittal, S.; Holloway, P.; Shukla, P.R.; Gallachóir, B.Ó.; Glynn, J. High Resolution Global Spatiotemporal Assessment of Rooftop Solar Photovoltaics Potential for Renewable Electricity Generation. Nat. Commun. 2021, 12, 5738. [Google Scholar] [CrossRef] [PubMed]
- Kapsalis, V.; Maduta, C.; Skandalos, N.; Wang, M.; Bhuvad, S.S.; D’Agostino, D.; Ma, T.; Raj, U.; Parker, D.; Peng, J.; et al. Critical Assessment of Large-Scale Rooftop Photovoltaics Deployment in the Global Urban Environment. Renew. Sust. Energ. Rev. 2024, 189, 114005. [Google Scholar] [CrossRef]
- Kiss, V.M.; Hetesi, Z.; Kiss, T. The Effect of Time Resolution on Energy System Simulation in Case of Intermittent Energies. Renew. Sust. Energ. Rev. 2024, 191, 114099. [Google Scholar] [CrossRef]
- Zhao, Y.; Yang, S.; Liu, S.; Zhang, S.; Zhong, Z. Optimal Economic Research of Microgrids Based on Multi-Strategy Integrated Sparrow Search Algorithm under Carbon Emission Constraints. Symmetry 2024, 16, 388. [Google Scholar] [CrossRef]
- Rahman, T.; Alharbi, T. Exploring Lithium-Ion Battery Degradation: A Concise Review of Critical Factors, Impacts, Data-Driven Degradation Estimation Techniques, and Sustainable Directions for Energy Storage Systems. Batteries 2024, 10, 220. [Google Scholar] [CrossRef]
- Wu, J.; Li, S.; Fu, A.; Cvetković, M.; Palensky, P.; Vasquez, J.C.; Guerrero, J.M. Hierarchical Online Energy Management for Residential Microgrids with Hybrid Hydrogen–Electricity Storage System. Appl. Energy 2024, 363, 123020. [Google Scholar] [CrossRef]
- Zhang, S.; Pan, G.; Li, B.; Gu, W.; Fu, J.; Sun, Y. Multi-Timescale Security Evaluation and Regulation of Integrated Electricity and Heating System. IEEE Trans. Smart Grid 2025, 16, 1088–1099. [Google Scholar] [CrossRef]
- Wang, W.; Yuan, B.; Sun, Q.; Wennersten, R. Application of energy storage in integrated energy systems—A solution to fluctuation and uncertainty of renewable energy. J. Energy Storage 2013, 52, 104812. [Google Scholar] [CrossRef]
- Li, X.; Hui, D.; Lai, X. Battery energy storage station (BESS)-based smoothing control of photovoltaic (PV) and wind power generation fluctuations. IEEE Trans. Sustain. Energy 2013, 4, 464–473. [Google Scholar] [CrossRef]
- Tani, A.; Camara, M.B.; Dakyo, B. Energy management in the decentralized generation systems based on renewable energy—Ultracapacitors and battery to compensate the wind/load power fluctuations. IEEE Trans. Ind. Appl. 2014, 51, 1817–1827. [Google Scholar] [CrossRef]
- Ling, J.; Mulani, F.I. Planning and Optimization of a Residential Microgrid Utilizing Renewable Resources and Integrated Energy Storage. J. Energy Storage 2024, 97, 112933. [Google Scholar] [CrossRef]
- Schwenzer, M.; Ay, M.; Bergs, T.; Abel, D. Review on model predictive control: An engineering perspective. J. Adv. Manuf. Technol. 2021, 117, 1327–1349. [Google Scholar] [CrossRef]
- Li, H.; Shi, Y. Robust distributed model predictive control of constrained continuous-time nonlinear systems: A robustness constraint approach. IEEE Trans. Autom. Control. 2013, 59, 1673–1678. [Google Scholar] [CrossRef]
- Conte, C.; Jones, C.N.; Morari, M.; Zeilinger, M.N. Distributed synthesis and stability of cooperative distributed model predictive control for linear systems. Automatica 2016, 69, 117–125. [Google Scholar] [CrossRef]
- Mai, W.; Chung, C.Y. Economic MPC of Aggregating Commercial Buildings for Providing Flexible Power Reserve. IEEE Trans. Power Syst. 2015, 30, 2685–2694. [Google Scholar] [CrossRef]
- Abedin, T.; Rahman M, M.; Alnamasi, K.; Badruddin, I.A.; Bashir, M.N.; Nur-E-Alam, M. Advancing Comfort and Efficiency: Radiant Heating and Cooling Systems for Sustainable Architecture. Build. Environ. 2025, 113234. [Google Scholar] [CrossRef]
- Hu, M.; Xiao, F.; Wang, S. Neighborhood-level Coordination and Negotiation Techniques for Managing Demand-side Flexibility in Residential Microgrids. Renew. Sust. Energ. Rev. 2021, 135, 110248. [Google Scholar] [CrossRef]
- Wang, C.; Wang, M.; Wang, A.; Zhang, X.; Zhang, J.; Ma, H.; Yang, N.; Zhao, Z.; Lai, C.S.; Lai, L.L. Multiagent Deep Reinforcement Learning-based Cooperative Optimal Operation with Strong Scalability for Residential Microgrid Clusters. Energy 2025, 314, 134165. [Google Scholar] [CrossRef]
- Ghodusinejad, M.H.; Peirov, S.; Yousefi, H.; Astaraei, F.R. Multi-objective Optimal Design and Performance Analysis of a Residential Microgrid. J. Energy Storage 2024, 92, 112201. [Google Scholar] [CrossRef]
- Valencia-Díaz, A.; Toro, E.M.; Hincapié, R.A. Optimal Planning and Management of the Energy–Water–Carbon Nexus in Hybrid AC/DC Microgrids for Sustainable Development of Remote Communities. Appl. Energy 2025, 377, 124517. [Google Scholar] [CrossRef]
- Li, Z.; Wu, L.; Xu, Y.; Zheng, X. Stochastic-Weighted Robust Optimization Based Bilayer Operation of a Multi-Energy Building Microgrid Considering Practical Thermal Loads and Battery Degradation. IEEE Trans. Sustain. Energy 2022, 13, 668–682. [Google Scholar] [CrossRef]
- Yilmaz, S.; Dener, M. Security with Wireless Sensor Networks in Smart Grids: A Review. Symmetry 2024, 16, 1295. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, Z.; Yuan, X.; Su, L.; Li, K. Optimal Control Strategies for Demand Response in Buildings Under Penetration of Renewable Energy. Buildings 2022, 12, 371. [Google Scholar] [CrossRef]
- Chen, X.; Lei, J.; Zhang, X. Bi-Level Optimization Scheduling Strategy for PIES Considering Uncertainties of Price-Based Demand Response. Symmetry 2025, 17, 43. [Google Scholar] [CrossRef]
- Correia, A.; Ferreira, L.M.; Coimbra, P.; Moura, P.; De Almeida, A.T. Smart Thermostats for a Campus Microgrid: Demand Control and Improving Air Quality. Energies 2022, 15, 1359. [Google Scholar] [CrossRef]
- Nematirad, R.; Ardehali, M.M.; Khorsandi, A.; Mahmoudian, A. Optimization of Residential Demand Response Program Cost With Consideration for Occupants Thermal Comfort and Privacy. IEEE Access 2024, 12, 15194–15207. [Google Scholar] [CrossRef]
- Ma, Z.; Cui, S.; Chen, J. Demand Response Through Ventilation and Latent Load Adjustment For Commercial Buildings in Humid Climate Zones. Appl. Energy 2024, 373, 123940. [Google Scholar] [CrossRef]
- Xin, X.; Zhang, Z.; Zhou, Y.; Liu, Y.; Wang, D.; Nan, S. A comprehensive review of predictive control strategies in heating, ventilation, and air-conditioning (HVAC): Model-free VS model. J. Build. Eng. 2024, 94, 110013. [Google Scholar] [CrossRef]
- Shin, M.; Kim, S.; Kim, Y.; Song, A.; Kim, Y.; Kim, H. Development of an HVAC system control method using weather forecasting data with deep reinforcement learning algorithms. Build. Environ. 2024, 248, 111069. [Google Scholar] [CrossRef]
- Nguyen, A.T.; Pham, D.H.; Oo, B.L.; Santamouris, M.; Ahn, Y.; Lim, B.T.H. Modelling building HVAC control strategies using a deep reinforcement learning approach. Energ. Buildings. 2024, 310, 114065. [Google Scholar] [CrossRef]
- Qiu, W.; Yin, H.; Dong, Y.; Wei, X.; Liu, Y.; Yao, W. Synchro-waveform-based event identification using multi-task time-frequency transform networks. IEEE Trans. Smart Grid 2025, 16, 2647–2658. [Google Scholar] [CrossRef]
- Kaspar, K.; Ouf, M.; Eicker, U.A. Critical Review of Control Schemes for Demand-side Energy Management of building Clusters. Energy Buildings 2022, 257, 111731. [Google Scholar] [CrossRef]
- Shafiqurrahman, A.; Yahyaee, S.A.; Sreekumar, P.; Khadkikar, V. A Novel Decentralized Unbalance Load Sharing Approach for Islanded Microgrids. IEEE Trans. Ind. Appl. 2024, 60, 5714–5725. [Google Scholar] [CrossRef]
- Sen, S.; Kumar, M. Distributed-MPC type optimal EMS for renewables and EVs based grid-connected building integrated microgrid. IEEE Trans. Ind. Appl. 2023, 60, 2390–2408. [Google Scholar] [CrossRef]
- Mannini, R.; Darure, T.; Eynard, J.; Grieu, S. Predictive energy management of a building-integrated microgrid: A case study. Energies 2024, 17, 1355. [Google Scholar] [CrossRef]
- Mannini, R.; Eynard, J.; Grieu, S. Predictive control of a multi-energy building-integrated microgrid: A case study. In Proceedings of the 2024 IEEE Congress on Evolutionary Computation (CEC), Yokohama, Japan, 30 June–5 July 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1–8. [Google Scholar]
- Wu, X.; Kerekes, T. Flexible active power control for PV-ESS systems: A review. Energies 2021, 14, 7388. [Google Scholar] [CrossRef]
- Maasoumy, M. Controlling Energy-efficient Buildings in the Context of Smart Grid: A Cyber Physical System Approach. Doctoral Dissertation, Electrical Engineering Department, University of California, Berkeley, CA, USA, 2013. Tech. Rep. UCB/EECS-2013-244. [Google Scholar]
- Fiedler, F.; Karg, B.; Lüken, L.; Brandner, D.; Heinlein, M.; Brabender, F.; Lucia, S. do-mpc: Towards FAIR nonlinear and robust model predictive control. Control Eng. Pract. 2023, 140, 105676. [Google Scholar] [CrossRef]



| PI Control | The Proposed RPTC | |
|---|---|---|
| RMSE | 3.12 ± 0.22 | 2.21 ± 0.14 |
| MAE | 2.45 ± 0.15 | 1.78 ± 0.09 |
| Overshoot | 22.4% | 9.7% |
| Settling time | 4.2 s | 2.8 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, W.; Ma, L.; Li, W.; Zhu, Y.; Nan, D.; Peng, Y. Thermodynamic-Based Perceived Predictive Power Control for Renewable Energy Penetrated Resident Microgrids. Energies 2025, 18, 3027. https://doi.org/10.3390/en18123027
Shi W, Ma L, Li W, Zhu Y, Nan D, Peng Y. Thermodynamic-Based Perceived Predictive Power Control for Renewable Energy Penetrated Resident Microgrids. Energies. 2025; 18(12):3027. https://doi.org/10.3390/en18123027
Chicago/Turabian StyleShi, Wenhui, Lifei Ma, Wenxin Li, Yankai Zhu, Dongliang Nan, and Yinzhang Peng. 2025. "Thermodynamic-Based Perceived Predictive Power Control for Renewable Energy Penetrated Resident Microgrids" Energies 18, no. 12: 3027. https://doi.org/10.3390/en18123027
APA StyleShi, W., Ma, L., Li, W., Zhu, Y., Nan, D., & Peng, Y. (2025). Thermodynamic-Based Perceived Predictive Power Control for Renewable Energy Penetrated Resident Microgrids. Energies, 18(12), 3027. https://doi.org/10.3390/en18123027





