Active-Clamp Dual-Transformer ZVS Flyback Converter

Abstract

In order to upgrade the ability of the traditional flyback converter to transfer energy to the load, a dual-flyback converter with two active clamping circuits is added, using the same clamping capacitor to recover the leakage inductance energy. Furthermore, no additional resonant inductor is needed, and both the switches have zero voltage switching (ZVS) to reduce the switching loss. In addition, full-wave rectification is used on the secondary side to decrease the output voltage ripple frequency, which makes it easy to design the output filter.

1. Introduction

Power supply can be classified into two types: switching and linear. The former has the advantages of higher power density and higher efficiency. In recent years, switching power supplies have moved towards increasing the switching frequency to reduce the overall circuit size, thereby achieving high power density [1,2]. Switching methods can be classified into hard switching and soft switching. However, the former will experience switching loss. Consequently, in order to reduce the loss caused by the switching of switches, the soft switching method has been introduced There are four common technologies used for this, as described below.

(1)

Resonant Converter [3]

In order to solve the problem of low hard-switching efficiency, since the early 1980s, the literature [1] has described resonant converters with the capacitor connected in parallel with the switch or the inductor connected in series with the switch to form the LC resonant circuit. This is the first paper to address the concept of soft switching. When the voltage on the switch resonates to zero, the power switch is turned on to achieve zero voltage switching (ZVS); when the current in the switch resonates to zero, the switch is turned off to achieve zero current switching (ZCS). Although these techniques can improve the overall efficiency of the converter, the corresponding disadvantage is that the resonance generates a relatively large voltage and current. This not only adds extra voltage stress or current stress to the components, but also creates relatively serious conduction losses.

(2)

Quasi-resonant Converter (QRC) [4]

The quasi-resonant converter is designed to minimize switching losses by adding a winding and a sensor to detect the valley voltage on the switch. However, the quasi-resonant switching technique is not completely ZVS, and this structure requires variable-frequency control and operation in the discontinuous conduction mode (DCM). In addition, in order to improve the efficiency, the secondary side mostly adopts synchronous rectification (SR), but due to the unpredictability of the turn-on time, it is usually necessary to use an external SR chip to detect the current at zero point for switching to reduce the loss.

(3)

Zero Voltage/Zero Current Transition (ZV/ZCT) [5,6,7,8,9,10,11,12]

ZV/ZCT is a technique in which an auxiliary switch is transiently resonated before the main power switch is energized by means of an external circuit to reduce the stress on the switch, and at the same time to achieve ZV/ZCS of the switch.

However, when ZV/ZCT converters [5,6,7,8] were first developed, the converter was able to achieve ZV/ZCS of the main switch by means of an auxiliary circuit, but it was not possible to achieve ZV/ZCS of the auxiliary switch, since the auxiliary switch transfers the energy from the main power switch to the auxiliary switch, thereby resulting in heat buildup on the auxiliary switch. Accordingly, the literature [9] proposes adding ZV/ZCS to the auxiliary switch to reduce the switching loss. According to the literature [10,11,12], the auxiliary switch is turned on before the switch is turned on and off, so that the switch has ZVT and ZCT.

(4)

Active Clamp Converter [13,14,15,16,17,18,19,20]

Active clamp technology improves the efficiency of the converter by making the voltage on the switch as close to zero voltage as possible when the switch is turned on. The principle of this technology is to connect a clamping capacitor in series with an auxiliary switch, which can be used for energy storage and energy recycling functions when the main switch is turned on and off, respectively. In other words, before the main switch is turned on, the energy stored in the output parasitic capacitor of the switch is released to the clamping capacitor to realize ZVS; when the main switch is turned off, the auxiliary switch releases the energy stored in the clamping capacitor.

The literature [13] proposes a primary-side regulation (PSR) method to analyze and derive the equations, and then the results are used to compensate the secondary losses to improve the accuracy of the output voltage regulation. The literature [14] proposes an active-clamped flyback converter and an automatic adjustment of the length of the blanking time in each state to achieve ZVS under various operating conditions.

In recent years, an active clamping circuit has been applied to boost converters in [15,16,17,18,19], and both the main switch and the auxiliary switch are able to achieve ZVS.

On the other hand, most of the low and medium power DC/DC converters on the market use a flyback converter. Since the flyback converter is directly connected to the transformer, the leakage inductance energy of the transformer will cause the switch to be subjected to high-frequency spike and ringing voltages during the cutoff period. Traditionally, in order to solve this problem, a snubber is added to the primary side of the transformer [20]. This snubber circuit generally consists of capacitors, resistors, and diodes, which can effectively absorb the energy generated by voltage surge into the capacitor during the switch cutoff moment, and then transfer this energy to the resistor to be consumed when the switch is turned on. However, although this method can effectively reduce high-frequency spike and ringing voltages, the efficiency is quite low. Consequently, active-clamped ZVS flyback converters [13,14,15] have been proposed, not only to recycle leakage inductance energy but also to achieve ZVS turn-on of the main switch.

In this paper, an active-clamped dual-transformer ZVS flyback converter is presented to increase the ability of the traditional flyback converter to transfer energy to the load. To achieve ZVS, no additional magnetic components are required in the resonant tank.

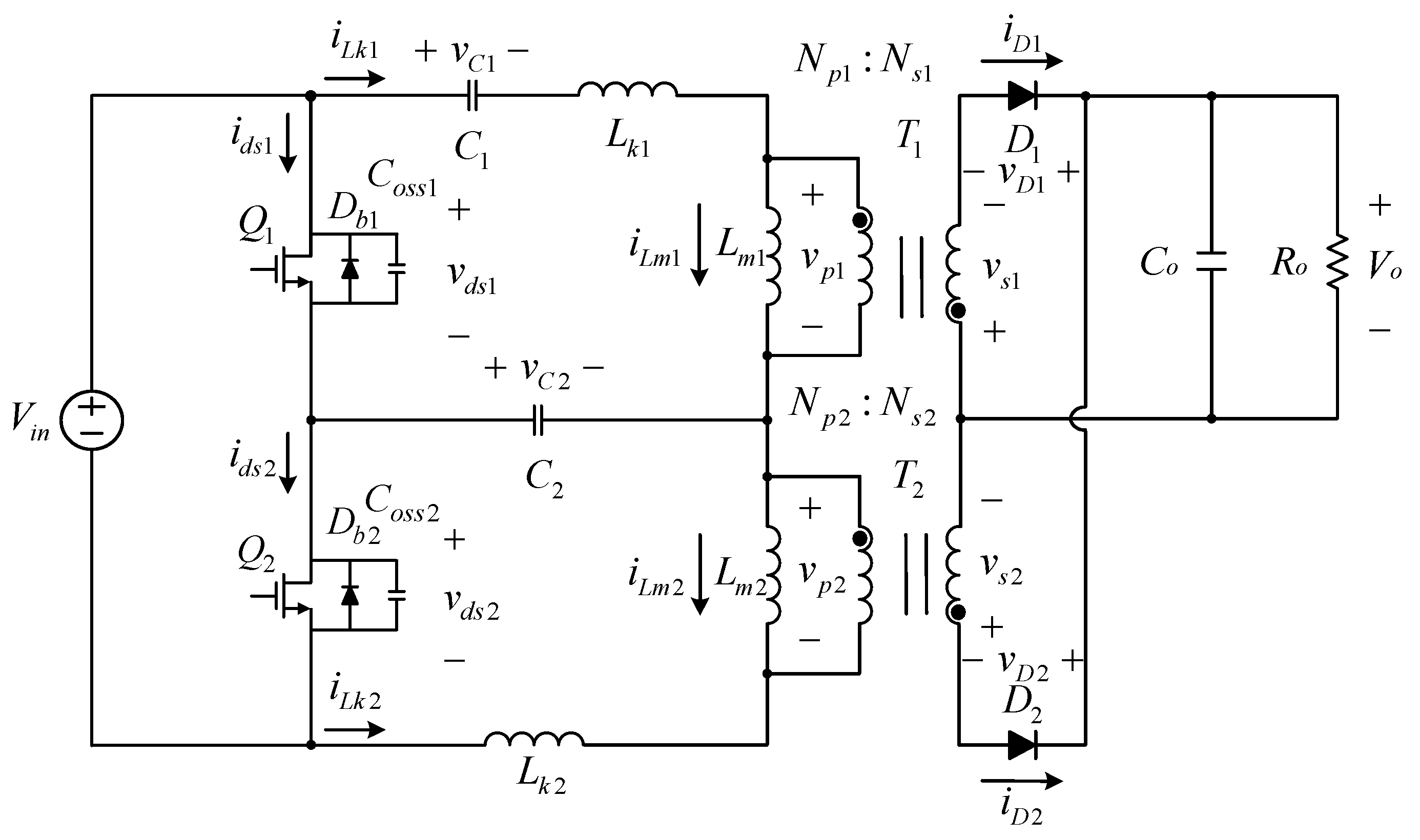
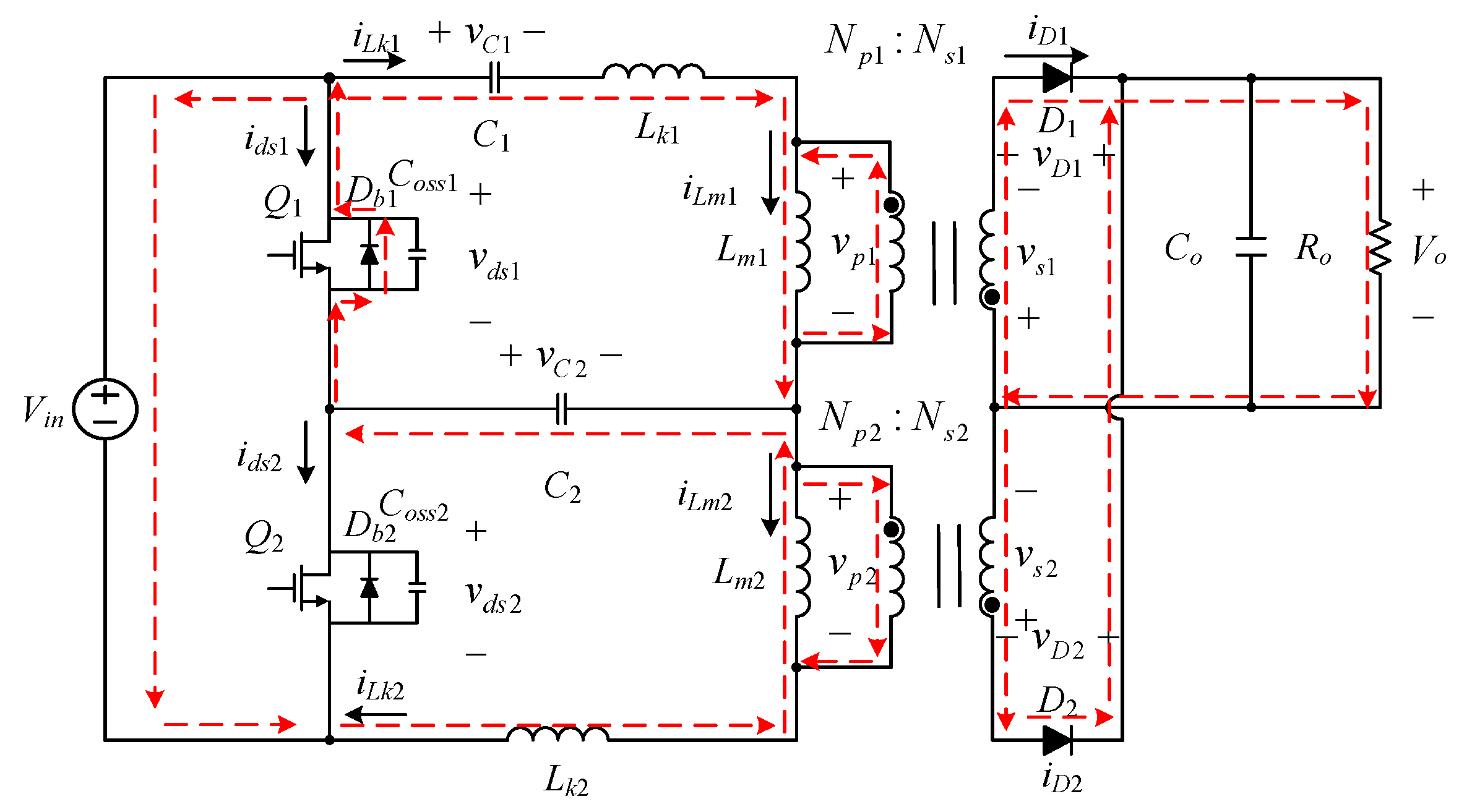
2. Proposed Active-Clamp Dual-Transformer ZVS Flyback Converter

Figure 1 shows the active-clamp flyback converter with two transformers. This circuit consists of an auxiliary switch Q₁, a main power switch Q₂, a clamping capacitor C₁, an energy-transferring capacitor C₂, an output capacitor C_o, two output rectifier diodes D₁ and D₂, two transformers T₁ and T₂. In addition, the load side is represented by an output resistor R_o.

2.1. Symbol Definitions and Assumptions

Prior to describing the operating principle of this circuit, the relevant variables in Figure 1 are defined as follows:

(1)

V_in is the input DC voltage, the output capacitance C_o is large enough, and the output voltage is denoted as V_o.

(2)

D_b1 and D_b2 are the body diodes of the auxiliary switch Q₁ and the main switch Q₂, respectively; C_oss1 and C_oss2 are the output capacitors of the auxiliary switch Q₁ and the main switch Q₂, respectively.

(3)

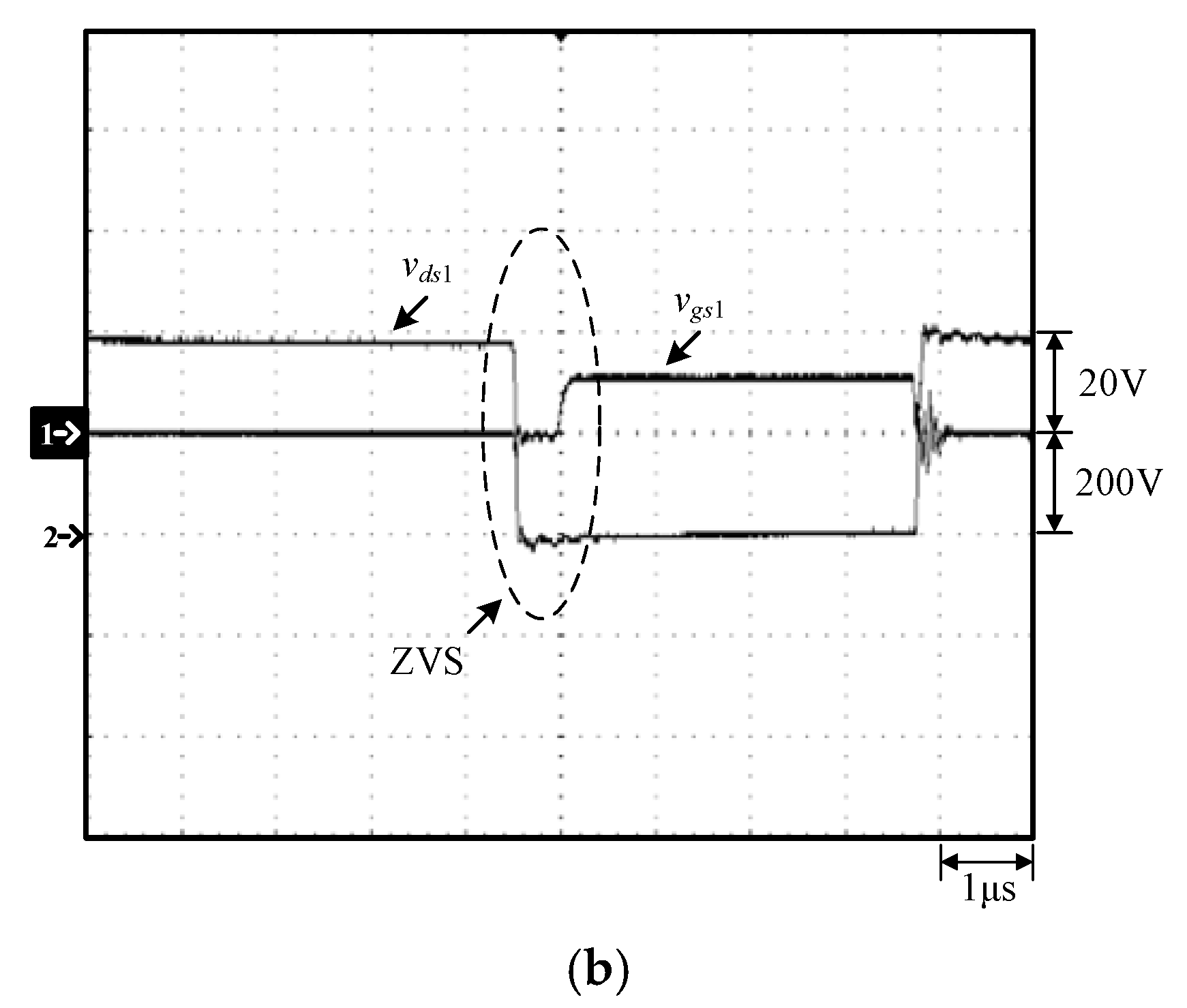
i_ds1 and i_ds2 are the currents in the auxiliary switch Q₁ and the main switch Q₂, respectively; v_ds1 and v_ds2 are the voltages on the auxiliary switch Q₁ and the main switch Q₂, respectively; v_gs1 is the gate driving signal for the auxiliary switch Q₁, v_gs2 is the gate driving signal for the main switch Q₂, and these two signals are complementary signals, namely, 1 − D and D for Q₁ and Q₂, respectively.

(4)

L_k1 and L_k2 are the leakage inductances of the first transformer and the second transformer, respectively, and are also the resonant inductances; L_m1 and L_m2 are the magnetizing inductances of the first transformer and the second transformer, respectively.

(5)

i_Lk1 and i_Lk2 are the leakage inductance currents of the first transformer and the second transformer, respectively, and are also the resonant inductor currents; i_Lm1 and i_Lm2 are the magnetizing inductance currents of the first transformer and the second transformer, respectively.

(6)

N_p1 and N_s1 are the turns of the primary and secondary sides of the first transformer, and their turns ratio is $n_1={\displaystyle \frac{N_{p1}}{N_{s1}}}$; N_p2 and N_s2 are the turns of the primary and secondary sides of the second transformer, and their ratio is $n_2={\displaystyle \frac{N_{p2}}{N_{s2}}}$; let $n_1=n_2=n$.

(7)

v_p1 and v_p2 are the primary-side voltages of the first transformer and the second transformer, respectively; v_s1 and v_s2 are the secondary-side voltages of the first transformer and the second transformer, respectively.

(8)

v_C1 and v_C2 are the voltages on the clamping capacitor C₁ and the energy-capacitor C₂, respectively.

(9)

v_D1 and v_D2 are the voltages on two output rectifier diodes D₁ and D₂, respectively; i_D1 and i_D2 are the currents in two output rectifier diodes D₁ and D₂, respectively.

(10)

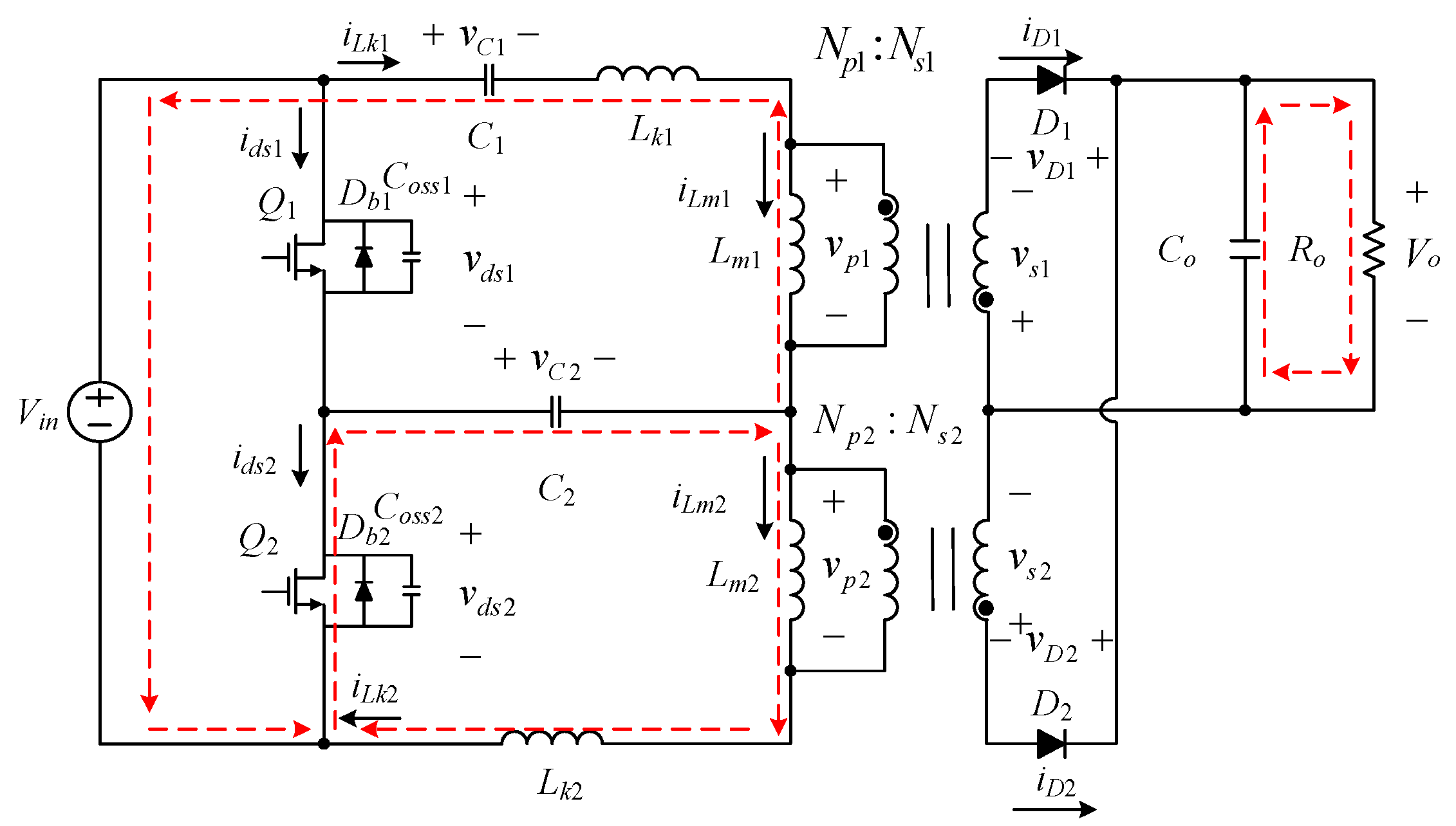
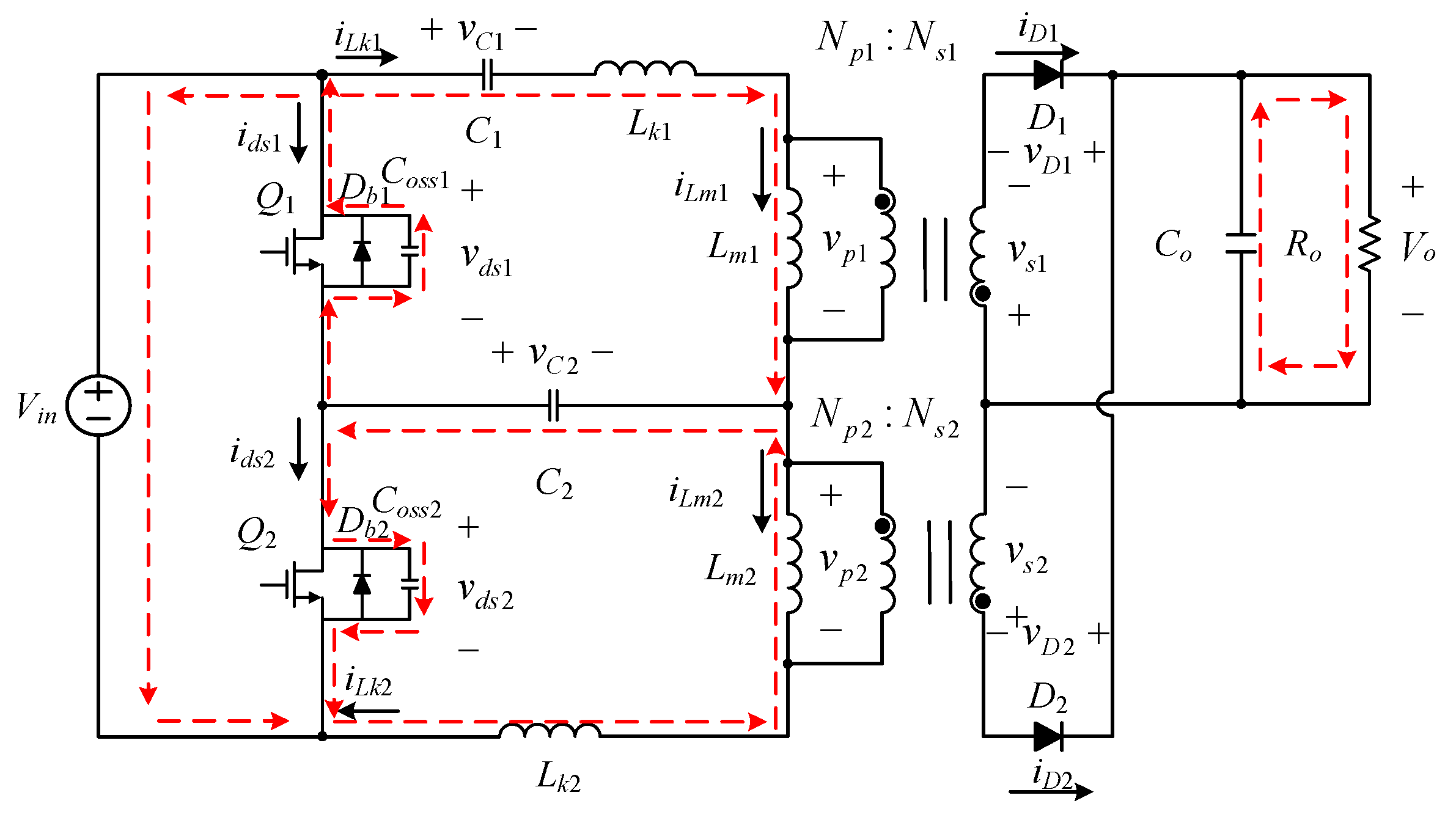
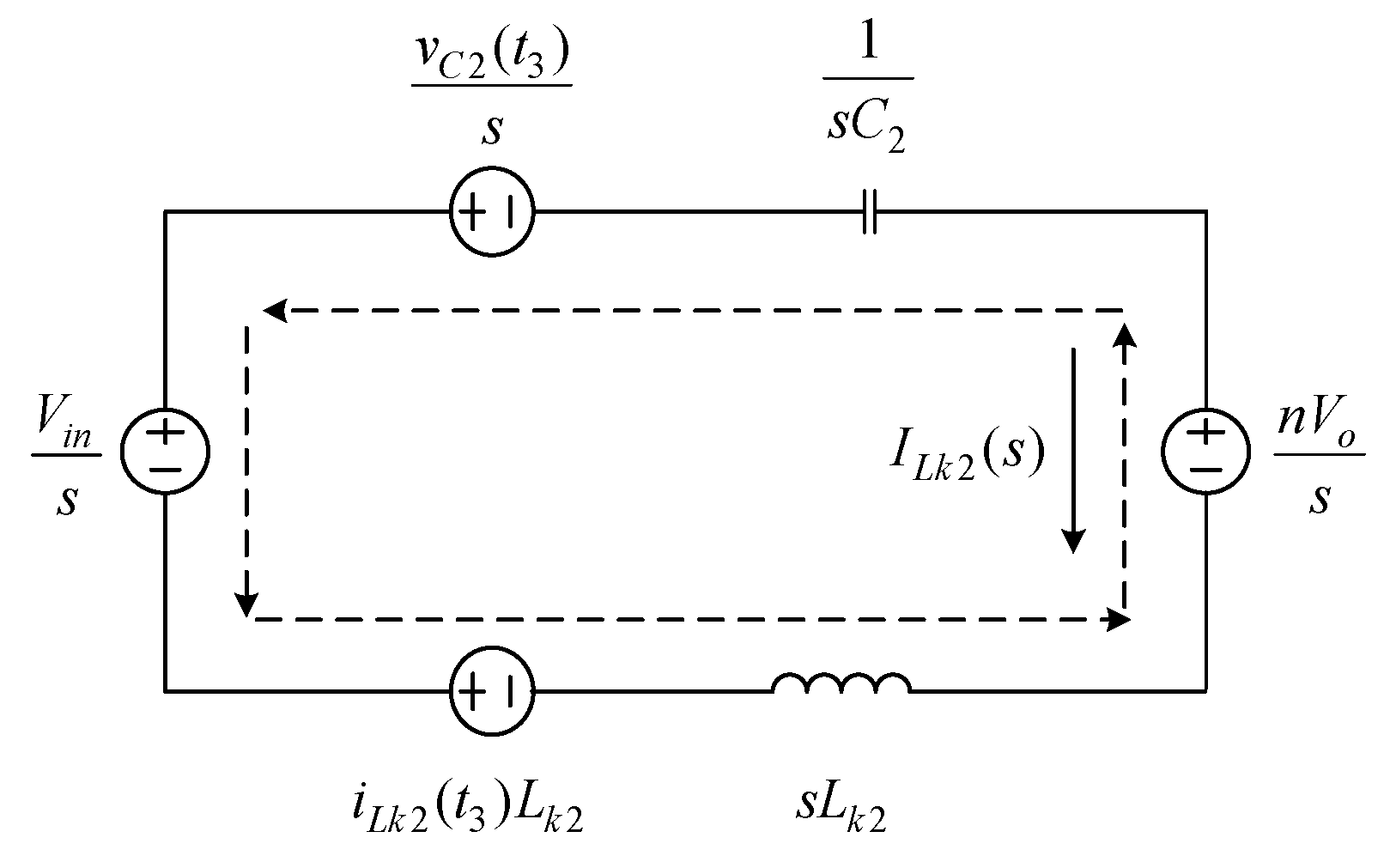
For brief analysis convenience, the circuit is operated under positive and negative currents, and Figure 2 shows the behavior of the circuit in one cycle. For brief analysis convenience, only the time interval between t₀ and t₆ will be taken into account; that is, the positive magnetizing current of T₁ and the negative magnetizing current of T₂ both occurring at the same time will be discussed.

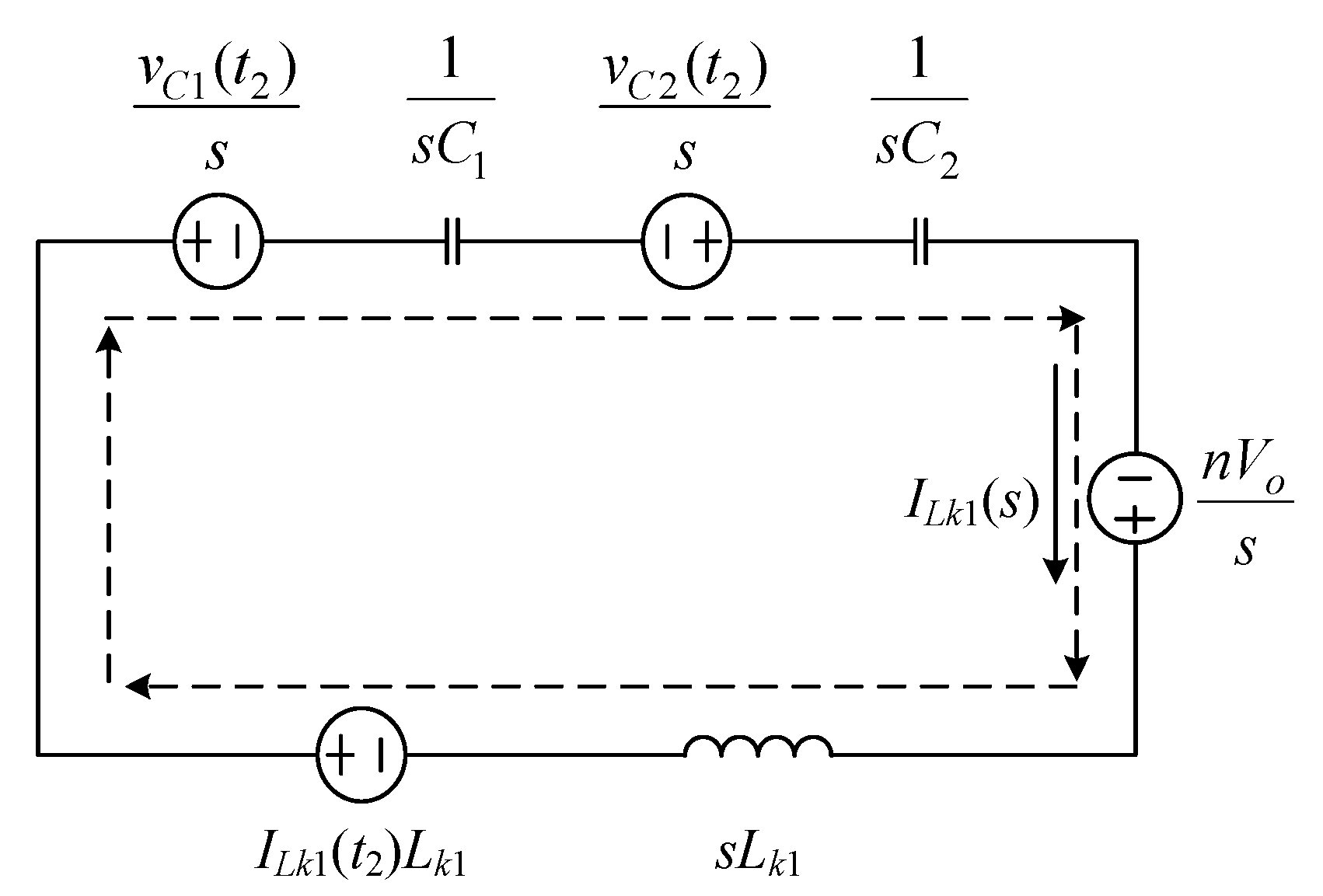
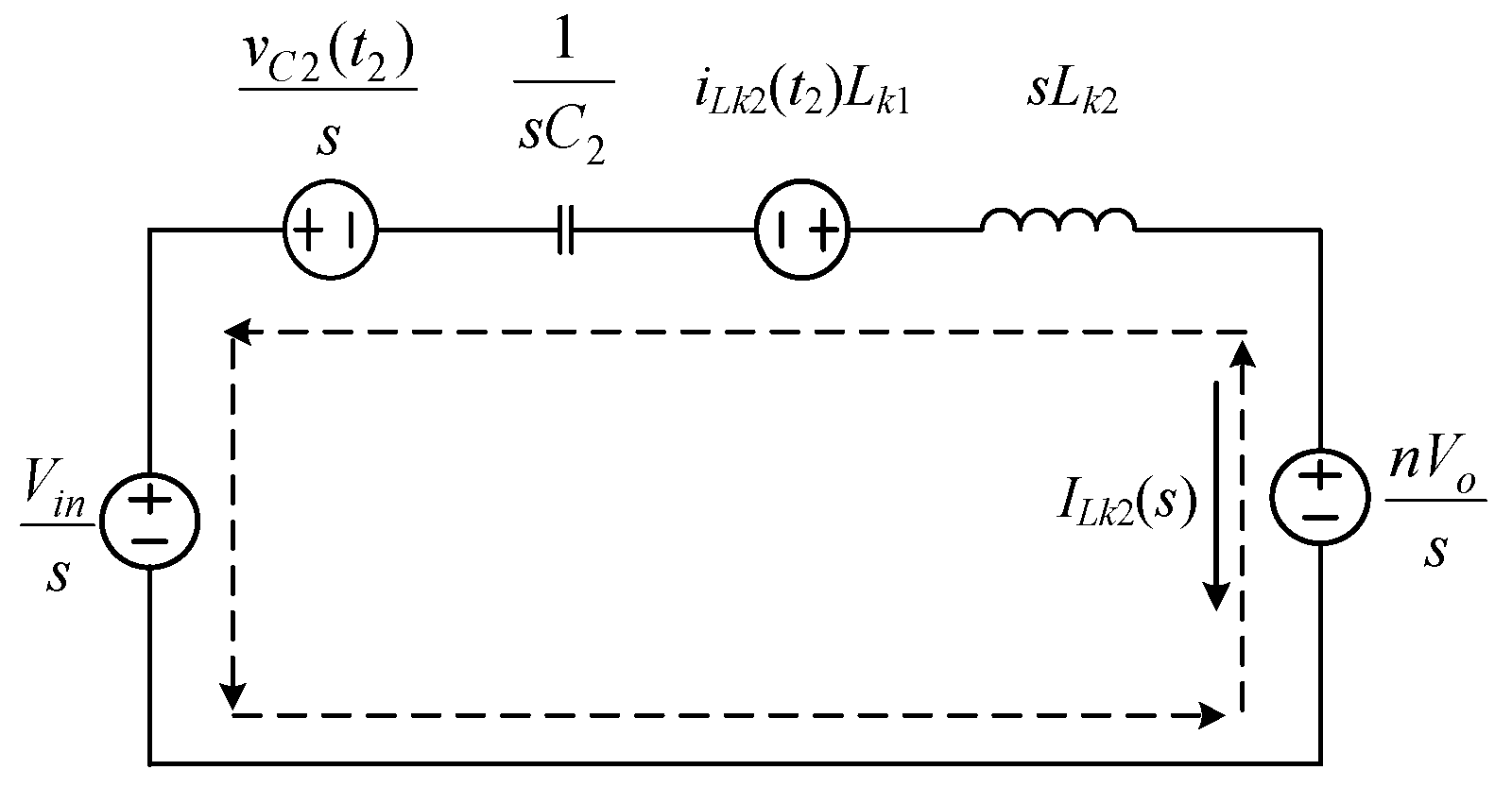
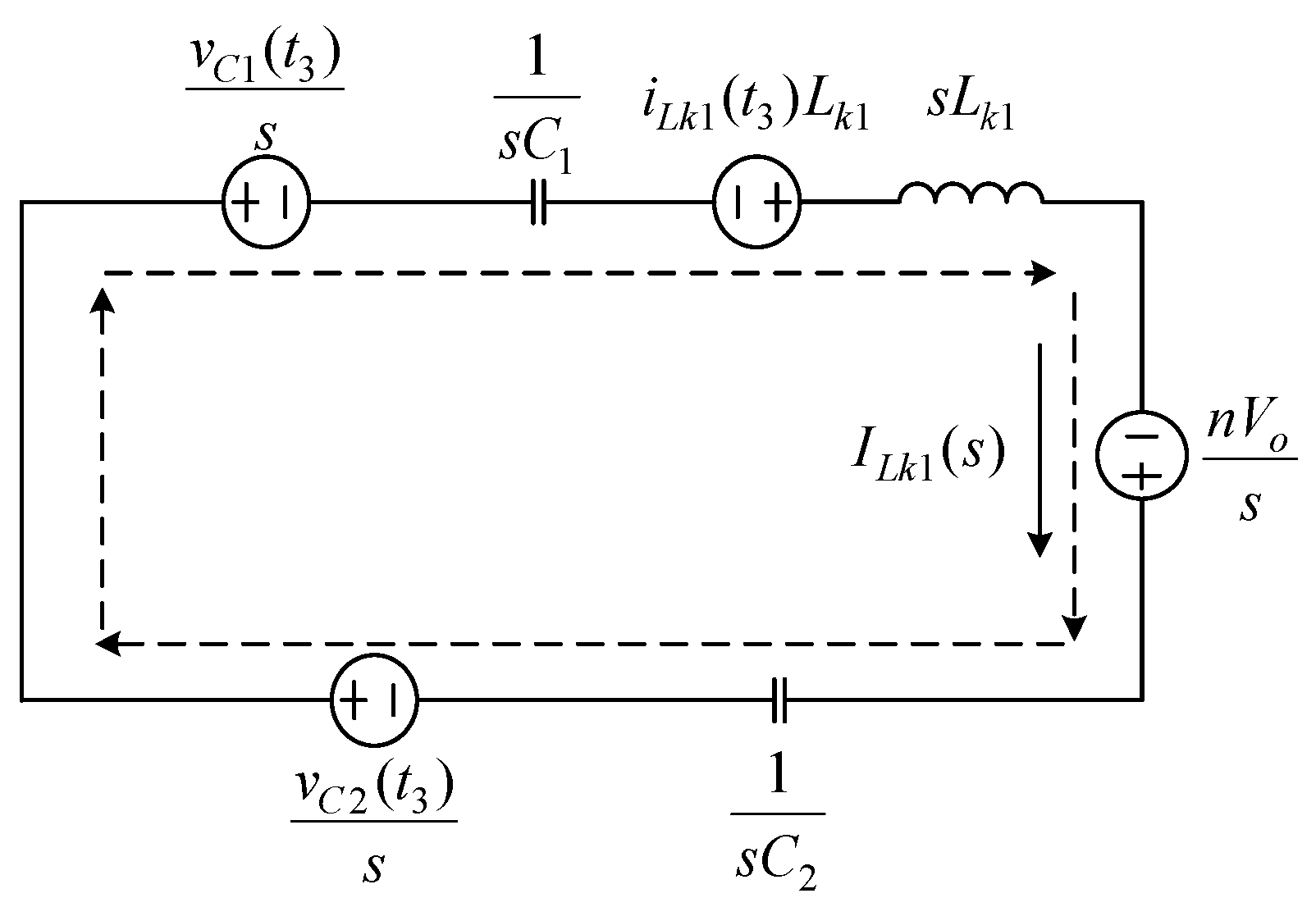
2.2. Operating Principle

State 1 [t₀ ≤ t ≤ t₁]: As shown in Figure 3, the auxiliary switch Q₁ is off and the main switch Q₂ is on. Assume v_C1(t₀) and v_C2(t₀) are constant. During this state, the voltage across the magnetizing inductance L_m1 of the first transformer is V_in − v_C1(t₀) + v_C2(t₀) (ignoring the voltage on L_k1), so the magnetizing inductance L_m1 is energized, whereas the voltage across the second inductance L_m2 of the second transformer is −v_C2(t₀) (ignoring the voltage on L_k2), so the magnetizing inductor L_m2 is de-energized. In addition, the energy required at the load side is supplied by the output capacitor C_o. As t = t₁, the main power switch Q₂ is turned off, and this state ends. The corresponding equations are as follows:

$$i_{Lk1}(t)=i_{Lk1}(t_0)+{\displaystyle \frac{V_{in}-v_{C1}(t_0)+v_{C2}(t_0)}{L_{m1}+L_{k1}}}(t-t_0)$$

(1)

$$i_{Lk2}(t)=i_{Lk2}(t_0)+{\displaystyle \frac{v_{C2}(t_0)}{L_{m1}+L_{k1}}}(t-t_0)$$

(2)

State 2 [t₁ ≤ t ≤ t₂]: As shown in Figure 4, at t = t₁, the auxiliary switch Q₁ is still off and the main power switch Q₂ is cut off. For analysis convenience, the voltages across the clamping capacitor C₁ and the energy-transferring capacitor C₂ are regarded as constant, namely, V_C1 and V_C2, respectively. Since this state belongs to the blanking time, the secondary output rectifier diodes D₁ and D₂ are in the off state, so the energy required at the output side is provided by the output capacitor C_o. At the same time, the first resonant tank is composed of L_k1, L_m1 and C_oss1, whereas the second resonant tank is composed of L_k2, L_m2 and C_oss2. In addition, the energy-transferring capacitor C₂ discharges C_oss1 and charges C_oss2. As t = t₂, C_oss1 is discharged to zero and C_oss2 is charged to V_in, and this state ends.

According to the equivalent circuits in Figure 5 and Figure 6, the equivalent impedances of the resonant tanks of the circuit, Z₁(s) and Z₂(s), are as follows:

$${ \mathrm{C}}_{eq1}\approx { \mathrm{C}}_{\mathrm{oss}1}$$

(3)

$${\mathrm{C}}_{eq2}\approx C_{oss2}$$

(4)

$$L_{eq1}=L_{k1}+L_{m1}$$

(5)

$$L_{eq2}=L_{k2}+L_{m2}$$

(6)

$$Z_1(s)=s{L}_{eq1}+{\displaystyle \frac{1}{s{C}_{eq1}}}$$

(7)

$$Z_2(s)=s{L}_{eq2}+{\displaystyle \frac{1}{s{C}_{eq2}}}$$

(8)

where C_eq1 and C_eq2 are the equivalent capacitances of the two resonant tanks, while L_eq1 and L_eq2 are the equivalent inductances of the two resonant tanks.

In this case, the corresponding resonant angular frequencies ω_r1 and ω_r2 and the corresponding characteristic impedances Z_r1 and Z_r2 are:

$${\omega }_{r1}={\displaystyle \frac{1}{\sqrt{L_{eq1}{C}_{eq1}}}}$$

(9)

$${\omega }_{r2}={\displaystyle \frac{1}{\sqrt{L_{eq2}{C}_{eq2}}}}$$

(10)

$${\mathrm{Z}}_{r1}=\sqrt{{\displaystyle \frac{L_{eq1}}{C_{eq1}}}}$$

(11)

$${\mathrm{Z}}_{r2}=\sqrt{{\displaystyle \frac{L_{eq2}}{C_{eq2}}}}$$

(12)

Based on Figure 5 and Figure 6, the resonant currents I_Lk1(s) and I_Lk2(s) of the two resonant tanks and the resonant voltages V_Cr1(s) and V_Cr2(s) of the two resonant tanks are expressed as follows:

$$I_{Lk1}(s)={\displaystyle \frac{\frac{V_{in}-V_{C1}+V_{C2}}{{\mathrm{Z}}_{r1}}{\omega }_{r1}+i_{Lk1}(t_1)s}{s^2+{\omega }_{r1}^2}}$$

(13)

$$I_{Lk2}(s)={\displaystyle \frac{\frac{V_{C2}}{{\mathrm{Z}}_{r2}}{\omega }_{r2}-i_{Lk2}(t_1)s}{s^2+{\omega }_{r2}^2}}$$

(14)

$$V_{Cr1}(s)={\displaystyle \frac{I_{Lk1}(s)}{s{C}_{eq1}}}+{\displaystyle \frac{v_{Cr1}(t_1)}{s}}$$

(15)

$$V_{Cr2}(s)={\displaystyle \frac{I_{Lk2}(s)}{s{C}_{eq2}}}+{\displaystyle \frac{v_{C2}(t_1)}{s}}$$

(16)

The expressions of i_Lk1(t), i_Lk2(t), v_Cr1(t) and v_Cr2(t) can be obtained by taking the inverse Laplace transform of (13), (14), (15) and (16), respectively, as shown below:

$$i_{Lk1}(t)={\displaystyle \frac{{\mathrm{V}}_{in}-V_{C1}+V_{C2}}{Z_{r1}}}\sin {\omega }_{r1}(t-t_1)+i_{Lk1}\cos {\omega }_{r1}(t-t_1)$$

(17)

$$i_{Lk2}(t)={\displaystyle \frac{V_{C2}}{Z_{r2}}}\sin {\omega }_{r2}(t-t_1)-i_{Lk2}\cos {\omega }_{r2}(t-t_1)$$

(18)

$$v_{Cr1}(t)=V_{in}-{\mathrm{V}}_{\mathrm{C}1}{+\mathrm{V}}_{\mathrm{C}2}+(V_{C1}-V_{in}-V_{C2})\cos {\omega }_{r1}(t-t_1)+Z_{r1}{i}_{Lk1}\sin {\omega }_{r1}(t-t_1)$$

(19)

$$v_{Cr2}(t){=\mathrm{V}}_{\mathrm{C}2}-V_{C2}\cos {\omega }_{r2}(t-t_1)-Z_{r2}{i}_{Lk2}\sin {\omega }_{r2}(t-t_1)$$

(20)

State 3 [t₂ ≤ t ≤ t₃]: As shown in Figure 7, Both the auxiliary switch Q₁ and the main switch Q₂ are off. This state still belongs to in the blanking time. Since the parasitic output capacitance C_oss2 of Q₂ has been discharged to zero voltage, the body diode D_b2 of Q₂ conducts. During this state, the voltages across the primary side of the first transformer and the voltage across the primary side of the second transformer are $v_{p1}=-n{V}_o$, $v_{p2}=n{V}_o$, respectively. Therefore, the secondary-side rectifier diodes D₁ and D₂ are forward biased. In addition, the first resonant tank is composed of C₁, C₂ and L_k1 and the second resonant tank is composed of C₂ and L_k2, so the resonant energy is transferred to the load side by the transformers. As t = t₃, the auxiliary switch Q₁ is turned on, and this state ends. It is noted that, since auxiliary switch Q₁ is turned on with v_ds1 =0, Q₁ has ZVS switching behavior.

According to the equivalent circuits in Figure 8 and Figure 9, the equivalent impedances of the resonant tanks of the circuit, Z₁(s) and Z₂(s), are as follows:

$$C_{eq3}={\displaystyle \frac{1}{\frac{1}{C_1}+\frac{1}{C_2}}}$$

(21)

$$C_{eq4}=C_2$$

(22)

$$L_{eq3}=L_{k1}$$

(23)

$$L_{eq4}=L_{k2}$$

(24)

$$Z_1(s)=s{L}_{eq3}+{\displaystyle \frac{1}{s{C}_{eq3}}}$$

(25)

$$Z_2(s)=s{L}_{eq4}+{\displaystyle \frac{1}{s{C}_{eq4}}}$$

(26)

where C_eq3 and C_eq4 are the equivalent capacitances of the two resonant tanks, while L_eq3 and L_eq4 are the equivalent inductances of the two resonant tanks.

In this case, the corresponding resonant angular frequencies ω_r3 and ω_r4 and the corresponding characteristic impedances Z_r3 and Z_r4 are

$${\omega }_{r3}={\displaystyle \frac{1}{\sqrt{L_{eq3}{C}_{eq3}}}}$$

(27)

$${\omega }_{r4}={\displaystyle \frac{1}{\sqrt{L_{eq4}{C}_{eq4}}}}$$

(28)

$$Z_{r3}=\sqrt{{\displaystyle \frac{L_{eq3}}{C_{eq3}}}}$$

(29)

$$Z_{r4}=\sqrt{{\displaystyle \frac{L_{eq4}}{C_{eq4}}}}$$

(30)

Based on Figure 8 and Figure 9, the resonant currents I_Lk1(s) and I_Lk2(s) of the two resonant tanks and the resonant voltages V_Cr1(s) and V_Cr2(s) of the two resonant tanks are expressed as follows:

$$I_{Lk1}(s)={\displaystyle \frac{\frac{v_{C2}(t_2)-v_{C1}(t_2)+n{V}_o}{Z_{r3}}{\omega }_{r3}+i_{Lk1}(t_2)s}{s^2+{\omega }_{r3}^2}}$$

(31)

$$I_{Lk2}(s)={\displaystyle \frac{\frac{v_{C2}(t_2)-V_{in}+n{V}_o}{Z_{r4}}{\omega }_{r4}-i_{Lk2}(t_2)s}{s^2+{\omega }_{r4}^2}}$$

(32)

$$V_{Cr1}(s)={\displaystyle \frac{I_{Lk1}(s)}{s{C}_{eq3}}}+{\displaystyle \frac{v_{Cr1}(t_2)}{s}}$$

(33)

$$V_{Cr2}(s)={\displaystyle \frac{I_{Lk2}(s)}{s{C}_{eq4}}}+{\displaystyle \frac{v_{Cr2}(t_2)}{s}}$$

(34)

The expressions of i_Lk1(t), i_Lk2(t), v_Cr1(t) and v_Cr2(t) can be obtained by taking the inverse Laplace transform of (31), (32), (33) and (34), respectively, as shown below:

$$i_{Lk1}(t)={\displaystyle \frac{[v_{C2}(t_2)-v_{C1}(t_2)+n{V}_o]}{Z_{r3}}}\sin {\omega }_{r3}(t-t_2)+i_{Lk1}\cos {\omega }_{r3}(t-t_2)$$

(35)

$$i_{Lk2}(t)={\displaystyle \frac{[v_{C2}(t_2)-V_{in}+n{V}_o]}{Z_{r4}}}\sin {\omega }_{r4}(t-t_2)-i_{Lk2}\cos {\omega }_{r4}(t-t_2)$$

(36)

$$v_{Cr1}(t)=n{V}_o+[v_{C1}(t_2)-v_{C2}(t_2)-n{V}_o]\cos {\omega }_{r3}(t-t_2)+Z_{r3}{i}_{Lk1}\sin {\omega }_{r3}(t-t_2)$$

(37)

$$v_{Cr2}(t)=-V_{in}+n{V}_o+[V_{in}-n{V}_o-v_{C2}(t_2)]\cos {\omega }_{r4}(t-t_2)-Z_{r4}{i}_{Lk2}\sin {\omega }_{r4}(t-t_2)$$

(38)

State 4 [t₃ ≤ t ≤ t₄]: As shown in Figure 10, at t = t₃, since the body diode of Q₁ in the previous state conducts, the voltage v_ds1 on the auxiliary switch Q₁ is zero, so the ZVS turn-on of Q₁ can be achieved. During this state, the voltages across the primary side of the first transformer and the voltage across the primary side of the second transformer are $v_{p1}=-n{V}_o$, $v_{p2}=n{V}_o$, respectively. Therefore, the secondary-side rectifier diodes D₁ and D₂ are forward biased. In addition, the first resonant tank is composed of C₁, C₂ and L_k1 and the second resonant tank is composed of C₂ and L_k2, so the resonant energy is transferred to the load side by the transformers.

According to the equivalent circuits in Figure 11 and Figure 12, the equivalent impedances of the resonant tanks of the circuit, Z₁(s) and Z₂(s), are as follows:

$$C_{eq5}={\displaystyle \frac{1}{\frac{1}{C_1}+\frac{1}{C_2}}}$$

(39)

$$C_{eq6}=C_2$$

(40)

$$L_{eq5}=L_{k1}$$

(41)

$$L_{eq6}=L_{k2}$$

(42)

$$Z_1(s)=s{L}_{eq5}+{\displaystyle \frac{1}{s{C}_{eq5}}}$$

(43)

$$Z_2(s)=s{L}_{eq6}+{\displaystyle \frac{1}{s{C}_{eq6}}}$$

(44)

where C_eq5 and C_eq6 are the equivalent capacitances of the two resonant tanks, while L_eq5 and L_eq6 are the equivalent inductances of the two resonant tanks.

In this case, the corresponding resonant angular frequencies ω_r5 and ω_r6 and the corresponding characteristic impedances Z_r5 and Z_r6 are

$${\omega }_{r5}={\displaystyle \frac{1}{\sqrt{L_{eq5}{C}_{eq5}}}}$$

(45)

$${\omega }_{r6}={\displaystyle \frac{1}{\sqrt{L_{eq6}{C}_{eq6}}}}$$

(46)

$${\mathrm{Z}}_{r5}=\sqrt{{\displaystyle \frac{L_{eq5}}{C_{eq5}}}}$$

(47)

$${\mathrm{Z}}_{r6}=\sqrt{{\displaystyle \frac{L_{eq6}}{C_{eq6}}}}$$

(48)

Based on Figure 11 and Figure 12, the resonant currents I_Lk1(s) and I_Lk2(s) of the two resonant tanks and the resonant voltages V_Cr1(s) and V_Cr2(s) of the two resonant tanks are expressed as follows:

$$I_{Lk1}(s)={\displaystyle \frac{\frac{v_{C2}(t_3)-v_{C1}(t_3)+n{V}_o}{{\mathrm{Z}}_{r5}}{\omega }_{r5}+i_{Lk1}(t_3)s}{s^2+{\omega }_{r5}^2}}$$

(49)

$$I_{Lk2}(s)={\displaystyle \frac{\frac{v_{C2}(t_3)-V_{in}-n{V}_o}{{\mathrm{Z}}_{r6}}{\omega }_{r6}-i_{Lk2}(t_3)s}{s^2+{\omega }_{r6}^2}}$$

(50)

$$V_{Cr1}(s)={\displaystyle \frac{I_{Lk1}(s)}{s{C}_{oss5}}}+{\displaystyle \frac{v_{Cr1}(t_3)}{s}}$$

(51)

$$V_{Cr2}(s)={\displaystyle \frac{I_{Lk2}(s)}{s{C}_{oss6}}}+{\displaystyle \frac{v_{Cr2}(t_3)}{s}}$$

(52)

The expressions of i_Lk1(t), i_Lk2(t), v_Cr1(t) and v_Cr2(t) can be obtained by taking the inverse Laplace transform of (49), (50), (51) and (52), respectively, as shown below:

$$i_{Lk1}(t)={\displaystyle \frac{[v_{C2}(t_3)-v_{Cr1}(t_3)+n{V}_o]}{Z_{r5}}}\sin {\omega }_{r5}(t-t_3)+i_{Lk1}\cos {\omega }_{r5}(t-t_3)$$

(53)

$$i_{Lk2}(t)={\displaystyle \frac{[v_{C2}(t_3)-V_{in}-n{V}_o]}{Z_{r6}}}\sin {\omega }_{r6}(t-t_3)-i_{Lk2}\cos {\omega }_{r6}(t-t_3)$$

(54)

$$v_{Cr1}(t)=n{V}_o+[v_{C1}(t_3)-v_{C2}(t_3)-n{V}_o]\cos {\omega }_{r5}(t-t_3)+Z_{r5}{i}_{Lk1}\sin {\omega }_{r5}(t-t_3)$$

(55)

$$v_{Cr2}(t)=-V_{in}+n{V}_o+[V_{in}-n{V}_o-v_{C2}(t_3)]\cos {\omega }_{r6}(t-t_3)-Z_{r6}{i}_{Lk2}\sin {\omega }_{r6}(t-t_3)$$

(56)

When t = t₄, the main switch Q₂ is turned off, and this state ends.

During state 5 [t₄ ≤ t ≤ t₅], state 6 [t₅ ≤ t ≤ t₆], state 7 [t₆ ≤ t ≤ t₇] and state 5 [t₇ ≤ t ≤ t₈], the magnetizing current is changed to the opposite direction, the resonant tanks and the corresponding operation behaviors are similar to state 4, state 3, state 2 and state 1, respectively; therefore, they are not elaborated here.

According to the equivalent circuits in Figure 11 and Figure 12, the equivalent impedances of the resonant tanks of the circuit, Z₁(s) and Z₂(s), are as follows:

$$C_{eq7}={\displaystyle \frac{1}{\frac{1}{C_1}+\frac{1}{C_2}}}$$

(57)

$$C_{eq8}=C_2$$

(58)

$$L_{eq7}=L_{k1}$$

(59)

$$L_{eq8}=L_{k2}$$

(60)

$$Z_1(s)=s{L}_{eq7}+{\displaystyle \frac{1}{s{C}_{eq7}}}$$

(61)

$$Z_2(s)=s{L}_{eq8}+{\displaystyle \frac{1}{s{C}_{eq8}}}$$

(62)

where C_eq7 and C_eq8 are the equivalent capacitances of the two resonant tanks, while L_eq7 and L_eq8 are the equivalent inductances of the two resonant tanks.

In this case, the corresponding resonant angular frequencies ω_r7 and ω_r8 and the corresponding characteristic impedances Z_r7 and Z_r8 are

$${\omega }_{r7}={\displaystyle \frac{1}{\sqrt{L_{eq7}{C}_{eq7}}}}$$

(63)

$${\omega }_{r8}={\displaystyle \frac{1}{\sqrt{L_{eq8}{C}_{eq8}}}}$$

(64)

$${\mathrm{Z}}_{r7}=\sqrt{{\displaystyle \frac{L_{eq7}}{C_{eq7}}}}$$

(65)

$${\mathrm{Z}}_{r8}=\sqrt{{\displaystyle \frac{L_{\mathrm{eq}8}}{C_{eq8}}}}$$

(66)

Additionally, the resonant currents I_Lk1(s) and I_Lk2(s) of the two resonant tanks and the resonant voltages V_Cr1(s) and V_Cr2(s) of the two resonant tanks are expressed as follows:

$$I_{Lk1}(s)={\displaystyle \frac{\frac{v_{C1}(t_4)-v_{C2}(t_4)-n{V}_o}{{\mathrm{Z}}_{r7}}{\omega }_{r7}-i_{Lk1}(t_4)s}{s^2+{\omega }_{r7}^2}}$$

(67)

$$I_{Lk2}(s)={\displaystyle \frac{\frac{V_{in}-v_{C2}(t_4)+n{V}_o}{{\mathrm{Z}}_{r8}}{\omega }_{r8}+i_{Lk2}(t_4)s}{s^2+{\omega }_{r8}^2}}$$

(68)

$$V_{Cr1}(s)={\displaystyle \frac{I_{Lk1}(s)}{s{C}_{eq7}}}+{\displaystyle \frac{v_{Cr1}(t_4)}{s}}$$

(69)

$$V_{Cr2}(s)={\displaystyle \frac{I_{Lk2}(s)}{s{C}_{eq8}}}+{\displaystyle \frac{v_{Cr2}(t_4)}{s}}$$

(70)

The expressions of i_Lk1(t), i_Lk2(t), v_Cr1(t) and v_Cr2(t) can be obtained by taking the inverse Laplace transform of (67), (68), (69) and (70), respectively, as shown below:

$$i_{Lk1}(t)={\displaystyle \frac{[v_{C1}(t_4)-v_{Cr2}(t_4)-n{V}_o]}{Z_{r5}}}\sin {\omega }_{r7}(t-t_4)-i_{Lk1}\cos {\omega }_{r7}(t-t_4)$$

(71)

$$i_{Lk2}(t)={\displaystyle \frac{[V_{in}-v_{C2}(t_4)+n{V}_o]}{Z_{r8}}}\sin {\omega }_{r8}(t-t_4)+i_{Lk2}\cos {\omega }_{r8}(t-t_4)$$

(72)

$$v_{Cr1}(t)=-n{V}_o+[v_{C2}(t_4)-v_{C1}(t_4)+n{V}_o]\cos {\omega }_{r7}(t-t_4)-Z_{r7}{i}_{Lk1}(t_4)\sin {\omega }_{r7}(t-t_4)$$

(73)

$$v_{Cr2}(t)=V_{in}-n{V}_o+[v_{C2}(t_4)-V_{in}+n{V}_o]\cos {\omega }_{r8}(t-t_4)-Z_{r8}{i}_{Lk2}(t_4)\sin {\omega }_{r8}(t-t_4)$$

(74)

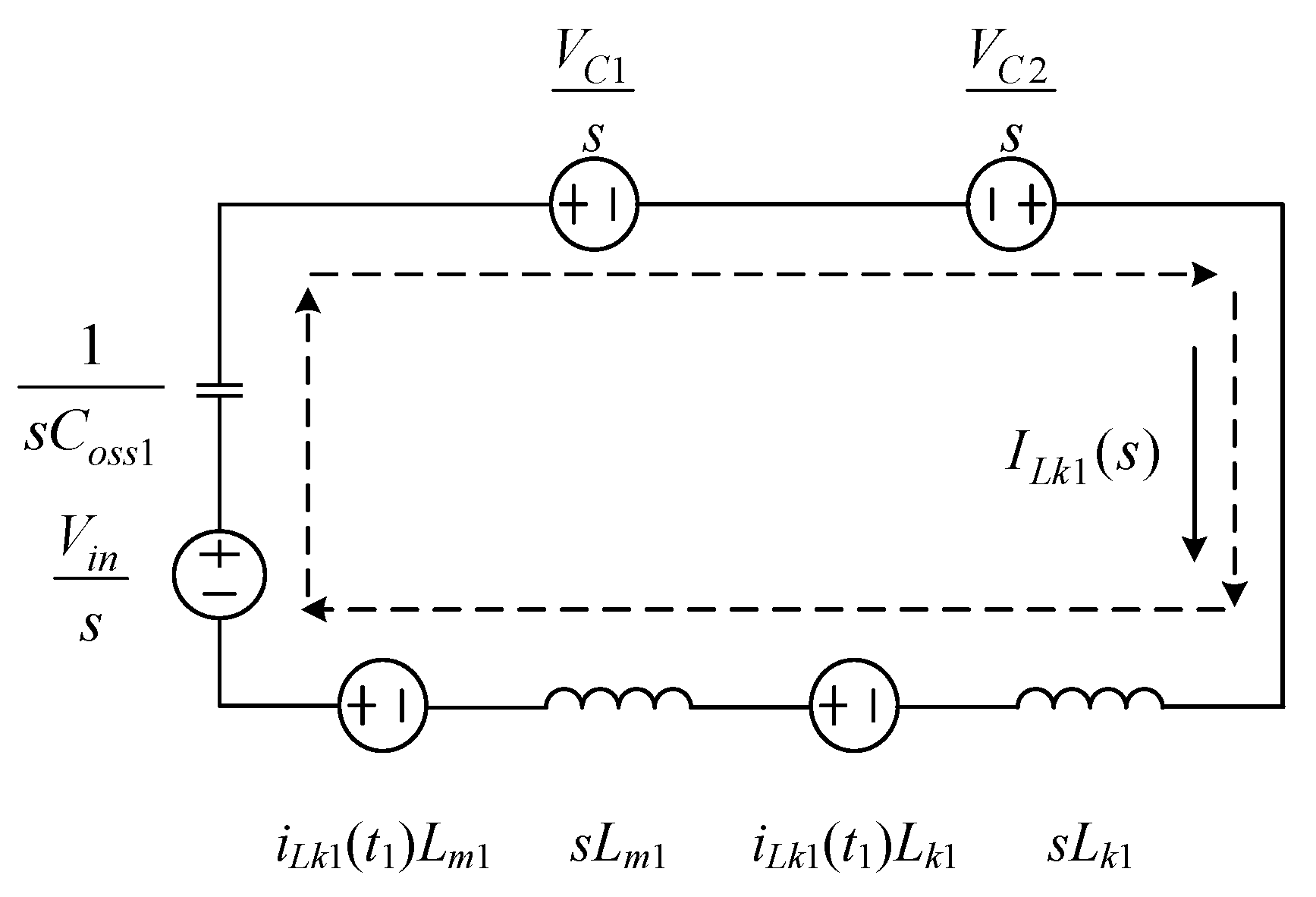
2.3. Voltage Gain

The voltage gain of this circuit, employing a set of upper and lower switches for high-frequency switching with complementary signals, will be analyzed herein. When the lower main switch is on, the magnetizing inductance is energized, while the energy required at the output side is provided by the output capacitor C_o. When the upper auxiliary switch is energized, the energy stored in the magnetizing inductance is transferred to the output side. The magnetizing inductance should obey the voltage-second balance. Assume v_C1 and v_C2 are constant.

Due to v_C1 = V_in, when the main switch Q₂ is turned on, the voltage v_Lm1 across the magnetizing inductance L_m1 is

$$v_{Lm1}=V_{in}-v_{C1}+v_{C2}=V_{in}-V_{C1}+V_{C2}=V_{C2}$$

(75)

When the auxiliary switch Q₁ is on, the voltage v_Lm1 across the magnetizing inductance L_m1 and the voltage V_C2 on the energy-transferring capacitor C₂ are shown below, respectively:

$$v_{Lm1}=-n{V}_o$$

(76)

Based on (75) and (76), the following equations (77) and (78) can be obtained:

$$V_{C2}=V_{in}\times (1-D)$$

(77)

$$V_{C2}\times D+(-n{V}_o)\times (1-D)=0$$

(78)

Rearranging (77) and (78) yields

$${\displaystyle \frac{V_o}{V_{in}}}=({\displaystyle \frac{D}{1-D}}\times {\displaystyle \frac{1}{n}})\times (1-D)={\displaystyle \frac{D}{n}}$$

(79)

3. Design Considerations

This section will describe the experimental porotype, including system specifications, transformers, and capacitors.

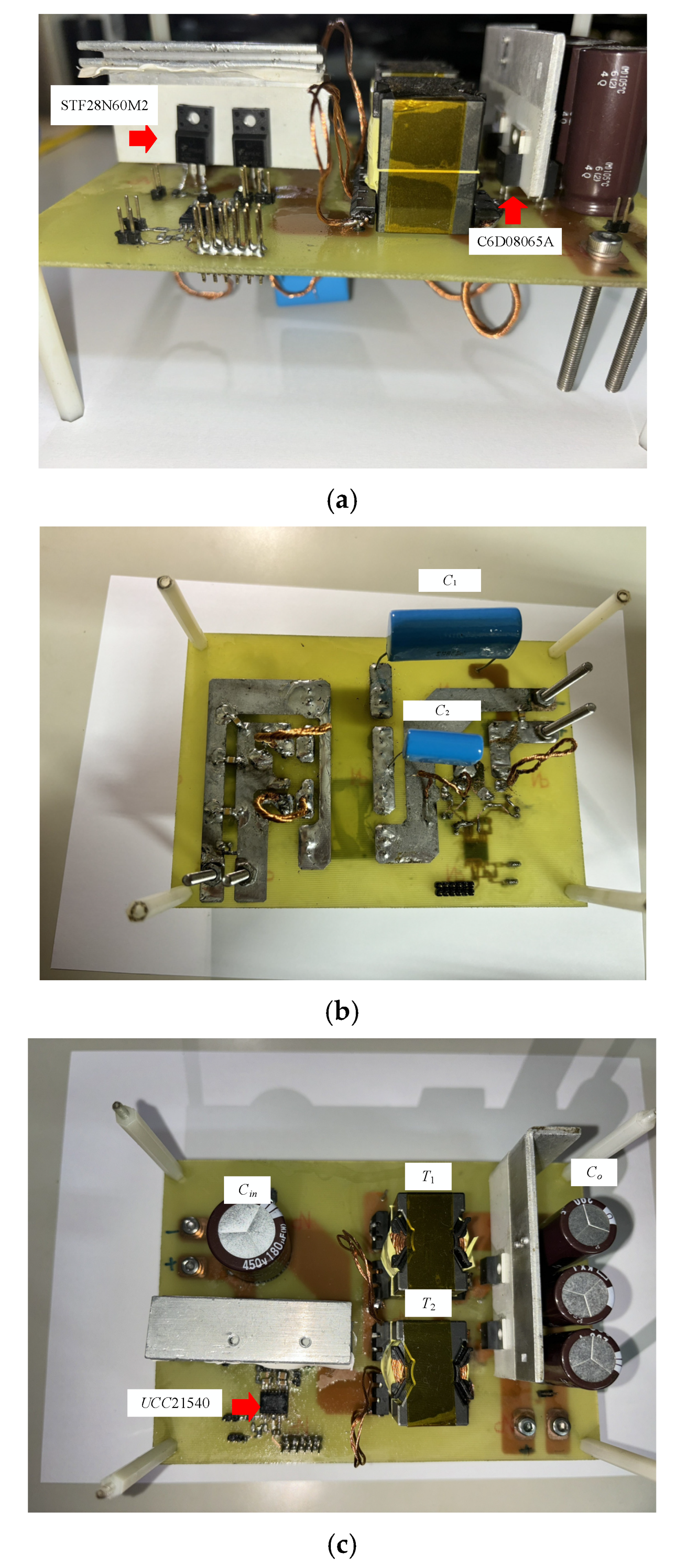
3.1. System Configuration

Figure 13 shows the proposed system configuration, which consists of a main power circuit and a feedback control circuit. The main circuit is constructed by an active-clamp flyback converter with dual transformers. Regarding the feedback circuit, a voltage feedback is used, where the output voltage is divided by two resistors R₁ and R₂, and then sent to an analog-to-digital converter (ADC), which converts it into a digital signal and then feeds it to the proportional-integral (PI) controller embedded in the FPGA. Finally, the pulse width modulation (PWM) generator embedded in the field programmable gate array (FPGA) is used to obtain the corresponding gate driving signals to drive the switches.

3.2. System Specifications

Table 1. System specifications.

Input Voltage (Vin)	380 V
Output Voltage (Vo)	48 V
Rated Output Power (Po,rated)	500 W
Minimum Output Power (Po,min)	100 W
Switching Frequency (fs)	100 kHz
Maximum Duty Cycle of Main Switch (Dmax)	0.4

shows the system specifications of the proposed circuit, and this table will be used to design the required components of this circuit.

3.3. Parameter Design

The main power circuit consists of two transformers, a clamping capacitor C₁, an energy-transferring capacitor C₂, an output capacitor C_o, and two resonant inductors L_k1 and L_k2. It is noted that, as design of the two transformers are completed, then the two leakage inductances L_k1 and L_k2 are measured to be about 5.6 μH.

3.3.1. Design of Magnetizing Inductance L_m1 of First Transformer

First, the turns ratio n₁ can be obtained based on Table 1 and (79), and after this, the magnetizing inductance can be obtained.

Turns Ratio n₁

$$n_1=n=D_{max}\times {\displaystyle \frac{V_{in}}{V_o}}=0.4\times {\displaystyle \frac{380}{48}}=3.17$$

(80)

In order to facilitate the winding, the turns ratio n = 3 is chosen for the following design.

Design of Magnetizing Inductance L_m.1 for the First Transformer

As has previously been mentioned, the magnetizing inductor current should be operated under positive and negative magnetizing inductance currents to obtain ZVS turn-on of the switches, so it is necessary to calculate the magnetizing inductance required in the boundary current mode (BCM), and then select the magnetizing inductance smaller than that the calculated in the BCM.

Also, the relationship between the secondary-side voltage v_s1 and the secondary-side BCM current i_sb1, obtained by demagnetizing the first transformer, is as follows:

$$v_{s1}=L_{s1}{\displaystyle \frac{d{i}_{sb1}}{dt}}$$

(81)

Based on (81), the secondary-side self-inductance of the first transformer, called L_s1, can be obtained at rated load:

$$L_{s1}=v_{s1}\times {\displaystyle \frac{dt}{d{i}_{sb1}}}={\displaystyle \frac{v_{s1}\times (1-D_{max})\times T_s}{d{i}_{sb1}}}={\displaystyle \frac{48\times (1-0.4)}{10.41\times 100\times {10}^3}}\approx 27.67\mathsf{\mu }\mathrm{H}$$

(82)

At the same time, the relationship between (82) and n of the transformer can be used to find the primary-side self-inductance L_p1 as follows:

$$\begin{array}{l}{L}_{p1}=n^2\times L_{s1}\\ =3^2\times 27.67\mathsf{\mu }\mathrm{H}\approx 248.4\mathsf{\mu }\mathrm{H}\end{array}$$

(83)

By assuming that the transformer has perfect coupling, the magnetizing inductance L_m1 is equal to L_p1.

Finally, based on the simulation software PSIM 9.11, the value of L_m1 is set at 180 $\mathsf{\mu }\mathrm{H}$.

3.3.2. Design of Magnetizing Inductance L_m2 of Second Transformer

The design of the magnetizing inductance L_m2 is the same as that of the first transformer.

3.3.3. Design of Clamping Capacitor C₁ and Energy-Transferring Capacitor C₂

In this circuit, the clamping capacitor C₁ and the energy-transferring capacitor C₂ resonate with the resonant inductor L_k1 during the de-energization of the magnetizing inductor L_m1 from state 3 to state 6. However, in order to avoid too short a resonant time, which may result in too little energy being transferred to the secondary side, or too long a resonant time, which may result in a ZVS failure. Therefore, the resonant frequency f_r1 of this resonant tank is set to be equal to the switching frequency f_s (=100 kHz). Similarly, the resonant frequency f_r2 of the resonant tank formed by the energy-transferring capacitor C₂ and the leakage inductor L_k2 from state 3 to state 6 is equal to the switching frequency f_s. The corresponding expressions are shown below:

$$f_{r1}=f_s={\displaystyle \frac{1}{2\mathsf{\pi }\sqrt{L_{k1}\times \frac{C_1\times C_2}{C_1+C_2}}}}$$

(84)

$$f_{r2}=f_s={\displaystyle \frac{1}{2\mathsf{\pi }\sqrt{L_{k2}\times C_2}}}$$

(85)

Based on (86), it can be obtained that

$$\begin{array}{l}{f}_{r2}={\displaystyle \frac{1}{2\mathsf{\pi }\sqrt{5.6\times {10}^{-6}\times C_2}}}=100\mathrm{kHz} \\ \Rightarrow C_2=450\mathrm{nF}\end{array}$$

(86)

Thus, a 470 nF/630 V plastic film capacitor is selected as the energy-transferring capacitor C₂.

Based on (84), it can be obtained that

$$\begin{array}{l}{f}_{r1}={\displaystyle \frac{1}{2\mathsf{\pi }\sqrt{5.6\times {10}^{-6}\times \frac{C_1\times 470\mathrm{n}}{C_1+470\mathrm{n}}}}}=100\mathrm{kHz} \\ \Rightarrow C_1=12\mathsf{\mu }\mathrm{F}\end{array}$$

(87)

Therefore, a 10 $\mathsf{\mu }\mathrm{F}$/630 V plastic film capacitor and a 2.2 $\mathsf{\mu }\mathrm{F}$/630 V plastic film capacitor are used in parallel as the clamping capacitor C₁.

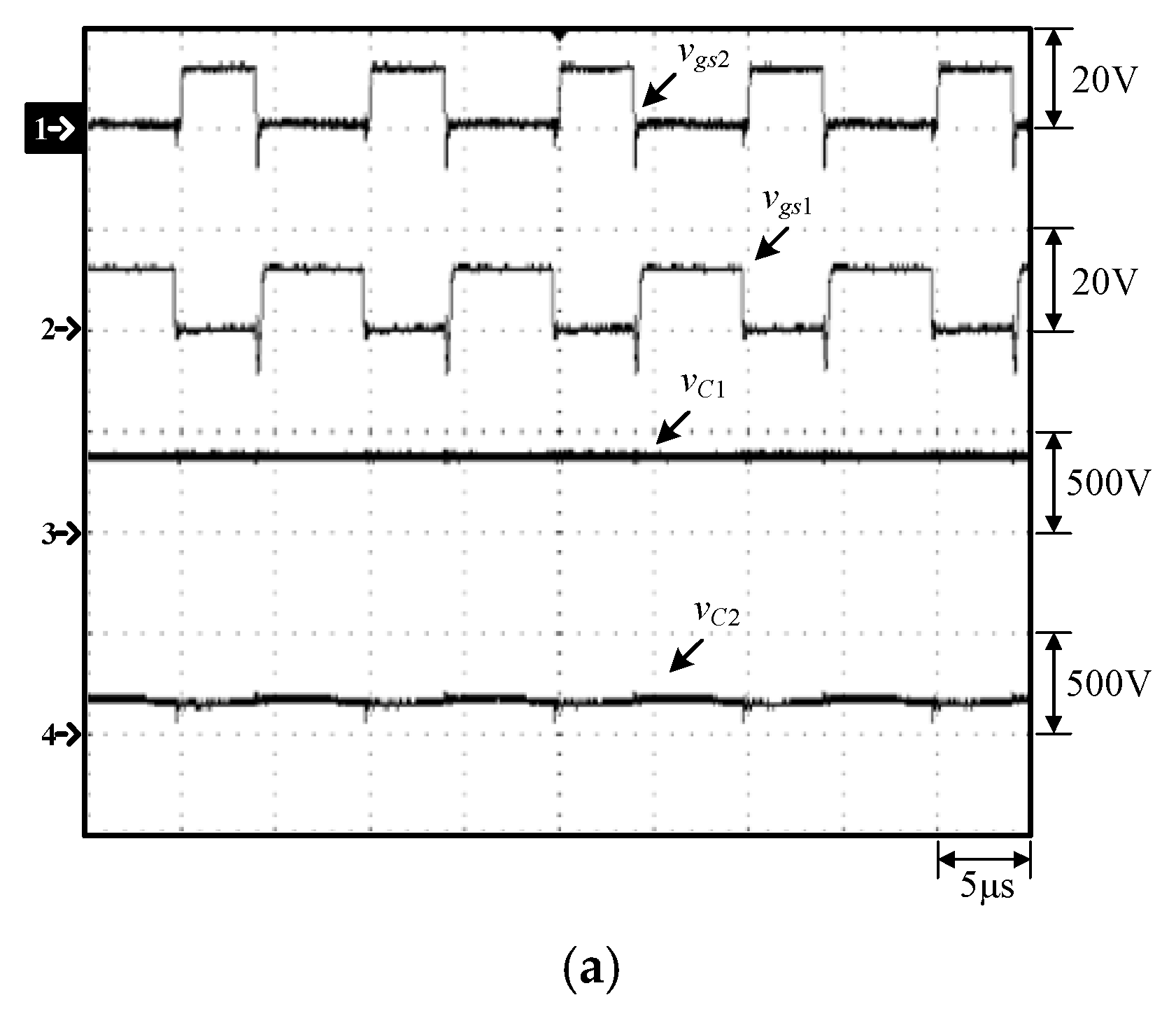
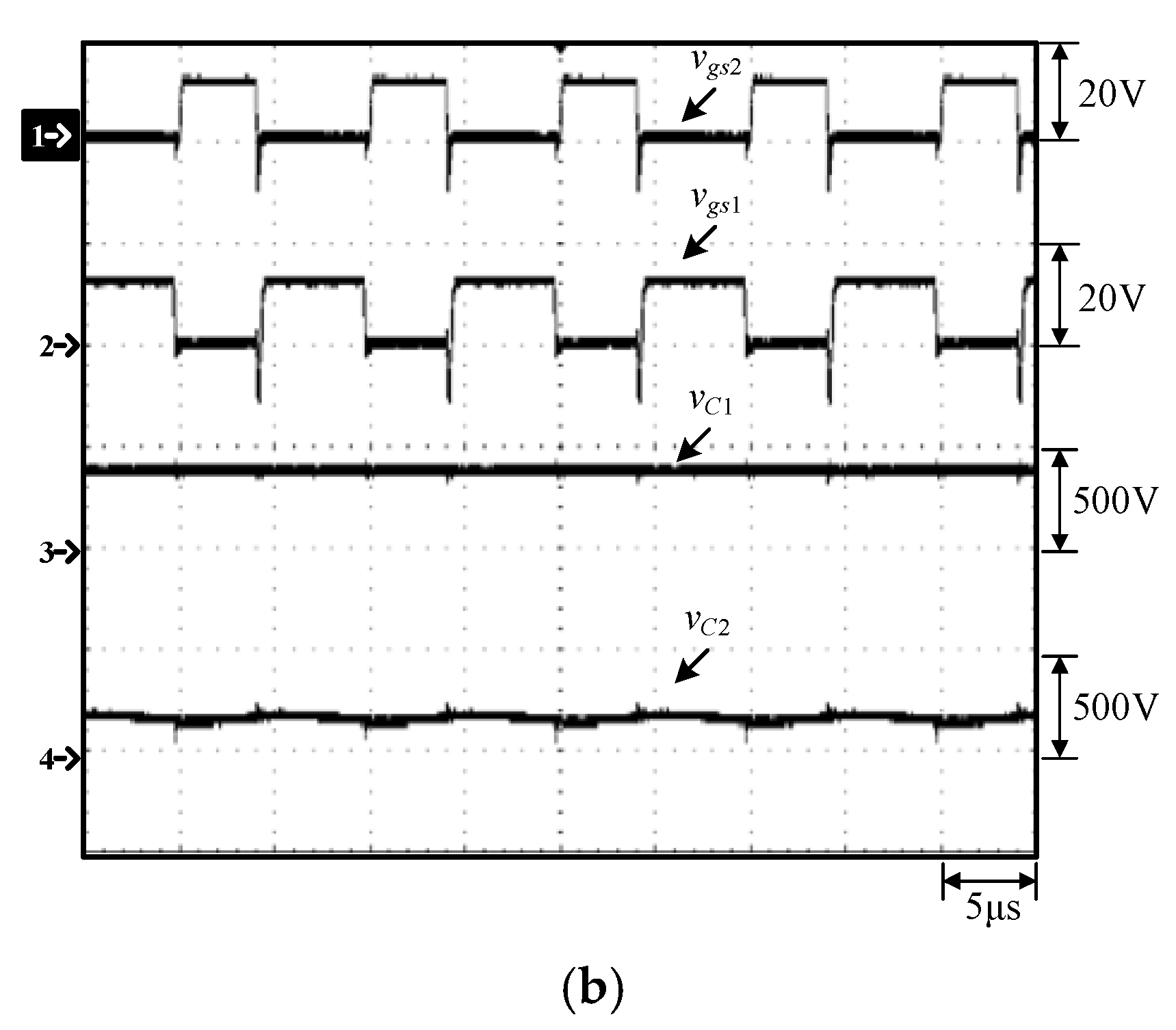
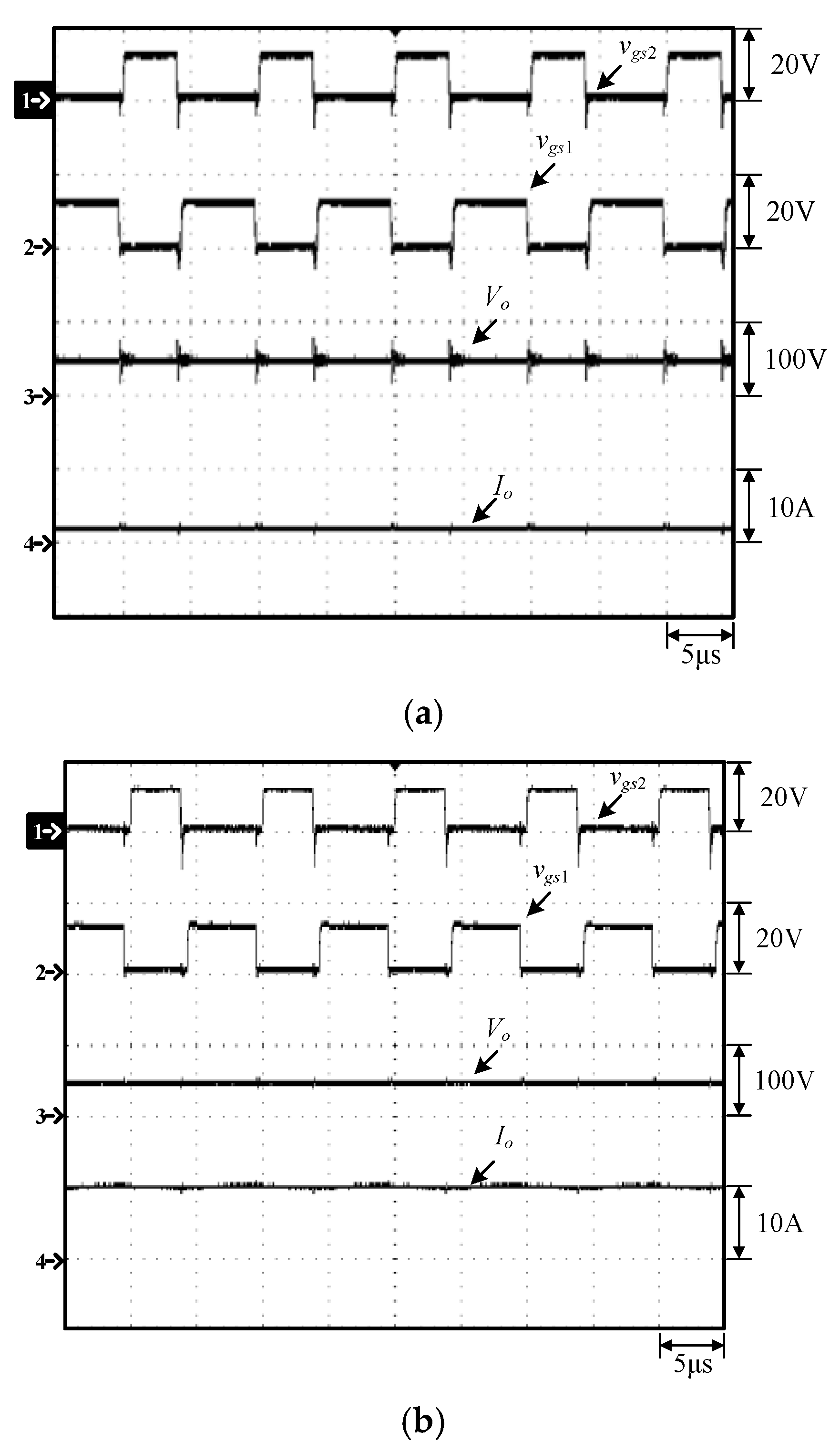
4. Experimental Results

4.1. Measured Waveforms and Discussions

In this section, the experimental waveforms at the light and rated loads are presented to verify the design’s feasibility. Finally, the digital control will be realized by the FPGA to demonstrate its effectiveness. At light load, it can be seen that both the switches have ZVS turn-on for the main switch Q₂ and the auxiliary switch Q₁.

Figure 14 displays the gate driving signal v_gs1 of the auxiliary switch Q₁, the gate driving signal v_gs2 of the main power switch Q₂, the current i_ds1 of the auxiliary switch Q₁, and the current i_ds2 of the main power switch Q₂. Figure 15 displays the gate driving signal v_gs1 of the auxiliary switch Q₁, the gate driving signal v_gs2 of the main switch Q₂, the voltage v_C1 of the clamping capacitor C₁, and the voltage v_C2 of the energy-transferring capacitor C₂. Figure 16 displays the gate driving signal v_gs1 of the auxiliary switch Q₁, the gate driving signal v_gs2 of the main switch Q₂, the voltage v_p1 on the primary side of the first transformer, and the voltage v_p2 on the primary side of the second transformer. Figure 17 displays the gate driving signal v_gs1 of the auxiliary switch Q₁, the gate driving signal v_gs2 of the main switch Q₂, the output voltage V_o, and the output current I_o. Figure 18 displays in the zoom-in gate driving signal v_gs1 of the auxiliary switch Q₁ and the voltage v_ds1 of the auxiliary switch Q₁. Figure 19 displays the zoom-in gate driving signal v_gs2 of the main switch Q₂ and the voltage v_ds2 of the main switch Q₂. Figure 20 displays a curve of efficiency versus load. Figure 21 shows the experimental setup.

Figure 14 shows that the currents in the two switches have negative currents, so the two switches Q₁ and Q₂ have ZVS turn-on, as shown in Figure 18 and Figure 19. Figure 16 displays that the magnetizing inductances L_m1 and L_m2 have voltage second balance. Figure 17 shows that the output voltage V_o is about 48 V and I_o is about 2 A and 10 A, corresponding to the system specifications. Figure 20 displays the efficiency curve, which is up to 94.5% over all the load range; the maximum efficiency is about 96.4% at around half load, and the rated-load efficiency is about 94.5%.

4.2. Comparison Between Proposed and Other Topologies

Comparisons of the proposed converter with the existing active-clamp ZVS DC/DC converters [14,15,16,17,18,19] in various items are tabulated in

Table 2. Comparisons between the proposed converter and existing active-clamp ZVS DC/DC converters.

	[14]	[15]	[16]	[17]	[18]	[19]	Proposed
Rated-load Power (W)	100	65	250	400	200	120	500
Input Voltage (V)	400	150	30	40	30	250	380
Output Voltage (V)	48	19.5	360	400	200	48	48
Voltage Gain	${\displaystyle \frac{D}{n(1-D)}}$	${\displaystyle \frac{D}{n(1-D)}}$	${\displaystyle \frac{2+3n-nD}{{(1-D)}^2}}$	${\displaystyle \frac{2nD+1}{1-D}}$	${\displaystyle \frac{nD+1}{1-D}}$	---	${\displaystyle \frac{D}{n}}$
Switching Frequency (kHz)	100	600	70	100	66	1000	100
No. of Switches	MOSFET (2)	GaN (2) + MOSFET (1)	MOSFET (2)	MOSFET (2)	MOSFET (2)	MOSFET (2)	MOSFET (2)
No. of Transformers (Coupled Inductors)	1(0)	1(0)	1(2)	0(2)	0(2)	1(0)	2(0)
No. of Capacitors	1	1	5	3	1	3	2
No. of Diodes	1	0	5	2	1	4	2
Maximum Efficiency (%)	---	93.74	96.1	94.6	92.0	92.4	96.4
Control Strategy	PSRS	PHCM	PWM	PWM	PWM	PWM	PWM
Isolation	v	v	x	x	x	v	v

. From this table, only the proposed converter has the highest efficiency.

5. Conclusions

A dual-transformer active-clamp is developed herein, where the two active clamping circuits utilize the same clamping capacitor to recycle the leakage inductance energy, and two resonant loops cause the main switch and the auxiliary switch to have ZVS turn-on to minimize the switching loss. From the efficiency measurement, the efficiency is above 94.5% for all the load range.