Enhanced MMC-HVDC Power Control via Adaptive VSG-PBC in Weak Grid Environments
Abstract
1. Introduction
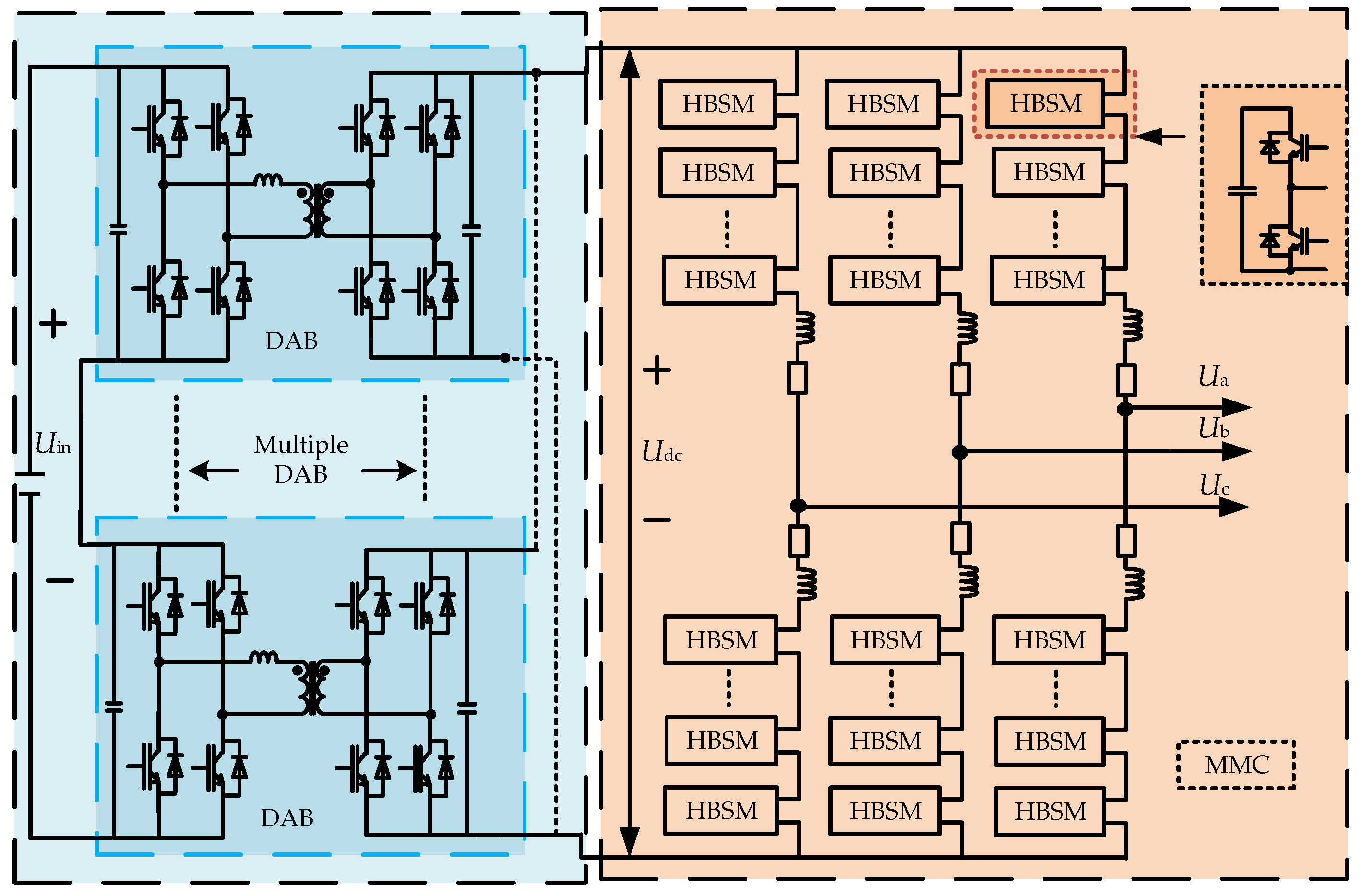
2. MMC-HVDC System Structure
3. MMC-HVDC Output Stage Control Strategy
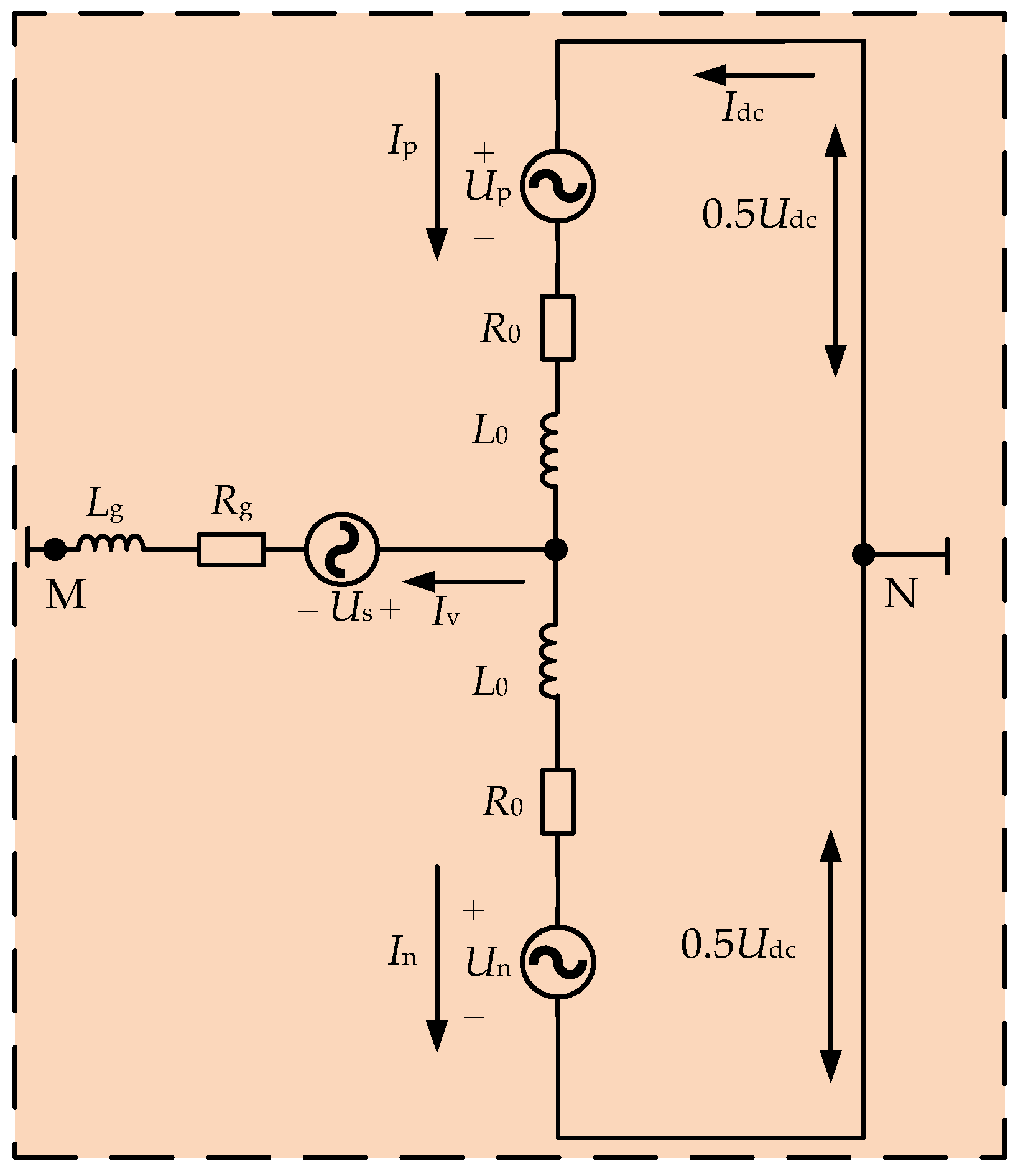
3.1. MMC Mathematical Model
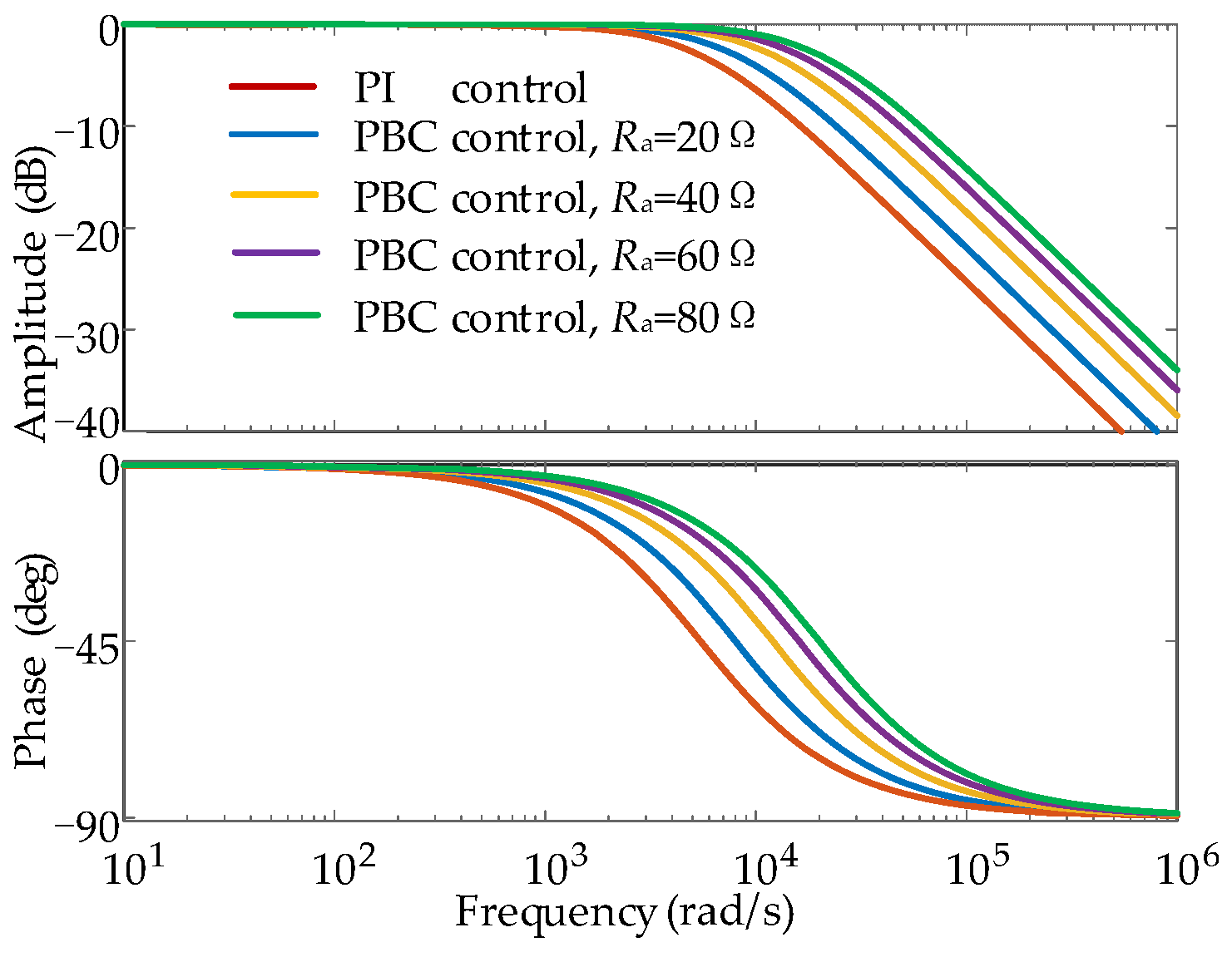
3.2. MMC Current Inner Loop PBC Control
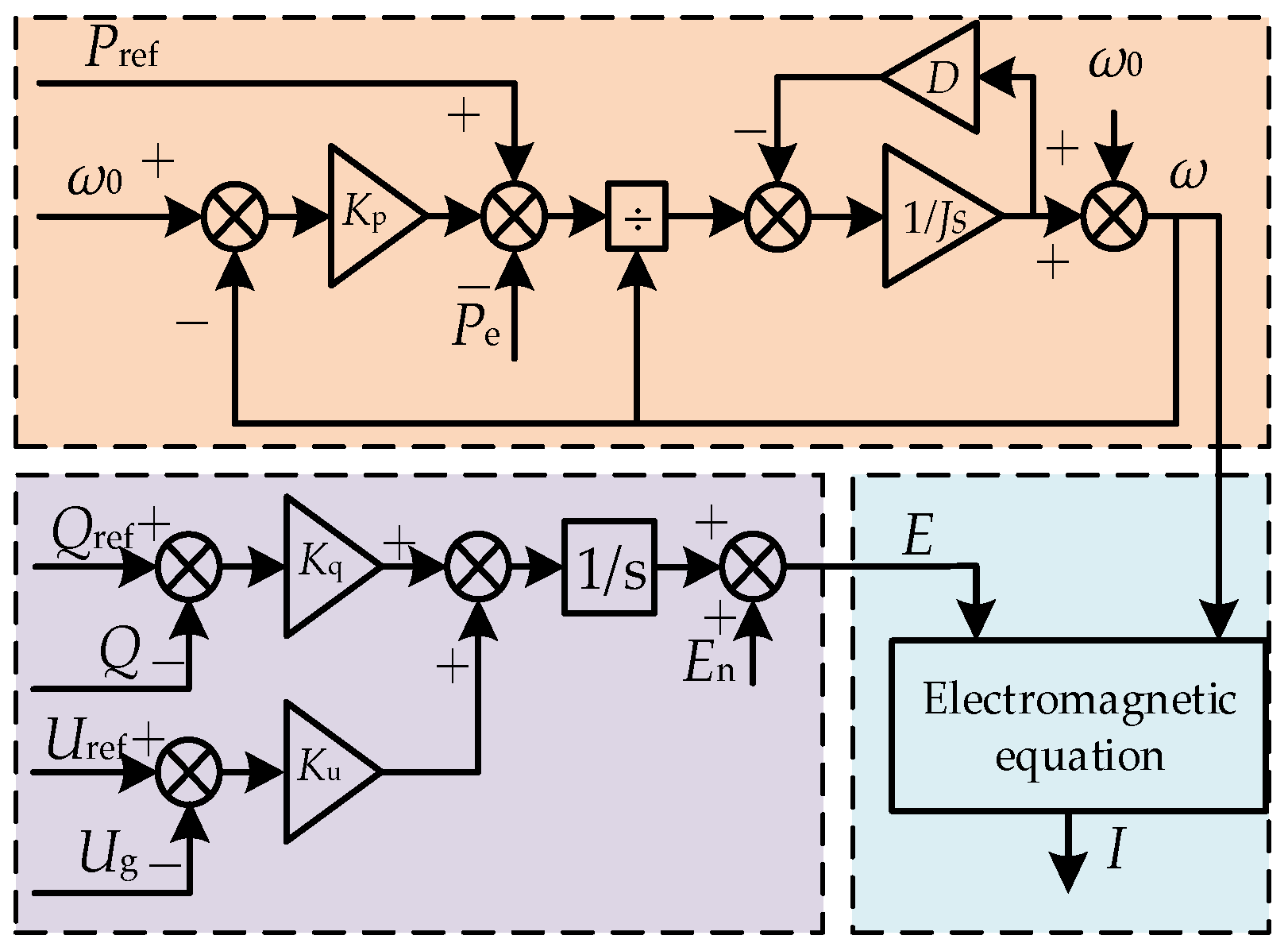
3.3. MMC Power Outer Loop VSG Control
3.3.1. MMC-VSG Control
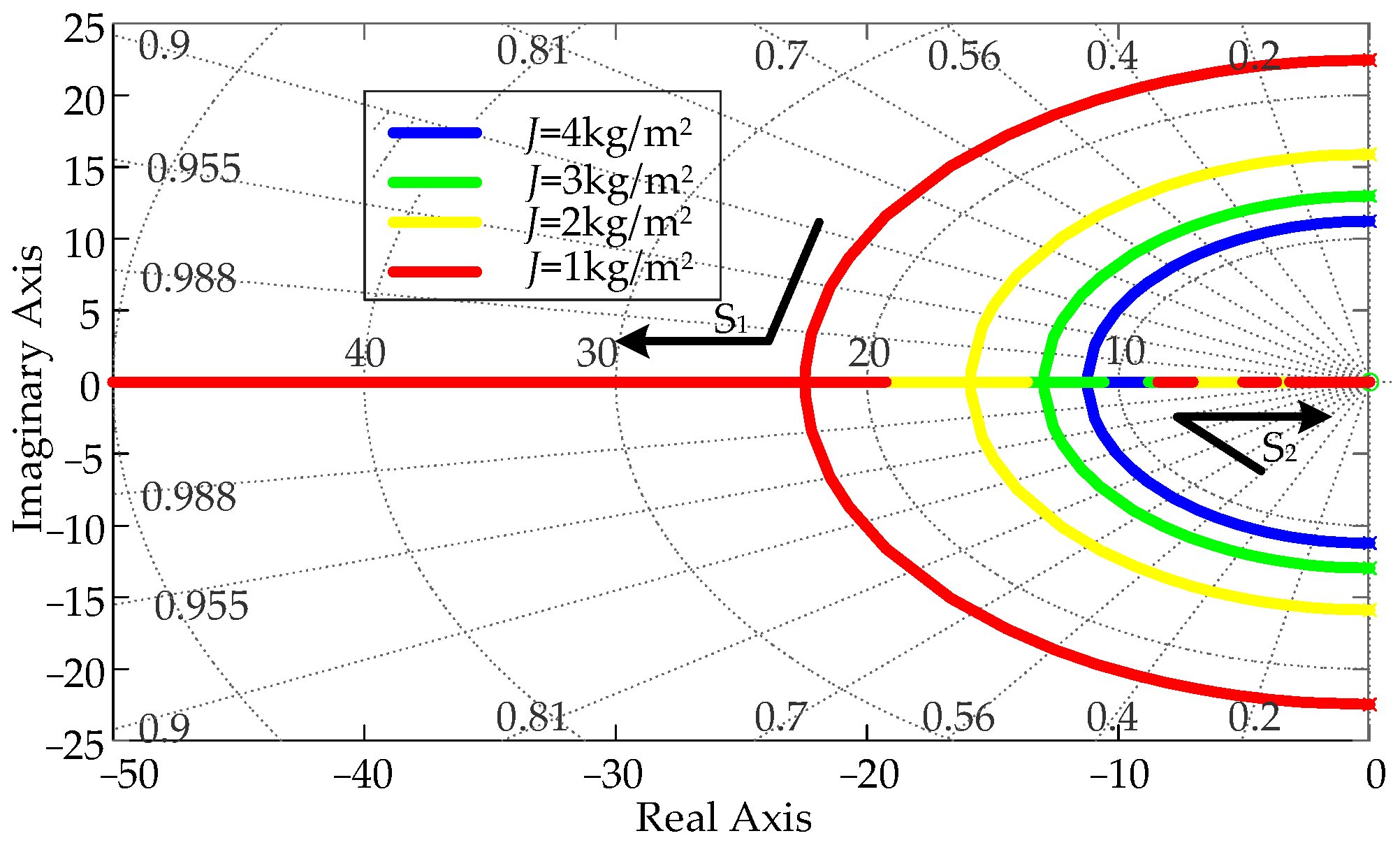
3.3.2. The Influence of J and D on the Dynamic Response of MMC-VSG Control
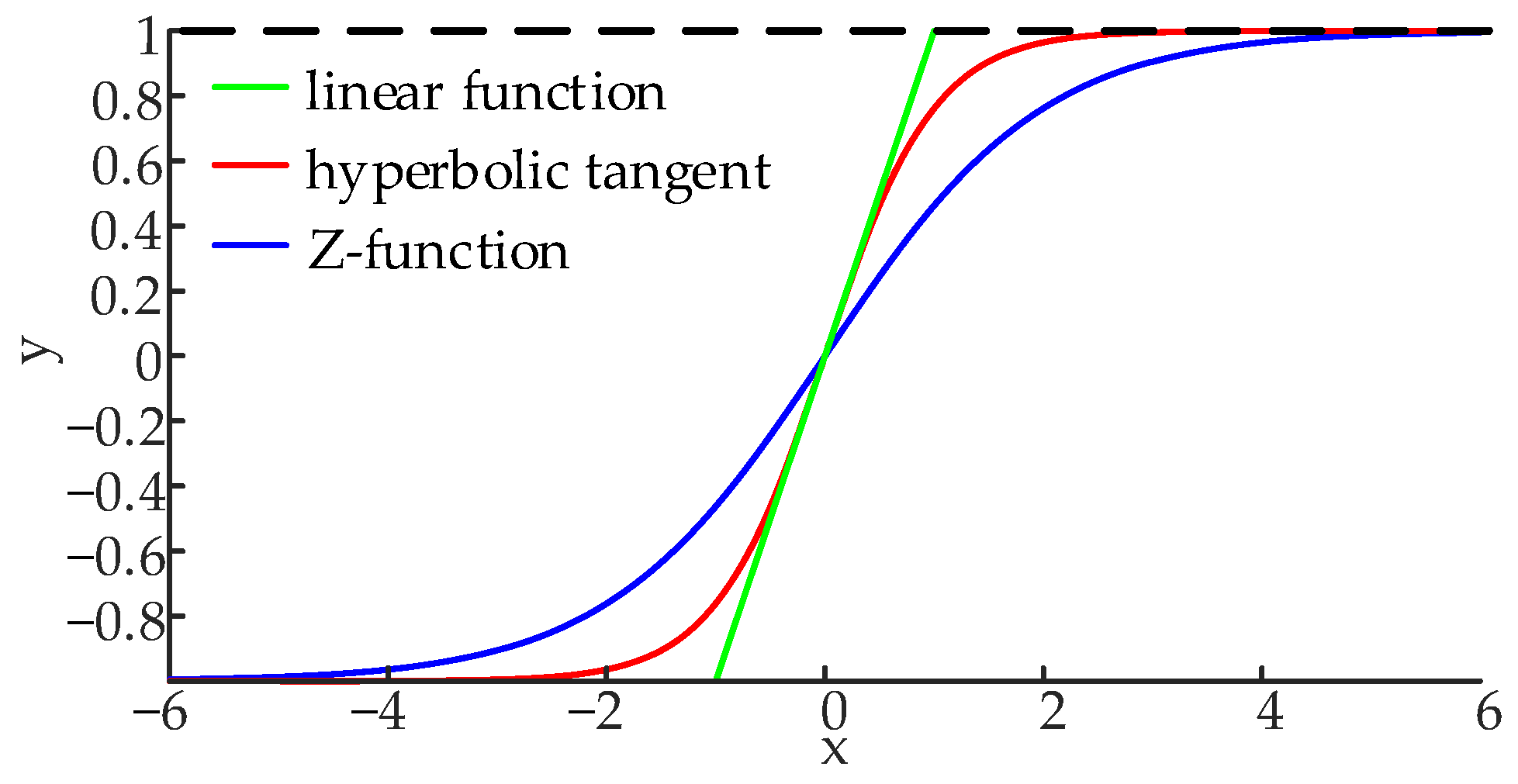
3.3.3. VSG Parameter Adaptive Control
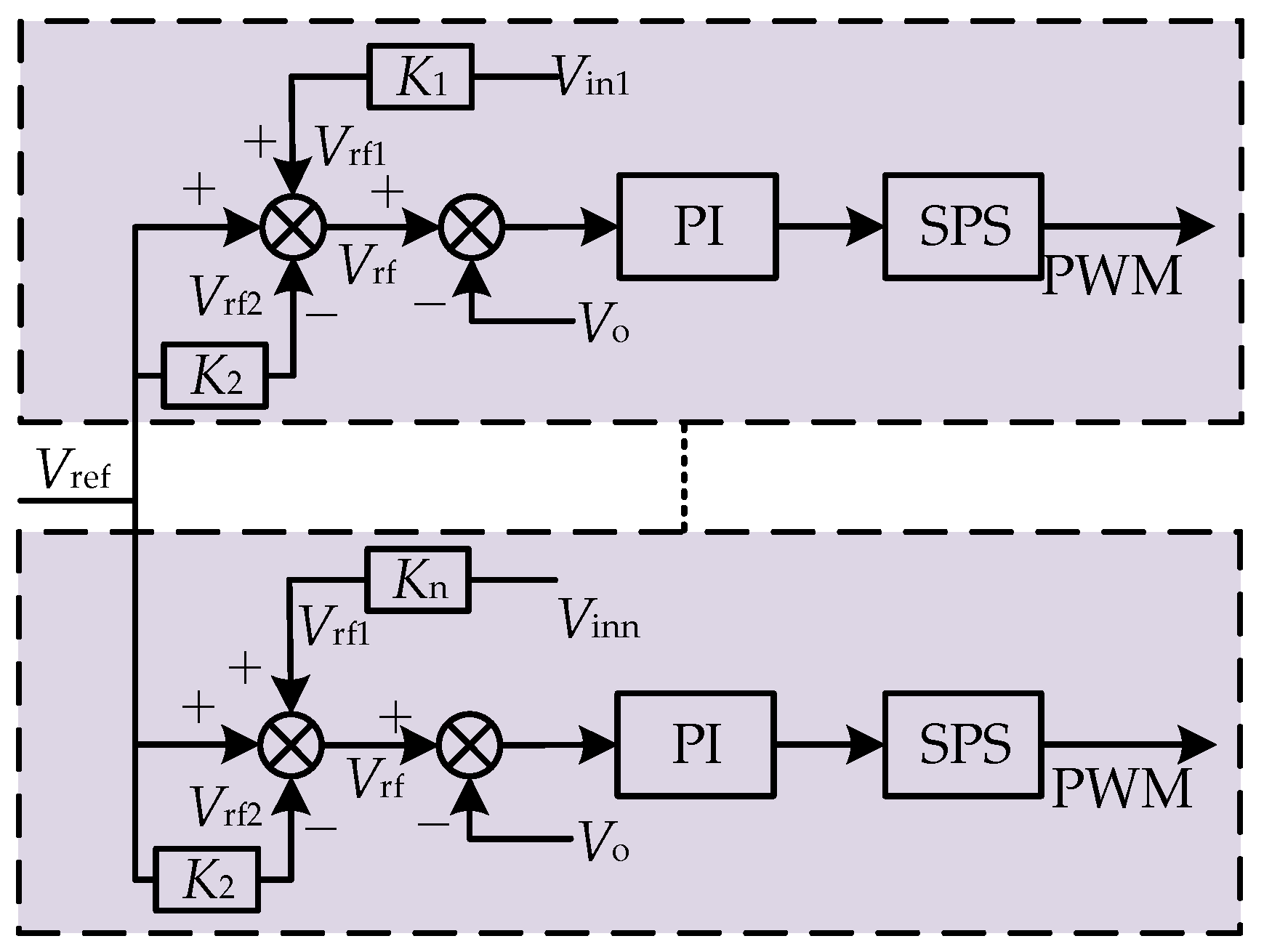
4. MMC-HVDC Isolation Stage Control Strategy
5. Simulation Results and Analysis
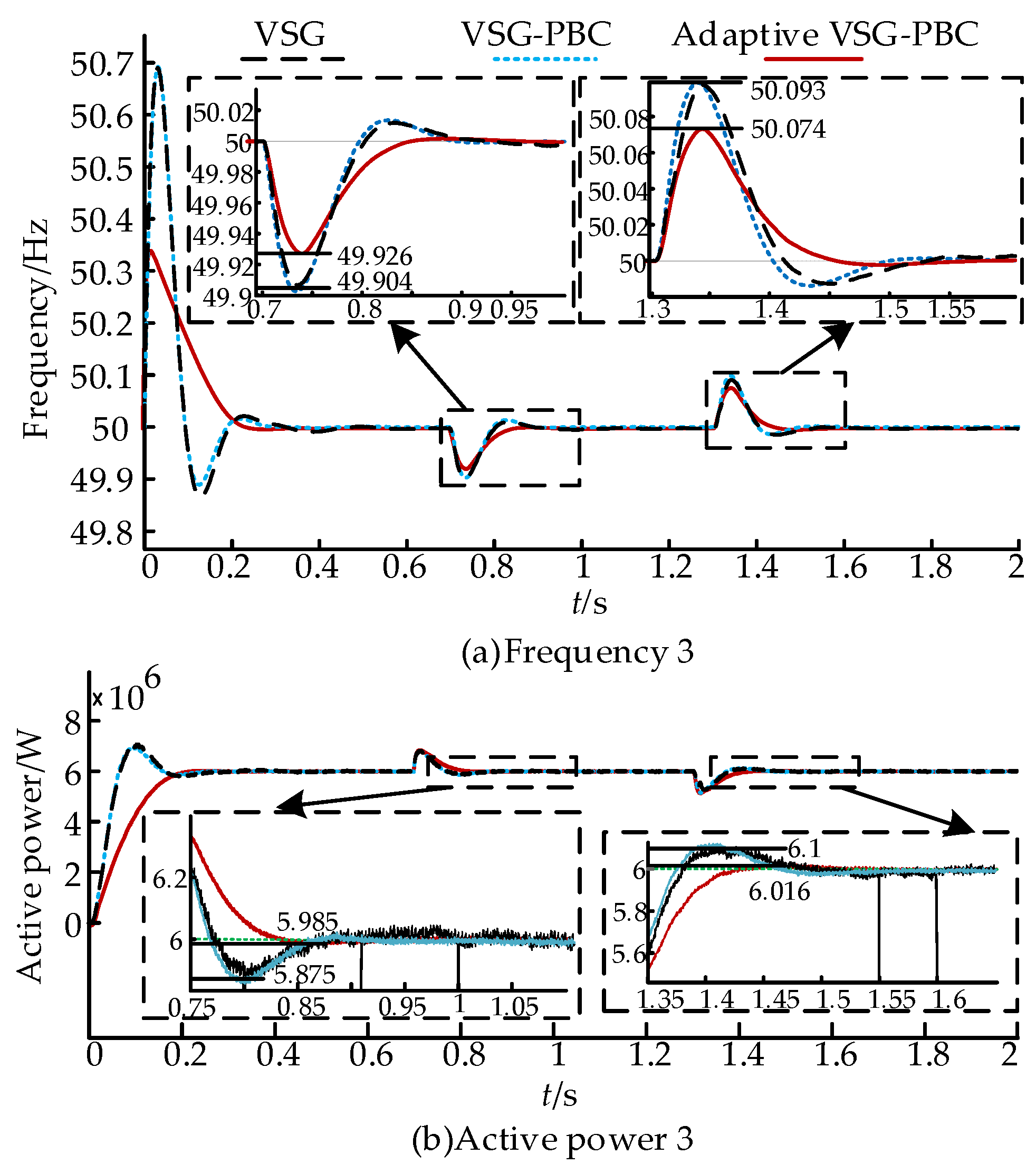
5.1. Given Output Power Variations
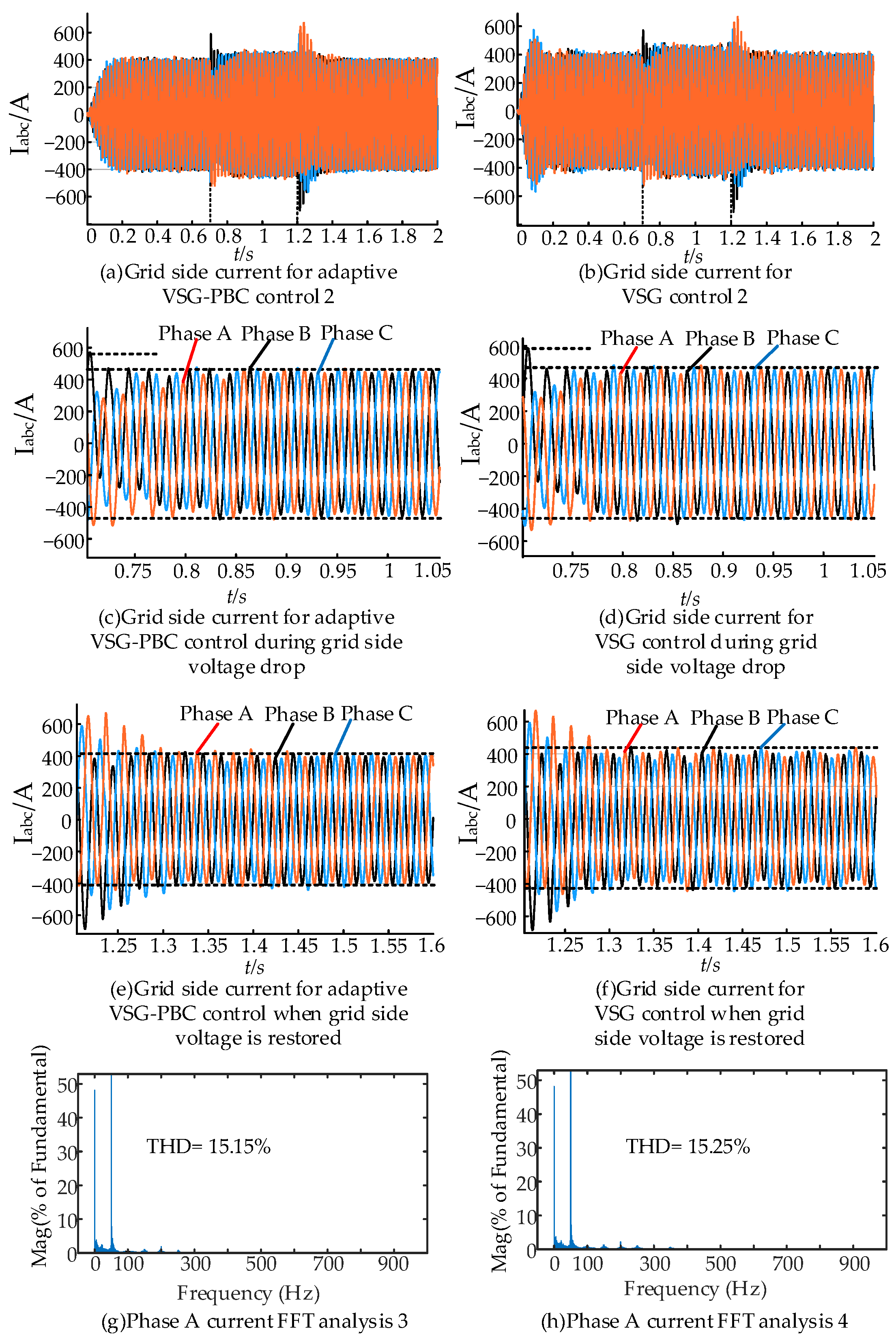
5.2. Operating Conditions of Variations in Voltage Amplitude on the Grid Side
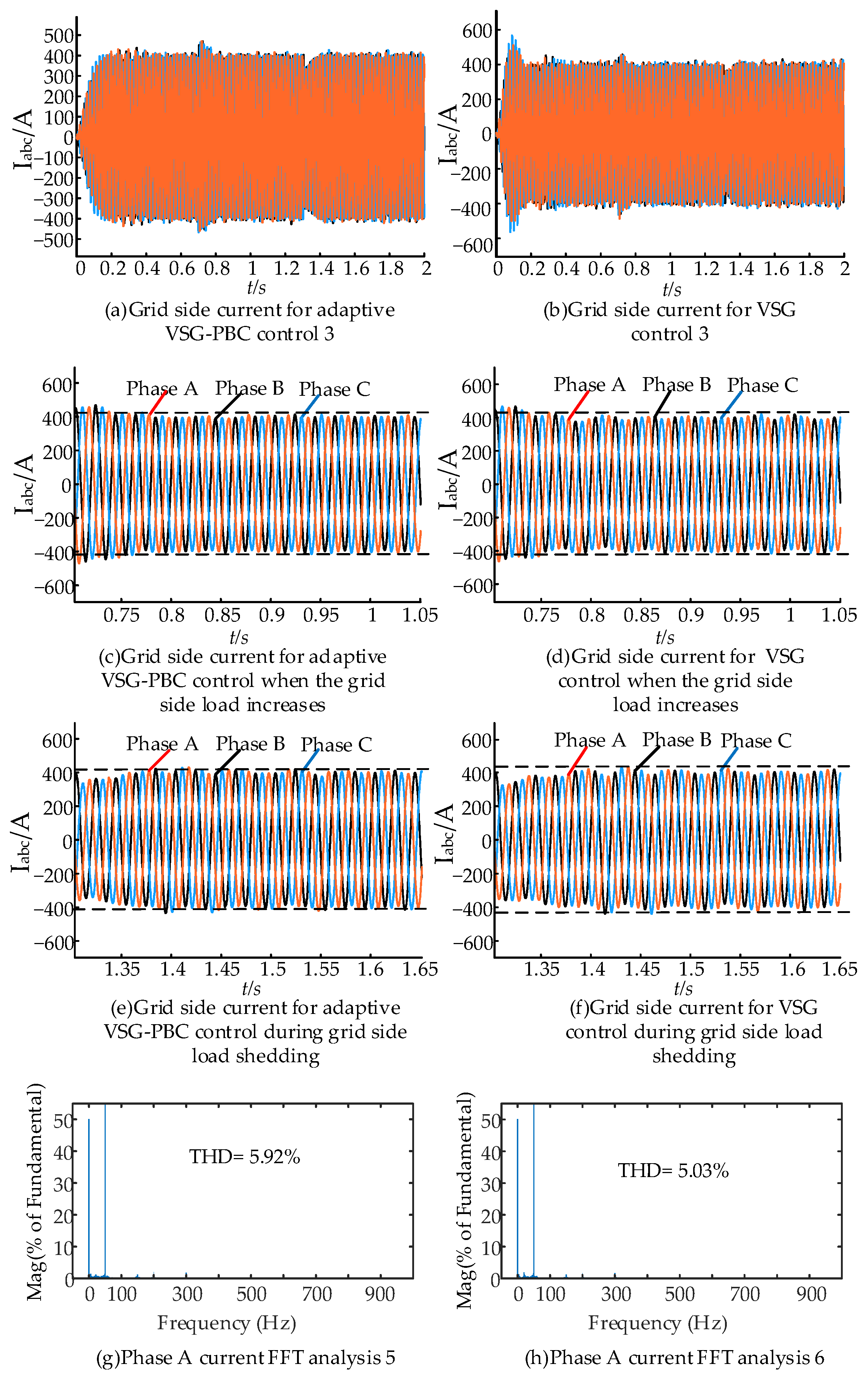
5.3. Grid-Side Load Mutation Condition
6. Conclusions
- (1)
- The adaptive VSG-PBC control strategy, when compared to traditional VSG control methods, integrates PBC in the current inner loop. The control strategy is based on the passivity of the system and injects additional damping into the control system to enhance energy dissipation and accelerate system regulation. In addition, the PBC control improves the power quality of the grid-connected currents in the MMC-HVDC system by changing the cut-off frequency of the current inner-loop control system.
- (2)
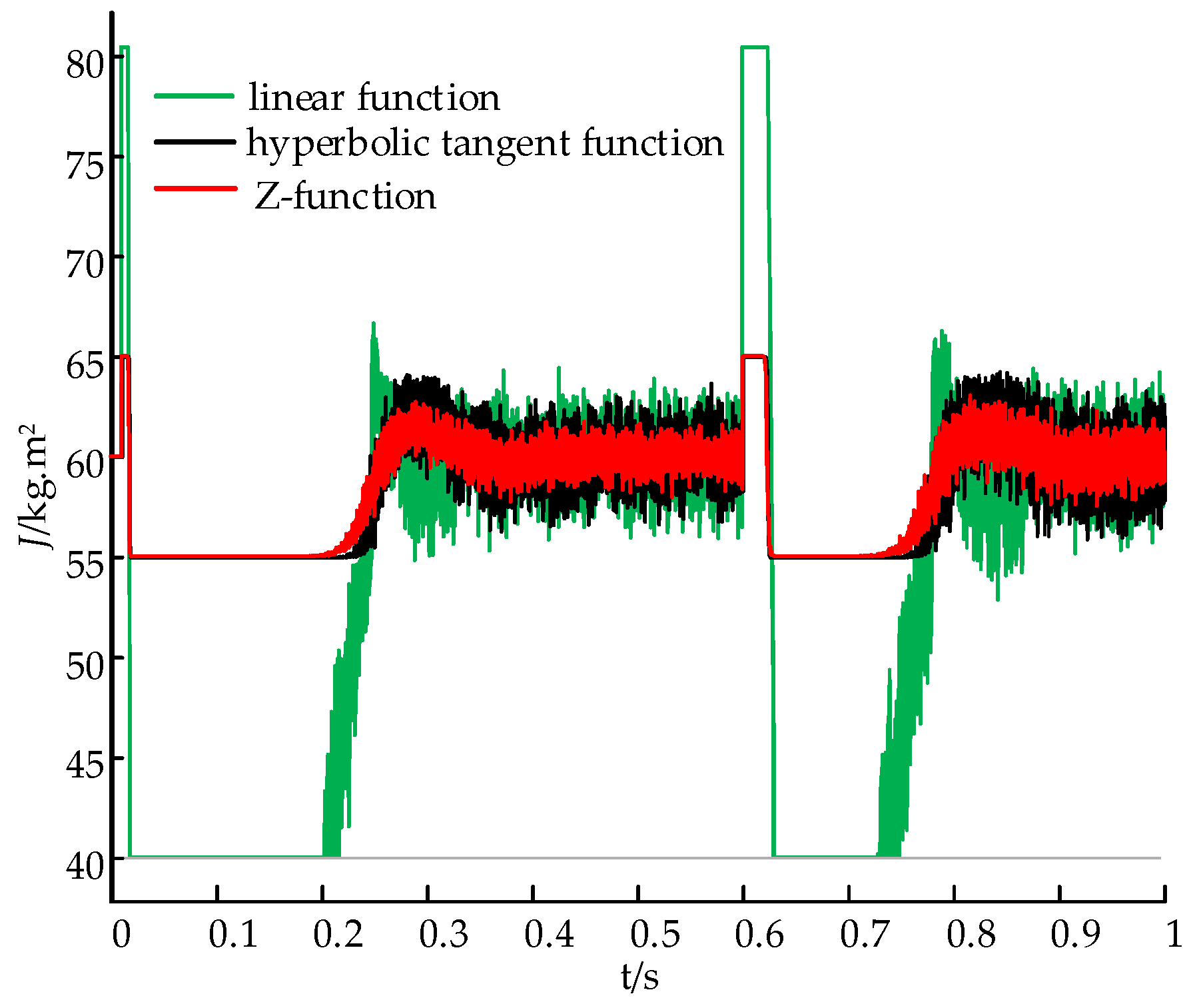
- The adaptive VSG-PBC control strategy, when compared to traditional VSG control methods, incorporates adaptive VSG control in the power outer loop. The strategy includes a mechanism for virtual inertia compensation that employs a sigmoid function, as well as an adaptive damping compensation mechanism. The control strategy designs the change rule of J and D parameters by analyzing the power and frequency oscillation characteristics of the MMC-HVDC system, combining the difference ∆ω between the VSG angular velocity and the reference angular velocity, and the angular velocity change rate dω/dt. In addition, the boundedness and smoothness of the sigmoid function are utilized to optimize the adjustment of the moment of inertia. Simulation results show that this approach effectively reduces the amplitude of power and frequency fluctuations in the MMC-HVDC system when operating in weak grid environments.
- (3)
- The adaptive VSG-PBC control strategy combines the advantages of adaptive VSG control and PBC and their interaction further improves the dynamic performance of the MMC-HVDC system in weak grid environments.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mi, Y.; Chen, Y.; Yuan, M.; Li, Z.; Tao, B.; Han, Y. Multi-Timescale Optimal Dispatching Strategy for Coordinated Source-Grid-Load-Storage Interaction in Active Distribution Networks Based on Second-Order Cone Planning. Energies 2023, 16, 1356. [Google Scholar] [CrossRef]
- Zhang, T.; Zhou, X.; Gao, Y.; Zhu, R. Optimal Dispatch of the Source-Grid-Load-Storage under a High Penetration of Photovoltaic Access to the Distribution Network. Processes 2023, 11, 2824. [Google Scholar] [CrossRef]
- Nazif, P.B.; Ahmad, S.; Saeed, M.; Guerrero, J.M.; Ortega, D.; Zelaa, B.; Larrazabal, I.; Briz, F. Assessment of Parameter Identification Methods for Digital Twins of Two-Level Bidirectional Converters. In Proceedings of the 2024 Energy Conversion Congress & Expo Europe (ECCE Europe), Darmstadt, Germany, 2–6 September 2024; pp. 1–6. [Google Scholar]
- Rajan, G.S.; Memala, W.A.; Sivachidambaranathan, V.; Jebaseelan, S.S.; Babu, A.R.; Glady, J.B.P. Implementation of Unidirectional Single Phase AC-DC-AC Three-Leg Three Level Converter. In Proceedings of the 2024 International Conference on Science Technology Engineering and Management (ICSTEM), Coimbatore, India, 26–27 April 2024; pp. 1–5. [Google Scholar]
- Patel, H.; Bhawal, S.; Harikrishnan, P.; Hatua, K.; Bhattacharya, S. Three Stage Power Electronic Transformer based MVAC Collection System and its Control System Design for Offshore Wind Power Generation Mills. IEEE Trans. Energy Convers. 2024, 39, 2216–2229. [Google Scholar] [CrossRef]
- Vipin, V.N.; Venkatramanan, D.; Mohan, N. An Online-Optimization-Based High-Frequency Link Control of an MMC-Driven Power Electronic Transformer for Wind-Energy Systems. IEEE Trans. Energy Convers. 2023, 38, 1986–1998. [Google Scholar] [CrossRef]
- Chandio, R.H.; Chachar, F.A.; Soomro, J.B.; Ansari, J.A.; Munir, H.M.; Zawbaa, H.M.; Kamel, S. Control and protection of MMC-based HVDC systems: A review. Energy Rep. 2023, 9, 1571–1588. [Google Scholar] [CrossRef]
- Soomro, J.B.; Akhtar, F.; Hussain, R.; Ahmed Ansari, J.; Munir, H.M. A detailed review of MMC circuit topologies and modelling issues. Int. Trans. Electr. Energy Syst. 2022, 2022, 8734010. [Google Scholar] [CrossRef]
- Abdolahi, M.; Adabi, J.; Mousazadeh Mousavi, S.Y. A passivity control and developed nonlinear disturbance observer for boost converter with constant power load in DC microgrid. Int. J. Circuit Theory Appl. 2024, 52, 5859–5876. [Google Scholar] [CrossRef]
- Baazouzi, K.; Drid, S.; Chrifi-Alaoui, L. Improving the Scalar Control of Induction Motor Using Passivity Based Control. In Proceedings of the 2024 2nd International Conference on Electrical Engineering and Automatic Control (ICEEAC), Setif, Algeria, 12–14 May 2024; pp. 1–6. [Google Scholar]
- Zhou, J.; Zhou, J.; Yang, H.; Huang, L.J.E. Passive Super-Twisting Second-Order Sliding Mode Control Strategy for Input Stage of MMC-PET. Energies 2024, 17, 2036. [Google Scholar] [CrossRef]
- Yang, X.; Chen, W.; Yin, C.; Cheng, Q. Fractional-Order Sliding-Mode Control and Radial Basis Function Neural Network Adaptive Damping Passivity-Based Control with Application to Modular Multilevel Converters. Energies 2024, 17, 580. [Google Scholar] [CrossRef]
- Hosseinnataj, S.; Mehrasa, M.; Rezanejad, M.; Gholamian, S.A.; Rodrigues, E.M.; Melicio, R. Virtual Inertia-based Control Strategy for Stable Operation of a Weak Grid Using Modular Multilevel Converter. In Proceedings of the 2024 IEEE 22nd Mediterranean Electrotechnical Conference (MELECON), Porto, Portugal, 25–27 June 2024; pp. 1198–1203. [Google Scholar]
- Liivik, E.; Yang, Y.; Sangwongwanich, A.; Blaabjerg, F. Advancing Grid-Connected Renewable Generation Systems. Appl. Sci. 2021, 11, 3058. [Google Scholar] [CrossRef]
- Al-Saadi, M.; Mahafzah, K.A.; Hatmi, A. Improved Frequency Response of Parallel Virtual Synchronous Generators Using Grey Wolf Optimization. J. Eur. Systèmes Autom. 2023, 56, 409. [Google Scholar] [CrossRef]
- Sun, X.; Cai, J.; Wang, D.; Lin, J.; Li, K. Small-disturbance stability analysis and control-parameter optimization of grid-connected virtual synchronous generator. Front. Energy Res. 2024, 12, 1428748. [Google Scholar] [CrossRef]
- Yao, L.; Li, M.; Liang, Z.; Zheng, X. Parameter Adaptive Control of Virtual Synchronous Generator Based on Ant Colony Optimization Fuzzy. In Advanced Intelligent Technologies for Industry, Proceedings of the 2nd International Conference on Advanced Intelligent Technologies (ICAIT 2021), Xi’an, China, 15–17 October 2021; Springer Nature: Singapore, 2022; pp. 339–349. [Google Scholar]
- Najjar, M.; Shahparasti, M.; Heydari, R.; Nymand, M. Model predictive controllers with capacitor voltage balancing for a single-phase five-level SiC/Si based ANPC inverter. IEEE Open J. Power Electron. 2021, 2, 202–211. [Google Scholar] [CrossRef]
- Hou, S.; Du, C.; Geng, Z.; Han, Y. An improved modular multilevel converter-high voltage direct current (MMC-HVDC) control method based on fuzzy adaptive proportional integral (PI) integrating model predicitve control. J. Beijing Univ. Chem. Technol. 2023, 50, 55–65. [Google Scholar]
- Hu, C.; Chen, H.; Tang, A. Sliding mode control strategy of grid-forming energy storage converter with fast active support of frequency and voltage. Front. Energy Res. 2024, 12, 1416591. [Google Scholar] [CrossRef]
- Ban, G.; Xu, Y.; Guo, D.; Zhou, W.; Zheng, H.; Yuan, X. Research on adaptive VSG control strategy based on inertia and damping. In Proceedings of the 2021 IEEE Sustainable Power and Energy Conference (iSPEC), Nanjing, China, 23–25 December 2021; pp. 1584–1589. [Google Scholar]
- Han, J.; Feng, X.; Zhao, H.; Hu, P.; He, C. Adaptive VSG control strategy considering energy storage SOC constraints. Front. Energy Res. 2023, 11, 1278648. [Google Scholar] [CrossRef]
- Zhang, C.; Zhu, Z. Research on VSG Control Strategy of Optical Storage Microgrid Based on Energy Storage Coordination. J. Electr. Eng. 2023, 18, 228–234. [Google Scholar]
- Wang, Y.; Cheng, Q.; Cheng, Y. Passivity-based control of MMC-based active power filter under non-ideal conditions. Int. Trans. Electr. Energy Syst. 2020, 30, e12178. [Google Scholar] [CrossRef]


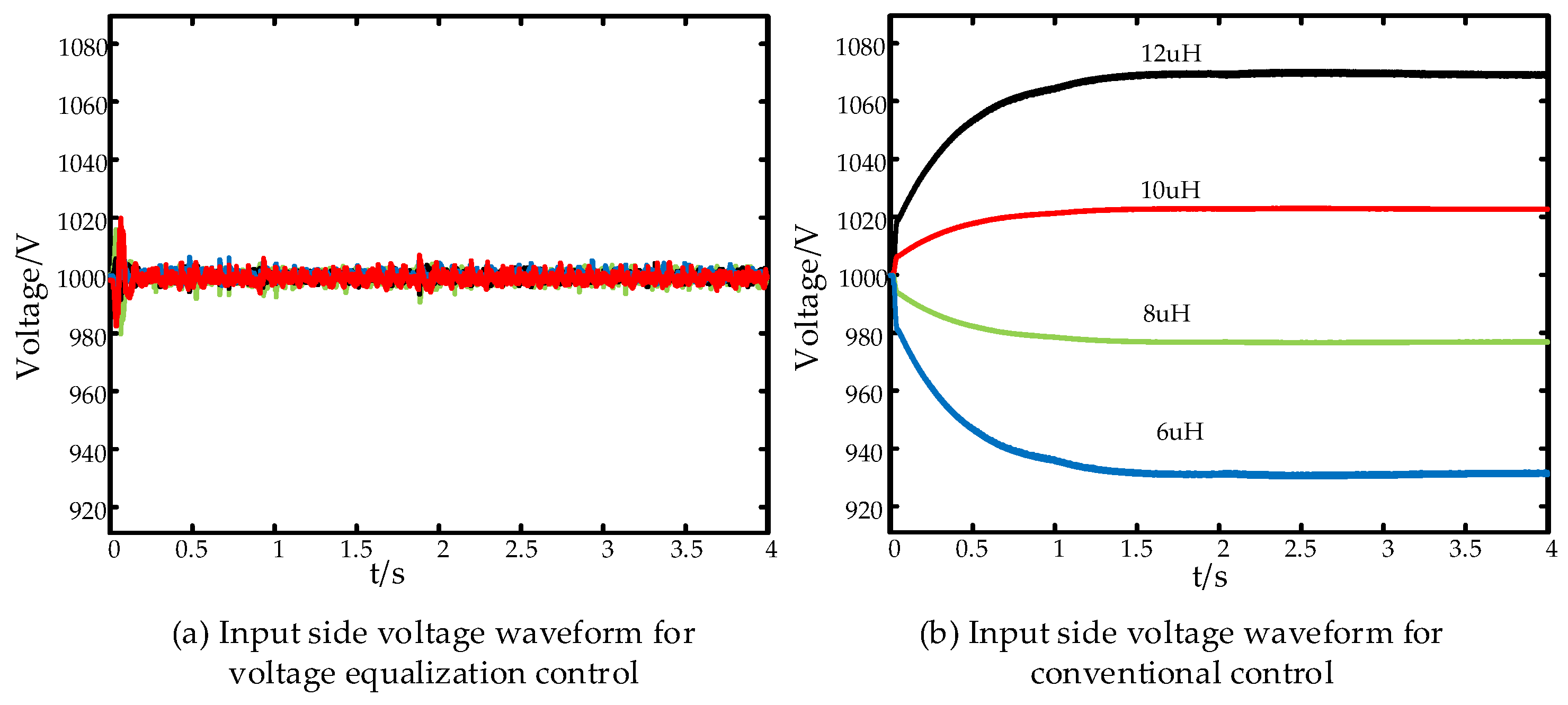
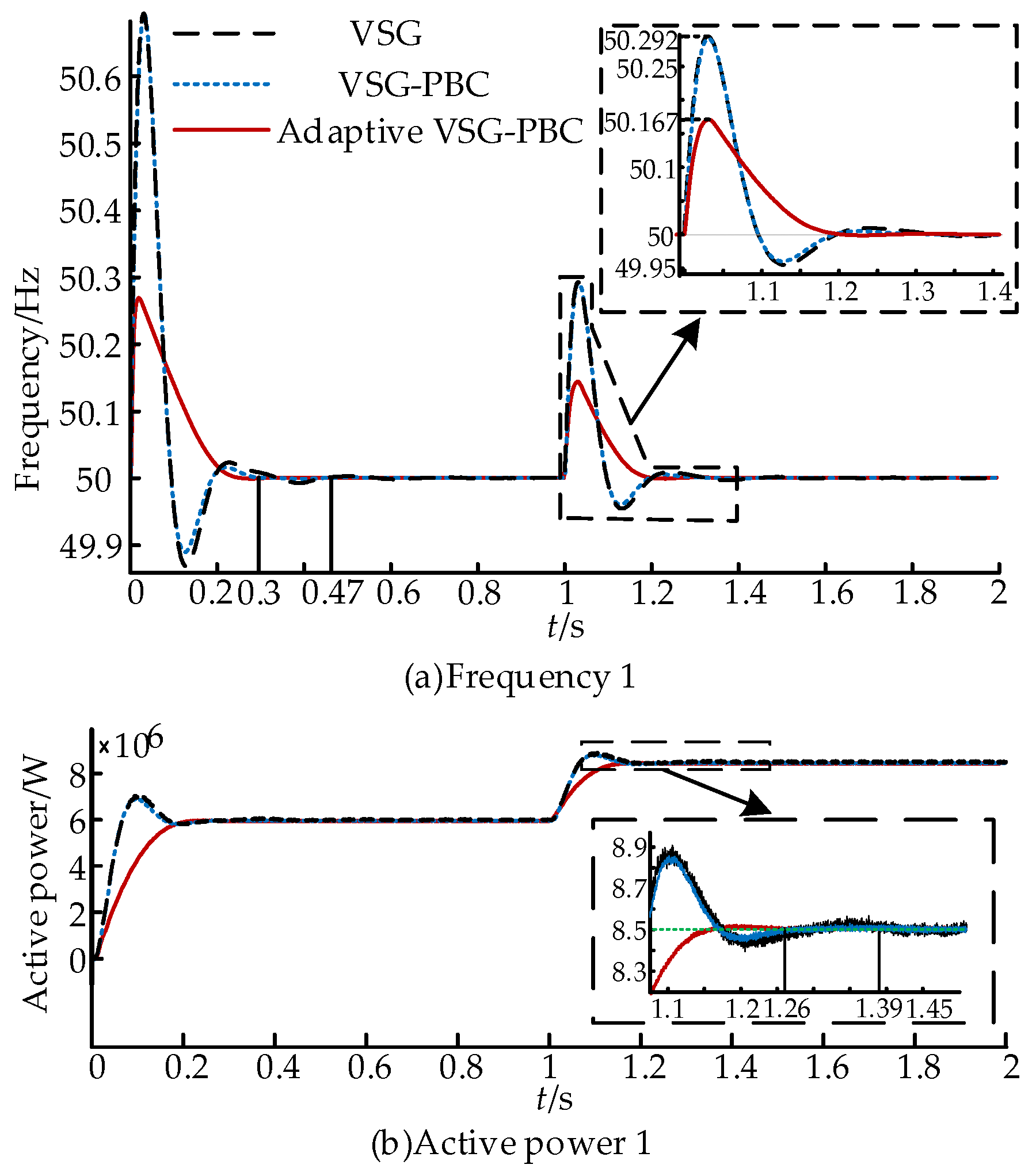
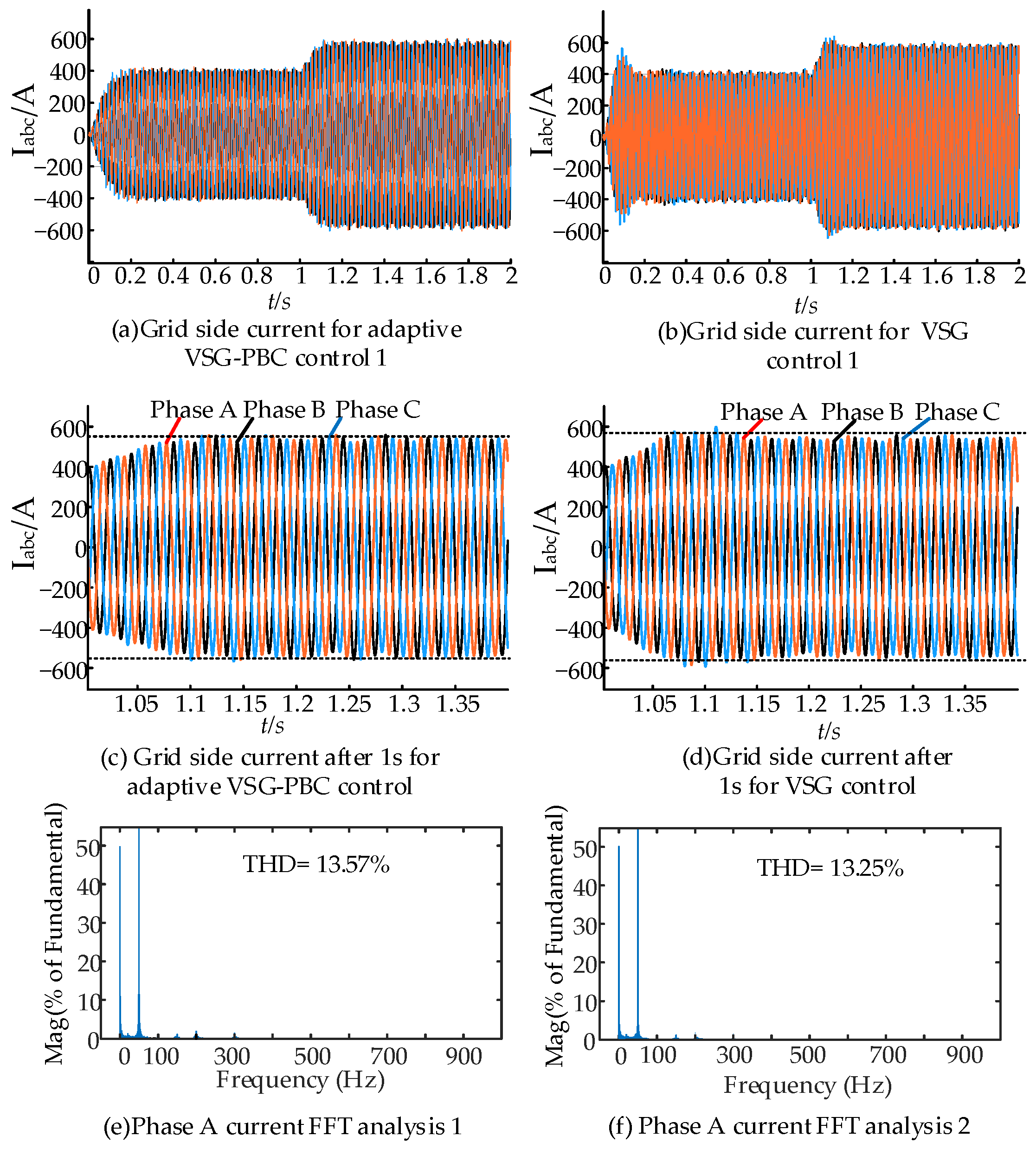
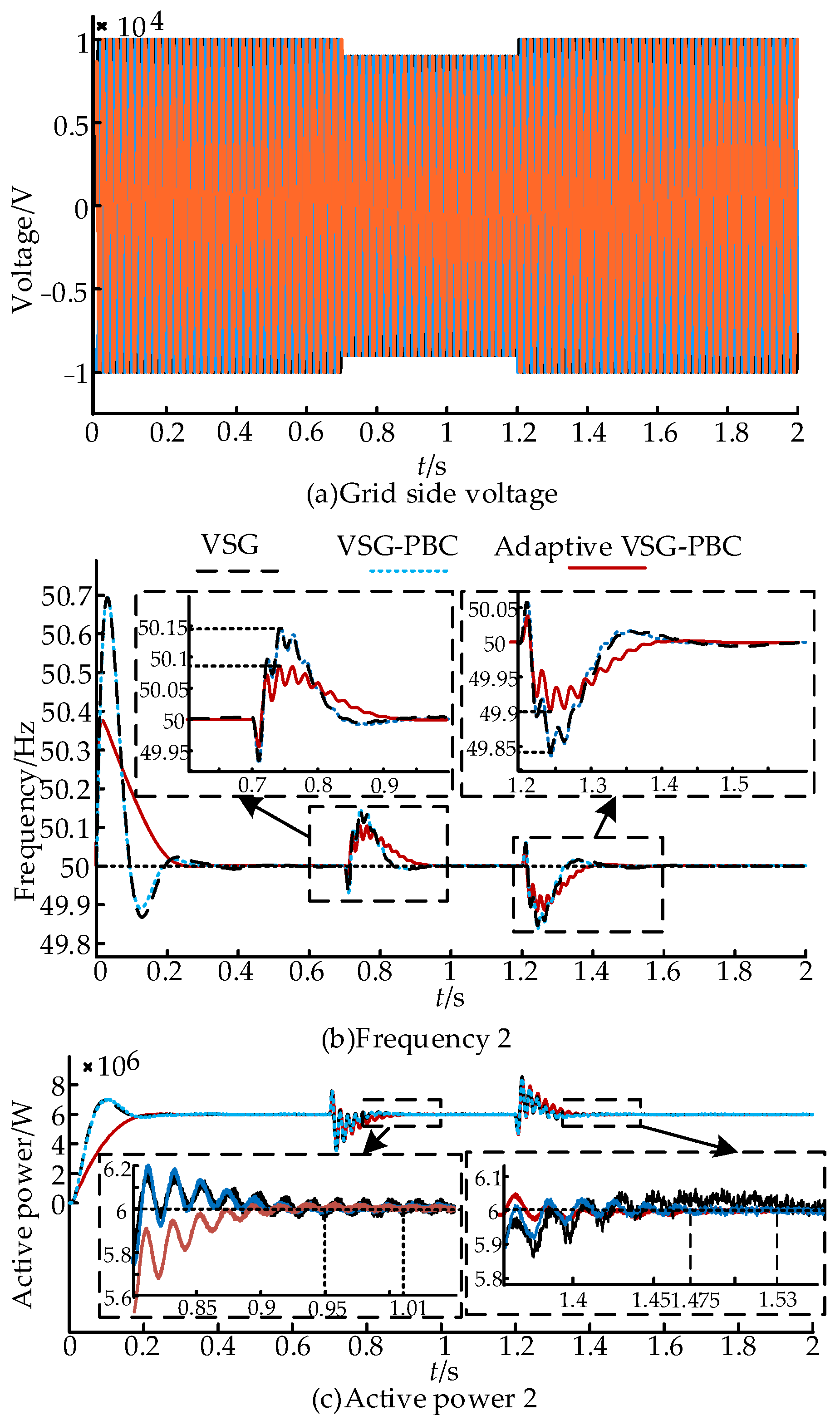
| Parameter | Value | |
|---|---|---|
| MMC | Grid-side voltage/kV Grid-side resistance/Ω Grid-side inductance/mH Number of upper or lower bridge arm submodules Bridge arm resistance/Ω Bridge arm inductance/mH Submodule capacitance/μF DC-side voltage reference value/kV | 10 0.4 6.58 12 0.01 5 700 20 |
| High-voltage-side capacitor/mF | 1 | |
| DAB | Low-voltage-side capacitor/mF | 8 |
| Rated frequency/Hz Rated ratio DC-side input voltage value/kV | 50 4:1 110 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, Y.; Li, H.; Ye, S.; Shi, J.; Yang, Y.; Li, K. Enhanced MMC-HVDC Power Control via Adaptive VSG-PBC in Weak Grid Environments. Energies 2025, 18, 3327. https://doi.org/10.3390/en18133327
Xia Y, Li H, Ye S, Shi J, Yang Y, Li K. Enhanced MMC-HVDC Power Control via Adaptive VSG-PBC in Weak Grid Environments. Energies. 2025; 18(13):3327. https://doi.org/10.3390/en18133327
Chicago/Turabian StyleXia, Yan, Huizhu Li, Shengyong Ye, Jinhui Shi, Yili Yang, and Ke Li. 2025. "Enhanced MMC-HVDC Power Control via Adaptive VSG-PBC in Weak Grid Environments" Energies 18, no. 13: 3327. https://doi.org/10.3390/en18133327
APA StyleXia, Y., Li, H., Ye, S., Shi, J., Yang, Y., & Li, K. (2025). Enhanced MMC-HVDC Power Control via Adaptive VSG-PBC in Weak Grid Environments. Energies, 18(13), 3327. https://doi.org/10.3390/en18133327




