A Review of Optimization Strategies for Energy Management in Microgrids
Abstract
1. Introduction
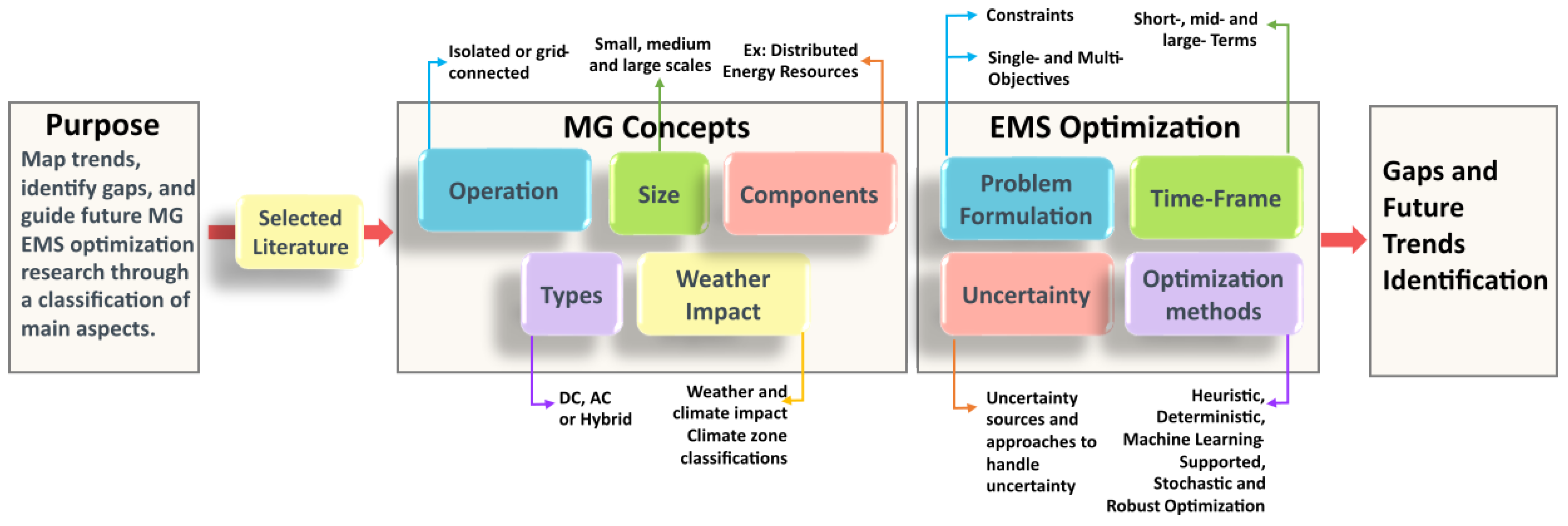
- Explores the main aspects of MGs that incorporate RESs, such as sizes, operational components, types of MGs, and implications of weather and climate on performance. This includes an analysis of how weather can influence energy generation and demand, thereby affecting system performance.
- Provides an up-to-date review of published research on the fundamentals of optimization EMS of MGs from 2020 to 2025. Main aspects such as problem formulation, time frames, sources of uncertainty, techniques for managing uncertainties, and various optimization methods are thoroughly discussed. It also addresses MOO, detailing the main objectives and constraints based on MG components.
- Identifies contributions and limitations of existing research, along with recommendations for future work. This section highlights areas that require further exploration or methodological refinement, ensuring that new studies can build on the identified gaps and deficiencies in the current literature. This comprehensive examination not only informs current practices but also sets the stage for innovative developments in EMS.
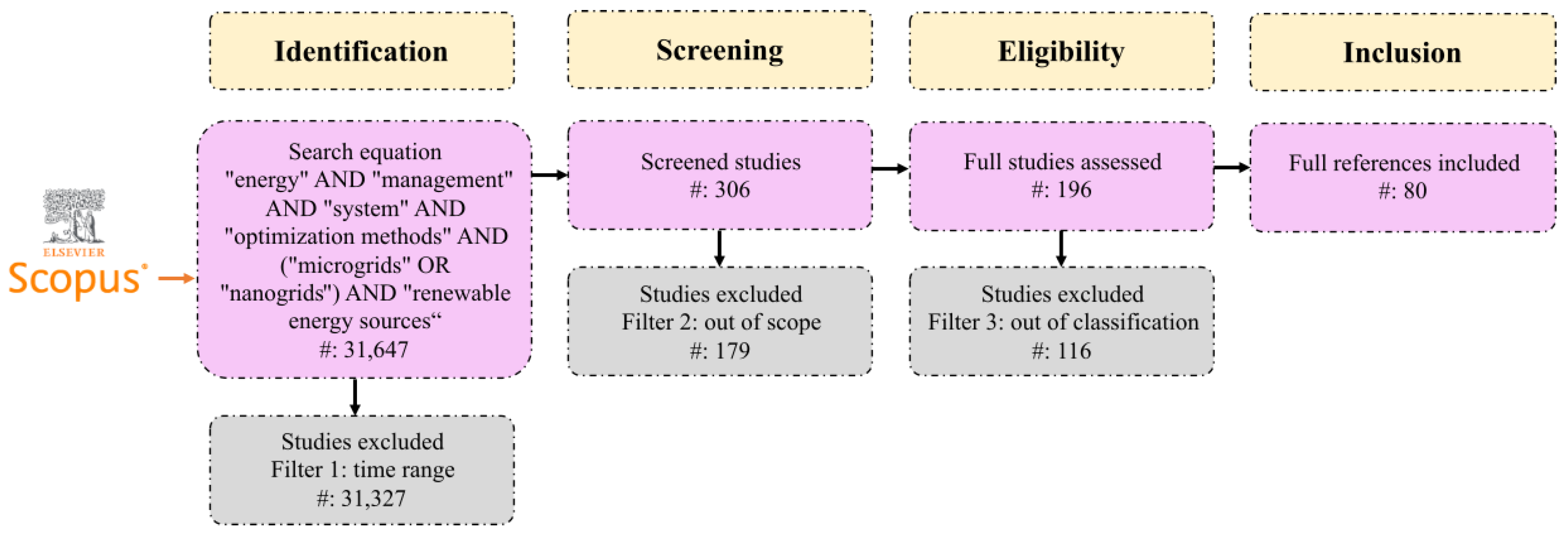
2. Literature Search Methodology
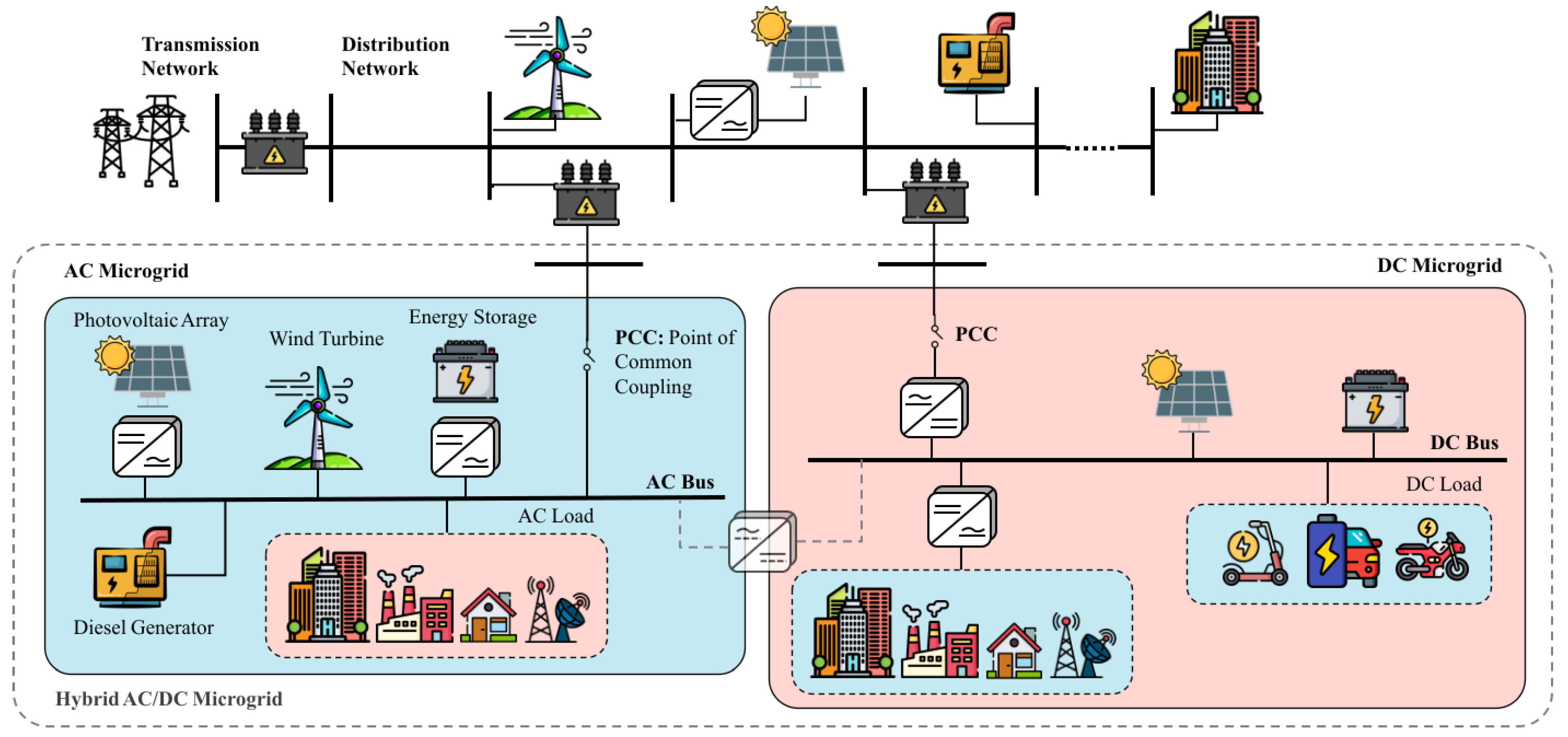
3. Microgrids Concepts and Implications
- AC MGs: power electronic devices connect DGs and ESSs to an AC bus. Depending on the on/off control at the Point of Common Connection (PCC), they can operate in grid-connected or standalone modes. AC MGs facilitate the integration of various RESs, supporting the existing AC power infrastructure.
- DC MGs: DC MGs supply AC and DC loads at different voltage levels via power electronic converters. They feature DERs connected to the DC bus, with ESSs linked to the DC network. DC MGs are more cost-effective when there are multiple DC power sources and loads, such as solar panels and batteries.
- Hybrid AC-DC MGs: these systems combine AC and DC buses, allowing them to serve both AC and DC loads. The DC grid connects to the AC bus through an inverter as a versatile power source. Hybrid MGs leverage the advantages of both AC and DC systems, effectively optimizing the feeding of various loads.
4. Optimization EMS
| Ref. Year | (MG) Information | Objective | Multi-Objective | Optimizer | Optimization Method | Timeframe | Uncertainty | Highlights |
|---|---|---|---|---|---|---|---|---|
| [44] (2020) | Photovoltaic (PV), Wind Turbine (WT), Battery Energy Storage System (BESS), Diesel Generator (DG); Standalone; Small Scale; Hybrid AC/DC; Nigeria, Yobe State; Tropical | Minimizing Cost of Energy (COE) and Deficiency of Power Supply Probability (DPSP) | Yes | Grasshopper Optimization Algorithm (GOA) | Metaheuristic | Long-Term | No | GOA—Reduced fuel consumption by 92.4%, Carbon Dioxide (CO2) emissions by 92.3%, and COE by 79.8%. Compared against Hybrid Optimization of Multiple Energy Resources (HOMER) software and traditional EMSs. |
| [50] (2021) | PV, WT, Flat-Plate Collector (FPC), BESS, Electric Water Heater (EWH); Grid-Connected; Medium Scale; Hybrid AC/DC; Spain, Public University of Navarre (UPNa); Temperate | Minimizing positive grid power peaks and negative grid power peaks, as well as Maximum Power Derivative (MPD), average power derivative (APD), and power profile variability (PPV) | No | Fuzzy Logic Control (FLC) | Heuristic | Mid-Term | Yes | FLC—Improved grid power stability, enhanced battery State of Charge (SOC) stability, and reduced power fluctuations. Compared against heuristic optimization. |
| [45] (2021) | PV, DG, BESS; Standalone; Large Scale; AC; Colombia; Tropical | Priority EMS reduces fuel consumption using predefined rules, while Optimal EMS optimizes total marginal cost for efficient Energy Management (EM). | No | Priority EMS (Rule-Based); Optimal EMS (Mixed-Integer Linear Programming (MILP)-Based) | Priority EMS: Heuristic; Optimal EMS: Deterministic | Mid-Term | No | Priority EMS vs. Optimal EMS—Priority EMS ensures simplicity and robustness, while Optimal EMS (MILP-based) improves BESS utilization and reduces diesel consumption. |
| [47] (2021) | PV, WT, BESS, Supercapacitor (SC); Both Grid-Connected and Standalone; Small Scale; DC; Iran, Shiraz; Arid | Particle Swarm Optimization (PSO) lowers maintenance costs and prevents battery life reduction, while Fuzzy Logic Control (FLC) minimizes peak current of the battery. | No | FLC and PSO | Metaheuristic | Short-Term | No | FLC + PSO—Improved stability against grid fluctuations in islanded and grid-connected modes. |
| [48] (2021) | PV, DG, BESS; Standalone; Medium Scale; Hybrid AC/DC; Somalia, Garowe; Arid | Minimizing operating costs by reducing DG power consumption. | No | Tunable Rule-Based Heuristic (TRBH) optimized using Evolutionary Algorithms | Heuristic | Mid-Term | No | TRBH + Evolutionary Algorithms—Achieved near-optimal performance while maintaining simplicity. Compared against MILP, Evolutionary Algorithms (SNO), and Rule-Based EMS. |
| [51] (2025) | PV, BESS; Grid-Connected; Small Scale; DC; France, École Polytechnique (Palaiseau); Temperate | Maintaining a specific SOC in the battery while minimizing electricity costs. | No | Scenario-Based Stochastic Model Predictive Control (MPC) | Stochastic | Short-Term and Mid-Term | Yes | Scenario-Based Stochastic MPC—Reduced operational cost by 6% and 22%. Compared against Chance-Constrained MPC, Rule-Based EMS, Single-Layer Scenario-Based MPC, and Two-Stage Stochastic Programming. |
| [59] (2024) | PV, WT, Fuel Cell (FC), Microturbine (MT), DG, BESS; Both Grid-Connected and Standalone; Medium Scale; AC; N/A; N/A | Minimizing main-grid energy costs, fuel and generator startup costs, renewable energy generation costs, greenhouse gas emissions costs, demand response incentive costs, and power loss costs. | Yes | Golden Jackal Optimization (GJO) | Metaheuristic | Mid-Term | No | GJO—Achieved 96% efficiency, significantly lowered operational costs. Compared against PSO, Artificial Bee Colony (ABC), and Tabu Search (TS). |
| [20] (2023) | DG, PV, WT, BESS; Standalone; Medium Scale; Hybrid AC/DC; Denmark, Sønderborg; Temperate | Optimizing system sizing while minimizing the Loss of Power Supply Probability (LPSP) and the Levelized Cost of Energy (LCOE). | Yes | multi-objective Moth Flame Optimization (MOMFO) | Metaheuristic | Long-Term | No | MOMFO—Improved reliability, increased renewable energy penetration, and reduced costs. Compared against NSGA-II, MOPSO, and MOSEO. |
| [21] (2022) | MT, WT, BESS, FC; Grid-Connected; Large Scale; N/A; N/A | Minimizing operational costs and emissions. | Yes | Oppositional Gradient-Based Grey Wolf Optimizer (OGGWO) | Metaheuristic | Mid-Term | Yes | OGGWO—Achieved efficient cost and emission reduction. Compared against NSGA-II, PSO, and Grey Wolf Optimizer (GWO). |
| [22] (2025) | WT, PV, BESS; Standalone; Medium Scale; N/A; China, Tianjin; Temperate | Minimizing the Tracking Assessment Cost of the Wind-PV Energy Storage System (ESS) and reduce Energy Storage charging and discharging costs. | Yes | State-Action-Reward-State-Action (SARSA) Algorithm | Machine Learning-Supported | Mid-Term | Yes | SARSA—Improved power tracking, enhanced storage efficiency, and reduced operational costs. Compared against Model Predictive Control (MPC) and Deep Q-Network (DQN) methods. |
| [23] (2022) | PV, WT, DG, MT, BESS; Standalone; Medium Scale; Hybrid AC/DC; N/A; N/A | Minimizing the optimization function by reducing generation, emissions, and maintenance costs. | Yes | Mixed-Integer Programming (MIP) | Deterministic | Mid-Term | No | MIP—Reduced operation costs, improved BESS utilization, and integrated demand response. Compared against Genetic Algorithm (GA). |
| [24] (2023) | PV, WT, DG, MT, BESS; Both Grid-Connected and Standalone; Medium Scale MG; All Types; Iran; Temperate | Minimizing operating costs and emissions. | Yes | Salp Swarm Algorithm (SSA) | Metaheuristic | Mid-Term | Yes | SSA—Achieved cost and emission reductions, ensuring feasible planning under uncertainty. The comparison focused on effectiveness in grid-connected and islanded scenarios. |
| [60] (2021) | PV, WT, BESS, DG; Grid-Connected; Medium Scale; Hybrid AC/DC; N/A; N/A | Minimizing fuel consumption, operation and maintenance costs, emissions, ES operation costs, and costs related to DG and grid interactions. | No | Column and Constraints Generation (C&CG) | Deterministic | Mid-Term | Yes | C&CG—Enhanced scheduling under Renewable Energy Source (RES) uncertainty, reducing operational costs. Validated through simulations on the IEEE-33 bus distribution network model. |
| [52] (2023) | Controllable Distributed Generators (CDG), PV; Grid-Connected; Large Scale; N/A; China, Nanjing; Temperate | Minimizing user load dispatch and emission dispatch. | Yes | Deep Reinforcement Learning (DRL) | Machine Learning-Supported | Mid-Term | Yes | DRL—Improved solving speed by 56.74% over NSGA-II and 15.62% over CVX, effectively managing renewable energy uncertainties. Compared against heuristic optimization. |
| [49] (2023) | PV, WT, BESS; Grid-Connected; Large Scale; N/A; Saudi Arabia, Wadi Alddawasir; Arid | Two-stage optimization to minimize operational costs and enhance self-consumption rates. | Yes | Harris Hawks Optimizer (HHO) | Metaheuristic | Mid-Term | Yes | HHO—Increased self-consumption (100% SCR), improved hosting capacity (8.863 MW to 10.213 MW), and reduced daily operating costs by 23.8%. Compared against standard optimization algorithms. |
| [53] (2023) | PV, BESS; Grid-Connected; Small Size; DC; Canada, Vancouver; Temperate | Maximizing power supply availability, minimizing Net Present Cost (NPC), and maximizing power efficiency. | No | GA | Metaheuristic Algorithm | Long-Term | Yes | GA—Achieved 93.76% energy efficiency, reduced costs by 14%, and provided 100 times lower downtime. Compared against HOMER software for MG design optimization. |
| [57] (2023) | DG, BESS, WT Farm; Standalone; Medium Scale; N/A; N/A | Minimizing total costs by considering unit operating costs, diesel generator emissions, ES degradation, and adjustment costs from wind power forecasting errors. | No | Mixed-Integer Second-Order Cone Programming (SOCP) | Deterministic | Mid-Term | Yes | SOCP—Improved reliability (99%) while balancing cost reductions. Compared against Deterministic and Stochastic Programming-Based models. |
| [61] (2022) | PV, WT Farm, DG, BESS; Grid-Connected; Medium Scale; N/A; Singapore; Tropical | Minimizing total economic energy costs. | No | Proximal Policy Optimization (PPO) | Machine Learning-Supported | Mid-Term | Yes | PPO—Achieved 32.8% cost savings and 28.5% carbon emission reduction. Compared to conventional grid-based power reliance. |
| [62] (2023) | RES, Combined Heat and Power (CHP), ESSs, Heat Energy Storage (HES); Both Grid-Connected and Standalone; Medium Scale; AC; N/A; N/A | Minimizing Cost of Energy Use (CET). | No | Myopic Optimization with Linear Programming (LP) and Reinforcement Learning (RL) | Hybrid Deterministic and Machine Learning-Supported | Long-Term and Short-Term | No | LP + RL—Improved operating cost by 90.98% compared to myopic model alone. |
| [63] (2023) | Exhaust Air WT, Concentrated Photovoltaic Thermal (CPVT), BESS, HES, DG; Grid-Connected; Medium Scale; AC; Iran; N/A | Minimizing the total CET and BESS degradation. | No | State-Action-Reward-State-Action (SARSA)-based Composite Differential Evolution (DE) Algorithm | Hybrid Machine Learning-Supported and Metaheuristic | Mid-Term and Short-Term | Yes | SARSA-Based Composite DE—Reduced energy and battery degradation costs, optimized renewable resource usage. Compared against Q-Learning and various DE-based methods. |
| [64] (2023) | MT, PV, WT, BESS; Both Grid-Connected and Standalone; Large Scale; AC; N/A; N/A | Minimizing operating costs and imbalance costs by penalizing power shortages and surpluses caused by renewable generation variability. | No | Data-Driven Robust Optimization Approach | Robust Optimization (RO) | Mid-Term and Short-Term | Yes | Data-Driven Robust Optimization—Reduced operational costs by 28% (MG1), 21% (MG2), and 19% (MG3). Compared against Traditional polyhedral set-based RO models. |
| [65] (2024) | BESS, FC, Natural Gas Storage (NGS), CHP Units; Both Grid-Connected and Standalone; Small Scale; AC; Iran (Zabol, Tabriz, Urmia); Continental | Minimizing the operational cost, including generation and reserve costs of MTs, ESS operation costs, and total trading payments. A two-stage RO model ensures feasibility against uncertainties by optimizing day-ahead scheduling and real-time adjustments, minimizing imbalance costs from renewable generation variations. | No | RO Techniques | RO | Mid-Term and Short-Term | Yes | RO—Achieved 67.54% reduction in load decrease, improved network performance from 15.48% to 69.85%, and enhanced recovery speed (61.59%). |
| [66] (2024) | PV, WT, BESS; Grid-Connected; Medium Scale; DC; India, Bhubaneswar; Tropical | Minimizing total operational costs, including EM of PV, wind, and batteries, maintenance expenses, and penalties for maintaining battery SOC within 20%-80%, while maximizing power availability to meet active and reactive power demands. | Yes | Modified MPC with Firefly Algorithm (FA) | Hybrid Model-Based and Metaheuristic Optimization | Short-Term | Yes | MPC + FA—Improved voltage stability, optimized active/reactive power, and reduced operational costs. Compared against Proportional-Integral PSO, Active Disturbance Rejection Control, and standard MPC variants. |
| [18] (2024) | PV, WT, BESS; Both Grid-Connected and Standalone; Small Scale; Hybrid AC/DC; Malaysia, Johor Bahru; Tropical | Maximizing reliability, minimize total costs, and reduce unutilized surplus power. | Yes | Iterative Pareto-Fuzzy (IPF) Method | Fuzzy Logic-Based | Mid-Term | Yes | IPF—Achieved a total cost of $5.12M, minimized surplus power to 201,364.45 kW, and ensured high reliability (>90% Index of Independence, >77% Reliability Test Efficiency). Compared against NSGA-II, Modified PSO, and GWO. |
| [46] (2024) | PV Plant, WT Farm, DG, BESS; Grid-Connected; Large Scale; DC; Egypt, Greater Cairo; Tropical | Minimizing operational costs by reducing total daily expenses, including grid electricity purchases, energy sales, battery operations, and diesel generator costs, while also minimizing deviations from target load profiles. | No | Honey Badger Algorithm (HBA) | Metaheuristic | Mid-Term | Yes | HBA—Achieving 4.56% cost reduction, and 2.3% savings in real-time operations under uncertainties. Comparison focused on real-time performance vs. theoretical optimal cost under perfect foresight. |
| [67] (2024) | WT, PV, BESS, Plug-in (EVs); Both Grid-Connected and Standalone; Medium Scale; N/A; N/A | Minimizing energy loss costs over 24 h, power purchase costs from the upstream grid, load curtailment costs, diesel DG operation costs, and battery and EV operational expenses. | No | Column and Constraints Generation (C&CG) | RO | Mid-Term | Yes | C&CG—Minimized total costs (86,978 vs. 93,936 for GA and 91,326 for PSO), reduced energy purchases and PV curtailment, and optimized peak charge. Compared against GA and PSO. |
| [68] (2024) | BESS, WT, PV; Grid-Connected; Small Scale; N/A; N/A | Minimizing the cost of energy trading for MGs, including buying, selling, and transportation costs. | No | Stochastic Dual Dynamic Programming (SDDP) | Stochastic | Mid-Term | Yes | SDDP—Improved MG EM efficiency, achieving cost reductions and optimizing decisions under uncertainty. Compared against Deterministic Equivalent Model (DEM). |
| [69] (2025) | DG, FC, WT, PV; Grid-Connected; N/A; Hybrid Ac/DC; Northwestern China; Dry | Minimization of economic dispatch cost. | No | Large-Scale Solvers like CONOPT and GUROBI | Deterministic | Mid-Term | No | Model of MGs to achieve a fully convex. Computational time reduction using the model III. |
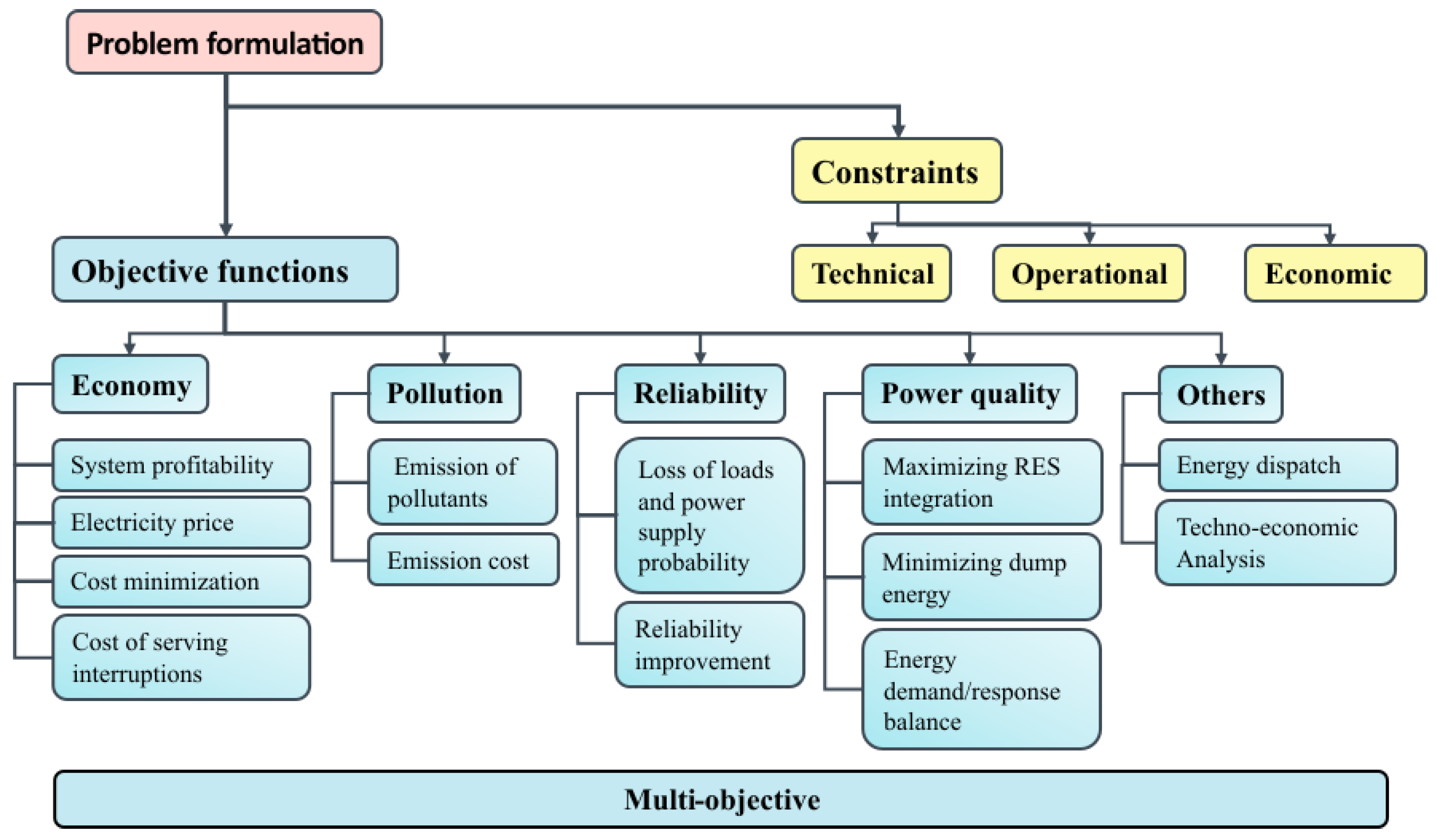
4.1. Problem Formulation
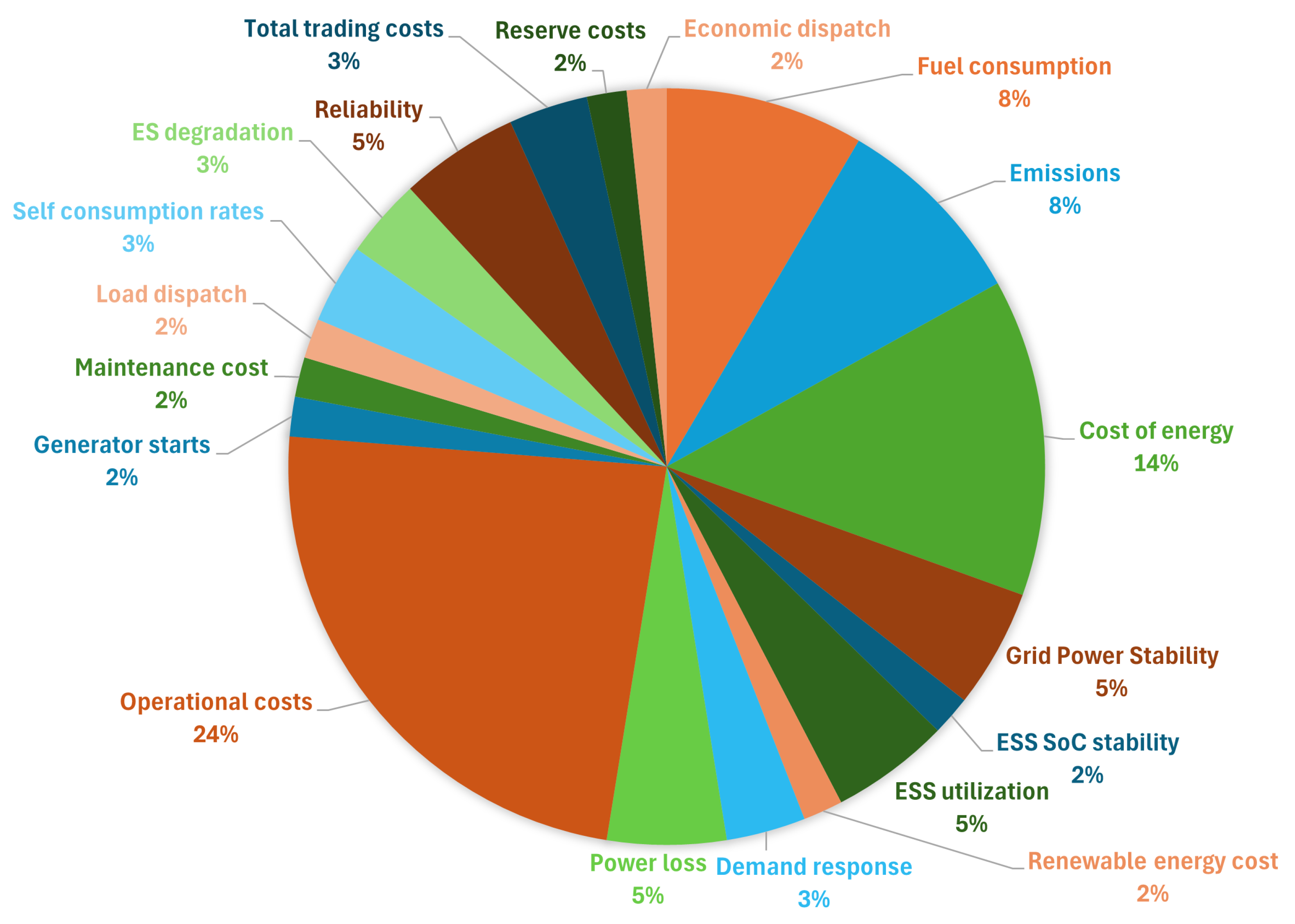
4.1.1. Optimization Objectives
4.1.2. Constraints
4.2. Time Frame
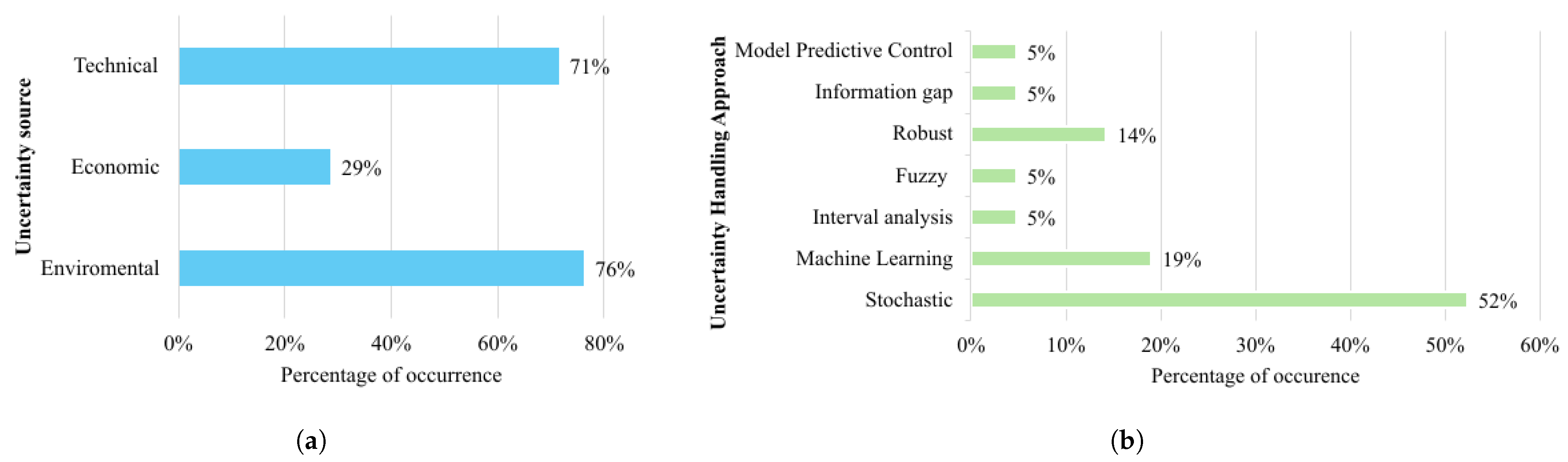
4.3. Uncertainty
4.3.1. Sources of Uncertainty
4.3.2. Handling Uncertainty
- Stochastic modeling: models uncertainty in renewable energy generation, demand fluctuations, and pricing. Techniques include Monte Carlo simulations, probability distribution models, and scenario-based optimization [18,64,68]. It enables the analysis of a spectrum of potential future scenarios by employing probability functions [27].
- Fuzzy Logic Optimization: this technique confronts imprecise and linguistically defined uncertainties, mirroring human-like reasoning [31]. It handles imprecise and ambiguous data (e.g., user energy behavior and uncertain weather conditions). Methods such as fuzzy clustering and fuzzy rule-based models provide greater flexibility in EMS decision-making [27,49].
- Robust Optimization: ensures EMS remains feasible under worst-case deviations, particularly for fuel prices, demand spikes, and battery degradation [65,81]. This method defines an uncertainty set and seeks solutions that are resilient to all possible scenarios within that set, offering a degree of guaranteed performance [27].
- Model Predictive Control: it is a real-time control technique that optimizes energy dispatch and system operation by continuously adjusting decisions based on short-term forecasts. MPC is particularly effective in battery management, demand response, and optimizing hybrid energy systems, where it adapts to fluctuations in generation and consumption [27].
- Interval Analysis: a technique that models uncertainty by defining upper and lower bounds for unknown parameters rather than assuming a probability distribution [31]. It is useful when data are incomplete or lack precise statistical properties, ensuring that optimization accounts for all possible values within a given range [23].
- Information Gap Decision Theory: applied in extreme uncertainty scenarios where probability distributions are unknown, ensuring that solutions remain robust even with limited information [31], such as in [46,67]. This approach addresses uncertainty by starting with a predicted value for each uncertain parameter [31]. It then explores how much these parameters can deviate from the predicted value without causing the system to fail [31]. It also aids decision-makers by identifying the maximum uncertainty range within which the system remains reliable [27].
- Machine Learning Approaches: improve forecasting accuracy for energy demand, renewable generation, and real-time EMS control. This technique enables more responsive handling of uncertainties in EMS operation by identifying patterns in historical data [27]. Examples include reinforcement learning for ESS optimization [62] and deep learning for load forecasting [82].
4.4. Optimization Methods
5. Discussion and Future Trends
5.1. Discussion and Key Points
- The use of hybrid models incorporating multiple energy resources, such as PV and WT, besides ESS, emphasizes the versatility and complexity of modern optimization EMS. The studies show advancements in balancing various components, optimizing battery use, and enhancing overall system efficiency.
- This review analyzes various optimization EMS, covering essential aspects like objective functions, constraints, optimization techniques, uncertainty, and time frame. It emphasizes how EMS can enhance system efficiency, reliability, and cost-effectiveness while addressing challenges like renewable energy intermittency.
- There are notable contributions regarding the economic benefits of optimized EMS. Optimized EMS can significantly reduce dependence on fossil fuels by minimizing operational costs and maximizing renewable energy utilization, thereby promoting financial sustainability.
- The necessity of MOO is emphasized for effectively handling conflicting objectives, such as balancing cost reduction with environmental sustainability. This approach helps avoid biases in decision-making, allowing the EMS to consider multiple goals comprehensively, which enhances overall system performance.
- Various strategies are explored in the literature for managing conflicts and uncertainties, including robust optimization techniques that consider worst-case scenarios, ML for improved forecasting, and stochastic programming, which incorporates randomness into decision-making. These more complete techniques could better handle the objectives with better-informed decisions regarding the objectives of the MG.
- Various optimization EMS, including metaheuristic algorithms, machine learning, robust and deterministic optimization, have been explored. This diversity aims to achieve optimal solutions under different operational conditions, ensuring MGs can flexibly adapt to changing situations.
- The review concludes that it is essential to select the appropriate EMS carefully to ensure stable and reliable operations within MG systems. Tailoring the EMS to the specific requirements of the MG facilitates better integration of RESs, enhances operational reliability, and improves overall system performance.
5.2. Research Gaps and Future Trend
- A critical limitation highlighted in the analysis is the lack of validation for optimization EMS under different weather scenarios and real data. RES power production is closely linked to weather, thus seasonal patterns, making incorporating regional uncertainties and seasonal validation essential. Future research must focus on validations to assess the efficacy of optimization strategies across seasonal conditions and real data.
- The analysis of limitations reveals a significant challenge concerning data scarcity and clarity, as shown in Table 4, where most were not mentioned. Many studies depend on historical data that may not adequately represent future scenarios or unusual events. Improved data collection is necessary to enhance the EMS validation, create optimization results that match real-world conditions or account for uncertainties.
- Adaptive EMS is essential to ensure reliable MG performance, especially given the global impacts of climate change, the variability of renewable energy sources, and the seasonal differences in weather. Future research should focus on validating the performance of EMS in different climate zones, seasons and under failure conditions.
- Many current studies focus on mid-term time frames without addressing short- and long-term strategies. This creates a gap when applying EMS strategies to other operational needs. Future research should expand to include exploring sizing, real-time applications, power quality, and other EMS aspects, ensuring that optimization strategies extend beyond scheduling.
- The analysis indicates that many optimization EMS may not fully account for the dynamic nature of user behavior and technological evolutions. As energy consumption patterns change, particularly with the rise of EV integration and smart technologies, EMS must adapt accordingly.
- Some methods, while ensuring accuracy, introduce complexity that may limit their practical application. For example, stochastic, robust, and MPC approaches are often difficult to implement [91]. Future efforts should focus on validating these methods in real-world scenarios and comparing optimization strategies to ensure alignment with MG performance under realistic conditions.
- Dynamic Pricing models, such as the one proposed in [92], promote local energy use in MGs and reduce grid dependence. EMS must incorporate dynamic pricing as energy markets move toward this model. This integration remains an underexplored area in current research.
- Future research should also consider the impact of regulatory frameworks, such as grid interconnection policies, tariff structures, and government subsidies, on the deployment and operation of MGs. Without supportive government policies, renewable energy-based MG projects can struggle to be implemented, particularly in remote or developing regions, where upfront costs and logistical challenges often arise. These considerations are especially important in studies focused on system sizing and energy pricing, where regulatory constraints and incentives can influence design and economic outcomes.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- International Energy Agency. Electricity 2025. Available online: https://www.iea.org/reports/electricity-2025 (accessed on 14 May 2025).
- Regulator, C.E. Canada’s Energy Futures 2021 Fact Sheet: Overview. 2021. Available online: https://publications.gc.ca/collections/collection_2021/one-neb/NE2-12-2021-eng.pdf (accessed on 15 May 2025).
- IEEE Std 2030.7-2017; IEEE Standard for the Specification of Microgrid Controllers. IEEE: Piscataway, NJ, USA, 2018; pp. 1–43. [CrossRef]
- Allwyn, R.G.; Al-Hinai, A.; Margaret, V. A comprehensive review on energy management strategy of microgrids. Energy Rep. 2023, 9, 5565–5591. [Google Scholar] [CrossRef]
- Joshi, A.; Capezza, S.; Alhaji, A.; Chow, M.Y. Survey on AI and machine learning techniques for microgrid energy management systems. IEEE/CAA J. Autom. Sin. 2023, 10, 1513–1529. [Google Scholar] [CrossRef]
- Alghamdi, A.S. Microgrid energy management and scheduling utilizing energy storage and exchange incorporating improved gradient-based optimizer. J. Energy Storage 2024, 97, 112775. [Google Scholar] [CrossRef]
- Rong, H.; Wang, J.; Kuang, H. A two-stage, four-layer robust optimisation model for distributed cooperation in multi-microgrids. IET Energy Syst. Integr. 2024, 6, 406–420. [Google Scholar] [CrossRef]
- He, W.; Wu, X.; Li, X.; He, M.; Cao, B.; Wang, X. Low-carbon economic operation of multi-energy microgrid based on multi-level robust optimisation. IET Energy Syst. Integr. 2024, 6, 606–621. [Google Scholar] [CrossRef]
- Chakraborty, A.; Ray, S. Multi-objective energy management using a smart charging technique of a microgrid with the charging impact of plug-in hybrid electric vehicles. Sustain. Cities Soc. 2024, 117, 105923. [Google Scholar] [CrossRef]
- Gholampour, K.; Adabi, J.; Gholinezhad, H.; Inegbedion, O. Optimal hierarchical energy management system with plug-and-play capability for neighborhood home microgrids. IEEE Trans. Ind. Electron. 2024, 71, 9067–9076. [Google Scholar] [CrossRef]
- Moradi Nezhad, S.; Saghafi, H.; Delshad, M.; Sadeghi, R. Nonparametric correlative-probabilistic microgrid power energy management based sine-cosine algorithm. IEEE Access 2021, 9, 156323–156336. [Google Scholar] [CrossRef]
- Liu, C.; Abdulkareem, S.S.; Rezvani, A.; Samad, S.; Aljojo, N.; Foong, L.K.; Nishihara, K. Stochastic scheduling of a renewable-based microgrid in the presence of electric vehicles using modified harmony search algorithm with control policies. Sustain. Cities Soc. 2020, 59, 102183. [Google Scholar] [CrossRef]
- Xu, Q.; Zhao, T.; Xu, Y.; Xu, Z.; Wang, P.; Blaabjerg, F. A distributed and robust energy management system for networked hybrid AC/DC microgrids. IEEE Trans. Smart Grid 2020, 11, 3496–3508. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Q.; Ding, J.; Shen, W.; Ma, J.; Li, G. Multiobjective particle swarm optimization for microgrids Pareto optimization dispatch. Math. Probl. Eng. 2020, 2020, 5695917. [Google Scholar] [CrossRef]
- Dey, B.; Bhattacharyya, B.; Márquez, F.P.G. A hybrid optimization-based approach to solve environment constrained economic dispatch problem on microgrid system. J. Clean. Prod. 2021, 307, 127196. [Google Scholar] [CrossRef]
- Moazeni, F.; Khazaei, J.; Pera Mendes, J.P. Maximizing energy efficiency of islanded micro water-energy nexus using co-optimization of water demand and energy consumption. Appl. Energy 2020, 266, 114863. [Google Scholar] [CrossRef]
- Ling, J.M.; Mulani, F.I. Planning and optimization of a residential microgrid utilizing renewable resources and integrated energy storage. J. Energy Storage 2024, 97, 112933. [Google Scholar] [CrossRef]
- Ibrahim, N.N.; Jamian, J.J.; Md Rasid, M. Optimal multi-objective sizing of renewable energy sources and battery energy storage systems for formation of a multi-microgrid system considering diverse load patterns. Energy 2024, 304, 131921. [Google Scholar] [CrossRef]
- Daniel, H.; Antunes, C.H.; Trovão, J.P.F.; Williams, D. Shore operations enhancement of bulk carriers based on a multi-objective sizing approach. Energy Convers. Manag. 2023, 276, 116497. [Google Scholar] [CrossRef]
- Heydari, A.; Nezhad, M.M.; Keynia, F.; Fekih, A.; Shahsavari-Pour, N.; Garcia, D.A.; Piras, G. A combined multi-objective intelligent optimization approach considering techno-economic and reliability factors for hybrid-renewable microgrid systems. J. Clean. Prod. 2023, 383, 135249. [Google Scholar] [CrossRef]
- Rajagopalan, A.; Nagarajan, K.; Montoya, O.D.; Dhanasekaran, S.; Kareem, I.A.; Perumal, A.S.; Lakshmaiya, N.; Paramasivam, P. Multi-Objective Optimal Scheduling of a Microgrid Using Oppositional Gradient-Based Grey Wolf Optimizer. Energies 2022, 15, 9024. [Google Scholar] [CrossRef]
- Meng, Q.; Hussain, S.; Luo, F.; Wang, Z.; Jin, X. An online reinforcement learning-based energy management strategy for microgrids with centralized control. IEEE Trans. Ind. Appl. 2025, 61, 1501–1510. [Google Scholar] [CrossRef]
- Nguyen-Duc, T.; Hoang-Tuan, L.; Ta-Xuan, H.; Do-Van, L.; Takano, H. A mixed-integer programming approach for unit commitment in micro-grid with incentive-based demand response and battery energy storage system. Energies 2022, 15, 7192. [Google Scholar] [CrossRef]
- Mansouri, S.; Zishan, F.; Montoya, O.D.; Azimizadeh, M.; Giral-Ramírez, D.A. Using an intelligent method for microgrid generation and operation planning while considering load uncertainty. Results Eng. 2023, 17, 100978. [Google Scholar] [CrossRef]
- Zhang, G.; Ge, Y.; Pan, X.; Zheng, Y.; Yang, Y. Hybrid robust-stochastic multi-objective optimization of combined cooling, heating, hydrogen and power-based microgrids. Energy 2023, 274, 127266. [Google Scholar] [CrossRef]
- Akter, A.; Zafir, E.I.; Dana, N.H.; Joysoyal, R.; Sarker, S.K.; Li, L.; Muyeen, S.M.; Das, S.K.; Kamwa, I. A review on microgrid optimization with meta-heuristic techniques: Scopes, trends and recommendation. Energy Strategy Rev. 2024, 51, 101298. [Google Scholar] [CrossRef]
- Cabrera-Tobar, A.; Massi Pavan, A.; Petrone, G.; Spagnuolo, G. A review of the optimization and control techniques in the presence of uncertainties for the energy management of microgrids. Energies 2022, 15, 9114. [Google Scholar] [CrossRef]
- Zeinal-Kheiri, S.; Ghassem-Zadeh, S.; Shotorbani, A.M.; Mohammadi-Ivatloo, B. Real-time energy management in a microgrid with renewable generation, energy storages, flexible loads and combined heat and power units using Lyapunov optimisation. IET Renew. Power Gener. 2020, 14, 526–538. [Google Scholar] [CrossRef]
- Canadian Climate Normals 1991–2020 Data—Climate—Environment and Climate Change Canada. 2025. Available online: https://climate.weather.gc.ca/climate_normals/results_1991_2020_e.html?searchType=stnProv&lstProvince=QC&txtCentralLatMin=0&txtCentralLatSec=0&txtCentralLongMin=0&txtCentralLongSec=0&stnID=150000000&dispBack=0 (accessed on 14 May 2025).
- Raya-Armenta, J.M.; Bazmohammadi, N.; Avina-Cervantes, J.G.; Sáez, D.; Vasquez, J.C.; Guerrero, J.M. Energy management system optimization in islanded microgrids: An overview and future trends. Renew. Sustain. Energy Rev. 2021, 149, 111327. [Google Scholar] [CrossRef]
- Abbasi, A.R.; Baleanu, D. Recent developments of energy management strategies in microgrids: An updated and comprehensive review and classification. Energy Convers. Manag. 2023, 297, 117723. [Google Scholar] [CrossRef]
- Page, M.J.; McKenzie, J.E.; Bossuyt, P.M.; Boutron, I.; Hoffmann, T.C.; Mulrow, C.D.; Shamseer, L.; Tetzlaff, J.M.; Akl, E.A.; Brennan, S.E.; et al. The PRISMA 2020 statement: An updated guideline for reporting systematic reviews. Int. J. Surg. 2021, 88, 105906. [Google Scholar] [CrossRef]
- Caballero-Peña, J.; Osma-Pinto, G.; Rey, J.M.; Nagarsheth, S.; Henao, N.; Agbossou, K. Analysis of the building occupancy estimation and prediction process: A systematic review. Energy Build. 2024, 313, 114230. [Google Scholar] [CrossRef]
- Marzbani, F.; Abdelfatah, A. Economic dispatch optimization strategies and problem formulation: A comprehensive review. Energies 2024, 17, 550. [Google Scholar] [CrossRef]
- IEEEXtreme Team. IEEEXtreme 17: Thesaurus; IEEE DataPort: Porto, Portugal, 2024. [Google Scholar] [CrossRef]
- Jamal, S.; Tan, N.M.L.; Pasupuleti, J. A review of energy management and power management systems for microgrid and nanogrid applications. Sustainability 2021, 13, 10331. [Google Scholar] [CrossRef]
- de Witt, M.; Stefánsson, H.; Valfells, Á.; Larsen, J.N. Energy resources and electricity generation in Arctic areas. Renew. Energy 2021, 169, 144–156. [Google Scholar] [CrossRef]
- Dutta, R.; Chanda, K.; Maity, R. Future of solar energy potential in a changing climate across the world: A CMIP6 multi-model ensemble analysis. Renew. Energy 2022, 188, 819–829. [Google Scholar] [CrossRef]
- Guo, K.; Liu, Y.; Cao, S.; Zhai, X.; Ji, Q. Can climate factors improve the forecasting of electricity price volatility? Evidence from Australia. Energy 2025, 315, 134332. [Google Scholar] [CrossRef]
- Gernaat, D.; De Boer, H.S.; Daioglou, V.; Yalew, S.; Müller, C.; Vuuren, D. Climate change impacts on renewable energy supply. Nat. Clim. Change 2021, 11, 119–125. [Google Scholar] [CrossRef]
- Nabil, T.; Mansour, T.M. Augmenting the performance of photovoltaic panel by decreasing its temperature using various cooling techniques. Results Eng. 2022, 15, 100564. [Google Scholar] [CrossRef]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World Map of the Köppen-Geiger climate classification updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef]
- World Bank. Climate Change Knowledge Portal. 2025. Available online: https://climateknowledgeportal.worldbank.org/ (accessed on 8 April 2024).
- Bukar, A.L.; Tan, C.W.; Yiew, L.K.; Ayop, R.; Tan, W.S. A rule-based energy management scheme for long-term optimal capacity planning of grid-independent microgrid optimized by multi-objective grasshopper optimization algorithm. Energy Convers. Manag. 2020, 221, 113161. [Google Scholar] [CrossRef]
- Azuara-Grande, L.S.; Arnaltes, S.; Alonso-Martinez, J.; Rodriguez-Amenedo, J.L. Comparison of two energy management system strategies for real-time operation of isolated hybrid microgrids. Energies 2021, 14, 6770. [Google Scholar] [CrossRef]
- Hassaballah, E.; Keshta, H.; Abdel-Latif, K.; Ali, A. A novel strategy for real-time optimal scheduling of grid-tied microgrid considering load management and uncertainties. Energy 2024, 299, 131419. [Google Scholar] [CrossRef]
- Sepehrzad, R.; Moridi, A.R.; Hassanzadeh, M.E.; Seifi, A.R. Intelligent energy management and multi-objective power distribution control in hybrid micro-grids based on the advanced fuzzy-PSO method. ISA Trans. 2021, 112, 199–213. [Google Scholar] [CrossRef] [PubMed]
- Moretti, L.; Meraldi, L.; Niccolai, A.; Manzolini, G.; Leva, S. An innovative tunable rule-based strategy for the predictive management of hybrid microgrids. Electronics 2021, 10, 1162. [Google Scholar] [CrossRef]
- Alhaider, M.M.; Ali, Z.M.; Mostafa, M.H.; Aleem, S.H.E.A. Economic viability of NaS batteries for optimal microgrid operation and hosting capacity enhancement under uncertain conditions. Sustainability 2023, 15, 15133. [Google Scholar] [CrossRef]
- Arcos-Aviles, D.; Pascual, J.; Guinjoan, F.; Marroyo, L.; Garcia-Gutierrez, G.; Gordillo-Orquera, R.; Llanos-Proano, J.; Sanchis, P.; Motoasca, T.E. An energy management system design using fuzzy logic control: Smoothing the grid power profile of a residential electro-thermal microgrid. IEEE Access 2021, 9, 25172–25188. [Google Scholar] [CrossRef]
- Hamdipoor, V.; Nguyen, H.N.; Mekhaldi, B.; Parra, J.; Badosa, J.; Obaldia, F.C. Experimental validation of scenario-based stochastic model predictive control of nanogrids. Control Eng. Pract. 2025, 157, 106249. [Google Scholar] [CrossRef]
- Wang, R.; Xu, T.; Xu, H.; Gao, G.; Zhang, Y.; Zhu, K. Robust multi-objective load dispatch in microgrid involving unstable renewable generation. Int. J. Electr. Power Energy Syst. 2023, 148, 108991. [Google Scholar] [CrossRef]
- May Alvarez, J.A.; Zurbriggen, I.G.; Paz, F.; Ordonez, M. Microgrids multiobjective design optimization for critical loads. IEEE Trans. Smart Grid 2023, 14, 17–28. [Google Scholar] [CrossRef]
- Esparza, A.; Blondin, M.; Trovão, J.P. Sensitivity Analysis of Battery Degradation Concerning Control Parameters of a Hybrid Nanogrid. In Proceedings of the IECON 2024—50th Annual Conference of the IEEE Industrial Electronics Society, Chicago, IL, USA, 3–6 November 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Vermeer, W.; Chandra Mouli, G.R.; Bauer, P. A comprehensive review on the characteristics and modeling of lithium-ion battery aging. IEEE Trans. Transp. Electrif. 2022, 8, 2205–2232. [Google Scholar] [CrossRef]
- Downie, J.; Stubbs, W. Corporate carbon ctrategies and greenhouse gas emission assessments: The implications of scope 3 emission factor selection. Bus. Strategy Environ. 2012, 21, 412–422. [Google Scholar] [CrossRef]
- Zhou, A.; Yang, M.; Wu, T.; Yang, L. Distributionally robust energy management for islanded microgrids with variable moment information: An MISOCP approach. IEEE Trans. Smart Grid 2023, 14, 3668–3680. [Google Scholar] [CrossRef]
- Trivedi, R.; Patra, S.; Khadem, S. A data-driven short-term PV generation and load forecasting approach for microgrid applications. IEEE J. Emerg. Sel. Top. Ind. Electron. 2022, 3, 911–919. [Google Scholar] [CrossRef]
- Kumar, R.P.; Karthikeyan, G. A multi-objective optimization solution for distributed generation energy management in microgrids with hybrid energy sources and battery storage system. J. Energy Storage 2024, 75, 109702. [Google Scholar] [CrossRef]
- Hein, K.; Xu, Y.; Gary, W.; Gupta, A.K. Robustly coordinated operational scheduling of a grid-connected seaport microgrid under uncertainties. IET Gener. Transm. Distrib. 2020, 15, 347–358. [Google Scholar] [CrossRef]
- Pravin, P.; Luo, Z.; Li, L.; Wang, X. Learning-based scheduling of industrial hybrid renewable energy systems. Comput. Chem. Eng. 2022, 159, 107665. [Google Scholar] [CrossRef]
- Gassi, K.B.; Baysal, M. Improving real-time energy decision-making model with an actor-critic agent in modern microgrids with energy storage devices. Energy 2023, 263, 126105. [Google Scholar] [CrossRef]
- Mughees, N.; Jaffery, M.H.; Mughees, A.; Ansari, E.A.; Mughees, A. Reinforcement learning-based composite differential evolution for integrated demand response scheme in industrial microgrids. Appl. Energy 2023, 342, 121150. [Google Scholar] [CrossRef]
- Mohseni, S.; Pishvaee, M.S.; Dashti, R. Privacy-preserving energy trading management in networked microgrids via data-driven robust optimization assisted by machine learning. Sustain. Energy Grids Netw. 2023, 34, 101011. [Google Scholar] [CrossRef]
- Ahrari, M.; Shirini, K.; Gharehveran, S.S.; Ahsaee, M.G.; Haidari, S.; Anvari, P. A security-constrained robust optimization for energy management of active distribution networks with presence of energy storage and demand flexibility. J. Energy Storage 2024, 84, 111024. [Google Scholar] [CrossRef]
- Anjaiah, K.; Dash, P.; Bisoi, R.; Dhar, S.; Mishra, S. A new approach for active and reactive power management in renewable based hybrid microgrid considering storage devices. Appl. Energy 2024, 367, 123429. [Google Scholar] [CrossRef]
- Hematian, H.; Askari, M.T.; Ahmadi, M.A.; Sameemoqadam, M.; Nik, M.B. Robust optimization for microgrid management with compensator, EV, storage, demand response, and renewable integration. IEEE Access 2024, 12, 73413–73425. [Google Scholar] [CrossRef]
- Tabares, A.; Cortés, P. Using stochastic dual dynamic programming to solve the multi-stage energy management problem in microgrids. Energies 2024, 17, 2628. [Google Scholar] [CrossRef]
- Liang, Z.; Chung, C.Y.; Zhang, W.; Wang, Q.; Lin, W.; Wang, C. Enabling high-efficiency economic dispatch of hybrid AC/DC networked microgrids: Steady-state convex bi-directional converter models. IEEE Trans. Smart Grid 2025, 16, 45–61. [Google Scholar] [CrossRef]
- Ghiasi, M.; Niknam, T.; Dehghani, M.; Siano, P.; Alhelou, H.H.; Al-Hinai, A. Optimal multi-operation energy management in smart microgrids in the presence of ress based on multi-objective improved de algorithm: Cost-emission based optimization. Appl. Sci. 2021, 11, 3661. [Google Scholar] [CrossRef]
- Hai, T.; Singh, N.S.S.; Jamal, F. Energy management of a microgrid with integration of renewable energy sources considering energy storage systems with electricity price. J. Energy Storage 2025, 110, 115191. [Google Scholar] [CrossRef]
- Yu, J.; Li, T.; Pan, J. Optimizing hydrogen-integrated Micro-CHP systems with demand response for sustainable energy management. J. Build. Eng. 2025, 99, 111625. [Google Scholar] [CrossRef]
- Miettinen, K. Nonlinear Multiobjective Optimization, 1st ed.; Springer: New York, NY, USA, 1998; p. 78. [Google Scholar] [CrossRef]
- Bai, Q.; Labi, S.; Sinha, K.C. Trade-Off Analysis for Multiobjective Optimization in Transportation Asset Management by Generating Pareto Frontiers Using Extreme Points Nondominated Sorting Genetic Algorithm II. J. Transp. Eng. 2012, 138, 798–808. [Google Scholar] [CrossRef]
- Hwang Goh, H.; Shi, S.; Liang, X.; Zhang, D.; Dai, W.; Liu, H.; Yuong Wong, S.; Agustiono Kurniawan, T.; Chen Goh, K.; Leei Cham, C. Optimal energy scheduling of grid-connected microgrids with demand side response considering uncertainty. Appl. Energy 2022, 327, 120094. [Google Scholar] [CrossRef]
- Aguila-Leon, J.; Vargas-Salgado, C.; Chiñas-Palacios, C.; Díaz-Bello, D. Energy management model for a standalone hybrid microgrid through a particle Swarm optimization and artificial neural networks approach. Energy Convers. Manag. 2022, 267, 115920. [Google Scholar] [CrossRef]
- Alamo, D.H.; Medina, R.N.; Ruano, S.D.; García, S.S.; Moustris, K.P.; Kavadias, K.K.; Zafirakis, D.; Tzanes, G.; Zafeiraki, E.; Spyropoulos, G.; et al. An advanced forecasting system for the optimum energy management of island microgrids. Energy Procedia 2019, 159, 111–116. [Google Scholar] [CrossRef]
- Antoniadou-Plytaria, K.E.; Eriksson, L.; Johansson, J.; Johnsson, R.C.B.; Kötz, L.; Lamm, J.; Lundblad, E.; Steen, D.; Tuan, L.A.; Carlson, O. Effect of short-term and high-resolution load forecasting errors on microgrid operation costs. In Proceedings of the 2022 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe), Novi Sad, Serbia, 10–12 October 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Pourbehzadi, M.; Niknam, T.; Aghaei, J.; Mokryani, G.; Shafie-khah, M.; Catalão, J.P. Optimal operation of hybrid AC/DC microgrids under uncertainty of renewable energy resources: A comprehensive review. Int. J. Electr. Power Energy Syst. 2019, 109, 139–159. [Google Scholar] [CrossRef]
- Ma, G.; Li, J.; Zhang, X.P. A review on optimal energy management of multimicrogrid system considering uncertainties. IEEE Access 2022, 10, 77081–77098. [Google Scholar] [CrossRef]
- Zhou, K.; Fei, Z.; Hu, R. Hybrid robust decentralized optimization of emission-aware multi-energy microgrids considering multiple uncertainties. Energy 2023, 265, 126405. [Google Scholar] [CrossRef]
- Aybar-Mejía, M.; Villanueva, J.; Mariano-Hernández, D.; Santos, F.; Molina-García, A. A review of low-voltage renewable microgrids: Generation forecasting and demand-side management strategies. Electronics 2021, 10, 2093. [Google Scholar] [CrossRef]
- Nazari-Heris, M.; Mohammadi-Ivatloo, B.; Gharehpetian, G. A comprehensive review of heuristic optimization algorithms for optimal combined heat and power dispatch from economic and environmental perspectives. Renew. Sustain. Energy Rev. 2018, 81, 2128–2143. [Google Scholar] [CrossRef]
- Zhu, H.; Wang, Y.; Wang, K.; Chen, Y. Particle Swarm Optimization (PSO) for the constrained portfolio optimization problem. Expert Syst. Appl. 2011, 38, 10161–10169. [Google Scholar] [CrossRef]
- Floudas, C.; Lin, X. Mixed integer linear programming in process scheduling: Modeling, algorithms, and applications. Ann. Oper. Res. 2005, 139, 131–162. [Google Scholar] [CrossRef]
- Eddy, S.R. What is dynamic programming? Nat. Biotechnol. 2004, 22, 909–910. [Google Scholar] [CrossRef]
- Jafari, M.; Malekjamshidi, Z.; Zhu, J.; Khooban, M.H. A novel predictive fuzzy logic-based energy management system for grid-connected and off-grid operation of residential smart microgrids. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 1391–1404. [Google Scholar] [CrossRef]
- Fayyazi, M.; Sardar, P.; Thomas, S.I.; Daghigh, R.; Jamali, A.; Esch, T.; Kemper, H.; Langari, R.; Khayyam, H. Artificial intelligence/machine learning in energy management systems, control, and optimization of hydrogen fuel cell vehicles. Sustainability 2023, 15, 5249. [Google Scholar] [CrossRef]
- Jeyaraj, T.; Ponnusamy, A.; Selvaraj, D. Hybrid renewable energy systems stability analysis through future advancement technique: A review. Appl. Energy 2025, 383, 125355. [Google Scholar] [CrossRef]
- Elmouatamid, A.; Ouladsine, R.; Bakhouya, M.; Kamoun, N.E.; Khaidar, M.; Zine-Dine, K. Review of control and energy management approaches in micro-grid systems. Energies 2021, 14, 168. [Google Scholar] [CrossRef]
- Meliani, M.; Barkany, A.E.; Abbassi, I.E.; Darcherif, A.M.; Mahmoudi, M. Energy management in the smart grid: State-of-the-art and future trends. Int. J. Eng. Bus. Manag. 2021, 13, 184797902110329. [Google Scholar] [CrossRef]
- Boiarkin, V.; Rajarajan, M.; Al-Zaili, J.; Asif, W. A novel dynamic pricing model for a microgrid of prosumers with photovoltaic systems. Appl. Energy 2023, 342, 121148. [Google Scholar] [CrossRef]

| Objective Function | Description | Ref. |
|---|---|---|
| Conventional Distributed Energy Resources (CDERs)—DGs and MTs | ||
| Minimization of Fuel Consumption | Reducing dependency on fossil fuel generators to improve efficiency and sustainability. | [21,23,44,45,48,59,60] |
| Minimization of Generator Cycling | Reducing startup/shutdown cycles to extend generator lifespan and enhance operational efficiency. | [21,23,59,60] |
| Minimization of Emissions | Reducing greenhouse gas emissions, and integrating cleaner energy alternatives. | [15,21,23,24,59,60,70] |
| RES—PV and WT | ||
| Maximization of Renewable Energy Utilization | Increasing self-consumption of solar, wind, and hybrid renewable energy to reduce reliance on fossil fuels. | [21,23,49,57,59,66,67] |
| Mitigation of Renewable Intermittency | Smoothing power output variability from renewable sources to enhance grid stability. | [49,50,52,64,65,71] |
| ESS—Batteries, Hydrogen, and Supercapacitors | ||
| Optimization of Battery SOC and Charging Strategies | Managing SOC to maximize battery efficiency and lifespan. | [21,22,23,49,51,60,63,65,66,68] |
| Minimization of Battery Degradation | Reducing degradation by optimizing Depth of Discharge (DOD) and charge-discharge cycles. | [10,21,23,47,49,63,66] |
| Battery System Resilience | Ensuring energy storage readiness in emergencies or blackouts. | [49,65] |
| Optimization of Hydrogen Storage and Utilization | Enhancing hydrogen efficiency for energy storage and demand response integration. | [72] |
| Grid Interaction and Demand-Side Management | ||
| Reduction of Grid Energy Costs | Optimizing electricity purchases to minimize dependency on external energy sources. | [21,23,49,51,59,61,62,68,71,72] |
| Demand-Side Management | Implementing load shifting, demand response, and real-time energy balancing strategies, including emission-aware dispatching. | [21,23,49,52,59,65,66,71,72] |
| Enhancement of Energy Trading Mechanisms | Optimizing market participation, MG energy trading, and vehicle-to-grid (V2G) strategies. | [49,65,68,71] |
| System Reliability and Energy Balance | ||
| Minimization of LPSP | Ensuring reliable power supply and reducing the probability of outages. | [20,44] |
| Enhancement of Grid Resilience | Improving system reliability through advanced grid control and autonomous operation. | [18,20,21,23,49,53] |
| Power Flow and Stability Optimization | Ensuring stable voltage and frequency regulation across MG operations. | [21,23,49,50,59,64,65,66,71] |
| Constraint | CDERS | RES | ESS | Load | System | Ref. |
|---|---|---|---|---|---|---|
| Power Balance | X | [20,21,23,24,45,49,51,57,59,61,65,67,68,75] | ||||
| SOC and DOD Limits | X | [20,45,47,48,49,50,51,62,63,67,68,76] | ||||
| Charging and Discharging Constraints | X | [21,23,46,49,57,59,60,65,68,71] | ||||
| Generation Power Limits | X | X | [22,23,44,45,47,48,49,52,57,60,63,64,67] | |||
| Spinning Reserve Requirements | X | [45,48] | ||||
| Capacity Constraints | X | X | X | [18,20,21,22,24,59,65,67,68,71,76] | ||
| Grid Power Trade Limits | X | [51,67,68,71] | ||||
| Renewable Energy Fraction | X | [20,44] | ||||
| Voltage Limits | X | [18,47,49,65,67,71] | ||||
| Load-Demand/Flow Constraints | X | [18,46,59,66,76] | ||||
| Energy-Balance Constraints | X | X | [22,62,63] | |||
| Power-Flow Constraints | X | [61,66,71] | ||||
| Demand-Response Constraints | X | [23,57] | ||||
| Ramp-Rate Constraints | X | X | [21,57,60,61] | |||
| System-Imbalance Constraints | X | X | [64] | |||
| Thermal-Demand Constraints | X | [62,63] | ||||
| Budget and Investment Limits | X | [53] | ||||
| Power-Availability Constraints | X | [53] | ||||
| Curtailment Constraints | X | [45] | ||||
| Converter Limits | X | [53] | ||||
| Energy-Demand Constraints | X | [62,63] | ||||
| Energy-Flow Constraints | X | [62,63] | ||||
| Power Supply | X | [44,67] |
| Ref. | Purpose/Source of Uncertainties | Method Category | Method | Data Source |
|---|---|---|---|---|
| [50] | Renewable power generation and load demand | Stochastic | Numerical Weather Prediction Model | MeteoGalicia THREDDS Server and Public University of Navarre dataset |
| [76] | Optimize demand response and hydrogen utilization under fluctuating renewable energy conditions | Machine Learning | Artificial Neural Network (ANN)-Based Load and Renewable Energy Forecasting | Historical operational data from the LabDER experimental MG |
| [51] | Quantify the effect of PV generation and load uncertainties on the performance of stochastic model predictive control | Stochastic | Scenario Generation with Stochastic Optimization | Historical PV and load profiles from NRLab (2016–2020) |
| [72] | To capture the uncertainty associated with prices, RES yields, and energy demand, a random model is employed | Stochastic | Random Model with Normal Distribution | Simulated renewable energy variability and demand fluctuations |
| [71] | Models various factors, including the number of plug-in electric vehicles, their arrival and departure times, prediction errors in hourly load and pricing, and power output variations from wind turbines and photovoltaic systems | Stochastic | Unscented Transform | N/A |
| [22] | Forecast EV charging demand and renewable generation variability for optimal scheduling | Stochastic | Monte Carlo Simulation | Predicted EV charging load and renewable energy forecast |
| [23] | The uncertainty of the load and renewable energy sources. Ensure power balance under uncertain demand and generation conditions | Interval Analysis | Standard Deviation Estimation with Spinning Reserve Adjustment | Synthetic data |
| [52] | The volatile nature of renewable energy generation | Stochastic | Probability Distribution Model | Solar Radiation Intensity Data from NREL, User Load Statistics Data |
| [49] | Modelling the volatility in market prices, RESs output, and electrical load using stochastic optimization techniques | Fuzzy | Fuzzy Clustering Method | N/A |
| [53] | Ambient Conditions Uncertainty and Load Uncertainty | Stochastic | Markov Chain and Degradation Models | Statistical Field Data |
| [57] | Manage uncertainties primarily related to both power generation and demand within the energy | Robust | Moment-Based Distributionally Robust Optimization | N/A |
| [61] | Determine the optimal schedule of the energy mix | Machine Learning | PPO | Weather Databases (Meteorological, from 12 September 2013 to 18 September 2013) |
| [62] | Energy storage charging and discharging decisions within an MG under specific constraints | Machine Learning | Reinforcement Learning | Open Energy Information Datasets, U.S. Department of Energy |
| [63] | Wind and solar power generation and the buying/selling costs of electrical and thermal energy | Machine Learning | SARSA Algorithm | Synthetic Data |
| [64] | Extracting probability distribution information in the uncertainty data of renewable generation | Stochastic | Robust Kernel Density Estimation (RKDE) | Synthetic Data |
| [65] | Addressing uncertainties that arise during planning processes | Robust | Robust Optimization Techniques | Synthetic Data |
| [66] | Uncertainty in PV irradiance, wind speed, and load variations | Stochastic | Modified MPC | Laboratory Data |
| [18] | Renewable energy uncertainty modeled using Gaussian noise for solar irradiance and Weibull noise for wind speed | Stochastic | Gaussian and Weibull Noise Models | Synthetic Data |
| [46] | Uncertainty in solar irradiance, wind speed, and grid tariff; actual demand load uncertainty up to 20% | Information Gap Decision Theory | Consideration of Forecasted Errors | N/A |
| [67] | Accounts for uncertainty in load demand, renewable generation, and influencing factors in optimization constraints | Robust | Robust Optimization Technique | N/A |
| [68] | Stochastic models for energy pricing and Stochastic representations of energy generation and demand | Stochastic | Monte Carlo Simulation | N/A |
| Method | Pros | Cons | MG Applications |
|---|---|---|---|
| Metaheuristic Optimization |
|
|
|
| Deterministic Optimization |
|
|
|
| Machine Learning-Supported Optimization |
|
|
|
| Stochastic Optimization |
|
| |
| Robust Optimization |
|
|
|
| Ref. | Contribution | Limitations/Future Work |
|---|---|---|
| [44] | Develops a mathematical model for a hybrid PV-WT-Diesel-Battery MG with a rule-based EMS using queuing theory. Applies a nature-inspired optimization algorithm for capacity planning, outperforming PSO and Crow Search Algorithm. Demonstrates environmental and economic benefits over diesel generators and assesses system resilience to future uncertainties. | Enhances EMS with MG pooling and harmonic mitigation. Incorporates uncertainty analysis like robust programming and Monte Carlo simulations. Explores hydrogen storage, Direct DC MG feasibility, and advanced optimization algorithms to improve renewable energy system performance and resilience. |
| [50] | Develops an EMS framework using two 25-rule FLC to smooth power fluctuations in a residential electro-thermal MG. One optimizes grid power exchange; the other manages demand-side response. One-year simulations with real data validate superior power smoothing using quantified smoothing indexes. | Enhances online optimization for EMS with advanced FLC to improve power smoothing while managing complexity. Integrates economic variables to assess tariff policy impacts. Addresses long-term historical consumption data availability for more accurate demand-side management. |
| [45] | Compares rule-based Priority EMS and optimization-based Optimal EMS for isolated hybrid MGs. Optimal EMS enhances BESS utilization, boosts renewable penetration, and cuts diesel use, while Priority EMS provides a simpler, more robust solution with lower computational demands. | Analyzes forecasting errors that may impact the advantage of Optimal EMS over Priority EMS. Enhances real-time decision-making to improve EMS performance under uncertainties. |
| [47] | Proposes an intelligent EMS combining FLC and PSO to improve power distribution and voltage stability in hybrid AC/DC MGs. Optimizes battery usage, reduces maintenance costs, and prevents battery life degradation through PSO. | Refines forecasting accuracy, integrates economic factors into optimization, and assesses scalability under various grid configurations. Includes battery performance analysis and compares the proposed EMS against alternative strategies for enhanced evaluation. |
| [76] | Develops a self-adaptive EMS with cascade ANN optimized by PSO to improve decision-making in standalone hybrid MGs, enhancing forecasting accuracy and system efficiency. | Expands the model to incorporate more energy generation and storage subsystems, enhances ANN training with additional experimental data, and integrates an automated control system for improved efficiency. |
| [48] | Introduces a TRBH EMS for hybrid MGs, enhancing rule-based scheduling with predictive capabilities to achieve near-optimal performance comparable to MILP. | Evaluates TRBH adoption in real systems, extends comparisons with predictive methods, addresses forecast uncertainty, and implements stochastic training with scenario-based evaluation for improved performance. |
| [51] | Develops a two-layer scenario-based stochastic MPC for real-time EM of nanogrids, integrating an Alternating Direction Method of Multipliers (ADMM) to reduce the computational burden. | Extends to islanded nanogrids with programmable loads, integrates diverse energy sources like wind turbines and distributed generators, and explores advanced EM methods, including learning-based and state-of-the-art approaches. |
| [72] | Enhances energy generation and consumption by integrating fuel cells, hydrogen fueling stations, and multi-energy storage. Uses multi-objective optimization with the SSA to manage renewable uncertainties, balance electrical and thermal systems, and optimize load shifting through demand response, ensuring energy transitions, resilience, and adaptability. | Limited to a single MG configuration, restricting broader applicability. Future work explores scalability, integrates emerging technologies, and includes life cycle assessments for hydrogen production. |
| [71] | Develops a management system for multiple renewable sources and plug-in EVs for short-term MG scheduling. Optimized with the Modified Marine Predators Algorithm, it minimizes total network costs, addressing energy shortages, reliability, and power supply interactions with the main grid. | Integrating demand response, improving forecast reliability. |
| [59] | Introduces GJO for energy storage scheduling in MG management, overcoming computational inefficiencies of PSO, TS, and ABC. It ensures faster convergence, improved efficiency, and lower operational costs, validated through case studies with hybrid energy sources and BESSs. | Implements the multi-objective optimization in a real-world MG, integrating hybrid energy and battery storage systems, monitoring performance, and refining the model for validation. |
| [20] | Presents a multi-objective optimization for hybrid renewable MGs, balancing techno-economic and reliability goals. Combines the Taguchi method, moth flame optimization, and fuzzy decision-making to minimize costs and power losses while maximizing renewable energy utilization. | Enhances wind model accuracy in optimization by exploring Weibull and least squares models, improving precision over the cubic model used in this study. |
| [21] | Proposes the OGGWO for multi-objective optimal scheduling in grid-connected MGs, balancing operational cost reduction and emissions minimization. | Improves uncertainty modeling, compares with additional optimization techniques, and extends the approach to various MG configurations for broader applicability. |
| [22] | Proposes an online reinforcement learning-based EMS using the SARSA algorithm to optimize MG operation under uncertainty, reducing energy storage operation costs and improving power tracking efficiency. | Expands the approach to larger MG networks and evaluates its performance by comparing it with other reinforcement learning techniques. |
| [23] | Develops an advanced MG model incorporating an incentive-based demand response program and a Vanadium Redox Battery for optimal scheduling. Uses MILP to optimize scheduling and evaluates its impact on battery operation, comparing performance with case studies using a genetic algorithm. | Integrates a hybrid battery model combining VRB with lithium-ion or absorbed glass mat batteries to enhance performance and flexibility in MG energy storage. |
| [24] | Proposes a Salp Swarm Algorithm for optimal MG operation, handling in generation, load, and pricing uncertainties. It minimizes generation and emission costs for grid-connected and standalone modes, solving a mixed-integer optimization problem. | Requires accounting for real-world complexities beyond tested variables and investigating further optimization techniques. |
| [60] | Develops a coordinated scheduling method for seaport MGs, integrating renewable energy with the main grid. It uses Adaptive Robust Optimization and time-shiftable load scheduling to minimize operational costs, emissions, and uncertainties across multiple timescales while ensuring distribution network constraints. | Future improvements include incorporating multi-energy carriers (heating and cooling) and analyzing electricity pricing schemes on seaport operations. |
| [52] | Proposes a robust multi-objective Load Dispatch Model using DRL to handle uncertainties in renewable generation. | Incorporating ESSs (batteries or EVs) for controlled charging/discharging can mitigate fluctuations but introduces investment costs and complexity, warranting further research. |
| [49] | Introduces a Two-Stage Optimization Approach for MG performance and hosting capacity by optimizing BESS sizing and placement under uncertainty. | Future work suggests hybridizing BESS instead of relying solely on sodium-sulfur batteries. |
| [53] | Proposes a Vectorial Microgrid Optimization (VMO) method integrating power architecture selection and sizing for flexibility and performance. Uses Graph Theory and Stochastic models to automate MG architecture selection. | Limited reliance on initial performance metrics and environmental variability. Future work suggests extending VMO with additional renewable sources and adaptive strategies. |
| [57] | Develops a Distributionally Robust Joint Chance-Constrained Energy Management Model for standalone MGs. Uses a Moment-Based Ambiguity Set and Bonferroni Approximation for reduced conservativeness, leading to a SOCP formulation. | Future improvements include integrating additional operational constraints (voltage and power loss), exploring tractable reformulations for time-dependent scenarios, and alternative ambiguity sets for robustness. |
| [61] | Uses an RL approach with PPO to enhance energy dispatch in hybrid renewable energy systems, achieving a 32.8% cost reduction and 28.5% decrease in carbon emissions. | Enhancing scheduling by integrating sequential neural networks and off-policy learning methods, eliminating reliance on model simulators. |
| [62] | Integrates RL with Myopic Optimization for MG energy management, optimizing electrical, cooling, and heating power-flow decisions without relying on forecasting. | Model performance constrained by learning episodes and agent action space, requiring high computational resources. Future research to address limitations before deployment. |
| [63] | Introduces an Industrial Demand Response program for Industrial Multi-Energy MGs, optimizing power and heat supply while maximizing renewable energy utilization. | Future work includes expanding the IDR framework by integrating additional renewable sources and considering real-time market fluctuations. |
| [64] | Develops a Data-Driven Peer-to-Peer Trading Mechanism for networked MGs using Nash Bargaining Theory and robust optimization. Introduces RKDE for improved data reliability and employs ADMM and Augmented Lagrangian-Based Alternating Direction Inexact Newton (ALADIN) for computational efficiency. | Future improvements include MT Startup/Shutdown Integration, addressing privacy concerns in ALADIN, and shifting from single-machine to parallel computing for performance analysis. |
| [65] | Enhances Distribution Network Security by modeling severe incidents with a Security Measurement Index, utilizing distributed generation resources, storage, and demand management. Implements MG partitioning for power exchange and robust optimization to address uncertainties. | Future research will focus on advanced optimization techniques (ML, Power-to-Gas Units, EV Charging Integration, and Standardized Resilience Metrics). |
| [66] | Proposes an Energy Management Approach for hybrid MGs, minimizing power loss and maximizing generation. The Multi-MPC-Improved Firefly Algorithm (IFA) strategy combines MPC with improved IFA) for power regulation. | Future work will improve Hybrid Microgrid (HMG) control via Fault Management Integration (FMI), EV Charging/V2G Optimization, and adaptive methods like ML and DRL. |
| [18] | Introduces a Spectral Clustering Algorithm improving clustering via the Silhouette Coefficient. Proposes a multi-objective Sizing Framework for RESs and BESSs) using the IPF technique. | Future work to test scalability on larger Active Distribution Networks beyond IEEE 33-bus systems to address real-world applicability. |
| [46] | Proposes a Two-Level Energy Management Strategy for grid-connected MGs integrating Demand-Side Management for day-ahead scheduling and real-time rescheduling based on demand, weather, and tariff fluctuations. Uses a Hybrid Bat Algorithm for enhanced efficiency. | Enhancing model with additional renewable sources, testing under different climatic conditions, and incorporating advanced predictive algorithms. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Esparza, A.; Blondin, M.; Trovão, J.P.F. A Review of Optimization Strategies for Energy Management in Microgrids. Energies 2025, 18, 3245. https://doi.org/10.3390/en18133245
Esparza A, Blondin M, Trovão JPF. A Review of Optimization Strategies for Energy Management in Microgrids. Energies. 2025; 18(13):3245. https://doi.org/10.3390/en18133245
Chicago/Turabian StyleEsparza, Astrid, Maude Blondin, and João Pedro F. Trovão. 2025. "A Review of Optimization Strategies for Energy Management in Microgrids" Energies 18, no. 13: 3245. https://doi.org/10.3390/en18133245
APA StyleEsparza, A., Blondin, M., & Trovão, J. P. F. (2025). A Review of Optimization Strategies for Energy Management in Microgrids. Energies, 18(13), 3245. https://doi.org/10.3390/en18133245






