A Real Options Model for CCUS Investment: CO2 Hydrogenation to Methanol in a Chinese Integrated Refining–Chemical Plant
Abstract
1. Introduction
2. Literature Review
3. Problem Formulation and Model Establishment
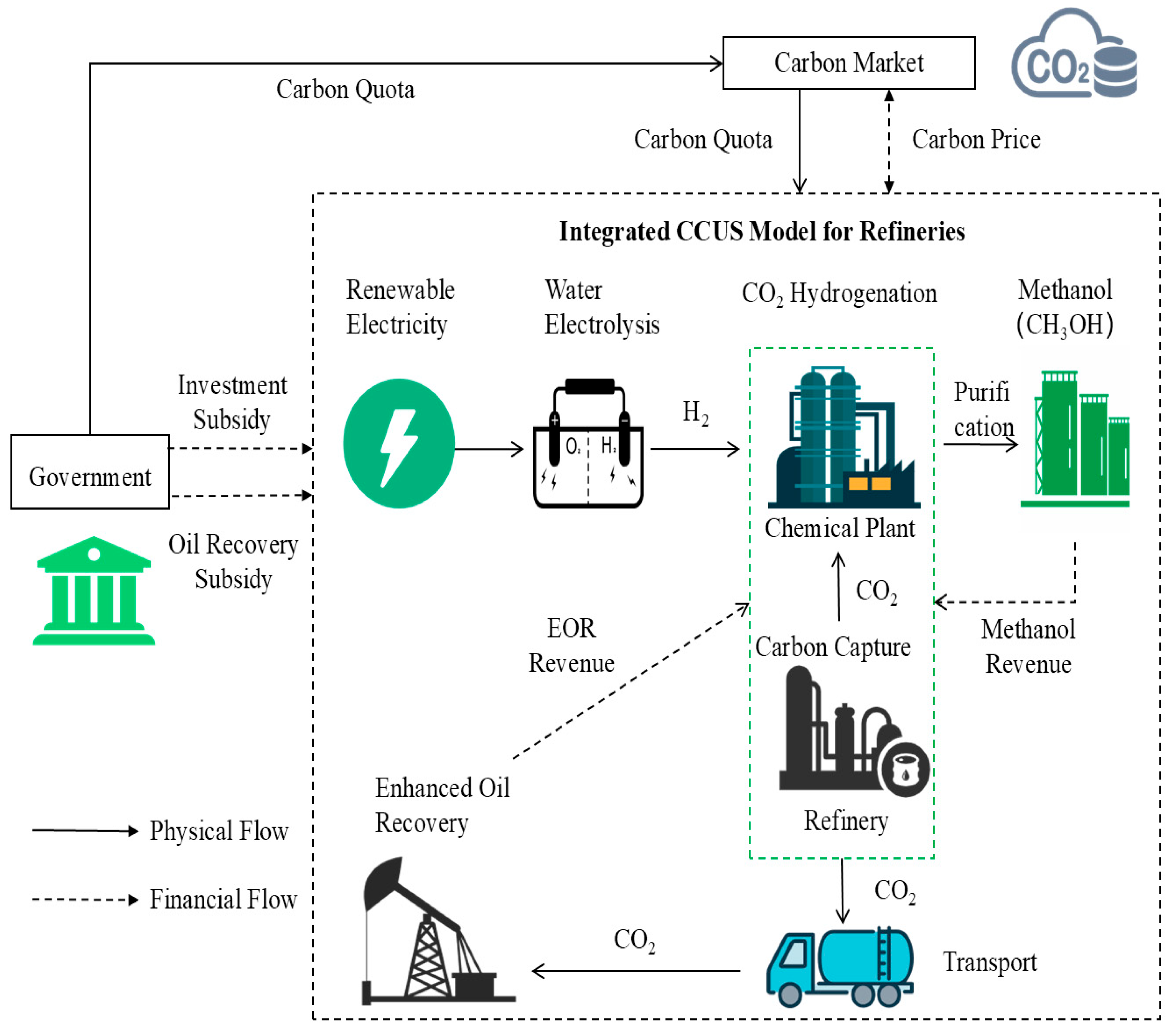
3.1. Description of Issue
3.2. Theoretical Assumptions
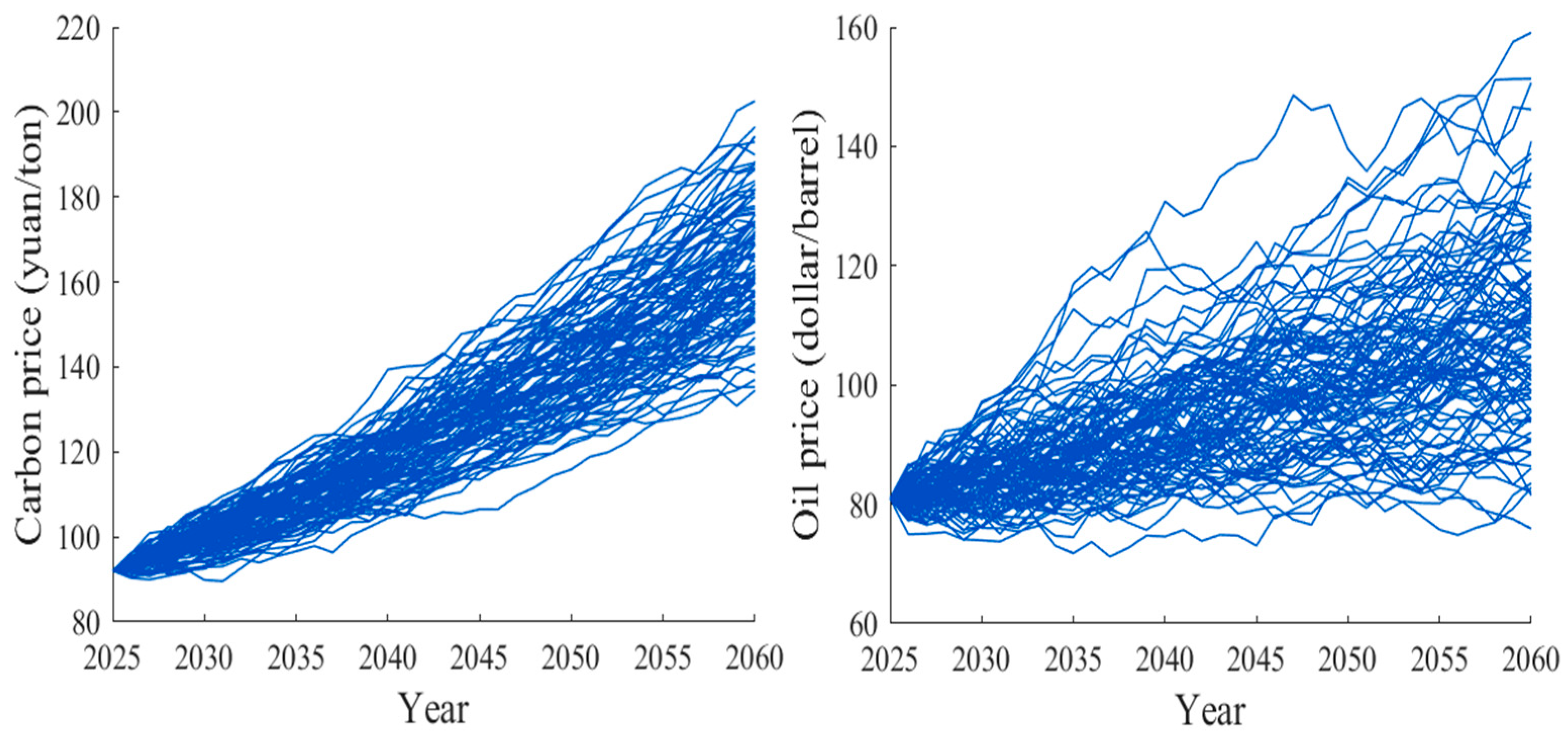
3.2.1. Carbon Price
3.2.2. Oil Price
3.2.3. Equipment Investment and Operating Costs
3.2.4. Assumptions on Project Lifespan and Investment Period
3.3. Model Framework
3.3.1. Investment Return Model
3.3.2. Investment Decision Model
4. Model Solution
4.1. Solution Method
4.2. Solution Process
5. Case Analysis
5.1. Model Parameters
5.2. Calculation Results
5.3. Sensitivity Analysis
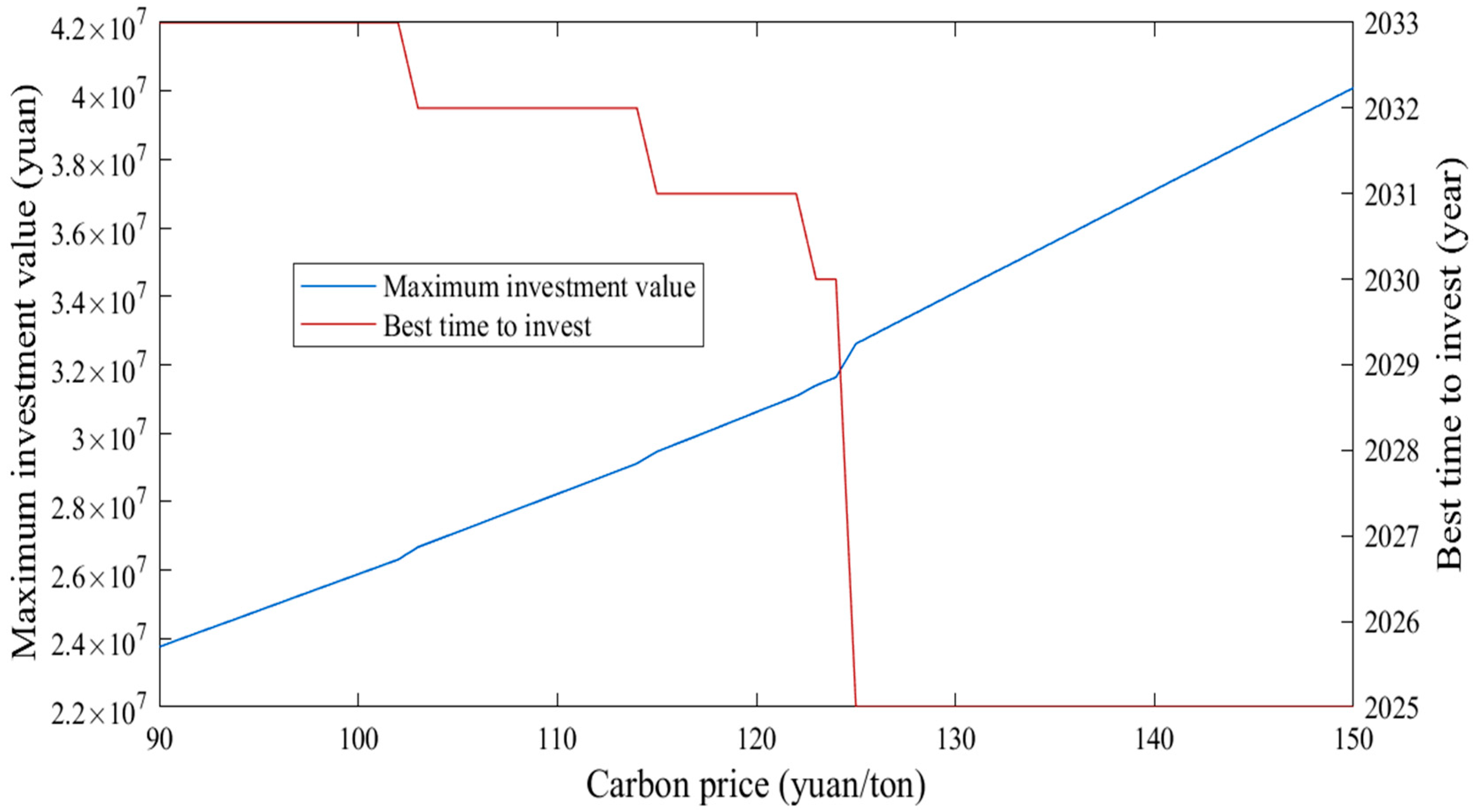
5.3.1. Sensitivity of Carbon Price
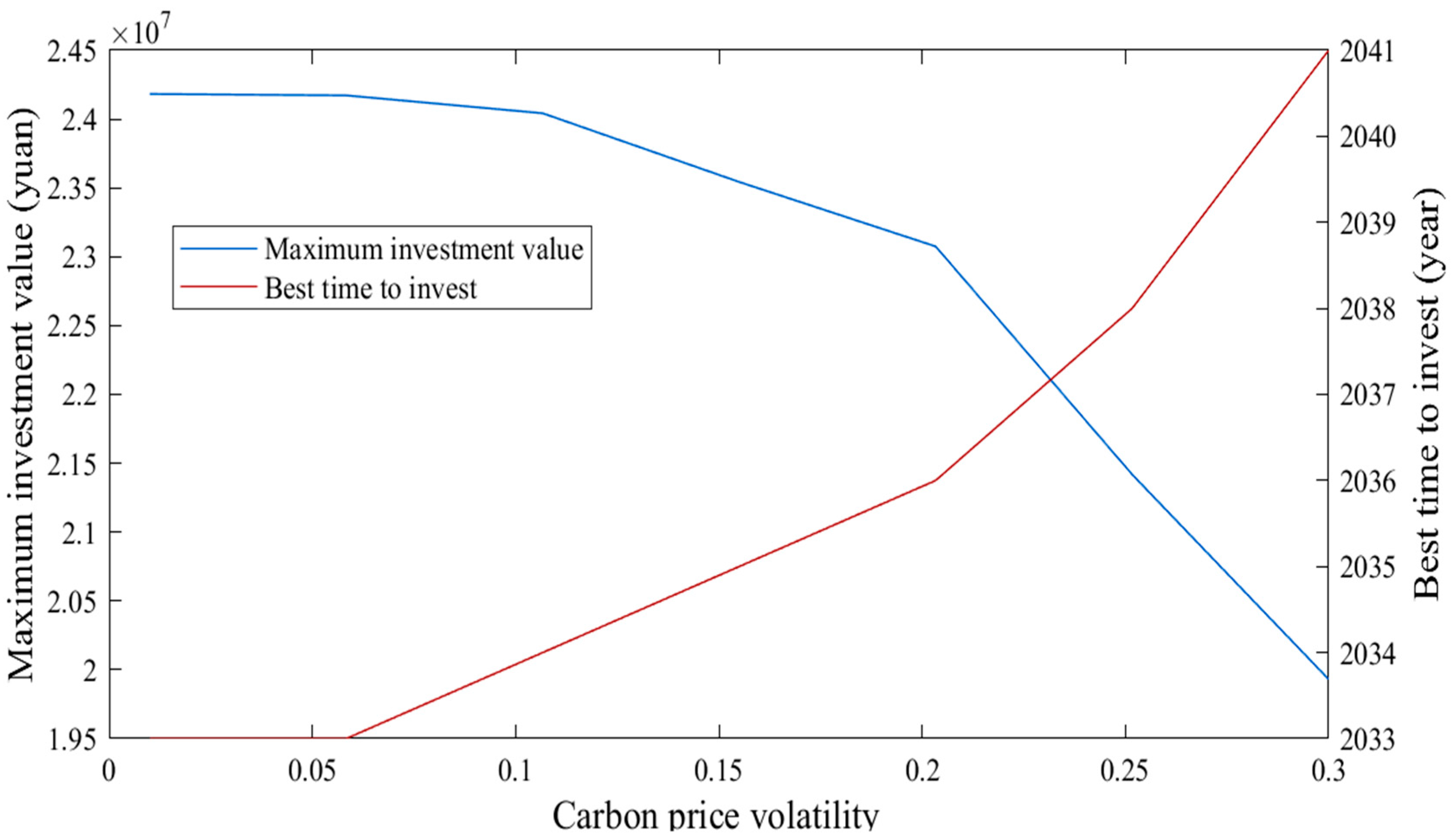
5.3.2. Sensitivity of Carbon Price Volatility
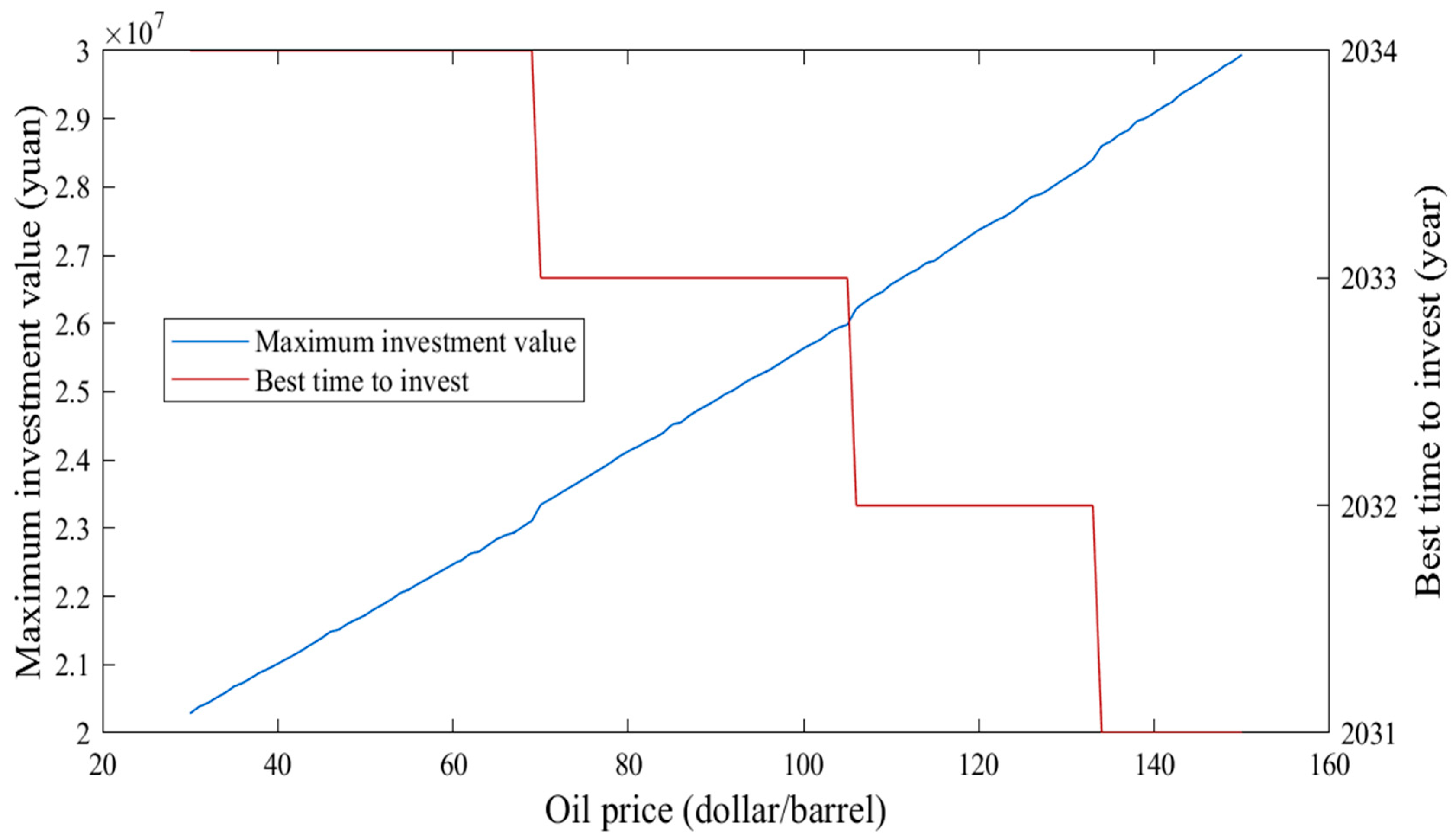
5.3.3. Sensitivity of Oil Price Levels
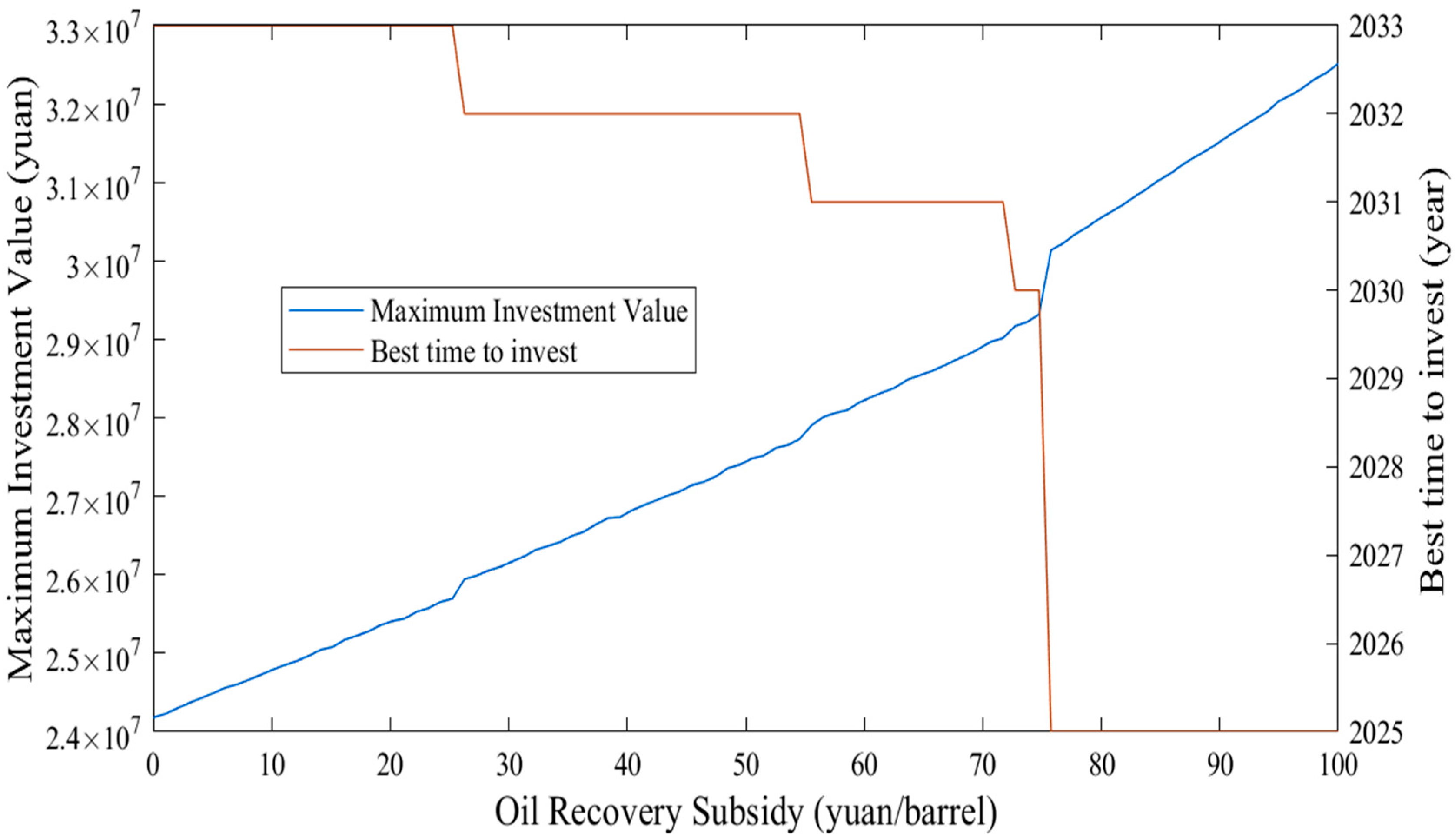
5.3.4. Sensitivity of EOR Subsidies
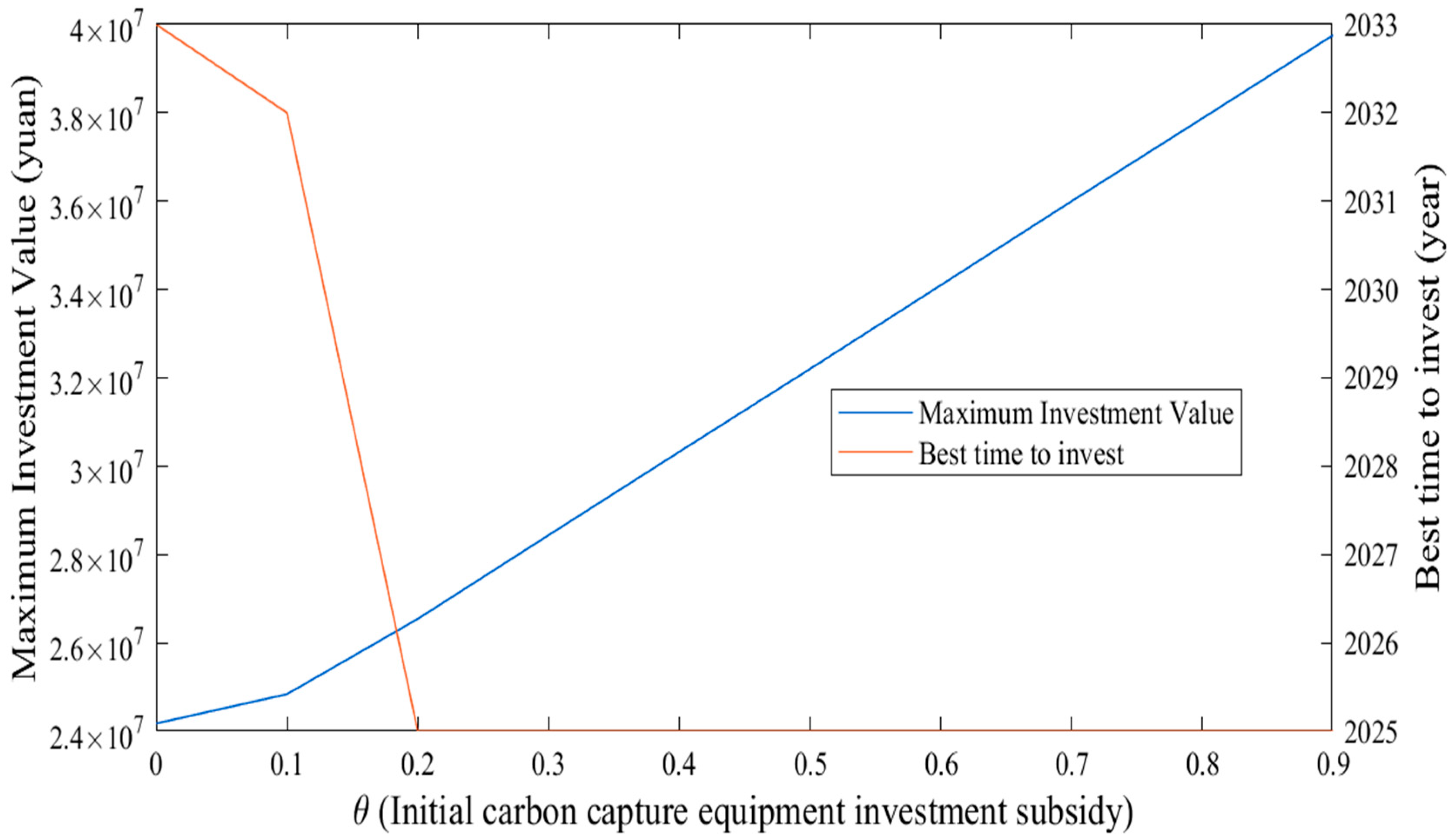
5.3.5. Sensitivity of Equipment Investment Subsidy Coefficient
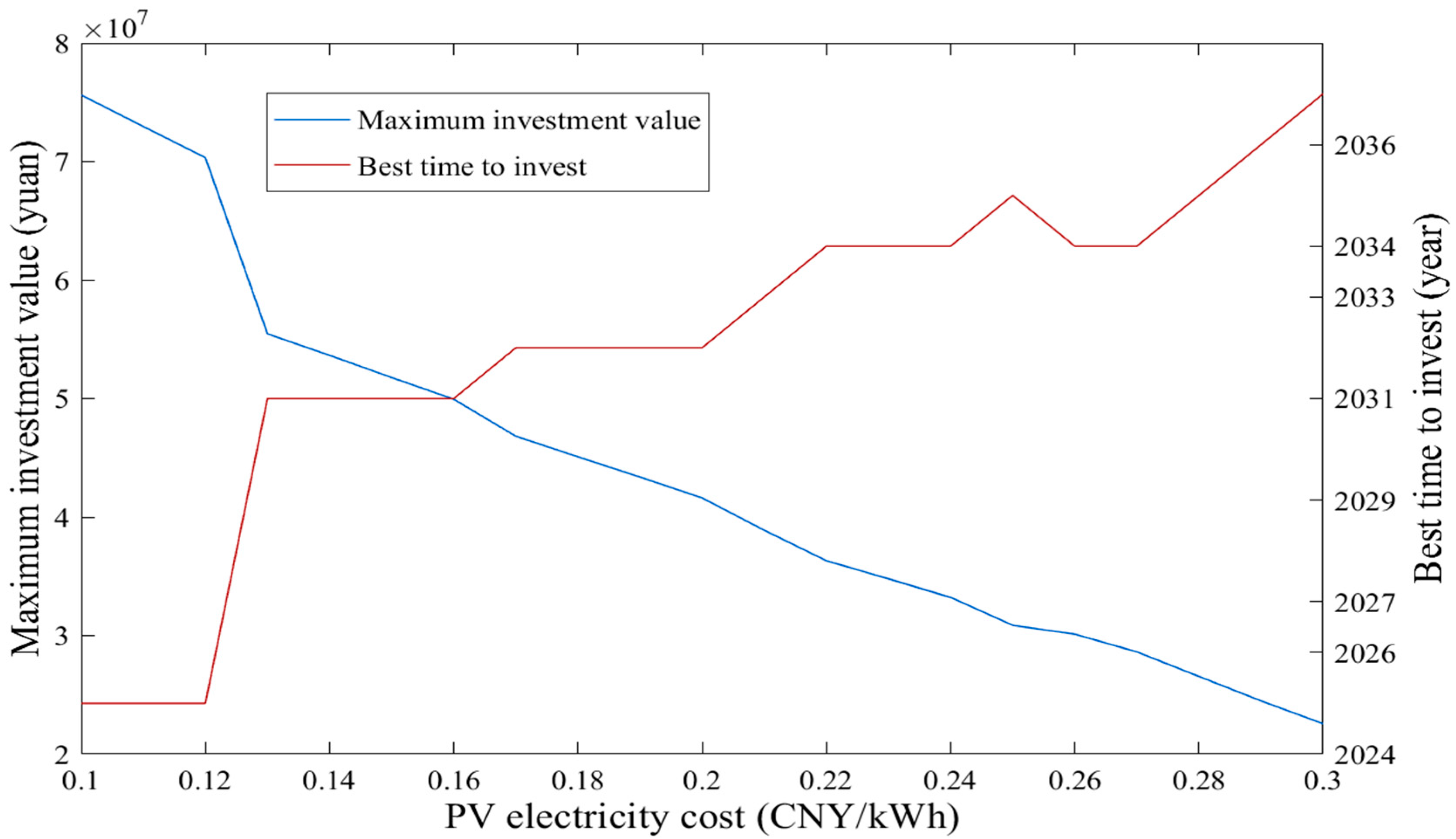
5.3.6. Sensitivity of Photovoltaic Levelized Electricity Cost Coefficient
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hill, L.B.; Li, X.; Wei, N. CO2-EOR in China: A comparative review. Int. J. Greenh. Gas Control 2020, 103, 103173. [Google Scholar] [CrossRef]
- Metz, B.; Davidson, O.; de Coninck, H.; Loos, M.; Meyer, L. IPCC Special Report on Carbon Dioxide Capture and Storage; Intergovernmental Panel on Climate Change: Geneva, Switzerland, 2005. Available online: https://www.osti.gov/biblio/20740954 (accessed on 25 April 2025).
- Qin, J.; Han, H.; Liu, X. Application and enlightenment of carbon dioxide flooding in the United States of America. Pet. Explor. Dev. 2015, 42, 232–240. [Google Scholar] [CrossRef]
- International Energy Agency. CCUS Projects Database; IEA: Paris, France, 2024; Available online: https://www.iea.org/data-and-statistics/data-product/ccus-projects-database (accessed on 25 April 2025).
- International Energy Agency. Net Zero by 2050: A Roadmap for the Global Energy Sector; IEA: Paris, France, 2023; Available online: https://www.iea.org/reports/net-zero-by-2050 (accessed on 25 April 2025).
- Zhang, X.; Yang, X.; Lu, X.; Chen, J.; Cheng, J.; Diao, Y.; Fan, J.; Gao, L.; Gao, S.; Han, L.; et al. China Carbon Capture, Utilization, and Storage (CCUS) Annual Report 2023; The Administrative Centre for China’s Agenda 21: Beijing, China, 2023; Available online: https://file.jgvogel.cn/124/upload/resources/file/421008.pdf (accessed on 25 April 2025).
- Da, H.; Xu, D.; Li, J.; Tang, Z.; Li, J.; Wang, C.; Luan, H.; Zhang, F.; Zeng, Y. Influencing factors of carbon emission from typical refining units: Identification, analysis, and mitigation potential. Energies 2023, 16, 6527. [Google Scholar] [CrossRef]
- Ma, S.; Lei, T.; Meng, J.; Liang, X.; Guan, D. Global oil refining’s contribution to greenhouse gas emissions from 2000 to 2021. Innovation 2023, 4, 100361. [Google Scholar] [CrossRef]
- Liang, B.; Chen, C.; Jia, C.; Wang, C.; Wang, X.; Zha, Y.; Wang, R.; Meng, Z.; Wang, H. Carbon capture, utilization and storage (CCUS) in oil and gas reservoirs in China: Status, opportunities and challenges. Fuel 2024, 375, 132353. [Google Scholar] [CrossRef]
- Qiao, Y.; Liu, W.; Guo, R.; Sun, S.; Zhang, S.; Bailey, J.J.; Fang, M.; Wu, C. Techno-economic analysis of integrated carbon capture and utilisation compared with carbon capture and utilisation with syngas production. Fuel 2023, 332, 125972. [Google Scholar] [CrossRef]
- Zang, G.; Sun, P.; Elgowainy, A.; Wang, M. Technoeconomic and life cycle analysis of synthetic methanol production from hydrogen and industrial byproduct CO2. Environ. Sci. Technol. 2021, 55, 5248–5257. [Google Scholar] [CrossRef] [PubMed]
- Sollai, S.; Porcu, A.; Tola, V.; Ferrara, F.; Pettinau, A. Renewable methanol production from green hydrogen and captured CO2: A techno-economic assessment. J. CO2 Util. 2023, 68, 102345. [Google Scholar] [CrossRef]
- 2024 China Green Methanol Industry Overview: Trillion-Level Clean Energy Track Driven by Dual-Carbon Strategy, Outlook for Explosive Growth in the Industrial Chain (Executive Summary). Available online: https://pdf.dfcfw.com/pdf/H3_AP202504251662297519_1.pdf?1745611283000.pdf (accessed on 21 May 2025).
- Wu, N.; Parsons, J.E.; Polenske, K.R. The impact of future carbon prices on CCS investment for power generation in China. Energy Policy 2013, 54, 160–172. [Google Scholar] [CrossRef]
- Sekar, R.C.; Parsons, J.E.; Herzog, H.J.; Jacoby, H.D. Future Carbon Regulations and Current Investments in Alternative Coal-Fired Power Plant Designs; MIT Joint Program on the Science and Policy of Global Change: Cambridge, MA, USA, 2005; Available online: https://dspace.mit.edu/handle/1721.1/30594 (accessed on 25 April 2025).
- Bohm, M.C.; Herzog, H.J.; Parsons, J.E.; Sekar, R.C. Capture-ready coal plants–Options, technologies and economics. Int. J. Greenh. Gas Control 2007, 1, 113–120. [Google Scholar] [CrossRef]
- Rubin, E.S.; Chen, C.; Rao, A.B. Cost and performance of fossil fuel power plants with CO2 capture and storage. Energy Policy 2007, 35, 4444–4454. [Google Scholar] [CrossRef]
- Zhai, H.; Ou, Y.; Rubin, E.S. Opportunities for decarbonizing existing U.S. coal-fired power plants via CO2 capture, utilization and storage. Environ. Sci. Technol. 2015, 49, 7571–7579. [Google Scholar] [CrossRef]
- Liang, X.; Reiner, D.; Gibbins, J.; Li, J. Assessing the value of CO2 capture ready in new-build pulverised coal-fired power plants in China. Int. J. Greenh. Gas Control 2009, 3, 787–792. [Google Scholar] [CrossRef]
- Dahowski, R.T.; Davidson, C.L.; Li, X.C.; Wei, N. A $70/tCO2 greenhouse gas mitigation backstop for China’s industrial and electric power sectors: Insights from a comprehensive CCS cost curve. Int. J. Greenh. Gas Control 2012, 11, 73–85. [Google Scholar] [CrossRef]
- Wang, X.; Cai, Y.; Dai, C. Evaluating China’s biomass power production investment based on a policy benefit real options model. Energy 2014, 73, 751–761. [Google Scholar] [CrossRef]
- Fan, Y.; Mo, J.-L.; Zhu, L. Evaluating coal bed methane investment in China based on a real options model. Resour. Policy 2013, 38, 50–59. [Google Scholar] [CrossRef]
- Myers, S.C. Determinants of corporate borrowing. J. Financ. Econ. 1977, 5, 147–175. [Google Scholar] [CrossRef]
- Fuss, S.; Szolgayová, J. Fuel price and technological uncertainty in a real options model for electricity planning. Appl. Energy 2010, 87, 2938–2944. [Google Scholar] [CrossRef]
- Laurikka, H. Option value of gasification technology within an emissions trading scheme. Energy Policy 2006, 34, 3916–3928. [Google Scholar] [CrossRef]
- Agaton, C.B. Application of real options in carbon capture and storage literature: Valuation techniques and research hotspots. Sci. Total Environ. 2021, 795, 148683. [Google Scholar] [CrossRef]
- Zhang, W.; Dai, C.; Luo, X.; Ou, X. Policy incentives in carbon capture utilization and storage (CCUS) investment based on real options analysis. Clean Technol. Environ. Policy 2021, 23, 1311–1326. [Google Scholar] [CrossRef]
- Fan, J.-L.; Li, Z.; Ding, Z.; Li, K.; Zhang, X. Investment decisions on carbon capture utilization and storage retrofit of Chinese coal-fired power plants based on real option and source-sink matching models. Energy Econ. 2023, 126, 106972. [Google Scholar] [CrossRef]
- Li, Z.; Yu, P.; Xian, Y.; Fan, J.-L. Investment benefit analysis of coal-to-hydrogen coupled CCS technology in China based on real option approach. Energy 2024, 294, 130293. [Google Scholar] [CrossRef]
- Wang, X.; Du, L. Study on carbon capture and storage (CCS) investment decision-making based on real options for China’s coal-fired power plants. J. Clean. Prod. 2016, 112, 4123–4131. [Google Scholar] [CrossRef]
- Geske, J.; Herold, J. Carbon capture and storage investment and management in an environment of technological and price uncertainties. SSRN Working Paper, 2010; 20 pages. [Google Scholar] [CrossRef]
- Zhu, L.; Fan, Y. A real options–based CCS investment evaluation model: Case study of China’s power generation sector. Appl. Energy 2011, 88, 4320–4333. [Google Scholar] [CrossRef]
- Zhu, L.; Fan, Y. Modelling the investment in carbon capture retrofits of pulverized coal-fired plants. Energy 2013, 57, 66–75. [Google Scholar] [CrossRef]
- Chen, H.; Wang, C.; Ye, M. An uncertainty analysis of subsidy for carbon capture and storage (CCS) retrofitting investment in China’s coal power plants using a real-options approach. J. Clean. Prod. 2016, 137, 200–212. [Google Scholar] [CrossRef]
- Chu, H.; Ran, L.; Zhang, R. Evaluating CCS investment of China by a novel real option-based model. Math. Probl. Eng. 2016, 2016, 8180674. [Google Scholar] [CrossRef]
- Yao, X.; Fan, Y.; Xu, Y.; Zhang, X.; Zhu, L.; Feng, L. Is it worth to invest?—An evaluation of CTL-CCS project in China based on real options. Energy 2019, 182, 920–931. [Google Scholar] [CrossRef]
- Yao, X.; Zhong, P.; Zhang, X.; Zhu, L. Business model design for the carbon capture utilization and storage (CCUS) project in China. Energy Policy 2018, 121, 519–533. [Google Scholar] [CrossRef]
- Jarvis, S.M.; Samsatli, S. Technologies and infrastructures underpinning future CO2 value chains: A comprehensive review and comparative analysis. Renew. Sustain. Energy Rev. 2018, 85, 46–68. [Google Scholar] [CrossRef]
- Mikhelkis, L.; Govindarajan, V. Techno-economic and partial environmental analysis of carbon capture and storage (CCS) and carbon capture, utilization, and storage (CCUS): Case study from proposed waste-fed district-heating incinerator in Sweden. Sustainability 2020, 12, 5922. [Google Scholar] [CrossRef]
- Wang, X.; Tang, R.; Meng, M.; Su, T. Research on CCUS business model and policy incentives for coal-fired power plants in China. Int. J. Greenh. Gas Control 2023, 125, 103871. [Google Scholar] [CrossRef]
- Wang, X.; Gao, Z. Research on CCUS investment decision-making in coal-fired power plants based on real options. Clean Coal Technol. 2023. Available online: http://kns.cnki.net/kcms/detail/11.3676.TD.20230816.1054.002.html (accessed on 25 April 2025).
- Cai, B.F.; Li, Q.; Zhang, X.; Cao, C.; Cao, L.; Chen, W.; Chen, Z.; Dong, J.; Fan, J.; Jiang, Y.; et al. Annual Report of China’s CO2 Capture, Utilization and Storage (CCUS) (2021)—China CCUS Path Study; Chinese Academy of Environmental Planning of the Ministry of Ecology and Environment: Beijing, China, 2021; Available online: https://www.caep.org.cn/sy/dqhj/gh/202107/W020210726513427451694.pdf (accessed on 25 April 2025).
- Yang, L.; Xu, M.; Yang, Y.; Fan, J.; Zhang, X. Comparison of subsidy schemes for carbon capture utilization and storage (CCUS) investment based on real option approach: Evidence from China. Appl. Energy 2019, 255, 113828. [Google Scholar] [CrossRef]
- Nikolova, C.; Gutierrez, T. Use of microorganisms in the recovery of oil from recalcitrant oil reservoirs: Current state of knowledge, technological advances and future perspectives. Front. Microbiol. 2020, 10, 2996. [Google Scholar] [CrossRef]
- Tan, X.; Luo, D.; Song, X. Analysis and discussion on the economics and development models of CCUS-EOR considering dual benefits of oil displacement and carbon emission reduction. Pet. Geol. Recovery Effic. 2024, 31, 70–78. [Google Scholar] [CrossRef]
- Lin, B.; Tan, Z. How much impact will low oil price and carbon trading mechanism have on the value of carbon capture utilization and storage (CCUS) project? Analysis based on real option method. J. Clean. Prod. 2021, 298, 126768. [Google Scholar] [CrossRef]
- Rubin, E.S.; Yeh, S.; Antes, M.; Berkenpas, M.; Davison, J. Use of experience curves to estimate the future cost of power plants with CO2 capture. Int. J. Greenh. Gas Control 2007, 1, 188–197. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Y. Techno-economic analysis of green methanol production processes. Mod. Chem. Ind. 2023, 43, 209–212. [Google Scholar] [CrossRef]
- Zhu, C.; Tian, D.; Zhang, H.; Qu, C.; Dong, L. Techno-economic analysis of methanol production systems via CO2 hydrogenation and electrolysis. Low-Carbon Chem. Chem. Eng. 2023, 48, 117–124. Available online: https://link.cnki.net/urlid/51.1336.TQ.20221212.1504.001 (accessed on 25 April 2025).
- Wang, Y.; Jin, Q.; Pan, F. Feasibility study on low-carbon methanol production based on green hydrogen. Mod. Chem. Ind. 2024, 44, 229–234. [Google Scholar] [CrossRef]
- Shu, B.; Fan, M.; Xiong, J. Cost estimation and prediction of green methanol production via CO2 hydrogenation. Electr. Power Technol. Environ. Prot. 2024, 40, 191–197. [Google Scholar] [CrossRef]
| Technical Route | Current Cost (CNY/ton) | Future Cost (CNY/ton) | Cost-Driving Factors | Development Potential |
|---|---|---|---|---|
| Coal-based methanol | 1800–2700 | 2700–3600 | Coal price, carbon price | Low, constrained by carbon prices |
| Gas-based methanol | 1600–3000 | 2800–3500 | Gas price, carbon price | Low, constrained by limited domestic resources and volatile global gas prices |
| Biomass-based methanol | 3800–5000 | 1900–2500 | Biomass pellet prices | Moderate, dependent on biomass pellet price reduction |
| Electricity-based methanol | 4400–4600 | 2100–2200 | Green electricity price, carbon capture cost | High, may become mainstream |
| Parameter | Unit | Value | Data Source |
|---|---|---|---|
| μc | Carbon Price Drift Rate (%) | 0.01726 | Using China’s carbon market price data (up to 2024), calculate using Formula (4) |
| σc | Carbon Price Volatility (%) | 0.01419 | |
| μ0 | Crude Oil Price Drift Rate (%) | 0.0092 | With reference to Brent crude oil prices over the past 5 years, perform calculations based on a modified version of Formula (4) |
| σ0 | Crude Oil Price Volatility (%) | 0.0252 | |
| poil | Initial Crude Oil Price (USD/barrel) | 72 | Using the 5-year average Brent crude price, converted at the 2024 USD to CNY exchange rate |
| pc | Initial Carbon Price (CNY/ton) | 92 | With reference to the average carbon price in China’s carbon market in 2024 |
| qc | Carbon Dioxide Reduction (ton) | 280,000 | |
| w1 | Carbon Dioxide Capture Rate (%) | 90 | Wang and Gao, 2025 [41] |
| w2 | Proportion of Carbon Dioxide Used for EOR (%) | 40 | |
| uc | Unit Carbon Dioxide Capture Cost (CNY/ton) | 250 | Zhang, X., Yang, X., Lu, X. et al., 2023 [6] |
| Unit Carbon Dioxide EOR Cost (CNY/ton) | 349 | ||
| ut | Unit Carbon Dioxide Transportation Cost (CNY/(ton·km)) | 1 | Cai, B. F., Li, Q., Zhang, X. et al., 2021 [42] |
| IC,0 | Initial carbon capture unit retrofit cost (CNY 10,000) | 22,644 | Yang et al., 2019 [43] |
| YC,0 | Initial operating cost for carbon capture system (10,000 CNY/year) | 377 | |
| i | The impact of technological advancements on the retrofit cost of carbon capture units | 0.021 | |
| l | The effect of technological progress on the cost of retrofitting carbon capture equipment | 0.057 | |
| py | Unit EOR incremental subsidy (CNY/barrel) | 0 | Set the parameters based on current Chinese policies |
| α | Enhanced the oil recovery rate (%) | 15 | Nikolova, C., and Gutierrez, T., 2020 [44] |
| θ | Government’s Initial Subsidy Coefficient for CCUS (%) | 0 | Set the parameters based on current Chinese policies |
| S | Transportation distance of tank trucks from the plant to the oil displacement site (kilometers) | 100 | |
| Investment period for the CCUS project (years) | 20 | Tan et al., 2024 [45]; Lin and Tan, 2021 [46] | |
| Project operational lifespan (years) | 30 | ||
| Risk-free interest rate (%) | 6 | Rubin et al., 2007 [47] | |
| qH | Hydrogen consumption for methanol production (tons) | 21,000 | This parameter is primarily based on the green methanol synthesis unit of the 100,000 tons per year Liquid Sunshine Project in Ordos, Inner Mongolia, China |
| uH | Water and electricity cost per unit of hydrogen produced via water electrolysis (CNY/ton) | 3526 | Zhang et al., 2023 [48] |
| WH | Employee welfare costs for the hydrogen production unit (10,000 CNY/year) | 1200 | |
| IH | Investment cost for the hydrogen synthesis unit (CNY 10,000) | 81,000 | Zhang et al., 2023 [48]. The hydrogen production capacity is up to 48,000 m3/h, with an annual hydrogen output of 20,000 tons. Alkaline water electrolysis equipment was selected as the primary hydrogen production technology |
| YH | Operation and maintenance costs of the hydrogen production facility (10,000 CNY/year) | 1620 | |
| qM | Methanol production volume (tons) | 110,080 | A standard commercial unit size for methanol plants |
| pM | Unit price of methanol (CNY) | 4300 | Zhu et al., 2023 [49]; the price represents a reasonable mid-term expectation and falls within the cost range of CO2 hydrogenation-based methanol production in China |
| Transportation cost per unit of methanol sold (CNY/ton) | 145 | Wang et al., 2024 [50] | |
| IM | Investment cost for the methanol synthesis unit(CNY 10,000) | 60,000 | |
| YM | Operation and maintenance costs of the methanol production facility (10,000 CNY/year) | 900 | Shu et al., 2024 [51] |
| WM | Employee welfare costs for the methanol synthesis unit (10,000 CNY/year) | 800 | 40 staff, with an annual average salary of CNY 200,000 per person |
| UM | Water and electricity costs for methanol production (10,000 CNY/year) | 11,516.8 | Power usage: 13,961 kWh/h; water usage: 435 tons/h |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, R.; Gan, X.; Bai, Y.; Feng, L. A Real Options Model for CCUS Investment: CO2 Hydrogenation to Methanol in a Chinese Integrated Refining–Chemical Plant. Energies 2025, 18, 3092. https://doi.org/10.3390/en18123092
Fang R, Gan X, Bai Y, Feng L. A Real Options Model for CCUS Investment: CO2 Hydrogenation to Methanol in a Chinese Integrated Refining–Chemical Plant. Energies. 2025; 18(12):3092. https://doi.org/10.3390/en18123092
Chicago/Turabian StyleFang, Ruirui, Xianxiang Gan, Yubing Bai, and Lianyong Feng. 2025. "A Real Options Model for CCUS Investment: CO2 Hydrogenation to Methanol in a Chinese Integrated Refining–Chemical Plant" Energies 18, no. 12: 3092. https://doi.org/10.3390/en18123092
APA StyleFang, R., Gan, X., Bai, Y., & Feng, L. (2025). A Real Options Model for CCUS Investment: CO2 Hydrogenation to Methanol in a Chinese Integrated Refining–Chemical Plant. Energies, 18(12), 3092. https://doi.org/10.3390/en18123092




