High-Precision Experimental Data for Thermal Model Validation of Flat-Plate Hybrid Water PV/T Collectors
Abstract
1. Introduction
2. Modeling and Experimental Methods
2.1. Experimental Hybrid PV/T with Monitoring System
2.1.1. Technological Description of the Used PV/T Collector
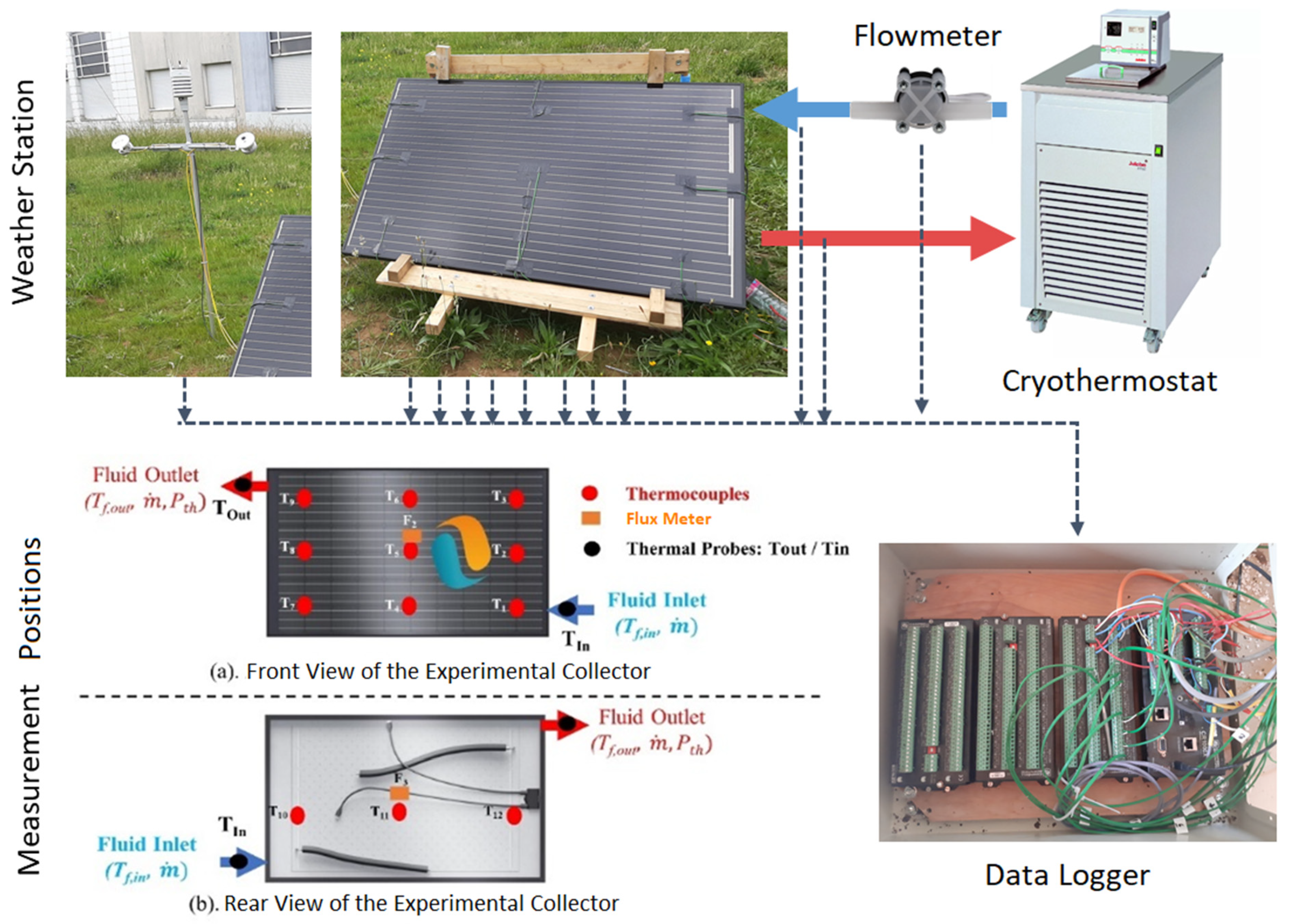
2.1.2. Experimental Setup and Monitoring System
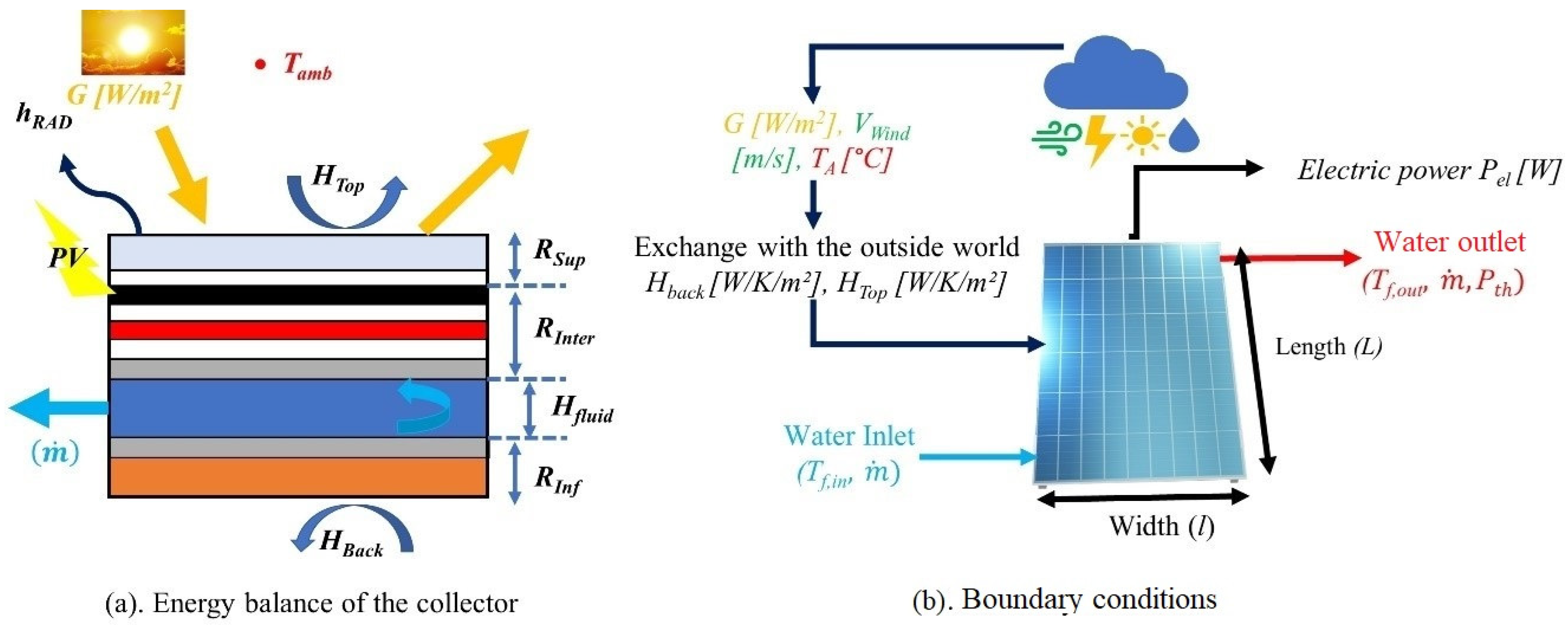
2.2. Literature-Based Mathematical Modeling of the Hybrid PV/T Collector
2.2.1. Thermal Balance of Photovoltaic Cells
2.2.2. Thermal Balance of the Heat Transfer Fluid
3. Comparative Analysis: Results and Discussion
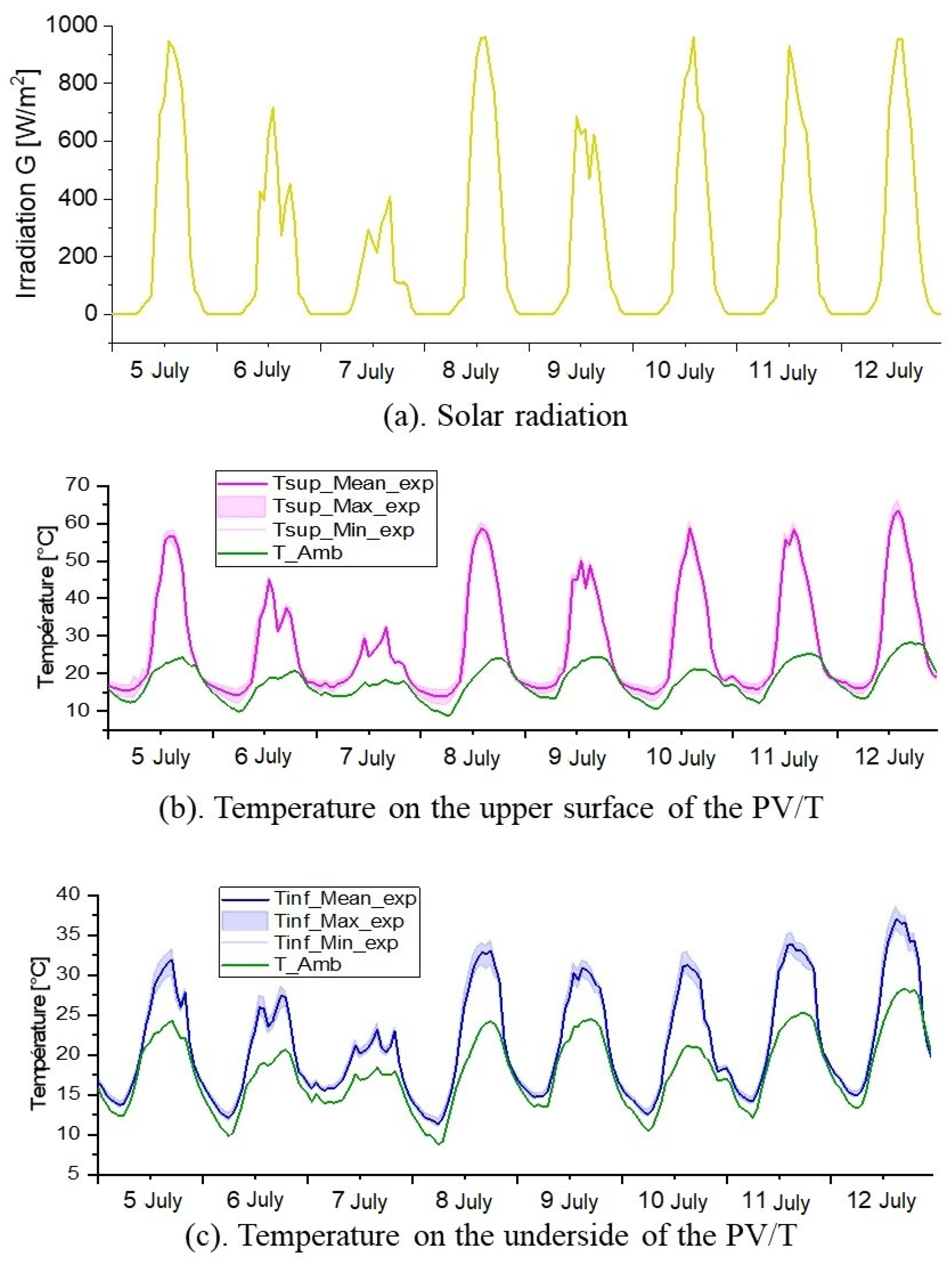
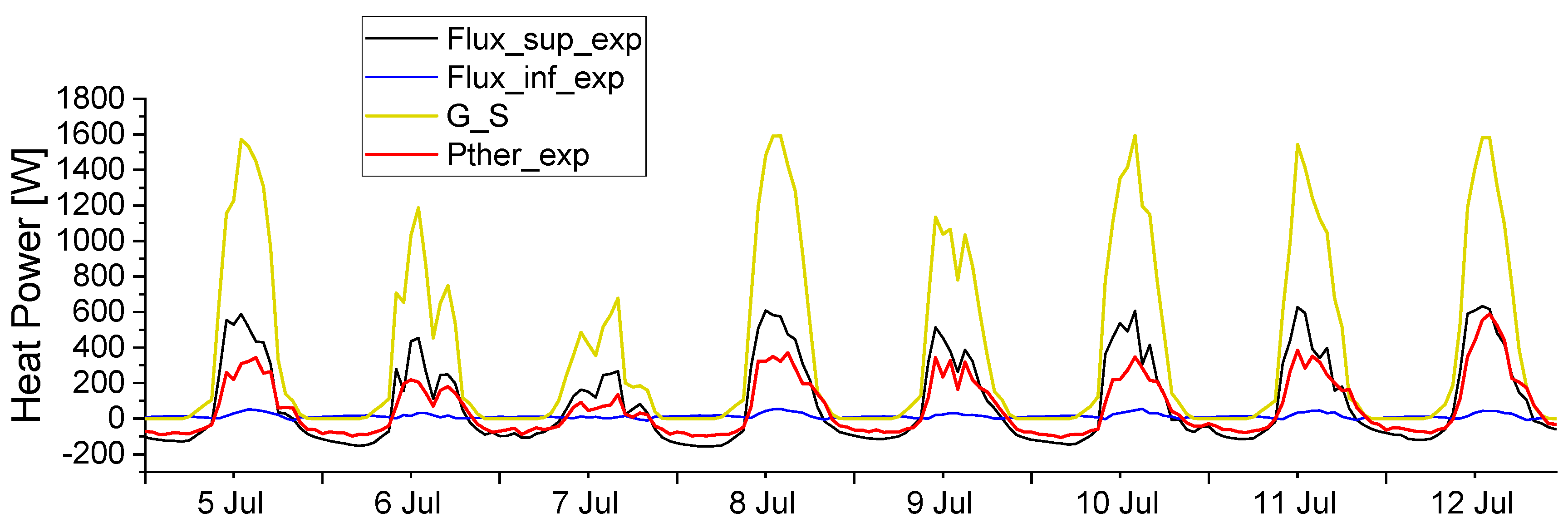
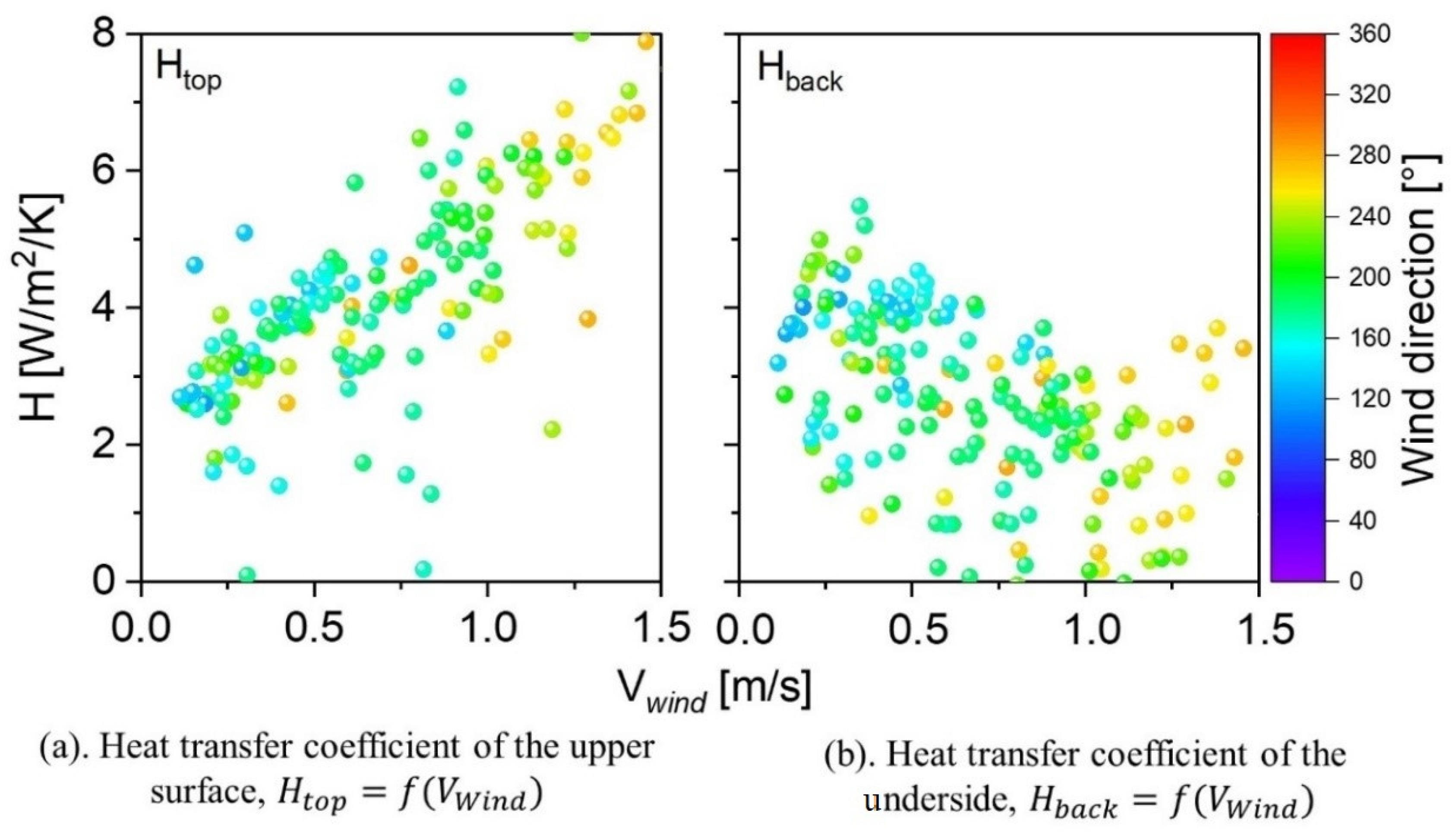
3.1. Analysis of Thermal Measurements
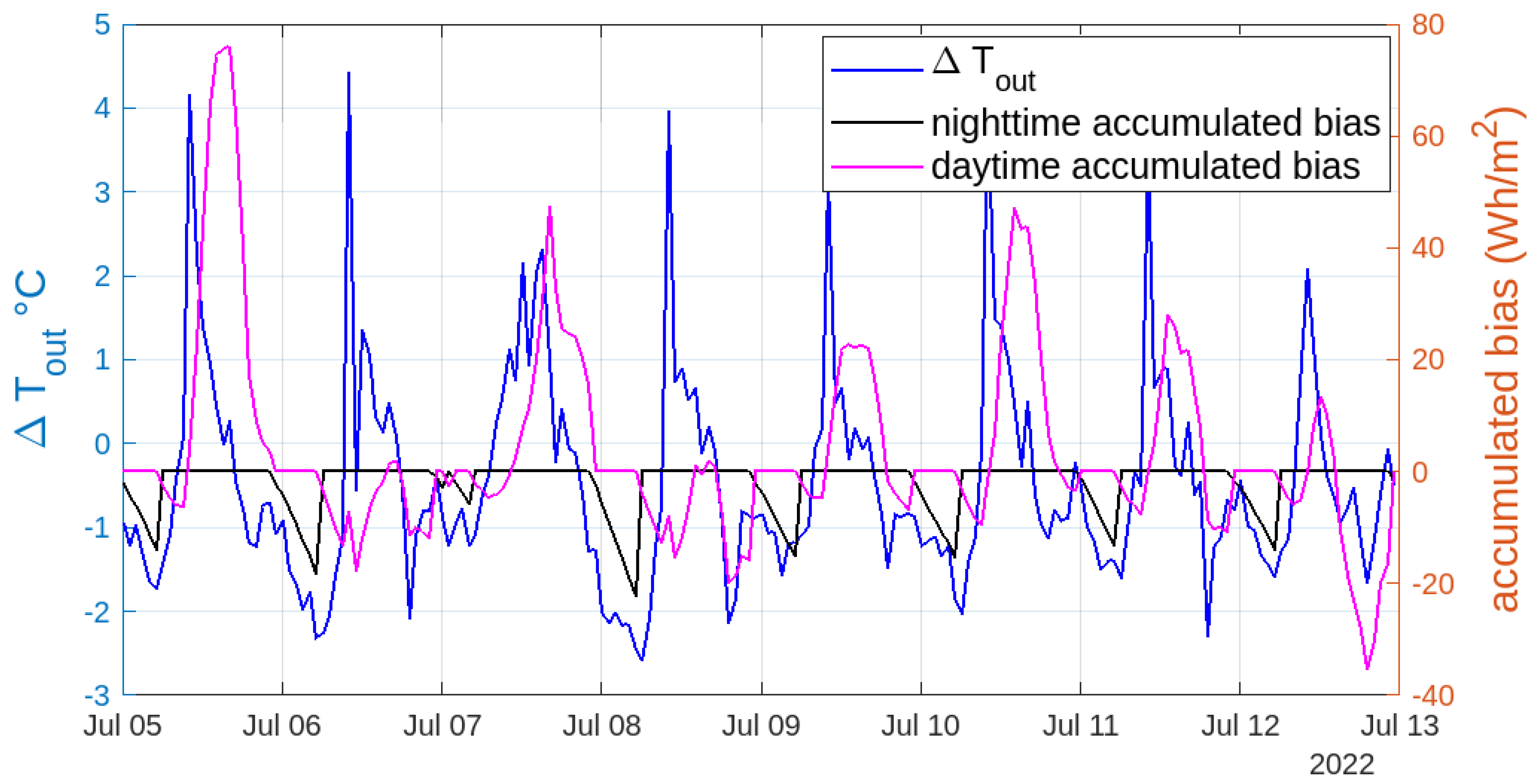
3.2. Comparison and Validation of Computational Results with Experimental Data
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature and Abbreviations
| T | Temperature [°C] |
| η | Efficiency [%] |
| ηPV/T | Overall efficiency of PV/T hybrid collector [%] |
| k | Thermal conductivity [W/mK] |
| δ | Thickness [m] |
| Area | Collector area [m2] |
| Mass flow rate [kg/s] | |
| α | Absorptivity [-] |
| H | Heat transfer coefficient [W/(m2K)] |
| h | Penalty factor [-] |
| Tsky | Temperature of the sky [°C] |
| G | Solar irradiance [W/m2] |
| TFluid and TF,Mean | Calculated fluid and mean fluid temperatures [°C] |
| Tout and Tin | Measured fluid outlet and inlet temperature [°C] |
| TPV | Photovoltaic panel temperature [°C] |
| τα | Transmittance-absorption product of solar collector [-] |
| IAM | Incidence angle modifier [-] |
| STC | Standard test conditions |
| DHW | Domestic hot water (English) |
| ECS | Domestic hot water (French) |
| TMY | Typical meteorological year |
| PV/T | Photovoltaic–thermal |
| PV | Photovoltaic |
References
- Tiwari, A.K.; Chatterjee, K.; Agrawal, S.; Singh, G.K. A comprehensive review of photovoltaic-thermal (PVT) technology: Performance evaluation and contemporary development. Energy Rep. 2023, 10, 2655–2679. [Google Scholar] [CrossRef]
- Kern, J.; Russell, M.C. Combined Photovoltaic and Thermal Hybrid Collector Systems, Massachusetts Inst. of Tech., Lexington (USA). Lincoln Lab. 1978. Available online: https://www.osti.gov/biblio/6352146 (accessed on 17 April 2025).
- Garg, H.; Agarwal, R. Some aspects of a PV/T collector/forced circulation flat plate solar water heater with solar cells. Energy Convers. Manag. 1995, 36, 87–99. [Google Scholar] [CrossRef]
- Garg, H.; Agarwal, R.; Joshi, J. Experimental study on a hybrid photovoltaic-thermal solar water heater and its performance predictions. Energy Convers. Manag. 1994, 35, 621–633. [Google Scholar] [CrossRef]
- Prakash, J. Transient analysis of a photovoltaic-thermal solar collector for co-generation of electricity and hot air/water. Energy Convers. Manag. 1994, 35, 967–972. [Google Scholar] [CrossRef]
- Rejeb, O.; Dhaou, H.; Jemni, A. A numerical investigation of a photovoltaic thermal (PV/T) collector. Renew. Energy 2015, 77, 43–50. [Google Scholar] [CrossRef]
- Al-Shamani, A.N.; Alghoul, M.; Elbreki, A.; Ammar, A.; Abed, A.M.; Sopian, K. Mathematical and experimental evaluation of thermal and electrical efficiency of PV/T collector using different water based nano-fluids. Energy 2018, 145, 770–792. [Google Scholar] [CrossRef]
- Altharwanee, H.; Jurado, F.; Vera, D. Experimental study on the performance of the photovoltaic thermal (PVT) connected in series with flat plate solar collector (ST). Sol. Energy 2024, 283, 113010. [Google Scholar] [CrossRef]
- Fang, H.; Zhang, N.; Cai, G.; Chen, H.; Ma, J.; Wu, D.; Du, T.; Wang, Y. Operation strategy optimization and heat transfer characteristic analysis of photovoltaic/thermal module series connected with flat plate solar collector: System experimental study. Renew. Energy 2024, 229, 120770. [Google Scholar] [CrossRef]
- Abdul-Ganiyu, S.; Quansah, D.A.; Ramde, E.W.; Seidu, R.; Adaramola, M.S. Study effect of flow rate on flat-plate water-based photovoltaic-thermal (PVT) system performance by analytical technique. J. Clean. Prod. 2021, 321, 128985. [Google Scholar] [CrossRef]
- Abdul-Ganiyu, S.; Quansah, D.A.; Ramde, E.W.; Seidu, R.; Adaramola, M.S. Techno-economic analysis of solar photovoltaic (PV) and solar photovoltaic thermal (PVT) systems using exergy analysis. Sustain. Energy Technol. Assess. 2021, 47, 101520. [Google Scholar] [CrossRef]
- Maoulida, F.; Djedjig, R.; Kassim, M.A.; El Ganaoui, M. Numerical Study for the Evaluation of the Effectiveness and Benefits of Using Photovoltaic-Thermal (PV/T) System for Hot Water and Electricity Production under a Tropical African Climate: Case of Comoros. Energies 2022, 16, 240. [Google Scholar] [CrossRef]
- Yue, H.; Xu, Z.; Chu, S.; Cheng, C.; Zhang, H.; Chen, H.; Ai, D. Study on the Performance of Photovoltaic/Thermal Collector–Heat Pump–Absorption Chiller Tri-Generation Supply System. Energies 2023, 16, 3034. [Google Scholar] [CrossRef]
- Brottier, L.; Bennacer, R. Thermal performance analysis of 28 PVT solar domestic hot water installations in Western Europe. Renew. Energy 2020, 160, 196–210. [Google Scholar] [CrossRef]
- Nedjar, A.; Chaker, A.; Absi, R.; Lahmer, Y.; Bennacer, R. Performance Study of Photovoltaic/Thermal Collector System for Cold Production by Adsorption in a Mediterranean Climate: Foodstuffs Preservation. J. Therm. Sci. Eng. Appl. 2023, 15, 101011. [Google Scholar] [CrossRef]
- Delachaux, V.; Daix, S.; Bennacer, R.; Brottier, L. CFD Modelling for the Design of a Photovoltaic-Thermal Solar Panel Dedicated to Solar-Assisted Heat Pump. In Advances in Computational Heat and Mass Transfer, Icchmt 2023; Benim, A.C., Bennacer, R., Mohamad, A.A., Oclon, P., Suh, S.H., Taler, J., Eds.; Springer International Publishing Ag: Cham, Switzerland, 2024; Volume 2, pp. 469–480. [Google Scholar] [CrossRef]
- Hazami, M.; Riahi, A.; Mehdaoui, F.; Nouicer, O.; Farhat, A. Energetic and exergetic performances analysis of a PV/T (photovoltaic thermal) solar system tested and simulated under to Tunisian (North Africa) climatic conditions. Energy 2016, 107, 78–94. [Google Scholar] [CrossRef]
- Brottier, L. Optimisation Biénergie d’un Panneau Solaire Multifonctionnel: Du Capteur aux Installations In Situ, Phdthesis, Université Paris-Saclay. 2019. Available online: https://tel.archives-ouvertes.fr/tel-02133891 (accessed on 12 March 2021).
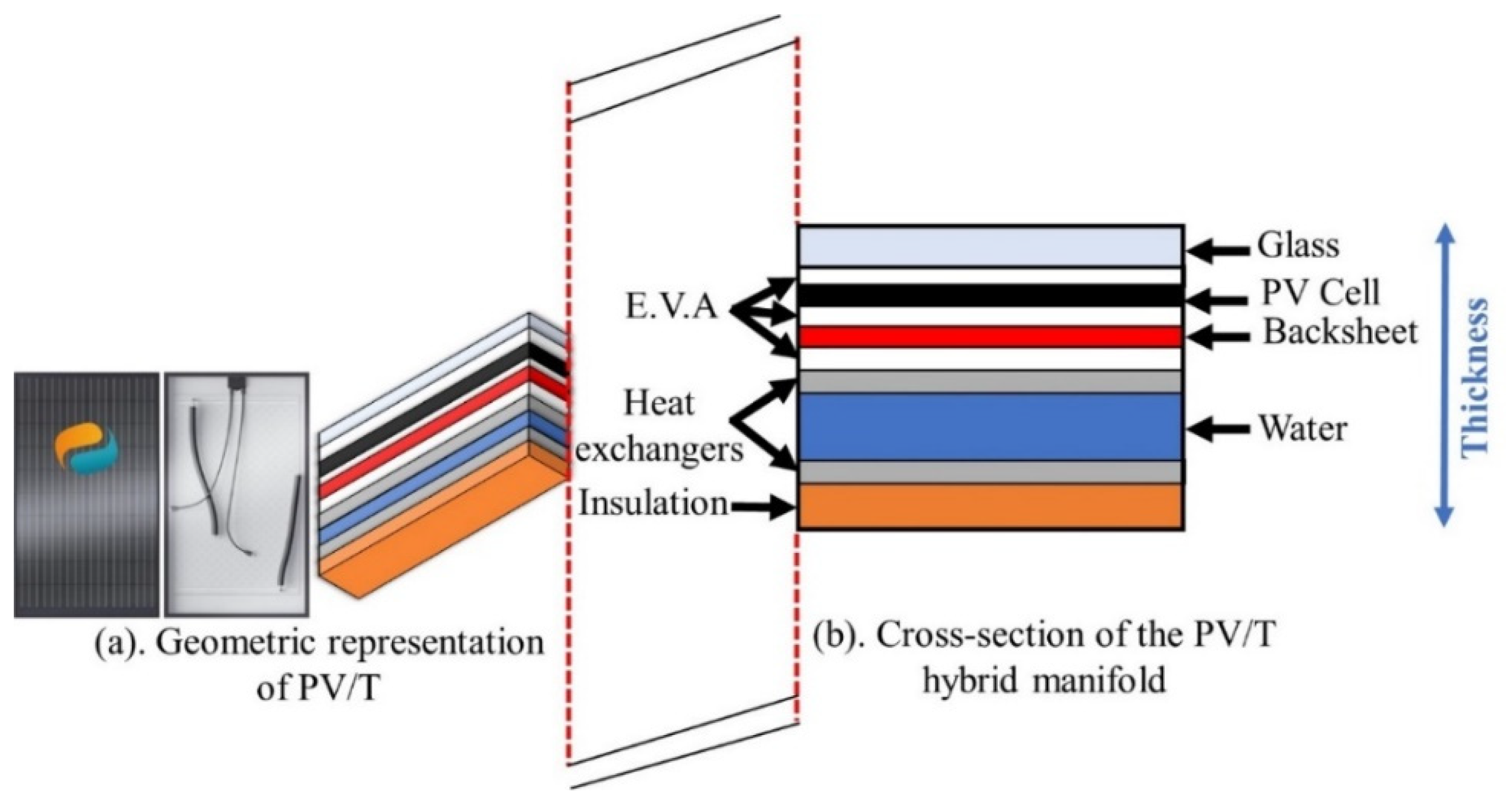



| Layer | Thickness (mm) | Thermal Conductivity (W/(m·K)) |
|---|---|---|
| Glass | 2 | ~1 |
| E.V.A. (encapsulant) | 0.6 | 0.23 |
| Silicon cells | 0.6 | 130 |
| E.V.A. | 0.6 | 0.23 |
| Backsheet | 0.14 | 0.2 |
| E.V.A. | 0.6 | 0.23 |
| Stainless steel (SS) plate 1 (exchanger 1) | 0.6 | 25 |
| Heat transfer fluid | 2 | 0.6 |
| Stainless steel (SS) plate 2 (exchanger 2) | 0.6 | 25 |
| Insulation (INS) | 30 | 0.04 |
| Tout deviation | |||||
|---|---|---|---|---|---|
| Day | Night | ||||
| MAX | 2.6 °C | 5.2% | MAX | 2.5 °C | 5.0% |
| MIN | −4.4 °C | −8.9% | MIN | 0.4 °C | 0.8% |
| MEAN | 0.1 °C | 0.3% | MEAN | 1.3 °C | 2.7% |
| Tpv deviation | |||||
| Day | Night | ||||
| MAX | 0.8 °C | 1.7% | MAX | 0.9 °C | 1.8% |
| MIN | −8.7 °C | −17.5% | MIN | −0.2 °C | −0.5% |
| MEAN | −2.7 °C | −5.5% | MEAN | 0.4 °C | 0.8% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maoulida, F.; Djedjig, R.; Rahim, M.; Kassim, M.A.; El Ganaoui, M. High-Precision Experimental Data for Thermal Model Validation of Flat-Plate Hybrid Water PV/T Collectors. Energies 2025, 18, 2972. https://doi.org/10.3390/en18112972
Maoulida F, Djedjig R, Rahim M, Kassim MA, El Ganaoui M. High-Precision Experimental Data for Thermal Model Validation of Flat-Plate Hybrid Water PV/T Collectors. Energies. 2025; 18(11):2972. https://doi.org/10.3390/en18112972
Chicago/Turabian StyleMaoulida, Fahad, Rabah Djedjig, Mourad Rahim, Mohamed Aboudou Kassim, and Mohammed El Ganaoui. 2025. "High-Precision Experimental Data for Thermal Model Validation of Flat-Plate Hybrid Water PV/T Collectors" Energies 18, no. 11: 2972. https://doi.org/10.3390/en18112972
APA StyleMaoulida, F., Djedjig, R., Rahim, M., Kassim, M. A., & El Ganaoui, M. (2025). High-Precision Experimental Data for Thermal Model Validation of Flat-Plate Hybrid Water PV/T Collectors. Energies, 18(11), 2972. https://doi.org/10.3390/en18112972










