Continuous-Control-Set Model Predictive Control Strategy for MMC-UPQC Under Non-Ideal Conditions
Abstract
1. Introduction
2. System Structure and Mathematical Model of the MMC-UPQC
2.1. MMC-UPQC System Structure
2.2. Mathematical Model of the MMC-UPQC
3. Model Predictive Control Based on a Continuous Control Set
3.1. Design of Model Predictive Controller Based on a Continuous Control Set
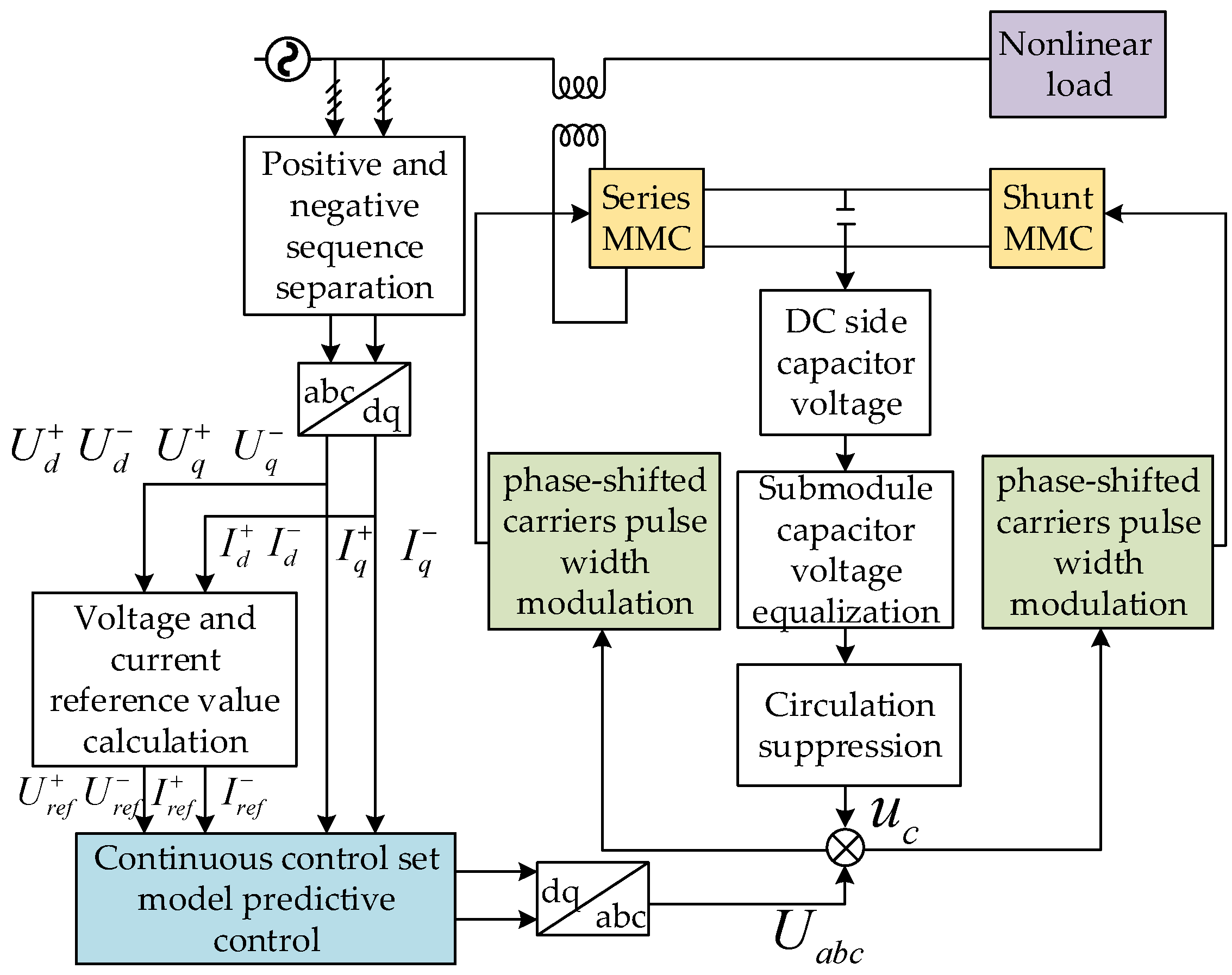
3.2. Overall Control Diagram of MMC-UPQC
4. Simulation Analysis
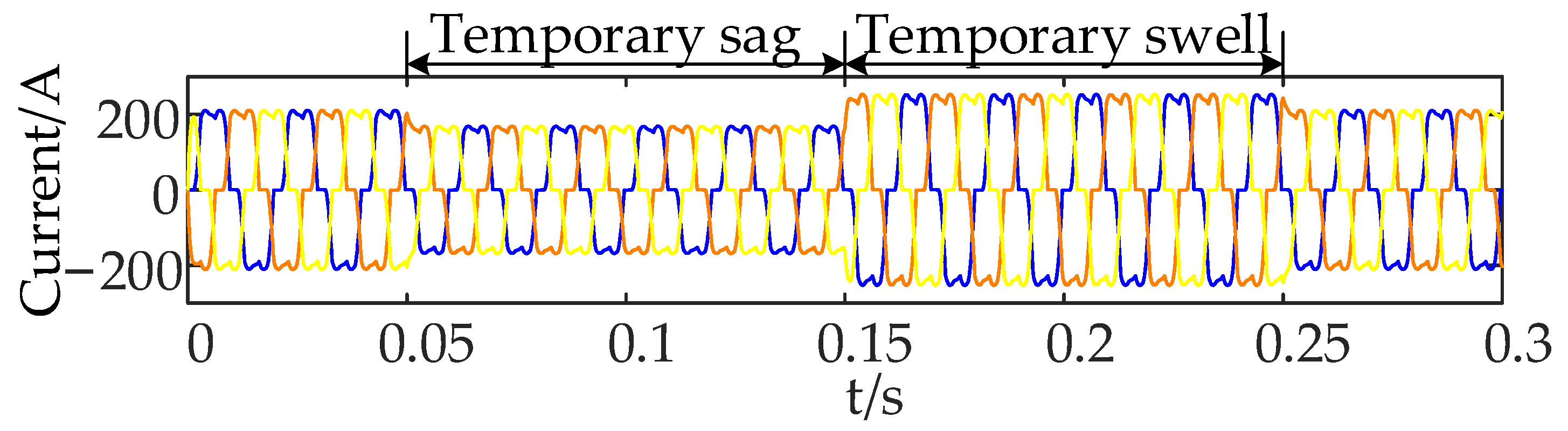
4.1. Single-Phase Grid Voltage Sag and Swell
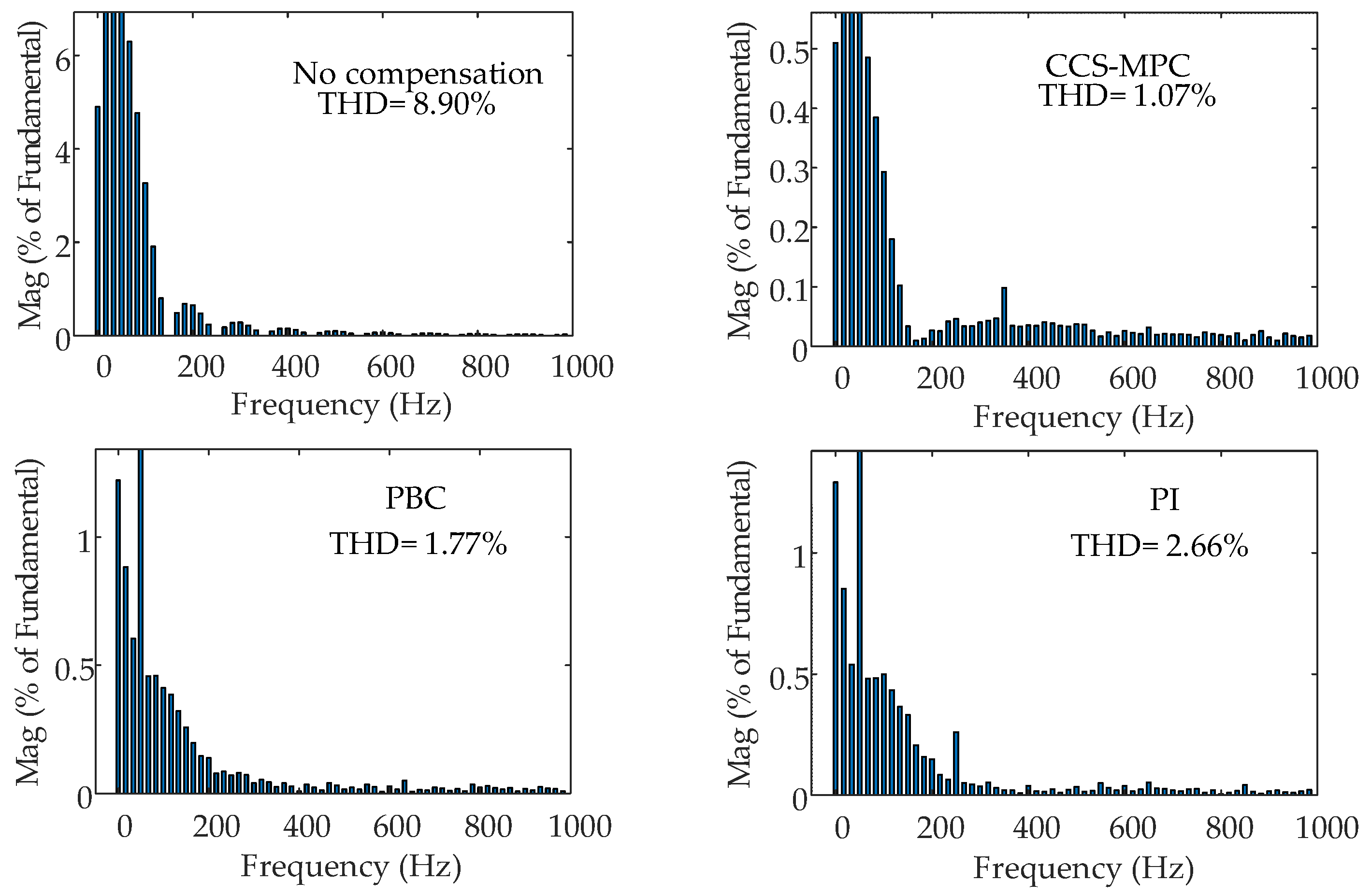
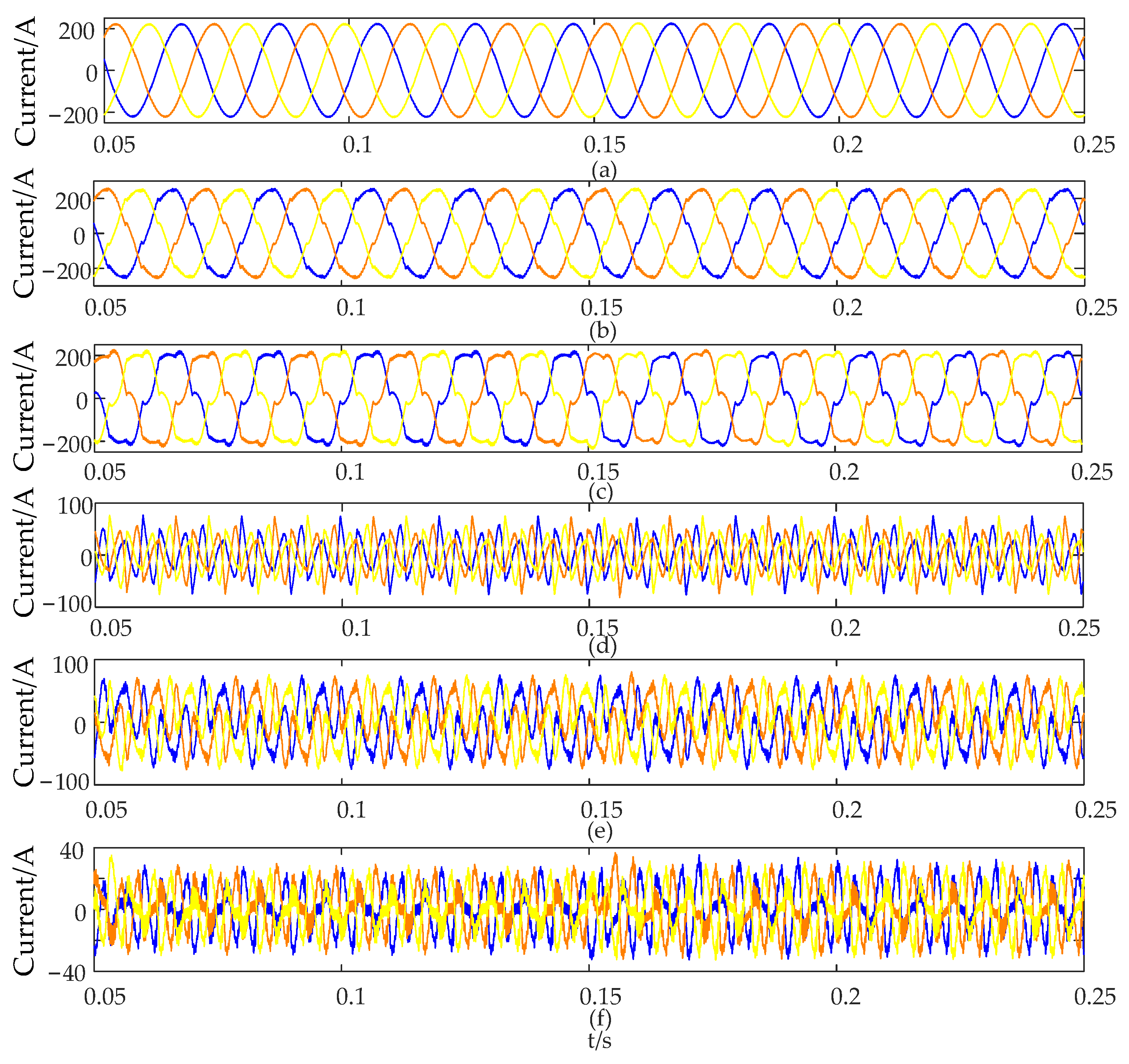
4.2. High-Order Harmonic Injection
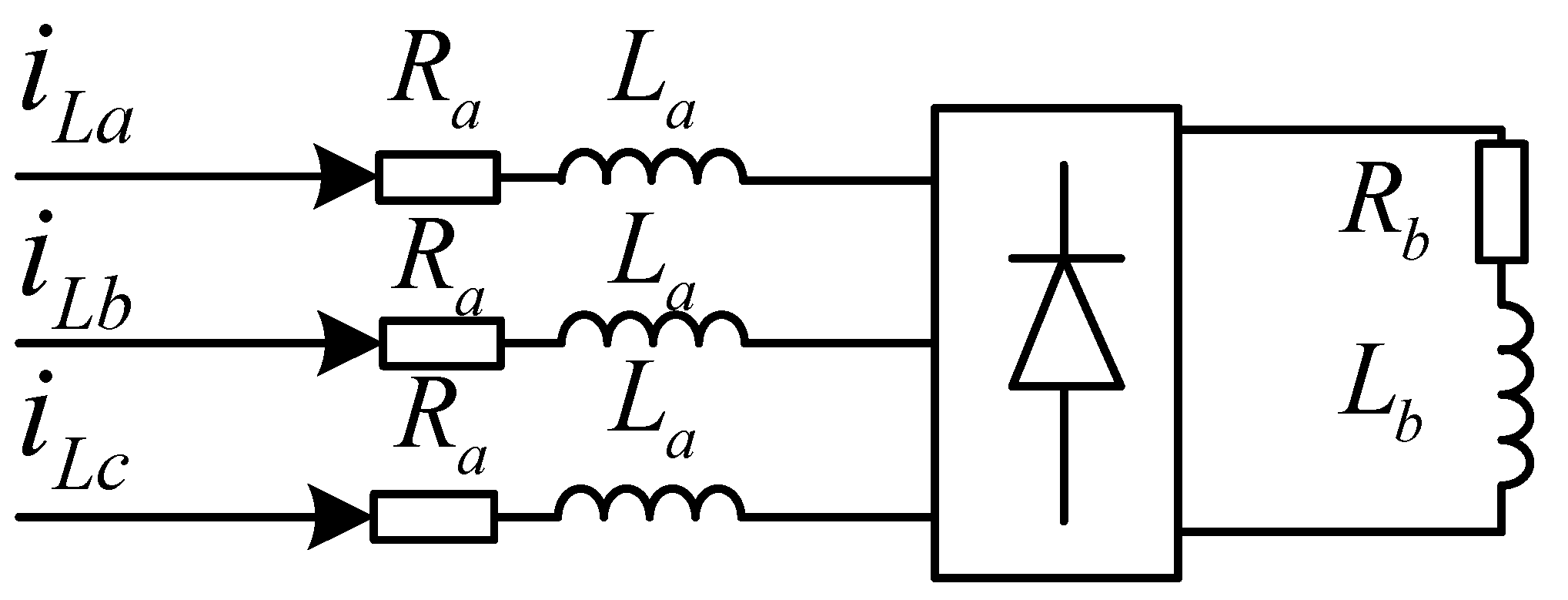
4.3. Grid Voltage Sag and Swell with Nonlinear Load
5. Conclusions
- (1)
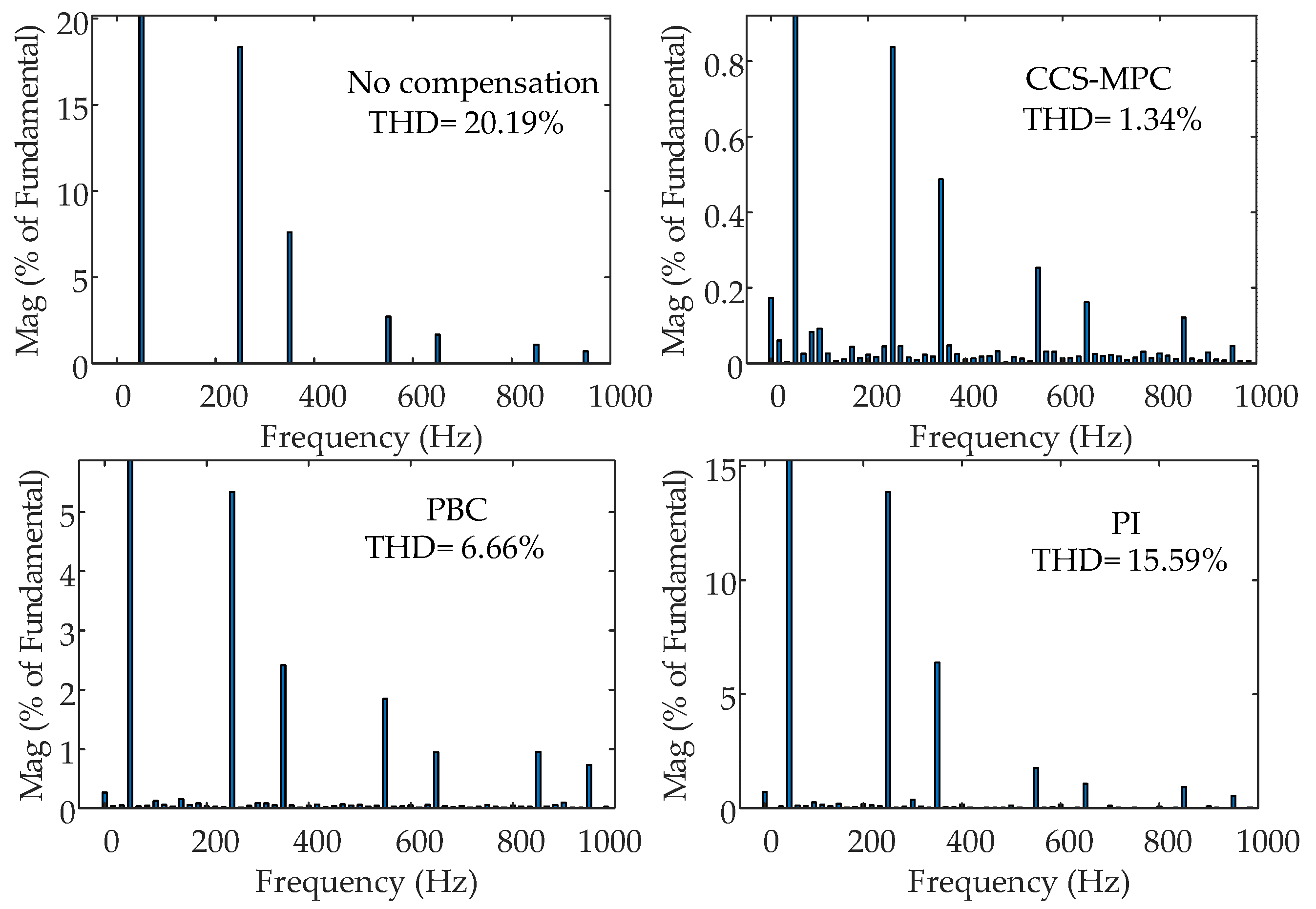
- CCS-MPC can fully utilize its fast response advantage, enabling MMC-UPQC to quickly and accurately track the required compensation signals. This allows the series-side MMC to output more precise compensation voltage and the shunt-side MMC to output more precise compensation current, effectively reducing the THD of the load-side voltage and grid-side current.
- (2)
- Compared with PI control and PBC, CCS-MPC exhibits higher compensation accuracy, stronger harmonic suppression capability, and superior performance in handling complex operating conditions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, F.; Quan, X.; Ren, L. Review of power quality disturbance detection and identification methods. Proc. CSEE 2021, 41, 4104–4121. [Google Scholar]
- He, J.; Meng, W.; Jiang, W.; Yin, X. Power quality problems in renewable energy power distribution systems: Analysis and solutions. High Volt. Eng. 2023, 49, 2983–2994. [Google Scholar]
- Khadkikar, V. Enhancing electric power quality using UPQC: A comprehensive overview. IEEE Trans. Power Electron. 2012, 27, 2284–2297. [Google Scholar] [CrossRef]
- Fuyin, N.; Zhengming, L. Overview of unified power quality conditioner research development. Power Syst. Prot. Control. 2020, 48, 177–187. [Google Scholar]
- Lu, J.; Xiao, X.; Zhang, J.; Xu, Y. MMC-UPQC coordinated control method based on fixed active current limit value control. Trans. China Electrotech. Soc. 2015, 30, 196–203. [Google Scholar]
- Isik, S.; Alharbi, M.; Bhattacharya, S. An optimized circulating current control method based on PR and PI controller for MMC applications. IEEE Trans. Ind. Appl. 2021, 57, 5074–5085. [Google Scholar] [CrossRef]
- Yang, Y.; Xiao, X.; Guo, S.; Gao, Y.; Yuan, C.; Yang, W. Energy storage characteristic analysis of voltage sags compensation for UPQC based on MMC for medium voltage distribution system. Energies 2018, 11, 923. [Google Scholar] [CrossRef]
- Liu, H.M.; Jiang, C.H.; Cheng, Q.M. Research on integrated management of MMC-UPQC power quality based on passivity control under unbalanced grid. High Volt. Eng. 2021, 47, 1344–1355. [Google Scholar]
- Wang, Y.; Cheng, Q.; Cheng, Y. Passivity-based control of MMC-based active power filter under non-ideal conditions. Int. Trans. Electr. Energy Syst. 2020, 30, e12178. [Google Scholar] [CrossRef]
- Ma, X.; Cheng, Q.; Cheng, Y.; Rui, X.; Zhao, J. Dual-passivity-based control strategy of modular multilevel matrix converter. Int. Trans. Electr. Energy Syst. 2021, 31, e12692. [Google Scholar] [CrossRef]
- Zhou, J.; Zhou, J.; Yang, H.; Huang, L. Passive Super-Twisting Second-Order Sliding Mode Control Strategy for Input Stage of MMC-PET. Energies 2024, 17, 2036. [Google Scholar] [CrossRef]
- Jiang, C.; Zhang, S. Power quality compensation strategy of MMC-UPQC based on passive sliding mode control. IEEE Access 2022, 11, 3662–3679. [Google Scholar] [CrossRef]
- Yang, X.; Chen, W.; Yin, C.; Cheng, Q. Fractional-Order Sliding-Mode Control and Radial Basis Function Neural Network Adaptive Damping Passivity-Based Control with Application to Modular Multilevel Converters. Energies 2024, 17, 580. [Google Scholar] [CrossRef]
- Qiming, C.; Weisha, S.U.N.; Yinman, C. Nonlinear control strategy based on Lyapunov function for MMC under grid voltage unbalance condition. High Volt. Eng. 2019, 45, 3984–3992. [Google Scholar]
- Cheng, Q.; Jiang, C.; Wang, Y. Lyapunov function control strategy of MMC-SAPF under non-ideal conditions. Electr. Power Autom. Equip. 2020, 40, 68–79. [Google Scholar]
- Ghadi, R.J.; Mehrasa, M.; Adabi, M.E.; Bacha, S. Lyapunov theory-based control strategy for multi-terminal MMC-HVDC systems. Int. J. Electr. Power Energy Syst. 2021, 129, 106778. [Google Scholar] [CrossRef]
- Chang, J.; Qiming, C.; Qiao, M. Differential flat control for unified power quality controller based on modular multilevel converter under unbalanced grid voltage. Trans. China Electrotech. Soc. 2021, 36, 3410–3421. [Google Scholar]
- Bo, L.I.N.; Bin, W.; Qiming, C. Differential flatness controller strategy of MMC-HVDC to supply power to passive network under asymmetric faults. High Volt. Eng. 2021, 47, 4023–4032. [Google Scholar]
- Zhou, D.; Tu, P.; Qiu, H.; Tang, Y. Finite-control-set model predictive control of modular multilevel converters with cascaded open-circuit fault ride-through. IEEE J. Emerg. Sel. Topics Power Electron. 2019, 8, 2943–2953. [Google Scholar] [CrossRef]
- Gong, Z.; Dai, P.; Yuan, X.; Wu, X.; Guo, G. Design and experimental evaluation of fast model predictive control for modular multilevel converters. IEEE Trans. Ind. Electron. 2015, 63, 3845–3856. [Google Scholar] [CrossRef]
- Bocker, J.; Freudenberg, B.; The, A.; Dieckerhoff, S. Experimental comparison of model predictive control and cascaded control of the modular multilevel converter. IEEE Trans. Power Electron. 2014, 30, 422–430. [Google Scholar] [CrossRef]
- Zhang, J.; Zeng, G.; Zhao, J.; Huang, B.; Xiao, B. Modular multilevel converter capacitor voltage balancing strategy based on improved bubble sorting. Power Syst. Prot. Control 2020, 48, 92–99. [Google Scholar]
- Zhou, D.; Yang, S.; Tang, Y. Model-predictive current control of modular multilevel converters with phase-shifted pulse width modulation. IEEE Trans. Ind. Electron. 2018, 66, 4368–4378. [Google Scholar] [CrossRef]
- Wang, Z.; Yin, X.; Chen, Y. Model predictive arm current control for modular multilevel converter. IEEE Access 2021, 9, 54700–54709. [Google Scholar] [CrossRef]
- Wang, F.; Wei, Y.; Young, H.; Ke, D.; Xie, H.; Rodríguez, J. A continuous-control-set type model-free predictive current control based on time-series for permanent magnet synchronous motor drives. Trans. China Electrotech. Soc. 2023, 38, 6027–6038. [Google Scholar]
- Karimi, M.H.; Rostami, M.A.; Zamani, H. Continuous control set model predictive control for the optimal current control of permanent magnet synchronous motors. Control Eng. Pract. 2023, 138, 105590. [Google Scholar] [CrossRef]






| System Parameter | Parameter Values |
|---|---|
| Number of bridge-arm submodules (N) | 6 |
| Grid-side line voltage/kV | 2 |
| Sub-module capacitance/mF | 1.2 |
| Bridge-arm inductance/mH | 4 |
| DC-side capacitance voltage/kV | 6 |
| DC-side capacitance/mF | 12 |
| Series-side inductance/mH | 2 |
| Shunt-side inductance/mH | 3 |
| Series-side resistance/Ω | 0.1 |
| Shunt-side resistance/Ω | 0.2 |
| Transformer ratio | 1 |
| N | 2 | 4 | 6 | 8 | 10 |
|---|---|---|---|---|---|
| CCS-MPC | 1 | 1 | 1 | 1 | 1 |
| IFCS-MPC | 9 | 25 | 49 | 81 | 121 |
| FCS-MPC | 16 | 256 | 4096 | 65,536 | 1,048,576 |
| Control Strategy | Overshoot/% | Recovery Time/s |
|---|---|---|
| CCS-MPC | 0.30 | 0.015 |
| PBC | 1.40 | 0.030 |
| PI | 3.50 | 0.075 |
| Control Strategy | Overshoot/% | Recovery Time/s |
|---|---|---|
| CCS-MPC | 0.80 | 0.015 |
| PBC | 2.70 | 0.040 |
| PI | 4.90 | 0.080 |
| Control Strategy | Overshoot/% | Recovery Time/s |
|---|---|---|
| CCS-MPC | 1.20 | 0.015 |
| PBC | 3.70 | 0.045 |
| PI | 5.20 | 0.090 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Zhou, J.; Zhai, J.; Yang, L.; Qian, X.; Tao, Z. Continuous-Control-Set Model Predictive Control Strategy for MMC-UPQC Under Non-Ideal Conditions. Energies 2025, 18, 2946. https://doi.org/10.3390/en18112946
Chen L, Zhou J, Zhai J, Yang L, Qian X, Tao Z. Continuous-Control-Set Model Predictive Control Strategy for MMC-UPQC Under Non-Ideal Conditions. Energies. 2025; 18(11):2946. https://doi.org/10.3390/en18112946
Chicago/Turabian StyleChen, Lianghua, Jianping Zhou, Jiayu Zhai, Lisheng Yang, Xudong Qian, and Zhiyong Tao. 2025. "Continuous-Control-Set Model Predictive Control Strategy for MMC-UPQC Under Non-Ideal Conditions" Energies 18, no. 11: 2946. https://doi.org/10.3390/en18112946
APA StyleChen, L., Zhou, J., Zhai, J., Yang, L., Qian, X., & Tao, Z. (2025). Continuous-Control-Set Model Predictive Control Strategy for MMC-UPQC Under Non-Ideal Conditions. Energies, 18(11), 2946. https://doi.org/10.3390/en18112946





