Robust Wide-Speed-Range Control of IPMSM with Multi-Axis Coordinated Extended State Observer for Dynamic Performance Enhancement
Abstract
1. Introduction
2. Current Bias Compensation Analysis
2.1. Mathematical Model of IPMSM
2.2. Current Sampling Bias Error Impact Analysis
2.3. Analysis of ESO-Based Current Bias Error Algorithm
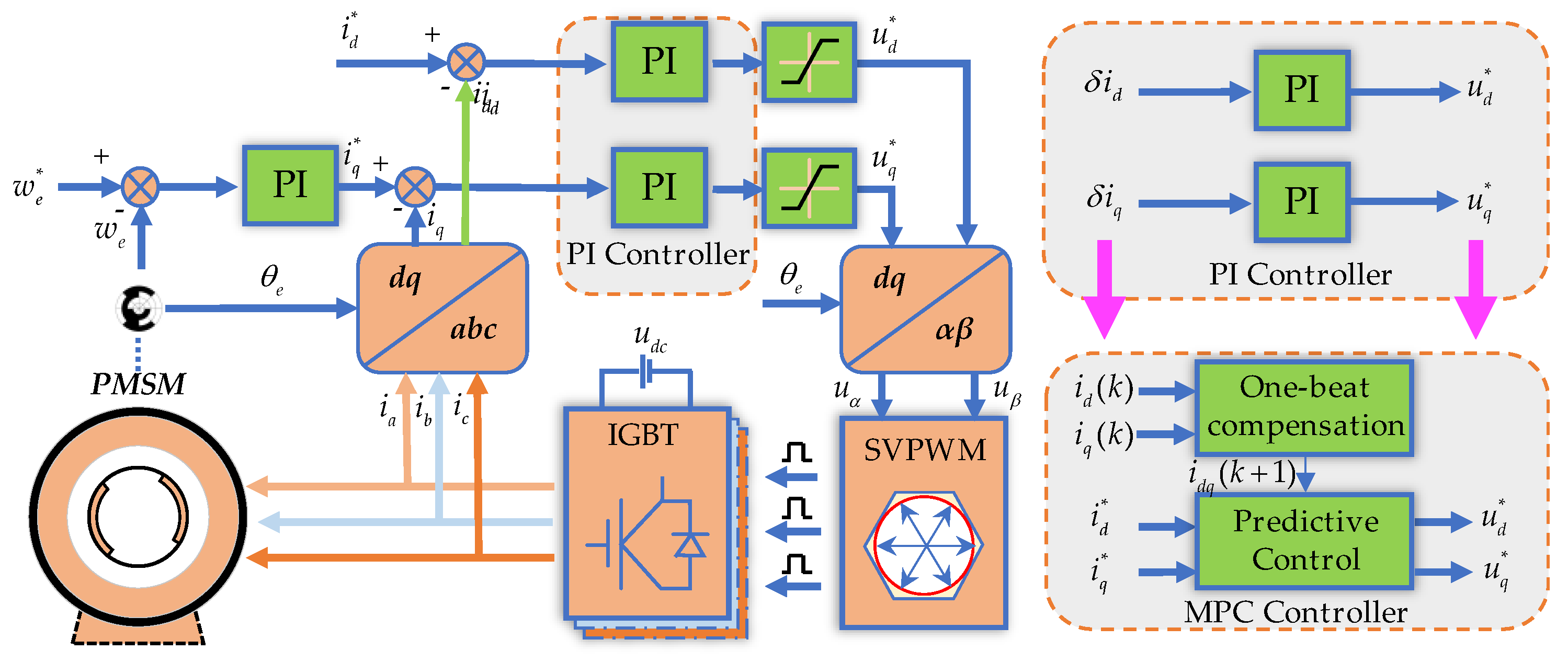
3. DPCC-Based Fast-Response Robust Current Control
3.1. Current Predictive Control Based on Deadbeat Principle
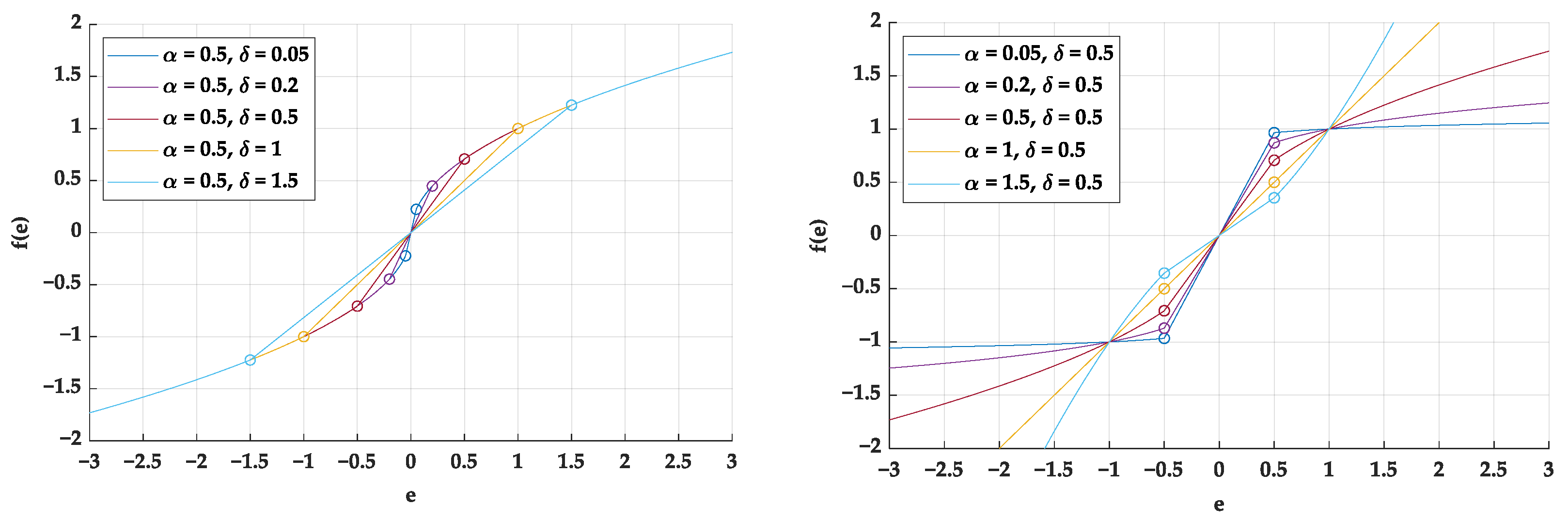
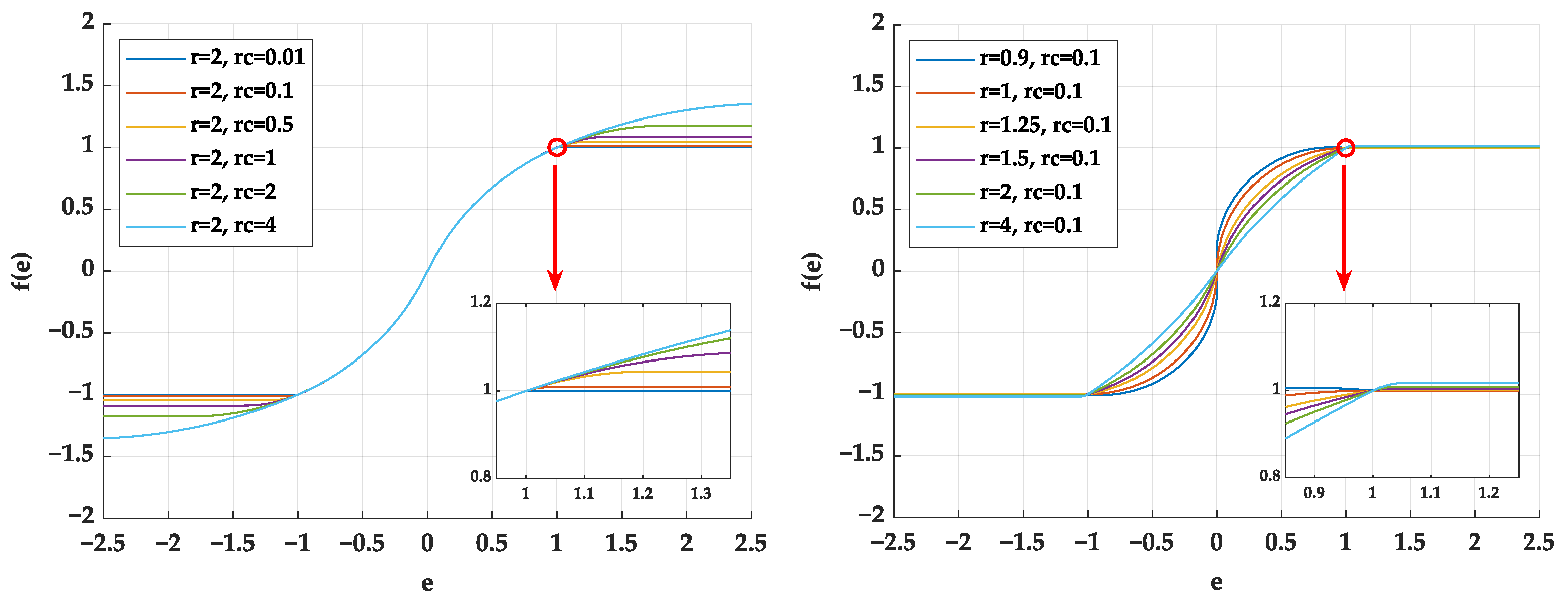
3.2. Parameter Mismatch Analysis and Robust Control Strategy
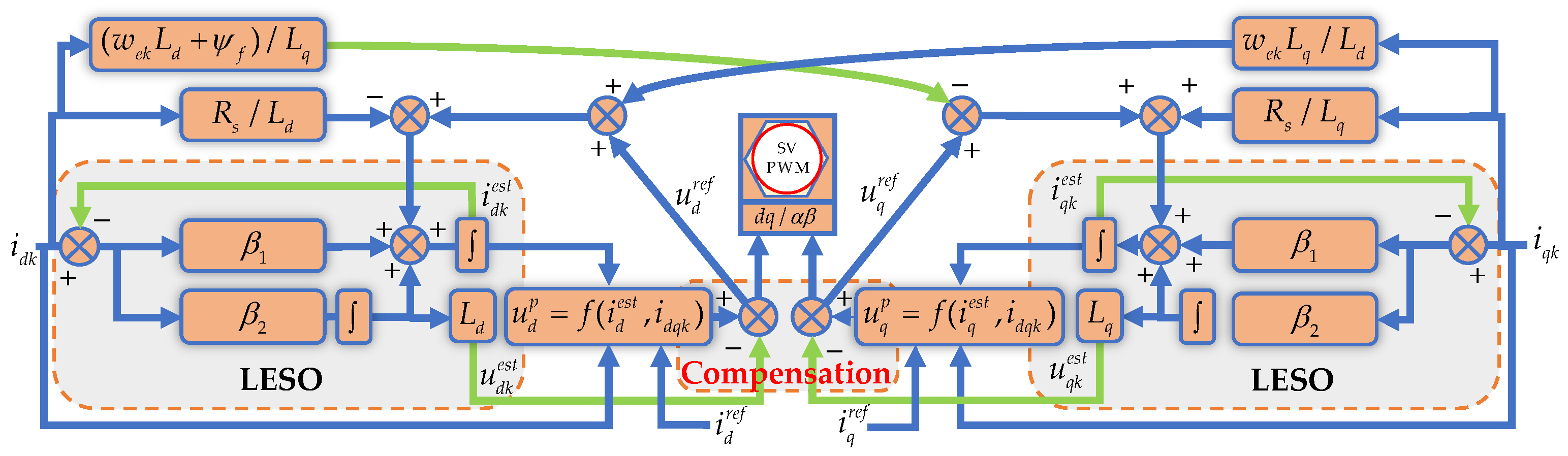
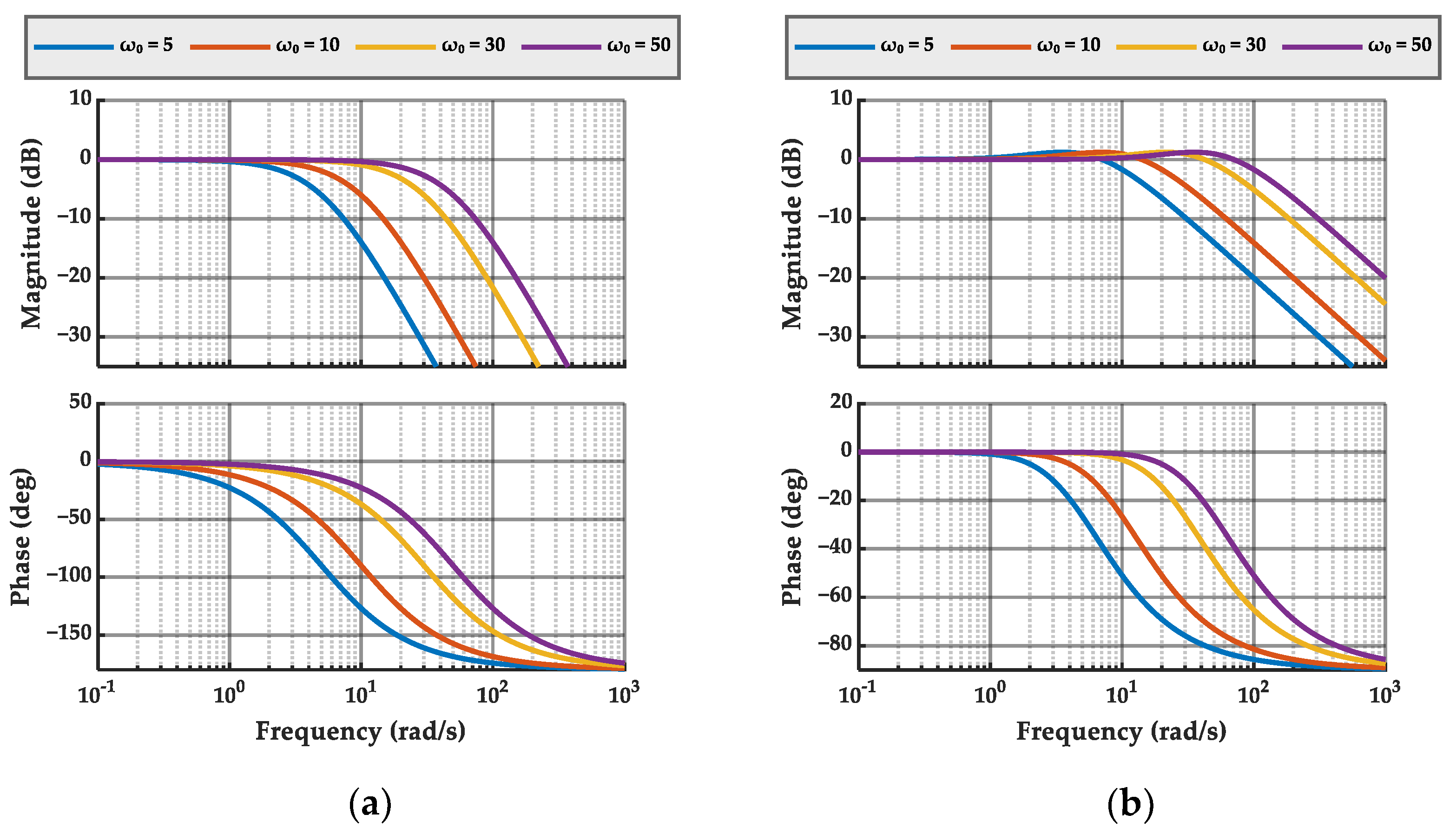
3.3. Proposed NESO Method Analysis
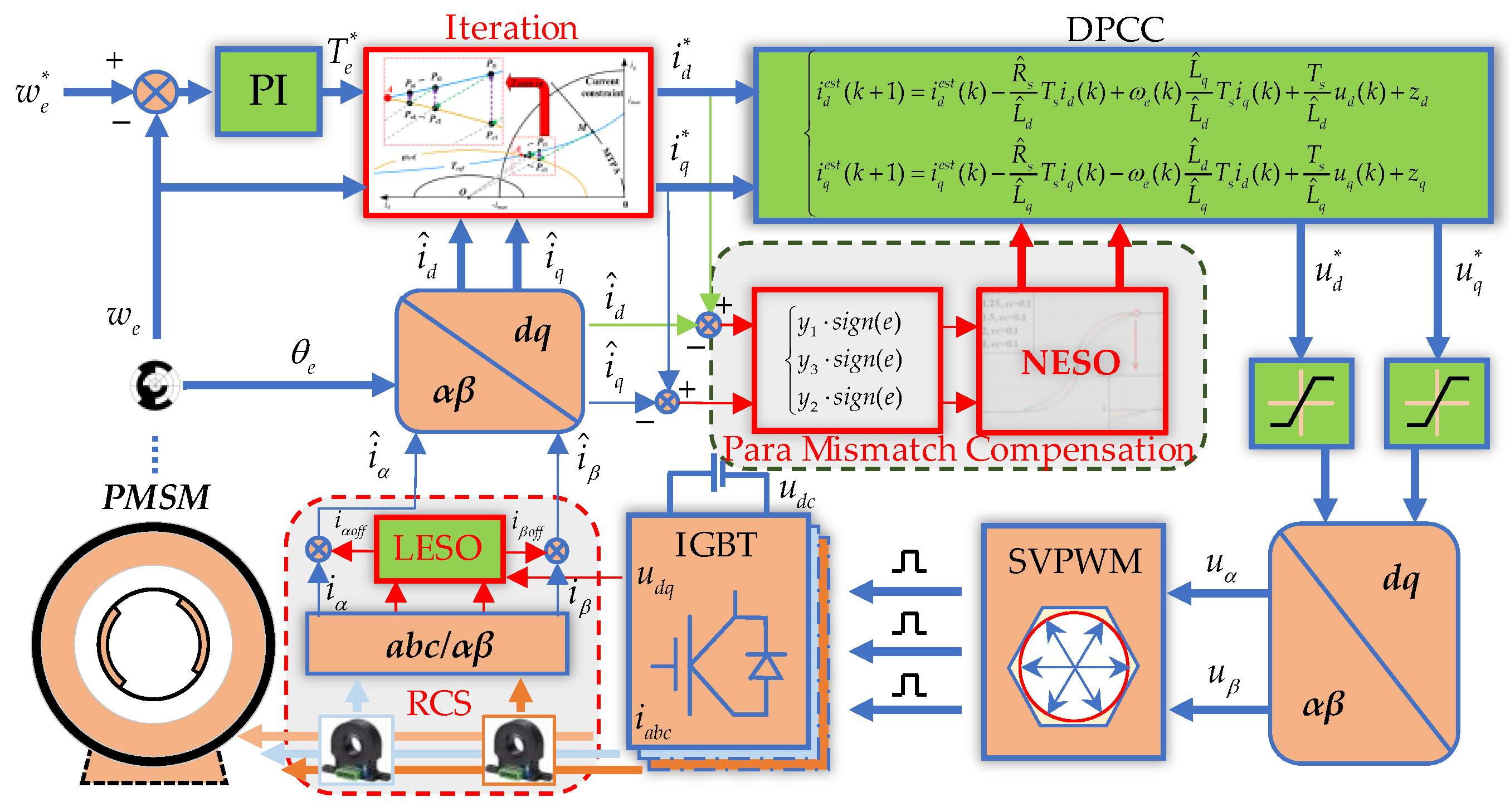
4. MCESO Architecture and Robustness Analysis
5. Experimental Results and Discussion
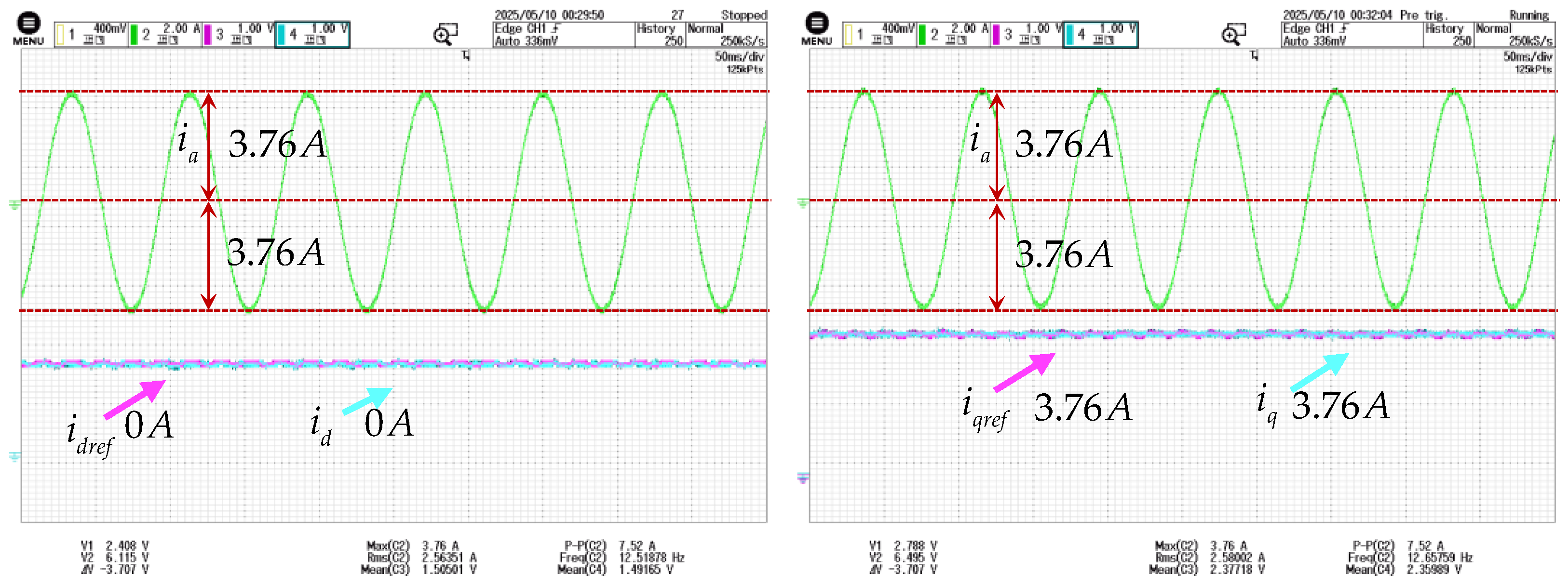
5.1. Introduction to Experimental Equipment
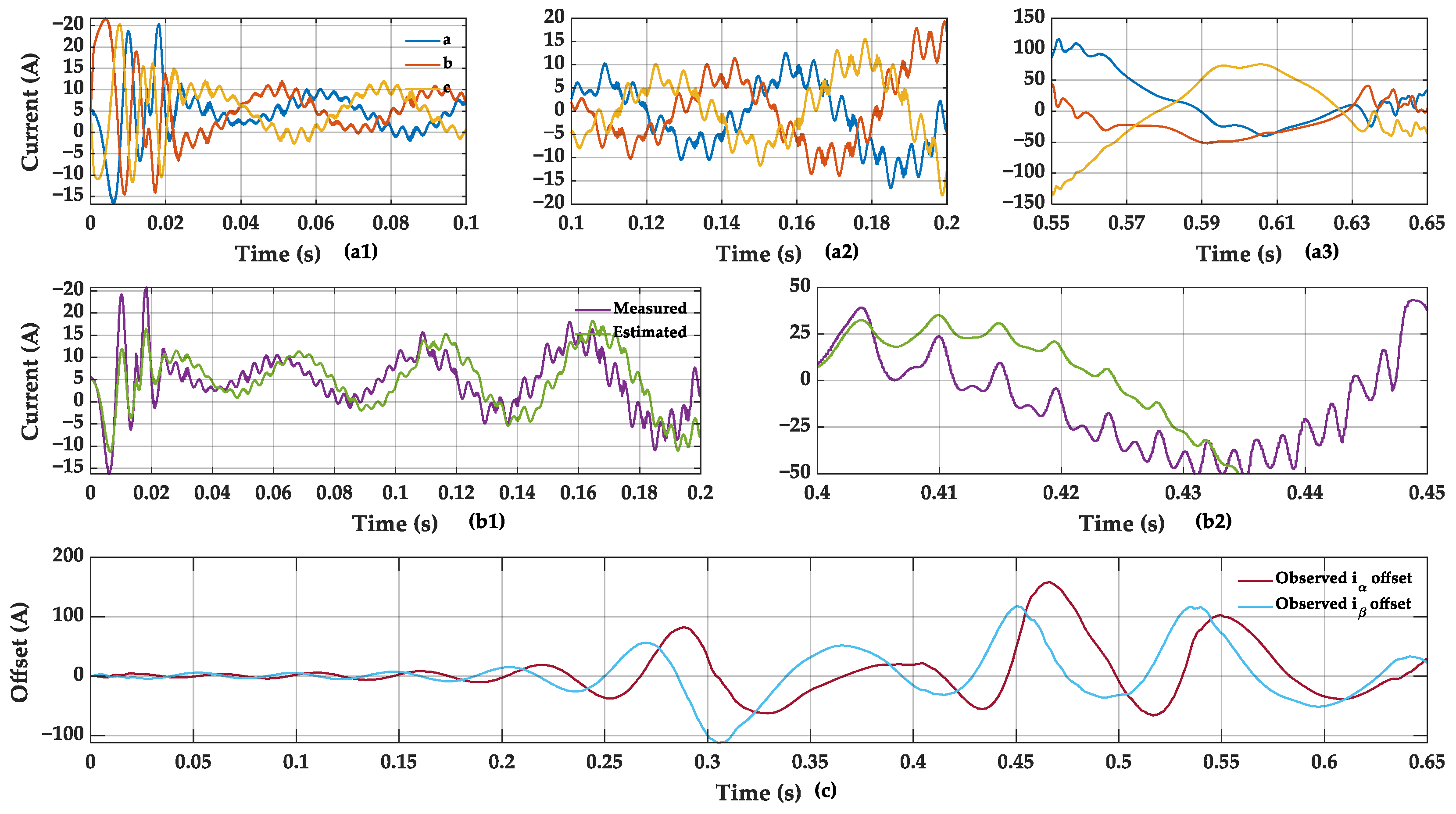
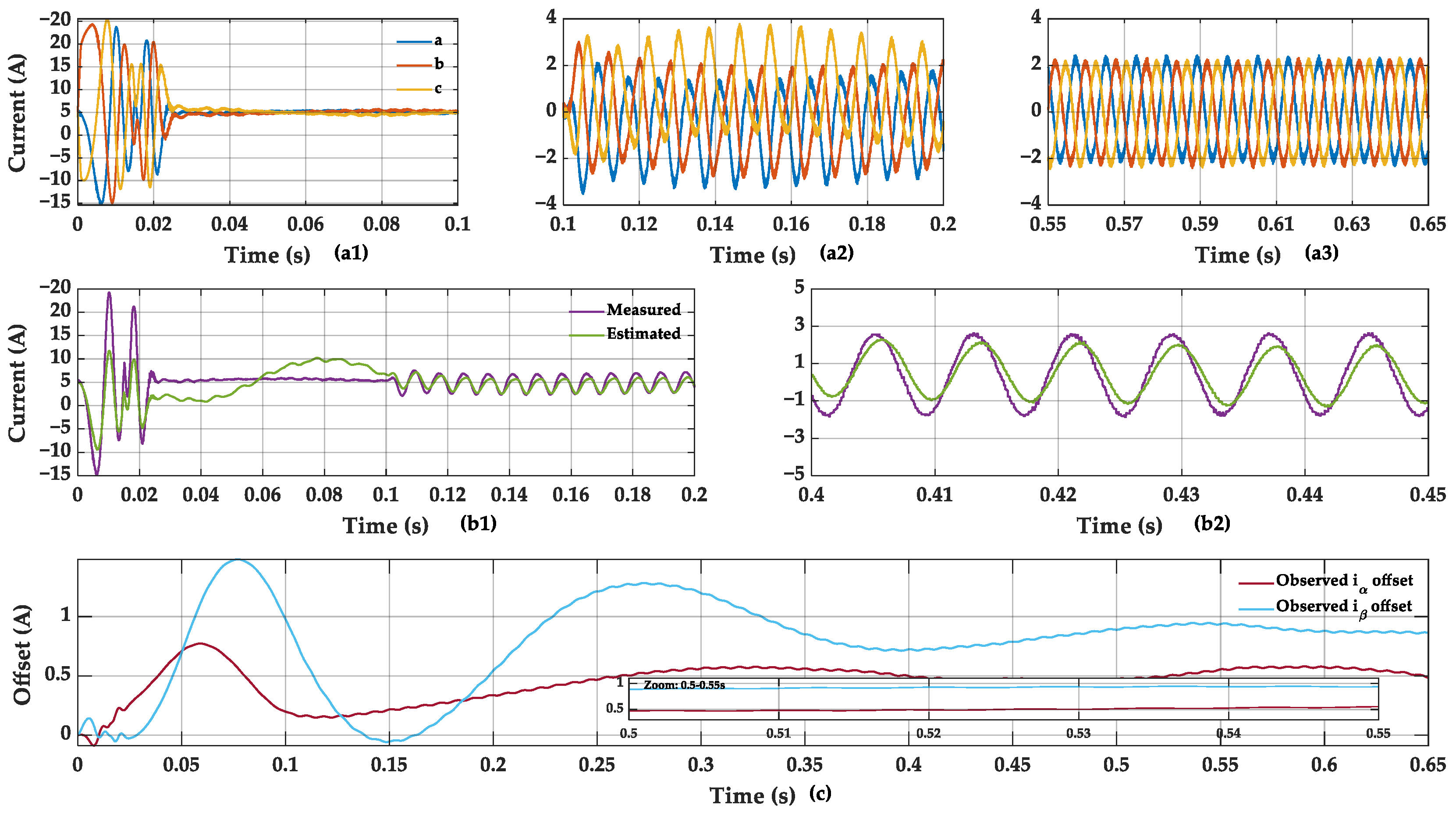
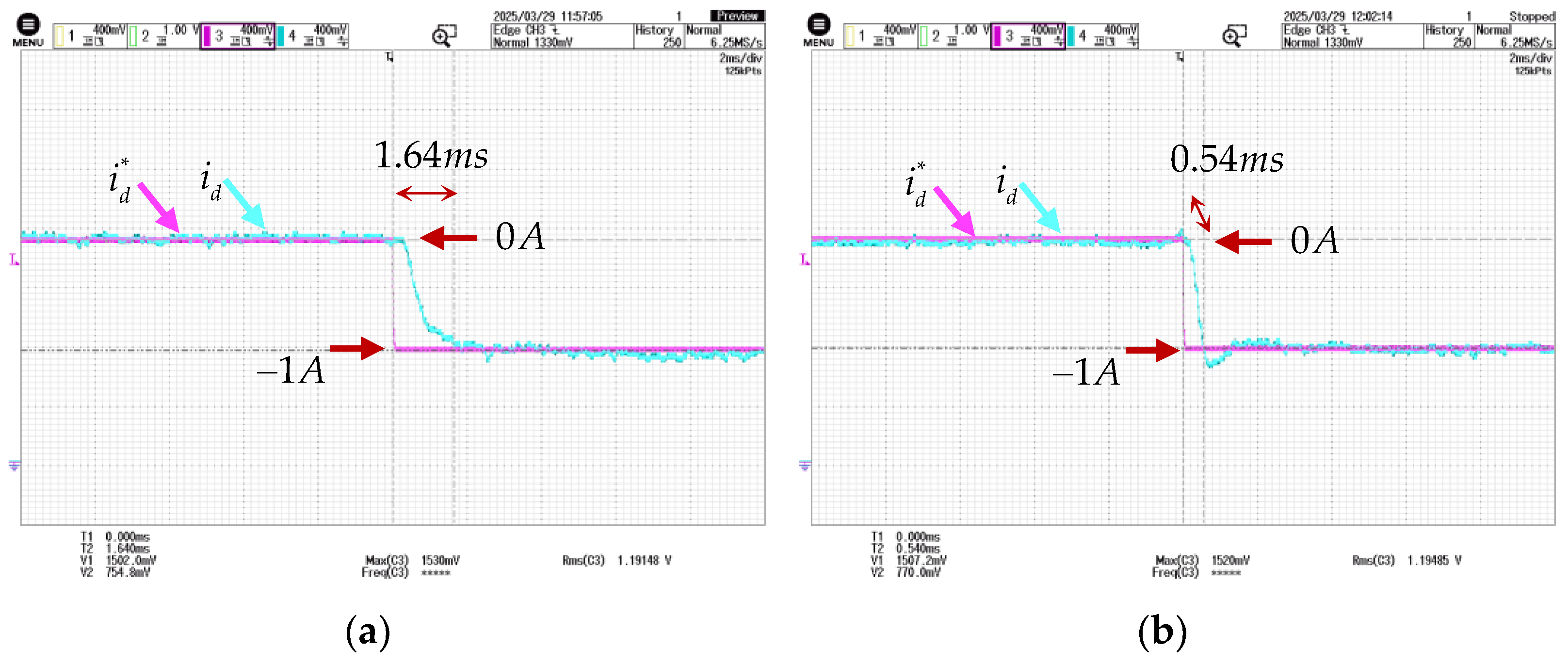
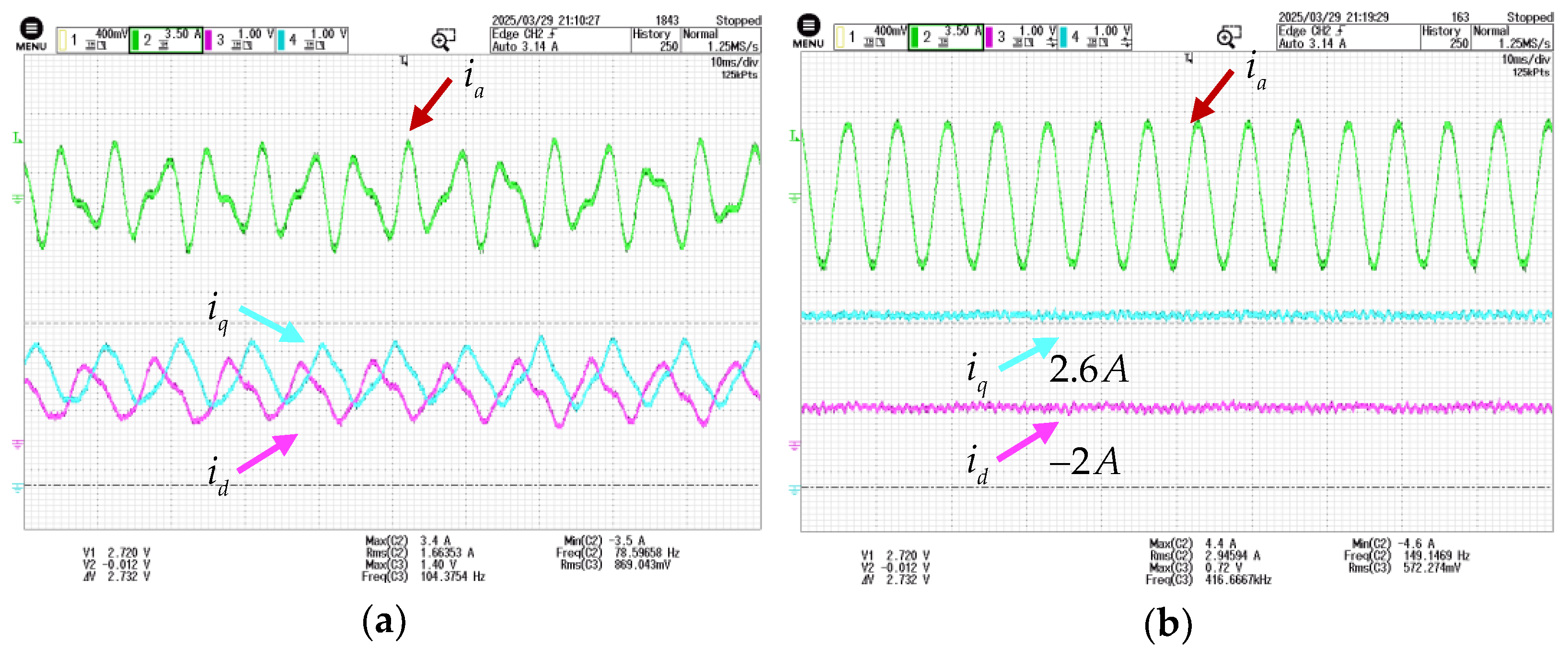
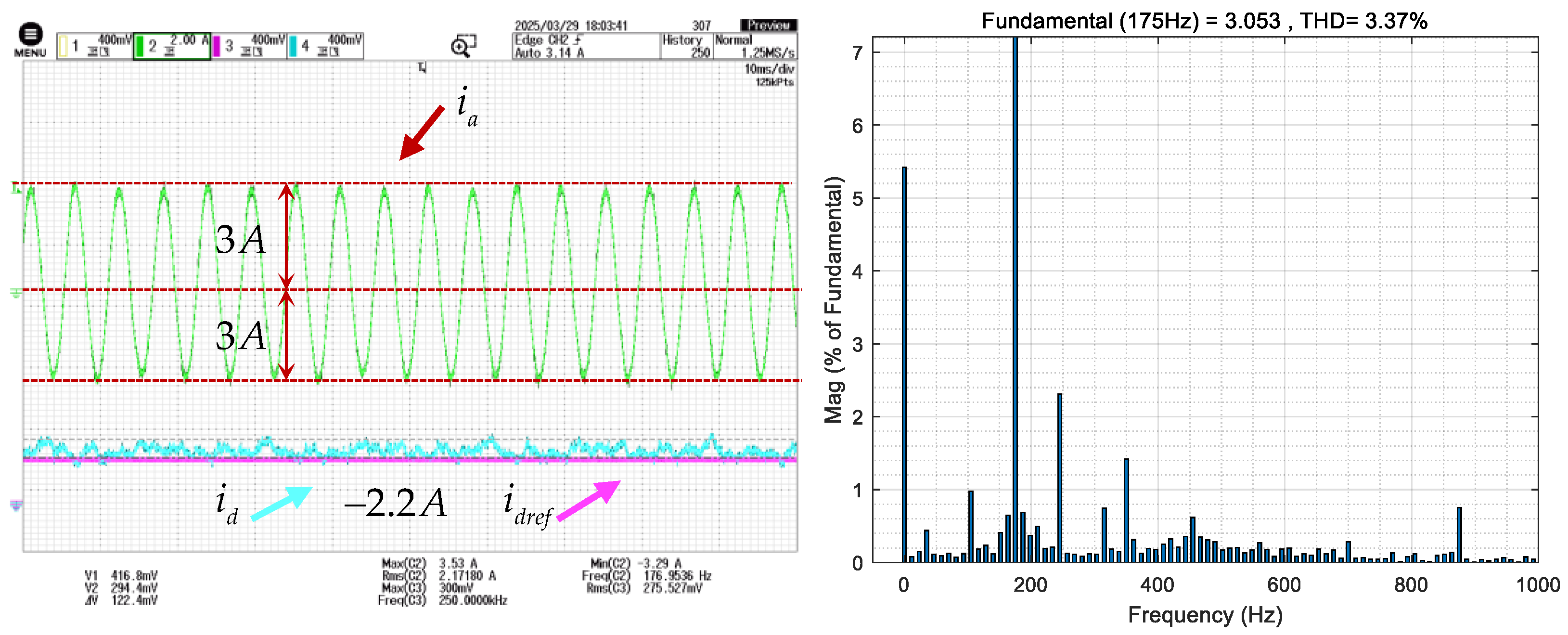
5.2. Experimental Results of Front-Stage MCESO
5.3. Experimental Results of Post-Stage MCESO
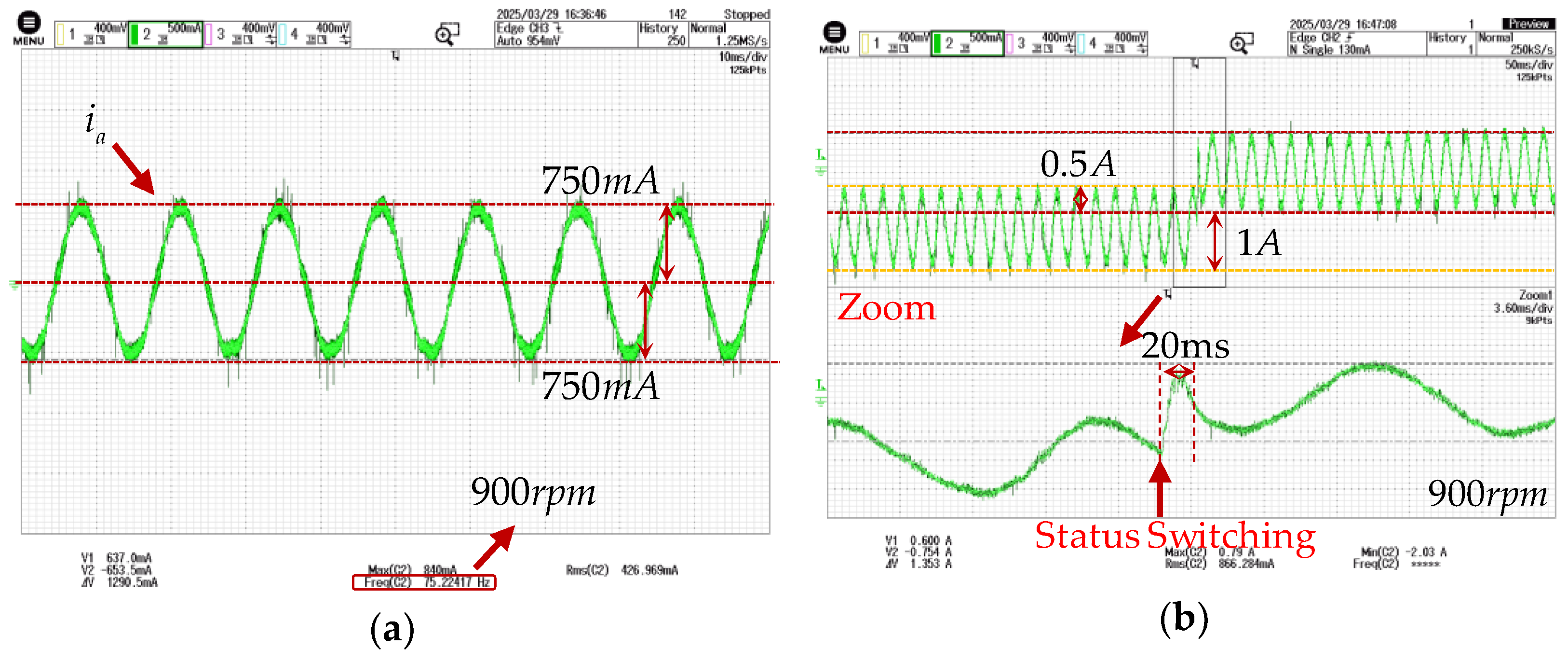
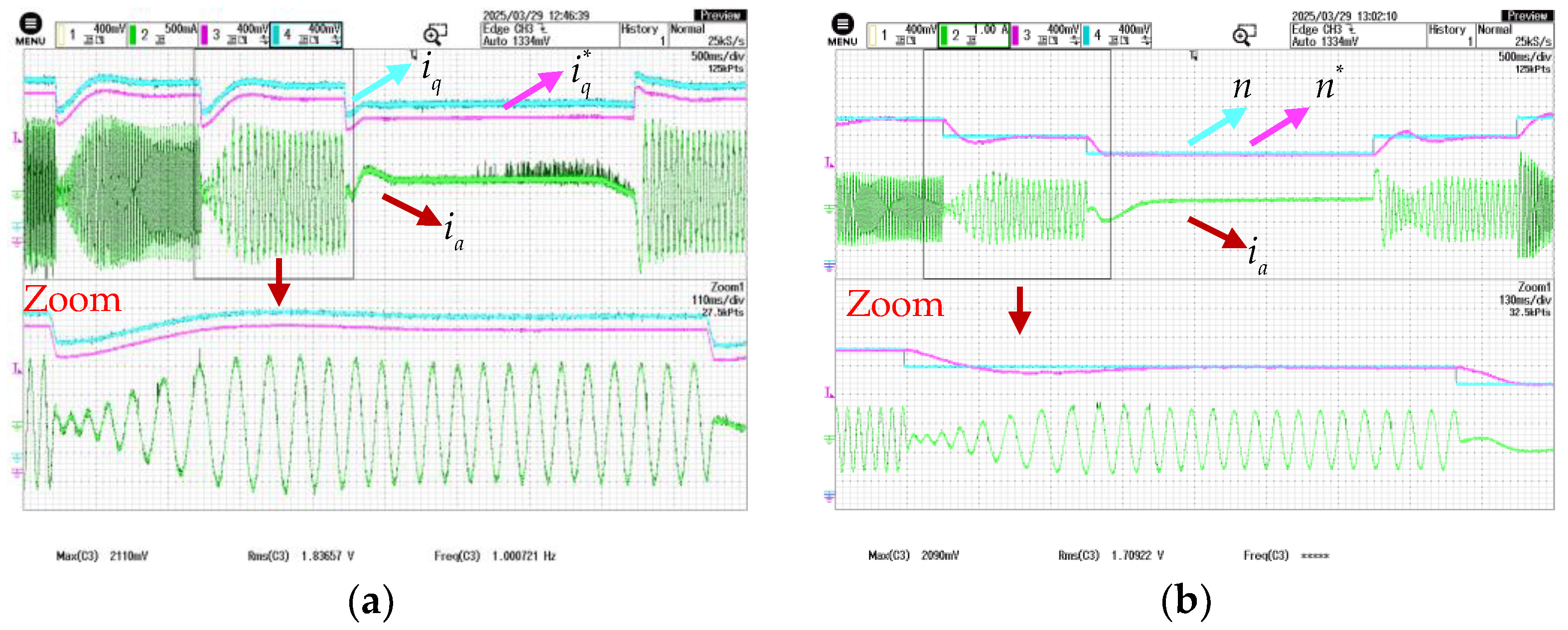
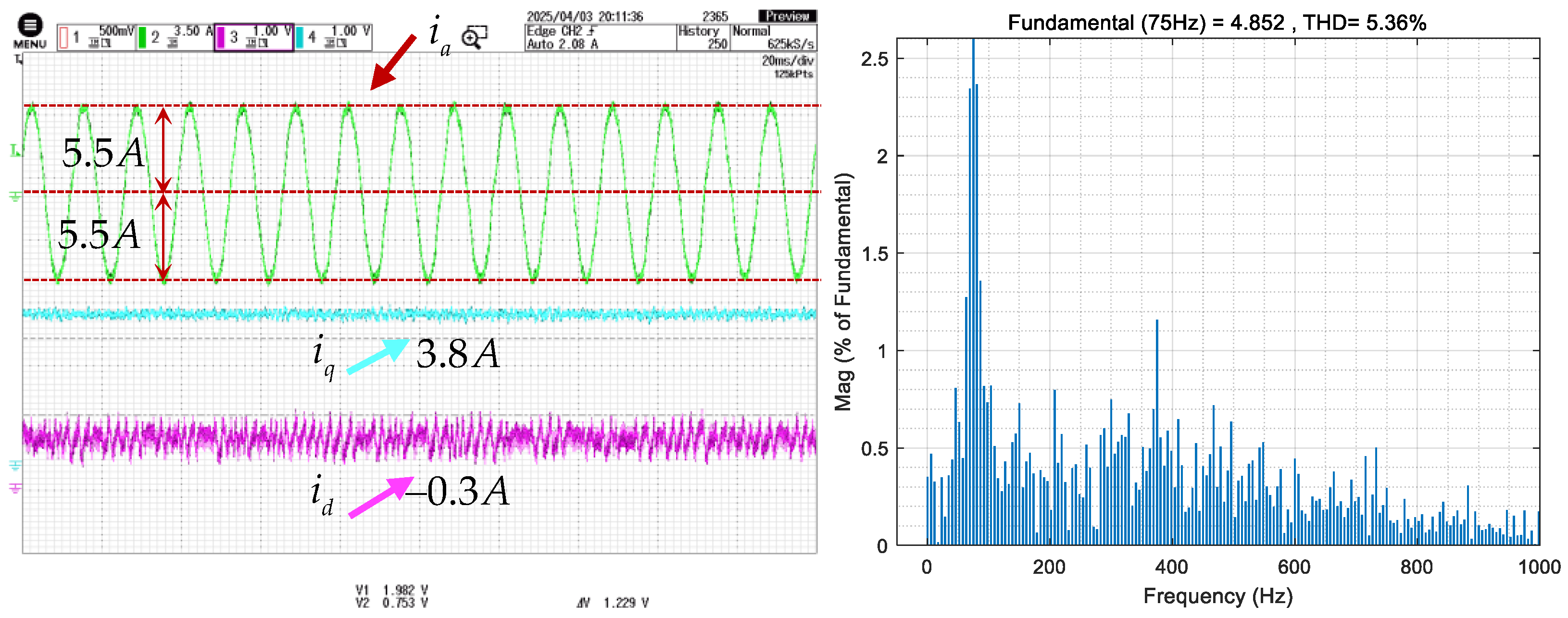
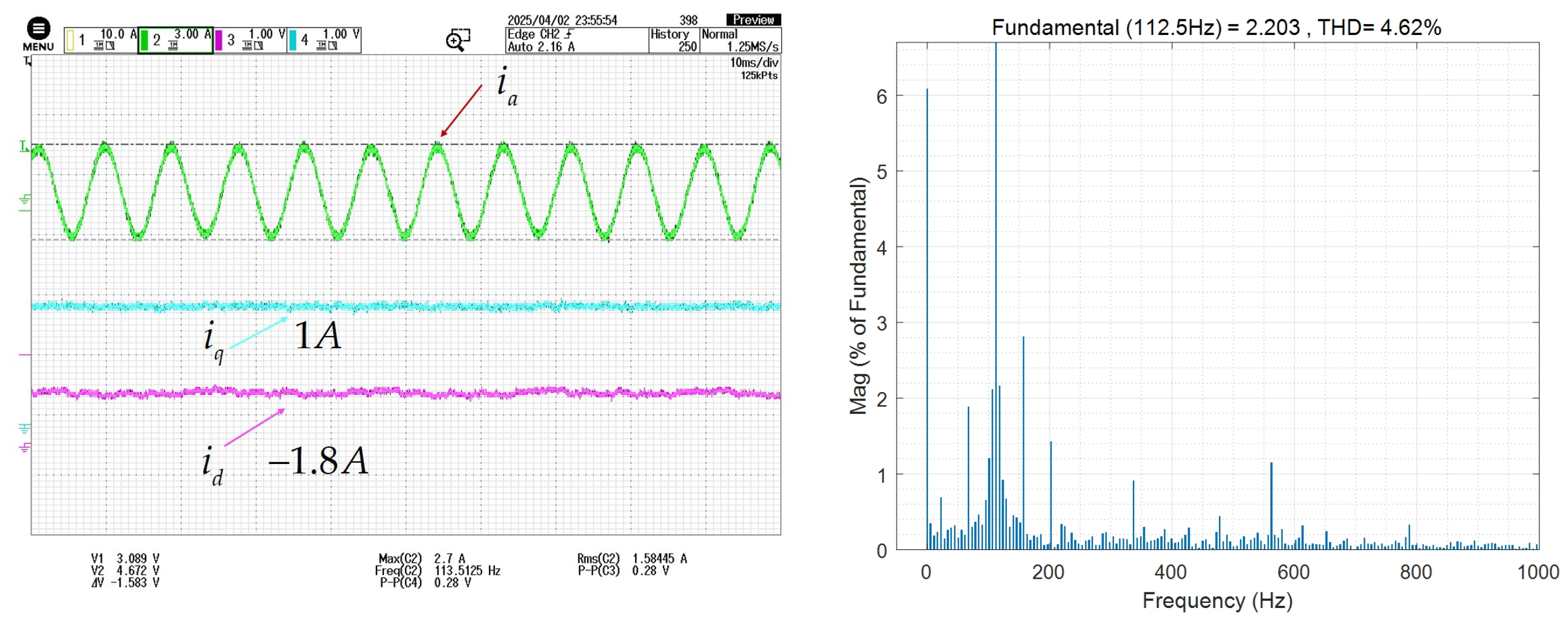
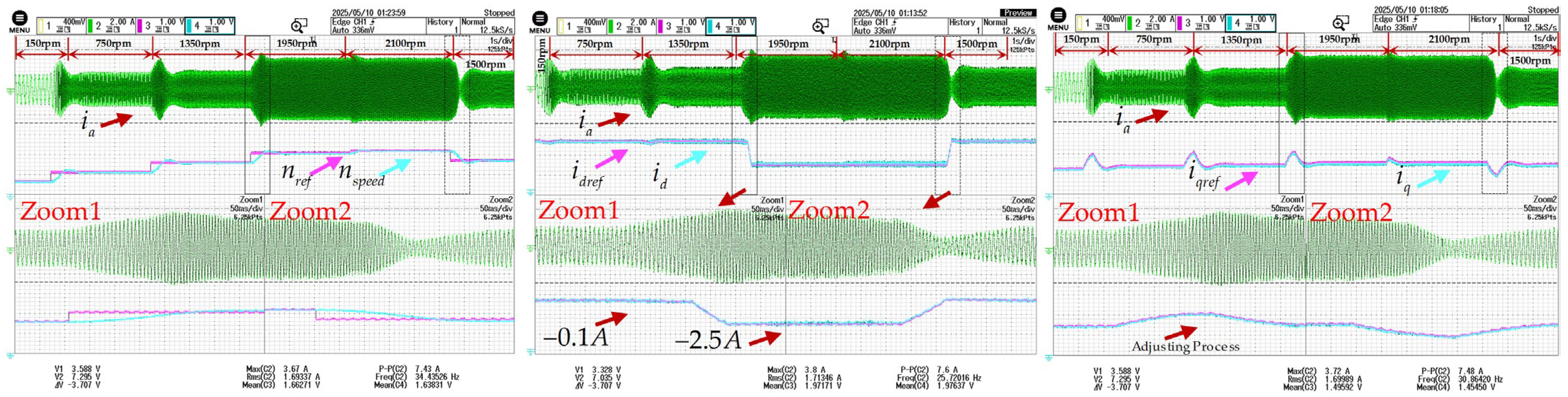
5.4. Experimental Results of MCESO Under Full-Speed-Range Operation
5.4.1. Operation Below Base Speed
5.4.2. Operation Above Base Speed
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Three-phase voltage, current, back EMF. | |
| Alpha-beta axis voltage and current. | |
| Dq axis voltage and current. | |
| Differential operator. | |
| Phase resistance and inductance. | |
| Alpha-beta axis inductance. | |
| Dq axis inductance and permanent magnet flux linkage. | |
| Point angular velocity and electrical angle. | |
| Measured current in different coordinate systems. | |
| The actual current in different coordinate systems. | |
| Current bias in different coordinate systems. | |
| Electromagnetic torque, measuring torque, torque bias. | |
| Alpha-beta axis current and bias estimation. | |
| The real value minus the observed value. | |
| Pi parameters. | |
| Resistance and inductance mismatch variation. | |
| Extended state variables—actual. | |
| Extended state variables—estimates. | |
| ESO coefficient. | |
| Interrupt cycle. | |
| Dq axis current reference given value. | |
| Resistance-inductance mismatch value under dq axis. | |
| Equivalent value of nonlinear voltage disturbance. | |
| Estimate dq axis voltage and current. | |
| non-linear function parameter. | |
| Alpha-beta axis lumped disturbance. | |
| DC disturbance and AC disturbance. | |
| Alpha-beta axis current error. |
Appendix A
References
- Zhou, M.; Fei, X.; Xu, W.; Cai, W.; Xie, Y.; Qiu, Z. Adaptive Gain-Based Double-Loop Full-Order Terminal Sliding Mode Control of a Surface-Mounted PMSM System. Energies 2025, 18, 2112. [Google Scholar] [CrossRef]
- Zhu, B.; Zhu, D.; Tao, T. Model-Free Adaptive Fuzzy Sliding-Mode Observer Control for PMSM. Energies 2025, 18, 1877. [Google Scholar] [CrossRef]
- Zou, J.; Zhu, P.; Zhang, W.; Xu, Y.; Zou, J. Software-Based Resolver-to-Digital Converter Using an α–β–γ Filter. IEEE Trans. Instrum. Meas. 2024, 73, 7502211. [Google Scholar] [CrossRef]
- Zhai, Y.; Zhang, W.; Xu, Y.; Zou, J. Parameter Identification of Permanent Magnet Synchronous Motor Based on Long Short Term Memory Neural Network. In Proceedings of the 2024 IEEE 10th International Power Electronics and Motion Control Conference (IPEMC2024-ECCE Asia), Chengdu, China, 17 May 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 3873–3878. [Google Scholar]
- Cheng, S.; Zhang, W.; Wang, J.; Ji, Q. Research on a Sensorless Control System for Dual-Branch Permanent Magnet Synchronous Motor with a Nonlinear Observer Based on Parameter Identification. In Proceedings of the 2024 7th International Conference on Power and Energy Applications (ICPEA), Taiyuan, China, 18 October 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 240–245. [Google Scholar]
- Cao, M.; Egashira, J.; Kaneko, K. High Efficiency Control of IPMSM for Electric Motorcycles. In Proceedings of the 2009 IEEE 6th International Power Electronics and Motion Control Conference, Wuhan, China, 17–20 May 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 1893–1897. [Google Scholar]
- Sun, T.; Wang, J. Extension of Virtual-Signal-Injection-Based MTPA Control for Interior Permanent-Magnet Synchronous Machine Drives Into the Field-Weakening Region. IEEE Trans. Ind. Electron. 2015, 62, 6809–6817. [Google Scholar] [CrossRef]
- Xia, Z.; Filho, S.R.; Xiao, D.; Fang, G.; Sun, Y.; Wiseman, J.; Emadi, A. Computation-Efficient Online Optimal Tracking Method for Permanent Magnet Synchronous Machine Drives for MTPA and Flux-Weakening Operations. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 5341–5353. [Google Scholar] [CrossRef]
- Xu, Q.; Cai, L. Developing an Approach in Calculating Reference Currents for Field-Weakening Control. IEEE Trans. Transp. Electrif. 2023, 9, 60–74. [Google Scholar] [CrossRef]
- Zhang, X.; Fang, S.; Zhang, H. Predictive Current Error Compensation Based Strong Robust Model Predictive Control for PMSM Drive Systems. IEEE Trans. Ind. Electron. 2024, 71, 15280–15289. [Google Scholar] [CrossRef]
- Fan, Y.; Chen, J.; Zhang, Q.; Cheng, M. An Improved Inertia Disturbance Suppression Method for PMSM Based on Disturbance Observer and Two-Degree-of-Freedom PI Controller. IEEE Trans. Power Electron. 2023, 38, 3590–3599. [Google Scholar] [CrossRef]
- Xue, W.; Madonski, R.; Lakomy, K.; Gao, Z.; Huang, Y. Add-On Module of Active Disturbance Rejection for Set-Point Tracking of Motion Control Systems. IEEE Trans. Ind. Appl. 2017, 53, 4028–4040. [Google Scholar] [CrossRef]
- Yan, Z.; Deng, S.; Yang, Z.; Zhao, X.; Yang, N.; Lu, Y. Improved Nonlinear Active Disturbance Rejection Control for a Continuous-Wave Pulse Generator with Cascaded Extended State Observer. Control Eng. Pract. 2024, 146, 105897. [Google Scholar] [CrossRef]
- Zhang, Y.; Yin, Z.; Bai, C.; Wang, G.; Liu, J. A Rotor Position and Speed Estimation Method Using an Improved Linear Extended State Observer for IPMSM Sensorless Drives. IEEE Trans. Power Electron. 2021, 36, 14062–14073. [Google Scholar] [CrossRef]
- Zeng, X.; Wang, W.; Wang, H. Adaptive PI and RBFNN PID Current Decoupling Controller for Permanent Magnet Synchronous Motor Drives: Hardware-Validated Results. Energies 2022, 15, 6353. [Google Scholar] [CrossRef]
- Yu, K.; Wang, Z.; Hua, W.; Cheng, M. Robust Cascaded Deadbeat Predictive Control for Dual Three-Phase Variable-Flux PMSM Considering Intrinsic Delay in Speed Loop. IEEE Trans. Ind. Electron. 2022, 69, 12107–12118. [Google Scholar] [CrossRef]
- Zhong, L.; Rahman, M.F.; Hu, W.Y.; Lim, K.W. Analysis of Direct Torque Control in Permanent Magnet Synchronous Motor Drives. IEEE Trans. Power Electron. 1997, 12, 528–536. [Google Scholar] [CrossRef]
- Casadei, D.; Profumo, F.; Serra, G.; Tani, A. FOC and DTC: Two Viable Schemes for Induction Motors Torque Control. IEEE Trans. Power Electron. 2002, 17, 779–787. [Google Scholar] [CrossRef]
- Sheikh, I.; Krishna, M.S.R.; Seshadrinath, J. Performance Comparison of FOC and DTC Techniques for SynRM in EV Applications. In Proceedings of the 2024 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Mangalore, India, 18 December 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1–6. [Google Scholar]
- Cortes, P.; Kazmierkowski, M.P.; Kennel, R.M.; Quevedo, D.E.; Rodriguez, J. Predictive Control in Power Electronics and Drives. IEEE Trans. Ind. Electron. 2008, 55, 4312–4324. [Google Scholar] [CrossRef]
- Morel, F.; Lin-Shi, X.; Retif, J.-M.; Allard, B.; Buttay, C. A Comparative Study of Predictive Current Control Schemes for a Permanent-Magnet Synchronous Machine Drive. IEEE Trans. Ind. Electron. 2009, 56, 2715–2728. [Google Scholar] [CrossRef]
- Moon, H.T.; Kim, H.S.; Youn, M.J. A Discrete-Time Predictive Current Control for PMSM. IEEE Trans. Power Electron. 2003, 18, 464–472. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, D.; Liu, J.; Gao, S.; Xu, W. Performance Improvement of Model-Predictive Current Control of Permanent Magnet Synchronous Motor Drives. IEEE Trans. Ind. Appl. 2017, 53, 3683–3695. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, D.; Huang, L. Generalized Multiple-Vector-Based Model Predictive Control for PMSM Drives. IEEE Trans. Ind. Electron. 2018, 65, 9356–9366. [Google Scholar] [CrossRef]
- Wei, Y.; Young, H.; Ke, D.; Wang, F.; Qi, H.; Rodríguez, J. Model-Free Predictive Control Using Sinusoidal Generalized Universal Model for PMSM Drives. IEEE Trans. Ind. Electron. 2024, 71, 13720–13731. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, L.; Zhang, Y. Model Predictive Current Control for PMSM Drives With Parameter Robustness Improvement. IEEE Trans. Power Electron. 2019, 34, 1645–1657. [Google Scholar] [CrossRef]
- Moreno, J.C.; Espi Huerta, J.M.; Gil, R.G.; Gonzalez, S.A. A Robust Predictive Current Control for Three-Phase Grid-Connected Inverters. IEEE Trans. Ind. Electron. 2009, 56, 1993–2004. [Google Scholar] [CrossRef]
- Young, H.A.; Perez, M.A.; Rodriguez, J. Analysis of Finite-Control-Set Model Predictive Current Control With Model Parameter Mismatch in a Three-Phase Inverter. IEEE Trans. Ind. Electron. 2016, 63, 3100–3107. [Google Scholar] [CrossRef]
- Attaianese, C.; D’Arpino, M.; Monaco, M.D.; Noia, L.P.D. Model-Based Detection and Estimation of DC Offset of Phase Current Sensors for Field Oriented PMSM Drives. IEEE Trans. Ind. Electron. 2023, 70, 6316–6325. [Google Scholar] [CrossRef]
- Kang, Y.G.; Reigosa, D.D. Dq-Transformed Error and Current Sensing Error Effects on Self-Sensing Control. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 1935–1945. [Google Scholar] [CrossRef]
- Zhang, Q.; Guo, H.; Liu, Y.; Guo, C.; Zhang, F.; Zhang, Z.; Li, G. A Novel Error-Injected Solution for Compensation of Current Measurement Errors in PMSM Drive. IEEE Trans. Ind. Electron. 2023, 70, 4608–4619. [Google Scholar] [CrossRef]
- Zuo, Y.; Wang, H.; Ge, X.; Zuo, Y.; Woldegiorgis, A.T.; Feng, X.; Lee, C.H.T. A Novel Current Measurement Offset Error Compensation Method Based on the Adaptive Extended State Observer for IPMSM Drives. IEEE Trans. Ind. Electron. 2024, 71, 3371–3382. [Google Scholar] [CrossRef]
- Lee, S.; Kim, H.; Lee, K. Current Measurement Offset Error Compensation in Vector-Controlled SPMSM Drive Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 2619–2628. [Google Scholar] [CrossRef]









| Motor Specification | Value | Motor Specification | Value |
|---|---|---|---|
| Motor Type | IPMSM | Stator Resistance | 0.425 Ω |
| Rated Power | 500 W | D-axis Inductance | 7.8 mH |
| Rated Current | 4 A | Q-axis Inductance | 10.5 mH |
| Rated Speed | 2000 rpm | Flux Linkage | 0.12475 Wb |
| Rated Voltage | 200 V | Switching Frequency | 10 kHz |
| Pairs of Poles | 5 | Rotational Inertia | 0.9 × 10−3 Kg·m2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Zhai, Y.; Zhu, P.; Liu, Y. Robust Wide-Speed-Range Control of IPMSM with Multi-Axis Coordinated Extended State Observer for Dynamic Performance Enhancement. Energies 2025, 18, 2938. https://doi.org/10.3390/en18112938
Zhang W, Zhai Y, Zhu P, Liu Y. Robust Wide-Speed-Range Control of IPMSM with Multi-Axis Coordinated Extended State Observer for Dynamic Performance Enhancement. Energies. 2025; 18(11):2938. https://doi.org/10.3390/en18112938
Chicago/Turabian StyleZhang, Wentao, Yanchen Zhai, Pengcheng Zhu, and Yiwei Liu. 2025. "Robust Wide-Speed-Range Control of IPMSM with Multi-Axis Coordinated Extended State Observer for Dynamic Performance Enhancement" Energies 18, no. 11: 2938. https://doi.org/10.3390/en18112938
APA StyleZhang, W., Zhai, Y., Zhu, P., & Liu, Y. (2025). Robust Wide-Speed-Range Control of IPMSM with Multi-Axis Coordinated Extended State Observer for Dynamic Performance Enhancement. Energies, 18(11), 2938. https://doi.org/10.3390/en18112938






