Economic Analysis of Nuclear Energy Cogeneration: A Comprehensive Review on Integrated Utilization
Abstract
1. Introduction
2. Technical Landscape of Nuclear Cogeneration
2.1. Classification of Nuclear Cogeneration Applications
2.1.1. Low-Temperature Applications (<250 °C)
2.1.2. Medium-Temperature System (250–550 °C)
2.1.3. High-Temperature Applications (>550 °C)
2.2. Reactor Technologies for Cogeneration
2.2.1. Light Water Reactors
2.2.2. Light Water Graphite Reactor
2.2.3. Pressurized Heavy Water Reactors
2.2.4. Advanced Reactors
2.3. Integration Methodologies
2.3.1. Thermal Extraction Techniques
2.3.2. Coupling with Thermal Energy Storage
3. Economic Models for Nuclear Cogeneration
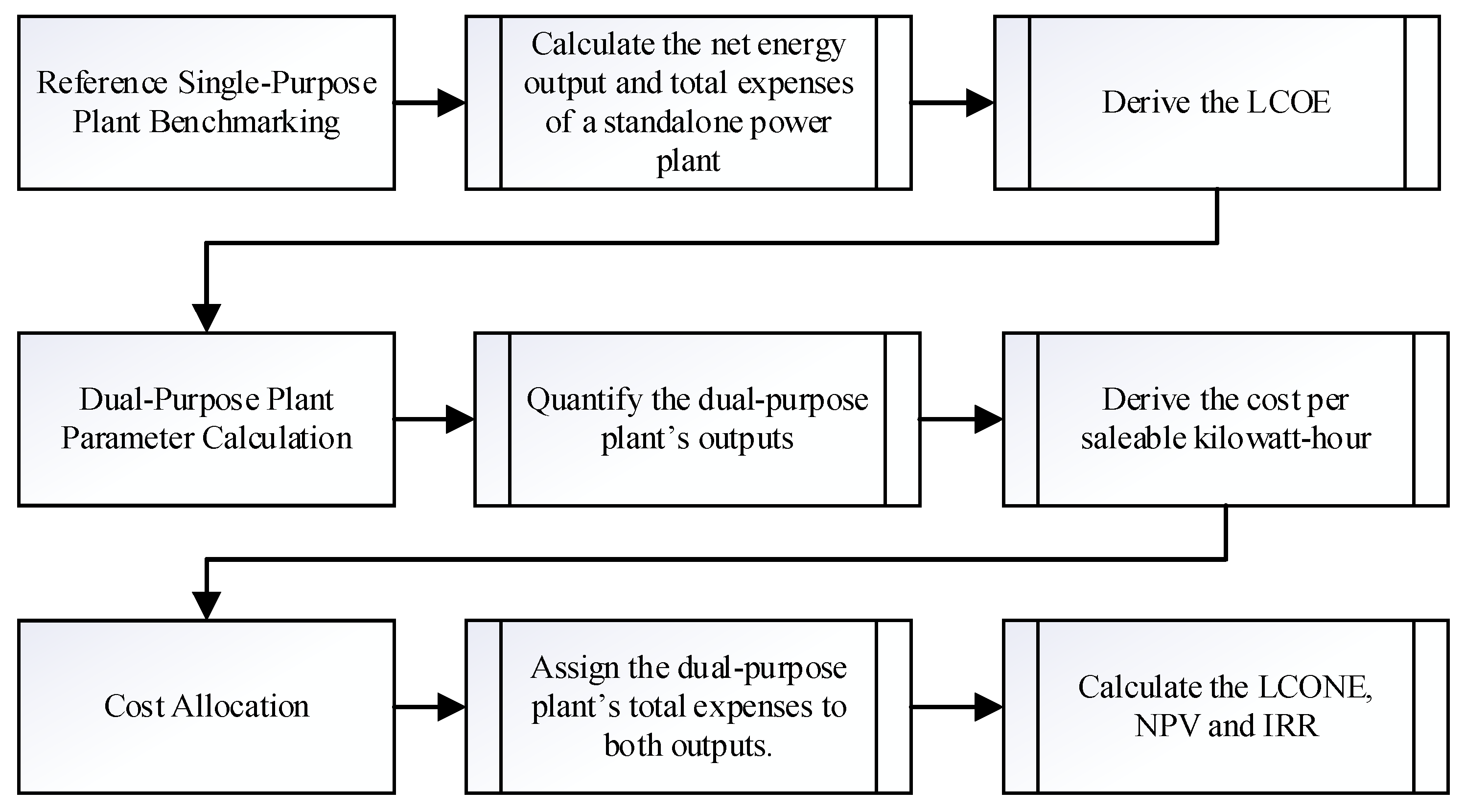
3.1. Economic Evaluation Models
3.1.1. LCOE Model
- (1)
- Standard LCOE with Time Discounting
- (2)
- Static LCOE
- (3)
- Monte Carlo LCOE with Endogenous Risks
3.1.2. Levelized Cost of Non-Electricity Model
3.1.3. Profitability Indicators
3.2. Cost Allocation
3.2.1. Energy Credit Method
3.2.2. Exergy-Based Method
3.2.3. Opportunity Cost Approach
3.2.4. Proportional Benefit Method
3.3. Policy-Driven Economics
3.3.1. Carbon Pricing Mechanisms
3.3.2. Value-Added Tax Exemption
3.3.3. Subsidized Loans
4. Sector-Specific Economic Analyses of Nuclear Cogeneration
4.1. District Heating Systems
4.2. Industrial Process Heat Applications
4.3. Hydrogen Economy Synergies
4.4. Desalination Economics
5. Market Dynamics and Policy Drivers
5.1. Regulatory Frameworks and Safety Paradigms
5.2. Carbon Pricing and Emission Trading Mechanisms
5.3. Subsidies and Tax Incentives
5.3.1. Direct Subsidies
5.3.2. Tax Credits
6. Future Prospects
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| LWR | light water reactor |
| HTGR | high-temperature gas-cooled reactor |
| MSR | molten salt reactor |
| VAT | value-added tax |
| NPP | nuclear power plant |
| CHP | combined heat and power |
| TES | thermal energy storage |
| BWR | boiling water reactor |
| VHTR | very-high-temperature reactor |
| PHWR | pressurized heavy water reactor |
| LWGR | light water graphite reactor |
| LCOE | levelized cost of electricity |
| LCONE | levelized cost of non-electricity |
| NPV | net present value |
| IRR | internal rate of return |
| LFR | lead-cooled fast reactor |
| HT | high temperature |
| CRF | capital recovery factor |
| SFF | sinking fund factor |
References
- Shcheklein, S.E.; Tashlykov, O.L.; Dubinin, A.M. Improving the energy efficiency of NPP. Nucl. Energy Technol. 2016, 2, 30–36. [Google Scholar] [CrossRef]
- Congedo, T.; Lahoda, E.; Matzie, R.; Task, K. The Nuclear Industry. In Handbook of Industrial Chemistry and Biotechnology; Kent, J.A., Ed.; Springer: Boston, MA, USA, 2012; pp. 829–874. [Google Scholar]
- Zakharikhina, L.V.; Lesnikova, P.S.; Kerimzade, V.V. Exploring secondary contamination in river and spring waters: A novel phenomenon arising from seawater intrusion into deep coastal aquifers. Mar. Pollut. Bull. 2025, 211, 117364. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.-T.; Jan, S.; Chen, M.-H.; Liu, L.-L.; Huang, J.-F.; Yang, Y.-J. Far-Field Influences Shadow the Effects of a Nuclear Power Plant’s Discharges in a Semi-Enclosed Bay. Sustainability 2023, 15, 9092. [Google Scholar] [CrossRef]
- Guimarães, L.S.F.; de Carvalho-Junior, L.; Façanha, G.L.; Resende, N.d.S.; Neves, L.M.; Cardoso, S.J. Meta-analysis of the thermal pollution caused by coastal nuclear power plants and its effects on marine biodiversity. Mar. Pollut. Bull. 2023, 195, 115452. [Google Scholar] [CrossRef]
- Sukhorukov, Y.G.; Smolkin, Y.V.; Kazarov, G.I.; Kulakov, E.N.; Kondurov, E.P.; Popov, A.V. Directions for Increasing Thermal Efficiency of an NPP with PWR. Therm. Eng. 2024, 71, 583–590. [Google Scholar] [CrossRef]
- Novotný, V.; Kim, J.; Cho, S.-B.; Saeed, R.M. Nuclear—Thermal energy storage configurations for industrial combined heat and power supply—Conceptual and thermodynamic study with high temperature gas-cooled reactor. Energy 2025, 322, 135544. [Google Scholar] [CrossRef]
- Khan, S.U.-D.; Khan, S.U.-D.; Danish, S.N.; Orfi, J.; Rana, U.A.; Haider, S. Chapter 6—Nuclear Energy Powered Seawater Desalination. In Renewable Energy Powered Desalination Handbook; Gude, V.G., Ed.; Butterworth-Heinemann: Oxford, UK, 2018; pp. 225–264. [Google Scholar]
- Ding, L.; Zhang, R.; Wang, C.; Xing, J. Research on Nuclear Seawater Desalination Technology Based on Small Modular Reactor ACP100. In Proceedings of the 23rd Pacific Basin Nuclear Conference, Beijing&Chengdu, China, 1–4 November 2022; Spring: Singapore, 2023; Volume 3, pp. 853–866. [Google Scholar]
- IAEA. New Technologies for Seawater Desalination Using Nuclear Energy; International Atomic Energy Agency: Vienna, Austria, 2015. [Google Scholar]
- Leurent, M.; Da Costa, P.; Rämä, M.; Persson, U.; Jasserand, F. Cost-benefit analysis of district heating systems using heat from nuclear plants in seven European countries. Energy 2018, 149, 454–472. [Google Scholar] [CrossRef]
- Tulkki, V.; Pursiheimo, E.; Lindroos, T.J. District Heat with Small Modular Reactors (SMR); VTT Technical Research Centre of Finland: Espoo, Finland, 2017. [Google Scholar]
- Samoilov, O.B.; Kurachenkov, A.V. Nuclear district heating plants AST-500. Present status and prospects for future in Russia. Nucl. Eng. Des. 1997, 173, 109–117. [Google Scholar] [CrossRef]
- Angulo, C.; Bogusch, E.; Bredimas, A.; Delannay, N.; Viala, C.; Ruer, J.; Muguerra, P.; Sibaud, E.; Chauvet, V.; Hittner, D.; et al. EUROPAIRS: The European project on coupling of High Temperature Reactors with industrial processes. Nucl. Eng. Des. 2012, 251, 30–37. [Google Scholar] [CrossRef]
- Hampe, J.; Madlener, R. Economics of High-Temperature Nuclear Reactors for Industrial Cogeneration; E.ON Energy Research Center, Future Energy Consumer Needs and Behavior (FCN): Aachen, Germany, 2012. [Google Scholar]
- Ruth, M.F.; Zinaman, O.R.; Antkowiak, M.; Boardman, R.D.; Cherry, R.S.; Bazilian, M.D. Nuclear-renewable hybrid energy systems: Opportunities, interconnections, and needs. Energy Convers. Manag. 2014, 78, 684–694. [Google Scholar] [CrossRef]
- IAEA. Guidance on Nuclear Energy Cogeneration; International Atomic Energy Agency: Vienna, Austria, 2019. [Google Scholar]
- NEA. Beyond Electricity: The Economics of Nuclear Cogeneration; Nuclear Energy Agency (NEA): Paris, France, 2022. [Google Scholar]
- Dincer, I.; Bicer, Y. Chapter 5—Integration of nuclear energy systems for multigeneration. In Integrated Energy Systems for Multigeneration; Dincer, I., Bicer, Y., Eds.; Elsevier: Amsterdam, The Netherlands, 2020; pp. 223–285. [Google Scholar]
- Choudhury, M.; Roy, P. Challenges with microplastic pollution in the regime of UN sustainable development goals. World Dev. Sustain. 2025, 6, 100216. [Google Scholar] [CrossRef]
- Moeen, M.S.; Jupesta, J.; Hanaoka, T. Integrated energy planning: Review of global practices for energy security and Paris Agreement implementation in Pakistan. Energy Nexus 2025, 18, 100413. [Google Scholar] [CrossRef]
- Leurent, M.; Jasserand, F.; Locatelli, G.; Palm, J.; Rämä, M.; Trianni, A. Driving forces and obstacles to nuclear cogeneration in Europe: Lessons learnt from Finland. Energy Policy 2017, 107, 138–150. [Google Scholar] [CrossRef]
- Jasserand, F.; Devezeaux de Lavergne, J.-G. Initial economic appraisal of nuclear district heating in France. EPJ—Nucl. Sci. Technol. 2016, 2, 39. [Google Scholar] [CrossRef]
- Lee, S.W.; Kim, D.; Seo, J.; Jo, H. Economic evaluations of hydrogen production and storage systems coupled with high-temperature gas-cooled reactors. Int. J. Hydrogen Energy 2025, 124, 191–203. [Google Scholar] [CrossRef]
- Huang, J.-L.; Jia, G.-B.; Han, L.-F.; Liu, W.-Q.; Huang, L.; Yang, Z.-H. Dynamic simulation analysis of molten salt reactor-coupled air–steam combined cycle power generation system. Nucl. Sci. Tech. 2024, 35, 30. [Google Scholar] [CrossRef]
- Sato, H.; Yan, X.L.; Tachibana, Y.; Kunitomi, K. GTHTR300—A nuclear power plant design with 50% generating efficiency. Nucl. Eng. Des. 2014, 275, 190–196. [Google Scholar] [CrossRef]
- Peng, C.; Zhang, H.; Wu, Y.; Guo, J.; Peng, W.; Zhang, P.; Li, F. Assessment of hydrogen leakage hazards in VHTR-based nuclear hydrogen production systems: A variable pressure analysis model. Int. J. Hydrogen Energy 2025, 128, 223–235. [Google Scholar] [CrossRef]
- Mignacca, B.; Locatelli, G. Economics and finance of Molten Salt Reactors. Prog. Nucl. Energy 2020, 129, 103503. [Google Scholar] [CrossRef]
- Yang, Q.; Zheng, Y.; Wu, H. Advancements and challenges in small modular lead/lead bismuth eutectic cooled fast reactors: A 30-year overview. Ann. Nucl. Energy 2025, 218, 111434. [Google Scholar] [CrossRef]
- Lindroos, T.; Pursiheimo, E.; Sahlberg, V.; Tulkki, V. A techno-economic assessment of NuScale and DHR-400 reactors in a district heating and cooling grid. Energy Sources Part B-Econ. Plan. Policy 2019, 14, 13–24. [Google Scholar] [CrossRef]
- Yoo, Y.; Arunachalam, M.; Elmakki, T.; Al-Ghamdi, A.S.; Bassi, H.M.; Mohammed, A.M.; Ryu, S.; Yong, S.; Shon, H.K.; Park, H.; et al. Evaluating the economic and environmental viability of small modular reactor (SMR)-powered desalination technologies against renewable energy systems. Desalination 2025, 602, 118624. [Google Scholar] [CrossRef]
- IAEA. Opportunities for Cogeneration with Nuclear Energy; International Atomic Energy Agency: Vienna, Austria, 2017. [Google Scholar]
- Thilagam, L.; Mohapatra, D.K. Preliminary neutronics analysis for generation III+ VVER design—VVER-1200. Nucl. Part. Phys. Proc. 2023, 341, 98–103. [Google Scholar] [CrossRef]
- Vasilyev, B.A.; Vasyaev, A.V.; Gusev, D.V.; Marova, E.V.; Staroverov, A.I.; Shepelev, S.F. Current status of BN-1200M reactor plant design. Nucl. Eng. Des. 2021, 382, 111384. [Google Scholar] [CrossRef]
- Kalyakin, S.G.; Kozlov, F.A.; Sorokin, A.P.; Bogoslovskaya, G.P.; Ivanov, A.P.; Konovalov, M.A.; Morozov, A.V.; Stogov, V.Y. Investigations for the substantiation of high-temperature nuclear power generation technology using fast sodium-cooled reactor for hydrogen production and other innovative applications (Part 1). Nucl. Energy Technol. 2016, 2, 282–286. [Google Scholar] [CrossRef]
- Li, Y.; Chen, C.; Hu, J.; Su, J.; Liu, H. Analysis of Current Status and Development Trend of Nuclear District Heating. In Proceedings of the 23rd Pacific Basin Nuclear Conference, Volume 3, Beijing&Chengdu, China, 1–4 November 2022; Spring: Singapore, 2023; pp. 301–307. [Google Scholar]
- Weiqi, L.; Jinshi, W.; Kai, X.; Zhiyong, S.; Xingmin, L.; Gen, L.; Junjie, Y. Capacity Configuration and Operation Optimization of a Low-Temperature Reactor Nuclear Heating System with Heat Storage. Nucl. Power Eng. 2024, 45, 213–220. [Google Scholar]
- Liu, W.; Zhao, Q.; Sun, Z.; Liu, X.; Li, G.; Yan, J.; Wang, J. Economic optimization and thermodynamic analysis of a novel nuclear district cooling system. Appl. Therm. Eng. 2024, 247, 123042. [Google Scholar] [CrossRef]
- Kontu, K.; Rinne, S.; Olkkonen, V.; Lahdelma, R.; Salminen, P. Multicriteria evaluation of heating choices for a new sustainable residential area. Energy Build. 2015, 93, 169–179. [Google Scholar] [CrossRef]
- Kim, K.; Kim, D.; Ju, H. Nuclear Power Plant Cogeneration System, Has District Heating Heat Exchanger for Producing Hot Water, and Thermal Storage Tank for Storing Thermal Energy by Using Steam Extracted from Turbine; Korea Hydro & Nuclear Power Co., Ltd. (Kepc-C): Gyeongju, Republic of Korea, 2025. [Google Scholar]
- Sundarrajan, P.; Thakur, J.; Meha, D. Harnessing hydrogen and thermal energy storage: Sweden’s path to a 100 % renewable energy system by 2045. Renew. Sustain. Energy Rev. 2025, 210, 115041. [Google Scholar] [CrossRef]
- Sanongboon, P.; Pettigrew, T.; Moore, M. Techno-economic analysis of small modular reactor for oil sands extraction and upgrading in Canada. Nucl. Eng. Des. 2024, 425, 113325. [Google Scholar] [CrossRef]
- Xing, J.; Song, D.; Wu, Y. HPR1000: Advanced Pressurized Water Reactor with Active and Passive Safety. Engineering 2016, 2, 79–87. [Google Scholar] [CrossRef]
- IAEA. Nuclear–Renewable Hybrid Energy Systems for Decarbonized Energy Production and Cogeneration; International Atomic Energy Agency: Vienna, Austria, 2019. [Google Scholar]
- Kang, S.; Yim, M. Coupled system model analysis for a small modular reactor cogeneration (combined heat and power) application. Energy 2023, 262, 125481. [Google Scholar] [CrossRef]
- Lin, N.; Xu, L. Navigating the Implementation of Tax Credits for Natural-Gas-Based Low-Carbon-Intensity Hydrogen Projects. Energies 2024, 17, 1604. [Google Scholar] [CrossRef]
- Iakovleva, M.; Rayner, J. Accelerating the deployment of SMRs in Canada: The importance of intermediaries. Environ. Innov. Soc. Transit. 2024, 53, 100918. [Google Scholar] [CrossRef]
- Dong, Z.; Zhang, Z.; Dong, Y.; Shi, L.; Huang, X.; Zhu, Y.; Jiang, D. Testing the feasibility of multi-modular design in an HTR-PM nuclear plant. Nat. Commun. 2025, 16, 2778. [Google Scholar] [CrossRef]
- Mansouri, N.Y.; Ghoniem, A.F. Does nuclear desalination make sense for Saudi Arabia? Desalination 2017, 406, 37–43. [Google Scholar] [CrossRef]
- Ahmad, A.; Ramana, M.V. Too costly to matter: Economics of nuclear power for Saudi Arabia. Energy 2014, 69, 682–694. [Google Scholar] [CrossRef]
- Sawicki, J.; Brett, M. Mossbauer Study of Corrosion Products from a CANDU Secondary System. Nucl. Instrum. Methods Phys. Res. Sect. B-Beam Interact. Mater. At. 1993, 76, 254–257. [Google Scholar] [CrossRef]
- Starkov, S.O.; Lavrenkov, Y.N. Prediction of the moderator temperature field in a heavy water reactor based on a cellular neural network. Nucl. Energy Technol. 2017, 3, 133–140. [Google Scholar] [CrossRef]
- Yan, X.; Sato, H.; Sumita, J.; Nomoto, Y.; Horii, S.; Imai, Y.; Kasahara, S.; Suzuki, K.; Iwatsuki, J.; Terada, A.; et al. Design of HTTR-GT/H2 test plant. Nucl. Eng. Des. 2018, 329, 223–233. [Google Scholar] [CrossRef]
- Kunitomi, K.; Yan, X.; Nishihara, T.; Sakaba, N.; Mouri, T. Jaea’s VHTR for hydrogen and electricity cogeneration: GTHTR300C. Nucl. Eng. Technol. 2007, 39, 9–20. [Google Scholar] [CrossRef]
- 2—Features of a PWR plant. In Pressurized Water Reactors; Mimaki, H., Kanzaki, Y., Yamamoto, T., Eds.; Elsevier: Amsterdam, The Netherlands, 2024; pp. 43–262. [Google Scholar]
- Nishio, H.; Kitani, T.; Kurashige, T. 5—Advanced PWRs. In Pressurized Water Reactors; Mimaki, H., Kanzaki, Y., Yamamoto, T., Eds.; Elsevier: Amsterdam, The Netherlands, 2024; pp. 347–402. [Google Scholar]
- Matsuura, M.; Shirahama, H.; Kawai, H.; Suzuki, H.; Katayama, Y.; Ikeda, H. 2—Features of BWR plant. In Boiling Water Reactors; Nishida, K., Morooka, S., Mori, M., Koizumi, Y., Eds.; Elsevier: Amsterdam, The Netherlands, 2023; Volume 4, pp. 59–165. [Google Scholar]
- Duffey, R.B.; Pioro, I.L.; Pioro, R. 1—Introduction. World energy production and the contribution of PHWRs. In Pressurized Heavy Water Reactors; Riznic, J.R., Ed.; Elsevier: Amsterdam, The Netherlands, 2022; Volume 7, pp. 1–44. [Google Scholar]
- Filburn, T.; Bullard, S. Russian Reactor Design History. In Three Mile Island, Chernobyl and Fukushima: Curse of the Nuclear Genie; Springer International Publishing: Cham, Switzerland, 2016; pp. 43–53. [Google Scholar]
- Locatelli, G.; Mancini, M.; Todeschini, N. Generation IV nuclear reactors: Current status and future prospects. Energy Policy 2013, 61, 1503–1520. [Google Scholar] [CrossRef]
- Ingersoll, D.; Houghton, Z.; Bromm, R.; Desportes, C. NuScale small modular reactor for Co-generation of electricity and water. Desalination 2014, 340, 84–93. [Google Scholar] [CrossRef]
- Squarer, D.; Schulenberg, T.; Struwe, D.; Oka, Y.; Bittermann, D.; Aksan, N.; Maraczy, C.; Kyrki-Rajamäki, R.; Souyri, A.; Dumaz, P. High performance light water reactor. Nucl. Eng. Des. 2003, 221, 167–180. [Google Scholar] [CrossRef]
- Kraemer, J.; Bauer, H. New Russian reactor concepts. Atw-Int. Z. Kernenerg. 1996, 41, 237–243. [Google Scholar]
- Khalid, F.; Dincer, I.; Rosen, M.A. Comparative assessment of CANDU 6 and Sodium-cooled Fast Reactors for nuclear desalination. Desalination 2016, 379, 182–192. [Google Scholar] [CrossRef]
- Zohuri, B. Nuclear Hydrogen Production Plants. In Hydrogen Energy: Challenges and Solutions for a Cleaner Future; Springer International Publishing: Cham, Switzerland, 2019; pp. 185–227. [Google Scholar]
- LeBlanc, D.; Rodenburg, C. 18—Integral molten salt reactor. In Molten Salt Reactors and Thorium Energy; Dolan, T.J., Ed.; Woodhead Publishing: Cambridge, UK, 2017; pp. 541–556. [Google Scholar]
- Johar, D.; Sharma, D.; Soni, S. Comparative studies on micro cogeneration, micro cogeneration with thermal energy storage and micro trigeneration with thermal energy storage system using same power plant. Energy Convers. Manag. 2020, 220, 113082. [Google Scholar] [CrossRef]
- Al Rashdi, M.R.; Alaabed, S.; El Tokhi, M.; Howari, F.M.; El Mowafi, W.; Arabi, A.A. Distribution of heavy metals around the Barakah nuclear power plant in the United Arab Emirates. Environ. Sci. Pollut. Res. 2017, 24, 19835–19851. [Google Scholar] [CrossRef]
- Moore, M.; Korinny, A.; Shropshire, D.; Sadhankar, R. Benchmarking of nuclear economics tools. Ann. Nucl. Energy 2017, 103, 122–129. [Google Scholar] [CrossRef]
- Geissmann, T. A probabilistic approach to the computation of the levelized cost of electricity. Energy 2017, 124, 372–381. [Google Scholar] [CrossRef]
- Stoiljkovic, V. Net present value analysis-Comparing engineering projects by financial return. IEEE Potentials 2010, 29, 17–21. [Google Scholar] [CrossRef]
- Barry, P.; Robison, L. Technical Note: Economic Rates of Return and Investment Analysis. Eng. Econ. 2014, 59, 231–236. [Google Scholar] [CrossRef]
- Gupta, R.; Soini, M.; Patel, M.; Parra, D. Levelized cost of solar photovoltaics and wind supported by storage technologies to supply firm electricity. J. Energy Storage 2020, 27, 101027. [Google Scholar] [CrossRef]
- Tariq, S.; Safder, U.; Yoo, C. Exergy-based weighted optimization and smart decision-making for renewable energy systems considering economics, reliability, risk, and environmental assessments. Renew. Sustain. Energy Rev. 2022, 162, 112445. [Google Scholar] [CrossRef]
- Carlsson, J.; Shropshire, D.; van Heek, A.; Fütterer, M. Economic viability of small nuclear reactors in future European cogeneration markets. Energy Policy 2012, 43, 396–406. [Google Scholar] [CrossRef]
- Correljé, A. The European Natural Gas Market. Curr. Sustain./Renew. Energy Rep. 2016, 3, 28–34. [Google Scholar] [CrossRef]
- Yue, X.-L.; Gao, Q.-X. Contributions of natural systems and human activity to greenhouse gas emissions. Adv. Clim. Change Res. 2018, 9, 243–252. [Google Scholar] [CrossRef]
- Ashoori, S.; Gates, I.D. Small modular nuclear reactors: A pathway to cost savings and environmental progress in SAGD operations. Next Energy 2024, 4, 100128. [Google Scholar] [CrossRef]
- Zhang, Z.; Dong, Y.; Li, F.; Zhang, Z.; Wang, H.; Huang, X.; Li, H.; Liu, B.; Wu, X.; Wang, H.; et al. The Shandong Shidao Bay 200 MWe High-Temperature Gas-Cooled Reactor Pebble-Bed Module (HTR-PM) Demonstration Power Plant: An Engineering and Technological Innovation. Engineering 2016, 2, 112–118. [Google Scholar] [CrossRef]
- Schulenberg, T.; Leung, L.K.H.; Oka, Y. Review of R&D for supercritical water cooled reactors. Prog. Nucl. Energy 2014, 77, 282–299. [Google Scholar]
- Hada, K.; Shibata, T.; Nishihara, T.; Shiozawa, S. Universally applicable design concept of stably controlling an HTGR-hydrogen production system. J. At. Energy Soc. Jpn. 1996, 38, 834–844. [Google Scholar] [CrossRef]
- Hino, R.; Miyamoto, Y. Preliminary Test of Hydrogen-Production by High-Temperature Electrolysis of Steam. J. At. Energy Soc. Jpn. 1993, 35, 546–548. [Google Scholar] [CrossRef]
- Bleischwitz, R.; Bader, N. Policies for the transition towards a hydrogen economy: The EU case. Energy Policy 2010, 38, 5388–5398. [Google Scholar] [CrossRef]
- Baig, M.B.; Al Kutbi, A.A. Design features of a 20 migd SWRO desalination plant, Al Jubail, Saudi Arabia. Desalination 1998, 118, 5–12. [Google Scholar] [CrossRef]
- Yan, H.-m.; Cao, C.-y.; Bai, G.; Bai, W. Seawater Desalination Technology Route and Analysis of Production Capacity for Large Commercial Nuclear Power Plant; Spring: Singapore, 2017; pp. 865–872. [Google Scholar]
- Shahmansouri, A.; Min, J.; Jin, L.; Bellona, C. Feasibility of extracting valuable minerals from desalination concentrate: A comprehensive literature review. J. Clean. Prod. 2015, 100, 4–16. [Google Scholar] [CrossRef]
- Boev, B. Non-Electric Applications of Nuclear Energy—A Theoretical Overview and Socioeconomic Opportunities. 2023. Available online: https://www.researchgate.net/publication/374701541_NON-ELECTRIC_APPLICATIONS_OF_NUCLEAR_ENERGY_-_A_THEORETICAL_OVERVIEW_AND_SOCIOECONOMIC_OPPORTUNITIES (accessed on 28 May 2025).
- Salant, S.W. What ails the European Union׳s emissions trading system? J. Environ. Econ. Manag. 2016, 80, 6–19. [Google Scholar] [CrossRef]
- Schultz, E.; Swieringa, J. Catalysts for price discovery in the European Union Emissions Trading System. J. Bank. Financ. 2014, 42, 112–122. [Google Scholar] [CrossRef]
- Weng, Q.; Xu, H. A review of China’s carbon trading market. Renew. Sustain. Energy Rev. 2018, 91, 613–619. [Google Scholar] [CrossRef]
- Brink, C.; Vollebergh, H.R.J.; van der Werf, E. Carbon pricing in the EU: Evaluation of different EU ETS reform options. Energy Policy 2016, 97, 603–617. [Google Scholar] [CrossRef]
- Weng, Y.; Da, Z.; Lanlan, L.; and Zhang, X. A general equilibrium analysis of floor prices for China’s national carbon emissions trading system. Clim. Policy 2018, 18 (Suppl. S1), 60–70. [Google Scholar] [CrossRef]
- Zhang, M.; Liu, Y.; Su, Y. Comparison of Carbon Emission Trading Schemes in the European Union and China. Climate 2017, 5, 70. [Google Scholar] [CrossRef]
- Elder, R.; Allen, R. Nuclear heat for hydrogen production: Coupling a very high/high temperature reactor to a hydrogen production plant. Prog. Nucl. Energy 2009, 51, 500–525. [Google Scholar] [CrossRef]
- Katebah, M.; Al-Rawashdeh, M.m.; Linke, P. Analysis of hydrogen production costs in Steam-Methane Reforming considering integration with electrolysis and CO2 capture. Clean. Eng. Technol. 2022, 10, 100552. [Google Scholar] [CrossRef]
- Jordaan, S.M.; Romo-Rabago, E.; McLeary, R.; Reidy, L.; Nazari, J.; Herremans, I.M. The role of energy technology innovation in reducing greenhouse gas emissions: A case study of Canada. Renew. Sustain. Energy Rev. 2017, 78, 1397–1409. [Google Scholar] [CrossRef]
- deLlano-Paz, F.; Calvo-Silvosa, A.; Iglesias Antelo, S.; Soares, I. The European low-carbon mix for 2030: The role of renewable energy sources in an environmentally and socially efficient approach. Renew. Sustain. Energy Rev. 2015, 48, 49–61. [Google Scholar] [CrossRef]
- Zhang, Z.; Sun, Y. Economic potential of modular reactor nuclear power plants based on the Chinese HTR-PM project. Nucl. Eng. Des. 2007, 237, 2265–2274. [Google Scholar] [CrossRef]
- Borenstein, S.; Davis, L.W. The Distributional Effects of US Clean Energy Tax Credits. Tax Policy Econ. 2016, 30, 191–234. [Google Scholar] [CrossRef]
- Berry, A. The distributional effects of a carbon tax and its impact on fuel poverty: A microsimulation study in the French context. Energy Policy 2019, 124, 81–94. [Google Scholar] [CrossRef]
- Miyamoto, Y.; Shiozawa, S.; Ogawa, M.; Hada, K.; Inagaki, Y.; Takeda, T.; Nishihara, T. Overview of hydrogen production program in HTTR. In Proceedings of the IAEA Technical Committee Meeting on High Temperature Gas Cooled Reactor Applications and Future Prospects, Petten, The Netherlands, 10–12 November 1997; pp. 121–131. [Google Scholar]
- Chebac, R.; Cammi, A.; Ricotti, M.E.; Lorenzi, S.; Sadeghi, K.; Hadi Ghazaie, S.; Sokolova, E.; Fedorovich, E. ALFRED reactor and hybrid systems: A test case. Ann. Nucl. Energy 2023, 191, 109934. [Google Scholar] [CrossRef]

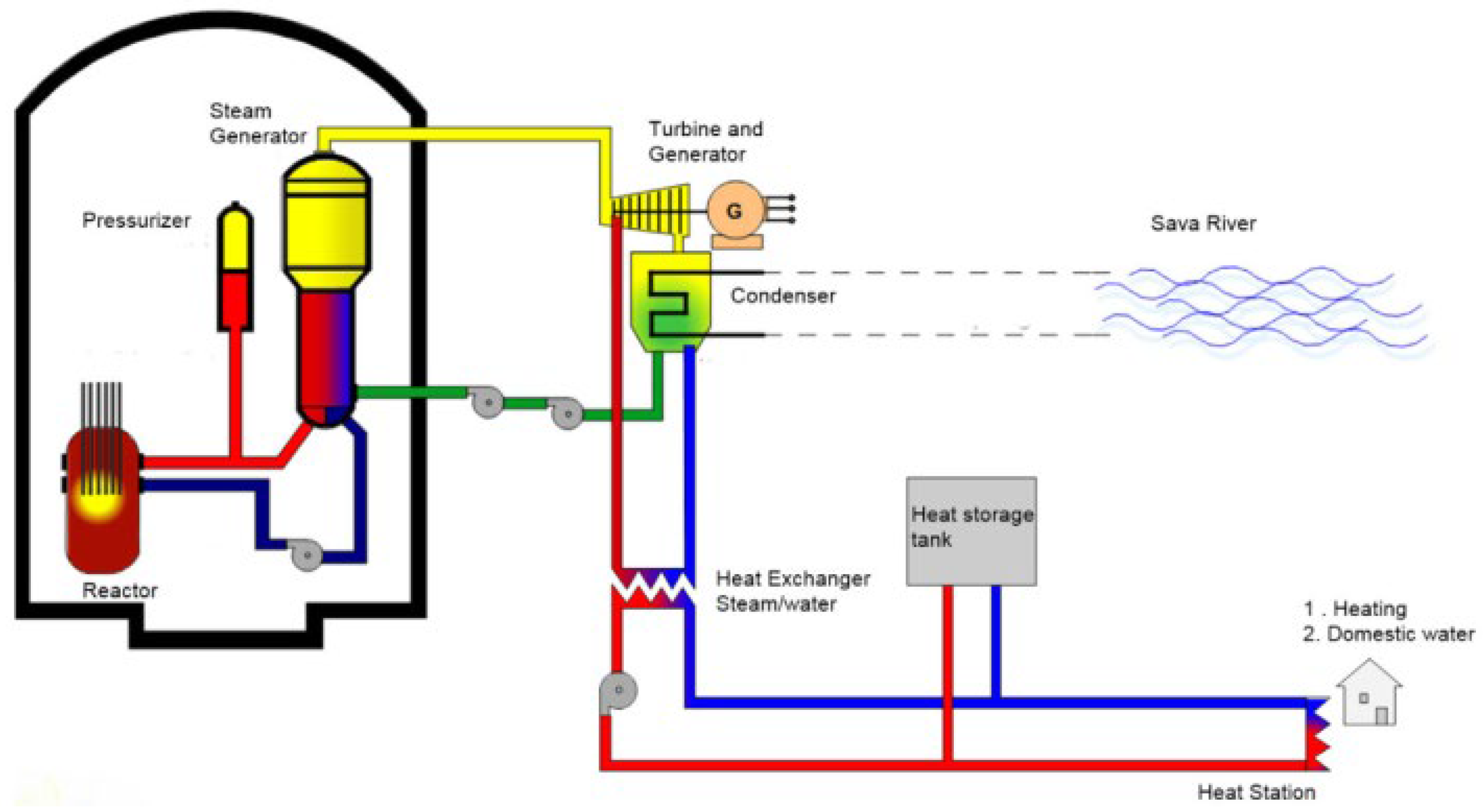
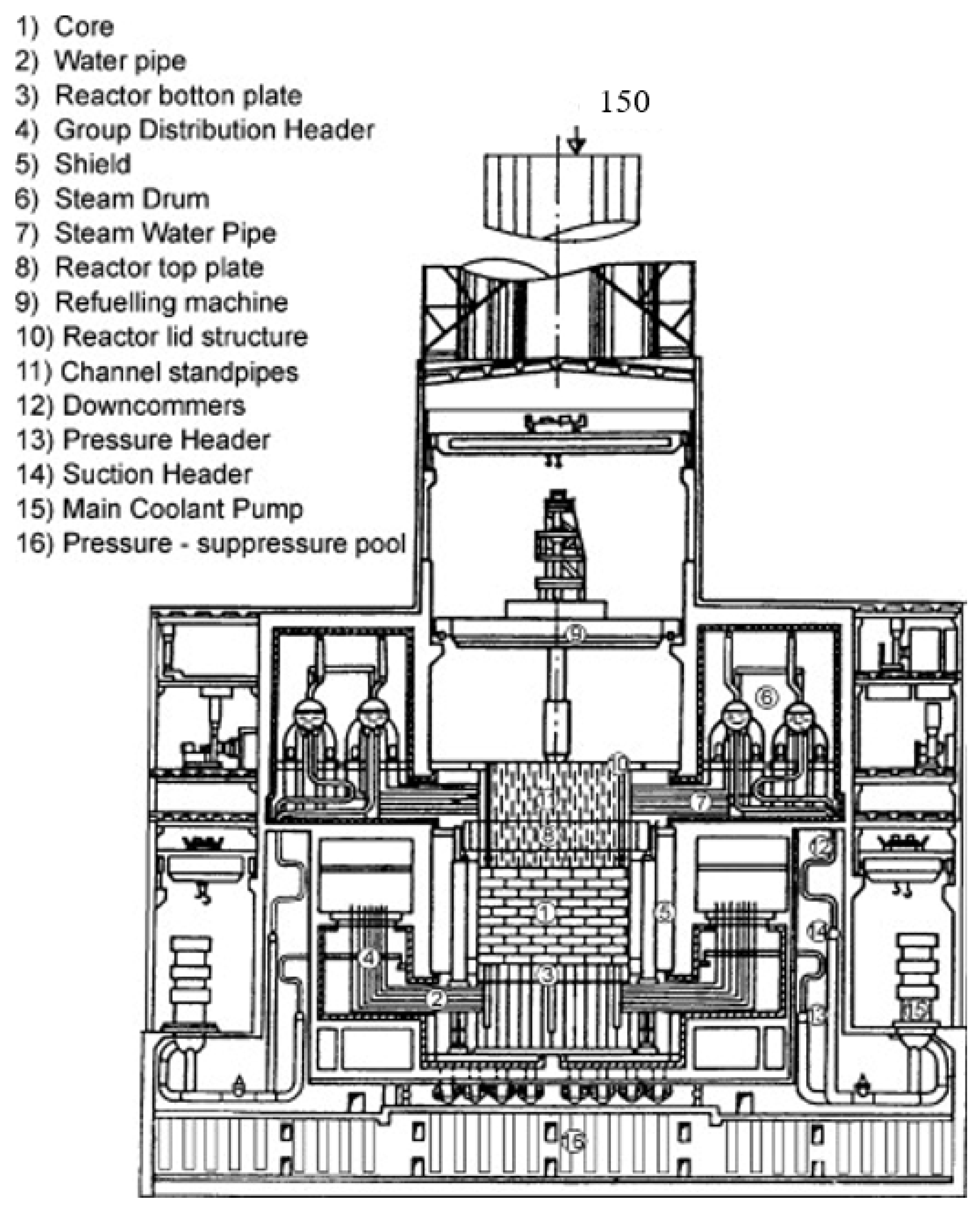
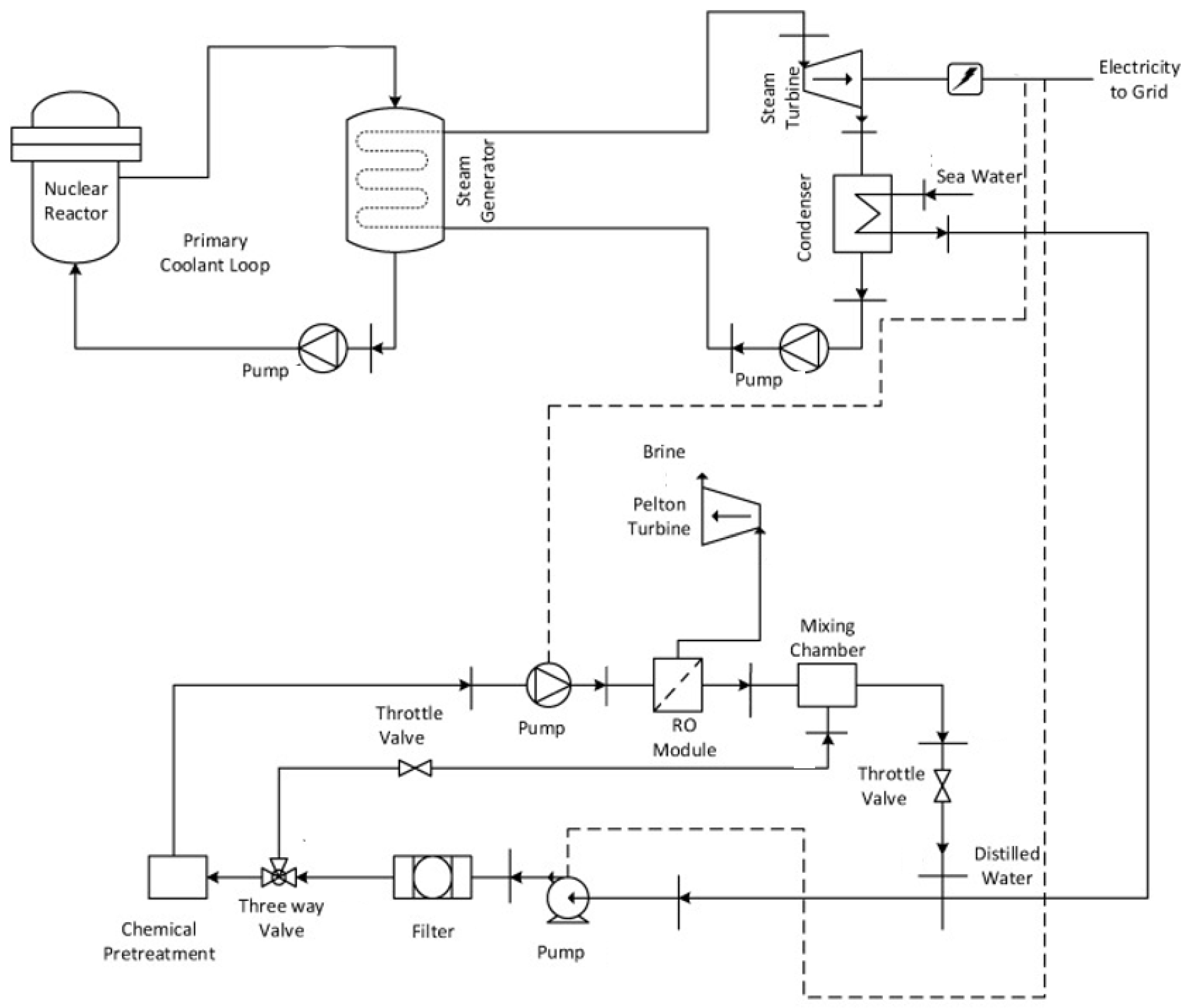
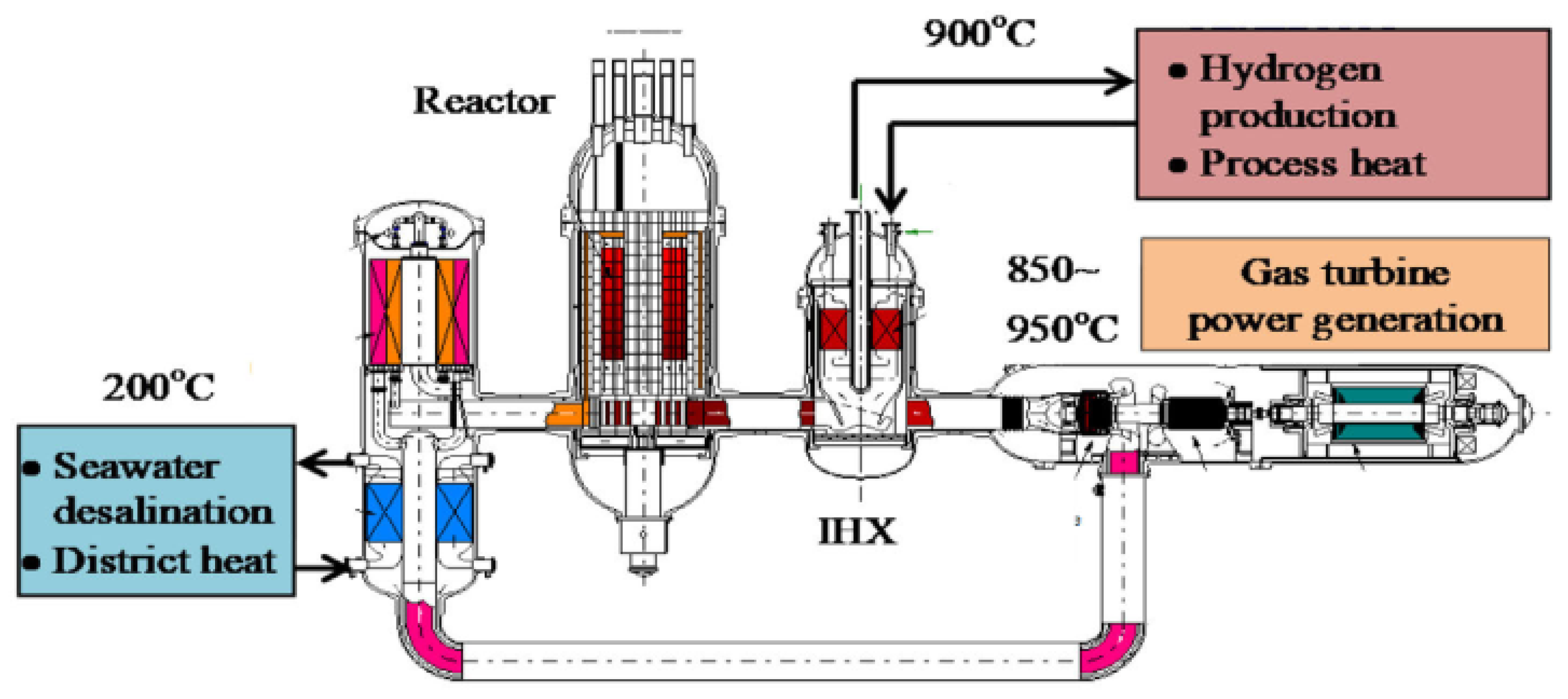
| Country and Plant | Reactor Type | Net Capacity [MWe] | Thermal Capacity [MWth] | Temperature/Pressure | Remarks |
|---|---|---|---|---|---|
| Desalination | |||||
| Japan, Ohi-1,2 | PWR | 2 × 1175 | 2 × 3120 | 130 °C/0.3 MPa | MSF (1 × 1300 m3/d), MED (2 × 1300 m3/d) |
| Japan, Ohi-3,4 | PWR | 2 × 1180 | 2 × 3415 | 150 °C/0.4 MPa | RO (1 × 1300 m3/d) |
| Kazakhstan, BN-350 (Aktau) | LMFR | 150 | 750 | 150 °C/0.5 MPa | Largest nuclear desalination plant; MED & MSF |
| India, Kalpakkam-1,2 | PHWR | 235 | 760 | 120 °C/0.25 MPa | Hybrid MSF/RO |
| Saudi Arabia, KA-CARE (planned) | HTGR | 2 × 105 | 2 × 450 | 250 °C/6.0 MPa | High-temperature MED-TVC feasibility study |
| District heating | |||||
| Russia, Novovoronezh-3,4 | VVER-440 | 2 × 385 | 2 × 1375 | 130 °C/0.8 MPa | 50 km pipeline network |
| China, Haiyang-1,2 | PWR | 2 × 1000 | 2 × 3415 | 130 °C/1.5 MPa | 23 km pipeline; integrated with urban heating |
| Czech Republic, Temelin-1,2 | VVER-1000 | 2 × 1086 | 2 × 3120 | 150 °C/1.0 MPa | 5 km & 26 km dual pipelines |
| Switzerland, Beznau-1,2 | PWR | 365, 357 | 2 × 1130 | 128 °C/0.7 MPa | 35 km pipeline; seasonal load management |
| Slovakia, Bohunice-3,4 | VVER-440 | 2 × 365 | 2 ×1471 | 150 °C/1.2 MPa | 18 km pipeline; peak demand via HP extraction |
| Process heat | |||||
| Canada, Bruce A | PHWR | 811, 777 | 2 × 2620 | 190 °C/1.8 MPa | Heavy water production; Bruce Energy Centre |
| Germany, Stade | PWR | 640 | 1900 | 190 °C/1.5 MPa | Salt refinery integration |
| Norway, Halden (experimental) | BWR | - | 35 | 240 °C/3.4 MPa | Intermittent operation for pulp/paper plant |
| China, Tianwan-1,2 | PWR (VVER-1000) | 2 × 1000 | 2 × 3000 | 248 °C/1.8 MPa | Refinery and chemical plants; 23 km steam pipeline |
| Romania, Cernavoda-1 | PHWR (CANDU-6) | 660 | 2180 | 150 °C/0.6 MPa | 2 km pipeline; low-temperature process heat |
| Advanced reactors (R&D) | |||||
| USA, Xe-100 (demonstration) | HTGR (Xe-100) | 80 | 200 | 750 °C/7.0 MPa | Flexible CHP with molten-salt TES; hydrogen co-production |
| Russia, BN-800 | LMFR | 789 | 2100 | 500 °C/14.0 MPa | High-temperature process heat for petrochemicals |
| South Korea, SMART | PWR | 100 | 330 | 250 °C/4.2 MPa | SMR-based desalination and district heating |
| France, Astrid (canceled) | Sodium-cooled fast reactor | 600 | 1500 | 550 °C/18.0 MPa | Planned for industrial heat; canceled in 2019 |
| UK, U-Battery (concept) | HTGR (microreactor) | 4 | 10 | 750 °C/5.0 MPa | Modular design for decentralized industrial parks |
| Historical Projects | |||||
| USSR, Beloyarsk-3 | LMFR (BN-600) | 560 | 1470 | 500 °C/10.0 MPa | Pioneering nuclear process heat for aluminum production (1980–2015) |
| East Germany, Rheinsberg | PWR (VVER-70) | 70 | 265 | 200 °C/1.0 MPa | District heating until 1990 |
| Canada, Gentilly-2 | HWR (CANDU-6) | 675 | 2100 | 180 °C/1.2 MPa | Heavy water and isotope production (1983–2012) |
| Emerging SMRs | |||||
| USA, NuScale VOYGR | PWR | 77 × 12 | 250 × 12 | 300 °C/8.0 MPa | Multi-module desalination and hydrogen production |
| Argentina, CAREM-25 | PWR | 25 | 100 | 220 °C/3.5 MPa | Compact design for remote industrial complexes |
| Russia, RITM-200 | PWR | 175 | 500 | 300 °C/6.0 MPa | Arctic industrial heat and power solutions |
| Thermal Range | Applications | Reactor Types | Case |
|---|---|---|---|
| <250 °C | District heating, RO desalination | PWR, BWR | Finland Loviisa [22], China Haiyang [36] |
| 250–550 °C | MED desalination, petrochemicals | CANDU, PHWR | Canada Darlington SMR [47] |
| >550 °C | HT electrolysis, steel production | HTGR, MSR, VHTR | Japan GTHTR300C [26], China HTR-PM [48] |
| Reactor Type | Thermal Efficiency (%) | Temperature Range | Advantage | Disadvantage |
|---|---|---|---|---|
| PWR (pressurized water reactor) [55,56] | 33–35 | 280–320 | Mature technology, high operational reliability | Limited temperature for industrial heat |
| BWR (boiling water reactor) [57] | 32–34 | 285–315 | Simplified design, direct steam cycle | Lower thermal efficiency, limited scalability |
| PHWR (CANDU) [58] | 29–30 | 250–300 | Natural uranium fuel, high neutron economy | Lower thermal efficiency, high heavy water costs |
| LWGR (RBMK) [59] | 28–30 | 250–280 | Enhanced neutron economy | Safety concerns, low thermal efficiency |
| HTGR (high-temperature gas-cooled reactor) [24] | 40–50 | 700–950 | High-temperature output, inherent safety | High capital costs, limited large-scale deployment |
| MSR (molten salt reactor) [60] | 45–50 | 700–1000 | Fuel flexibility, passive safety | Corrosion challenges, low TRL |
| Model | Time Handling | Strengths | Weaknesses |
|---|---|---|---|
| IAEA standard [18] | Full discounting | Benchmarking; lifecycle transparency | Overreliance on discount rate; ignores fuel-phase links |
| Static (Gen-IV) [69] | No discounting on O&M or fuel cost | Simplicity; rapid scenario testing | Misleading for long-term projects on operational cost and fuel cost |
| Monte Carlo [70] | Probabilistic discounting | Risk quantification; endogenous correlations | Computational cost; expert dependency |
| Method | Basis | Strengths | Weaknesses | Typical Applications |
|---|---|---|---|---|
| Energy credit [73] | Energy quantity (enthalpy) | Simplicity; regulatory compliance | Ignores energy quality; undervalues high-T heat | District heating |
| Exergy-based [74] | Thermodynamic work potential | Reflects energy grade; technical rigor | Data-intensive; limited policy adoption | High-temperature hydrogen |
| Opportunity cost [75] | Foregone electricity revenue | Market-aligned; flexible for retrofits | Volatility in electricity prices | Retrofitted PWRs |
| Proportional benefit [18] | Revenue share | Aligns with economic value; market-responsive | Requires stable revenue data | Deregulated markets |
| Region | Carbon Price | Breakeven Threshold | Key Sector |
|---|---|---|---|
| EU | EUR 105/tCO2 (2025) | EUR 50/tCO2 (district heating) | District heating |
| China | USD 28/tCO2 | USD 35/tCO2 (district heating) | Hydrogen/steel |
| Canada | Multi-credit | USD 80–90/tCO2 (HTGR hydrogen) | Industrial hydrogen |
| Region | Subsidy Program | Funding/Coverage | Target Technology |
|---|---|---|---|
| EU | Innovation fund (N-RHES) | EUR 4B (2021–2030), 40% TES | Molten salt reactors |
| China | VAT exemption | 13% tax relief on outputs | HTR-PM reactors |
| Region | Tax Credit | Value | Target Output |
|---|---|---|---|
| U.S. | 45X clean hydrogen credit | USD 3/kg for nuclear hydrogen | Industrial hydrogen |
| France | Heat premium | EUR 18/MWh (gas-indexed) | District heating |
| Reactor Type | Coolant | Core Outlet Temperature Range (°C) | Key Cogeneration Applications |
|---|---|---|---|
| VHTR | Helium | 750–1000 | Hydrogen, ammonia, steelmaking |
| SFR | Sodium | 500–550 | Desalination, synthetic fuels |
| MSR | Fluoride | 700–800 | Hydrogen, chemical synthesis |
| GFR | Helium | 850–950 | Industrial process heat |
| LFR | Lead | 480–800 | District heating, desalination |
| SCWR | Water | 374–625 | High-efficiency power + heat |
| Project | Country | Reactor Type | Output (MWth) | Application |
|---|---|---|---|---|
| HTTR | Japan | VHTR | 30 | Hydrogen production |
| BN-1200 | Russia | SFR | 600 | Hydrogen/desalination |
| ELFR | EU | LFR | 300 | Desalination |
| IMSR | Canada | MSR | 600 | District heating |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, G.; Zhu, G.; Zou, Y.; Ma, Y.; Dai, Y.; Wu, J.; Tian, J. Economic Analysis of Nuclear Energy Cogeneration: A Comprehensive Review on Integrated Utilization. Energies 2025, 18, 2929. https://doi.org/10.3390/en18112929
Jia G, Zhu G, Zou Y, Ma Y, Dai Y, Wu J, Tian J. Economic Analysis of Nuclear Energy Cogeneration: A Comprehensive Review on Integrated Utilization. Energies. 2025; 18(11):2929. https://doi.org/10.3390/en18112929
Chicago/Turabian StyleJia, Guobin, Guifeng Zhu, Yang Zou, Yuwen Ma, Ye Dai, Jianhui Wu, and Jian Tian. 2025. "Economic Analysis of Nuclear Energy Cogeneration: A Comprehensive Review on Integrated Utilization" Energies 18, no. 11: 2929. https://doi.org/10.3390/en18112929
APA StyleJia, G., Zhu, G., Zou, Y., Ma, Y., Dai, Y., Wu, J., & Tian, J. (2025). Economic Analysis of Nuclear Energy Cogeneration: A Comprehensive Review on Integrated Utilization. Energies, 18(11), 2929. https://doi.org/10.3390/en18112929







