Melting in Shell-and-Tube and Shell-and-Coil Thermal Energy Storage: Analytical Correlation for Melting Fraction
Abstract
1. Introduction
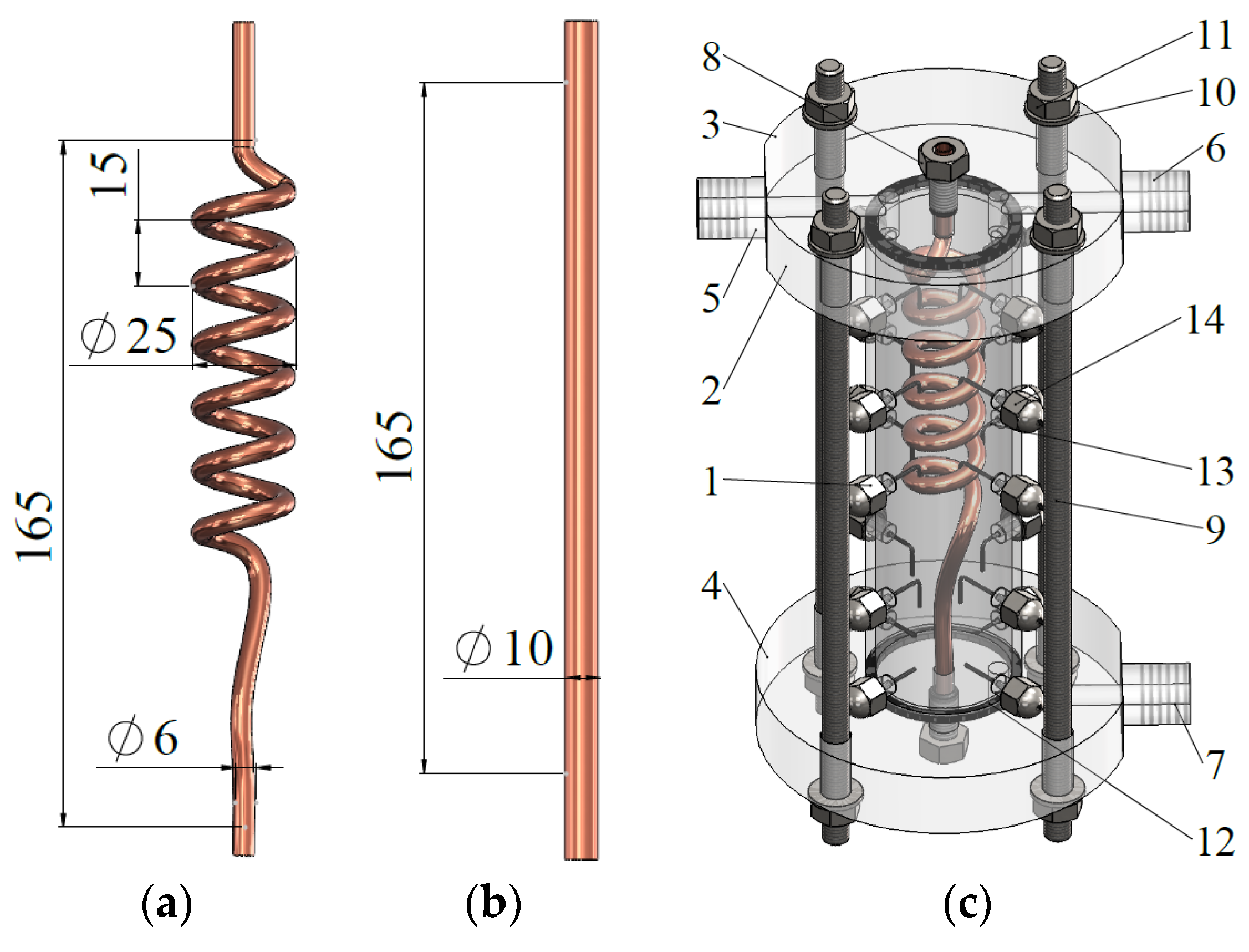
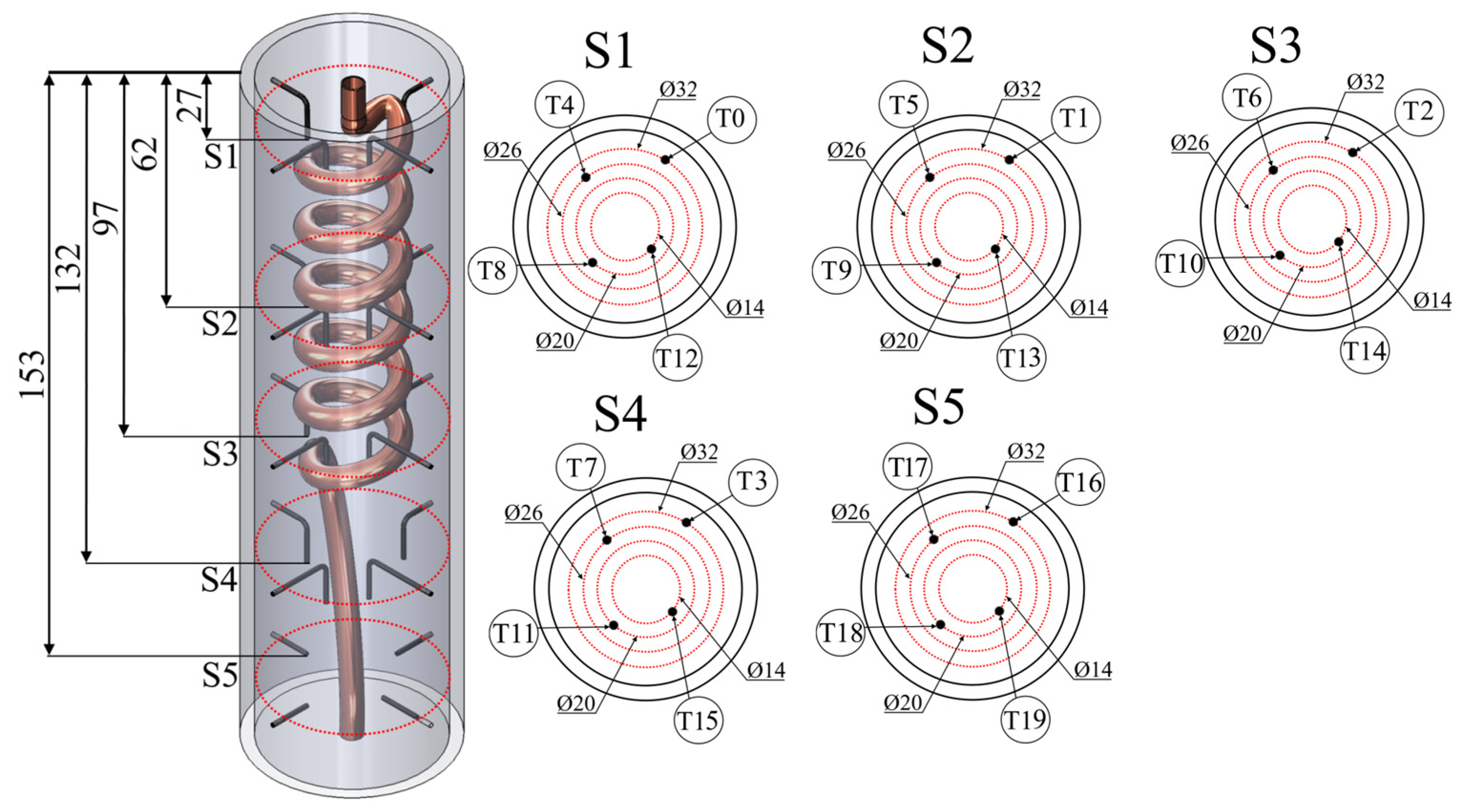
2. Materials and Methods
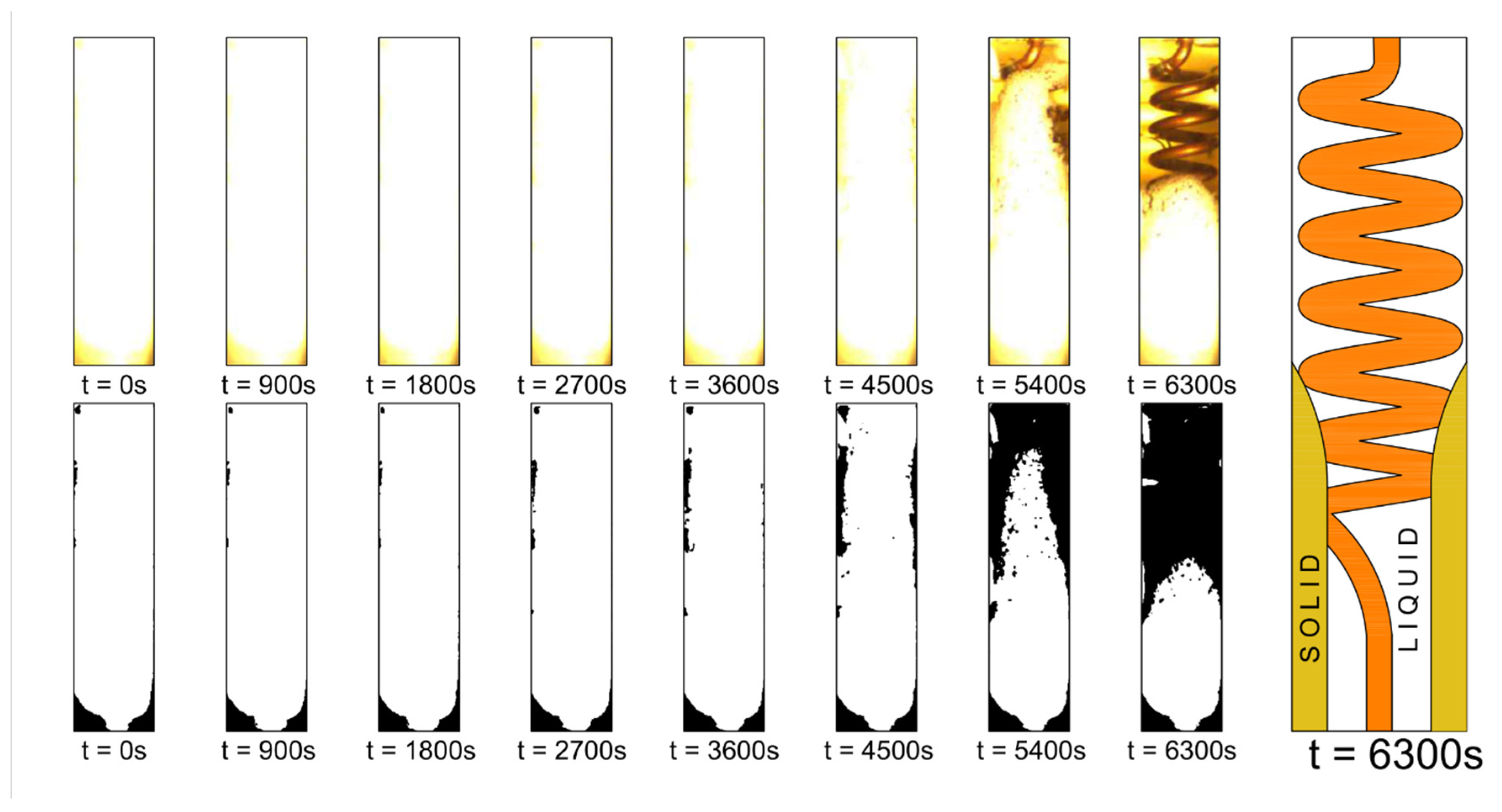
3. Visual Observations
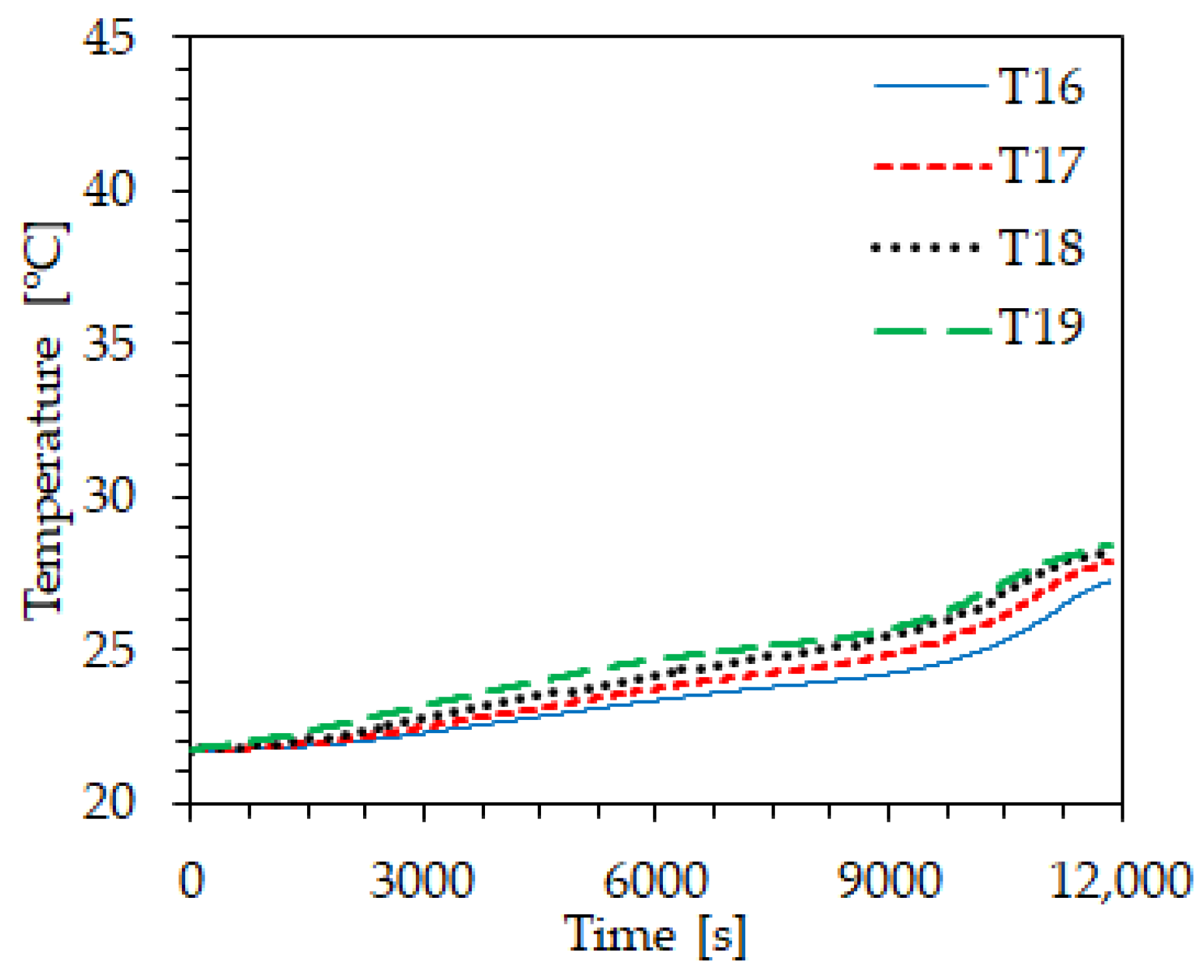
4. Thermal Analysis
5. Modeling
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Symbols | density [kg/m3] | ||
| surface area [m2] | liquid fraction [-] | ||
| specific heat capacity [J/kg·K] | Abbreviations | ||
| diameter [m] | ANN | artificial neural network | |
| Fourier number [-] | CPV | concentrator photovoltaic | |
| gravitational acceleration [m/s2] | DC | direct current | |
| latent heat [J/kg] | DSC | differential scanning calorimeter | |
| characteristic dimension [m] | HTF | heat-transfer fluid | |
| length [m] | HVAC | heat, ventilation, and air conditioning | |
| mass [kg] | LHTES | latent heat thermal energy storage | |
| Nusselt number [-] | PCM | phase-change material | |
| Prandtl number [-] | PV | photovoltaic panel | |
| heat flux [W/m2] | PVT | photovoltaic thermal collector | |
| Rayleigh number [-] | RES | renewable energy sources | |
| modified Rayleigh number [-] | TES | thermal energy storage | |
| Reynolds number [-] | Subscripts | ||
| Stefan number [-] | avg | average | |
| modified Stefan number [-] | eq | equivalent | |
| t | time [s] | in | inlet |
| temperature [°C] | m | melting | |
| thermal diffusivity [m2/s] | out | outside | |
| thermal expansion coefficient [1/K] | s | solidification | |
| thermal conductivity [W/m·K] | t | total | |
| dynamic viscosity [Pa·s] | V_avg | volume-averaged | |
| kinematic viscosity [m2/s] | w | wall |
References
- Zayed, M.E.; Zhao, J.; Elsheikh, A.H.; Hammad, F.A.; Ma, L.; Du, Y.; Kabeel, A.; Shalaby, S. Applications of cascaded phase change materials in solar water collector storage tanks: A review. Sol. Energy Mater. Sol. Cells 2019, 199, 24–49. [Google Scholar] [CrossRef]
- Mao, Q. Recent developments in geometrical configurations of thermal energy storage for concentrating solar power plant. Renew. Sustain. Energy Rev. 2016, 59, 320–327. [Google Scholar] [CrossRef]
- Zondag, H.; de Boer, R.; Smeding, S.; van der Kamp, J. Performance analysis of industrial PCM heat storage lab prototype. J. Energy Storage 2018, 18, 402–413. [Google Scholar] [CrossRef]
- Royo, P.; Acevedo, L.; Ferreira, V.J.; García-Armingol, T.; López-Sabirón, A.M.; Ferreira, G. High-temperature PCM-based thermal energy storage for industrial furnaces installed in energy-intensive industries. Energy 2019, 173, 1030–1040. [Google Scholar] [CrossRef]
- Hordov, J.B.; Nižetić, S.; Jurčević, M.; Čoko, D.; Ćosić, M.; Jakić, M.; Arıcı, M. Review of organic and inorganic waste-based phase change composites in latent thermal energy storage: Thermal properties and applications. Energy 2024, 306, 132421. [Google Scholar] [CrossRef]
- Okogeri, O.; Stathopoulos, V.N. What about greener phase change materials? A review on biobased phase change materials for thermal energy storage applications. Int. J. Thermofluids 2021, 10, 100081. [Google Scholar] [CrossRef]
- Kamaraj, D.; Senthilkumar, S.R.R.; Ramalingam, M.; Vanaraj, R.; Kim, S.-C.; Prabakaran, M.; Kim, I.-S. A Review on the Effective Utilization of Organic Phase Change Materials for Energy Efficiency in Buildings. Sustainability 2024, 16, 9317. [Google Scholar] [CrossRef]
- Ghalambaz, M.; Mohammed, H.I.; Mahdi, J.M.; Eisapour, A.H.; Younis, O.; Ghosh, A.; Talebizadehsardari, P.; Yaïci, W. Intensifying the charging response of a phase-change material with twisted fin arrays in a shell-and-tube storage system. Energies 2021, 14, 1619. [Google Scholar] [CrossRef]
- Seddegh, S.; Wang, X.; Joybari, M.M.; Haghighat, F. Investigation of the effect of geometric and operating parameters on thermal behavior of vertical shell-and-tube latent heat energy storage systems. Energy 2017, 137, 69–82. [Google Scholar] [CrossRef]
- Pakalka, S.; Valančius, K.; Streckienė, G. Experimental and theoretical investigation of the natural convection heat transfer coefficient in phase change material (PCM) based fin-and-tube heat exchanger. Energies 2021, 14, 716. [Google Scholar] [CrossRef]
- Motahar, S. Experimental study and ANN-based prediction of melting heat transfer in a uniform heat flux PCM enclosure. J. Energy Storage 2020, 30, 101535. [Google Scholar] [CrossRef]
- Dhaidan, N.S.; Khodadadi, J.; Al-Hattab, T.A.; Al-Mashat, S.M. Experimental and numerical investigation of melting of NePCM inside an annular container under a constant heat flux including the effect of eccentricity. Int. J. Heat Mass Transf. 2013, 67, 455–468. [Google Scholar] [CrossRef]
- Chintakrinda, K.; Weinstein, R.D.; Fleischer, A.S. A direct comparison of three different material enhancement methods on the transient thermal response of paraffin phase change material exposed to high heat fluxes. Int. J. Therm. Sci. 2011, 50, 1639–1647. [Google Scholar] [CrossRef]
- Kachalov, A.B.; Sánchez, P.S.; Porter, J.; Ezquerro, J. The combined effect of natural and thermocapillary convection on the melting of phase change materials in rectangular containers. Int. J. Heat Mass Transf. 2021, 168, 120864. [Google Scholar] [CrossRef]
- Emam, M.; Ookawara, S.; Ahmed, M. Thermal management of electronic devices and concentrator photovoltaic systems using phase change material heat sinks: Experimental investigations. Renew. Energy 2019, 141, 322–339. [Google Scholar] [CrossRef]
- Fadl, M.; Eames, P.C. An experimental investigations of the melting of RT44HC inside a horizontal rectangular test cell subject to uniform wall heat flux. Int. J. Heat Mass Transf. 2019, 140, 731–742. [Google Scholar] [CrossRef]
- García-Roco, R.; Sánchez, P.S.; Bello, A.; Olfe, K.; Rodríguez, J. Dynamics of PCM melting driven by a constant heat flux at the free surface in microgravity. Therm. Sci. Eng. Prog. 2024, 48, 102378. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, Z.; Wang, Q.; Wu, Q. Melting in an Enclosure with Discrete Heating at a Constant Rate. Exp. Therm. Fluid Sci. 1993, 6, 196–201. [Google Scholar] [CrossRef]
- Pal, D.; Joshi, Y.K. Melting in a side heated tall enclosure by a uniformly dissipating heat source. Int. J. Heat Mass Transf. 2001, 44, 375–387. [Google Scholar] [CrossRef]
- Hajjar, A.; Jamesahar, E.; Shirivand, H.; Ghalambaz, M.; Mahani, R.B. Transient phase change heat transfer in a metal foam-phase change material heatsink subject to a pulse heat flux. J. Energy Storage 2020, 31, 101701. [Google Scholar] [CrossRef]
- Huang, S.; Lu, J.; Li, Y.; Xie, L.; Yang, L.; Cheng, Y.; Chen, S.; Zeng, L.; Li, W.; Zhang, Y.; et al. Experimental study on the influence of PCM container height on heat transfer characteristics under constant heat flux condition. Appl. Therm. Eng. 2020, 172, 115159. [Google Scholar] [CrossRef]
- Ghasemi, B.; Aminossadati, S. Periodic natural convection in a nanofluid-filled enclosure with oscillating heat flux. Int. J. Therm. Sci. 2009, 49, 1–9. [Google Scholar] [CrossRef]
- Gupta, A.K.; Mishra, G.; Singh, S. Numerical study of MWCNT enhanced PCM melting through a heated undulated wall in the latent heat storage unit. Therm. Sci. Eng. Prog. 2022, 27, 101172. [Google Scholar] [CrossRef]
- Ben-David, O.; Levy, A.; Mikhailovich, B.; Azulay, A. 3D numerical and experimental study of gallium melting in a rectangular container. Int. J. Heat Mass Transf. 2013, 67, 260–271. [Google Scholar] [CrossRef]
- Ho, J.; See, Y.; Leong, K.; Wong, T. An experimental investigation of a PCM-based heat sink enhanced with a topology-optimized tree-like structure. Energy Convers. Manag. 2021, 245, 114608. [Google Scholar] [CrossRef]
- Karimi, G.; Azizi, M.; Babapoor, A. Experimental study of a cylindrical lithium ion battery thermal management using phase change material composites. J. Energy Storage 2016, 8, 168–174. [Google Scholar] [CrossRef]
- Verma, A.; Shashidhara, S.; Rakshit, D. A comparative study on battery thermal management using phase change material (PCM). Therm. Sci. Eng. Prog. 2019, 11, 74–83. [Google Scholar] [CrossRef]
- Huo, Y.; Rao, Z. Lattice Boltzmann simulation for solid–liquid phase change phenomenon of phase change material under constant heat flux. Int. J. Heat Mass Transf. 2015, 86, 197–206. [Google Scholar] [CrossRef]
- Raut, D.; Lanjewar, S.; Kalamkar, V.R. Effect of geometrical and operational parameters on paraffin’s melting performance in helical coiled latent heat storage for solar application: A numerical study. Int. J. Therm. Sci. 2022, 176, 107509. [Google Scholar] [CrossRef]
- Andrzejczyk, R.; Kozak, P.; Muszyński, T. Experimental investigations on the influence of coil arrangement on melting/solidification processes. Energies 2020, 13, 6334. [Google Scholar] [CrossRef]
- Andrzejczyk, R.; Muszynski, T.; Kowalczyk, T.; Saqib, M. Experimental and numerical investigation on shell and coil storage unit with biodegradable PCM for modular thermal battery applications. Int. J. Therm. Sci. 2022, 185, 108076. [Google Scholar] [CrossRef]
- Joneidi, M.; Hosseini, M.; Ranjbar, A.; Bahrampoury, R. Experimental investigation of phase change in a cavity for varying heat flux and inclination angles. Exp. Therm. Fluid Sci. 2017, 88, 594–607. [Google Scholar] [CrossRef]
- Shatikian, V.; Ziskind, G.; Letan, R. Numerical investigation of a PCM-based heat sink with internal fins. Int. J. Heat Mass Transf. 2005, 48, 3689–3706. [Google Scholar] [CrossRef]
- Andrzejczyk, R.; Saqib, M.; Rogowski, M. A New Approach of Solidification Analysis in Modular Latent Thermal Energy Storage Unit Based on Image Processing. Appl. Therm. Eng. 2024, 236, 121925. [Google Scholar] [CrossRef]
- Andrzejczyk, R.; Kowalczyk, T.; Kozak, P.; Muszyński, T. Experimental and theoretical study of a vertical tube in shell storage unit with biodegradable PCM for low temperature thermal energy storage applications. Appl. Therm. Eng. 2020, 183, 116216. [Google Scholar] [CrossRef]
- Andrzejczyk, R.; Saqib, M.; Kowalczyk, T.; Ali, H.M. Study on effective front region thickness of PCM in thermal energy storage using a novel semi-theoretical model. Int. Commun. Heat Mass Transf. 2023, 146, 106901. [Google Scholar] [CrossRef]
- Li, Z.-R.; Hu, N.; Liu, J.; Zhang, R.-H.; Fan, L.-W. Revisiting melting heat transfer of nano-enhanced phase change materials (NePCM) in differentially-heated rectangular cavities using thermochromic liquid crystal (TLC) thermography. Int. J. Heat Mass Transf. 2020, 159, 120119. [Google Scholar] [CrossRef]
- Wang, S.; Guo, Y.; Peng, C.; Wang, W. Experimental study of paraffin melting in cylindrical cavity with central electric heating rod. J. Environ. Manag. 2019, 237, 264–271. [Google Scholar] [CrossRef]
- Martinez-Garcia, J.; Gwerder, D.; Wahli, F.; Guarda, D.; Fenk, B.; Stamatiou, A.; Worlitschek, J.; Schuetz, P. Volumetric quantification of melting and solidification of phase change materials by in-situ X-ray computed tomography. J. Energy Storage 2023, 61, 106726. [Google Scholar] [CrossRef]
- Rogowski, M.; Andrzejczyk, R. Recent advances of selected passive heat transfer intensification methods for phase change material-based latent heat energy storage units: A review. Int. Commun. Heat Mass Transf. 2023, 144, 106795. [Google Scholar] [CrossRef]
- Raj, L.S.; Sreenivasulu, S.; Prasad, B.D. Numerical analysis of melting time and melt fraction for bottom charged tube in tube phase change material heat exchanger. Sadhana 2023, 48, 1–13. [Google Scholar] [CrossRef]
- Gau, C.; Viskanta, R. Melting and solidification of a pure metal on a vertical wall. J. Heat Transf. 1986, 108, 174–181. [Google Scholar] [CrossRef]
- Wang, Y.; Amiri, A.; Vafai, K. An experimental investigation of the melting process in a rectangular enclosure. Int. J. Heat Mass Transf. 1999, 42, 3659–3672. [Google Scholar] [CrossRef]
- Xu, Y.; Li, M.-J.; Zheng, Z.-J.; Xue, X.-D. Melting performance enhancement of phase change material by a limited amount of metal foam: Configurational optimization and economic assessment. Appl. Energy 2018, 212, 868–880. [Google Scholar] [CrossRef]
- Kalapala, L.; Devanuri, J.K. Parametric investigation to assess the melt fraction and melting time for a latent heat storage material based vertical shell and tube heat exchanger. Sol. Energy 2019, 193, 360–371. [Google Scholar] [CrossRef]
- EN 1057+A1; Copper and Copper Alloys—Seamless, Round Copper Tubes for Water and Gas in Sanitary and Heating Applications. European Committee for Standardization: Brussels, Belgium, 2006.
- Rhinehart, R.R. Nonlinear Regression Modeling for Engineering Applications; Wiley: Hoboken, NJ, USA, 2016. [Google Scholar]
- Boroojerdian, A.; Nemati, H.; Selahi, E. Direct and non-contact measurement of liquid fraction in unconstrained encapsulated PCM melting. Energy 2023, 284, 129359. [Google Scholar] [CrossRef]
- Petryniak, R. Algorytmy Komputerowej Detekcji Dużych Obiektów w Obrazach o Wysokim Poziomie Szumu i Niejednorodności. Ph.D. Thesis, AGH University of Krakow, Kraków, Poland, 2011. [Google Scholar]
- Punniakodi, B.M.S.; Senthil, R. Effect of conical coiled heat transfer fluid tube on charging of phase-change material in a vertical shell and coil type cylindrical thermal energy storage. Energy Sources Part A Recover. Util. Environ. Eff. 2020, 44, 8611–8626. [Google Scholar] [CrossRef]
- Punniakodi, B.M.S.; Senthil, R. Experimental study on melting enhancement of phase change material in a vertical cylindrical latent heat storage using a short concentric helical heat transfer tube. J. Energy Storage 2021, 41, 102879. [Google Scholar] [CrossRef]
- Lorente, S.; Bejan, A.; Niu, J. Constructal design of latent thermal energy storage with vertical spiral heaters. Int. J. Heat Mass Transf. 2015, 81, 283–288. [Google Scholar] [CrossRef]
- Tian, S.; Bai, H.; Hui, N.; Gao, H.; Shao, S.; Sun, Z.; Liu, S. A dynamic analytical model to predict and parametrically analyze charging and discharging process of tube-in-tank PCM systems. Therm. Sci. Eng. Prog. 2021, 22, 100866. [Google Scholar] [CrossRef]
- Liu, Z.; Ma, C. Numerical analysis of melting with constant heat flux heating in a thermal energy storage system. Energy Convers. Manag. 2002, 43, 2521–2538. [Google Scholar] [CrossRef]
- Bathelt, A.G.; Viskanta, R.; Leidenfrost, W. Latent Heat-of-Fusion Energy Storage: Experiments on Heat Transfer from Cylinders During Melting. J. Heat Transf. 1979, 101, 453–458. [Google Scholar] [CrossRef]








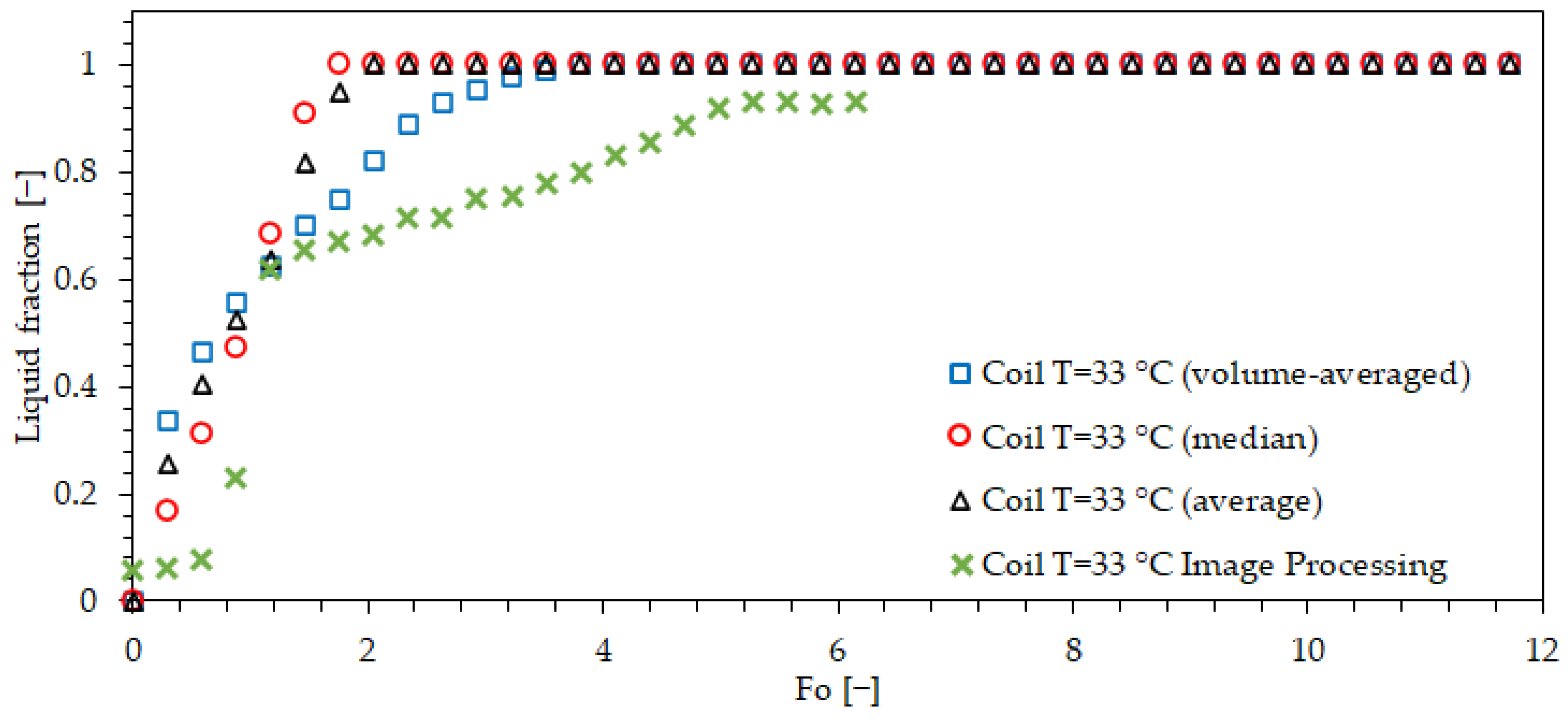
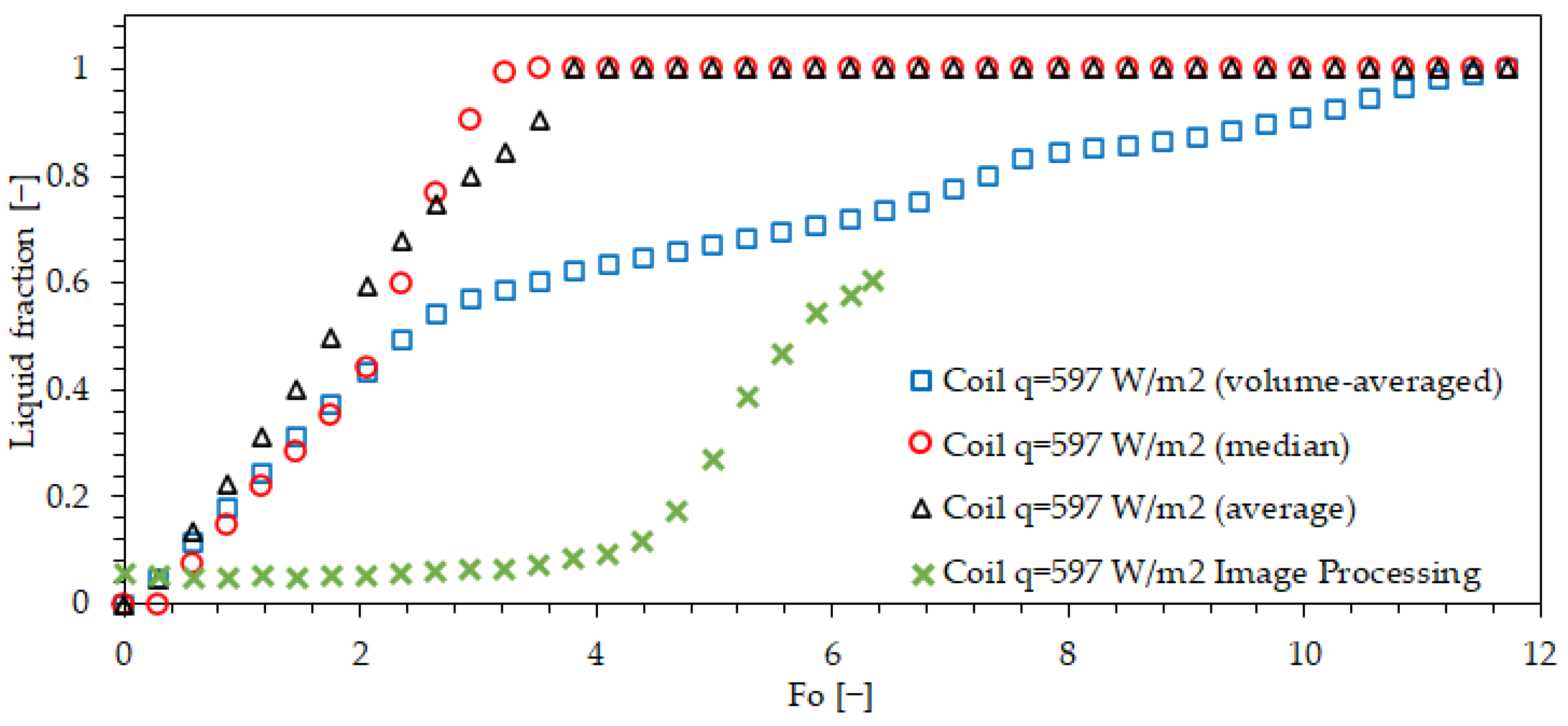


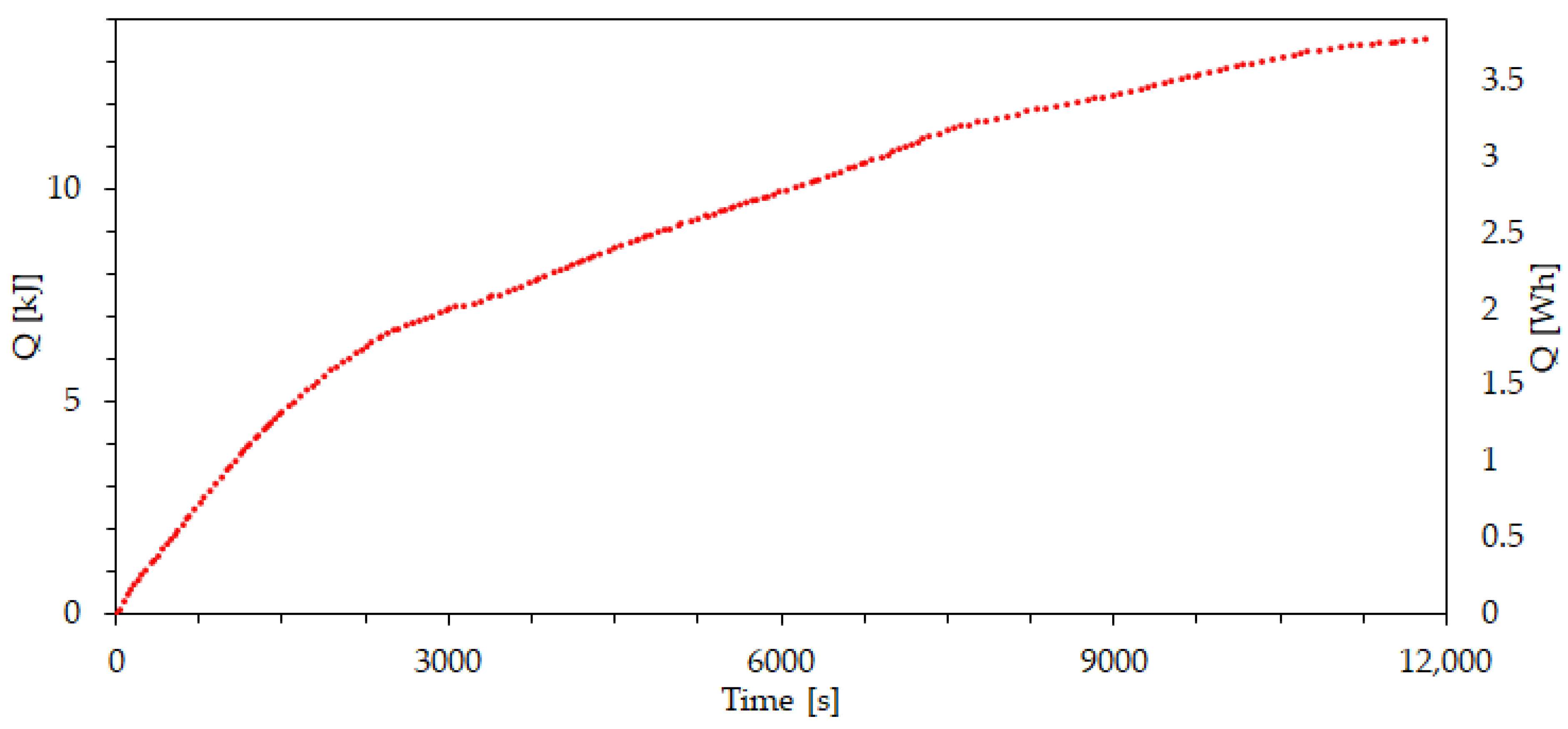
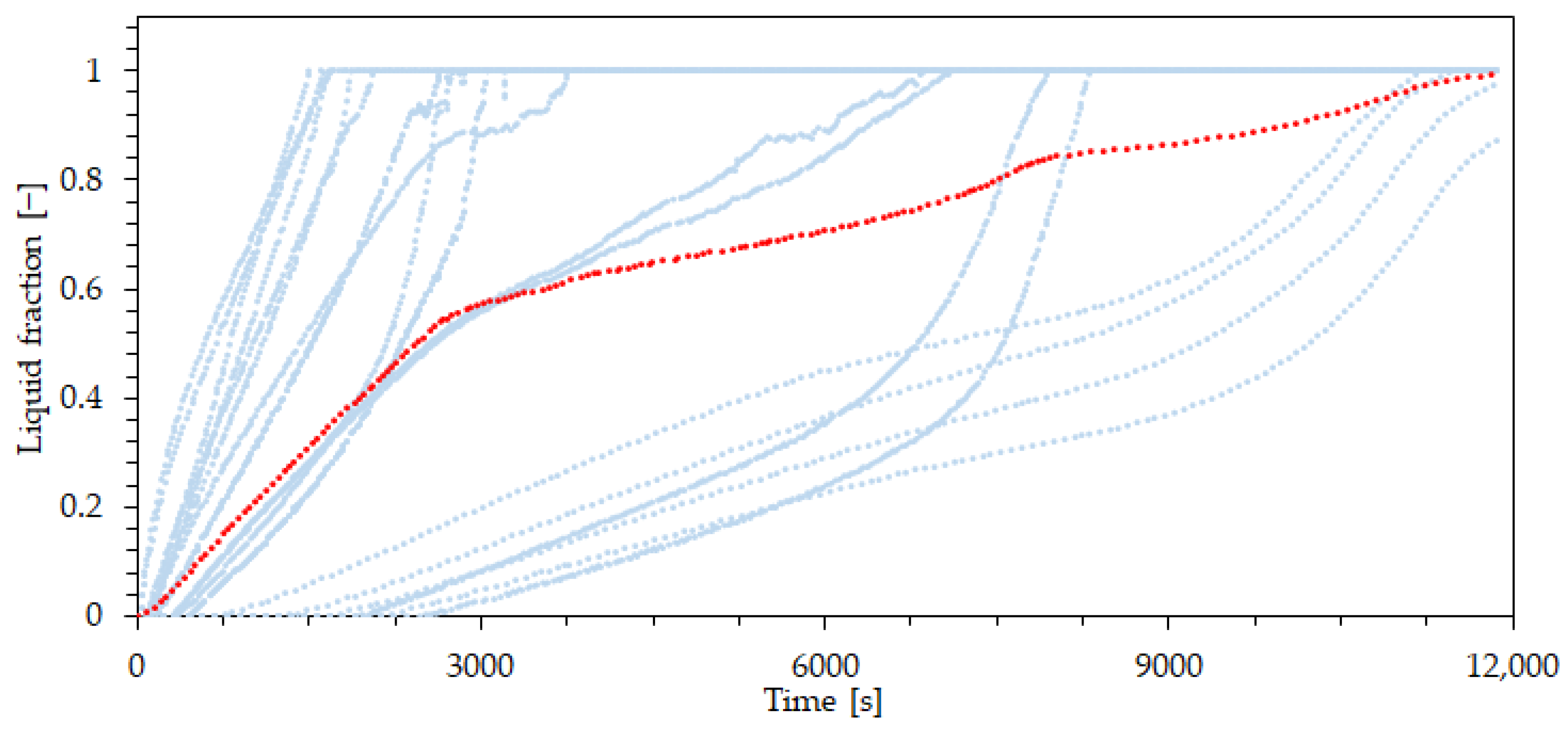
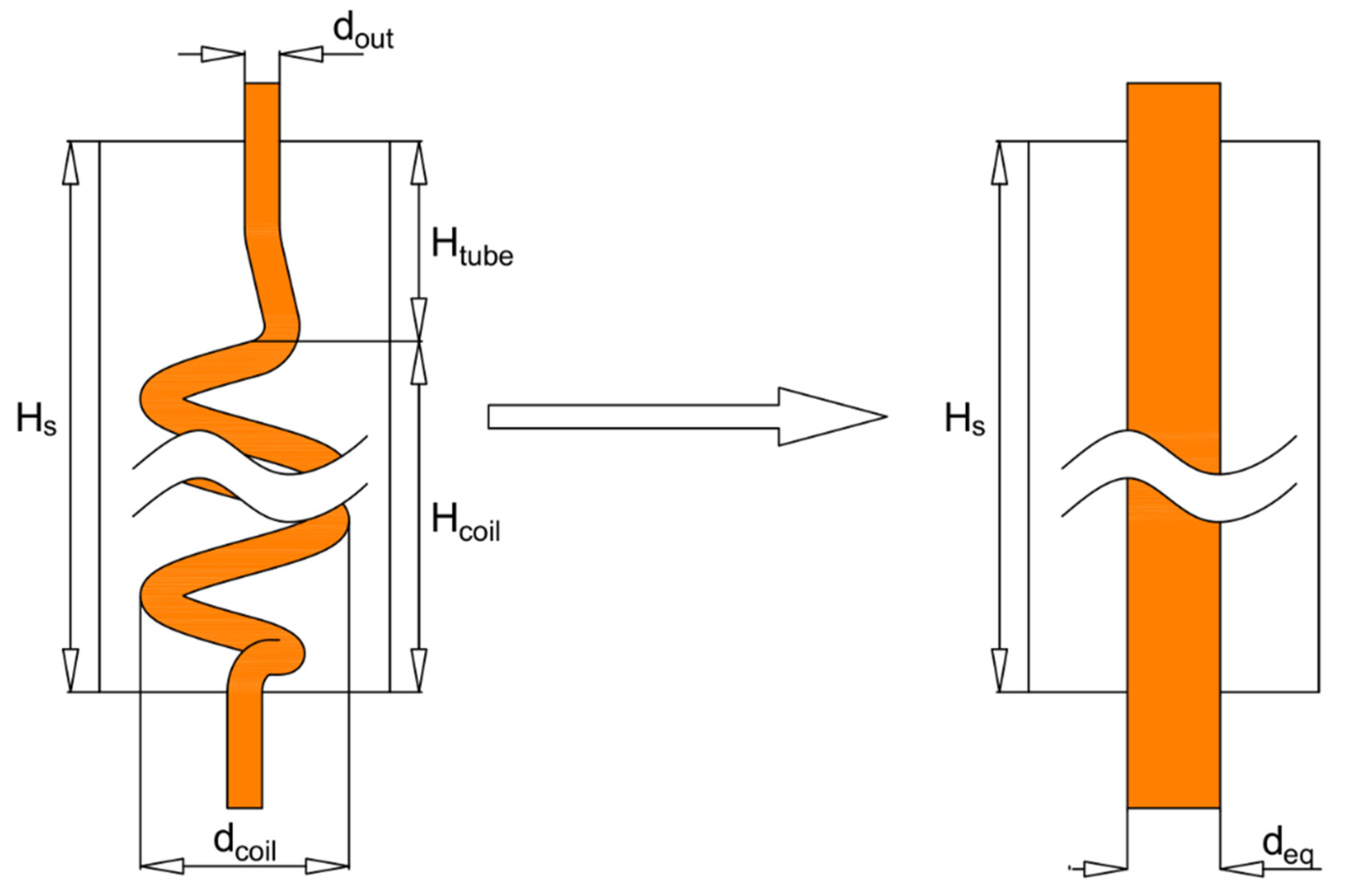
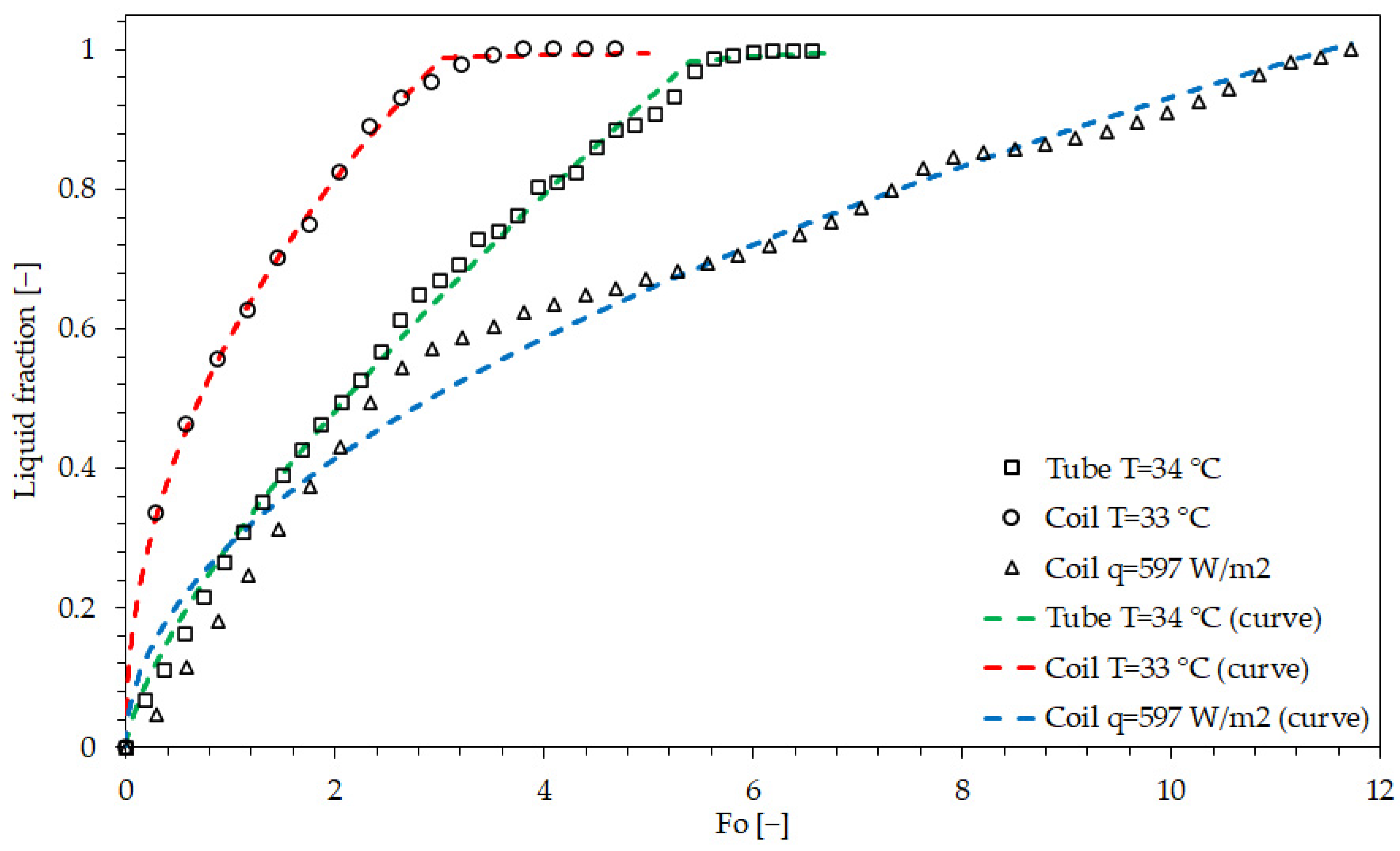
| Property | Value | Unit |
|---|---|---|
| 0.329 | W/mK | |
| 1130 | Kg/m3 | |
| 146.7 | kJ/kg | |
| 2.07 | kJ/kg·K | |
| 25.5 | °C | |
| 0.02 | Pa·s | |
| 1.77 × 10−5 | m2/s | |
| 7.61 × 10−4 | 1/K | |
| 1.4 × 10−7 | m2/s | |
| 125.8 | - |
| Year | Article | Correlation | Boundary Condition | PCM |
|---|---|---|---|---|
| 1986 | [42] | gallium (pure) | ||
| 1993 | [18] | n-Octadecane (pure) | ||
| 1999 | [43] | PEG900 | ||
| 2001 | [19] | gallium (pure) n-Eicosane (pure) n-Tricontane (pure) | ||
| 2018 | [44] | Li2CO3–K2CO3 | ||
| 2019 | [45] | lauric acid (pure) | ||
| 2023 | [41] | RT35 |
| Parameter | Units | Operating Range | Uncertainty | Error |
|---|---|---|---|---|
| °C | 10–60 | ±0.2 | - | |
| V | 1 | ±2 × 10−3 | - | |
| A | 5.13 | ±0.01 | - | |
| W | 50 | ±0.02 | - | |
| m | 0.46 | ±5 × 10−4 | - | |
| m | 6 × 10−3 | ±4 × 10−6 [46] | - | |
| A | m2 | 8.67 × 10−3 | 7.23 × 10−4 | ±8% |
| W/m2 | 597 | ±4 | ±0.8% |
| Studied Case | Parameter | Value |
|---|---|---|
| Tube | 0.105807 | |
| 75,908.44 | ||
| 16.5 | ||
| Coil | 0.11286 | |
| 41,456.13 | ||
| 10.3125 | ||
| Coil | 0.38078 | |
| 1111.5 | ||
| 10.3125 |
| Studied Case | Threshold | A | B | C | E | F | |
|---|---|---|---|---|---|---|---|
| Tube | −9.115 | −3.508 | 0.6725 | 0.469 | 6.981 | 0.9953 | |
| −0.09181 | 0.7105 | 0.05595 | 0.0117 | 2.098 | 0.5268 | ||
| Coil | 0.2438 | 0.3932 | 0.08631 | 0.7176 | 0.9447 | 0.9989 | |
| 0.3567 | 0.47 | 0.1006 | 0.05653 | 0.8187 | 0.1148 | ||
| Coil | 0.2753 | 0.5387 | 0.08948 | 0.5043 | 0.9987 | 0.9764 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rogowski, M.; Fabrykiewicz, M.; Andrzejczyk, R. Melting in Shell-and-Tube and Shell-and-Coil Thermal Energy Storage: Analytical Correlation for Melting Fraction. Energies 2025, 18, 2923. https://doi.org/10.3390/en18112923
Rogowski M, Fabrykiewicz M, Andrzejczyk R. Melting in Shell-and-Tube and Shell-and-Coil Thermal Energy Storage: Analytical Correlation for Melting Fraction. Energies. 2025; 18(11):2923. https://doi.org/10.3390/en18112923
Chicago/Turabian StyleRogowski, Michał, Maciej Fabrykiewicz, and Rafał Andrzejczyk. 2025. "Melting in Shell-and-Tube and Shell-and-Coil Thermal Energy Storage: Analytical Correlation for Melting Fraction" Energies 18, no. 11: 2923. https://doi.org/10.3390/en18112923
APA StyleRogowski, M., Fabrykiewicz, M., & Andrzejczyk, R. (2025). Melting in Shell-and-Tube and Shell-and-Coil Thermal Energy Storage: Analytical Correlation for Melting Fraction. Energies, 18(11), 2923. https://doi.org/10.3390/en18112923








