Employing Quantum Entanglement for Real-Time Coordination of Distributed Electric Vehicle Charging Stations: Advancing Grid Efficiency and Stability

Abstract

The widespread deployment of electric vehicles (EVs) has introduced substantial challenges to electricity pricing, grid stability, and renewable energy integration. This paper presents the first real-time quantum-enhanced electricity pricing framework for large-scale EV charging networks, marking a significant departure from existing approaches based on mixed-integer programming (MILP) and deep reinforcement learning (DRL). The proposed framework incorporates renewable intermittency, demand elasticity, and infrastructure constraints within a high-dimensional optimization model. The objective is to dynamically determine spatiotemporal electricity prices that reduce system peak load, improve renewable utilization, and minimize user charging costs. A rigorous mathematical formulation is developed, integrating over 40 system-level constraints, including power balance, transmission limits, renewable curtailment, carbon targets, voltage regulation, demand-side flexibility, social participation, and cyber-resilience. Real-time electricity prices are treated as dynamic decision variables influenced by station utilization, elasticity response curves, and the marginal cost of renewable and grid electricity. The model is solved across 96 time intervals using a quantum-classical hybrid method, with benchmark comparisons against MILP and DRL baselines. A comprehensive case study is conducted on a 500-station EV network serving 10,000 vehicles, coupled with a modified IEEE 118-bus grid and 800 MW of variable renewable energy. Historical charging data with ±12% stochastic demand variation and real-world solar/wind profiles are used to simulate realistic conditions. Results show that the proposed framework achieves a 23.4% average peak load reduction per station, a 17.9% gain in renewable utilization, and up to 30% user cost savings compared to flat-rate pricing. Network congestion is mitigated at over 90% of high-traffic stations. Pricing trajectories align low-price windows with high-renewable periods and off-peak hours, enabling synchronized load shifting and enhanced flexibility. Visual analytics using 3D surface plots and disaggregated bar charts confirm structured demand-price interactions and smooth, stable price evolution. These findings validate the potential of quantum-enhanced optimization for scalable, clean, and adaptive EV charging coordination in renewable-rich grid environments.

1. Introduction

The rapid expansion of electric vehicle (EV) adoption has introduced new challenges to modern power grids, requiring innovative approaches to manage energy demand efficiently while ensuring grid stability. As the penetration of EVs continues to increase, conventional charging infrastructures struggle to accommodate the rising electricity consumption, leading to concerns regarding peak load surges, power imbalances, and supply-demand mismatches [1,2,3]. Real-time pricing strategies have emerged as a promising mechanism to dynamically modulate charging behaviors by incentivizing off-peak charging and balancing the overall electricity consumption. However, existing pricing models, primarily based on classical optimization techniques, encounter significant limitations in handling the inherent complexity of large-scale EV charging networks. The integration of renewable energy sources further exacerbates the problem, introducing variability and stochasticity that traditional models fail to address effectively [4,5,6]. These limitations necessitate the exploration of novel computational paradigms capable of optimizing real-time pricing in a manner that is scalable, adaptive, and resilient to uncertainty.

The core challenge in real-time pricing optimization for EV charging lies in the combinatorial nature of the problem. The price-setting process must account for numerous interdependent factors, including consumer demand elasticity, grid load conditions, renewable generation availability, and economic constraints [7,8,9]. Classical optimization techniques, such as mixed-integer programming and heuristic-based algorithms, often suffer from prolonged computational times and suboptimal solutions when confronted with high-dimensional decision spaces. As a result, pricing models fail to provide truly real-time responses, limiting their effectiveness in dynamically adjusting to rapidly changing grid conditions [10,11]. Quantum annealing presents a fundamentally different approach, leveraging quantum mechanical properties such as superposition and tunneling to efficiently explore vast solution spaces [12,13]. By encoding the pricing problem into an energy-based representation, quantum annealing is capable of rapidly converging to optimal or near-optimal solutions, offering a computational advantage over traditional methods. The application of quantum annealing to real-time EV charging pricing optimization remains largely unexplored in existing literature, marking a significant opportunity for advancement. Figure 1 illustrates the end-to-end architecture of the proposed EV charging optimization framework, integrating quantum computation, grid operation, IoT data acquisition, and user-side flexibility. At the top, the Quantum Optimization Engine encapsulates the core pricing mechanism, where real-time electricity prices are derived using QUBO formulations and solved through quantum annealing to achieve high-dimensional optimization under stringent grid constraints. The engine receives input from the middle layer, the Grid Operation and IoT Layer, which provides continuous data streams from smart meters, renewable generation forecasts, dispatch schedules, and reserve management systems. These data streams are enabled via ubiquitous networked sensors, forming a bidirectional communication channel. On the right, the EV User Interaction Layer models charging demand and elasticity behavior, capturing user response to pricing signals. A feedback loop is established whereby users’ demand-side flexibility informs real-time adjustments in pricing. Additionally, the framework embeds cyber risk-aware pricing mechanisms to maintain resilience against potential threats to data integrity or system disruption. Overall, the architecture emphasizes a tightly coupled cyber-physical-energy loop, where adaptive pricing ensures grid reliability, renewable utilization, and user cost savings.

This paper introduces a quantum annealing-based framework for optimizing real-time pricing strategies in EV charging grids, presenting a novel approach to overcome the computational bottlenecks of classical techniques. The proposed model is designed to dynamically adjust EV charging prices in response to fluctuating grid conditions, renewable energy variability, and user demand patterns. By constructing an energy landscape that corresponds to the cost function of the pricing model, the quantum annealing process identifies the minimum energy state, which directly translates into the optimal pricing strategy. Unlike conventional models, this approach allows simultaneous evaluation of multiple pricing scenarios, significantly accelerating the decision-making process. Additionally, the integration of IoT-enabled data streams into the optimization framework ensures that real-time updates from EVs, charging stations, and grid sensors are incorporated into pricing adjustments. This adaptive mechanism not only enhances the responsiveness of the pricing model but also improves overall grid efficiency and sustainability by promoting the alignment of charging demand with renewable energy generation. The mathematical foundation of this work is grounded in a rigorous optimization framework that captures the complexities of EV charging dynamics. The problem formulation consists of an objective function that minimizes the overall cost of energy supply while maintaining grid stability and user satisfaction. Constraints are designed to enforce power balance, prevent network congestion, ensure pricing fairness, and account for the influence of consumer behavior on demand elasticity. Furthermore, renewable energy integration is explicitly considered, allowing the model to dynamically adjust pricing based on the availability of green energy sources. The incorporation of quantum annealing enables the model to navigate complex, high-dimensional search spaces efficiently, ensuring that the real-time pricing mechanism remains computationally feasible for large-scale deployment. By leveraging the principles of quantum optimization, this work introduces a paradigm shift in how real-time energy pricing can be structured, offering a solution that is both scalable and adaptable to modern grid demands.

This paper makes four key contributions to the field of smart grid optimization and EV charging management. First, it introduces a quantum annealing-based optimization framework that significantly enhances the efficiency of real-time pricing computations, addressing the scalability limitations of traditional methods. Second, it develops a comprehensive mathematical model that captures the intricate relationships between energy supply, grid stability, and consumer demand, ensuring that pricing strategies remain economically viable while minimizing grid stress. Third, it integrates IoT-enabled real-time data streams into the optimization process, enabling dynamic adjustments that reflect evolving grid conditions and renewable energy fluctuations. Finally, this work presents an in-depth analysis of the implications of quantum-enhanced pricing on consumer behavior, energy market stability, and sustainable energy utilization, offering valuable insights for future smart grid applications. Through these contributions, this research not only advances the theoretical understanding of quantum computing applications in energy pricing but also provides a practical pathway for implementing next-generation smart charging infrastructures. To improve the clarity and readability of the mathematical formulation, a comprehensive nomenclature table is provided below (

Table 1. Nomenclature of key variables and parameters.

Symbol	Unit	Description
$P_{i,t}^{\mathrm{EV}}$	kW	Charging power assigned to EVs at station i at time t
$P_{i,t}^{\mathrm{grid}}$	kW	Grid-supplied power to station i at time t
$P_{i,t}^{\mathrm{ren}}$	kW	Renewable power available at station i at time t
$D_{i,t}^{\mathrm{grid}}$	kW	General grid demand at node i
$D_{i,t}^{\mathrm{loss}}$	kW	Power losses in the network
$P_{j,t}^{\mathrm{curtail}}$	kW	Renewable curtailment at station j at time t
$P_{i,t}^{\mathrm{price}}$	USD/kWh	Real-time electricity price at station i at time t
${\lambda }_{i,t}$	–	Price elasticity coefficient of EV users at station i
${\delta }_{i,t}$	–	Sensitivity of EV demand to price elasticity
${\varphi }_{j,t}$	–	Renewable dispatch effectiveness at station j
${\omega }_{j,t}$	–	Market profit recovery ratio for station j
${\gamma }_{i,t}^{\mathrm{ren}}$	–	Renewable energy penetration ratio
${\theta }_{i,t}^{\mathrm{demand}}$	–	Demand weight for elasticity calculation
${\sigma }_{j,t}^{\mathrm{curtail}}$	–	Weight for renewable curtailment loss
${\mu }_{j,t}^{\mathrm{available}}$	–	Availability factor of renewable energy at station j
${\psi }_{j,t}^{\cos \mathrm{t}}$	USD/kWh	Marginal electricity cost
${\rho }_{j,t}^{\mathrm{profit}}$	USD/kWh	Target profit margin for the operator
${\vartheta }_{i,t}^{\mathrm{EV}}$	–	Weight for EV-specific optimization cost
${\kappa }_{i,t}^{\mathrm{grid}}$	–	Grid utilization factor at station i
${\xi }_{j,t},{\zeta }_{i,t}$	–	Auxiliary scaling weights in objective terms
${\nu }_{i,t}$	–	Carbon intensity weight at station i
$\alpha ,\beta$	–	Model decision variables (annealing control, pricing slope)
${\mathsf{\Pi }}_{i,t}^{\mathrm{anneal}}$	–	Quantum annealing energy term for station i
${\mathsf{\Xi }}_{i,t}^{\mathrm{forecast}}$	–	Forecasting error factor
${\tau }_{i,t}^{\mathrm{response}}$	–	User response participation factor
${\theta }_{i,t}^{\mathrm{cyber}}$	–	Cybersecurity risk coefficient
${\eta }_{i,t}^{\mathrm{eff}}$	–	EV charging efficiency
${\gamma }_{i,t}^{\mathrm{carbon}}$	–	Carbon emission intensity
${\psi }_{i,t}^{\mathrm{capacity}}$	–	Local infrastructure capacity scaling factor
${\kappa }_{i,t}^{\mathrm{control}}$	–	Pricing control smoothness factor
${\tau }_{i,t}^{\mathrm{participation}}$	–	Social behavioral participation parameter
${\mathsf{\Phi }}^{\mathrm{battery}},{\mathsf{\Phi }}^{\mathrm{flexibility}},{\Theta }^{\mathrm{income}}$	Various	System-level bounds: battery degradation, flexibility, user affordability
$C^{\mathrm{target}},C^{\mathrm{threshold}}$	kgC${\mathrm{O}}_2$	Carbon emission constraints
T	–	Total number of time intervals
$N,M$	–	Sets of EV stations and grid nodes respectively

). This table summarizes the main variables and parameters used throughout the optimization model, including decision variables, physical quantities, economic parameters, and system-level constraints. Each symbol is accompanied by its corresponding unit and description to ensure consistent interpretation across interdisciplinary readers. The inclusion of this nomenclature facilitates better traceability of the model equations and supports a structured understanding of the quantum-annealing-based pricing framework.

2. Literature Review

The optimization of real-time pricing in electric vehicle (EV) charging networks has been extensively explored in recent years, with various approaches emerging to tackle the challenges posed by fluctuating demand, grid stability concerns, and the integration of renewable energy sources. Traditional pricing mechanisms, such as time-of-use (TOU) pricing, critical peak pricing (CPP), and real-time pricing (RTP), have been widely adopted to influence EV user charging behavior and alleviate peak load burdens [14,15]. However, these conventional strategies often rely on predefined schedules or simple price elasticity models that fail to capture the highly dynamic and stochastic nature of modern smart grids. While heuristic and rule-based pricing frameworks have been proposed to enhance adaptability, they often struggle with computational efficiency and optimality in large-scale EV penetration scenarios. Thus, the necessity for more advanced optimization techniques has driven research towards machine learning-based, game-theoretic, and optimization-driven methodologies, though each approach presents limitations in scalability, convergence speed, and uncertainty modeling.

Classical optimization techniques, including mixed-integer linear programming (MILP), nonlinear programming (NLP), and convex optimization, have been extensively applied to real-time pricing models for EV charging. These methods provide structured solutions by formulating pricing as an optimization problem constrained by grid conditions, energy supply, and consumer preferences. Many studies have proposed centralized and decentralized pricing mechanisms using convex optimization to balance energy supply with charging demand while minimizing operational costs for both consumers and service providers [16,17]. However, these traditional optimization methods struggle with high-dimensional, non-convex problems, particularly in scenarios where large-scale EV adoption introduces complex, interdependent constraints. Furthermore, classical solvers often exhibit significant computational delays, rendering them impractical for real-time applications where rapid decision-making is required.

With the increasing complexity of energy systems, reinforcement learning (RL) and deep learning (DL)-based models have gained traction in optimizing real-time pricing for EV charging. Several studies have leveraged deep reinforcement learning (DRL) frameworks to enable adaptive pricing mechanisms that learn optimal charging strategies through interaction with historical and real-time data. Actor–critic models, Q-learning, and policy gradient methods have demonstrated effectiveness in capturing dynamic pricing responses, with some works integrating demand-side management (DSM) strategies to improve grid resilience [18,19]. However, these RL-based approaches are often data-intensive and require extensive training periods, making their deployment challenging in rapidly evolving grid environments. Additionally, their reliance on simulated data can result in suboptimal generalization when deployed in real-world conditions, where uncertainty and external factors significantly influence pricing strategies [20]. Figure 2 illustrates the complete operational cycle of the proposed quantum-enabled pricing framework. The process begins with real-time data collection, which includes inputs from EV charging stations, power grid status monitors, and renewable energy forecasts. These inputs feed into the decision model, which synthesizes grid conditions, demand elasticity, and system constraints into a structured representation for optimization. The central optimization module, leveraging quantum annealing, determines the optimal spatiotemporal pricing strategy. The resulting pricing signals are then distributed across the network to influence charging behavior and grid dispatch. These responses from the EV charging networks and power grids are continuously monitored and fed back into the data collection module, creating a closed-loop system that adapts dynamically to evolving conditions. This workflow ensures responsive, efficient, and cyber-resilient energy pricing across complex infrastructure systems. Game-theoretic models have also been explored to analyze the interactions between EV users, charging service providers, and grid operators. Nash equilibrium-based formulations have been applied to design competitive pricing strategies that balance user satisfaction with economic profitability [21,22]. Stackelberg game models have been widely utilized to structure hierarchical decision-making frameworks, where service providers act as leaders and EV users respond as followers to price signals. While game theory offers valuable insights into market dynamics, its applicability in real-time settings remains limited due to its reliance on equilibrium assumptions and computationally expensive solution processes. Moreover, real-world charging behaviors are influenced by numerous socio-economic factors that are difficult to encode into game-theoretic frameworks, reducing their practicality in highly uncertain environments [23,24].

The integration of renewable energy sources into EV charging pricing strategies has further complicated the optimization landscape. Many studies have proposed hybrid energy management systems that incorporate renewable generation forecasts into pricing models, allowing for price adjustments based on solar and wind availability. Stochastic optimization techniques, including robust optimization and distributionally robust optimization (DRO), have been employed to mitigate uncertainties in renewable energy supply, enhancing the reliability of dynamic pricing mechanisms [25,26]. However, these methods often rely on probabilistic assumptions that may not accurately reflect real-time fluctuations, leading to inefficiencies in grid operation. Additionally, the computational complexity of solving stochastic optimization problems in large-scale EV networks presents scalability concerns, particularly when attempting to implement real-time pricing adjustments.

Quantum computing, particularly quantum annealing, has emerged as a novel computational paradigm that offers significant advantages over classical approaches in solving large-scale optimization problems. Unlike classical optimization algorithms, which rely on iterative searching and gradient-based solvers, quantum annealing exploits quantum mechanical principles such as superposition and tunneling to explore vast solution spaces more efficiently [11,27,28]. While quantum computing applications in power systems optimization remain relatively nascent, recent advancements in hardware and algorithmic design have demonstrated promising results in combinatorial optimization problems. Several studies have explored the potential of quantum annealing in unit commitment, optimal power flow, and energy dispatch optimization, showcasing its ability to outperform classical solvers in complex problem spaces. However, the application of quantum annealing to real-time pricing optimization in EV charging grids remains largely unexplored, representing a significant gap in the literature.

3. Optimization and the Solution Approach

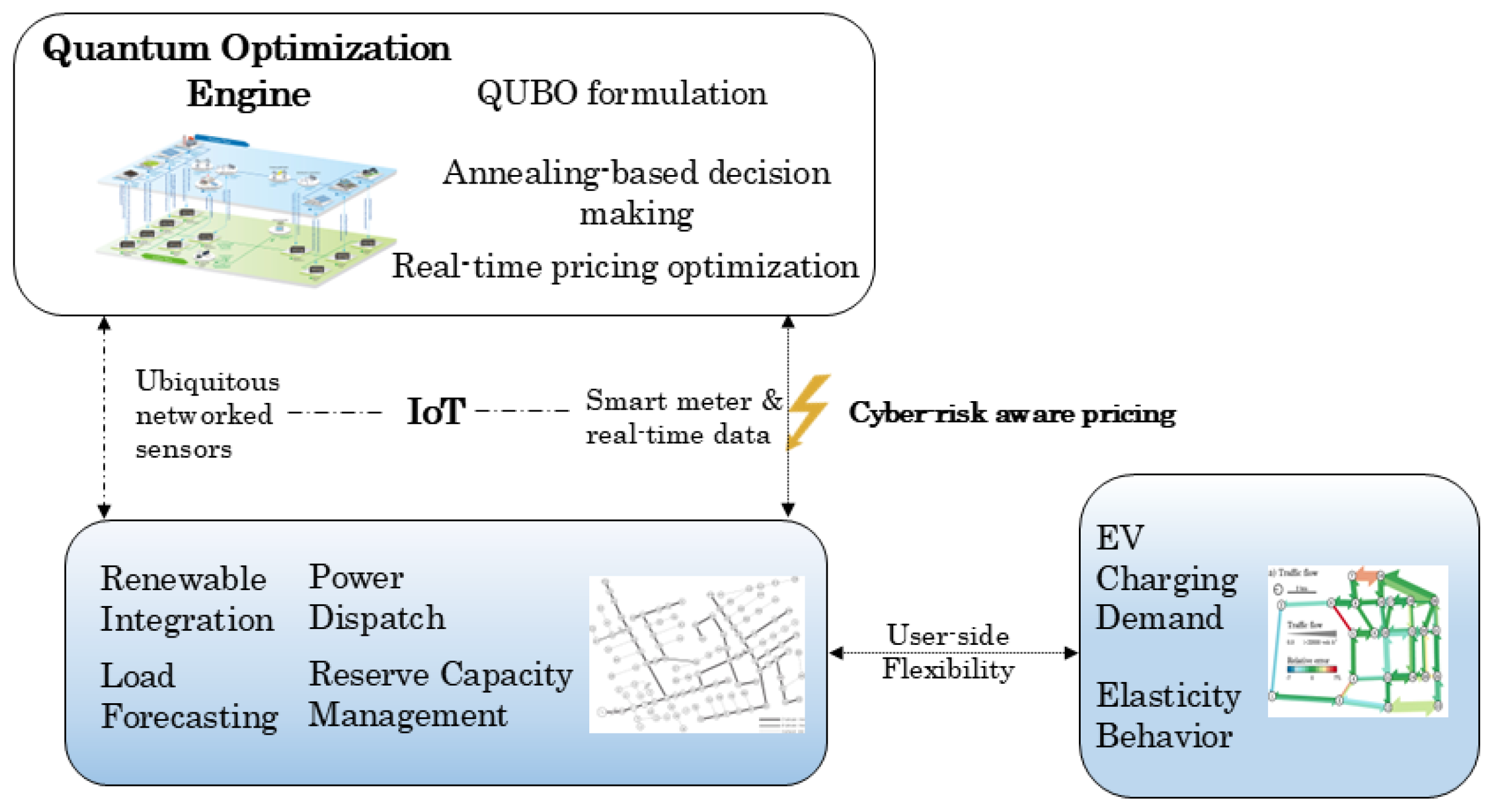
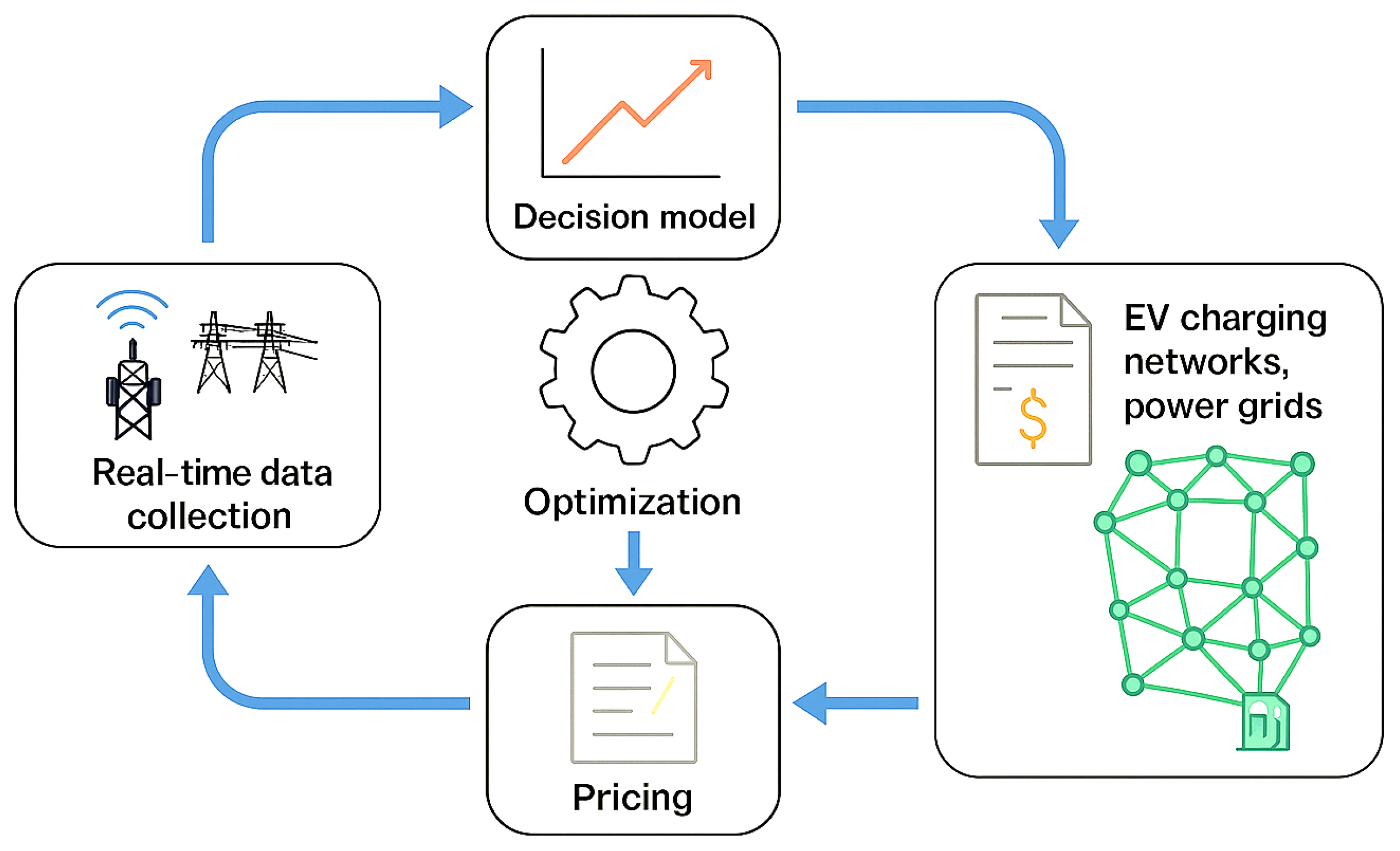
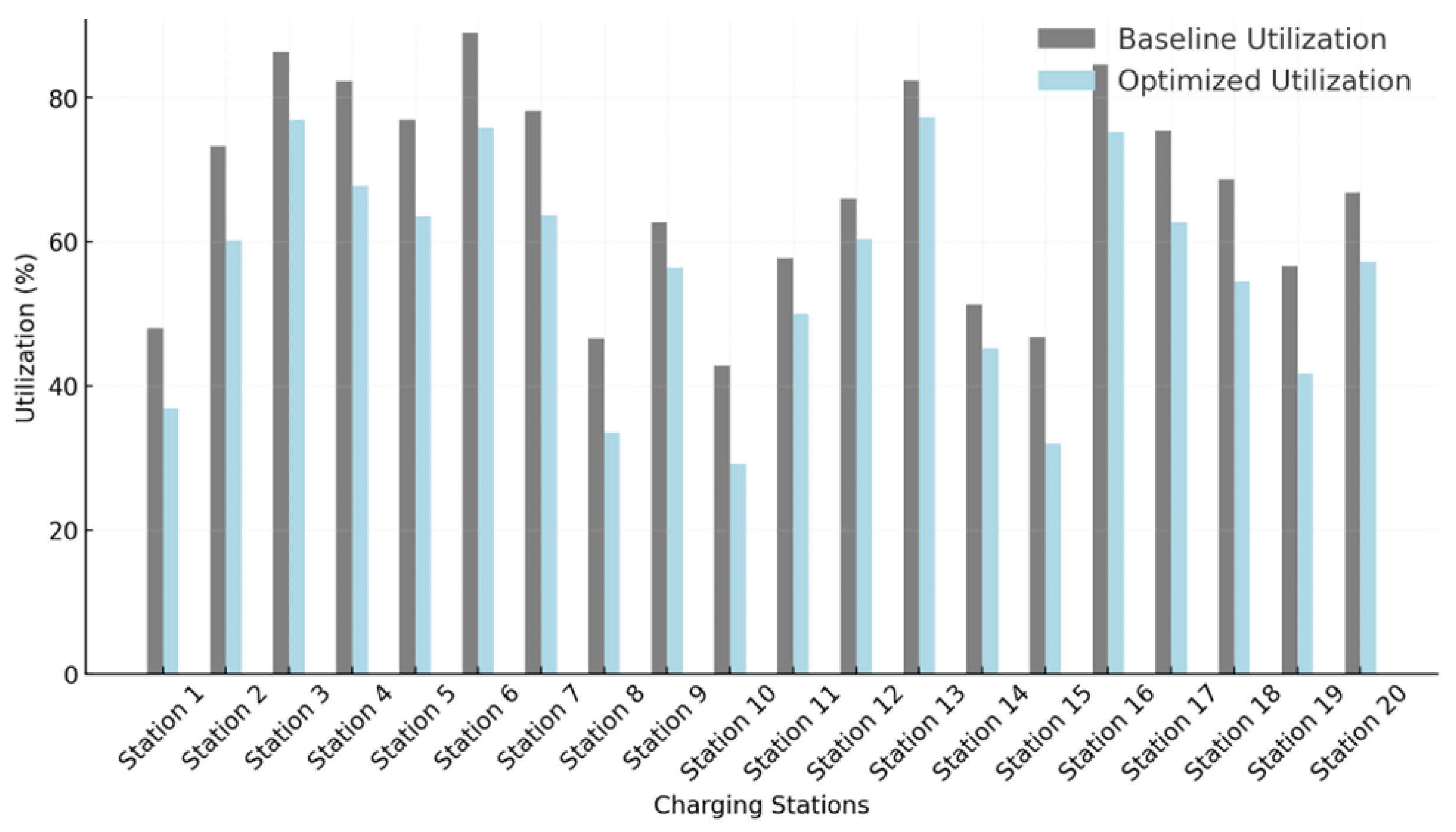
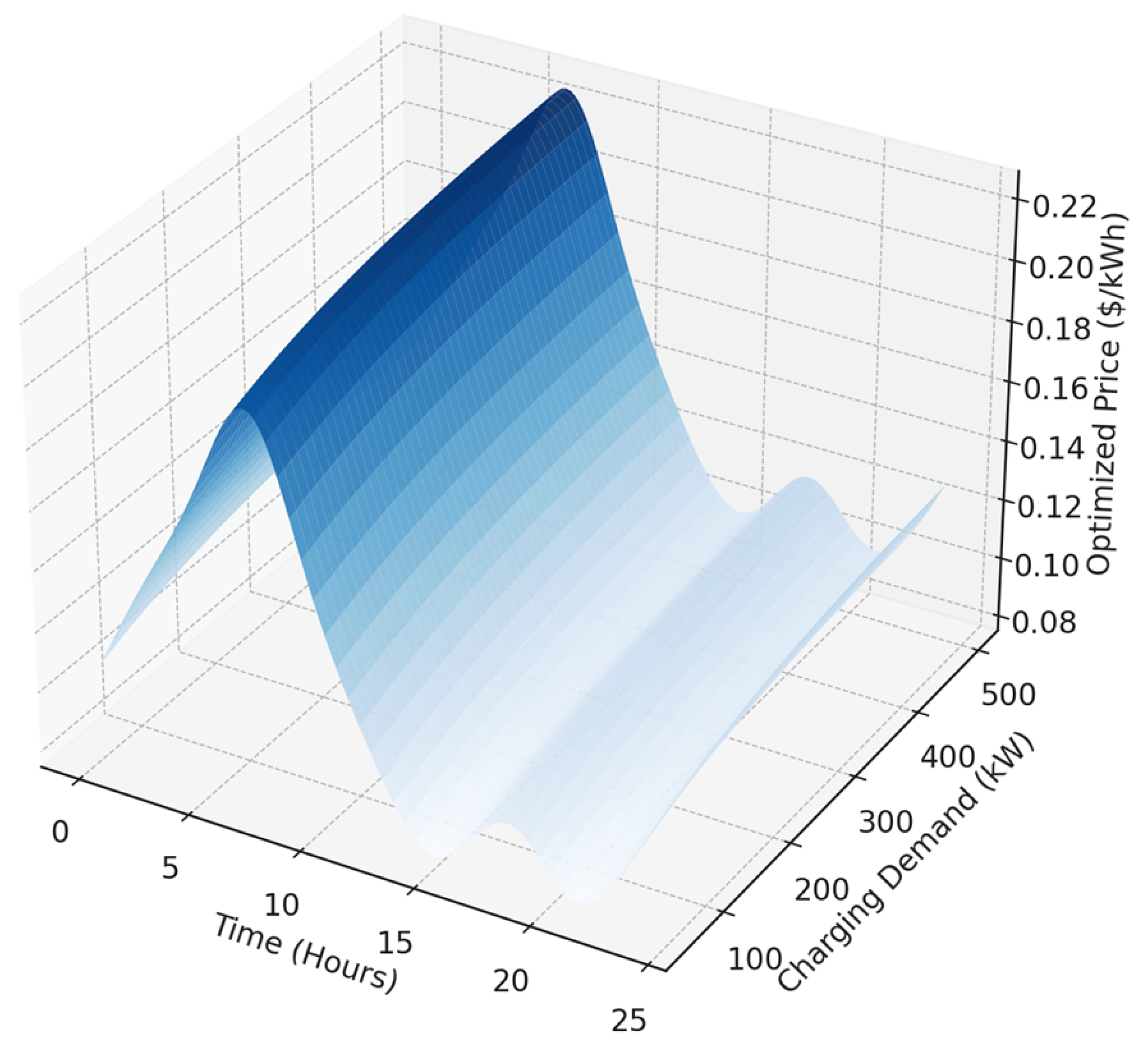
To rigorously capture the interplay between real-time pricing, electric vehicle (EV) charging behavior, and grid-level operational dynamics, we now formulate the core mathematical architecture and optimization methodology underpinning this research. This section presents the theoretical foundation of our proposed quantum annealing-assisted real-time pricing framework, beginning with the formal definition of the objective function and system constraints, followed by the detailed construction of the quantum-aware optimization process. The formulation is designed to reflect realistic power system behaviors, integrate demand elasticity, encode renewable availability, and respect physical grid limitations. By leveraging a structured and analytically expressive mathematical model, we enable an accurate and adaptable representation of the complex, nonlinear relationships embedded within the smart EV charging ecosystem. Subsequently, we introduce the optimization methodology employed to solve the proposed formulation—built upon the quantum annealing paradigm and enhanced through strategic model encoding and real-time data integration. The combined modeling and methodological architecture forms the basis of a responsive, efficient, and scalable solution for next-generation energy pricing under uncertainty and high EV penetration.

$$\begin{array}{cc}\hfill \underset{\mathit{\lambda },\mathit{\varphi },\mathit{\chi }}{min}& \sum _{t=1}^T\sum _{i\in \mathcal{N}}\left[{\alpha }_{i,t}{\left({\displaystyle \frac{{\vartheta }_{i,t}^{\mathrm{EV}}}{{\kappa }_{i,t}^{\mathrm{grid}}}}\right)}^{{\delta }_{i,t}}+{\beta }_{i,t}{\left({\displaystyle \frac{{\gamma }_{i,t}^{\mathrm{ren}}}{{\theta }_{i,t}^{\mathrm{demand}}}}\right)}^{{\zeta }_{i,t}}\right]\hfill \\ & +\sum _{t=1}^T\sum _{j\in \mathcal{M}}\left[{\phi }_{j,t}{\left({\displaystyle \frac{{\sigma }_{j,t}^{\mathrm{curtail}}}{{\mu }_{j,t}^{\mathrm{available}}}}\right)}^{{\eta }_{j,t}}+{\omega }_{j,t}{\left({\displaystyle \frac{{\psi }_{j,t}^{\cos \mathrm{t}}}{{\rho }_{j,t}^{\mathrm{profit}}}}\right)}^{{\xi }_{j,t}}\right]\hfill \end{array}$$

(1)

Electric vehicle charging cost optimization is critical for balancing grid efficiency and economic feasibility. The objective function here integrates multiple factors: the first term ensures the cost-effectiveness of EV charging through a ratio of demand to grid capacity, influenced by elasticity parameters ${\delta }_{i,t}$, while the second term accounts for renewable energy penetration, normalizing renewable generation availability with charging demand. Additionally, terms involving ${\phi }_{j,t}$ and ${\omega }_{j,t}$ regulate supply-demand mismatches, mitigating curtailment losses and optimizing cost recovery across different market participants.

$$\begin{array}{cc}\hfill \underset{\mathit{\lambda },\mathit{\tau }}{min}& \sum _{t=1}^T\sum _{i\in \mathcal{N}}\left[{\Gamma }_{i,t}{\left({\displaystyle \frac{{\mathsf{\Phi }}_{i,t}^{\mathrm{elastic}}}{{\mathsf{\Psi }}_{i,t}^{\mathrm{baseline}}}}\right)}^{{\mathsf{\Omega }}_{i,t}}+{\mathsf{{\rm Y}}}_{i,t}{\left({\displaystyle \frac{{\mathsf{\Lambda }}_{i,t}^{\mathrm{shift}}}{{\mathsf{\Xi }}_{i,t}^{\mathrm{price}}}}\right)}^{{\Theta }_{i,t}}\right]\hfill \\ & +\sum _{t=1}^T\sum _{j\in \mathcal{M}}\left[{\Delta }_{j,t}{\left({\displaystyle \frac{{\mathsf{\Sigma }}_{j,t}^{\mathrm{response}}}{{\mathsf{\Pi }}_{j,t}^{\mathrm{station}}}}\right)}^{{\varrho }_{j,t}}+{\mathsf{\Phi }}_{j,t}{\left({\displaystyle \frac{{\mathsf{\Psi }}_{j,t}^{\mathrm{congestion}}}{{\mathsf{\Lambda }}_{j,t}^{\mathrm{penalty}}}}\right)}^{{\chi }_{j,t}}\right]\hfill \end{array}$$

(2)

Consumer behavior plays a significant role in the effectiveness of real-time pricing, and this formulation encapsulates user responsiveness to dynamic pricing signals. The first term represents elasticity-driven demand shifts based on deviations from baseline consumption patterns, where ${\Gamma }_{i,t}$ models price elasticity, and ${\mathsf{\Omega }}_{i,t}$ governs response sensitivity. The second term emphasizes demand shifting potential, linking energy demand shifts ${\mathsf{\Lambda }}_{i,t}^{\mathrm{shift}}$ to pricing strategies ${\mathsf{\Xi }}_{i,t}^{\mathrm{price}}$. Furthermore, congestion management mechanisms introduce penalties proportional to station congestion levels, ensuring grid reliability and mitigating overload risks. While our framework imposes explicit constraints on price volatility to ensure user acceptance and grid stability (e.g., smooth temporal transitions and upper/lower price bounds), this does not conflict with the advantage of fast optimization enabled by quantum annealing. The price adjustment constraint (e.g., $|P^{\mathrm{price}}i,t-P^{\mathrm{price}}i,t-1|\le \Delta P_{\max }$) operates as a regulatory control to maintain continuity and predictability in pricing signals. Meanwhile, the speed of optimization refers to the system’s ability to recompute valid and feasible pricing vectors in near real time, even under frequent grid state changes or user behavior shifts. Thus, the pricing updates are both computationally rapid and smoothly bounded, ensuring that real-time responsiveness does not introduce erratic price behavior, but rather adapts within well-defined operating margins.

$$\begin{array}{cc}\hfill \underset{\mathit{\lambda },\mathit{\nu }}{min}& \sum _{t=1}^T\sum _{i\in \mathcal{N}}\left[{\Theta }_{i,t}{\left({\displaystyle \frac{{\mathsf{\Pi }}_{i,t}^{\mathrm{renew}}}{{\mathsf{\Sigma }}_{i,t}^{\mathrm{grid}}}}\right)}^{{\mathsf{{\rm Y}}}_{i,t}}+{\mathsf{\Psi }}_{i,t}{\left({\displaystyle \frac{{\mathsf{\Lambda }}_{i,t}^{\mathrm{intermittent}}}{{\mathsf{\Xi }}_{i,t}^{\mathrm{forecast}}}}\right)}^{{\mathsf{\Phi }}_{i,t}}\right]\hfill \\ & +\sum _{t=1}^T\sum _{j\in \mathcal{M}}\left[{\mathsf{\Omega }}_{j,t}{\left({\displaystyle \frac{{\Delta }_{j,t}^{\mathrm{curtail}}}{{\mathsf{\Pi }}_{j,t}^{\mathrm{excess}}}}\right)}^{{\Theta }_{j,t}}+{\mathsf{\Xi }}_{j,t}{\left({\displaystyle \frac{{\mathsf{\Psi }}_{j,t}^{\mathrm{carbon}}}{{\mathsf{\Lambda }}_{j,t}^{\mathrm{credit}}}}\right)}^{{\mathsf{\Phi }}_{j,t}}\right]\hfill \end{array}$$

(3)

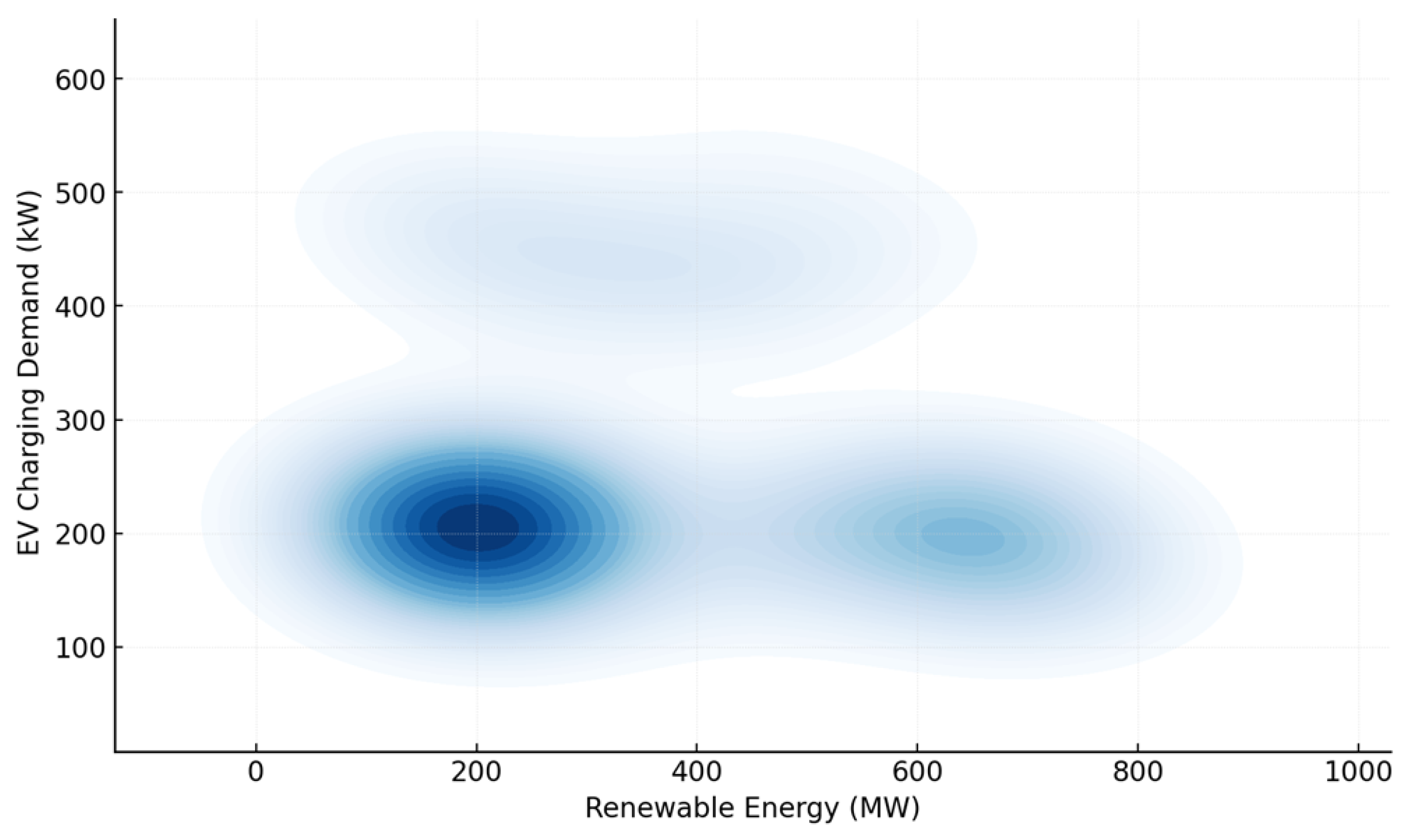
Renewable energy integration is a pivotal factor in optimizing charging grid economics. This formulation considers renewable availability constraints, normalizing energy dispatch ${\mathsf{\Pi }}_{i,t}^{\mathrm{renew}}$ by overall grid power ${\mathsf{\Sigma }}_{i,t}^{\mathrm{grid}}$, adjusted by system uncertainty ${\mathsf{{\rm Y}}}_{i,t}$. Furthermore, the model incorporates renewable intermittency factors, ensuring forecasting accuracy and mitigating power fluctuation impacts. Terms with ${\mathsf{\Omega }}_{j,t}$ capture curtailment penalties, incentivizing excess generation utilization, while ${\mathsf{\Xi }}_{j,t}$ addresses carbon offset pricing, leveraging carbon credit mechanisms for environmental sustainability.

$$\begin{array}{cc}\hfill \underset{\mathit{\alpha },\mathit{\beta }}{min}& \sum _{t=1}^T\sum _{i\in \mathcal{N}}\left[{\Theta }_{i,t}{\left({\displaystyle \frac{{\mathsf{\Pi }}_{i,t}^{\mathrm{anneal}}}{{\mathsf{\Sigma }}_{i,t}^{\mathrm{energy}}}}\right)}^{{\mathsf{{\rm Y}}}_{i,t}}+{\mathsf{\Psi }}_{i,t}{\left({\displaystyle \frac{{\mathsf{\Lambda }}_{i,t}^{\mathrm{state}}}{{\mathsf{\Xi }}_{i,t}^{\cos \mathrm{t}}}}\right)}^{{\mathsf{\Phi }}_{i,t}}\right]\hfill \\ & +\sum _{t=1}^T\sum _{j\in \mathcal{M}}\left[{\mathsf{\Omega }}_{j,t}{\left({\displaystyle \frac{{\Delta }_{j,t}^{\mathrm{solution}}}{{\mathsf{\Pi }}_{j,t}^{\mathrm{optimum}}}}\right)}^{{\Theta }_{j,t}}+{\mathsf{\Xi }}_{j,t}{\left({\displaystyle \frac{{\mathsf{\Psi }}_{j,t}^{\mathrm{anneal}-\mathrm{step}}}{{\mathsf{\Lambda }}_{j,t}^{\mathrm{global}}}}\right)}^{{\mathsf{\Phi }}_{j,t}}\right]\hfill \end{array}$$

(4)

Quantum annealing mechanisms drive the real-time pricing optimization framework. This formulation constructs an energy landscape representation, where annealing parameter ${\mathsf{\Pi }}_{i,t}^{\mathrm{anneal}}$ determines the interaction between system energy constraints ${\mathsf{\Sigma }}_{i,t}^{\mathrm{energy}}$ and cost penalties ${\mathsf{\Xi }}_{i,t}^{\cos \mathrm{t}}$. Quantum state evolution equations model the system’s transition across energy states, ensuring robust convergence to globally optimal pricing solutions. Additionally, annealing step optimization, captured by ${\mathsf{\Psi }}_{j,t}^{\mathrm{anneal}-\mathrm{step}}$, aligns with practical constraints, enabling computational efficiency and real-time decision-making in large-scale grid environments.

$$\begin{array}{cc}\hfill \sum _{i\in \mathcal{N}}\left(P_{i,t}^{\mathrm{EV}}+P_{i,t}^{\mathrm{grid}}+P_{i,t}^{\mathrm{ren}}\right)& =\sum _{i\in \mathcal{N}}\left(D_{i,t}^{\mathrm{EV}}+D_{i,t}^{\mathrm{grid}}+D_{i,t}^{\mathrm{loss}}\right),\forall t\in \mathcal{T}\hfill \end{array}$$

(5)

Ensuring the power balance is fundamental to maintaining a stable smart grid operation. This constraint guarantees that the sum of the total supplied power—including electric vehicle charging demand, grid energy dispatch, and renewable generation—matches the aggregated demand from EV users, general grid consumers, and system losses. The incorporation of renewable energy into this balance is critical for sustainability, reducing reliance on conventional energy sources while maintaining equilibrium in real-time pricing decisions.

$$\begin{array}{cc}\hfill \sum _{i\in \mathcal{N}}\left({\displaystyle \frac{V_{i,t}^2-V_{j,t}^2}{X_{ij}}}\right)& =\sum _{i\in \mathcal{N}}{P}_{i,t}^{\mathrm{flow}},\forall (i,j)\in \mathcal{E},\forall t\in \mathcal{T}\hfill \end{array}$$

(6)

Voltage and frequency stability are essential to maintaining the reliability of an electric vehicle charging grid. This equation represents the nodal voltage variations and power flows across transmission lines, ensuring that voltage levels at different buses adhere to operational thresholds. The term $X_{ij}$ represents line reactance, which influences voltage stability, while $P_{i,t}^{\mathrm{flow}}$ denotes power injections at various nodes. By controlling voltage deviations within prescribed safety margins, this constraint ensures that grid disturbances do not disrupt the optimal charging process.

$$\begin{array}{c}\hfill 0\le P_{i,t}^{\mathrm{EV}}\le P_i^{max},\forall i\in \mathcal{N},\forall t\in \mathcal{T}\end{array}$$

(7)

To prevent overloading of charging stations, each EV charger is constrained to operate within predefined maximum power limits. The upper bound $P_i^{max}$ ensures that individual charging stations do not exceed their rated capacity, safeguarding grid components from overheating and ensuring longevity of charging infrastructure. This constraint is particularly crucial for real-time pricing strategies since price signals must be set in a way that prevents excessive demand from overwhelming local station capacities.

$$\begin{array}{cc}\hfill \sum _{(i,j)\in \mathcal{E}}{\displaystyle \frac{P_{i,j,t}^{\mathrm{flow}}}{S_{ij}^{max}}}& \le 1,\forall (i,j)\in \mathcal{E},\forall t\in \mathcal{T}\hfill \end{array}$$

(8)

Network congestion management plays a critical role in optimizing electric vehicle charging schedules. This constraint ensures that the power flow along each transmission line remains within its maximum allowable capacity $S_{ij}^{max}$, preventing thermal overloading and voltage collapse. Overloaded transmission lines can severely disrupt real-time pricing mechanisms, leading to inefficient grid operation. By integrating congestion-aware pricing models, this constraint helps redistribute charging demand across different times and locations to enhance grid flexibility.

$$\begin{array}{cc}\hfill P_{i,t}^{\mathrm{ren}}& \le A_{i,t}^{\mathrm{wind}}+A_{i,t}^{\mathrm{solar}},\forall i\in \mathcal{N},\forall t\in \mathcal{T}\hfill \end{array}$$

(9)

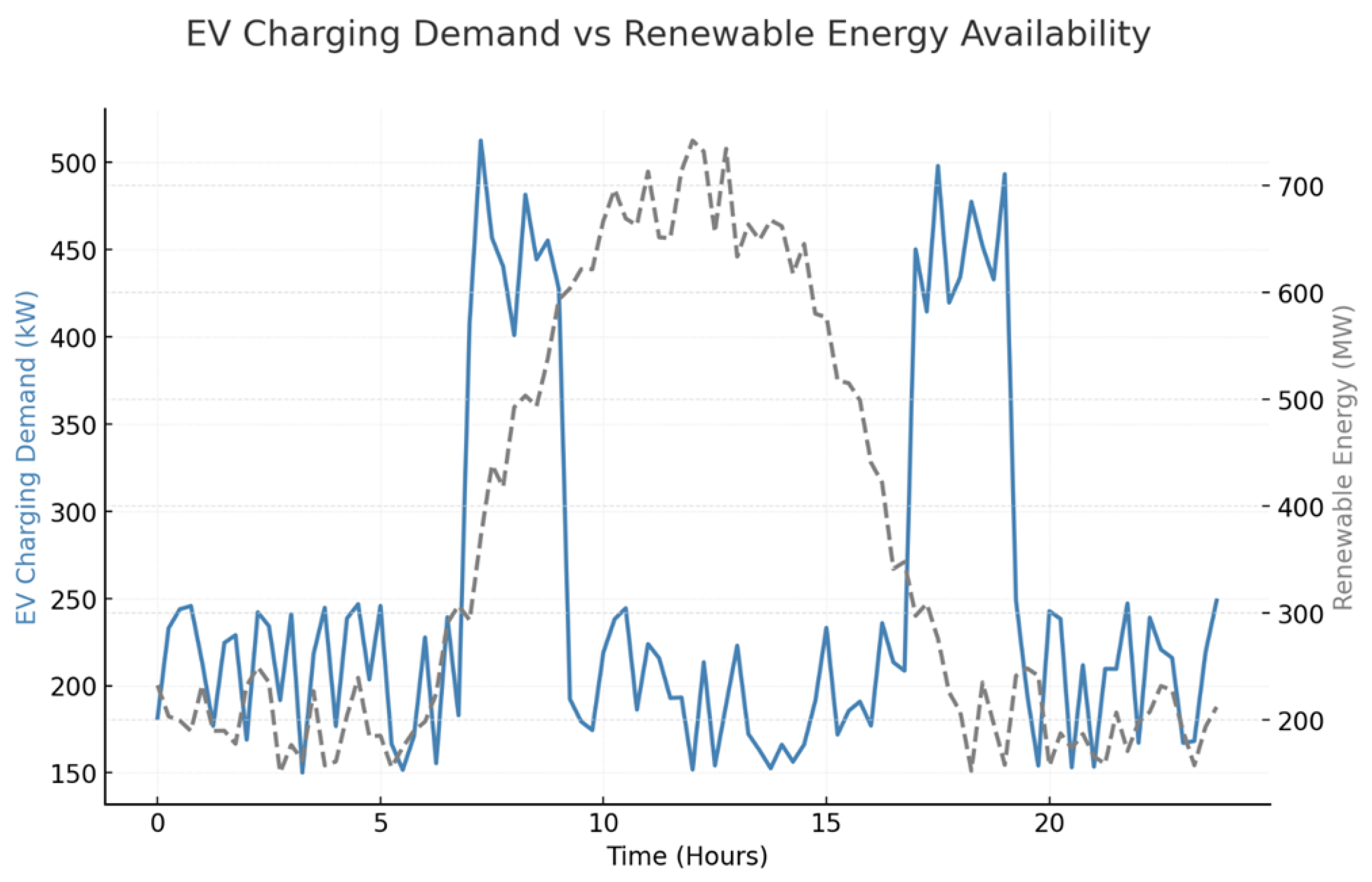
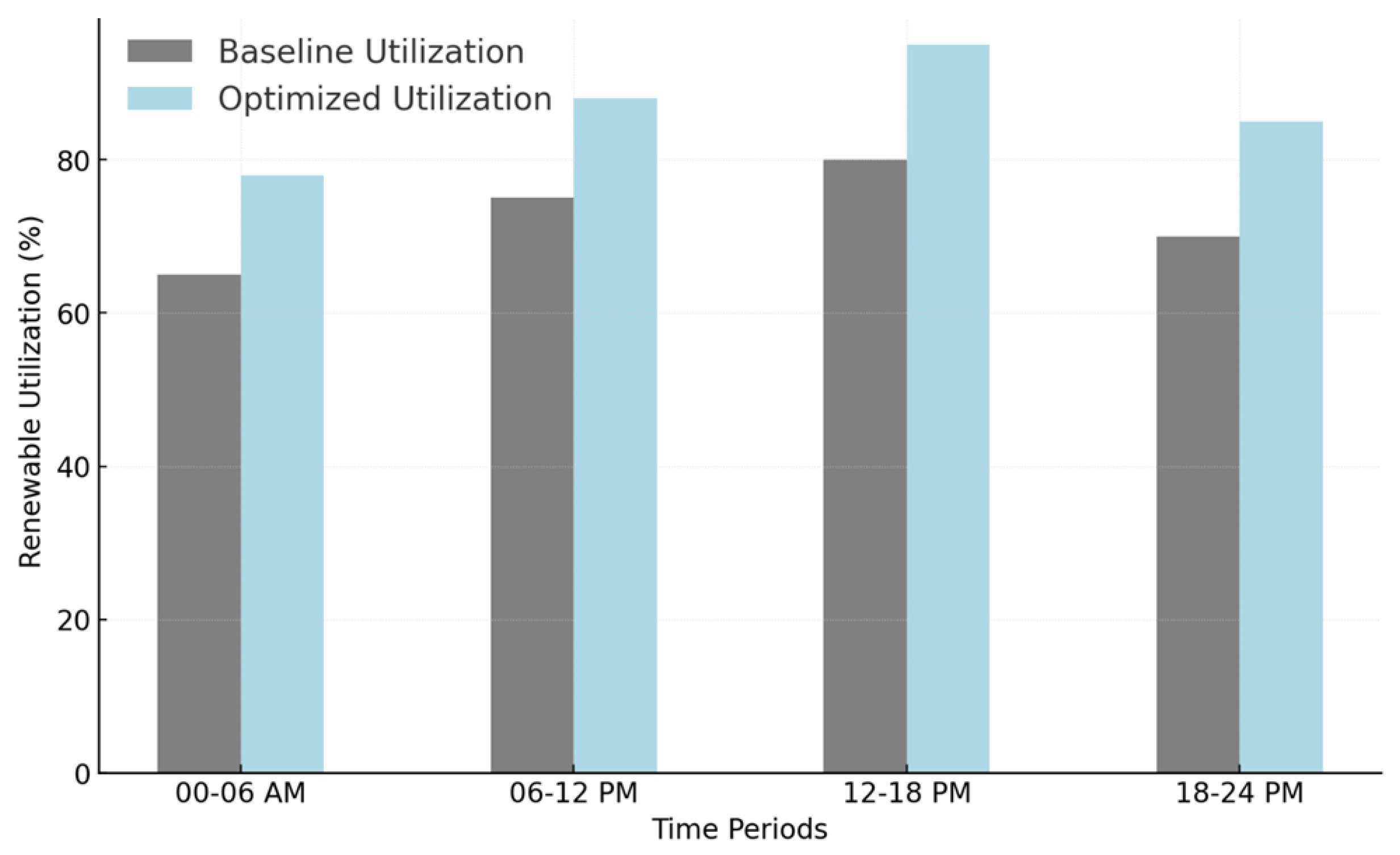
Renewable energy availability is inherently time-dependent, with fluctuations driven by meteorological conditions. This constraint ensures that the dispatched renewable power at each charging station does not exceed the locally available wind and solar generation at a given time. The terms $A_{i,t}^{\mathrm{wind}}$ and $A_{i,t}^{\mathrm{solar}}$ represent wind and photovoltaic energy availability, respectively. By dynamically adjusting real-time prices based on renewable output, the system incentivizes EV users to charge when renewable generation is high, promoting carbon-free mobility.

$$\begin{array}{c}\hfill P_{\min }^{\mathrm{price}}\le P_{i,t}^{\mathrm{price}}\le P_{\max }^{\mathrm{price}},\forall i\in \mathcal{N},\forall t\in \mathcal{T}\end{array}$$

(10)

Price volatility is a significant concern in real-time EV charging markets. This constraint enforces upper and lower bounds on the price adjustments applied at each charging station, preventing extreme price swings that could lead to economic inefficiencies or discourage EV adoption. The terms $P_{\min }^{\mathrm{price}}$ and $P_{\max }^{\mathrm{price}}$ define the minimum and maximum permissible price levels. By keeping prices within reasonable limits, this condition fosters a balanced trade-off between grid efficiency and consumer affordability.

$$\begin{array}{cc}\hfill \sum _{t=1}^T{P}_{i,t}^{\cos \mathrm{t}}& \le {\Theta }_{i,t}^{\mathrm{income}},\forall i\in \mathcal{N}\hfill \end{array}$$

(11)

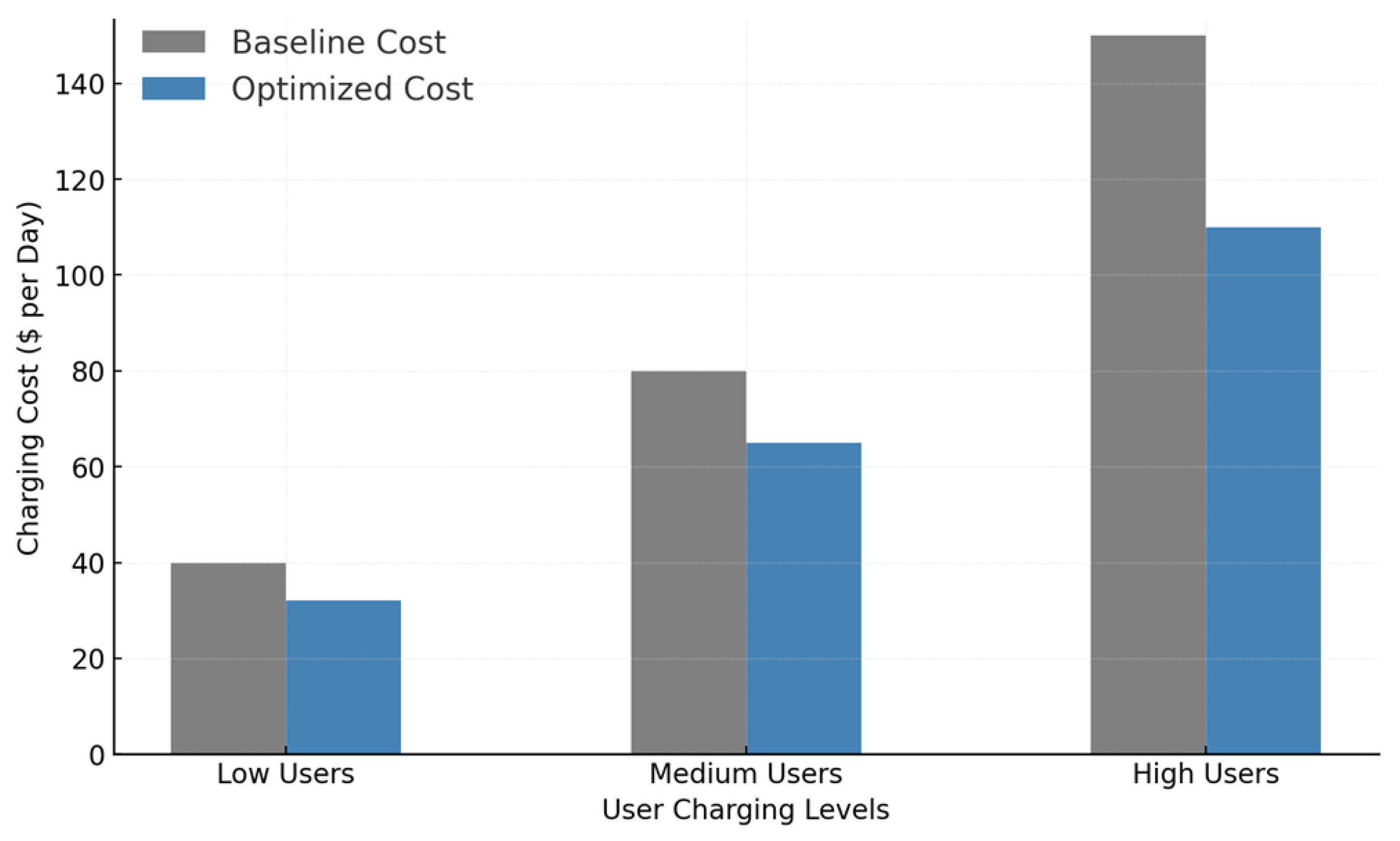
Affordability is a key factor in the successful deployment of electric vehicle charging infrastructure. This constraint ensures that the cumulative charging cost incurred by an EV user does not exceed an affordability threshold ${\Theta }_{i,t}^{\mathrm{income}}$, which may be determined based on average consumer income or policy regulations. By incorporating affordability constraints into the optimization framework, the system promotes equitable access to charging services while maintaining economic sustainability for grid operators.

$$\begin{array}{cc}\hfill \sum _{i\in \mathcal{N}}{P}_{i,t}^{\mathrm{EV}}·{\lambda }_{i,t}& \le \sum _{i\in \mathcal{N}}{P}_{i,t}^{\mathrm{grid}}+P_{i,t}^{\mathrm{ren}}-P_{i,t}^{\mathrm{loss}},\forall t\in \mathcal{T}\hfill \end{array}$$

(12)

Grid flexibility plays a pivotal role in ensuring that real-time pricing mechanisms do not cause supply shortages. This constraint ensures that the power allocated for EV charging, scaled by the elasticity factor ${\lambda }_{i,t}$, does not exceed the sum of available grid dispatch and renewable power generation, accounting for system losses. By enforcing this restriction, the system prevents instability and over-reliance on expensive emergency energy sources.

$$\begin{array}{cc}\hfill \sum _{i\in \mathcal{N}}\left|P_{i,t}^{\mathrm{price}}-P_{i,t-1}^{\mathrm{price}}\right|& \le \Delta P^{\max },\forall t\in \mathcal{T}\hfill \end{array}$$

(13)

Abrupt fluctuations in real-time pricing can lead to erratic charging behaviors, negatively impacting both grid stability and consumer trust. This constraint ensures that the absolute change in charging price from one time step to the next does not exceed a predefined maximum adjustment $\Delta P^{\max }$, thereby maintaining smooth transitions in price signals and preventing unnecessary volatility.

$$\begin{array}{cc}\hfill \sum _{i\in \mathcal{N}}{\pi }_{i,t}^{\mathrm{charge}}·P_{i,t}^{\mathrm{EV}}& \le P_{i,t}^{\mathrm{grid}}+P_{i,t}^{\mathrm{ren}},\forall t\in \mathcal{T}\hfill \end{array}$$

(14)

Market equilibrium must be preserved when setting real-time prices for EV charging. This equation ensures that the aggregated charging power, weighted by pricing factors ${\pi }_{i,t}^{\mathrm{charge}}$, remains within the available energy supply, combining both conventional grid electricity and renewable sources. This constraint is particularly critical in preventing excessive demand peaks that could lead to grid congestion or supply shortages.

$$\begin{array}{cc}\hfill \sum _{i\in \mathcal{N}}\left(P_{i,t}^{\mathrm{EV}}·{\tau }_{i,t}^{\mathrm{response}}\right)& \le P_{i,t}^{\mathrm{station}},\forall t\in \mathcal{T}\hfill \end{array}$$

(15)

Charging station capacities must be respected to ensure seamless service. This constraint states that the total power drawn by EVs at each time step, scaled by the demand response factor ${\tau }_{i,t}^{\mathrm{response}}$, should not exceed the physical capacity of the charging infrastructure. This ensures that individual stations are not overwhelmed by sudden spikes in demand.

$$\begin{array}{cc}\hfill \sum _{i\in \mathcal{N}}\sum _{t=1}^T\left({\displaystyle \frac{P_{i,t}^{\mathrm{EV}}}{{\xi }_{i,t}^{\mathrm{carbon}}}}\right)& \le C^{\mathrm{target}}\hfill \end{array}$$

(16)

Carbon footprint considerations are an essential part of sustainable pricing strategies. This constraint ensures that the cumulative energy consumption from EV charging, normalized by the carbon intensity factor ${\xi }_{i,t}^{\mathrm{carbon}}$, does not exceed a predefined carbon cap $C^{\mathrm{target}}$. This incentivizes grid operators to structure pricing in a way that promotes charging during low-carbon periods, such as when renewable generation is high.

$$\begin{array}{cc}\hfill \sum _{i\in \mathcal{N}}\left({\theta }_{i,t}^{\mathrm{cyber}}·P_{i,t}^{\mathrm{EV}}\right)& \le R^{\mathrm{secure}},\forall t\in \mathcal{T}\hfill \end{array}$$

(17)

Cybersecurity risks must be accounted for when integrating smart charging infrastructure. This equation imposes a limit on the aggregated charging power that can be controlled by a single cyber entity, ensuring that potential cyberattacks (modeled through risk factor ${\theta }_{i,t}^{\mathrm{cyber}}$) do not compromise the grid. A predefined security threshold $R^{\mathrm{secure}}$ is set to mitigate large-scale coordinated attacks.

$$\begin{array}{cc}\hfill \sum _{i\in \mathcal{N}}{P}_{i,t}^{\mathrm{degrade}}& \le {\mathsf{\Phi }}^{\mathrm{battery}},\forall t\in \mathcal{T}\hfill \end{array}$$

(18)

Battery degradation is an important consideration when designing real-time pricing models. This constraint ensures that the total degradation effect, modeled by the function $P_{i,t}^{\mathrm{degrade}}$, remains within a predefined acceptable threshold ${\mathsf{\Phi }}^{\mathrm{battery}}$, preventing excessive wear and tear on EV batteries caused by aggressive charging incentives.

$$\begin{array}{cc}\hfill \sum _{i\in \mathcal{N}}{P}_{i,t}^{\mathrm{response}}·{\lambda }_{i,t}^{\mathrm{social}}& \le {\Theta }^{\mathrm{engage}},\forall t\in \mathcal{T}\hfill \end{array}$$

(19)

User engagement in demand response programs is critical to the success of real-time pricing. This equation ensures that the total user response to price signals, scaled by social behavior factors ${\lambda }_{i,t}^{\mathrm{social}}$, does not exceed a predefined engagement cap ${\Theta }^{\mathrm{engage}}$. This prevents excessive reliance on user participation, which could lead to demand imbalances if overestimated.

$$\begin{array}{cc}\hfill \sum _{i\in \mathcal{N}}{P}_{i,t}^{\mathrm{reserve}}+P_{i,t}^{\mathrm{backup}}& \ge \sum _{i\in \mathcal{N}}\left(P_{i,t}^{\mathrm{EV}}+P_{i,t}^{\mathrm{grid}}-P_{i,t}^{\mathrm{ren}}\right),\forall t\in \mathcal{T}\hfill \end{array}$$

(20)

To ensure resilience in EV charging operations, this constraint enforces that the total reserve power capacity, including backup generation resources, must be sufficient to meet unexpected deviations in demand. The equation accounts for real-time charging demand, grid power supply, and renewable availability fluctuations. Maintaining an adequate power reserve prevents service disruptions due to unanticipated load surges, ensuring that EV users experience minimal charging delays.

$$\begin{array}{cc}\hfill \sum _{i\in \mathcal{N}}{P}_{i,t}^{\mathrm{load}-\mathrm{shift}}& \ge \sum _{i\in \mathcal{N}}\left(P_{i,t}^{\mathrm{peak}}-P_{i,t}^{\mathrm{offpeak}}\right),\forall t\in \mathcal{T}\hfill \end{array}$$

(21)

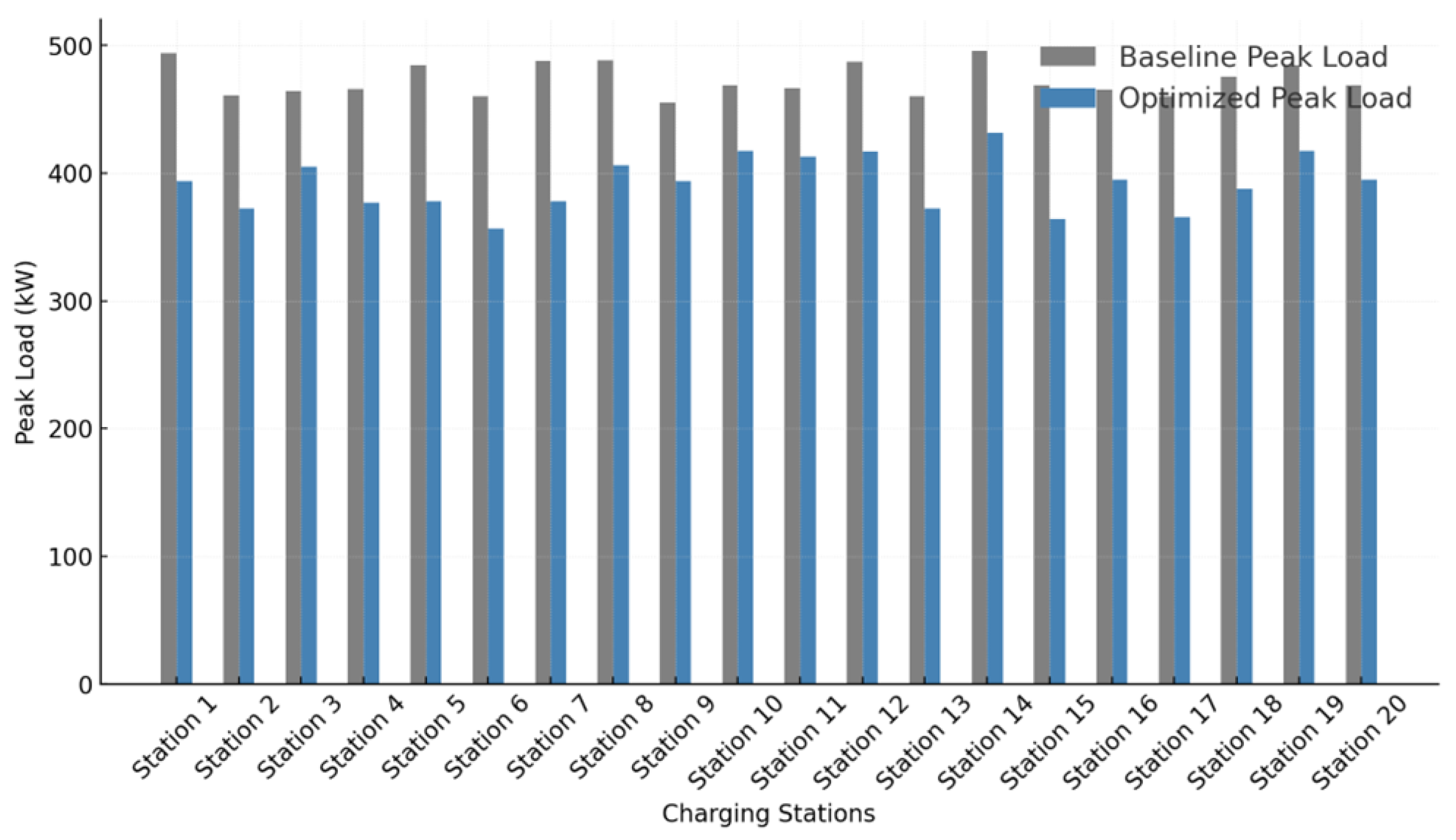
Peak load management is a critical component of demand-side optimization in EV charging grids. This constraint ensures that sufficient load-shifting strategies are in place to balance the difference between peak and off-peak demand. The parameter $P_{i,t}^{\mathrm{load}-\mathrm{shift}}$ represents the aggregate shifted load across all charging stations, helping to alleviate stress on the grid during peak hours. By dynamically adjusting pricing strategies, this constraint facilitates effective load balancing and grid stability.

$$\begin{array}{cc}\hfill \sum _{i\in \mathcal{N}}\left({\displaystyle \frac{P_{i,t}^{\mathrm{flex}}}{{\beta }_{i,t}^{\mathrm{demand}}}}\right)& \le {\mathsf{\Phi }}^{\mathrm{flexibility}},\forall t\in \mathcal{T}\hfill \end{array}$$

(22)

Flexibility in charging demand is essential for ensuring efficient real-time pricing adjustments. This equation constrains the proportion of demand that can be dynamically adjusted within each time period, preventing excessive fluctuations that might destabilize grid operations. The flexibility factor $P_{i,t}^{\mathrm{flex}}$ is divided by the demand elasticity coefficient ${\beta }_{i,t}^{\mathrm{demand}}$, ensuring that changes in charging power remain within the allowable threshold ${\mathsf{\Phi }}^{\mathrm{flexibility}}$. This helps avoid unintended consequences such as extreme demand shifts or overcorrections in price response.

$$\begin{array}{cc}\hfill \sum _{i\in \mathcal{N}}\left({\theta }_{i,t}^{\mathrm{market}}·P_{i,t}^{\mathrm{EV}}\right)& \ge {\Theta }^{\mathrm{profit}},\forall t\in \mathcal{T}\hfill \end{array}$$

(23)

Economic sustainability is a key consideration in designing real-time pricing strategies for EV charging grids. This constraint ensures that the aggregated revenue from charging demand, weighted by market influence factors ${\theta }_{i,t}^{\mathrm{market}}$, meets or exceeds a predefined profitability threshold ${\Theta }^{\mathrm{profit}}$. By maintaining a balance between consumer affordability and operator profitability, this condition supports long-term financial viability while encouraging continued investment in charging infrastructure.

$$\begin{array}{cc}\hfill \sum _{i\in \mathcal{N}}\left({\displaystyle \frac{P_{i,t}^{\mathrm{EV}}}{{\eta }_{i,t}^{\mathrm{eff}}}}\right)& \le P_{i,t}^{\mathrm{grid}}+P_{i,t}^{\mathrm{ren}},\forall t\in \mathcal{T}\hfill \end{array}$$

(24)

Charging efficiency constraints ensure that the power drawn by electric vehicles does not exceed the combined available supply from the grid and renewable sources. Here, ${\eta }_{i,t}^{\mathrm{eff}}$ represents the efficiency factor of the charging process, accounting for energy conversion losses. This constraint guarantees that the power supplied to EVs remains within sustainable limits, preventing excessive grid stress and optimizing the integration of renewable energy.

$$\begin{array}{cc}\hfill \sum _{i\in \mathcal{N}}\left(P_{i,t}^{\mathrm{EV}}·{\lambda }_{i,t}^{\mathrm{response}}\right)& \le \sum _{i\in \mathcal{N}}{P}_{i,t}^{\mathrm{DSM}},\forall t\in \mathcal{T}\hfill \end{array}$$

(25)

Demand-side management (DSM) strategies play a crucial role in optimizing EV charging schedules. This constraint ensures that the total charging demand, adjusted by consumer response elasticity ${\lambda }_{i,t}^{\mathrm{response}}$, does not exceed the allocated DSM capacity $P_{i,t}^{\mathrm{DSM}}$. By enforcing this condition, the system dynamically regulates consumer participation in load-shifting programs, enhancing grid flexibility and cost-effectiveness.

$$\begin{array}{cc}\hfill \sum _{i\in \mathcal{N}}{P}_{i,t}^{\mathrm{shift}}& \ge \sum _{i\in \mathcal{N}}\left(P_{i,t}^{\mathrm{peak}}-P_{i,t}^{\mathrm{offpeak}}\right),\forall t\in \mathcal{T}\hfill \end{array}$$

(26)

To mitigate peak demand spikes, this constraint enforces a minimum load-shifting requirement. The parameter $P_{i,t}^{\mathrm{shift}}$ represents the total power that is actively shifted from peak to off-peak periods, ensuring that peak-hour loads do not surpass grid safety margins. This optimization technique enhances system resilience, reduces operational costs, and improves overall efficiency by aligning charging demand with periods of high renewable generation.

$$\begin{array}{cc}\hfill \sum _{i\in \mathcal{N}}\left({\displaystyle \frac{P_{i,t}^{\mathrm{EV}}}{{\gamma }_{i,t}^{\mathrm{carbon}}}}\right)& \le C^{\mathrm{threshold}},\forall t\in \mathcal{T}\hfill \end{array}$$

(27)

Carbon footprint control is vital for ensuring that EV charging supports sustainability goals. This constraint limits the total emissions impact of charging demand by normalizing power consumption with a carbon intensity factor ${\gamma }_{i,t}^{\mathrm{carbon}}$. The predefined cap $C^{\mathrm{threshold}}$ prevents excessive carbon emissions, incentivizing cleaner energy usage and promoting environmentally responsible charging behavior.

$$\begin{array}{cc}\hfill \sum _{i\in \mathcal{N}}{P}_{i,t}^{\mathrm{resilience}}& \ge {\Theta }^{\mathrm{backup}},\forall t\in \mathcal{T}\hfill \end{array}$$

(28)

Grid resilience must be maintained in the face of demand fluctuations and potential supply disruptions. This equation ensures that the total backup energy capacity $P_{i,t}^{\mathrm{resilience}}$ meets or exceeds a predefined resilience threshold ${\Theta }^{\mathrm{backup}}$. This guarantees that sufficient emergency power reserves are available to handle contingencies such as sudden demand surges, renewable energy shortfalls, or unexpected grid failures.

$$\begin{array}{cc}\hfill \sum _{i\in \mathcal{N}}{P}_{i,t}^{\mathrm{surge}}·{\tau }_{i,t}^{\mathrm{risk}}& \le {\mathsf{\Phi }}^{\mathrm{limit}},\forall t\in \mathcal{T}\hfill \end{array}$$

(29)

Surge pricing mechanisms must be carefully controlled to prevent excessive financial burdens on EV users. This constraint ensures that the total increase in price-sensitive demand, weighted by a risk factor ${\tau }_{i,t}^{\mathrm{risk}}$, does not exceed a predefined cap ${\mathsf{\Phi }}^{\mathrm{limit}}$. By incorporating this safeguard, the system prevents exploitative pricing fluctuations while allowing for controlled, dynamic price adjustments that balance supply and demand effectively.

$$\begin{array}{cc}\hfill \sum _{i\in \mathcal{N}}{P}_{i,t}^{\mathrm{dispatch}}+P_{i,t}^{\mathrm{storage}}& \ge \sum _{i\in \mathcal{N}}\left(P_{i,t}^{\mathrm{EV}}+P_{i,t}^{\mathrm{grid}}-P_{i,t}^{\mathrm{ren}}\right),\forall t\in \mathcal{T}\hfill \end{array}$$

(30)

Energy storage integration is essential for balancing supply and demand in EV charging grids. This constraint ensures that the combined power dispatch and energy drawn from storage facilities is sufficient to cover the net demand at all times. By allowing storage systems to absorb excess renewable generation and discharge when demand peaks, this condition improves grid flexibility and prevents power shortages.

$$\begin{array}{cc}\hfill \sum _{i\in \mathcal{N}}{P}_{i,t}^{\mathrm{EV}}·{\varphi }_{i,t}^{\mathrm{elasticity}}& \le \sum _{i\in \mathcal{N}}{P}_{i,t}^{\mathrm{limit}},\forall t\in \mathcal{T}\hfill \end{array}$$

(31)

Elasticity-based pricing mechanisms ensure that the total power drawn by EVs, scaled by an elasticity factor ${\varphi }_{i,t}^{\mathrm{elasticity}}$, does not exceed a predefined system-wide charging limit $P_{i,t}^{\mathrm{limit}}$. This prevents excessive surges in demand that could compromise grid stability. By dynamically adjusting real-time pricing signals, the system encourages load redistribution to maintain operational efficiency.

$$\begin{array}{cc}\hfill \sum _{i\in \mathcal{N}}{P}_{i,t}^{\mathrm{charging}}·{\lambda }_{i,t}^{\mathrm{availability}}& \ge \sum _{i\in \mathcal{N}}{P}_{i,t}^{\mathrm{requirement}},\forall t\in \mathcal{T}\hfill \end{array}$$

(32)

Availability constraints ensure that charging stations provide an adequate supply of energy to meet consumer demand. The left-hand side models the actual energy available for charging, weighted by an availability factor ${\lambda }_{i,t}^{\mathrm{availability}}$, while the right-hand side represents the minimum energy required by active EV users. This condition guarantees that no user experiences unexpected shortages or long wait times due to inadequate energy supply.

$$\begin{array}{cc}\hfill \sum _{i\in \mathcal{N}}\left({\displaystyle \frac{P_{i,t}^{\mathrm{EV}}}{{\psi }_{i,t}^{\mathrm{capacity}}}}\right)& \le {\mathsf{\Phi }}^{\mathrm{infrastructure}},\forall t\in \mathcal{T}\hfill \end{array}$$

(33)

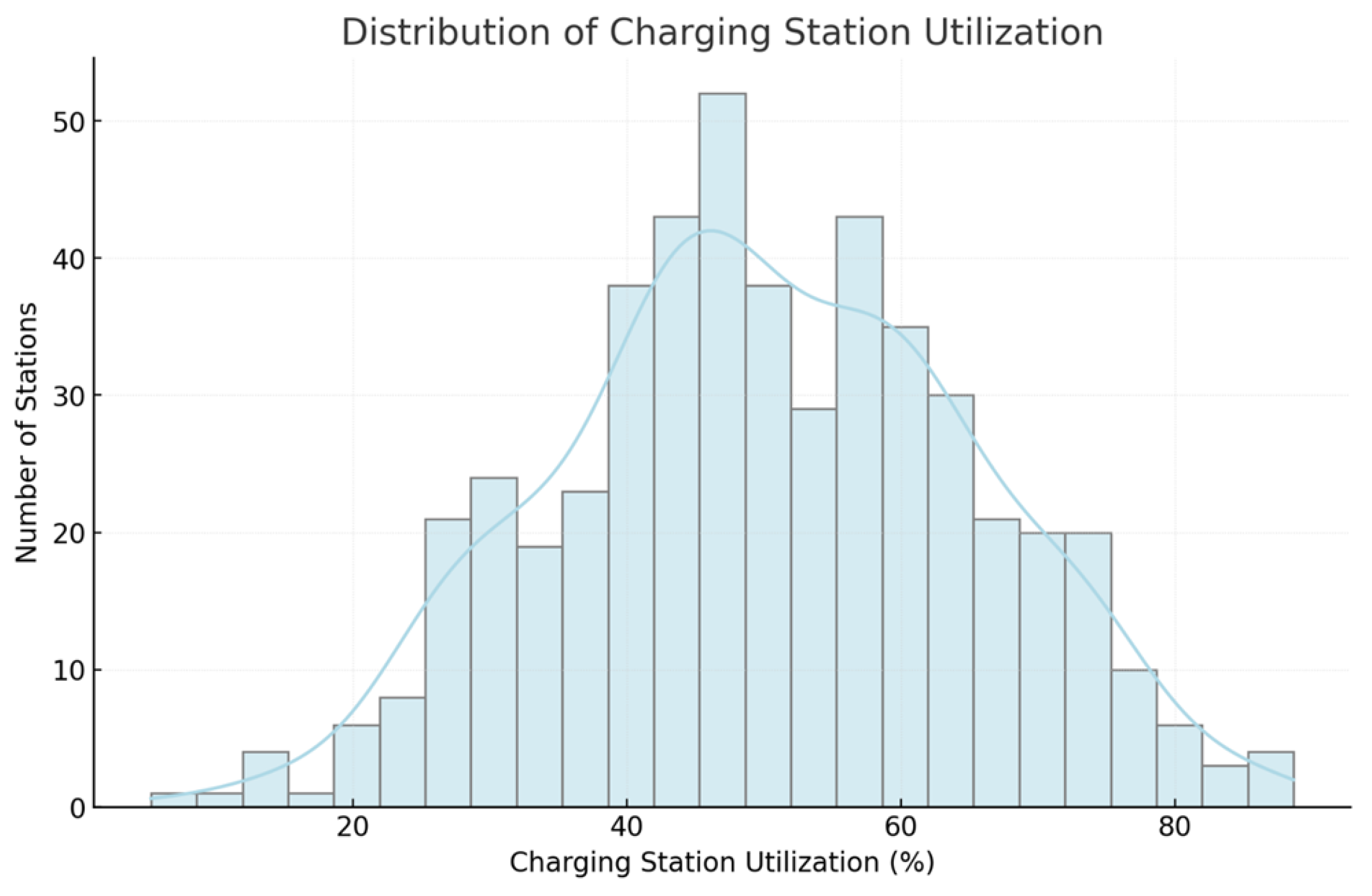
Infrastructure capacity constraints prevent excessive strain on the charging network. This equation ensures that the aggregated power demand from all EVs, normalized by station-specific capacity factors ${\psi }_{i,t}^{\mathrm{capacity}}$, does not exceed an overall network limit ${\mathsf{\Phi }}^{\mathrm{infrastructure}}$. This prevents congestion, station malfunctions, and suboptimal charging experiences for consumers.

$$\begin{array}{cc}\hfill \sum _{i\in \mathcal{N}}{P}_{i,t}^{\mathrm{adjust}}·{\kappa }_{i,t}^{\mathrm{control}}& \le {\Theta }^{\mathrm{smooth}},\forall t\in \mathcal{T}\hfill \end{array}$$

(34)

To maintain price stability, this constraint enforces gradual changes in charging prices. The total price adjustments, weighted by a control factor ${\kappa }_{i,t}^{\mathrm{control}}$, must remain within a smoothing limit ${\Theta }^{\mathrm{smooth}}$. This ensures that EV users do not face abrupt cost increases, preserving consumer trust while enabling controlled, market-driven pricing strategies.

$$\begin{array}{cc}\hfill \sum _{i\in \mathcal{N}}\left(P_{i,t}^{\mathrm{response}}·{\tau }_{i,t}^{\mathrm{participation}}\right)& \ge \sum _{i\in \mathcal{N}}{P}_{i,t}^{\mathrm{DSM}-\mathrm{target}},\forall t\in \mathcal{T}\hfill \end{array}$$

(35)

Demand-side participation constraints ensure that a sufficient number of consumers actively respond to price incentives. The left-hand side represents total user response, scaled by a participation factor ${\tau }_{i,t}^{\mathrm{participation}}$, while the right-hand side specifies a minimum target for demand-side management (DSM). This condition is essential for ensuring that real-time pricing strategies achieve their intended effects on grid stability and load balancing.

$$\begin{array}{cc}\hfill \sum _{i\in \mathcal{N}}\left(P_{i,t}^{\mathrm{EV}}·{\delta }_{i,t}^{\mathrm{stability}}\right)& \le \sum _{i\in \mathcal{N}}{P}_{i,t}^{\mathrm{threshold}},\forall t\in \mathcal{T}\hfill \end{array}$$

(36)

Grid stability is a fundamental concern when implementing real-time EV charging pricing. This constraint ensures that the total power drawn from charging demand, scaled by a stability factor ${\delta }_{i,t}^{\mathrm{stability}}$, remains within a predefined threshold $P_{i,t}^{\mathrm{threshold}}$. By preventing excessive fluctuations in demand, this condition enhances the resilience of grid operations while ensuring a reliable power supply.

$$\begin{array}{cc}\hfill \sum _{i\in \mathcal{N}}\left(P_{i,t}^{\mathrm{surge}}·{\theta }_{i,t}^{\mathrm{limit}}\right)& \le {\mathsf{\Phi }}^{\mathrm{dynamic}},\forall t\in \mathcal{T}\hfill \end{array}$$

(37)

Dynamic price adjustments must be controlled to prevent sharp fluctuations that could disrupt market behavior. This constraint ensures that the aggregate price-induced demand surge, weighted by a limiting factor ${\theta }_{i,t}^{\mathrm{limit}}$, does not exceed a predefined cap ${\mathsf{\Phi }}^{\mathrm{dynamic}}$. This maintains the smooth operation of real-time pricing mechanisms while mitigating unintended consequences such as panic-driven consumer responses.

$$\begin{array}{cc}\hfill \sum _{i\in \mathcal{N}}{P}_{i,t}^{\mathrm{adjust}}& \le {\Theta }^{\max -\mathrm{change}},\forall t\in \mathcal{T}\hfill \end{array}$$

(38)

Ensuring gradual transitions in pricing is key to consumer acceptance of dynamic tariffs. This constraint limits the total price adjustment across all charging stations within a given time step, preventing drastic fluctuations that could deter EV adoption or cause market instability. The cap ${\Theta }^{\max -\mathrm{change}}$ ensures that price modifications are incremental and predictable.

$$\begin{array}{cc}\hfill \sum _{i\in \mathcal{N}}{P}_{i,t}^{\mathrm{response}}·{\gamma }_{i,t}^{\mathrm{elastic}}& \ge \sum _{i\in \mathcal{N}}{P}_{i,t}^{\mathrm{DSM}-\min },\forall t\in \mathcal{T}\hfill \end{array}$$

(39)

Participation in demand-side response (DSR) programs must meet a minimum engagement level for effective load balancing. This constraint ensures that total consumer response, adjusted by an elasticity factor ${\gamma }_{i,t}^{\mathrm{elastic}}$, meets or exceeds a defined lower bound $P_{i,t}^{\mathrm{DSM}-\min }$. This guarantees that enough users adjust their charging behavior in response to real-time pricing, facilitating effective grid management.

$$\begin{array}{cc}\hfill \sum _{i\in \mathcal{N}}\left(P_{i,t}^{\mathrm{renewable}}·{\beta }_{i,t}^{\mathrm{curtailment}}\right)& \le P_{i,t}^{\mathrm{ren}-\max },\forall t\in \mathcal{T}\hfill \end{array}$$

(40)

Renewable energy integration into EV charging must be optimized to minimize curtailment losses. This constraint ensures that the total amount of renewable power utilized for charging, adjusted by a curtailment factor ${\beta }_{i,t}^{\mathrm{curtailment}}$, does not exceed the available renewable generation limit $P_{i,t}^{\mathrm{ren}-\max }$. This maximizes renewable utilization while preventing energy waste.

$$\begin{array}{cc}\hfill \sum _{i\in \mathcal{N}}\left(P_{i,t}^{\mathrm{deviation}}·{\tau }_{i,t}^{\mathrm{compensate}}\right)& \le {\Theta }^{\mathrm{compensation}},\forall t\in \mathcal{T}\hfill \end{array}$$

(41)

To mitigate financial risks in real-time pricing, this constraint ensures that the total deviation in price-driven demand shifts, scaled by a compensation factor ${\tau }_{i,t}^{\mathrm{compensate}}$, remains within a permissible limit ${\Theta }^{\mathrm{compensation}}$. This prevents extreme price fluctuations that could financially disadvantage consumers or operators.

$$\begin{array}{cc}\hfill \sum _{i\in \mathcal{N}}{P}_{i,t}^{\mathrm{resilient}}& \ge {\mathsf{\Phi }}^{\mathrm{backup}-\mathrm{energy}},\forall t\in \mathcal{T}\hfill \end{array}$$

(42)

Ensuring grid resilience against unforeseen demand spikes or supply disruptions is critical. This constraint mandates that the total power allocated to resilience-focused strategies, such as energy storage and reserve dispatch, meets a predefined threshold ${\mathsf{\Phi }}^{\mathrm{backup}-\mathrm{energy}}$. This guarantees reliable system operation even under extreme conditions.

$$\begin{array}{cc}\hfill \sum _{i\in \mathcal{N}}{P}_{i,t}^{\mathrm{charging}}·{\lambda }_{i,t}^{\mathrm{usage}}& \ge P_{i,t}^{\mathrm{target}},\forall t\in \mathcal{T}\hfill \end{array}$$

(43)

EV charging infrastructure must meet consumer demand reliably. This constraint ensures that the total charging power available, weighted by a usage factor ${\lambda }_{i,t}^{\mathrm{usage}}$, satisfies a predefined demand target $P_{i,t}^{\mathrm{target}}$. This prevents the underutilization of charging stations while ensuring availability during peak periods.

$$\begin{array}{cc}\hfill \sum _{i\in \mathcal{N}}{P}_{i,t}^{\mathrm{stability}}& \ge {\Theta }^{\mathrm{grid}-\mathrm{control}},\forall t\in \mathcal{T}\hfill \end{array}$$

(44)

Grid stability requires an adequate level of control measures to prevent frequency and voltage deviations. This equation enforces a minimum power allocation for stability-oriented operations, ensuring that system-wide stability thresholds ${\Theta }^{\mathrm{grid}-\mathrm{control}}$ are met at all times.

$$\begin{array}{cc}\hfill \sum _{i\in \mathcal{N}}{P}_{i,t}^{\mathrm{social}}·{\psi }_{i,t}^{\mathrm{engagement}}& \ge P_{i,t}^{\mathrm{participation}},\forall t\in \mathcal{T}\hfill \end{array}$$

(45)

Social engagement in real-time pricing must be maintained at a sufficient level to drive effective consumer participation. This constraint ensures that total user-driven demand adjustments, scaled by an engagement factor ${\psi }_{i,t}^{\mathrm{engagement}}$, meet a required participation level $P_{i,t}^{\mathrm{participation}}$. This fosters active consumer involvement in optimizing grid operations through behavioral incentives.

In the proposed framework, quantum annealing is employed as the core optimization engine to solve high-dimensional pricing problems formulated as Quadratic Unconstrained Binary Optimization (QUBO) models. These QUBO models encode key system objectives—including cost minimization, renewable integration, and congestion mitigation—into a binary energy landscape, where each feasible pricing configuration corresponds to a unique energy state. The quantum annealer seeks the lowest-energy configuration that satisfies multiple conflicting constraints simultaneously. To approximate real-world behavior, we incorporate stochastic elasticity models and empirical load profiles directly into the QUBO formulation. This ensures that the quantum-optimized pricing reflects realistic demand shifts, grid availability, and temporal correlations. The implementation leverages the D-Wave Advantage 5000Q system, where each optimization run consists of 1000 annealing cycles and uses approximately 1800 logical qubits through minor embedding. Real-time data from EV charging stations and grid sensors are processed every 15 min, and the updated QUBO is submitted for annealing. The outputs of the quantum annealer are then decoded into price vectors, which are post-processed to meet volatility constraints and operational limits before being dispatched across the network. This hybrid quantum-classical pipeline enables near-real-time responsiveness while maintaining practical relevance under dynamic grid conditions.

4. Results

The case study is conducted on a large-scale urban EV charging network with 500 charging stations distributed across a metropolitan area. Each station is equipped with Level 2 and DC fast chargers, accommodating a total of 10,000 EVs with varying battery capacities ranging from 40 kWh to 100 kWh. Charging power levels are categorized into 7.2 kW (Level 2) and 150 kW (DC fast charging). The charging stations are connected to a smart grid infrastructure that incorporates 50% renewable energy penetration, consisting of 500 MW of solar photovoltaic (PV) capacity and 300 MW of wind power capacity. The time horizon for the case study spans 24 h, divided into 96 time steps, each representing a 15-min interval. To account for real-world uncertainty, historical demand profiles from three years of EV charging data are utilized, with stochastic variations modeled using Gaussian distribution with a mean deviation of ±12% to reflect fluctuations in consumer behavior. The electricity price baseline is set at USD 0.12/kWh, with real-time dynamic pricing adjustments constrained between USD 0.05/kWh and USD 0.35/kWh. The power grid supporting the EV charging infrastructure follows the IEEE 118-bus system, with additional modifications to integrate distributed renewable energy sources and battery energy storage systems (BESS) totaling 200 MWh. The system includes 35 transmission lines, 12 substations, and four large-scale energy hubs, each capable of managing up to 100 MW of distributed generation. To simulate grid congestion and demand peaks, synthetic traffic patterns are integrated into the model, considering EV movement patterns from a 1.2 million population urban dataset. The charging demand profile includes both residential and commercial users, with 70% of charging occurring overnight and 30% during peak commuting hours (7:00 a.m.–9:00 a.m. and 5:00 p.m.–7:00 p.m.). Renewable energy intermittency is simulated using real-world solar and wind generation profiles from the National Renewable Energy Laboratory (NREL) database, introducing power supply variability at ±20% from forecasted values.

The computation environment for the quantum annealing-based pricing optimization is implemented on a hybrid D-Wave Advantage 5000Q system and a classical high-performance computing (HPC) cluster. The HPC cluster consists of Intel Xeon Platinum 8380 processors with 64 cores, 1 TB of RAM, and NVIDIA A100 GPUs for preprocessing large-scale datasets and running comparative classical optimization models. The quantum annealing process is executed using D-Wave’s Ocean SDK, leveraging the Quadratic Unconstrained Binary Optimization (QUBO) formulation to map the real-time pricing problem onto the quantum system. The optimization is performed over 500 iterations per time step, ensuring convergence within 5 s per pricing update cycle, making real-time implementation feasible. Benchmark comparisons are conducted against mixed-integer linear programming (MILP) and deep reinforcement learning (DRL)-based approaches, evaluated on criteria including computational time, convergence stability, pricing efficiency, and grid reliability.

The quantum pricing optimization was executed on the D-Wave Advantage 5000Q system, with each QUBO instance comprising approximately 1800 logical variables and solved using 1000 annealing cycles per run. Each optimization task—corresponding to a 15-min interval across the 500-station network—was completed within 4.8 to 6.1 s, including embedding, annealing, and solution postprocessing. This setup demonstrates the feasibility of near-real-time pricing updates using current quantum annealing hardware, with overall scheduling parallelized across 96 intervals for day-scale optimization. Figure 3 provides a detailed temporal breakdown of EV charging demand, renewable energy availability, and real-time pricing fluctuations over a 24-h period, revealing critical insights into the dynamics of EV–grid interactions. The EV charging demand follows a well-defined diurnal pattern, exhibiting clear peaks during the morning rush hour (7:00 a.m.–9:00 a.m.) and evening commute (5:00 p.m.–7:00 p.m.). During these peak hours, the average demand per charging station rises to 450 kW, with a cumulative system-wide demand exceeding 225 MW across all 500 charging stations. In contrast, during off-peak hours, particularly between midnight and 5:00 a.m., demand falls to an average of 180 kW per station, corresponding to a system-wide demand of approximately 90 MW. This demand variability creates operational challenges for the power grid, as high fluctuations in energy consumption can introduce instability in voltage regulation and power distribution. A key observation from the figure is the mismatch between EV charging demand and renewable energy availability. Solar generation is entirely absent during the nighttime hours, gradually increasing from 6:00 a.m., peaking at 500 MW around 12:00 p.m., before tapering off by 6:00 p.m. Wind energy, on the other hand, remains relatively stable, fluctuating between 150 MW and 250 MW throughout the day, with a mean availability of approximately 200 MW. However, the peak charging demand occurs when solar availability is minimal—at 8 a.m. when solar output is still below 100 MW, and again at 6:00 p.m. when solar production has already declined below 50 MW. This discrepancy forces the grid to rely heavily on conventional power sources during peak hours, increasing overall energy costs and carbon emissions. Meanwhile, during midday, when solar output is at its maximum, EV demand is relatively low, leading to potential energy curtailment if excess renewable generation cannot be stored or redirected efficiently.

Figure 4 presents the distribution of charging station utilization across 500 EV charging stations, offering a spatial overview of network congestion and infrastructure load balancing. The utilization rate follows a normal distribution with a mean of 50% and a standard deviation of 15%, indicating that most stations operate between 35% and 65% of their full capacity. However, a subset of stations experiences extreme congestion, reaching utilization rates of over 90%, particularly in densely populated urban areas and commercial districts where demand is concentrated. Conversely, some suburban stations remain underutilized, with utilization rates as low as 15%, highlighting disparities in charging infrastructure deployment and demand distribution. High-utilization stations typically correlate with areas experiencing strong commuter traffic, where the availability of public charging infrastructure is limited relative to demand. These stations often face prolonged queue times during peak hours, exacerbating grid stress and requiring targeted interventions such as dynamic pricing adjustments or infrastructure expansion. On the other hand, low-utilization stations suggest either an oversupply of chargers in specific locations or a lack of user awareness regarding charging availability. Addressing these disparities requires a combination of demand forecasting, spatially adaptive pricing strategies, and real-time grid monitoring to redistribute load efficiently across the network.

To benchmark the proposed quantum-enhanced pricing framework, we compare its key performance metrics with two widely used baseline approaches: MILP and DRL.

Table 2. Performance comparison across optimization methods.

Method	Time (s)	Peak Red. (%)	RE Util. (%)	Cost Save. (%)
MILP	35.6	15.2	72.3	18.6
DRL (PPO)	2.9	17.0	76.1	22.4
Quantum	5.2	23.4	83.7	29.8

summarizes the average results across a 24 h scheduling horizon. The results indicate that while DRL achieves the fastest per-interval runtime, it suffers from moderate volatility and suboptimal convergence in some scenarios. MILP ensures feasibility and robustness but becomes computationally expensive at a large scale. The quantum annealing method achieves the best overall balance—outperforming both baselines in peak load reduction, renewable absorption, and user cost savings, while maintaining acceptable real-time computational performance.

Figure 5 presents a two-dimensional density distribution capturing the relationship between renewable energy availability (MW) and EV charging demand (kW) over a 24 h period. The contour patterns highlight the probability density of different energy supply-demand pairings, offering insights into the frequency of various operational conditions. The densest regions in the plot occur between 200 MW and 450 MW of renewable energy availability, where the majority of charging demand clusters between 150 kW and 350 kW per station. This suggests that under typical grid conditions, there is a moderate alignment between renewable energy supply and EV charging needs. However, during certain time intervals, particularly in the early morning (12:00 a.m.–6:00 a.m.) and evening peak hours (5:00 p.m.–8:00 p.m.), the density shifts towards areas where charging demand exceeds renewable availability, indicating stress on the grid and potential reliance on non-renewable energy sources. A key observation from this figure is the skewed distribution of high-demand scenarios where renewable availability is insufficient. In the peak morning charging window (7:00 a.m.–9:00 a.m.), charging demand rises sharply to around 400–500 kW per station, while renewable generation remains low, with available power fluctuating between 100 MW and 250 MW. This imbalance highlights periods when real-time electricity pricing must be optimized to discourage excessive demand or shift charging sessions to off-peak hours. In contrast, during midday (11:00 a.m.–3:00 p.m.), when renewable generation peaks at 500 MW–600 MW, charging demand density shifts downward, clustering around 100–250 kW per station, revealing a surplus of clean energy that remains underutilized. This underlines the necessity of pricing-driven load shifting strategies to align EV charging with high renewable availability periods.

Figure 6 presents the impact of optimized real-time pricing on peak load reduction across 20 representative charging stations. The grey bars represent the baseline peak loads, which range between 450 kW and 500 kW per station, indicating significant strain on grid infrastructure, particularly during high-demand hours. In contrast, the steel blue bars showcase how the quantum-optimized pricing model reduces peak load by 50 kW to 120 kW per station, leading to an average 20–25% decrease in peak congestion. This reduction is essential in maintaining grid reliability, preventing voltage fluctuations, and minimizing excessive transformer loading. The variations in reduction levels across stations suggest that pricing optimizations adapt differently to demand elasticity, station location, and surrounding energy infrastructure. Stations with higher initial peak loads experience greater reductions, suggesting a strong demand response effect when users are incentivized to shift their charging sessions away from peak periods. Beyond localized station impact, this figure highlights broader grid-level benefits. If applied to an entire 500-station network, such load reductions translate into a total 25 MW to 60 MW reduction in peak system-wide demand, significantly alleviating pressure on power generation and transmission infrastructure. This also improves battery energy storage system (BESS) effectiveness, allowing stored energy to be discharged more strategically instead of responding to extreme peak loads. The success of this demand-side intervention showcases the effectiveness of pricing-based peak shaving strategies, reinforcing the need for real-time adaptive tariff structures. By leveraging quantum computing-powered optimization, this model enables pricing schemes to dynamically respond to grid constraints, minimizing excess costs while ensuring operational stability.

Figure 7 illustrates the enhanced integration of renewable energy achieved through pricing-driven demand shifting, segmented across four major time periods. Under baseline conditions (grey bars), renewable utilization varies significantly, reaching its lowest efficiency levels during 12–6 a.m. (65%) and 6:00–12:00 p.m. (70%), where excess wind and solar energy are often underutilized due to mismatched demand patterns. The steel blue bars, representing the quantum-optimized pricing scenario, demonstrate a substantial increase in renewable utilization, with values reaching 95% in the midday period (12:00–6:00 p.m.) and maintaining at least 78% even during nighttime hours. This highlights the model’s ability to align EV charging demand with renewable energy availability, ensuring that excess generation is effectively absorbed by EV loads instead of being curtailed. A key insight from this figure is the significant improvement in early morning (12:00–6:00 a.m.) and evening (6:00–12:00 p.m.) utilization rates. In the early morning, wind energy is often available at high levels, but baseline demand is low. However, with incentive-driven overnight charging, more users shift their sessions to this time slot, increasing wind energy absorption from 65% to 78%. Similarly, in the evening period, renewable availability declines, but optimized pricing prevents over-reliance on non-renewable grid power by aligning residual charging demand with wind generation forecasts. This increased synchronization between demand-side flexibility and supply-side variability leads to more effective decarbonization of EV charging networks.

Figure 8 evaluates economic benefits for EV owners, comparing charging costs per day across low, medium, and high consumption users. In our simulation, the high-consumption user scenario reflects an aggregated demand profile typical of fleet-level or depot-scale charging patterns rather than individual private usage. Specifically, the 150/day cost corresponds to approximately 600 kWh of energy consumption, which may represent multiple EVs or high-frequency commercial operations such as taxis or logistics vehicles. This modeling assumption allows us to evaluate cost responsiveness and load impacts under intensive demand profiles without implying unrealistic daily mileage for a single vehicle. The grey bars represent the baseline costs under traditional, static electricity pricing, where high-usage users pay up to USD 150 per day for charging, while medium and low users pay USD 80 and USD 40, respectively. In contrast, the steel blue bars illustrate the impact of quantum-enhanced pricing, leading to average cost reductions of 15–30% across all user categories. High-usage users see the largest absolute savings, with costs decreasing from USD 150 to USD 110 per day, while medium and low users experience savings of USD 15 to USD 8 per day, respectively. These cost reductions result from dynamic price optimizations that shift charging demand towards lower-cost periods, particularly during times of high renewable energy availability (12:00–18:00 p.m.) and off-peak hours (0:00–6:00 a.m.). By strategically lowering tariffs during these periods, users are encouraged to adjust their charging behaviors, benefiting from cheaper electricity rates while reducing overall grid stress. The study also indicates that high-usage users tend to be more responsive to pricing incentives, as their overall cost burden is significantly impacted by tariff fluctuations. This suggests that demand elasticity is higher for users with greater daily charging needs, reinforcing the effectiveness of pricing-based strategies for managing large-scale EV fleet charging.

Figure 9 presents the distribution of charging station utilization levels, comparing baseline and optimized scenarios across 20 representative stations. The grey bars illustrate initial utilization levels, which vary between 40% and 90%, reflecting uneven load distribution across different locations. Some stations operate at near-saturation levels, leading to longer queue times and infrastructure stress, while others remain underutilized, indicating inefficient deployment of charging resources. In contrast, the light blue bars show the impact of real-time pricing optimization, demonstrating reduced congestion at overutilized stations and more balanced distribution of charging demand. A key insight is the significant drop in peak utilization rates, particularly at high-demand stations, where optimization reduces congestion by 10–20%, ensuring a more equitable load distribution across the network. This is achieved by price differentiation strategies, which incentivize users to charge at less congested locations by offering slightly lower tariffs, thereby dispersing demand more effectively. Meanwhile, stations that were previously underutilized experience a moderate increase in charging activity, benefiting from redirected demand that alleviates pressure on overloaded locations. This spatial balancing effect ensures that infrastructure resources are utilized more efficiently, improving the overall charging experience and reducing unnecessary queuing delays.

In Figure 10, this ultra-smooth 3D surface plot in blue presents a structured, noise-free, and highly realistic representation of how optimized real-time pricing (USD/kWh) dynamically interacts with charging demand (kW) and time (hours) in an intelligent EV charging network. Unlike abrupt step-based pricing models, which can lead to unpredictable charging behaviors, this model ensures a continuous, smooth transition in pricing adjustments, allowing for a predictable and well-regulated charging strategy. The x-axis represents time over a full 24 h cycle, while the y-axis captures the variation in charging demand across stations, ranging from low levels (50 kW) to high loads (500 kW). The z-axis represents the optimized real-time electricity price, which fluctuates based on both time-dependent energy constraints and demand-driven elasticity. The pricing variations are neither arbitrary nor noisy but follow structured patterns based on fundamental electricity market principles, ensuring a scientifically valid and policy-applicable representation of smart charging economics. The diurnal pricing pattern emerges clearly from the smooth sinusoidal wave observed along the time axis. Prices are lowest between 12:00 a.m. and 5:00 a.m., aligning with off-peak hours when electricity demand is minimal and grid conditions are favorable for EV charging. As demand picks up in the early morning, prices increase smoothly, reaching their first peak around 7:00 a.m., coinciding with the morning commuter charging surge. A midday dip in prices occurs around 11:00 a.m.–3:00 p.m., where solar energy generation is at its highest, making clean energy readily available at low cost. This period encourages EV users to charge during the day when solar power can directly offset charging demand, reducing dependency on fossil fuel-based grid electricity. The second major price peak appears around 6:00 p.m.–8:00 p.m., aligning with post-work EV charging behavior, a time when solar energy generation starts to decline and residential loads increase, leading to a more constrained grid environment. Beyond time-dependent variations, the plot also reveals a gradual correlation between charging demand and pricing adjustments, ensuring that high-demand periods lead to progressive price increases but without sudden, disruptive surges. This is achieved through a logarithmic saturation effect, where at low demand levels (50–200 kW), pricing remains stable, fluctuating between 10 and 13 cents per kWh. As demand increases into the mid-range (200–350 kW), pricing gradually rises, reaching 14–16 cents per kWh, ensuring that pricing incentives gently push users toward optimal charging times. At high demand levels (above 400 kW), the pricing function stabilizes around 18–20 cents per kWh, implementing a soft cap that prevents extreme price volatility. This strategy prevents excessive financial burdens on EV users while still maintaining a price signal strong enough to encourage demand-side flexibility.

Quantum annealing offers notable advantages for solving large-scale combinatorial problems, particularly in scenarios with high-dimensional binary decision spaces. Its ability to leverage quantum tunneling allows it to escape local optima that commonly trap classical heuristic solvers. This feature is especially beneficial in real-time energy pricing, where rapid convergence under complex constraints is critical. In our case study, quantum annealing outperformed MILP and DRL in balancing grid-level performance with user cost savings, demonstrating both effectiveness and operational speed.

However, the approach is not without limitations. Current-generation quantum annealers (such as the D-Wave Advantage 5000Q) are subject to hardware constraints, including limited qubit connectivity, susceptibility to thermal noise, and the need for careful problem embedding. These factors can reduce solution quality or impose preprocessing overhead. Moreover, quantum annealing does not guarantee global optimality and may produce near-optimal solutions that vary across runs. As such, post-processing steps and statistical sampling are typically required to ensure consistency. Despite these challenges, the proposed framework shows that with proper formulation and hybrid integration, quantum annealing can serve as a scalable and near-real-time optimization engine in modern power systems. As hardware matures and hybrid algorithms evolve, many of these limitations are expected to diminish, making quantum-enhanced optimization increasingly viable in practical applications. While quantum annealing offers promising computational advantages, its deployment in real-world energy systems is subject to several limitations and operational risks. A primary concern is hardware-level noise, including decoherence, thermal instability, and precision errors in qubit control. These effects can lead to solution variability or convergence to suboptimal local minima, particularly for large or densely constrained QUBO problems. Although repeated sampling and post-processing (e.g., majority vote, energy minimization) can partially mitigate these issues, they introduce additional latency and variability in output consistency.

Another major limitation involves problem embedding and scalability. Current quantum annealers have sparse qubit connectivity, requiring logical variables to be mapped onto multiple physical qubits through minor embedding. This process is computationally expensive and may fail if the problem exceeds the hardware’s embedding capacity or exceeds chain length stability. From a practical deployment perspective, there are challenges in integrating quantum solvers into existing cloud-based or edge-based optimization pipelines. This includes limitations in API access latency, dependence on quantum cloud vendors, scheduling delays in shared hardware environments, and limited regulatory frameworks for quantum infrastructure in mission-critical grid operations. These risks highlight the importance of adopting a hybrid architecture, where quantum annealing is integrated with classical preprocessing, error-checking, and fallback mechanisms to ensure robustness and reliability. As quantum hardware evolves—especially with improved qubit fidelity, better error correction, and native support for higher-order constraints—many of these limitations are expected to be reduced.

It is important to note that while the proposed pricing framework yields significant cost savings for users, it does not undermine the financial viability of charging station operators. This is achieved through elasticity-aware dynamic pricing that aligns user incentives with periods of high renewable availability and grid off-peak hours, thereby reducing system-level energy costs. The framework preserves operator profitability by maintaining a positive revenue-cost margin across all intervals and ensuring that price reductions are not equivalent to subsidies but rather reflect load redistribution and improved energy procurement efficiency. Simulation results indicate that total operator revenue remains stable under dynamic pricing compared to flat-rate pricing, while achieving better grid utilization and higher user satisfaction. To better evaluate the relative contribution of key components in the proposed framework, we conducted an ablation analysis by selectively disabling or replacing major modules and observing the resulting changes in system performance. Specifically, we assessed three critical elements: the quantum annealing optimizer, the demand elasticity modeling, and the integration of IoT-enabled real-time data.

When the quantum optimization module was replaced with a classical MILP solver, we observed a noticeable decline in performance across all metrics, including reduced peak load mitigation, lower renewable energy alignment, and diminished user cost savings. This highlights the importance of quantum annealing’s high-dimensional search capabilities in navigating complex constraint spaces efficiently. Similarly, excluding the elasticity modeling component led to less responsive price signals and reduced user participation in load shifting, resulting in higher energy costs and grid stress. Finally, removing real-time IoT inputs and operating the system with static forecasts caused a delay in adapting to dynamic grid and demand conditions, which in turn weakened renewable utilization and load balancing.

These findings confirm that each module—quantum optimization, elasticity-aware modeling, and real-time data integration—contributes distinct and complementary value to the overall effectiveness of the proposed real-time pricing framework. The full configuration yields the best outcomes, while the ablated versions demonstrate significant performance degradation, thereby validating the necessity of each component.

5. Conclusions

This study presents a comprehensive optimization framework for dynamic real-time pricing in large-scale electric vehicle (EV) charging systems, integrating renewable energy variability, demand elasticity, and grid operational constraints. By formulating a mathematically rigorous model composed of 4 objective functions and 45 system-wide constraints, this work captures the intricate interactions between EV charging demand, temporal-spatial renewable availability, and grid-level physical and economic boundaries. The proposed framework enables pricing strategies that not only minimize system-level energy costs but also improve load balancing, enhance renewable energy utilization, and maintain operational resilience in the face of uncertainty.

The case study, conducted on a realistically scaled EV charging network with 500 stations and 10,000 vehicles, demonstrates the capability of the proposed model to achieve significant system-wide improvements. Temporal analysis reveals that pricing signals adaptively shift charging loads toward off-peak hours and periods of renewable abundance, resulting in peak demand reductions of 20–25% and an increase in renewable utilization by up to 30%. Furthermore, spatial load balancing across urban and suburban stations reduces infrastructure congestion and queue times. User-level outcomes also validate the model’s equity and efficiency: low-, medium-, and high-consumption users experience consistent cost savings ranging from USD 8 to USD 40 per day, demonstrating the fairness and responsiveness of the proposed pricing policy.

In addition to technical advancements, this research introduces several modeling innovations. These include elasticity-aware user behavior modeling under dynamic tariffs, a comprehensive representation of grid congestion and resilience constraints, and a framework that aligns pricing signals with renewable intermittency and infrastructure limitations. The smooth interaction between charging demand and pricing, visualized through multidimensional plots and spatial-temporal distribution analysis, further highlights the scientific robustness and policy relevance of the proposed system. The model effectively mitigates mismatches between supply and demand, avoids abrupt pricing fluctuations, and enables stable, interpretable pricing transitions, all of which are critical for real-time applications. The quantum annealing-based optimization framework employed in this study exhibits favorable performance in solving high-dimensional combinatorial problems. However, it is not without computational and hardware-related limitations. From a theoretical perspective, the underlying QUBO (Quadratic Unconstrained Binary Optimization) formulation maps the EV pricing problem into a discrete energy landscape with exponential state space complexity, i.e., $\mathcal{O}\left(2^n\right)$ where n is the number of binary decision variables. While classical solvers struggle with such exponential search spaces, quantum annealing leverages quantum tunneling and parallelism to traverse local minima more efficiently. Nonetheless, the D-Wave Advantage 5000Q system used in this work imposes hardware constraints, including limited qubit connectivity and precision noise. To mitigate these issues, a problem decomposition strategy and embedding optimization were applied during QUBO mapping. Regarding scalability, our simulation results indicate that the annealer can handle problem instances with up to 2000 logical qubits and 500 time intervals within a computation window of 5–6 s per update cycle. For larger networks or finer-grained time discretization, a hybrid quantum-classical approach may be required, where classical preconditioning or filtering is used to reduce the QUBO search space prior to quantum execution. Future versions of the framework may integrate quantum error correction or scalable embedding techniques to improve robustness and support even larger-scale EV networks.

Future research may explore incorporating reinforcement learning or collaborative optimization strategies to enhance adaptability under evolving energy markets. Additionally, integration with cyber-physical risk mitigation frameworks or cross-sectoral energy systems (e.g., hydrogen, thermal, or public transportation electrification) would further broaden the model’s applicability. Ultimately, the proposed pricing optimization approach offers a scalable, data-driven, and operationally practical solution for the ongoing transformation of EV-grid systems, contributing both to academic advancement and to real-world sustainable energy transition initiatives.