Abstract
Heat exchangers are critical components in various industrial applications, requiring efficient thermal management to enhance thermal performance and energy efficiency. Longitudinal vortex generators (LVGs) have emerged as a potent mechanism to enhance heat transfer within these devices. A precise knowledge of the thermal performance enhancement of HE through LVGs is missing in the literature. Therefore, this study aims to provide a critical review of both numerical simulations and experimental studies focusing on the enhancement of heat transfer through LVGs to further enhance the knowledge of the field. It begins with elucidating the fundamental principles behind LVGs and delineating their role in manipulating flow patterns to augment heat transfer. This is followed by an exploration of the various numerical methods employed in the field, including computational fluid dynamics techniques such as Reynolds-Averaged Navier–Stokes (RANS) models, Large Eddy Simulation (LES), and Direct Numerical Simulation (DNS). Various experimental methods are then summarised, including differential pressure measuring instruments, temperature measurements, velocity measurements, heat transfer coefficient measurements, and flow visualisation techniques. The effectiveness of these methods in capturing the complex fluid dynamics and thermal characteristics induced by LVGs is critically assessed. The review covers a wide range of LVG configurations, including their geometry, placements, and orientations, and their effects on the thermal performance of heat exchangers. Different from previous reviews that mainly focus on classical configurations and historical studies, this review also emphasizes recent developments in computational fluid dynamics and progress in interdisciplinary fields such as innovative materials, additive manufacturing, surface finishing, and machine learning. By bridging the gap between fluid dynamics, thermal enhancement, and emerging manufacturing technologies, this paper provides a forward-looking, comprehensive analysis that is valuable for both academic and industrial innovations.
1. Introduction
To achieve high energy efficiency and performance optimization, the engineering community continues to seek innovative methods to enhance heat transfer mechanisms in thermal systems. Heat exchangers, as critical components in industrial, automotive, and HVAC applications, are the focal point of such innovations due to their significant role in energy conservation and system efficiency. The efficiency of heat exchangers is pivotal in minimizing energy consumption and improving the overall thermal performance of systems. Traditional methods, such as increasing surface area or operational adjustments, often lead to higher costs and complex operational strategies [1]. Among various enhancement techniques, the integration of longitudinal vortex generators (LVGs) in heat exchanger design has emerged as a promising solution to enhance thermal performance without substantially increasing the pressure drop or the footprint of the equipment. LVGs are typically designed as small protrusions aligned with the flow direction and are integrated into heat transfer surfaces through various methods such as embossing, mounting, attaching, stamping, and punching [2]. Their main function is to generate longitudinal vortices, thus swirling flows that effectively mix fluid layers. This mixing action disrupts the thermal boundary layer, a thin layer of fluid that normally acts as a thermal insulator, thereby enhancing the overall heat transfer rate [2,3]. Numerous studies have demonstrated that the incorporation of LVGs in heat exchangers can increase the Nusselt number compared to baseline configurations, depending on their geometry, positioning, and Reynolds number range, leading to more compact, energy-efficient, and effective systems [2,3,4,5]. However, this enhancement is often accompanied by a rise in the friction factor, which can result in increased pumping power and operational costs if not carefully evaluated and optimized. Despite this trade-off, systems equipped with LVGs can still achieve energy savings, particularly when optimized for specific applications. While several previous reviews have explored classical LVG configurations and their historical development, a more comprehensive, contemporary, and forward-looking review is still needed. The special feature of this review is that it not only integrates numerical and experimental research methods and findings on traditional LVG designs but also emphasizes the latest advances in CFD, including topology optimization and multi-objective algorithms. In addition, this review highlights progress in interdisciplinary areas, such as the use of innovative materials (e.g., shape memory alloys) for generating adaptive vortex generators, additive manufacturing techniques for fabricating complex LVG geometries, surface adjustment methods (e.g., surface abrasive finishing) for reducing flow resistance, and machine learning algorithms for design optimization and surrogate models. By integrating these advances, this review provides a comprehensive and up-to-date perspective on the heat transfer enhancement role of LVGs in heat exchangers. It aims to serve as a fundamental reference for researchers and engineers exploring the next generation of thermal management technologies.
2. Longitudinal Vortex Generators
2.1. Heat Transfer Enhancement Characteristics
Vortices can be classified by their rotational axes: transverse vortices (TVs) have perpendicular axes to the main flow direction; longitudinal vortices (LVs), also referred to as streamwise vortices, on the other hand, have parallel ones. LVs are typically more efficient at improving heat transfer while only causing a minimal rise in pressure drop compared to TVs [2,6,7]. LVGs are utilized as a passive technique for augmenting heat transfer, involving the generation of streamwise vortices, as depicted in Figure 1, which induces heightened turbulence within the fluid flow across heat transfer surfaces [8].
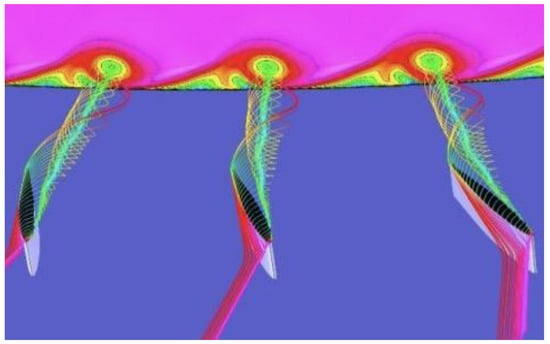
Figure 1.
Longitudinal vortices generated by LVGs [8].
When the fluid traverses LVGs, a potent secondary swirling flow is induced, where the tangential velocity of the vortices may reach twice that of the main flow. This high-velocity swirling action not only facilitates the fluid mixing within the main and peripheral flow regions but also introduces high-energy fluid into the boundary layer, which effectively suppresses and postpones the separation of the boundary layer, consequently leading to the profile drag reduction and heat transfer enhancement. Conventional heat transfer augmentation methods like louvered, slit, and wave fins operate by disrupting the flow, reducing the thickness of boundary layer or halting its progression, and generating small transverse vortices. However, the contribution of these transverse vortices to heat transfer enhancement is somewhat limited under conditions of steady-state laminar flow, whereas longitudinal vortices have a pronounced effect on increasing both the average and local heat transfer coefficients throughout the channel [9]. Consequently, LVGs are markedly advantageous in augmenting heat transfer within heat exchangers operating under laminar flow regimes.
2.2. Types of Longitudinal Vortex Generators Studied in Recent Decades
Due to the significant effect of LVGs on the heat transfer capacity of heat exchangers, more and more geometrical and positional parameters of LVGs have been investigated to obtain optimal design configurations of LVGs to achieve maximum heat transfer enhancement.
Four prevalent LVGs are illustrated in Figure 2, encompassing delta wings, delta winglets, rectangular wings, and rectangular winglets [10,11,12]. In addition to the primary four types, a variety of other LVGs have been explored and studied extensively in recent years. Studies on a range of winglet VGs were conducted by Zhou and Feng [13], Lu and Zhou [14], including delta, trapezoidal, and rectangular shapes, plane and curved designs, with and without holes, as depicted in Figure 3a. Wang et al. [5], and Lin et al. [15] proposed the application of annular winglet VGs to finned-tube heat exchangers, as shown in Figure 3b. Gholami et al. investigated the heat transfer enhancement in a finned-tube heat exchanger with wavy rectangular winglet VGs, as illustrated in Figure 3c [16]. He et al. introduced arrays of V-deployed VGs, inspired by animal locomotion in nature, as illustrated in Figure 3d [17]. Lotfi et al. explored the use of four distinct VG designs on wavy-finned elliptical-tube heat exchangers, including the wheeler wishbone (WW), angle rectangular winglet (ARW), curved angle rectangular winglet (CARW), and rectangular trapezoidal winglet (RTW), depicted in Figure 3e [18,19]. In addition to WW, ARW, and RTW, Samadifar and Toghraie also investigated the effect of the intended vortex generator (IVG) and waved vortex generator (WVG) on heat transfer in finned plate heat exchangers, as shown in Figure 3f [20].
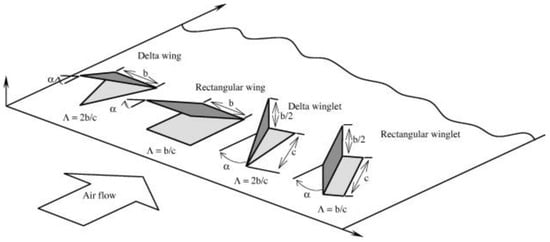
Figure 2.
Diagram of four common longitudinal vortex generators [10,11,12].
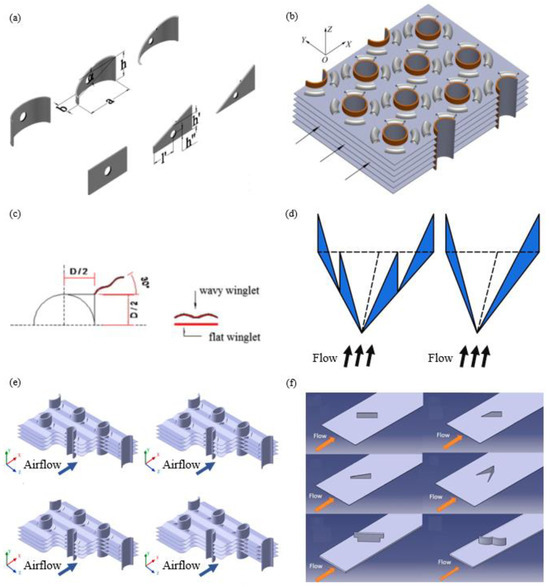
Figure 3.
Other longitudinal vortex generators studied in recent years (a) Plane and curved delta winglet, trapezoidal winglet, and rectangular winglet VGs with circular holes [13,14]; (b) Annular winglet VGs mounted in finned circular-tube heat exchanger [5,15]; (c) Wavy rectangular winglet VGs [16]; (d) Arrays of V-deployed VGs [17]; (e) WW, ARW, CARW, and RTW VGs mounted in wavy-finned elliptical-tube heat exchanger [18,19]; (f) rectangular winglet, WW, ARW, RTW, IVG, and WVG mounted in finned plate heat exchanger [20].
Representative numerical studies focusing on LVGs in recent decades are thoroughly investigated in this paper. The author(s) of these studies, year of publication, LVG type, application, and Reynolds number range are summarized in Table 1 as shown below. This paper also provides a comprehensive review of representative experimental studies focusing on LVGs in recent decades, as listed in Table 2 below.

Table 1.
Representative numerical studies of LVGs in recent decades.

Table 2.
Representative experimental studies of LVGs in recent decades.
3. Numerical Methods
Computational Fluid Dynamics (CFD) analysis of LVGs in heat exchangers involves a complex process that depends on several numerical elements such as solver selection, assumptions on the model used to analyse LVGs, modelling strategies employed and discretization methods. Each of these elements is critical to produce accurate and reliable simulation results.
3.1. Solvers
CFD analysis relies heavily on its solver, which numerically solves fluid flow and heat transfer equations to produce results. Selecting an optimal solver depends on multiple variables, including flow state (laminar or turbulent), geometry complexity, and available computational resources. Solvers optimized for incompressible turbulent flows tend to be preferred when performing LVG analysis in heat exchangers. Solvers typically employ the Finite Volume Method (FVM), which is known for conservation of fluxes within the control volume, or the Finite Element Method (FEM), which excels at handling complex geometries. Common computational solvers for CFD analysis include Solution Algorithm (SOLA), Modified Marker-and-Cell (MAC) algorithm, FORTRAN code, and FLUENT, CFX, and STAR-CD. Table 3 offers an in-depth review of computational solvers used in numerical studies of LVGs, along with examples of numerical studies conducted using these solvers. Ideal solvers would allow for coupled heat transfer and fluid flow simulation as well as managing turbulent interactions associated with LVGs.

Table 3.
Comparative overview of representative computational solvers used in CFD studies and their applications.
3.2. Assumptions
Assumptions in CFD are necessary to simplify real-world scenarios into computationally manageable models. Common assumptions for LVG analysis include steady-state or transient flow, incompressible flow, or neglect of gravity effects, depending on the specific application and analysis objectives.
3.3. Models
Numerous numerical solvers and turbulence models have been used to simulate heat transfer enhancement induced by LVGs. These models range from simplified laminar assumptions to highly detailed Direct Numerical Simulation (DNS), each with its own advantages and disadvantages in terms of accuracy, computational cost, and applicability to real-world conditions. For low Reynolds number flows, the laminar model can provide reasonable predictions, especially in microchannel heat exchangers, where the flow remains steady, and vortex shedding is minimal. However, this model neglects turbulence effects and becomes unreliable in transitional or turbulent flows, where secondary flow interactions play a dominant role in heat transfer enhancement. For LVGs in heat exchangers, the flow is often turbulent due to the vortex generation. Thus, a turbulence model is generally more appropriate. RANS models, such as the standard k–ε model, the RNG k–ε model, and the SST k–ω model, are widely used due to their low computational requirements and acceptable accuracy in steady-state simulations. The RNG k–ε model is more suitable for the swirling flows and recirculation regions generated by LVGs, while the SST k–ω model is better at predicting vortex structures near walls and under adverse pressure gradients. However, RANS models are usually unable to resolve the unsteady vortex structures that are critical to LVG performance. To obtain higher fidelity, Large Eddy Simulation (LES), and Detached Eddy Simulation (DES) can more effectively capture large-scale unsteady vortex dynamics and flow anisotropy. LES shows good agreement with experimental results in predicting turbulent kinetic energy and local heat transfer enhancement, albeit at a significantly increased computational cost. LES requires substantially more computational resources, typically one to two orders of magnitude higher than RANS models. DNS resolves all scales of turbulence with the highest accuracy, without the need for turbulence models. DNS comprehensively captures the entire spectrum of eddies, including integral, Taylor scale, and Kolmogorov scales. DNS provides unparalleled insight into vortex-wall interactions, boundary layer behaviour, and local Nu variations induced by LVGs. However, the computational power of DNS limits its use in practical applications, which are usually limited to low Reynolds numbers, simplified geometries, and fundamental studies. The comparative properties of these models are summarized in Table 4, providing guidance for model selection in future studies of LVG-based heat exchangers. The choice of these models depends on the available computational resources and the level of detail required.

Table 4.
A detailed comparison of the laminar and various turbulence models used for numerical investigations of LVGs.
3.4. Boundary Conditions
CFD simulations rely on boundary conditions to provide an operating environment for the physical model and obtain realistic and reliable results. When simulating heat exchangers equipped with LVGs, setting accurate boundary conditions becomes particularly important due to their huge impact on fluid dynamics and heat transfer characteristics. Accurate boundary conditions are essential in describing the flow behaviour around LVGs, which create secondary flows with complex dynamics. They can accurately predict heat transfer rates in regions with steep temperature gradients and validate experimental data by accurately replicating physical setups. Most researchers assume a constant velocity and temperature at the flow channel inlet; however, a few studies utilize periodic fully developed fluid flow conditions at both computational domain inlets and outlets. In order to save computing resources, the physical model needs to be simplified, and periodic boundary conditions are usually adopted in the simulation domain, such as symmetric boundary conditions or periodic boundary conditions. Table 5 offers an overview of some common boundary conditions used in CFD simulations of heat exchangers with LVGs.

Table 5.
A detailed overview of the discretization methods used in CFD studies of LVGs in heat exchangers.
3.5. Discretization Techniques
Discretization techniques are an important part of CFD, as it transforms continuous partial differential equations into discrete algebraic equations that can be solved numerically. Table 6 offers an in-depth review of discretization methods employed in LVG studies of heat exchangers using CFD. Table 5 contains spatial and temporal discretization as well as grid independence studies to illustrate their importance in discussing the modelling results.

Table 6.
A detailed comparison of typical experimental techniques used for experimental investigations of LVGs.
4. Experimental Methods
The comprehensive experimental analysis of LVGs covers a wide range of measurements and techniques. This includes pressure difference assessments using tools like differential pressure meters, gauges, transmitters, transducers, and micro-manometers; temperature evaluations employing thermocouples, Resistance Temperature Detectors (RTDs), infrared thermography, and Liquid Crystal Thermography (LCT); velocity determinations via hot-wire anemometry, Laser Doppler Velocimetry (LDV), and Particle Image Velocimetry (PIV); calculations of heat transfer coefficients through methods such as the naphthalene sublimation technique; and flow visualization utilizing dye-injection technique, Laser Light Sheets (LLS), and PIV. Table 6 compiles a summary of the experimental techniques outlined above, detailing their development, fundamental principles, applications, and research conducted applying these methods.
5. Different Configurations of Longitudinal Vortex Generators in Heat Exchangers and Their Effects
5.1. Geometric Parameters
5.1.1. Plane Longitudinal Vortex Generators
There are many studies focusing on the difference in the effect of different shapes of plane VGs on heat transfer enhancement. For a specified heat load, DWPs have significant potential to substantially decrease the mass and size of heat exchangers. Fiebig et al. experimentally determined that in an inline tube configuration, the use of DWPs resulted in a 55–65% enhancement in heat transfer, accompanied by a 20–45% increase in the apparent friction factor [114]. Tiggelbeck et al. found that winglets outperformed wings in terms of heat transfer enhancement, with a DWP capable of enhancing heat transfer by 46% at a Reynolds number of 2000, and up to 120% at a Reynolds number of 8000, compared to the heat transfer on a flat plate [115]. Fiebig et al. investigated the performance differences of DWPs used in FTHEs with different tube shapes (circular tubes and flat tubes). [116]. Study findings indicated that in a staggered fin-and-tube configuration, longitudinal vortices generated by DWPs led to a modest heat transfer increase of about 10% for circular tubes, but a significant 100% increase for flat tubes [116]. A heat exchanger element equipped with flat tubes and DWPs achieved nearly double the heat transfer and only half the pressure loss compared to an equivalent element with circular tubes [116]. In the study carried out by Torii et al., for staggered tube banks, the addition of delta winglets resulted in a heat transfer augmentation ranging from 30% to 10%, and a pressure loss reduction of 55% to 34%, across Reynolds numbers from 350 to 2100; for in-line tube banks, the heat transfer augmentation was observed to be between 20% to 10%, with a corresponding pressure loss reduction of 15% to 8% [120]. Kwak et al. discovered that in an in-line fin–tube bundle configuration, the application of delta winglets led to an overall heat transfer enhancement of 10–25% and a pressure loss increase of 20–35%, across a range of Reynolds numbers from 300 to 2700 [121]. In a follow-up study, they observed that in a configuration with three rows of tubes and a single transverse row of delta winglets adjacent to the front row of tubes, heat transfer increased by 30–10%, while pressure loss decreased by 55–34% as the Reynolds number rose from 350 to 2100 [125]. O’Brien et al. conducted research on the effect of DWPs on finned oval-tube heat exchangers, and they revealed that incorporating a single DWP into the oval-tube geometry resulted in a notable average heat transfer enhancement of 38% compared to the setup without DWP, with only a modest increase in the friction factor observed [127]. The experimental results of Pesteei et al. showed that utilizing DWPs led to a significant enhancement of the heat transfer coefficient, on the order of 46%, accompanied by an 18% increase in pressure drop compared to a plain fin–tube heat exchanger [130]. Wang et al. experimentally determined that the application of RWPs can increase heat transfer rate by 10–45% across the investigated Reynolds number range of 3000 to 20,000 [133]. Joardar and Jacobi compared the performance difference between a single DWP and three DWPs, and they identified that within the Reynolds number range of 220 to 960, the air-side heat transfer coefficient experienced an increase of 16.5–44% with the arrangement of a single DWP and 30–68.8% with the arrangement of 3 DWPs [134]. Although the 3 DWP array demonstrated superior heat transfer performance over the single DWP, it incurred a greater pressure drop penalty, which notably diminished as the Reynolds number increased [134]. In comparison to the wavy fin without delta winglets, Tian et al. noted that the wavy fin using delta winglets in staggered and in-line setups experienced respective Colburn factor and friction factor enhancements of 13.1%, 7.0% and 15.4%, 10.5%, while the delta winglet amplified the fin channel’s pressure drop, the heat transfer saw a greater increase [47]. Chu et al. found that for Reynolds numbers between 500 and 880, the introduction of RWP to the baseline configuration resulted in a substantial increase in the air-side heat transfer coefficient, ranging from 28.1% to 131%, accompanied by a corresponding increase in pressure drop between 11.3% and 121.4% [49]. Experimental findings of Promvonge et al. [138] and Chompookham et al. [139] revealed a notable impact of the ribs and DWPs on both the heat transfer rate and friction loss, compared to a smooth wall channel. The Nusselt number and friction factor values for configurations employing both the ribs and DWPs were significantly higher than those using either the ribs or DWPs alone [138,139]. Hwang et al. found that the presence of delta winglet VGs on fins enhanced heat transfer performance, particularly at high Reynolds numbers or air velocities, while also maintaining a lower pressure loss compared to plain fins, primarily due to improved flow mixing and delayed flow separation [57]. According to Du et al., when 6 DWPs were punched onto the wavy fin surface, the average friction factor rose by 13–83% with the Reynolds number varying from 500 to 4500, while the average Nusselt number exhibited an increase of 21–60% as the Reynolds number ranged from 1500 to 4500 [144]. Additionally, the average Performance Evaluation Criteria (PEC) reached a value of up to 1.31 [144]. As illustrated in Figure 4, Huisseune et al. numerically explored the impact of integrating delta winglet VGs into the surfaces of louvered fins, specifically in each tubes near wake region. They pointed out that the incorporation of delta winglets resulted in an elevated net core pressure drop and a more efficient heat transfer compared to the baseline design devoid of delta winglets [63]. Three significant mechanisms contributing to the enhancement of heat transfer were identified: improved fluid mixing, thinned boundary layer, and delayed flow separation from tube walls [63]. Tian et al. [48] and Caliskan [145] indicated that the DWP-equipped channel outshone the one with RWPs in heat transfer performance. The use of delta winglet VGs in pipes can also significantly enhance heat transfer [146,152,153]. Khoshvaght-Aliabadi et al. stated that using a specialized arrangement of delta-winglets on the VG insert of circular pipes, an ideal balance between enhanced heat transfer and friction can be attained, yielding the highest heat transfer coefficient and a peak PEC value of 1.41 at a Reynolds number of 8715 [146]. Zhai et al. observed that the Nusselt number (Nu) tended to rise with an increase in Reynolds number (Re), whereas the friction factor showed a decreasing trend with Re [153].
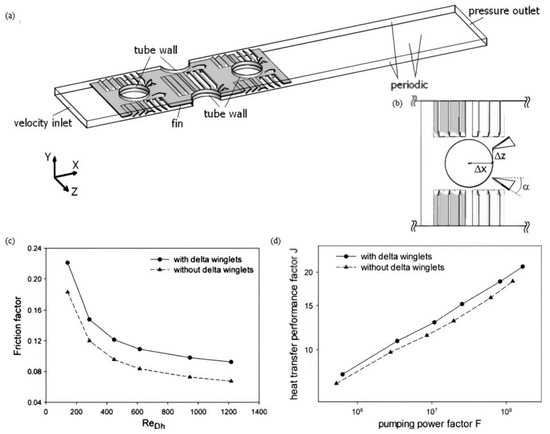
Figure 4.
(a) Schematic view of 3D computational domain; (b) DWP configuration diagram; (c) variation of friction factor versus Reynolds number; (d) variation of heat transfer performance factor versus pumping power factor; heat flux distribution at Reynolds number of 616 [63].
5.1.2. Curved Longitudinal Vortex Generators
Zhou and Ye compared the thermohydraulic performance of curved TWPs and plane RWPs, TWPs, DWPs in the Reynolds number range of 700–26,800, indicating that in laminar and transitional flow regions, plane DWPs performed optimally, while in fully turbulent regions, curved TWPs stood out for their excellent thermohydraulic performance, primarily due to their streamlined configuration that led to reduced pressure drop [142]. They also revealed that a greater angle of inclination (α = 20°), a larger curvature ratio (b/a = 1/2), and a smaller attack angle (β = 0° and 15°) led to improved thermohydraulic performance for curved TWPs [142]. Among six winglet VGs without holes (plane and curved RWPs, TWPs, DWPs) investigated by Zhou and Feng, the curved DWPs exhibited the best thermohydraulic performance across Reynolds numbers from 650 to 21,000 [13]. The experimental outcomes of Wu et al. also demonstrated that curved DWPs were highly effective in improving heat transfer when compared to equivalent plain fin geometries [151]. In the study carried out by Gong et al., under working conditions encompassing a range of Reynolds numbers (800–3000), optimal heat transfer performance was achieved by curved RWPs when the leading edge of VGs was aligned with the transversal axis of the tube, the fin spacing to tube outer diameter ratio was 0.239, the height of VGs was about 0.8 times the fin spacing, and the base arc length diameter of VGs was approximately 3.8 times their optimal height [71]. According to Lin et al., at a Reynolds number of 2000, optimal heat transfer performance was observed when the fin spacing was 0.293 times the fin collar outer diameter and the base arc diameter of curved DWPs was 1.95 times the fin collar outer diameter [73]. Curved VGs, due to their streamlined design, outperform plane VGs in heat transfer and pressure loss by 8.2–15.8% under identical conditions [14]. Deshmukh et al. conducted a study on curved delta wings and pointed out that the implementation of curved delta wings resulted in Nusselt number enhancements ranging approximately from 5.0 to 15.0 times greater than those observed with smooth tubes [149]. According to Esmaeilzadeh et al., curved TWPs demonstrated a superior overall performance and a lower pressure drop in comparison to the plane one [79]. In the study conducted by Naik et al., curved rectangular winglet VGs exhibited a maximum heat transfer enhancement of 3% and a notable 32% decrease in friction factor when contrasted with plane rectangular winglet VGs, as indicated in Figure 5 [86]. Among the variants, concave rectangular winglet VGs led in heat transfer enhancement and pressure loss, with a 75° arc angle concave rectangular winglet VGs achieving a peak heat transfer enhancement of 22% relative to the channel without rectangular winglet VGs [86]. However, convex rectangular winglets VGs demonstrated superior thermodynamic efficiency and overall thermal performance, surpassing both plane and concave rectangular winglet VGs [86].
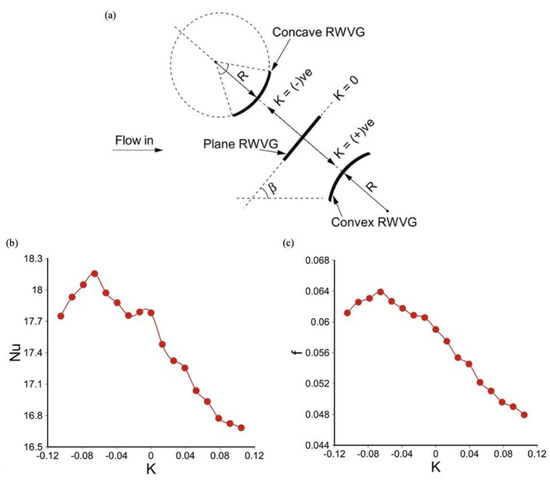
Figure 5.
(a) K notation for plane, concave, and convex rectangular winglet VGs; (b) variation of Nusselt number versus K values; (c) variation of friction factor versus K values [86].
Lu and Zhai showed that curved VGs possessing a curvature of 0.25 and oriented at an angle of attack of 15° demonstrated superior thermal hydraulic performance [88]. They also observed that curved VGs featuring decreased inclination angle and increased height exhibited improved thermal hydraulic performance at high Reynolds numbers (Re > 1620), while those with greater inclination angle and reduced height yielded enhanced thermal hydraulic performance at low Reynolds numbers (Re < 1620) [88]. As depicted in Figure 6, Song et al. conducted a numerical analysis on the enhancement of heat transfer in plate heat exchangers using concave and convex curved delta winglet VGs, examining the impacts of varying central angles (θ = 10–80°) and angles of attack (β = 20°, 30°, 40°) on thermal hydraulic performance across Reynolds numbers ranging from 200 to 1400 [90]. Compared to plane VGs, concave curved VGs proved to be advantageous for enhancing heat transfer, with the Nusselt number increasing alongside both the attack angle and the central angle [90]. Conversely, convex curved VGs were found to be less effective for heat transfer enhancement relative to plane VGs, with Nu rising as the attack angle increased but decreasing as the central angle increased [90]. Concave curved delta winglet VGs exhibited a 19.7% higher Nu and an 11.35% greater surface goodness factor (JF) compared to those measured for convex curved delta winglet versions within the examined parameter range [90]. An optimal configuration for concave curved VGs was found to significantly enhance heat transfer performance, with the highest efficiency achieved at a β of 30° for θ less than 60°, and for θ greater than 60°, VGs with a β of 20° were markedly more effective, particularly at an optimal θ of around 70° [90]. Naik et al. examined how variations in the arc angle of curved rectangular winglet VGs affected the flow dynamics and thermal properties, while maintaining a constant chord length [102]. They found that the concave rectangular winglet VGs with a 90-degree arc angle produced the strongest longitudinal vortices and the highest heat transfer augmentation of 39.4% at a Reynolds number of 2000, compared to the channel without VGs [102]. However, the convex rectangular winglet VGs with a 30-degree arc angle offered a better thermal performance factor due to lower friction losses [102]. Hu et al. revealed that concave curved VGs created robust longitudinal vortices that intensified fluid mixing and enhanced heat transfer, resulting in maximum increases of 30.4% in the Nusselt number and 25.9% in the surface goodness factor compared to a smooth wavy channel [108]. While curved VGs can enhance heat transfer performance, they are not inherently superior to traditional VGs and require specific positional and geometric criteria to achieve optimal performance [98].
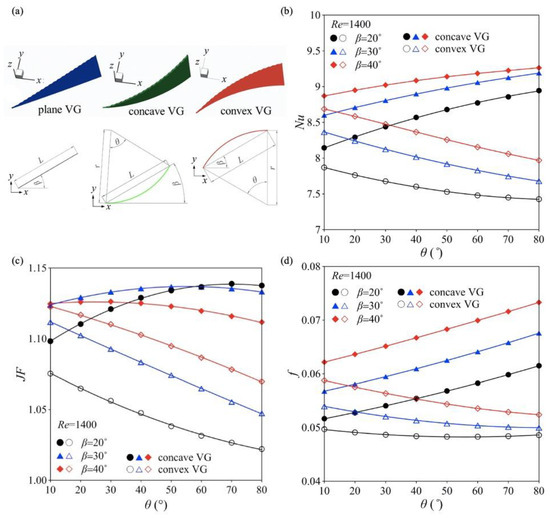
Figure 6.
(a) Dimensional details of delta winglet VGs; (b) comparisons of Nusselt number between concave and convex curved VGs for different values of β and θ; (c) comparisons of surface goodness factor between concave and convex curved VGs for different values of β and θ; (d) comparisons of friction factor between concave and convex curved VGs for different values of β and θ [90].
5.1.3. Wavy Longitudinal Vortex Generators
Gholami et al. numerically examined the impact of pressure loss and heat transfer enhancement in finned circular-tube heat exchangers featuring wavy-down and wavy-up rectangular winglets, focusing on flows with relatively low Reynolds numbers (400–800) [16]. As shown in Figure 7, wavy-up rectangular winglets yielded the highest heat transfer enhancement, outperforming conventional and wavy-down rectangular winglets, while wavy-down rectangular winglets were associated with lower friction factor and pressure drop penalty compared to both conventional and wavy-up rectangular winglets [16]. Sawhney et al. investigated wavy delta winglets with different wave numbers (3, 5, and 7) as depicted in Figure 8, and they concluded that these winglets offered superior thermal performance compared to smooth channels, with the inline setup achieving a higher Nusselt Number than the staggered arrangement [150]. Using five-wave delta winglets (ϕ = 5) with a relative longitudinal pitch of 3 (P/H = 3) at a Reynolds number of 4000, the Nusselt number enhancement reached 223% over a flat plate, accompanied by a 10.3-fold increase in the friction factor, resulting in a thermohydraulic performance of 2.09 for this configuration [150].
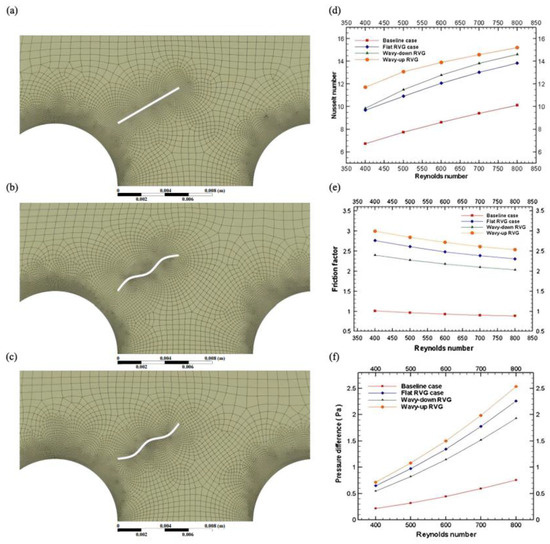
Figure 7.
(a) flat rectangular winglet case; (b) wavy-down rectangular winglet case; (c) wavy-up rectangular winglet case; (d) variation of Nusselt number versus Reynolds number; (e) variation of friction factor with Reynolds number; (f) variation of pressure drop with Reynolds number [16].
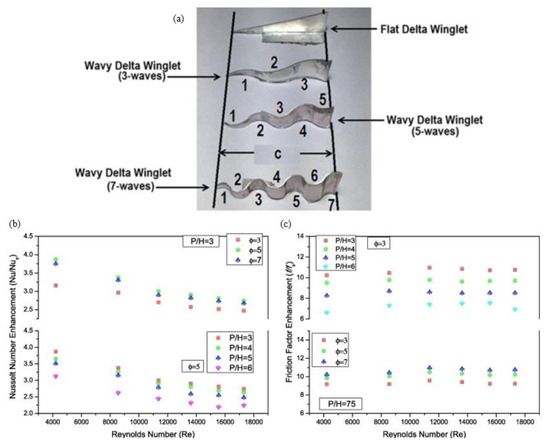
Figure 8.
(a) Diagram of flat and wavy delta winglet with different wave numbers (3, 5, and 7); (b) variation of Nusselt number enhancement for various wave number (ϕ), relative longitudinal pitch (P/H), and Re; (c) variation of friction factor enhancement for various ϕ, P/H, and Re [150].
5.1.4. Other Innovative Geometries
Wang et al. introduced wave-type VGs and identified that the application of these VGs significantly improved mixing characteristics [2]. When compared to plain fin geometry, the frictional penalty associated with these VGs was approximately 25–55% higher, with their pressure drop penalty exhibiting relatively low sensitivity to Reynolds number changes [2]. Wang et al. then compared the performance of annular and delta winglets, and they indicated that with identical winglet heights, the delta winglet induced more intense vortical motion and flow unsteadiness compared to the annular winglet, resulting in superior mixing [5]. Despite this enhanced mixing, the delta winglet incurred lower pressure drops than the annular winglet [5]. Additionally, when compared to plain fin geometry, the extra pressure drop penalty associated with these winglet VGs showed relatively little sensitivity to Reynolds number changes [5]. Wang et al. also investigated the heat transfer performance of semi-simple winglets, comparing their effectiveness to that of louvered fins [148]. The louver fin geometry exhibited superior heat transfer coefficients compared to the semi-dimple winglet geometry, largely attributed to enhanced fluid mixing [148]. For heat exchangers with 2 or 4 tube rows, the louver fin’s heat transfer coefficients were about 2–15% greater than those of the semi-dimple winglet setup [148]. As shown in Figure 9, Min et al. introduced modified RWPs created by cutting off the four corners of rectangular winglets, and the experimental findings demonstrated that these modified RWPs possess superior flow and heat transfer properties compared to traditional RWPs [140].
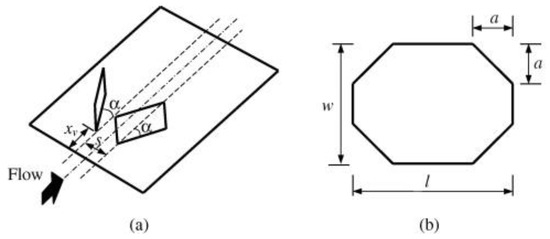
Figure 9.
Diagram of modified rectangular winglet vortex generator and layout (a) common-flow-down configuration; (b) modified rectangular winglet [140].
Oneissi et al. conducted numerical simulations on the classical DWP as a baseline, and then examined a novel vortex generator configuration, the inclined projected winglet pair (IPWP), which exhibited superior performance [77]. The IPWP configuration demonstrated a 50% reduction in peak friction magnitude, a 30% improvement in vorticity, and a 6% increase in the thermal enhancement factor relative to the DWP [77]. Zhang et al. investigated five different types of VGs, which are streamlined winglet pairs (SWPs), isosceles right-angled triangular winglet pairs (IRATWPs), equilateral triangular winglet pairs (ETWPs), spline curve winglet pairs (SCWPs), and semicircle winglet pairs (SEWPs) [94]. They observed that SWPs exhibited the lowest pressure drop, and utilizing these VGs resulted in a 46% increase in heat transfer coefficients compared to a heat exchanger without VGs [94]. As illustrated in Figure 10, Dogan and Igci conducted experimental research on a novel type of VG (NTVG) and revealed that NTVG delivered both a lower friction factor and a higher Nusselt number compared to DWP across all tested Reynolds numbers, indicating that NTVG achieved superior heat transfer enhancement relative to DWP [154]. The highest thermal enhancement factor (TEF) reached approximately 1.15 for DWP and was recorded at about 1.34 for NTVG at a Reynolds number of 5000 [154]. At a transverse pitch ratio of 0.4, the NTVG achieved its highest TEF value [154]. A single delta winglet was able to generate one longitudinal vortex, while a single NTVG was capable of generating two longitudinal vortices; the creation of longitudinal vortices persistently interfered with the thermal boundary layer, promoting the intermingling of cold and hot fluids and consequently leading to improved heat transfer [154].
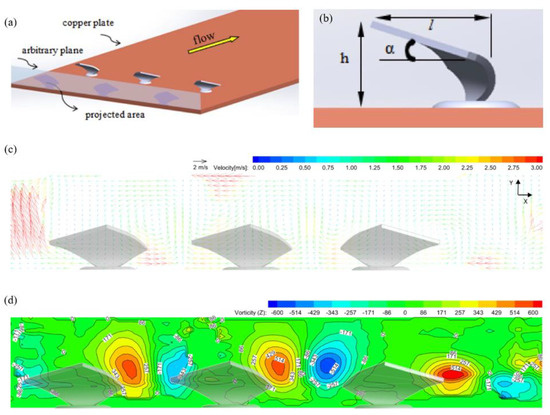
Figure 10.
(a) isometric view of NTVG; (b) side view of NTVG; (c) vectors of secondary flow for NTVG at Re = 20,000; (d) vorticity contours for NTVG at Re = 20,000 [154].
5.1.5. Height, Length, and Thickness
The influence of height, length, and thickness of VGs on heat transfer and flow structure has also been extensively studied. Wu and Tao noted that the thickness of rectangular winglets marginally impacted heat transfer near VGs and negligibly affected the channel’s total pressure drop [7,43]. Tang et al. identified that enhancing the heat transfer performance of a vortex-generator fin can be achieved by increasing the length of DWPs or by decreasing their height [45]. However, Zeng et al. presented a differing observation, exhibiting that elevating the height and length of DWPs significantly boosts heat transfer intensity, albeit with a corresponding rise in pressure drop [53]. Sharma et al. observed that the escalation in the dimensions of the winglets resulted in a more pronounced diversion of the primary flow towards the thermal isolation region, thereby intensifying thermal mixing and mitigating the formation of large eddies, leading to a marked improvement in heat transfer at the cost of a moderate increase in pressure losses [105]. Lotfi et al. revealed that wheeler wishbone (WW) VGs with a width-to-length aspect ratio of 0.5 achieved the most effective heat transfer performance [18]. As indicated in Figure 11, Zeeshan et al. examined four VG heights (40%, 50%, 60%, and 70% of the channel height), employing the Multi-Objective Optimization on the basis of Ratio Analysis (MOORA) method to identify the optimal performance configuration [80]. Based on the area goodness factor, VGs with a height constituting 60% of the channel’s height demonstrated superior thermal hydraulic performance in comparison to alternative height configurations considered [87]. At this height, heat transfer was enhanced by 27.40% to 35.42%, albeit with a 17.79% to 25.76% higher pressure loss, relative to the baseline case across the examined Reynolds number range from 500 to 900 [87]. Tang et al. demonstrated that heat transfer intensity was significantly enhanced by lessening the position of VGs and by raising their height, although this was accompanied by an increased pressure drop [78]. Additionally, they also observed that both the friction factor and Nusselt number exhibited an initial increase followed by a decrease as the length of VGs was extended [78]. Sun et al. found that the Nusselt number and friction factor both escalated with the quantity and height ratio of rectangular winglets, with the thermal enhancement factor reaching a maximum value of up to 1.27 at a height ratio of 0.05 [95]. However, the height of the winglet exerted a negligible influence on the Colburn factor across varying Reynolds numbers [83].
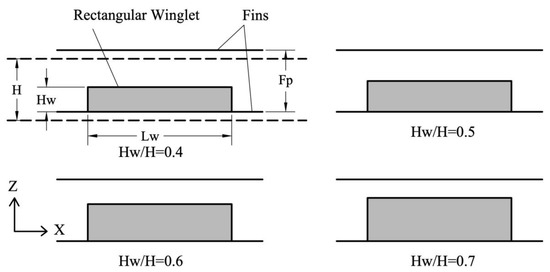
Figure 11.
Geometric description of the RWP [87].
5.2. Positional Parameters
5.2.1. Common-Flow-Down and Common-Flow-Up Setups
Various studies have demonstrated that the placement and alignment of VGs in a heat exchanger or a channel significantly influence its heat transfer efficiency. Kwak et al. discovered that in a staggered three-row tube bundle, a single transverse row of DWPs arranged in the common-flow-down (CFD) setup enhanced heat transfer by 5–15% and increased pressure loss by 2–10%, while DWPs arranged in the common-flow-up (CFU) setup improved heat transfer by 10–30% and decreased pressure loss by 34–55%, both compared to fin–tube bundles without winglets and measured across Reynolds numbers from 350 to 2100 [129]. However, Tian et al. noted that in the channel with DWPs, there is a minimal distinction between the CFU and CFD setups, whereas in the channel with RWPs, the CFD configuration notably surpassed the CFU configuration in overall performance [48]. Sinha et al. evaluated five distinct strategic placements of the VGs: common-flow down in series (CFD–CFD), common-flow up in series (CFU–CFU), combined (CFD–CFU), staggered rows of winglet (SRW), and inline rows of winglet (IRW) as illustrated in Figure 12 [61]. They indicated that, among the various VG arrangements, the CFU–CFU configuration excelled in both quality factor and heat transfer performance at Reynolds numbers in the range of 250–1580 [61]. According to Abdelatie et al., maximum heat transfer efficiency, characterized by elevated values of efficiency index (η), area goodness factor (G), and effectiveness (ε), alongside minimized fluid-flow parameters such as the friction factor, is attained at orientations of +5° counterclockwise common-flow down (CFDn) downstream and −15° clockwise common-flow up (CFUp) downstream [83]. Zhang et al. found that DWPs set up in the CFD configuration consistently delivered the best overall thermal performance across various Reynolds numbers, achieving up to a 5.51% improvement in heat transfer performance compared to setups featuring five continuous ribs [155].
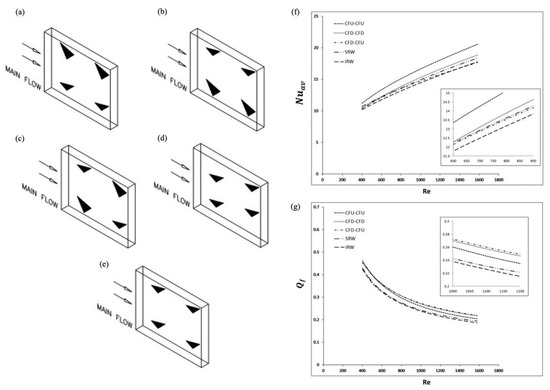
Figure 12.
(a) CFU-CFU configuration; (b) CFD-CFD configuration; (c) CFD-CFU configuration; (d) SRW configuration; (e) IRW configuration; (f) variation of average combined spanwise Nusselt number for various setups versus Reynolds number; (g) variation of average Quality factor for various setups versus Reynolds number [61].
5.2.2. Angle of Attack
Fiebig et al. stated that longitudinal vortices remained stable at higher angles of attack [111]. Within a Reynolds number spectrum of 500 to 2500, the three-row fin-and-oval-tube heat exchanger equipped with VGs demonstrated a 13.6–32.9% enhancement in the average Nusselt number and a 29.2–40.6% increase in pressure loss compared to the baseline scenario, and optimal heat transfer performance was attained with VGs positioned downstream, set at an angle of attack of 30°, and configured with the minimum number of tube rows [50]. Zeng et al. [53], Promvonge et al. [138], and Zhai et al. [153] noted that elevating the attack angle of VGs significantly boosted heat transfer intensity, albeit with a corresponding rise in pressure drop and friction factors. As represented in Figure 13, the experimental findings of Wu and Tao indicated that the average Nusselt number on the surface of a flat plate with DWP increased as the attack angle was raised, compared to a flat plate without DWP within the tested Reynolds number range of 500–2000 [141]. Lotfi et al. found that rectangular trapezoidal winglet (RTW) VGs excelled in heat transfer enhancement at larger attack angles between 15° and 75°, outperforming angle rectangular winglet (ARW) and curved angle rectangular winglet (CARW) VGs, due to their larger surface area interacting with airflow and inducing robust streamwise vortices [18]. Conversely, at smaller attack angles, CARW VGs demonstrated superior thermo-hydraulic performance [18]. Li et al. noted that rectangular winglets outperformed delta winglets in heat transfer enhancement at identical angles of attack, with the former achieving optimal performance between 20° and 30°, and the latter at 45° [72]. Samadifar and Toghraie identified that rectangular winglet VGs had the optimal effectiveness in enhancing heat transfer at the angle of attack of 45° [20]. Luo et al. pointed out that the optimal attack angle for delta winglet VGs in wavy fin plate heat exchangers was 45°, which, along with the integration of wavy fins, boosted the thermal performance factor by 26.4% [89]. The results of Zhai et al. showed that a peak thermal enhancement factor of 1.44 can be obtained at an angle of attack of 30° for a Reynolds number of 5000 in a circular pipe equipped with DWPs [153]. The effect of angle of attack on the heat transfer enhancement properties of curved winglets was evaluated by Berber et al., and they observed that the increase in the attack angle of curved winglets led to higher Nusselt numbers, performance evaluation criteria values, and friction factors [156]. Specifically, curved winglets at attack angles of 0°, 30°, and 60° enhanced heat transfer by 217.39–291.30%, 260.86–465.21%, and 278.26–476.08%, respectively, compared to a plain tube [156]. The PEC values for curved winglets at these angles were in the ranges of 1.22–1.78, 1.28–1.86, and 1.32–1.89, respectively [156]. Correspondingly, the friction factors in the inner rectangular channel for these attack angles were about 8.93–10.33, 10.66–14.16, and 14.96–19.13 times higher than that of a plain tube [156].
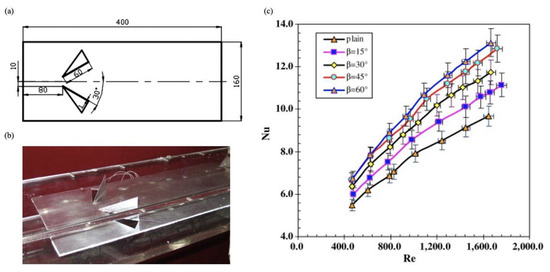
Figure 13.
(a) Dimensions and position of DWP on the plate at the angle of attack of = 30°; (b) tested plate punched with DWP; (c) variation of average Nusselt number for various attack angles versus Reynolds number [141].
5.2.3. Location
Mitra and Fiebig stated that aligned double rows of delta winglets demonstrated a greater enhancement in heat transfer compared to their staggered counterparts [113]. Longitudinal vortices induced by DWPs can markedly boost the heat transfer performance of finned flat-tube heat exchangers, but this enhancement is reliant on the positioning of DWPs [117]. Among the three locations evaluated by Valencia et al., the optimal one resulted in a 50% increase in heat transfer and a 36% rise in pressure loss [117]. The experimental research conducted by Pesteei et al. exhibited that the optimal placement for the delta winglets was at a streamwise distance (Δx) of 0.5D (where D was the tube diameter) and a spanwise distance (Δy) of 0.5D from the tube [130]. The positioning of delta winglet VGs adjacent to circular tubes fosters stronger longitudinal vortices and creates nozzle-like flow passages that accelerate the flow, significantly enhancing heat transfer by eliminating zones of poor heat transfer [58]. Whereas delta winglets positioned entirely within tube wakes failed to contribute to heat transfer enhancement [62]. Song and Wang indicated that the transverse pitches of VGs were associated with the interaction between longitudinal vortices, and this interaction significantly impacted both the intensity and the heat transfer performance of the longitudinal vortices [76]. Thus, selecting the optimal transverse pitch for VGs is crucial for achieving peak heat transfer performance while avoiding transverse pitches that could lead to suboptimal results [76]. Sarangi and Mishra found that positioning winglets near the central tube proved to be more efficacious in heat transfer, with a significant boost observed when the streamwise and spanwise distances were determined to be −3.201 mm and 7.2 mm, respectively, resulting in a 60% improvement in the Nusselt number compared to the baseline [80]. Chimres et al. revealed that elliptical winglets, featuring a vertical distance of 6 mm, a horizontal distance of 0 mm, a 30° angle of attack, and a 120° trailing angle, delivered the highest performance [81]. Relative to the baseline plain fin, these configurations yielded pressure drops and heat transfer coefficients that were elevated by approximately 35% and 13%, respectively [81]. Song and Tagawa examined the impact of the transverse distance of VGs on the heat transfer performance and the interaction of longitudinal vortices, revealing that for the highest Reynolds number investigated (Re = 1600), the maximal variations in the increments of friction factor, Nusselt number, and longitudinal vortex intensity across different VG transverse distances are 18.5%, 33.9%, and 34.0%, respectively [82]. Shi et al. noted that the vortex generator had an ideal longitudinal position for maximum heat transfer performance, where the Nusselt number rose by 43.9% compared to the plain fin and 9.8% over its original position; additionally, the thermal performance factor at this optimal spot grew by 8.1% from its original location, achieving a value of 1.38 [100]. Naik and Tiwari numerically investigated how various locations of RWPs affect the thermodynamic and thermohydraulic performances of staggered finned circular-tube heat exchangers [101]. As displayed in Figure 14, adjacent RWP locations yielded a higher augmentation in heat transfer but incurred a higher friction loss, resulting in a lower thermal performance factor [101]. In contrast, upstream RWP locations, with stronger longitudinal and horseshoe vortices, enhanced fluid mixing and transport, leading to a notable improvement in heat transfer augmentation and a higher JF due to a reduced friction loss penalty [101]. Hu et al. employed a neural network and a multi-objective genetic algorithm to optimize the arrangement of VGs and used the Pareto optimal strategy to determine the ideal transverse distances, leading to an optimal configuration that enhances heat transfer power by up to 34.6% [108]. Dogan and Erzincan determined that the ratios of transverse and longitudinal pitch play crucial roles in determining thermal performance, with an inline arrangement proving more effective for heat transfer than a staggered one [158]. The optimal thermal enhancement factor was attained with a transverse pitch ratio of 0.16, a longitudinal pitch ratio of 1.5, and an inline arrangement [158].
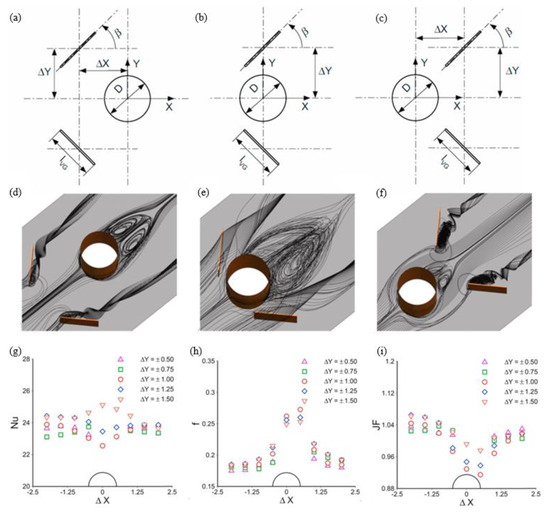
Figure 14.
(a) Upstream RWP location (ΔX < 0); (b) adjacent RWP location (ΔX = 0); (c) downstream RWP location (ΔX > 0); (d) flow pattern for upstream located RWP; (e) flow pattern for adjacent located RWP; (f) flow pattern for downstream located RWP; (g) variation of Nusselt number versus RWP locations; (h) variation of friction factor versus RWP locations; (i) variation of JF versus RWP locations [101].
5.3. Punched Holes
To figure out the effect of punching holes in winglet VGs on heat transfer enhancement, many studies have been conducted to investigate the punched winglet VGs and the parameters of holes, including hole shape, size, location, and number of holes. Wu and Tao [7,43], Modi and Rathod [157] indicated that compared to unpunched setups, rectangular winglets with punched holes exhibited superior heat transfer enhancement near VGs and a decreased flow frictional coefficient. Zhou and Feng noted that the introduction of punched holes significantly reduced flow resistance and enhanced the thermohydraulic performance across all cases [13]. However, the optimal diameter of these holes should correspond to the face area of VGs, with smaller VGs benefiting from relatively smaller holes [13]. Holes punched lower in the vertical direction and at the lateral centreline yield better thermohydraulic performance and heat transfer enhancement [13]. Nonetheless, the positioning of these holes had a minimal impact on the VGs’ flow resistance [13]. As indicated in Figure 15, Lu and Zhou also conducted research on the dimensions of holes and their placement, identifying that punched VGs boosted heat transfer and lessened flow resistance, with an optimal hole-to-vortex generator area ratio of 0.06 for best overall performance [14]. Holes placed lower vertically and near the leading-edge enhanced heat transfer, but their positioning had minimal effect on flow resistance [14].
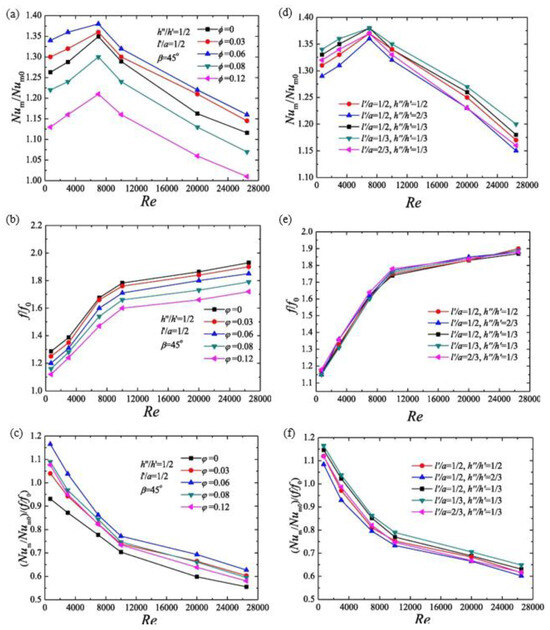
Figure 15.
For various hole diameters: (a) variation of Num/Num0 versus Reynolds number; (b) variation of f/f0 versus Reynolds number; (c) variation of (Num/Num0)/(f/f0) versus Reynolds number; for different hole position: (d) variation of Num/Num0 versus Reynolds number; (e) variation of f/f0 versus Reynolds number; (f) variation of (Num/Num0)/(f/f0) versus Reynolds number [14].
According to Han et al., rectangular winglet VGs with a hole excelled in thermo-hydraulic performance compared to those without, and based on PEC, Colburn factor and friction factor values, the optimal hole diameter was 5 mm, with its position mildly affecting heat transfer enhancement but greatly influencing VGs’ flow resistance [85]. For the given Reynolds number range (1500–9000), using rectangular winglets with a punched hole in the CFU configuration at an upstream location in a FTHE resulted in a heat transfer increase of up to 34% compared to its non-punched counterpart in the same setup [96]. The punched delta winglet increased the Nusselt number by 78.21 times compared to the plain flat plate and offered a peak thermal enhancement factor of 2.1, while the flapped delta winglet’s thermal enhancement factor was approximately 2.16, which was about 2.9% higher than the punched version [99]. As shown in Figure 16, Modi et al. conducted numerical studies to assess the thermo-hydraulic performance of finned circular-tube heat exchangers outfitted with rectangular winglet VGs with different numbers of circular punched holes (1, 2, 4, and 6) [97]. They noted that rectangular winglet VGs featuring circular punched holes significantly enhanced FTHE’s thermo-hydraulic performance, with the 6-hole variant outshining others by raising the Nusselt number approximately 45.95% at a Reynolds number of 400 and 57.37% at 2000 [97]. Among various configurations of rectangular winglet VGs, the version with 6 holes demonstrated the highest values for both Hydro Thermal Performance Factor (HTPF = (Nu/Nu0)/(f/f0)^(1/3)) and Performance Evaluation Criteria (PEC = (j/j0)/(f/f0)), indicating a superior thermo-hydraulic performance for the 6-hole variant [97]. Using curved trapezoidal winglet VGs with circular punched holes notably boosted FTHE’s thermo-hydraulic performance, with the 6-hole variant excelling other curved trapezoidal winglet vortex generator designs, showing a Nusselt number increase of approximately 75.25% and 40.10% at Reynolds numbers of 400 and 2000, respectively [106]. In addition to punched curved trapezoidal winglet VGs, Saini et al. also conducted research on punched curved delta winglet VGs. They observed that FTHE’s thermo-hydraulic performance was notably enhanced by curved delta winglet VGs with circular punched holes, especially the 6-hole variant, which elevated the Nusselt number by about 77.25% and 42.51% at Reynolds numbers of 400 and 2000, compared to the heat exchanger without VGs [107].
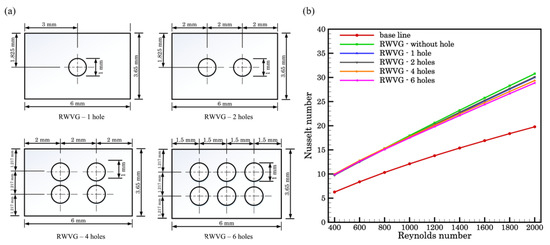
Figure 16.
(a) Dimensional details of rectangular winglet VGs with 1, 2, 4, and 6 punched holes; (b) variation of Nusselt number versus Reynolds number [97].
6. Recent Advances and Emerging Technologies in Heat Transfer Enhancement
Heat transfer enhancement technologies have made significant progress in recent years, integrating innovative materials, manufacturing techniques, computational methods, and multidisciplinary approaches. This section briefly explores these advanced solutions and highlights potential synergistic applications with LVGs.
6.1. Shape Memory Alloys (SMAs)
Shape memory alloys are smart materials that can deform significantly under thermal stimulation and return to their original shape after heating. In recent years, SMAs have been explored as adaptive vortex generators in heat exchangers [56,166,167,168,169,170,171]. SMA-based vortex generators can passively respond to temperature fluctuations and dynamically change their shape to optimize the vortex strength and turbulence intensity according to operational requirements. This adaptive capability allows active and autonomous control of heat transfer performance without the need for external mechanical actuation, thereby significantly improving thermal efficiency and operational stability. Aris et al. introduced a memory-alloy-based vortex generator for active regulation of heat transfer performance [166]. Subsequently, Aris et al. extended this approach by integrating this vortex generator into a fin-and-tube heat exchanger, performing comprehensive experimental investigations and numerical simulations [56]. Their findings demonstrated that the device achieved a 16% improvement in heat transfer performance under the activated state, and a 19% decrease in pressure losses when deactivated [56]. Vilarrubi et al. introduced a self-adaptive vortex generator made of SMA, showing its effectiveness in sustaining a steady wall temperature under increasing heat flux conditions [167]. Chu et al. conducted both experimental and numerical analyses to evaluate the heat transfer performance of microchannel heat exchangers equipped with SMA-based vortex generators [168]. The microchannel equipped with the SMA vortex generator demonstrated enhanced localized disturbance effects. At a heat flux of 100,000 W/m2, the Nusselt number improved by 112% compared to the plain channel and was 9% higher than that of the channel featuring a non-deformed vortex generator [168]. According to Regany et al., implementing a self-adaptive vortex generator enhances wall temperature uniformity by 63.1% compared to a plain channel configuration [169]. Wang et al. [170] and Li et al. [171] introduced a heat exchanger design incorporating SMAs, where a two-way SMA strip functions as a self-adaptive vortex generator to improve heat transfer performance. As fluid temperature rises, heat transfer enhancement ranges between 110% and 125%. Conversely, when thermal demand decreases, the Darcy friction factor drops by 74% to 90%, in line with their proposed mechanism.
6.2. Soft Abrasive Flow (SAF) Finishing Methods
Curved thin-walled structures, such as winglet-type vortex generators, are likely to experience brittle failure or deformation during fabrication because of their complex stress distribution. Traditional processing techniques often struggle to deliver high precision in both geometric accuracy and surface finish. The SAF surface finishing methods offer a more effective solution by establishing flexible contact with the surface, making it particularly suitable for machining complex structure surfaces [172]. The process involves flowing a semi-solid abrasive media through complex internal geometries, smoothing surface roughness without destroying structural integrity. By lowering surface roughness, the SAF finishing techniques can reduce flow friction and inhibit boundary layer separation, significantly improving convective heat transfer and thermal hydraulic performance. Applying the SAF finishing methods to LVG surfaces can further enhance heat transfer efficiency by optimizing vortex shedding characteristics and minimizing undesirable pressure drops.
6.3. Additive Manufacturing (AM) Technologies
The advancement of additive manufacturing technologies, particularly Selective Laser Melting (SLM) [173,174,175,176], Electron Beam Melting (EBM) [177,178], and Fused Deposition Modelling (FDM) [179,180,181,182,183,184,185,186,187,188,189,190,191], has provided new perspectives for the fabrication of vortex generators and heat exchanger surfaces. The FDM technology, also referred to as Fused Filament Fabrication (FFF) technology, is widely recognized for its advantages in rapid prototyping, including affordability, broad material compatibility, ease of operation, and a high level of design flexibility [179,180,181,182,183,184]. This layer-by-layer additive process enables the fabrication of complex geometries. However, it also has several challenges during the extrusion deposition process. Insufficient contact pressure, inadequate interfacial temperature, or limited molding time can affect interlayer healing strength. Weak interlayer healing strength between layers can substantially reduce the mechanical strength of the printed object, thereby restricting the use of FDM in applications requiring high-performance structural components [185,186]. As a result, considerable research has recently focused on improving the interlayer healing strength of components produced by FDM [187,188,189,190,191]. For example, Xu et al. investigated the underlying mechanisms influencing interlayer healing strength in multi-path deposition configurations and demonstrated that optimizing nozzle geometry can significantly improve interlayer healing strength [191]. In summary, additive manufacturing technologies provide design flexibility and the ability to produce complex three-dimensional geometries that are difficult or impossible to achieve using traditional manufacturing methods. Novel structures such as triply periodic minimal surfaces, lattice-based fins, and integrated vortex generators can be easily manufactured and contribute to enhanced heat transfer performance by increasing the surface-to-volume ratio and optimizing the flow channel structure.
6.4. Topology Optimization
Originally introduced by Bendsøe and Kikuchi in 1988 [192], topology optimization reformulates structural optimization as a problem of material distribution. In this approach, design variables indicate the presence or absence of material at specific locations within the design space. Through iterative updates of these variables using mathematical programming techniques, the optimal configuration is achieved. This method has found widespread application across numerous areas of physics [193,194,195,196,197,198,199,200,201,202,203,204,205]. Zeng et al. developed a simplified 2D model to approximate a 3D conjugate heat transfer model for the design of a heatsink and validated the resulting optimized configuration through both experimental testing and numerical simulations [206]. Sun et al. employed topology optimization in the development of a fin-and-tube heat exchanger, proposing an innovative fin configuration featuring surface embossments [207]. These features were optimized to reduce pressure drop, and the approach allowed extensive flexibility in fin geometry design [207]. However, employing topology optimization to the tube-and-fin heat exchanger design presents certain challenges. Firstly, the optimized fin structures are often impractical for direct use due to manufacturing restrictions. Secondly, conventional topology optimization methods typically neglect the influence of heat transfer in the design process. To address these issues, Kobayashi et al. developed a method for designing freeform winglets that incorporates both heat transfer performance and manufacturability of the topology-optimized fin [208]. As a result, the proposed configuration achieved a 16% improvement in the performance factor j/f compared to a fin equipped with traditional rectangular winglet pairs [208]. In conclusion, topology optimization employs advanced computational techniques to determine the optimal material layout within a given design domain, maximizing performance under specified constraints. Applying topology optimization to LVGs can generate innovative designs that maximize vortex strength and heat transfer performance while minimizing pressure losses. Integrating these optimized geometries into heat exchangers can lead to significant improvements in energy efficiency and compactness.
6.5. Machine Learning (ML) Integration with CFD
Recent advancements integrate machine learning algorithms with CFD, creating hybrid frameworks that rapidly predict flow behaviour and heat transfer characteristics with high accuracy. ML-driven CFD approaches can efficiently explore extensive design spaces for LVGs, rapidly identifying optimal configurations. Furthermore, predictive models trained on CFD simulation data could accelerate the design cycle and enhance real-time operational adaptability. Various ML models are employed, including supervised learning algorithms such as Random Forest (RF), Gradient Boosting (GB), Support Vector Regression (SVR), and Artificial Neural Network (ANN) to approximate CFD outputs such as temperature distribution, velocity profiles, and Nusselt number predictions. For example, Berber et al. used ANN algorithms to explore the effects of the innovative fin configuration and different attack angles of winglets (30°, 60°, and 90°) on convective heat transfer in a rectangular channel, considering variations in Reynolds number and plate temperature [209]. Kang et al. employed three machine learning techniques, that is, RF, ANN, and SVR, to predict average heat transfer and net energy loss [210]. The input features included gap distance, bending rigidity, and inclination angle of flexible vortex generators [210]. Among all the models, SVR and ANN delivered the most accurate predictions on both thermal performance and mean energy loss [210]. Wu et al. conducted a study utilizing four machine learning methods, that is, SVR, GB, RF, and XGBoost regression, to develop prediction models for dimensionless heat transfer coefficients in microchannel heat sinks equipped with flexible vortex generators [211]. Xie et al. proposed using Response Surface Methodology (RSM) and ANN for optimizing the design of fin-and-tube heat exchangers equipped with vortex generators [212]. The findings indicated that while both methods provided reliable predictions, ANN demonstrated superior accuracy in predicting the friction factor and Nusselt number compared to RSM [212]. Liang et al. also applied RSM and ANN to analyse how design variations influence the Nusselt number and pressure drop in microchannel heat sinks, and they obtained similar results, that is, ANN provided more accurate predictions than the RSM approach [213]. Li et al. proposed a multi-objective optimization method for designing microchannels featuring a delta winglet pair to achieve optimal hydrothermal performance under conditions of high heat flux [214]. The optimization integrated Non-dominated Sorting Genetic Algorithm II (NSGA-II), ANN, and grey relational analysis [214]. Among the models tested, the genetic algorithm-enhanced back-propagation neural network demonstrated superior accuracy and generalization capabilities in predicting both the friction factor and Nusselt number, outperforming the conventional back-propagation neural network model [214]. Deep learning models, especially Convolutional Neural Network (CNN) algorithms, are increasingly applied to capture spatial features from CFD-generated flow fields, enabling efficient surrogate modelling and flow regime classification. For example, Seal et al. achieved over 98% accuracy in predicting flow pattern images of R-134a refrigerant condensation using CNN algorithms [215]. In this study, principal component analysis and multilayer perceptron neural networks were also employed to visualize the dataset and reduce computational requirements [215]. Reinforcement learning is emerging as a tool to optimize flow control strategies. For example, Ren et al. integrated various machine learning techniques, including reinforcement learning based on the non-Oberbeck-Boussinesq (NOB) approximation and proximal policy optimization (PPO) approximation [216]. An intelligent active flow control approach was developed to enhance fluid heat transfer under laminar flow conditions [216]. Following extensive training, the method demonstrated a 76.7% improvement in heat transfer performance [216]. Unsupervised learning methods like clustering and dimensionality reduction are also used to discover patterns in high-dimensional simulation outputs.
6.6. Potential Synergistic Applications with LVGs
The integration of SMA materials with AM technologies presents a promising pathway for the development of advanced LVG designs in heat exchangers. AM technologies facilitate the fabrication of complex and optimized geometries that can be precisely tailored to enhance thermal efficiency, while SMA materials offer dynamic shape adaptability, enabling components to passively respond to changing thermal conditions. This synergy has the potential to produce self-adaptive LVGs that can adjust vortex strength and distribution in real time, thereby significantly improving both thermal performance and operational flexibility. Future research should focus on improving AM techniques, embedding SMA wires or layers into printed LVGs, investigating the adaptive thermal response mechanisms of these SMA-integrated structures under actual operating conditions, and conducting long-term evaluations to assess their fatigue behaviour and overall durability.
Integrating ML algorithms into topology optimization frameworks provides a novel and powerful approach to enhance LVG designs. By quickly predicting flow behaviour and heat transfer characteristics, ML significantly speeds up the optimization process, allowing topology optimization algorithms to more effectively explore complex design spaces. This synergistic effect helps create efficient, lightweight, and turbulence-optimized LVG configurations to meet specific thermal and fluid conditions. Future research should focus on developing hybrid ML-based topology optimization frameworks specifically for LVG design, validating ML-predicted CFD results against experimental benchmarks to ensure robustness and accuracy, and conducting comparative studies to evaluate the performance and manufacturability of ML-optimized LVGs in contrast to those produced by traditional methods.
SAF applied to AM vortex generators offers an attractive solution for improving surface finish, thereby significantly reducing friction losses and minimizing boundary-layer disruptions. By enhancing the surface properties of complex AM-fabricated vortex generators, SAF contributes to improved aerodynamic performance, greater turbulence generation efficiency, and ultimately more effective heat transfer enhancement. Future research should include experimental investigations into the effects of SAF-treated AM vortex generators on flow turbulence and thermal enhancement, optimization of SAF process parameters specifically for complex AM geometries, and comprehensive evaluations of long-term performance gains and structural durability resulting from SAF application.
7. Recommendations for Future Research
Despite the significant progress in the application of LVGs for heat transfer enhancement in heat exchangers, there are still some research gaps that deserve further investigation. The following suggestions are proposed to guide future research work:
- Develop more sophisticated numerical models that incorporate complex geometric structures and fluid dynamics phenomena. These models should aim to reduce the existing differences between simulation results and experimental data. Attention should be paid to combining actual operating conditions to improve the predictive ability of the model.
- Investigate the application and effectiveness of LVGs in miniaturized heat exchangers commonly used in portable and microscale devices. Research focus should be on optimizing LVG design to minimize space occupation without affecting efficiency, including exploring microfabrication techniques for LVG manufacturing.
- Study the integration of LVGs with other heat transfer enhancement methods, including active techniques such as spray cooling, electrohydrodynamic techniques, fluid vibration, magnetic fields, etc., and passive techniques such as nanofluids, extended surfaces, rough surfaces, porous materials, dimples and protrusions, other inserts, etc. Such integrative approaches could potentially lead to breakthroughs in heat transfer rates and efficiency.
- Design adaptive LVG systems equipped with sensors and actuators that can dynamically adjust their behaviour based on real-time feedback from the heat exchanger’s performance. This approach allows for continuous optimization of energy consumption and performance under a wide range of operating conditions.
- Explore the use of advanced materials in LVGs, such as composites or metamaterials that can withstand extreme conditions while maintaining performance. Research into environmentally friendly materials that are both effective and sustainable for long-term use is also crucial.
- Conduct a comprehensive cost–benefit and environmental impact analysis to evaluate the feasibility of implementing LVGs in industrial settings. The study should include a lifecycle assessment to fully understand the environmental impacts of widespread LVG adoption.
- Expand experimental methods to include long-term performance studies under varying operating pressures. Such studies will help to understand the durability and maintenance requirements of LVGs in industrial applications.
8. Conclusions
This literature review systematically examines a large number of numerical and experimental studies on the enhancement of heat transfer in heat exchangers through the use of LVGs. The review highlights the effectiveness of LVGs in improving heat exchanger performance by generating coherent vortex structures that augment the thermal boundary layer mixing, thereby significantly enhancing heat transfer rates while minimally impacting pressure drop. A comprehensive review of the results from numerous studies indicates that the geometry, size, orientation, and location of LVGs play a key role in optimizing heat transfer enhancement. Numerical simulations are essential to understand the complex fluid dynamics and thermal characteristics induced by LVGs, providing insights into the mechanisms of heat transfer enhancement and facilitating the design of more efficient heat exchanger configurations. Experimental activities, on the other hand, validate the numerical models and provide empirical data that are crucial for the practical application and further development of LVG technologies. Despite some progress, gaps remain in the current knowledge base, particularly regarding the long-term performance, fouling resistance, and economic feasibility of heat exchangers equipped with LVGs. In addition, more comprehensive studies are needed to explore the integration of LVGs in various types of heat exchangers and their performance under different operating conditions. Future research should aim to address these gaps, including developing more sophisticated numerical models, conducting long-term performance studies, and exploring innovative materials and manufacturing techniques for LVGs. Additionally, the environmental impact and sustainability of LVG-enhanced heat exchangers warrant further investigation to ensure that these technologies can actively contribute to energy efficiency goals and carbon footprint reduction. In summary, the use of LVGs presents a promising avenue for enhancing the performance of heat exchangers. Based on the foundation laid by the extensive numerical and experimental activities reviewed in this paper, future advances are expected to lead to more efficient, reliable, and sustainable heat exchange technologies.
Funding
This work was supported in part by the CSC PhD scholarship fund of the China Scholarship Council under Grant 202308200023. The support of ARC Discovery Project Grant DP240102559 is gratefully acknowledged.
Acknowledgments
The authors thank the publishers for giving permission for the reproductions of the figures. The first author confirms that this manuscript was written independently without the assistance of AI writing tools. All content reflects the authors’ original analysis and synthesis.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Nomenclature
| Curvature ratio | |
| Diameter (mm) | |
| Hydraulic diameter (mm) | |
| Friction factor | |
| Pumping power factor | |
| Fin pitch (mm) | |
| Height (mm) | |
| Colburn factor | |
| Heat transfer performance factor | |
| Surface goodness factor | |
| Length (mm) | |
| Nusselt number | |
| Prandtl number | |
| Pressure difference (Pa) | |
| Relative longitudinal pitch | |
| Radius (mm) | |
| Reynolds number | |
| Cartesian coordinates (mm) | |
| Greek letters | |
| Angle of inclination | |
| Angle of attack | |
| Central angle | |
| Wave number; hole-to-vortex generator area ratio | |
| Efficiency index | |
| Effectiveness | |
| Abbreviations | |
| ARW | Angle rectangular winglet |
| CARW | Curved angle rectangular winglet |
| CFD | Computational fluid dynamics |
| CFD | Common-flow-down |
| CFDn | Counterclockwise common-flow down |
| CFD-CFD | Common-flow down in series |
| CFD-CFU | Combined common-flow-down and common-flow-up |
| CFU | Common-flow-up |
| CFUp | Clockwise common-flow up |
| CFU-CFU | Common-flow up in series |
| DNS | Direct numerical simulation |
| DWP | Delta winglet pair |
| ETWP | Equilateral triangular winglet pair |
| FTHE | Finned tube heat exchanger |
| FVM | Finite Volume Method |
| HTPF | Hydro thermal performance factor |
| IPWP | Inclined projected winglet pair |
| IRATWP | Isosceles right-angled triangular winglet pair |
| IRW | Inline rows of winglet |
| IVG | Intended vortex generator |
| LCT | Liquid crystal thermography |
| LDV | Laser Doppler velocimetry |
| LES | Large eddy simulation |
| LLS | Laser light sheets |
| LV | Longitudinal vortex |
| LVG | Longitudinal vortex generator |
| MAC | Marker-and-cell |
| MOORA | Multi objective optimization on the basis of ratio analysis |
| NTVG | Novel type of vortex generator |
| PEC | Performance evaluation criteria |
| PIV | Particle image velocimetry |
| RANS | Reynolds-Averaged Navier–Stokes |
| RTD | Resistance temperature detector |
| RTW | Rectangular trapezoidal winglet |
| RWP | Rectangular winglet pair |
| SCWP | Spline curve winglet pair |
| SEWP | Semicircle winglet pair |
| SRW | Staggered rows of winglet |
| SST | Shear stress transport |
| SWP | Streamlined winglet pair |
| TEF | Thermal enhancement factor |
| TV | Transverse vortex |
| TWP | Trapezoidal winglet pair |
| VG | Vortex generator |
| WVG | Waved vortex generator |
| WW | Wheeler wishbone |
References
- Incropera, F.P.; DeWitt, D.P.; Bergman, T.L.; Lavine, A.S. Fundamentals of Heat and Mass Transfer; Wiley: New York, NY, USA, 1996; Volume 6, p. 116. [Google Scholar]
- Wang, C.C.; Lo, J.; Lin, Y.T.; Liu, M.S. Flow visualization of wave-type vortex generators having inline fin-tube arrangement. Int. J. Heat Mass Transf. 2002, 45, 1933–1944. [Google Scholar] [CrossRef]
- Depaiwa, N.; Chompookham, T.; Promvonge, P. Thermal enhancement in a solar air heater channel using rectangular winglet vortex generators. In Proceedings of the International Conference on Energy and Sustainable Development: Issues and Strategies (ESD 2010), Chiang Mai, Thailand, 2–4 June 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 1–7. [Google Scholar]
- Jacobi, A.M.; Shah, R.K. Heat transfer surface enhancement through the use of longitudinal vortices: A review of recent progress. Exp. Therm. Fluid Sci. 1995, 11, 295–309. [Google Scholar] [CrossRef]
- Wang, C.C.; Lo, J.; Lin, Y.T.; Wei, C.S. Flow visualization of annular and delta winlet vortex generators in fin-and-tube heat exchanger application. Int. J. Heat Mass Transf. 2002, 45, 3803–3815. [Google Scholar] [CrossRef]
- Fiebig, M. Vortices and heat transfer. ZAMM-J. Appl. Math. Mech./Z. Angew. Math. Mech. 1997, 77, 3–18. [Google Scholar] [CrossRef]
- Wu, J.M.; Tao, W.Q. Numerical study on laminar convection heat transfer in a rectangular channel with longitudinal vortex generator. Part A: Verification of field synergy principle. Int. J. Heat Mass Transf. 2008, 51, 1179–1191. [Google Scholar] [CrossRef]
- He, Y.L.; Zhang, Y. Advances and outlooks of heat transfer enhancement by longitudinal vortex generators. In Advances in Heat Transfer; Elsevier: Amsterdam, The Netherlands, 2012; Volume 44, pp. 119–185. [Google Scholar]
- Fiebig, M. Embedded vortices in internal flow: Heat transfer and pressure loss enhancement. Int. J. Heat Fluid Flow 1995, 16, 376–388. [Google Scholar] [CrossRef]
- Aris, M.S.; Owen, I.; Sutcliffe, C.J. The development of active vortex generators from shape memory alloys for the convective cooling of heated surfaces. Int. J. Heat Mass Transf. 2011, 54, 3566–3574. [Google Scholar] [CrossRef]
- Ahmed, H.E.; Mohammed, H.A.; Yusoff, M.Z. An overview on heat transfer augmentation using vortex generators and nanofluids: Approaches and applications. Renew. Sustain. Energy Rev. 2012, 16, 5951–5993. [Google Scholar] [CrossRef]
- Chai, L.; Tassou, S.A. A review of airside heat transfer augmentation with vortex generators on heat transfer surface. Energies 2018, 11, 2737. [Google Scholar] [CrossRef]
- Zhou, G.; Feng, Z. Experimental investigations of heat transfer enhancement by plane and curved winglet type vortex generators with punched holes. Int. J. Therm. Sci. 2014, 78, 26–35. [Google Scholar] [CrossRef]
- Lu, G.; Zhou, G. Numerical simulation on performances of plane and curved winglet type vortex generator pairs with punched holes. Int. J. Heat Mass Transf. 2016, 102, 679–690. [Google Scholar] [CrossRef]
- Lin, Z.M.; Wang, L.B.; Zhang, Y.H. Numerical study on heat transfer enhancement of circular tube bank fin heat exchanger with interrupted annular groove fin. Appl. Therm. Eng. 2014, 73, 1465–1476. [Google Scholar] [CrossRef]
- Gholami, A.A.; Wahid, M.A.; Mohammed, H.A. Heat transfer enhancement and pressure drop for fin-and-tube compact heat exchangers with wavy rectangular winglet-type vortex generators. Int. Commun. Heat Mass Transf. 2014, 54, 132–140. [Google Scholar] [CrossRef]
- He, J.; Liu, L.; Jacobi, A.M. Air-side heat-transfer enhancement by a new winglet-type vortex generator array in a plain-fin round-tube heat exchanger. J. Heat Transf. 2010, 132, 071801. [Google Scholar] [CrossRef]
- Lotfi, B.; Zeng, M.; Sundén, B.; Wang, Q. 3D numerical investigation of flow and heat transfer characteristics in smooth wavy fin-and-elliptical tube heat exchangers using new type vortex generators. Energy 2014, 73, 233–257. [Google Scholar] [CrossRef]
- Lotfi, B.; Sundén, B.; Wang, Q. An investigation of the thermo-hydraulic performance of the smooth wavy fin-and-elliptical tube heat exchangers utilizing new type vortex generators. Appl. Energy 2016, 162, 1282–1302. [Google Scholar] [CrossRef]
- Samadifar, M.; Toghraie, D. Numerical simulation of heat transfer enhancement in a plate-fin heat exchanger using a new type of vortex generators. Appl. Therm. Eng. 2018, 133, 671–681. [Google Scholar] [CrossRef]
- Biswas, G.; Mitra, N.K.; Fiebig, M. Computation of laminar mixed convection flow in a channel with wing type built-in obstacles. J. Thermophys. Heat Transf. 1989, 3, 447–453. [Google Scholar] [CrossRef]
- Fiebig, M.; Brockmeier, U.; Mitra, N.K.; Gü Termann, T. Structure of velocity and temperature fields in laminar channel flows with longitudinal vortex generators. Numer. Heat Transf. 1989, 15, 281–302. [Google Scholar] [CrossRef]
- Biswas, G.; Chattopadhyay, H. Heat transfer in a channel with built-in wing-type vortex generators. Int. J. Heat Mass Transf. 1992, 35, 803–814. [Google Scholar] [CrossRef]
- Zhu, J.X.; Mitra, N.K.; Fiebig, M. Effects of longitudinal vortex generators on heat transfer and flow loss in turbulent channel flows. Int. J. Heat Mass Transf. 1993, 36, 2339–2347. [Google Scholar] [CrossRef]
- Zhu, J.X.; Fiebig, M.; Mitra, N.K. Comparison of numerical and experimental results for a turbulent flow field with a longitudinal vortex pair. J. Fluids Eng. 1993, 115, 270–274. [Google Scholar] [CrossRef]
- Biswas, G.; Deb, P.; Biswas, S. Generation of longitudinal streamwise vortices—A device for improving heat exchanger design. J. Heat Transf. 1994, 116, 588–597. [Google Scholar] [CrossRef]
- Biswas, G.; Mitra, N.K.; Fiebig, M. Heat transfer enhancement in fin-tube heat exchangers by winglet type vortex generators. Int. J. Heat Mass Transf. 1994, 37, 283–291. [Google Scholar] [CrossRef]
- Deb, P.; Biswas, G.; Mitra, N.K. Heat transfer and flow structure in laminar and turbulent flows in a rectangular channel with longitudinal vortices. Int. J. Heat Mass Transf. 1995, 38, 2427–2444. [Google Scholar] [CrossRef]
- Biswas, G.; Torii, K.; Fujii, D.; Nishino, K. Numerical and experimental determination of flow structure and heat transfer effects of longitudinal vortices in a channel flow. Int. J. Heat Mass Transf. 1996, 39, 3441–3451. [Google Scholar] [CrossRef]
- Vasudevan, R.; Eswaran, V.; Biswas, G. Winglet-type vortex generators for plate-fin heat exchangers using triangular fins. Numer. Heat Transf. Part A Appl. 2000, 38, 533–555. [Google Scholar]
- Chen, Y.; Fiebig, M.; Mitra, N.K. Heat transfer enhancement of finned oval tubes with staggered punched longitudinal vortex generators. Int. J. Heat Mass Transf. 2000, 43, 417–435. [Google Scholar] [CrossRef]
- Davidson, A.S.L. Effect of inclined vortex generators on heat transfer enhancement in a three-dimensional channel. Numer. Heat Transf. Part A Appl. 2001, 39, 433–448. [Google Scholar] [CrossRef]
- Jain, A.; Biswas, G.; Maurya, D. Winglet-type vortex generators with common-flow-up configuration for fin-tube heat exchangers. Numer. Heat Transf. Part A Appl. 2003, 43, 201–219. [Google Scholar] [CrossRef]
- Prabhakar, V.; Biswas, G.; Eswaran, V. Numerical prediction of heat transfer in a channel with a built-in oval tube and various arrangements of the vortex generators. Numer. Heat Transf. Part A Appl. 2003, 44, 315–333. [Google Scholar] [CrossRef]
- Tiwari, S.; Maurya, D.; Biswas, G.; Eswaran, V. Heat transfer enhancement in cross-flow heat exchangers using oval tubes and multiple delta winglets. Int. J. Heat Mass Transf. 2003, 46, 2841–2856. [Google Scholar] [CrossRef]
- Leu, J.S.; Wu, Y.H.; Jang, J.Y. Heat transfer and fluid flow analysis in plate-fin and tube heat exchangers with a pair of block shape vortex generators. Int. J. Heat Mass Transf. 2004, 47, 4327–4338. [Google Scholar] [CrossRef]
- Sohankar, A. The LES and DNS simulations of heat transfer and fluid flow in a plate-fin heat exchanger with vortex generators. Iran. J. Sci. Technol. Trans. B 2004, 28, 443–452. [Google Scholar]
- Srikanth, J.; Biswas, G. Large eddy simulation of flow past built-in winglet-pair in a rectangular channel. Int. J. Fluid Mech. Res. 2005, 32, 310–326. [Google Scholar] [CrossRef]
- Ferrouillat, S.; Tochon, P.; Garnier, C.; Peerhossaini, H. Intensification of heat-transfer and mixing in multifunctional heat exchangers by artificially generated streamwise vorticity. Appl. Therm. Eng. 2006, 26, 1820–1829. [Google Scholar] [CrossRef]
- Sohankar, A. Heat transfer augmentation in a rectangular channel with a vee-shaped vortex generator. Int. J. Heat Fluid Flow 2007, 28, 306–317. [Google Scholar] [CrossRef]
- Wu, J.M.; Tao, W.Q. Investigation on laminar convection heat transfer in fin-and-tube heat exchanger in aligned arrangement with longitudinal vortex generator from the viewpoint of field synergy principle. Appl. Therm. Eng. 2007, 27, 2609–2617. [Google Scholar] [CrossRef]
- Joardar, A.; Jacobi, A.M. A numerical study of flow and heat transfer enhancement using an array of delta-winglet vortex generators in a fin-and-tube heat exchanger. J. Heat Transf. 2007, 129, 1156–1167. [Google Scholar] [CrossRef]
- Wu, J.M.; Tao, W.Q. Numerical study on laminar convection heat transfer in a channel with longitudinal vortex generator. Part B: Parametric study of major influence factors. Int. J. Heat Mass Transf. 2008, 51, 3683–3692. [Google Scholar] [CrossRef]
- Song, K.W.; Wang, L.B.; Fan, J.F.; Zhang, Y.H.; Liu, S. Numerical study of heat transfer enhancement of finned flat tube bank fin with vortex generators mounted on both surfaces of the fin. Heat Mass Transf. 2008, 44, 959–967. [Google Scholar] [CrossRef]
- Tang, L.H.; Zeng, M.; Wang, Q.W. Experimental and numerical investigation on air-side performance of fin-and-tube heat exchangers with various fin patterns. Exp. Therm. Fluid Sci. 2009, 33, 818–827. [Google Scholar] [CrossRef]
- Chang, L.M.; Wang, L.B.; Song, K.W.; Sun, D.L.; Fan, J.F. Numerical study of the relationship between heat transfer enhancement and absolute vorticity flux along main flow direction in a channel formed by a flat tube bank fin with vortex generators. Int. J. Heat Mass Transf. 2009, 52, 1794–1801. [Google Scholar] [CrossRef]
- Tian, L.; He, Y.; Tao, Y.; Tao, W. A comparative study on the air-side performance of wavy fin-and-tube heat exchanger with punched delta winglets in staggered and in-line arrangements. Int. J. Therm. Sci. 2009, 48, 1765–1776. [Google Scholar] [CrossRef]
- Tian, L.T.; He, Y.L.; Lei, Y.G.; Tao, W.Q. Numerical study of fluid flow and heat transfer in a flat-plate channel with longitudinal vortex generators by applying field synergy principle analysis. Int. Commun. Heat Mass Transf. 2009, 36, 111–120. [Google Scholar] [CrossRef]
- Chu, P.; He, Y.L.; Tao, W.Q. Three-dimensional numerical study of flow and heat transfer enhancement using vortex generators in fin-and-tube heat exchangers. J. Heat Transf. 2009, 131, 091903–9. [Google Scholar] [CrossRef]
- Chu, P.; He, Y.L.; Lei, Y.G.; Tian, L.T.; Li, R. Three-dimensional numerical study on fin-and-oval-tube heat exchanger with longitudinal vortex generators. Appl. Therm. Eng. 2009, 29, 859–876. [Google Scholar] [CrossRef]
- Lei, Y.G.; He, Y.L.; Tian, L.T.; Chu, P.; Tao, W.Q. Hydrodynamics and heat transfer characteristics of a novel heat exchanger with delta-winglet vortex generators. Chem. Eng. Sci. 2010, 65, 1551–1562. [Google Scholar] [CrossRef]
- Onishi, H.; Yonekura, H.; Tada, Y.; Takimoto, A. Heat transfer performance of finless flat tube heat exchanger with vortex generator. In Proceedings of the International Heat Transfer Conference, Washington, DC, USA, 8–13 August 2010; Volume 49392, pp. 799–807. [Google Scholar]
- Zeng, M.; Tang, L.H.; Lin, M.; Wang, Q.W. Optimization of heat exchangers with vortex-generator fin by Taguchi method. Appl. Therm. Eng. 2010, 30, 1775–1783. [Google Scholar] [CrossRef]
- Lemouedda, A.; Breuer, M.; Franz, E.; Botsch, T.; Delgado, A. Optimization of the angle of attack of delta-winglet vortex generators in a plate-fin-and-tube heat exchanger. Int. J. Heat Mass Transf. 2010, 53, 5386–5399. [Google Scholar] [CrossRef]
- Wu, J.M.; Tao, W.Q. Impact of delta winglet vortex generators on the performance of a novel fin-tube surfaces with two rows of tubes in different diameters. Energy Convers. Manag. 2011, 52, 2895–2901. [Google Scholar] [CrossRef]
- Aris, M.S.; McGlen, R.; Owen, I.; Sutcliffe, C.J. An experimental investigation into the deployment of 3-D, finned wing and shape memory alloy vortex generators in a forced air convection heat pipe fin stack. Appl. Therm. Eng. 2011, 31, 2230–2240. [Google Scholar] [CrossRef]
- Hwang, S.W.; Kim, D.H.; Min, J.K.; Jeong, J.H. CFD analysis of fin tube heat exchanger with a pair of delta winglet vortex generators. J. Mech. Sci. Technol. 2012, 26, 2949–2958. [Google Scholar] [CrossRef]
- Pal, A.; Bandyopadhyay, D.; Biswas, G.; Eswaran, V. Enhancement of heat transfer using delta-winglet type vortex generators with a common-flow-up arrangement. Numer. Heat Transf. Part A Appl. 2012, 61, 912–928. [Google Scholar]
- He, Y.L.; Han, H.; Tao, W.Q.; Zhang, Y.W. Numerical study of heat-transfer enhancement by punched winglet-type vortex generator arrays in fin-and-tube heat exchangers. Int. J. Heat Mass Transf. 2012, 55, 5449–5458. [Google Scholar] [CrossRef]
- He, Y.L.; Chu, P.; Tao, W.Q.; Zhang, Y.W.; Xie, T. Analysis of heat transfer and pressure drop for fin-and-tube heat exchangers with rectangular winglet-type vortex generators. Appl. Therm. Eng. 2013, 61, 770–783. [Google Scholar] [CrossRef]
- Sinha, A.; Raman, K.A.; Chattopadhyay, H.; Biswas, G. Effects of different orientations of winglet arrays on the performance of plate-fin heat exchangers. Int. J. Heat Mass Transf. 2013, 57, 202–214. [Google Scholar] [CrossRef]
- Huisseune, H.; T’Joen, C.; De Jaeger, P.; Ameel, B.; De Schampheleire, S.; De Paepe, M. Influence of the louver and delta winglet geometry on the thermal hydraulic performance of a compound heat exchanger. Int. J. Heat Mass Transf. 2013, 57, 58–72. [Google Scholar] [CrossRef]
- Huisseune, H.; T’joen, C.; De Jaeger, P.; Ameel, B.; De Schampheleire, S.; De Paepe, M. Performance enhancement of a louvered fin heat exchanger by using delta winglet vortex generators. Int. J. Heat Mass Transf. 2013, 56, 475–487. [Google Scholar] [CrossRef]
- Song, K.W.; Wang, L.B. The effectiveness of secondary flow produced by vortex generators mounted on both surfaces of the fin to enhance heat transfer in a flat tube bank fin heat exchanger. J. Heat Transf. 2013, 135, 041902. [Google Scholar] [CrossRef]
- Hu, W.L.; Song, K.W.; Guan, Y.; Chang, L.M.; Liu, S.; Wang, L.B. Secondary flow intensity determines Nusselt number on the fin surfaces of circle tube bank fin heat exchanger. Int. J. Heat Mass Transf. 2013, 62, 620–631. [Google Scholar] [CrossRef]
- Jang, J.Y.; Hsu, L.F.; Leu, J.S. Optimization of the span angle and location of vortex generators in a plate-fin and tube heat exchanger. Int. J. Heat Mass Transf. 2013, 67, 432–444. [Google Scholar] [CrossRef]
- Saha, P.; Biswas, G.; Sarkar, S. Comparison of winglet-type vortex generators periodically deployed in a plate-fin heat exchanger–A synergy based analysis. Int. J. Heat Mass Transf. 2014, 74, 292–305. [Google Scholar] [CrossRef]
- Wu, X.; Zhang, W.; Gou, Q.; Luo, Z.; Lu, Y. Numerical simulation of heat transfer and fluid flow characteristics of composite fin. Int. J. Heat Mass Transf. 2014, 75, 414–424. [Google Scholar] [CrossRef]
- Zhao, X.B.; Tang, G.H.; Ma, X.W.; Jin, Y.; Tao, W.Q. Numerical investigation of heat transfer and erosion characteristics for H-type finned oval tube with longitudinal vortex generators and dimples. Appl. Energy 2014, 127, 93–104. [Google Scholar] [CrossRef]
- Lin, Z.M.; Wang, L.B. A multi-domain coupled numerical method for a flat tube bank fin heat exchanger with delta-winglet vortex generators. Numer. Heat Transf. Part A Appl. 2014, 65, 1204–1229. [Google Scholar] [CrossRef]
- Gong, B.; Wang, L.B.; Lin, Z.M. Heat transfer characteristics of a circular tube bank fin heat exchanger with fins punched curve rectangular vortex generators in the wake regions of the tubes. Appl. Therm. Eng. 2015, 75, 224–238. [Google Scholar] [CrossRef]
- Li, L.; Du, X.; Zhang, Y.; Yang, L.; Yang, Y. Numerical simulation on flow and heat transfer of fin-and-tube heat exchanger with longitudinal vortex generators. Int. J. Therm. Sci. 2015, 92, 85–96. [Google Scholar] [CrossRef]
- Lin, Z.M.; Liu, C.P.; Lin, M.; Wang, L.B. Numerical study of flow and heat transfer enhancement of circular tube bank fin heat exchanger with curved delta-winglet vortex generators. Appl. Therm. Eng. 2015, 88, 198–210. [Google Scholar] [CrossRef]
- Behfard, M.; Sohankar, A. Numerical investigation for finding the appropriate design parameters of a fin-and-tube heat exchanger with delta-winglet vortex generators. Heat Mass Transf. 2016, 52, 21–37. [Google Scholar] [CrossRef]
- Sinha, A.; Chattopadhyay, H.; Iyengar, A.K.; Biswas, G. Enhancement of heat transfer in a fin-tube heat exchanger using rectangular winglet type vortex generators. Int. J. Heat Mass Transf. 2016, 101, 667–681. [Google Scholar] [CrossRef]
- Song, K.; Wang, L. Effects of longitudinal vortex interaction on periodically developed flow and heat transfer of fin-and-tube heat exchanger. Int. J. Therm. Sci. 2016, 109, 206–216. [Google Scholar] [CrossRef]
- Oneissi, M.; Habchi, C.; Russeil, S.; Bougeard, D.; Lemenand, T. Novel design of delta winglet pair vortex generator for heat transfer enhancement. Int. J. Therm. Sci. 2016, 109, 1–9. [Google Scholar] [CrossRef]
- Tang, L.H.; Tan, S.C.; Gao, P.Z.; Zeng, M. Parameters optimization of fin-and-tube heat exchanger with a novel vortex generator fin by Taguchi method. Heat Transf. Eng. 2016, 37, 369–381. [Google Scholar] [CrossRef]
- Esmaeilzadeh, A.; Amanifard, N.; Deylami, H.M. Comparison of simple and curved trapezoidal longitudinal vortex generators for optimum flow characteristics and heat transfer augmentation in a heat exchanger. Appl. Therm. Eng. 2017, 125, 1414–1425. [Google Scholar] [CrossRef]
- Sarangi, S.K.; Mishra, D.P. Effect of winglet location on heat transfer of a fin-and-tube heat exchanger. Appl. Therm. Eng. 2017, 116, 528–540. [Google Scholar] [CrossRef]
- Chimres, N.; Wang, C.C.; Wongwises, S. Effect of elliptical winglet on the air-side performance of fin-and-tube heat exchanger. Int. J. Heat Mass Transf. 2018, 123, 583–599. [Google Scholar] [CrossRef]
- Song, K.; Tagawa, T. The optimal arrangement of vortex generators for best heat transfer enhancement in flat-tube-fin heat exchanger. Int. J. Therm. Sci. 2018, 132, 355–367. [Google Scholar] [CrossRef]
- Abdelatief, M.A.; Sayed Ahmed, S.A.E.; Mesalhy, O.M. Experimental and numerical study on thermal-hydraulic performance of wing-shaped-tubes-bundle equipped with winglet vortex generators. Heat Mass Transf. 2018, 54, 727–744. [Google Scholar] [CrossRef]
- Chamoli, S.; Lu, R.; Xu, D.; Yu, P. Thermal performance improvement of a solar air heater fitted with winglet vortex generators. Sol. Energy 2018, 159, 966–983. [Google Scholar] [CrossRef]
- Han, Z.; Xu, Z.; Wang, J. Numerical simulation on heat transfer characteristics of rectangular vortex generators with a hole. Int. J. Heat Mass Transf. 2018, 126, 993–1001. [Google Scholar] [CrossRef]
- Naik, H.; Harikrishnan, S.; Tiwari, S. Numerical investigations on heat transfer characteristics of curved rectangular winglet placed in a channel. Int. J. Therm. Sci. 2018, 129, 489–503. [Google Scholar] [CrossRef]
- Zeeshan, M.; Nath, S.; Bhanja, D. Determination of optimum winglet height of longitudinal vortex generators for the best thermo-hydraulic performance of compact heat exchangers. J. Mech. Sci. Technol. 2019, 33, 4529–4534. [Google Scholar] [CrossRef]
- Lu, G.; Zhai, X. Effects of curved vortex generators on the air-side performance of fin-and-tube heat exchangers. Int. J. Therm. Sci. 2019, 136, 509–518. [Google Scholar] [CrossRef]
- Luo, C.; Wu, S.; Song, K.; Hua, L.; Wang, L. Thermo-hydraulic performance optimization of wavy fin heat exchanger by combining delta winglet vortex generators. Appl. Therm. Eng. 2019, 163, 114343. [Google Scholar] [CrossRef]
- Song, K.; Tagawa, T.; Chen, Z.; Zhang, Q. Heat transfer characteristics of concave and convex curved vortex generators in the channel of plate heat exchanger under laminar flow. Int. J. Therm. Sci. 2019, 137, 215–228. [Google Scholar] [CrossRef]
- Tang, S.Z.; Wang, F.L.; He, Y.L.; Yu, Y.; Tong, Z.X. Parametric optimization of H-type finned tube with longitudinal vortex generators by response surface model and genetic algorithm. Appl. Energy 2019, 239, 908–918. [Google Scholar] [CrossRef]
- Bjerg, A.; Christoffersen, K.; Sørensen, H.; Hærvig, J. Flow structures and heat transfer in repeating arrangements of staggered rectangular winglet pairs by Large Eddy Simulations: Effect of winglet height and longitudinal pitch distance. Int. J. Heat Mass Transf. 2019, 131, 654–663. [Google Scholar] [CrossRef]
- Jeong, M.; Ha, M.Y.; Park, Y.G. Numerical investigation of heat transfer enhancement in a dimpled cooling channel with different angles of the vortex generator. Int. J. Heat Mass Transf. 2019, 144, 118644. [Google Scholar] [CrossRef]
- Zhang, L.; Yan, X.; Zhang, Y.; Feng, Y.; Li, Y.; Meng, H.; Zhang, J.; Wu, J. Heat transfer enhancement by streamlined winglet pair vortex generators for helical channel with rectangular cross section. Chem. Eng. Process. Process Intensif. 2020, 147, 107788. [Google Scholar] [CrossRef]
- Sun, Z.; Zhang, K.; Li, W.; Chen, Q.; Zheng, N. Investigations of the turbulent thermal-hydraulic performance in circular heat exchanger tubes with multiple rectangular winglet vortex generators. Appl. Therm. Eng. 2020, 168, 114838. [Google Scholar] [CrossRef]
- Gupta, A.; Roy, A.; Gupta, S.; Gupta, M. Numerical investigation towards implementation of punched winglet as vortex generator for performance improvement of a fin-and-tube heat exchanger. Int. J. Heat Mass Transf. 2020, 149, 119171. [Google Scholar] [CrossRef]
- Modi, A.J.; Kalel, N.A.; Rathod, M.K. Thermal performance augmentation of fin-and-tube heat exchanger using rectangular winglet vortex generators having circular punched holes. Int. J. Heat Mass Transf. 2020, 158, 119724. [Google Scholar] [CrossRef]
- Oh, Y.; Kim, K. Effects of position and geometry of curved vortex generators on fin-tube heat-exchanger performance characteristics. Appl. Therm. Eng. 2021, 189, 116736. [Google Scholar] [CrossRef]
- Promvonge, P.; Promthaisong, P.; Skullong, S. Numerical heat transfer in a solar air heater duct with punched delta-winglet vortex generators. Case Stud. Therm. Eng. 2021, 26, 101088. [Google Scholar] [CrossRef]
- Shi, W.; Liu, T.; Song, K.; Zhang, Q.; Hu, W.; Wang, L. The optimal longitudinal location of curved winglets for better thermal performance of a finned-tube heat exchanger. Int. J. Therm. Sci. 2021, 167, 107035. [Google Scholar] [CrossRef]
- Naik, H.; Tiwari, S. Thermal performance analysis of fin-tube heat exchanger with staggered tube arrangement in presence of rectangular winglet pairs. Int. J. Therm. Sci. 2021, 161, 106723. [Google Scholar] [CrossRef]
- Naik, H.; Tiwari, S.; Kim, H.D. Flow and thermal characteristics produced by a curved rectangular winglet vortex generator in a channel. Int. Commun. Heat Mass Transf. 2022, 135, 106103. [Google Scholar] [CrossRef]
- Pérez, R.B.; Pérez, A.M.; Suárez, D.S. Influence of the punched holes on thermohydraulic performance and flow pattern of rectangular channels with a pair of perforated vortex generators. Int. J. Heat Mass Transf. 2022, 184, 122291. [Google Scholar] [CrossRef]
- Pérez, A.M.; Altamirano, C.F.A.; Pérez, R.B. Parametric analysis of the influence of geometric variables of vortex generators on compact louver fin heat exchangers. Therm. Sci. Eng. Prog. 2022, 27, 101151. [Google Scholar] [CrossRef]
- Sharma, R.; Mishra, D.P.; Wasilewski, M.; Brar, L.S. Application of Response Surface Methodology and Artificial Neural Network to Optimize the Curved Trapezoidal Winglet Geometry for Enhancing the Performance of a Fin-and-Tube Heat Exchanger. Energies 2023, 16, 4209. [Google Scholar] [CrossRef]
- Saini, P.; Dhar, A.; Powar, S. Performance enhancement of fin and tube heat exchanger employing curved trapezoidal winglet vortex generator with circular punched holes. Int. J. Heat Mass Transf. 2023, 209, 124142. [Google Scholar] [CrossRef]
- Saini, P.; Dhar, A.; Powar, S. Performance enhancement of fin and tube heat exchanger employing curved delta winglet vortex generator with circular punched holes. Int. J. Thermofluids 2023, 20, 100452. [Google Scholar] [CrossRef]
- Hu, D.; Zhang, Q.; Song, K.; Gao, C.; Zhang, K.; Su, M.; Wang, L. Performance optimization of a wavy finned-tube heat exchanger with staggered curved vortex generators. Int. J. Therm. Sci. 2023, 183, 107830. [Google Scholar] [CrossRef]
- Feng, Y.; Xu, R.; Cao, Y.; Wu, X.; Liang, C.; Zhang, L. Optimization of H-type finned tube heat exchangers with combinations of longitudinal vortex generator, dimples/protrusions and grooves by Taguchi method. Int. Commun. Heat Mass Transf. 2023, 143, 106709. [Google Scholar] [CrossRef]
- Garimella, S.V.; Eibeck, P.A. Enhancement of single phase convective heat transfer from protruding elements using vortex generators. Int. J. Heat Mass Transf. 1991, 34, 2431–2433. [Google Scholar] [CrossRef]
- Fiebig, M.; Kallweit, P.; Mitra, N.; Tiggelbeck, S. Heat transfer enhancement and drag by longitudinal vortex generators in channel flow. Exp. Therm. Fluid Sci. 1991, 4, 103–114. [Google Scholar] [CrossRef]
- Tiggelbeck, S.; Mitra, N.; Fiebig, M. Flow structure and heat transfer in a channel with multiple longitudinal vortex generators. Exp. Therm. Fluid Sci. 1992, 5, 425–436. [Google Scholar] [CrossRef]
- Mitra, N.K.; Fiebig, M. Experimental investigations of heat transfer enhancement and flow losses in a channel with double rows of longitudinal vortex generators. Int. J. Heat Mass Transf. 1993, 36, 2327–2337. [Google Scholar]
- Fiebig, M.; Valencia, A.; Mitra, N.K. Wing-type vortex generators for fin-and-tube heat exchangers. Exp. Therm. Fluid Sci. 1993, 7, 287–295. [Google Scholar] [CrossRef]
- Tiggelbeck, S.; Mitra, N.K.; Fiebig, M. Comparison of wing-type vortex generators for heat transfer enhancement in channel flows. J. Heat Transf. 1994, 116, 880–885. [Google Scholar] [CrossRef]
- Fiebig, M.; Valencia, A.; Mitra, N.K. Local heat transfer and flow losses in fin-and-tube heat exchangers with vortex generators: A comparison of round and flat tubes. Exp. Therm. Fluid Sci. 1994, 8, 35–45. [Google Scholar] [CrossRef]
- Valencia, A.; Fiebig, M.; Mitra, N.K. Heat transfer enhancement by longitudinal vortices in a fin-tube heat exchanger element with flat tubes. J. Heat Transf. 1996, 118, 209–211. [Google Scholar] [CrossRef]
- Gentry, M.C.; Jacobi, A.M. Heat transfer enhancement by delta-wing vortex generators on a flat plate: Vortex interactions with the boundary layer. Exp. Therm. Fluid Sci. 1997, 14, 231–242. [Google Scholar] [CrossRef]
- KOTCİOĞLU, İ. Heat transfer and flow structure in a rectangular channel with wing-type vortex generator. Turk. J. Eng. Environ. Sci. 1998, 22, 185–196. [Google Scholar]
- Torii, K.; Kwak, K.M.; Nishino, K. Heat transfer enhancement accompanying pressure-loss reduction with winglet-type vortex generators for fin-tube heat exchangers. Int. J. Heat Mass Transf. 2002, 45, 3795–3801. [Google Scholar] [CrossRef]
- Kwak, K.; Torii, K.; Nishino, K. Heat transfer and flow characteristics of fin-tube bundles with and without winglet-type vortex generators. Exp. Fluids 2002, 33, 696–702. [Google Scholar] [CrossRef]
- Gentry, M.C.; Jacobi, A.M. Heat transfer enhancement by delta-wing-generated tip vortices in flat-plate and developing channel flows. J. Heat Transf. 2002, 124, 1158–1168. [Google Scholar] [CrossRef]
- Yoo, S.Y.; Park, D.S.; Chung, M.H.; Lee, S.Y. Heat transfer enhancement for fin-tube heat exchanger using vortex generators. KSME Int. J. 2002, 16, 109–115. [Google Scholar] [CrossRef]
- Yuan, Z.X.; Tao, W.Q.; Yan, X.T. Experimental study on heat transfer in ducts with winglet disturbances. Heat Transf. Eng. 2003, 24, 76–84. [Google Scholar] [CrossRef]
- Kwak, K.M.; Torii, K.; Nishino, K. Heat transfer and pressure loss penalty for the number of tube rows of staggered finned-tube bundles with a single transverse row of winglets. Int. J. Heat Mass Transf. 2003, 46, 175–180. [Google Scholar] [CrossRef]
- Chen, T.Y.; Shu, H.T. Flow structures and heat transfer characteristics in fan flows with and without delta-wing vortex generators. Exp. Therm. Fluid Sci. 2004, 28, 273–282. [Google Scholar] [CrossRef]
- O’Brien, J.E.; Sohal, M.S.; Wallstedt, P.C. Local heat transfer and pressure drop for finned-tube heat exchangers using oval tubes and vortex generators. J. Heat Transf. 2004, 126, 826–835. [Google Scholar] [CrossRef]
- Sommers, A.D.; Jacobi, A.M. Air-side heat transfer enhancement of a refrigerator evaporator using vortex generation. Int. J. Refrig. 2005, 28, 1006–1017. [Google Scholar] [CrossRef]
- Kwak, K.M.; Torii, K.; Nishino, K. Simultaneous heat transfer enhancement and pressure loss reduction for finned-tube bundles with the first or two transverse rows of built-in winglets. Exp. Therm. Fluid Sci. 2005, 29, 625–632. [Google Scholar] [CrossRef]
- Pesteei, S.M.; Subbarao, P.M.V.; Agarwal, R.S. Experimental study of the effect of winglet location on heat transfer enhancement and pressure drop in fin-tube heat exchangers. Appl. Therm. Eng. 2005, 25, 1684–1696. [Google Scholar] [CrossRef]
- Shi, B.; Wang, L.; Gen, F.; Zhang, Y. The optimal fin spacing for three-row flat tube bank fin mounted with vortex generators. Heat Mass Transf. 2006, 43, 91–101. [Google Scholar] [CrossRef]
- Allison, C.B.; Dally, B.B. Effect of a delta-winglet vortex pair on the performance of a tube–fin heat exchanger. Int. J. Heat Mass Transf. 2007, 50, 5065–5072. [Google Scholar] [CrossRef]
- Wang, Q.; Chen, Q.; Wang, L.; Zeng, M.; Huang, Y.; Xiao, Z. Experimental study of heat transfer enhancement in narrow rectangular channel with longitudinal vortex generators. Nucl. Eng. Des. 2007, 237, 686–693. [Google Scholar] [CrossRef]
- Joardar, A.; Jacobi, A.M. Heat transfer enhancement by winglet-type vortex generator arrays in compact plain-fin-and-tube heat exchangers. Int. J. Refrig. 2008, 31, 87–97. [Google Scholar] [CrossRef]
- Tang, L.H.; Min, Z.; Xie, G.N.; Wang, Q.W. Fin pattern effects on air-side heat transfer and friction characteristics of fin-and-tube heat exchangers with large number of large-diameter tube rows. Heat Transf. Eng. 2009, 30, 171–180. [Google Scholar] [CrossRef]
- Hernon, D.; Patten, N. Hotwire measurements downstream of a delta winglet pair at two angles of attack. In Proceedings of the Heat Transfer Summer Conference, San Francisco, CA, USA, 19–23 July 2009; Volume 43567, pp. 777–784. [Google Scholar]
- Yang, K.S.; Li, S.L.; Chen, Y.; Chien, K.H.; Hu, R.; Wang, C.C. An experimental investigation of air cooling thermal module using various enhancements at low Reynolds number region. Int. J. Heat Mass Transf. 2010, 53, 5675–5681. [Google Scholar] [CrossRef]
- Promvonge, P.; Chompookham, T.; Kwankaomeng, S.; Thianpong, C. Enhanced heat transfer in a triangular ribbed channel with longitudinal vortex generators. Energy Convers. Manag. 2010, 51, 1242–1249. [Google Scholar] [CrossRef]
- Chompookham, T.; Thianpong, C.; Kwankaomeng, S.; Promvonge, P. Heat transfer augmentation in a wedge-ribbed channel using winglet vortex generators. Int. Commun. Heat Mass Transf. 2010, 37, 163–169. [Google Scholar] [CrossRef]
- Min, C.; Qi, C.; Kong, X.; Dong, J. Experimental study of rectangular channel with modified rectangular longitudinal vortex generators. Int. J. Heat Mass Transf. 2010, 53, 3023–3029. [Google Scholar] [CrossRef]
- Wu, J.M.; Tao, W.Q. Effect of longitudinal vortex generator on heat transfer in rectangular channels. Appl. Therm. Eng. 2012, 37, 67–72. [Google Scholar] [CrossRef]
- Zhou, G.; Ye, Q. Experimental investigations of thermal and flow characteristics of curved trapezoidal winglet type vortex generators. Appl. Therm. Eng. 2012, 37, 241–248. [Google Scholar] [CrossRef]
- Wu, J.M.; Zhang, H.; Yan, C.H.; Wang, Y. Experimental study on the performance of a novel fin-tube air heat exchanger with punched longitudinal vortex generator. Energy Convers. Manag. 2012, 57, 42–48. [Google Scholar] [CrossRef]
- Du, X.; Feng, L.; Yang, Y.; Yang, L. Experimental study on heat transfer enhancement of wavy finned flat tube with longitudinal vortex generators. Appl. Therm. Eng. 2013, 50, 55–62. [Google Scholar] [CrossRef]
- Caliskan, S. Experimental investigation of heat transfer in a channel with new winglet-type vortex generators. Int. J. Heat Mass Transf. 2014, 78, 604–614. [Google Scholar] [CrossRef]
- Khoshvaght-Aliabadi, M.; Sartipzadeh, O.; Alizadeh, A. An experimental study on vortex-generator insert with different arrangements of delta-winglets. Energy 2015, 82, 629–639. [Google Scholar] [CrossRef]
- Khoshvaght-Aliabadi, M.; Zangouei, S.; Hormozi, F. Performance of a plate-fin heat exchanger with vortex-generator channels: 3D-CFD simulation and experimental validation. Int. J. Therm. Sci. 2015, 88, 180–192. [Google Scholar] [CrossRef]
- Wang, C.C.; Chen, K.Y.; Liaw, J.S.; Tseng, C.Y. An experimental study of the air-side performance of fin-and-tube heat exchangers having plain, louver, and semi-dimple vortex generator configuration. Int. J. Heat Mass Transf. 2015, 80, 281–287. [Google Scholar] [CrossRef]
- Deshmukh, P.W.; Prabhu, S.V.; Vedula, R.P. Heat transfer enhancement for laminar flow in tubes using curved delta wing vortex generator inserts. Appl. Therm. Eng. 2016, 106, 1415–1426. [Google Scholar] [CrossRef]
- Sawhney, J.S.; Maithani, R.; Chamoli, S. Experimental investigation of heat transfer and friction factor characteristics of solar air heater using wavy delta winglets. Appl. Therm. Eng. 2017, 117, 740–751. [Google Scholar] [CrossRef]
- Wu, X.; Lin, Z.M.; Liu, S.; Su, M.; Wang, L.C.; Wang, L.B. Experimental study on the effects of fin pitches and tube diameters on the heat transfer and fluid flow characteristics of a fin punched with curved delta-winglet vortex generators. Appl. Therm. Eng. 2017, 119, 560–572. [Google Scholar] [CrossRef]
- Xu, Y.; Islam, M.D.; Kharoua, N. Experimental study of thermal performance and flow behaviour with winglet vortex generators in a circular tube. Appl. Therm. Eng. 2018, 135, 257–268. [Google Scholar] [CrossRef]
- Zhai, C.; Islam, M.D.; Simmons, R.; Barsoum, I. Heat transfer augmentation in a circular tube with delta winglet vortex generator pairs. Int. J. Therm. Sci. 2019, 140, 480–490. [Google Scholar] [CrossRef]
- Dogan, M.; Igci, A.A. An experimental comparison of delta winglet and novel type vortex generators for heat transfer enhancement in a rectangular channel and flow visualization with stereoscopic PIV. Int. J. Heat Mass Transf. 2021, 164, 120592. [Google Scholar] [CrossRef]
- Zhang, G.; Liu, J.; Sundén, B.; Xie, G. Combined experimental and numerical studies on flow characteristic and heat transfer in ribbed channels with vortex generators of various types and arrangements. Int. J. Therm. Sci. 2021, 167, 107036. [Google Scholar] [CrossRef]
- Berber, A.; Gürdal, M.; Yetimoğlu, M. Experimental study on the heat transfer enhancement in a rectangular channel with curved winglets. Exp. Heat Transf. 2022, 35, 797–817. [Google Scholar] [CrossRef]
- Modi, A.J.; Rathod, M.K. Experimental investigation of heat transfer enhancement and pressure drop of fin-and-circular tube heat exchangers with modified rectangular winglet vortex generator. Int. J. Heat Mass Transf. 2022, 189, 122742. [Google Scholar] [CrossRef]
- Dogan, M.; Erzincan, S. Experimental investigation of thermal performance of novel type vortex generator in rectangular channel. Int. Commun. Heat Mass Transf. 2023, 144, 106785. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D.; Romero, N.C. SOLA: A Numerical Solution Algorithm for Transient Fluid Flows; No. LA-5852; Los Alamos National Lab.(LANL): Los Alamos, NM, USA, 1975. [Google Scholar]
- Harlow, F.H.; Welch, J.E. Numerical calculation of time-dependent viscous incompressible flow of fluid with free surface. Phys. Fluids 1965, 8, 2182. [Google Scholar] [CrossRef]
- Welch, J.E.; Harlow, F.H.; Shannon, J.P.; Daly, B.J. The MAC Method—A Computing Technique for Solving Viscous, Incompressible, Transient Fluid-Flow Problems Involving Free Surfaces; No. LA-3425; Los Alamos National Lab.(LANL): Los Alamos, NM, USA, 1965. [Google Scholar]
- Versteeg, H.K. An Introduction to Computational Fluid Dynamics the Finite Volume Method, 2/E; Pearson Education India: Noida, India, 2007. [Google Scholar]
- Anderson, D.; Tannehill, J.C.; Pletcher, R.H.; Munipalli, R.; Shankar, V. Computational Fluid Mechanics and Heat Transfer; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Moin, P.; Mahesh, K. Direct numerical simulation: A tool in turbulence research. Annu. Rev. Fluid Mech. 1998, 30, 539–578. [Google Scholar] [CrossRef]
- Roache, P.J. Verification and Validation in Computational Science and Engineering; Hermosa: Albuquerque, NM, USA, 1998; Volume 895, p. 895. [Google Scholar]
- Aris, M.S.; Owen, I.; Sutcliffe, C.J. The application of shape memory alloy as vortex generators and flow control devices for enhanced convective heat transfer. In Proceedings of the Fluids Engineering Division Summer Meeting, San Diego, CA, USA, 30 July–2 August 2007; Volume 42886, pp. 1465–1470. [Google Scholar]
- Vilarrubí, M.; Morell, G.; Rosell, J.; Fréchette, L.G.; Barrau, J. Experimental characterization of a self-adaptive shape memory alloy cooling approach to regulate temperature under varying heat loads. Int. J. Heat Mass Transf. 2019, 139, 632–640. [Google Scholar] [CrossRef]
- Chu, X.; You, H.; Tang, X.; Zhou, W.; Li, X.; Yuan, D.; Zhou, S. Smart microchannel heat exchanger based on the adaptive deformation effect of shape memory alloys. Energy Convers. Manag. 2021, 250, 114910. [Google Scholar] [CrossRef]
- Regany, D.; Majós, F.; Barrau, J.; Rosell, J.; Ibáñez, M.; Fréchette, L.G.; Vilarrubí, M. Design and test of shape memory alloy fins for self-adaptive liquid cooling device. Appl. Therm. Eng. 2022, 206, 118010. [Google Scholar] [CrossRef]
- Wang, B.; Deng, H.; Li, L.A.; Li, H. Design and test of smart heat exchanger based on shape memory alloys. Appl. Therm. Eng. 2023, 221, 119911. [Google Scholar] [CrossRef]
- Li, L.A.; Deng, H.; Li, H.; Wang, J.; Wang, B.; Huang, Y. Shape memory alloys enabled smart heat exchangers. Appl. Therm. Eng. 2023, 224, 120067. [Google Scholar] [CrossRef]
- Tan, Y.; Ni, Y.; Xu, W.; Xie, Y.; Li, L.; Tan, D. Key technologies and development trends of the soft abrasive flow finishing method. J. Zhejiang Univ. Sci. A 2023, 24, 1043–1064. [Google Scholar] [CrossRef]
- Meier, C.; Penny, R.W.; Zou, Y.; Gibbs, J.S.; Hart, A.J. Thermophysical phenomena in metal additive manufacturing by selective laser melting: Fundamentals, modeling, simulation, and experimentation. Annu. Rev. Heat Transf. 2017, 20, 241–316. [Google Scholar] [CrossRef]
- Zhang, X.; Yocom, C.J.; Mao, B.; Liao, Y. Microstructure evolution during selective laser melting of metallic materials: A review. J. Laser Appl. 2019, 31, 031201. [Google Scholar] [CrossRef]
- Mishra, A.K.; Kumar, A. Numerical and experimental analysis of the effect of volumetric energy absorption in powder layer on thermal-fluidic transport in selective laser melting of Ti6Al4V. Opt. Laser Technol. 2019, 111, 227–239. [Google Scholar] [CrossRef]
- Razavykia, A.; Brusa, E.; Delprete, C.; Yavari, R. An overview of additive manufacturing technologies—A review to technical synthesis in numerical study of selective laser melting. Materials 2020, 13, 3895. [Google Scholar] [CrossRef]
- Gong, H.; Rafi, K.; Gu, H.; Starr, T.; Stucker, B. Analysis of defect generation in Ti–6Al–4V parts made using powder bed fusion additive manufacturing processes. Addit. Manuf. 2014, 1, 87–98. [Google Scholar] [CrossRef]
- Galati, M.; Iuliano, L. A literature review of powder-based electron beam melting focusing on numerical simulations. Addit. Manuf. 2018, 19, 1–20. [Google Scholar] [CrossRef]
- Vyavahare, S.; Teraiya, S.; Panghal, D.; Kumar, S. Fused deposition modelling: A review. Rapid Prototyp. J. 2020, 26, 176–201. [Google Scholar] [CrossRef]
- Wang, S.; Ma, Y.; Deng, Z.; Zhang, S.; Cai, J. Effects of fused deposition modeling process parameters on tensile, dynamic mechanical properties of 3D printed polylactic acid materials. Polym. Test. 2020, 86, 106483. [Google Scholar] [CrossRef]
- Shanmugam, V.; Pavan, M.V.; Babu, K.; Karnan, B. Fused deposition modeling based polymeric materials and their performance: A review. Polym. Compos. 2021, 42, 5656–5677. [Google Scholar] [CrossRef]
- Xu, X.; Ren, H.; Chen, S.; Luo, X.; Zhao, F.; Xiong, Y. Review on melt flow simulations for thermoplastics and their fiber reinforced composites in fused deposition modeling. J. Manuf. Process. 2023, 92, 272–286. [Google Scholar] [CrossRef]
- Kumar, S.; Singh, H.; Singh, I.; Bharti, S.; Kumar, D.; Siebert, G.; Koloor, S.S.R. A comprehensive review of FDM printing in sensor applications: Advancements and future perspectives. J. Manuf. Process. 2024, 113, 152–170. [Google Scholar] [CrossRef]
- Tientcheu, S.W.T.; Djouda, J.M.; Bouaziz, M.A.; Lacazedieu, E. A review on fused deposition modeling materials with analysis of key process parameters influence on mechanical properties. Int. J. Adv. Manuf. Technol. 2024, 130, 2119–2158. [Google Scholar] [CrossRef]
- Casavola, C.; Cazzato, A.; Moramarco, V.; Pappalettere, C. Orthotropic mechanical properties of fused deposition modelling parts described by classical laminate theory. Mater. Des. 2016, 90, 453–458. [Google Scholar] [CrossRef]
- Mishra, P.K.; Senthil, P. Prediction of in-plane stiffness of multi-material 3D printed laminate parts fabricated by FDM process using CLT and its mechanical behaviour under tensile load. Mater. Today Commun. 2020, 23, 100955. [Google Scholar] [CrossRef]
- Zhang, W.; Cotton, C.; Sun, J.; Heider, D.; Gu, B.; Sun, B.; Chou, T.W. Interfacial bonding strength of short carbon fiber/acrylonitrile-butadiene-styrene composites fabricated by fused deposition modeling. Compos. Part B Eng. 2018, 137, 51–59. [Google Scholar] [CrossRef]
- Yin, J.; Lu, C.; Fu, J.; Huang, Y.; Zheng, Y. Interfacial bonding during multi-material fused deposition modeling (FDM) process due to inter-molecular diffusion. Mater. Des. 2018, 150, 104–112. [Google Scholar] [CrossRef]
- Gao, X.; Qi, S.; Zhang, D.; Su, Y.; Wang, D. The role of poly (ethylene glycol) on crystallization, interlayer bond and mechanical performance of polylactide parts fabricated by fused filament fabrication. Addit. Manuf. 2020, 35, 101414. [Google Scholar] [CrossRef]
- Lepoivre, A.; Boyard, N.; Levy, A.; Sobotka, V. Methodology to assess interlayer quality in the material extrusion process: A temperature and adhesion prediction on a high performance polymer. Addit. Manuf. 2022, 60, 103167. [Google Scholar] [CrossRef]
- Xu, P.; Li, Q.; Wang, C.; Li, L.; Tan, D.; Wu, H. Interlayer healing mechanism of multipath deposition 3D printing models and interlayer strength regulation method. J. Manuf. Process. 2025, 141, 1031–1047. [Google Scholar] [CrossRef]
- Bendsøe, M.P.; Kikuchi, N. Generating optimal topologies in structural design using a homogenization method. Comput. Methods Appl. Mech. Eng. 1988, 71, 197–224. [Google Scholar] [CrossRef]
- Borrvall, T.; Petersson, J. Topology optimization of fluids in Stokes flow. Int. J. Numer. Methods Fluids 2003, 41, 77–107. [Google Scholar] [CrossRef]
- Gersborg-Hansen, A.; Sigmund, O.; Haber, R.B. Topology optimization of channel flow problems. Struct. Multidiscip. Optim. 2005, 30, 181–192. [Google Scholar] [CrossRef]
- Gersborg-Hansen, A.; Bendsøe, M.P.; Sigmund, O. Topology optimization of heat conduction problems using the finite volume method. Struct. Multidiscip. Optim. 2006, 31, 251–259. [Google Scholar] [CrossRef]
- Bruns, T.E. Topology optimization of convection-dominated, steady-state heat transfer problems. Int. J. Heat Mass Transf. 2007, 50, 2859–2873. [Google Scholar] [CrossRef]
- Iga, A.; Nishiwaki, S.; Izui, K.; Yoshimura, M. Topology optimization for thermal conductors considering design-dependent effects, including heat conduction and convection. Int. J. Heat Mass Transf. 2009, 52, 2721–2732. [Google Scholar] [CrossRef]
- Koga, A.A.; Lopes, E.C.C.; Nova, H.F.V.; De Lima, C.R.; Silva, E.C.N. Development of heat sink device by using topology optimization. Int. J. Heat Mass Transf. 2013, 64, 759–772. [Google Scholar] [CrossRef]
- Matsumori, T.; Kondoh, T.; Kawamoto, A.; Nomura, T. Topology optimization for fluid–thermal interaction problems under constant input power. Struct. Multidiscip. Optim. 2013, 47, 571–581. [Google Scholar] [CrossRef]
- Yaji, K.; Yamada, T.; Kubo, S.; Izui, K.; Nishiwaki, S. A topology optimization method for a coupled thermal–fluid problem using level set boundary expressions. Int. J. Heat Mass Transf. 2015, 81, 878–888. [Google Scholar] [CrossRef]
- Yoon, G.H. Topology optimization for turbulent flow with Spalart–Allmaras model. Comput. Methods Appl. Mech. Eng. 2016, 303, 288–311. [Google Scholar] [CrossRef]
- Dilgen, S.B.; Dilgen, C.B.; Fuhrman, D.R.; Sigmund, O.; Lazarov, B.S. Density based topology optimization of turbulent flow heat transfer systems. Struct. Multidiscip. Optim. 2018, 57, 1905–1918. [Google Scholar] [CrossRef]
- Zhao, X.; Zhou, M.; Sigmund, O.; Andreasen, C.S. A “poor man’s approach” to topology optimization of cooling channels based on a Darcy flow model. Int. J. Heat Mass Transf. 2018, 116, 1108–1123. [Google Scholar] [CrossRef]
- Haertel, J.H.; Engelbrecht, K.; Lazarov, B.S.; Sigmund, O. Topology optimization of a pseudo 3D thermofluid heat sink model. Int. J. Heat Mass Transf. 2018, 121, 1073–1088. [Google Scholar] [CrossRef]
- Liu, A.; Wang, G.; Wang, D.; Peng, X.; Yuan, H. Study on the thermal and hydraulic performance of fin-and-tube heat exchanger based on topology optimization. Appl. Therm. Eng. 2021, 197, 117380. [Google Scholar] [CrossRef]
- Zeng, S.; Kanargi, B.; Lee, P.S. Experimental and numerical investigation of a mini channel forced air heat sink designed by topology optimization. Int. J. Heat Mass Transf. 2018, 121, 663–679. [Google Scholar] [CrossRef]
- Sun, C.; Lewpiriyawong, N.; Khoo, K.L.; Zeng, S.; Lee, P.S. Thermal enhancement of fin and tube heat exchanger with guiding channels and topology optimisation. Int. J. Heat Mass Transf. 2018, 127, 1001–1013. [Google Scholar] [CrossRef]
- Kobayashi, H.; Yaji, K.; Yamasaki, S.; Fujita, K. Freeform winglet design of fin-and-tube heat exchangers guided by topology optimization. Appl. Therm. Eng. 2019, 161, 114020. [Google Scholar] [CrossRef]
- Berber, A.; Guerdal, M. Estimation of forced heat convection in a rectangular channel with curved-winglet vortex generator: A machine learning approach. Therm. Sci. Eng. Prog. 2023, 37, 101563. [Google Scholar] [CrossRef]
- Kang, M.S.; Park, S.G.; Dinh, C.T. Heat transfer enhancement by a pair of asymmetric flexible vortex generators and thermal performance prediction using machine learning algorithms. Int. J. Heat Mass Transf. 2023, 200, 123518. [Google Scholar] [CrossRef]
- Wu, W.; Wang, Y.; Zhao, L.; Dong, H. Optimization of microchannel heat sinks with flexible vortex generators using GWO-SVR: A CFD and machine learning approach. Int. Commun. Heat Mass Transf. 2025, 164, 108900. [Google Scholar] [CrossRef]
- Xie, C.; Yan, G.; Ma, Q.; Elmasry, Y.; Singh, P.K.; Algelany, A.M.; Wae-hayee, M. Flow and heat transfer optimization of a fin-tube heat exchanger with vortex generators using Response Surface Methodology and Artificial Neural Network. Case Stud. Therm. Eng. 2022, 39, 102445. [Google Scholar] [CrossRef]
- Liang, X.; Kumar, N.B.; Mansir, I.B.; Singh, P.K.; Abed, A.M.; Dahari, M.; Nasr, S.; Albalawi, H.; Cherif, A.; Wae-Hayee, M. Management of heat transfer and hydraulic characteristics of a micro-channel heat sink with various arrangements of rectangular vortex generators utilizing artificial neural network and response surface methodology. Case Stud. Therm. Eng. 2023, 44, 102850. [Google Scholar] [CrossRef]
- Li, Z.; Feng, Z.; Zhang, Q.; Zhou, J.; Zhang, J.; Guo, F. Thermal-hydraulic performance and multi-objective optimization using ANN and GA in microchannels with double delta-winglet vortex generators. Int. J. Therm. Sci. 2023, 193, 108489. [Google Scholar] [CrossRef]
- Seal, M.K.; Abadi, S.N.R.; Mehrabi, M.; Meyer, J.P. Machine learning classification of in-tube condensation flow patterns using visualization. Int. J. Multiph. Flow 2021, 143, 103755. [Google Scholar] [CrossRef]
- Ren, F.; Zhang, F.; Zhu, Y.; Wang, Z.; Zhao, F. Enhancing heat transfer from a circular cylinder undergoing vortex induced vibration based on reinforcement learning. Appl. Therm. Eng. 2024, 236, 121919. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).