Abstract
This study investigates the influence of modifications in the geometry of the blades—specifically, the introduction of a gap blade into the impeller blades—on the hydraulic performance of a low specific speed centrifugal pump. The research addresses the problem of efficiency losses in such pumps and explores whether implementing a blade gap can improve energy characteristics without altering the primary flow path. A set of impellers with different gap configurations was designed and manufactured using 3D printing. Experimental tests were carried out on a laboratory test rig equipped with standard pressure, flow, and power measurement instruments. Next, numerical simulations were performed using CFD methods in Ansys CFX, using the k-ω SST turbulence model. The results show that impellers with gap blades achieved higher efficiency—up to 4 percentage points compared to the reference design—and an increase in the maximum pump capacity. CFD analysis confirmed more uniform velocity distributions and reduced separation zones in the interscapular channels, along with a smoother pressure gradient across the blade surfaces. The results demonstrate that modifying impeller geometry using gap blades can improve hydraulic efficiency and expand the range of stable operation. These conclusions support further research on performance optimisation in low-specific-speed centrifugal pumps.
1. Introduction
Pumps constitute the largest group of machines used in industry, second only to electric motors in terms of applications [1,2]. In 2000, industrial energy consumption in European countries amounted to approximately 951 TWh, of which up to 65% was attributable to electrical machinery, with pumps playing a dominant role [3]. In Europe, pumps account for about 22% of total electricity consumption [2]. In Poland, annual pump energy consumption is estimated at 32 TWh, representing approximately 20% of the country’s total electricity production [4]. Consequently, reducing the energy consumption in pumping processes has become a significant issue. This can be achieved through the appropriate selection of new pumps combined with suitable control systems or by improving the efficiency of existing units. In both cases, it is crucial to match the pump characteristics to the varying demands of the system and, thus, to different operating points.
1.1. Losses in Centrifugal Pumps
Among centrifugal pumps, the most commonly used type is the radial-flow centrifugal pump [1], designed for flow rates greater than 10 m3/h and specific speed values above 15 (nq > 15). These pumps account for approximately 80% of all pump applications [3]. During operation, centrifugal pumps are subject to various losses that affect their performance. Understanding the mechanisms responsible for these losses is essential for analysing the efficiency and energy performance of such machines.
Power losses in centrifugal pumps are the result of leakage, flow resistance, and friction in mechanical components [5,6]. Volumetric losses are associated with seal leakages; hydraulic losses are due to flow resistance, and mechanical losses, including disk friction losses, arise from the movement of rotating parts [5,6]. In pumps with a low kinematic specific speed nq, defined by Equation (1) according to Troskolanski [7]:
where
- n-rotational speed (rpm);
- Q-flow rate (m3/s);
- H-head (m).
Moreover, disk friction losses and volumetric losses dominate. A diameter ratio d2/d1 greater than 2 significantly increases mechanical losses (ΔPt ~ ω3 d25), while a decrease in nq increases the pressure differential across the seals, leading to higher leakage rates [8]. For nq = 10, disk friction losses can account for up to 50% of total power, whereas for nq = 30 they decrease to about 5% [8]. Hydraulic losses tend to increase as the size of the pump decreases, whereas mechanical losses depend on the overall dimensions of the pump [8]. In pumps with nq = 13.4, the main sources of losses are liquid drainage (34%) and the front chamber of the impeller (29%), collectively accounting for 63% [9]. Losses within the impeller and seals contribute the remaining 37%, while losses in the volute depend on the operating [9]. In addition to experimental studies, Computational Fluid Dynamics (CFD) methods are increasingly used to evaluate losses and optimize pump designs for improved energy efficiency [9].
Due to the efficiency drop caused by increasing disk friction and volumetric losses [5,6], the design of low-specific-speed pumps with acceptable efficiency levels remains a major challenge. Therefore, improving the efficiency and operational stability of low-speed centrifugal pumps is an important area of ongoing research [10,11].
A key aspect is the adaptation of the pump characteristics to the requirements of the system, which directly affects its energy efficiency. Modern methods are being explored to enhance pump performance, such as impeller outer surface structure, trim of the impeller blade trailing edge, or the application of gap blades.
1.2. Novelty Methods to Increase Efficiency of Centrifugal Pumps
In modern centrifugal pumps, microgeometry modifications are applied to reduce energy losses. Bieganowski et al. [12] demonstrated that an appropriate selection of the microgroove geometry in the impeller channels can increase the head and efficiency without altering the main impeller geometry. Sosnowski et al. [13] reported that trimming the trailing edge of the impeller blade reduces flow resistance, thus improving efficiency under load conditions. CFD analysis by Gangipamula et al. [14] confirmed that impeller trimming reduces pressure pulsations by 10.3% and lowers hydraulic noise by 2 dB, while additional tongue trimming increases flow instability and acoustic pressure. Skrzypacz et al. [15] showed that surface structuring of the outer faces of the impeller disks, through the application of surface indentations, reduces disk friction losses and improves efficiency, particularly at low flow rates. In subsequent sections, the use of gap blades is discussed as an additional method to improve the efficiency of centrifugal pumps.
1.3. Application of Splitter Blades in Rotating Machinery
A gap blade is a modified form of a classical impeller blade used in turbomachinery, featuring an intentional gap or discontinuity in the blade profile. This gap can vary in length, width, and position, and its geometry can be selected according to the type of machine, flow conditions, and specific design objectives. Splitter blades are classified as passive flow control solutions, which means that they do not have moving parts and that their primary function is to modify the flow structure within the interscapular channel.
The introduction of splitter blades in turbomachinery, such as centrifugal pumps, axial compressors, and fans, aims to improve flow characteristics and increase machine efficiency. One of the main objectives of implementing a splitter blade is to reduce adverse flow phenomena such as boundary layer separation, flow detachment, cavitation, or pressure fluctuations. The presence of the gap enables a more uniform velocity distribution within the interscapular channel and reduces local hydraulic loads, leading to more stable operation and lower energy losses. The applications of splitter blades in rotating machinery are summarised and described in Table 1.

Table 1.
Application of split blades in rotor machines.
1.4. Gap Blades in Impellers of Centrifugal Pumps
Studies on the application of gaps in the blades of rotating machinery, summarised in Table 1, have demonstrated the potential to improve performance and reduce starting power requirements. This method, previously successfully implemented in fans and compressors, has also been introduced in centrifugal pumps. Calculations involving various gap parameters, based on optimisation methods, showed that their impact on efficiency depends on both the operating conditions and the gap geometry.
The study [28] presents a centrifugal pump with a specific speed ns = 85 (in SI units nq = 23.34) with blades with a slot structure. Numerical simulations and experimental tests were performed for 16 different slot geometries, covering variations in position, width, depth, and angle of inclination. The best results were obtained for a configuration with a narrow slot (0.5 mm), a depth equal to one quarter of the width of the blade, and a deviation angle of 30°. Under low-flow conditions (0.6Q), the head increased from 38.5 m to 39.3 m, while under high-flow conditions (1.4Q), the efficiency improved from 77.09% to 77.86%. The application of the slot structure improved the pressure and velocity distributions within the interscapular channel, reducing backflow and increasing overall efficiency.
Another study [29] analysed a low-specific-speed centrifugal pump with ns = 55 (in SI units nq = 15.17), focusing on the optimization of slot geometry on the impeller blades. Using an orthogonal experimental design L16(45), five geometric parameters were investigated: slot diameter, mid-width, deviation angle, depth, and contraction ratio. Numerical simulations combined with the entropy-weighted TOPSIS method indicated that the optimal configuration consisted of a 200 mm slot diameter, 3 mm mid-width, 20° deviation angle, 6 mm depth, and a contraction ratio of 0.5. This con-figuration improved the total head from 24.13 m to 24.58 m and the hydraulic efficiency from 55.33% to 57.82%, confirming the potential of slotted blades to enhance pump performance by reducing internal flow losses.
A review of the literature indicates that in new designs of low-specific-speed pumps, the use of impellers with groove drain blades [30] and gap drainage blades [31] can potentially improve the energy efficiency of centrifugal pumps [30,31,32]. In the first approach [30], a groove is created that connects the suction and pressure sides of the blade. The authors suggest that the pressure difference across the groove drives a flow that supplies energy to the backflow region at the impeller inlet. The goal is to reduce the size of this region and decrease the risk of flow separation. This solution can also be combined with the application of splitter blades. In the second approach [31], by retracting the leading edge of the main blade and placing a shorter auxiliary blade in front of it, a gap is formed to control flow in the inlet zone. Within a specific speed range of 35 to 70, the efficiency of the pump equipped with a gap drainage impeller was higher compared to the traditional version. The critical net positive suction head value (NPSHc) was lower at all operating points, with a maximum difference of 0.37 m observed at a flow rate of 48 m3/h. The pump with a drainage impeller with a gap reached cavitation conditions at higher flow rates compared to the conventional design.
According to the literature, such modifications to the blade geometry can improve the hydraulic efficiency of low-speed centrifugal pumps. For example, in the study [32], it was shown that the use of a gap blade reduces the intensity of vortices that form at the leading edge, leading to a more ordered flow in the interscapular channel. Three impeller variants were analysed: without a gap, with a 1.5 mm gap, and with a 6 mm gap. Numerical and experimental studies showed that a 1.5 mm gap increased hydraulic efficiency to 28.62% (an improvement of 7.2 percentage points compared to the variant without a gap) with only a minor decrease in head by 0.11 m. For the 6 mm gap, efficiency increased only to 27%, and the head dropped by 2.47 m. However, the authors emphasized the need to properly match the gap dimensions to the machine’s geometric scale to avoid performance deterioration. The effectiveness of both concepts was initially evaluated through CFD simulations and was later supported by preliminary experimental tests [32].
In the article [33], the effect of gap drainage blades was investigated in a centrifugal pump with a specific speed of approximately SI units nq = 9.56. A classical impeller with continuous blades was compared to an impeller equipped with gap drainage blades. CFD calculations were performed using ANSYS CFX 2023 R1 with the k-ω SST turbulence model and the Rayleigh–Plesset cavitation model. At a cavitation number of σ = 0.178, the cavitation volume was smaller for the impeller with the gap. For a flow rate Q = 14 m3/h, a head H = 20 m, and a rotational speed of n = 1450 rpm, the efficiency reached 66.7%, which was higher than that of the impeller without gaps. The gap blades reduced the intensity of cavitation and improved flow stability. Studies confirmed that modifications to the blade gaps can enhance performance and expand the operating range of centrifugal pumps [33].
The research problem of this article focuses on the existing knowledge gaps related to the design and application of gaps in the impeller blades of low-speed centrifugal pumps. Although previous studies have included selected results from numerical and experimental analyses, they do not provide a comprehensive characterisation of the gap blade geometry that would clearly contribute to improving the performance parameters of low-specific-speed centrifugal pumps.
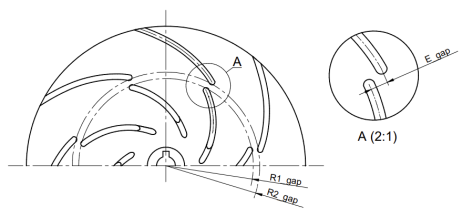
The aim of the preliminary research was to identify and verify the geometric variables that influence pump performance. These variables include the gap position radius (R1gap), the gap length (Lgap = |R1gap − R2gap|), and the gap width (Egap). The study was conducted based on a single-factor, completely randomized design (CRD) [34] with seven levels of the factor. The objective was to test the research hypothesis stating that the application of a gap in impeller blades positively affects the energy characteristics of a single-stage, low-specific-speed centrifugal pump.
This article presents the results of preliminary experimental and numerical investigations concerning the optimal positioning of the gap in the impeller blade.
2. Research Object
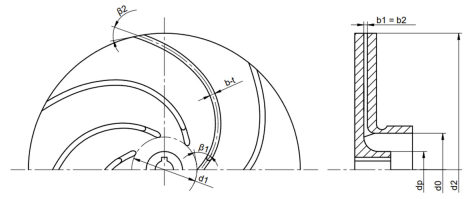
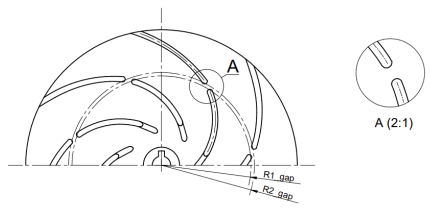
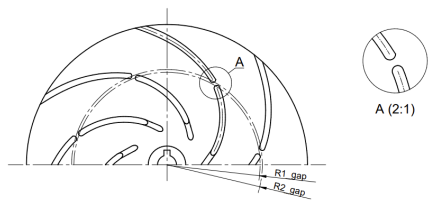
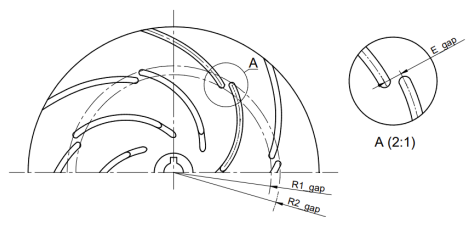
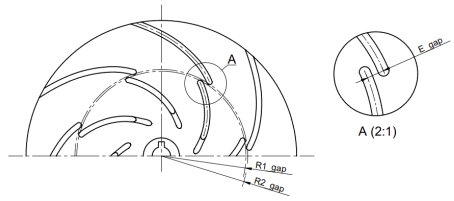
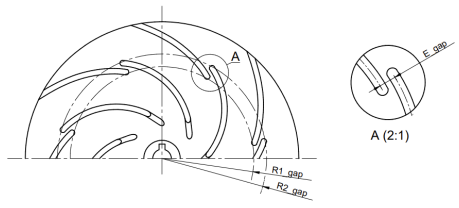
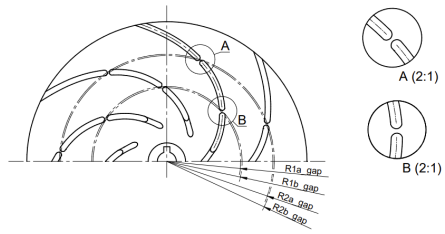
For the initial studies, an impeller with a specific speed nq = 12.68 (Q = 6.78 m3/h, H = 21.02 m, n = 2870 rpm) was selected, which was designed from scratch specifically for the experiment using Solid Edge 2023 software. The reference impeller is characterised by the following parameters: d2 = 150 mm, d1 = 36 mm, β1 = 45°, β2 =30°, and z = 7. Its modifications involved altering the geometry of the blade by introducing designated gaps. Several variants of gap positioning were prepared. One approach involved cutting the blade along its length, resulting in a larger gap (W1), a smaller gap (W2), and a double gap (W7). In these cases, the gap geometry is described by two parameters: R1gap and R2gap.
In addition, the impellers were designed with a gap formed by displacing part of the main blade to the pressure side (W3, W5) or the suction side (W4, W6), analysed from the inlet. In this case, the blade consists of two parts: the main and the secondary part, forming a gap defined by the parameters R1gap, Lgap, and Egap.
The impellers were manufactured using 3D printing technology based on the FDM (Fused Deposition Modelling) method, employing a Prusa MK3 printer (PrusaResearch, Prague, Czech Republic) and PLA (polylactide) material (Rosa3D, Gdansk, Poland), which enabled rapid prototyping. The shroud and hub of the impellers were bonded with cyanoacrylate adhesive and subsequently pressed together uniformly using a hydraulic press. All analysed geometric parameters, illustrative drawings, and photographs of the printed models are compiled in Table 2 and Table 3.

Table 2.
Geometric parameters of the impellers.

Table 3.
Geometry of the impellers.
Subsequently, comparative studies were conducted to determine the energy characteristics of the reference impeller (without a gap blade) and the modified impellers.
3. Methodology
The experimental investigations were carried out on a laboratory test rig designed to measure and analyse the performance characteristics of the pump. The test setup is equipped with appropriate sensors for pressure measurement (manometers on the suction and discharge sides of the pump), flow rate measurement (electromagnetic flowmeter), input power measurement (power transducer), and liquid temperature measurement (temperature sensor). The system also includes actuators and control devices, such as a three-phase inverter with integrated power measurement, electric rotary actuators on the suction and discharge lines, a three-phase motor, and a frequency converter. Table 4 presents the specifications of the measurement instruments used.

Table 4.
Characteristics of measuring instruments.
Throughout the experimental campaign, throttle control was applied to adjust and regulate pump operating conditions across the full operating range, with measurements performed on an automated test stand equipped with a computer-monitored control system to ensure consistent testing conditions. Data acquisition followed the procedures defined by the PN-EN ISO 9906:2012 standard, accuracy class 1 [35]. The setup of the test rig, the measurement methodology, and the evaluation of instrument accuracy are comprehensively explained in a separate publication [36]. A photograph of the test setup is shown in Figure 1.

Figure 1.
Measurement stand; 1—tank, 2—pump, 3—electric motor, 4—suction pressure sensor, 5—discharge pressure sensor, 6—control valve, 7—flow meter behind control cabinet.
4. Experimental Studies
Analysis of the head characteristics obtained H = f(Q) (Figure 2) indicates that the introduction of gaps in most of the cases analysed had a positive effect on increasing the pump head. Impellers W3, W4, and W7 exhibited significantly lower head values in the low flow rate range (up to approximately 6 m3/h) compared to the reference impeller W0; however, beyond this flow rate, they achieved higher head values. The head curves for all gapped impellers were also observed to be less steep compared to the curve for the reference impeller (W0).
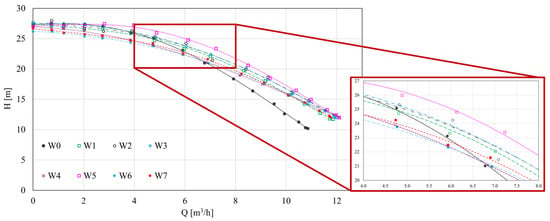
Figure 2.
Pump head characteristics.
When comparing the efficiency characteristics η = f(Q) (Figure 3), it was noted that all impellers with gaps exhibited higher efficiency than the reference impeller, particularly at flow rates greater than approximately 6 m3/h. The increase in efficiency was approximately 4% at the optimal flow rate (reference impeller efficiency η = 39.47%, gapped impeller efficiency η = 43.33%). Furthermore, both characteristics demonstrated an increase in the maximum pump capacity from approximately 11 m3/h to 12 m3/h. For the gapped impellers, the point of maximum efficiency shifted toward higher flow rates, and the efficiency peak became flatter.
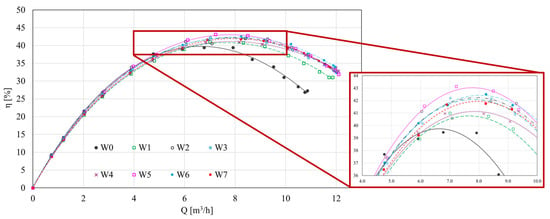
Figure 3.
Efficiency characteristics.
The power at the pump shaft curves Pw = f(Q) (Figure 4) show minimal differences between all tested impellers, including the reference design W0. The values of power at the pump shaft are nearly identical across the flow range, indicating that the observed improvements in hydraulic performance and efficiency for the gap blade variants result primarily from reduced hydraulic losses rather than increased power input. This suggests that the enhanced performance is due to better internal flow organization and lower energy dissipation rather than higher energy consumption.
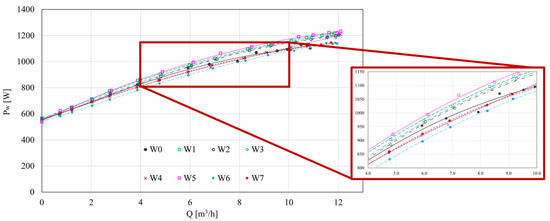
Figure 4.
Power at the pump shaft characteristics.
The results obtained at this stage allow for the identification of dependencies between the geometric variables. Preliminary research confirms the rationale for continuing investigations on this type of impeller design. The findings are very promising and suggest that a more detailed determination of the influence of gap geometry on energy characteristics will enable the development of design guidelines for low-specific-speed centrifugal pump impellers with improved flow parameters.
5. Numerical Simulations
Computational Fluid Dynamics (CFD) is an advanced numerical method used for the analysis of liquid and gas flows as well as heat transfer. Thanks to the growing computational capabilities, CFD has found wide application in the design and optimisation of flow devices, such as pumps. In the field of centrifugal pump research, CFD enables detailed analysis of internal flow conditions and evaluation of the influence of geometry on hydraulic characteristics.
In the present study, the computational model was divided into three separate domains: the suction pipe section, the volute casing, and the impeller (Figure 5). This division allows for the separation of stationary and rotating parts and facilitates the computation process. Flow information between domains was exchanged via appropriate interfaces. The computational mesh was generated using Ansys Meshing 2023 R1 software, creating unstructured tetrahedral elements. Wall layers were modelled using the Inflation function, with individual adjustments of parameters for each domain geometry.
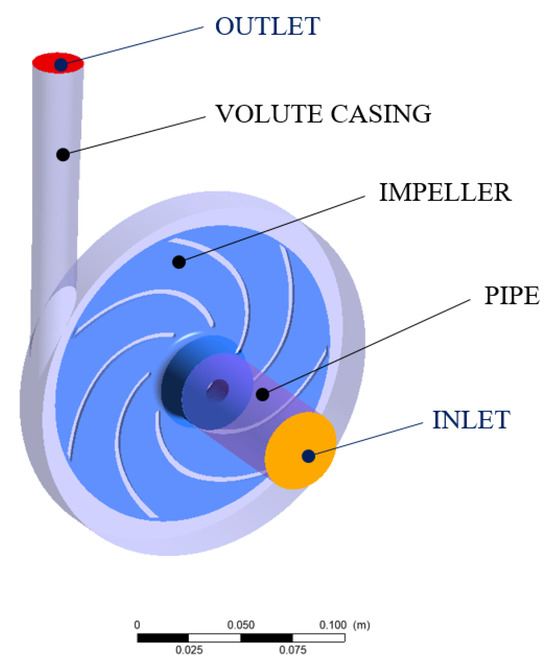
Figure 5.
Fluid bodies; boundary conditions.
Details regarding the applied meshes are summarised in Table 5. Numerical flow analysis through the centrifugal pump was carried out as a steady-state simulation. The Ansys CFX solver and the k-ω SST turbulence model were used due to their ability to accurately capture near-wall behaviour [37]. The convergence criteria for the calculations were set to 10−6. According to the given boundary conditions (reference pressure of 1 atm and optimum flow for a given rotor), the head and efficiency at the optimum point (BEP) were determined for the reference rotor W0 and selected rotor design solutions with gap blades: impeller with the best energy performance W5-gap blade formed by displacing part of the main blade to the pressure side (analysing from the inlet), W6-gap blade formed by displacing part of the main blade to the suction side (analysing from the inlet), and W7-impeller with double gap. The convergence of the calculated values of head and efficiency oscillates within 5% for W0 and W7 and 2% for W5 and W6.

Table 5.
Key specifications of the computational meshes.
Figure 6 presents the velocity contours (left-index 1) and velocity vectors (right-index 2) in the inter-blade channels of four impeller variants: (a) W0-reference impeller with continuous blades, (b) W5, (c) W6, and (d) W7-impellers with gap blades. Across all cases, the flow accelerates radially from the impeller inlet toward the outlet, consistent with the expected behaviour in radial-flow pumps. For the W0 configuration, the velocity field appears relatively uniform; however, noticeable recirculation zones and secondary flows develop near the suction side, particularly close to the blade leading edges. These disturbances indicate inefficient flow control and may lead to increased internal energy losses.
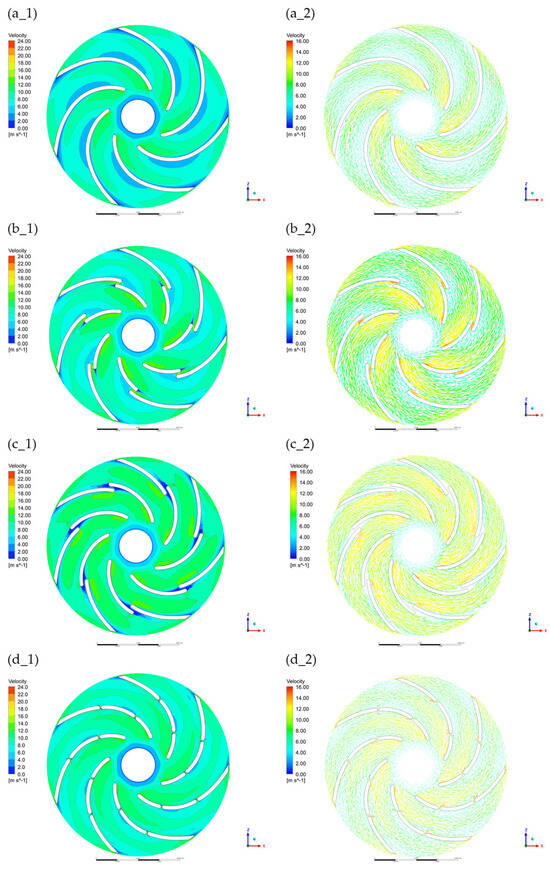
Figure 6.
Velocity distribution (index 1-left) and velocity vectors distribution (index 2-right); (a_1,a_2) W0-continuous blade, (b_1,b_2) W5, (c_1,c_2) W6, (d_1,d_2) W7-gap blade.
The W5 variant shows a distinctly more ordered distribution of velocity. Flow acceleration along the blade passages is consistent, with vectors remaining well aligned with the blade surfaces. Flow separation is largely suppressed, and the interaction between the main and secondary blades supports more coherent fluid motion. This efficient redirection of the streamlines results in lower turbulence and reduced hydraulic losses, correlating directly with the highest experimentally measured parameter performance in this group.
By contrast, impellers W6 and W7 exhibit less favourable characteristics. Although velocity magnitudes remain comparable, the vector fields show increased irregularities. In W6, regions of low momentum and reversed flow appear near the suction sides, while W7 presents scattered velocity directions, especially near the blade tips and exits. These flow instabilities contribute to greater energy dissipation and reduce the overall efficiency of the pumping process.
Overall, the velocity field analysis reinforces the experimental findings: configuration of the blade gap in W5 proceeds an advantageous interaction between the main and gap blades, enhancing flow uniformity and minimizing losses. As a result, W5 delivers the most effective energy transfer among all tested impellers.
Figure 7 shows the absolute pressure distribution in the impeller of the centrifugal pump. In all cases, the pressure increases from the inlet to the outlet, which is typical behaviour in radial-flow machines. In the W0 configuration (continuous blade), the pressure contours are more uniform and concentric, indicating a steady increase of pressure along the blade channel. However, the pressure difference between the pressure side and suction side of the blades is the highest in this case. This can lead to increased hydraulic loading on the blade surface and higher local pressure gradients, which are unfavourable from the perspective of minimizing energy losses and cavitation risk.
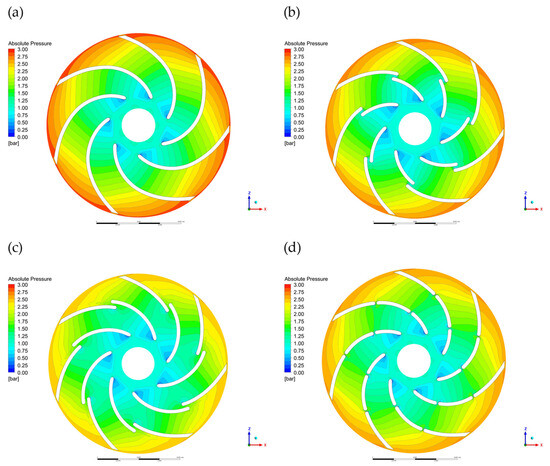
Figure 7.
Absolute pressure distribution: (a) W0-continuous blade, (b) W5, (c) W6, (d) W7-gap blade.
In impeller W5, the pressure distribution near the leading edge is less abrupt. The pressure gradient along the main blade is reduced compared to W0. The pressure on the suction side is also higher, indicating improved guidance of the working fluid and a more stable flow in this region. The low-pressure zones are smaller and less concentrated, which reduces the potential for cavitation. These features suggest better internal flow conditions and more efficient energy conversion within the impeller.
In impeller W6, the pressure field is similar to W5, but larger low-pressure areas appear near the inlet. The pressure gradient along the blade channel is steeper, and the suction side exhibits lower absolute pressure, which may promote local flow separation or cavitation. W7 shows the least favourable pressure distribution among the gap blade variants. The inlet region contains the largest low-pressure zones, and the pressure contours are less uniform, indicating disturbed flow conditions and possible increases in hydraulic losses.
Based on pressure distribution, impeller W5 offers the most favourable conditions, with reduced local gradients, improved suction side pressure, and minimized low-pressure areas.
The CFD simulations were conducted for four impeller designs: W0 (reference), W5, W6, and W7 (gap blade variants). The reference impeller W0 with continuous blades showed stable but less optimized internal flow, with clear signs of recirculation and high local pressure gradients near the suction side.
The W5 impeller, featuring a gap blade formed by shifting part of the main blade to the pressure side (viewed from the inlet), demonstrated the best parameter performance. The flow was more uniform, with reduced recirculation zones and a smoother pressure gradient near the leading edge. This resulted in improved energy conversion and higher hydraulic efficiency. The W6 impeller, where the blade gap was directed toward the suction side, showed increased low-pressure regions and less stable flow, with a higher risk of separation. The W7 impeller, with a double gap, exhibited the least improved flow structure, with scattered vectors and significant pressure non-uniformity near the inlet.
The application of the pressure-side gap blade (W5) improved the internal flow pattern and reduced losses, confirming its potential for performance optimization. Nevertheless, further experimental and numerical research is recommended—particularly in the context of model validation and assessment of long-term operating behaviour.
6. Conclusions
The article presents the results of preliminary research on the application of gap blades in a single-stage centrifugal pump with low specific speed. The aim was to determine how changes in the geometry and positioning of the blade gap influence the energy performance of the pump. The experimental and numerical analyses conducted allowed the evaluation of the influence of the selected gap geometry parameters on the pump energy characteristics, leading to the following conclusions:
- Head measurements showed that, above 6 m3/h, most gap blade configurations provided a higher head compared to the reference impeller—Figure 2. The power at the pump shaft (Figure 4) remained largely unchanged, indicating that the efficiency gains resulted primarily from reduced internal hydraulic losses.
- The most significant improvement—up to approximately 4 percentage points (from 39.47% for the reference impeller to 43.33% for the gap blade impeller)—was observed for the W5 variant, where the gap was introduced by shifting a part of the main blade toward the pressure side (viewed from the inlet)—Figure 3;
- The efficiency curves η(Q)—Figure 3, for all gap blade designs, were flatter than that of W0, and the best efficiency point (BEP) was shifted toward higher flow rates. This suggests an extended range of efficient operation and more stable performance at partial load conditions;
- Numerical simulations supported the experimental findings by showing that the W5 impeller generated a more uniform velocity field in the blade channels and reduced recirculation zones. Pressure contours also revealed a lower pressure gradient near the leading edge and a reduced pressure difference between the pressure and suction sides of the blade.
- Impellers W6 (gap toward the suction side) and W7 (double gap) showed less coherent flow patterns and larger low-pressure areas, which may increase the risk of cavitation and flow instabilities. These results were consistent across both experimental and CFD analyses.
- The combination of experimental testing and CFD confirmed that the W5 configuration offers the most advantageous hydraulic performance among all tested designs, thanks to improved flow guidance and pressure recovery.
Preliminary research results confirm the potential for optimisation of blade geometry modification through the use of gaps. They highlight the necessity of continuing work within the framework of fundamental research, particularly involving the validation of numerical models by comparison with extended experimental data and conducting higher-order experimental design studies to analyse the influence of gap geometry variables.
Author Contributions
Conceptualization, A.N.; methodology, A.N.; software, J.S.; validation, A.N.; formal analysis, A.N.; investigation, A.N. and P.S.; resources, J.S.; data curation, A.N., J.S. and P.S.; writing—original draft preparation, A.N.; writing—review and editing, J.S. and P.S.; visualization, A.N.; supervision, J.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available from the corresponding author upon reasonable request.
Acknowledgments
Created using resources provided by Wroclaw Centre for Networking and Supercomputing (http://wcss.pl).
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| Symbol | Name | Unit |
| b1 | impeller width at the inlet | mm |
| b2 | impeller width impeller width at the outlet | mm |
| d1 | impeller inlet diameter | mm |
| d2 | impeller outlet diameter | mm |
| Egap | gap width | mm |
| g | gravity acceleration | m/s2 |
| H | pump lifting height | m |
| Lgap | gap length | mm |
| M | total torque on the moving walls of the impeller | Nm |
| NPSH | net positive suction head | m |
| n | rotational speed | rpm |
| ns | kinematic specific speed factor, in USA units, (gpm, ft) | - |
| nq | kinematic specific speed factor, in SI units, (m3/s, m) | - |
| Pw | power input | W |
| Rgap | gap position radius | mm |
| Q | capacity | m3/h |
| T | temperature | °C |
| t | time | s |
| Greek Symbols | ||
| β | inflow angle, offset angle | ° |
| Δ | variability, difference | - |
| η | efficiency | - |
| μ | dynamic viscosity coefficient | Pa·s |
| ν | kinematic viscosity coefficient | m2/s |
| π | number, dimensionless variable | - |
| ρ | fluid density | kg/m3 |
| ω | angular velocity | rad/s |
| Subscripts | ||
| c | critical | - |
| CFD | Computational Fluid Dynamics, applies to results obtained using CFD | - |
| EXP | experimental | - |
| h | hydraulic | - |
| H2O | applies to water | - |
| i | next value | - |
| n | nominal | - |
| opt | optimal | - |
References
- The Pump Market Report; Resolute Research BV: Deventer, The Netherlands, 2017.
- Arun Shankar, V.K.; Umashankar, S.; Paramasivam, S.; Hanigovszki, N.A. Comprehensive Review on Energy Efficiency Enhancement Initiatives in Centrifugal Pumping System. Appl. Energy 2016, 181, 495–513. [Google Scholar] [CrossRef]
- Vogelesang, H. An Introduction to Energy Consumption in Pumps. World Pumps 2008, 496, 28–31. [Google Scholar] [CrossRef]
- Jędral, W. Efektywne Energetycznie Układy Pompowe; Oficyna Wydawnicza Politechniki Warszawskiej: Warszawa, Poland, 2018. [Google Scholar]
- Gülich, J.F. Centrifugal Pumps, 2nd ed.; Springer: New York, NY, USA, 2010. [Google Scholar]
- Jędral, W. Pompy Wirowe; Wydawnictwo Naukowe PWN: Warszawa, Poland, 2001. [Google Scholar]
- troskolański, T.A.; Łazarkiewicz, S.z. Pompy Wirowe; Państwowe Wydawnictwa Techniczne: Warszawa, Poland, 1973. [Google Scholar]
- Gülich, J.F. Disk Friction Losses of Closed Turbomachine Impellers. Forschung im Ingenieurwesen/Eng. Res. 2003, 68, 87–95. [Google Scholar] [CrossRef]
- Juckelandt, K.; Bleeck, S.; Wurm, F. H Analysis of Losses in Centrifugal Pumps with Low Specific Speed with Smooth and Rough Walls. In Proceedings of the 11th European Conference on Turbomachinery Fluid Dynamics & Thermodynamic, Madrid, Spain, 23–27 March 2015. [Google Scholar]
- Visser, F.C.; Brouwers, J.J.H.; Jonker, J.B. Fluid Flow in a Rotating Low-Specific-Speed Centrifugal Impeller Passage. Fluid. Dyn. Res. 1999, 24, 275–292. [Google Scholar] [CrossRef]
- Peng, G.; Hong, S.; Chang, H.; Fan, F.; Zhang, Y.; Shi, P. Numerical and Experimental Research on the Influence of Clearance Between Impeller and Cover on the Pump Performance. Mechanika 2022, 28, 67–72. [Google Scholar] [CrossRef]
- Bieganowski, M.; Skrzypacz, J.; Chomiuk, B. The Influence of the Geometry of Grooves on the Operating Parameters of the Impeller in a Centrifugal Pump with Microgrooves. Energies 2024, 17, 2807. [Google Scholar] [CrossRef]
- Sosnowski, M.; Skrzypacz, J.; Szulc, P. Wpływ ukształtowania krawędzi wylotowej wirnika na parametry energetyczne pompy. Kierunek Pompy 2024, 1/2024, 92–97. [Google Scholar]
- Gangipamula, R.; Ranjan, P.; Patil, R.S. Study on Fluid Dynamic Characteristics of a Low Specific Speed Centrifugal Pump with Emphasis on Trimming Operations. Int. J. Heat. Fluid. Flow. 2022, 95. [Google Scholar] [CrossRef]
- Skrzypacz, J.; Szulc, P.; Chomiuk, B.; Bieganowski, M.; Nycz, A. Strukturyzacja Powierzchni Zewnętrznych Wirnika. Kierunek Pompy 2025, 1/2025, 88–91. [Google Scholar]
- Qiu, X.; Dang, T. 3D Inverse Method for Turbomachine Blading with Splitter Blades. In Proceedings of the ASME Turbo Expo 2000: Power for Land, Sea, and Air, 2000-GT-0526, Munich, Germany, 8–11 May 2000. [Google Scholar]
- Pham, K.-Q.; Le, X.-T.; Dinh, C.-T. Effects of Stator Splitter Blades on Aerodynamic Performance of a Single-Stage Transonic Axial Compressor. J. Mech. Eng. Sci. 2020, 14, 7369–7378. [Google Scholar] [CrossRef]
- Heo, M.W.; Kim, J.H.; Kim, K.Y. Design Optimization of a Centrifugal Fan with Splitter Blades. Int. J. Turbo Jet Engines 2015, 32, 143–154. [Google Scholar] [CrossRef]
- Jang, C.M.; Choi, K.R.; Yang, S.H. Performance Analysis of a Centrifugal Fan with Splitters. Trans. Korean Soc. Mech. Eng. B 2011, 35, 1067–1073. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, H.; Xia, X.; Li, X.; Zuo, Q.; Xie, B.; Chen, W. Optimization of a Radial Inflow Turbine Rotor with Splitter Blades Based on Entropy Production Theory and Artificial Neural Network. Appl. Therm. Eng. 2024, 252, 123759. [Google Scholar] [CrossRef]
- Zhao, T.; Jiang, Z.; Mo, G.; Wang, G.J.; Gao, J. Control of Separation Flows of Turbine-Blade-Tip Turbines by Splitter Blades. Proc. Inst. Mech. Eng. Part A J. Power Energy 2024, 238, 985–998. [Google Scholar] [CrossRef]
- Chen, J.; Qu, H.; Li, P.; Li, Y.; Xie, Y.; Zhang, D. Numerical Study on Flow Separation Control for High-Lift Low-Pressure Turbine Split Blade. In Proceedings of the ASME 2013 Fluids Engineering Division Summer Meeting, Incline Village, NV, USA, 7–11 July 2013. proceeding paper: 13 December 2013. [Google Scholar] [CrossRef]
- Moshfeghi, M.; Hur, N. Power Generation Enhancement in a Horizontal Axis Wind Turbine Blade Using Split Blades. J. Wind. Eng. Ind. Aerodyn. 2020, 206, 104352. [Google Scholar] [CrossRef]
- Jia, Y.; Wei, X.; Wang, Q.; Cui, J.; Li, F. Experimental Study of the Effect of Splitter Blades on the Performance Characteristics of Francis Turbines. Energies 2019, 12, 1676. [Google Scholar] [CrossRef]
- Yang, S.; Kong, F.; Fu, J.; Xue, L. Numerical Research on Effects of Splitter Blades to the Influence of Pump as Turbine. Int. J. Rotating Mach. 2012, 2012, 1542–3034. [Google Scholar] [CrossRef]
- Bezdíček, J.; Chabannes, L.; Štefan, D. Effect of Splitter Blades on Turbine Mode of Low Specific Speed Pump. EPJ Web Conf. 2024, 299, 01003. [Google Scholar] [CrossRef]
- Xiao, W.; Chen, L.; Ren, S.; Yan, B.; Liu, Z.; Xiao, Y. Analysis of Pressure Fluctuation of a Pump-Turbine with Splitter Blades on Small Opening in Turbine Mode. Energies 2024, 17, 2967. [Google Scholar] [CrossRef]
- Wang, H.; Long, B.; Wang, C.; Han, C.; Li, L. Effects of the Impeller Blade with a Slot Structure on the Centrifugal Pump Performance. Energies 2020, 13, 1628. [Google Scholar] [CrossRef]
- Ke, Q.; Tang, L. Performance Optimization of Slotted Blades for Low-Specific Speed Centrifugal Pumps. Adv. Civil. Eng. 2023, 2023, 1–16. [Google Scholar] [CrossRef]
- Hongxun, C.; Weiwei, L.; Wen, J.; Peiru, W. Impellers of Low Specific Speed Centrifugal Pump Based on the Draughting Technology. IOP Conf. Ser. Earth Environ. Sci. 2010, 12, 012018. [Google Scholar] [CrossRef]
- Chen, H.; He, J.; Liu, C. Design and Experiment of the Centrifugal Pump Impellers with Twisted Inlet Vice Blades. J. Hydrodyn. 2017, 29, 1085–1088. [Google Scholar] [CrossRef]
- Wei, Y.; Yang, Y.; Zhou, L.; Jiang, L.; Shi, W.; Huang, G. Influence of Impeller Gap Drainage Width on the Performance of Low Specific Speed Centrifugal Pump. J. Mar. Sci. Eng. 2021, 9, 106. [Google Scholar] [CrossRef]
- Zhu, B.; Chen, H.X. Cavitating Suppression of Low Specific Speed Centrifugal Pump with Gap Drainage Blades. J. Hydrodyn. 2012, 24, 729–736. [Google Scholar] [CrossRef]
- Montgomery, D.C. Design and Analysis of Experiments, 8th ed.; John Wiley & Sons, Inc: Hoboken, NJ, USA, 2013; ISBN 9781118146927. [Google Scholar]
- EN ISO 9906:2012; Rotodynamic Pumps—Hydraulic Performance, Acceptance Tests—Grades 1, 2 and 3. International Organization for Standardization: Geneva, Switzerland, 2012.
- Skrzypacz, J. Numerical Modelling of Flow Phenomena in a Pump with a Multi-Piped Impeller. Chem. Eng. Process. Process Intensif. 2014, 75, 58–66. [Google Scholar] [CrossRef]
- Nycz, A.; Szulc, P.; Skrzypacz, J. Identyfikacja Zjawisk Przepływowych w Rurze Ssącej Średniobieżnej Turbiny Wodnej z Wykorzystaniem CFD. Rynek Energii 2024, 4, 64–73. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).