Rapid, Precise Parameter Optimization and Performance Prediction for Multi-Diode Photovoltaic Model Using Puma Optimizer
Abstract
1. Introduction
1.1. Contribution
1.2. Research Framework
- Collect experimental data from photovoltaic cells and modules.
- Develop multi-diode models to represent the behavior of photovoltaic cells and modules.
- Construct Puma Optimizer algorithm and the objective function.
- Comprehensively compare the search performance of the system with calculated results.
- Predict the performance and maximum power point of several photovoltaic systems under various temperature conditions.
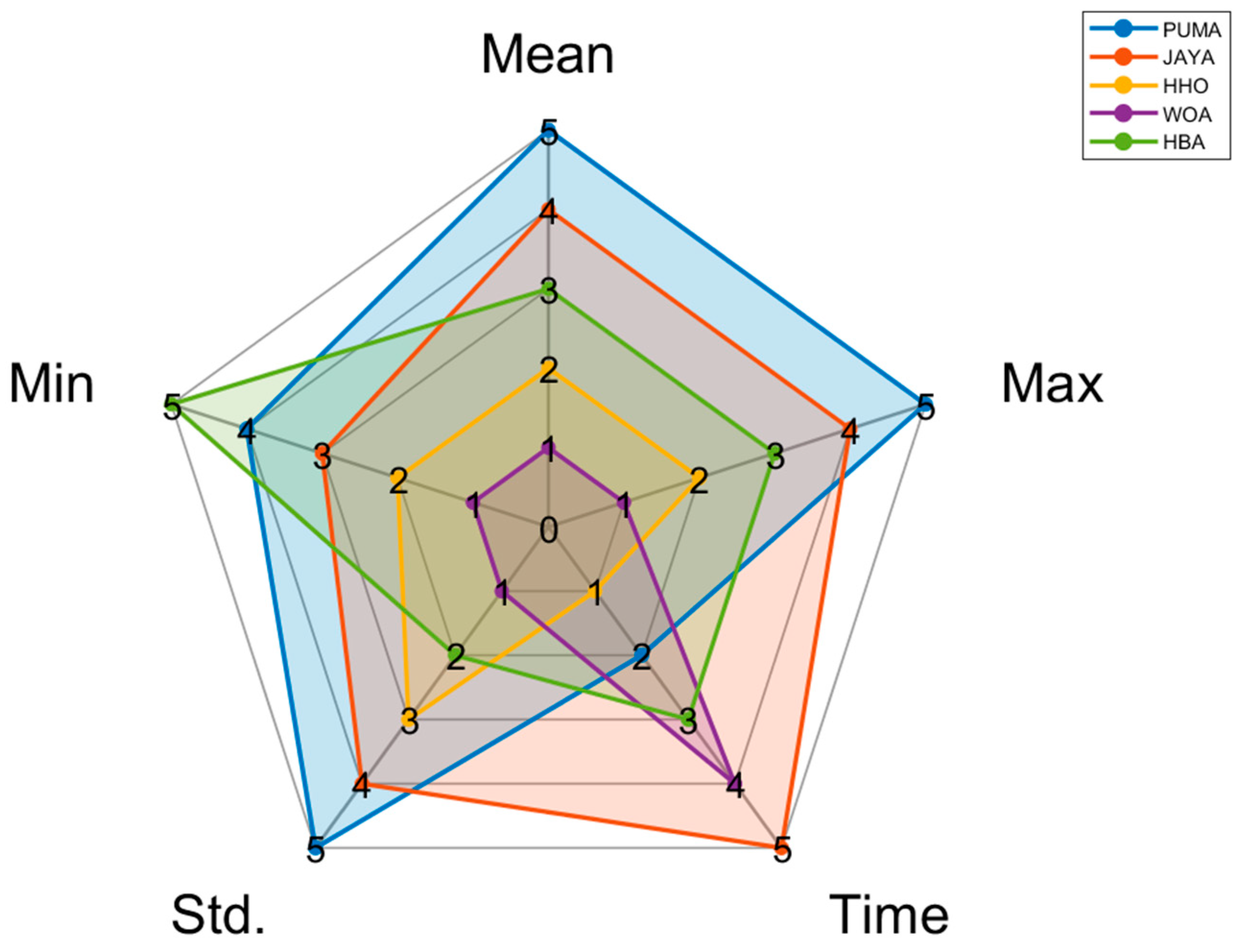
- Integrate the algorithm performance variables into a visual analysis using radar charts.
- Use a one-factor-at-a-time approach to analyze the sensitivity of system parameters.
2. Methodology
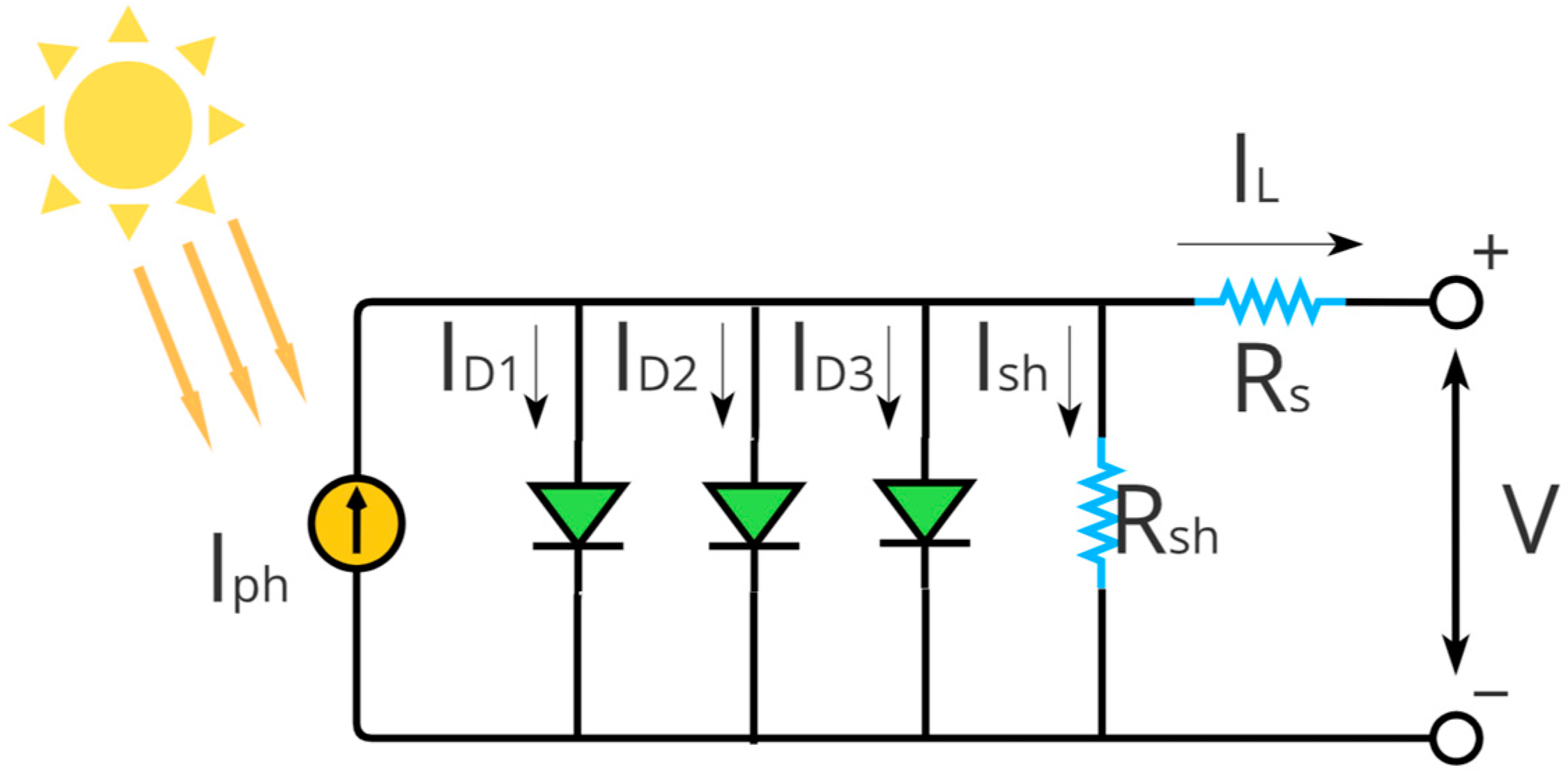
2.1. Photovoltaics Modeling
2.1.1. Single Diode Model
2.1.2. Double Diode Model
2.1.3. Triple Diode Model
2.1.4. Photovoltaic Module Model
2.2. Puma Optimizer
2.2.1. Initialization
2.2.2. Inexperienced Phase
2.2.3. Experienced Phase
2.2.4. Exploration Phase
2.2.5. Exploitation Phase
2.3. Objective Function
2.4. Parameter Setting
3. Results and Discussion
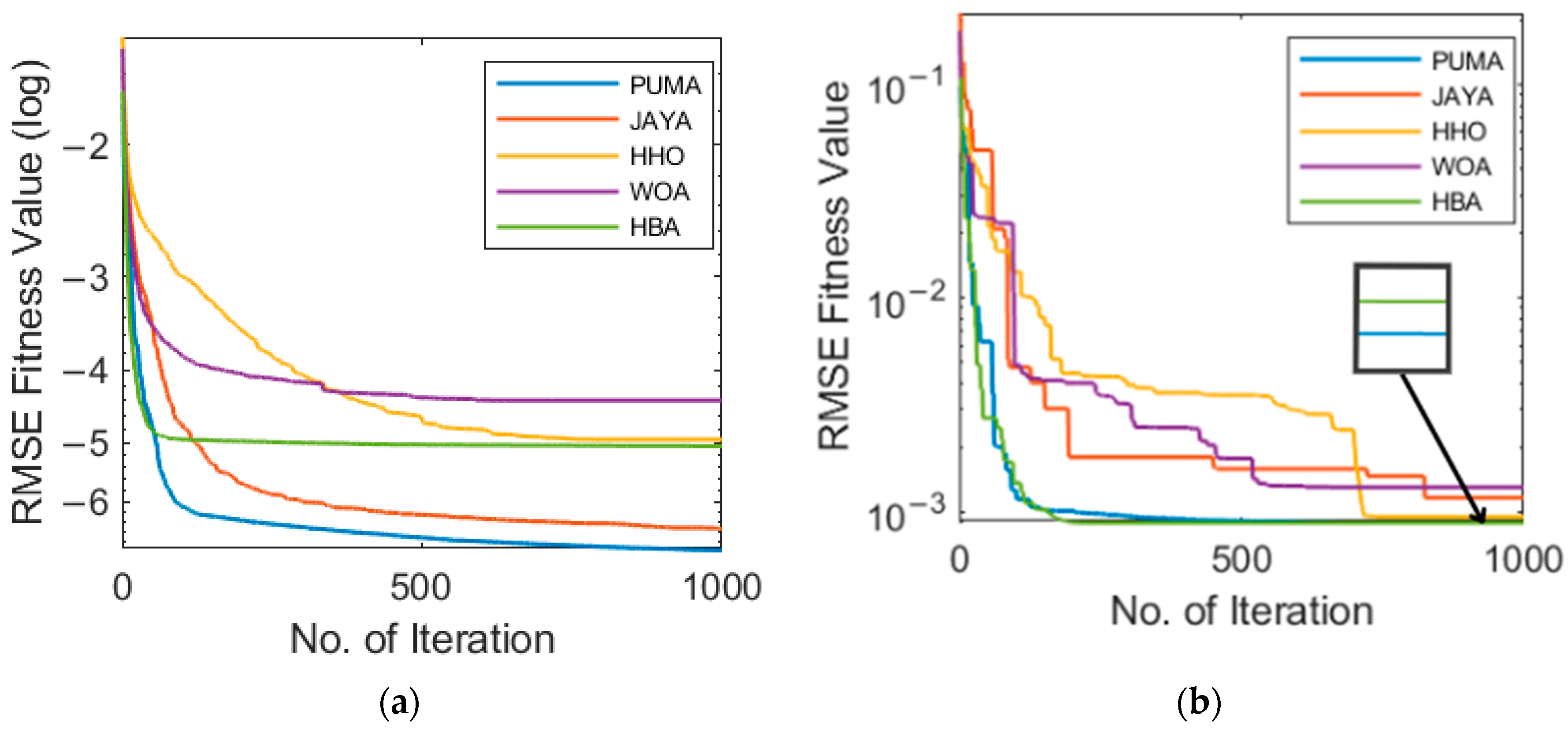
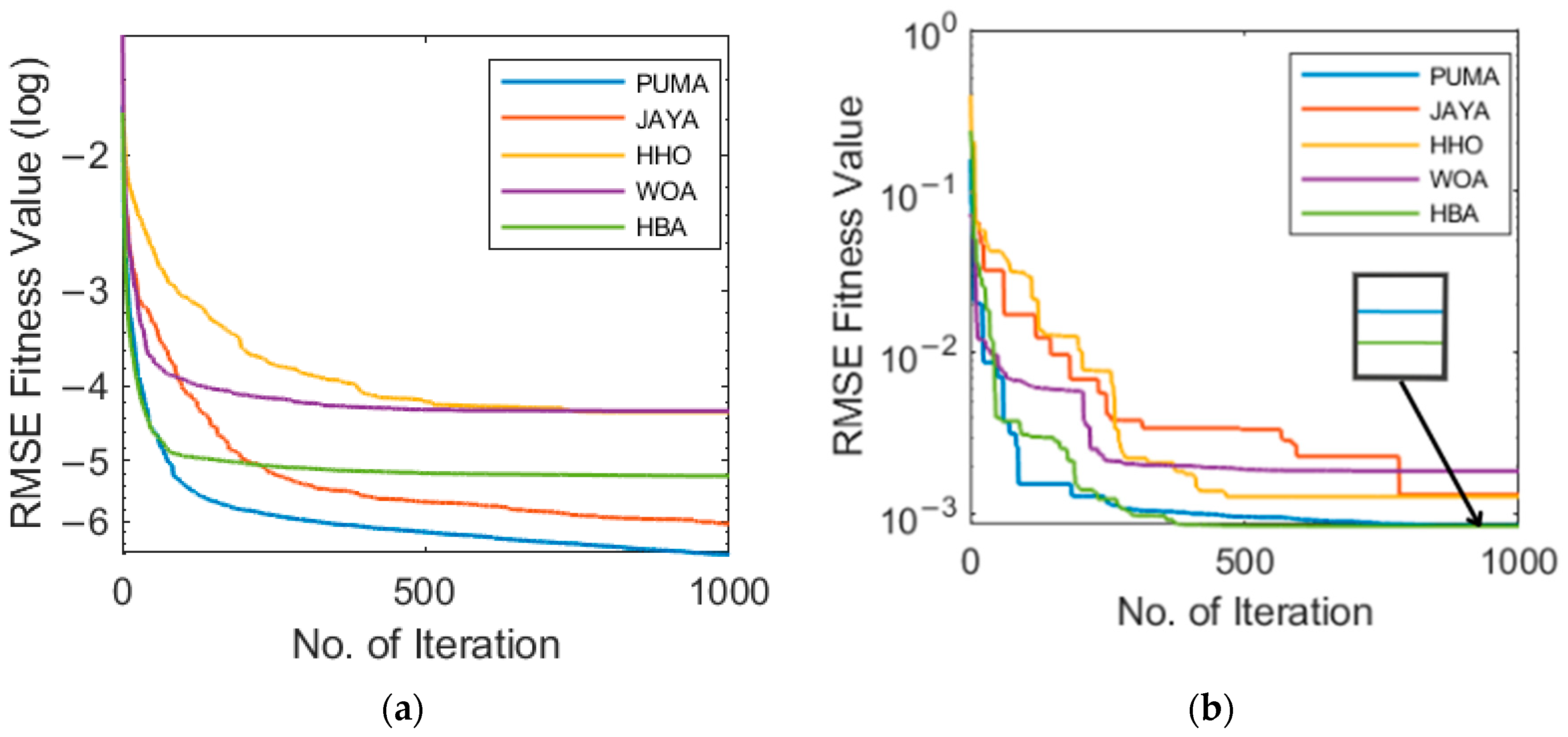
3.1. Single Diode Model
3.2. Double Diode Model
3.3. Triple Diode Model
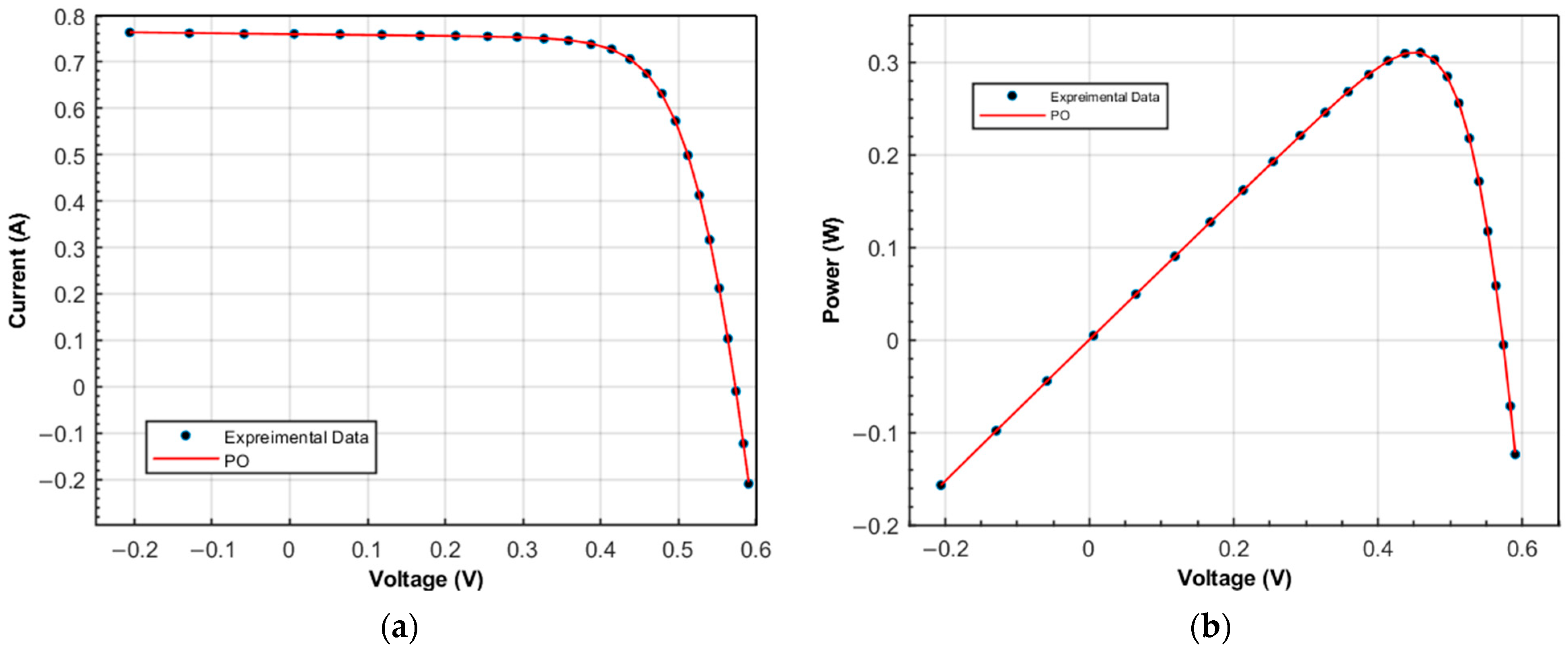
3.4. Photovolataic Module Model
3.5. Data Visualization Analysis
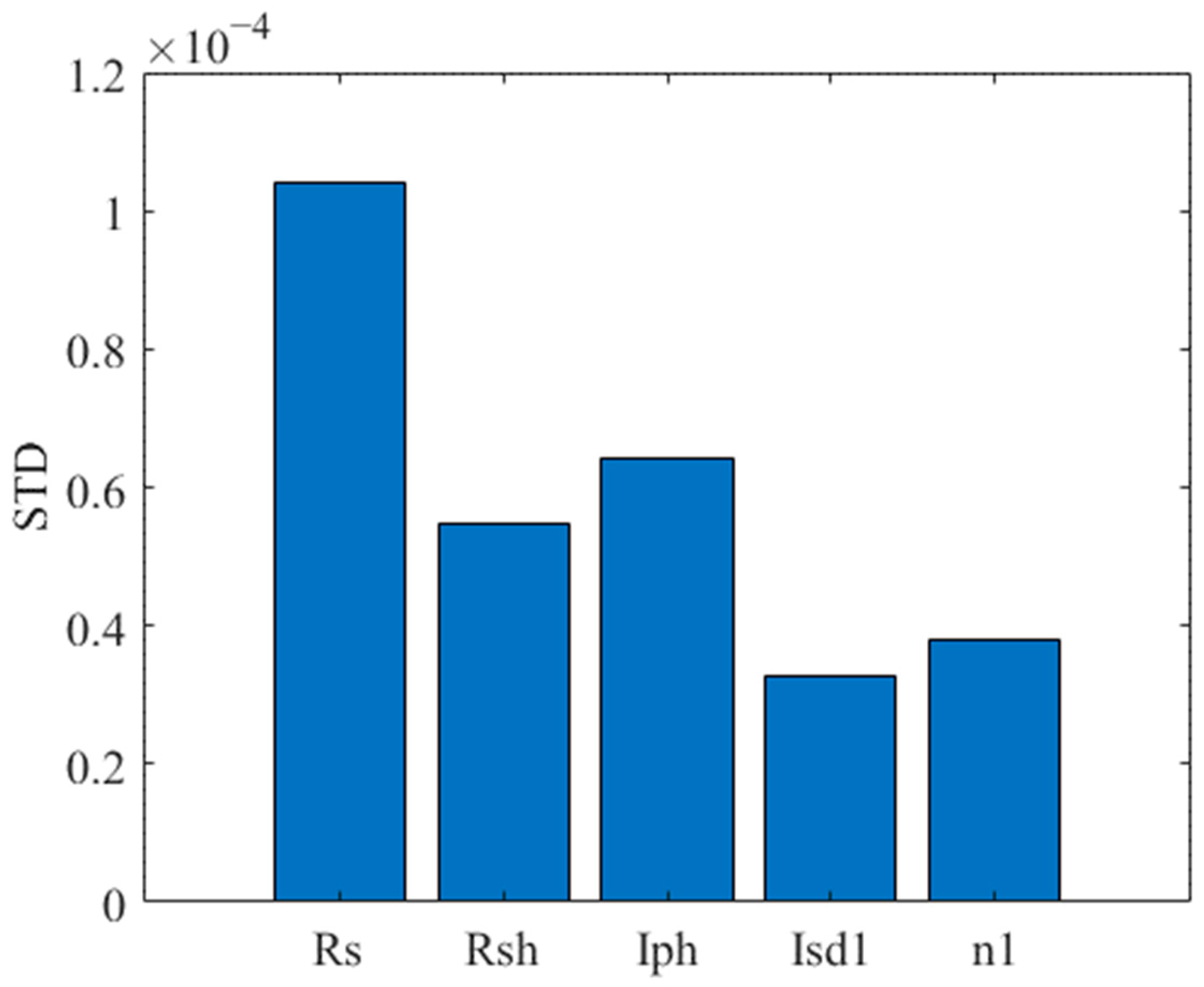
3.6. System Parameter Sensitivity
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Acronym | |
| PV | Photovoltaic |
| MPP | Maximum power point |
| PO | Puma optimizer |
| WOA | Whale optimization algorithm |
| HBA | Honey badger algorithm |
| HHO | Harris Hawks optimization |
| SDM | Single diode model |
| DDM | Double diode model |
| TDM | Triple diode model |
| PMM | Photovoltaic module model |
| RMSE | Root means square error |
| Symbol | |
| Iph | Photocurrent |
| Rs | Series resistance |
| Rsh | Shunt resistance |
| Isd | Reverse saturation current |
| n | Ideality factor |
| K | Boltzmann constant |
| T | Temperature in Kelvin |
| q | Elementary charge |
| Terminal current | |
| Terminal voltage | |
| Random number between 0 and 1 | |
| Random number from the standard normal distribution | |
| Subscript | |
| i | The i-th agent |
| t | The t-th iteration |
| Old | The old best solution |
| New | The new best solution |
| The dimension of models | |
References
- O’Neill, S. COP26: Some progress, but nations still fiddling while world warms. Engineering 2022, 11, 6–8. [Google Scholar] [CrossRef]
- Sivasankar, S.M.; de Oliveira Amorim, C.; da Cunha, A.F. Progress in thin-film photovoltaics: A review of key strategies to enhance the efficiency of CIGS, CdTe, and CZTSSe solar cells. J. Compos. Sci. 2025, 9, 143. [Google Scholar] [CrossRef]
- Abubaker, S.A.; Pakhuruddin, M.Z. Progress and development of organic photovoltaic cells for indoor applications. Renew. Sustain. Energy Rev. 2024, 203, 114738. [Google Scholar] [CrossRef]
- Hao, M.; Ding, S.; Gaznaghi, S.; Cheng, H.; Wang, L. Perovskite quantum dot solar cells: Current status and future outlook: Focus review. ACS Energy Lett. 2024, 9, 308–322. [Google Scholar] [CrossRef]
- Shin Thant, K.K.; Seriwattanachai, C.; Jittham, T.; Thamangraksat, N.; Sakata, P.; Kanjanaboos, P. Comprehensive review on slot-die-based perovskite photovoltaics: Mechanisms, materials, methods, and marketability. Adv. Energy Mater. 2025, 15, 2403088. [Google Scholar] [CrossRef]
- Cuce, E.; Cuce, P.M.; Bali, T. An experimental analysis of illumination intensity and temperature dependency of photovoltaic cell parameters. Appl. Energy 2013, 111, 374–382. [Google Scholar] [CrossRef]
- Tajuddin, M.F.N.; Arif, M.; Ayob, S.; Salam, Z. Perturbative methods for maximum power point tracking (MPPT) of photovoltaic (PV) systems: A review. Int. J. Energy Res. 2015, 39, 1153–1178. [Google Scholar] [CrossRef]
- Ismail, H.A.; Diab, A.A.Z. An efficient, fast, and robust algorithm for single diode model parameters estimation of photovoltaic solar cells. IET Renew. Power Gener. 2024, 18, 863–874. [Google Scholar] [CrossRef]
- Tifidat, K.; Maouhoub, N.; Ait Salah, F.E.; Askar, S.; Abouhawwash, M. An adaptable method for efficient modeling of photovoltaic generators’ performance based on the double-diode model. Heliyon 2024, 10, e33946. [Google Scholar] [CrossRef]
- Nafack Nihako, J.; Simo, E.; Abada Essouma, D.D.; Nanmegne Leutchouang, M.; Atteutsia Tsakem, C.R.; Tchienou Tchienou, C.Y.; Kenhago Watia, J.S.; Logerais, P.O.; Marae Djouda, J. Realistic Modeling of Photovoltaic Solar Cell: A Simple and Accurate Two-Diode Model. Appl. Res. 2025, 4, e70010. [Google Scholar] [CrossRef]
- Gao, X.; Feng, S.; Zhao, X.; Zhou, K.; Qu, J. Special trans function based exact expressions for the double and triple diode models of solar cells: Superior fitness, accuracy and convergence. Energy Rep. 2024, 11, 5252–5270. [Google Scholar] [CrossRef]
- Hali, A.; Khlifi, Y. Fast and efficient way of PV parameters estimation based on combined analytical and numerical approaches. Appl. Sol. Energy 2023, 59, 135–151. [Google Scholar] [CrossRef]
- Gu, Z.; Xiong, G.; Fu, X. Parameter extraction of solar photovoltaic cell and module models with metaheuristic algorithms: A review. Sustainability 2023, 15, 3312. [Google Scholar] [CrossRef]
- Yang, B.; Wang, J.; Zhang, X.; Yu, T.; Yao, W.; Shu, H.; Zeng, F.; Sun, L. Comprehensive overview of meta-heuristic algorithm applications on PV cell parameter identification. Energy Convers. Manag. 2020, 208, 112595. [Google Scholar] [CrossRef]
- Younis, A.; Bakhit, A.; Onsa, M.; Hashim, M. A comprehensive and critical review of bio-inspired metaheuristic frameworks for extracting parameters of solar cell single and double diode models. Energy Rep. 2022, 8, 7085–7106. [Google Scholar] [CrossRef]
- Sanin-Villa, D.; Rodriguez-Cabal, M.A.; Grisales-Noreña, L.F.; Ramirez-Neria, M.; Tejada, J.C. A Comparative Analysis of Metaheuristic Algorithms for Enhanced Parameter Estimation on Inverted Pendulum System Dynamics. Mathematics 2024, 12, 1625. [Google Scholar] [CrossRef]
- Kumar, C.; Mary, D.M. A novel chaotic-driven Tuna Swarm Optimizer with Newton-Raphson method for parameter identification of three-diode equivalent circuit model of solar photovoltaic cells/modules. Optik 2022, 264, 169379. [Google Scholar] [CrossRef]
- Raj, S.; Kumar Sinha, A.; Panchal, A.K. Solar cell parameters estimation from illuminated IV characteristic using linear slope equations and Newton-Raphson technique. J. Renew. Sustain. Energy 2013, 5, 033105. [Google Scholar] [CrossRef]
- Reis, L.; Camacho, J.R.; Novacki, D. The Newton Raphson method in the extraction of parameters of PV modules. Renew. Energy Power Qual. J. 2017, 1, 634–639. [Google Scholar]
- Et-Torabi, K.; Nassar-Eddine, I.; Obbadi, A.; Errami, Y.; Rmaily, R.; Sahnoun, S.; Agunaou, M. Parameters estimation of the single and double diode photovoltaic models using a Gauss-Seidel algorithm and analytical method: A comparative study. Energy Convers. Manag. 2017, 148, 1041–1054. [Google Scholar] [CrossRef]
- Wang, M.; Xu, X.; Yan, Z.; Wang, H. An online optimization method for extracting parameters of multi-parameter PV module model based on adaptive Levenberg-Marquardt algorithm. Energy Convers. Manag. 2021, 245, 114611. [Google Scholar] [CrossRef]
- Jordehi, A.R. Parameter estimation of solar photovoltaic (PV) cells: A review. Renew. Sustain. Energy Rev. 2016, 61, 354–371. [Google Scholar] [CrossRef]
- Chin, V.J.; Salam, Z.; Ishaque, K. Cell modelling and model parameters estimation techniques for photovoltaic simulator application: A review. Appl. Energy 2015, 154, 500–519. [Google Scholar] [CrossRef]
- Senthilkumar, S.; Mohan, V.; Krithiga, G. Brief review on solar photovoltaic parameter estimation of single and double diode model using evolutionary algorithms. Int. J. Eng. Technol. Manag. Res. 2023, 10, 64–78. [Google Scholar] [CrossRef]
- Ramadan, A.; Kamel, S.; Hassan, M.H.; Ahmed, E.M.; Hasanien, H.M. Accurate photovoltaic models based on an adaptive opposition artificial hummingbird algorithm. Electronics 2022, 11, 318. [Google Scholar] [CrossRef]
- Singh, A.; Sharma, A.; Rajput, S.; Bose, A.; Hu, X. An investigation on hybrid particle swarm optimization algorithms for parameter optimization of PV cells. Electronics 2022, 11, 909. [Google Scholar] [CrossRef]
- Kanimozhi, G.; Kumar, H. Modeling of solar cell under different conditions by Ant Lion Optimizer with LambertW function. Appl. Soft Comput. 2018, 71, 141–151. [Google Scholar]
- Ramadan, A.; Kamel, S.; Korashy, A.; Almalaq, A.; Domínguez-García, J.L. An enhanced Harris Hawk optimization algorithm for parameter estimation of single, double and triple diode photovoltaic models. Soft Comput. 2022, 26, 7233–7257. [Google Scholar] [CrossRef]
- Guo, W.; Hou, Z.; Dai, F.; Wang, J.; Li, S. Global information enhanced adaptive bald eagle search algorithm for photovoltaic system optimization. Energy Rep. 2025, 13, 2129–2152. [Google Scholar] [CrossRef]
- Devarajah, L.A.; Ahmad, M.A.; Jui, J.J. Identifying and estimating solar cell parameters using an enhanced slime mould algorithm. Optik 2024, 311, 171890. [Google Scholar] [CrossRef]
- Diab, A.A.Z.; Sultan, H.M.; Do, T.D.; Kamel, O.M.; Mossa, M.A. Coyote optimization algorithm for parameters estimation of various models of solar cells and PV modules. IEEE Access 2020, 8, 111102–111140. [Google Scholar] [CrossRef]
- El-Dabah, M.A.; El-Sehiemy, R.A.; Hasanien, H.M.; Saad, B. Photovoltaic model parameters identification using Northern Goshawk Optimization algorithm. Energy 2023, 262, 125522. [Google Scholar] [CrossRef]
- Gafar, M.; Sarhan, S.; Ginidi, A.R.; Shaheen, A.M. An Improved Bio-Inspired Material Generation Algorithm for Engineering Optimization Problems Including PV Source Penetration in Distribution Systems. Appl. Sci. 2025, 15, 603. [Google Scholar] [CrossRef]
- Chaib, L.; Tadj, M.; Choucha, A.; El-Rifaie, A.M.; Shaheen, A.M. Hybrid Brown-Bear and Hippopotamus Algorithms with Fractional Order Chaos Maps for Precise Solar PV Model Parameter Estimation. Processes 2024, 12, 2718. [Google Scholar] [CrossRef]
- Hakmi, S.H.; Alnami, H.; Moustafa, G.; Ginidi, A.R.; Shaheen, A.M. Modified rime-ice growth optimizer with polynomial differential learning operator for single-and double-diode PV parameter estimation problem. Electronics 2024, 13, 1611. [Google Scholar] [CrossRef]
- Smaili, I.H.; Moustafa, G.; Almalawi, D.R.; Ginidi, A.; Shaheen, A.M.; Mansour, H.S. Enhanced Artificial Rabbits Algorithm Integrating Equilibrium Pool to Support PV Power Estimation via Module Parameter Identification. Int. J. Energy Res. 2024, 2024, 8913560. [Google Scholar] [CrossRef]
- Kullampalayam Murugaiyan, N.; Chandrasekaran, K.; Manoharan, P.; Derebew, B. Leveraging opposition-based learning for solar photovoltaic model parameter estimation with exponential distribution optimization algorithm. Sci. Rep. 2024, 14, 528. [Google Scholar] [CrossRef]
- Saleh Alluhaidan, A.; Salama AbdElminaam, D.; Ghanim, T.M.; El-Rahman, S.A.; Shawky Farahat, I.; Al Tawil, A.; Alkady, Y.; Elashmawi, W.H. Refined photovoltaic parameters estimation via an improved Sinh Cosh Optimizer with trigonometric operators. Sci. Rep. 2025, 15, 4481. [Google Scholar] [CrossRef]
- Almansuri, M.A.K.; Yusupov, Z.; Rahebi, J.; Ghadami, R. Parameter Estimation of PV Solar Cells and Modules Using Deep Learning-Based White Shark Optimizer Algorithm. Symmetry 2025, 17, 533. [Google Scholar] [CrossRef]
- Kumar, M.; Panda, K.P.; Naayagi, R.T.; Thakur, R.; Panda, G. Enhanced Optimization Techniques for Parameter Estimation of Single-Diode PV Modules. Electronics 2024, 13, 2934. [Google Scholar] [CrossRef]
- Gafar, M.; El-Sehiemy, R.A.; Hasanien, H.M.; Abaza, A. Optimal parameter estimation of three solar cell models using modified spotted hyena optimization. J. Ambient Intell. Humaniz. Comput. 2024, 15, 361–372. [Google Scholar] [CrossRef]
- Elshara, R.; Hançerlioğullari, A.; Rahebi, J.; Lopez-Guede, J.M. PV cells and modules parameter estimation using coati optimization algorithm. Energies 2024, 17, 1716. [Google Scholar] [CrossRef]
- Choulli, I.; Elyaqouti, M.; Saadaoui, D.; Lidaighbi, S.; Elhammoudy, A.; Abazine, I. Diwjaya: Jaya driven by individual weights for enhanced photovoltaic model parameter estimation. Energy Convers. Manag. 2024, 305, 118258. [Google Scholar] [CrossRef]
- Beşkirli, A.; Dağ, İ.; Kiran, M.S. A tree seed algorithm with multi-strategy for parameter estimation of solar photovoltaic models. Appl. Soft Comput. 2024, 167, 112220. [Google Scholar] [CrossRef]
- Moustafa, G.; Alnami, H.; Ginidi, A.R.; Shaheen, A.M. An improved Kepler optimization algorithm for module parameter identification supporting PV power estimation. Heliyon 2024, 10, e39902. [Google Scholar] [CrossRef]
- Joyce, T.; Herrmann, J.M. A review of no free lunch theorems, and their implications for metaheuristic optimisation. Nat.-Inspired Algorithms Appl. Optim. 2017, 744, 27–51. [Google Scholar]
- Jiang, L.; Zhang, Z.; Lu, L.; Shang, X.; Wang, W. Nonparametric modelling of ship dynamics using puma optimizer algorithm-optimized twin support vector regression. J. Mar. Sci. Eng. 2024, 12, 754. [Google Scholar] [CrossRef]
- Al Faiya, B.; Moustafa, G.; Alnami, H.; Ginidi, A.R.; Shaheen, A.M. Puma algorithm for environmental emissions and generation costs minimization dispatch in power systems. Sci. Afr. 2025, 27, e02547. [Google Scholar]
- Maurya, P.; Tiwari, P.; Pratap, A. Puma optimizer technique for optimal planning of different types of distributed generation units in radial distribution network considering different load models. Electr. Eng. 2024, 107, 2777–2828. [Google Scholar] [CrossRef]
- Maurya, P.; Tiwari, P.; Pratap, A. Puma optimiser technique for efficient distributed generation planning in electrical distribution network with different load models. Int. J. Ambient Energy 2025, 46, 2478140. [Google Scholar] [CrossRef]
- Shaikh, A.M.; Shaikh, M.F.; Shaikh, S.A.; Krichen, M.; Rahimoon, R.A.; Qadir, A. Comparative analysis of different MPPT techniques using boost converter for photovoltaic systems under dynamic shading conditions. Sustain. Energy Technol. Assess. 2023, 57, 103259. [Google Scholar]
- Huang, C.-M.; Chen, S.-J.; Yang, S.-P. A parameter estimation method for a photovoltaic power generation system based on a two-diode model. Energies 2022, 15, 1460. [Google Scholar] [CrossRef]
- Rezk, H.; Abdelkareem, M.A. Optimal parameter identification of triple diode model for solar photovoltaic panel and cells. Energy Rep. 2022, 8, 1179–1188. [Google Scholar] [CrossRef]
- Fahim, S.R.; Hasanien, H.M.; Turky, R.A.; Aleem, S.H.A.; Ćalasan, M. A comprehensive review of photovoltaic modules models and algorithms used in parameter extraction. Energies 2022, 15, 8941. [Google Scholar] [CrossRef]
- Abdollahzadeh, B.; Khodadadi, N.; Barshandeh, S.; Trojovský, P.; Gharehchopogh, F.S.; El-kenawy, E.-S.M.; Abualigah, L.; Mirjalili, S. Puma optimizer (PO): A novel metaheuristic optimization algorithm and its application in machine learning. Clust. Comput. 2024, 27, 5235–5283. [Google Scholar] [CrossRef]
- Easwarakhanthan, T.; Bottin, J.; Bouhouch, I.; Boutrit, C. Nonlinear minimization algorithm for determining the solar cell parameters with microcomputers. Int. J. Sol. Energy 1986, 4, 1–12. [Google Scholar] [CrossRef]
- Rezk, H.; Olabi, A.; Wilberforce, T.; Sayed, E.T. A comprehensive review and application of metaheuristics in solving the optimal parameter identification problems. Sustainability 2023, 15, 5732. [Google Scholar] [CrossRef]
- Słowik, A.; Cpałka, K.; Xue, Y.; Hapka, A. An efficient approach to parameter extraction of photovoltaic cell models using a new population-based algorithm. Appl. Energy 2024, 364, 123208. [Google Scholar] [CrossRef]
























| Year | Algorithm | Modeling | Objective Function | Reference |
|---|---|---|---|---|
| 2025 | OBEDO | SDM, DDM, TDM | RMSE | [37] |
| 2025 | I_SCHO | SDM, DDM, TDM | RMSE | [38] |
| 2025 | WSO | SDM, DDM, PV module | RMSE | [39] |
| 2024 | GPSO | SDM | RMSE | [40] |
| 2024 | MSHOA | SDM, DDM, TDM | RMSE | [41] |
| 2024 | ICOA | SDM, DDM, PV module | RMSE | [42] |
| 2024 | DIWJAYA | SDM, DDM, PMM | RMSE | [43] |
| 2024 | MS-TSA | SDM, DDM, PVM | RMSE | [44] |
| 2024 | IKOA | SDM, DDM, TDM | RMSE | [45] |
| Function | Parameter Vector |
|---|---|
| ] | |
| ] | |
| ] | |
| ] |
| 57 mm Diameter R.T.C France Solar Cell | |
|---|---|
| Operation Temperature (K) | 303.15 |
| Operation radiation (W/m2) | 1000 |
| Maximum power (Pmpp) (W) | 0.3101 |
| Voltage at MPP (VMPP) (V) | 0.4507 |
| Current at MPP (IMPP) (A) | 0.6880 |
| Open circuit voltage (VOC) (V) | 0.5728 |
| Short circuit current (ISC) (A) | 0.7603 |
| Parameter | Range | Parameter | Range | ||
|---|---|---|---|---|---|
| 1 | Iph (A) | [0, 1] | 6 | Isd2 (μA) | [0.001, 1] |
| 1 | Rs (Ω) | [0, 0.5] | 7 | n2 | [1, 2] |
| 2 | Rsh (Ω) | [0, 100] | 8 | Isd3 (μA) | [0.001, 1] |
| 4 | Isd1 (μA) | [0.001, 1] | 9 | n3 | [1, 2] |
| 5 | n1 | [1, 2] | - | - | - |
| Photowatt-PWP 201 Solar Module | |
|---|---|
| Operation Temperature (K) | 318.15 |
| Operation radiation (W/m2) | 1000 |
| Maximum power (Pmpp) (W) | 11.54 |
| Voltage at MPP (VMPP) (V) | 12.6490 |
| Current at MPP (IMPP) (A) | 0.9120 |
| Open circuit voltage (VOC) (V) | 16.7785 |
| Short circuit current (ISC) (A) | 1.0317 |
| Parameter | Range | Parameter | Range | ||
|---|---|---|---|---|---|
| 1 | Iph (A) | [0, 2] | 4 | Isd1 (μA) | [0, 50] |
| 2 | Rs (Ω) | [0, 2] | 5 | n1 | [1, 50] |
| 3 | Rsh (Ω) | [0, 2000] |
| Algorithm Setting | |
|---|---|
| Independent run time | 30 |
| Population size | 30 |
| Iteration time | 1000 |
| Experimental Data | HBA | WOA | HHO | JAYA | PO | |
|---|---|---|---|---|---|---|
| Vt(V) | It(A) | Computed It(A) | ||||
| −0.2057 | 0.7640 | 0.7642 | 0.7632 | 0.7637 | 0.7629 | 0.7642 |
| −0.1291 | 0.7620 | 0.7628 | 0.7620 | 0.7623 | 0.7618 | 0.7628 |
| −0.0588 | 0.7605 | 0.7614 | 0.7609 | 0.7611 | 0.7607 | 0.7614 |
| 0.0057 | 0.7605 | 0.7602 | 0.7600 | 0.7600 | 0.7598 | 0.7602 |
| 0.0646 | 0.7600 | 0.7590 | 0.7591 | 0.7590 | 0.7589 | 0.7590 |
| 0.1185 | 0.7590 | 0.7580 | 0.7582 | 0.7581 | 0.7581 | 0.7580 |
| 0.1678 | 0.7570 | 0.7570 | 0.7574 | 0.7572 | 0.7573 | 0.7570 |
| 0.2132 | 0.7570 | 0.7560 | 0.7566 | 0.7563 | 0.7565 | 0.7560 |
| 0.2545 | 0.7555 | 0.7550 | 0.7557 | 0.7553 | 0.7556 | 0.7550 |
| 0.2924 | 0.7540 | 0.7535 | 0.7543 | 0.7540 | 0.7542 | 0.7535 |
| 0.3269 | 0.7505 | 0.7513 | 0.7520 | 0.7517 | 0.7519 | 0.7513 |
| 0.3585 | 0.7465 | 0.7473 | 0.7478 | 0.7476 | 0.7478 | 0.7473 |
| 0.3873 | 0.7385 | 0.7401 | 0.7404 | 0.7403 | 0.7403 | 0.7401 |
| 0.4137 | 0.7280 | 0.7275 | 0.7273 | 0.7275 | 0.7273 | 0.7275 |
| 0.4373 | 0.7065 | 0.7071 | 0.7066 | 0.7069 | 0.7065 | 0.7071 |
| 0.4590 | 0.6755 | 0.6755 | 0.6747 | 0.6750 | 0.6745 | 0.6755 |
| 0.4784 | 0.6320 | 0.6309 | 0.6301 | 0.6303 | 0.6298 | 0.6309 |
| 0.4960 | 0.5730 | 0.5720 | 0.5715 | 0.5714 | 0.5710 | 0.5720 |
| 0.5119 | 0.4990 | 0.4995 | 0.4996 | 0.4990 | 0.4990 | 0.4995 |
| 0.5265 | 0.4130 | 0.4134 | 0.4143 | 0.4132 | 0.4135 | 0.4134 |
| 0.5398 | 0.3165 | 0.3171 | 0.3187 | 0.3172 | 0.3179 | 0.3171 |
| 0.5521 | 0.2120 | 0.2118 | 0.2137 | 0.2121 | 0.2131 | 0.2118 |
| 0.5633 | 0.1035 | 0.1022 | 0.1038 | 0.1026 | 0.1036 | 0.1022 |
| 0.5736 | −0.0100 | −0.0083 | −0.0079 | −0.0080 | −0.0073 | −0.0083 |
| 0.5833 | −0.1230 | −0.1243 | −0.1257 | −0.1243 | −0.1242 | −0.1243 |
| 0.5900 | −0.2100 | −0.2065 | −0.2101 | −0.2070 | −0.2077 | −0.2065 |
| RMSE | ||||||
| PARAM/ALGO | OBEDO [37] | AFCSO [58] | ESMA [30] | HBA | WOA | HHO | JAYA | PO |
|---|---|---|---|---|---|---|---|---|
| Rs (Ω) | 0.0364 | 0.03639 | 0.036373 | 0.037 | 0.0349 | 0.0363 | 0.0354 | 0.037 |
| (Ω) | 53.7185 | 52.64088 | 53.724744 | 51.8812 | 65.4335 | 58.5555 | 67.1110 | 52.1089 |
| (A) | 0.7608 | 0.76091 | 0.760776 | 0.7608 | 0.7605 | 0.7606 | 0.7602 | 0.7608 |
| (μA) | 0.32168 | 0.323260 | 0.2905 | 0.4395 | 0.3476 | 0.4258 | 0.2918 | |
| n1 | 1.4812 | 1.48077 | 1.481095 | 1.4719 | 1.5142 | 1.4899 | 1.5109 | 1.4723 |
| Best | (5) | (4) | (6) | (2) | (8) | (3) | (7) | (1) |
| Mean | (3) | (2) | (5) | (6) | (8) | (7) | (4) | (1) |
| Std. | (1) | (2) | (5) | (7) | (8) | (6) | (4) | (3) |
| Experimental Data | HBA | WOA | HHO | JAYA | PO | |
|---|---|---|---|---|---|---|
| Vt(V) | It(A) | Computed It(A) | ||||
| −0.2057 | 0.7640 | 0.7641 | 0.7662 | 0.7611 | 0.7636 | 0.7641 |
| −0.1291 | 0.7620 | 0.7627 | 0.7645 | 0.7603 | 0.7624 | 0.7627 |
| −0.0588 | 0.7605 | 0.7614 | 0.7630 | 0.7595 | 0.7613 | 0.7614 |
| 0.0057 | 0.7605 | 0.7602 | 0.7616 | 0.7588 | 0.7603 | 0.7602 |
| 0.0646 | 0.7600 | 0.7591 | 0.7603 | 0.7581 | 0.7594 | 0.7590 |
| 0.1185 | 0.7590 | 0.7581 | 0.7591 | 0.7575 | 0.7586 | 0.7580 |
| 0.1678 | 0.7570 | 0.7571 | 0.7579 | 0.7570 | 0.7577 | 0.7571 |
| 0.2132 | 0.7570 | 0.7561 | 0.7568 | 0.7563 | 0.7569 | 0.7561 |
| 0.2545 | 0.7555 | 0.7551 | 0.7555 | 0.7555 | 0.7560 | 0.7551 |
| 0.2924 | 0.7540 | 0.7536 | 0.7539 | 0.7543 | 0.7546 | 0.7536 |
| 0.3269 | 0.7505 | 0.7513 | 0.7513 | 0.7522 | 0.7523 | 0.7513 |
| 0.3585 | 0.7465 | 0.7472 | 0.7469 | 0.7483 | 0.7481 | 0.7473 |
| 0.3873 | 0.7385 | 0.7400 | 0.7392 | 0.7412 | 0.7406 | 0.7401 |
| 0.4137 | 0.7280 | 0.7273 | 0.7260 | 0.7286 | 0.7275 | 0.7274 |
| 0.4373 | 0.7065 | 0.7070 | 0.7051 | 0.7082 | 0.7066 | 0.7070 |
| 0.4590 | 0.6755 | 0.6754 | 0.6729 | 0.6765 | 0.6745 | 0.6754 |
| 0.4784 | 0.6320 | 0.6309 | 0.6281 | 0.6318 | 0.6297 | 0.6308 |
| 0.4960 | 0.5730 | 0.5721 | 0.5692 | 0.5726 | 0.5708 | 0.5719 |
| 0.5119 | 0.4990 | 0.4996 | 0.4971 | 0.4998 | 0.4986 | 0.4995 |
| 0.5265 | 0.4130 | 0.4135 | 0.4115 | 0.4132 | 0.4130 | 0.4134 |
| 0.5398 | 0.3165 | 0.3172 | 0.3160 | 0.3166 | 0.3172 | 0.3172 |
| 0.5521 | 0.2120 | 0.2118 | 0.2114 | 0.2110 | 0.2122 | 0.2119 |
| 0.5633 | 0.1035 | 0.1021 | 0.1025 | 0.1014 | 0.1024 | 0.1022 |
| 0.5736 | −0.0100 | −0.0084 | −0.0074 | −0.0086 | −0.0089 | −0.0083 |
| 0.5833 | −0.1230 | −0.1243 | −0.1229 | −0.1238 | −0.1262 | −0.1243 |
| 0.5900 | −0.2100 | −0.2063 | −0.2049 | −0.2049 | −0.2100 | −0.2065 |
| RMSE | ||||||
| PARAM/ALGO | OBEDO [37] | AFCSO [58] | ESMA [30] | HBA | WOA | HHO | JAYA | PO |
|---|---|---|---|---|---|---|---|---|
| (Ω) | 0.0367 | 2.00000 | 0.036685 | 0.0375 | 0.0367 | 0.0382 | 0.0353 | 0.0370 |
| (Ω) | 55.3995 | 55.38775 | 55.226233 | 53.7479 | 45.2503 | 91.8191 | 64.2008 | 53.5530 |
| (A) | 0.7608 | 0.76078 | 0.760780 | 0.7608 | 0.7623 | 0.7592 | 0.7608 | 0.7608 |
| (μA) | 0.71140 | 0.645229 | 0.4878 | 0.5837 | 0.9081 | 0.4319 | 0.2866 | |
| (μA) | 0.03672 | 0.238374 | 0.1255 | 0.0430 | 0.1188 | 0 | 0.2591 | |
| n1 | 1.4529 | 0.23038 | 1.999999 | 1.7341 | 1.6200 | 1.8644 | 1.5122 | 1.9852 |
| n2 | 2.0000 | 1.45263 | 1.455321 | 1.4106 | 1.3637 | 1.4008 | 1.9608 | 1.4627 |
| Best | (3) | (3) | (5) | (1) | (8) | (7) | (6) | (2) |
| Mean | (3) | (4) | (2) | (6) | (8) | (7) | (5) | (1) |
| Std. | (1) | (3) | (5) | (7) | (8) | (6) | (4) | (2) |
| Experimental Data | HBA | WOA | HHO | JAYA | PO | |
|---|---|---|---|---|---|---|
| Vt(V) | It(A) | Computed It(A) | ||||
| −0.2057 | 0.7640 | 0.7639 | 0.7617 | 0.7624 | 0.7640 | |
| −0.1291 | 0.7620 | 0.7626 | 0.7609 | 0.7614 | 0.7602 | 0.7626 |
| −0.0588 | 0.7605 | 0.7613 | 0.7601 | 0.7606 | 0.7595 | 0.7613 |
| 0.0057 | 0.7605 | 0.7602 | 0.7594 | 0.7597 | 0.7589 | 0.7602 |
| 0.0646 | 0.7600 | 0.7591 | 0.7587 | 0.7590 | 0.7583 | 0.7591 |
| 0.1185 | 0.7590 | 0.7582 | 0.7581 | 0.7583 | 0.7577 | 0.7581 |
| 0.1678 | 0.7570 | 0.7573 | 0.7575 | 0.7576 | 0.7572 | 0.7572 |
| 0.2132 | 0.7570 | 0.7563 | 0.7569 | 0.7569 | 0.7566 | 0.7562 |
| 0.2545 | 0.7555 | 0.7552 | 0.7560 | 0.7560 | 0.7558 | 0.7551 |
| 0.2924 | 0.7540 | 0.7537 | 0.7547 | 0.7547 | 0.7546 | 0.7537 |
| 0.3269 | 0.7505 | 0.7513 | 0.7525 | 0.7524 | 0.7524 | 0.7513 |
| 0.3585 | 0.7465 | 0.7472 | 0.7484 | 0.7482 | 0.7483 | 0.7472 |
| 0.3873 | 0.7385 | 0.7399 | 0.7410 | 0.7406 | 0.7409 | 0.7400 |
| 0.4137 | 0.7280 | 0.7272 | 0.7281 | 0.7274 | 0.7280 | 0.7272 |
| 0.4373 | 0.7065 | 0.7068 | 0.7075 | 0.7065 | 0.7074 | 0.7069 |
| 0.4590 | 0.6755 | 0.6753 | 0.6754 | 0.6743 | 0.6755 | 0.6753 |
| 0.4784 | 0.6320 | 0.6309 | 0.6304 | 0.6295 | 0.6308 | 0.6309 |
| 0.4960 | 0.5730 | 0.5721 | 0.5708 | 0.5707 | 0.5718 | 0.5721 |
| 0.5119 | 0.4990 | 0.4997 | 0.4976 | 0.4987 | 0.4992 | 0.4997 |
| 0.5265 | 0.4130 | 0.4136 | 0.4109 | 0.4133 | 0.4129 | 0.4135 |
| 0.5398 | 0.3165 | 0.3172 | 0.3143 | 0.3178 | 0.3164 | 0.3172 |
| 0.5521 | 0.2120 | 0.2117 | 0.2091 | 0.2131 | 0.2108 | 0.2118 |
| 0.5633 | 0.1035 | 0.1020 | 0.1003 | 0.1035 | 0.1011 | 0.1020 |
| 0.5736 | −0.0100 | −0.0084 | −0.0083 | −0.0076 | −0.0090 | −0.0084 |
| 0.5833 | −0.1230 | −0.1243 | −0.1216 | −0.1248 | −0.1246 | −0.1243 |
| 0.5900 | −0.2100 | −0.2061 | −0.2008 | −0.2087 | −0.2057 | −0.2061 |
| RMSE | ||||||
| PARAM/ALGO | OBEDO [37] | AFCSO [58] | HBA | WOA | HHO | JAYA | PO |
|---|---|---|---|---|---|---|---|
| (Ω) | 0.0367 | 0.03666 | 0.0379 | 0.0394 | 0.0351 | 0.0391 | 0.0378 |
| (Ω) | 55.7780 | 55.12808 | 56.8628 | 90.4876 | 78.773 | 100 | 55.1974 |
| (A) | 0.7608 | 0.76078 | 0.7608 | 0.7598 | 0.7601 | 0.7592 | 0.7608 |
| (μA) | 0.23805 | 0.6863 | 0.5061 | 0.3012 | 0.0010 | 0.0102 | |
| (μA) | 0.00098 | 0.8779 | 0.0434 | 0.0718 | 0.0010 | 0.0771 | |
| (μA) | 0.57956 | 0.1206 | 0.6807 | 0.2946 | 0.6901 | 0.6860 | |
| n1 | 1.9995 | 1.45564 | 1.9774 | 1.7883 | 1.4947 | 1.1294 | 1.9999 |
| n2 | 1.4537 | 1.70165 | 0.0379 | 0.0394 | 0.0351 | 1.6918 | 1.3752 |
| n3 | 2.7316 | 1.97191 | 56.8628 | 90.4876 | 78.773 | 1.6042 | 1.7352 |
| Best | (3) | (4) | (1) | (7) | (5) | (6) | (2) |
| Mean | (1) | (3) | (5) | (7) | (6) | (4) | (2) |
| Std. | (1) | (3) | (5) | (6) | (7) | (4) | (2) |
| Experimental Data | HBA | WOA | HHO | JAYA | PO | |
|---|---|---|---|---|---|---|
| Vt(V) | It(A) | Computed It(A) | ||||
| −1.9426 | 1.0345 | 1.0327 | 1.0365 | 1.0272 | 1.0283 | 1.0310 |
| 0.1248 | 1.0315 | 1.0302 | 1.0329 | 1.0270 | 1.0281 | 1.0291 |
| 1.8093 | 1.0300 | 1.0282 | 1.0300 | 1.0268 | 1.0279 | 1.0275 |
| 3.3511 | 1.0260 | 1.0263 | 1.0273 | 1.0266 | 1.0277 | 1.0260 |
| 4.7622 | 1.0220 | 1.0244 | 1.0247 | 1.0261 | 1.0273 | 1.0245 |
| 6.0538 | 1.0180 | 1.0223 | 1.0221 | 1.0252 | 1.0265 | 1.0227 |
| 7.2364 | 1.0155 | 1.0198 | 1.0191 | 1.0234 | 1.0248 | 1.0204 |
| 8.3189 | 1.0140 | 1.0161 | 1.0152 | 1.0200 | 1.0216 | 1.0168 |
| 9.3097 | 1.0100 | 1.0102 | 1.0093 | 1.0136 | 1.0156 | 1.0108 |
| 10.2163 | 1.0035 | 1.0003 | 0.9996 | 1.0027 | 1.0050 | 1.0007 |
| 11.0449 | 0.9880 | 0.9843 | 0.9839 | 0.9850 | 0.9878 | 0.9842 |
| 11.8018 | 0.9630 | 0.9594 | 0.9592 | 0.9580 | 0.9613 | 0.9588 |
| 12.4929 | 0.9255 | 0.9228 | 0.9225 | 0.9195 | 0.9232 | 0.9218 |
| 13.1231 | 0.8725 | 0.8727 | 0.8717 | 0.8680 | 0.8718 | 0.8713 |
| 13.6983 | 0.8075 | 0.8075 | 0.8049 | 0.8024 | 0.8059 | 0.8060 |
| 14.2221 | 0.7265 | 0.7285 | 0.7239 | 0.7240 | 0.7270 | 0.7272 |
| 14.6995 | 0.6345 | 0.6372 | 0.6305 | 0.6343 | 0.6365 | 0.6363 |
| 15.1346 | 0.5345 | 0.5362 | 0.5274 | 0.5354 | 0.5366 | 0.5359 |
| 15.5311 | 0.4275 | 0.4294 | 0.4195 | 0.4306 | 0.4308 | 0.4296 |
| 15.8929 | 0.3185 | 0.3186 | 0.3087 | 0.3216 | 0.3208 | 0.3193 |
| 16.2229 | 0.2085 | 0.2071 | 0.1987 | 0.2112 | 0.2097 | 0.2082 |
| 16.5241 | 0.1010 | 0.0960 | 0.0903 | 0.1003 | 0.0982 | 0.0971 |
| 16.7987 | −0.0080 | −0.0083 | −0.0092 | −0.0055 | −0.0078 | −0.0076 |
| 17.0499 | −0.1110 | −0.1107 | −0.1058 | −0.1101 | −0.1123 | −0.1105 |
| 17.2793 | −0.2090 | −0.2087 | −0.1969 | −0.2113 | −0.2132 | −0.2093 |
| 17.4885 | −0.3030 | −0.2999 | −0.2801 | −0.3068 | −0.3082 | −0.3016 |
| RMSE | ||||||
| PARAM/ALGO | OBEDO [37] | AFCSO [58] | ESMA [30] | HBA | WOA | HHO | JAYA | PO |
|---|---|---|---|---|---|---|---|---|
| Rs (Ω) | 1.2013 | 0.03337 | 1.201129 | 0.03367 | 0.03698 | 0.02984 | 0.03079 | 0.0327 |
| (Ω) | 981.98 | 27.27673 | 983.44499 | 23.0581 | 16.0008 | 389.6039 | 360.344 | 30.0367 |
| (A) | 1.0305 | 1.03051 | 1.03051 | 1.0319 | 1.0355 | 1.0271 | 1.02823 | 1.03035 |
| (μA) | 3.48 | 3.48211 | 3.48703 | 3.1442 | 1.6401 | 10.0554 | 7.80723 | 4.24014 |
| n1 | 48.6428 | 1.35118 | 48.642708 | 1.3410 | 1.2759 | 1.4749 | 1.44282 | 1.37310 |
| Best | (1) | (1) | (4) | (3) | (8) | (7) | (6) | (5) |
| Mean | (1) | (2) | (7) | 0.10694 (6) | 0.13499 (8) | (4) | (5) | (3) |
| Std. | (1) | (2) | (8) | 0.11847 (7) | 0.10889 (6) | (5) | (4) | (3) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, E.-J.; Huang, Y.-H.; Lin, W.-L.; Wen, C.-K.; Lin, C.-I. Rapid, Precise Parameter Optimization and Performance Prediction for Multi-Diode Photovoltaic Model Using Puma Optimizer. Energies 2025, 18, 2855. https://doi.org/10.3390/en18112855
Liu E-J, Huang Y-H, Lin W-L, Wen C-K, Lin C-I. Rapid, Precise Parameter Optimization and Performance Prediction for Multi-Diode Photovoltaic Model Using Puma Optimizer. Energies. 2025; 18(11):2855. https://doi.org/10.3390/en18112855
Chicago/Turabian StyleLiu, En-Jui, Yan-Hao Huang, Wei-Lun Lin, Chen-Kai Wen, and Chun-I Lin. 2025. "Rapid, Precise Parameter Optimization and Performance Prediction for Multi-Diode Photovoltaic Model Using Puma Optimizer" Energies 18, no. 11: 2855. https://doi.org/10.3390/en18112855
APA StyleLiu, E.-J., Huang, Y.-H., Lin, W.-L., Wen, C.-K., & Lin, C.-I. (2025). Rapid, Precise Parameter Optimization and Performance Prediction for Multi-Diode Photovoltaic Model Using Puma Optimizer. Energies, 18(11), 2855. https://doi.org/10.3390/en18112855






