Cluster Partitioning Method for High-PV-Penetration Distribution Network Based on mGA-PSO Algorithm
Abstract
1. Introduction
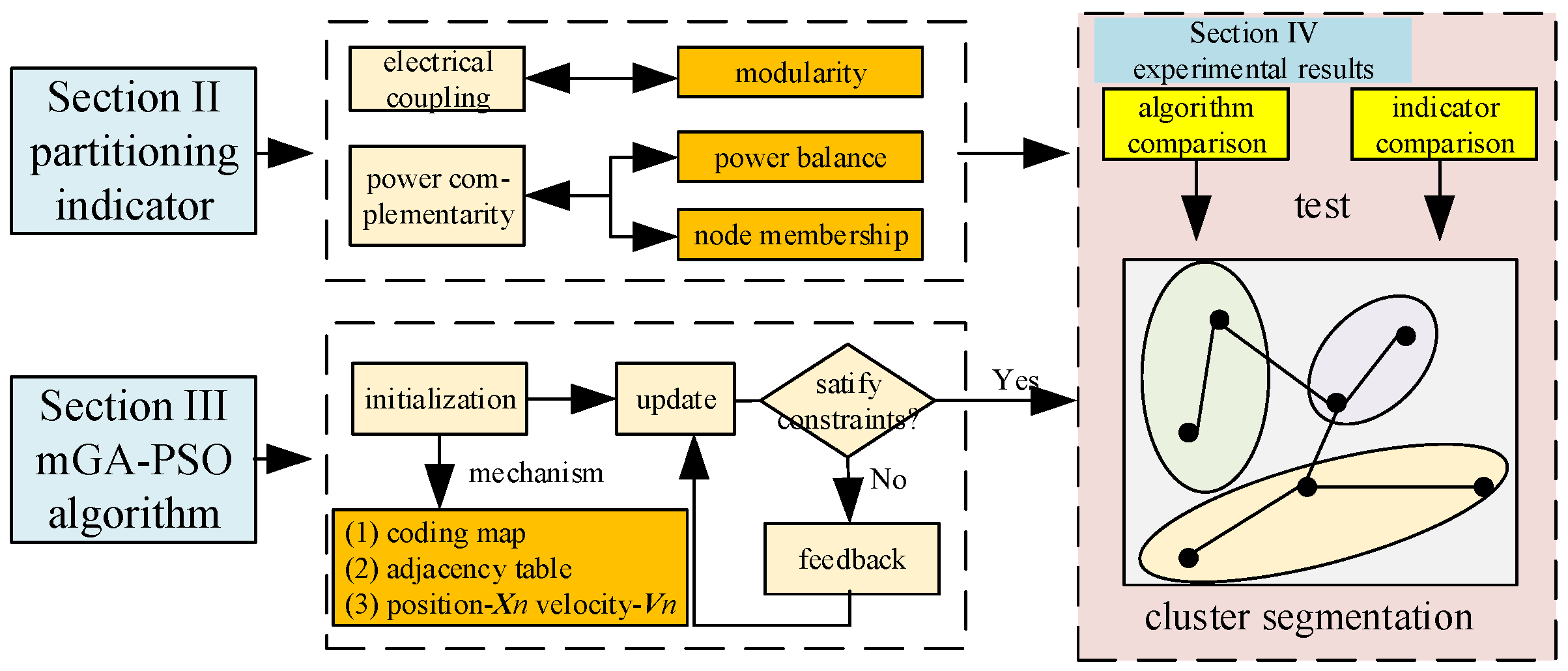
2. Distributed Cluster Partitioning Indicators
2.1. Modularity Index
2.2. Power Balance Index
2.3. Node Membership Index
2.4. Comprehensive Cluster Partitioning Index
3. Clustering Partitioning Method Based on mGA-PSO
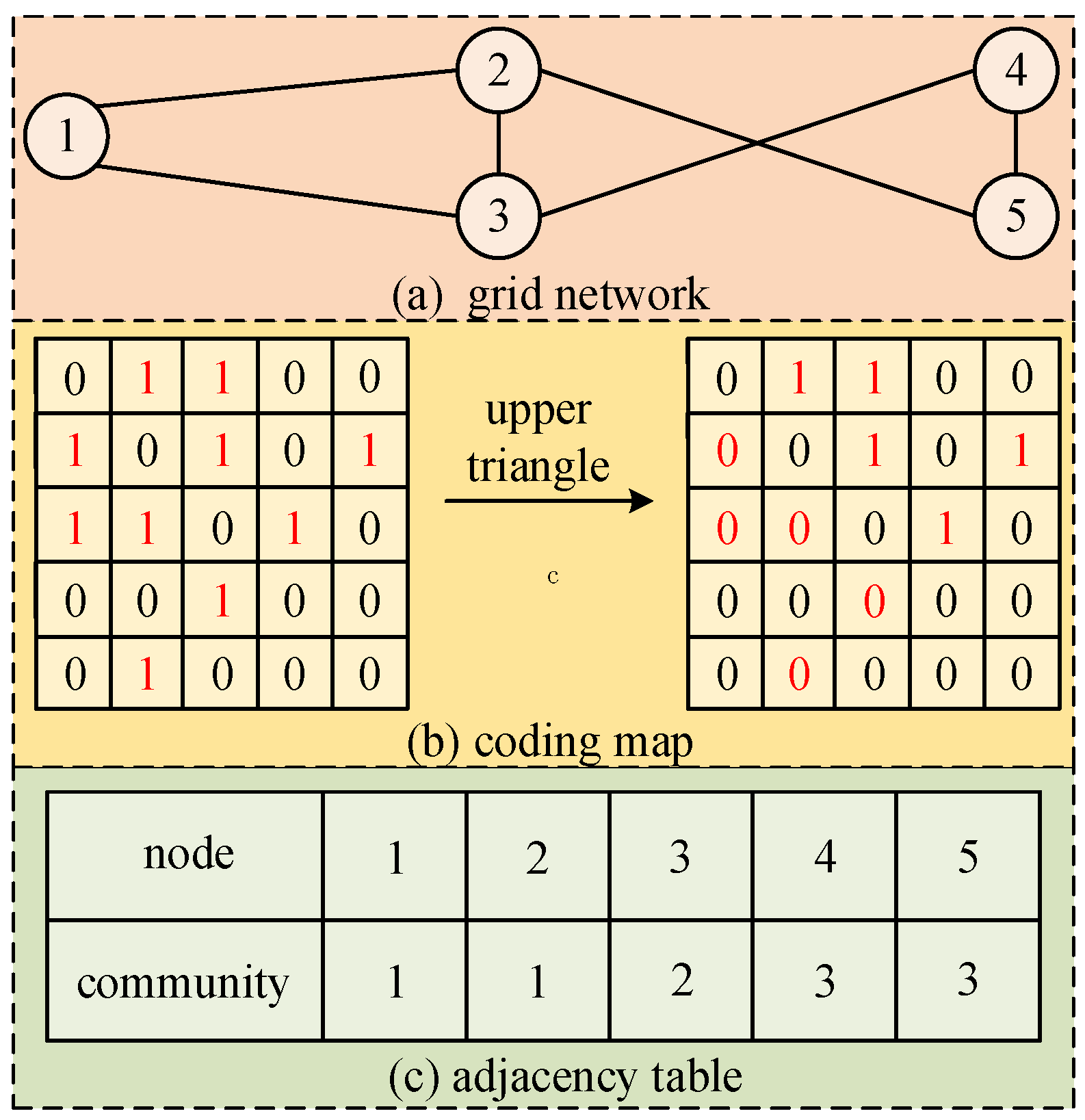
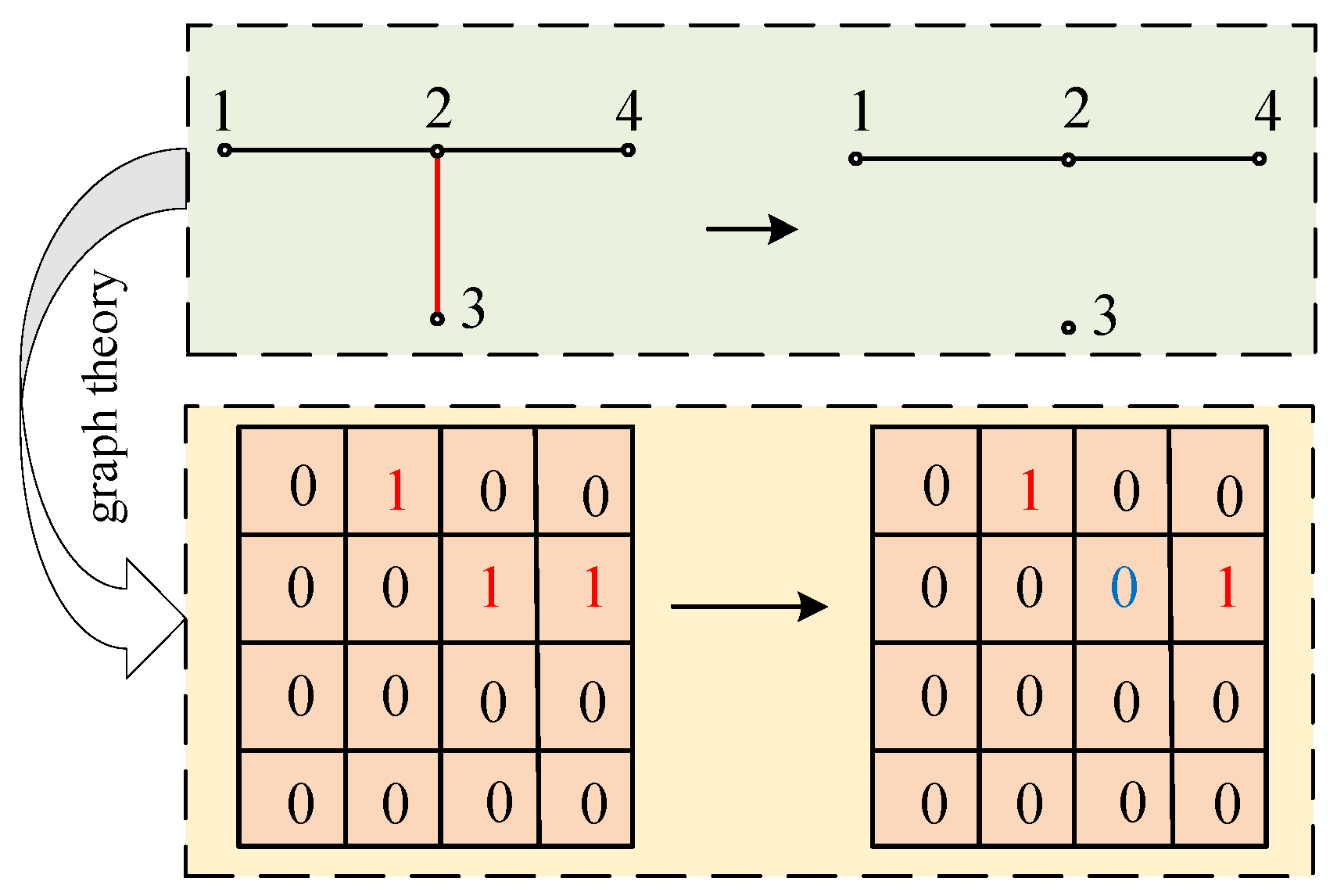
3.1. Encoding and Initialization
3.2. mGA-PSO for Cluster Partitioning
3.2.1. Micro-GA Optimization Mechanism
3.2.2. PSO Optimization Mechanism
3.2.3. Update Strategy of PSO Optimization Mechanism
- (1)
- Individual search update
- (2)
- Modification factor during iteration
- (3)
- Individual transfer based on historical population information
- (4)
- Individual feedback
3.2.4. Algorithm Flowchart
4. Experiments and Analysis
4.1. IEEE 34-Node Case Analysis
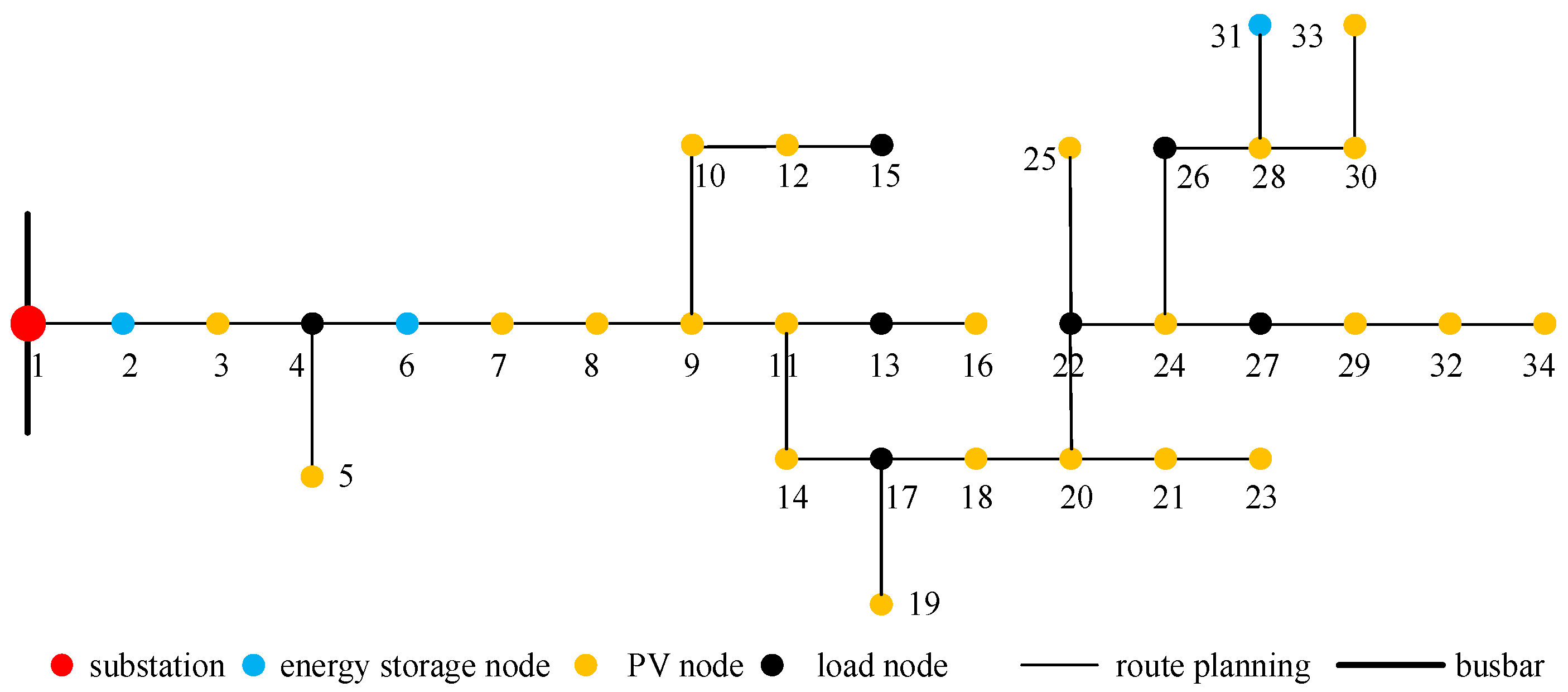
4.1.1. Distributed PV Network Design
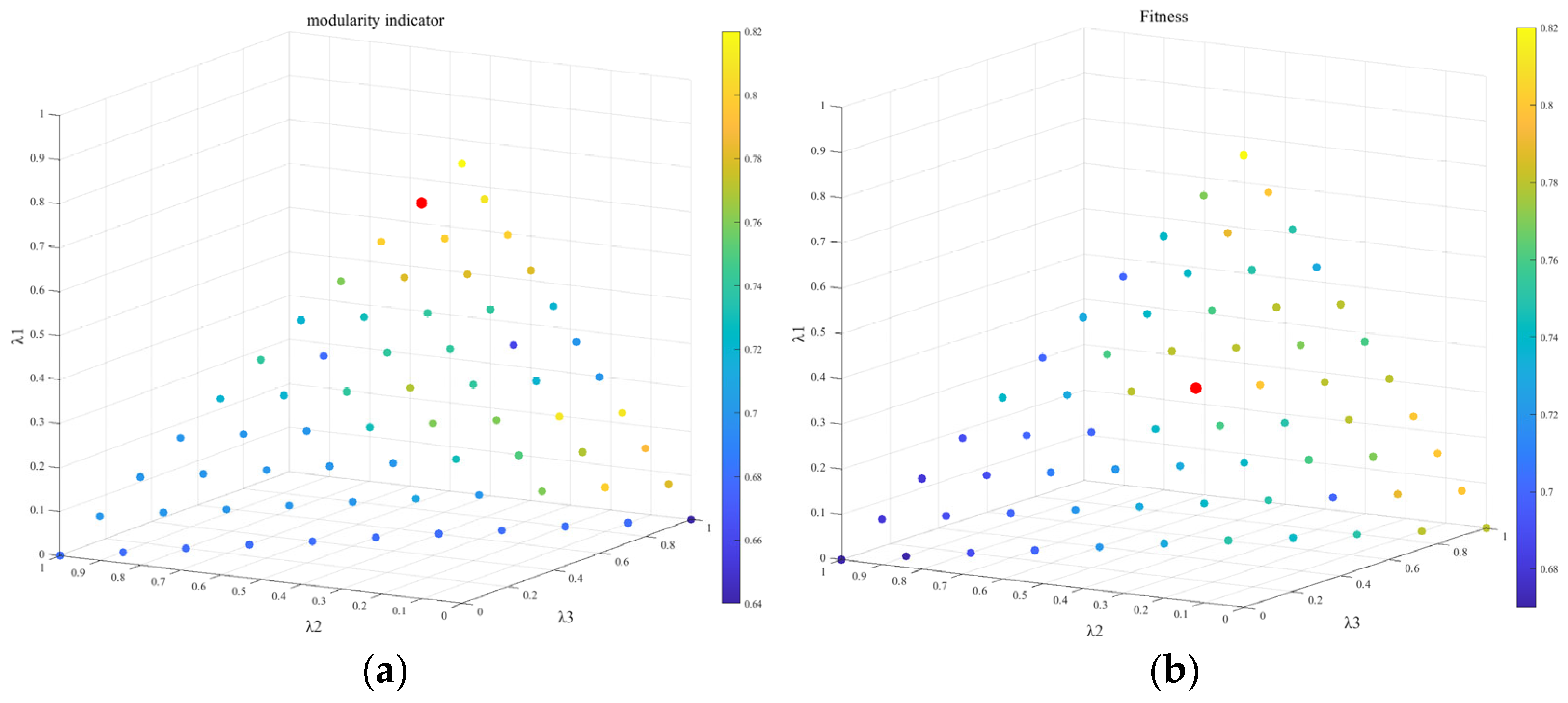
4.1.2. Analysis of the Impact of Index Weights on Cluster Partitioning
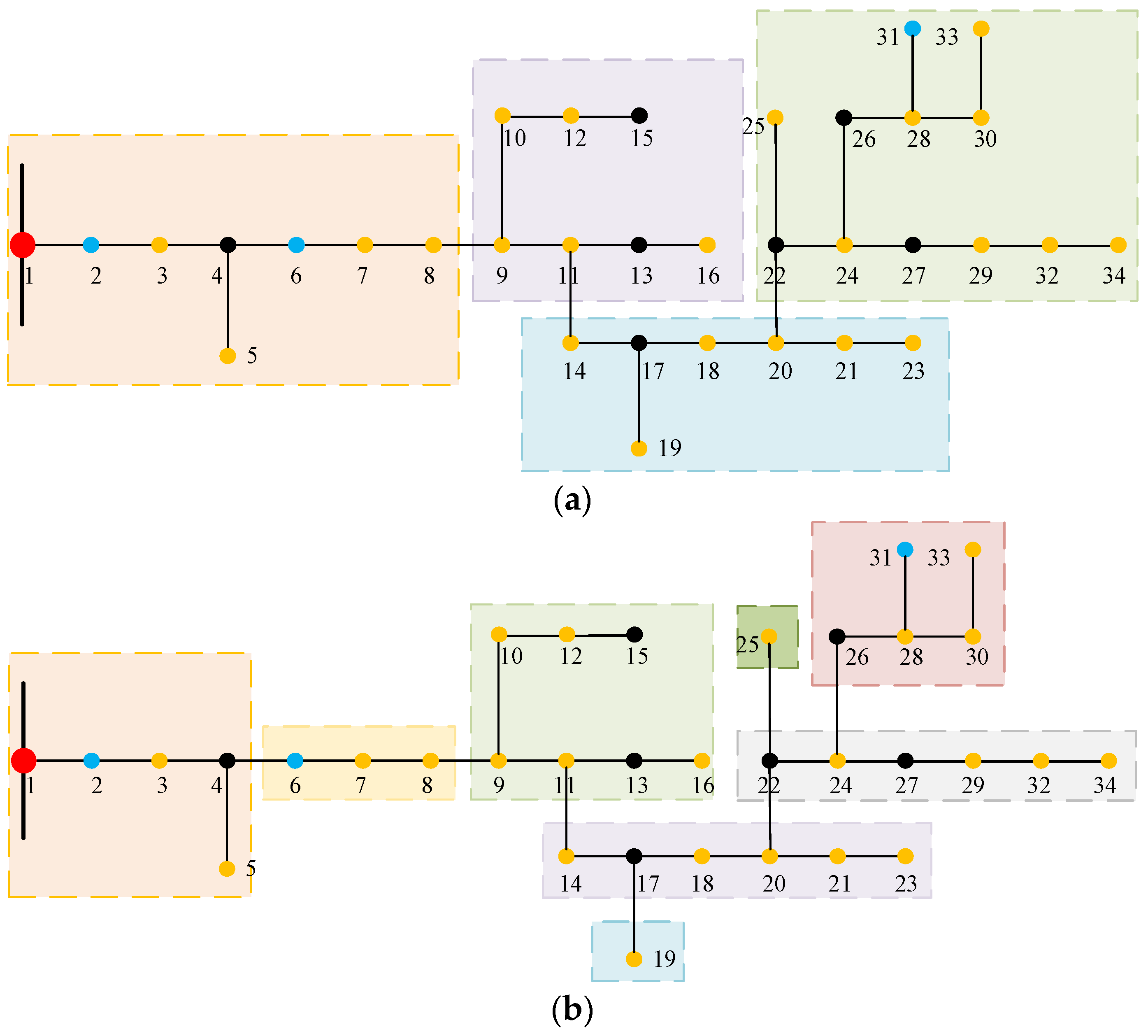
4.1.3. Analysis of the Indicator
4.1.4. Algorithmic Analysis of 34-Node
4.2. IEEE 110-Node Case Analysis
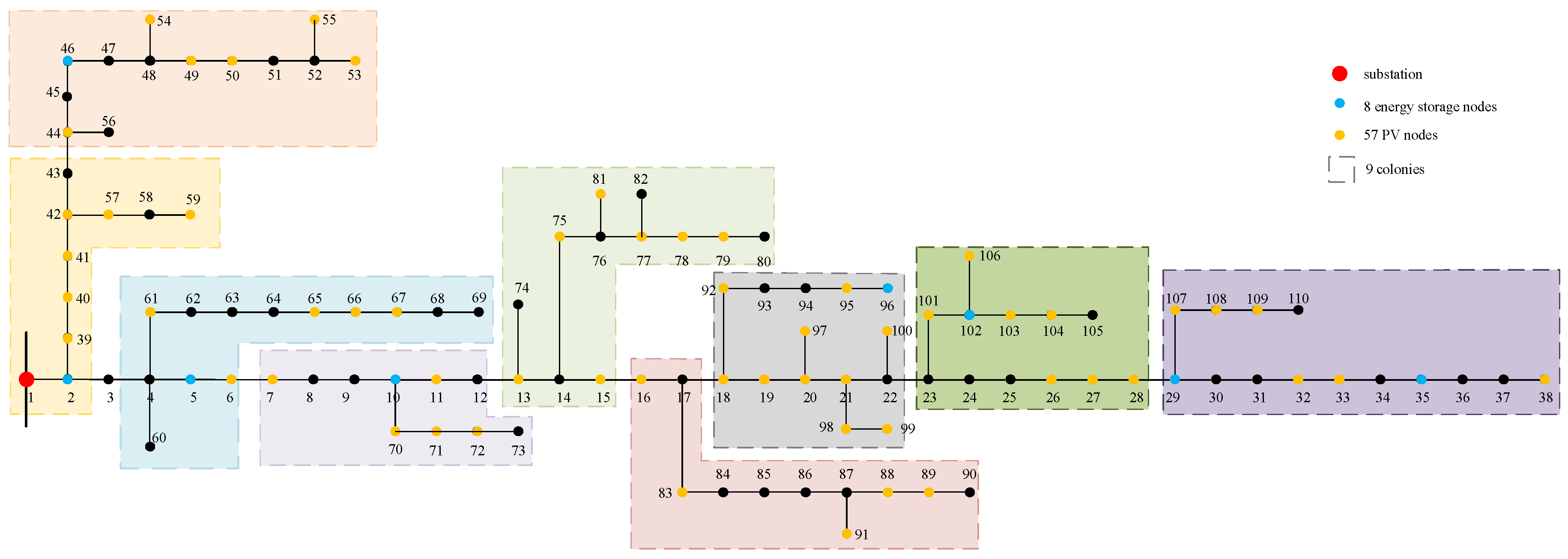
4.2.1. Distribution Network Design and Partition Results
4.2.2. Analysis of Algorithm Performance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bai, M.; Yao, P.; Dong, H.; Fang, Z.; Jin, W.; Yang, X.; Liu, J.; Yu, D. Spatial-temporal characteristics analysis of solar irradiance forecast errors in Europe and North America. Energy 2024, 297, 131187. [Google Scholar] [CrossRef]
- Li, F.; Ding, J.; Zhou, C.; Yong, W.; Huang, Y.; Wang, J.; Xu, X. Key technologies of large-scale grid-connected operation of distributed photovoltaic under new-type power system. Power Syst. Technol. 2024, 48, 184–196. [Google Scholar]
- Zhang, Z.F.; Kang, C.Q. Challenges and prospects for constructing the new-type power system towards a carbon neutrality future. Proc. CSEE 2022, 42, 2806–2819. [Google Scholar]
- Fei, Z.; Yang, H.; Du, L.; Guerrero, J.M.; Meng, K.; Li, Z. Two-stage coordinated operation of a green multi-energy ship microgrid with underwater radiated noise by distributed stochastic approach. IEEE Trans. Smart Grid 2024, 16, 1062–1074. [Google Scholar] [CrossRef]
- Xu, X.; Gao, Y.; Wang, H.; Yan, Z.; Shahidehpour, M.; Tan, Z. Distributionally robust optimization of photovoltaic power with lifted linear decision rule for distribution system voltage regulation. IEEE Trans. Sustain. Energy 2023, 15, 758–772. [Google Scholar] [CrossRef]
- Sheng, W.; Wu, M.; Ji, Y.; Kou, L.; Pan, J.; Shi, H.; Niu, G.; Wang, Z.G. Key techniques and engineering practice of distributed renewable generation clusters integration. Proc. CSEE 2019, 39, 2175–2186. [Google Scholar]
- Peng, H.; Gu, J.; Hu, Y.; Song, B. Forecasting model of saturated load based on chaotic particle swarm and optimization-gaussian process regression. Autom. Electr. Power Syst. 2017, 41, 9–14. [Google Scholar]
- Liu, S.Y. Multi-objective model predictive control of grid-connected inverters in unbalanced grids. J. Electr. Eng. 2023, 18, 77–85. [Google Scholar]
- Li, B.T.; Sun, M.Y.; Chen, X.L.; Li, B.; Ji, X.; Xiao, F. Line parameter identification method for multi-ring medium-voltage distribution network based on phaseless measurement. Autom. Electr. Power Syst. 2023, 47, 22–30. [Google Scholar]
- Li, B.; Lei, C.; Fan, B.; Huang, Y.; Jia, W.; Ma, Y. Research on typical electricity consumption law based on daily load indicator and improved distributed k-means clustering. Electr. Meas. Instrum. 2023, 60, 104–111. [Google Scholar]
- Xie, Q.; Xu, H.L.; Wang, T.; Zhao, F.; Zhang, G.; Dang, J. Disconnector fault diagnosis method based on autonomous-cognition deep temporal clustering representation. J. Electr. Eng. 2024, 19, 281–289. [Google Scholar]
- Dong, M.; Liu, K.Z.; Zhao, Q.L.; Chen, L.; Yao, Y.; Zhao, X. Multi-objective optimal operation of integrated energy system based on improved particle swarm optimization algorithm. Electr. Drive 2024, 54, 41–47. [Google Scholar]
- Chai, Y.; Guo, L.; Wang, C. Network partition and voltage coordination control for distribution networks with high penetration of distributed PV units. IEEE Trans. Power Syst. 2018, 33, 3396–3407. [Google Scholar] [CrossRef]
- Ding, M.; Liu, X.; Bi, R.; Hu, D.; Ye, B.; Zhang, J. Method for cluster partition of high-penetration distributed generators based on comprehensive performance index. Autom. Electr. Power Syst. 2018, 42, 47–52. [Google Scholar]
- Yu, L.; Sun, Y.; Xu, R.; Li, K. Improved particle swarm optimization algorithm and its application in reactive power partitioning of power grid. Autom. Electr. Power Syst. 2017, 41, 89–95. [Google Scholar]
- Pan, M.Y.; Liu, N.; Lei, J.Y. Dynamic partition method for distributed energy cluster with combined heat and power unit. Autom. Electr. Power Syst. 2021, 45, 168–176. [Google Scholar]
- Gao, Y.Q.; Wang, W.; Yu, N.P. Consensus multi-agent reinforcement learning for volt-VAR control in power distribution networks. IEEE Trans. Smart Grid 2021, 12, 3594–3604. [Google Scholar] [CrossRef]
- Newman, M.E.J. Modularity and community structure in networks. Proc. Natl. Acad. Sci. USA 2006, 103, 8577–8582. [Google Scholar] [CrossRef]
- Cotilla-Sanchez, E.; Hines, P.D.; Barrows, C.; Blumsack, S.; Patel, M. Multi-attribute partitioning of power networks based on electrical distance. IEEE Trans. Power Syst. 2013, 28, 4979–4987. [Google Scholar] [CrossRef]
- Wang, J.L.; Zhang, Y.; Wang, C.M.; Sun, J.S. Power system reactive power/voltage assessment based on sensitivity analysis and optimal power flow. Power Syst. Technol. 2005, 29, 65–69. [Google Scholar]
- Xu, H.D.; Ding, Y.F.; Wang, R.S.; Geng, G.C.; Jiang, Q.Y.; Sun, F.F. Optimal allocation of shared energy storage based on transmission network zoning. Proc. CSEE 2024. Available online: http://kns.cnki.net/kcms/detail/11.2107.tm.20240624.1645.024.html (accessed on 10 January 2025).
- Kennedy, J.; Eberhart, R.C. A discrete binary version of the particle swarm algorithm. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics, Orlando, FL, USA, 12–15 October 1997; pp. 4104–4108. [Google Scholar]
- Mesloub, S.; Mansour, A. Hybrid PSO and GA for global maximization. Int. J. Open Probl. Compt. Math 2009, 2, 597–608. [Google Scholar]
- Wang, L.; Zhang, F.; Kou, L.F.; Xu, Y.H.; Hou, X.G. Large-scale distributed PV cluster division based on fast unfolding clustering algorithm. Acta Energiae Solaris Sin. 2021, 42, 29–34. [Google Scholar]
- Chen, J.H.; Zhang, L.J.; Lu, D.; Guo, P.; Ren, J.; Li, J.; Li, Z. Cluster partition method of distributed power supply based on improved particle swarm optimization algorithm. J. Zhengzhou Univ. (Eng. Sci.) 2023, 44, 77–85. [Google Scholar]

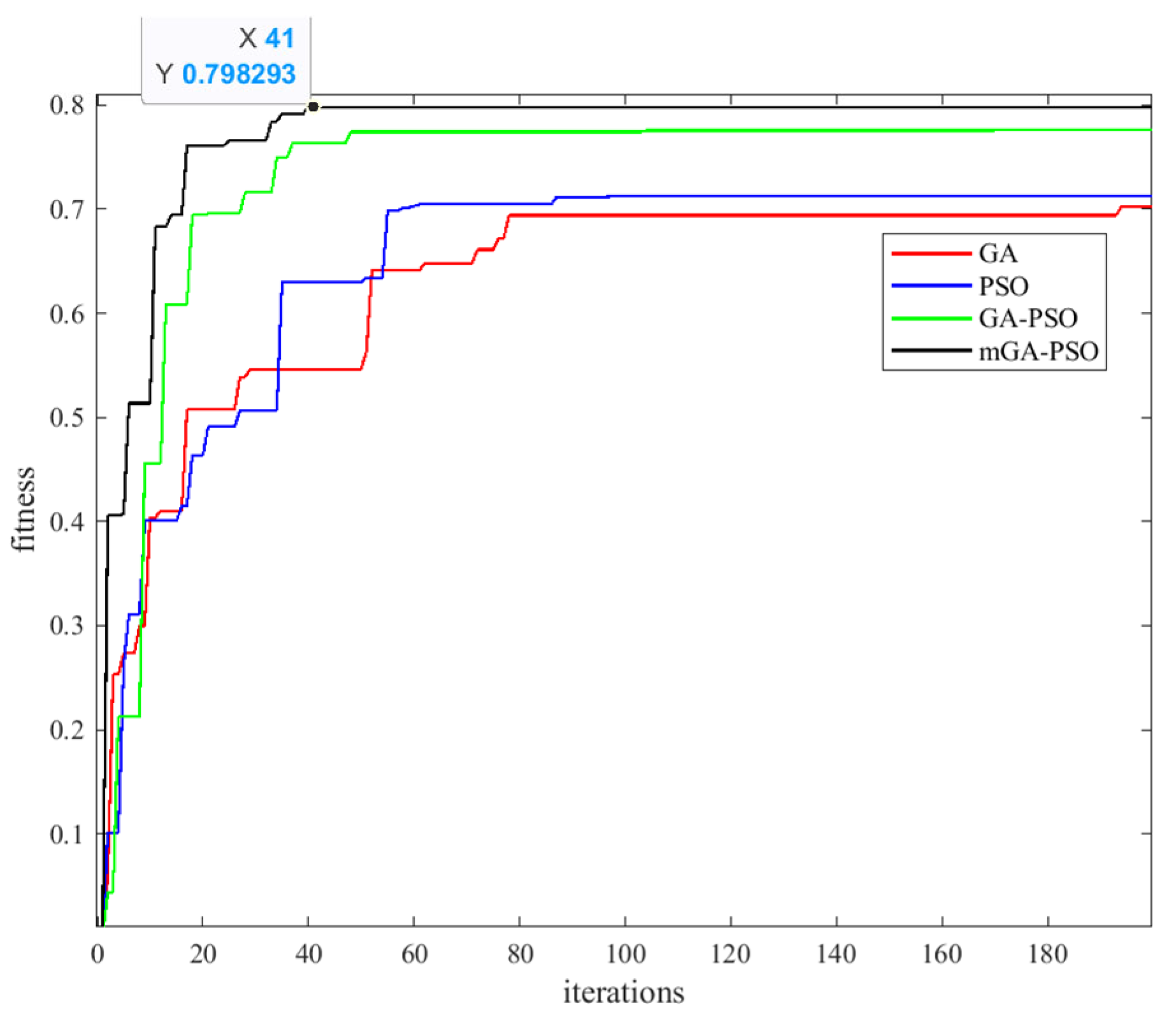

| Algorithm | GA | PSO | GA-PSO | Ours |
|---|---|---|---|---|
| optimal fitness value | 0.696 | 0.712 | 0.784 | 0.798 |
| modularity index | 0.672 | 0.724 | 0.773 | 0.786 |
| power balance index | 0.683 | 0.684 | 0.763 | 0.781 |
| node membership index | 0.741 | 0.721 | 0.821 | 0.832 |
| percentage of optimal solutions % | 58 | 68 | 76 | 86 |
| index of average convergence | 81 | 62.5 | 48 | 43.5 |
| cost time/s | >60 | 10 | 24 | 32 |
| Indicator | f | σm | φ | Cluster Number |
|---|---|---|---|---|
| this paper’s clustering indicator | 0.79 | 0.83 | 0.76 | 9 |
| modularity indicator | 0.74 | 0.74 | 0.64 | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Guo, G.; Gong, D.; Xuan, L.; He, F.; Wan, X.; Zhou, D. Cluster Partitioning Method for High-PV-Penetration Distribution Network Based on mGA-PSO Algorithm. Energies 2025, 18, 1197. https://doi.org/10.3390/en18051197
Liu Z, Guo G, Gong D, Xuan L, He F, Wan X, Zhou D. Cluster Partitioning Method for High-PV-Penetration Distribution Network Based on mGA-PSO Algorithm. Energies. 2025; 18(5):1197. https://doi.org/10.3390/en18051197
Chicago/Turabian StyleLiu, Zhu, Guowei Guo, Dehuang Gong, Lingfeng Xuan, Feiwu He, Xinglin Wan, and Dongguo Zhou. 2025. "Cluster Partitioning Method for High-PV-Penetration Distribution Network Based on mGA-PSO Algorithm" Energies 18, no. 5: 1197. https://doi.org/10.3390/en18051197
APA StyleLiu, Z., Guo, G., Gong, D., Xuan, L., He, F., Wan, X., & Zhou, D. (2025). Cluster Partitioning Method for High-PV-Penetration Distribution Network Based on mGA-PSO Algorithm. Energies, 18(5), 1197. https://doi.org/10.3390/en18051197





