A Novel Control Method for Current Waveform Reshaping and Transient Stability Enhancement of Grid-Forming Converters Considering Non-Ideal Grid Conditions
Abstract
1. Introduction
2. Topology and Control Strategies of GFM
2.1. System Description
2.2. Control Strategies of GFM
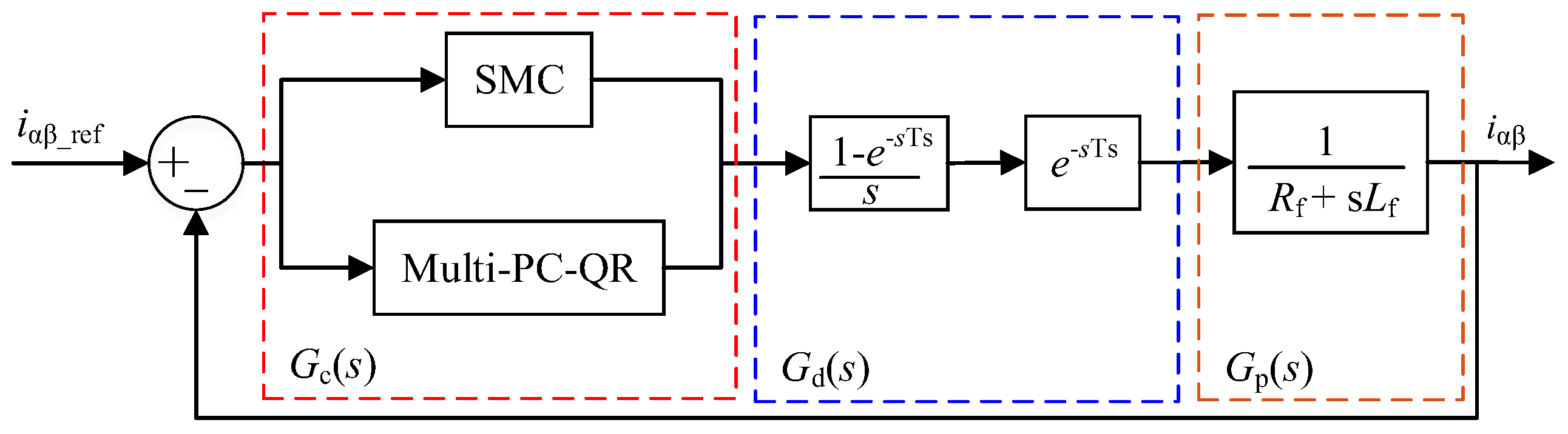
3. Improved Composite Reaching Law-Based Current Controller
3.1. Sliding Surface Selection in SMC
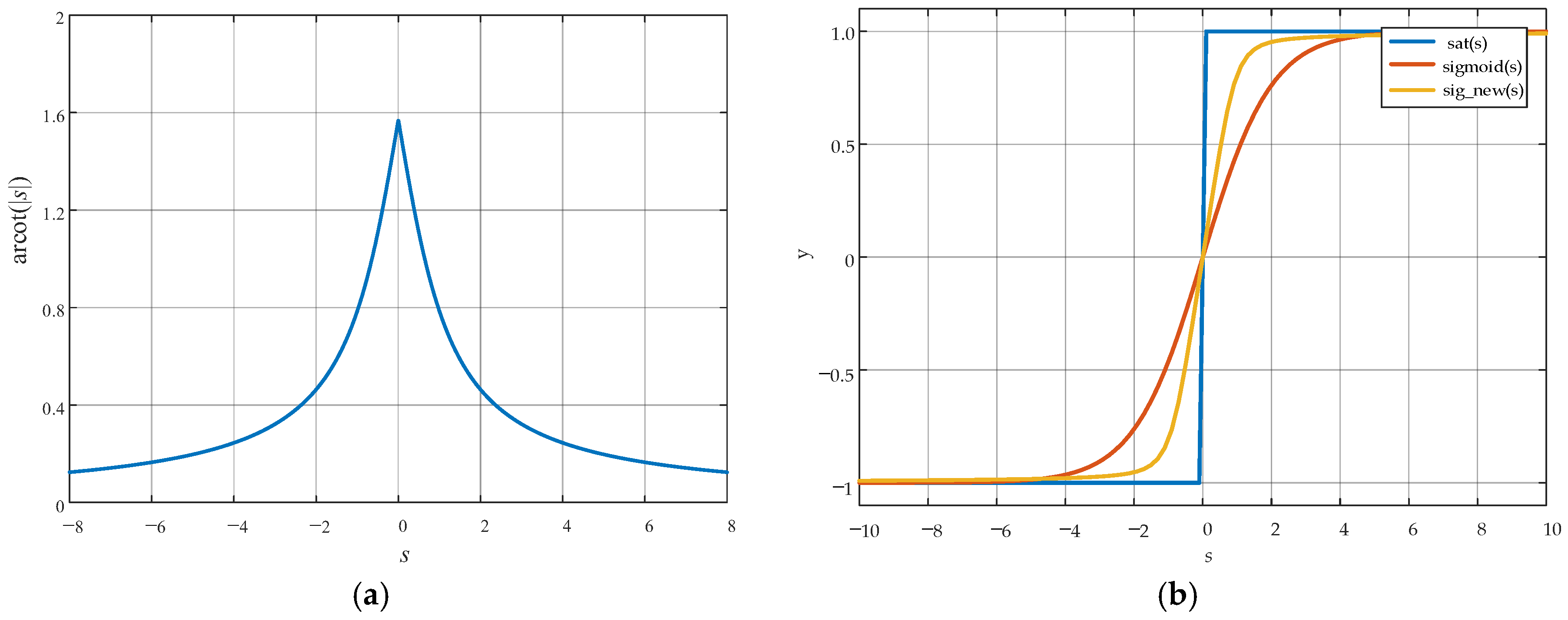
3.2. Design of an Improved Composite Reaching Law
3.3. Reachability and Finite-Time Convergence Analysis of Reaching Law
3.4. Derivation of Control Law
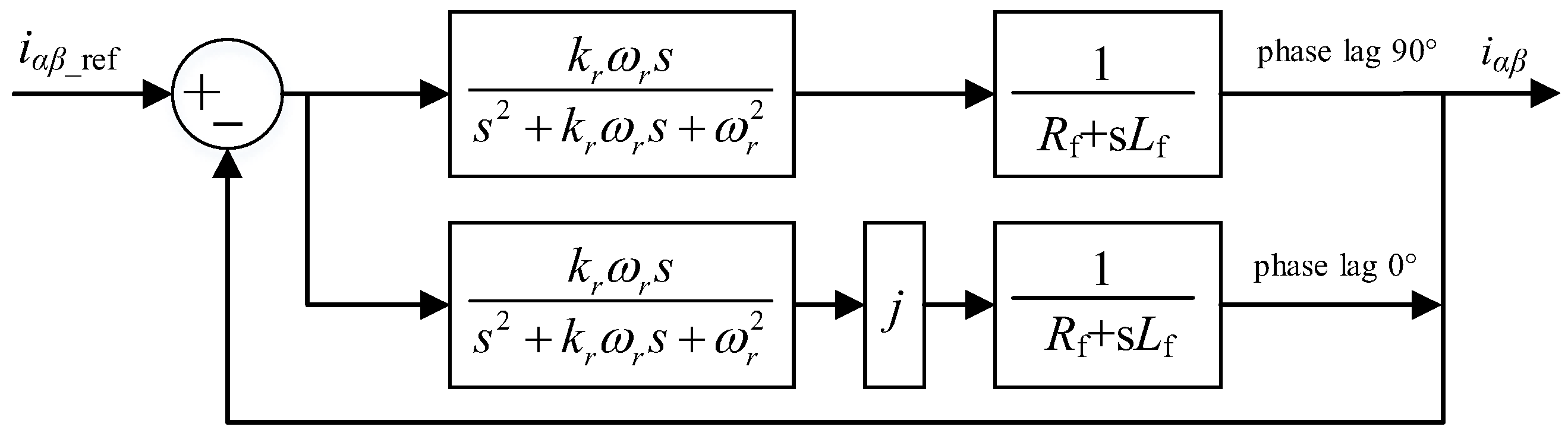
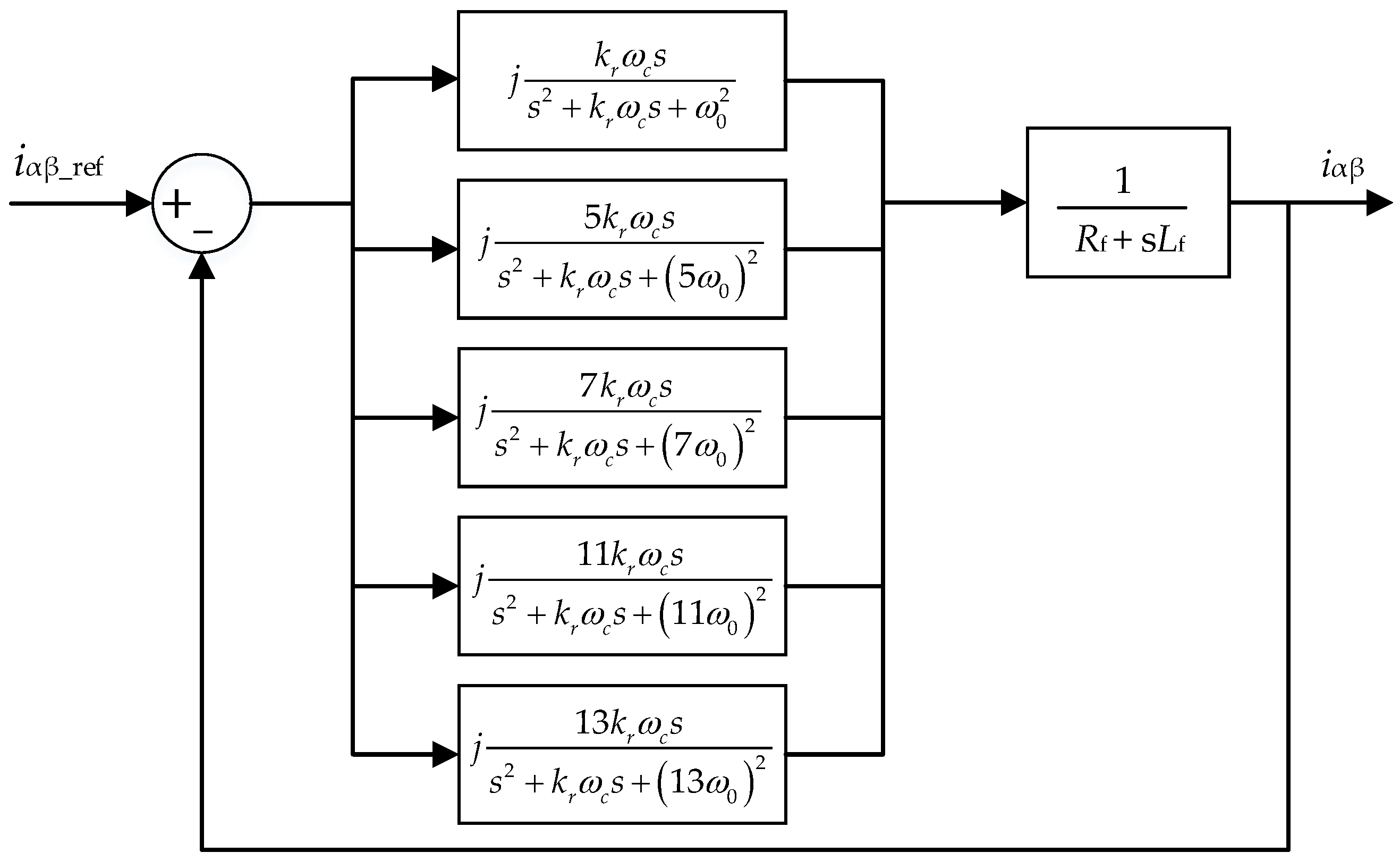
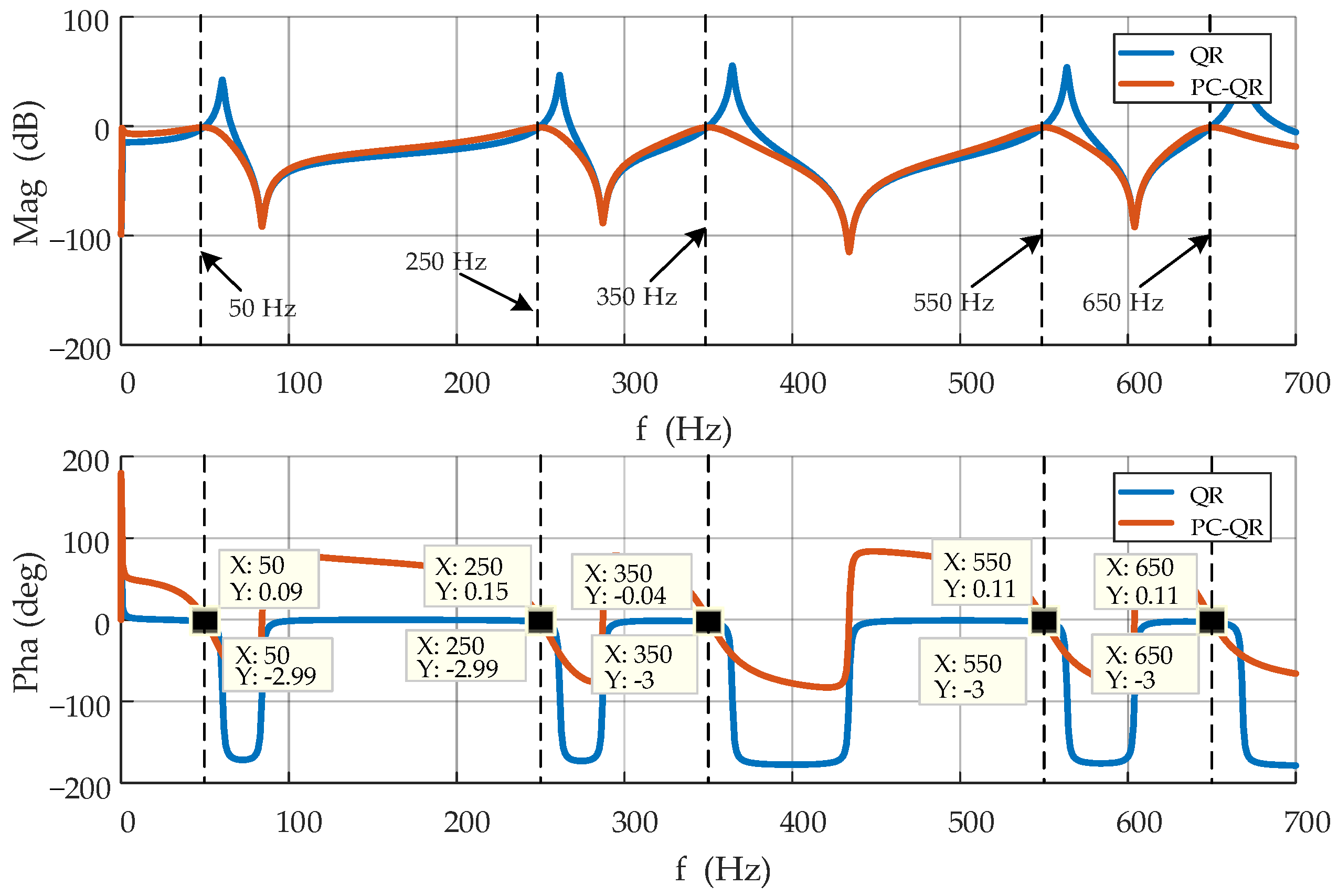
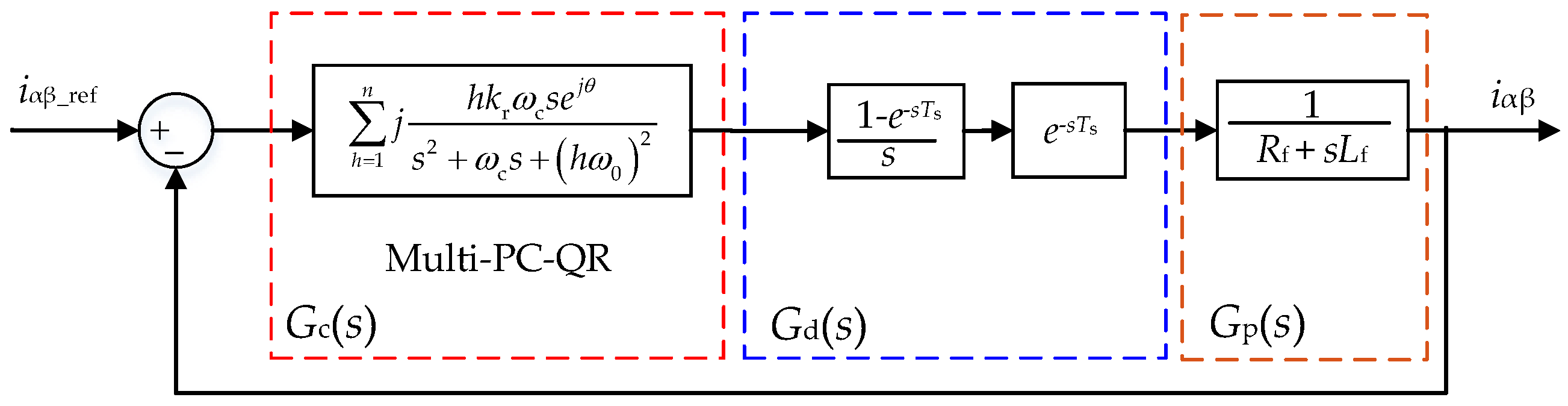
4. Improved Complex Quasi-Resonant Strategy Controller Design Considering Phase Compensation
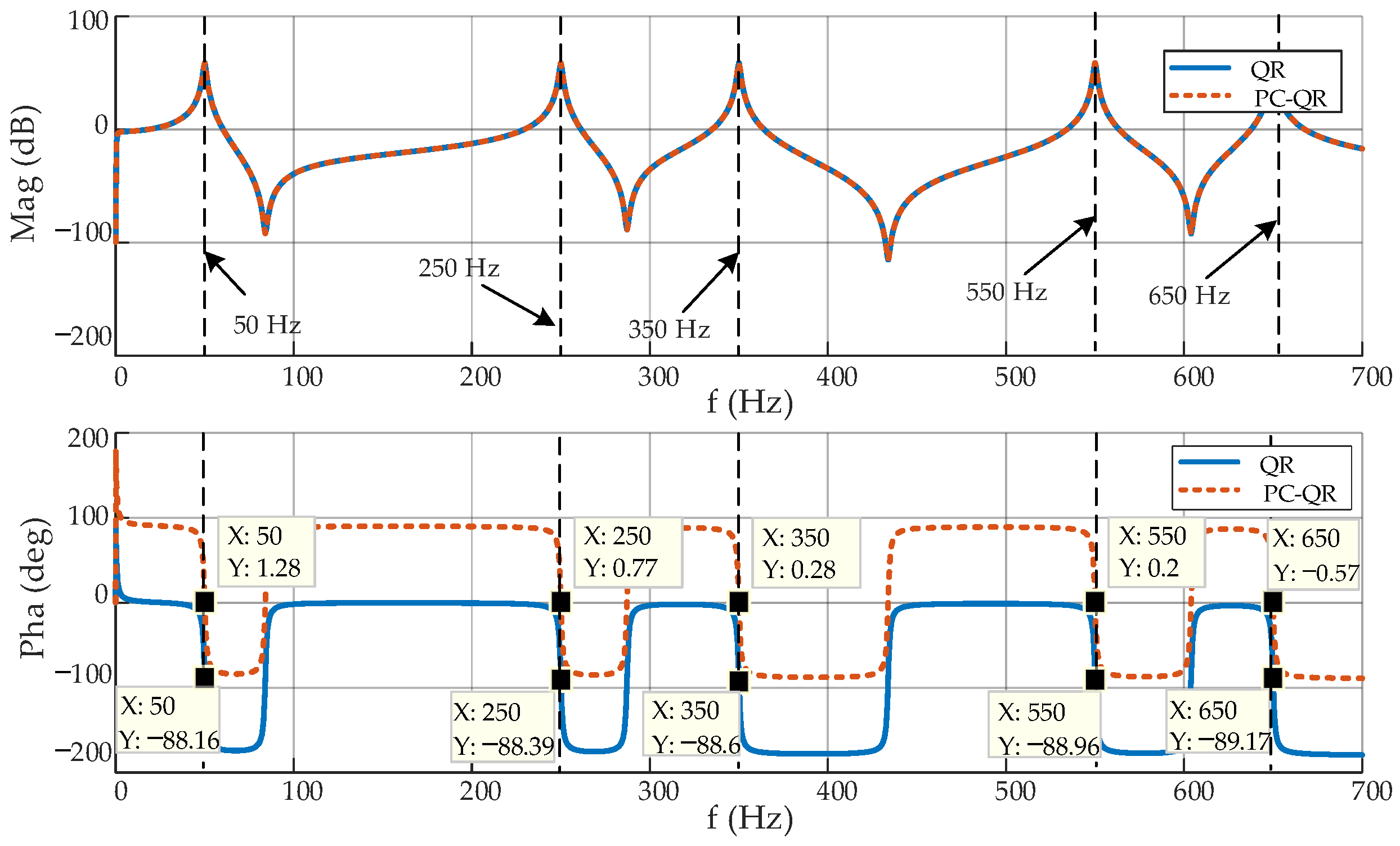
4.1. Improved Quasi-Resonant Controller Based on Phase Compensation
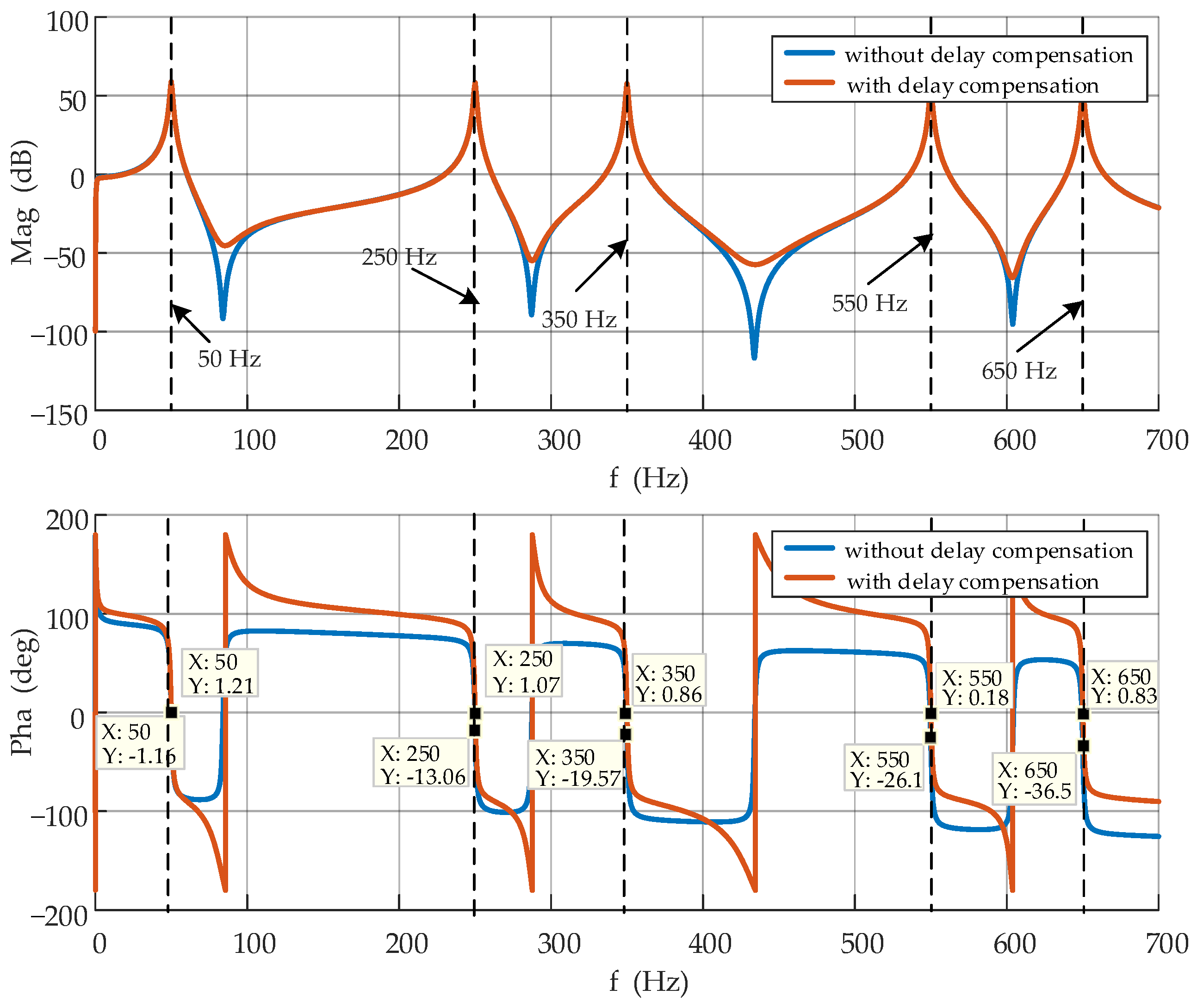
4.2. Phase Compensation Strategy
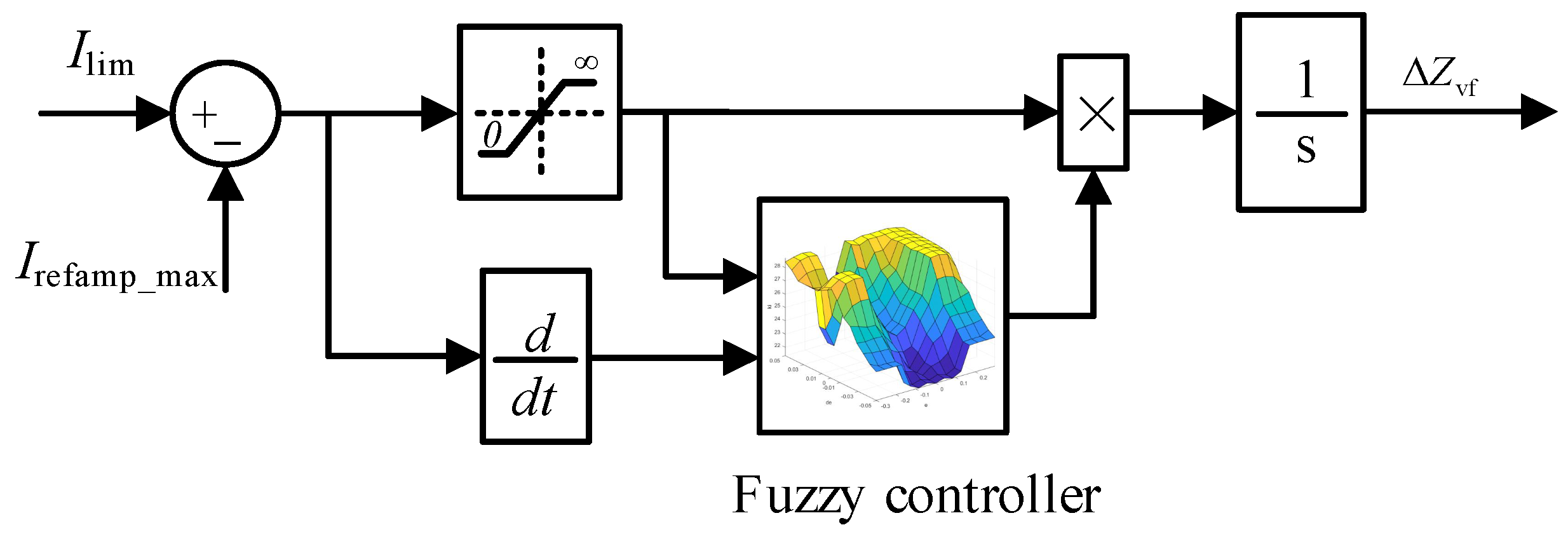
5. Individual-Phase Fuzzy Control-Based Dynamic VI Strategy for Current Limiting and Transient Stability Improvement
5.1. Fuzzy-Based Transient Adaptive VI Strategy for Current Limitation
5.2. Investigation of Current Limiting and Transient Stability Under Unbalanced Voltage Sag
5.2.1. Study of Current Limiting Strategies for Unbalanced Voltage Sag
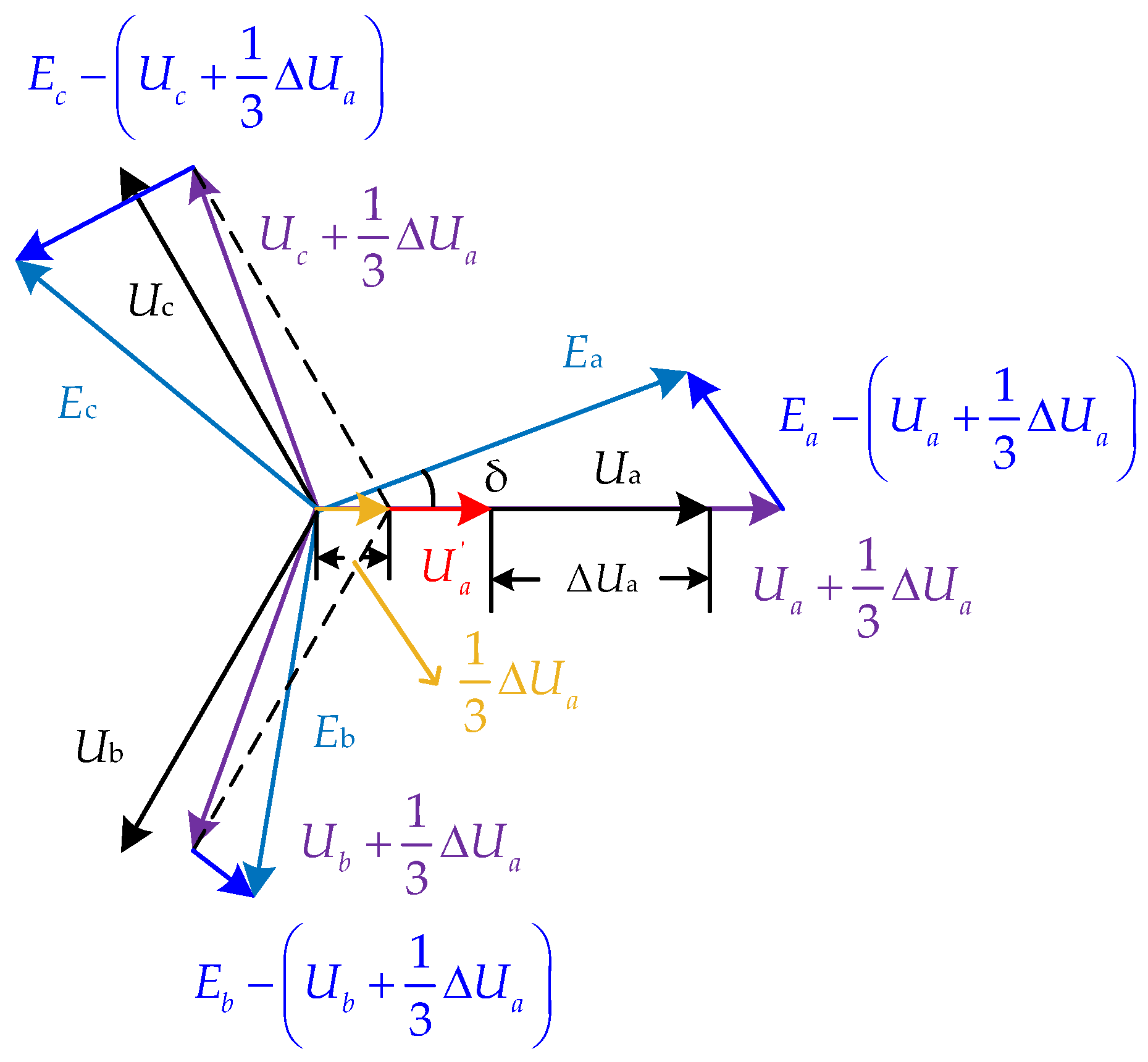
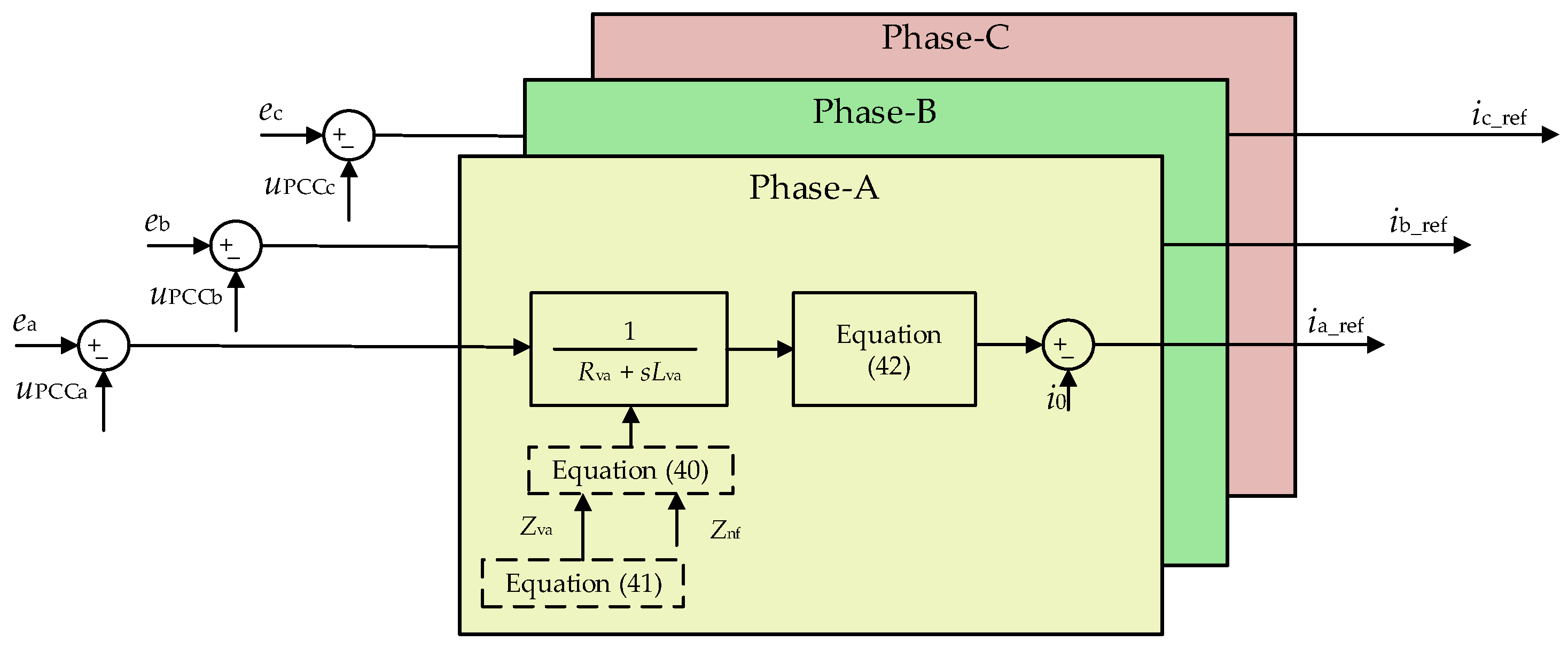
5.2.2. Individual-Phase VI Strategy for Transient Stability Enhancement via Zero-Sequence Current Separation
Effects of Zero-Sequence Current
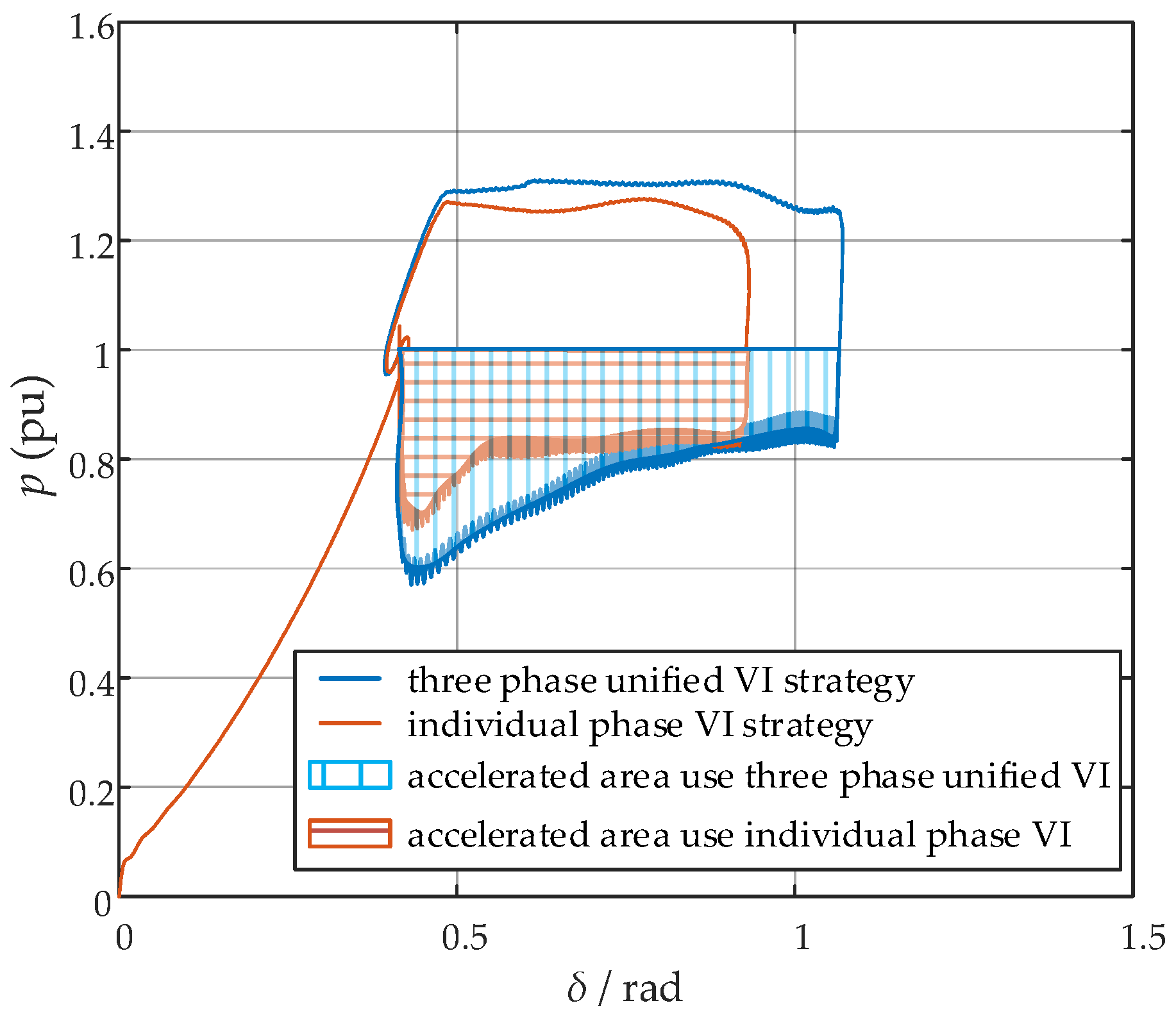
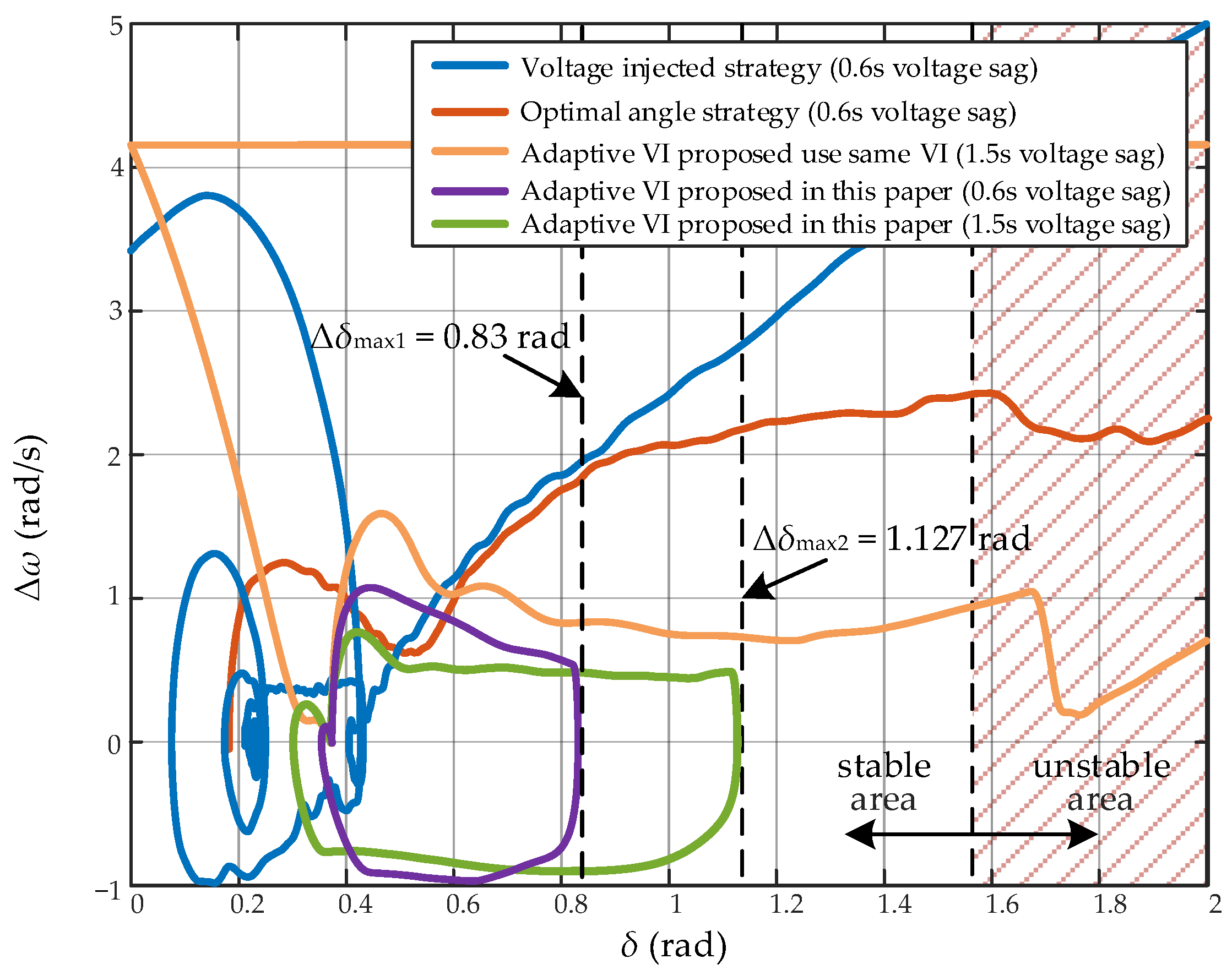
Transient Stability Enhancement Analysis
6. Simulation and Experimental Verification
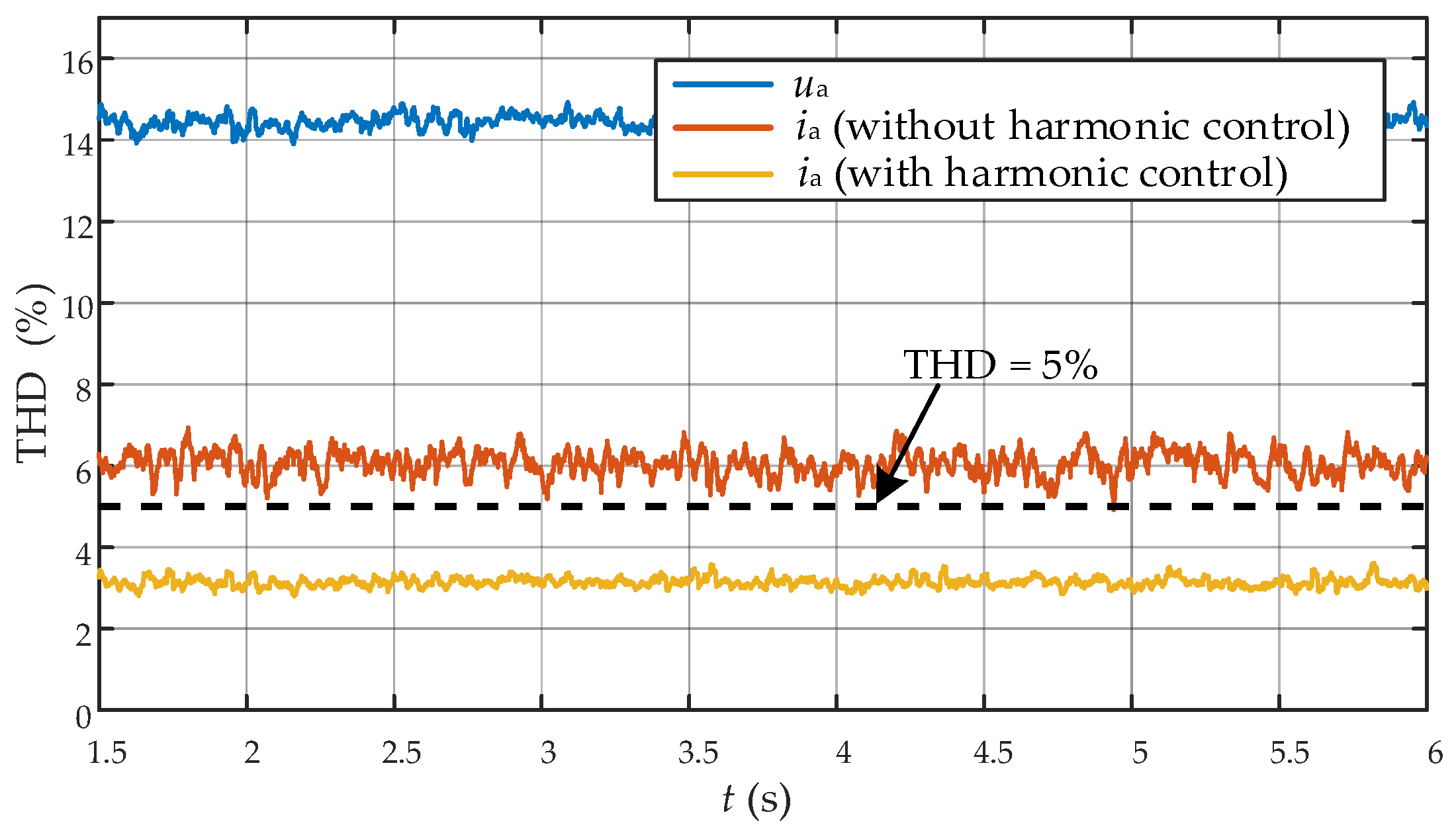
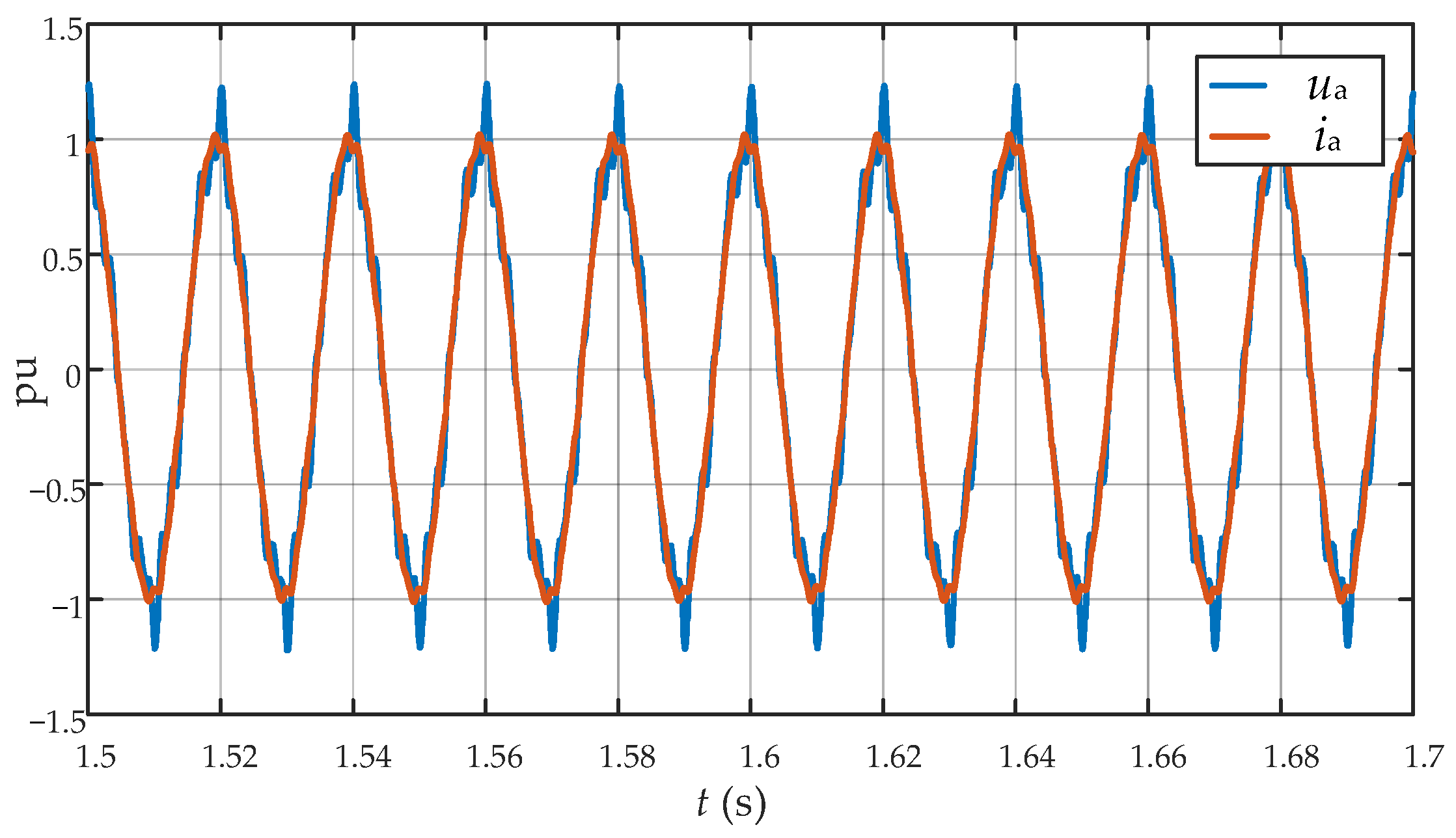
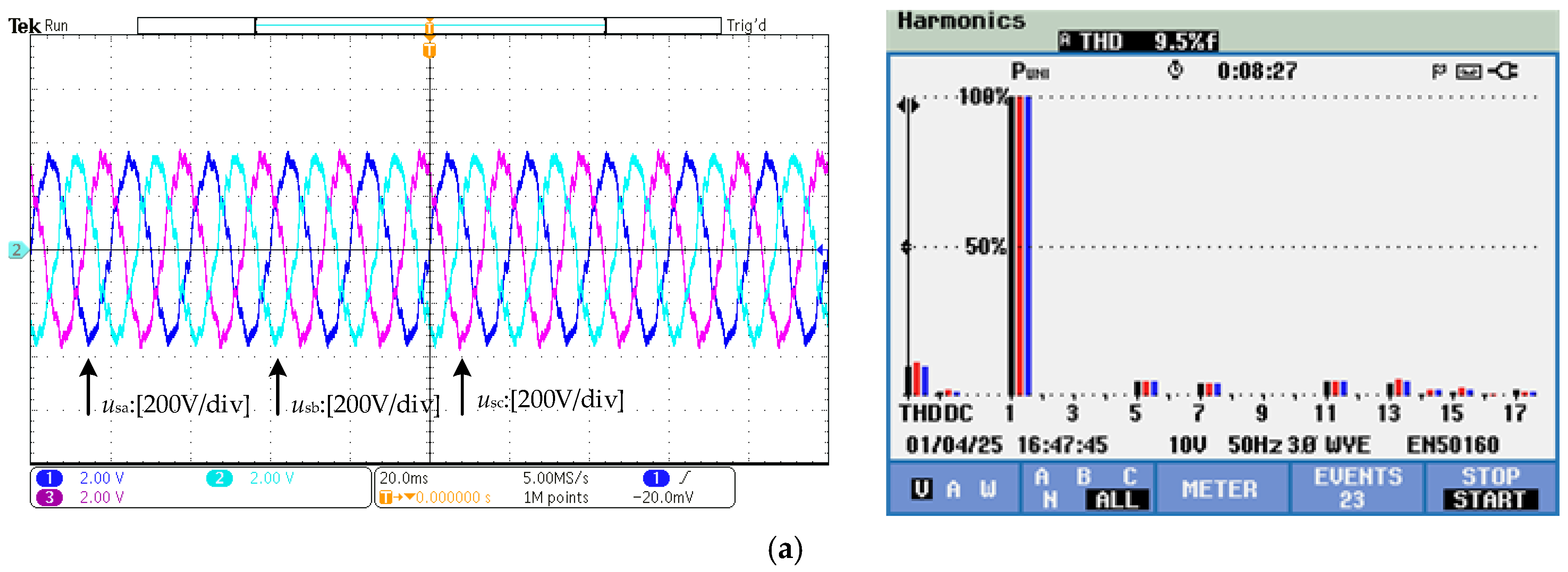
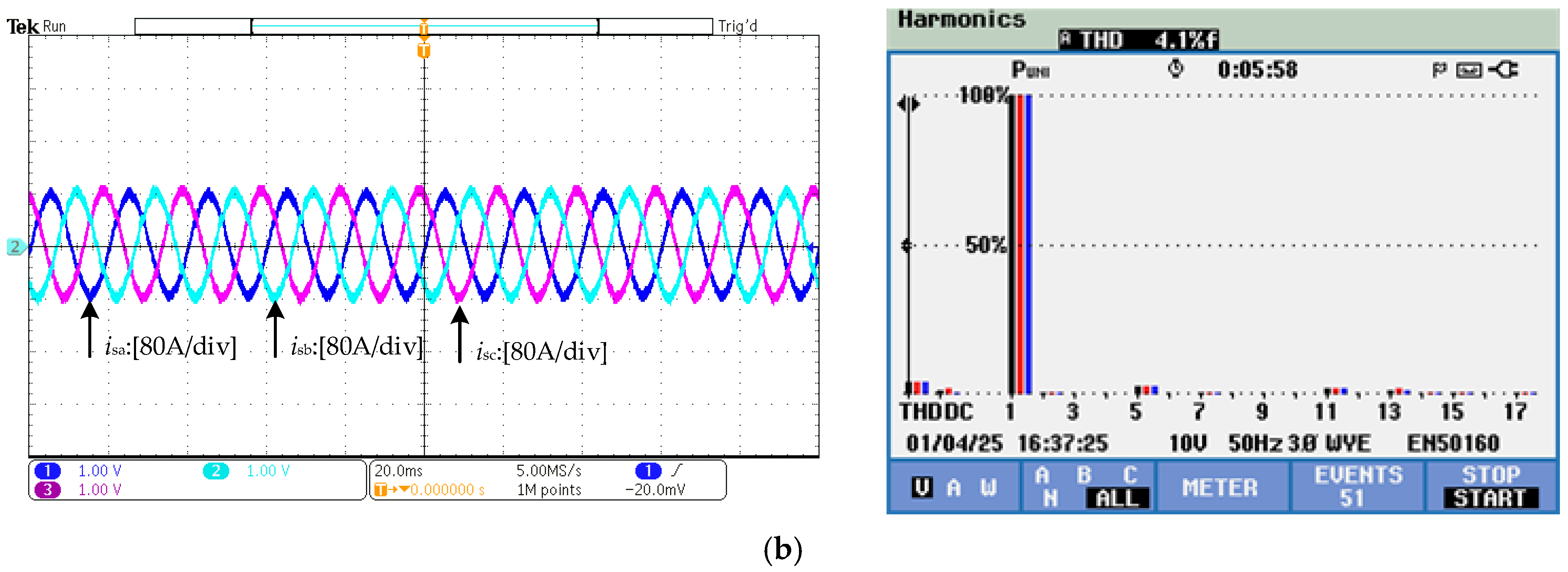
6.1. Testing Under Grid Background Harmonics Conditions
6.2. Testing Under Grid Voltage Sag Conditions
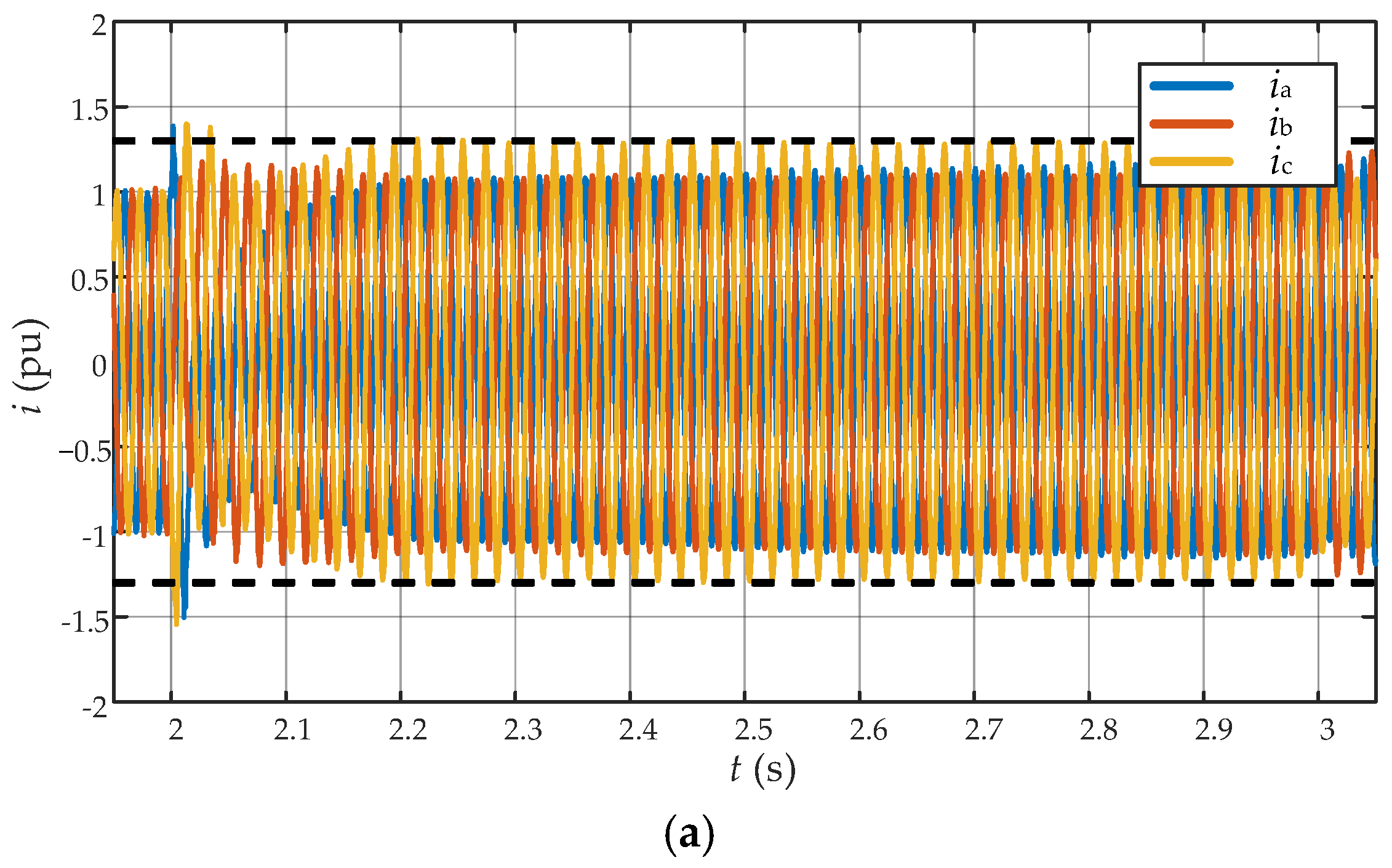
6.2.1. Single-Phase Voltage Sag Condition
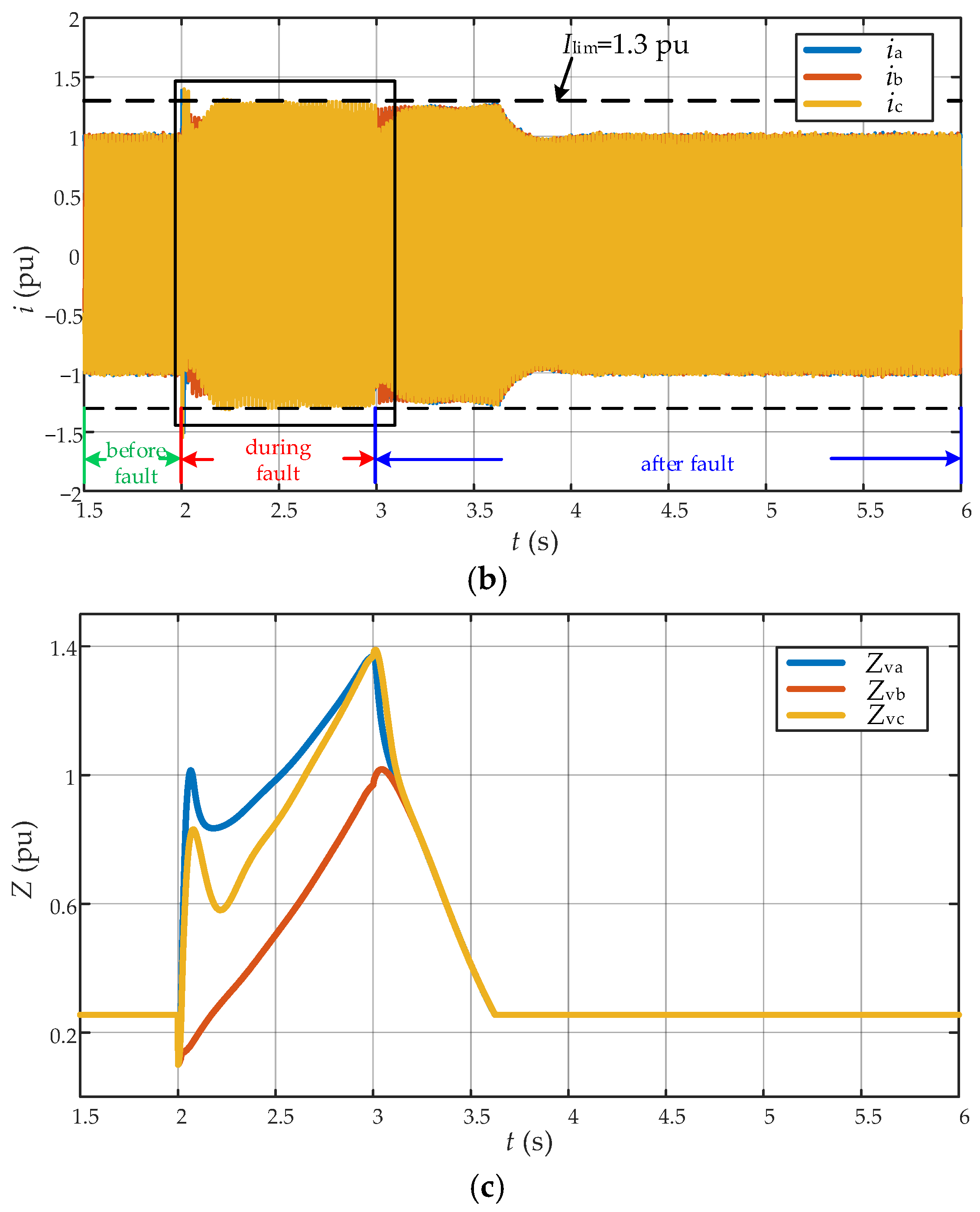
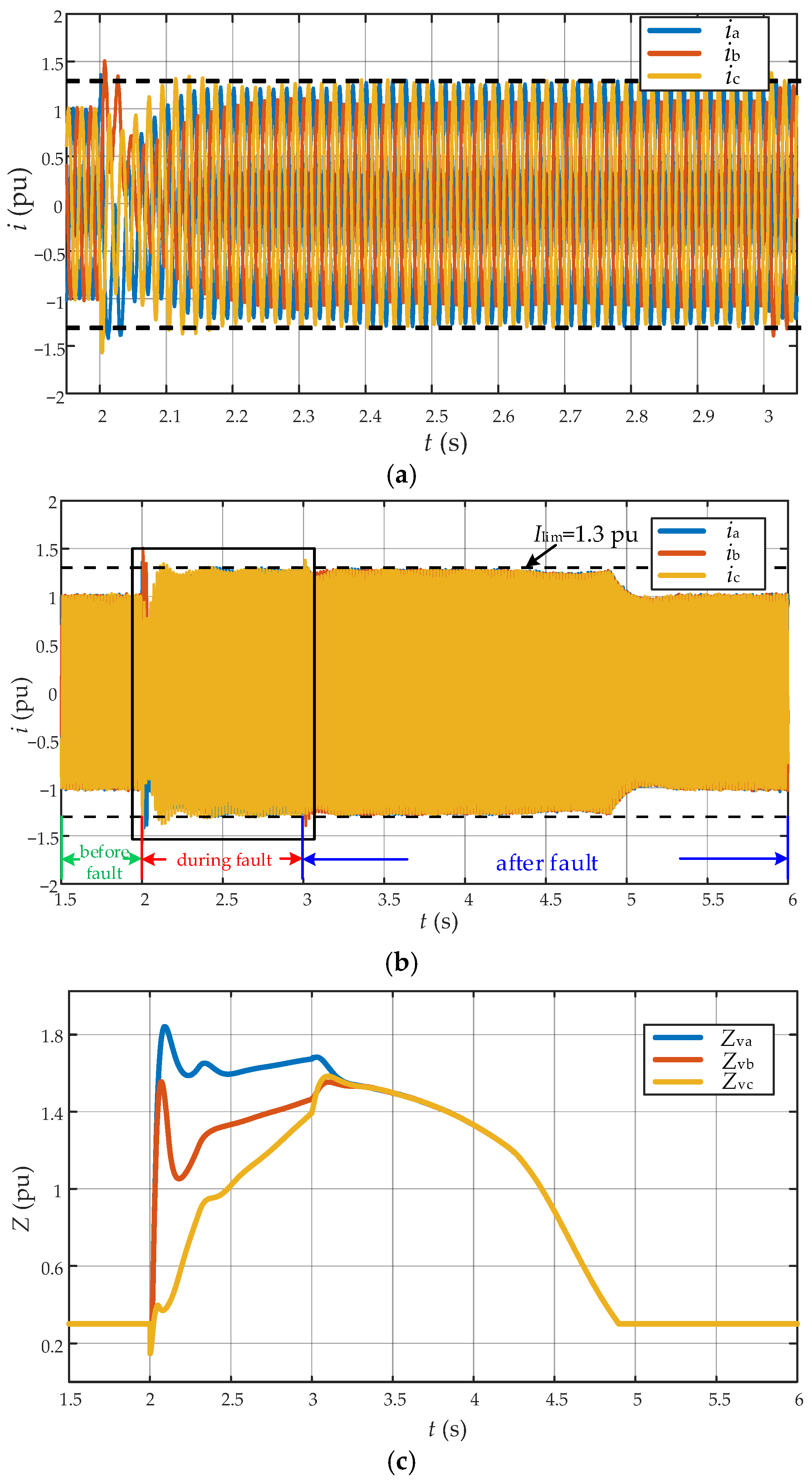
6.2.2. Two-Phase Voltage Sags Condition
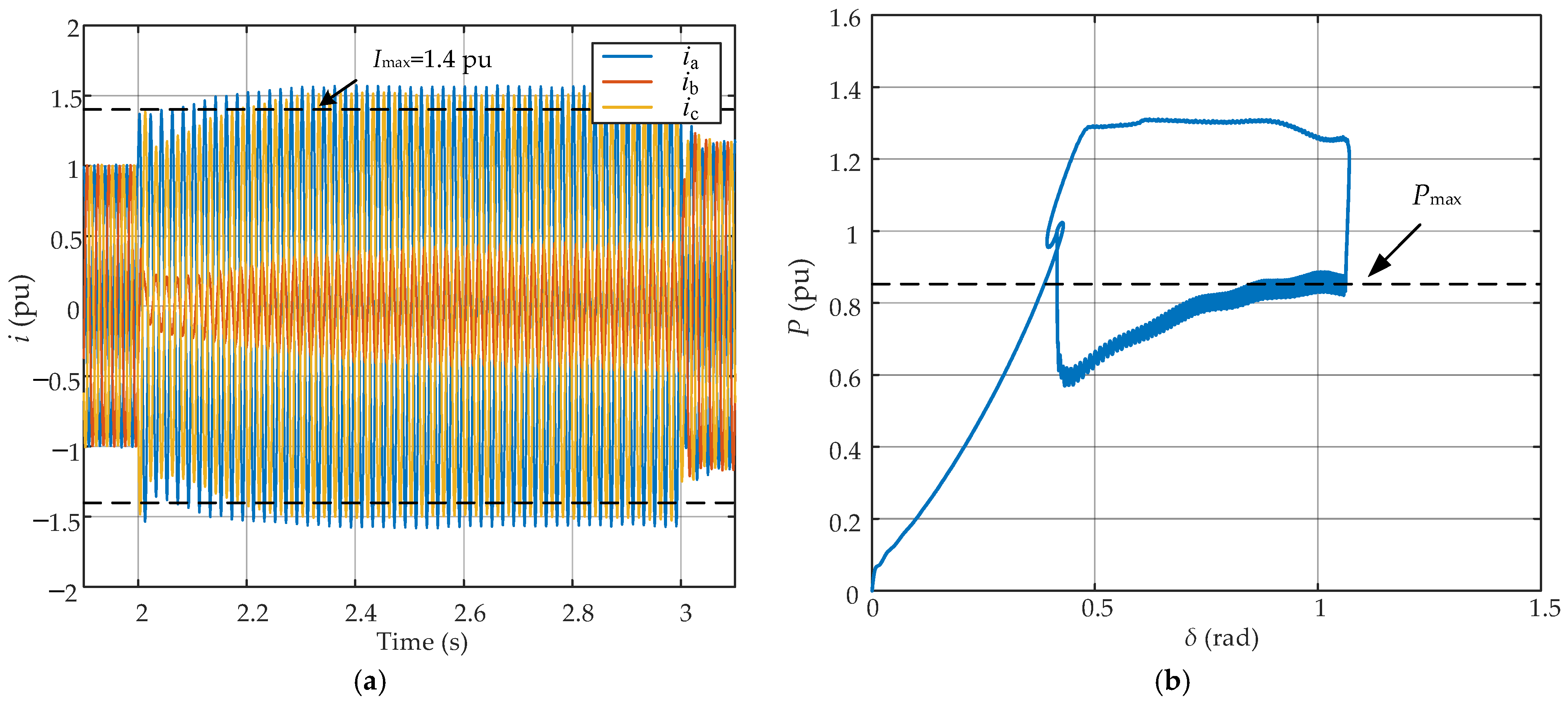
6.3. Verification of Transient Stability Improvement
6.4. Hardware-in-the-Loop Experiments
6.4.1. Test 1: Testing Under Grid Background Harmonics Conditions
6.4.2. Test 2: Unbalanced Grid Voltage Sag Conditions
6.4.3. Test 3: Verification of Transient Stability Improvement
7. Discussion
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Park, J.-Y.; Chang, J.-W. Novel Autonomous Control of Grid-Forming DGs to Realize 100% Renewable Energy Grids. IEEE Trans. Smart Grid 2024, 15, 2866–2880. [Google Scholar] [CrossRef]
- Xu, J.; Liu, W.; Liu, S.; Chang, F.; Xie, X. Current State and Development Trends of Power System Converter Grid-Forming Control Technology. Power Syst. Technol. 2022, 46, 3586–3594. [Google Scholar]
- Eroğlu, H.; Cuce, E.; Cuce, P.M.; Gul, F.; Iskenderoğlu, A. Harmonic Problems in Renewable and Sustainable Energy Systems: A Comprehensive Review. Sustain. Energy Technol. Assess. 2021, 48, 101566. [Google Scholar] [CrossRef]
- Hu, S.; Meng, Y.; Gong, W.; Wang, L. Operation Control Strategy of DFIG Wind Turbine Under Non-Ideal Grid Conditions. Trans. China Electrotech. Soc. 2013, 28, 99–104. [Google Scholar]
- Taul, M.G.; Wang, X.; Davari, P.; Blaabjerg, F. Current Limiting Control with Enhanced Dynamics of Grid-Forming Converters During Fault Conditions. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 1062–1073. [Google Scholar] [CrossRef]
- Martínez-Turégano, J.; Añó-Villalba, S.; Bernal-Perez, S.; Peña, R.; Blasco-Gimenez, R. Small-Signal Stability and Fault Performance of Mixed Grid Forming and Grid Following Offshore Wind Power Plants Connected to a HVDC-Diode Rectifier. IET Renew. Power Gener. 2020, 14, 2166–2175. [Google Scholar] [CrossRef]
- Si, W.; Fang, J. Transient Stability Improvement of Grid-Forming Converters Through Voltage Amplitude Regulation and Reactive Power Injection. IEEE Trans. Power Electron. 2023, 38, 12116–12125. [Google Scholar] [CrossRef]
- Rokrok, E.; Qoria, T.; Bruyere, A.; Francois, B.; Guillaud, X. Transient Stability Assessment and Enhancement of Grid-Forming Converters Embedding Current Reference Saturation as Current Limiting Strategy. IEEE Trans. Power Syst. 2022, 37, 1519–1531. [Google Scholar] [CrossRef]
- Fang, J.; Si, W.; Xing, L.; Goetz, S.M. Analysis and Improvement of Transient Voltage Stability for Grid-Forming Converters. IEEE Trans. Ind. Electron. 2024, 71, 7230–7240. [Google Scholar] [CrossRef]
- Liu, B.; Xiang, X.; Li, Y.; Yang, H.; Li, W.; He, X. Stability Constrained Transient Overcurrent Capability Enhancement of Grid Forming Converters Based on Switching Frequency Adjustment. IEEE Trans. Power Electron. 2025, 40, 2987–3004. [Google Scholar] [CrossRef]
- Rosso, R.; Engelken, S.; Liserre, M. On the Implementation of an FRT Strategy for Grid-Forming Converters Under Symmetrical and Asymmetrical Grid Faults. IEEE Trans. Ind. Appl. 2021, 57, 4385–4397. [Google Scholar] [CrossRef]
- GB/T 33593-2017; Technical Requirements for Grid Connection of Distributed Resources. Standardization Administration of China: Beijing, China, 2017.
- IEEE Std 1547-2018; IEEE Standard for Interconnection and Interoperability of Distributed Energy Resources with Associated Electric Power Systems Interfaces. IEEE: Piscataway, NJ, USA, 2018.
- Das, T.S.; Annakkage, U.D.; Muthumuni, D.; Park, I.K. Robust higher order sliding mode control of grid-forming converters with LCL filter in weak grid scenarios for fast frequency support. IET Gener. Transm. Distrib. 2024, 18, 3851–3862. [Google Scholar] [CrossRef]
- Fu, C.; Zhang, C.; Zhang, G.; Zhang, C.; Su, Q. Finite-Time Command Filtered Control of Three-Phase AC/DC Converter Under Unbalanced Grid Conditions. IEEE Trans. Ind. Electron. 2023, 70, 6876–6886. [Google Scholar] [CrossRef]
- Komurcugil, H.; Biricik, S.; Bayhan, S.; Zhang, Z. Sliding Mode Control: Overview of Its Applications in Power Converters. IEEE Ind. Electron. Mag. 2021, 15, 40–49. [Google Scholar] [CrossRef]
- Wang, Z.; Li, S.; Li, Q. Discrete-Time Fast Terminal Sliding Mode Control Design for DC–DC Buck Converters with Mismatched Disturbances. IEEE Trans. Ind. Inform. 2020, 16, 1204–1213. [Google Scholar] [CrossRef]
- Pal, A.; Hosseinabadi, P.A.; Panigrahi, B.K.; Pota, H.R. A Fixed-Time Sliding Mode Controller for Black-Starting of Grid-Forming Inverter-Based Generations. In Proceedings of the 2024 IEEE 4th International Conference on Sustainable Energy and Future Electric Transportation (SEFET), Hyderabad, India, 31 July–3 August 2024; pp. 1–5. [Google Scholar]
- Haroon, F.; Aamir, M.; Waqar, A.; Qaisar, S.M.; Ali, S.U.; Almaktoom, A.T. A Composite Exponential Reaching Law Based SMC with Rotating Sliding Surface Selection Mechanism for Two Level Three Phase VSI in Vehicle to Load Applications. Energies 2023, 16, 346. [Google Scholar] [CrossRef]
- Jeeranantasin, N.; Nungam, S. Sliding Mode Control of Three-Phase AC/DC Converters Using Exponential Rate Reaching Law. J. Syst. Eng. Electron. 2022, 33, 210–221. [Google Scholar] [CrossRef]
- Ye, T.; Dai, N.; Lam, C.-S.; Wong, M.-C.; Guerrero, J.M. Analysis, Design and Implementation of a Quasi-Proportional-Resonant Controller for a Multifunctional Capacitive-Coupling Grid-Connected Inverter. IEEE Trans. Ind. Appl. 2016, 52, 4269–4280. [Google Scholar] [CrossRef]
- Mishra, M.K.; Lal, V.N. An Advanced Proportional Multiresonant Controller for Enhanced Harmonic Compensation with Power Ripple Mitigation of Grid-Integrated PV Systems Under Distorted Grid Voltage Conditions. IEEE Trans. Ind. Appl. 2021, 57, 5318–5331. [Google Scholar] [CrossRef]
- Hans, F.; Schumacher, W.; Chou, S.-F.; Wang, X. Design of Multifrequency Proportional–Resonant Current Controllers for Voltage-Source Converters. IEEE Trans. Power Electron. 2020, 35, 13573–13589. [Google Scholar] [CrossRef]
- Qoria, T.; Gruson, F.; Colas, F.; Denis, G.; Prevost, T.; Guillaud, X. Critical Clearing Time Determination and Enhancement of Grid-Forming Converters Embedding Virtual Impedance as Current Limitation Algorithm. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 1050–1061. [Google Scholar] [CrossRef]
- Jin, Z.; Wang, X. A DQ-Frame Asymmetrical Virtual Impedance Control for Enhancing Transient Stability of Grid-Forming Inverters. IEEE Trans. Power Electron. 2022, 37, 4535–4544. [Google Scholar] [CrossRef]
- Zhou, L.; Liu, S.; Chen, Y.; Yi, W.; Wang, S.; Zhou, X. Harmonic Current and Inrush Fault Current Coordinated Suppression Method for VSG Under Non-Ideal Grid Condition. IEEE Trans. Power Electron. 2021, 36, 1030–1042. [Google Scholar] [CrossRef]
- Baeckeland, N.; Venkatramanan, D.; Kleemann, M.; Dhople, S. Stationary-Frame Grid-Forming Inverter Control Architectures for Unbalanced Fault-Current Limiting. IEEE Trans. Energy Convers. 2022, 37, 2813–2825. [Google Scholar] [CrossRef]
- Narula, A.; Imgart, P.; Bongiorno, M.; Beza, M.; Svensson, J.R.; Hasler, J.-P. Voltage-Based Current Limitation Strategy to Preserve Grid-Forming Properties Under Severe Grid Disturbances. IEEE Open J. Power Electron. 2023, 4, 176–188. [Google Scholar] [CrossRef]
- Mahamedi, B.; Eskandari, M.; Fletcher, J.E.; Zhu, J. Sequence-Based Control Strategy with Current Limiting for the Fault Ride-Through of Inverter-Interfaced Distributed Generators. IEEE Trans. Sustain. Energy 2020, 11, 165–174. [Google Scholar] [CrossRef]
- Jia, Q.; Liu, J.; Liu, J.; Xu, J. A General Current Limiting Strategy of Grid-Forming Converters Based on Adaptive Virtual Impedance Regulated by Fuzzy PI Control. In Proceedings of the 2024 IEEE 10th International Power Electronics and Motion Control Conference (IPEMC2024-ECCE Asia), Chengdu, China, 17–20 May 2024; pp. 4836–4841. [Google Scholar]
- Sebaaly, F.; Vahedi, H.; Kanaan, H.Y.; Moubayed, N.; Al-Haddad, K. Sliding Mode Fixed Frequency Current Controller Design for Grid-Connected NPC Inverter. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 1397–1405. [Google Scholar] [CrossRef]
- Zhao, S.; Shao, B.; Gao, B.; Li, R.; Pei, J. Sliding Mode Current Control Design and Stability Analysis of VSC-HVDC Based on Combinatorial Reaching Law. High Volt. Eng. 2019, 45, 3603–3611. [Google Scholar]
- Liu, J. Sliding Mode Control Design and MATLAB Simulation: The Basic Theory and Design Method, 3rd ed.; Tsinghua University Press: Beijing, China, 2015. [Google Scholar]
- Qiao, Z.; Shi, T.; Wang, Y.; Yan, Y.; Xia, C.; He, X. New Sliding-Mode Observer for Position Sensorless Control of Permanent-Magnet Synchronous Motor. IEEE Trans. Ind. Electron. 2013, 60, 710–719. [Google Scholar] [CrossRef]
- Sarpturk, S.; Istefanopulos, Y.; Kaynak, O. On the Stability of Discrete-Time Sliding Mode Control Systems. IEEE Trans. Autom. Control 1987, 32, 930–932. [Google Scholar] [CrossRef]
- Li, T.; Li, Y.; Li, S.; Zhang, W. Research on Current-Limiting Control Strategy Suitable for Ground Faults in AC Microgrid. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 1736–1750. [Google Scholar] [CrossRef]
- Yepes, A.G.; Freijedo, F.D.; Doval-Gandoy, J.; López, Ó.; Malvar, J.; Fernandez-Comesaña, P. Effects of Discretization Methods on the Performance of Resonant Controllers. IEEE Trans. Power Electron. 2010, 25, 1692–1712. [Google Scholar] [CrossRef]
- Zhao, F.; Zhu, T.; Harnefors, L.; Fan, B.; Wu, H.; Zhou, Z. Closed-Form Solutions for Grid-Forming Converters: A Design-Oriented Study. IEEE Open J. Power Electron. 2024, 5, 186–200. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, C.; Yang, R.; Molinas, M.; Cai, X. Current-Constrained Power-Angle Characterization Method for Transient Stability Analysis of Grid-Forming Voltage Source Converters. IEEE Trans. Energy Convers. 2023, 38, 1338–1349. [Google Scholar] [CrossRef]
- Rodriguez, P.; Candela, I.; Citro, C.; Rocabert, J.; Luna, A. Control of Grid-Connected Power Converters Based on a Virtual Admittance Control Loop. In Proceedings of the 15th European Conference on Power Electronics and Applications (EPE), Lille, France, 2–6 September 2013; pp. 1–10. [Google Scholar]
- Cai, S.; Liang, D.; Zhou, K.; Zhang, L.; Liu, Y. Switching Strategy with the Improved Single-Phase dq0 Voltage Detection Method for the Load Voltage Compensation Unit of Hybrid Distribution Transformer. Trans. China Electrotech. Soc. 2021, 36, 126–132. [Google Scholar]
- Tavakoli, S.D.; Prieto-Araujo, E.; Gomis-Bellmunt, O.; Galceran-Arellano, S. Fault ride-through control based on voltage prioritization for grid-forming converters. IET Renew. Power Gener. 2023, 17, 1370–1384. [Google Scholar] [CrossRef]



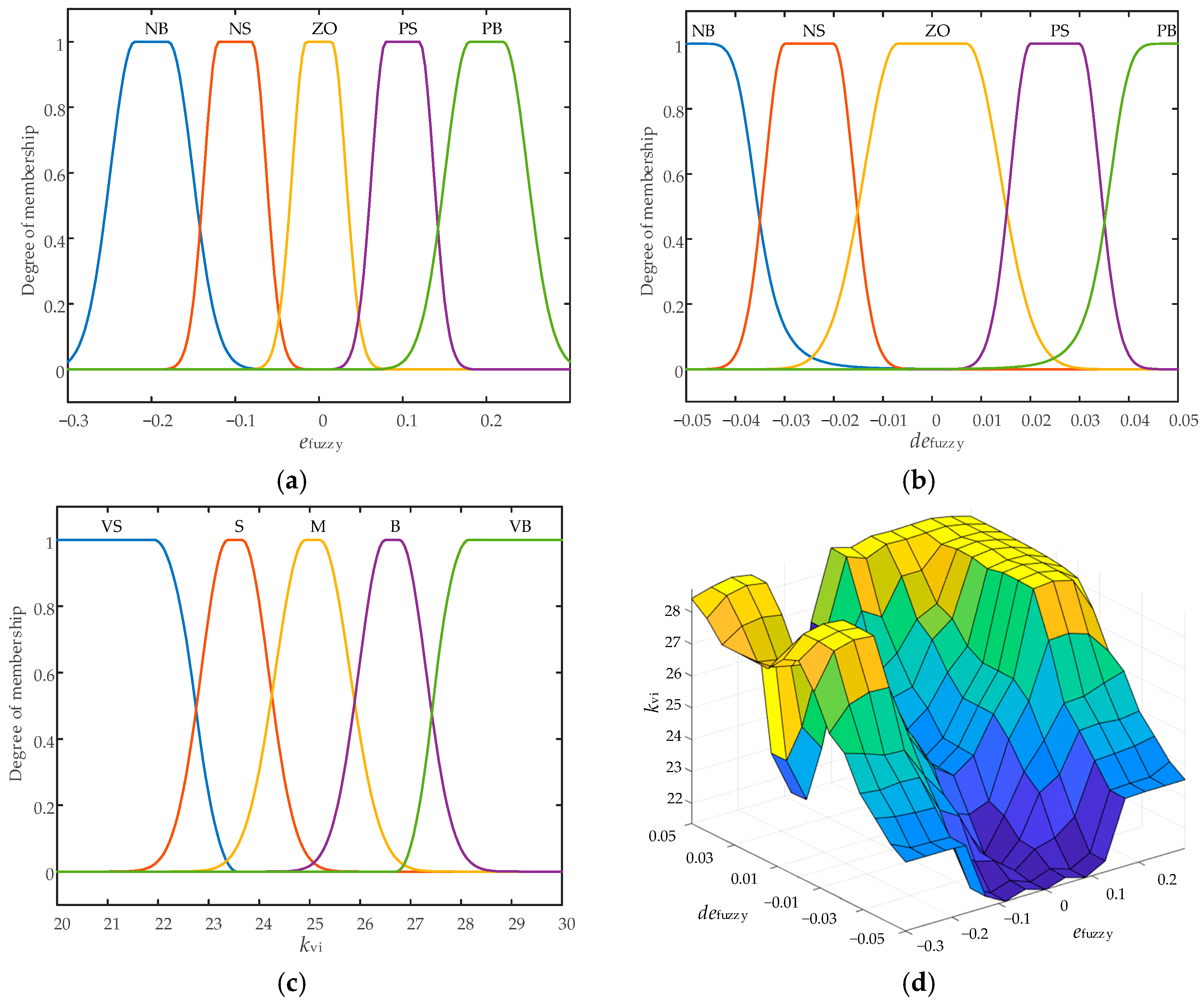







| e | ||||||
|---|---|---|---|---|---|---|
| NB | NS | ZO | PS | PB | ||
| de | NB | VS | VS | S | S | M |
| NS | VS | VS | S | M | B | |
| ZO | S | S | S | B | B | |
| PS | S | M | S | VB | VB | |
| PB | M | B | VB | VB | VB | |
| Quantity | Symbol | Value | Units |
|---|---|---|---|
| Grid Parameters | |||
| Rated voltage | Un | 0.4 | kV |
| Rated angular frequency | ω0 | 100π | rad/s |
| Gird impedance | Lg | 1.133 | mH |
| Filter inductance | Lf | 0.2 | pu |
| Filter capacitance | Cf | 0.05 | pu |
| Inverter Parameters | |||
| Rated capacity | Sn | 0.0346 | MW |
| Static Virtual inductance | Lv_n | 0.3 | pu |
| Static Virtual resistance | Rv_n | 0.06 | pu |
| DC voltage | Udc | 1.1 | kV |
| Sample frequency | fs | 9 | kHz |
| Damping coefficient | Dp | 3.5 × 10−5 | N.m.s/rad |
| Inertia constant | H | 2.0 | s |
| Speed governor coefficient | kω | 20 | pu |
| Reactive power control loop proportional coefficient | kpv | 0.1 | pu |
| Reactive power control loop integral coefficient | kiv | 20 | |
| SMC parameters | a | 1.25 | |
| b | 10.0 | ||
| c | 0.05 | ||
| d | 0.005 | ||
| α | 0.8 | ||
| X/R ratio | σ | 5 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, T.; Liang, J.; Rong, S.; Shu, Z.; Pan, C.; Liang, Y. A Novel Control Method for Current Waveform Reshaping and Transient Stability Enhancement of Grid-Forming Converters Considering Non-Ideal Grid Conditions. Energies 2025, 18, 2834. https://doi.org/10.3390/en18112834
Yu T, Liang J, Rong S, Shu Z, Pan C, Liang Y. A Novel Control Method for Current Waveform Reshaping and Transient Stability Enhancement of Grid-Forming Converters Considering Non-Ideal Grid Conditions. Energies. 2025; 18(11):2834. https://doi.org/10.3390/en18112834
Chicago/Turabian StyleYu, Tengkai, Jifeng Liang, Shiyang Rong, Zhipeng Shu, Cunyue Pan, and Yingyu Liang. 2025. "A Novel Control Method for Current Waveform Reshaping and Transient Stability Enhancement of Grid-Forming Converters Considering Non-Ideal Grid Conditions" Energies 18, no. 11: 2834. https://doi.org/10.3390/en18112834
APA StyleYu, T., Liang, J., Rong, S., Shu, Z., Pan, C., & Liang, Y. (2025). A Novel Control Method for Current Waveform Reshaping and Transient Stability Enhancement of Grid-Forming Converters Considering Non-Ideal Grid Conditions. Energies, 18(11), 2834. https://doi.org/10.3390/en18112834






