Dynamic Characteristics Analysis of a Multi-Pile Wind Turbine Under the Action of Wind–Seismic Coupling
Abstract
1. Introduction
2. Numerical Models
2.1. Wind Turbine Geometry Model
2.2. Finite Element Model for Wind Turbines
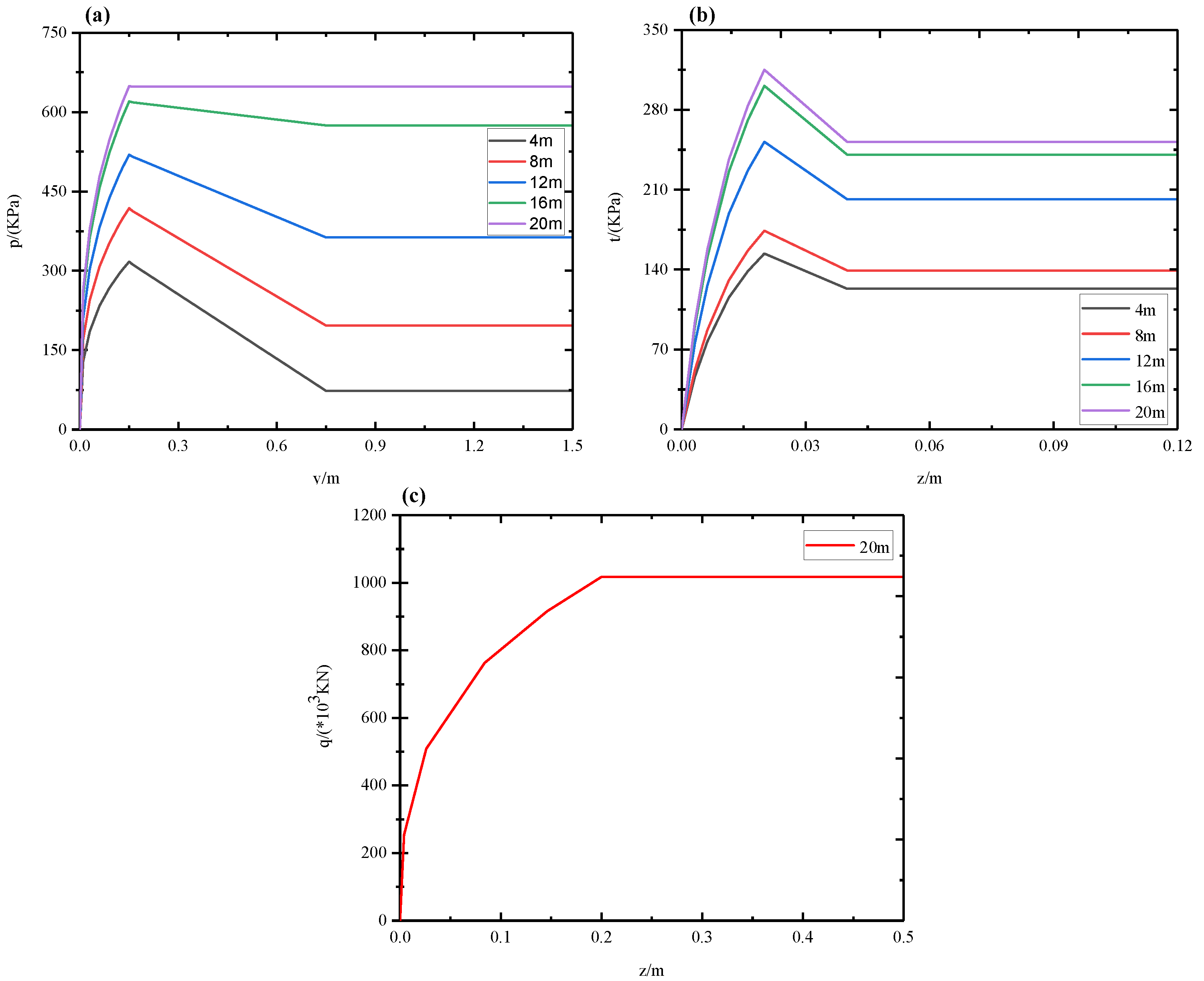
2.3. SSI Model
2.4. System Damping
3. Wind Loads and Ground Motion
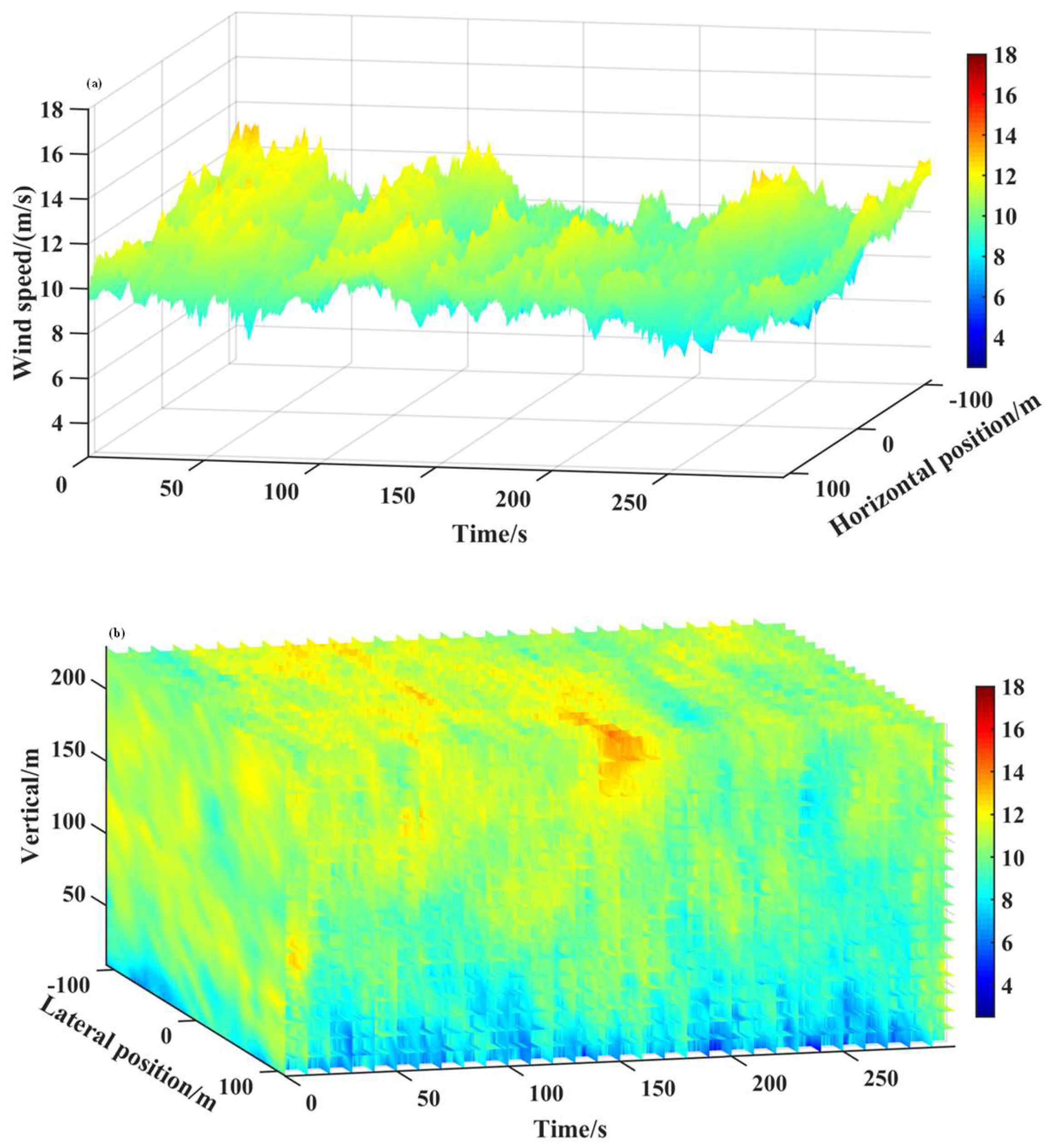
3.1. Turbulent Wind Fields
3.2. Ground Motion
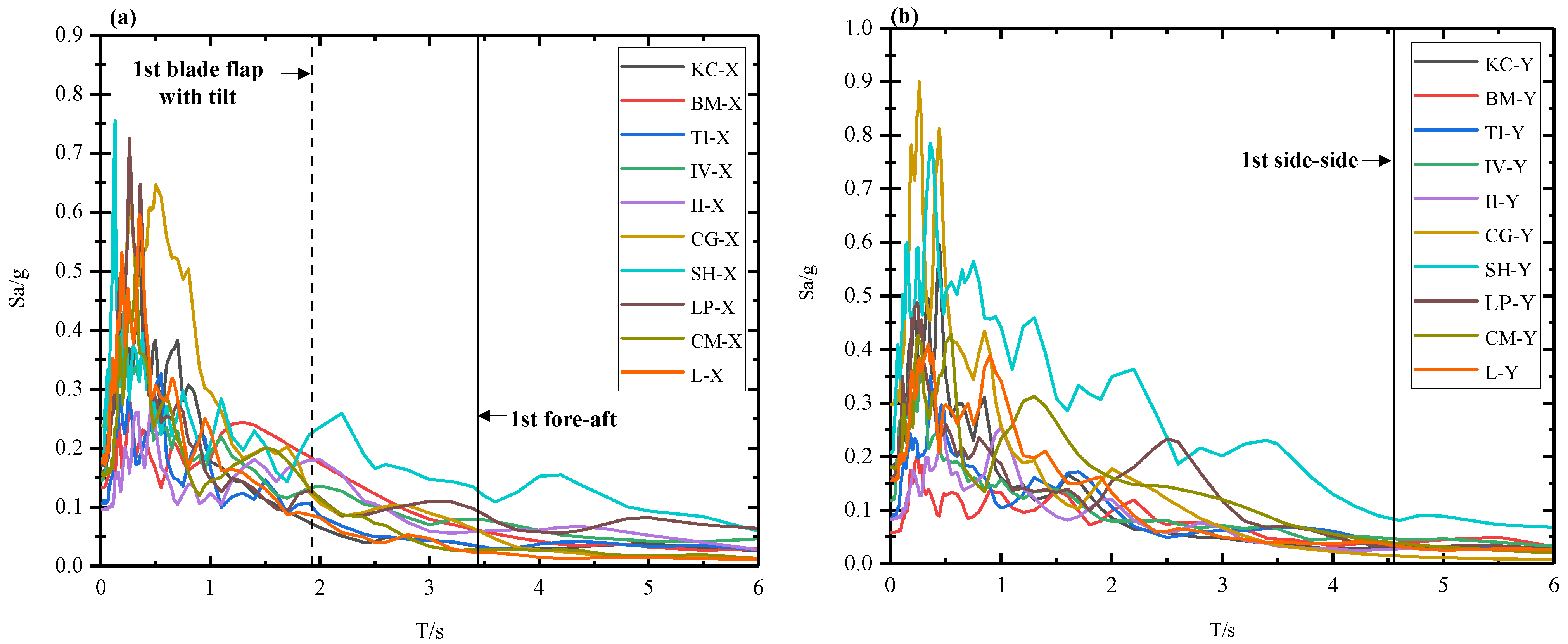
4. Vibration Characteristics of Wind Turbines During Wind Interaction
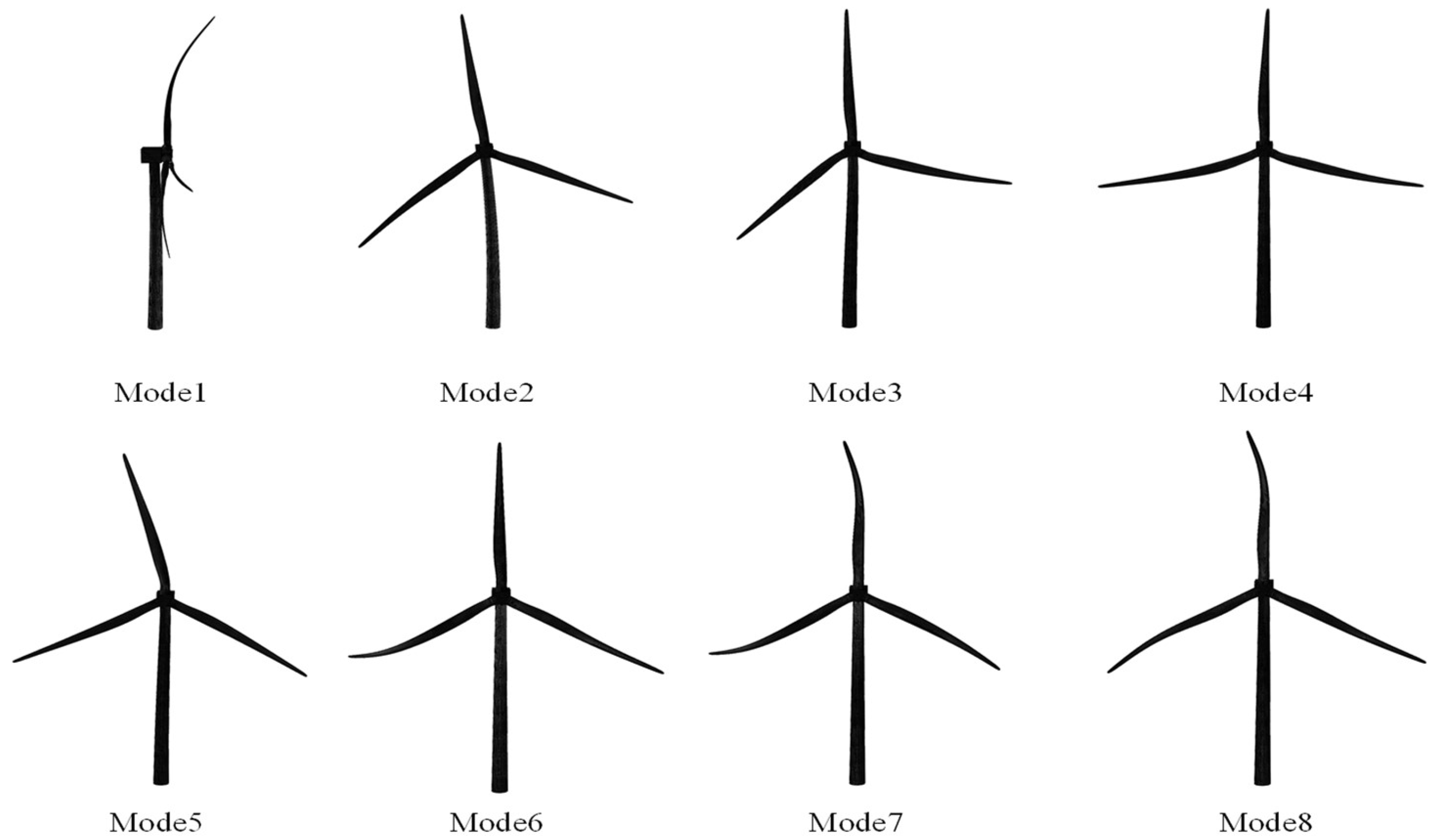
4.1. Analysis of the Natural Frequency of Wind Turbines
4.2. Vibration Characteristics Under Wind Load
5. Vibration Characteristics Under Wind–Seismic Interaction
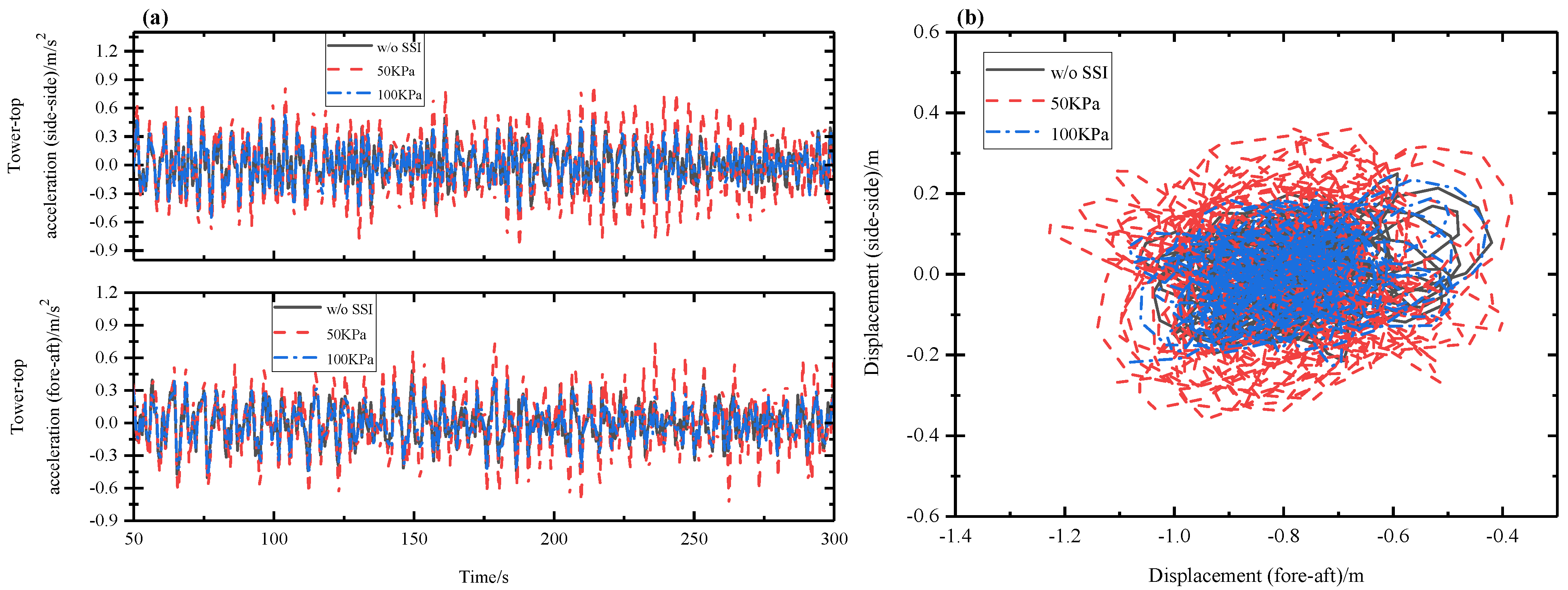
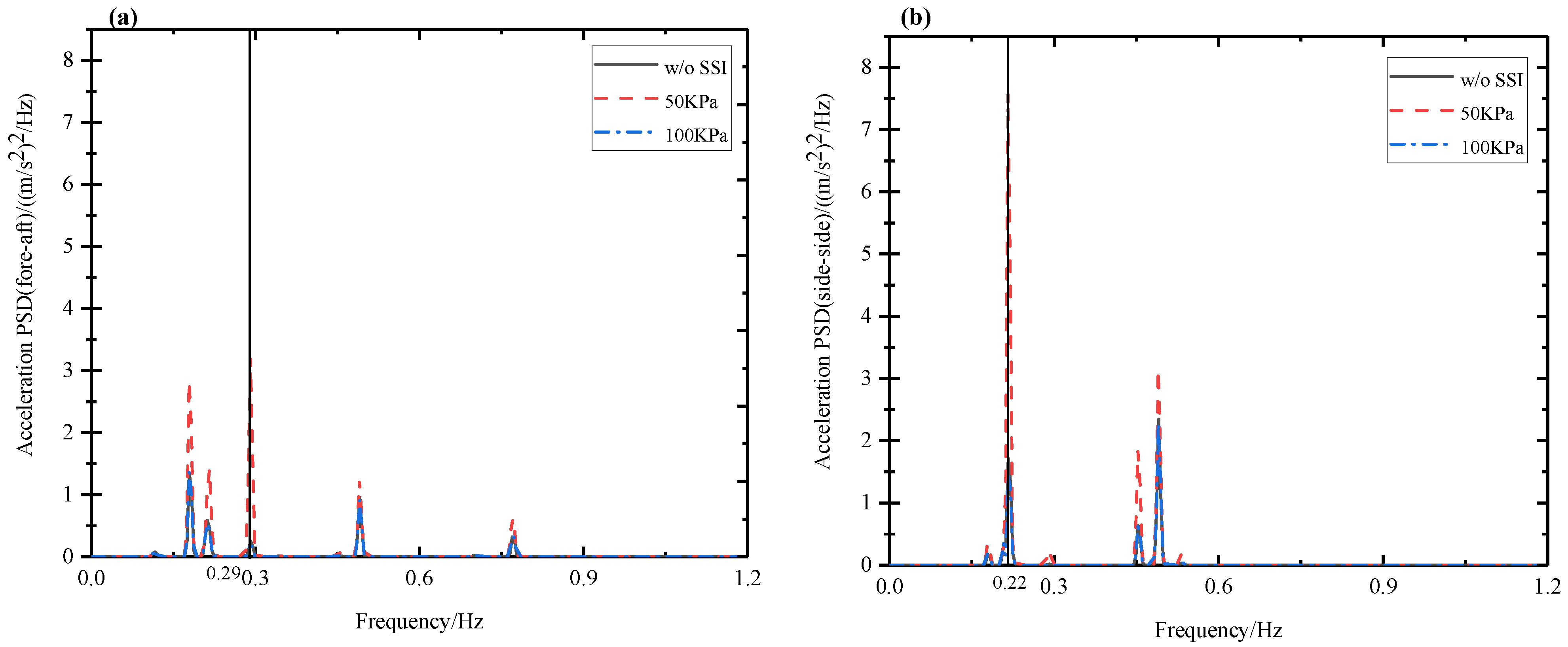
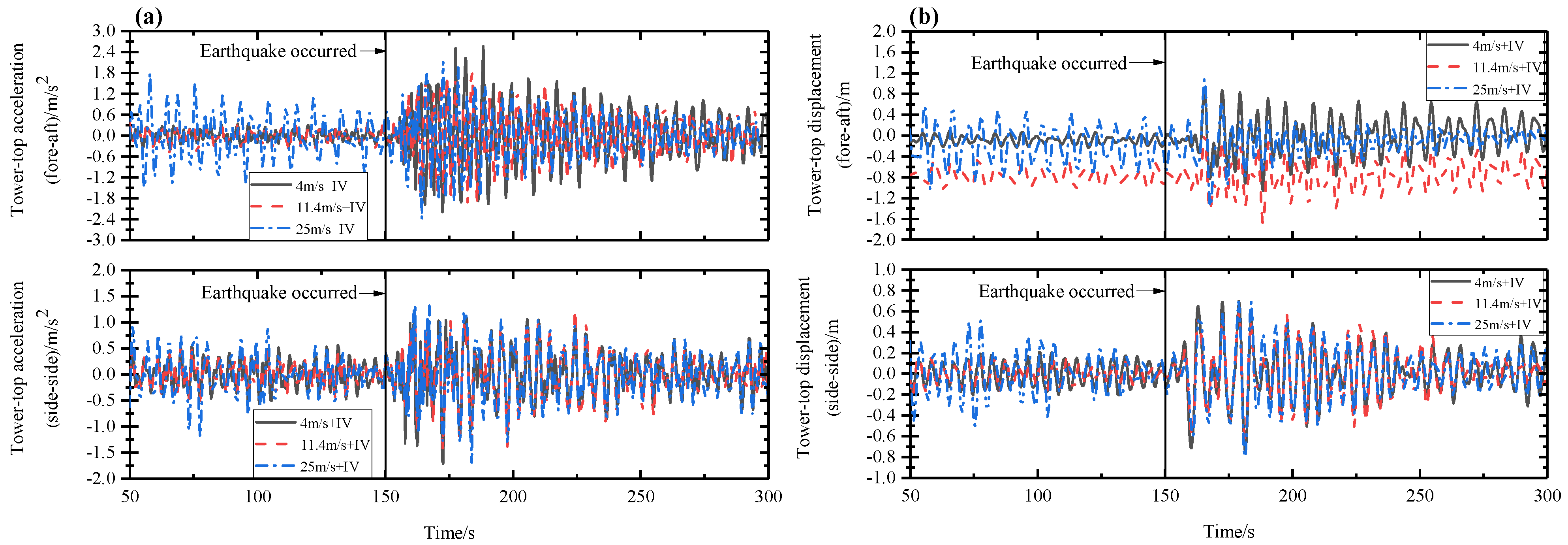
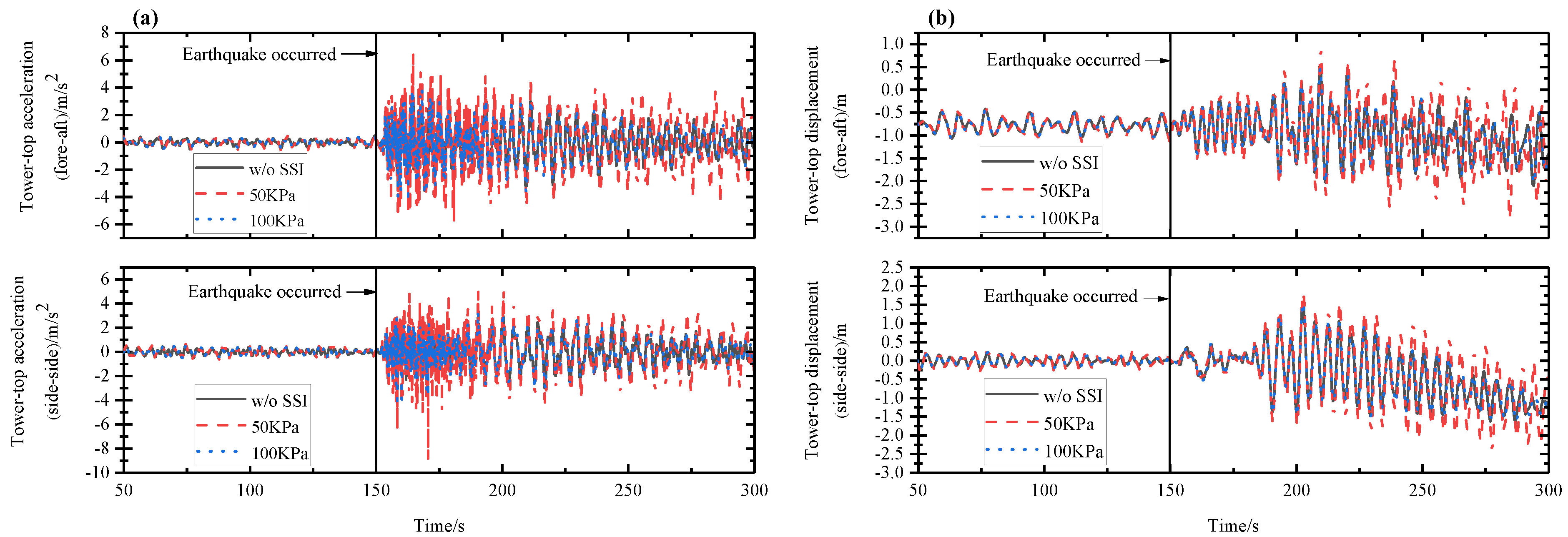
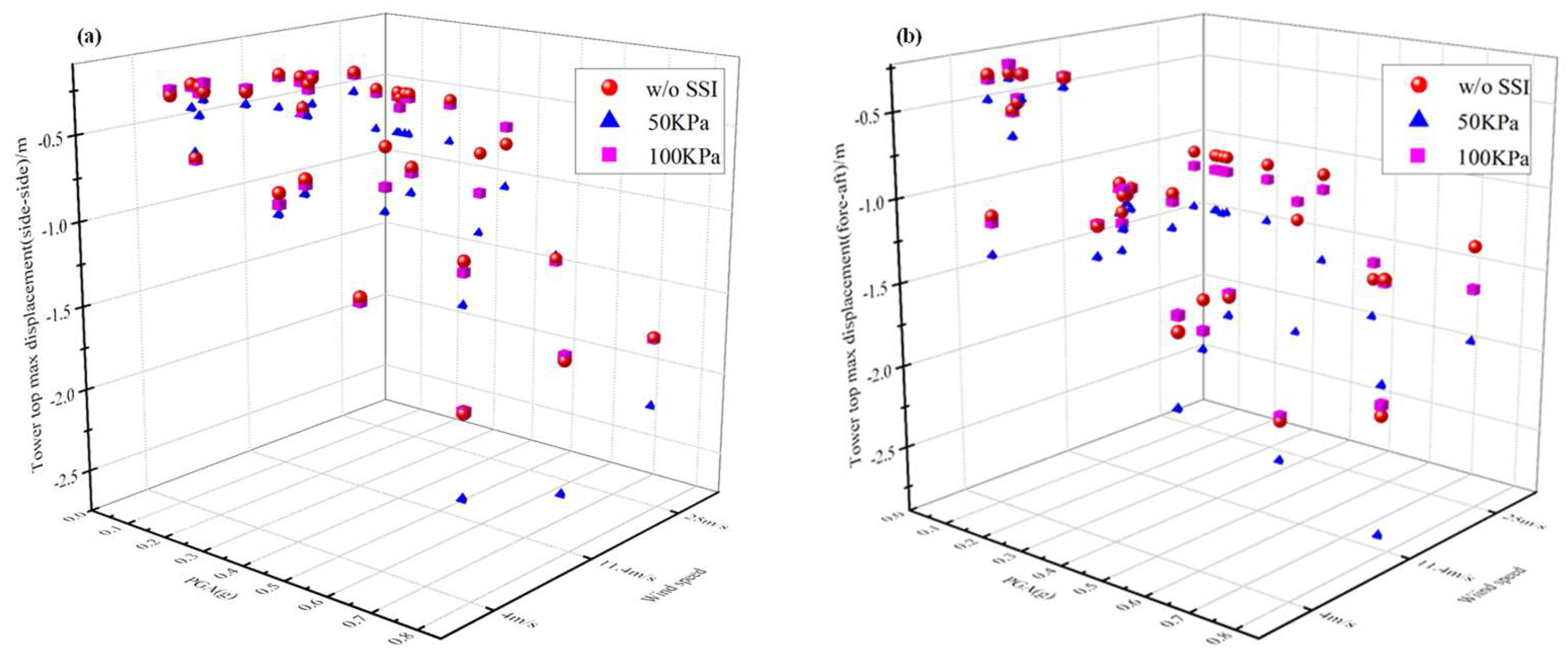
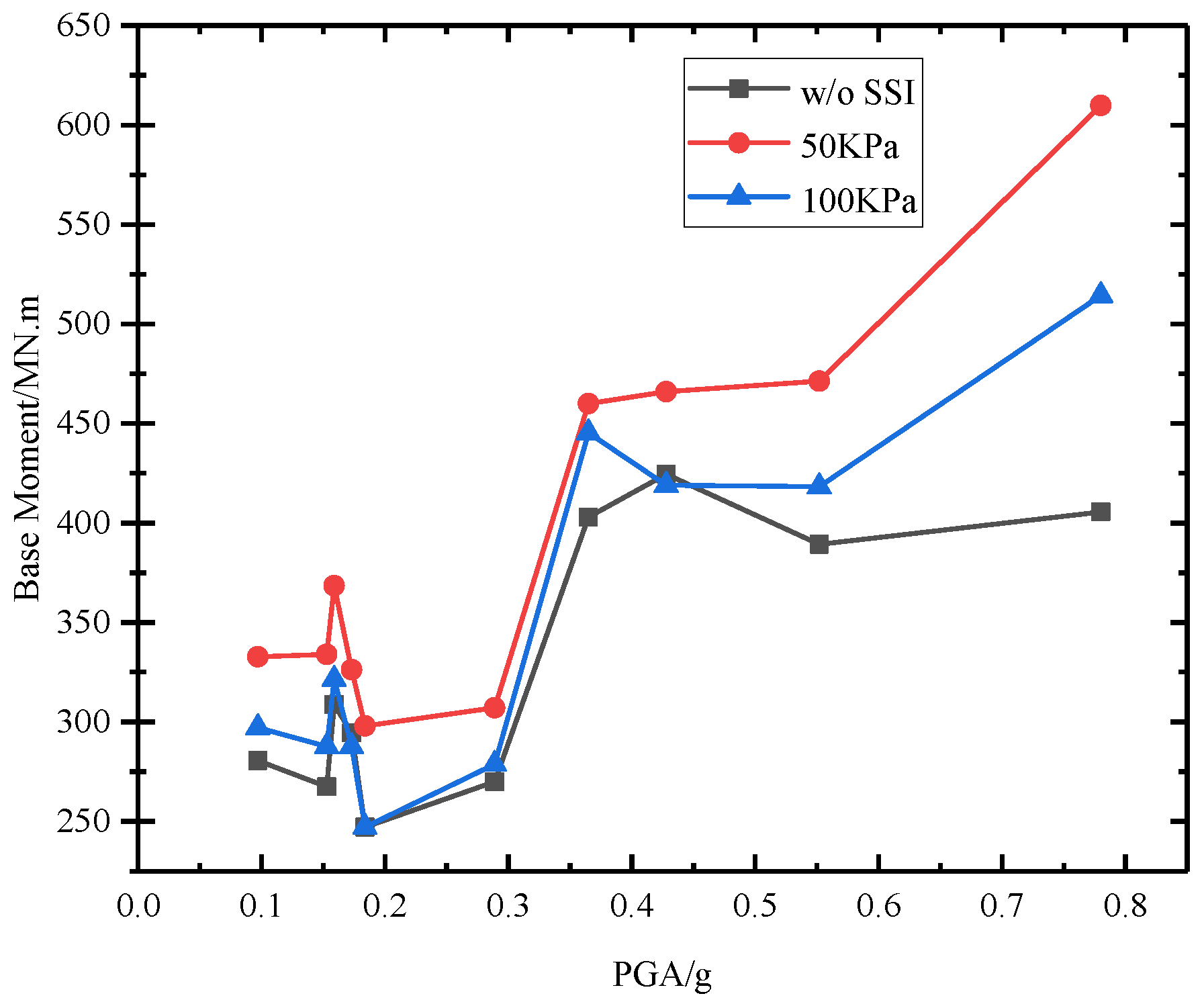
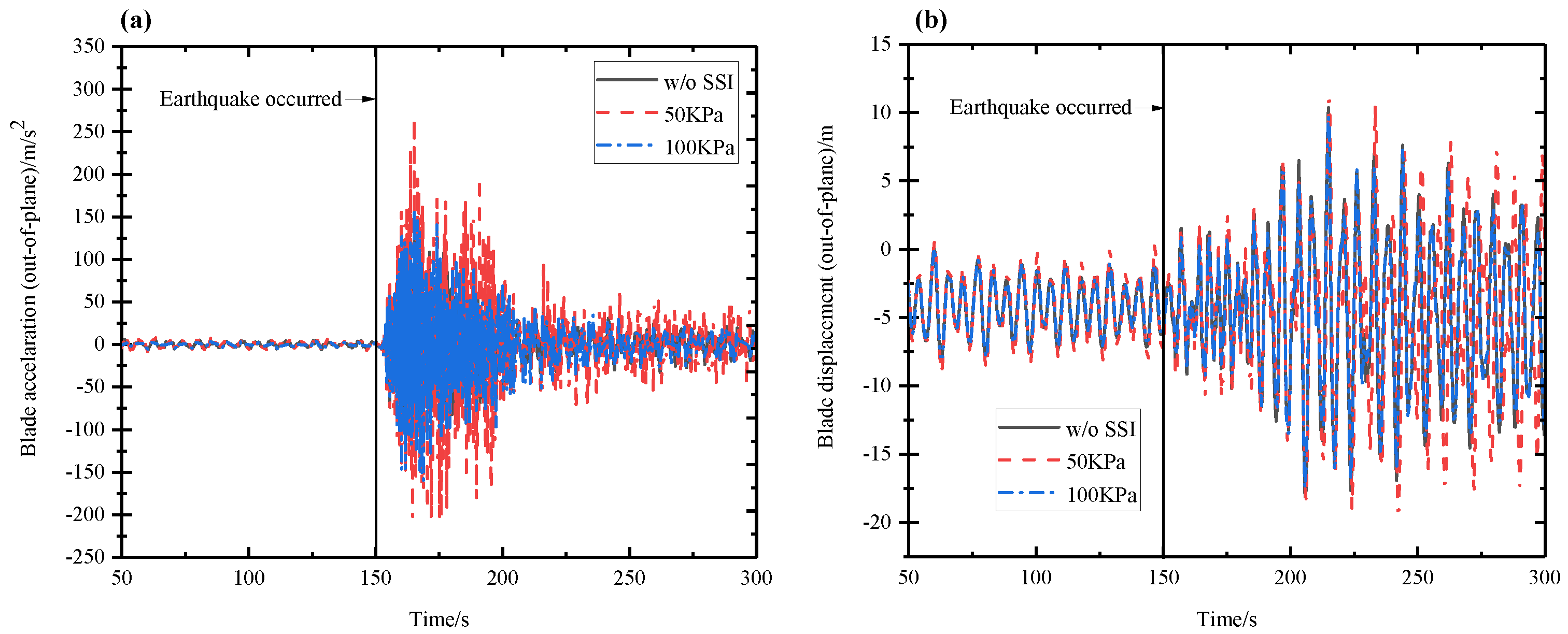
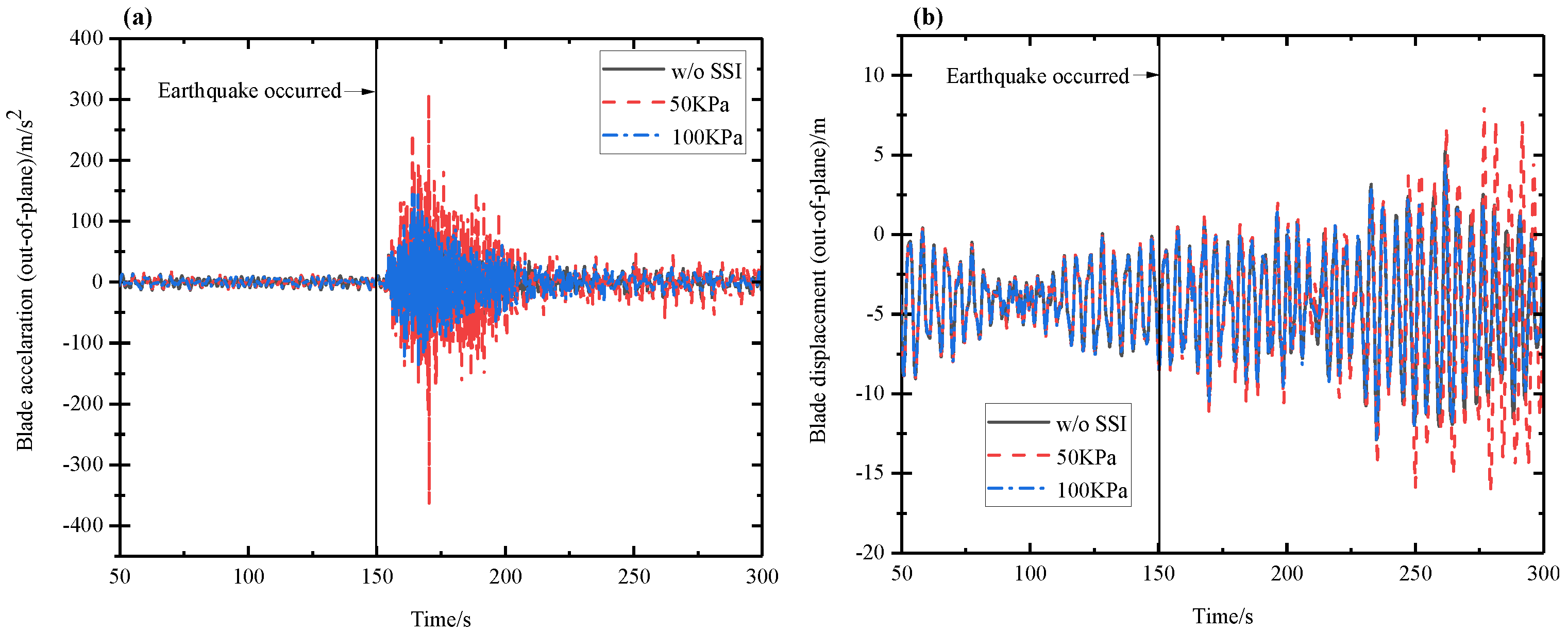
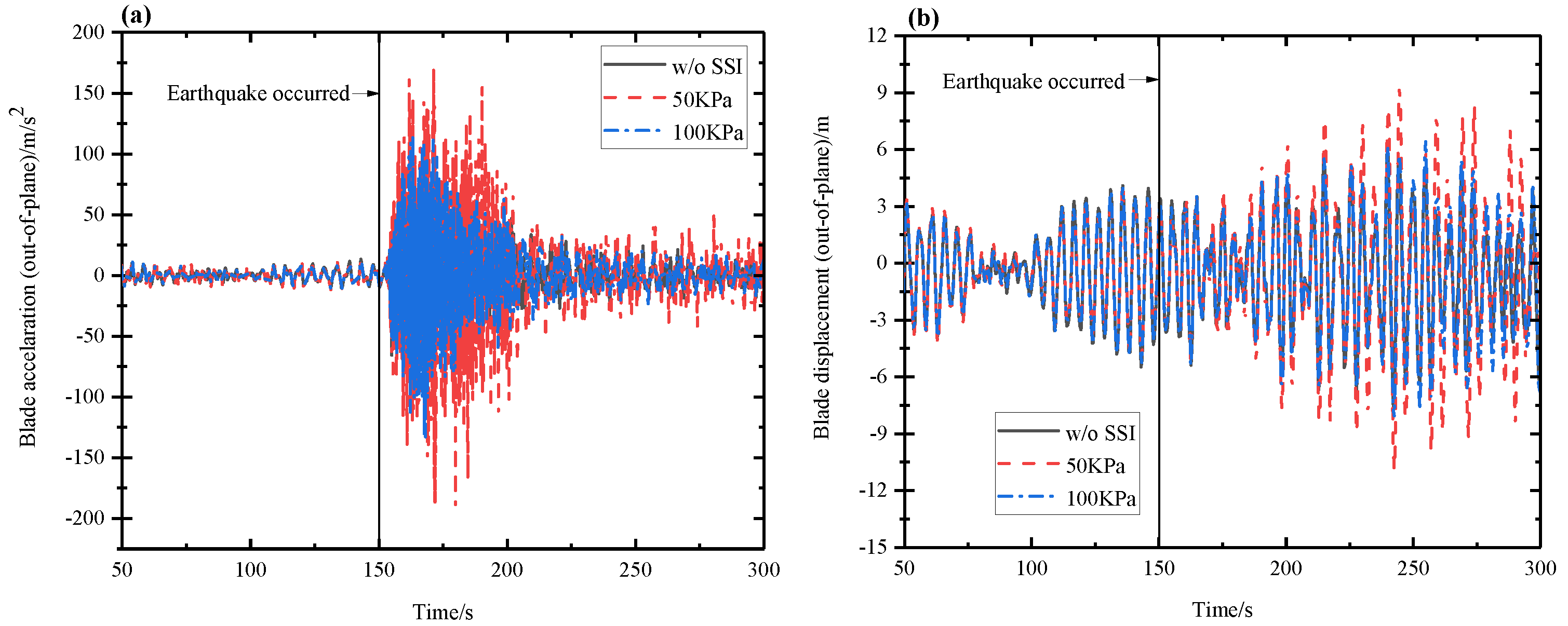
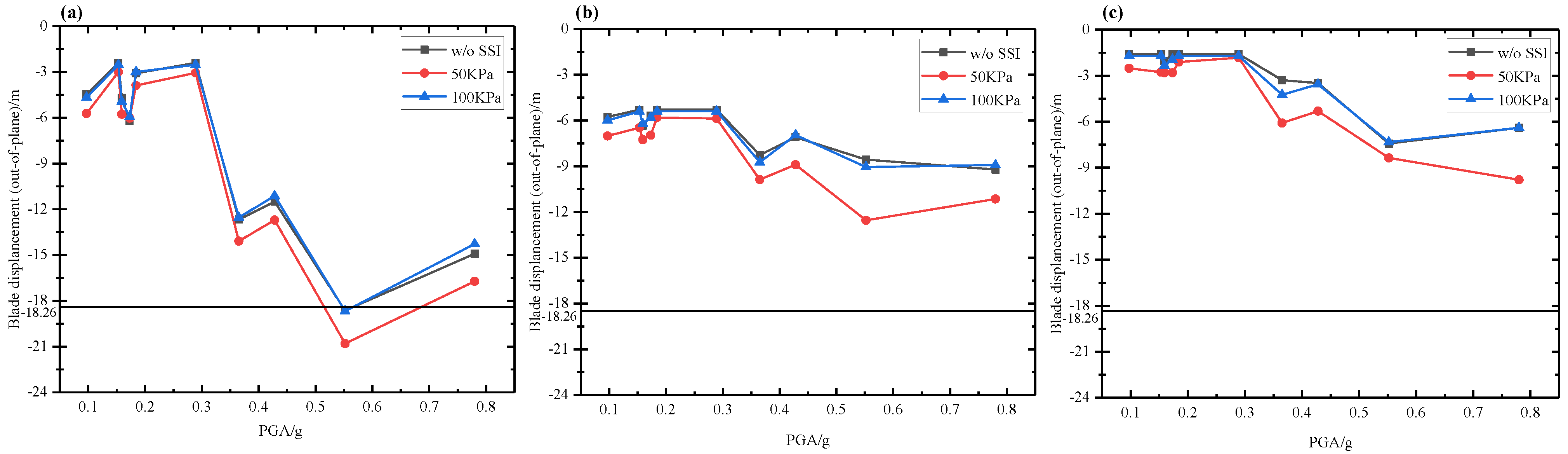
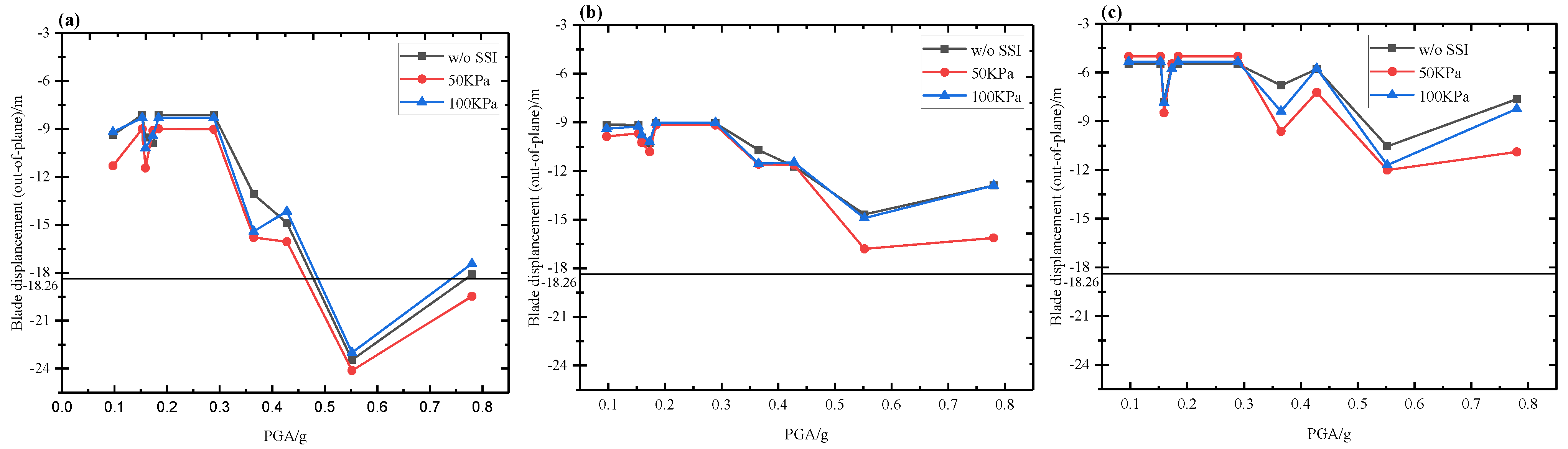
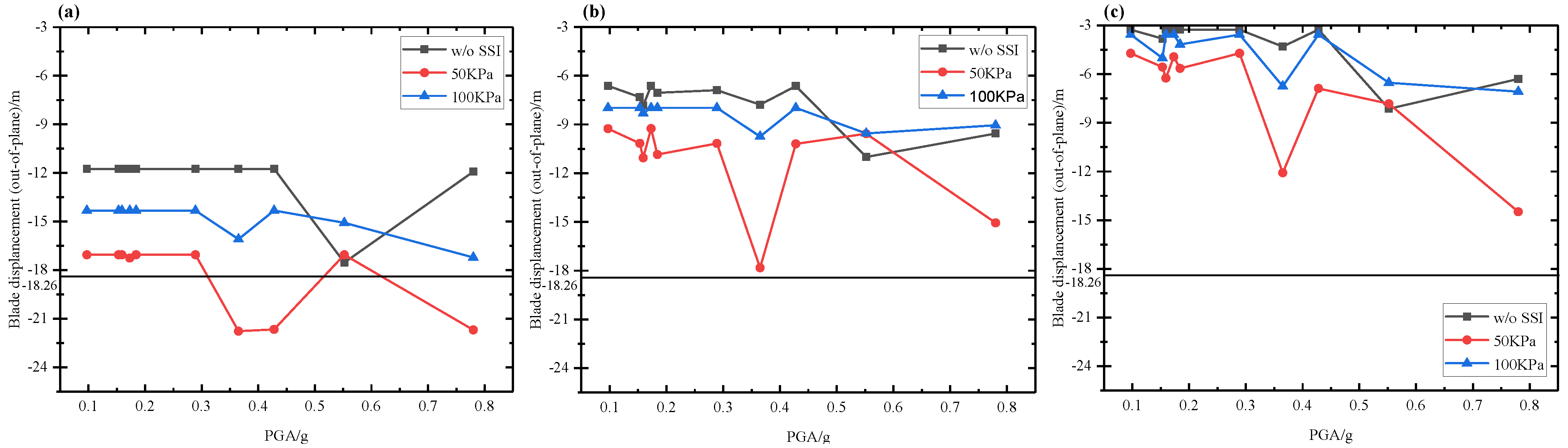
5.1. Wind–Seismic Coupled Tower Vibration Behavior
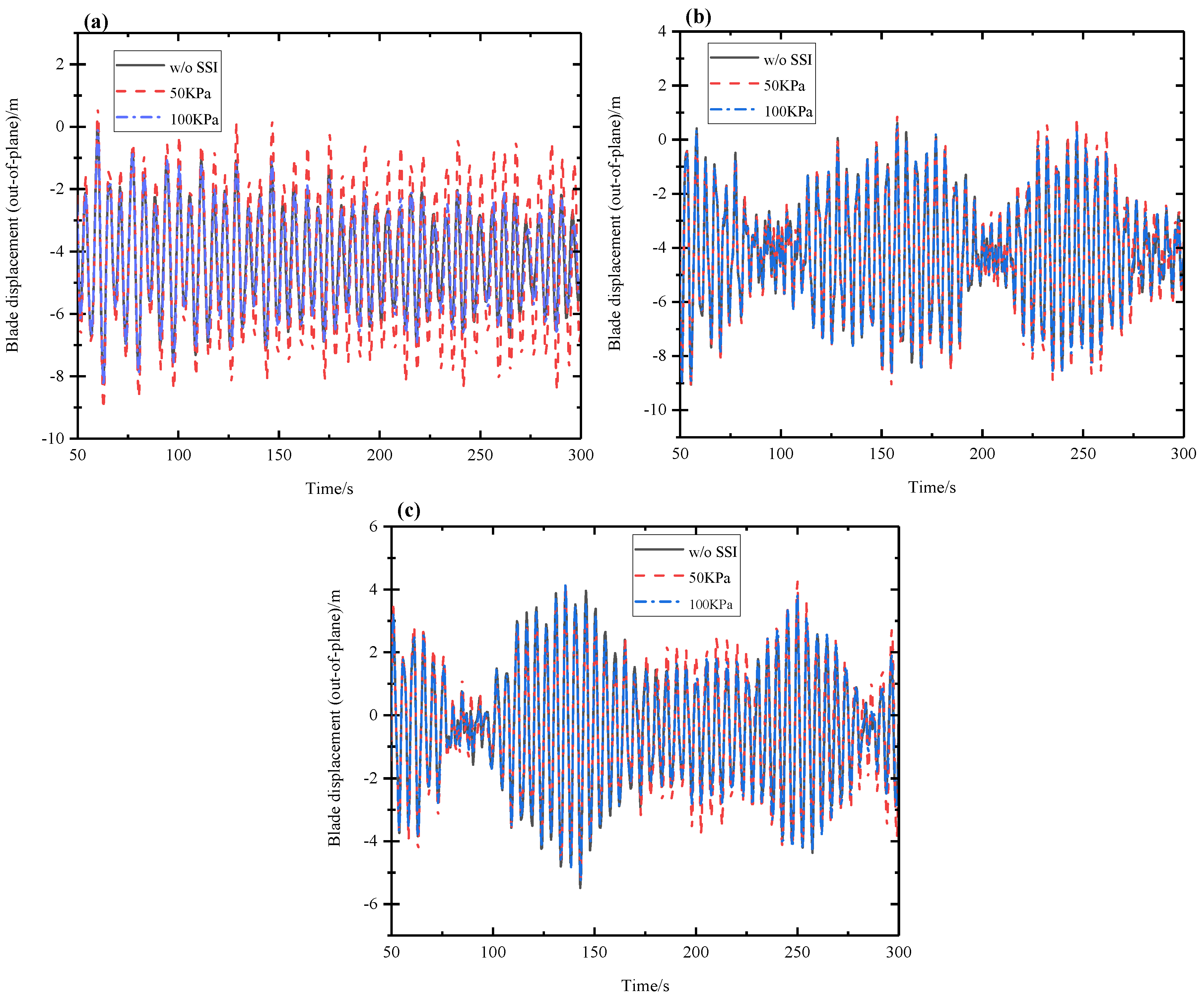
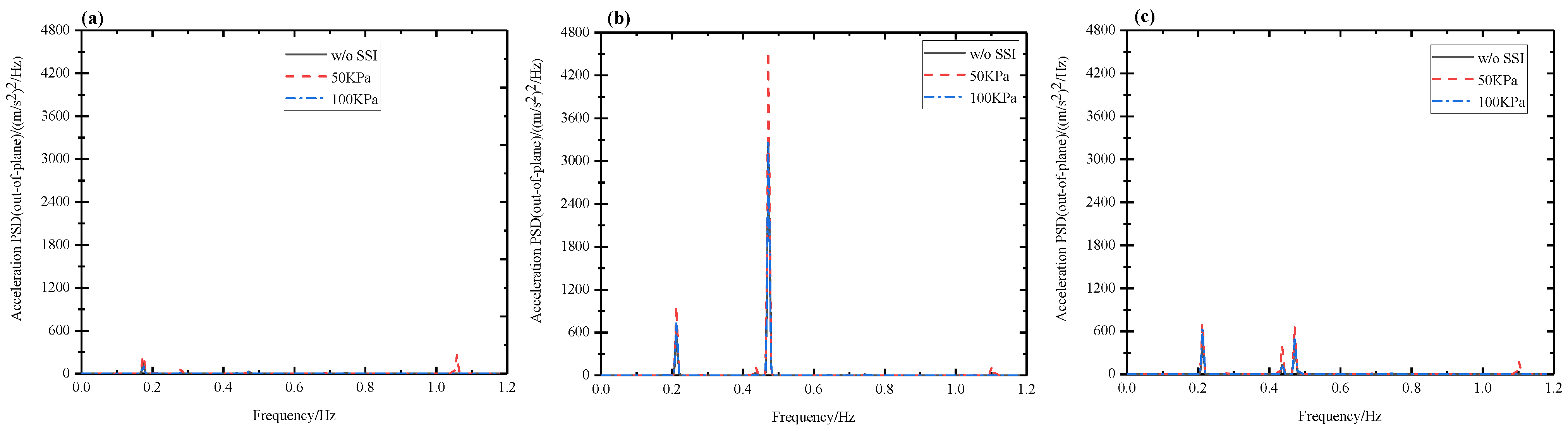
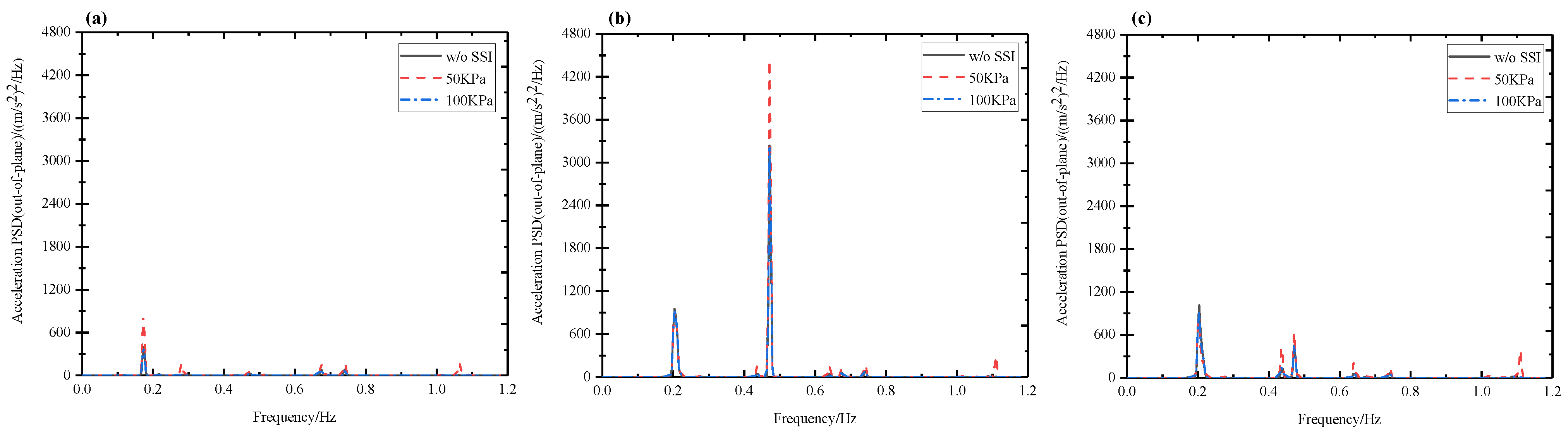
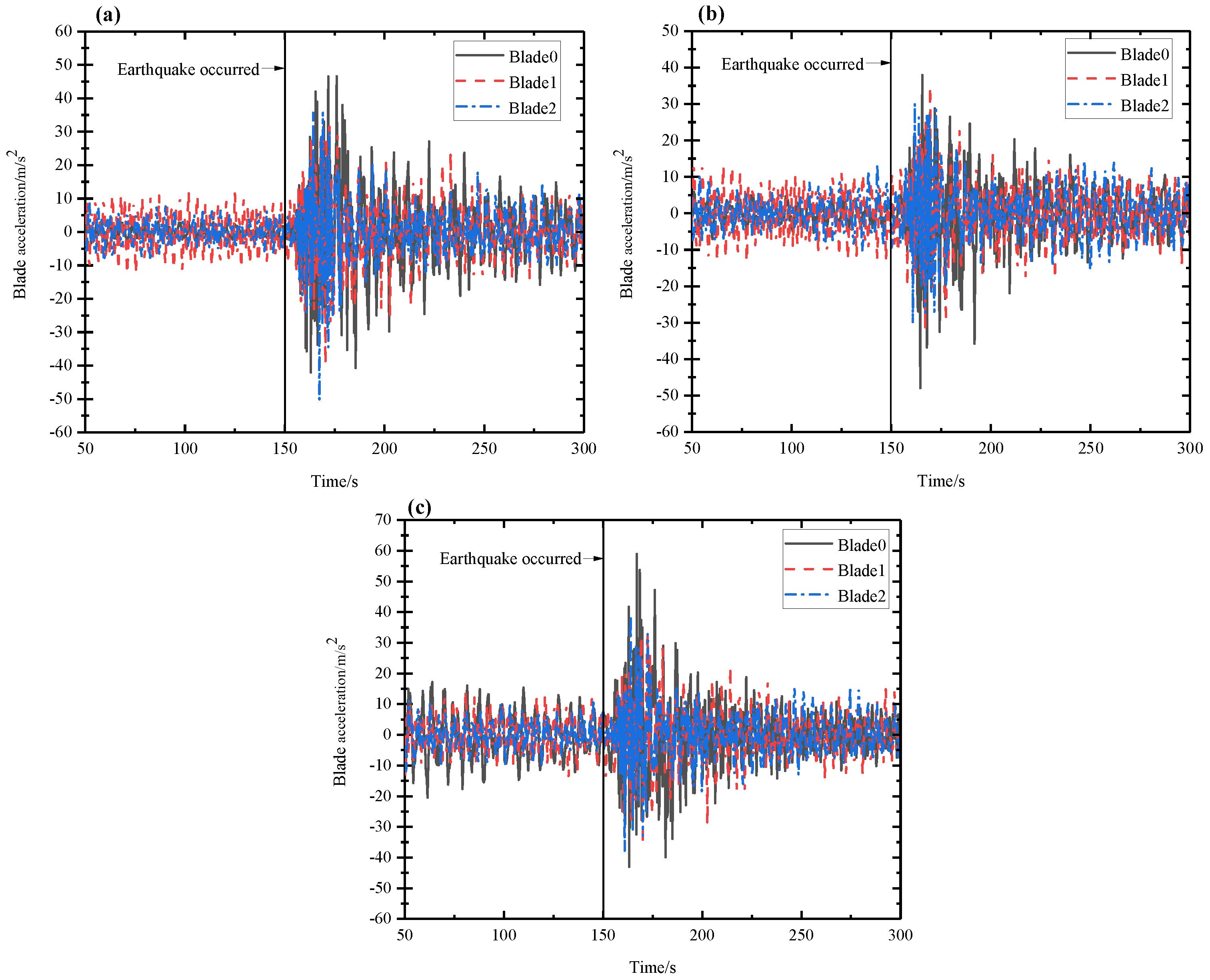
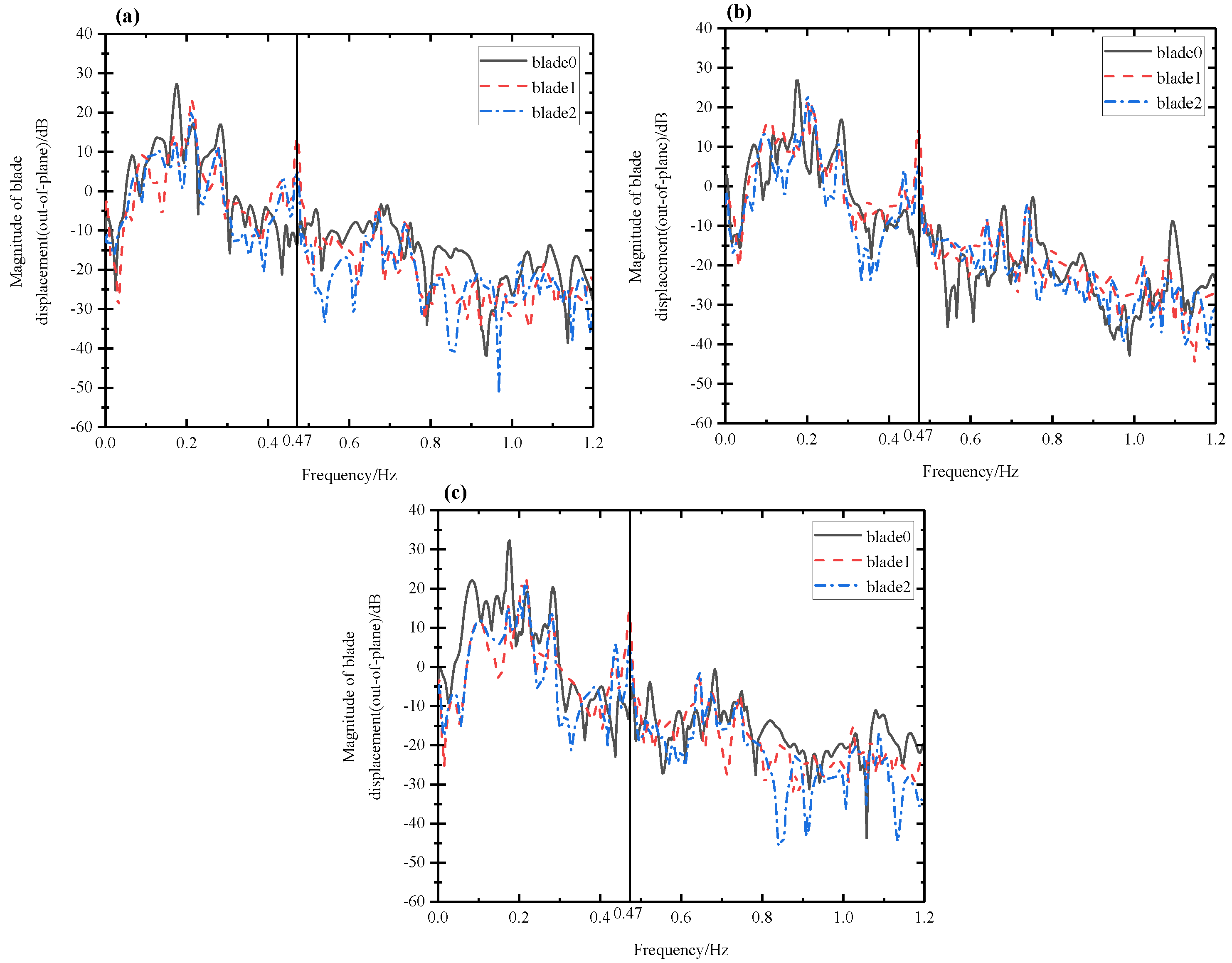
5.2. Wind–Seismic Coupled Blade Vibration Behavior
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Meng, D.; Yang, S.; de Jesus, A.M.; Zhu, S.-P. A novel Kriging-model-assisted reliability-based multidisciplinary design optimization strategy and its application in the offshore wind turbine tower. Renew. Energy 2022, 203, 407–420. [Google Scholar] [CrossRef]
- Li, H.; Diaz, H.; Guedes Soares, C. A developed failure mode and effect analysis for floating offshore wind turbine support structures. Renew. Energy 2021, 164, 133–145. [Google Scholar] [CrossRef]
- Nuta, E.; Christopoulos, C.; Packer, J.A. Methodology for seismic risk assessment for tubular steel wind turbine towers: Application to Canadian seismic environment. Can. J. Civ. Eng. 2011, 38, 293–304. [Google Scholar] [CrossRef]
- Sadowski, A.J. On the advantages of hybrid beam-shell structural finite element models for the efficient analysis of metal wind turbine support towers. Finite Elem. Anal. Des. 2019, 162, 19–33. [Google Scholar] [CrossRef]
- Sadowski, A.J.; Camara, A.; Málaga-Chuquitaype, C.; Dai, K. Seismic analysis of a tall metal wind turbine support tower with realistic geometric imperfections. Earthq. Eng. Struct. Dyn. 2017, 46, 201–219. [Google Scholar] [CrossRef]
- Witcher, D. Seismic analysis of wind turbines in the time domain. Wind Energy 2005, 8, 81–91. [Google Scholar] [CrossRef]
- Bossanyi, E.A. Bladed for Windows User Manual; Garrad Hassan and Partners: Bristol, UK, 2000. [Google Scholar]
- Prowell, I.; Elgamal, A.; Uang, C.-M.; Luco, J.E.; Romanowitz, H.; Duggan, E. Shake table testing and numerical simulation of a utility-scale wind turbine including operational effects. Wind Energy 2014, 17, 997–1016. [Google Scholar] [CrossRef]
- Prowell, I.; Uang, C.-M.; Elgamal, A.; Luco, J.E.; Guo, L. Shake Table Testing of a Utility-Scale Wind Turbine. J. Eng. Mech. 2012, 138, 900–909. [Google Scholar] [CrossRef]
- Jonkman, J.M.; Buhl, M.L., Jr. FAST User’s Guide; National renewable energy Laboratory: Golden, CO, USA, 2005; EL500-38230. [Google Scholar]
- Zhu, J.; Zhou, Z.; Cai, X. Multi-objective aerodynamic and structural integrated optimization design of wind turbines at the system level through a coupled blade-tower model. Renew. Energy 2020, 150, 523–537. [Google Scholar] [CrossRef]
- Asareh, M.-A.; Schonberg, W.; Volz, J. Fragility analysis of a 5-MW NREL wind turbine considering aero-elastic and seismic interaction using finite element method. Finite Elem. Anal. Des. 2016, 120, 57–67. [Google Scholar] [CrossRef]
- Asareh, M.-A.; Schonberg, W.; Volz, J. Effects of seismic and aerodynamic load interaction on structural dynamic response of multi-megawatt utility scale horizontal axis wind turbines. Renew. Energy 2016, 86, 49–58. [Google Scholar] [CrossRef]
- Prowell, I.; Veletzos, M.; Elgamal, A.; Restrepo, J. Experimental and Numerical Seismic Response of a 65 kW Wind Turbine. J. Earthq. Eng. 2009, 13, 1172–1190. [Google Scholar] [CrossRef]
- Meng, D.B.; Yang, H.F.; Yang, S.Y.; de Jesus, A.M.P.; Zhu, S.P. Kriging-assisted hybrid reliability design and optimization of offshore wind turbine support structure based on a portfolio allocation strategy. Ocean Eng. 2023, 203, 407–420. [Google Scholar] [CrossRef]
- Meng, D.B.; Yang, H.F.; Yang, S.Y.; de Jesus, A.M.P.; Correia, J.; Zhu, S.P. Intelligent-inspired framework for fatigue reliability evaluation of offshore wind turbine support structures under hybrid uncertainty. Ocean Eng. 2024, 307, 118213. [Google Scholar] [CrossRef]
- Guo, S.X.; Li, Y.L.; Chen, W.M. Analysis on dynamic interaction between flexible bodies of large-sized wind turbine and its response to random wind loads. Renew. Energy 2021, 163, 123–137. [Google Scholar] [CrossRef]
- Andersen, L.V.; Vahdatirad, M.J.; Sichani, M.T.; Sorensen, J.D. Natural frequencies of wind turbines on monopile foundations in clayey soils-A probabilistic approach. Comput. Geotech. 2012, 43, 1–11. [Google Scholar] [CrossRef]
- Arany, L.; Bhattacharya, S.; Macdonald, J.H.G.; Hogan, S.J. Closed form solution of Eigen frequency of monopile supported offshore wind turbines in deeper waters incorporating stiffness of substructure and SSI. Soil Dyn. Earthq. Eng. 2016, 83, 18–32. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Adhikari, S. Experimental validation of soil-structure interaction of offshore wind turbines. Soil Dyn. Earthq. Eng. 2011, 31, 805–816. [Google Scholar] [CrossRef]
- Lombardi, D.; Bhattacharya, S.; Wood, D.M. Dynamic soil-structure interaction of monopile supported wind turbines in cohesive soil. Soil Dyn. Earthq. Eng. 2013, 49, 165–180. [Google Scholar] [CrossRef]
- Zuo, H.; Bi, K.; Hao, H. Dynamic analyses of operating offshore wind turbines including soil-structure interaction. Eng. Struct. 2018, 157, 42–62. [Google Scholar] [CrossRef]
- Zuo, H.; Bi, K.; Hao, H.; Li, C. Influence of earthquake ground motion modelling on the dynamic responses of offshore wind turbines. Soil Dyn. Earthq. Eng. 2019, 121, 151–167. [Google Scholar] [CrossRef]
- Amani, S.; Prabhakaran, A.; Bhattacharya, S. Design of monopiles for offshore and nearshore wind turbines in seismically liquefiable soils: Methodology and validation. Soil Dyn. Earthq. Eng. 2022, 157, 107252. [Google Scholar] [CrossRef]
- Bisoi, S.; Haldar, S. Dynamic analysis of offshore wind turbine in clay considering soil–monopile–tower interaction. Soil Dyn. Earthq. Eng. 2014, 63, 19–35. [Google Scholar] [CrossRef]
- Filho, H.A.N.C.; Avila, S.M.; de Brito, J.L.V. Dynamic analysis of onshore wind turbines including soil–structure interaction. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 143. [Google Scholar] [CrossRef]
- Bak, C.; Bitsche, R.; Kim, T.; Hansen, M.H.; Zahle, F. Light Rotor: The 10-MW reference wind turbine. In Proceedings of the European Wind Energy Association (EWEA) Annual Event, Copenhagen, Denmark, 16–19 April 2012. [Google Scholar]
- Hong, Y.; He, B.; Wang, L.Z.; Wang, Z.; Ng, C.W.W.; Mašín, D. Cyclic lateral response and failure mechanisms of semi-rigid pile in soft clay: Centrifuge tests and numerical modelling. Can. Geotech. J. 2017, 54, 806–824. [Google Scholar] [CrossRef]
- Wang, L.; Lai, Y.; Hong, Y.; Mašín, D. A unified lateral soil reaction model for monopiles in soft clay considering various length-to-diameter (L/D) ratios. Ocean. Eng. 2020, 212, 107492. [Google Scholar] [CrossRef]
- ISO 19901-10:2021; Petroleum and Natural Gas Industries-Specific Requirements for Offshore Structures. ISO: Geneva, Switzerland, 2021.
- DNV-OS-J101; Design of Offshore Wind Turbine Structures. DNV: Copenhagen, Denmark, 2014.
- Meng, J.; Dai, K.; Zhao, Z.; Mao, Z.; Camara, A.; Zhang, S.; Mei, Z. Study on the aerodynamic damping for the seismic analysis of wind turbines in operation. Renew. Energy 2020, 159, 1224–1242. [Google Scholar] [CrossRef]
- Bajrić, A.; Høgsberg, J.; Rüdinger, F. Evaluation of damping estimates by automated Operational Modal Analysis for offshore wind turbine tower vibrations. Renew. Energy 2018, 116, 153–163. [Google Scholar] [CrossRef]
- Hu, W.-H.; Thöns, S.; Rohrmann, R.G.; Said, S.; Rücker, W. Vibration-based structural health monitoring of a wind turbine system. Part I: Resonance phenomenon. Eng. Struct. 2015, 89, 260–272. [Google Scholar] [CrossRef]
- Valamanesh, V.; Myers, A.T. Aerodynamic Damping and Seismic Response of Horizontal Axis Wind Turbine Towers. J. Struct. Eng. 2014, 140, 04014090. [Google Scholar] [CrossRef]
- Dai, J.C.; Liu, Z.Q.; Liu, X.; Yang, S.Y.; Shen, X.B. Structural parameters multi-objective optimisation and dynamic characteristics analysis of large-scale wind turbine towers. Aust. J. Mech. Eng. 2017, 16, 43–49. [Google Scholar] [CrossRef]
- International Electrotechnical Commission. Wind Turbines-Part 1: Design Requirements, 3rd ed.; International Electrotechnical Commission: Geneva, Switzerland, 2005. [Google Scholar]
- Yang, Y.; Ye, K.; Li, C.; Michailides, C.; Zhang, W. Dynamic behavior of wind turbines influenced by aerodynamic damping and earthquake intensity. Wind Energy 2018, 21, 303–319. [Google Scholar] [CrossRef]
- Yang, Y.; Bashir, M.; Li, C.; Michailides, C.; Wang, J. Mitigation of coupled wind-wave-earthquake responses of a 10 MW fixed-bottom offshore wind turbine. Renew. Energy 2020, 157, 1171–1184. [Google Scholar] [CrossRef]
- Yang, Y.; Li, C.; Bashir, M.; Wang, J.; Yang, C. Investigation on the sensitivity of flexible foundation models of an offshore wind turbine under earthquake loadings. Eng. Struct. 2019, 183, 756–769. [Google Scholar] [CrossRef]
- Ancheta, T.D.; Darragh, R.B.; Stewart, J.P. PEER NGA-West2 Database, PEER Report 2013/03; Pacific Earthquake Engineering Research Center: Berkeley, CA, USA, 2013. [Google Scholar]
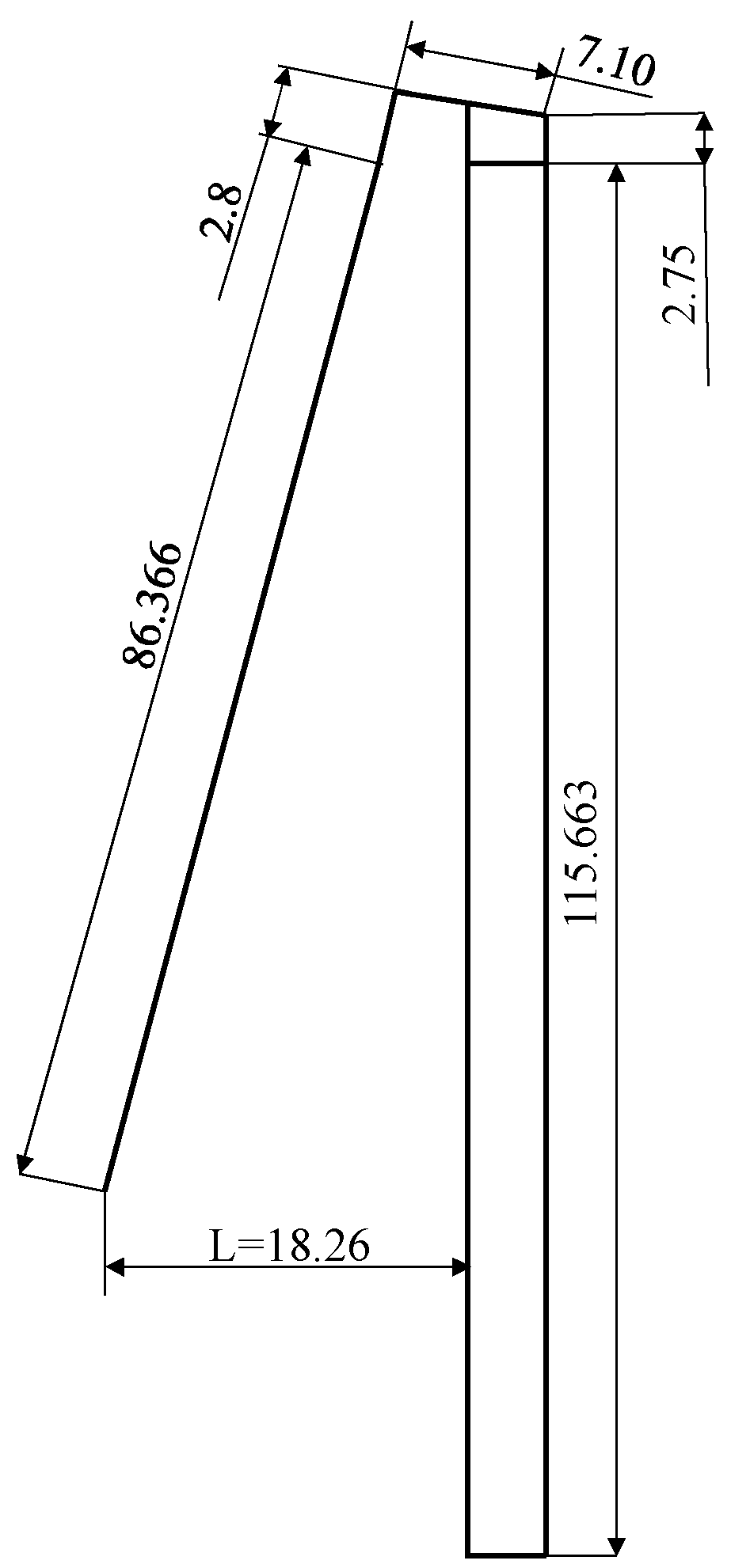
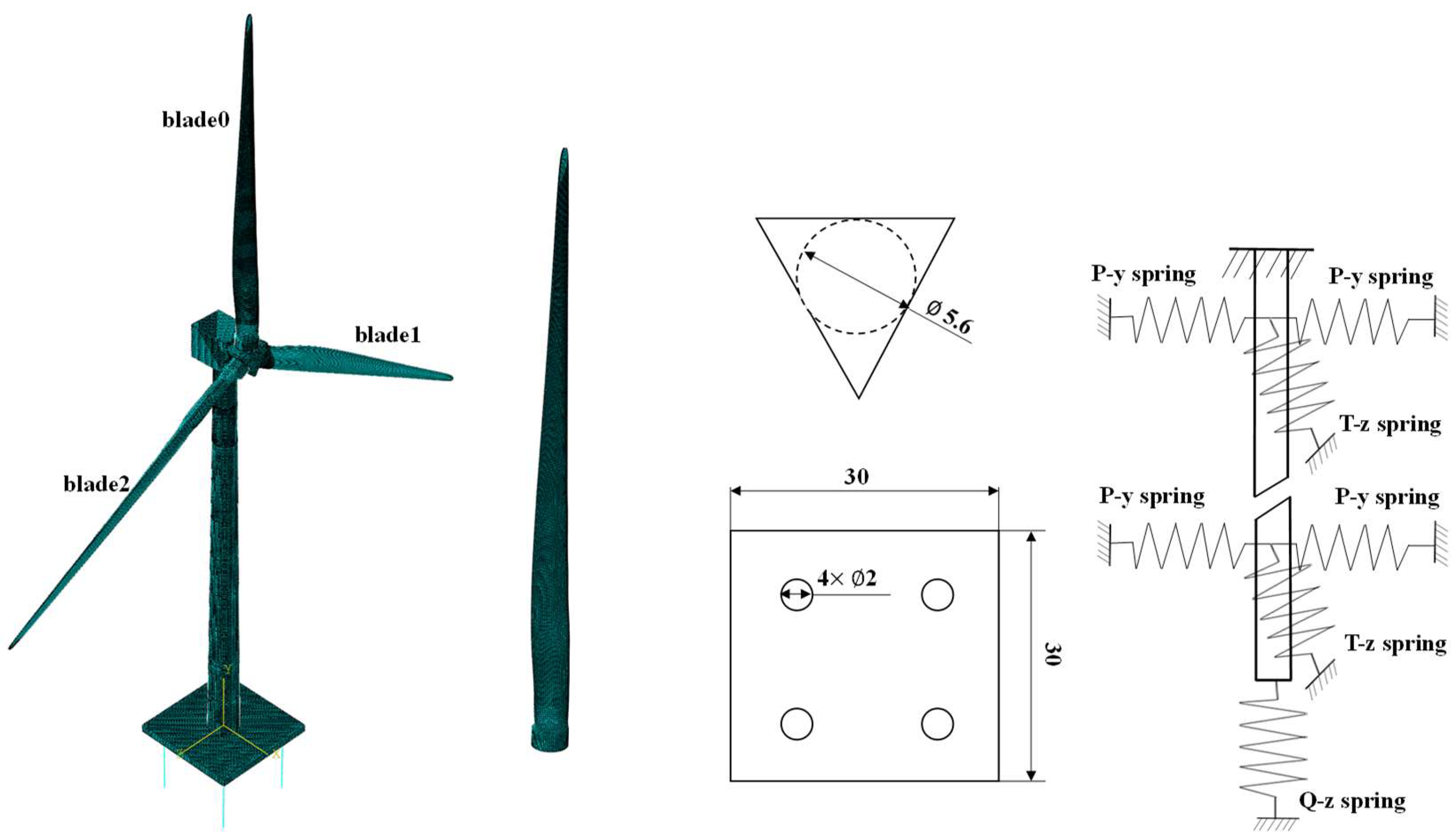
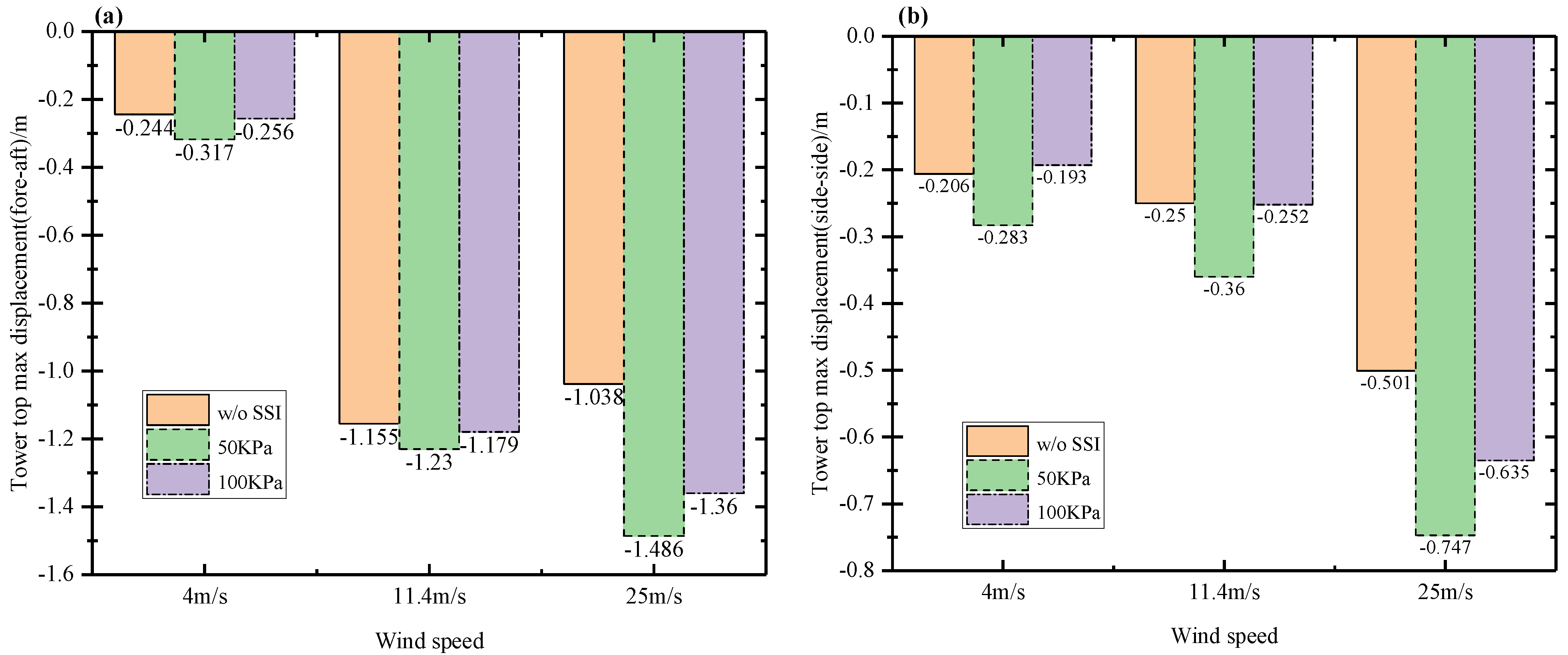
| DTU 10 MW Baseline Wind Turbine Properties | ||
|---|---|---|
| Basic description | Rated power | 10 MW |
| Blade | Number of blades | 3 |
| Rotor Diameter | 178.3 m | |
| Cut in wind speed | 4 m/s | |
| Cut out wind speed | 25 m/s | |
| Rated wind speed | 11.4 m/s | |
| Rotor Mass | 227,962 kg | |
| Structural damping ratio | 0.5% | |
| Hub and Nacelle | Hub Diameter | 5.6 m |
| Hub Height | 119.0 m | |
| Nacelle Mass | 446,036 kg | |
| Tower | Height | 115.663 m |
| Tower Mass | 628,442 kg | |
| Structural damping ratio | 1% | |
| Component | Material | Density (kg/m3) | Young’s Modulus (GPa) | Poisson’s Ratio | Yield Strength (MPa) |
|---|---|---|---|---|---|
| Blade | Polyester fiber | 1850 | 38 | 0.3 | 700 |
| Tower | Steel | 8500 | 210 | 0.3 | 355 |
| Pile | - | 2400 | 31 | 0.3 | - |
| No. | Earthquake Names | Year | Scale Factor | PGA(g) |
|---|---|---|---|---|
| 1 | Kern County | 1952 | 5 | 0.78 |
| 2 | Borrego Mtn | 1968 | 4 | 0.55 |
| 3 | Tabas-Iran | 1978 | 4 | 0.43 |
| 4 | Imperial Valley-06 | 1979 | 2.5 | 0.37 |
| 5 | Irpinia-Italy-01 | 1980 | 1 | 0.01 |
| 6 | Corinth- Greece | 1981 | 1 | 0.29 |
| 7 | Superstition Hills-02 | 1987 | 1 | 0.16 |
| 8 | Loma Prieta | 1989 | 1 | 0.17 |
| 9 | Cape Mendocino | 1992 | 1 | 0.15 |
| 10 | Landers | 1992 | 1 | 0.18 |
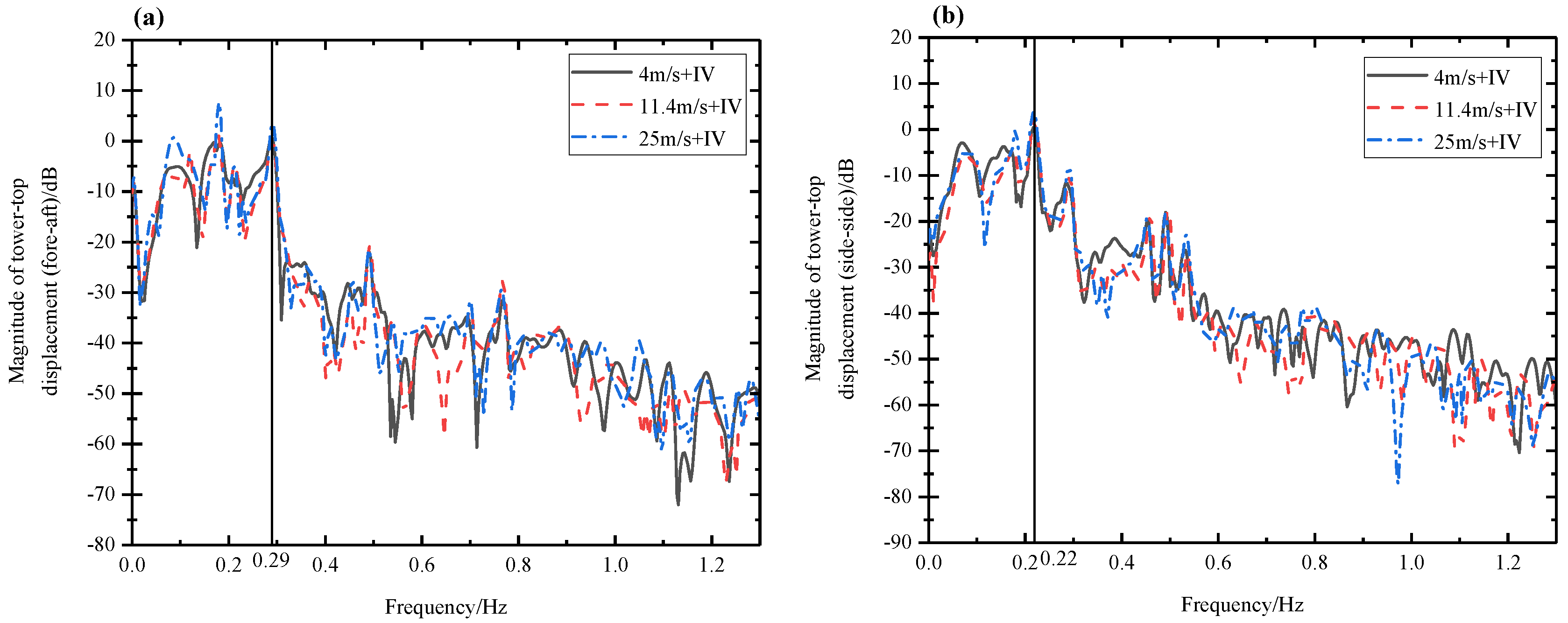
| Modal | Description | Literature [27] (Hz) | In Paper (60 mm) (Hz) | Difference (%) | In Paper (34 mm) (Hz) | Difference (%) |
|---|---|---|---|---|---|---|
| 1 | 1st tower fore–aft mode | 0.25 | 0.29 | 16.0 | 0.28 | 12.0 |
| 2 | 1st tower side–side mode | 0.25 | 0.22 | −12.0 | 0.24 | −4.0 |
| 3 | 1st fix-free mode | 0.50 | 0.44 | −12.0 | 0.48 | −4.0 |
| 4 | 1st blade flap with yaw | 0.55 | 0.47 | −14.5 | 0.51 | −7.2 |
| 5 | 1st blade flap with tilt | 0.59 | 0.52 | −11.8 | 0.54 | −5.0 |
| 6 | 1st collective flap mode | 0.63 | 0.64 | 1.6 | 0.68 | 7.9 |
| 7 | 1st blade edge1 | 0.92 | 0.68 | −25.5 | 0.72 | −21.7 |
| 8 | 1st blade edge2 | 0.94 | 0.75 | −20.2 | 0.76 | −19.1 |
| 9 | 2nd blade flap with yaw | 1.38 | 1.41 | 2.2 | 1.45 | 5.0 |
| 10 | 2nd blade flap with tilt | 1.55 | 1.47 | 5.2 | 1.51 | 2.6 |
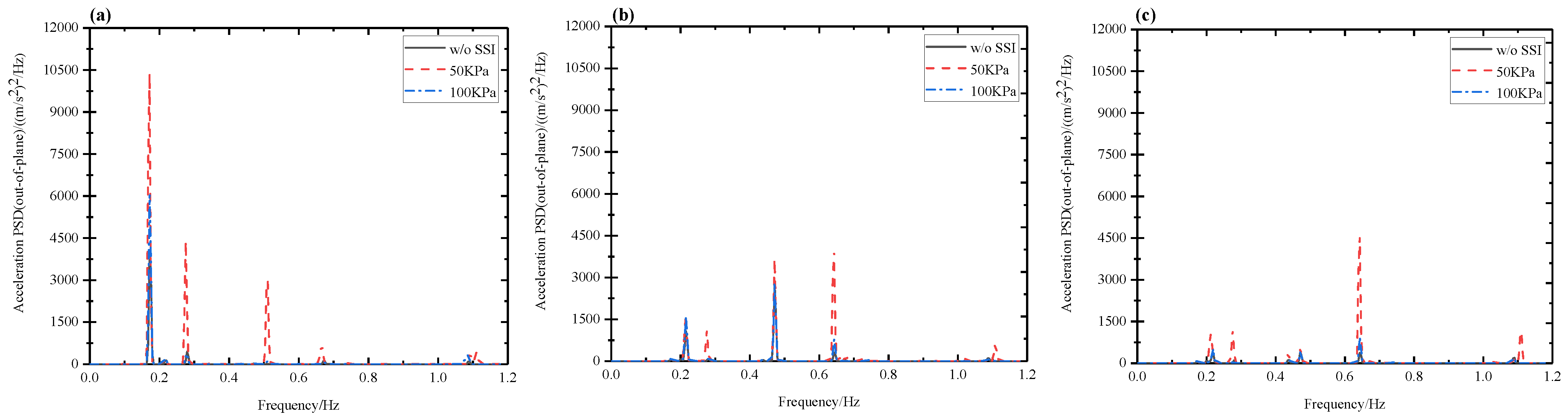
| Modal | Description | w/o SSI | 50 KPa | 100 KPa | ||
|---|---|---|---|---|---|---|
| Frequency (Hz) | Frequency (Hz) | Difference (%) | Frequency (Hz) | Difference (%) | ||
| 1 | 1st tower fore–aft mode | 0.29 | 0.29 | 0 | 0.29 | 0 |
| 2 | 1st tower side–side mode | 0.22 | 0.21 | 4.5 | 0.21 | 4.5 |
| 3 | 1st fix-free mode | 0.44 | 0.44 | 0 | 0.44 | 0 |
| 4 | 1st blade flap with yaw | 0.47 | 0.47 | 0 | 0.47 | 0 |
| 5 | 1st blade flap with tilt | 0.52 | 0.52 | 0 | 0.52 | 0 |
| 6 | 1st collective flap mode | 0.64 | 0.64 | 0 | 0.64 | 0 |
| 7 | 1st blade edge1 | 0.68 | 0.68 | 0 | 0.68 | 0 |
| 8 | 1st blade edge2 | 0.75 | 0.75 | 0 | 0.75 | 0 |
| 9 | 2nd blade flap with yaw | 1.41 | 1.41 | 0 | 1.41 | 0 |
| 10 | 2nd blade flap with tilt | 1.47 | 1.47 | 0 | 14.7 | 0 |
| Wind Speed (m/s) | w/o SSI | 50 KPa | 100 KPa | ||
|---|---|---|---|---|---|
| Max Bending Moment (MN · m) | Max Bending Moment (MN · m) | Difference (%) | Max Bending Moment (MN · m) | Difference (%) | |
| 4 | 81.3 | 104 | 27.9 | 85 | 4.6 |
| 11.4 | 265 | 307 | 15.8 | 267 | 0.8 |
| 25 | 282 | 335 | 18.8 | 288 | 2.1 |
| Wind Speed (m/s) | Blade | w/o SSI | 50 KPa | 100 KPa | ||
|---|---|---|---|---|---|---|
| Max Displacement (m) | Max Displacement (m) | Difference (%) | Max Displacement (m) | Difference (%) | ||
| 4 | 0 | 2.403 | 2.989 | 24.38 | 2.539 | 5.6 |
| 1 | 5.292 | 5.797 | 9.54 | 5.384 | 1.74 | |
| 2 | 1.581 | 1.84 | 16.38 | 1.679 | 6.2 | |
| 11.4 | 0 | 8.116 | 9.055 | 11.57 | 8.305 | 2.28 |
| 1 | 9.051 | 9.148 | 1.07 | 9.048 | −0.03 | |
| 2 | 5.483 | 5.175 | −5.6 | 5.261 | −4.05 | |
| 25 | 0 | 11.756 | 16.824 | 43.11 | 14.237 | 21.1 |
| 1 | 7.019 | 10.164 | 44.81 | 8.081 | 15.13 | |
| 2 | 3.264 | 4.697 | 43.9 | 3.689 | 13.02 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, C.; Wang, Y.; Weng, J.; Ding, B.; Zhong, J. Dynamic Characteristics Analysis of a Multi-Pile Wind Turbine Under the Action of Wind–Seismic Coupling. Energies 2025, 18, 2833. https://doi.org/10.3390/en18112833
Zheng C, Wang Y, Weng J, Ding B, Zhong J. Dynamic Characteristics Analysis of a Multi-Pile Wind Turbine Under the Action of Wind–Seismic Coupling. Energies. 2025; 18(11):2833. https://doi.org/10.3390/en18112833
Chicago/Turabian StyleZheng, Chaoyang, Yongtao Wang, Jiahua Weng, Bingxiao Ding, and Jianhua Zhong. 2025. "Dynamic Characteristics Analysis of a Multi-Pile Wind Turbine Under the Action of Wind–Seismic Coupling" Energies 18, no. 11: 2833. https://doi.org/10.3390/en18112833
APA StyleZheng, C., Wang, Y., Weng, J., Ding, B., & Zhong, J. (2025). Dynamic Characteristics Analysis of a Multi-Pile Wind Turbine Under the Action of Wind–Seismic Coupling. Energies, 18(11), 2833. https://doi.org/10.3390/en18112833







