A Topology Identification Strategy of Low-Voltage Distribution Grids Based on Feature-Enhanced Graph Attention Network
Abstract
1. Introduction
1.1. Motivation
1.2. Literature Review and Research Gaps
- (1)
- The effectiveness of the aforementioned topology identification methods in practical LVDGs is predominantly constrained by measurement device reliability and data quality. Notably, there are quite a few hidden nodes without installed measuring devices in LVDGs. Moreover, due to equipment aging, communication interference or environmental factors, the measurement data may contain noise or errors, which poses a challenge to the performance of the model.
- (2)
- In the existing research on the topology recognition of the LVDG, the network is often merely regarded as a simple homogeneous graph or only relies on the correlations of traditional electrical quantities (such as voltage and current). As a result, critical information, such as the hierarchical relationships within distribution areas and the diversity of equipment types, is often overlooked. In addition, the existing methods lack deep modeling of graph structure features (such as node neighbor relationship and path dependence), making it difficult to capture the complex interaction patterns among devices.
1.3. Contributions
- (1)
- A topology identification architecture based on F-GAT, which integrates basic information and structural characteristics of LVDGs, is proposed to realize topology identification by graph learning to represent the relationship between measurement data and topology connection. The proposed topology recognition strategy achieves topology identification based on existing AMI system data without requiring additional measurement devices, effectively addressing current challenges in low-voltage distribution grids, such as insufficient data collection capabilities and untimely record updates, thereby demonstrating significant engineering practicality.
- (2)
- A meta-path random walk node enhancement model for LVDGs is proposed. According to the connection characteristics of LVDGs, the meta-path form is designed, and the node type and connection mode are explicitly distinguished to avoid the information loss caused by the homogenous graph assumption. A heterogeneous skip-gram model was employed to derive embedding representations of node-specific structural characteristics, which significantly enhances the model’s feature extraction and mining capabilities.
- (3)
- A GAT with an attention mechanism is adopted to learn the low-dimensional representations of topological nodes and to excavate the potential association patterns and structural information in the graph structure topology. The accuracy of topology recognition has been enhanced through joint representation of electrical properties and graph-structural semantics.
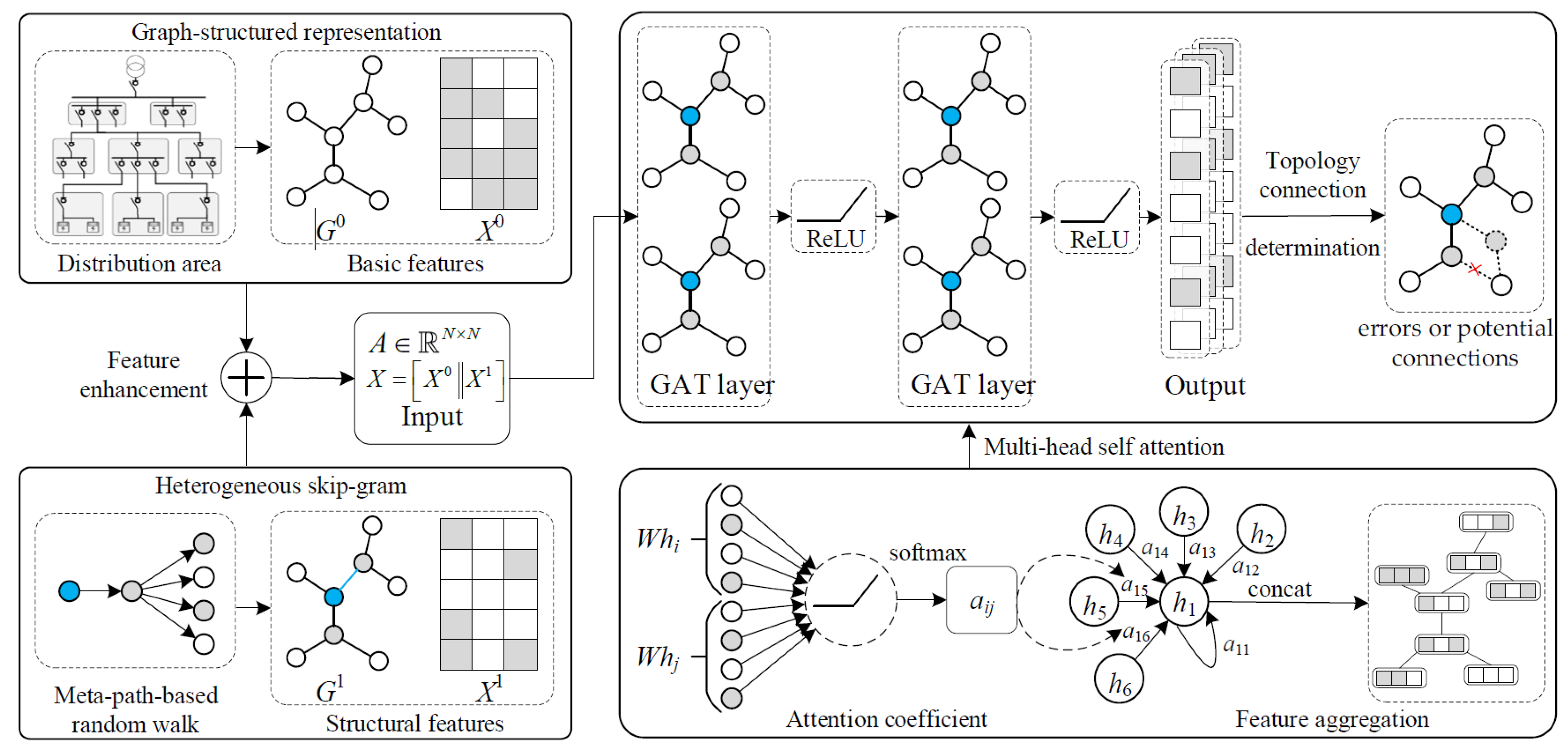
2. Topology Identification Architecture of LVDGs Based on F-GAT
3. Problem Modeling
3.1. Graph-Structured Representation of the Distribution Grid Topology
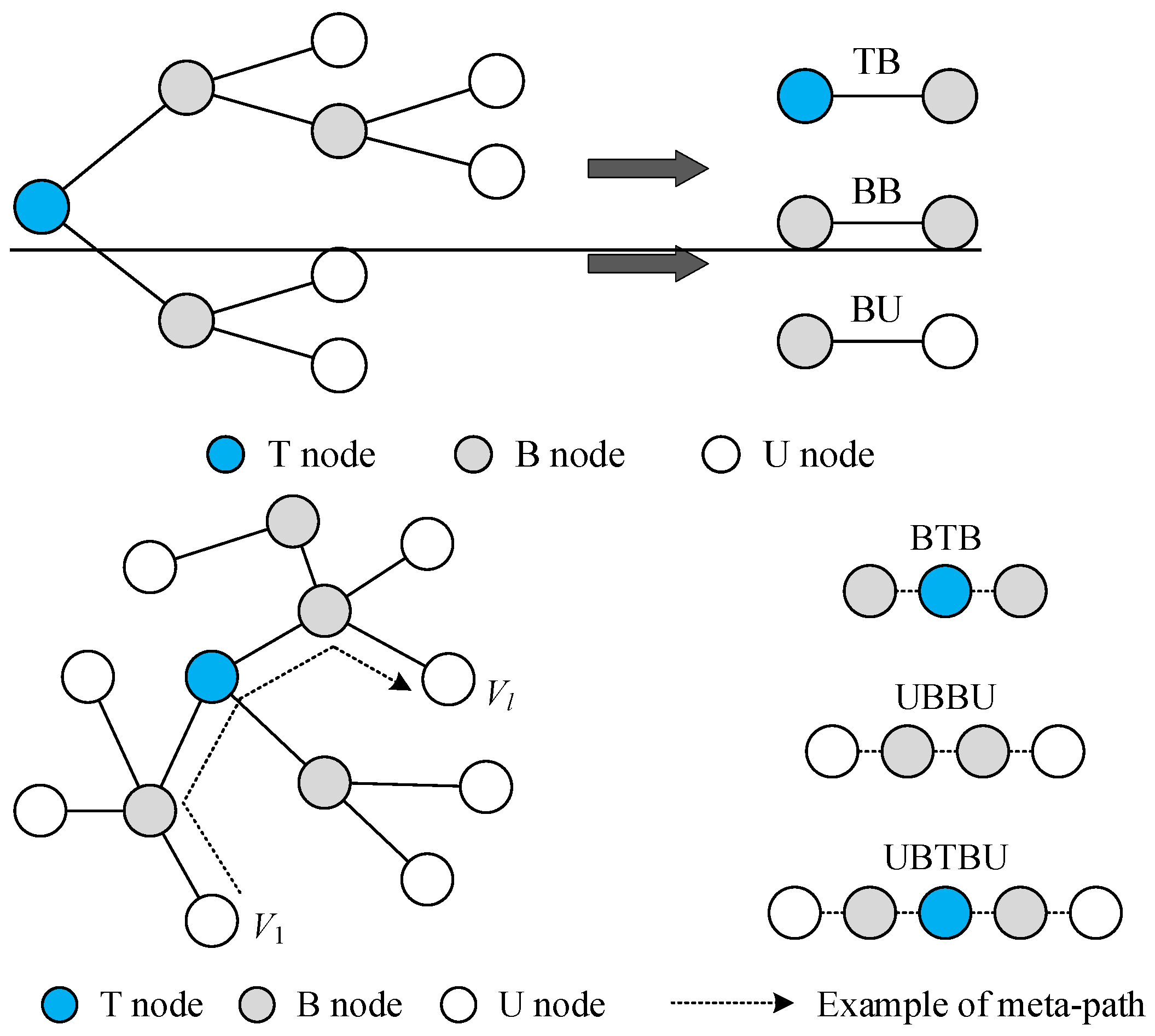
3.2. Feature Enhancement Based on Meta-Path Random Walk
- (1)
- Definition of meta-path transition probability
- (2)
- Meta-path form design
- (3)
- Feature enhancement scheme based on heterogeneous skip-gram
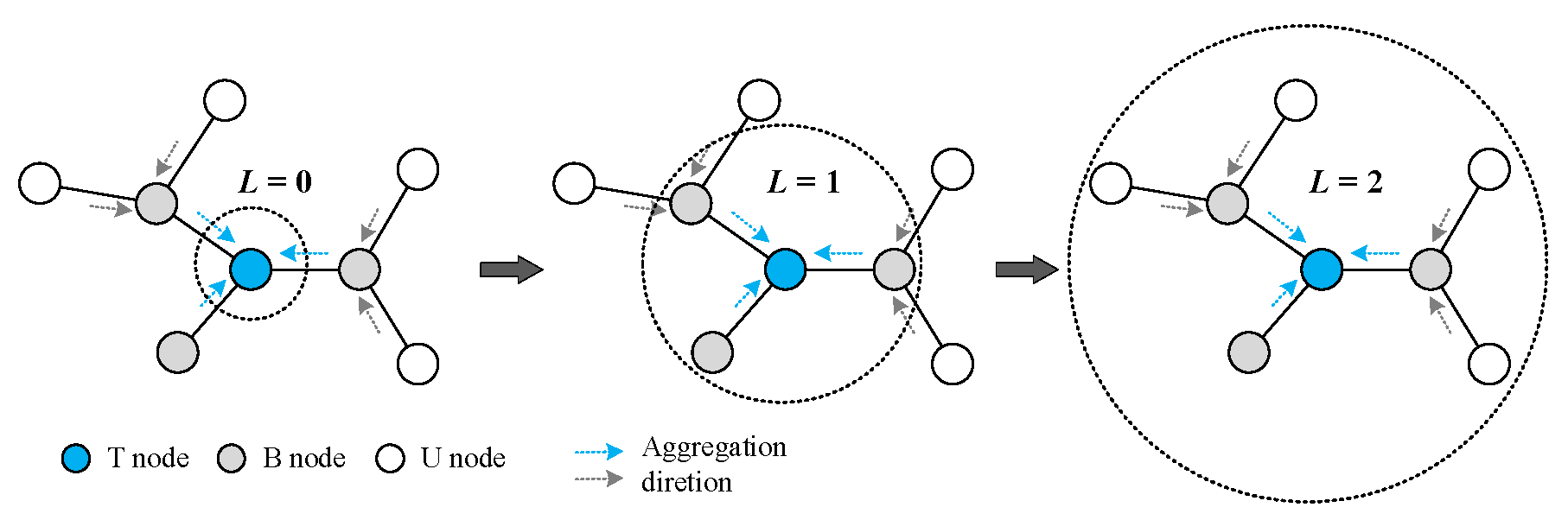
3.3. Feature Fusion Based on F-GAT
4. Proposed Solution Based on F-GAT
| Algorithm 1: Proposed solution based on F-GAT |
 |
5. Case Studies
5.1. Case Study Setup
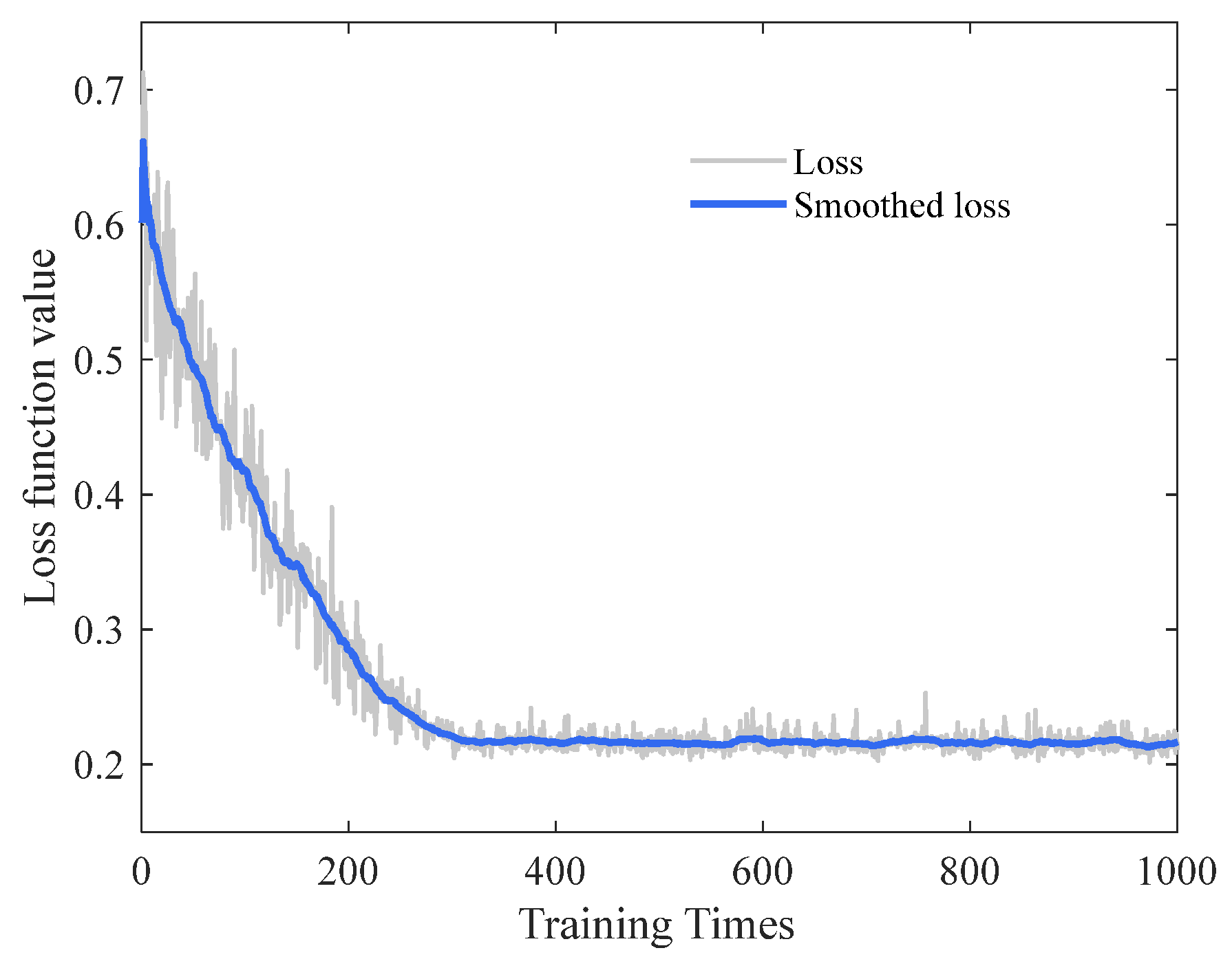
5.2. Analysis of the Model Training Process
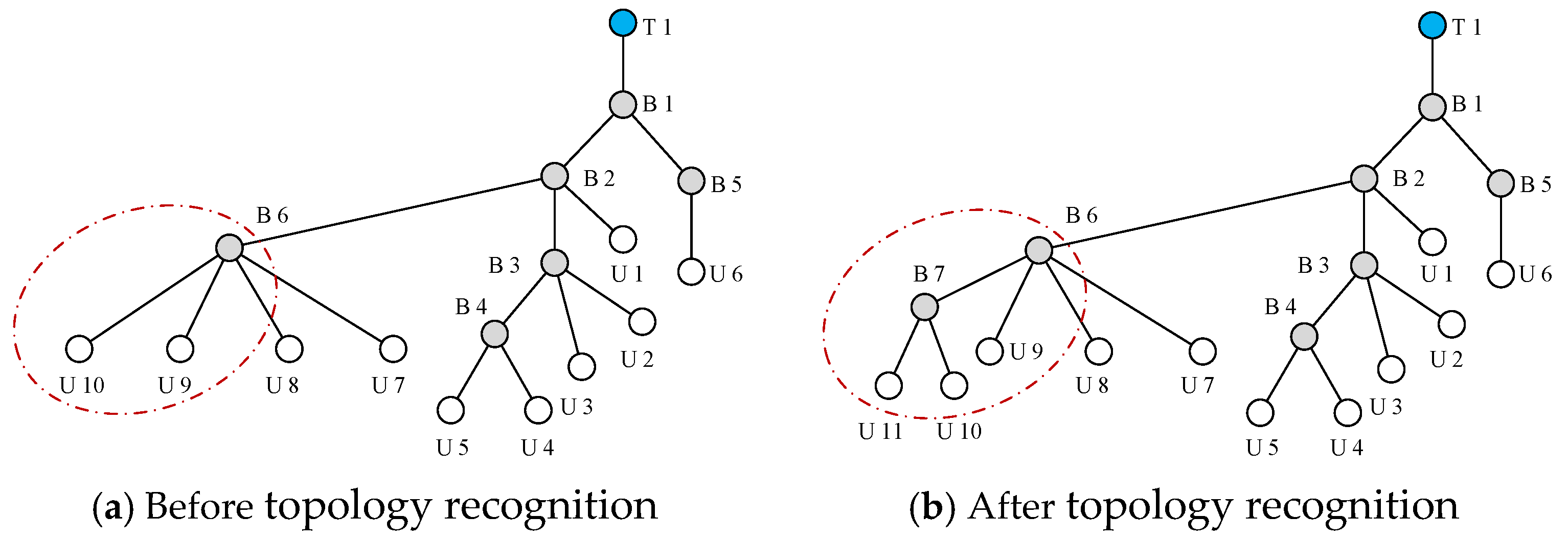
5.3. Analysis of the Topology Identification Result
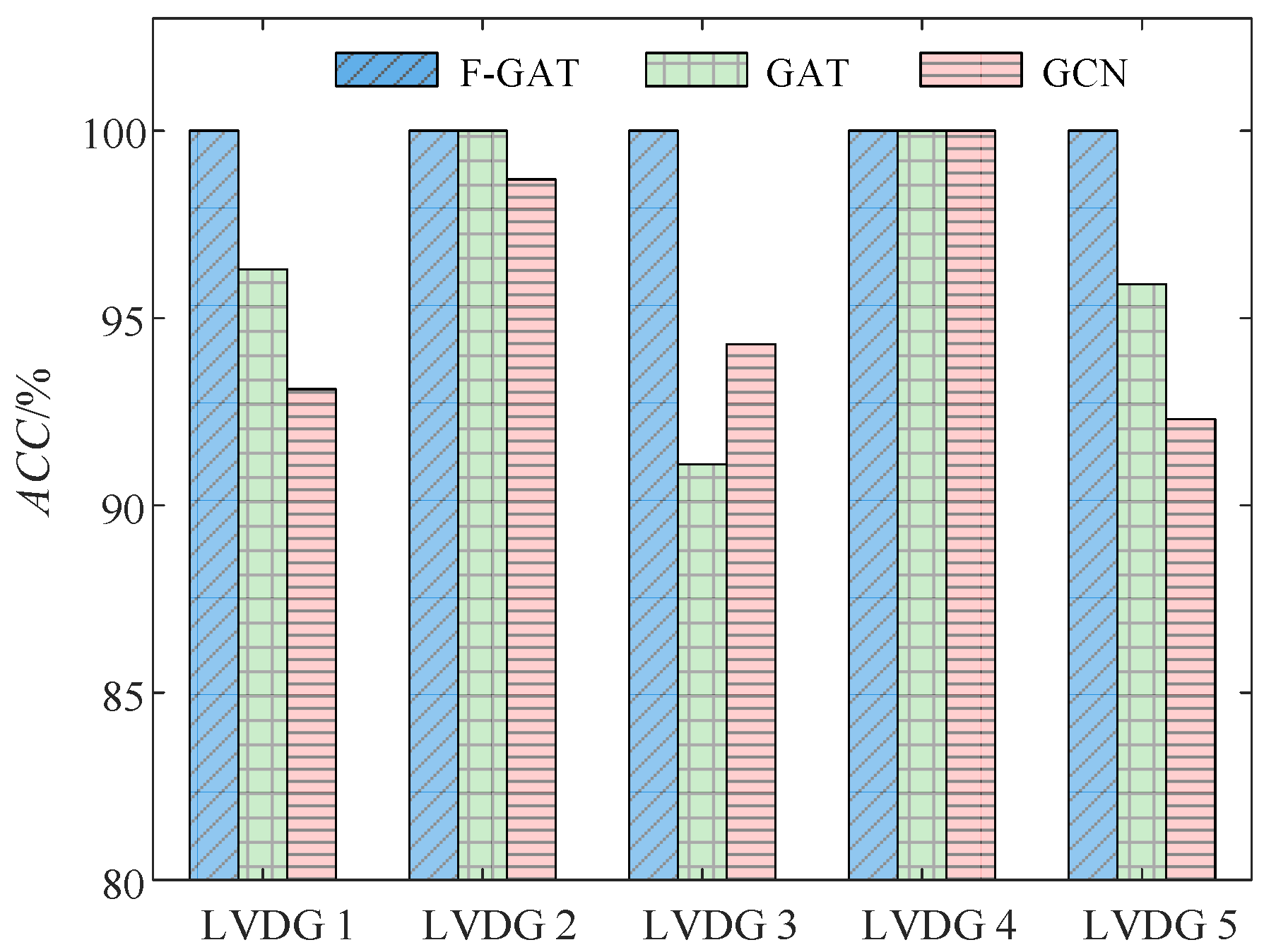
5.4. Comparison of Different Algorithms
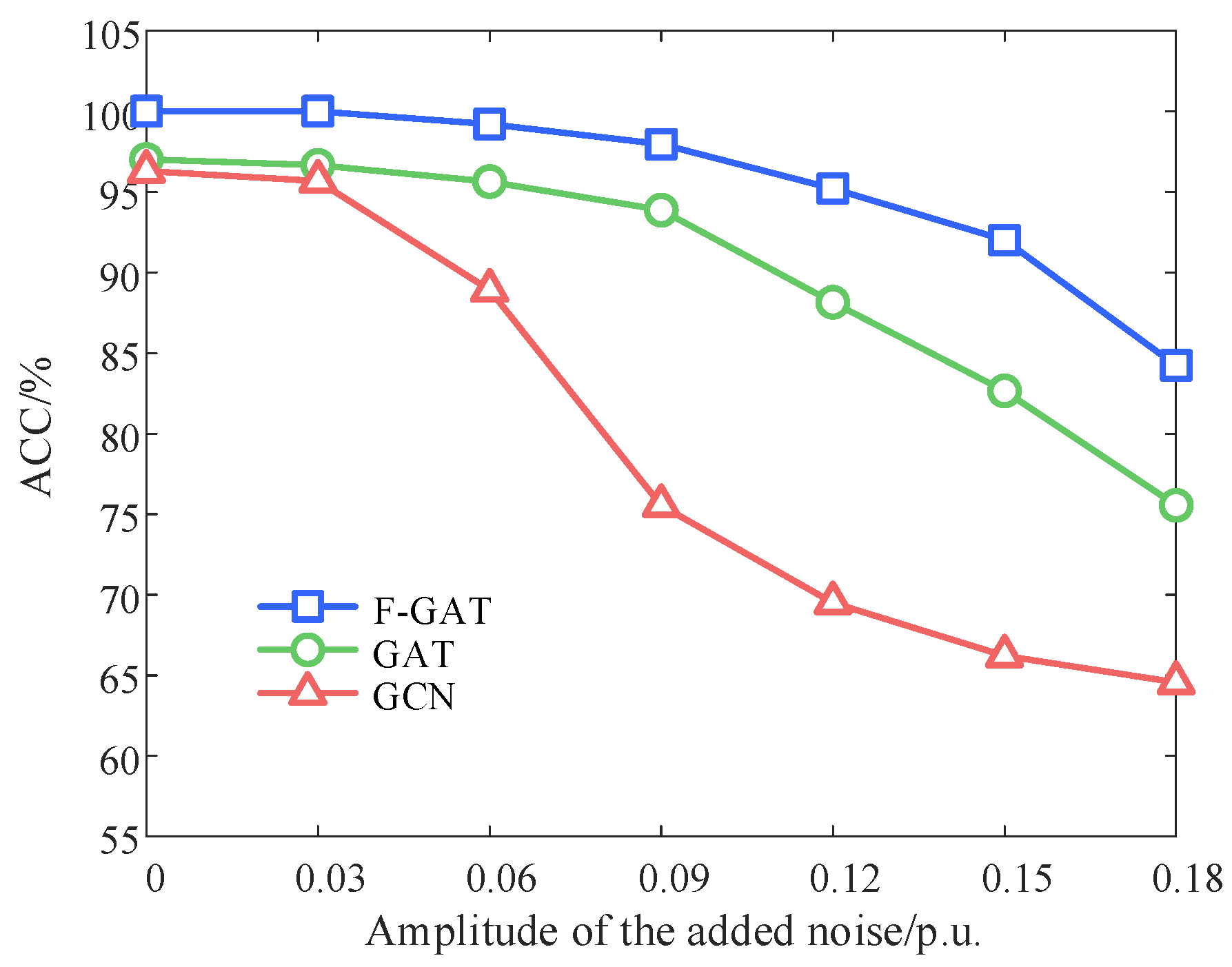
5.5. Analysis of the Model Anti-Noise Performance
6. Conclusions
- (1)
- The topology identification model of LVDGs based on F-GAT is used to obtain the embedded representation of node structure characteristics by means of a meta-path random walk and to judge node connections by means of GAT. Case studies across five distribution transformer areas of varying scales demonstrate that the proposed F-GAT model establishes dynamic topological mapping relationships for LVDGs, overcomes the time latency inherent in conventional manual inspections and achieves precision correction of archival errors.
- (2)
- The GAT with multi-head attention automatically adjusts neighboring node weights, accurately identifying six abnormal and two disconnected lines in 100 test samples, enhancing robustness in abnormal scenarios.
- (3)
- Compared with graph structure learning algorithms, such as GCN and GAT, the proposed F-GAT model utilizes meta-path random walks to generate embedded representations of node structural features, which are then fused with basic node information for enhanced feature perception and mining capabilities. The F-GAT algorithm achieves 4.32% and 3.34% improvements in the ACC index compared to GCN and GAT, respectively.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Parameters | Value |
|---|---|
| Number of hidden units (evaluation network) | {128, 128} |
| Output feature dimension | 16 |
| Number of attention heads | 4 |
| Learning rate | 0.001 |
| Dropout rate | 0.4 |
| Optimizer | Adam |
| Parameters | Value |
|---|---|
| Number of hidden units (evaluation network) | {128, 128} |
| Output feature dimension | 64 |
| Number of attention heads | / |
| Learning rate | 0.001 |
| Dropout rate | 0.4 |
| Optimizer | Adam |
References
- García, S.; Mora-Merchán, J.M.; Larios, D.F.; Personal, E.; Parejo, A.; León, C. Phase topology identification in low-voltage distribution networks: A Bayesian approach. Int. J. Electr. Power Energy Syst. 2023, 144, 108525. [Google Scholar] [CrossRef]
- Wang, L.; Chiang, H.D. Group-based line switching for enhancing contingency-constrained static voltage stability. IEEE Trans. Power Syst. 2019, 35, 1489–1498. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Y.; Weng, Y.; Zhang, N. Topology identification and line parameter estimation for non-PMU distribution network: A numerical method. IEEE Trans. Smart Grid 2020, 11, 4440–4453. [Google Scholar] [CrossRef]
- Athanasiadis, C.L.; Papadopoulos, T.A.; Kryonidis, G.C.; Doukas, D.I. A review of distribution network applications based on smart meter data analytics. Renew. Sustain. Energy Rev. 2024, 191, 114151. [Google Scholar] [CrossRef]
- Ge, H.; Xu, B.; Zhang, X.; Bi, Y. Low-voltage overhead lines topology identification method based on high-frequency signal injection. Arch. Electr. Eng. 2021, 70, 791–800. [Google Scholar]
- Byun, H.J.; Zheng, Y.P.; Choi, S.J.; Shon, S.G. New identification method for power transformer and phase in distribution systems. Appl. Mech. Mater. 2018, 878, 291–295. [Google Scholar] [CrossRef]
- Byun, H.J.; Shon, S. Phase shift analysis and phase identification for distribution system with 3-phase unbalanced constant current loads. J. Electr. Eng. Technol. 2013, 8, 729–736. [Google Scholar] [CrossRef]
- Wang, J.; Ji, X.; Li, K.; Sun, Q. Topology verification of low voltage distribution network based on k-means clustering algorithm. IOP Conf. Ser. Mater. Sci. Eng. 2019, 569, 052096. [Google Scholar] [CrossRef]
- Al Khafaf, N.; Song, H.; McGrath, B.; Jalili, M. Identification of low voltage distribution transformer–customer connectivity based on unsupervised learning. Energy Rep. 2023, 9, 72–79. [Google Scholar] [CrossRef]
- Lian, Z.; Yao, L.; Liu, S.; Yu, Y.; Tang, X. Phase and meter box identification for single-phase users based on t-SNE dimension reduction and BIRCH clustering. Autom. Electr. Power Syst. 2020, 44, 176–184. [Google Scholar]
- Jiao, F.; Li, Z.; Ai, J.; Yang, H.; Deng, Y.; Li, D.; Gao, W.; Lai, Z.; Fu, X. Topology Identification Method for Low-Voltage Distribution Node Networks Based on Density Clustering Using Smart Meter Real-time Measurement Data. IEEE Access 2024, 12, 83600–83610. [Google Scholar] [CrossRef]
- Tian, Z.; Wu, W.; Zhang, B. A mixed integer quadratic programming model for topology identification in distribution network. IEEE Trans. Power Syst. 2015, 31, 823–824. [Google Scholar] [CrossRef]
- Liu, B.; Chen, J.; Li, J. Distribution network topology identification method based on state estimation with mixed integer programming and structural equation model. Int. J. Electr. Power Energy Syst. 2024, 162, 110251. [Google Scholar] [CrossRef]
- Farajollahi, M.; Shahsavari, A.; Mohsenian-Rad, H. Topology identification in distribution systems using line current sensors: An MILP approach. IEEE Trans. Smart Grid 2019, 11, 1159–1170. [Google Scholar] [CrossRef]
- Karimi, H.S.; Natarajan, B. Joint topology identification and state estimation in unobservable distribution grids. IEEE Trans. Smart Grid 2021, 12, 5299–5309. [Google Scholar] [CrossRef]
- Ma, L.; Wang, L.; Liu, Z. Topology identification of distribution networks using a split-EM based data-driven approach. IEEE Trans. Power Syst. 2021, 37, 2019–2031. [Google Scholar] [CrossRef]
- Tong, L.; Chai, W.; Wu, D. Topology and impedance identification method of low-voltage distribution network based on smart meter measurements. Front. Energy Res. 2022, 10, 895397. [Google Scholar] [CrossRef]
- Xu, D.; Wu, Z.; Xu, J.; Hu, Q. A data-model hybrid driven topology identification framework for distribution networks. CSEE J. Power Energy Syst. 2023, 10, 1478–1490. [Google Scholar]
- Ni, Q.; Jiang, H. Topology identification of low-voltage distribution network based on deep convolutional time-series clustering. Energies 2023, 16, 4274. [Google Scholar] [CrossRef]
- Wu, H.; Xu, Z.; Zhao, J.; Chai, S. Gridtopo-GAN for distribution system topology identification. IEEE Trans. Ind. Inform. 2022, 19, 5356–5366. [Google Scholar] [CrossRef]
- Poudel, S.; Ramachandran, T.; Veeramany, A.; Francis, C.; Reiman, A.P. Topology identification using graph theory informed state estimation-based model selection for power distribution systems. IEEE Trans. Ind. Inform. 2023, 20, 3563–3573. [Google Scholar] [CrossRef]
- Li, H.; Liang, W.; Liang, Y.; Li, Z.; Wang, G. Topology identification method for residential areas in low-voltage distribution networks based on unsupervised learning and graph theory. Electr. Power Syst. Res. 2023, 215, 108969. [Google Scholar] [CrossRef]
- Flynn, C.; Pengwah, A.B.; Razzaghi, R.; Andrew, L.L. An improved algorithm for topology identification of distribution networks using smart meter data and its application for fault detection. IEEE Trans. Smart Grid 2023, 14, 3850–3861. [Google Scholar] [CrossRef]
- Dong, Y.; Chawla, N.V.; Swami, A. metapath2vec: Scalable representation learning for heterogeneous networks. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13–17 August 2017; pp. 135–144. [Google Scholar]
- Huang, C.; Fang, Y.; Lin, X.; Cao, X.; Zhang, W. ABLE: Meta-path prediction in heterogeneous information networks. ACM Trans. Knowl. Discov. Data (TKDD) 2022, 16, 1–21. [Google Scholar] [CrossRef]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
- Vujović, Ž. Classification model evaluation metrics. Int. J. Adv. Comput. Sci. Appl. 2021, 12, 599–606. [Google Scholar] [CrossRef]
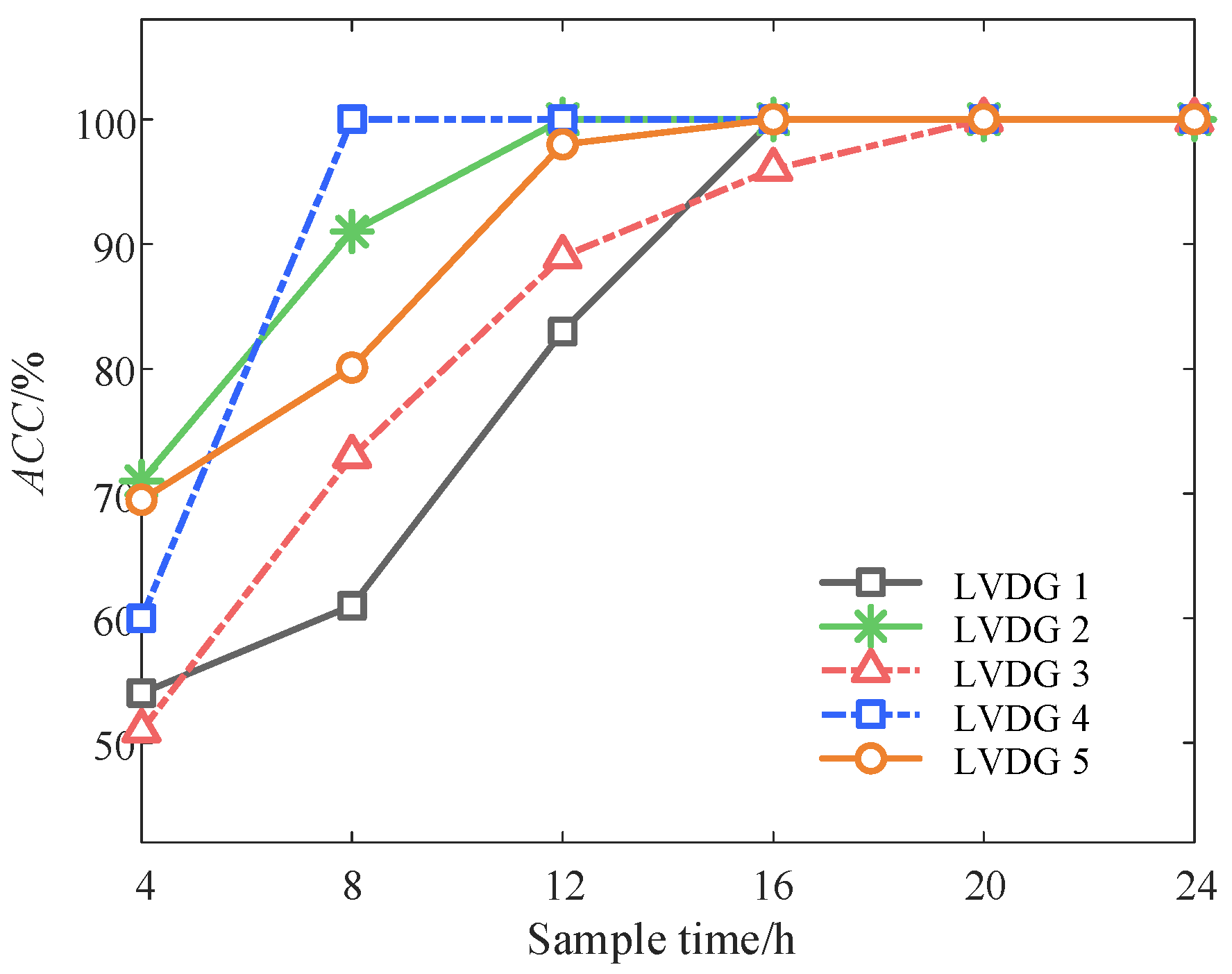

| LVDG 1 | LVDG 2 | LVDG 3 | LVDG 4 | LVDG 5 | |
|---|---|---|---|---|---|
| Number of branch nodes | 19 | 7 | 28 | 5 | 10 |
| Number of user nodes | 62 | 11 | 51 | 12 | 28 |
| Number of all nodes | 81 | 19 | 79 | 18 | 39 |
| Computational Complexity | Time Consumption/s | ACC/% | P/% | R/% | F1/% | |
|---|---|---|---|---|---|---|
| GCN | 0.58 | 95.68 | 98.39 | 97.14 | 97.76 | |
| GAT | 0.58 | 96.66 | 98.42 | 98.11 | 98.26 | |
| F-GAT | 0.61 | 100 | 100 | 100 | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, Y.; Yang, F.; Feng, Y.; Hu, W.; Cheng, Y. A Topology Identification Strategy of Low-Voltage Distribution Grids Based on Feature-Enhanced Graph Attention Network. Energies 2025, 18, 2821. https://doi.org/10.3390/en18112821
Lei Y, Yang F, Feng Y, Hu W, Cheng Y. A Topology Identification Strategy of Low-Voltage Distribution Grids Based on Feature-Enhanced Graph Attention Network. Energies. 2025; 18(11):2821. https://doi.org/10.3390/en18112821
Chicago/Turabian StyleLei, Yang, Fan Yang, Yanjun Feng, Wei Hu, and Yinzhang Cheng. 2025. "A Topology Identification Strategy of Low-Voltage Distribution Grids Based on Feature-Enhanced Graph Attention Network" Energies 18, no. 11: 2821. https://doi.org/10.3390/en18112821
APA StyleLei, Y., Yang, F., Feng, Y., Hu, W., & Cheng, Y. (2025). A Topology Identification Strategy of Low-Voltage Distribution Grids Based on Feature-Enhanced Graph Attention Network. Energies, 18(11), 2821. https://doi.org/10.3390/en18112821





