Optimizing Automatic Voltage Control Collaborative Responses in Chain-Structured Cascade Hydroelectric Power Plants Using Sensitivity Analysis
Abstract
1. Introduction
- (1)
- Analyze the mechanism of reactive power pulling induced by AVCs in CC-HPP networks.
- (2)
- Construct a reactive power–voltage coupling model on the basis of sensitivity analysis.
- (3)
- Propose a coordinated optimization strategy, and develop a regional voltage control system.
- (4)
- Conduct simulations and field-data-based validations to evaluate the effectiveness of the proposed strategy.
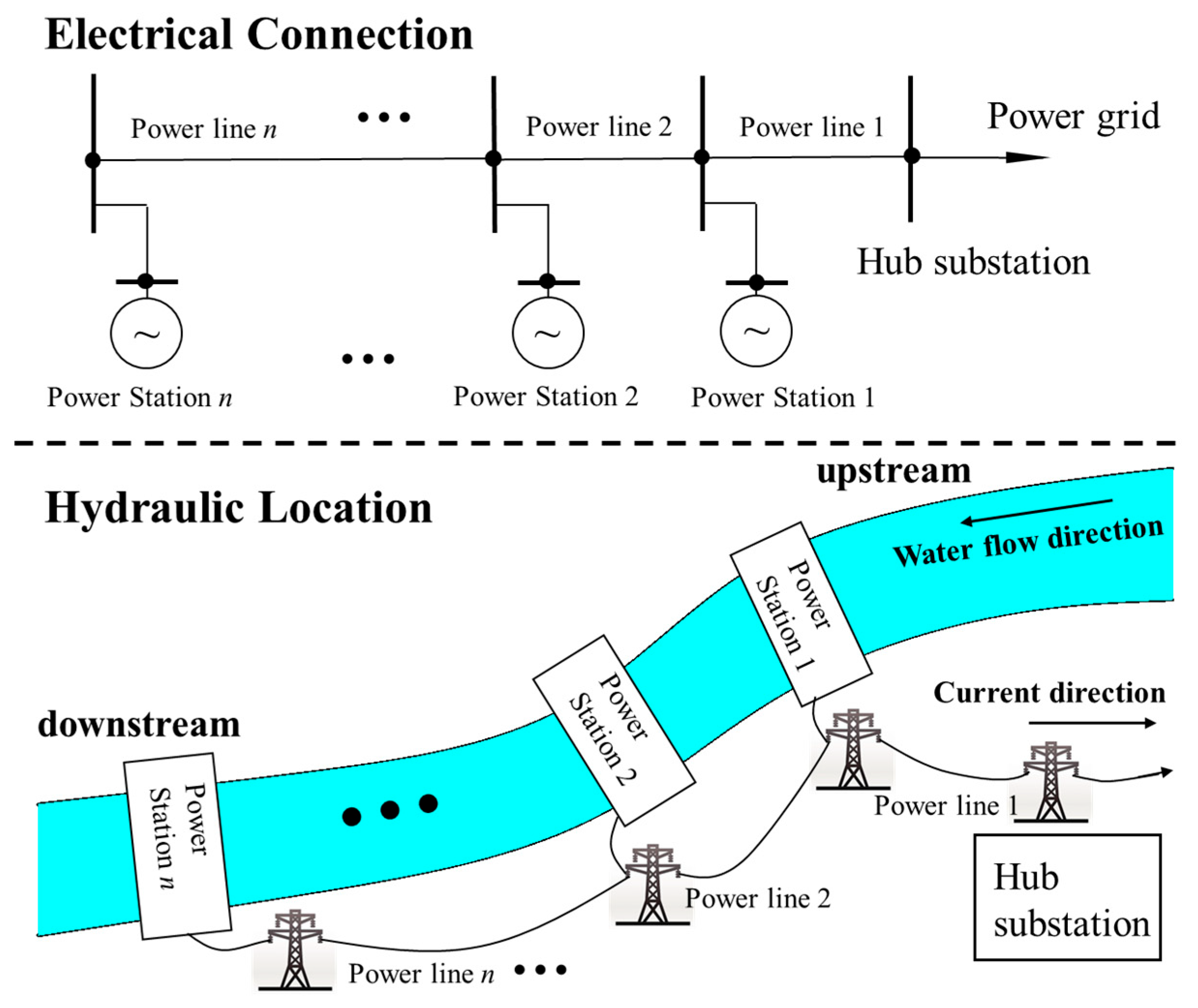
2. Problem Statements
3. Sensitivity Analysis
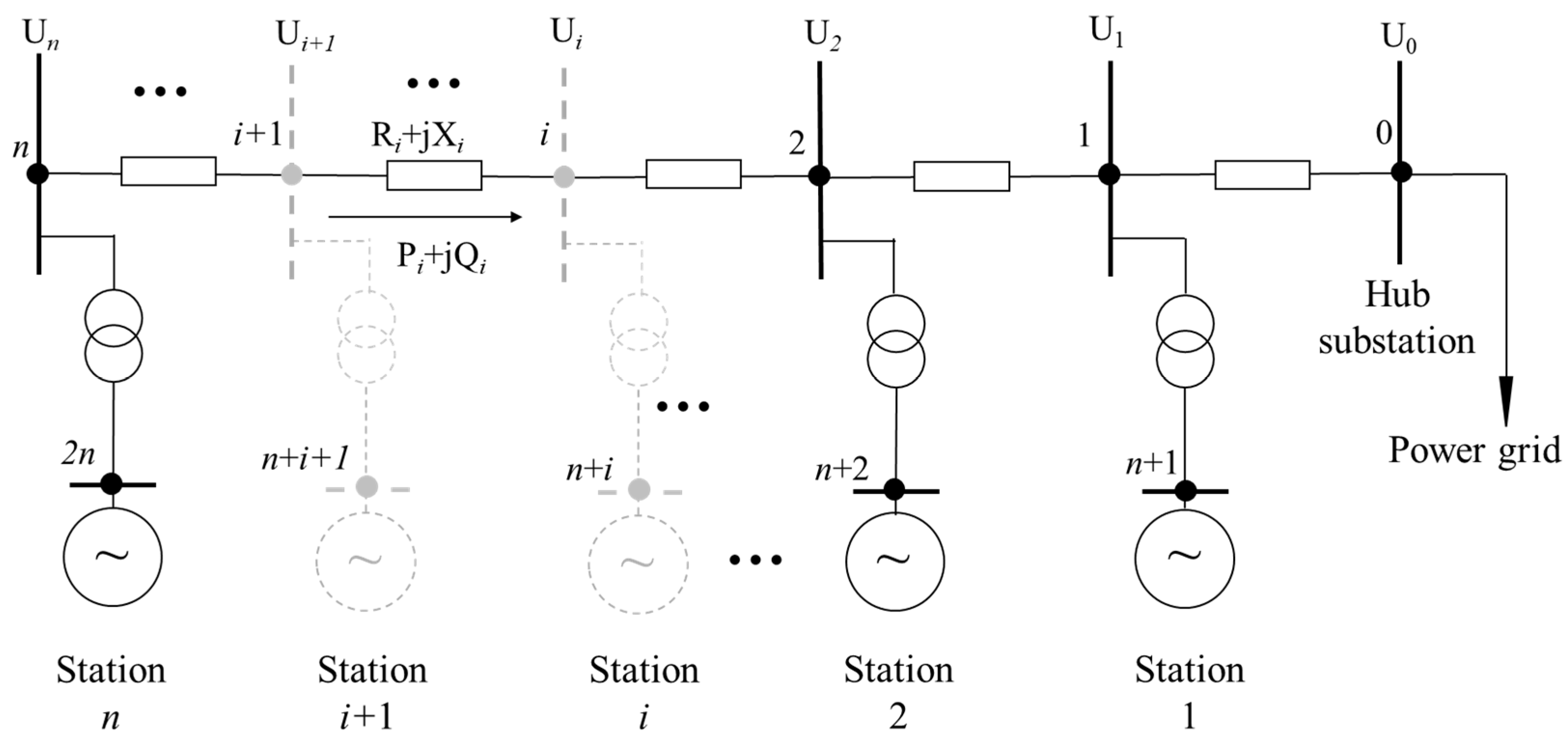
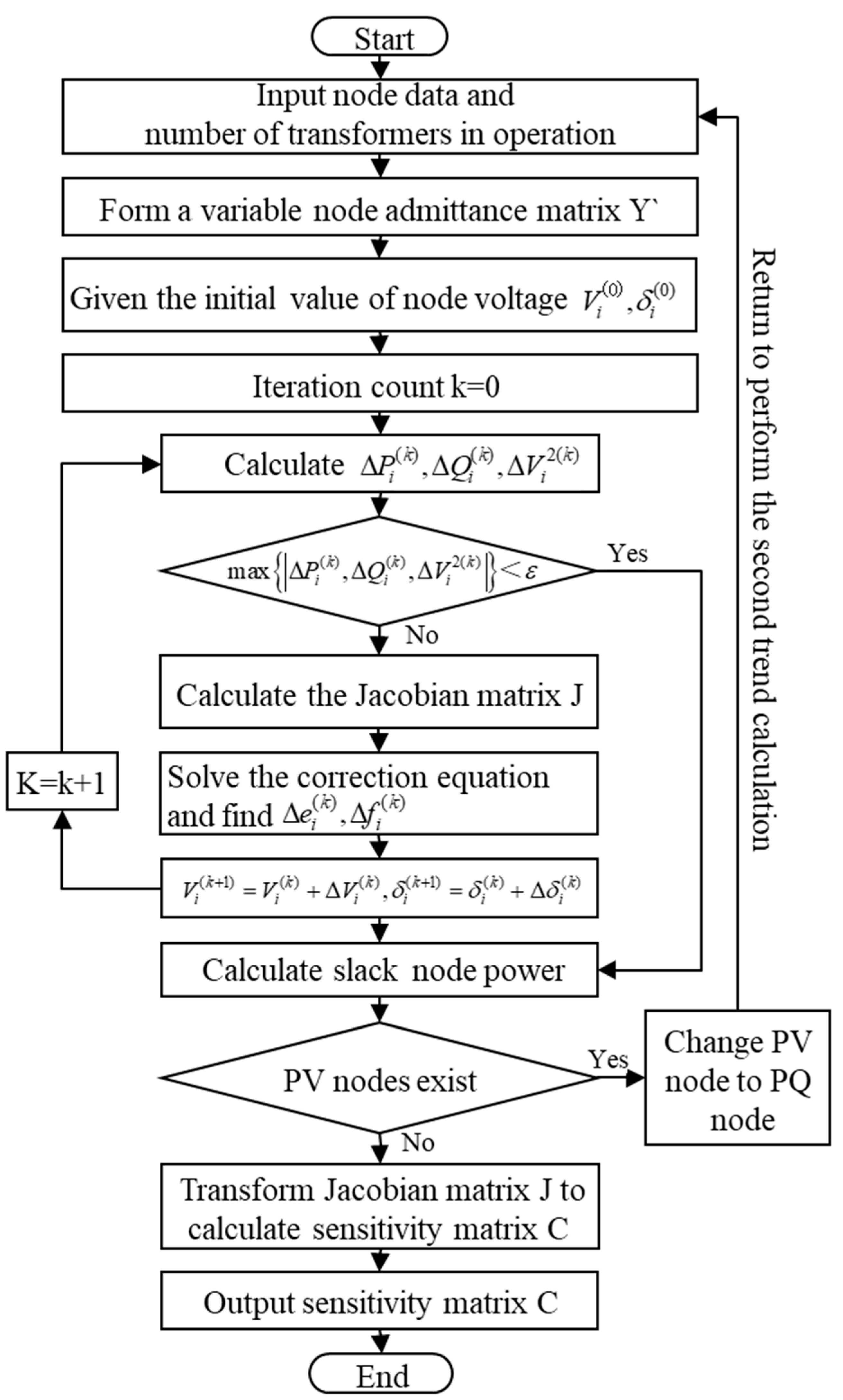
3.1. Sensitivity Modeling
3.2. Reactive Power–Voltage Sensitivity Analysis of CC-HPPs
4. Control Strategy
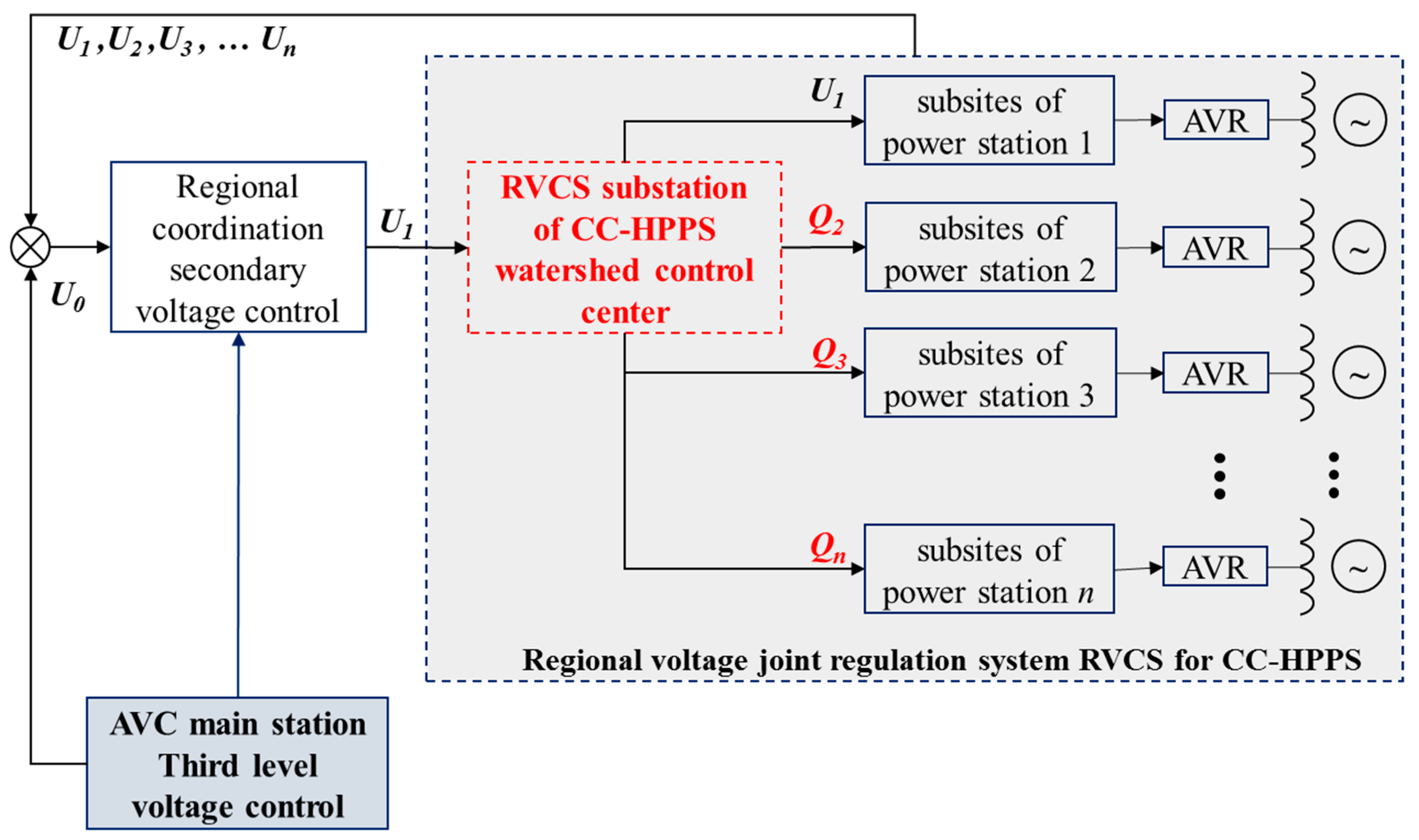
4.1. Control Model
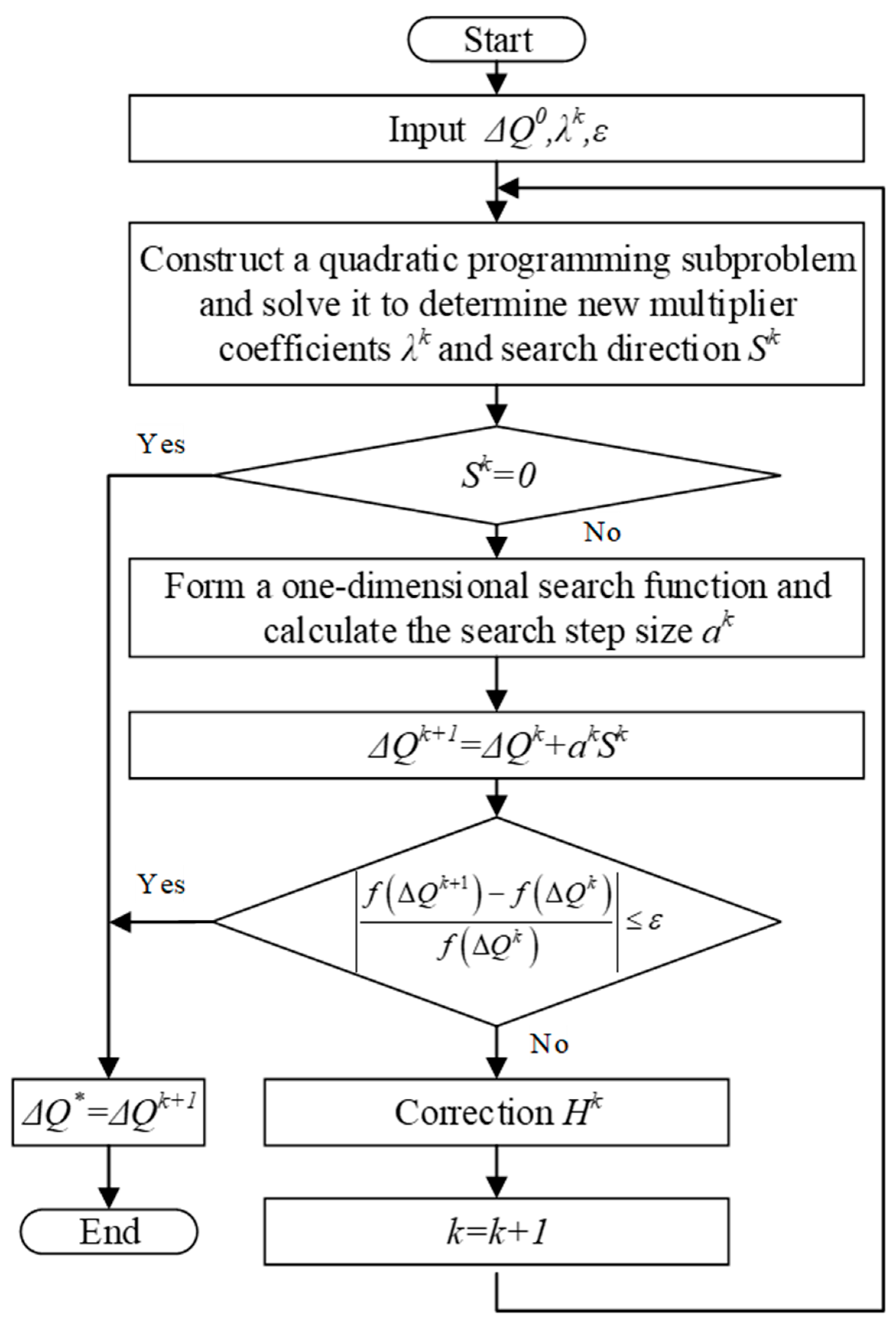
4.2. Mathematical Modeling
4.2.1. Objective Function
4.2.2. Constraints
- (1)
- Constraint on Voltage Variation at the Centralized Grid Connection Point of the CC-HPP Network
- (2)
- Constraint on the Voltage Gradient Difference Across High-Voltage Bus Nodes in the CC-HPP Network
- (3)
- Constraint on the Single-Station Adjustment Step Size
- (4)
- Constraint on Single-Station Voltage Limits
- (5)
- Constraint on the Single-Station Reactive Power Output Limits
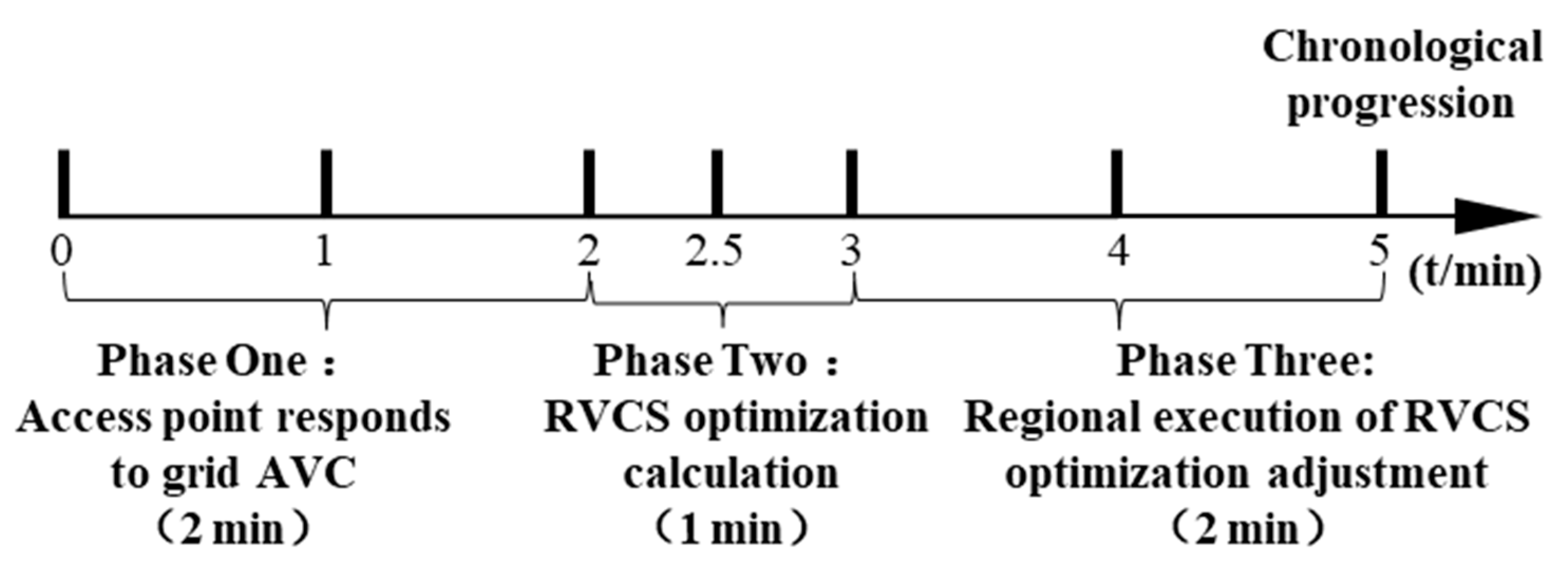
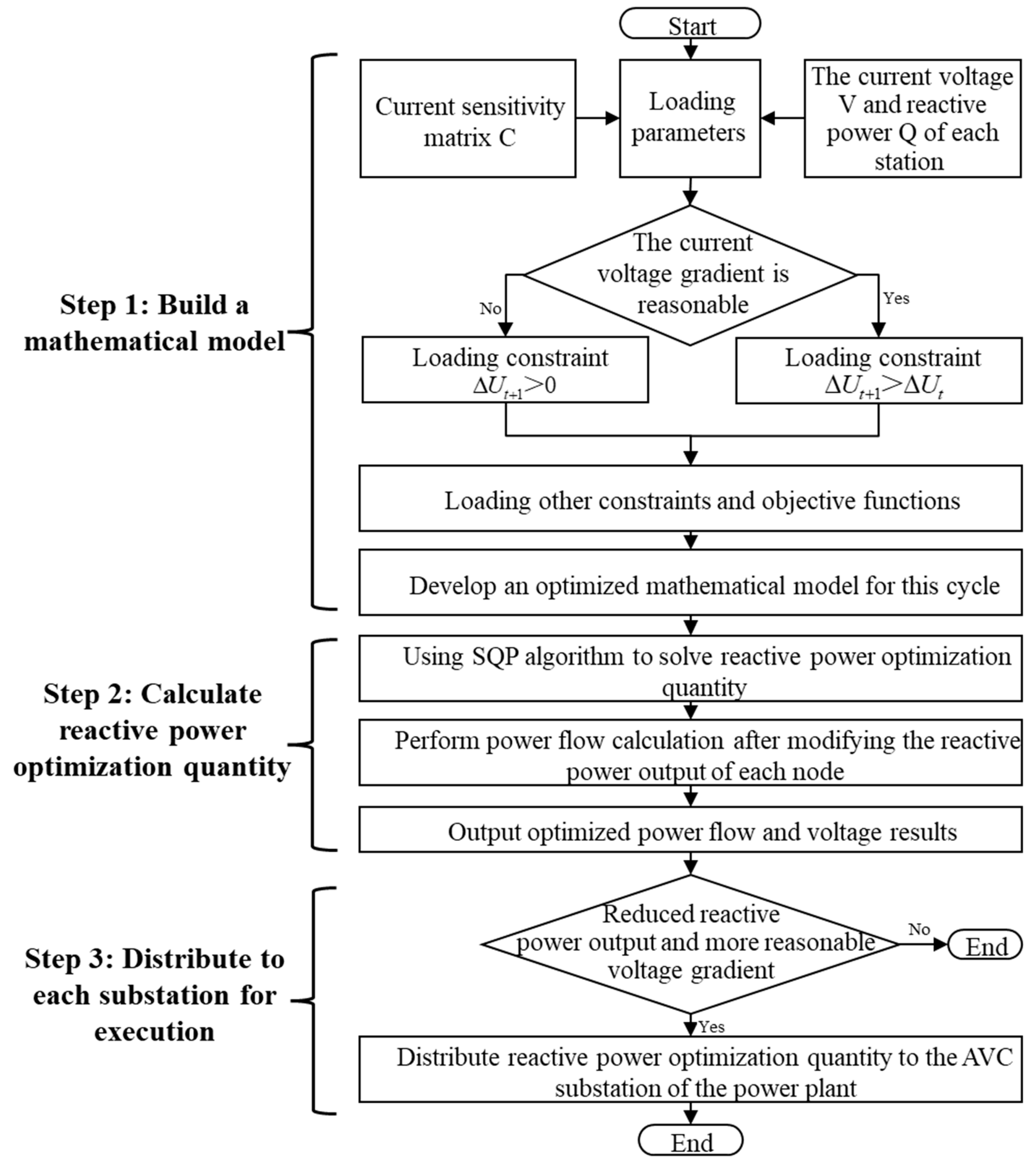
4.3. Working Flow
4.4. Key Indicators
- (1)
- Absolute Value of the Reactive Power-Pulling Amplitude
- (2)
- Reasonable Voltage Gradient Operation Rate
5. Case Study
5.1. Parameter Settings and Scene Division
5.2. Result Analysis
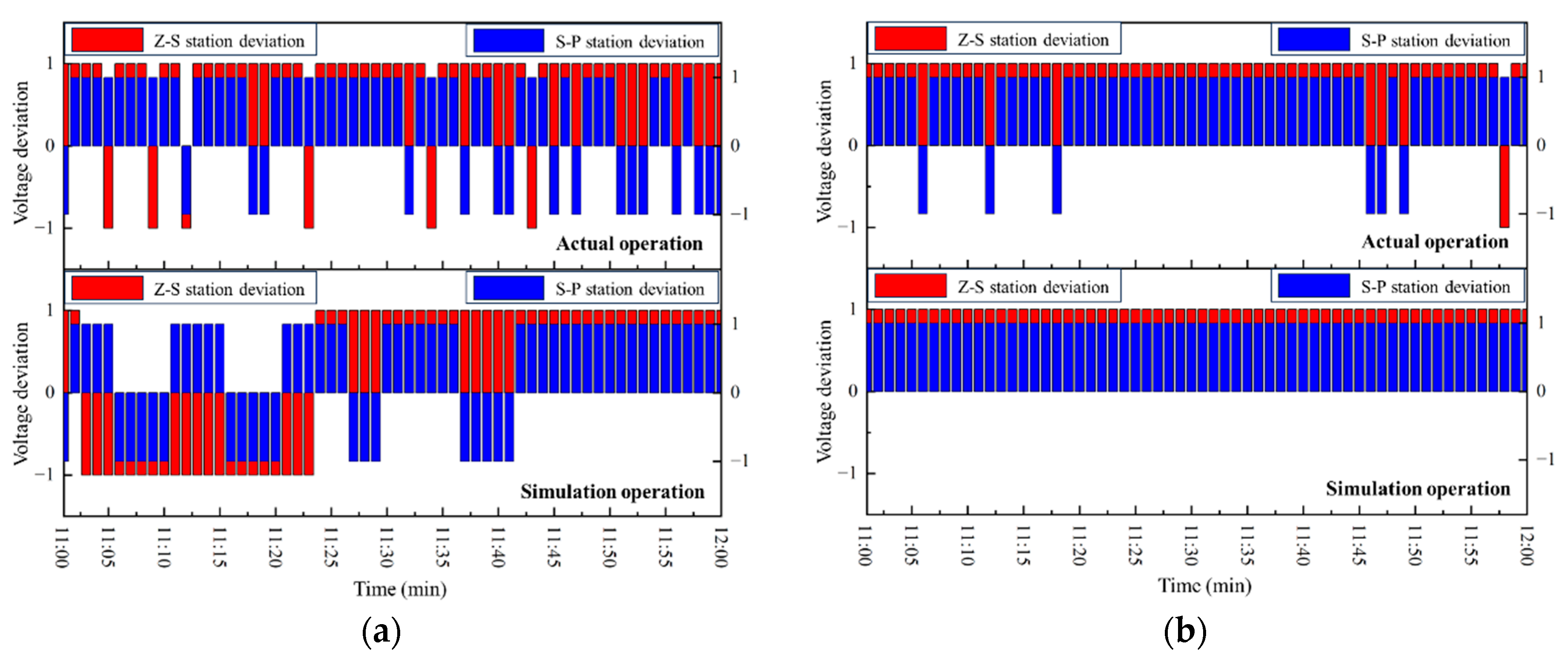
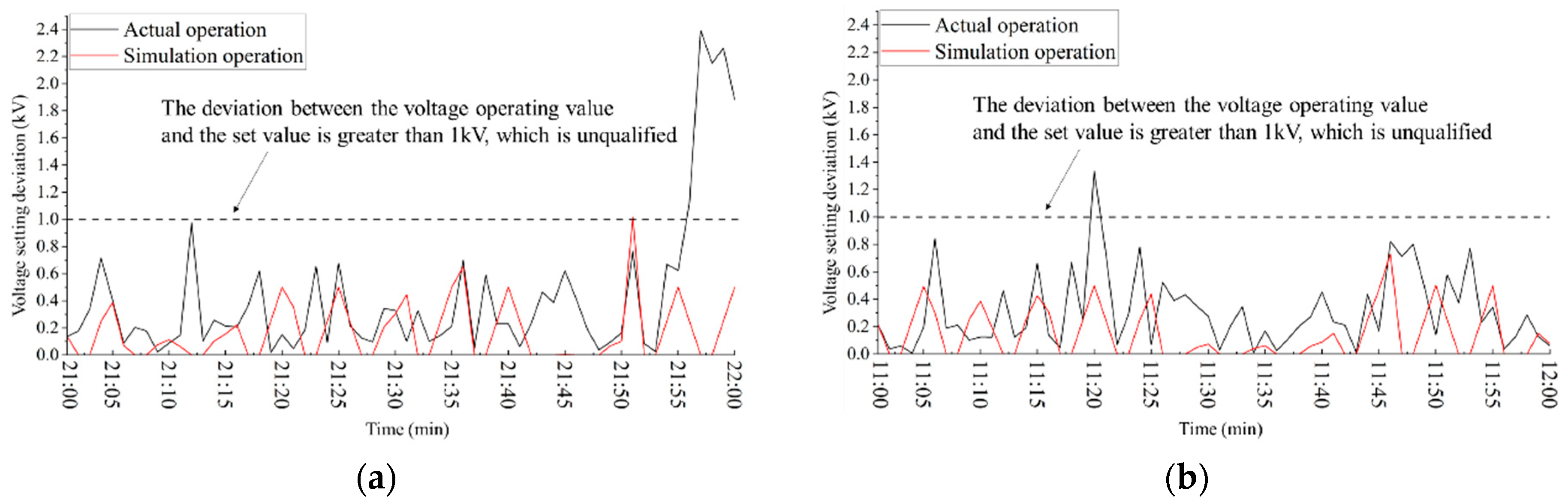
- (1)
- Simulation Results for the Absolute Reactive Power Pulling Amplitude
- (2)
- Simulation Results for the Reasonable Voltage Gradient Operation Rate
- (3)
- Simulation Results for AVC Qualification Rate
6. Conclusions and Discussion
6.1. Conclusions
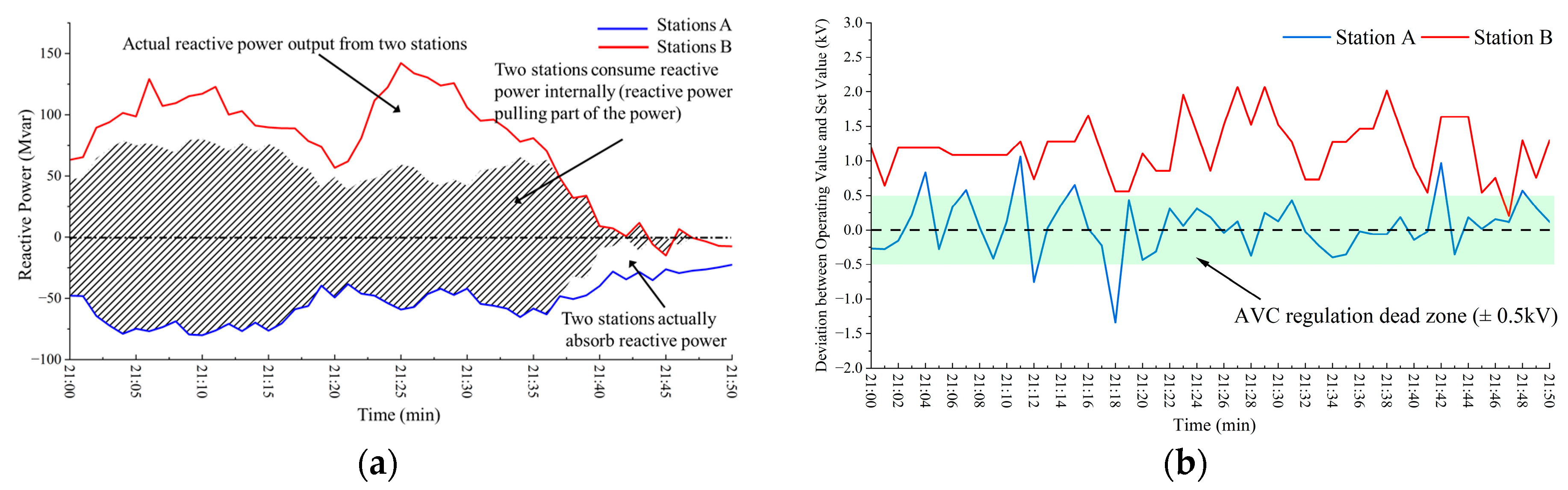
- In a cascade hydropower system, when transferred reactive power causes bus voltage deviations surpassing the AVC dead band, counter-responses from AVC substations may trigger reactive power–voltage anomalies across the entire CC-HPP network.
- Compared to traditional two-stage voltage control, the proposed RVCS accounts for interstation interactions within the network. While ensuring compliance with grid reactive power requirements, it also boosts the power factor performance of regional hydropower stations.
- In optimized simulations, early RVCS implementation prevents reactive power pulling and maintains a reasonable voltage gradient. However, if corrective measures are applied after the onset of reactive power pulling, multiple adjustment cycles are required for system stabilization.
6.2. Discussion
- Adaptability Analysis under Multi-Scenario and Renewable-Integrated Conditions: To enhance the applicability of the proposed strategy, future research will evaluate its adaptability across a range of hydropower operation scenarios, including reservoir regulation, intra-day peak-shaving, fluctuating load levels, and seasonal variations in water availability during wet and dry periods. In addition, this study explores the reactive power coordination mechanism of hydropower under hybrid configurations with renewable sources (e.g., PV integration), aiming to enhance the strategy’s applicability in complex source-load coupled systems. Qiu et al.’s work on the real-time scheduling of cascaded run-of-river hydro plants provides a useful reference for such hybrid operation control [49].
- Exploration of Alternative Coordinated Control Methods in CC-HPPs: Future work will explore the applicability of alternative coordinated control frameworks in chain-structured hydropower systems, including model predictive control (MPC), distributed optimization, and deep learning-based approaches. Given the unique hierarchical structure and heterogeneous control objectives of CC-HPPs, future work should evaluate how these advanced methods can be tailored and implemented for multi-station reactive power regulation. Notable references include the cascaded PID controller model for hybrid energy systems by Behera et al. [50] and the ML-enhanced Benders decomposition proposed by Borozan et al. [51].
- Forecast-aided Coordinated Control Enhancement: To improve proactive control capabilities, future work will investigate the integration of machine learning-based forecasting techniques into the strategy. By predicting the evolving system state, including voltage profiles and dynamic reactive power demands, forecast-aided optimization may significantly improve control precision and responsiveness. The forecasting framework proposed by Giannelos et al. [52], which ensures high prediction accuracy through a structured modeling process, offers practical guidance in this direction.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Time | Actual Value of Z Station (MVar) | Simulation Value of Z Station (MVar) | Actual Value of S Station (MVar) | Simulation Value of S Station (MVar) |
|---|---|---|---|---|
| 21:01 | −48.20 | −48.20 | 65.41 | 65.41 |
| 21:02 | −64.40 | −47.08 | 89.45 | 68.90 |
| 21:03 | −72.20 | −47.03 | 93.95 | 68.86 |
| 21:04 | −78.90 | −23.51 | 101.48 | 34.43 |
| 21:05 | −74.80 | −11.76 | 98.58 | 17.22 |
| 21:06 | −76.90 | −12.89 | 129.14 | 11.61 |
| 21:07 | −73.50 | −13.52 | 107.11 | 7.23 |
| 21:08 | −68.80 | −13.31 | 109.43 | 8.17 |
| 21:09 | −79.50 | −6.66 | 115.12 | 4.09 |
| 21:10 | −80.10 | −3.33 | 117.13 | 2.04 |
| 21:11 | −76.30 | −7.52 | 122.80 | 14.30 |
| 21:12 | −70.80 | −6.36 | 100.09 | 14.33 |
| 21:13 | −76.80 | −6.38 | 103.02 | 13.94 |
| 21:14 | −69.80 | −3.19 | 91.18 | 6.97 |
| 21:15 | −76.40 | −1.59 | 89.68 | 3.48 |
| 21:16 | −70.50 | −7.28 | 88.97 | −4.60 |
| 21:17 | −58.90 | −8.41 | 88.90 | −21.83 |
| 21:18 | −48.20 | −8.64 | 78.53 | −24.71 |
| 21:19 | −64.40 | −8.25 | 73.83 | −16.25 |
| 21:20 | −72.20 | −5.82 | 56.71 | −9.80 |
| 21:21 | −78.90 | −4.14 | 61.86 | 15.73 |
| 21:22 | −74.80 | −4.05 | 80.89 | 45.23 |
| 21:23 | −76.90 | −3.99 | 111.54 | 45.34 |
| 21:24 | −73.50 | 3.71 | 122.56 | 28.18 |
| 21:25 | −68.80 | 5.30 | 142.30 | 17.45 |
| 21:26 | −79.50 | 4.76 | 133.81 | 1.39 |
| 21:27 | −80.10 | 4.65 | 130.47 | −18.99 |
| 21:28 | −76.30 | 4.70 | 123.85 | −19.00 |
| 21:29 | −70.80 | 2.57 | 125.83 | −9.50 |
| 21:30 | −76.80 | 1.54 | 105.88 | −4.74 |
| 21:31 | −69.80 | 4.27 | 95.11 | 29.92 |
| 21:32 | −76.40 | 4.30 | 96.06 | 68.12 |
| 21:33 | −70.50 | 4.19 | 88.32 | 68.19 |
| 21:34 | −58.90 | 15.58 | 77.99 | 47.05 |
| 21:35 | −48.20 | 18.95 | 80.82 | 34.42 |
| 21:36 | −64.40 | 17.87 | 70.42 | −22.20 |
| 21:37 | −72.20 | 17.92 | 48.53 | −75.96 |
| 21:38 | −78.90 | 17.91 | 31.96 | −76.13 |
| 21:39 | −74.80 | 9.08 | 33.86 | −58.97 |
| 21:40 | −76.90 | 4.72 | 9.01 | −45.99 |
| 21:41 | −73.50 | 4.22 | 7.27 | −24.04 |
| 21:42 | −68.80 | 5.33 | 0.72 | −4.97 |
| 21:43 | −79.50 | 5.21 | 11.77 | −5.15 |
| 21:44 | −80.10 | 2.67 | −5.83 | −2.57 |
| 21:45 | −76.30 | 1.51 | −14.97 | −1.28 |
| 21:46 | −70.80 | 3.98 | 6.65 | −5.30 |
| 21:47 | −76.80 | 3.99 | −0.54 | −5.14 |
| 21:48 | −69.80 | 0.84 | −3.47 | −5.74 |
| 21:49 | −76.40 | 0.42 | −7.16 | −2.87 |
| 21:50 | −70.50 | 0.21 | −7.50 | −1.44 |
| 21:51 | −58.90 | −1.68 | −27.14 | 57.32 |
| 21:52 | −48.20 | 24.08 | −27.75 | 85.17 |
| 21:53 | −64.40 | 24.19 | −10.67 | 85.40 |
| 21:54 | −72.20 | 34.98 | 1.37 | 64.83 |
| 21:55 | −78.90 | 37.93 | −16.26 | 52.48 |
| 21:56 | −74.80 | 37.64 | −79.17 | 34.65 |
| 21:57 | −76.90 | 37.47 | −54.86 | 16.66 |
| 21:58 | −73.50 | 37.58 | −52.06 | 16.89 |
| 21:59 | −68.80 | 27.81 | −43.47 | 17.50 |
| 22:00 | −79.50 | 20.69 | −32.76 | 15.52 |
| Time | Actual Value of Z Station (MVar) | Simulation Value of Z Station (MVar) | Actual Value of S Station (MVar) | Simulation Value of S Station (MVar) |
|---|---|---|---|---|
| 11:01 | −12.00 | −12.00 | −17.22 | −17.22 |
| 11:02 | −19.90 | −11.25 | −11.11 | −15.65 |
| 11:03 | −23.40 | −11.25 | −4.29 | −15.65 |
| 11:04 | −27.50 | −7.80 | −5.93 | −9.97 |
| 11:05 | −27.30 | −3.90 | −14.28 | −4.98 |
| 11:06 | −12.10 | −4.00 | −13.84 | 20.29 |
| 11:07 | −16.70 | −2.82 | −11.01 | 22.56 |
| 11:08 | −11.50 | −2.83 | −14.35 | 22.46 |
| 11:09 | −2.10 | −1.20 | −20.05 | 11.44 |
| 11:10 | −9.20 | −0.60 | −16.94 | 5.72 |
| 11:11 | −5.40 | −2.01 | −17.42 | −5.39 |
| 11:12 | −23.40 | −5.18 | −1.91 | −17.12 |
| 11:13 | −16.80 | −5.01 | 4.30 | −17.06 |
| 11:14 | −25.50 | −3.45 | −3.03 | −9.47 |
| 11:15 | −18.40 | −1.73 | 8.73 | −4.74 |
| 11:16 | −20.20 | 3.57 | 11.22 | 10.55 |
| 11:17 | −20.80 | 5.51 | 9.62 | 26.15 |
| 11:18 | −18.40 | 5.60 | 15.52 | 26.10 |
| 11:19 | −25.90 | 6.08 | 21.83 | 12.96 |
| 11:20 | −30.30 | 4.01 | 39.59 | 5.79 |
| 11:21 | −33.30 | 4.31 | 55.24 | −15.94 |
| 11:22 | −43.80 | 2.25 | 57.70 | −24.44 |
| 11:23 | −38.00 | 2.34 | 50.03 | −25.20 |
| 11:24 | −35.30 | −0.01 | 50.71 | −13.78 |
| 11:25 | −40.80 | 0.00 | 54.36 | −6.89 |
| 11:26 | −47.40 | 1.14 | 62.51 | 2.74 |
| 11:27 | −45.40 | 1.22 | 62.81 | 2.68 |
| 11:28 | −41.00 | 1.04 | 59.92 | 2.55 |
| 11:29 | −51.60 | 0.52 | 60.67 | 1.27 |
| 11:30 | −47.80 | 0.26 | 63.12 | 0.64 |
| 11:31 | −51.10 | 0.89 | 43.96 | 2.25 |
| 11:32 | −55.10 | 0.89 | 37.48 | 2.19 |
| 11:33 | −49.30 | 0.89 | 34.00 | 2.13 |
| 11:34 | −53.00 | 0.45 | 28.85 | 1.07 |
| 11:35 | −49.10 | 0.22 | 25.07 | 0.53 |
| 11:36 | −40.40 | 1.29 | 15.96 | 2.94 |
| 11:37 | −37.10 | 1.29 | 6.28 | 3.00 |
| 11:38 | −32.50 | 1.29 | 4.37 | 3.00 |
| 11:39 | −36.90 | 0.65 | −11.59 | 1.50 |
| 11:40 | −31.70 | 0.32 | −9.95 | 0.75 |
| 11:41 | −27.20 | 2.77 | −12.71 | −17.51 |
| 11:42 | −31.60 | 1.10 | 1.33 | −26.38 |
| 11:43 | −36.90 | 1.10 | −1.60 | −26.38 |
| 11:44 | −36.50 | −1.23 | 2.36 | −14.97 |
| 11:45 | −37.60 | −0.61 | −0.20 | −7.49 |
| 11:46 | −39.00 | 3.00 | −11.35 | 47.53 |
| 11:47 | −35.30 | 10.75 | 1.61 | 74.31 |
| 11:48 | −40.70 | 10.84 | 9.62 | 74.32 |
| 11:49 | −41.20 | 22.02 | 17.26 | 53.22 |
| 11:50 | −46.20 | 25.17 | 43.31 | 40.57 |
| 11:51 | −46.10 | 21.68 | 38.71 | 26.40 |
| 11:52 | −52.00 | 23.58 | 41.33 | 3.42 |
| 11:53 | −41.80 | 26.54 | 34.38 | 3.43 |
| 11:54 | −44.10 | 16.12 | 33.39 | 4.57 |
| 11:55 | −40.80 | 8.64 | 33.35 | 2.86 |
| 11:56 | −50.30 | 8.40 | 27.90 | 2.29 |
| 11:57 | −55.70 | 8.40 | 27.18 | 2.34 |
| 11:58 | −55.30 | 8.51 | 29.06 | 2.53 |
| 11:59 | −56.30 | 4.26 | 24.59 | 1.27 |
| 12:00 | −53.10 | 2.13 | 36.93 | 0.63 |
References
- Kougias, I.; Aggidis, G.; Avellan, F.; Deniz, S.; Lundin, U.; Moro, A.; Muntean, S.; Novara, D.; Pérez-Díaz, J.I.; Quaranta, E. Analysis of emerging technologies in the hydropower sector. Renew. Sustain. Energy Rev. 2019, 113, 109257. [Google Scholar] [CrossRef]
- Azimov, U.; Avezova, N. Sustainable small-scale hydropower solutions in Central Asian countries for local and cross-border energy/water supply. Renew. Sustain. Energy Rev. 2022, 167, 112726. [Google Scholar] [CrossRef]
- Quaranta, E.; Bejarano, M.D.; Comoglio, C.; Fuentes-Pérez, J.F.; Pérez-Díaz, J.I.; Sanz-Ronda, F.J.; Schletterer, M.; Szabo-Meszaros, M.; Tuhtan, J.A. Digitalization and real-time control to mitigate environmental impacts along rivers: Focus on artificial barriers, hydropower systems and European priorities. Sci. Total Environ. 2023, 875, 162489. [Google Scholar] [CrossRef] [PubMed]
- Xiang, W. A brief discussion on voltage joint regulation of waterfall gully, Shenxigou, and pillow dam hydropower stations. Sichuan Hydroelectr. Power Gener. 2021, 2, 137–142. [Google Scholar]
- Wang, J.; Wang, L.; Yang, J.; Huang, E.; Zhang, L.; Liu, X.; Yang, K. Simulation analysis of reactive power and voltage for chain-structured cascade hydropower stations. J. Xihua Univ. (Nat. Sci. Ed.) 2025, 44, 1–9. [Google Scholar]
- Chou, M.H.; Su, C.L.; Lee, Y.C.; Chin, H.M.; Parise, G.; Chavdarian, P. Voltage-drop calculations and power cable designs for harbor electrical distribution systems with high voltage shore connection. IEEE Trans. Ind. Appl. 2016, 53, 1807–1814. [Google Scholar] [CrossRef]
- Thakur, R.; Chawla, P. Voltage drop calculations & design of urban distribution feeders. Int. J. Res. Eng. Technol. 2015, 4, 43–53. [Google Scholar]
- Hualiang, L.; Min, S.; Di, S.; Lei, Z.; Xiaozhen, J. Research on voltage drop of test transformer during combined voltage test. In Proceedings of the 16th IET International Conference on AC and DC Power Transmission (ACDC 2020), Online Conference, 2–3 July 2020. [Google Scholar]
- Khadka, S.; Wagle, A.; Dhakal, B.; Gautam, R.; Nepal, T.; Shrestha, A.; Gonzalez-Longatt, F. Agglomerative hierarchical clustering methodology to restore power system considering reactive power balance and stability factor analysis. Int. Trans. Electr. Energy Syst. 2024, 2024, 8856625. [Google Scholar] [CrossRef]
- Liu, B. The application of electrical engineering automation technology in the operation of power systems. Light. Source Illum. 2024, 12, 201–203. [Google Scholar]
- Dey, R.; Nath, S. A new active and reactive power control strategy for multifrequency microgrid in islanded mode. In Proceedings of the 2021 5th International Conference on Smart Grid and Smart Cities (ICSGSC), Tokyo, Japan, 18–20 June 2021. [Google Scholar]
- Sadeghi, S.E.; Akbari Foroud, A. A general index for voltage stability assessment of power system. Int. Trans. Electr. Energy Syst. 2021, 31, e13155. [Google Scholar] [CrossRef]
- Sahu, A.; Davis, K. Bayesian reinforcement learning for automatic voltage control under cyber-induced uncertainty. arXiv 2023, arXiv:2305.16469. [Google Scholar] [CrossRef]
- Yin, L.; Zhang, C.; Wang, Y.; Gao, F.; Yu, J.; Cheng, L. Emotional deep learning programming controller for automatic voltage control of power systems. IEEE Access 2021, 9, 31880–31891. [Google Scholar] [CrossRef]
- Lu, Z.; Zhao, G.; Kong, X.; Chen, J.; Guo, X.; Zhang, J. A detection based on particle filtering and multivariate time-series anomaly detection via graph attention network for automatic voltage control attack in smart grid. Sustain. Energy Grids Netw. 2024, 40, 101494. [Google Scholar] [CrossRef]
- Guo, Q.; Sun, H.; Zhang, B.; Wu, W.; Li, Q. Research on coordinated secondary voltage control. Power Syst. Autom. 2005, 29, 19–24. [Google Scholar]
- Tang, M.; Pang, X.; Li, M.; Liu, B.; Yin, X.; Zhang, B. Research and implementation plan of provincial local integration AVC system taking into account cascade hydropower stations. Power Autom. Equip. 2009, 29, 119–123. [Google Scholar]
- Wang, L.; Wang, J.; Zhang, L.; Yang, J.; Tang, Y.; Huang, E.; Liu, X. Research on automatic voltage control for chain-structured hydropower stations. In Proceedings of the 2023 3rd International Conference on Energy Engineering and Power Systems (EEPS), Dali, China, 28–30 July 2023. [Google Scholar]
- Wu, H.; Zhang, L.; Shu, A. Research on countermeasures for large hydropower plants participating in the ‘two regulations’ under asynchronous networking. Yunnan Hydrop. 2020, 8, 236–238. [Google Scholar]
- Yang, M.; Wu, B.; Yu, T. The application of weighted average algorithm in automatic voltage control system of hydropower station. Inn. Mong. Electr. Power Technol. 2023, 41, 7–13. [Google Scholar]
- Schwenzer, M.; Ay, M.; Bergs, T.; Abel, D. Review on model predictive control: An engineering perspective. Int. J. Adv. Manuf. Technol. 2021, 117, 1327–1349. [Google Scholar] [CrossRef]
- Molzahn, D.K.; Dörfler, F.; Sandberg, H. A survey of distributed optimization and control algorithms for electric power systems. IEEE Trans. Smart Grid 2017, 8, 2941–2962. [Google Scholar] [CrossRef]
- Mathew, A.; Amudha, P.; Sivakumari, S. Deep learning techniques: An overview. In Smart Intelligent Computing and Applications; Springer: Singapore, 2020; Volume 1141, pp. 599–608. [Google Scholar]
- Peschon, J.; Piercy, D.S.; Tinney, W.F.; Tveit, O.J. Sensitivity in power systems. IEEE Trans. Power Appar. Syst. 1968, 87, 1687–1696. [Google Scholar] [CrossRef]
- Kasturi, R.; Dorraju, P. Sensitivity analysis of power systems. IEEE Trans. Power Appar. Syst. 1969, 88, 1521–1529. [Google Scholar] [CrossRef]
- Lotufo, A.D.P.; Lopes, M.L.M.; Minussi, C.R. Sensitivity analysis by neural networks applied to power systems transient stability. Electr. Power Syst. Res. 2007, 77, 730–738. [Google Scholar] [CrossRef]
- Ni, F.; Nijhuis, M.; Nguyen, P.H.; Cobben, J.F.G. Variance-based global sensitivity analysis for power systems. IEEE Trans. Power Syst. 2017, 33, 1670–1682. [Google Scholar] [CrossRef]
- Ginocchi, M.; Ponci, F.; Monti, A. Sensitivity analysis and power systems: Can we bridge the gap? A review and a guide to getting started. Energies 2021, 14, 8274. [Google Scholar] [CrossRef]
- Wang, H.; Hou, K.; Liu, X.; Yu, X.; Jia, H.; Du, J. A method for enhancing the resilience of electrical interconnection systems based on global sensitivity analysis. Power Syst. Autom. 2023, 47, 59–67. [Google Scholar]
- Schyska, B.U.; Kies, A.; Schlott, M.; Von Bremen, L.; Medjroubi, W. The sensitivity of power system expansion models. Joule 2021, 5, 2606–2624. [Google Scholar] [CrossRef]
- Wang, C.; Feng, C.; Zeng, Y.; Zhang, F. Improved correction strategy for power flow control based on multi-machine sensitivity analysis. IEEE Access 2020, 8, 82391–82403. [Google Scholar] [CrossRef]
- Sun, H.; Guo, Q.; Zhang, B.; Li, Y.; Li, Q.; Wu, L.; Yu, Z. Automatic voltage control scheme for large-scale power networks. Power Grid Technol. 2006, 30, 13–18. [Google Scholar]
- Naresh, D. A distributed AC power grid with wind farms using ADMM-based active and reactive power control. Int. J. Eng. Sci. Adv. Technol. 2021, 23, 31–36. [Google Scholar]
- Yang, J.; Zhu, S.; Zhou, T. Distributed model predictive control for voltage coordination of distributed photovoltaic networks. J. Appl. Sci. Eng. 2023, 28, 1341–1350. [Google Scholar]
- Hamrouni, N.; Younsi, S.; Jraidi, M. A flexible active and reactive power control strategy of a LV grid connected PV system. Energy Proced. 2019, 162, 325–338. [Google Scholar] [CrossRef]
- Wu, Y.; Shang, B.; Yang, P.; Yang, L.; Yu, B.; Ma, T.; Qiao, J. Research on reactive power circulation suppression strategy for new energy clusters. Inn. Mong. Electr. Power Technol. 2023, 4, 13–19. [Google Scholar]
- Wang, B.; Guo, Q.; Sun, H.; Tang, L.; Zhang, B.; Wu, W. Research and practice on automatic voltage control of ultra high voltage near area power grid. Power Syst. Autom. 2013, 37, 99–105. [Google Scholar]
- Yu, H. Research on Optimal Method of Reactive Voltage Control for UHV Power Network. Mod. Ind. Econ. Informaionization 2024, 245, 261–262+267. [Google Scholar]
- Shi, X.; Wang, B.; Chen, P. Application of Coordinating Technology between Power Plants in Automatic Voltage Control System of Power Plants Near UHV Grid. Shanxi Electr. Power 2013, 183, 1–5. [Google Scholar]
- Wang, B.; Guo, Q.; Sun, H.; Tang, L.; Zhang, B.; Tian, J. Coordinated control method for strong coupling power plants in automatic voltage control. Power Syst. Autom. 2015, 12, 165–171. [Google Scholar]
- Han, B.; Wang, B.; Dai, F.; Wang, D.; Qin, J.; Wang, L. Research on automatic voltage control of power grid considering safety voltage constraints of large power grid. Electr. Meas. Instrum. 2020, 57, 6–11. [Google Scholar]
- Ibe, O.G.; Onyema, A.I. Concepts of reactive power control and voltage stability methods in power system network. IOSR J. Comput. Eng. 2013, 11, 15–25. [Google Scholar]
- Begovic, M.M.; Phadke, A.G. Control of voltage stability using sensitivity analysis. IEEE Trans. Power Syst. 1992, 7, 114–123. [Google Scholar] [CrossRef]
- Gomes, F.V.; Carneiro, S.; Pereira, J.L.R.; Vinagre, M.P.; Garcia, P.A.N.; De Araujo, L.R. A new distribution system reconfiguration approach using optimum power flow and sensitivity analysis for loss reduction. IEEE Trans. Power Syst. 2006, 21, 1616–1623. [Google Scholar] [CrossRef]
- Li, Y.; Wang, K.; Wang, D.; Zhu, H.; Wu, X. Fast VCA method for full dimensional sensitivity matrix considering weak coupling relationship. Electr. Meas. Instrum. 2022, 59, 69–76. [Google Scholar]
- Li, Y.; Wang, D.; Zhang, Q.; Du, J.; Wang, Q.; Wang, Q. Gradient descent based dynamic optimization for VSG dominated microgrid. J. Eng. 2024, 2024, e70040. [Google Scholar] [CrossRef]
- Long, G.; Wu, X.; Liu, H.; Lou, H.; Shen, B.; Yan, C.; Kong, W. Interior-point-method-based switching angle computation for selective harmonic elimination in high-frequency cascaded H-bridge multilevel inverters. J. Power Electron. 2024, 24, 1229–1240. [Google Scholar] [CrossRef]
- Hasan, M.S.; Chowdhury, M.M.-U.-T.; Kamalasadan, S. Sequential quadratic programming (SQP) based optimal power flow methodologies for electric distribution system with high penetration of DERs. IEEE Trans. Ind. Appl. 2024, 60, 4810–4820. [Google Scholar] [CrossRef]
- Qiu, Y.; Lin, J.; Liu, F.; Song, Y.; Chen, G. Stochastic online generation control of cascaded run-of-the-river hydropower for mitigating solar power volatility. IEEE Trans. Power Syst. 2020, 35, 4709–4722. [Google Scholar] [CrossRef]
- Behera, A.; Panigrahi, T.K.; Ray, P.K. A novel cascaded PID controller for automatic generation control analysis with renewable sources. IEEE/CAA J. Autom. Sin. 2019, 6, 1438–1451. [Google Scholar] [CrossRef]
- Borozan, S.; Giannelos, S.; Falugi, P.; Moreira, A. Machine learning-enhanced Benders decomposition approach for the multi-stage stochastic transmission expansion planning problem. Electr. Power Syst. Res. 2024, 237, 110895. [Google Scholar] [CrossRef]
- Giannelos, S.; Moreira, A.; Papadaskalopoulos, D.; Strbac, G. A machine learning approach for generating and evaluating forecasts on the environmental impact of the buildings sector. Energies 2023, 16, 2915. [Google Scholar] [CrossRef]


| Station | Capacity (MW) | Maximum Reactive Power (MVar) | Minimum Reactive Power (MVar) | Generator Terminal Voltage (kV) |
|---|---|---|---|---|
| Station Z | 720 | 349 | −280 | 15.75 |
| Station S | 660 | 320 | −480 | 15.75 |
| Station P | 3600 | 1746 | −1500 | 20.00 |
| Transformer | Capacity (MVA) | Impedance (Ω) | Transformation Ratio |
|---|---|---|---|
| Station Z | 200 | 0.002780 + j0.180838 | 15.75/550 |
| Station S | 375 | 0.001379 + j0.104186 | 15.75/550 |
| Station P | 667 | 0.001184 + j0.094633 | 20.00/550 |
| Line | Impedance (Ω) | Electrical Susceptance (10−6 S) | Charging Power (MVar) |
|---|---|---|---|
| Z–S Line | 0.72 + j8.585 | 119.226 | 32.86 |
| S–P Line | 0.44 + j6.072 | 94.922 | 26.16 |
| BP Line | 3.27 + j50.384 | 744.902 | 205.31 |
| Simulation Scenario | Actual Value Aav (MVar) | Simulate Value Aav (MVar) | Percentage Decrease (%) |
|---|---|---|---|
| Scenario 1 (21:00–22:00) | 39.14 | 3.34 | 91.47 |
| Scenario 2 (11:00–12:00) | 18.73 | 0.42 | 97.76 |
| Simulation Scenario | Actual Operation B (%) | Simulated Operation B (%) | Percentage Increase (%) | |
|---|---|---|---|---|
| Scenario 1 | Period 1 (21:00–21:30) | 86.67 | 41.67 | −45.00 |
| Period 2 (21:30–22:00) | 75.00 | 91.67 | 16.67 | |
| Scenario 2 | Period 1 (11:00–11:30) | 95.00 | 100.00 | 5.00 |
| Period 2 (11:30–12:00) | 93.33 | 100.00 | 6.67 | |
| Simulation Scenario | Actual Qualification Points | Simulated Qualification Points | Actual Qualification Rate | Simulated Qualification Rate |
|---|---|---|---|---|
| Scenario 1 (21:00–22:00) | 5 | 1 | 91.66% | 98.33% |
| Scenario 2 (11:00–12:00) | 1 | 0 | 98.33% | 100.00% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Yang, J.; Wang, J.; Wang, L.; Niu, H.; Liu, X.; Yang, S.X.; Yang, K. Optimizing Automatic Voltage Control Collaborative Responses in Chain-Structured Cascade Hydroelectric Power Plants Using Sensitivity Analysis. Energies 2025, 18, 2681. https://doi.org/10.3390/en18112681
Zhang L, Yang J, Wang J, Wang L, Niu H, Liu X, Yang SX, Yang K. Optimizing Automatic Voltage Control Collaborative Responses in Chain-Structured Cascade Hydroelectric Power Plants Using Sensitivity Analysis. Energies. 2025; 18(11):2681. https://doi.org/10.3390/en18112681
Chicago/Turabian StyleZhang, Li, Jie Yang, Jun Wang, Lening Wang, Haiming Niu, Xiaobing Liu, Simon X. Yang, and Kun Yang. 2025. "Optimizing Automatic Voltage Control Collaborative Responses in Chain-Structured Cascade Hydroelectric Power Plants Using Sensitivity Analysis" Energies 18, no. 11: 2681. https://doi.org/10.3390/en18112681
APA StyleZhang, L., Yang, J., Wang, J., Wang, L., Niu, H., Liu, X., Yang, S. X., & Yang, K. (2025). Optimizing Automatic Voltage Control Collaborative Responses in Chain-Structured Cascade Hydroelectric Power Plants Using Sensitivity Analysis. Energies, 18(11), 2681. https://doi.org/10.3390/en18112681








