Voltage Regulation Strategies in Photovoltaic-Energy Storage System Distribution Network: A Review

Abstract

With the increasing penetration of distributed photovoltaic-energy storage system (PV-ESS) access distribution networks, the safe and stable operation of the system has brought a huge impact, in which the voltage regulation of PV-ESS distribution networks is more prominent. This paper comprehensively reviews the voltage over-run mechanism in the PV-ESS distribution network and combs through the current mainstream voltage regulation strategies, of which two strategies of direct voltage regulation and current optimization are summarized. At the same time, this paper discusses the advantages and limitations of centralized, distributed, multi-timescale, voltage-reactive joint optimization and other regulation methods and focuses on the analysis of heuristic algorithms and algorithms based on deep reinforcement learning in the voltage regulation of the relevant research progress. Finally, this paper points out the main challenges currently facing voltage regulation in PV-ESS distribution networks, including cluster dynamic partitioning technologies, multi-timescale control of hybrid voltage regulation devices, and synergistic problems of demand-side resources, such as electric vehicle participation in voltage regulation, etc., and gives an outlook on future research directions. The aim of this paper is to provide a theoretical basis and practical guidance for voltage regulation of PV-ESS distribution networks and to promote the intelligent construction and sustainable development of power grids.

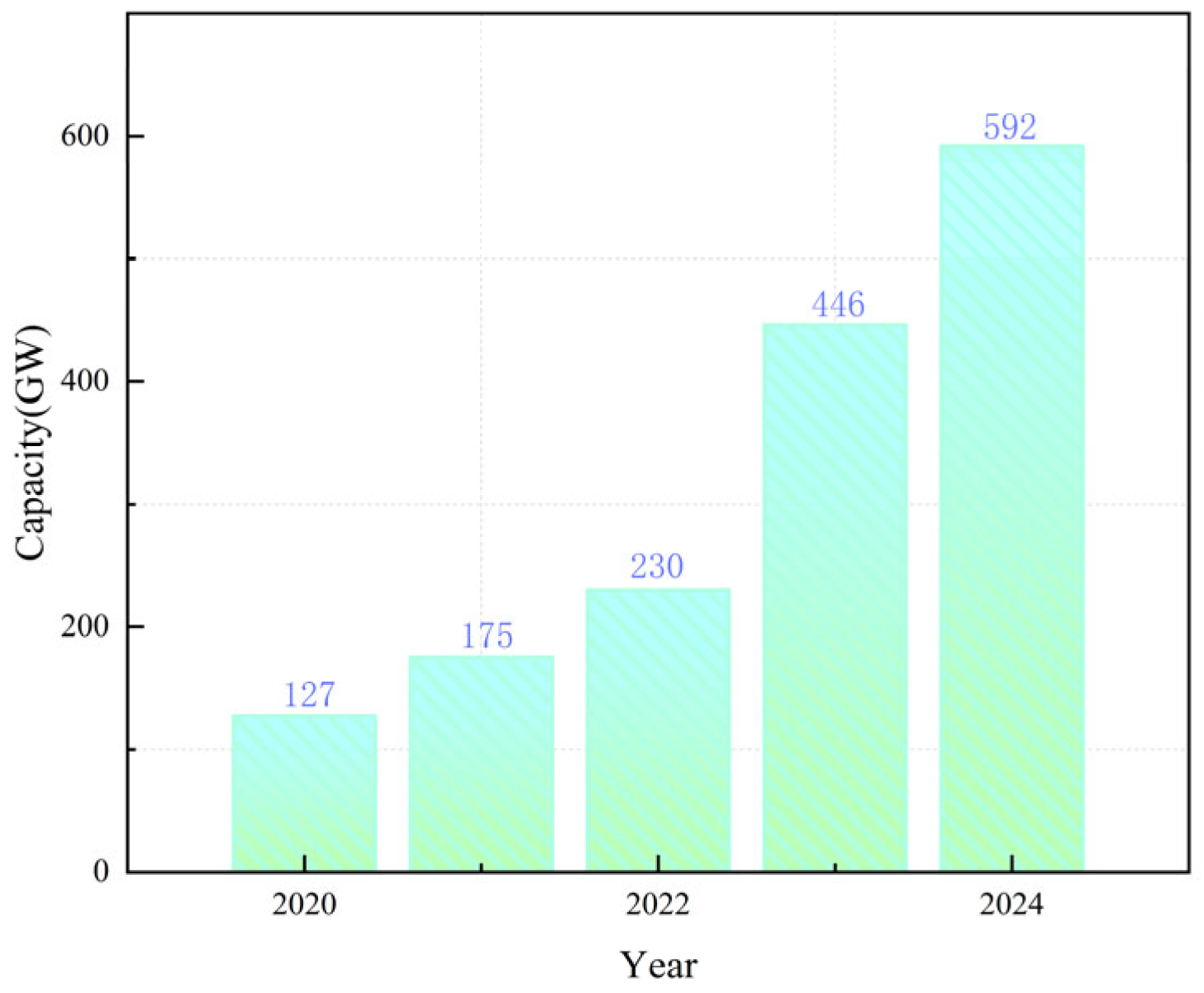
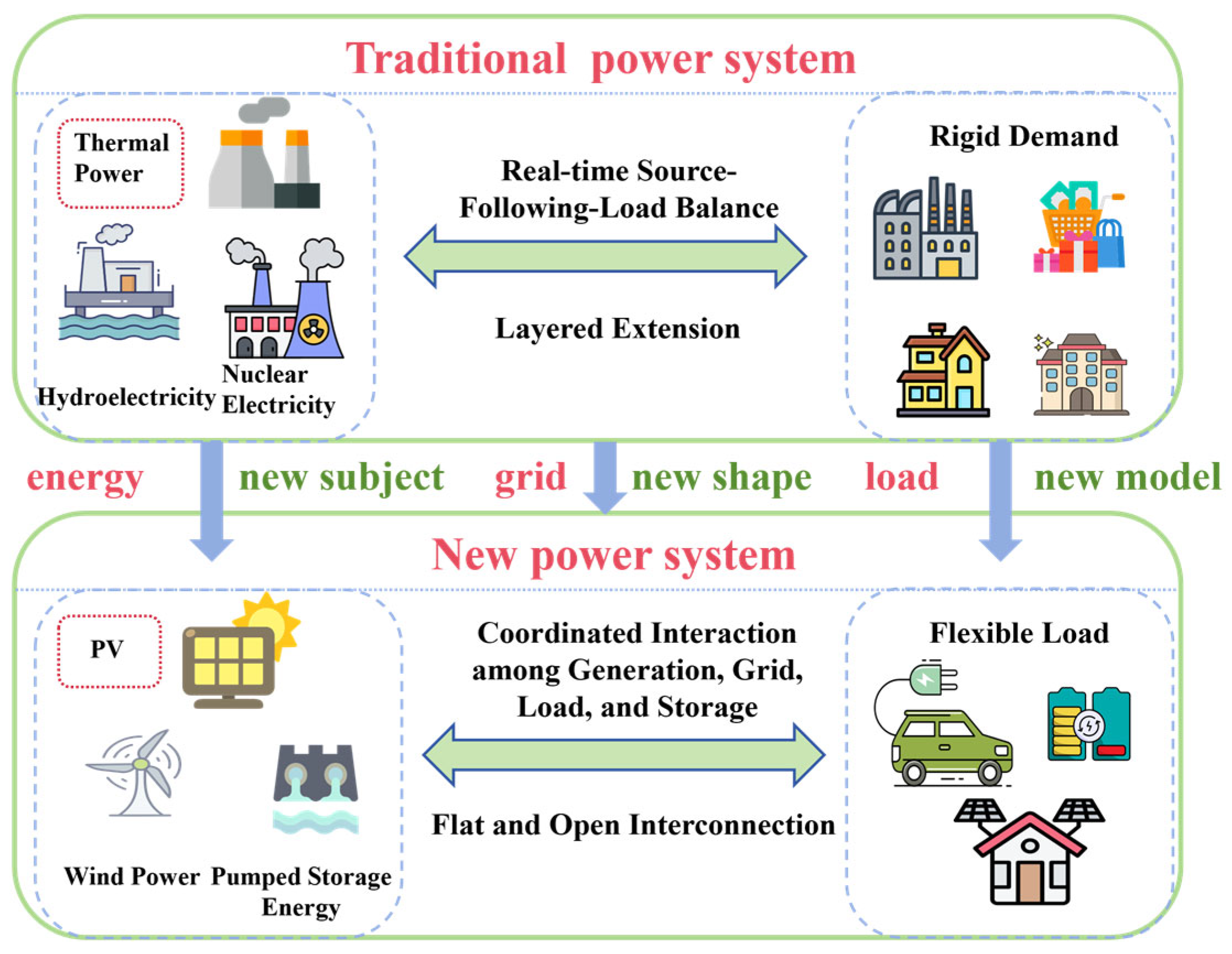
1. Introduction

With the continued global economic development, energy shortages and environmental pollution have become increasingly severe, making carbon emission reduction a key driver of future energy transition. As a major carbon-emitting sector, the power industry urgently requires structural transformation, with renewable energy—particularly photovoltaics (PVs)—emerging as a vital pathway toward green, low-carbon development. Among these, distributed photovoltaics (DPVs) have gained global attention due to their advantages in flexible deployment, short construction periods, low land dependency, and proximity to load centers.

As power demand grows and fossil fuel resources dwindle, pairing DPVs with appropriately scaled energy storage systems (ESSs) has become essential for improving energy utilization. The coordinated development of DPVs and ESSs is not only critical for addressing environmental and energy challenges but also serves as a foundational pillar for advancing distribution networks and smart grid integration [1,2].

Since reaching a global cumulative installed capacity of 127 GW in 2020, photovoltaic (PV) power generation has experienced rapid growth, climbing to 592 GW by 2024. This represents an increase of 465 GW over four years, with a particularly sharp rise between 2022 and 2023, outpacing previous years and signaling that global PV deployment has entered an accelerated phase. As shown in Figure 1, the annual growth in PV installations reflects the technology’s increasing market penetration, driven by the global push for energy transition and carbon neutrality. Looking ahead, ongoing technological advancements and strong policy support are expected to sustain high growth rates, further reinforcing PV’s pivotal role in the future energy landscape.

As the penetration of distributed photovoltaics (DPVs) continues to rise, their decentralized access to the distribution network introduces volatility and intermittency that significantly impact power quality. Among these challenges, voltage violations at the point of common coupling (PCC) are particularly prominent [3]. The active power injected by DPVs can cause reverse power flow, leading to elevated bus voltages. When system voltage deviates beyond acceptable limits, it can disrupt normal equipment operation, pose safety risks, or even result in equipment damage. Moreover, output fluctuations from DPVs can trigger overvoltage events that activate protective devices, forcing PV units offline and reducing the overall utilization efficiency of renewable energy sources [4].

With the global push for carbon neutrality, the energy transition has become an irreversible trend, driving rapid growth in the energy storage market. In 2024, newly installed global energy storage reached 79.2 GW/188.5 GWh, up 82.1% year on year, with the total demand projected to hit 828 GWh by 2030. Electricity market reforms have also prompted more industrial and commercial users to adopt energy storage to meet production needs and reduce costs. However, many energy storage systems remain underutilized: some operate less than four hours a day, while others sit idle for extended periods. This inefficiency not only wastes resources but also limits the role of storage in enhancing grid flexibility and stability. To address this, improved operational strategies and smarter coordination are urgently needed to fully realize the value of existing storage assets.

This review focuses on the voltage regulation challenges in distribution networks with high penetration of distributed photovoltaics (DPVs). The main structure of the article is shown in Figure 2. It begins with a systematic analysis of the causes of voltage violations, followed by a classification of overvoltage phenomena based on different mechanisms and corresponding mitigation strategies. A key innovation lies in shifting from traditional single-device control to coordinated regulation involving PV inverters, energy storage systems, and transformers. The review further outlines the technological evolution from passive response to active prediction and intelligent coordination. The main contributions include the construction of a comprehensive theoretical framework, a comparative analysis of mainstream voltage control methods, and the proposal of an intelligent voltage regulation paradigm that integrates PV forecasting, flexible network control, and resource coordination. These insights offer practical guidance for enhancing the stability and adaptability of future distribution networks under high PV penetration.

2. Analysis of Voltage Violation Mechanism in PV-ESS Distribution Network

In a traditional distribution network, voltage over-runs are common when a large number of loads are in operation, which are usually manifested as the bus voltage falling below the specified lower limit. In the new distribution network architecture with a high proportion of DPV access, the extensive access of PV resources has significantly changed the current distribution characteristics of the power systems, which makes the distribution network voltage exceed the lower voltage limit but also frequently exceed the upper voltage limit. In addition, the access of DPVs may exacerbate the three-phase imbalance and harmonic pollution in the distribution network, further inducing voltage over-runs. The differences in voltage control characteristics between the traditional distribution network and the new one with high penetration of DPVs are shown in Figure 3.

2.1. Over-Runs Caused by DPV Access

In general, DPVs are connected to the distribution network and have a significant impact on the stability and voltage level of the distribution network [5]. The connection of DPVs can change the original load characteristics and current distribution of the grids to a certain extent [6]. Specifically, their active power usually varies with the change of light conditions, which may lead to a rapid change in the active demand of the grid in a specific period of time [7]. When there is sufficient light, the PV power output may rise rapidly, causing the voltage of the grid to rise, while when there is insufficient light, the rapid decrease in PV power output may cause the active deficit of the grid, further affecting the stability of the grid. In Figure 4, ${\mathrm{P}}_1{,\mathrm{P}}_2{,\mathrm{P}}_3,\dots {,\mathrm{P}}_{\mathrm{N}}$ and ${\mathrm{Q}}_1{,\mathrm{Q}}_2{,\mathrm{Q}}_3,\dots {\mathrm{Q}}_{\mathrm{N}}$ are the active and reactive powers at each node of the line, respectively, ${\mathrm{P}}_{\mathrm{V}1}{,\mathrm{P}}_{\mathrm{V}2}{,\mathrm{P}}_{\mathrm{V}3},\dots {,\mathrm{P}}_{\mathrm{VN}}$ is the PV active power transmitted at each node of the line, ${\mathrm{U}}_0$ is the head voltage, ${\mathrm{U}}_1{,\mathrm{U}}_2{,\mathrm{U}}_3,\dots {,\mathrm{U}}_{\mathrm{N}}$ is the voltage corresponding to each node, $\nabla {\mathrm{U}}_1$ is the voltage drop in the first section of the line, $\nabla {\mathrm{U}}_2$ is the voltage drop between nodes 1 and 2, and ${\mathrm{R}}_1{,\mathrm{R}}_2$ and ${\mathrm{X}}_1{,\mathrm{X}}_2$ are the resistances and impedance of the line corresponding to $\nabla {\mathrm{U}}_1$ and $\nabla {\mathrm{U}}_2$, respectively.

In order to simplify the analysis process, the complex interactions between line reactance and reactive power are not considered; then, the voltage at the node is:

$${\displaystyle U_a=U_0-\sum _{k=1}^a\frac{{\displaystyle \sum _{n=k}^N(P_n-P_{Vn})r{l}_k}}{U_{k-1}}}$$

(1)

where $r$ is the resistance per unit length, ${\mathrm{l}}_{\mathrm{k}}(\mathrm{k}=1,2,\dots \mathrm{m})$ is the distance from the node $\mathrm{k}$ to the first end of the line, $\mathrm{n}$ is a calculation variable, $\mathrm{n}=\mathrm{k},\mathrm{k}+1,\dots ,\mathrm{N}$, and ${\mathrm{U}}_{\mathrm{k}-1}$ is the voltage at node $\mathrm{k}-1$.

At this time, the voltage difference between node $\mathrm{m}$ and node $\mathrm{m}-1$ is:

$$\begin{array}{c}\mathsf{\Delta }{U}_m=U_{m-1}-U_m=\\ {\displaystyle \sum _{k=1}^{m-1}}\frac{{\displaystyle \sum _{n=k}^N(P_n-P_{Vn})r{l}_k}}{U_{k-1}}-{\displaystyle \sum _{k=1}^m}{\displaystyle \frac{{\displaystyle \sum _{n=k}^N}(P_n-P_{Vn})}{U_{k-1}}}=\\ {\displaystyle \frac{{\displaystyle \sum _{n=m}^N}(P_n-P_{\nu n})r{l}_k}{U_{m-1}}}\end{array}$$

(2)

According to Equations (1) and (2), it can be seen that the voltage fluctuation is not only related to the active power output from the PV but also to the sum of the active power consumed by all the subsequent users from the node $\mathrm{m}$. Specifically, when the active power output from the PV increases or the active power consumed by the subsequent users decreases, the system voltage tends to increase.

With the increasing proportion of DPV access, its output has randomness and intermittency, and at the same time, there are differences with the user’s use of the law, which leads to backward transmission and disorder of the distribution network trend, causing some nodes of voltage fluctuations or even over the limit, and bringing challenges to the stable operation of the grid [8]. A reduction in ${\mathrm{P}}_{\mathrm{VN}}$ will cause instantaneous fluctuations in the voltage or even over the lower limit. This effect is more significant, especially in regions with a high percentage of photovoltaic power generation. On long distribution feeders, such voltage variations may be progressive along the line, ultimately leading to the exacerbation of the system’s voltage crossing the lower limit problem [9]. In addition, the change in load characteristics, such as a change in ${\mathrm{P}}_{\mathrm{N}}$, can also cause the problem of grid voltage crossing the lower limit. Unbalanced load distribution in the power system may lead to overloading in certain areas, and the overloaded areas will draw a large amount of active power ${\mathrm{P}}_{\mathrm{N}}$, which will lead to the voltage crossing the lower limit problem.

2.2. Over-Runs Caused by Charging and Discharging Behavior of Energy Storage System

The impact of the charging and discharging behavior of the ESS on the grid voltage is mainly reflected in its dynamic regulation of the current distribution [10,11]. By absorbing or releasing active and reactive power, the ESS changes the power balance at local nodes, which, in turn, affects the node voltage. The effect of the charging and discharging behavior of the ESS on the voltage is expressed by the following equation:

$$V_i\approx V_j+{\displaystyle \frac{(P_{ij}\pm P_{c/d})R_{ij}+(Q_{ij}\pm Q_{c/d})X_{ij}}{V_j}}$$

(3)

When the ESS is charged, it absorbs active power ${\mathrm{P}}_{\mathrm{c}}$ and reactive power ${\mathrm{Q}}_{\mathrm{c}}$, resulting in a reduction in active power ${\mathrm{P}}_{\mathrm{ij}}$ and reactive power ${\mathrm{Q}}_{\mathrm{ij}}$ in the line. In the case of a light load or large DPV output, if ${\mathrm{P}}_{\mathrm{c}}$ or ${\mathrm{Q}}_{\mathrm{c}}$ is large, the distribution network voltage will cross the lower limit. In contrast, a voltage crossing the upper limit occurs when the ESS is discharged.

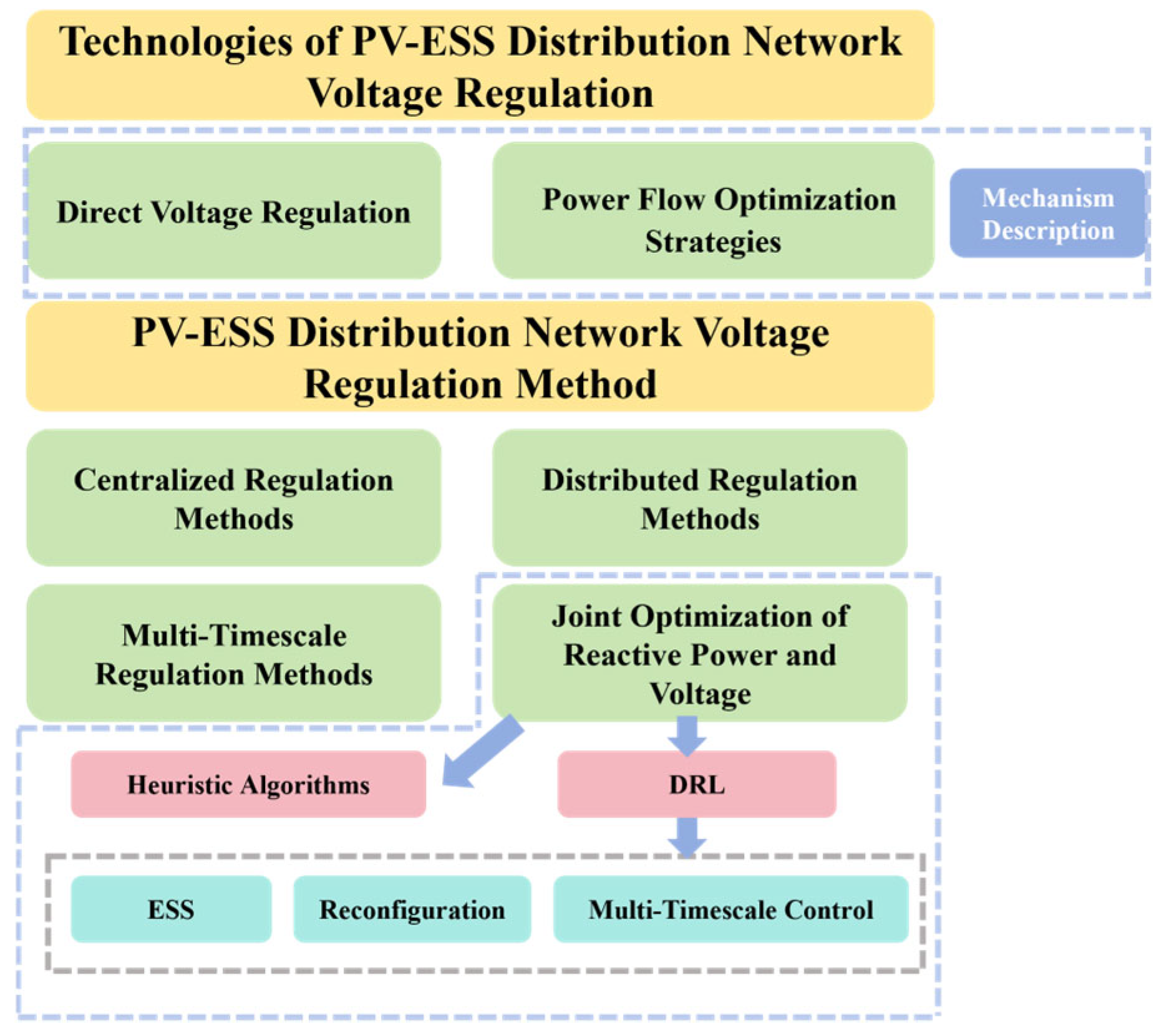
3. Technologies of PV-ESS Distribution Network Voltage Regulation

In actual operation, the voltage level is improved to a certain extent by the control scheduling of reactive power compensation equipment, such as the on-load voltage changer (OLTC), the shunt capacitor bank (SCB), and the static var generator (SVG) [12], but there are shortcomings such as limited voltage regulation accuracy or high voltage regulation cost. The partial conversion of active photovoltaic output through smart inverters also provides a more considerable reactive power resource for system voltage regulation [13], but the program must fully consider the user’s willingness and lacks flexibility. In contrast, the use of inherent flexibility of the ESS, flexible scheduling, and fast response characteristics [14], so that through reasonable configuration of the ESS, voltage distribution can be optimized, improve the stability of the system operation effect.

3.1. Direct Voltage Regulation

Traditional reactive power optimization methods for distribution networks are highly interpretable and offer reliable accuracy and stability. Such methods are usually based on mathematical modeling of various types of regulation devices in distribution networks [15] and need to simultaneously optimize continuous control variables for devices such as static reactive power compensators and PV inverters, as well as discrete control variables for devices such as capacitors and transformer taps. The objective is typically to minimize network losses and improve voltage quality, resulting in a nonconvex, nonlinear mixed-integer optimization problem. However, due to the high complexity and large feasible domain of the problem, it is still difficult for existing general-purpose solvers to obtain an efficient and globally optimal solution. Currently, traditional reactive power optimization methods mainly include linear programming and mixed-integer programming [16], which, although they can be used to simplify the problem-solving process to a certain extent, still have some limitations in dealing with the challenges of multivariable coupling and significant nonlinear characteristics in a real distribution network.

3.1.1. Principle of OLTC

An OLTC is a critical device in power systems that regulates voltage without interrupting power supply by adjusting the transformer turns ratio. It plays a key role in maintaining voltage levels, and its design and build quality directly impact transformer performance. The OLTC operates electromechanically, typically adjusting the tap position in steps of 1.25% or 1.43%, while the transformer remains energized and under load [17]. Each OLTC works in coordination with an automatic voltage control (AVC) relay to raise or lower the voltage as needed [18]. However, in distribution networks with high penetration of distributed energy resources, frequent voltage fluctuations pose a challenge. OLTCs cannot respond rapidly due to inherent time delays and mechanical wear concerns, limiting their effectiveness in such dynamic conditions [19,20].

3.1.2. Principle of Voltage Regulation Using SVC

Reactive power compensation devices play a vital role in power systems by improving power quality, regulating voltage, and optimizing transmission efficiency. This is mainly realized through compensation capacitors, SVCs and static reactive power generators, and other equipment. These devices can adjust reactive power output or absorption in real time to maintain voltage stability. This type of voltage regulation has the advantages of a fast response speed and wide adjustment range, which is especially suitable for occasions with large voltage fluctuations [21,22]. For example, ref. [23] implemented a dual-slope voltage control strategy, enabling the SVC to stabilize voltage within allowable limits while coordinating with OLTCs for upstream reactive voltage control. Ref. [24] developed an adaptive SVC controller capable of online parameter identification and real-time adjustment for optimized performance. Ref. [25] proposed a three-layer hybrid reactive power compensation scheme based on expert decision making, differential slope control, and fuzzy self-tuning PI control, which proved effective in mitigating voltage flicker and reactive power imbalances. Ref. [26] studied differential slope control and fuzzy self-tuning PI control, which proved effective in mitigating voltage flicker and reactive power imbalances. In addition, a static synchronous compensator (STATCOM) is a self-commutating converter consisting of a fully controlled switching device insulated-gate bipolar transistor (IGBT), which offers superior voltage regulation by precisely controlling the amplitude and phase of output voltage, allowing for dynamic reactive power support. Compared to traditional capacitor-based regulation, STATCOMs provide a faster response and higher accuracy, making them especially suitable for modern distribution networks with high penetration of distributed energy resources.

3.2. Power Flow Optimization Strategies

3.2.1. PV Inverter Voltage Regulation Principle

In the face of the distribution network voltage over-run problem triggered by a high proportion of DPV access, two effective regulation strategies can be applied. Firstly, by optimizing the active power scheduling of DPVs, reverse power flow into the grid can be reduced, helping to mitigate voltage rise. Secondly, the reactive power capabilities of PV inverters can be leveraged to enhance their inductive reactive power support, thereby improving local voltage regulation.

A PV inverter is the main module of photovoltaic power generation. Among various configurations, the two-stage PV inverter is the most widely adopted due to its high reliability, wide input voltage range, and simple control. In a two-stage PV inverter, the front stage DC/DC boost circuit realizes maximum power tracking by regulating the output voltage of the PV array. The backstage DC/AC inverter circuit includes a converter and a filter. Inverter control is typically based on an inner current loop with decoupling control, while the outer voltage loop provides the reference for active current, and the outer reactive power loop provides the reference for reactive current. The current is compared with the outer loop given, and the on–off of the switching devices of the main circuit is controlled through certain current control strategies and PWM modulation links to achieve the purpose of controlling the power output [27]. Generally, the reactive power output of the PV inverter is zero when grid connected, so the outer loop reactive power is given as zero.

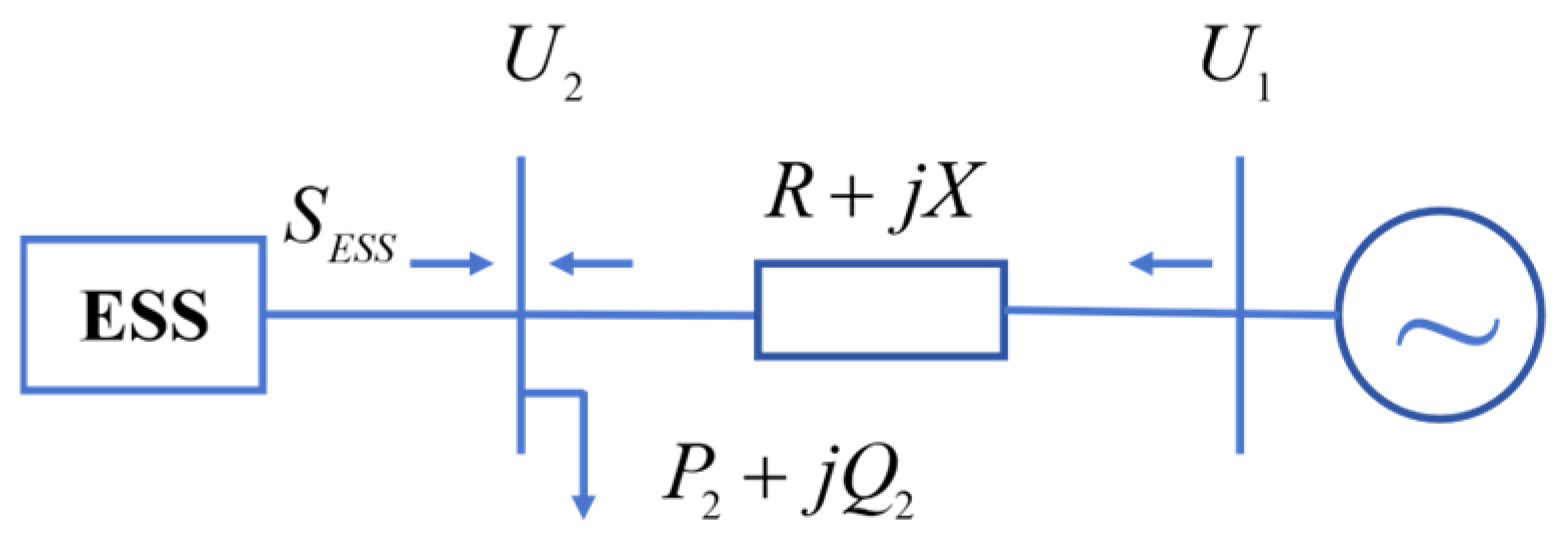
3.2.2. Voltage Regulation Principles for ESS

The ESS shows excellent flexibility and response speeds in dealing with the voltage over-run problem of distribution networks with high proportion of DPV access. When the line load is heavy node voltage over the lower limit, the ESS can discharge energy to reduce the active power flow along the line, helping to raise voltages at the end nodes; conversely, when excessive PV output causes voltages to exceed the upper limit, the ESS can absorb energy, ensuring reasonable power flow and bringing voltages back within acceptable limits. In addition, the ESS can provide a degree of reactive power compensation to further support voltage regulation.

The simplified model of a grid-connected ESS for distribution systems is shown in Figure 5.

In Figure 4, ${\mathrm{U}}_1$ is the distribution network bus voltage, ${\mathrm{U}}_2$ is the energy storage grid point voltage, ${\mathrm{S}}_{\mathrm{ESS}}$ is the apparent power of the ESS, ${\mathrm{P}}_2{+\mathrm{jQ}}_2$ is the user power at the point in ESS side, and $\mathrm{R}+\mathrm{jX}$ is the line impedance. From the simplified model, the node voltage ${\mathrm{U}}_1$ can be introduced as:

$$U_1=U_2+{\displaystyle \frac{\left(P_2-S_{\mathrm{ESS}}\cos \theta \right)R+\left(Q_2-S_{\mathrm{ESS}}\sin \theta \right)X}{U_2}}$$

(4)

where $\theta$ is the power factor angle of the stored power output.

The output is in the positive direction, and in Equation (4), when ${\mathrm{S}}_{\mathrm{ESS}}>0$, the ESS is discharged and plays the role of the power supply to lift the line voltage. When ${\mathrm{S}}_{\mathrm{ESS}}<0$, the ESS is charged and plays the role of the load to reduce the line voltage.

To address the voltage challenges caused by DPV integration, ref. [28] proposed an innovative method of ESS application, whereby the ESS device absorbs excess power during high PV generation periods and releases the energy when the PV output is insufficient in order to maintain the stability and quality of the voltage of the distribution network. Ref. [29] proposed a coordinated control strategy for distributed ESSs that includes two modes: multi-device cooperative control and stand-alone autonomous control. The former coordinates outputs via algorithms to stabilize node voltages, while the latter ensures the basic functionality of individual ESS units. Ref. [30] proposed a new method for voltage regulation and the control of PVs and ESSs cooperatively, where PV systems manage voltage through reactive power compensation, and the ESS employs a sag control strategy to enhance overall voltage quality. Ref. [31] further investigated the indirect control of PV output by regulating the storage charging and discharging rate to realize the regulation of access point voltage.

In addition to real-time control strategies, refs. [32,33] also emphasized the importance of developing optimal scheduling models for ESSs. Such models can help determine the most efficient operating strategies, improving both the economic and operational performances of ESSs. However, despite its strong potential in voltage regulation, ESS technology faces limitations, including a finite lifespan and cycle count. Over time, performance degradation may impact both its cost effectiveness and reliability.

3.2.3. Principles of Voltage Regulation Based on Cluster Partitioning in Distribution Network

With the transfer of renewable energy from the transmission system to the distribution network and the access of a large number of distributed power sources, distribution networks have evolved from passive to active systems. This transformation has introduced greater complexity in planning, operation, and dispatch. In order to improve the ability of distribution network to absorb distributed power sources and to solve the voltage management problems of distribution network, the concept of distribution network “clustering” has gradually attracted attention and been deeply studied.

The implementation of distributed cluster voltage regulation requires reasonable cluster partitioning for DPV access to the distribution network and reactive power optimization by identifying key nodes within each cluster. This process involves three main components: cluster partitioning index selection, algorithm design, and reactive power voltage control [34]. For index selection, most studies focus on structural features, particularly electrical distance between nodes. Refs. [35,36] proposed to characterize the electrical distance by the Euclidean distance between nodes and establish the modularity function as the partitioning index to find the optimal number of clusters. Ref. [37] further improved accuracy by using voltage sensitivity to characterize electrical coupling between nodes. However, these approaches primarily emphasize the scale of partitioning and often neglect cluster capacity. This can lead to imbalances in the DPV output and load across clusters, causing uneven voltage regulation efforts and overloading or idling of key nodes. To address this, some researchers have shifted focus from structural to functional indicators. Ref. [38] proposed a modular degree function partitioning method based on the improvement of the reactive/active balance index and carried out the cluster control of reactive power first, active power later, for the distribution network with scaled DPV access. However, this still results in capacity imbalances and delayed voltage response under limit violations. Based on the above exposed methodological deficiencies, ref. [39] introduced a graph-based genetic algorithm for DPV clustering, enhancing accuracy and stability by optimizing chromosome design and combining modularity with active power balance. Similarly, ref. [40] integrated simulated annealing into the genetic algorithm to further improve clustering outcomes and formulated an optimal scheduling model aimed at minimizing operational costs, thereby improving flexibility and reliability of renewable energy integration.

Overall, research on cluster partitioning for DPV integration in distribution networks has gradually shifted from structural to functional indicators, aiming to address issues such as uneven voltage regulation task distribution and imbalanced cluster capacity. While existing methods have improved cluster sizing and voltage regulation capability to some extent, challenges remain, particularly in dynamic responsiveness and capacity uniformity. In recent years, AI-based methods have enhanced clustering accuracy and stability by integrating modularity with active power balance, while the introduction of optimal scheduling models has improved the flexibility and reliability of renewable energy integration.

Most existing studies assess a cluster’s voltage regulation capability based on power supply–demand relationships, using indicators such as active/reactive power balance. However, from the perspective of what triggers node voltage violations, it is also essential to characterize the relationship between DPV output and load—i.e., cluster capacity—as a measure of the voltage regulation burden. A more comprehensive approach combines both perspectives: considering cluster capacity alongside regional regulation resources to quantify regulation capability and guide partitioning. This integrated strategy supports balanced voltage control tasks and power sharing, offering new insights into cluster-based voltage regulation.

Existing indicator systems have their own focus: power balance-based indicators are easy to construct and suitable for overall supply and demand analysis, but it is difficult to accurately reflect the node voltage fluctuations; indicators based on the voltage regulation task are more relevant to the actual problem, but they rely on real-time data, which makes their construction complicated. In the future, the two types of methods can be integrated to develop a composite indicator system that takes into account both accuracy and practicability, realizes more reasonable cluster division and assignment of regulating tasks, and improves voltage control in high PV penetration scenarios.

As shown in the

Table 1. Comparison of voltage regulation methods under different distribution network scenarios.

Method	Suitable Scenarios	Advantages	Limitations
OLTC	Older or stable power grids with few solar panels	Reliable and well tested	Slow response and inadequate for handling fast system fluctuations
SVC	Areas with frequent voltage changes	Adjusts voltage quickly	Expensive and only works in a limited area
PV inverter	Places with lots of solar power	Quick and easy to use and already built into solar systems	May not be strong enough alone and needs coordination
BESS	Areas with big voltage swings or peak usage times	Can respond quickly and help balance supply and demand	Costly and performance drops over time
Cluster partitioning	Grids with lots of solar and uneven electricity use	Smart way to group and manage resources	Needs fast computing and is hard to set up

, different voltage regulation methods suit different distribution network conditions. Traditional devices like OLTCs and SVCs are reliable for stable networks but respond slowly to fluctuations from high PV penetration. PV inverters and battery storage offer faster, more flexible control, making them better suited to modern solar-rich networks, although they face challenges such as capacity limits, cost, and degradation. Clustering provides a more adaptive, real-time solution but requires significant computational resources and coordination. Overall, no single method is universally ideal: integrated strategies tailored to specific grid conditions are likely to perform best in future smart grids.

4. PV-ESS Distribution Network Voltage Regulation Method

4.1. Centralized Regulation Methods

The centralized regulation method can effectively optimize and coordinate all controllable resources in the distribution network by using the central controller to directly access and obtain the operating conditions, operating status, and perfect network topology; parameters and other information of all control devices; and the operation and regulation scheme through centralized computing and send it down to the local controller of each device [41]. Based on the network parameter analysis to obtain the voltage sensitivity of each node, ref. [11] proposed an active and reactive power adjustment strategy based on the real-time measurement data to collaboratively control the controllable resources, so as to solve the voltage problem. A more general approach to centralized optimal regulation of an active distribution network is to construct the optimal tidal current problem. Considering that the power system tidal equations are nonconvex and nonlinear in nature, and the operational security domains of multiple controllable resources may also be nonconvex and discrete, the constructed centralized optimal regulation problem for distribution network is difficult to be solved directly using mature commercial solvers, and it can be optimized and computed using heuristic algorithms [42,43], interior-point methods [44], approximation methods [45,46], convex optimization [47,48], and other methods for optimization calculations.

For the multiple uncertainty problems brought by the large-scale access of distributed new energy sources in the distribution network, the current commonly used methods to cope with them mainly include stochastic optimization [49,50], robust optimization [51], and so on. Stochastic optimization models uncertainty using probability density functions and generates representative random scenarios through sampling techniques. It then constructs an optimization problem to minimize the expected objective value across all scenarios. However, this method relies on accurate probability distribution data, which are often unavailable in practice. To cope with this problem, robust optimization methods define deterministic uncertainty sets and solve for the worst-case scenario within these sets. While this enhances system resilience against uncertainty, it typically sacrifices operational efficiency under normal conditions. In order to balance robustness and operational performance, the distributional robust optimization method has been proposed. This method does not require an exact probability distribution but rather can effectively improve the adaptability and flexibility of power system optimization and regulation by constructing a fuzzified probability set and comprehensively considering the possibility and uncertainty of parameter distribution [52]. In addition, in order to dynamically respond to the impact of new energy output and load changes on distribution network operation, the model predictive control (MPC) method is widely used in the online optimization scheduling of active distribution network. Based on the short-term prediction information of new energy and loads [53], MPC continuously updates and solves the optimal control strategy in a rolling time horizon, significantly enhancing the system’s robustness and real-time responsiveness [54,55].

In addition, centralized control requires a global update and re-optimization whenever control devices are added or removed, which makes it difficult to meet real-time control requirements. As the system scales and the number of controllable resources increases, the computational burden also grows significantly, limiting the scalability of centralized methods.

4.2. Distributed Regulation Methods

The core idea of distributed regulation is that autonomous agents are set up at each node in the network, and each agent uses local information and partial message exchange with its neighbors to achieve a common cooperative goal [56,57]. Compared with the centralized regulation approach, this protects the privacy of individual agents, and the amount of data handled by each agent is significantly lower and relatively more computationally efficient, resulting in a faster control response from the controllable resources. Theoretically, distributed methods can approach the optimal regulation performance achieved using centralized approaches [58].

Distributed communication ensures the consistency of a certain state among the devices so that the devices can participate equally in the operation and control of the active distribution network, thus avoiding the situation that one device is over-utilized while the others are in an idle state. In [29], on the basis of ESS control, a consistency algorithm is used to equalize the utilization rate of all ESSs, so as to effectively utilize the storage capacity to achieve voltage regulation, but the influence of network parameters is not considered in the control method. Ref. [59] utilized voltage sensitivity to realize the effective response of distributed power reactive output to voltage over-runs and, at the same time, showed that local controllers can initiate additional reactive power support requests to other controllers in neighboring nodes based on the consistency algorithm to ensure the voltage security of the distribution network. However, voltage sensitivities are usually kept constant and computed offline using centralized methods, and since they usually vary according to the network operating conditions, fixed sensitivity coefficients may degrade the voltage control performance.

Despite their advantages, most distributed optimization methods require numerous iterations and long communication times to converge [60,61], which limits their suitability for real-time control. Moreover, many existing studies focus on single-resource control or oversimplify network currents and device operational states [62]. Updating dynamic voltage sensitivities necessitates handling network voltage coupling constraints in a distributed fashion. Coupled with the multitemporal operational constraints of distributed ESSs, this presents significant challenges for implementing distributed optimal control in time-varying active distribution networks.

4.3. Multi-Timescale Regulation Methods

In distribution networks, traditional voltage regulation equipment is primarily designed to address slow voltage variations caused by load fluctuations [63,64]. To ensure reactive power balance within distribution network, adjustable SCBs and SVCs are employed as reactive power compensation devices. The former can only provide discrete regulation and output capacitive reactive power, whereas the latter is capable of continuous compensation ranging from inductive to capacitive reactive power [65]. However, with a high percentage of DPV access, conventional regulation devices often struggle to respond effectively to rapid voltage fluctuations resulting from variable renewable generation [66]. In this case, PV inverter-based reactive power compensation methods have been used to improve the voltage distribution due to the large number of DTVs in the distribution network with inverters that can absorb and release reactive power, can be continuously regulated, have a fast response time, and are inexpensive to control [67]. Considering the large ratio of line resistance/reactance in distribution network, the ESS is applied on a large scale, which can regulate voltage more effectively through active power adjustment at different timescales, such as intraday and real time, or form an integrated PV-ESS, further improving the rate of PV consumption and smoothing out the high volatility of PV output. Influenced by the current characteristics of the grid, the voltage of each node is associated with the active and reactive powers of other nodes [30]. Because of the varying control characteristics and costs of flexible resources and traditional equipment, effective voltage control requires coordinated management of active/reactive power, multi-timescale operation, and system-wide resource optimization. This includes leveraging underutilized load-side resources, particularly electric vehicles (EVs). Ref. [68] proposed a strategy to introduce EVs to replace part of the ESS to participate in real-time voltage regulation under a multi-timescale voltage regulation framework. By harnessing the flexible charging/discharging capabilities of EVs, the scheme alleviates storage limitations and improves system responsiveness and user-side resource utilization. Similarly, ref. [69] proposed a reactive power optimization method that considers load characteristics to synergistically optimize the distribution network voltage through day-ahead and intraday timescales. Although the above methods have achieved some success in distribution network voltage regulation, their complex modeling, difficult nonlinear solution, and insufficient real-time response capability limit their effectiveness in large-scale DPVs access scenarios. For this reason, there is an urgent need to explore more efficient and accurate modeling and solving methods to cope with the rapid voltage fluctuations and complex regulation demands brought about by a high proportion of renewable energy access, so as to achieve real-time and stable control of distribution network voltage [70].

4.4. Joint Optimization of Reactive Power and Voltage

Joint optimization of reactive power and voltage is a key technical means to ensure the voltage stability of distribution networks and improve the operation economy and power supply quality. Under the background of a high proportion of distributed photovoltaic energy storage access, voltage fluctuation and reactive power distribution show a strong coupling relationship, and the traditional independent optimization method has shown difficultly in coping with multi-source, heterogeneous, and dynamically changing operation characteristics. Therefore, integrating reactive power allocation and voltage regulation into a unified optimization framework has become essential for enhancing the regulation capabilities of distribution networks. At present, the commonly used optimization methods mainly focus on two categories: heuristic algorithms and artificial intelligence algorithms. The following section summarizes the characteristics, advantages, and limitations of these approaches, providing a reference for selecting appropriate optimization strategies.

4.4.1. Application of Commonly Used Heuristic Algorithms for Voltage Regulation in PV-ESS Distribution Network

Heuristic algorithms are simple in structure and easy to implement and have received extensive attention from researchers. Particle swarm optimization (PSO), ant colony optimization (ACO), genetic algorithms (GAs), the simulated annealing (SA) method, and other heuristic methods are commonly used in power system optimization and scheduling due to their strong generality, which is not limited to the structure and characteristics of the optimization problem and is easy to program and implement. However, these algorithms cannot guarantee optimal solutions, and their computational complexity grows exponentially with problem scale. When applied to large distribution networks, they often require excessive computation time, exhibit low efficiency for real-time control, and frequently converge to local optima with unpredictable solution quality gaps [71].

The integration of distributed renewable energy introduces significant intermittency, posing challenges for centralized control methods, including massive data communication, model maintenance, strategy agility, system reliability, and privacy concerns. In contrast, distributed control methods can realize the efficient, orderly, safe, and economical integration of renewable energy into the grid through clustering control of distributed renewable energy generation. The consistency algorithm is a classic distributed control method in distribution network; however, it requires all controllers to keep synchronized updates, which increases the complexity of communication and the difficulty of execution and makes it difficult to ensure real-time algorithmic control and unable to cope with voltage fluctuations due to rapid changes in new energy output. The alternating direction multiplier method realizes the efficient solution of the distributed control problem by alternating iterations of the proximity intervals and solving them in parallel.

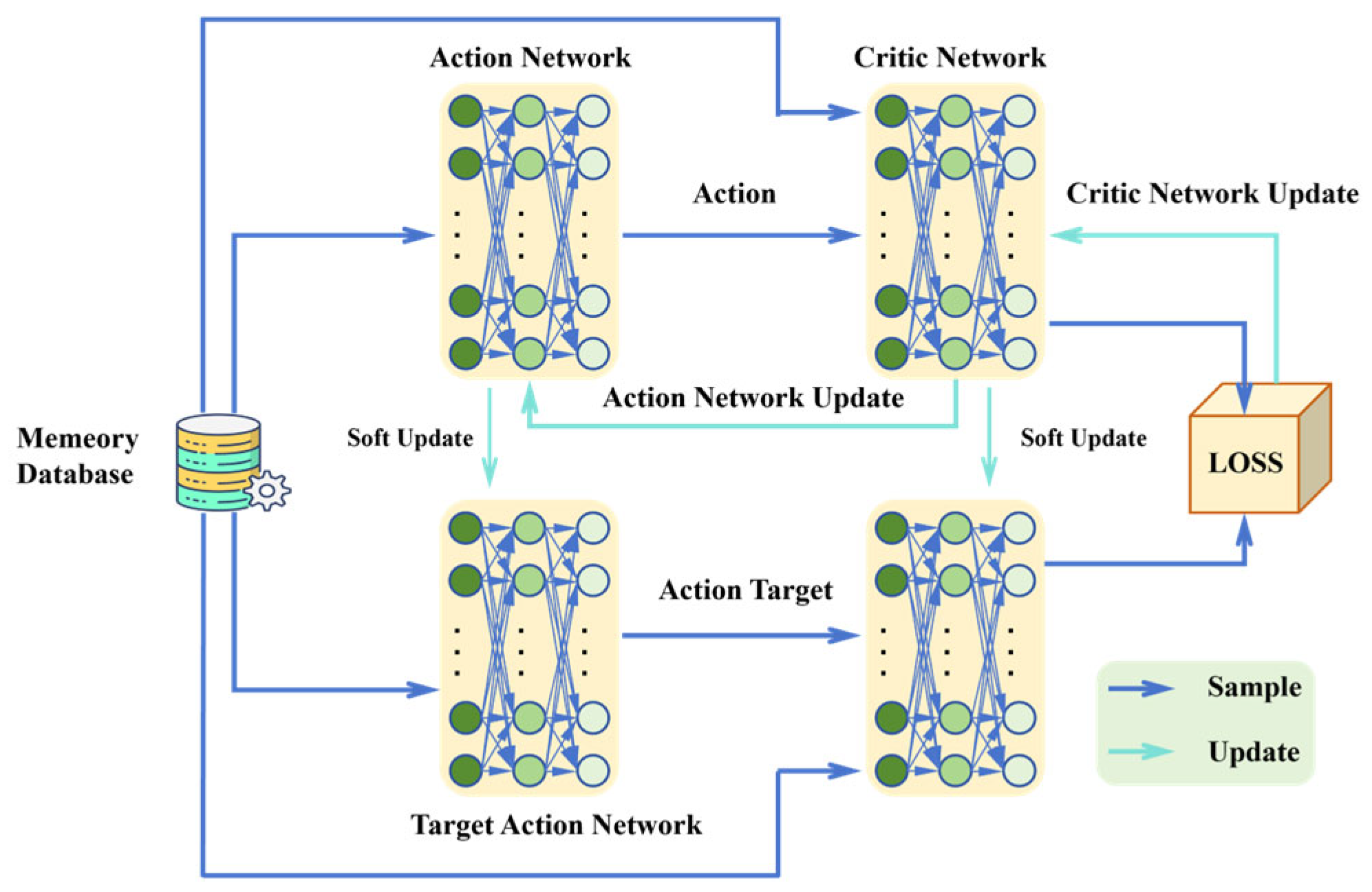
4.4.2. Deep Reinforcement Learning for Voltage Regulation in PV-ESS and Distribution Network

For the traditional research on optimal dispatch of distribution networks, the most common approach is based on optimization [72]. This type of method has the advantages of stable calculation results and strong interpretability, but it requires the establishment of an explicit mathematical model of the system, with which it is difficult to obtain the precise line parameters and topology of the system for large-scale distribution network systems, and in order to ensure solvability in the modeling process, it is usually necessary to make a certain degree of assumptions and simplification of the model, and too many assumptions and simplifications will cause the model to deviate from the actual situation.

Compared with traditional heuristic methods, deep reinforcement learning offers key advantages in distribution network optimization [73]. First, it does not rely on accurate physical models. In practice, distribution networks often suffer from poor observability, and obtaining precise line parameters or topology information requires extensive historical or measurement data, which may not be available. Traditional methods depend heavily on accurate models, and errors in model parameters can lead to control deviations. In contrast, deep reinforcement learning can learn control strategies directly from data, reducing reliance on detailed physical models and improving robustness under uncertain conditions [74]. Second, DRL is better at leveraging historical data. With the increasing use of measurement devices and smart terminals, distribution networks generate large volumes of time-series data with complex structures and interdependencies. Traditional optimization and heuristic methods often overlook this valuable information. In contrast, DRL can learn from historical records during offline training, allowing it to capture patterns and scheduling knowledge that improve decision making in real-time operations.

However, reinforcement learning is highly dependent on high-quality training environments, since the actual distribution network operating environment is complex, dynamic, and data constrained, making it difficult to directly construct an accurate simulation environment. Secondly, reinforcement learning models often require a lot of interactions and trial and error during the training process, which is unacceptable for real power grids with frequent non-optimal operations and, thus, can only rely on simulation training, which further exacerbates the uncertainty of policy migration. In addition, most of the current algorithms have high computational complexity and slow convergence when facing large-scale state space and multi-objective optimization problems, which makes it difficult to operate stably in systems with high real-time requirements. Furthermore, the interpretability of reinforcement learning strategies is poor, and it is difficult to gain operators’ trust in critical control scenarios; at the same time, when facing unexpected events or extreme perturbations, the training strategies may lack sufficient robustness and security. In summary, the practical application of reinforcement learning in PV distribution networks still needs to make further breakthroughs in terms of data accessibility, policy generalization ability, security guarantee and algorithm deployability.

• Reinforcement Learning

Reinforcement learning is an algorithm for learning state-to-action mappings with the goal of maximizing the value of the cumulative rewards received by an intelligent body in its interaction with the environment. Markov decision processes are commonly used to model reinforcement learning problems. The Markov decision process contains the following four elements [75]:

(1)

State set: S is the set of environment states, where the state of the intelligence at moment t is $st\in S$;

(2)

Action set: A is the set of actions of an agent, where the action of the agent at moment t is $at\in S$;

(3)

State transfer process: the state transfer process $\mathrm{T}(\mathrm{st},\mathrm{at},\mathrm{st}+1)\sim \mathrm{Pr}(\mathrm{st}+1|\mathrm{st},\mathrm{at})$ denotes the probability that an agent performs an action at in state $st$ and then transfers to the next moment state $st+1$;

(4)

Reward function: the reward function $rt$ is the immediate reward obtained by an agent after performing the action at in the state $st$.

At each turn, the agent first observes the current state $st$ of the environment and makes a decision based on the state out. When the action is executed, the environment feeds a reward value rt to the intelligent body, and then the environment shifts to the next state $st+1$, which is a Markov decision process.

• Deep Reinforcement Learning Algorithm Summary

Table 2. Comparison of common reinforcement learning algorithms in terms of efficiency, scalability, and complexity.

Algorithm	Execution Efficiency	Scalability	Computational Complexity
DQN	Moderate	Low	Low from the main grid
DDQN	Slightly higher than DQN	Low	Low
DDPG	Moderate	High	High
TD3	High	High	High
SAC	High	Very high	Very high
PPO	Moderate to high	High	Moderate

summarizes the evaluation criteria of classical and commonly used reinforcement learning algorithms in terms of operational efficiency, scalability, and computational complexity. In general, SAC and TD3 perform well in tasks that deal with complex and continuous action spaces but have higher computational complexity accordingly, while DQN and DDQN are more suitable for discrete tasks, with lower computational overhead but limited scalability. PPO, as a Policy Gradient method that combines stability and efficiency, has good overall performance in practical applications.

As shown in

Table 3. Classification and comparison of classical deep reinforcement learning algorithms.

Type	Algorithms	Characteristic	Advantages	Disadvantages
Value Function Based	DQN	Uses deep neural networks to approximate Q-values with experience replay and target networks	Handles high-dimensional state spaces effectively	Prone to overestimation of Q-values
	DDQN	Introduces Double Q-learning to separate action selection and evaluation	Reduces Q-value overestimation, improving policy stability	Slightly higher computational complexity
	Dueling DQN	Decomposes Q-values into state value and advantage	Better evaluation of state values, especially in large action spaces	More complex network architecture, requiring additional tuning
Actor–Critic	AC	Uses separate actor and critic networks to improve policy updates	More stable than pure policy-based methods	High variance and sample inefficiency
	A3C	Parallel training with multiple agents to speed up learning	Faster convergence, with better exploration	High computational cost and complex implementation
	DDPG	Off-policy, model-free, and uses deterministic policy with target networks	Handles continuous action spaces and undergoes stable updates with experience replay	Sensitive to hyperparameters and prone to overestimation bias
	TD3	Improves DDPG with twin Q-networks and delayed policy updates	Reduces overestimation bias and improves training stability	Higher computational complexity due to twin critics
	SAC	Uses entropy regularization for better exploration	More stable training, robust to hyperparameters, and effective in complex environments	Requires careful tuning of temperature parameter
Policy Gradient	PPO	Uses a clipped objective function to ensure stable policy updates	Simple to implement, computationally efficient, and widely used in deep RL applications	Still requires careful hyperparameter tuning and may struggle with highly stochastic environments
	TRPO	Constrains policy updates using a trust region to ensure monotonic improvement	Guarantees monotonic policy improvement and provides strong theoretical convergence properties	Computationally expensive due to second-order optimization and Hessian-vector product calculations

, classical deep reinforcement learning algorithms are summarized and classified into three groups based on their internal properties. Among them, the Value Function-Based algorithm mainly relies on the Q-value function to evaluate the value of state–action pairs and selects actions through a greedy strategy. These methods perform well in a discrete action space but require discretization or policy approximation in a continuous action space and may suffer from overestimation bias during training. Policy Gradient methods optimize policies directly, making them suitable for continuous action spaces and complex behaviors; however, the approach often suffers from high variance, leading to unstable convergence. PPO controls the magnitude of policy update by trimming the objective function, while TRPO uses trust regions to optimize the constraint update to improve the convergence; Actor–Critic combines the advantages of the previous two methods by using a critic network to evaluate the value function, while the actor network is responsible for the policy update. These methods can learn efficiently in the continuous action space and have good stability. DDPG uses a deterministic strategy as shown in Figure 6, which is suitable for high-dimensional continuous control tasks but suffers from the overestimation problem, which is alleviated by TD3 with a dual-Q network and delayed updating

• Deep Reinforcement Learning for PV-ESS and Distribution Network

In recent years, researchers have carried out many studies on the application of deep reinforcement learning in PV-ESS distribution networks. In this paper, we provide an in-depth description in terms of storage allocation calling, distribution network dynamic reconfiguration, and multi-timescale voltage control [76].

1.

Energy Storage System

An ESS has the ability to absorb and emit active power, which can smooth out the impact of new energy fluctuations on distribution network operation [77]. The charging and discharging power of an ESS affects its state of charge; therefore, the effect of future uncertainty needs to be considered when scheduling an ESS. Since the current action of the ESS has an impact on its charge state, in order to realize the optimal scheduling of the ESS at multiple moments, ref. [78] proposed a stochastic scheduling method for ESSs based on reinforcement learning. Monte Carlo tree search estimates the expected maximum Q-value. By embedding scheduling rules, it reduces inaction and enables efficient multi-stage optimization considering battery degradation. Ref. [79] proposed an ESS scheduling strategy based on Double DQN. First, the optimization problem considering ESS access is modeled as a Markov decision process, and the multitemporal optimization problem is split through the Bellman equation; then, the Double DQN solution is adopted, and the effect of future uncertainty is considered in solving the charging and discharging scheduling commands of the ESS at each moment, so as to realize the efficient solution of the sequential control problem containing the ESS. Ref. [80] proposed a DDPG-based EV scheduling strategy, in which the EV optimization problem considering the uncertainty of the state transfer process is first modeled as a Markov decision process and then solved by the DDPG algorithm. Comparative experiments show the advantages of the deep reinforcement learning-based method over the traditional stochastic optimization method in sequential control. Ref. [81] proposed a PPO-based distribution network scheduling strategy, and comparative experiments at IEEE 33 nodes show that the PPO-based control algorithm can achieve better control results compared with the DQN method. Ref. [82] considered the impact of distributed renewable energy access on the voltage of low-voltage distribution network and used reinforcement learning for real-time scheduling of energy storage systems in order to optimize the voltage regulation strategy across the whole day in a high-dimensional state–action space, to cope with the uncertainty of the distribution network, and to minimize the regulation cost.

Compared with traditional methods, deep reinforcement learning-based optimization strategies for distribution networks containing an ESS show significant advantages in the following two aspects [83]: (1) Deep reinforcement learning gets rid of the dependence on the probability distribution of random variables and, at the same time, does not need to explicitly construct the state transfer model of the system, which avoids the influence of assumptions and simplifications in the process of random variable modeling and state transfer on the optimization results and improves the method’s adaptability and robustness. (2) Through offline training, deep reinforcement learning can embed scheduling strategies into neural networks, significantly reducing the online computational burden and enabling the optimization problem to be solved in real time during the runtime phase. Compared with the traditional stochastic optimization methods, this feature shows stronger computational efficiency and real-time performance when dealing with high-dimensional and fine-grained optimization problems.

2.

Distribution Network Reconfiguration

Reconfiguration of the distribution network refers to a technology in which the distribution network improves operation economy and reliability of the power supply by changing its own topology. According to the different needs, the dynamic reconfiguration of a distribution network can be divided into two cases: (1) During normal operation, the distribution network changes the direction of network current flow through reconfiguration, which, in turn, achieves the purpose of optimizing the current and reducing the network loss. (2) In the event of faults in the distribution network due to extreme natural disasters and other influences, the switching state of the system is altered in order to minimize the outage loss of the users and to achieve the maximum degree of power supply. Ref. [84] proposed a data-driven control strategy based on a batch-based reinforcement learning algorithm. The proposed method approximates a supervised learning method, where the learning process does not depend on the interaction between the intelligentsia and the physical model of the distribution network, and the distribution network reconfiguration strategy can be learned directly based on historical operational data. However, this method requires a relatively high amount of historical data and a certain amount of “expert-level” data to assist the learning of the agents. Ref. [85] proposed a topology optimization method for distribution networks based on an action–evaluation deep reinforcement learning algorithm. The system topology state set and action set applicable to the deep reinforcement learning method are designed, and then the deep reinforcement learning algorithm is used to solve the problem. It is important to verify the robustness of algorithms under a full year (e.g., 8760 scenarios) in optimization and control tasks for complex power systems [86]. Ref. [87] proposed a reinforcement learning-based extended Q-routing method for fast reconfiguration of dynamic distribution networks under events such as grid faults. By constructing a dynamic model containing distributed power control and protection functions and combining it with an event-driven communication mechanism, the network reconfiguration is realized within 1.5 s, which verifies the real-time effectiveness of the method. The dynamic division of clusters can realize rapid area isolation and autonomous control during grid faults or fluctuations and improve system resilience. However, its practical application still faces many limitations: communication delays affect the response speed, missing data reduce the reconfiguration accuracy, coordination between traditional protection and intelligent control is difficult, and algorithms converge and stabilize in large-scale systems. Together, these factors constrain its efficient and reliable application in real-time scenarios.

Compared with traditional methods, the deep reinforcement learning-based reconfiguration and restoration strategy for distribution network shows significant advantages in the following aspects: (1) The method has excellent solving efficiency, can dynamically adjust the network topology based on the real-time operating state of the system, and, at the same time, realize rapid restoration and optimization after the occurrence of faults, so as to improve the adaptive ability and response speed of the power grid. (2) Relying on historical operation data, deep reinforcement learning can independently construct dynamic reconfiguration strategies, avoiding the deviations caused by assumptions and simplifications in the modeling process of traditional methods, thus improving the generalization ability of the model and the reliability of decision making.

3.

Multi-Timescale Control

Current distribution networks usually contain both types of controllable equipment. Mechanical equipment has a slow response time and is unable to perform frequent on–off actions, while power electronic equipment has a faster response time and can be adjusted frequently. The different characteristics of the two types of controllable devices determine the differences in their control timescales, and it is challenging to coordinate the control of mechanical devices and power electronic devices on two different timescales and give full play to the real-time response capability of the power electronic devices in order to inhibit the rapid fluctuation of voltage. Ref. [88] proposed a dual time-scale control strategy, in which the outer layer models the control of mechanical devices as a Markov decision process and solves it using a DQN; the inner layer coordinates the smart inverters within the dispatch network based on a centralized control strategy. The inner layer model uses linearized approximation to improve the solution speed to achieve fast regulation of the inverter devices. Ref. [89] proposed a multi-timescale distribution network reactive power optimization strategy for the control of long timescale capacitor banks and on-load regulator transformers, weather optimization is carried out using a hybrid second-order cone planning-based approach, and for the short timescale power electronic equipment, real-time scheduling methods based on multi-agent deep reinforcement learning are used. Simulation experiments show that the multi-agent deep reinforcement learning method can achieve online optimization while obtaining cooperative control of multiple controllable devices. However, the outer-layer optimization in both of the above methods depends on an accurate physical model of the system. In practice, such a model for the distribution network is often difficult to obtain. Moreover, the inner-layer in situ control strategy based on multi-agent deep reinforcement learning, as proposed in [90], is challenging to apply in scenarios with a high penetration of renewable energy sources. For this reason, ref. [91] proposed a dual time-scale control strategy based on a centralized–distributed hybrid control framework. The outer layer models the optimization problem considering long-term voltage offset and the cumulative number of mechanical device actions as a Markov decision process, which is solved using a single-agent deep reinforcement learning algorithm; the inner layer adopts a smart partition–multi-agent-based partition cooperative control strategy for coordinated scheduling of photovoltaic inverters and guides the inner and outer agents to learn the voltage control strategy through an agent model, which achieves the coordinated scheduling of multiple controllable devices without relying on physical models. Ref. [92] proposed a dual time-scale control method based on deep reinforcement learning, which models the coordinated control of slow discrete and fast continuous devices as a two-layer Markov decision process; then, two independent agents are used to solve the problem collaboratively, and importance sampling technique is introduced during the training process to ensure the stability of training. Comparative experiments show that the method can realize the coordinated control of multiple devices without relying on physical model information.

Abstracting the coordinated control of multiple devices as a multi-timescale optimization problem can not only accurately portray the dynamic characteristics of various types of devices but also fully exploit their operational advantages in order to achieve efficient cooperative scheduling [93,94]. Combining deep reinforcement learning with a variety of advanced control strategies, we give full play to the adaptive online decision-making ability of reinforcement learning in complex environments, so as to realize real-time scheduling of power electronic equipment, effectively cope with the impact of intermittent fluctuations of new energy power generation on the operation of the distribution network, and enhance the stability and regulation capability of the system.

As shown in

Table 4. Summarizes the application of different reinforcement learning algorithms to the distribution network.

Field of Application	Document	Algorithm	Purpose
ES device scheduling and control	[79]	DDQN	Minimize the cost of purchasing electricity from the main grid
	[80]	DDPG	Maximizing profits for distribution system operators
	[81]	PPO	Minimize network loss
	[82]	SAC	Minimizing system voltage offset
Dynamic reconfiguration	[84]	DQN	Minimizing network losses and switching action costs
Multi-timescale voltage regulation	[88]	DQN	Minimize system voltage excursion and capacitor operation costs
	[89]	SCOP+MLTI-DDPG	Minimizing system network losses on long timescales and minimizing them on short timescales
	[91]	MLTI-SAC	Minimizing system voltage excursions and mechanical device actions

, it demonstrates the specific application scenario examples of different algorithms. In practical grid regulation and other engineering applications, heuristic algorithms have the advantages of simple implementation and strong global search capability, which are especially suitable for solving nonconvex and discrete problems. However, they generally have limitations, such as slow convergence speed and poor adaptability to dynamic environments. In contrast, AI algorithms, especially reinforcement learning, have good adaptive and online decision-making capabilities and can continuously optimize strategies and adapt to environmental changes through interaction with complex systems. However, their shortcomings include high dependence on computing resources, high demand for training samples, as well as poor interpretability and difficult security verification in critical power scenarios. Therefore, it is necessary to weigh the advantages and disadvantages of the two in practical applications, and in recent years, some studies have also attempted to integrate heuristic and artificial intelligence algorithms to take into account the global and adaptive capabilities and to improve the regulation performance and practicality.

5. Challenges and Prospects of Voltage Regulation in PV-ESS Distribution Network

5.1. Challenges

This paper provides a systematic overview of the voltage regulation of a PV-ESS distribution network under high-penetration DPV access, analyzing voltage over-run mechanisms and mainstream regulation strategies. It compares direct voltage regulation with current optimization methods, examines centralized versus distributed control architectures, and evaluates traditional and intelligent algorithms for reactive power-voltage optimization. Aiming at the challenges of multi-device collaboration and timescale matching, it is proposed that centralized–distributed hybrid control and deep reinforcement learning should be developed in the future. Special attention is given to privacy protection and cooperative optimization when user-side resources participate in voltage regulation, with the key challenges summarized as follows:

• The contradiction between timeliness and accuracy of dynamic cluster partitioning: Traditional partitioning methods have minute delays in thousand-node systems, making it difficult to meet real-time requirements [95,96,97]; static models have a failure rate as high as 42% in photovoltaic fluctuation scenarios. The network loss in multidimensional optimization shows a significant negative correlation with the reliability index, and the heterogeneous nature of the resources also exacerbates the fragmentation of the resources. A breakthrough should be achieved through distributed computing, digital twin modeling, and multi-timescale collaborative optimization.
• Reinforcement learning policy migration and security issues: The current training mainly relies on a simulation environment, in which it is difficult to realistically reproduce the dynamic characteristics of a distribution network, and random policy exploration may threaten the system security. It is necessary to construct a high-fidelity digital twin system to achieve safe migration and to integrate data-driven methods with physical models to improve generalization ability and control credibility. Digital twins provide a real-time virtual replica of the power system, enabling safer testing and the adaptation of reinforcement learning policies. By bridging the gap between simulation and reality, they help reduce policy transfer risks and improve control reliability under dynamic grid conditions. The introduction of multi-objective learning, migration learning, and security constraint mechanisms is the key to improve the practicality of the algorithm.
• The multi-dimensional challenges of EV participation in voltage regulation: The privacy level requires the introduction of privacy computing frameworks such as federated learning; the control level faces response delay and control granularity issues. Interface differences lead to a decline in the accuracy of voltage regulation; the market mechanism lacks a universal solution that takes into account the interests of both the grid and the user; and, at the same time, frequent charging and discharging will exacerbate battery degradation, which requires the construction of a fine-grained battery life assessment model. The essence of the overall problem is the balance game between user flexibility, the real-time grid, and equipment life, which needs to be dealt with through edge computing, standardized interfaces, and digital evaluation system.
• Three-phase imbalance and harmonics on the grid voltage challenges are mainly manifested in the deterioration of voltage quality prone to neutral shift, waveform distortion, equipment loss and life reduction, resonance risk and protection false operation, as well as new energy grid-connected harmonic superposition, imbalance aggravation, and other issues. In the future, it is necessary to break through from intelligent monitoring and dynamic compensation, power electronic harmonic suppression using multi-level converter and AI predictive control, and new energy synergistic control and other multi-dimensional breakthroughs to build a highly resilient power grid system from intelligent perception to multi-dimensional analysis to efficient management.

5.2. Prospects

• Uncertainty modeling and distributed cooperative control: the strong volatility and uncertainty of distributed photovoltaic and customer-side loads make it difficult for traditional centralized regulation to fully cope with them. The centralized method based on probabilistic prediction can quantify the source-load bilateral uncertainty and improve the system robustness by combining stochastic optimization and robust optimization. In the distributed regulation framework, the existing methods mostly rely on point prediction results or measurement data and lack the comprehensive utilization of source-load probabilistic information. In the future, there is an urgent need to construct a distributed communication mechanism that supports probabilistic information transmission to maximize the benefits of multifaceted device regulation under multiple uncertainties.
• The enhancement of strategy migration and model adaptation: Existing deep reinforcement learning algorithms assume that the system model is static and unchanged, making it difficult to cope with dynamic changes in the physical model caused by changes in the grid topology or access to new energy sources, resulting in a decline in the performance of the trained strategy or even its failure [98]. To address these challenges, the integration of digital twins, edge computing, and federated learning is emerging as a promising solution. Digital twins provide a real-time virtual replica of the physical grid system, enabling rapid simulation and testing of control strategies under various operating scenarios. Edge computing brings computational intelligence closer to data sources, allowing for faster local decision making and reducing dependence on centralized infrastructure. Meanwhile, federated learning enables distributed devices to collaboratively train models without sharing raw data, thus enhancing adaptability while preserving data privacy. In the future, we need to develop learning algorithms with model-aware and adaptive capabilities so that they can quickly adjust their strategies after system changes to achieve continuous and stable control performance.
• Privacy protection mechanism and system governance model management: The participation of EVs in voltage regulation involves user privacy issues, reflecting the conflict between individual rights and system effectiveness in the process of energy digitization. It is crucial to build a “privacy–efficiency” balance mechanism. In the future, we can rely on homomorphic encryption, federated learning, and other technologies to shift from the data level to the knowledge level of regulation to realize secure dispatching. In addition, the integration of cryptography and market mechanism is expected to realize the orderly regulation of power grid public power while guaranteeing privacy and promote the transformation of energy governance mode [99].
• Unified framework under multi-device convergence: The key to achieving unified cooperative control of distributed resources such as photovoltaic, energy storage, and electric vehicles in the future lies in the breakthrough of the two core challenges of heterogeneous model integration and cross-timescale optimization. In terms of control models, a hybrid control mode combining distributed and centralized control can be explored, and distributed algorithms, such as the ADMM, can achieve the global optimization goal while guaranteeing the autonomous regulation capability of each device. In terms of modeling methodology, efforts should be made to develop hybrid modeling technology that integrates physical mechanisms and data-driven modeling, which not only portrays the dynamic characteristics of the equipment by using mechanism models such as state space equations but also predicts the fluctuation of photovoltaic output and EV charging behavior with the help of machine learning methods.