The Development of a MATLAB/Simulink-SCADA/EMS-Integrated Framework for Microgrid Pre-Validation
Abstract
1. Introduction
- The study presents a fully integrated SILS-EMS-SCADA framework that enables cost-effective and scalable pre-validation of microgrid operations.
- A detailed grid optimal operation algorithm is proposed and implemented on an IEEE 13-bus system with real-world constraints including ESS, EVCS, and DG.
- The proposed model demonstrates a 17.84% cost reduction and significant flattening of the load profile, improving grid flexibility.
- The framework supports both grid-connected and islanded scenarios and enables a real-time simulation interface via APIs and database management using Python.
- A novel SILS framework that seamlessly integrates with SCADA/EMS platforms through HTTP-based APIs for real-time simulation and monitoring.
- The implementation of a day-ahead optimal scheduling algorithm for DERs using MILP, validated through dynamic SILS testbed simulations.
- The demonstration of operational cost savings, load curve flattening, and stability enhancement in both connected and islanded modes.
2. Methodology
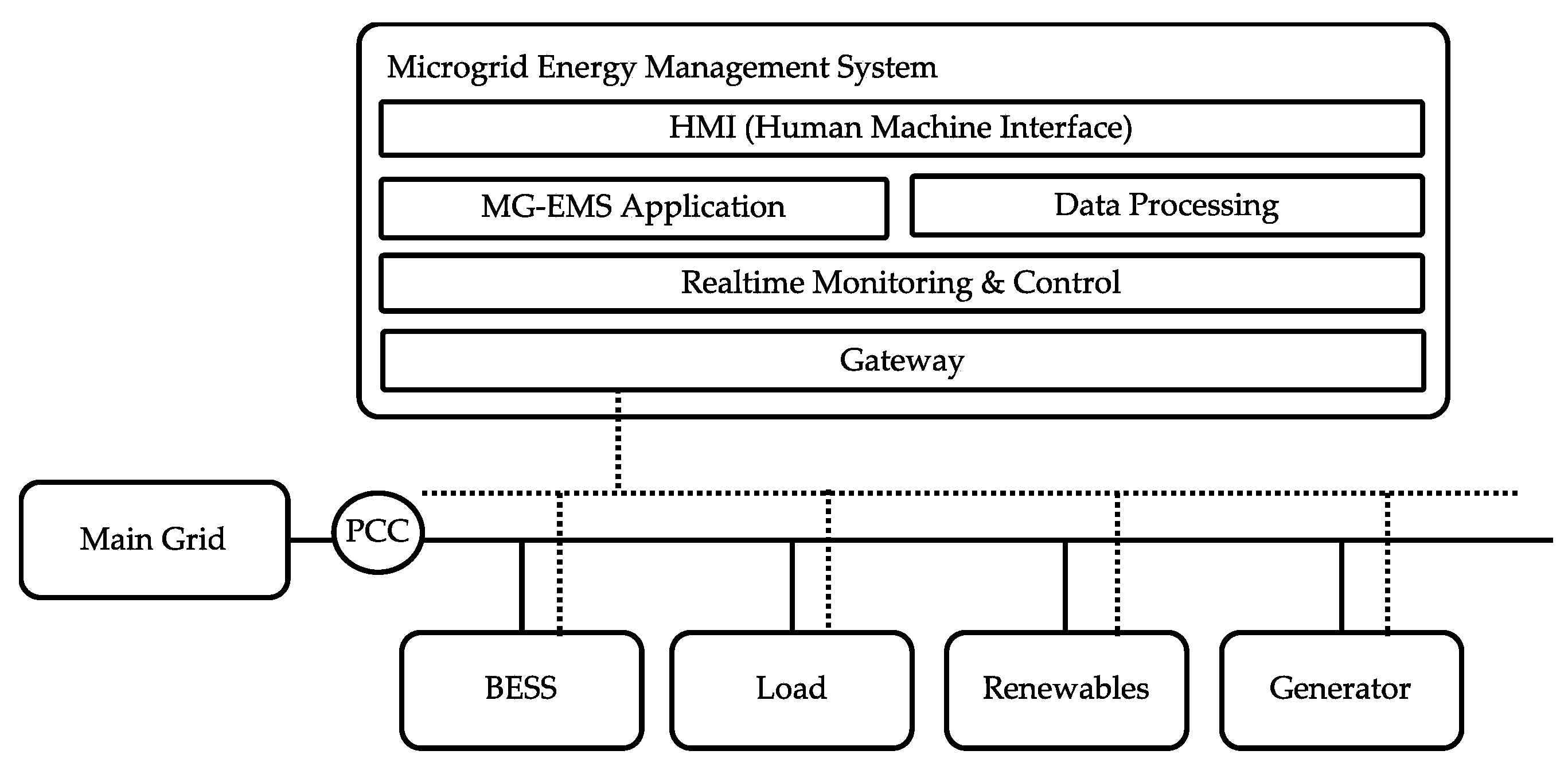
2.1. Energy Management System (EMS)
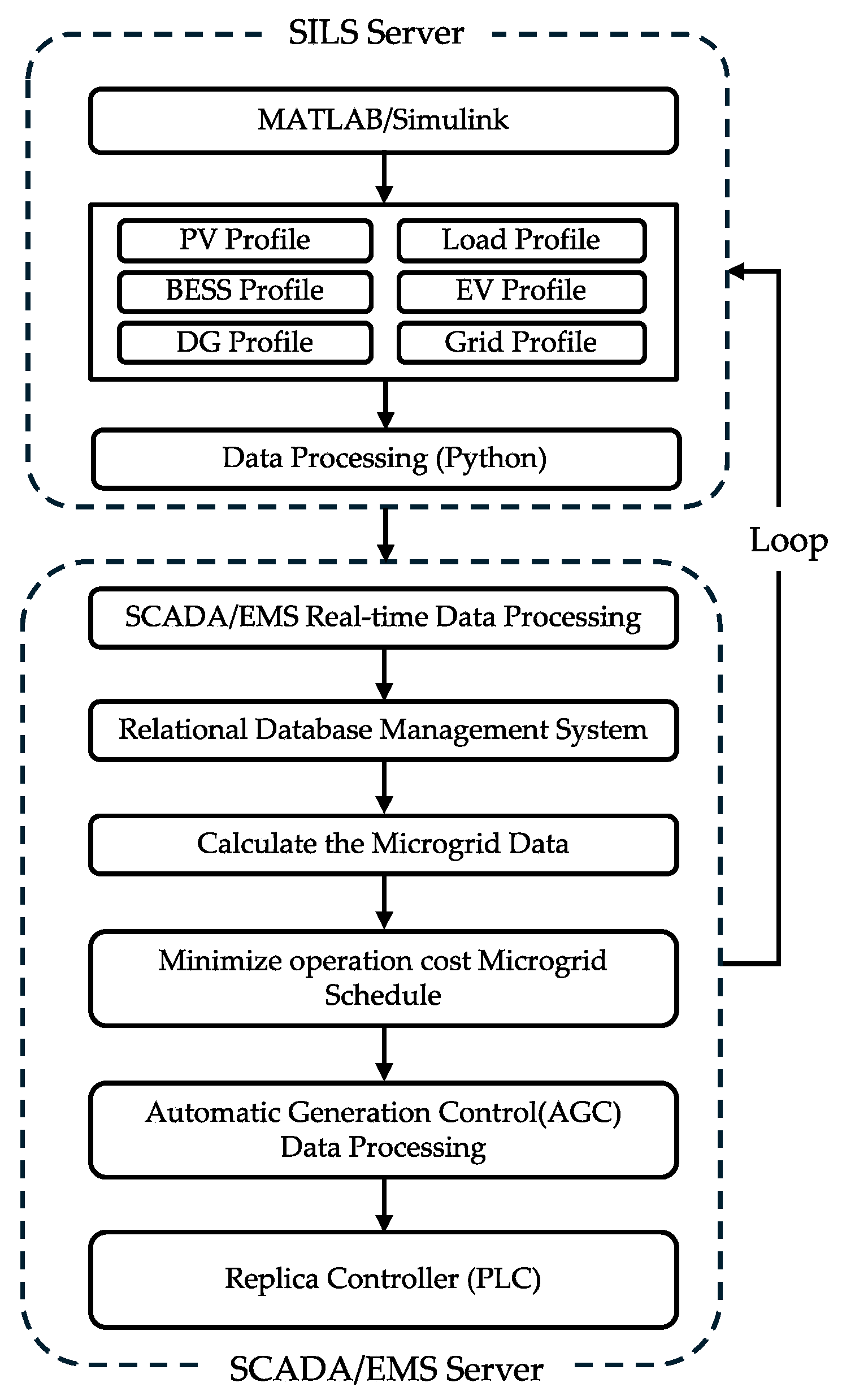
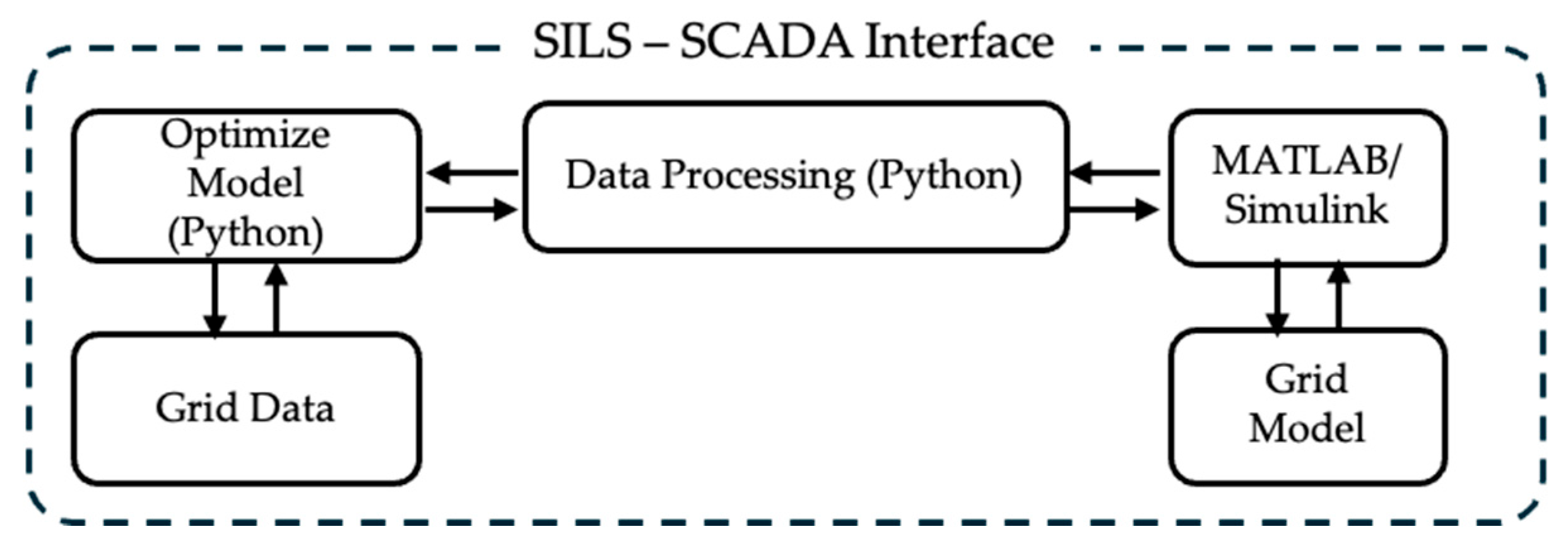
2.2. SILS (Software-in-the-Loop Simulation) Framework
2.3. Optimal Grid Operation Algorithm
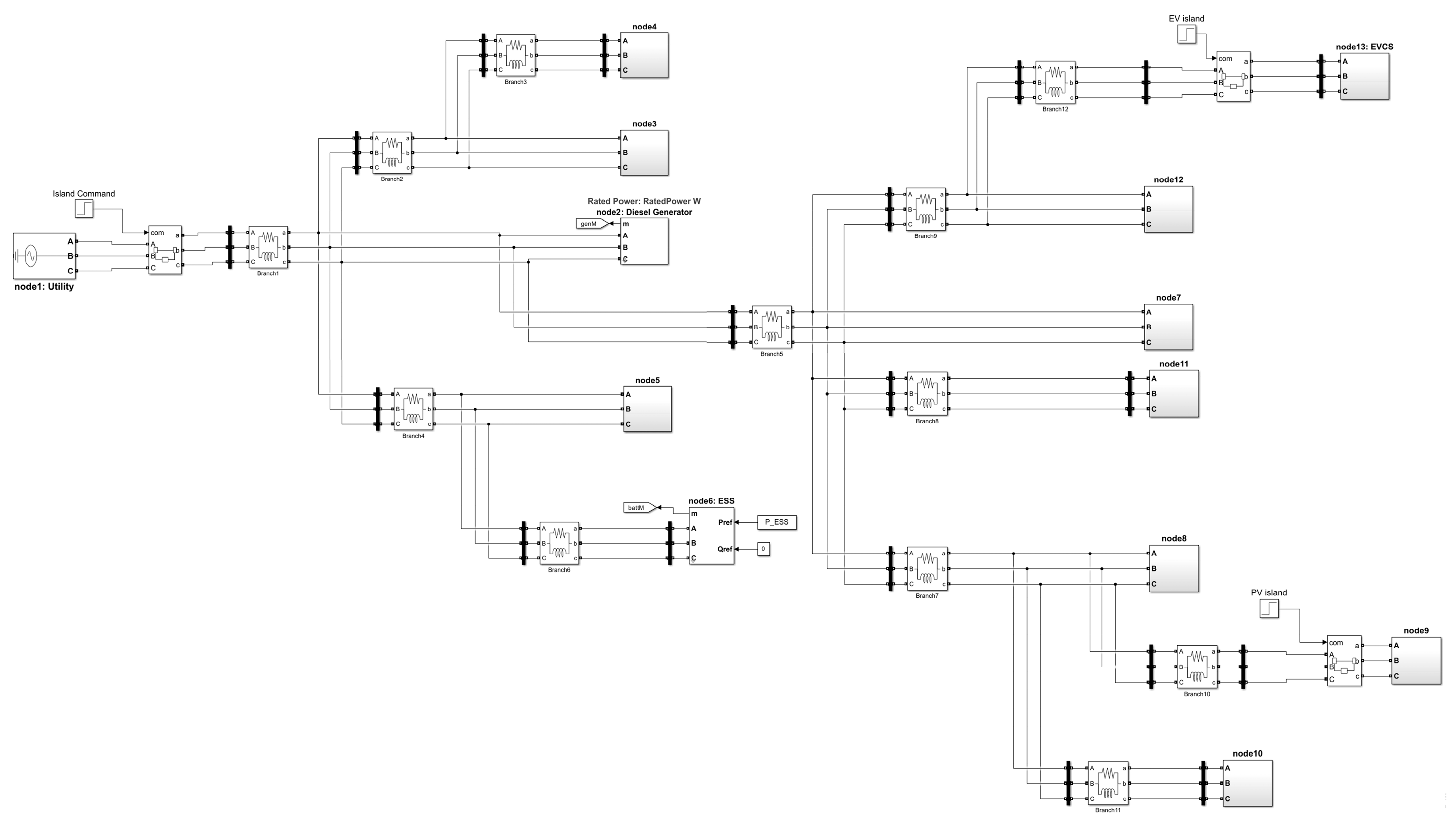
2.4. Grid Modeling
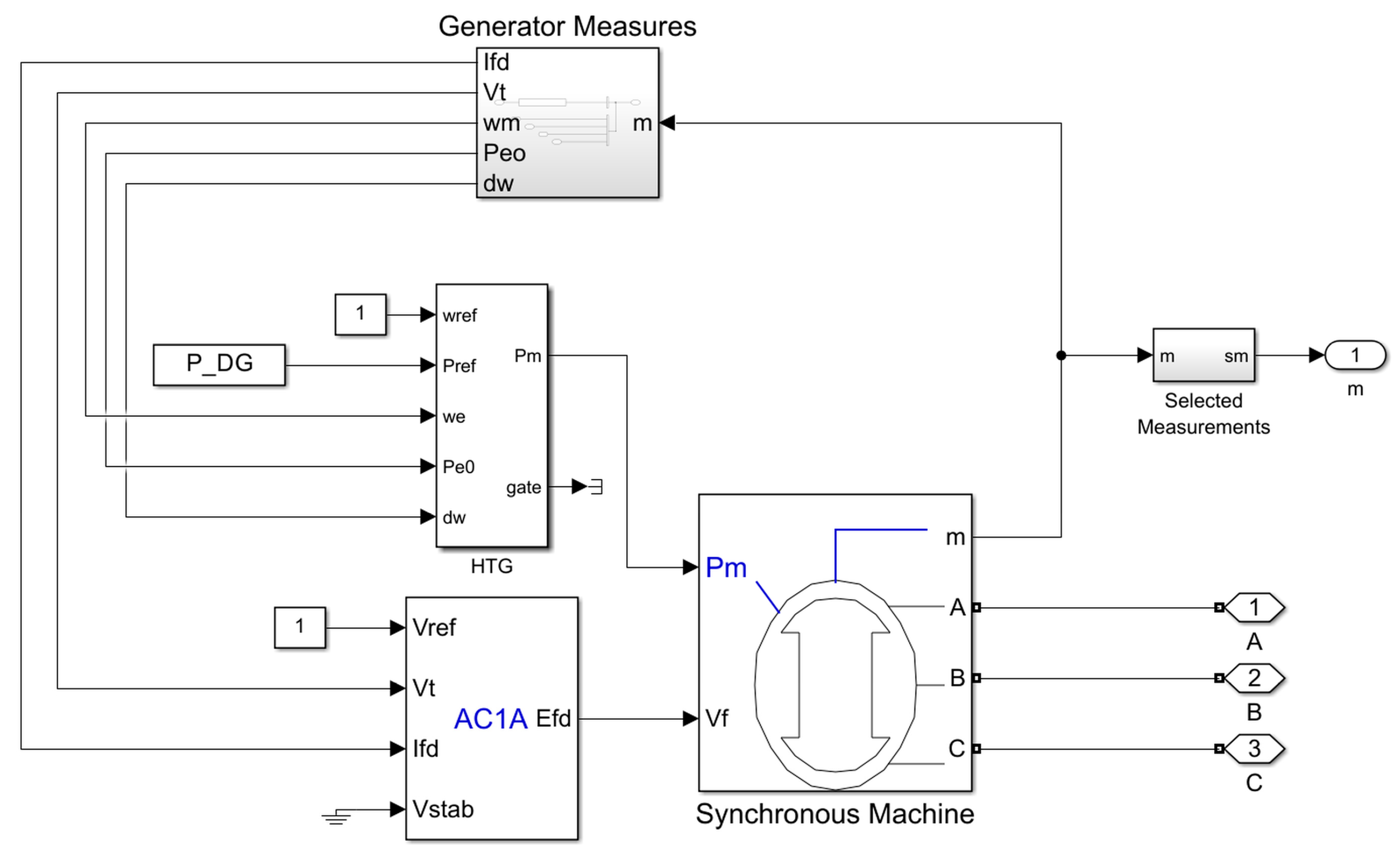
2.4.1. Diesel Generator Model
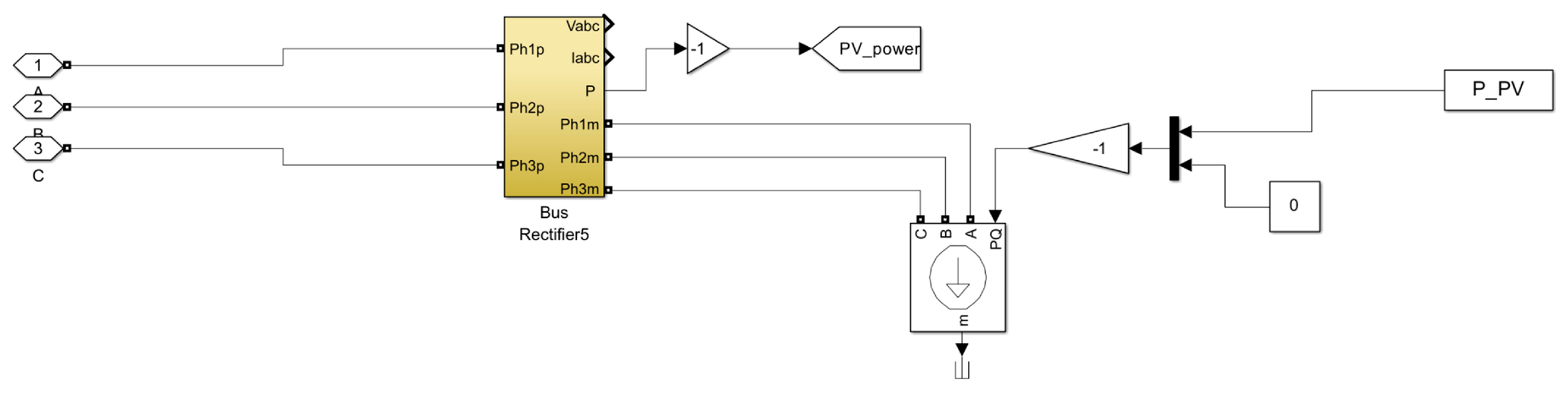
2.4.2. PV Generator Model
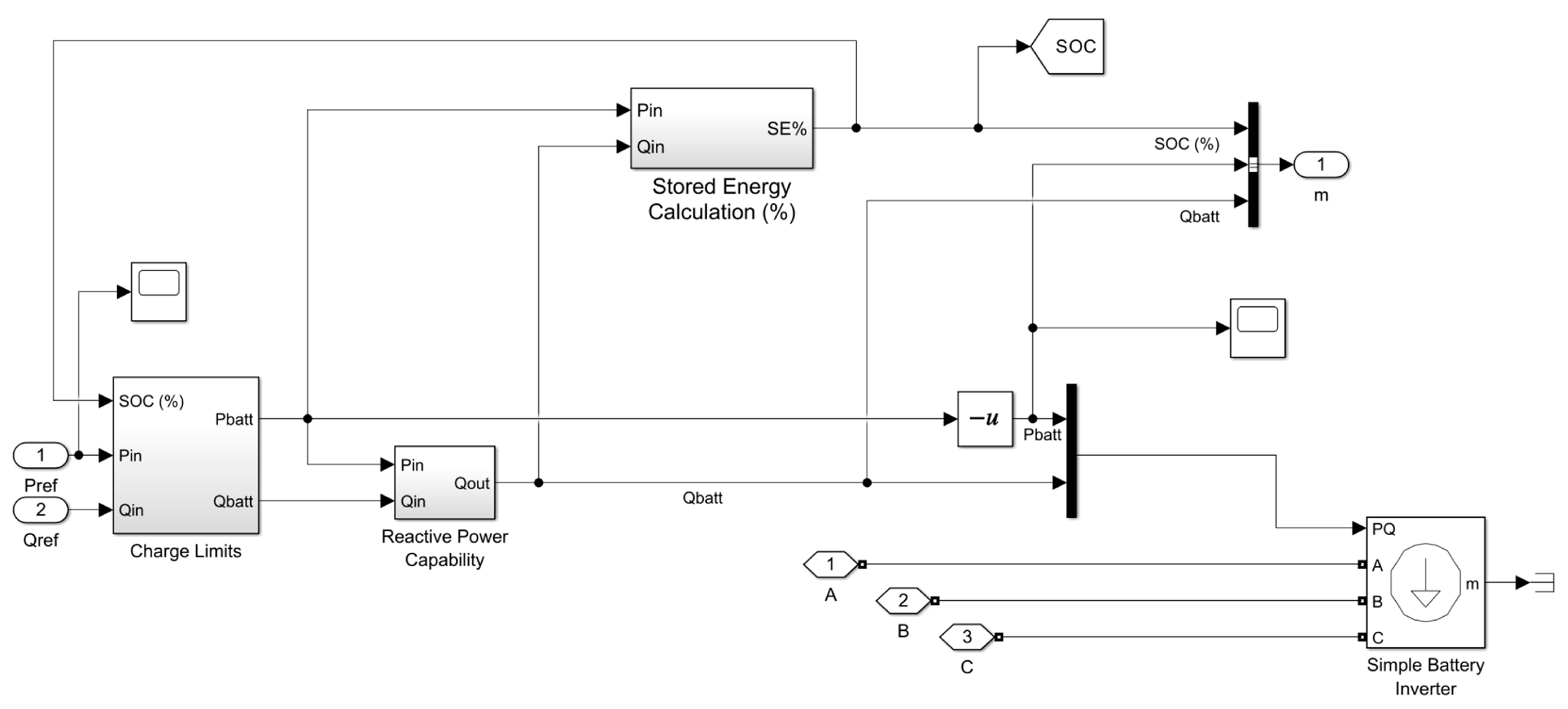
2.4.3. ESS Model
3. Results
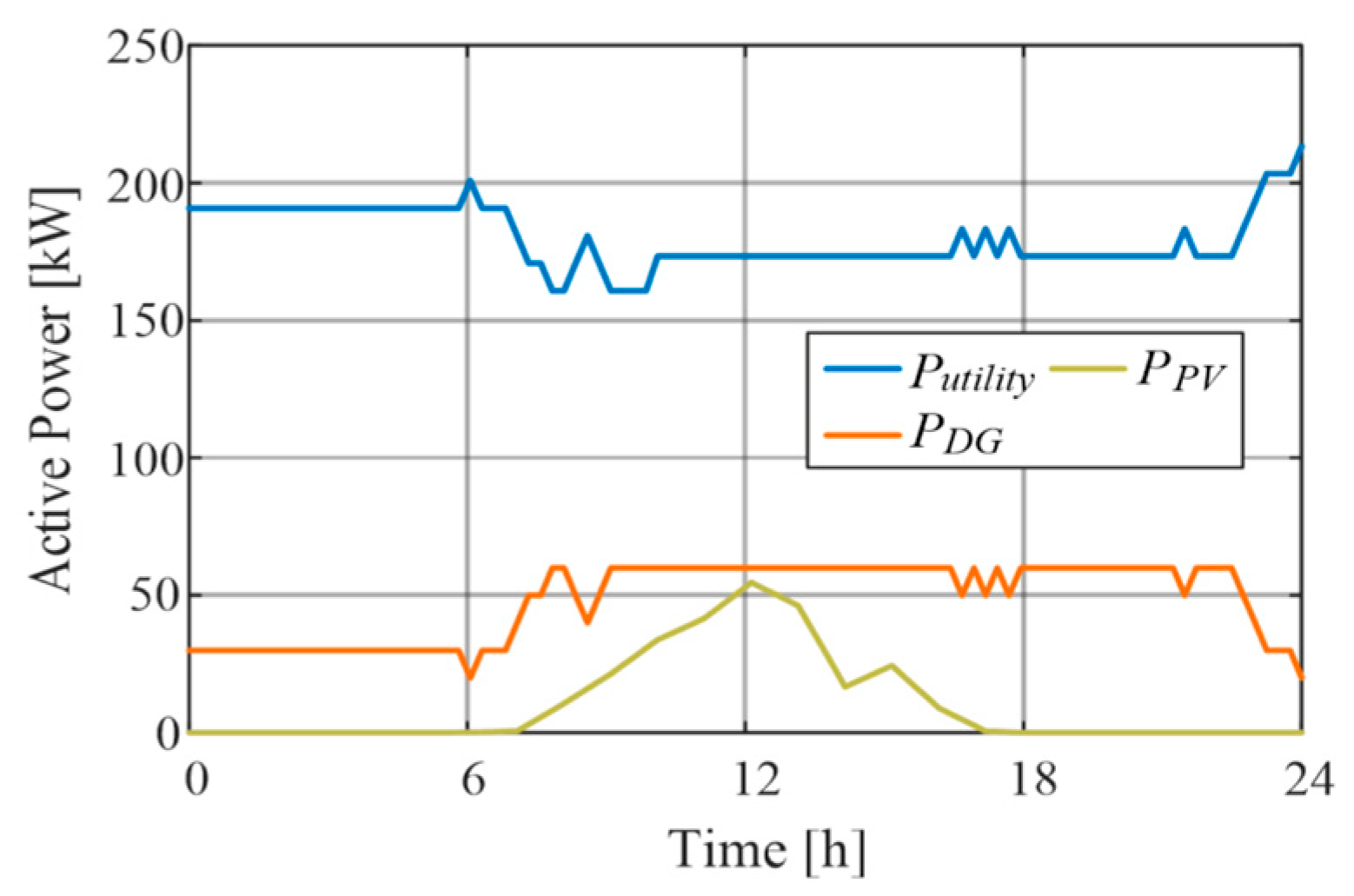
3.1. Optimal Grid Operation Algorithm Simulation
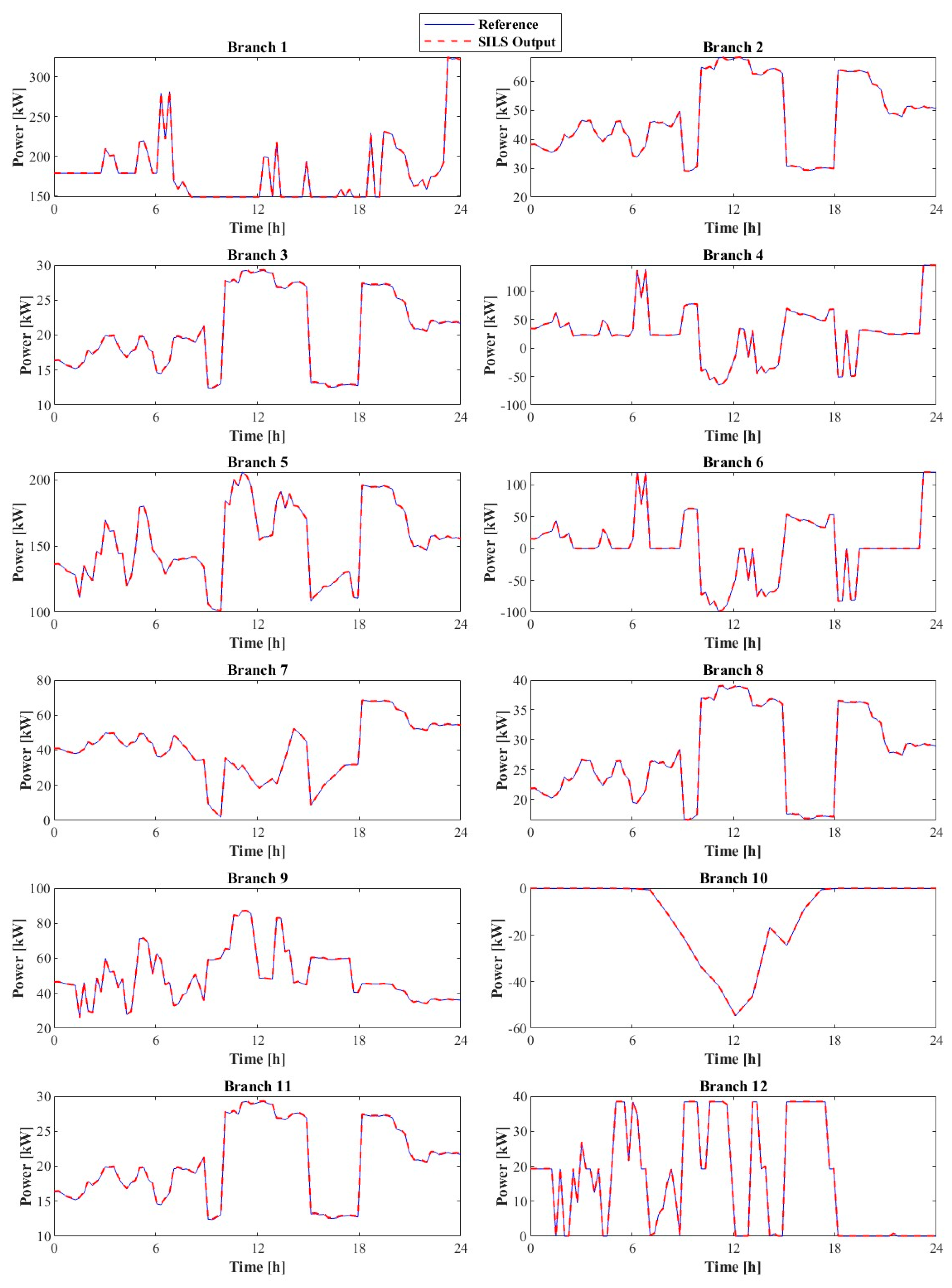
3.2. Modeling Validation Results
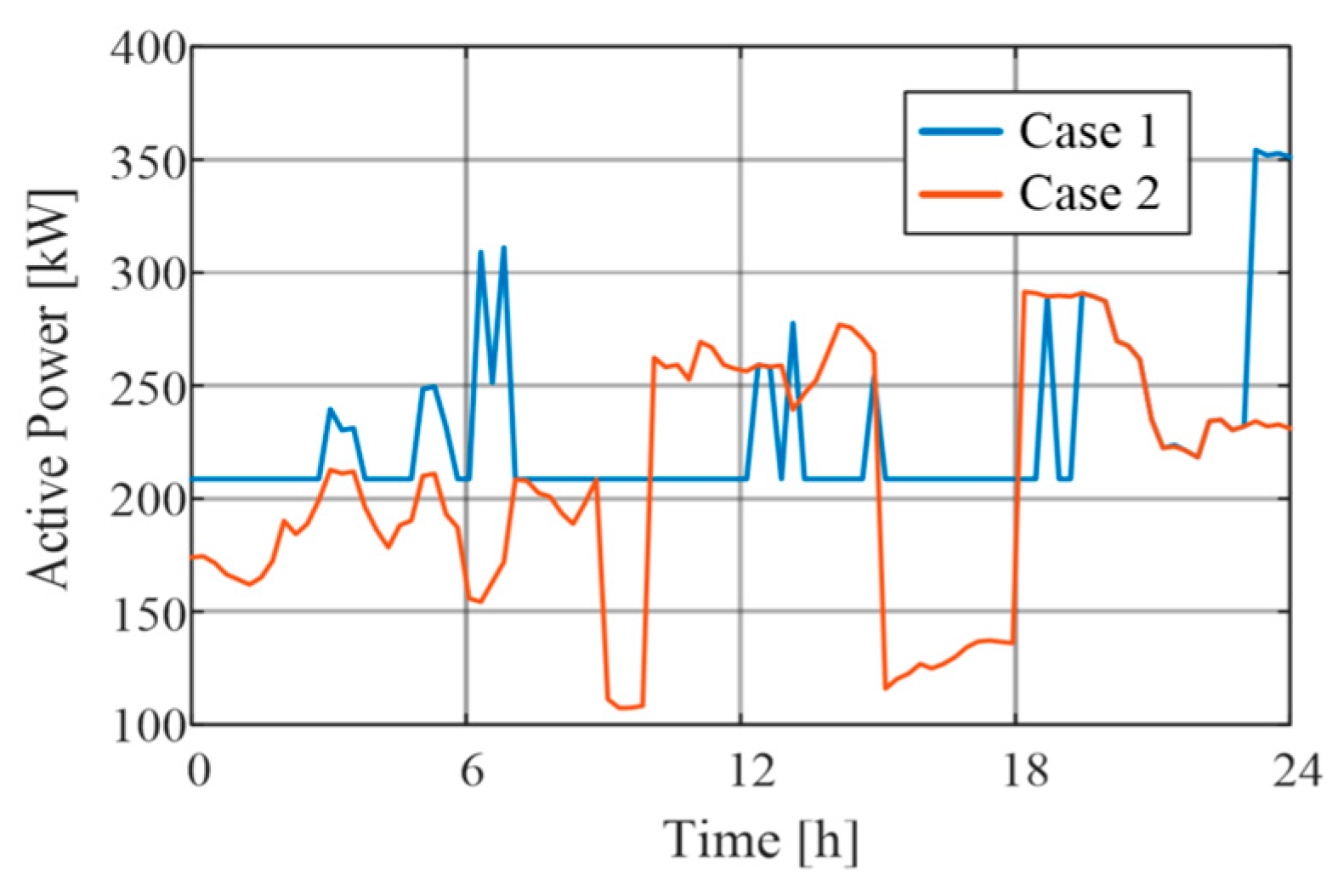
3.3. Case Study on Load Curve Flattening
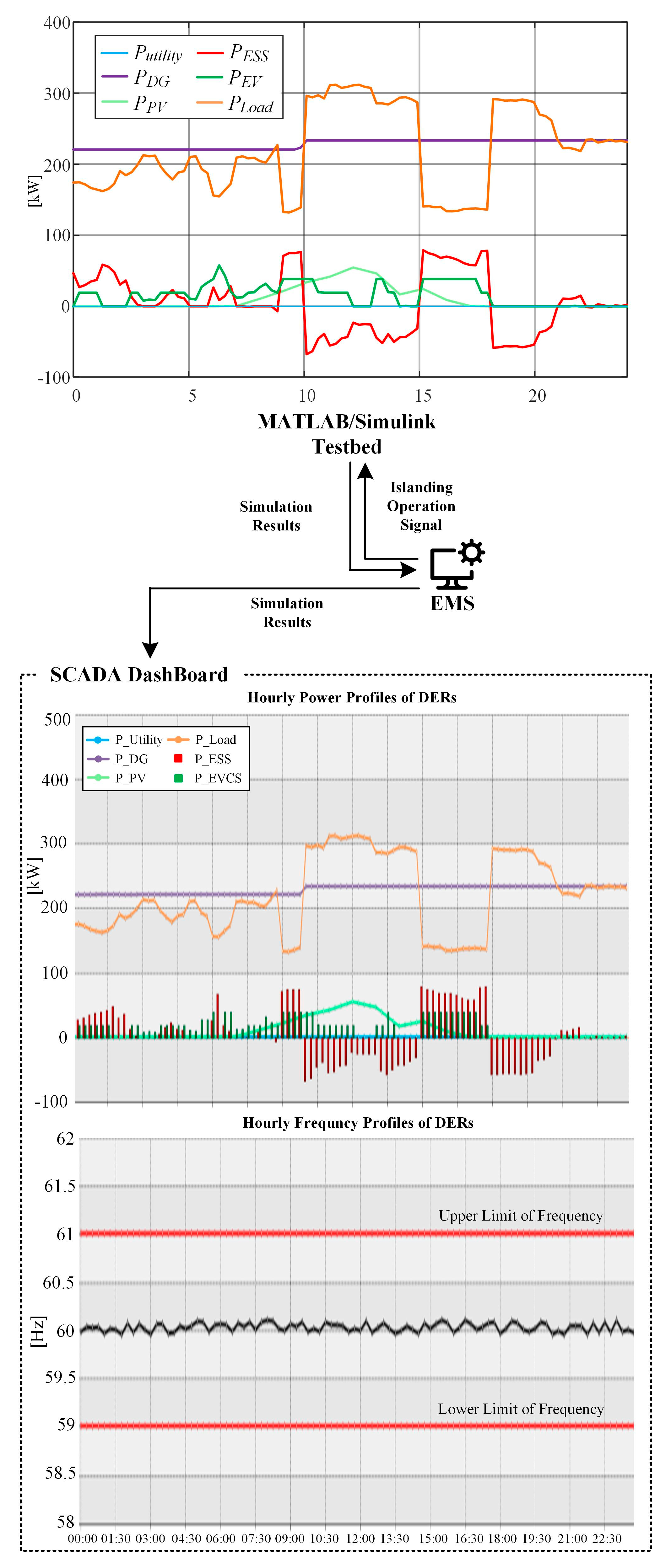
3.4. Case Study on Islanded Operation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| EMS | Energy Management System |
| ESS | Energy Storage System |
| BESS | Battery Energy Storage System |
| EVCS | Electric Vehicle Charging Station |
| DER | Distributed Energy Resources |
| SILS | Software-in-the-Loop Simulation |
| HILS | Hardware-in-the-Loop Simulation |
| SCADA | Supervisory Control and Data Acquisition |
| SOC | State of Charge |
| PQ | Active and Reactive Power Control |
| MILP | Mixed-Integer Linear Programming |
| API | Application Programming Interface |
| OPC-UA | Open Platform Communication Unified Architecture |
| R-MGC | Replica Microgrid Controller |
| PFC | Primary Frequency Control |
| SFC | Secondary Frequency Control |
| PCC | Point of Common Coupling |
| DG | Diesel Generator |
| PV | Photovoltaic |
| PLC | Programmable Logic Controller |
Nomenclature
| Symbols | Description |
| Power purchase from the grid at time t | |
| Section cost of diesel generator k at segment s and time t | |
| Binary variable for contracted power violation at time t | |
| Linearization coefficient for diesel generator k at section s | |
| Charging revenue at EVCS at time t | |
| State of charge of ESS n at time t | |
| Charging and discharging efficiency of ESS n | |
| Charging and discharging power of ESS n at time t | |
| Number of electric vehicles | |
| State of charge of EV at arrival (a) and departure (d) | |
| Bus voltage at node j | |
| Active and reactive power injection at bus j |
References
- Son, Y.; Woo, H.; Noh, J.; Dehghanian, P.; Zhang, X.; Choi, S. Optimization of energy storage scheduling considering variable-type minimum SOC for enhanced disaster preparedness. J. Energy Storage 2024, 93, 112366. [Google Scholar] [CrossRef]
- Clausen, C.S.B.; Jørgensen, B.N.; Ma, Z.G. A scoping review of In-the-loop paradigms in the energy sector focusing on software-in-the-loop. Energy Inform. 2024, 7, 12. [Google Scholar] [CrossRef]
- Vignati, M.; Debattisti, N.; Bacci, M.L.; Tarsitano, D. A Software-in-the-Loop Simulation of Vehicle Control Unit Algorithms for a Driverless Railway Vehicle. Appl. Sci. 2021, 11, 6730. [Google Scholar] [CrossRef]
- Kuntuarova, S.; Licklederer, T.; Huynh, T.; Zinsmeister, D.; Hamacher, T.; Perić, V. Design and simulation of district heating networks: A review of modeling approaches and tools. Energy 2024, 305, 132189. [Google Scholar] [CrossRef]
- Moustafa, A.M.; Abdelghany, M.B.; Younis, A.-S.A.; Moness, M.; Al-Durra, A.; Guerrero, J.M. Software-defined control of an emulated hydrogen energy storage for energy internet ecosystems. Int. J. Hydrog. Energy 2024, 50, 893–909. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Yang, G.; Nielsen, A.H.; Jensen, P.H. Hardware- and Software-in-the-Loop Simulation for Parameterizing the Model and Control of Synchronous Condensers. IEEE Trans. Sustain. Energy 2019, 10, 1593–1602. [Google Scholar] [CrossRef]
- Guerrero, C.A.V.; da Silveira, P.M.; Carvalho, J.M.; Bonatto, B.D.; Oliveira, D.Q.; Santos, M.; Marujo, D.; Zambroni, A.C.; Felver, L.A.; Oliveira, J.A.; et al. A new software-in-the-loop strategy for real-time testing of a coordinated Volt/Var Control. In Proceedings of the 2016 IEEE PES PowerAfrica, Livingstone, Zambia, 28 June–3 July 2016; pp. 6–10. [Google Scholar]
- Casolino, G.M.; AlizadehTir, M.; Andreoli, A.; Albanesi, M.; Marignetti, F. Software-in-the-loop simulation of a test system for automotive electric drives. In Proceedings of the IECON 2016-42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; pp. 1882–1887. [Google Scholar]
- Tan, R.H.G.; Tinakaran, G.K. Development of battery energy storage system model in MATLAB/Simulink. Int. J. Smart Grid Clean Energy 2020, 9, 180–188. [Google Scholar] [CrossRef]
- Faruque, M.D.O.; Strasser, T.; Lauss, G.; Jalili-Marandi, V.; Forsyth, P.; Dufour, C.; Dinavahi, V.; Monti, A.; Kotsampopoulos, P.; Martinez, J.A.; et al. Real-Time Simulation Technologies for Power Systems Design, Testing, and Analysis. IEEE Power Energy Technol. Syst. J. 2015, 2, 63–73. [Google Scholar] [CrossRef]
- Guillaud, X.; Faruque, M.O.; Teninge, A.; Hariri, A.H.; Vanfretti, L.; Paolone, M.; Dinavahi, V.; Mitra, P.; Lauss, G.; Dufour, C.; et al. Applications of Real-Time Simulation Technologies in Power and Energy Systems. IEEE Power Energy Technol. Syst. J. 2015, 2, 103–115. [Google Scholar] [CrossRef]
- JJeon, H.; Kim, J.-Y.; Kim, H.-M.; Kim, S.-K.; Cho, C.; Kim, J.-M.; Ahn, J.-B.; Nam, K.-Y. Development of Hardware In-the-Loop Simulation System for Testing Operation and Control Functions of Microgrid. IEEE Trans. Power Electron. 2010, 25, 2919–2929. [Google Scholar] [CrossRef]
- Gutiérrez-Escalona, J.; Roncero-Clemente, C.; González-Romera, E.; Milanés-Montero, M.I.; Husev, O.; Romero-Cadaval, E. PV-Battery Assisted Three-Level T-Type Inverter for AC Residential Nanogrid Realized With Small-Scale HIL Units. IEEE Access 2023, 11, 48007–48021. [Google Scholar] [CrossRef]
- Kotsampopoulos, P.; Lagos, D.; Hatziargyriou, N.; Faruque, M.O.; Lauss, G.; Nzimako, O.; Forsyth, P.; Steurer, M.; Ponci, F.; Monti, A.; et al. A Benchmark System for Hardware-in-the-Loop Testing of Distributed Energy Resources. IEEE Power Energy Technol. Syst. J. 2018, 5, 94–103. [Google Scholar] [CrossRef]
- Wang, J.; Song, Y.; Li, W.; Guo, J.; Monti, A. Development of a Universal Platform for Hardware In-the-Loop Testing of Microgrids. IEEE Trans. Ind. Inform. 2014, 10, 2154–2165. [Google Scholar] [CrossRef]
- Lin, F.J.; Liao, J.C.; Zhang, Y.M.; Huang, Y.C. Optimal Economic Dispatch and Power Generation for Microgrid Using Novel Lagrange Multipliers-Based Method With HIL Verification. IEEE Syst. J. 2023, 17, 4533–4544. [Google Scholar] [CrossRef]
- Bonassi, F.; La Bella, A.; Fagiano, L.; Scattolini, R.; Zarrilli, D.; Almaleck, P. Software-in-the-loop testing of a distributed optimal scheduling strategy for microgrids’ aggregators. In Proceedings of the 2020 IEEE PES Innovative Smart Grid Technologies Europe (ISGT-Europe), The Hague, The Netherlands, 26–28 October 2020; pp. 985–989. [Google Scholar]
- Mütherig, M.; Puleo, G.; Zdrallek, M.; Schönbauer, A. Development of a software in the loop environment to control a microgrid. In Proceedings of the 7th International Hybrid Power Plants & Systems Workshop (HYB 2023), Hybrid Conference, Tórshavn, Faroe Islands, 23–24 May 2023; pp. 103–107. [Google Scholar]
- Lee, G.-H.; Park, J.-Y.; Ham, S.-J.; Kim, Y.-J. Comparative Study on Optimization Solvers for Implementation of a Two-Stage Economic Dispatch Strategy in a Microgrid Energy Management System. Energies 2020, 13, 1096. [Google Scholar] [CrossRef]
- Lambert, M.; Hassani, R. Diesel genset optimization in remote microgrids. Appl. Energy 2023, 340, 121036. [Google Scholar] [CrossRef]
- Rajashekaraiah, K.; Iurlaro, C.; Bruno, S.; De Carne, G. Modelling of 3-Phase p-q Theory-Based Dynamic Load for Real-Time Simulation. IEEE Open Access J. Power Energy 2023, 10, 654–664. [Google Scholar] [CrossRef]
- Hwang, J.S.; Kim, J.-S.; Song, H. Handling Load Uncertainty during On-Peak Time via Dual ESS and LSTM with Load Data Augmentation. Energies 2022, 15, 3001. [Google Scholar] [CrossRef]




| Study (Ref.) | EMS Integration | SCADA Interaction | Real-Time Capability | Modeling Scope | Notes |
|---|---|---|---|---|---|
| [6] | x | x | x | Basic power flow control only | No EMS or SCADA interface |
| [7] | x | x | x | PV–ESS configuration validation | Lacks dynamic operation |
| [8] | x | o | x | SILS–Python interface | No control strategy validation |
| [9] | o (HIL) | o | o (via HILS) | Diesel–PV–ESS control | Requires physical HIL hardware |
| [17] | o | x | x | SILS-based EMS scheduling | No dynamic or SCADA integration |
| [18] | x | o | x | Python–MATLAB–SCADA interfacing | No EMS or optimization |
| Proposed work | o | o | o (sub-minute) | Full EMS–SCADA–SILS loop with PV/ESS/EVCS | Functional real-time validation without HIL |
| Parameter | Value |
|---|---|
| Rated Power | 2000 kW |
| Rated Voltage | 4.16 kV |
| Rated Frequency | 60 Hz |
| Initial Output Power | 0.1 pu |
| Friction and Inertia Constants | 3.7, 1 (H, pole pairs) |
| Stator Resistance | 0.003 ohms |
| Reactances | = 1.305 and = 0.296 |
| Parameter | Value |
|---|---|
| Exciter Gain/Time Constant | = 1.0 and = 0.80 |
| Voltage Limits (, ) | 4.8 pu and 14.0 pu |
| Saturation Curve ()) | ) = 0.1 and ) = 0.03 |
| Demagnetizing Factor () | 0.38 |
| Rectifier Loading Factor () | 0.20 |
| Parameter | Value |
|---|---|
| Rated Capacity | 480 kWh |
| Rated Voltage | 4.16 kV |
| Rated Frequency | 60 Hz |
| Overall Efficiency | 90% |
| SOC Operating Range | 10–90% |
| SOC to Recharge Trigger | 18% |
| Case | Total Cost [KRW] |
|---|---|
| Case 1 | 1,290,093 |
| Case 2 | 1,570,235 |
| Reduction Rate [%] | 17.84 |
| Symbol | Definition | Formula |
|---|---|---|
| Load factor | Utilization efficiency of installed capacity | |
| Peak-to-Average Ratio | Inverse of the load factor | |
| Peak–Valley Gap | Spread of extreme loads |
| Metric | Case 1 (with ESS, EVCS) | Case 2 (Without ESS, EVCS) |
|---|---|---|
| Load factor | 0.6445 | 0.7159 |
| PAR (=) | 1.552 | 1.397 |
| Peak–Valley Gap [kW] | 145.61 | 184.14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.; Kim, Y.-J.; Choi, S. The Development of a MATLAB/Simulink-SCADA/EMS-Integrated Framework for Microgrid Pre-Validation. Energies 2025, 18, 2739. https://doi.org/10.3390/en18112739
Kim S, Kim Y-J, Choi S. The Development of a MATLAB/Simulink-SCADA/EMS-Integrated Framework for Microgrid Pre-Validation. Energies. 2025; 18(11):2739. https://doi.org/10.3390/en18112739
Chicago/Turabian StyleKim, Seonghyeon, Young-Jin Kim, and Sungyun Choi. 2025. "The Development of a MATLAB/Simulink-SCADA/EMS-Integrated Framework for Microgrid Pre-Validation" Energies 18, no. 11: 2739. https://doi.org/10.3390/en18112739
APA StyleKim, S., Kim, Y.-J., & Choi, S. (2025). The Development of a MATLAB/Simulink-SCADA/EMS-Integrated Framework for Microgrid Pre-Validation. Energies, 18(11), 2739. https://doi.org/10.3390/en18112739







