Impact of Passive Modifications on the Efficiency of Darrieus Vertical Axis Wind Turbines Utilizing the Kline-Fogleman Blade Design at the Trailing Edge
Abstract
1. Introduction
2. Case Study Description
3. Governing Equations and Numerical Setup
3.1. Fluid Mechanics Equations
3.2. Turbulence Modeling Equations
3.3. Turbine Mathematical Relations
3.4. Computational Domain
3.5. Boundary Conditions
3.6. Solver Settings
3.7. Grid Study
3.8. Time Step Size Study
3.9. CFD Model Validation
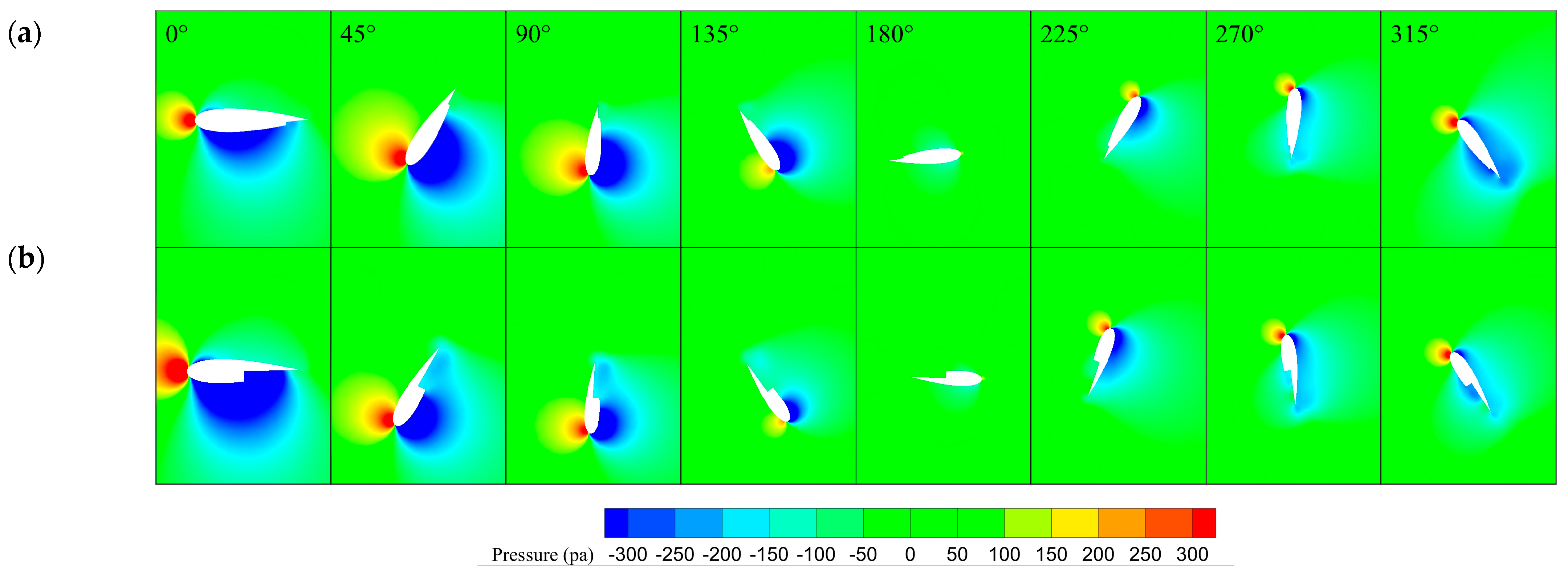
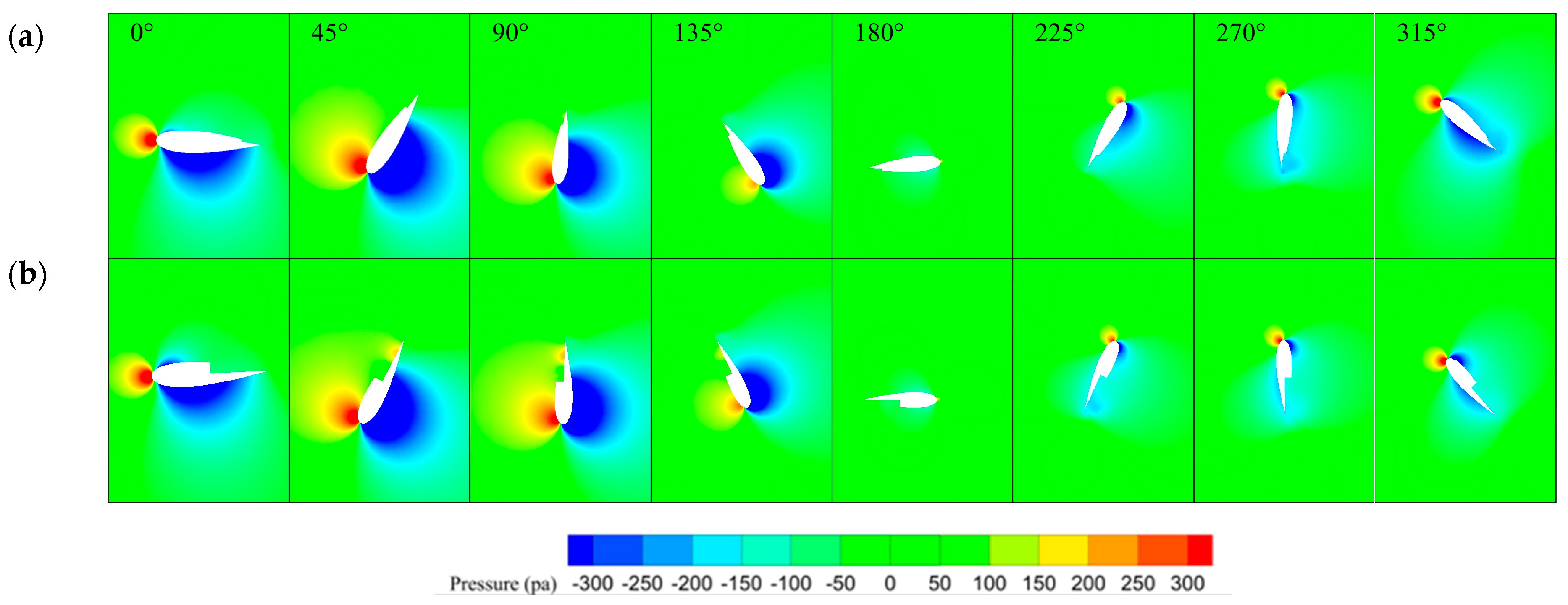
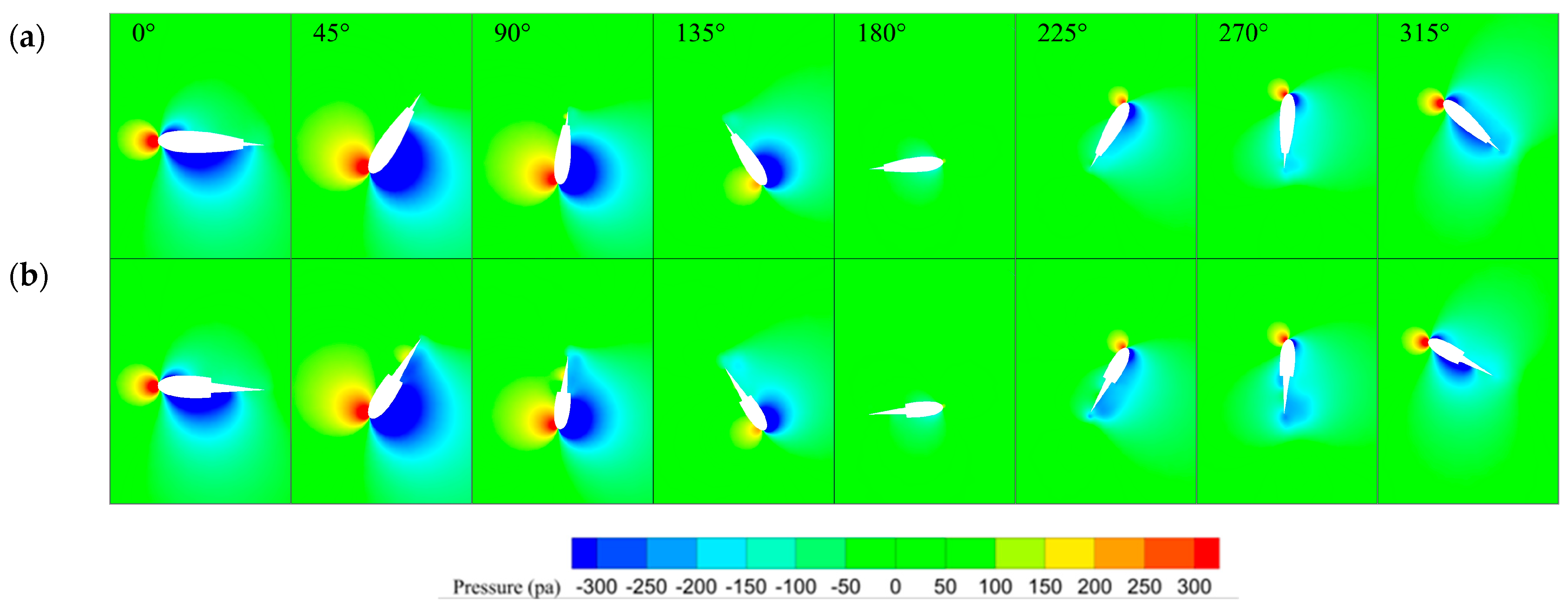
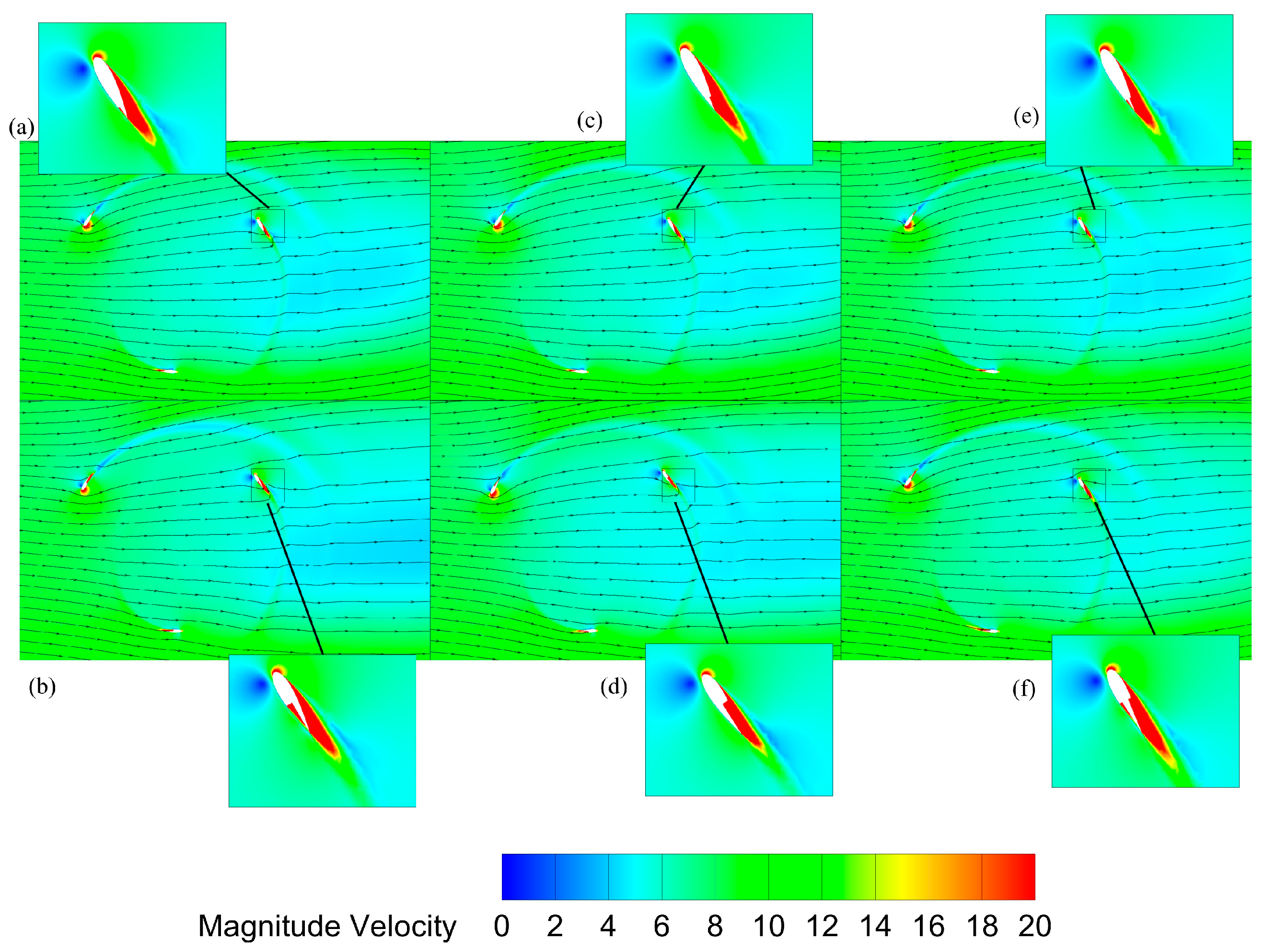
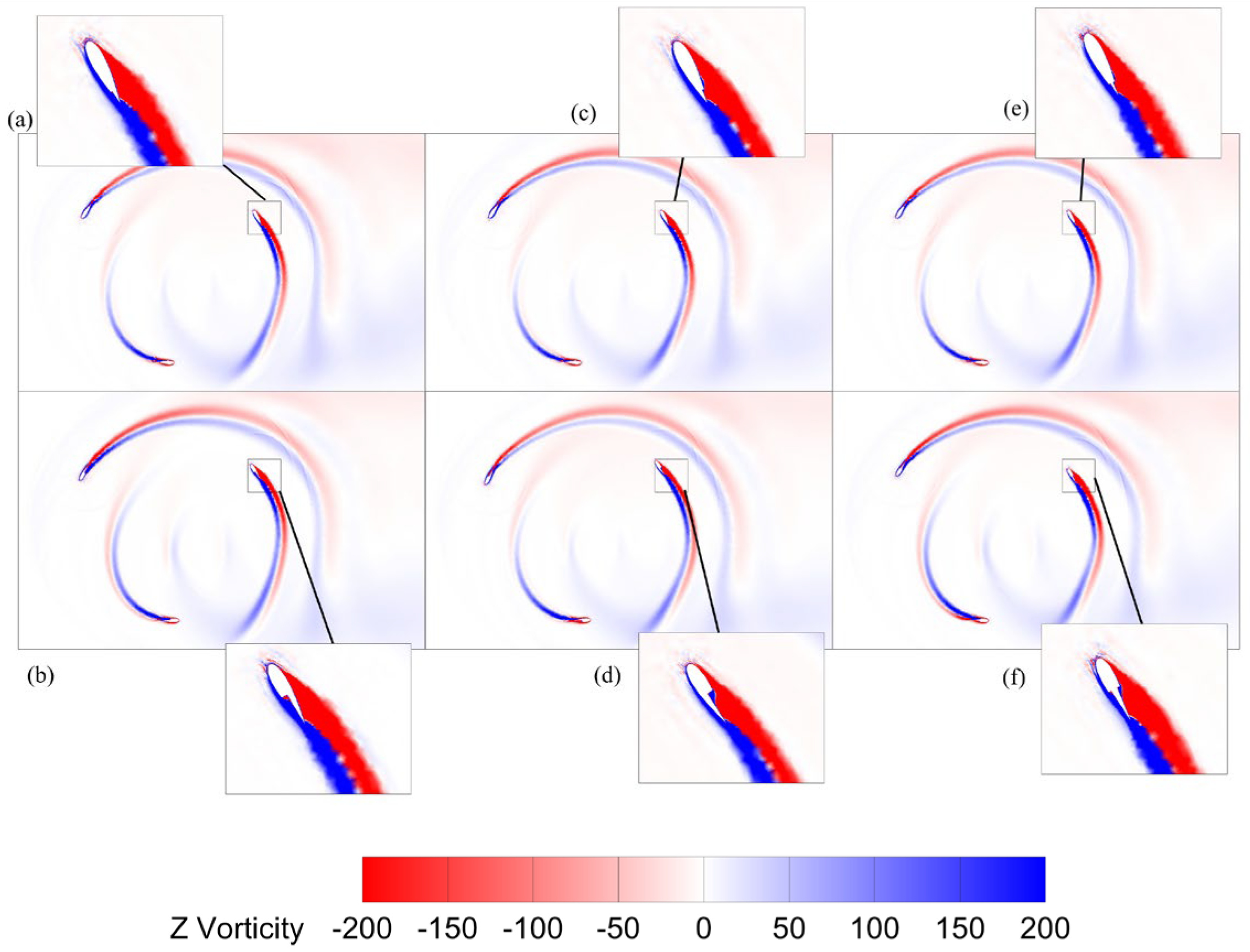
4. Results and Discussion
5. Conclusions
6. Further Study
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbols | Subscript | ||
| Inlet flow velocity (m/s) | t | Turbulence | |
| A | Swept Area (m2) | Abbreviations | |
| Torque (Nm) | VAWT | Vertical axis wind turbine | |
| Output power (W) | HAWT | Horizontal axis wind turbine | |
| Rotor radius (m) | CFD | Computational fluid dynamics | |
| Rotor height (m) | CFL | Courant number | |
| Rotor Diameter (m) | AoA | Angle of Attack | |
| Power coefficient | URANS | Unsteady Reynolds Averaged Navier Stokes | |
| Torque coefficient | TSR | Tip speed ratio | |
| Lift coefficient | KF | Kline–Fogleman | |
| Number of blades | SST | Shear stress transport | |
| Blade chord length | 2D | Two-dimensional | |
| Slot length (mm) | |||
| Slot depth (mm) | |||
| Greek | |||
| Azimuth angle (Degree) | |||
| Viscosity (Pas) | |||
| Angular velocity (rad/s) | |||
| Air density (kg/m3) | |||
| α | Angle of Attack (Degree) | ||
| Rotor solidity |
References
- Holechek, J.L.; Geli, H.M.E.; Sawalhah, M.N.; Valdez, R. A Global Assessment: Can Renewable Energy Replace Fossil Fuels by 2050? Sustainability 2022, 14, 4792. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, L.; Lu, J.; Zhang, X.; Wang, K.; Gan, Z.; Liu, X.; Jing, Z.; Cui, X.; Wang, H. Advances in urban wind resource development and wind energy harvesters. Renew. Sustain. Energy Rev. 2025, 207, 114943. [Google Scholar] [CrossRef]
- Shen, Z.; Gong, S.; Zuo, Z.; Chen, Y.; Guo, W. Darrieus vertical-axis wind turbine performance enhancement approach and optimized design: A review. Ocean. Eng. 2024, 311, 118965. [Google Scholar] [CrossRef]
- Selvarajoo, S.R.; Mohamed-Kassim, Z. The effects of dynamic stalls on the aerodynamics and performance of a Darrieus rotor during self-start. Phys. Fluids 2024, 36, 015143. [Google Scholar] [CrossRef]
- Redchyts, D.; Fernandez-Gamiz, U.; Tarasov, S.; Portal-Porras, K.; Tarasov, A.; Moiseienko, S. Comparison of aerodynamics of vertical-axis wind turbine with single and combine Darrieus and Savonius rotors. Results Eng. 2024, 24, 103202. [Google Scholar] [CrossRef]
- Abdolahifar, A.; Zanj, A. A review of available solutions for enhancing aerodynamic performance in Darrieus vertical-axis wind turbines: A comparative discussion. Energy Convers. Manag. 2025, 327, 119575. [Google Scholar] [CrossRef]
- Mohamed, O.S.; Ibrahim, A.A.; Etman, A.K.; Abdelfatah, A.A.; Elbaz, A.M.R. Numerical investigation of Darrieus wind turbine with slotted airfoil blades. Energy Convers. Manag. X 2020, 5, 100026. [Google Scholar] [CrossRef]
- Acarer, S. Peak lift-to-drag ratio enhancement of the DU12W262 airfoil by passive flow control and its impact on horizontal and vertical axis wind turbines. Energy 2020, 201, 117659. [Google Scholar] [CrossRef]
- Hosseini Rad, S.; Ghafoorian, F.; Taraghi, M.; Moghimi, M.; Ghoveisi Asl, F.; Mehrpooya, M. A systematic study on the aerodynamic performance enhancement in H-type Darrieus vertical axis wind turbines using vortex cavity layouts and deflectors. Phys. Fluids 2024, 36, 125170. [Google Scholar] [CrossRef]
- Javaid, M.T.; Sajjad, U.; Saddam ul Hassan, S.; Nasir, S.; Shahid, M.U.; Ali, A.; Salamat, S. Power enhancement of vertical axis wind turbine using optimum trapped vortex cavity. Energy 2023, 278, 127808. [Google Scholar] [CrossRef]
- Lee, K.-Y.; Cruden, A.; Ng, J.-H.; Wong, K.-H. Variable designs of vertical axis wind turbines—A review. Front. Energy Res. 2024, 12, 1437800. [Google Scholar] [CrossRef]
- Farzadi, R.; Zanj, A.; Bazargan, M. Effect of baffles on efficiency of darrieus vertical axis wind turbines equipped with J-type blades. Energy 2024, 305, 132305. [Google Scholar] [CrossRef]
- Naik, K.; Sahoo, N. Aerodynamic performance and starting torque enhancement of small-scale Darrieus type straight-bladed vertical axis wind turbines with J-shaped airfoil. J. Renew. Sustain. Energy 2024, 16, 033304. [Google Scholar] [CrossRef]
- Zereg, A.; Aksas, M.; Bouzaher, M.T.; Laghrouche, S.; Lebaal, N. Efficiency Improvement of Darrieus Wind Turbine Using Oscillating Gurney Flap. Fluids 2024, 9, 150. [Google Scholar] [CrossRef]
- Zhu, H.; Hao, W.; Li, C.; Luo, S.; Liu, Q.; Gao, C. Effect of geometric parameters of Gurney flap on performance enhancement of straight-bladed vertical axis wind turbine. Renew Energy 2021, 165, 464–480. [Google Scholar] [CrossRef]
- Eltayeb, W.A.; Somlal, J. Performance enhancement of Darrieus wind turbines using Plain Flap and Gurney Flap configurations: A CFD analysis. Results Eng. 2024, 24, 103400. [Google Scholar] [CrossRef]
- Chen, L.; Yang, P.; Zhang, B.; Chen, L. Aerodynamic Enhancement of Vertical-Axis Wind Turbines Using Plain and Serrated Gurney Flaps. Appl. Sci. 2023, 13, 12643. [Google Scholar] [CrossRef]
- Syawitri, T.P.; Yao, Y.; Yao, J.; Chandra, B. Drag reduction of lift-type Vertical axis wind turbine with slit modified Gurney flap. J. Wind. Eng. Ind. Aerodyn. 2024, 253, 105853. [Google Scholar] [CrossRef]
- Han, Z.; Chen, H.; Chen, Y.; Su, J.; Zhou, D.; Zhu, H.; Xia, T.; Tu, J. Aerodynamic performance optimization of vertical axis wind turbine with straight blades based on synergic control of pitch and flap. Sustain. Energy Technol. Assess. 2023, 57, 103250. [Google Scholar] [CrossRef]
- Seyhan, M.; Akbıyık, H. An experimental investigation on the flow control of the partially stepped NACA0012 airfoil at low Reynolds numbers. Ocean. Eng. 2024, 306, 118068. [Google Scholar] [CrossRef]
- Kabir, A.; Akib, Y.M.; Hasan, M.; Islam, M.J. Comparison of the aerodynamic performance of NACA 4415 and KFm based stepped airfoils. In AIP Conference Proceedings; AIP Publishing: Melville, NY, USA, 2021; Volume 2324. [Google Scholar]
- Akbıyık, H. The effect of cavity modified stepped geometry on aerodynamic performance of an airfoil at a low Reynolds number. Phys. Fluids 2025, 37, 047106. [Google Scholar] [CrossRef]
- Iddou, H.; Nait Bouda, N.; Benaissa, A.; Zereg, K. Numerical Analysis of the Kline and Fogleman Airfoil’s Effect on the Operation of Straight Darrieus Wind Turbine. J. Appl. Fluid Mech. 2024, 17, 1568–1592. [Google Scholar]
- Castelli, M.R.; Englaro, A.; Benini, E. The Darrieus wind turbine: Proposal for a new performance prediction model based on CFD. Energy 2011, 36, 4919–4934. [Google Scholar] [CrossRef]
- Sheidani, A.; Salavatidezfouli, S.; Stabile, G.; Rozza, G. Assessment of URANS and LES methods in predicting wake shed behind a vertical axis wind turbine. J. Wind Eng. Ind. Aerodyn. 2023, 232, 105285. [Google Scholar] [CrossRef]
- Menter, F.R. Review of the shear-stress transport turbulence model experience from an industrial perspective. Int. J. Comput. Fluid Dyn. 2009, 23, 305–316. [Google Scholar] [CrossRef]
- Meana-Fernández, A.; Fernández Oro, J.M.; Argüelles Díaz, K.M.; Velarde-Suárez, S. Turbulence-Model Comparison for Aerodynamic-Performance Prediction of a Typical Vertical-Axis Wind-Turbine Airfoil. Energies 2019, 12, 488. [Google Scholar] [CrossRef]
- Spalart, P.; Allmaras, S. A one-equation turbulence model for aerodynamic flows. In Proceedings of the 30th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1992; p. 439. [Google Scholar]
- Didane, D.H.; Rosly, N.; Zulkafli, M.F.; Shamsudin, S.S. Numerical investigation of a novel contra-rotating vertical axis wind turbine. Sustain. Energy Technol. Assess. 2019, 31, 43–53. [Google Scholar] [CrossRef]
- Moghimi, M.; Motawej, H. Developed DMST model for performance analysis and parametric evaluation of Gorlov vertical axis wind turbines. Sustain. Energy Technol. Assess. 2020, 37, 100616. [Google Scholar] [CrossRef]
- Bianchini, A.; Balduzzi, F.; Bachant, P.; Ferrara, G.; Ferrari, L. Effectiveness of two-dimensional CFD simulations for Darrieus VAWTs: A combined numerical and experimental assessment. Energy Convers. Manag. 2017, 136, 318–328. [Google Scholar] [CrossRef]
- Rezaeiha, A.; Kalkman, I.; Blocken, B. Effect of pitch angle on power performance and aerodynamics of a vertical axis wind turbine. Appl. Energy 2017, 197, 132–150. [Google Scholar] [CrossRef]
- Ghafoorian, F.; Enayati, E.; Mirmotahari, S.R.; Wan, H. Self-Starting Improvement and Performance Enhancement in Darrieus VAWTs Using Auxiliary Blades and Deflectors. Machines 2024, 12, 806. [Google Scholar] [CrossRef]
- Ghafoorian, F.; Hosseini Rad, S.; Moghimi, M. Enhancing Self-Starting Capability and Efficiency of Hybrid Darrieus–Savonius Vertical Axis Wind Turbines with a Dual-Shaft Configuration. Machines 2025, 13, 87. [Google Scholar] [CrossRef]
- Harris, M.J. Flow feature aligned mesh generation and adaptation. Ph.D. Thesis, University of Sheffield, Sheffield, UK, 2013. [Google Scholar]
- Lositaño, I.C.M.; Danao, L.A.M. Steady wind performance of a 5 kW three-bladed H-rotor Darrieus Vertical Axis Wind Turbine (VAWT) with cambered tubercle leading edge (TLE) blades. Energy 2019, 175, 278–291. [Google Scholar] [CrossRef]
- Marsh, P.; Ranmuthugala, D.; Penesis, I.; Thomas, G. The influence of turbulence model and two and three-dimensional domain selection on the simulated performance characteristics of vertical axis tidal turbines. Renew. Energy 2017, 105, 106–116. [Google Scholar] [CrossRef]
- Balduzzi, F.; Bianchini, A.; Ferrara, G.; Ferrari, L. Dimensionless numbers for the assessment of mesh and timestep requirements in CFD simulations of Darrieus wind turbines. Energy 2016, 97, 246–261. [Google Scholar] [CrossRef]
- Trivellato, F.; Castelli, M.R. On the Courant–Friedrichs–Lewy criterion of rotating grids in 2D vertical-axis wind turbine analysis. Renew. Energy 2014, 62, 53–62. [Google Scholar] [CrossRef]
- Raciti Castelli, M.; Ardizzon, G.; Battisti, L.; Benini, E.; Pavesi, G. Modeling Strategy and Numerical Validation for a Darrieus Vertical Axis Micro-Wind Turbine. In Proceedings of the IMECE2010, Vancouver, BC, Canada, 12–18 November 2010; Volume 7: Fluid Flow, Heat Transfer and Thermal Systems, Parts A and B, pp. 409–418. [Google Scholar]
- Chegini, S.; Asadbeigi, M.; Ghafoorian, F.; Mehrpooya, M. An investigation into the self-starting of darrieus-savonius hybrid wind turbine and performance enhancement through innovative deflectors: A CFD approach. Ocean. Eng. 2023, 287, 115910. [Google Scholar] [CrossRef]
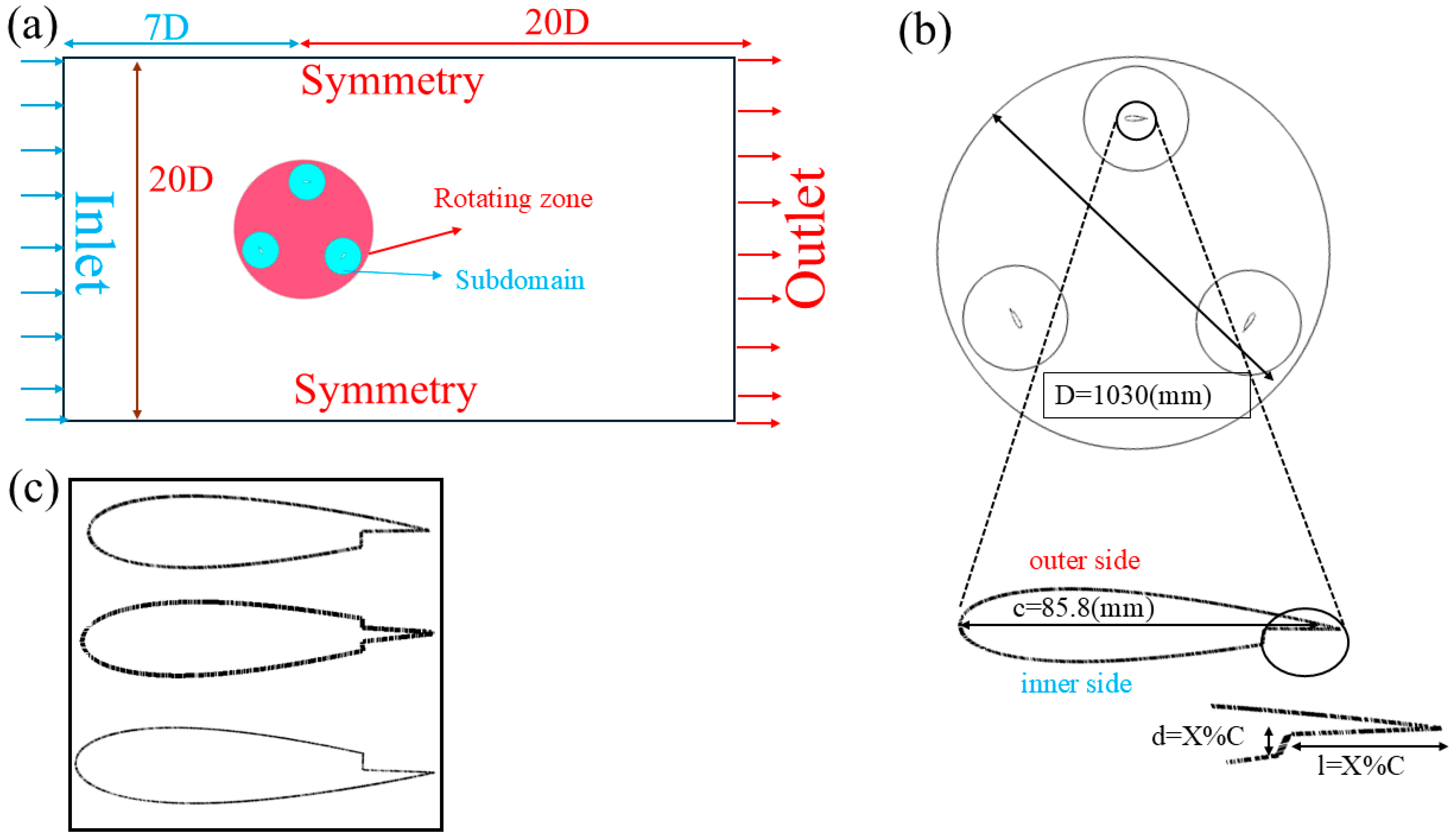
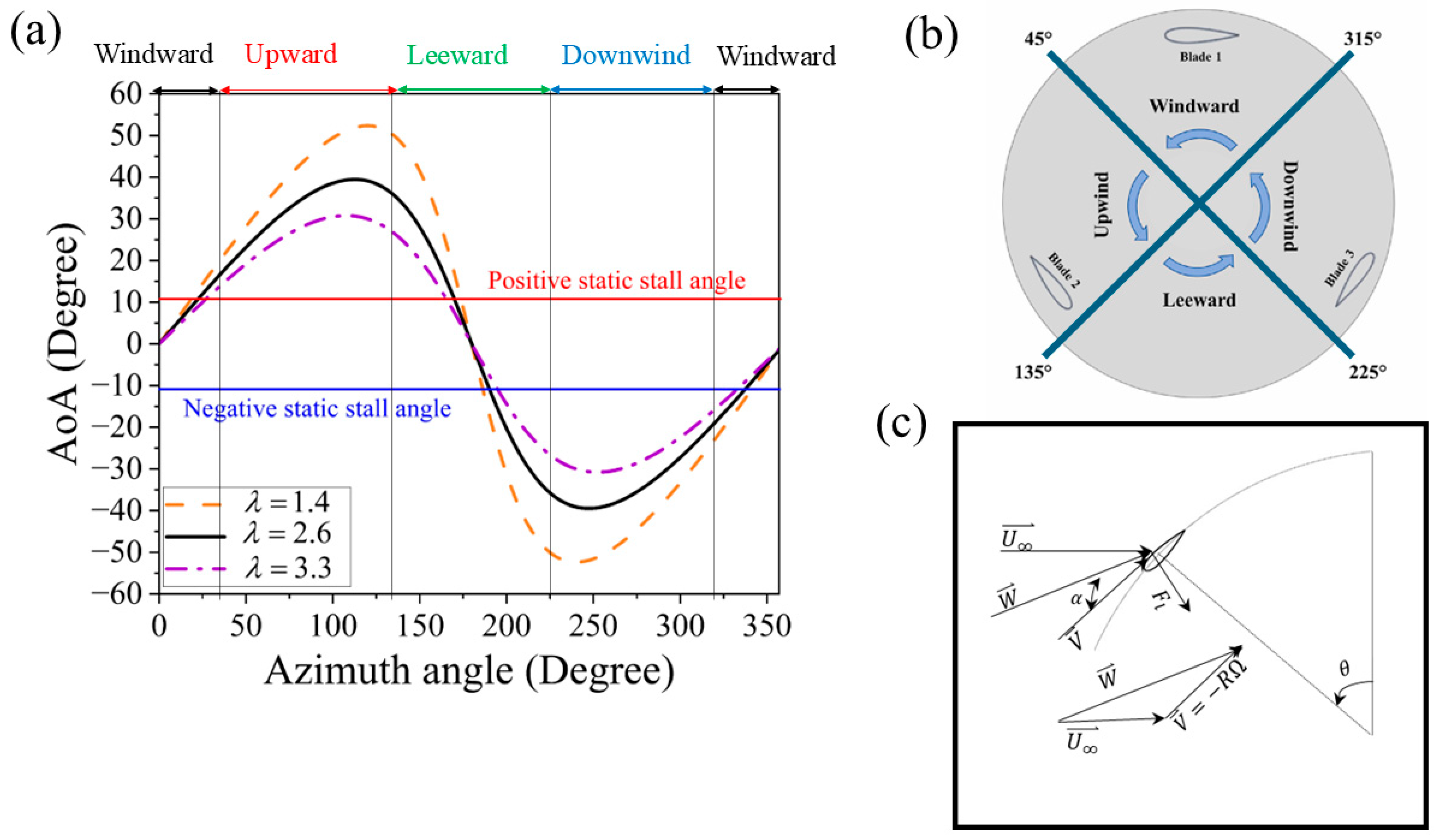
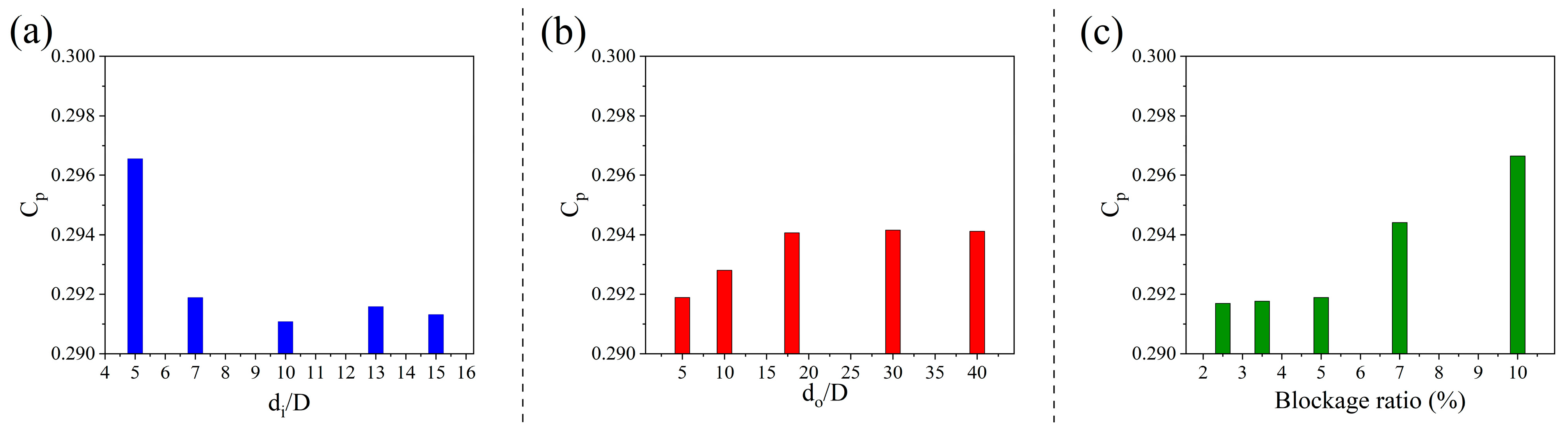

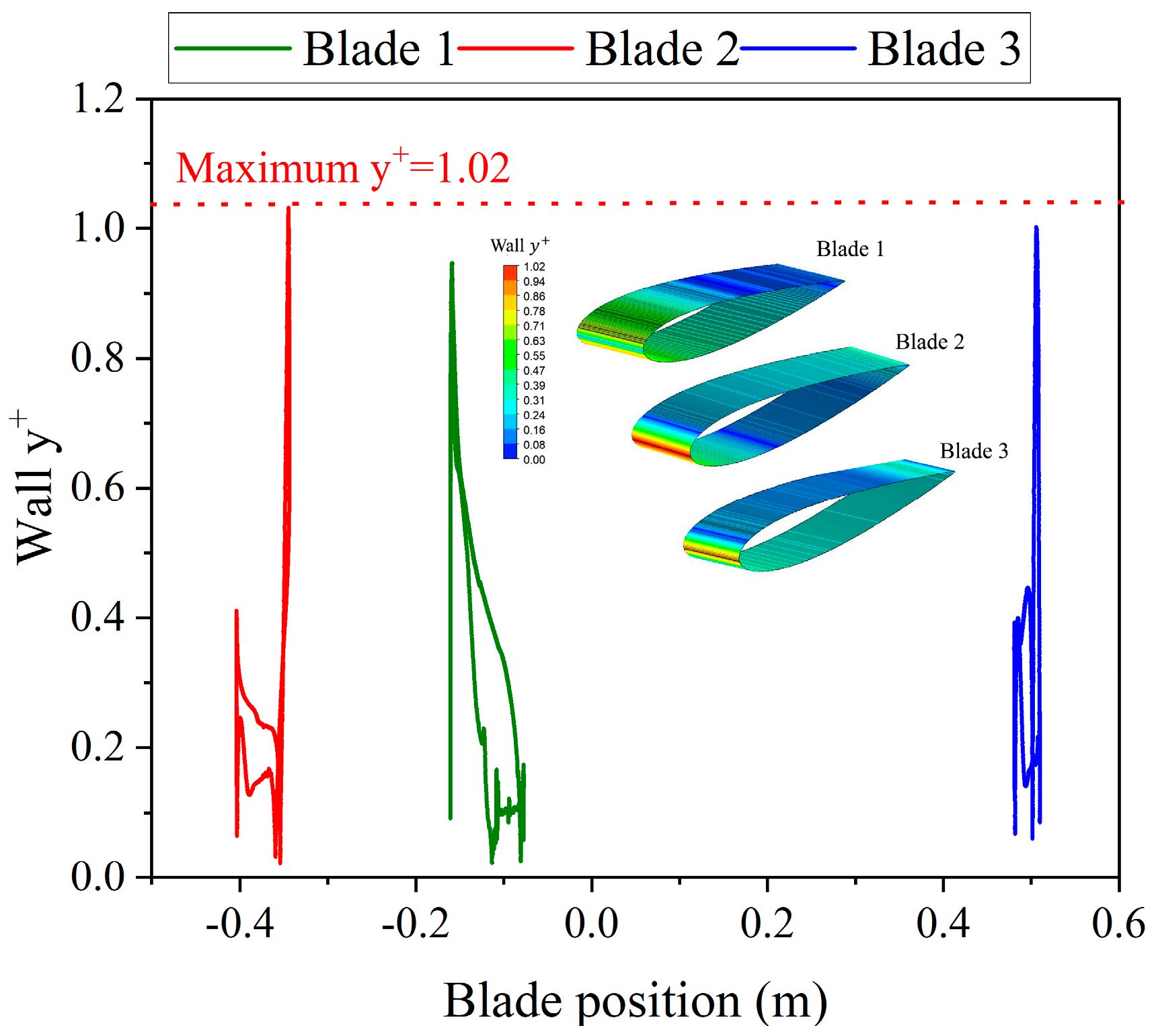
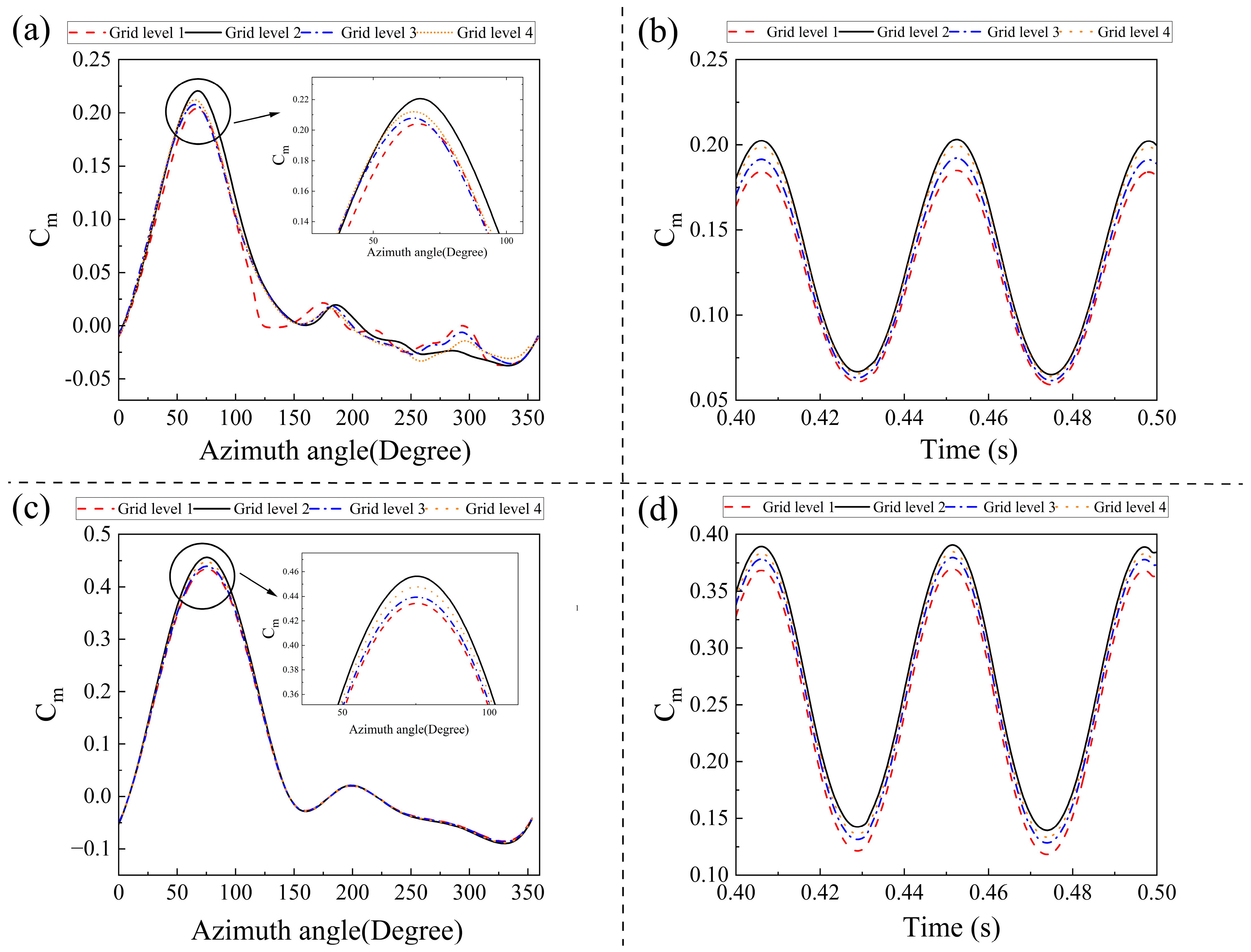

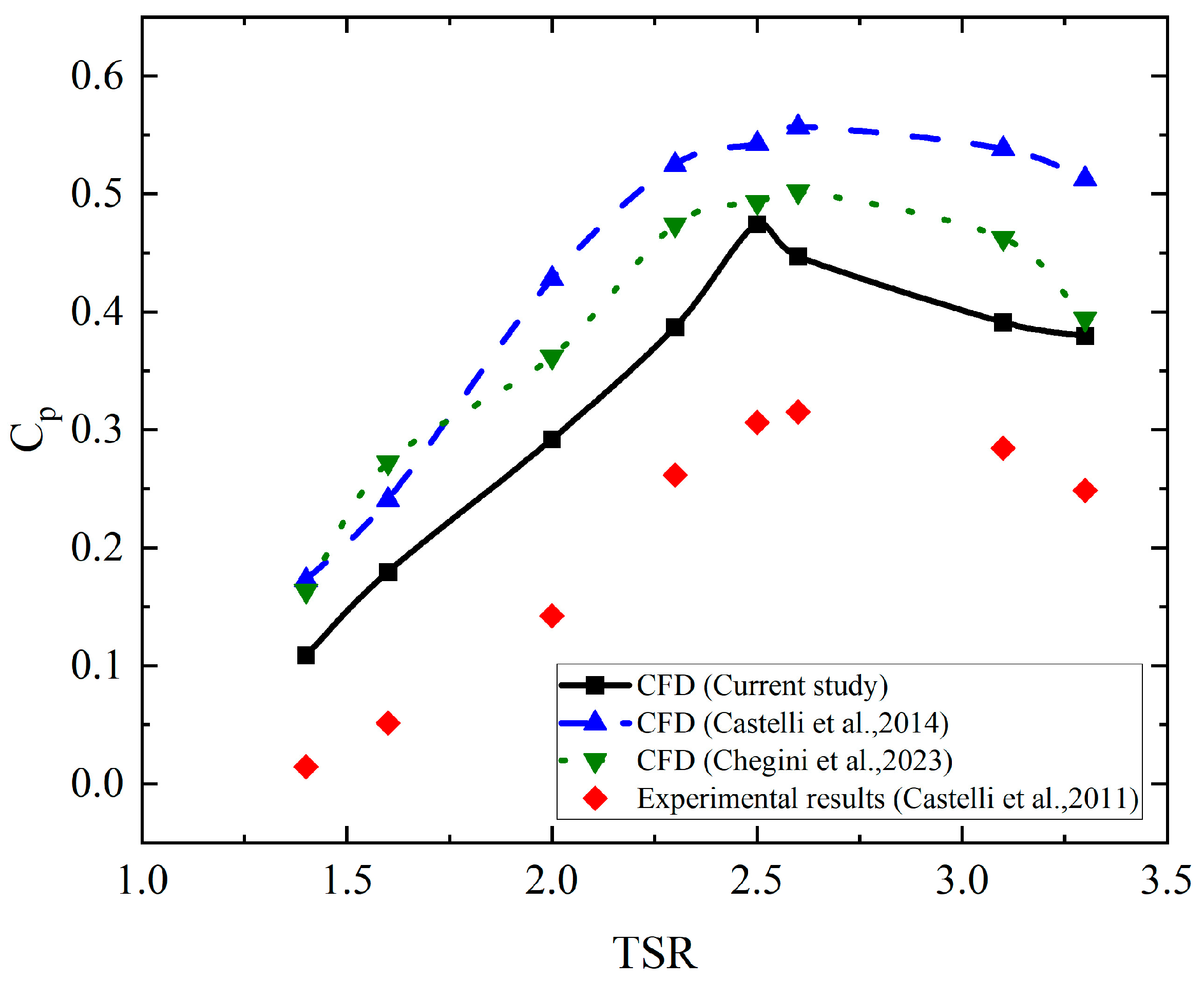

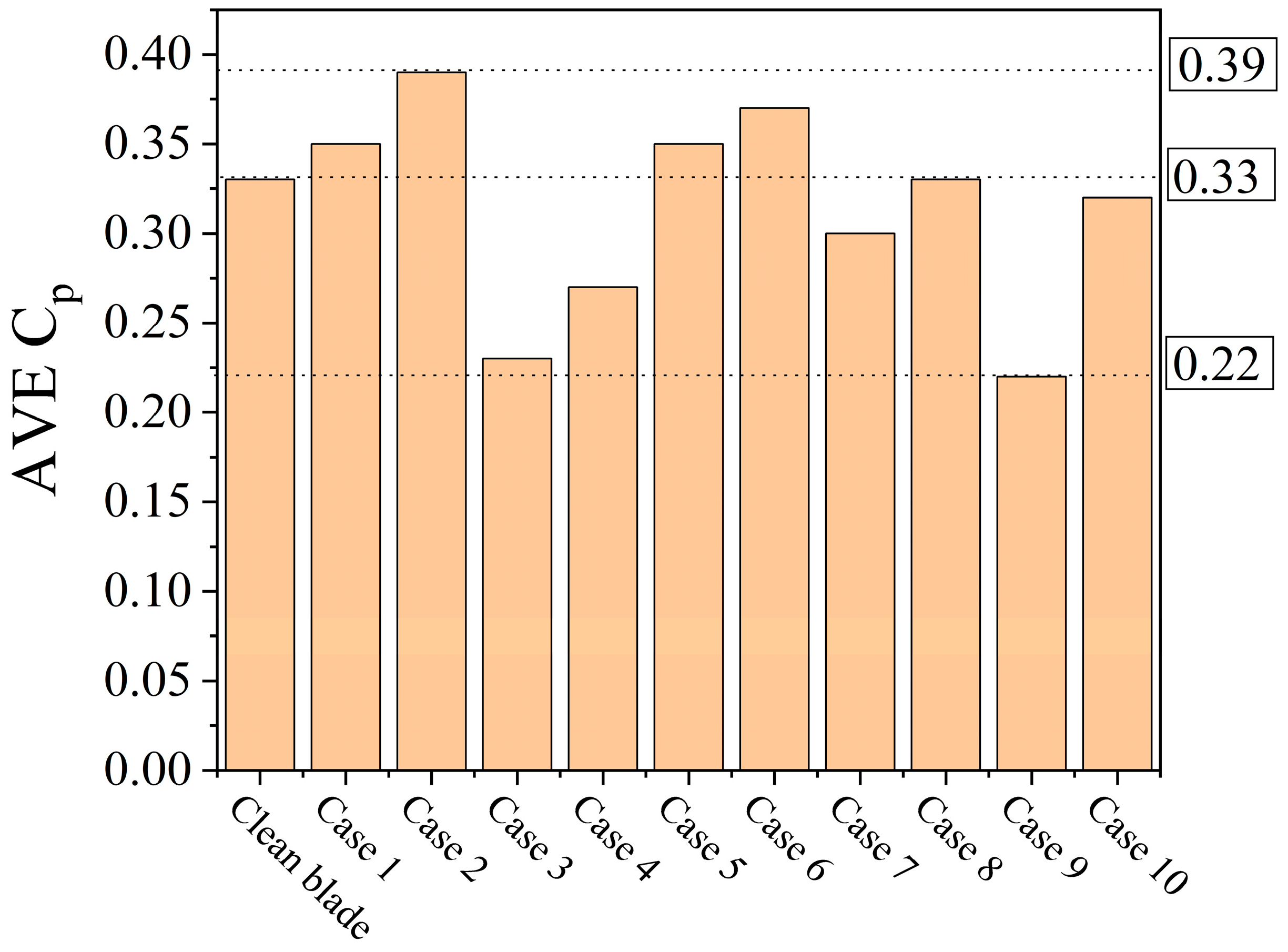
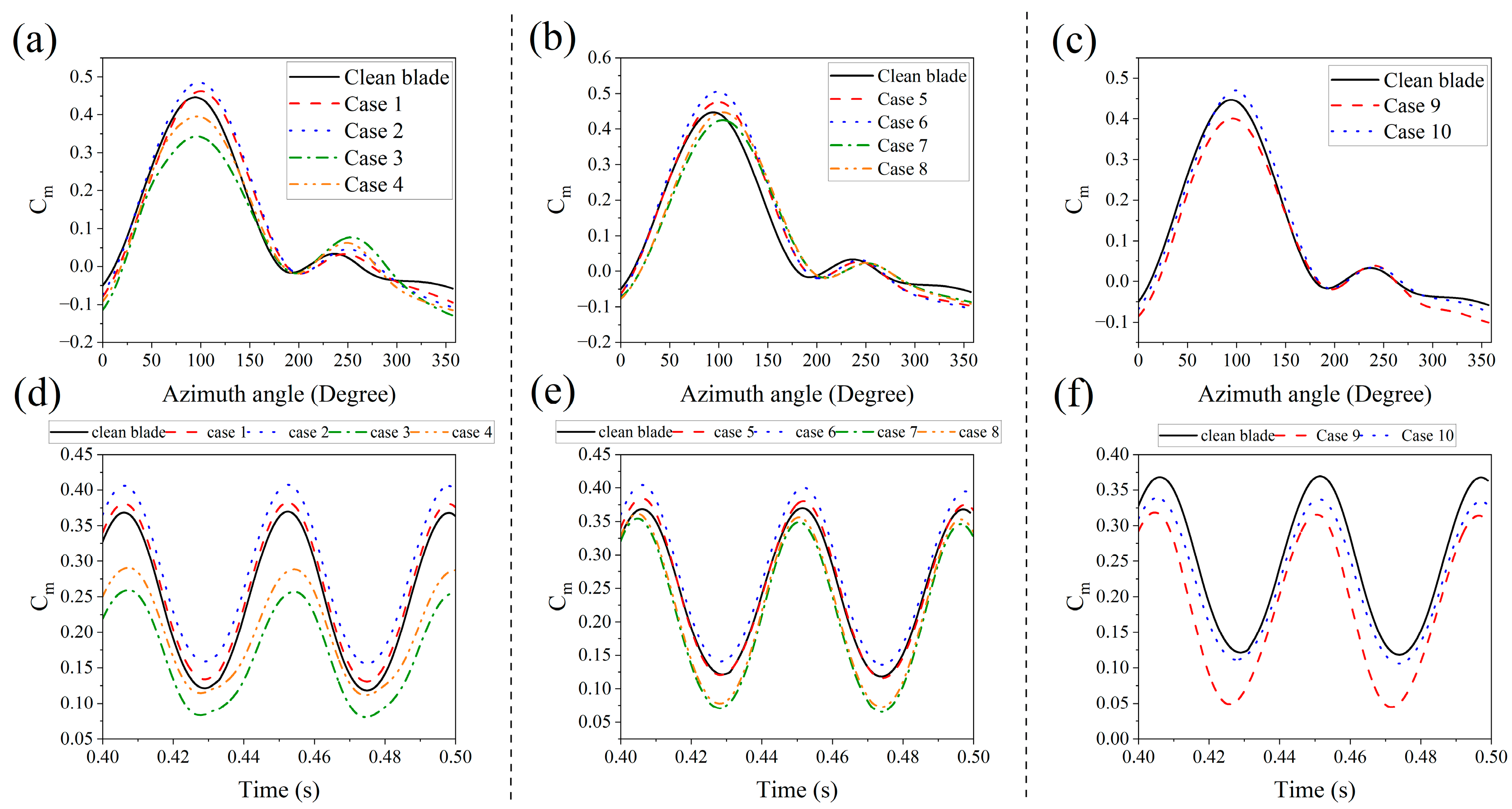

| Quantity | Value |
|---|---|
| Blade airfoil profile | NACA0021 |
| Blade chord length () | 85.8 (mm) |
| Rotor diameter () | 1030 (mm) |
| Rotor solidity | 0.5 |
| Number of blades | 3 |
| Case Number | Location | ||
|---|---|---|---|
| Case 1 | Inner side | 20% | 5% |
| Case 2 | Inner side | 20% | 2% |
| Case 3 | Inner side | 50% | 10% |
| Case 4 | Inner side | 50% | 5% |
| Case 5 | Outer side | 20% | 5% |
| Case 6 | Outer side | 20% | 2% |
| Case 7 | Outer side | 50% | 10% |
| Case 8 | Outer side | 50% | 5% |
| Case 9 | Both sides | 50% | 5% |
| Case 10 | Both sides | 20% | 2% |
| Grid Properties | Grid 1 | Grid 2 | Grid 3 | Grid 4 |
|---|---|---|---|---|
| Number of elements | 441 | 564 | 786 | 846 |
| Interface element size (mm) | 10 | 8 | 6 | 4 |
| Airfoil element size (mm) | 0.05 | 0.03 | 0.015 | 0.01 |
| Number of inflation layers | 12 | 14 | 16 | 18 |
| First layer thickness (mm) | 0.029 | 0.024 | 0.019 | 0.014 |
| Inflation growth rate | 1.2 | 1.15 | 1.1 | 1.05 |
| Maximum skewness | 0.946 | 0.979 | 0.969 | 0.984 |
| Averaged | 1.4 | 0.9 | 0.83 | 0.74 |
| 0.2918 | 0.2929 | 0.2939 | 0.2931 |
| TSR | (rad/s) | ||||||
|---|---|---|---|---|---|---|---|
| 2.5 Grid 1 | 2.1 Grid 2 | 1.7 Grid 3 | 1.3 Grid 4 | ||||
| 2 | 35.4 | 2 | 0.001 | 34 | 39.6 | 48.4 | 61.7 |
| 1 | 0.0005 | 17 | 19.8 | 24.2 | 30.8 | ||
| 0.5 | 0.00025 | 8.9 | 9.9 | 12.1 | 15.4 | ||
| 0.1 | 0.00005 | 1.7 | 2 | 2.4 | 3 | ||
| 3.3 | 57.3 | 2 | 0.0006 | 32.6 | 36.92 | 45.3 | 57.61 |
| 1 | 0.0003 | 16.3 | 18.5 | 22.6 | 28.8 | ||
| 0.5 | 0.00015 | 8.4 | 9.2 | 11.3 | 14.4 | ||
| 0.1 | 0.00003 | 1.7 | 1.8 | 2.2 | 2.9 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghafoorian, F.; Wan, H. Impact of Passive Modifications on the Efficiency of Darrieus Vertical Axis Wind Turbines Utilizing the Kline-Fogleman Blade Design at the Trailing Edge. Energies 2025, 18, 2718. https://doi.org/10.3390/en18112718
Ghafoorian F, Wan H. Impact of Passive Modifications on the Efficiency of Darrieus Vertical Axis Wind Turbines Utilizing the Kline-Fogleman Blade Design at the Trailing Edge. Energies. 2025; 18(11):2718. https://doi.org/10.3390/en18112718
Chicago/Turabian StyleGhafoorian, Farzad, and Hui Wan. 2025. "Impact of Passive Modifications on the Efficiency of Darrieus Vertical Axis Wind Turbines Utilizing the Kline-Fogleman Blade Design at the Trailing Edge" Energies 18, no. 11: 2718. https://doi.org/10.3390/en18112718
APA StyleGhafoorian, F., & Wan, H. (2025). Impact of Passive Modifications on the Efficiency of Darrieus Vertical Axis Wind Turbines Utilizing the Kline-Fogleman Blade Design at the Trailing Edge. Energies, 18(11), 2718. https://doi.org/10.3390/en18112718







