Flue Gas Temperature Distribution as a Function of Air Management in a High-Temperature Biomass Burner
Abstract
1. Introduction
- Low emissions of gaseous pollutants (CO, NOx);
- A sufficiently high flue gas temperature (minimum 1000 °C) to ensure proper heat transfer from the flue gases to the surface of the hot head of the Stirling engine (adequate heat flux density);
- Minimal variability in the flow rate and temperature of the flue gases exiting the burner;
- Unprocessed or minimally processed biomass as the fuel;
- Long operation time (degradation prevention).
- The development of a new biomass burner capable of achieving high flue gas temperatures (≥1000 °C) and suitable for coupling with micro-CHP systems based on Stirling engines;
- The use of a novel air supply system that enables both the preheating of combustion air and the partial cooling of the burner structure, thereby improving thermal efficiency and operational durability;
- The application of CFD modeling, validated in previous studies, to optimize the geometry and operational conditions of the burner for enhanced durability and minimized emissions.
2. Methods: Mathematical Modeling
- Release of H2O;
- Consumption of energy.
- Release of CH4;
- Release of CO2;
- Release of CO;
- Release of C6H6;
- Release of H2;
- Consumption of energy.
- Release of CO2;
- Release of CO;
- Consumption of O2;
- Consumption of energy.
3. Results
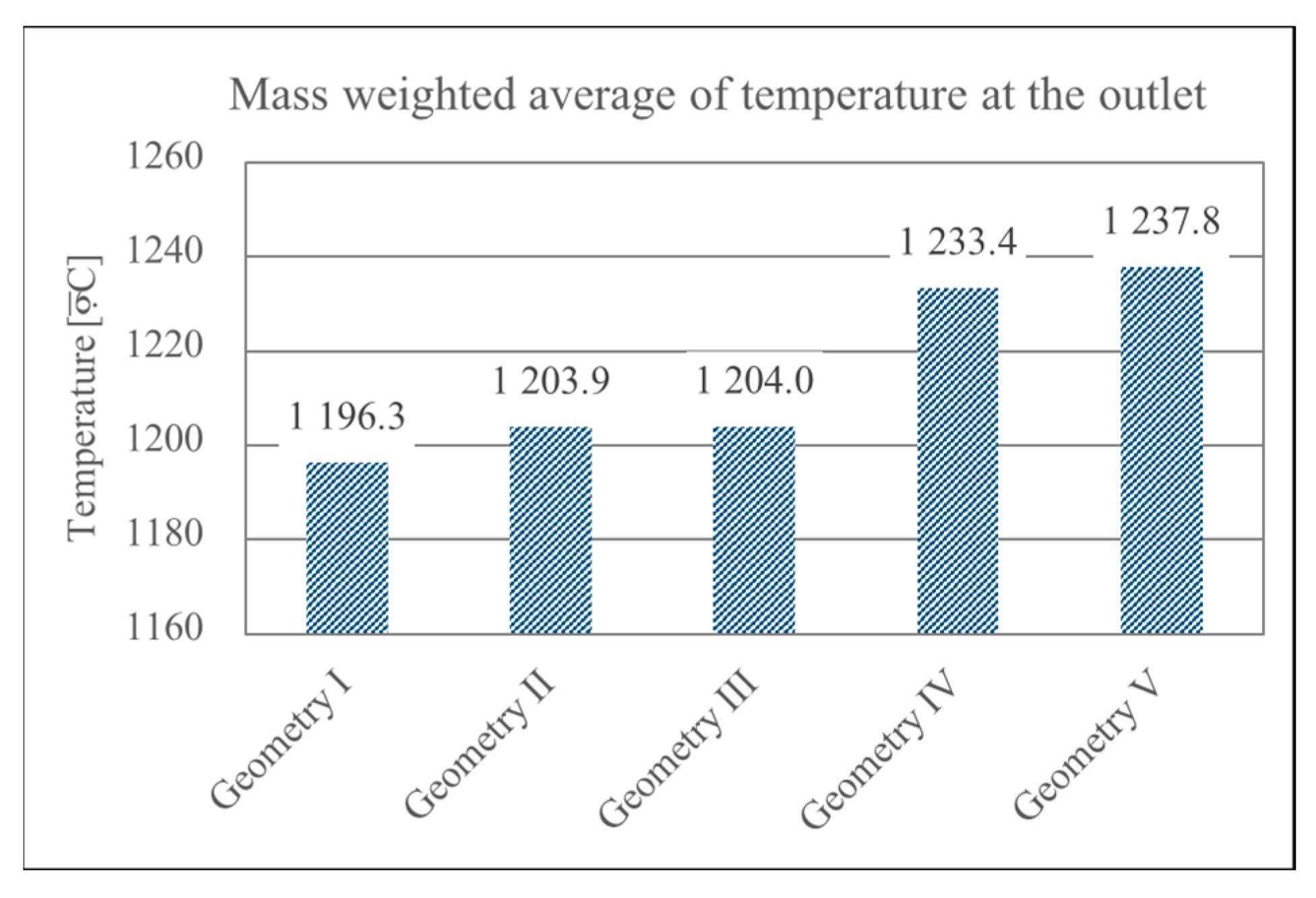
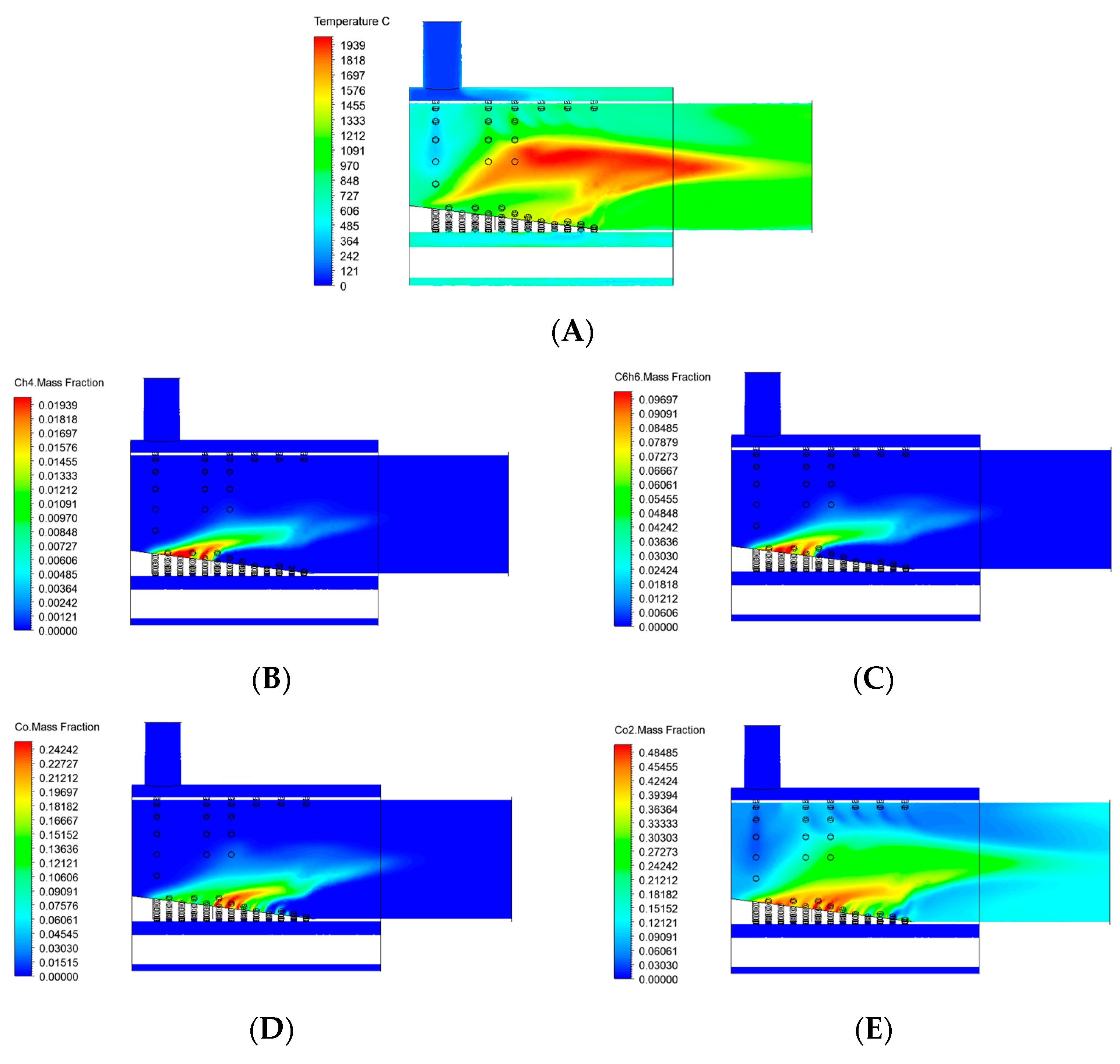
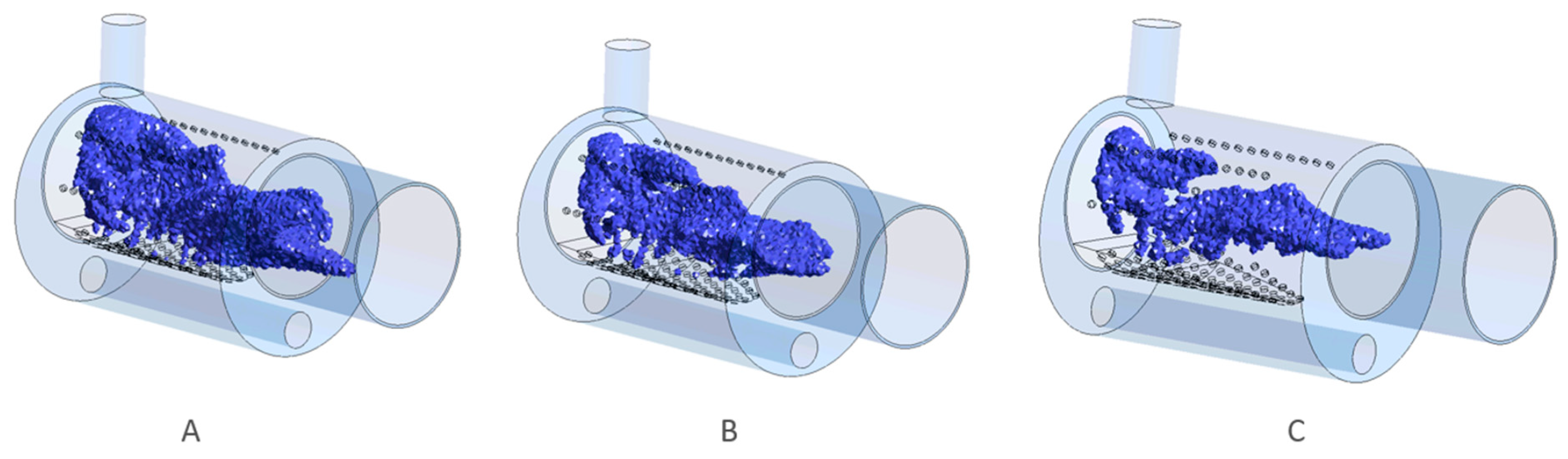
3.1. Geometry Optimization
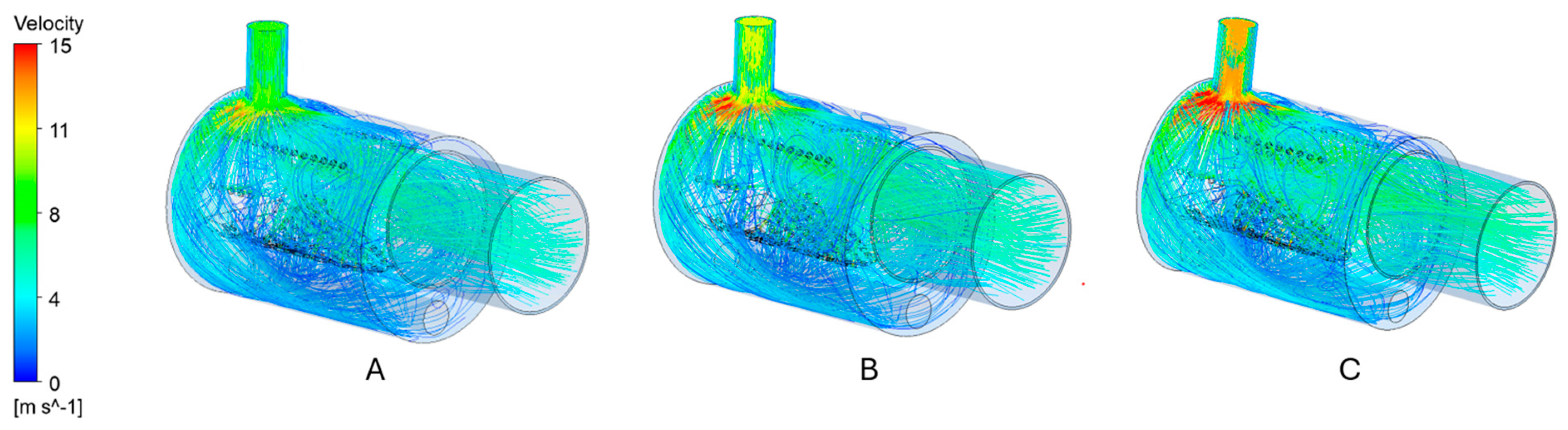
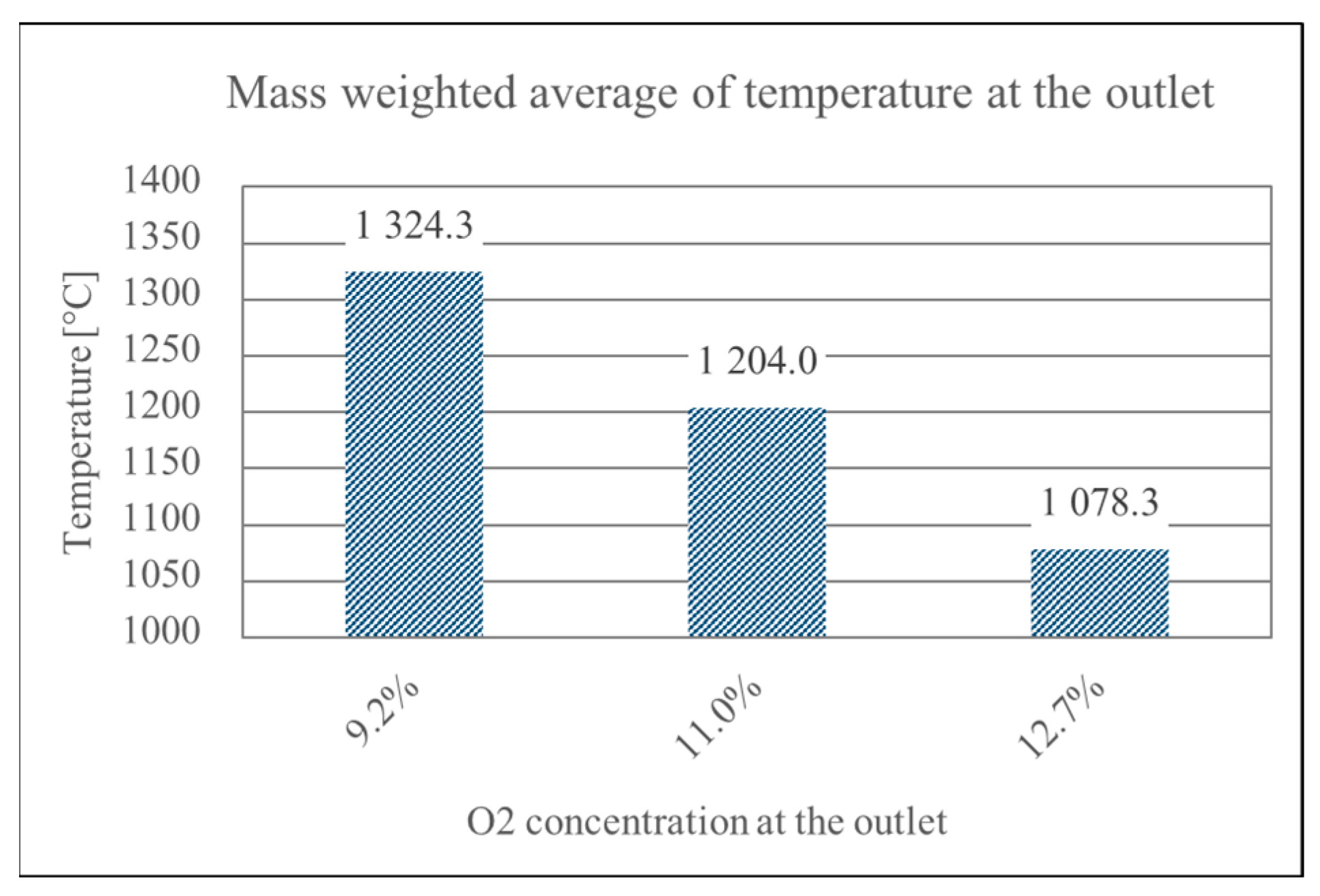
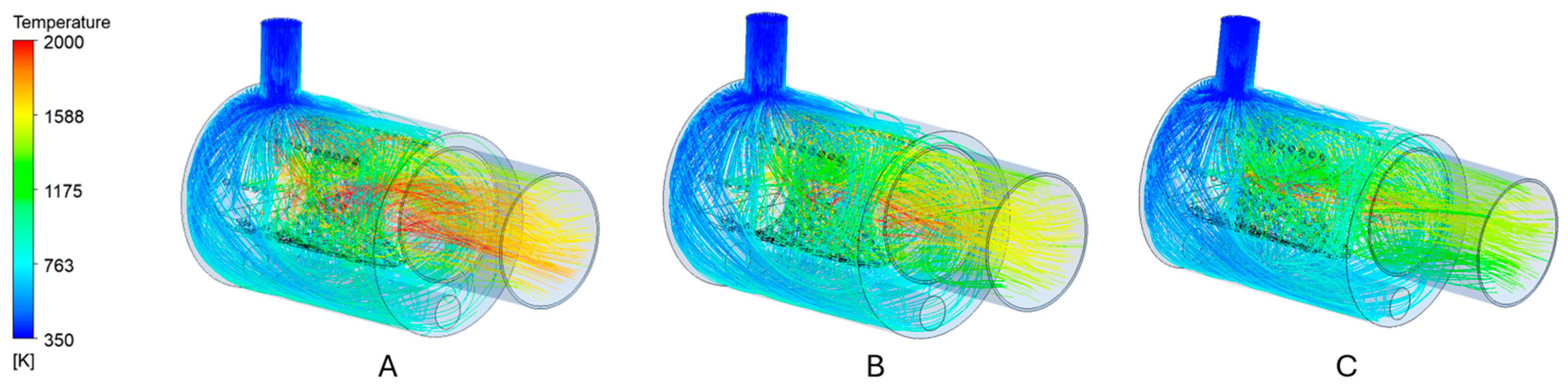
3.2. Air Mass Flow
4. Discussion
5. Conclusions
- Geometry optimization mitigates thermal degradation: Modifying the burner geometry, especially the distribution of secondary air holes, significantly reduced the risk of thermal degradation of the burner’s upper wall. Geometry V proved most effective, successfully shifting the high-temperature zone away from sensitive wall areas and improving combustion stability.
- A high outlet temperature ensures Stirling engine compatibility: All optimized geometries achieved flue gas temperatures above the critical 1000 °C threshold. Geometry V achieved the highest outlet temperature (1237.8 °C), fulfilling the requirements of efficient heat transfer to the Stirling engine in micro-CHP applications.
- Increased air mass flow reduces wall overheating: Operational optimization by increasing the air mass flow rate (e.g., via blower adjustment) successfully limits high-temperature zones near burner walls—even in suboptimal geometries. However, this also leads to reduced flue gas temperatures, requiring a balance between structural protection and thermal performance.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| empirical constant | |
| empirical constant, | |
| fluid total energy, J/kg | |
| force source term, N | |
| species mass fluxes, kg/s | |
| reaction rate constant, J/kg | |
| molecular weight, kg/mole | |
| fluid static pressure, Pa | |
| energy source term, J | |
| mass source term, kg/(m3 s) | |
| species creation source term, kg/s | |
| temperature, K | |
| velocity, m/s | |
| species mass fraction | |
| mass fraction of reactant | |
| mass fraction of product species | |
| Greek symbols | |
| turbulent kinetic energy dissipation rate | |
| thermal conductivity, W/(m K) | |
| stochiometric coefficient for reactant k in reaction r | |
| stochiometric coefficient for product k in reaction r | |
| gas density, kg/m3 | |
| stress tensor | |
| species production/destruction rate, kg/(m3 s) | |
| Subscripts and superscripts | |
| effective | |
| species index | |
| species index | |
| number of chemical species in the system | |
| product | |
| reaction | |
| reactant | |
References
- Gonzcalves, A.C.; Malico, I. Biomass for Domestic Heat BT—Forest Bioenergy: From Wood Production to Energy Use; Springer International Publishing: Evora, Portugal, 2024; pp. 209–233. ISBN 978-3-031-48224-3. [Google Scholar]
- World Bioegengy Association. Global Bioenergy Statistics 2022; World Bioegengy Association: Stockholm, Sweden, 2022. [Google Scholar]
- Niekurzak, M. The potential of using renewable energy sources in Poland taking into account the economic and ecological conditions. Energies 2021, 14, 7525. [Google Scholar] [CrossRef]
- Krawczyk, P.; Badyda, K.; Dzido, A. Techno-Economic Analysis of Increasing the Share of Renewable Energy Sources in Heat Generation Using the Example of a Medium-Sized City in Poland. Energies 2025, 18, 884. [Google Scholar] [CrossRef]
- Jonsson, R.; Rinaldi, F. The impact on global wood-product markets of increasing consumption of wood pellets within the European Union. Energy 2017, 133, 864–878. [Google Scholar] [CrossRef]
- Zhu, S.; Yu, G.; Liang, K.; Dai, W.; Luo, E. A review of Stirling-engine-based combined heat and power technology. Appl. Energy 2021, 294, 116965. [Google Scholar] [CrossRef]
- Chacón, J.; Sala, J.M.; Blanco, J.M. Investigation on the design and optimization of a low NOx-Co emission burner both experimentally and through computational fluid dynamics (CFD) simulations. Energy Fuels 2007, 21, 42–58. [Google Scholar] [CrossRef]
- Yan, W.; Li, K.; Yu, T.; Huang, X.; Yu, L.; Panahi, A.; Levendis, Y.A. Determination of Flame Temperatures and Soot Volume Fractions during Combustion of Biomass Pellets. Energy Fuels 2021, 35, 2313–2325. [Google Scholar] [CrossRef]
- Weng, W.; Feuk, H.; Li, S.; Richter, M.; Aldén, M.; Li, Z. Temporal temperature measurement on burning biomass pellets using phosphor thermometry and two-line atomic fluorescence. Proc. Combust. Inst. 2021, 38, 3929–3938. [Google Scholar] [CrossRef]
- Deore, S.P.; Gadkari, P.; Mahajani, S.M.; Kumar, S.; Kumar, S. Development of a new premixed burner for biomass gasifier generated low calorific value producer gas for industrial applications. Energy 2023, 279, 128140. [Google Scholar] [CrossRef]
- Costa, M.A.; Schiavon, N.C.B.; Felizardo, M.P.; Souza, A.J.D.; Dussán, K.J. Emission analysis of sugarcane bagasse combustion in a burner pilot. Sustain. Chem. Pharm. 2023, 32, 101028. [Google Scholar] [CrossRef]
- Zainith, P.; Mishra, N.K. Numerical study for the combustion analysis of wood volatiles in porous radiant burner for the application of biomass cooking stove. Int. J. Therm. Sci. 2024, 196, 108708. [Google Scholar] [CrossRef]
- Chen, C.Y.; Chen, W.H.; Hung, C.H. Combustion performance and emissions from torrefied and water washed biomass using a kg-scale burner. J. Hazard. Mater. 2021, 402, 123468. [Google Scholar] [CrossRef] [PubMed]
- He, F.; Wei, F.; Ma, C.; Zhao, H.; Fan, Y.; Wang, L.; Wang, J.A. Performance of an intelligent biomass fuel burner as an alternative to coal-fired heating for tobacco curing. Pol. J. Environ. Stud. 2020, 30, 131–140. [Google Scholar] [CrossRef]
- Marra, F.S.; Miccio, F.; Solimene, R.; Chirone, R.; Urciuolo, M.; Miccio, M. Coupling a Stirling engine with a fluidized bed combustor for biomass. Int. J. Energy Res. 2020, 44, 12572–12582. [Google Scholar] [CrossRef]
- Schneider, T.; Ruf, F.; Müller, D.; Karl, J. Performance of a fluidized bed-fired Stirling engine as micro-scale combined heat and power system on wood pellets. Appl. Therm. Eng. 2021, 189, 116712. [Google Scholar] [CrossRef]
- Borisov, I.; Khalatov, A.; Paschenko, D. The biomass fueled micro-scale CHP unit with stirling engine and two-stage vortex combustion chamber. Heat Mass Transf. Und Stoffuebertragung 2022, 58, 1091–1103. [Google Scholar] [CrossRef]
- Kropiwnicki, J. Low temperature rotary Stirling engine: Conceptual design and theoretical analysis. Appl. Therm. Eng. 2024, 257, 124276. [Google Scholar] [CrossRef]
- Sripakagorn, A.; Srikam, C. Design and performance of a moderate temperature difference Stirling engine. Renew. Energy 2011, 36, 1728–1733. [Google Scholar] [CrossRef]
- Krawczyk, P.; Kurkus-Gruszecka, M.; Wilczyński, M.; Dzido, A. Numerical analysis of design and operational parameters of low power pellet burners. Renew. Energy 2025, 243, 122577. [Google Scholar] [CrossRef]
- Ahn, J.; Kim, H.J. Combustion process of a Korean wood pellet at a low temperature. Renew. Energy 2020, 145, 391–398. [Google Scholar] [CrossRef]
- Biswas, A.K.; Rudolfsson, M.; Broström, M.; Umeki, K. Effect of pelletizing conditions on combustion behaviour of single wood pellet. Appl. Energy 2014, 119, 79–84. [Google Scholar] [CrossRef]
- Wiese, J.; Wissing, F.; Höhner, D.; Wirtz, S.; Scherer, V.; Ley, U.; Behr, H.M. DEM/CFD modeling of the fuel conversion in a pellet stove. Fuel Process. Technol. 2016, 152, 223–239. [Google Scholar] [CrossRef]
- Saldarriaga, J.F.; Aguado, R.; Pablos, A.; Amutio, M.; Olazar, M.; Bilbao, J. Fast characterization of biomass fuels by thermogravimetric analysis (TGA). Fuel 2015, 140, 744–751. [Google Scholar] [CrossRef]
- Cavalaglio, G.; Cotana, F.; Nicolini, A.; Coccia, V.; Petrozzi, A.; Formica, A.; Bertini, A. Characterization of various biomass feedstock suitable for small-scale energy plants as preliminary activity of biocheaper project. Sustainability 2020, 12, 6678. [Google Scholar] [CrossRef]
- Zadravec, T.; Rajh, B.; Kokalj, F.; Samec, N. CFD modelling of air staged combustion in a wood pellet boiler using the coupled modelling approach. Therm. Sci. Eng. Prog. 2020, 20, 100715. [Google Scholar] [CrossRef]
- Caretto, L.S. Modeling pollutant formation in combustion processes. Symp. Combust. 1973, 14, 803–817. [Google Scholar] [CrossRef]
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. In Numerical Prediction of Flow, Heat Transfer, Turbulence and Combustion; Elsevier: Amsterdam, The Netherlands, 1983; pp. 96–116. [Google Scholar]
- Fletcher, D.F.; Haynes, B.S.; Christo, F.C.; Joseph, S.D. A CFD based combustion model of an entrained flow biomass gasifier. Appl. Math. Model. 2000, 24, 165–182. [Google Scholar] [CrossRef]
- Dixon, T.F.; Mann, A.P.; Plaza, F.; Gilfillan, W.N. Development of advanced technology for biomass combustion—CFD as an essential tool. Fuel 2005, 84, 1303–1311. [Google Scholar] [CrossRef]
- Murthy, J.Y.; Mathur, S.R. Finite volume method for radiative heat transfer using unstructured meshes. J. Thermophys. Heat Transf. 1998, 12, 313–321. [Google Scholar] [CrossRef]
- Hernik, B. Numerical Research of Flue Gas Denitrification Using the SNCR Method in an OP 650 Boiler. Energies 2022, 15, 3427. [Google Scholar] [CrossRef]
- Skreiberg, A.; Skreiberg, O.; Sandquist, J.; Sørum, L. TGA and macro-TGA characterisation of biomass fuels and fuel mixtures. Fuel 2011, 90, 2182–2197. [Google Scholar] [CrossRef]
- Hermansson, S.; Thunman, H. CFD modelling of bed shrinkage and channelling in fixed-bed combustion. Combust. Flame 2011, 158, 988–999. [Google Scholar] [CrossRef]
- Gómez, M.A.; Martín, R.; Chapela, S.; Porteiro, J. Steady CFD combustion modeling for biomass boilers: An application to the study of the exhaust gas recirculation performance. Energy Convers. Manag. 2019, 179, 91–103. [Google Scholar] [CrossRef]
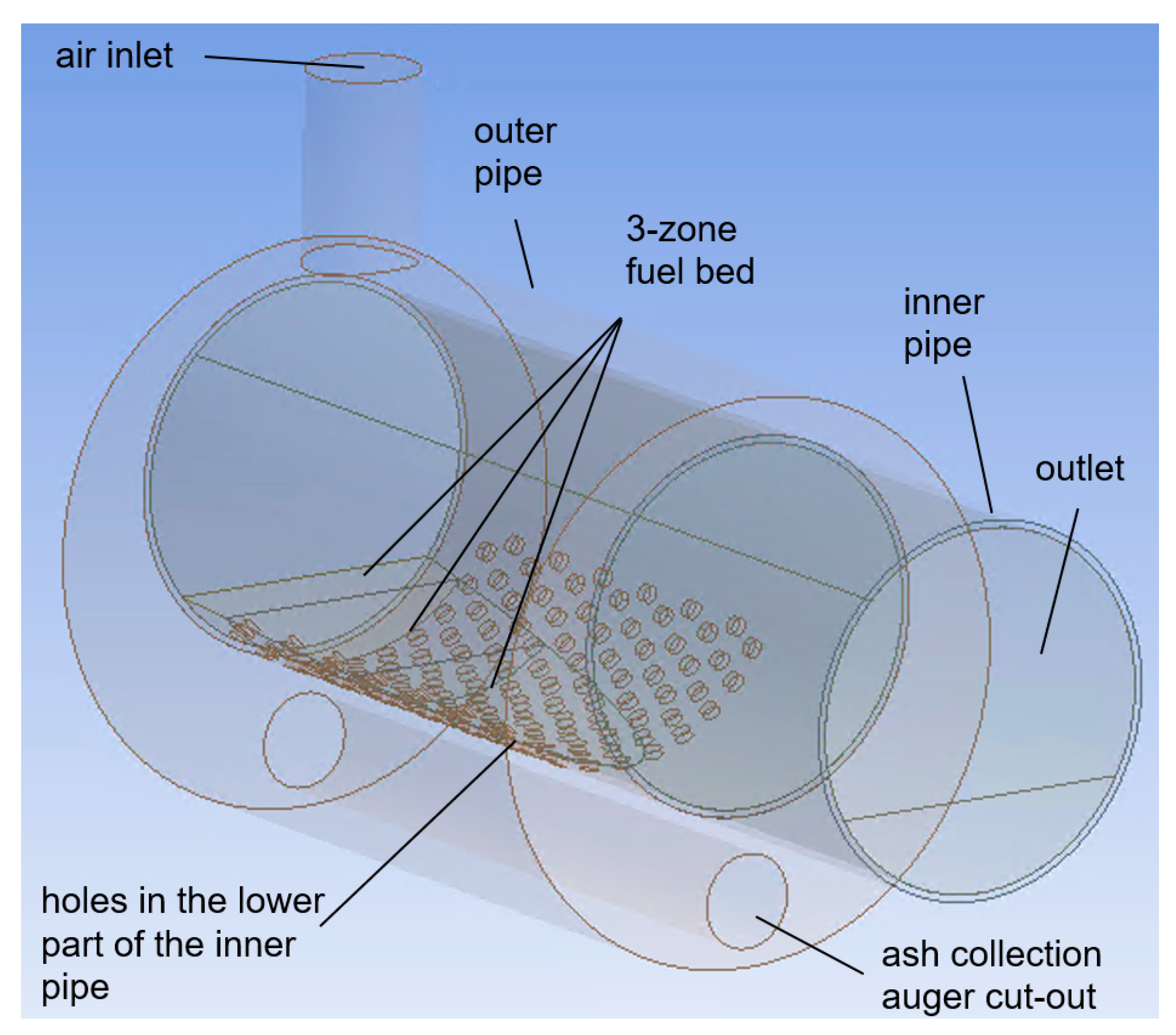
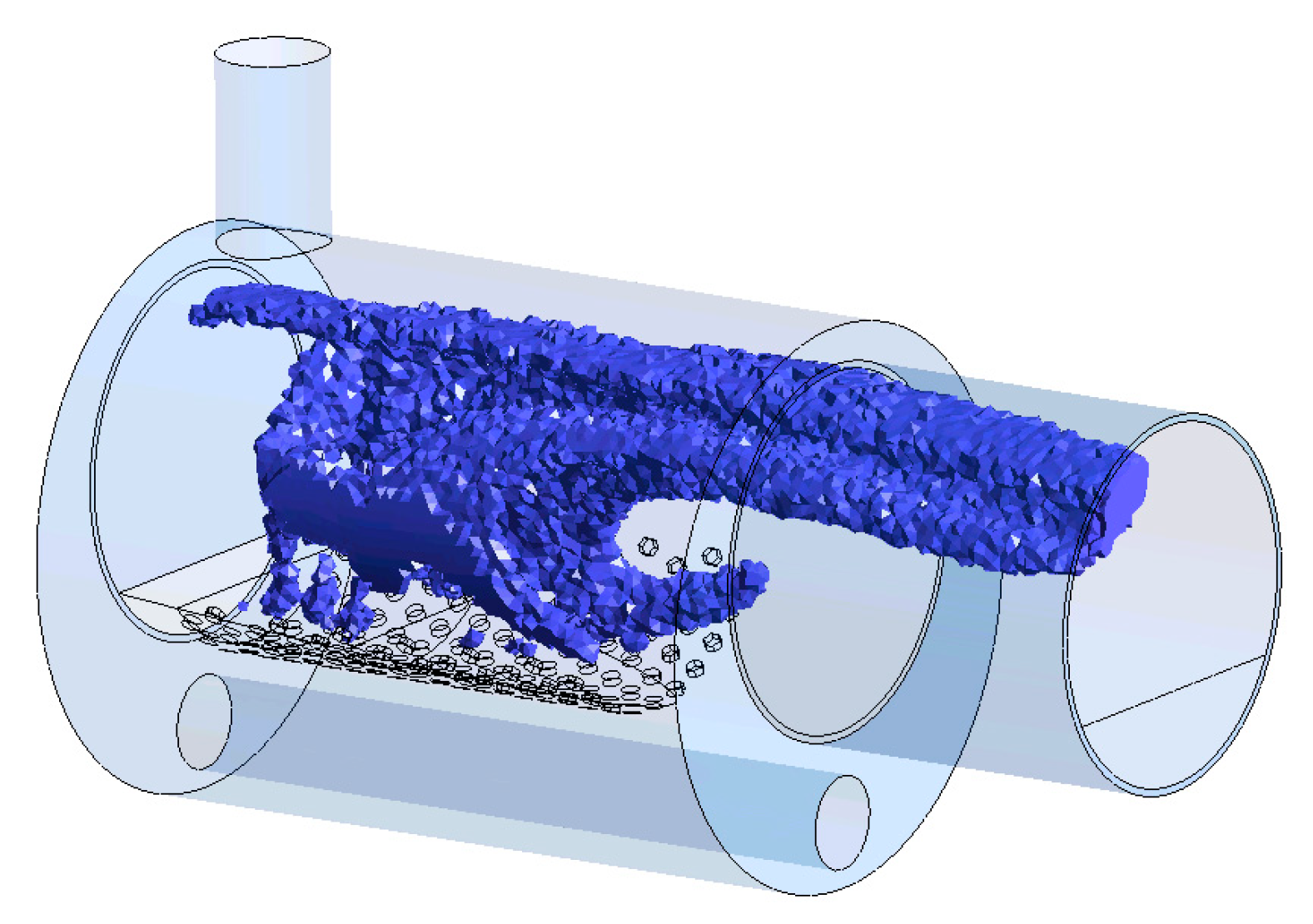


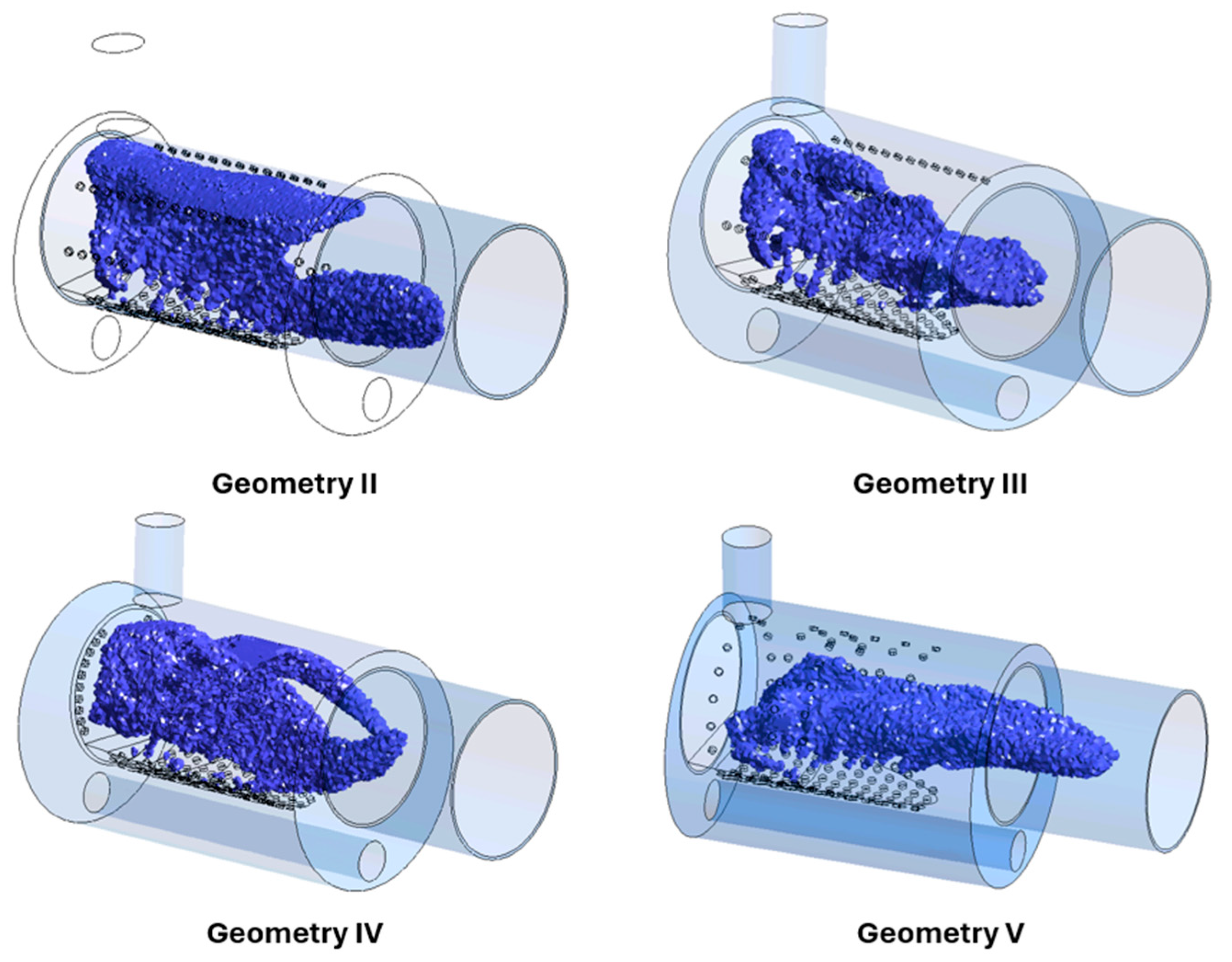
| Location | Conditions |
|---|---|
| Inlet | mass flow inlet, air, 25.3 kg/h, 373 K |
| Outlet | pressure outlet, opaque; external black body temperature: 623 K; internal emissivity: 1 |
| Outer walls | thermal conditions: mixed; heat transfer coefficient: 8 W/m2K; free stream temperature: 300 K; external emissivity: 0.05; external radiation temperature: 300 K; shell construction: two layers: steel, 0.0025 m; mineral wool, 0.03 m; internal emissivity: 1; opaque |
| Internal pipe wall | thermal conditions—coupled; opaque; internal emissivity: 1; steel |
| Geometry | I (Initial) | II | III | IV | V |
|---|---|---|---|---|---|
| Quantity of primary air holes | 136 | 102 | 136 | 136 | 102 |
| Quantity of secondary air holes | 0 | 36 | 36 | 20 | 38 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dzido, A.; Kurkus-Gruszecka, M.; Wilczyński, M.; Krawczyk, P. Flue Gas Temperature Distribution as a Function of Air Management in a High-Temperature Biomass Burner. Energies 2025, 18, 2719. https://doi.org/10.3390/en18112719
Dzido A, Kurkus-Gruszecka M, Wilczyński M, Krawczyk P. Flue Gas Temperature Distribution as a Function of Air Management in a High-Temperature Biomass Burner. Energies. 2025; 18(11):2719. https://doi.org/10.3390/en18112719
Chicago/Turabian StyleDzido, Aleksandra, Michalina Kurkus-Gruszecka, Marcin Wilczyński, and Piotr Krawczyk. 2025. "Flue Gas Temperature Distribution as a Function of Air Management in a High-Temperature Biomass Burner" Energies 18, no. 11: 2719. https://doi.org/10.3390/en18112719
APA StyleDzido, A., Kurkus-Gruszecka, M., Wilczyński, M., & Krawczyk, P. (2025). Flue Gas Temperature Distribution as a Function of Air Management in a High-Temperature Biomass Burner. Energies, 18(11), 2719. https://doi.org/10.3390/en18112719






