Enhancing Pumped Hydro Storage Regulation Through Adaptive Initial Reservoir Capacity in Multistage Stochastic Coordinated Planning
Abstract
1. Introduction
- (1)
- Coordinated Planning Model based on MSSP: We develop an MSSP model that dynamically adjusts investment and operational strategies for the CHWS-PHS system, effectively addressing uncertainties and temporal variations in RE output and NWIs. The model incorporates NACs, enabling dynamic adjustments in response to unfolding uncertainties.
- (2)
- Proposed HPHS-AIRC Strategy: To address the unique reservoir management challenges associated with switching between pumping and generating modes in HPHS, the HPHS-AIRC strategy is proposed. This strategy is integrated into the multistage optimization model to maximize the regulatory potential of HPHS under uncertainties in NWIs and RE generation.
2. Coordinated Planning Model
2.1. Proposed HPHS-AIRC Strategy
2.2. Objective Function
- (1)
- Investment Cost: The investment cost (Equation (4)) comprises four components: variable-speed HPHS (VS-HPHS) units, wind farms, PV power plants, and transmission lines.
- (2)
- Operation Cost: The operational cost (Equation (5)) includes the operational costs of thermal units (Equation (6)) and the penalty costs for load shedding (Equation (7)) and for wind and solar curtailment (Equation (8)).
2.3. Constraints
- (1)
- Planning decision constraints:
- (2)
- VS-HPHS unit constraints:
- (a)
- Power-generation unit:
- (b)
- Pumped-storage unit:
- (3)
- Thermal unit constraints:
- (4)
- Wind and solar constraints:
- (5)
- Power flow constraints:
- (6)
- Power balance constraints:
2.4. General Mathematical Formulation
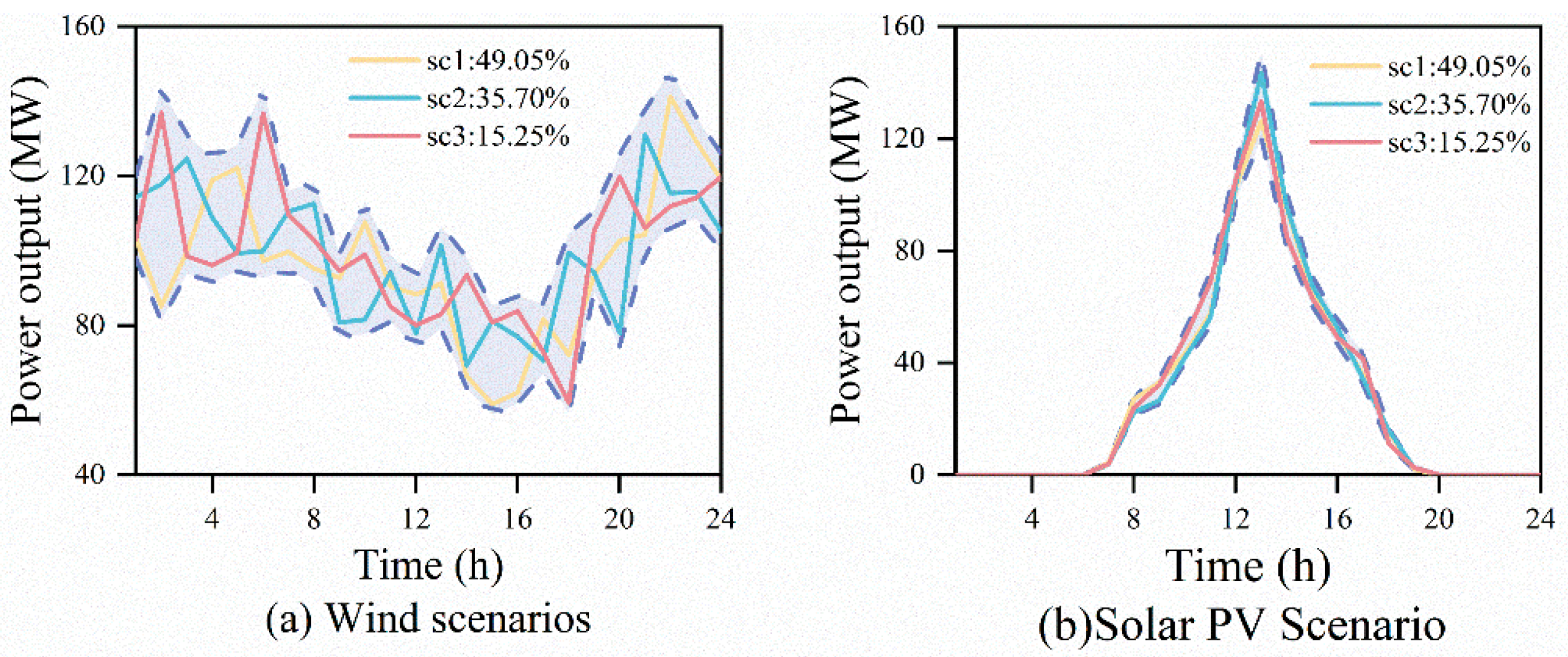
3. Modeling and Handling of Uncertainties in Renewable Generation and Natural Water Inflows
3.1. Comparative Analysis of NWIs, Wind, and Solar Uncertainties in Power System Planning
3.2. Handling Inter-Annual and Intra-Day Uncertainties with Instance Trees
3.3. Non-Anticipativity-Constrained Multistage Optimization
3.4. Implementation of the Proposed Model
- Step 1: Multistage Instance Tree Generation
- Step 2: Wind and Solar Scenario Generation
- Step 3: Multistage Stochastic Planning
- Step 4: Solution to the Model
4. Case Study
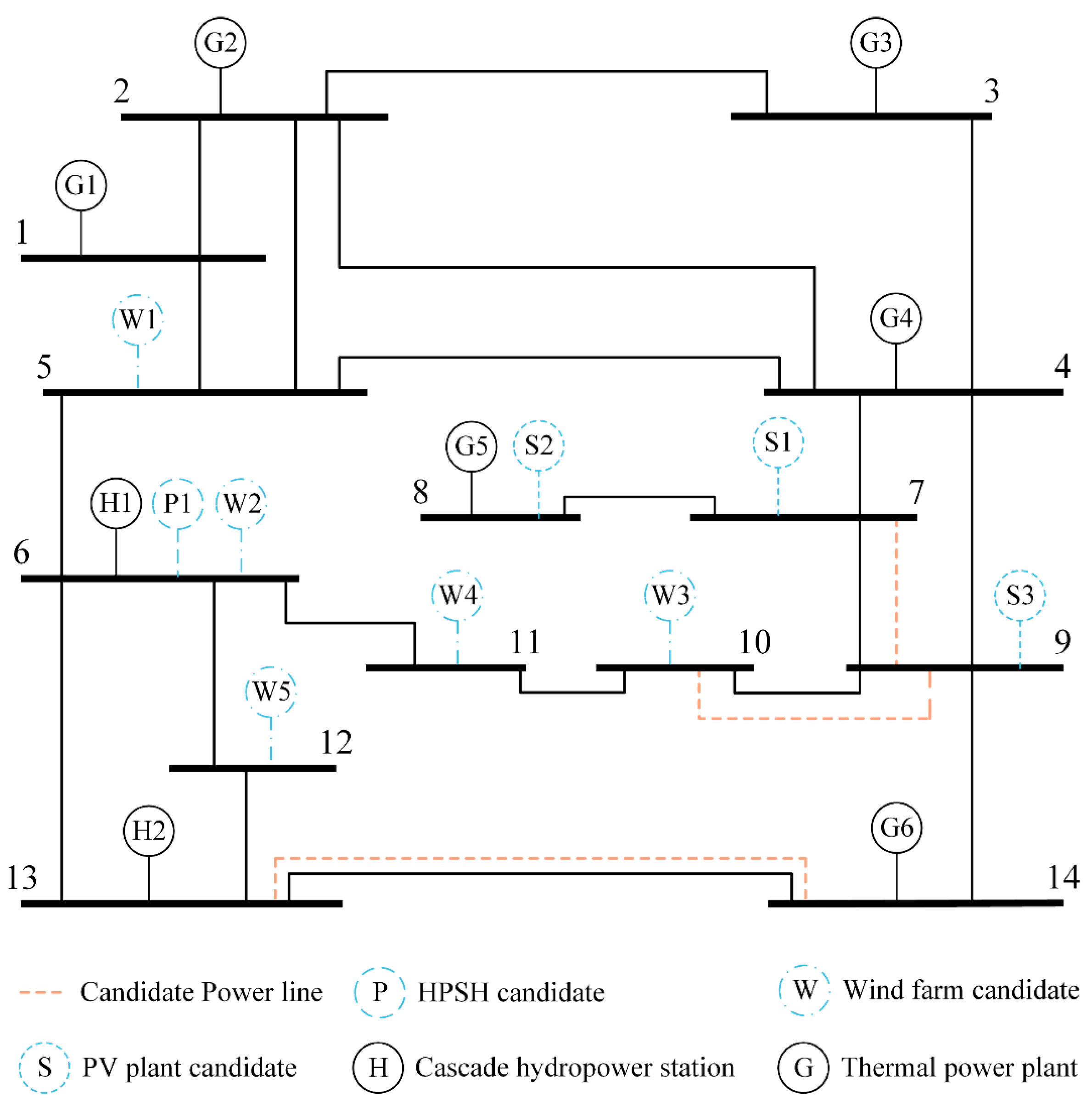
4.1. IEEE 14-Bus System
- (1)
- Proposed HPHS-AIRC Strategy
- (2)
- MSSP with NACs
4.2. Application of MSSP in the IEEE 118-Bus System
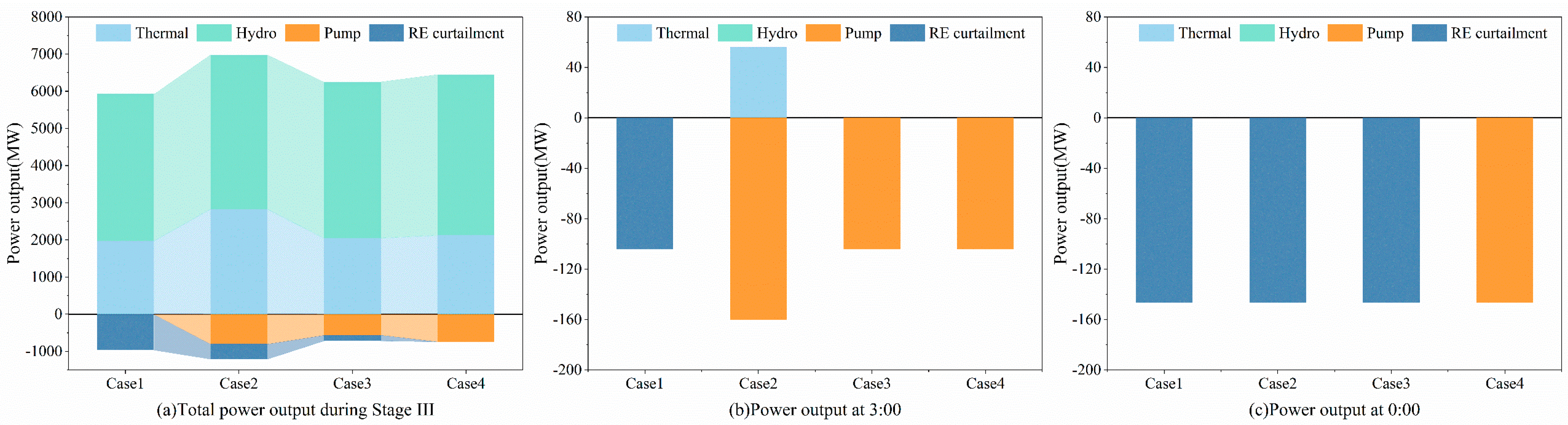
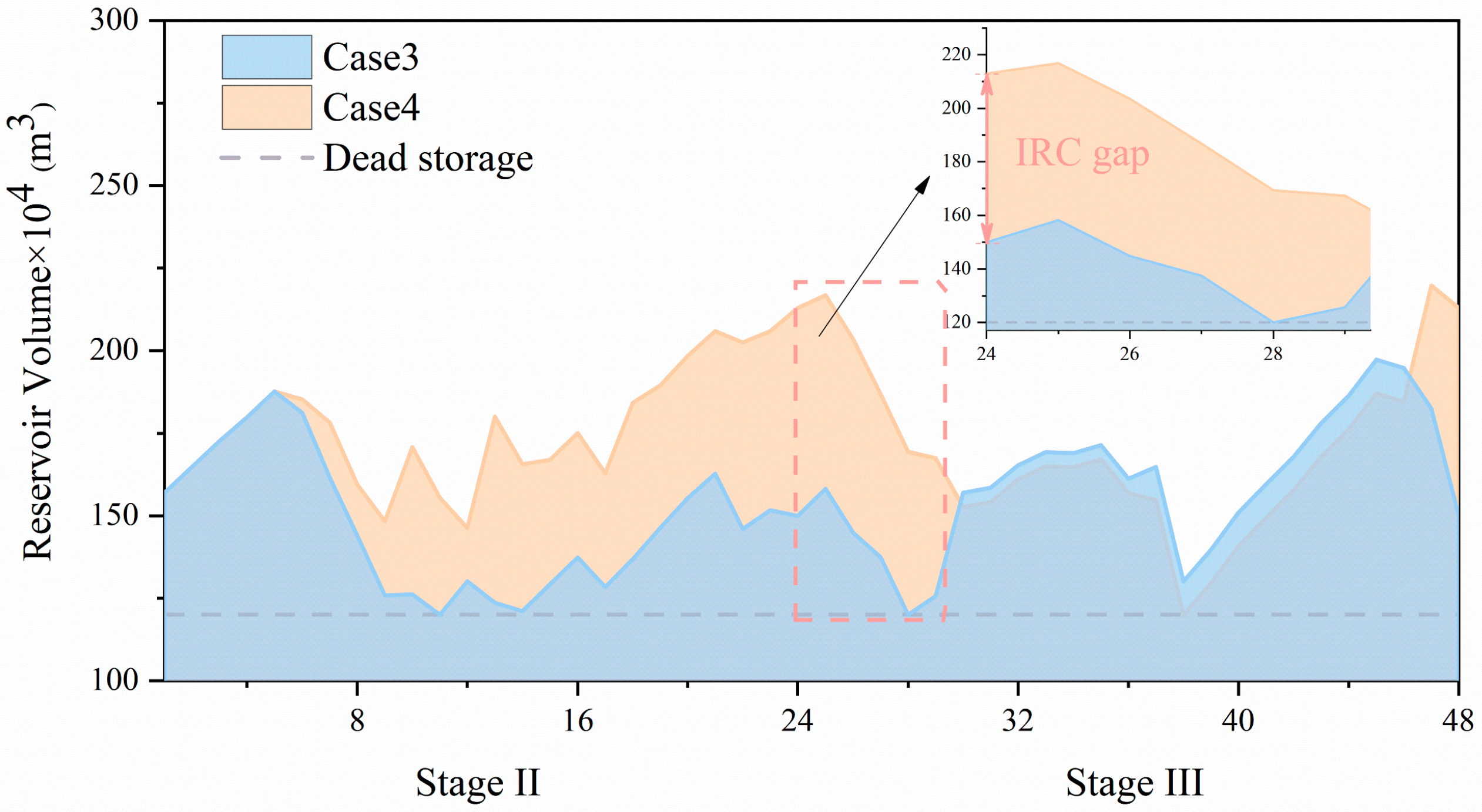
5. Discussion
5.1. Advantages of the HPHS-AIRC Strategy
5.2. Impact of Uncertainty and MSSP Modeling
5.3. Scalability and Practicality in Larger Systems
6. Conclusions
- (1)
- Topology Scalability: The current framework assumes a simplified PHS configuration. Future work could extend the HPHS-AIRC strategy to multistage cascaded reservoirs to evaluate its performance in complex hydropower topologies, where hydraulic coupling and sequential water-outflow constraints may challenge regulation stability.
- (2)
- Parameter Adaptability: The impact of adaptive control parameters δpump on regulation capability warrants systematic analysis. A sensitivity-driven parameter optimization framework could further enhance the strategy’s robustness across diverse operating scenarios.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Virah-Sawmy, D.; Sturmberg, B. Socio-economic and environmental impacts of renewable energy deployments: A review. Renew. Sustain. Energy Rev. 2025, 207, 114956. [Google Scholar] [CrossRef]
- Mitchell, C. Momentum is increasing towards a flexible electricity system based on renewables. Nat. Energy 2016, 1, 15030. [Google Scholar] [CrossRef]
- Qiu, X.; Chen, Y.; Cai, W.; Niu, M.; Li, J. LD-YOLOv10: A Lightweight Target Detection Algorithm for Drone Scenarios Based on YOLOv10. Electronics 2024, 13, 3269. [Google Scholar] [CrossRef]
- Bhandari, B. A novel off-grid hybrid power system comprised of solar photovoltaic, wind, and hydro energy sources. Appl. Energy 2014, 133, 236–242. [Google Scholar] [CrossRef]
- Gielen, D.; Boshell, F.; Saygin, D.; Bazilian, M.D.; Wagner, N.; Gorini, R. The role of renewable energy in the global energy transformation. Energy Strategy Rev. 2019, 24, 38–50. [Google Scholar] [CrossRef]
- Shair, J. Power system stability issues, classifications and research prospects in the context of high-penetration of renewables and power electronics. Renew. Sustain. Energy Rev. 2021, 145, 111111. [Google Scholar] [CrossRef]
- Sterl, S. Smart renewable electricity portfolios in West Africa. Nat. Sustain. 2020, 3, 710–719. [Google Scholar] [CrossRef]
- Rana, M.M.; Uddin, M.; Sarkar, M.R.; Meraj, S.T.; Shafiullah, G.M.; Muyeen, S.M.; Islam, M.A.; Jamal, T. Applications of energy storage systems in power grids with and without renewable energy integration—A comprehensive review. J. Energy Storage 2023, 68, 107811. [Google Scholar] [CrossRef]
- Javed, M.S.; Zhong, D.; Ma, T.; Song, A.; Ahmed, S. Hybrid pumped hydro and battery storage for renewable energy based power supply system. Appl. Energy 2020, 257, 114026. [Google Scholar] [CrossRef]
- Barbour, E.; Wilson, I.A.G.; Radcliffe, J.; Ding, Y.; Li, Y. A review of pumped hydro energy storage development in significant international electricity markets. Renew. Sustain. Energy Rev. 2016, 61, 421–432. [Google Scholar] [CrossRef]
- Tan, Q.; Nie, Z.; Wen, X.; Su, H.; Fang, G.; Zhang, Z. Complementary scheduling rules for hybrid pumped storage hydropower-photovoltaic power system reconstructing from conventional cascade hydropower stations. Appl. Energy 2024, 355, 122250. [Google Scholar] [CrossRef]
- Acuña, G.; Domínguez, R.; Arganis, M.L.; Fuentes, O. Optimal Schedule the Operation Policy of a Pumped Energy Storage Plant Case Study Zimapán, México. Electronics 2022, 11, 4139. [Google Scholar] [CrossRef]
- Sospiro, P.; Nibbi, L.; Liscio, M.C.; De Lucia, M. Cost–Benefit Analysis of Pumped Hydroelectricity Storage Investment in China. Energies 2021, 14, 8322. [Google Scholar] [CrossRef]
- Zhang, X. Capacity configuration of a hydro-wind-solar-storage bundling system with transmission constraints of the receiving-end power grid and its techno-economic evaluation. Energy Convers. Manag. 2022, 270, 116177. [Google Scholar] [CrossRef]
- Sun, K.; Li, K.-J.; Pan, J.; Liu, Y.; Liu, Y. An optimal combined operation scheme for pumped storage and hybrid wind-photovoltaic complementary power generation system. Appl. Energy 2019, 242, 1155–1163. [Google Scholar] [CrossRef]
- Zhang, S.; Xiang, Y.; Liu, J.; Liu, J.; Yang, J.; Zhao, X.; Jawad, S.; Wang, J. A Regulating Capacity Determination Method for Pumped Storage Hydropower to Restrain PV Generation Fluctuations. Csee J. Power Energy Syst. 2022, 8, 304–316. [Google Scholar]
- Hunt, J.D.; Freitas, M.A.V.; Pereira Junior, A.O. Enhanced-Pumped-Storage: Combining pumped-storage in a yearly storage cycle with dams in cascade in Brazil. Energy 2014, 78, 513–523. [Google Scholar] [CrossRef]
- Ak, M. Quantifying the revenue gain of operating a cascade hydropower plant system as a pumped-storage hydropower system. Renew. Energy 2019, 139, 739–752. [Google Scholar] [CrossRef]
- Lu, M.; Guan, J.; Wu, H.; Chen, H.; Gu, W.; Wu, Y.; Ling, C.; Zhang, L. Day-ahead optimal dispatching of multi-source power system. Renew. Energy 2022, 183, 435–446. [Google Scholar] [CrossRef]
- Zhang, J.; Cheng, C.; Yu, S.; Shen, J.; Wu, X.; Su, H. Preliminary feasibility analysis for remaking the function of cascade hydropower stations to enhance hydropower flexibility: A case study in China. Energy 2022, 260, 125163. [Google Scholar] [CrossRef]
- Wang, Z.; Fang, G.; Wen, X.; Tan, Q.; Zhang, P.; Liu, Z. Coordinated operation of conventional hydropower plants as hybrid pumped storage hydropower with wind and photovoltaic plants. Energy Convers. Manag. 2023, 277, 116654. [Google Scholar] [CrossRef]
- Niknam, T. An efficient scenario-based stochastic programming framework for multi-objective optimal micro-grid operation. Appl. Energy 2012, 99, 455–470. [Google Scholar] [CrossRef]
- Park, H. Multi-year stochastic generation capacity expansion planning under environmental energy policy. Appl. Energy 2016, 183, 737–745. [Google Scholar] [CrossRef]
- Mavromatidis, G.; Orehounig, K.; Carmeliet, J. Design of distributed energy systems under uncertainty: A two-stage stochastic programming approach. Appl. Energy 2018, 222, 932–950. [Google Scholar] [CrossRef]
- Ding, T.; Hu, Y.; Bie, Z. Multi-Stage Stochastic Programming With Nonanticipativity Constraints for Expansion of Combined Power and Natural Gas Systems. IEEE Trans. Power Syst. 2018, 33, 317–328. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, F.; Zhang, X.; Wang, Z.; Meng, K.; Dong, Z.Y. Mobile Emergency Generator Planning in Resilient Distribution Systems: A Three-Stage Stochastic Model With Nonanticipativity Constraints. IEEE Trans. Smart Grid 2020, 11, 4847–4859. [Google Scholar] [CrossRef]
- Cobos, N.G. Network-constrained unit commitment under significant wind penetration: A multistage robust approach with non-fixed recourse. Appl. Energy 2018, 232, 489–503. [Google Scholar] [CrossRef]
- Rahat, S.H.; Steissberg, T.; Chang, W.; Chen, X.; Mandavya, G.; Tracy, J.; Wasti, A.; Atreya, G.; Saki, S.; Bhuiyan, A.E.; et al. Remote sensing-enabled machine learning for river water quality modeling under multidimensional uncertainty. Sci. Total Environ. 2023, 898, 165504. [Google Scholar] [CrossRef]
- Prasad, A.A.; Taylor, R.A.; Kay, M. Assessment of solar and wind resource synergy in Australia. Appl. Energy 2017, 190, 354–367. [Google Scholar] [CrossRef]
- Heide, D.; Von Bremen, L.; Greiner, M.; Hoffmann, C.; Speckmann, M.; Bofinger, S. Seasonal optimal mix of wind and solar power in a future, highly renewable Europe. Renew. Energy 2010, 35, 2483–2489. [Google Scholar] [CrossRef]
- Yin, Y.; Liu, T.; He, C. Day-ahead stochastic coordinated scheduling for thermal-hydro-wind-photovoltaic systems. Energy 2019, 187, 115944. [Google Scholar] [CrossRef]
- Straume, M.; Johnson, M.L. [7] Monte Carlo Method for determining complete confidence probability distributions of estimated model parameters. In Methods in Enzymology; Elsevier: Amsterdam, The Netherlands, 1992; Volume 210, pp. 117–129. [Google Scholar] [CrossRef]
- Wu, L.; Shahidehpour, M.; Li, Z. GENCO’s Risk-Constrained Hydrothermal Scheduling. IEEE Trans. Power Syst. 2008, 23, 1847–1858. [Google Scholar] [CrossRef]
- Liu, Z.; He, X. Balancing-oriented hydropower operation makes the clean energy transition more affordable and simultaneously boosts water security. Nat. Water 2023, 1, 778–789. [Google Scholar] [CrossRef]
- Alnowibet, K.A.; Alrasheedi, A.F.; Alshamrani, A.M. Integrated stochastic transmission network and wind farm investment considering maximum allowable capacity. Electr. Power Syst. Res. 2023, 215, 108961. [Google Scholar] [CrossRef]
- Zhao, Z. Beyond fixed-speed pumped storage: A comprehensive evaluation of different flexible pumped storage technologies in energy systems. J. Clean. Prod. 2024, 434, 139994. [Google Scholar] [CrossRef]
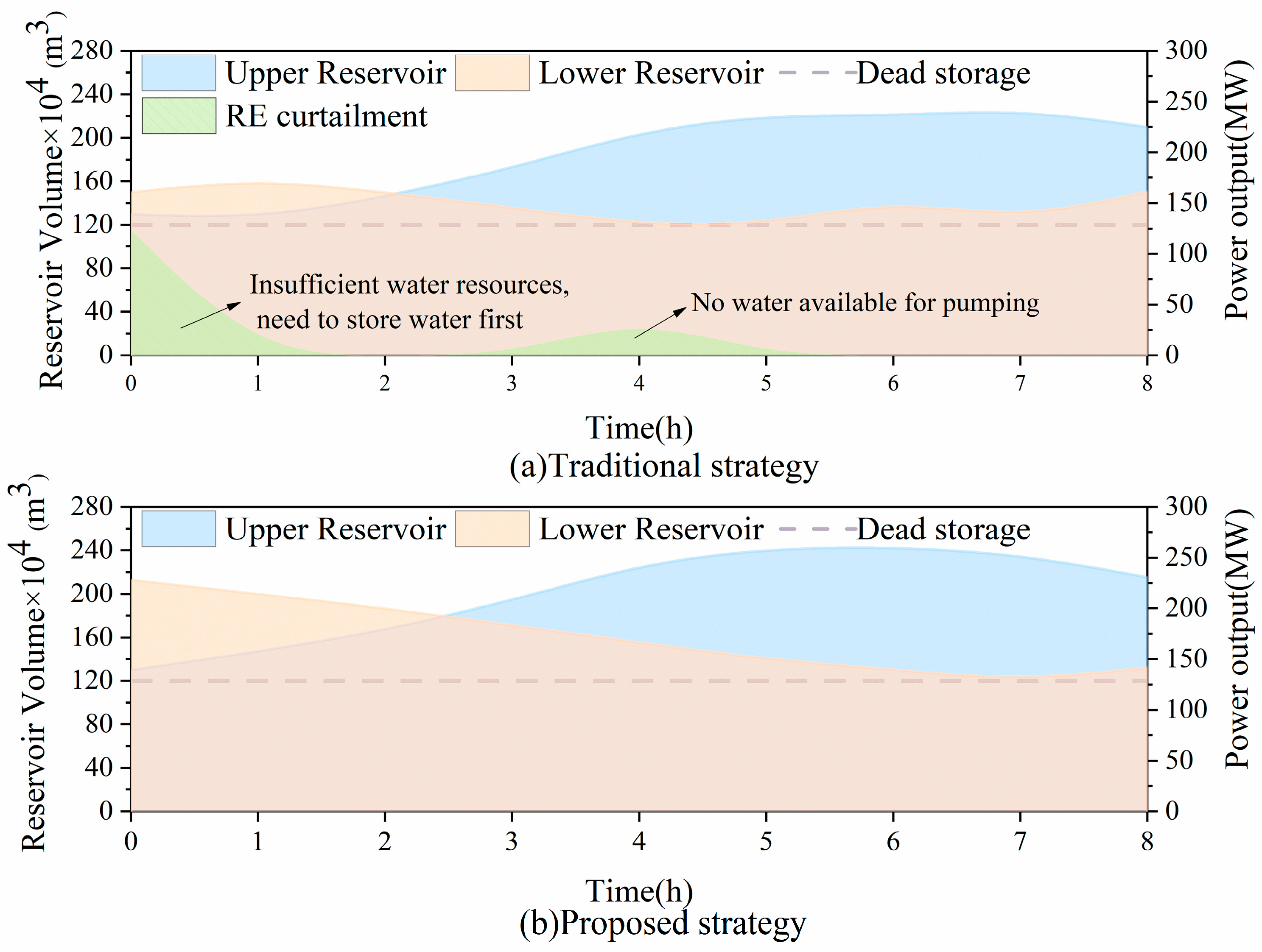
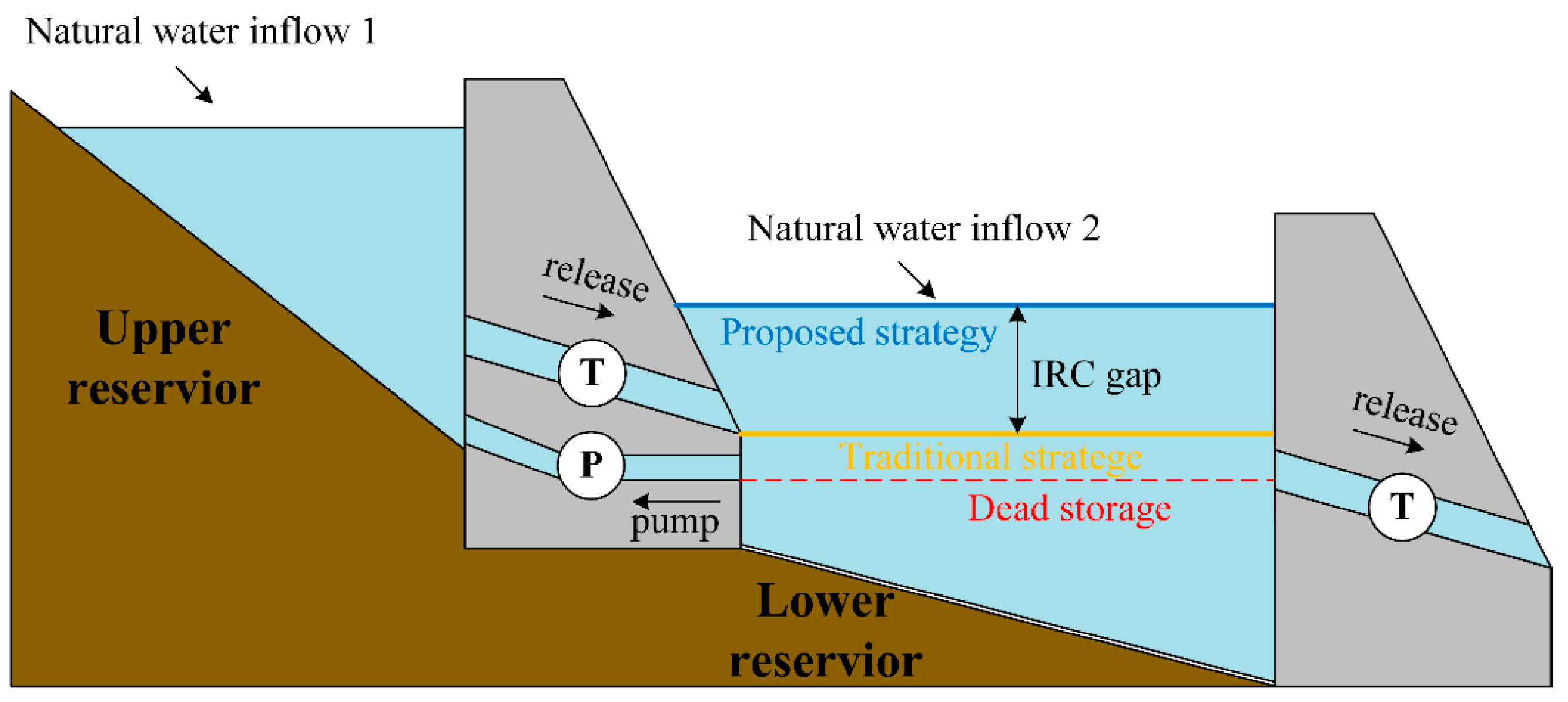
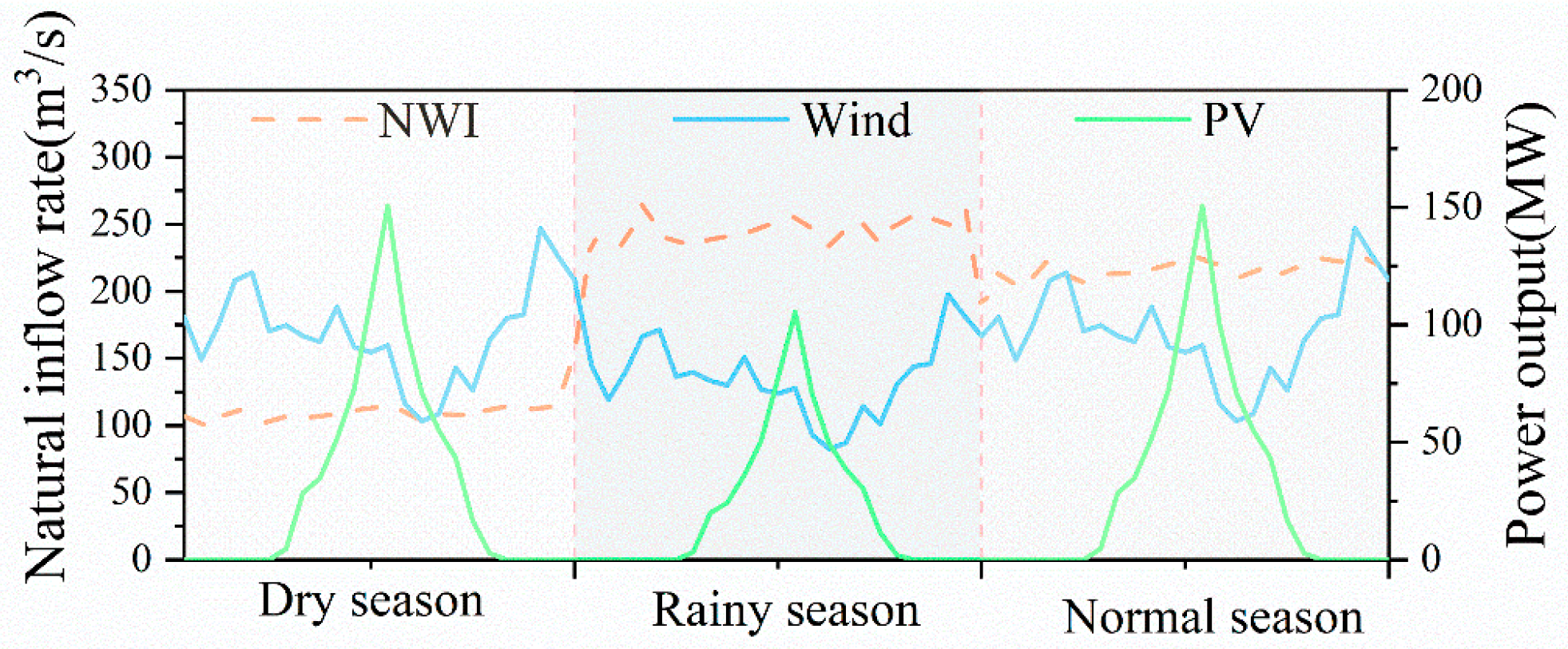
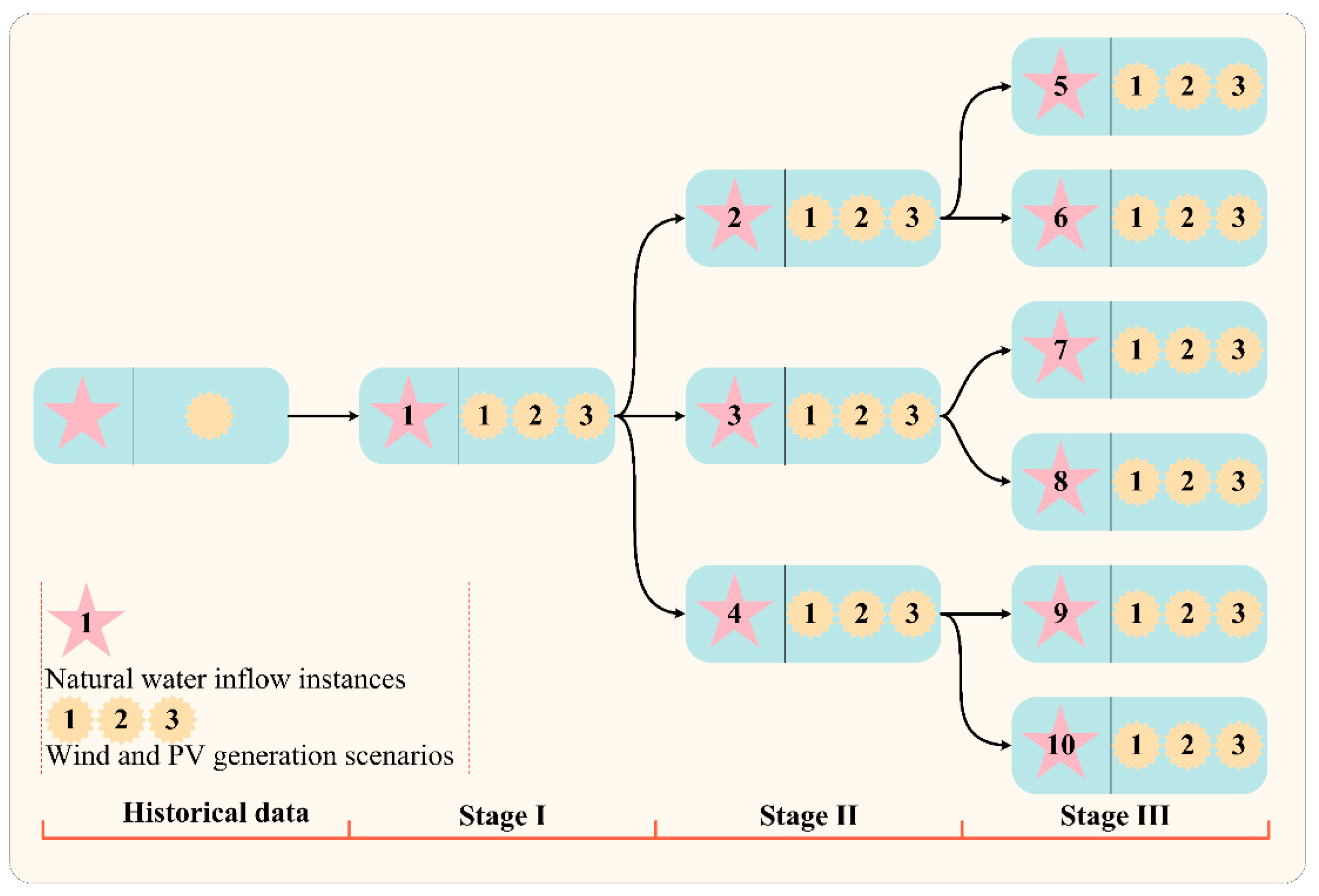



| Unit | Lower (MW) | Upper (MW) | Ramp (MW/h) | Retirement Stage |
|---|---|---|---|---|
| G1 | 25 | 100 | 50 | 2 |
| G2 | 75 | 300 | 150 | - |
| G3 | 50 | 200 | 100 | 3 |
| G4 | 100 | 300 | 150 | 2 |
| G5 | 25 | 100 | 50 | 2 |
| G6 | 50 | 250 | 125 | 3 |
| Case | Type of HPHS | IRC Strategy | ||
|---|---|---|---|---|
| FS | VS | FIRC | HPHS-AIRC | |
| Case 1 | - | - | - | - |
| Case 2 | √ | √ | ||
| Case 3 | √ | √ | ||
| Case 4 | √ | √ | ||
| Cost (USD Billion) | Total | ||||
|---|---|---|---|---|---|
| Case 1 | 2.30 | 1.48 | 5.42 | 0 | 9.20 |
| Case 2 | 2.33 | 1.49 | 2.30 | 0 | 6.13 |
| Case 3 | 2.36 | 1.49 | 0.82 | 0 | 4.67 |
| Case 4 | 2.36 | 1.51 | 0 | 0 | 3.87 |
| Case | Uncertainty | Model | ||
|---|---|---|---|---|
| NWI | RE | TSSP | MSSP | |
| Case 5 | √ | √ | ||
| Case 6 | √ | √ | ||
| Case 7 | √ | √ | √ | |
| Case | (USD Billion) | (USD Billion) | (USD Billion) | (USD Billion) | Total (USD Billion) | (MW) | Time (s) |
|---|---|---|---|---|---|---|---|
| Case 3 | 16.94 | 11.96 | 4.04 | 0 | 32.94 | 5671 | 113 |
| Case 4 | 16.94 | 12.19 | 0 | 0 | 29.13 | 7587 | 110 |
| Case 5 | 17.45 | 11.16 | 2.11 | 0 | 30.72 | - | 1142 |
| Case 6 | 17.26 | 11.54 | 0 | 0 | 28.80 | - | 2731 |
| Case 7 | 18.55 | 12.54 | 1.04 | 0 | 32.13 | - | 6482 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.; Huang, S.; Yin, Y.; Tang, Z.; Shuai, Q. Enhancing Pumped Hydro Storage Regulation Through Adaptive Initial Reservoir Capacity in Multistage Stochastic Coordinated Planning. Energies 2025, 18, 2707. https://doi.org/10.3390/en18112707
Chen C, Huang S, Yin Y, Tang Z, Shuai Q. Enhancing Pumped Hydro Storage Regulation Through Adaptive Initial Reservoir Capacity in Multistage Stochastic Coordinated Planning. Energies. 2025; 18(11):2707. https://doi.org/10.3390/en18112707
Chicago/Turabian StyleChen, Chao, Shan Huang, Yue Yin, Zifan Tang, and Qiang Shuai. 2025. "Enhancing Pumped Hydro Storage Regulation Through Adaptive Initial Reservoir Capacity in Multistage Stochastic Coordinated Planning" Energies 18, no. 11: 2707. https://doi.org/10.3390/en18112707
APA StyleChen, C., Huang, S., Yin, Y., Tang, Z., & Shuai, Q. (2025). Enhancing Pumped Hydro Storage Regulation Through Adaptive Initial Reservoir Capacity in Multistage Stochastic Coordinated Planning. Energies, 18(11), 2707. https://doi.org/10.3390/en18112707






