Modeling and Testing of 3D Wound Core Loss of Amorphous Alloy Transformer for Photovoltaic Inverter
Abstract
1. Introduction
2. Core Loss Characteristics Under Sinusoidal Excitation Low-Voltage Side Winding Model
2.1. Core Loss Characteristics Under Sinusoidal Excitation
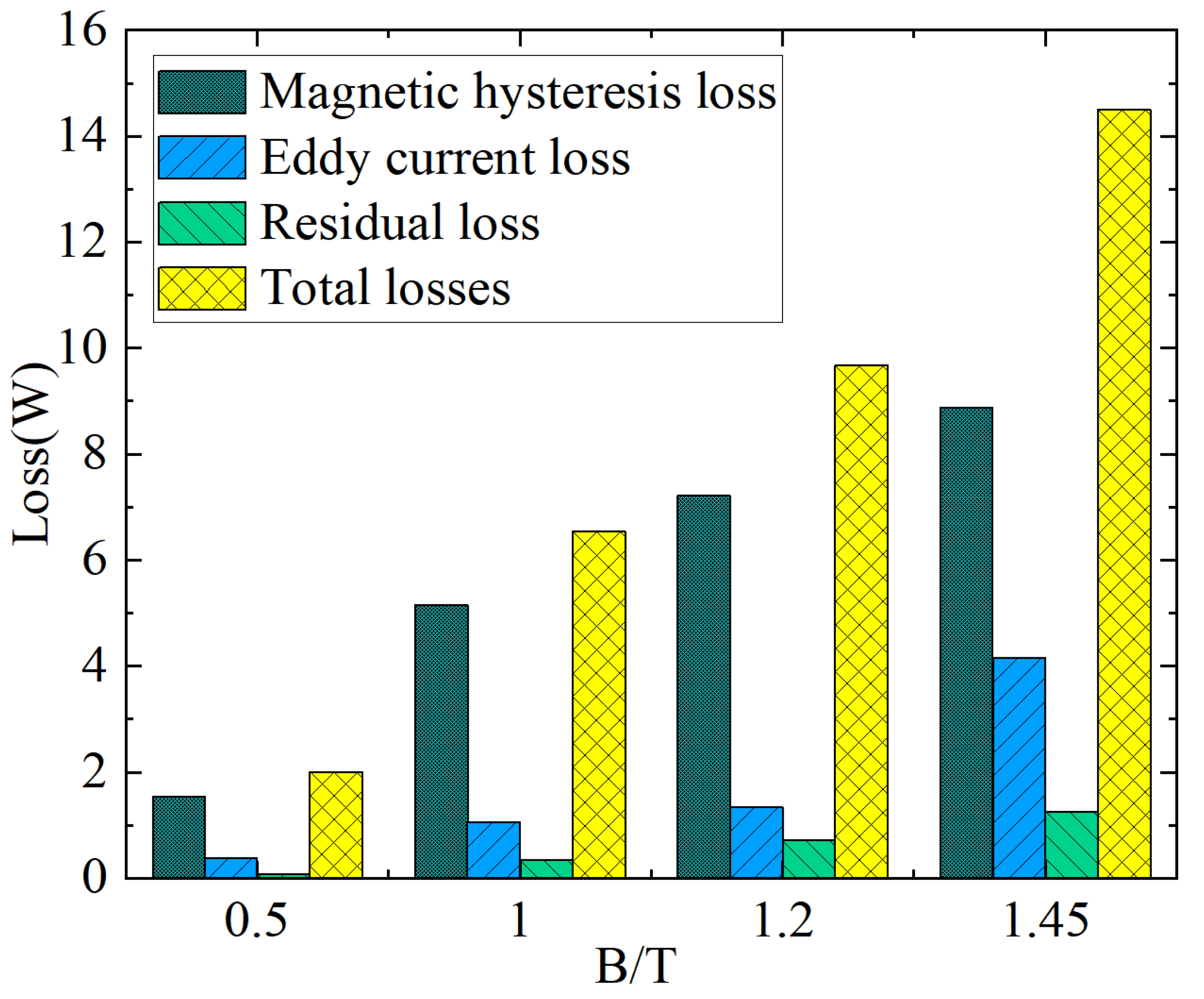
2.2. Loss Separation Method for Single-Frame Amorphous Alloy Iron Core
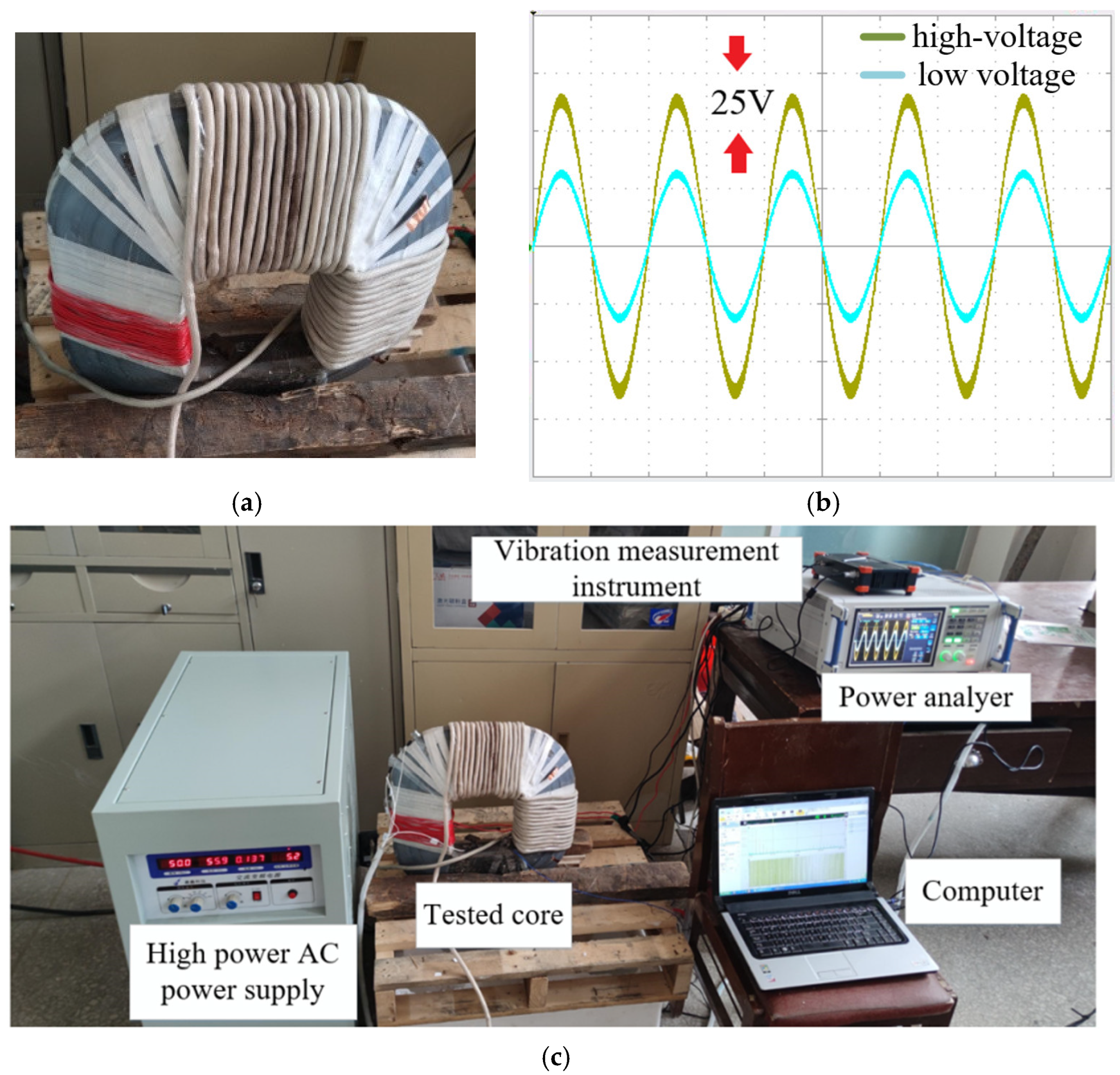
2.3. Construction of Finite Element Simulation
3. Core Loss Characteristics Under Non-Sinusoidal Excitation
4. Core Rotational Magnetization
5. Conclusions
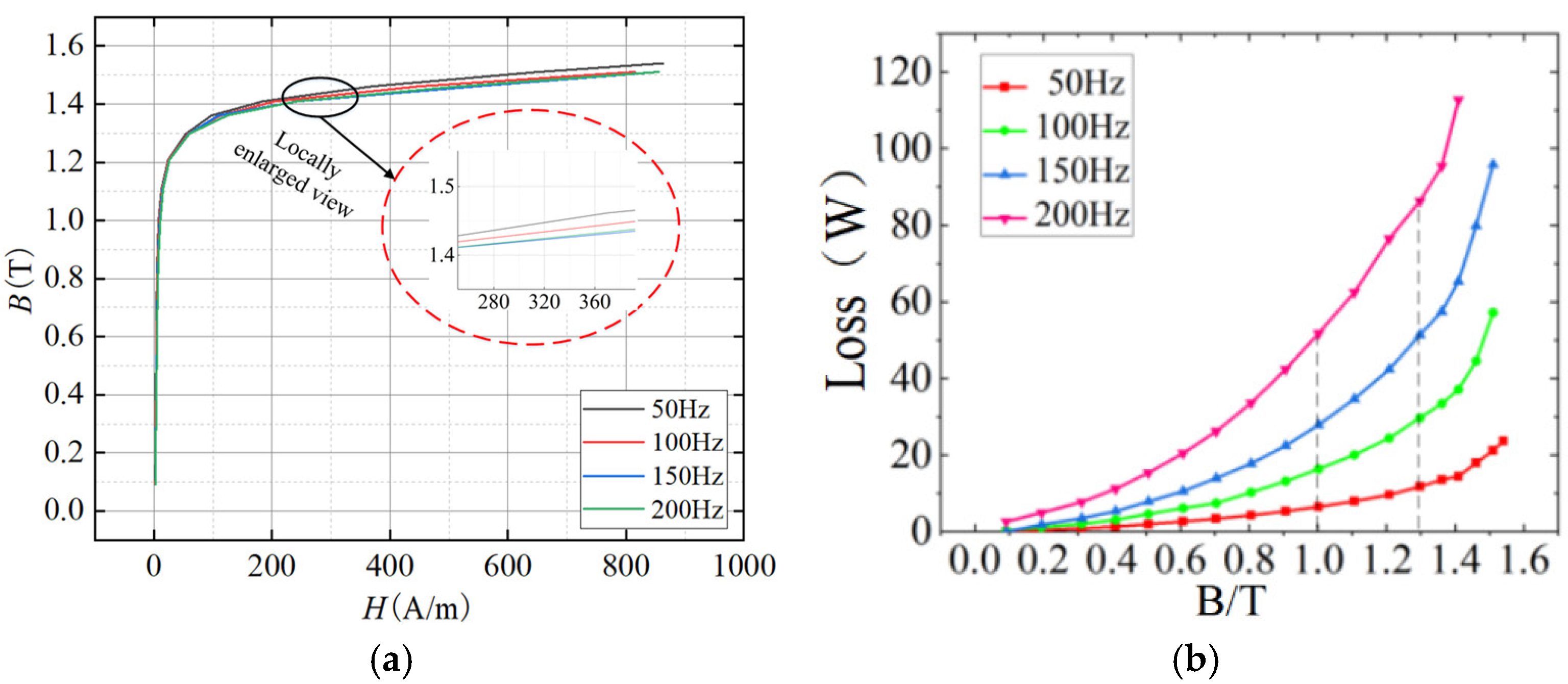
- Using the Brockhaus magnetic characteristic experimental measurement platform, we obtained the magnetization and loss characteristics of the amorphous alloy core under sinusoidal excitations at different frequencies. Results show that as frequency increases, the B-H curve slope decreases, and loss increases at the same magnetic flux density.
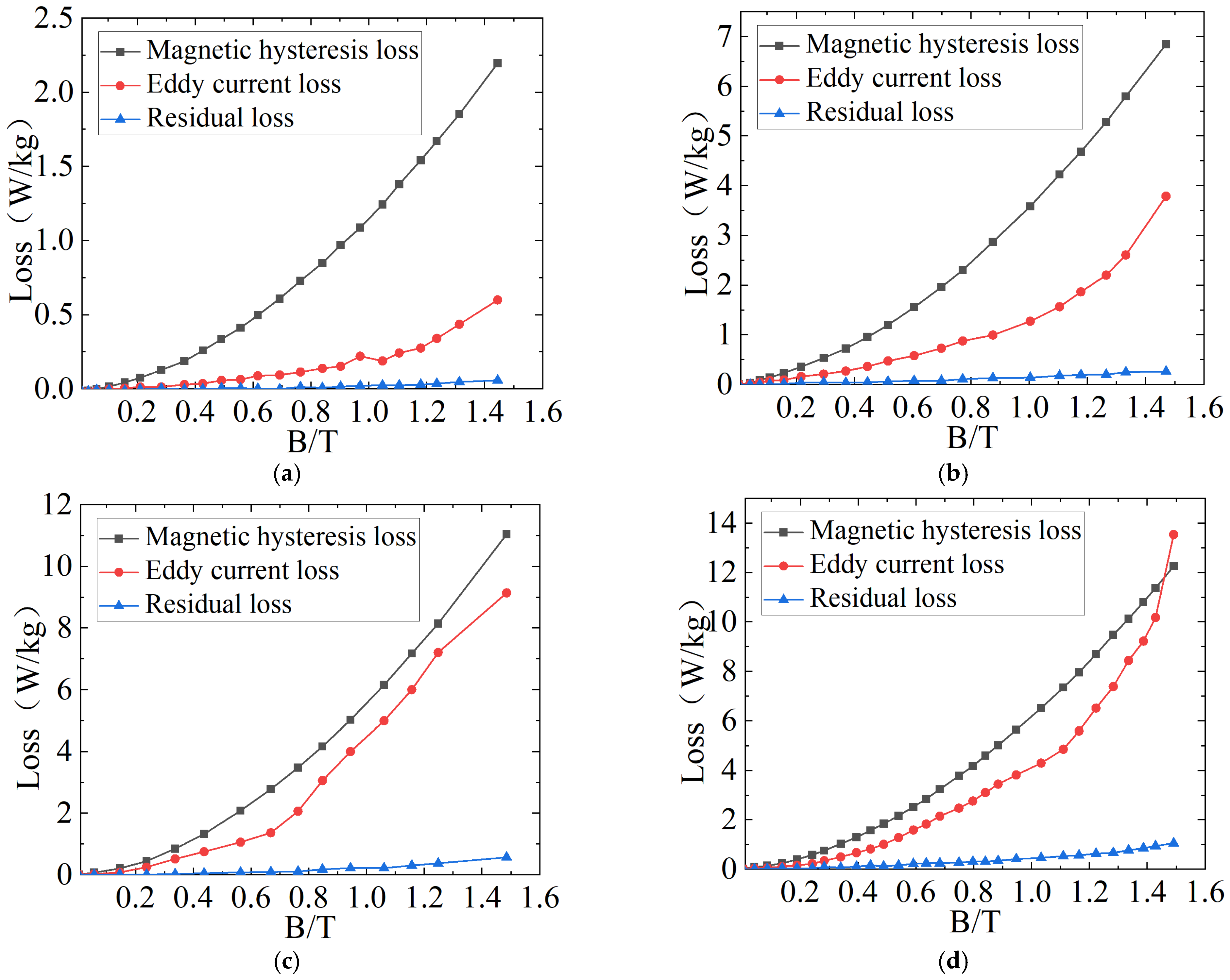
- Our proposed loss separation model for transformer cores can effectively separate hysteresis, eddy current, and residual losses after parameter fitting via the Levenberg–Marquardt optimization algorithm. Separated losses at different frequencies were obtained. The eddy current loss of the amorphous alloy is relatively small, while the hysteresis loss grows exponentially with the magnetic flux density peak.
- In an inter-harmonic environment, inter-harmonic components increase the transformer’s peak magnetic flux density, worsen saturation, and cause a large loss increase, hindering normal operation. Notably, core loss under inter-harmonic excitation is much greater than under sinusoidal excitation.
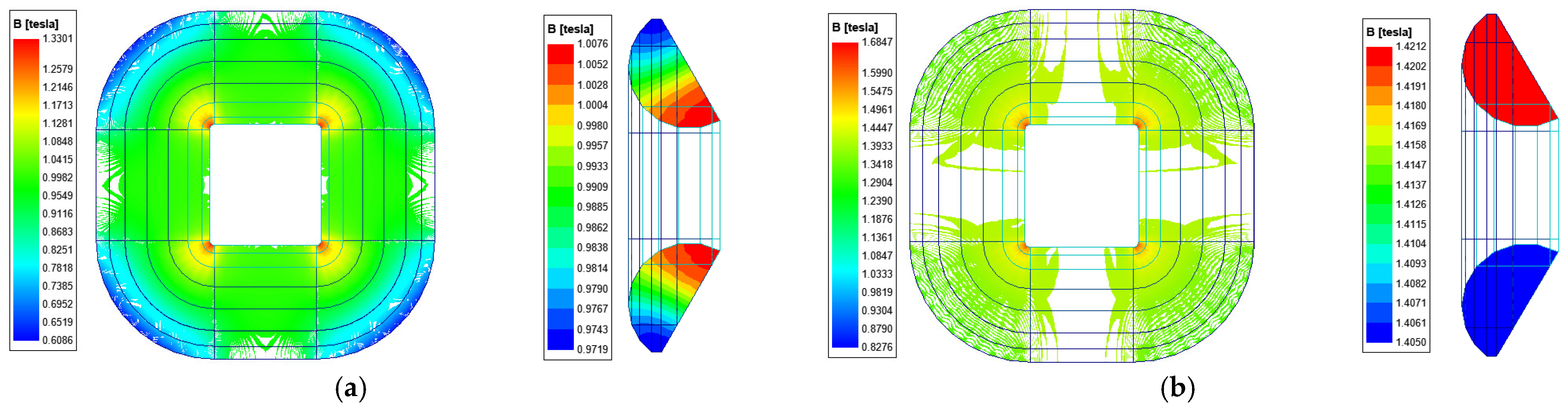
- In transformer cores, rotational and alternating magnetization occur. Analyzing the magnetization curves of characteristic points on different sections of the amorphous 3D wound core reveals that although the magnetic flux density at each point is sinusoidal, the radial and tangential magnetic flux density distributions are non-uniform. Their variation patterns differ across sections and from the outer to inner frame, and the influence extents of the two magnetization types on characteristic points also vary. This means that considering only alternating magnetization in core loss calculation increases error, and rotational magnetization of the amorphous core should be considered.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| 3D | three-dimensional wound core |
| J-A | Josephson–Anderson |
| PWM | pulse width modulation |
| B | magnetic induction |
| H | magnetic field strength |
References
- Krings, A.; Boglietti, A.; Cavagnino, A.; Sprague, S. Soft Magnetic Material Status and Trends in Electric Machines. IEEE Trans. Ind. Electron. 2017, 64, 2405–2414. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, L.; Zhu, J. Core Loss Calculation Based on Finite-Element Method With Jiles–Atherton Dynamic Hysteresis Model. IEEE Trans. Magn. 2018, 54, 1300105. [Google Scholar] [CrossRef]
- Zhao, H.; Ragusa, C.; de la Barrière, O.; Khan, M.; Appino, C.; Fiorillo, F. Magnetic Loss Versus Frequency in Non-Oriented Steel Sheets and Its Prediction: Minor Loops, PWM, and the Limits of the Analytical Approach. IEEE Trans. Magn. 2017, 53, 2003804. [Google Scholar] [CrossRef]
- Du, R.; Robertson, P. Dynamic Jiles–Atherton Model for Determining the Magnetic Power Loss at High Frequency in Permanent Magnet Machines. IEEE Trans. Magn. 2015, 51, 7301210. [Google Scholar]
- Hwang, S.; Lim, M.; Hong, J. Hysteresis Torque Estimation Method Based on Iron-Loss Analysis for Permanent Magnet Synchronous Motor. IEEE Trans. Magn. 2016, 52, 8204904. [Google Scholar] [CrossRef]
- Wei, W.; Nysveen, A.; Magnusson, N.; Nilssen, R. Fourier-based effective permeability for transformer iron losses computation under saturation. IET Electr. Power Appl. 2020, 14, 2609–2615. [Google Scholar]
- Li, Y.; Liu, H.; Sun, H.; Wan, Z. High-Frequency Loss Modeling of Amorphous and Nanocrystalline Cores With Different Air Gaps. IEEE Trans. Magn. 2022, 58, 8400105. [Google Scholar] [CrossRef]
- Zhu, L.; Fan, B.; Han, X.; Tang, R. Effects of shrink fitting on iron losses of a permanent magnet synchronous motor with an amorphous core. IET Electr. Power Appl. 2022, 16, 996–1003. [Google Scholar] [CrossRef]
- Xu, X.; Zhu, T.; Zhao, Z.; Liu, W. Loss calculation and temperature prediction method for High-Speed amorphous alloy PMSM considering the coupling effect of Multi-Physical field factors. J. Magn. Magn. Mater. 2025, 614, 172689. [Google Scholar] [CrossRef]
- Zhou, Y.; Sun, A. Simplified ferrite core loss separation model for switched mode power converter. IET Power Electron. 2016, 9, 529–535. [Google Scholar]
- Kampen, D.; Owzareck, M.; Beyer, S.; Parspour, N.; Schmitt, S. Analytical core loss models for electrical steel in power electronic applications. In Proceedings of the 2012 13th International Conference on Optimization of Electrical and Electronic Equipment (OPTIM), Brasov, Romania, 24–26 May 2012; pp. 109–117. [Google Scholar]
- Pfützner, H.; Shilyashki, G.; Christodoulou, N. Standardisation concept for rapid testing of effects of cutting on losses of electric steel and amorphous ribbon. IET Electr. Power Appl. 2024, 18, 1164–1173. [Google Scholar] [CrossRef]
- Barg, S.; Ammous, K.; Mejbri, H.; Ammous, A. An Improved Empirical Formulation for Magnetic Core Losses Estimation Under Nonsinusoidal Induction. IEEE Trans. Power Electron. 2017, 32, 2146–2154. [Google Scholar] [CrossRef]
- Seyedshenava, S.; Ahmadpour, A. Finite element method for optimal transformer connection based on induction motor characteristics analysis. Ain Shams Eng. J. 2021, 12, 1943–1957. [Google Scholar] [CrossRef]
- Deng, X.; Mecrow, B.; Martin, R.; Gadoue, S. Effects of Winding Connection on Performance of a Six-Phase Switched Reluctance Machine. IEEE Trans. Energy Convers. 2018, 33, 166–178. [Google Scholar] [CrossRef]
- Moses, P.S.; Masoum, M.A.S. Three-Phase Asymmetric Transformer Aging Considering Voltage-Current Harmonic Interactions, Unbalanced Nonlinear Loading, Magnetic Couplings, and Hysteresis. IEEE Trans. Energy Convers. 2012, 27, 318–327. [Google Scholar] [CrossRef]
- Monteiro, T.C.; Martinz, F.O.; Matakas, L.; Komatsu, W. Transformer Operation at Deep Saturation: Model and Parameter Determination. IEEE Trans. Ind. Appl. 2012, 48, 1054–1063. [Google Scholar] [CrossRef]
- Li, D.; Wang, W.; Liu, T.; Li, L.; Lu, Z. Reducing the Core Losses of Fe-Si-B Amorphous Alloy Ribbons by High Cooling Rate Planar Flow Casting. Materials 2022, 15, 894. [Google Scholar] [CrossRef] [PubMed]
- Dawood, K.; Komurgoz, G.; Isik, F. Modeling of Distribution Transformer for Analysis of Core Losses of Different Core Materials Using FEM. In Proceedings of the in 2019 8th International Conference on Modeling Simulation and Applied Optimization (ICMSAO), Manama, Bahrain, 15–17 April 2019; pp. 1–5. [Google Scholar]



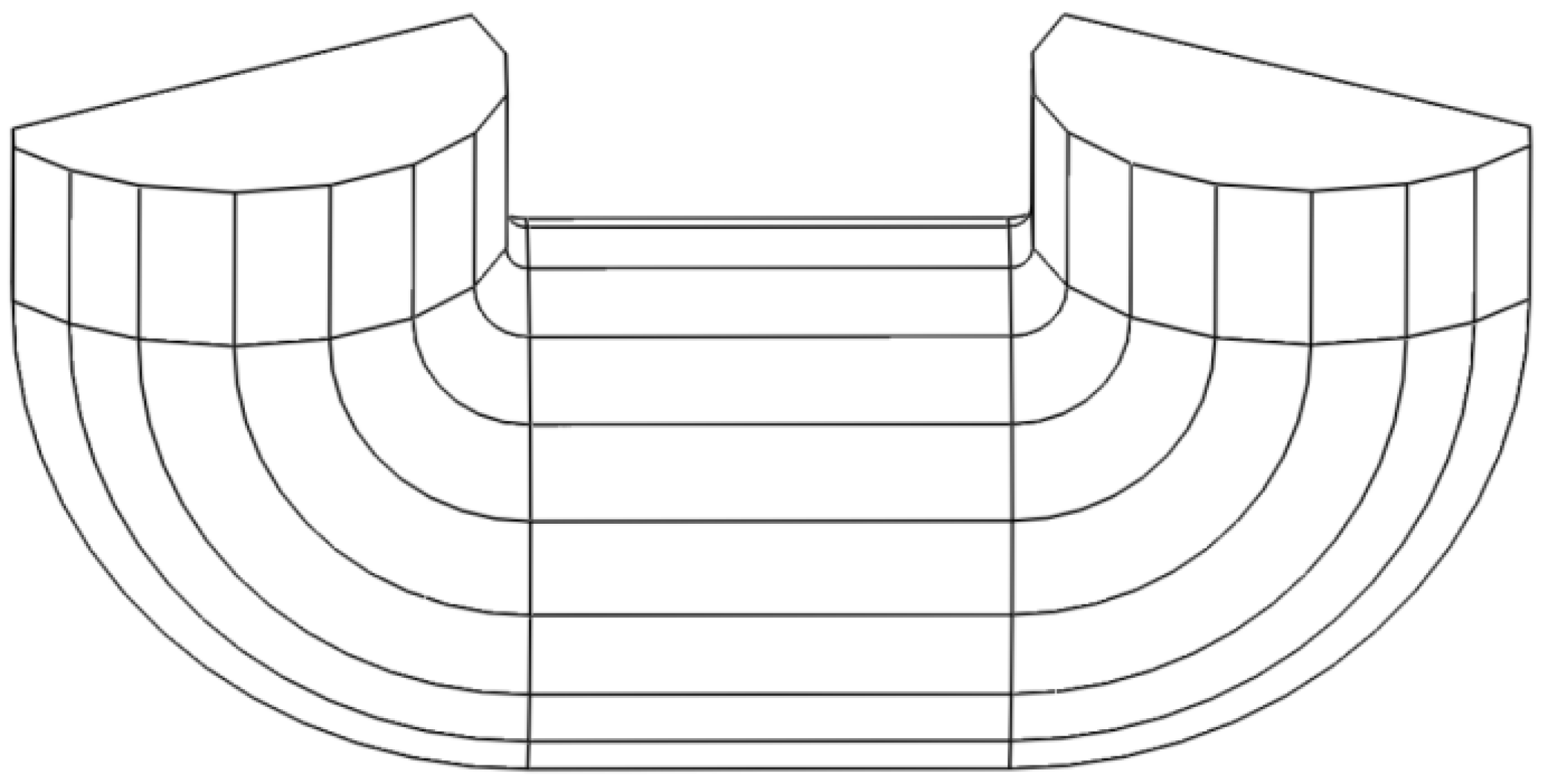
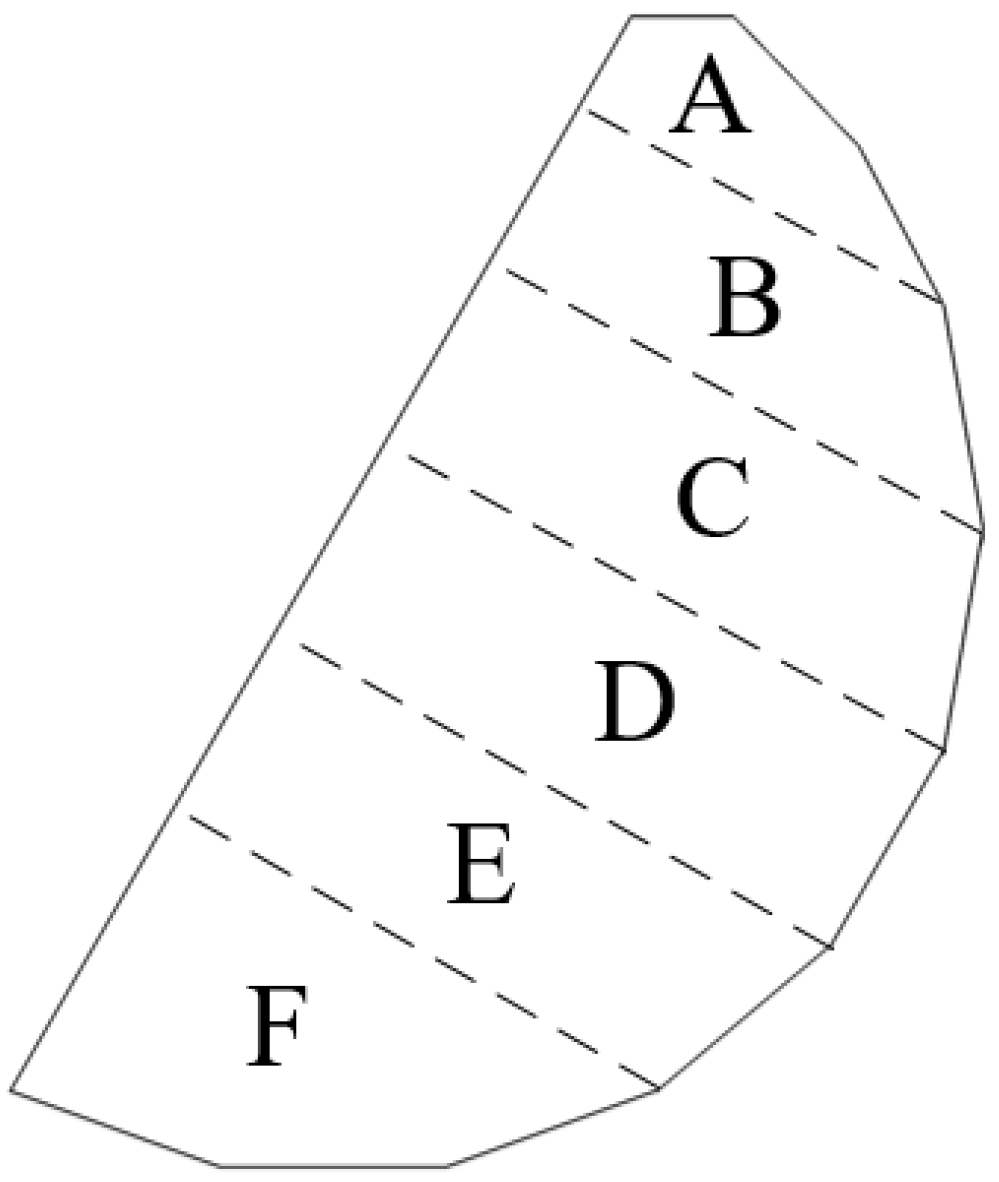
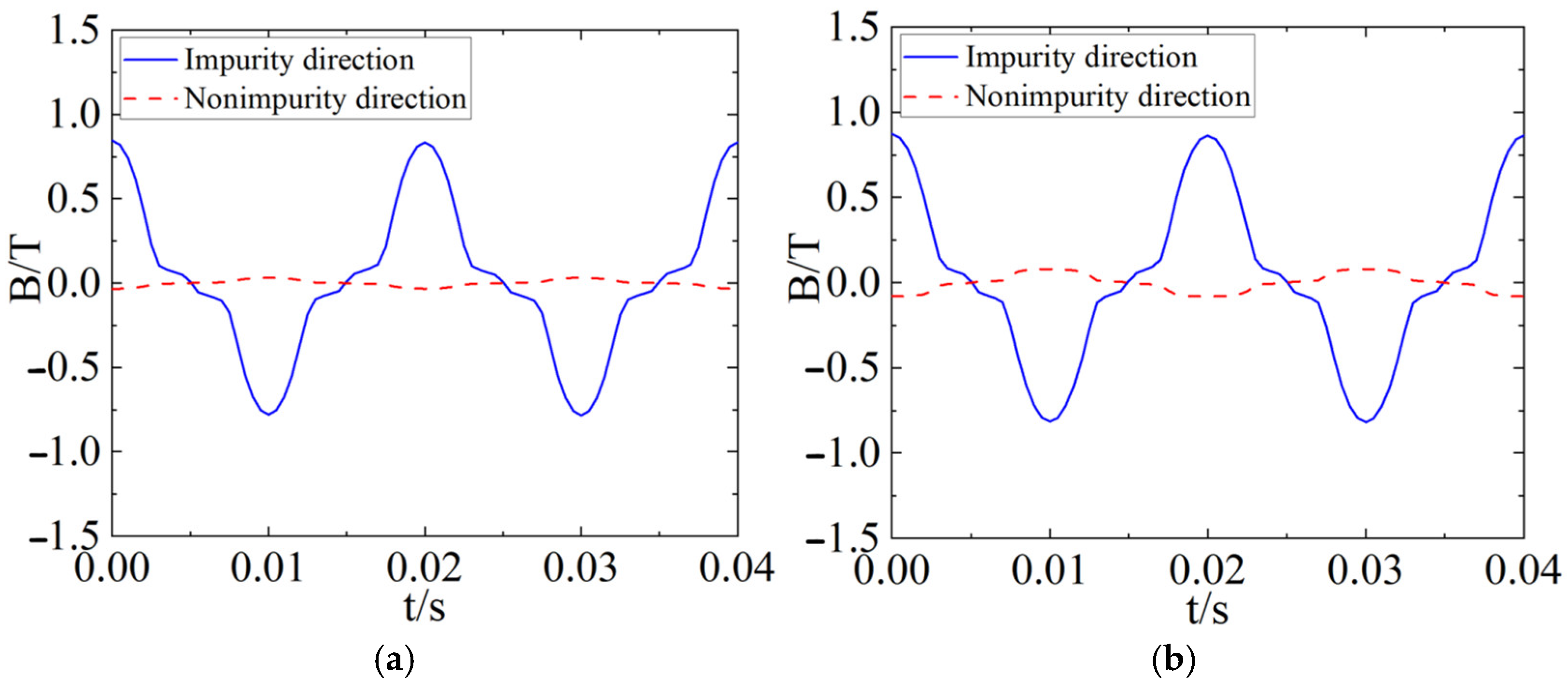

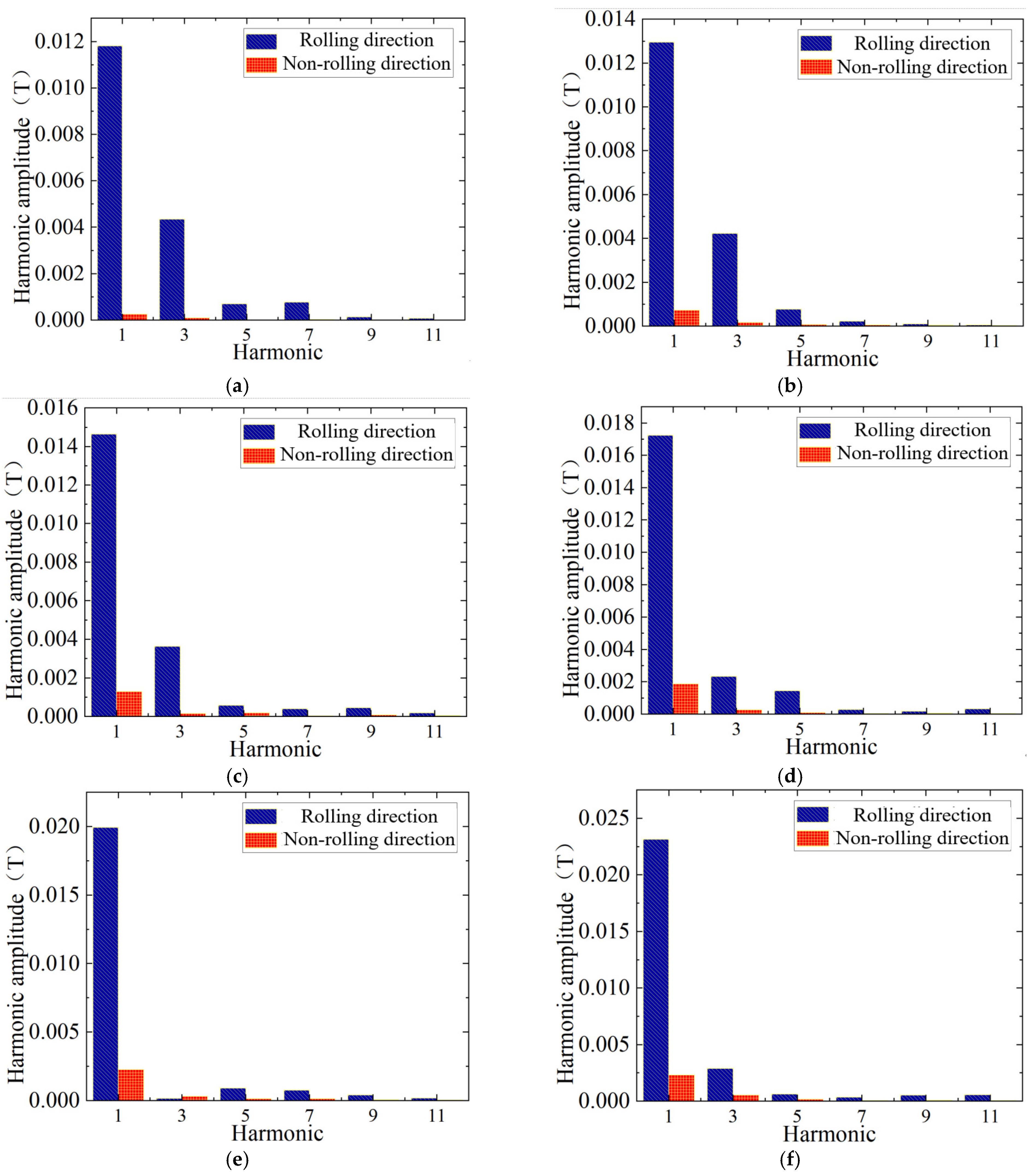
| Parameter | Value |
|---|---|
| Rated capacity (kV) | 10 × (1 ± 5%)/0.4 |
| Capacity (kVA) | 50 |
| Connection mode | Dyn11 |
| Core radius (mm) | 80.0 |
| Number of turns in primary side winding | 30 |
| Number of turns of secondary side winding | 15 |
| Low-voltage winding radius (mm) | 208/173 |
| High-voltage winding radius (mm) | 288/218 |
| Short-circuit impedance (%) | 4.26 |
| Sinusoidal Core | Parameter | Sinusoidal Core | Parameter |
|---|---|---|---|
| Kh | 0.045 | α2 | −6.114 |
| β1 | 0.547 | α3 | 0.421 |
| β2 | 6.221 | α4 | 2.054 |
| β3 | −11.151 | α5 | −2.247 |
| β4 | 6.124 | α6 | 4.698 |
| α1 | 9.012 | − | − |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, P.; Han, J.; Yao, X.; Wang, X.; Yan, Y.; Zhao, Z.; Zhang, L.; Yu, Z.; Li, H. Modeling and Testing of 3D Wound Core Loss of Amorphous Alloy Transformer for Photovoltaic Inverter. Energies 2025, 18, 2698. https://doi.org/10.3390/en18112698
Chen P, Han J, Yao X, Wang X, Yan Y, Zhao Z, Zhang L, Yu Z, Li H. Modeling and Testing of 3D Wound Core Loss of Amorphous Alloy Transformer for Photovoltaic Inverter. Energies. 2025; 18(11):2698. https://doi.org/10.3390/en18112698
Chicago/Turabian StyleChen, Peng, Jianwei Han, Xinglong Yao, Xiaohui Wang, Yunfei Yan, Zhe Zhao, Lisong Zhang, Zhanyang Yu, and Hao Li. 2025. "Modeling and Testing of 3D Wound Core Loss of Amorphous Alloy Transformer for Photovoltaic Inverter" Energies 18, no. 11: 2698. https://doi.org/10.3390/en18112698
APA StyleChen, P., Han, J., Yao, X., Wang, X., Yan, Y., Zhao, Z., Zhang, L., Yu, Z., & Li, H. (2025). Modeling and Testing of 3D Wound Core Loss of Amorphous Alloy Transformer for Photovoltaic Inverter. Energies, 18(11), 2698. https://doi.org/10.3390/en18112698






