PID Sliding Mode Control of PMSM Based on Improved Terminal Sliding Mode Reaching Law
Abstract
1. Introduction
- (1)
- An ITSMRL is proposed, which not only balances the reduction in chattering with the acceleration of convergence but also considers the complexity of the structure. It has been verified that the RL can reach a sliding mode surface within a finite time.
- (2)
- A novel speed composite controller based on a PID sliding mode surface with an ITSMRL and ESO is designed. The boundedness of the estimated error of the ESO and the stability of the closed-loop system are proven.
- (3)
- The validity and robustness of the proposed algorithm are evidenced by simulation and experimental tests.
2. Preliminaries
3. Design of Sliding Mode Controller Based on ESO and ITSMRL
3.1. Improved TSMRL Design
3.1.1. TSMRL
3.1.2. Proposed ITSMRL
3.2. Design of ESO
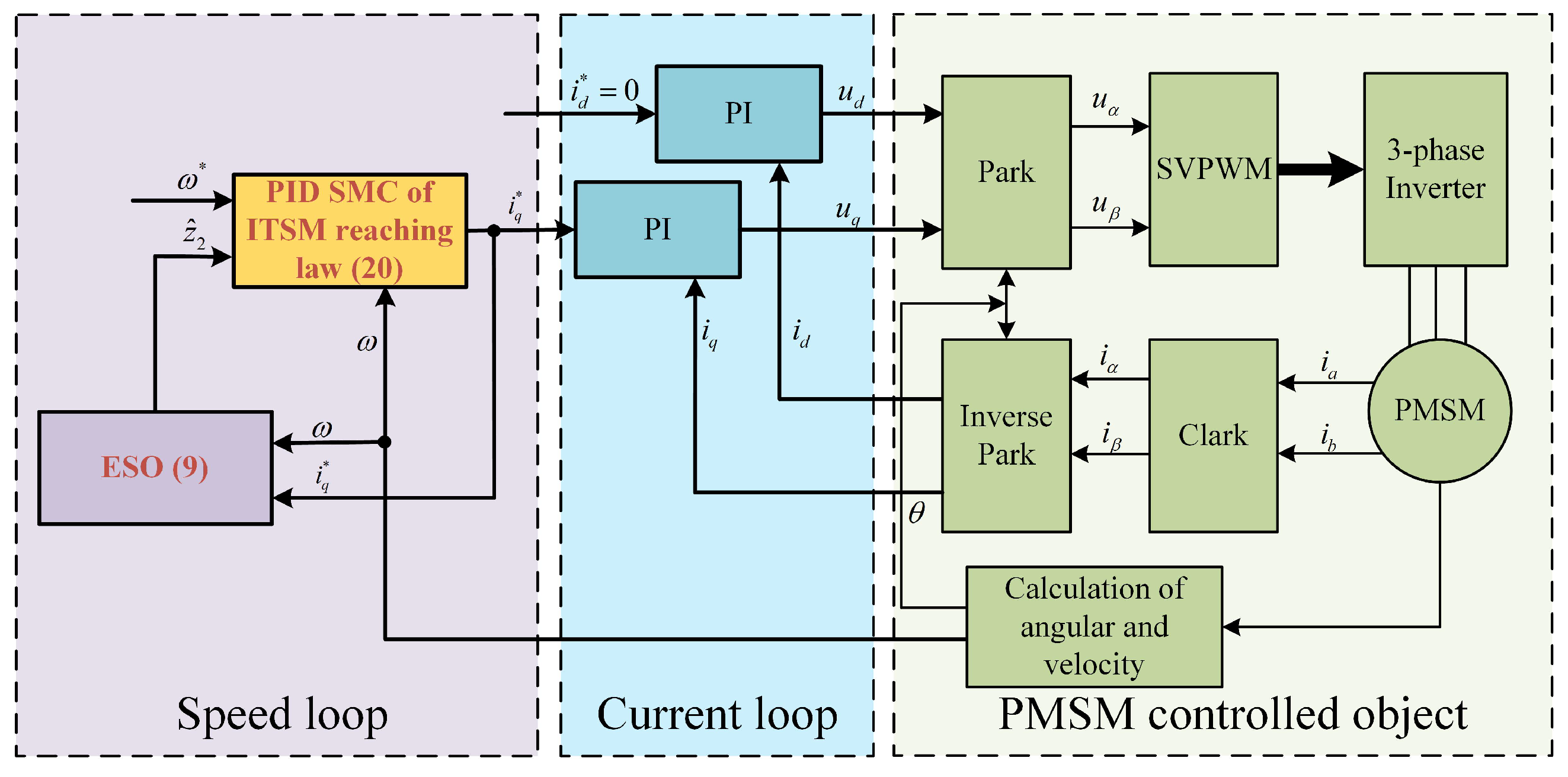
3.3. Design of Proposed Controller
4. Simulations and Experiments
4.1. Simulations
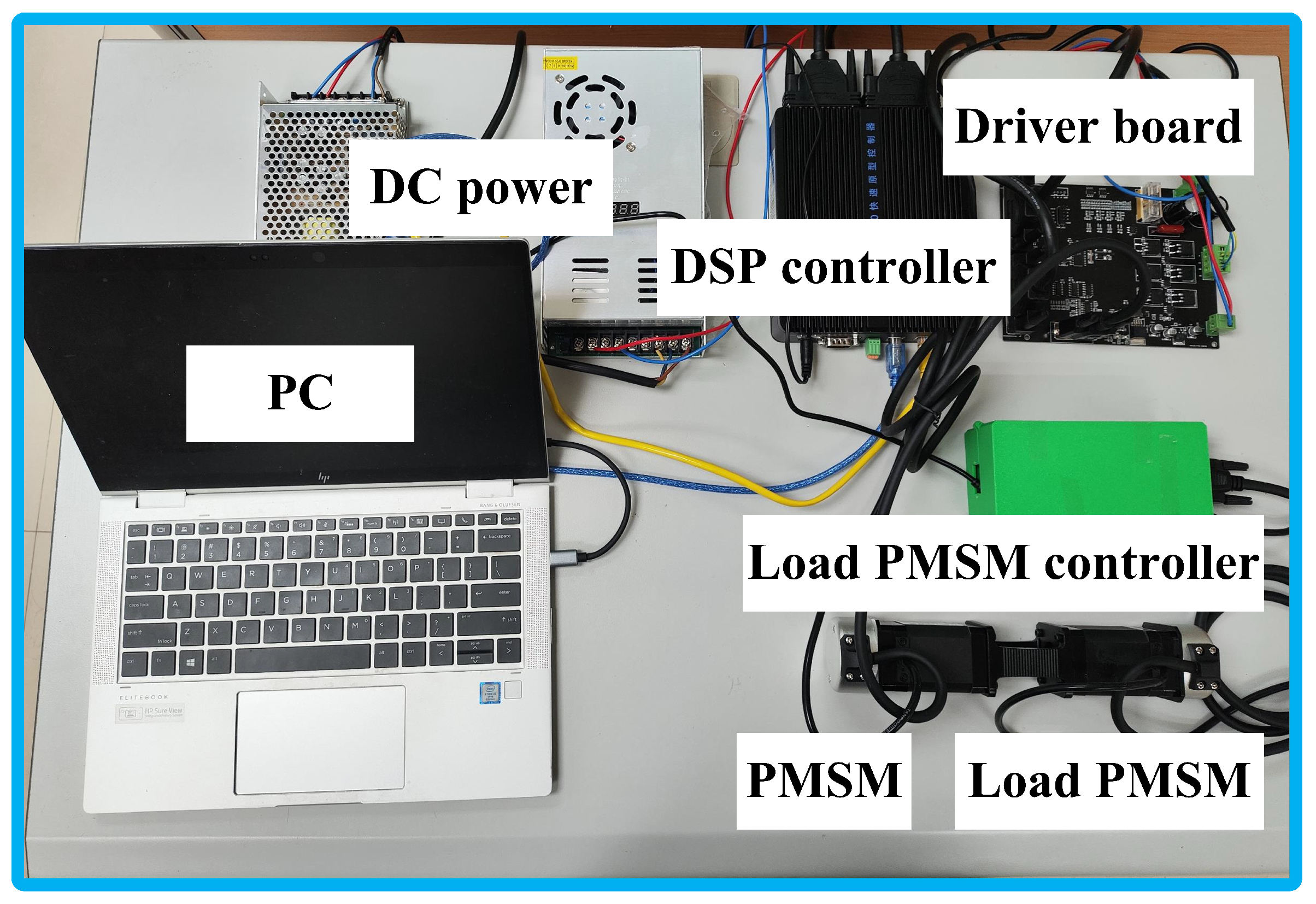
4.2. Experiments
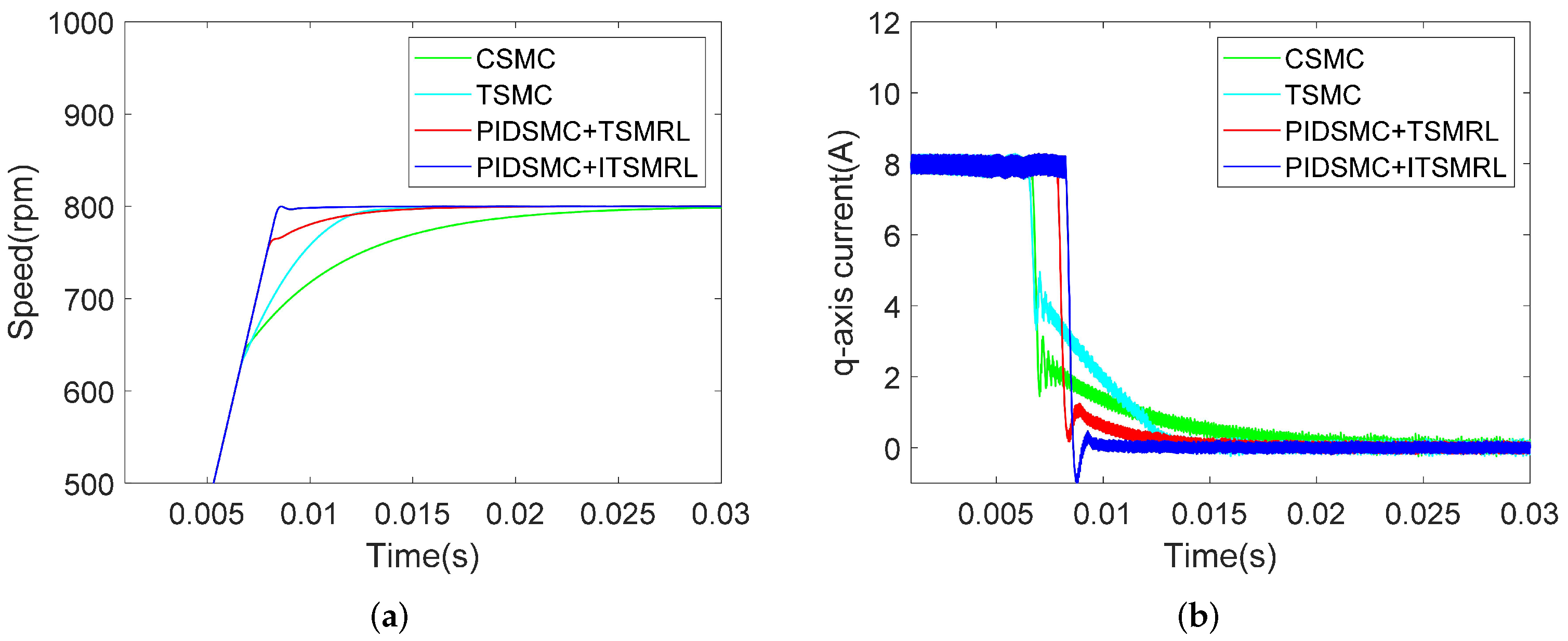
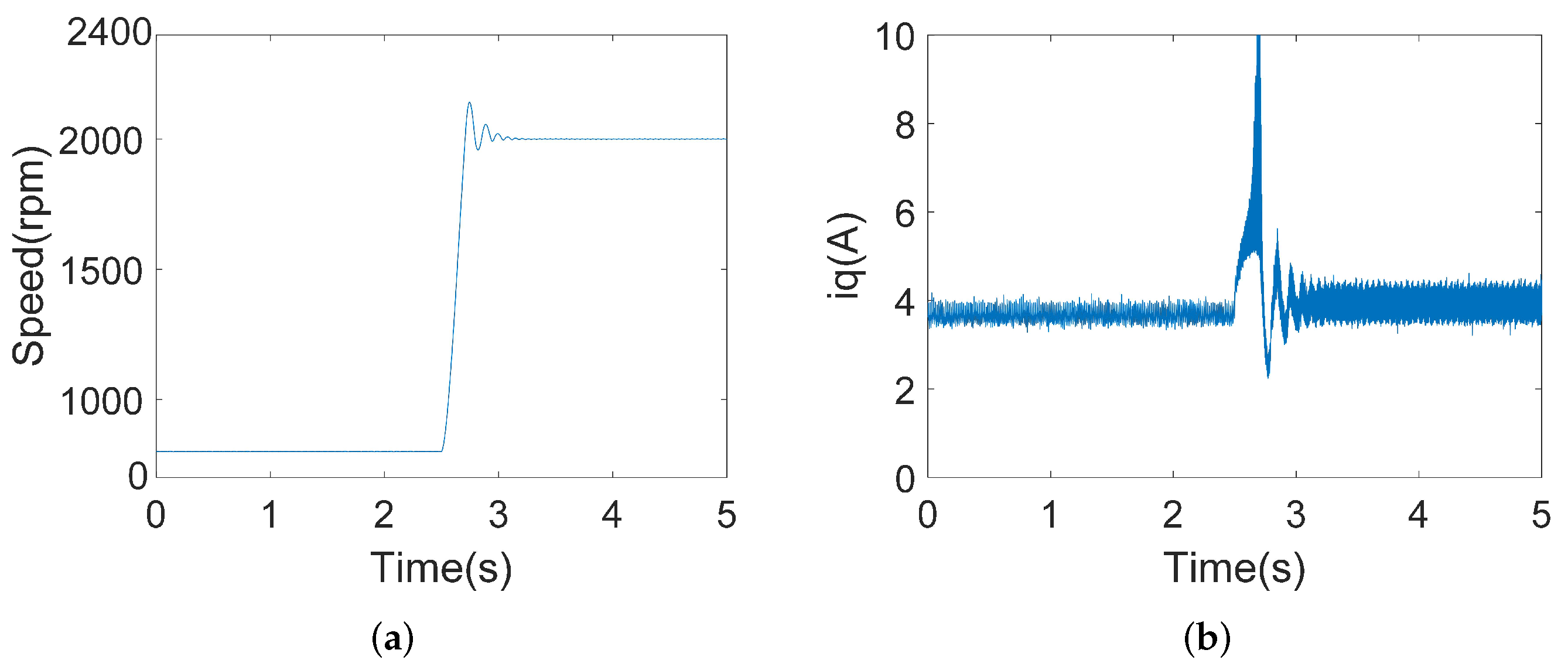
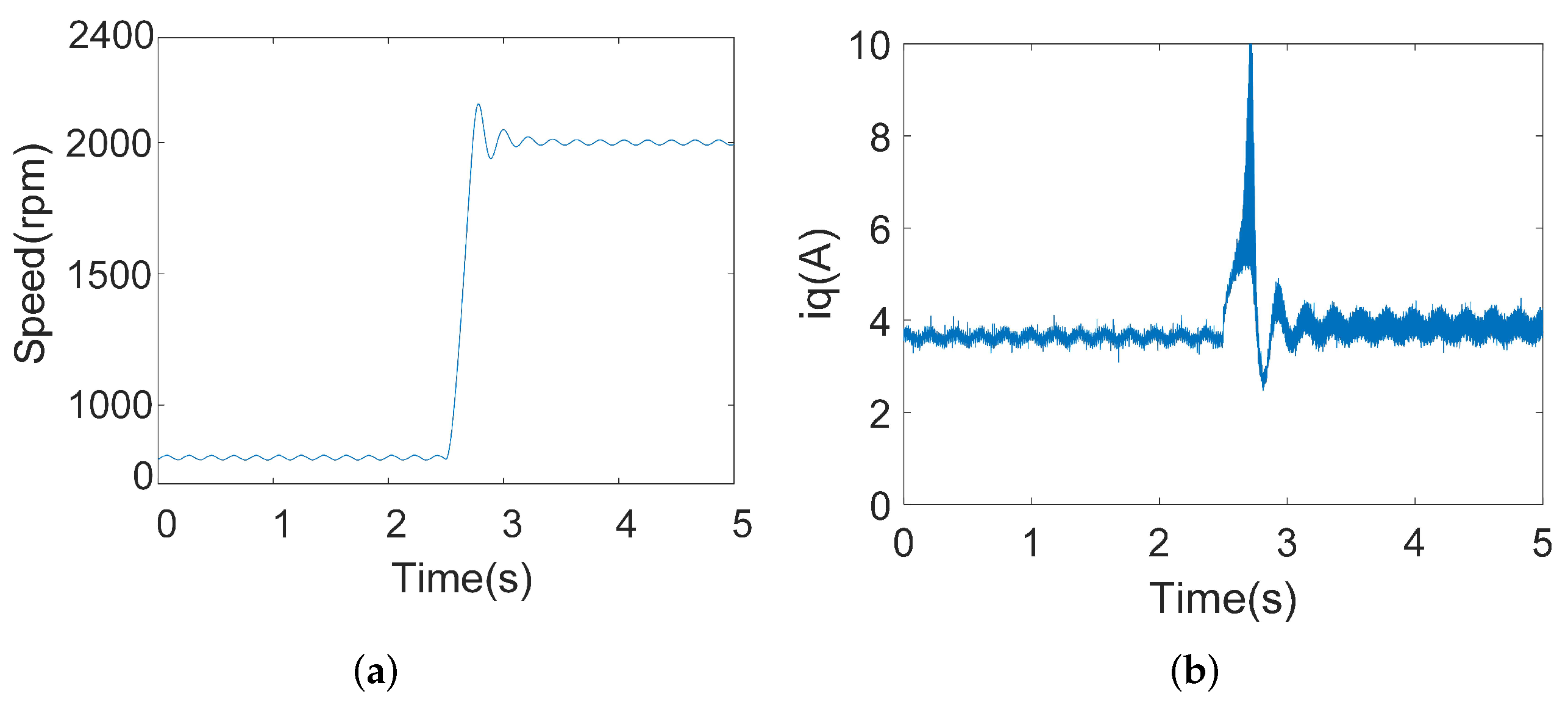
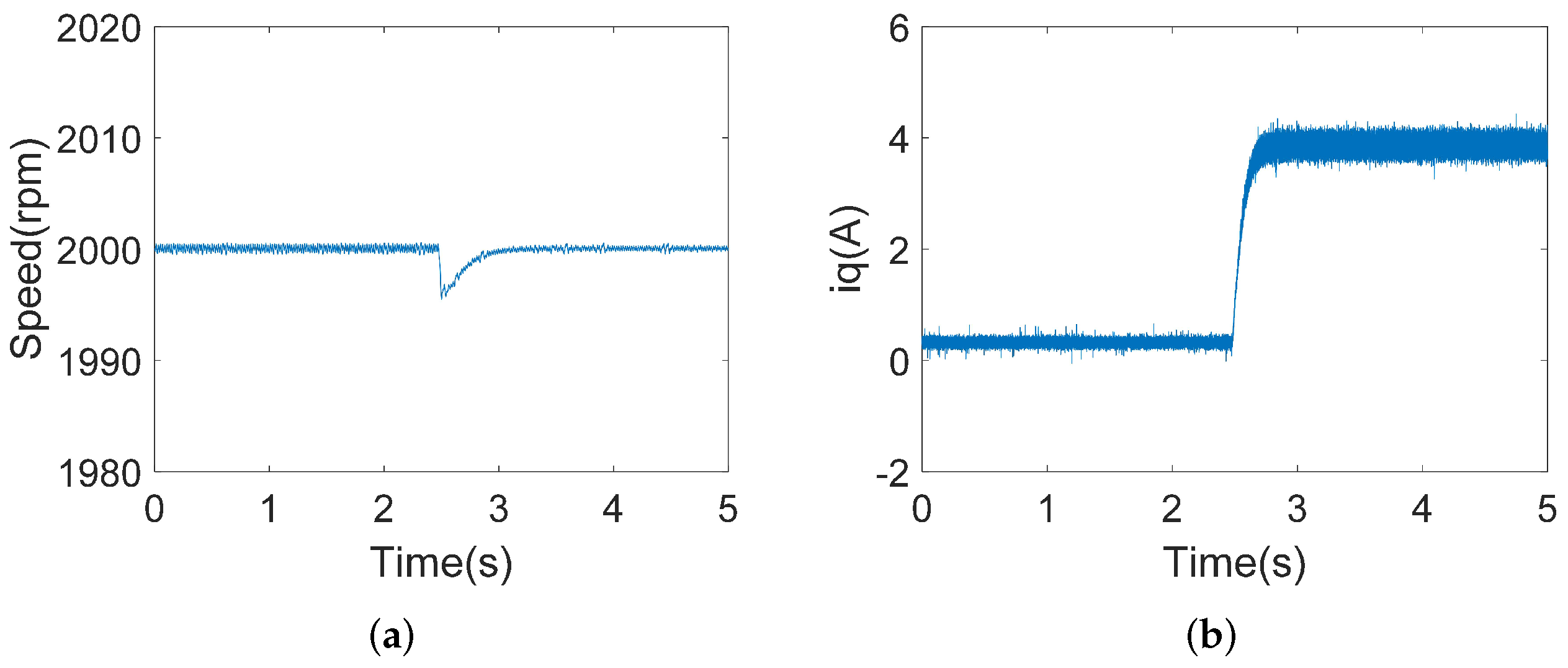
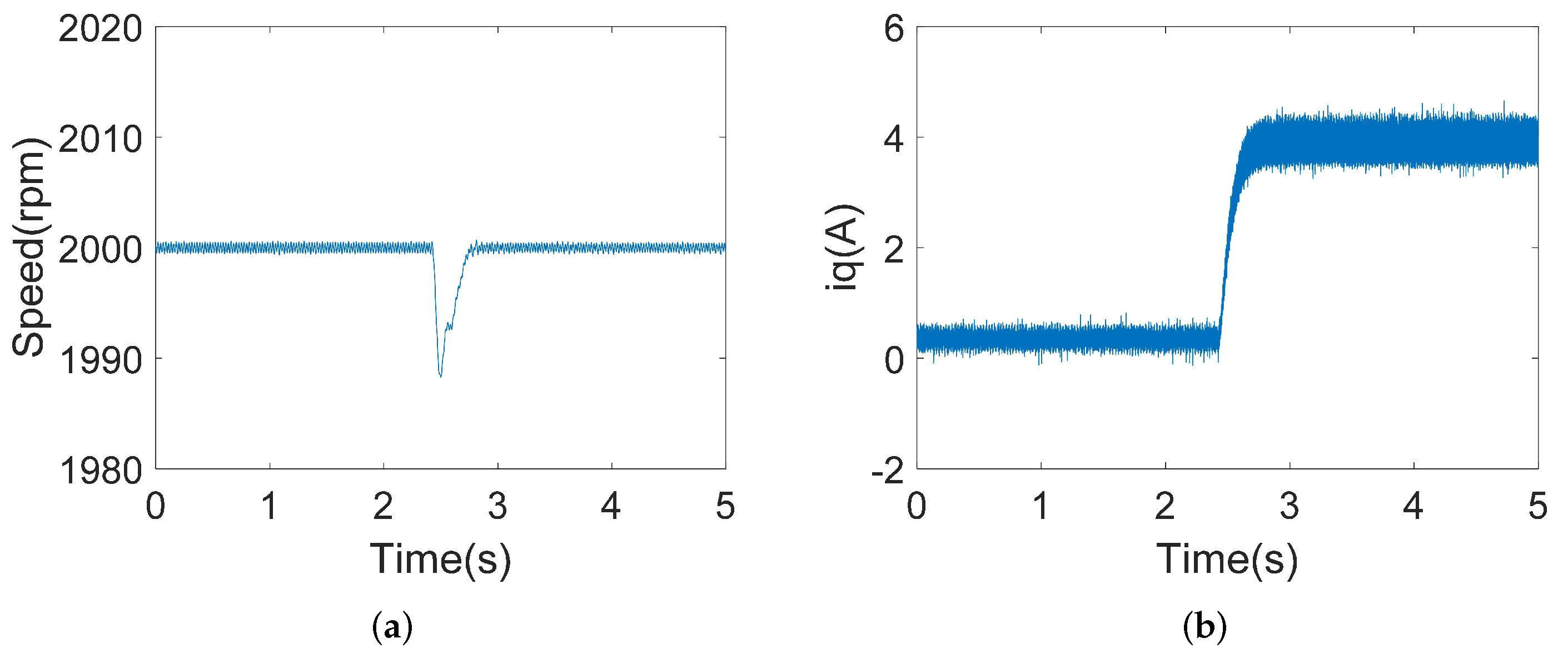
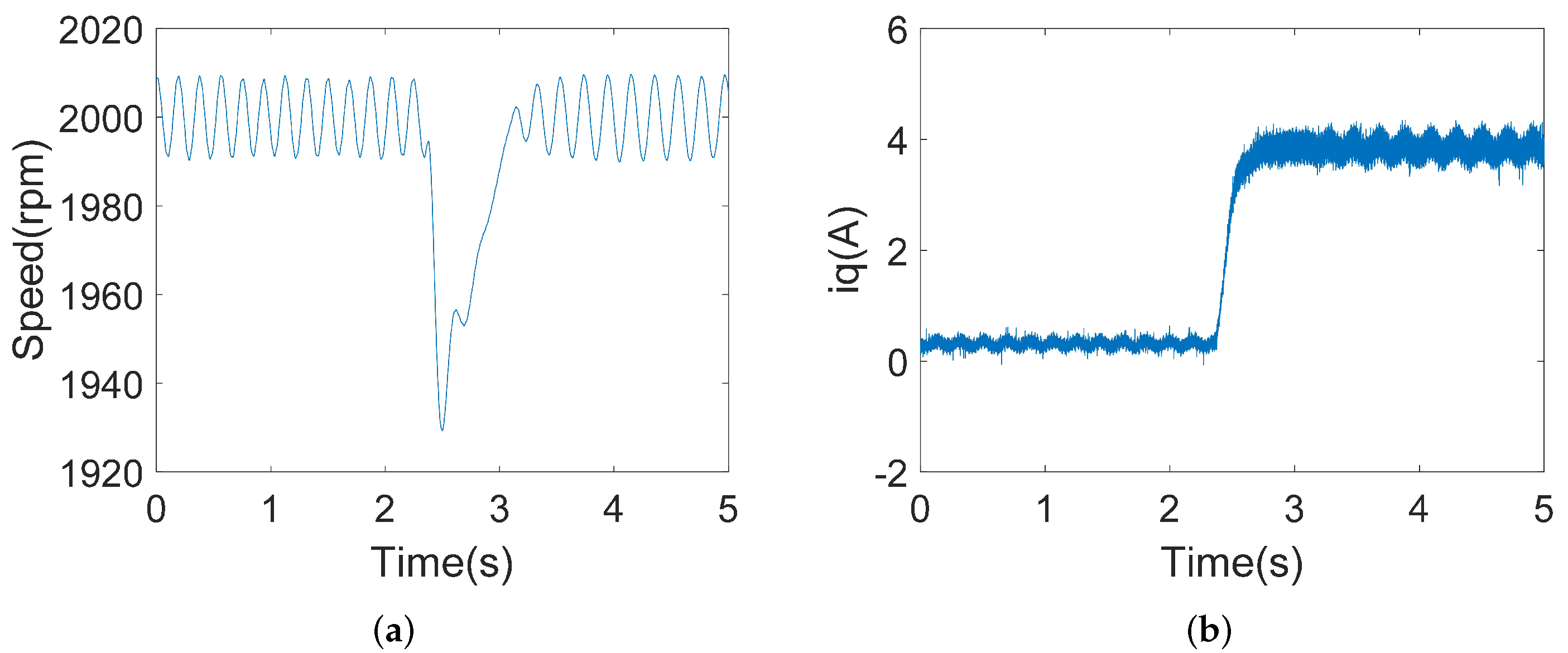
4.2.1. Acceleration Experiments
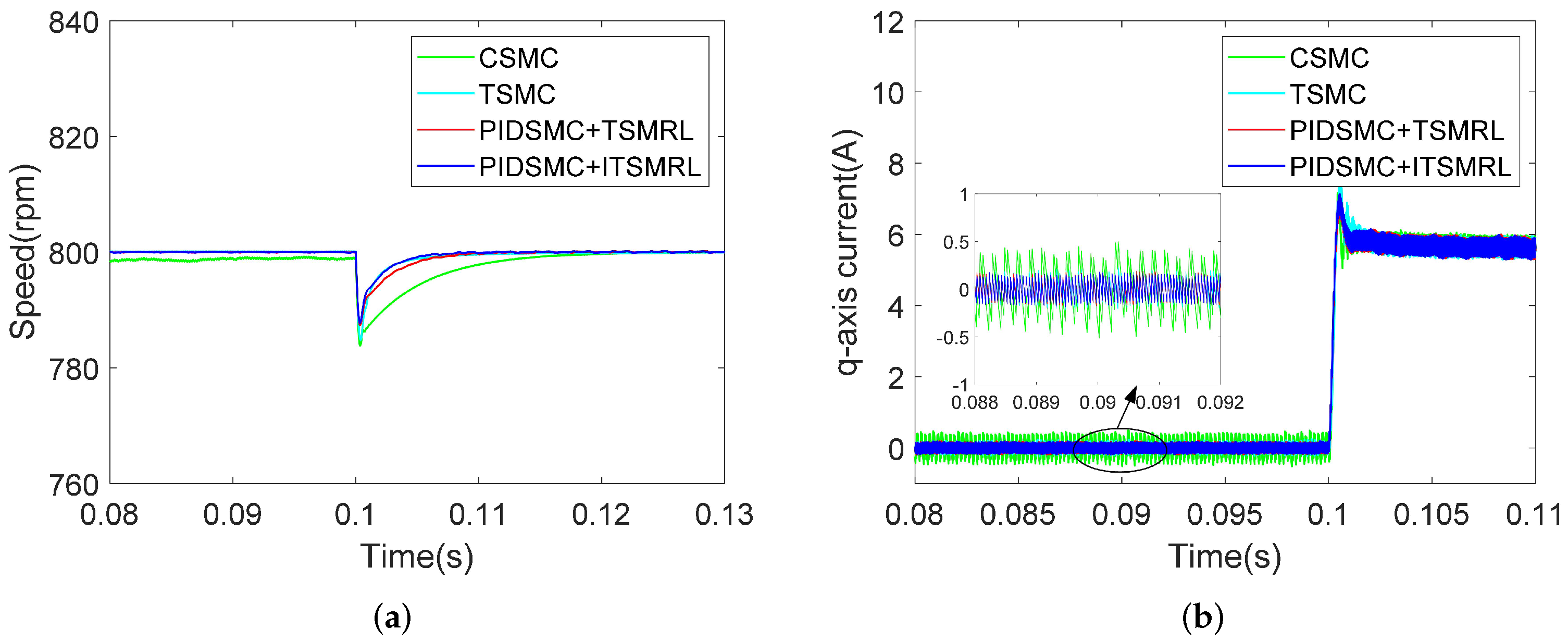
4.2.2. Loading Experiments
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kang, W.; Li, H. Improved Sliding Mode Observer Based Sensorless Control for PMSM. IEICE Electron. Express 2017, 14, 20170934. [Google Scholar] [CrossRef]
- Zerdali, E.; Rivera, M.; Wheeler, P. A Review on Weighting Factor Design of Finite Control Set Model Predictive Control Strategies for AC Electric Drives. IEEE Trans. Power Electron. 2024, 39, 9967–9981. [Google Scholar] [CrossRef]
- Wang, M.; Liu, Y.; Wang, Q.; Wheeler, P. Current-constraint Speed Regulation for PMSM Based on Port-controlled Hamiltonian Realization and Deep Deterministic Policy Gradient. IEICE Electron. Express 2024, 21, 20230516. [Google Scholar] [CrossRef]
- Guo, T.; Sun, Z.; Wang, X.; Li, S.; Zhang, K. A Simple Current-Constrained Controller for Permanent-Magnet Synchronous Motor. IEEE Trans. Ind. Inform. 2019, 15, 1486–1495. [Google Scholar] [CrossRef]
- Zhang, N.; Guo, K.; Guo, Y. Research on Low Speed Operation of PMSM Based on Improved Non-Singular Fast Terminal SMC. IEEE Trans. Appl. Supercond. 2024, 34, 5209705. [Google Scholar] [CrossRef]
- Rubio, F.; Pereda, J.; Mora, A.; Rojas, F. Optimal Switching Sequence MPC of a Three- Port-Converter for Variable-Speed PMSM with Hybrid Energy Storage. IEEE Trans. Power Electron. 2025, 40, 5069–5079. [Google Scholar] [CrossRef]
- Tian, M.; Wang, B.; Yu, Y.; Dong, Q.; Xu, D. Enhanced One Degree-of-Freedom ADRC with Sampled-Data Iterative Learning Controller for PMSM Uncertain Speed Fluctuations Suppression. IEEE Trans. Transp. Electrif. 2024, 10, 8321–8335. [Google Scholar] [CrossRef]
- Zou, W.; Shi, T.; Guo, J.; Xiang, Z. A Novel Adaptive Fuzzy Control Scheme for a Class of Nonlinear Planar Systems Under State Constraints. IEEE Trans. Circuits Syst. II Express Briefs 2024, 71, 827–831. [Google Scholar] [CrossRef]
- Carlet, P.G.; Favato, A.; Bolognani, S.; Dörfler, F. Data-Driven Continuous-Set Predictive Current Control for Synchronous Motor Drives. IEEE Trans. Power Electron. 2022, 37, 6637–6646. [Google Scholar] [CrossRef]
- Li, S.; Xu, Y.; Zhang, W.; Zou, J. A Novel Two-Phase Mode Switching Control Strategy for PMSM Position Servo Systems with Fast-Response and High-Precision. IEEE Trans. Power Electron. 2023, 38, 803–815. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, S.; Hu, J.; Huang, D. Multiscenarios Parameter Optimization Method for Active Disturbance Rejection Control of PMSM Based on Deep Reinforcement Learning. IEEE Trans. Ind. Electron. 2023, 70, 10957–10968. [Google Scholar] [CrossRef]
- Liu, X.; Yang, H.; Cai, S.; Lin, H.; Yu, F.; Yang, Y. A Novel Finite-Control-Set Model-Free Predictive Current Control Incorporating Event Triggering Mechanism for PMSM Drives. IEEE Trans. Ind. Appl. 2025, 61, 322–334. [Google Scholar] [CrossRef]
- Zhang, X.; Mao, J.; Zhao, F.; Wang, W.; Jia, R. Speed-current Composite Loop SPMSM Control Based on ADR-SMC. IEICE Electron. Express 2024, 21, 20240088. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, L.; Ji, W. Improved Non-Singular Fast Terminal Sliding Mode Control with Disturbance Observer for PMSM Drives. IEEE Trans. Transp. Electrif. 2021, 7, 2753–2762. [Google Scholar] [CrossRef]
- Wang, S. Nonlinear Uncertainty Estimator-Based Robust Control for PMSM Servo Mechanisms with Prescribed Performance. IEEE Trans. Transp. Electrif. 2023, 9, 2535–2543. [Google Scholar] [CrossRef]
- Repecho, V.; Waqar, J.B.; Biel, D.; Dòria-Cerezo, A. Zero Speed Sensorless Scheme for Permanent Magnet Synchronous Machine Under Decoupled Sliding-Mode Control. IEEE Trans. Ind. Electron. 2022, 69, 1288–1297. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, Z.; Yu, X.; Yang, J.; Li, S. Sliding-Mode-Based Robust Output Regulation and Its Application in PMSM Servo Systems. IEEE Trans. Ind. Electron. 2023, 70, 1852–1860. [Google Scholar] [CrossRef]
- Guo, X.; Huang, S.; Lu, K.; Peng, Y.; Wang, H.; Yang, J. A Fast Sliding Mode Speed Controller for PMSM Based on New Compound Reaching Law with Improved Sliding Mode Observer. IEEE Trans. Transp. Electrif. 2023, 9, 2955–2968. [Google Scholar] [CrossRef]
- Liu, Y.C.; Laghrouche, S.; Depernet, D.; Djerdir, A.; Cirrincione, M. Disturbance-Observer-Based Complementary Sliding-Mode Speed Control for PMSM Drives: A Super-Twisting Sliding-Mode Observer-Based Approach. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 5416–5428. [Google Scholar] [CrossRef]
- Lu, W.; Zhang, Z.; Wang, D.; Lu, K.; Wu, D.; Ji, K.; Guo, L. A New Load Torque Identification Sliding Mode Observer for Permanent Magnet Synchronous Machine Drive System. IEEE Trans. Power Electron. 2020, 35, 1156. [Google Scholar] [CrossRef]
- Cheng, M.B.; Radisavljevic, V.; Su, W.C. Sliding Mode Boundary Control of a Parabolic PDE System with Parameter Variations and Boundary Uncertainties. Automatica 2011, 47, 381–387. [Google Scholar] [CrossRef]
- Zhu, P.; Chen, Y.; Li, M.; Zhang, P.; Wan, Z. Fractional-Order Sliding Mode Position Tracking Control for Servo System with Disturbance. ISA Trans. 2020, 105, 269–277. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Li, D.; Li, Y.; Yang, L. A Novel Discrete Compound Integral Terminal Sliding Mode Control with Disturbance Compensation For PMSM Speed System. IEEE/ASME Trans. Mechatronics 2022, 27, 549–560. [Google Scholar] [CrossRef]
- Xu, W.; Junejo, A.; Liu, Y.; Islam, M.R. Improved Continuous Fast Terminal Sliding Mode Control with Extended State Observer for Speed Regulation of PMSM Drive System. IEEE Trans. Veh. Technol. 2019, 68, 10465–10476. [Google Scholar] [CrossRef]
- Qu, L.; Qiao, W.; Qu, L. An Extended-State-Observer-Based Sliding-Mode Speed Control for Permanent-Magnet Synchronous Motors. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 1605–1613. [Google Scholar] [CrossRef]
- Liu, Y.C.; Laghrouche, S.; Depernet, D.; N’Diaye, A.; Djerdir, A.; Cirrincione, M. Disturbance-observer-based Speed Control for SPMSM Drives Using Modified Super-Twisting Algorithm and Extended State Observer. Asian J. Control 2024, 26, 1089–1102. [Google Scholar] [CrossRef]
- Gao, W.; Hung, J. Variable Structure Control of Nonlinear Systems: A New Approach. IEEE Trans. Ind. Electron. 1993, 40, 45–55. [Google Scholar] [CrossRef]
- Ma, H.; Li, Y.; Xiong, Z. Discrete-Time Sliding-Mode Control with Enhanced Power Reaching Law. IEEE Trans. Ind. Electron. 2019, 66, 4629–4638. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, Y.; Zhang, X.; Tian, B.; Wang, K.; Liang, J. Antidisturbance Sliding Mode-Based Deadbeat Direct Torque Control for PMSM Speed Regulation System. IEEE Trans. Transp. Electrif. 2021, 7, 2705–2714. [Google Scholar] [CrossRef]
- Guo, X.G.; Ahn, C.K. Adaptive Fault-Tolerant Pseudo-PID Sliding-Mode Control for High-Speed Train with Integral Quadratic Constraints and Actuator Saturation. IEEE Trans. Intell. Transp. Syst. 2021, 22, 7421–7431. [Google Scholar] [CrossRef]
- Ventura, J.O.; Morales, D.B.; Oliver, J.P.O.; Quesada, E.S.E. Dynamic Sliding Mode Control with PID Surface for Trajectory Tracking of a Multirotor Aircraft. IEEE Access 2023, 11, 99878–99888. [Google Scholar] [CrossRef]
- Wang, Q.; Yu, H.; Wang, M.; Qi, X. An Improved Sliding Mode Control Using Disturbance Torque Observer for Permanent Magnet Synchronous Motor. IEEE Access 2019, 7, 36691–36701. [Google Scholar] [CrossRef]
- Gao, P.; Zhang, G.; Ouyang, H.; Mei, L. A Sliding Mode Control with Nonlinear Fractional Order PID Sliding Surface for the Speed Operation of Surface-Mounted PMSM Drives Based on an Extended State Observer. Math. Probl. Eng. 2019, 2019, 7130232. [Google Scholar] [CrossRef]
- Gao, P.; Zhang, G.; Ouyang, H.; Mei, L. An Adaptive Super Twisting Nonlinear Fractional Order PID Sliding Mode Control of Permanent Magnet Synchronous Motor Speed Regulation System Based on Extended State Observer. IEEE Access 2020, 8, 53498–53510. [Google Scholar] [CrossRef]
- Yang, L.; Yang, J. Nonsingular Fast Terminal Sliding-Control for Nonlinear Dynamical Systems. Int. J. Robust Nonlinear Control 2011, 21, 1865–1879. [Google Scholar] [CrossRef]
- Tian, M.; Wang, T.; Yu, Y.; Dong, Q.; Wang, B.; Xu, D. Integrated Observer-Based Terminal Sliding-Mode Speed Controller for PMSM Drives Considering Multisource Disturbances. IEEE Trans. Power Electron. 2024, 39, 7968–7979. [Google Scholar] [CrossRef]
- Dai, C.; Guo, T.; Yang, J.; Li, S. A Disturbance Observer-Based Current-Constrained Controller for Speed Regulation of PMSM Systems Subject to Unmatched Disturbances. IEEE Trans. Ind. Electron. 2021, 68, 767–775. [Google Scholar] [CrossRef]
- Dai, B.; Sun, J.; Yang, J.; Li, S. Dynamic Event-Triggered Disturbance Rejection Control for Speed Regulation of Networked PMSM. IEEE Trans. Ind. Inform. 2024, 20, 6436–6445. [Google Scholar] [CrossRef]
- Liu, J.; Yang, J.; Li, S.; Wang, X. Single-Loop Robust Model Predictive Speed Regulation of PMSM Based on Exogenous Signal Preview. IEEE Trans. Ind. Electron. 2023, 70, 12719–12729. [Google Scholar] [CrossRef]
- Wang, Q.; Yu, H.; Li, C.; Lang, X.; Yeoh, S.S.; Yang, T.; Rivera, M.; Bozhko, S.; Wheeler, P. A Low-Complexity Optimal Switching Time-Modulated Model-Predictive Control for PMSM with Three-Level NPC Converter. IEEE Trans. Transp. Electrif. 2020, 6, 1188–1198. [Google Scholar] [CrossRef]
- Wang, B.; Tian, M.; Yu, Y.; Dong, Q.; Xu, D. Enhanced ADRC with Quasi-Resonant Control for PMSM Speed Regulation Considering Aperiodic and Periodic Disturbances. IEEE Trans. Transp. Electrif. 2022, 8, 3568–3577. [Google Scholar] [CrossRef]
- Zhang, J.; Ren, W.; Sun, X. Extended-State-Observer-Based Nonlinear Control for PMSM Servo Systems with Current Constraints and Voltage Saturations. IEEE Trans. Transp. Electrif. 2024, 10, 2713–2726. [Google Scholar] [CrossRef]
- Gao, Z. Scaling and Parameterization Based Controller Tuning. In Proceedings of the American Control Conference, Denver, CO, USA, 4–6 June 2003. [Google Scholar]
- Wang, Y.; Yu, H.; Liu, Y. Speed-Current Single-Loop Control with Overcurrent Protection for PMSM Based on Time-Varying Nonlinear Disturbance Observer. IEEE Trans. Ind. Electron. 2022, 69, 179–189. [Google Scholar] [CrossRef]



| Parameters | Label | Value |
|---|---|---|
| rated power | 64 W | |
| rated voltage | 24 V | |
| rated current | 4 A | |
| rated speed | 3000 rpm | |
| rated torque | ||
| pole pairs | 4 | |
| stator inductance | L | mH |
| stator resistance | ||
| inertia constant |
| Algorithms | Parameters |
|---|---|
| The proposed method | , , , , , |
| PIDSMC+TSMRL | , , , , , |
| TSMC | , p = 25,000,000, , , |
| CSMC | , = 35,000,000 |
| Algorithms | ST (s) | RMSEA (A) | RT (s) | SF (rpm) | RMSEL (A) |
|---|---|---|---|---|---|
| The proposed method | |||||
| PIDSMC+TSMRL | |||||
| TSMC | |||||
| CSMC |
| Algorithms | Parameters |
|---|---|
| The proposed method | , , , , , |
| PIDSMC+TSMRL | , , , , , |
| TSMC | , , , , |
| CSMC | , |
| Algorithms | ST (s) | RMSEA (A) |
|---|---|---|
| The proposed method | ||
| PIDSMC+TSMRL | ||
| TSMC | ||
| CSMC |
| Algorithms | SF (rpm) | RMSEL (A) |
|---|---|---|
| The proposed method | ||
| PIDSMC+TSMRL | ||
| TSMC | ||
| CSMC |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, G.; Wang, M.; Cao, G.; Wang, Q.; Liao, Y. PID Sliding Mode Control of PMSM Based on Improved Terminal Sliding Mode Reaching Law. Energies 2025, 18, 2661. https://doi.org/10.3390/en18102661
Qin G, Wang M, Cao G, Wang Q, Liao Y. PID Sliding Mode Control of PMSM Based on Improved Terminal Sliding Mode Reaching Law. Energies. 2025; 18(10):2661. https://doi.org/10.3390/en18102661
Chicago/Turabian StyleQin, Guodong, Min Wang, Guizhou Cao, Qi Wang, and Yuefeng Liao. 2025. "PID Sliding Mode Control of PMSM Based on Improved Terminal Sliding Mode Reaching Law" Energies 18, no. 10: 2661. https://doi.org/10.3390/en18102661
APA StyleQin, G., Wang, M., Cao, G., Wang, Q., & Liao, Y. (2025). PID Sliding Mode Control of PMSM Based on Improved Terminal Sliding Mode Reaching Law. Energies, 18(10), 2661. https://doi.org/10.3390/en18102661






