Abstract
This paper investigates the distributed time-varying (TV) resource management problem (RMP) for microgrids (MGs) within a multi-agent system (MAS) framework. A novel fixed-time (FXT) distributed optimization algorithm is proposed, capable of operating over switching communication graphs and handling both local inequality and global equality constraints. By incorporating a time-decaying penalty function, the algorithm achieves an FXT consensus on marginal costs and ensures asymptotic convergence to the optimal TV solution of the original RMP. Unlike the prior methods with centralized coordination, the proposed algorithm is fully distributed, scalable, and privacy-preserving, making it suitable for real-time deployment in dynamic MG environments. Rigorous theoretical analysis establishes FXT convergence under both identical and nonidentical Hessian conditions. Simulations on the IEEE 14-bus system validate the algorithm’s superior performance in convergence speed, plug-and-play adaptability, and robustness to switching topologies.
1. Introduction
MGs have emerged as a pivotal component of modern energy systems, facilitating enhanced energy efficiency and the integration of renewable energy sources [1]. An MG typically consists of distributed generators (DGs), energy storage systems (ESSs), loads, and control devices, and is capable of operating either autonomously or in coordination with the main grid, thereby enhancing system flexibility and reliability.
Effective resource management within MGs remains a critical challenge, especially in dynamically balancing energy supply and demand while minimizing operational costs. In this context, MASs have gained increasing attention for MG control and optimization, owing to their inherent advantages in distributed decision-making, scalability, and fault tolerance. MASs enable autonomous agents to collaborate and solve complex optimization tasks in a fully distributed manner [2,3]. Moreover, the TV nature of MGs—characterized by intermittent renewable generation and fluctuating load demand—requires advanced optimization algorithms that can efficiently adapt to dynamic environments. In particular, ensuring fast consensus and convergence under varying operating conditions and communication topologies remains an ongoing issue.
Recent efforts have focused on distributed optimization strategies for resource scheduling in MGs [4,5,6,7,8]. For example, a fully distributed consensus-based control strategy was proposed to solve an optimal RMP in an island MG [4]. In [7], to boost the convergence speed, Li et al. presented a distributed and parallel optimization method for the RMP of MGs. This method improved the convergence speed of the algorithm without sacrificing optimal accuracy. The aforementioned methodologies [4,5,6,7,8] achieve distributed optimization asymptotically, i.e., convergence is guaranteed only as time approaches infinity. However, in many practical applications, faster convergence is crucial, which motivates the development of finite-time (FT) or FXT distributed optimization algorithms [3,9,10,11,12,13]. Despite the recent advances, most existing FT and FXT distributed optimization methods still have limitations. They often assume time-invariant cost functions [3,9,10,11,12,13], making them less suitable for dynamic environments with renewable fluctuations and varying loads. Moreover, global constraints like supply–demand balance are typically ignored or managed semi-centrally, which limits scalability and real-time application.
Nevertheless, most of the aforementioned works focus on static optimization problems, where objectives remain constant over time. In contrast, many real-world applications exhibit TV characteristics, with dynamically evolving objectives and constraints. This has motivated research on distributed TV optimization in areas such as resource allocation [14], visual tracking [15], robotic navigation [16], and transportation systems [17,18,19,20]. Several recent studies have proposed distributed algorithms for general TV optimization [21,22,23,24,25]. For example, an edge-based protocol was developed in [22], while [23] introduced a prediction–correction scheme for TV economic dispatch, and [25] designed gradient-based trackers for quadratic problems. However, these works are typically limited to fixed communication graphs and general problem formulations; they do not address the specific structure and constraints of RMPs in MGs. In power systems, the need for real-time monitoring and response increases communication demands and the risk of link failures, highlighting the requirement for flexible and adaptive communication models. Switching graphs, which better reflect these dynamic conditions, have recently drawn growing interest [26,27,28]. Yet few approaches jointly consider TV objectives, global constraints, and switching topologies in distributed RMPs, thereby motivating the present work.
Moreover, while FT algorithms can accelerate convergence, their settling time often depends on the initial state. In contrast, FXT algorithms ensure convergence within a uniform time bound—independent of initial conditions—offering more predictable performance. Distributed optimization problems have been extensively investigated under a range of conditions [3,9,10,11,12,13,21,22,23,24,25,26,27,28,29], including FT/FXT convergence, switching communication graphs, and both static and TV cost functions and loads. However, to the best of our knowledge, few existing studies have addressed the FXT distributed optimization of TV RMPs for MGs within an MAS framework, particularly under switching communication topologies. Addressing this challenge is essential for enhancing the efficiency, adaptability, and sustainability of energy systems in dynamic environments [30,31].
Motivated by these insights, this paper aims to develop an FXT distributed optimization algorithm to solve the TV RMP for MGs over switching communication graphs.
The main contributions of this paper are summarized as follows:
- (1)
- An FXT distributed optimization algorithm is proposed to solve penalized TV RMPs, guaranteeing fixed-time convergence to a tunable neighborhood of the original optimal solution, as well as asymptotic convergence to the exact optimum. Theoretical guarantees are established under both identical and nonidentical Hessian conditions. Compared with [3,9,10,11,12,13,21,22,23,24,25], the proposed algorithm exhibits improved efficiency and enhanced practical applicability.
- (2)
- Unlike prior studies that have primarily considered either equality or inequality constraints separately [21,22,23,24,25,26,27], the proposed algorithm is designed to handle TV RMPs in MGs with both local inequality and global equality constraints, enabling effective adaptation to dynamic resource and constraint variations [30,31].
- (3)
- To ensure robust performance in dynamic environments, the algorithm is designed to operate over switching communication topologies, thereby enhancing the resilience and adaptability of MASs under intermittent communication conditions.
In this work, we aim to solve a TV RMP for MGs, which features both local inequality constraints and a global power balance constraint. To this end, we develop a fully distributed control strategy that enables a network of MG agents—each with local TV objectives and constraints—to collaboratively solve a RMP over a dynamically switching communication network. The proposed algorithm is rooted in an FXT consensus-based optimization framework, where the agent updates its decision variables based solely on local computations and information exchanged with its neighbors. The FXT protocol guarantees that all agents achieve consensus on marginal costs and converge to the globally optimal power allocation of the penalized TV RMP within a fixed time, regardless of initial conditions. To handle inequality constraints, a time-decaying penalty function is employed to incorporate them into the optimization objective, ensuring that the original constrained problem is approximated asymptotically. In parallel, the global equality constraint is implicitly enforced by designing the dynamics to preserve the total power invariant, provided that the initial condition satisfies the constraint. This avoids the need for explicit projection or Lagrangian-based enforcement, thereby reducing control complexity.
Overall, the method efficiently carries out the distributed optimization process, allowing agents to pursue local objectives, gradually satisfy inequality constraints, achieve consensus, and maintain global power balance within a fixed time, even under switching networks. The resulting approach is scalable, resilient to communication variations, and suitable for real-time implementation in dynamic and decentralized MG environments.
The rest of this paper is structured as follows: Section 2 provides the preliminary information. The formation of the TV RMP is described in Section 3. Section 4 outlines the main results. Simulation examples are given in Section 5 to illustrate the effectiveness of the proposed control strategy. Finally, conclusions are drawn in Section 6.
2. Preliminaries
2.1. MAS Framework
As illustrated in Figure 1, the MG under consideration is structured within an MAS framework, comprising a utility grid, conventional dispatchable generators (CDGs), renewable generators (RGs), battery energy storage systems (BESSs), and a variety of loads (residential, commercial, industrial, and flexible loads). The utility grid connects to the MG via a point of common coupling (PCC), which monitors power exchange and determines the operational mode of the MG. Each MG component is managed by an autonomous agent capable of local control and inter-agent communication, enabling coordinated decision-making across the network.
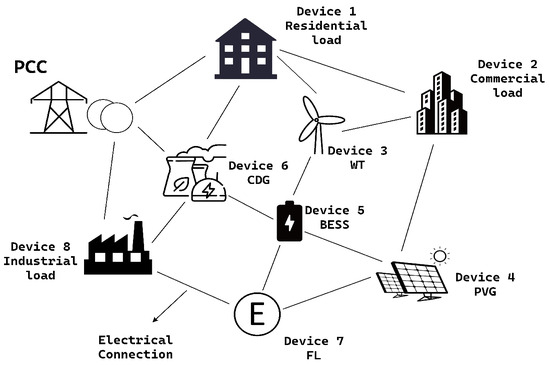
Figure 1.
Topology of the MAS-based MG.
As shown in Figure 2, the MAS adopts a two-level control architecture. The upper level consists of a communication network, where each agent exchanges information only with its neighbors to implement the distributed optimization strategy. The lower level comprises physical devices, where control commands are executed to regulate power generation or consumption in accordance with reference signals received from the upper level. Power is exchanged through physical electrical connections among devices.
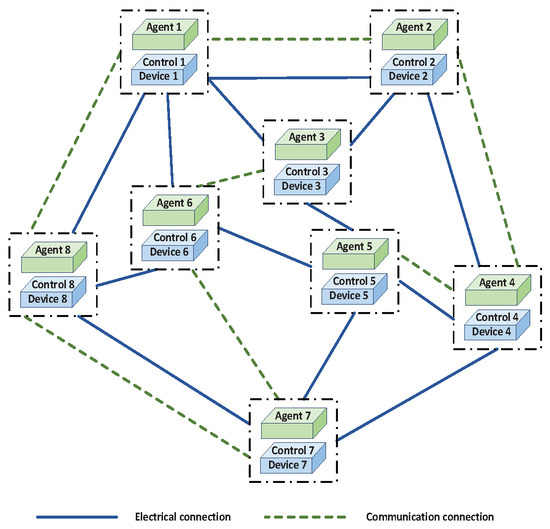
Figure 2.
Agent communication network in MGs.
2.2. Graph Theory
Denote an undirected graph with N nodes, where represents the set of nodes, and constitutes the set of edges. The nodes are connected by an adjacency matrix , where if there is an edge , and otherwise. Given the undirected of G, the matrix A satisfies . The neighborhood of any node i, denoted .
A path in G is defined as a sequence of edges connecting two nodes, and the graph is considered connected if a path exists between every pair of nodes. Associated with A is the Laplacian matrix , where for , and . Note that when G is connected, the eigenvalues of L are ordered as , with being the second smallest eigenvalue. Additionally, the concept of a switching graph sequence is introduced as , where is a piecewise constant signal dictating the graph configuration at any given time. Here, w represents the total number of distinct switching graphs possible. The corresponding Laplacian matrices, and the set of neighbors for any agent i, are denoted as , and , respectively.
2.3. Definitions and Lemmas
Consider the following nonlinear system:
where is a continuous function with , and denotes the system state at time t.
To facilitate the analysis of FXT distributed TV resource management, several mathematical preliminaries are introduced below.
Lemma 1
([32]). Let be a smooth, positive definite scalar function. If there exist constants and such that
then the origin of system (1) is finite-time stable, and the settling time satisfies
Lemma 2
([33]). Let be a positive definite scalar function. If there exist constants , , , and such that
then the origin of system (1) is fixed-time stable, and the settling time satisfies
Definition 1
(Filippov Solution [34]). Consider system (1), where may be discontinuous. The Filippov set-valued map associated with g at x is defined as follows:
where denotes the Lebesgue measure of the set S, denotes the convex hull, and is an open ball centered at x with radius δ. A function is called a Filippov solution to if it is absolutely continuous and satisfies almost everywhere.
Lemma 3
([22]). Let . Then, for any , the following inequalities hold
Lemma 4
([26]). For an undirected and connected graph G, when for , we have .
Lemma 5
([35]). Let be a symmetric positive semidefinite matrix, and let the global cost function be ω-strongly convex over for each fixed , with . Denote by the optimal solution to the TV regularized RMP at time t. Then, the following inequality holds for all :
where denotes the second smallest eigenvalue of B.
3. Problem Formulation
In this section, we define five types of agents within the MG context under the introduced MAS framework. Additionally, corresponding cost functions of each kind of agent are designed to facilitate optimal resource management modeling. In the following content, for convenience, we often omit t where it does not cause confusion.
3.1. Conventional Generator Agents
This class of agents includes natural gas turbines, fuel-fired generators, and other controllable power sources. These units typically exhibit convex cost characteristics due to thermal efficiency and fuel consumption laws. To capture such behavior under TV operating conditions, their generation cost is modeled as a TV quadratic function [3,11], as follows:
where are TV cost coefficients, and denotes the marginal cost function. The parameters and specify the operating limits of generator i. In resource management optimization, aligning marginal costs across generators is essential for achieving economic dispatch and system-wide efficiency. This design maintains power balance under demand fluctuations, mitigates resource over-utilization, and improves operational fairness and stability.
3.2. RG Agents
RG agents represent photovoltaic generators and wind turbines, which are inherently intermittent and uncertain. While conventionally treated as nondispatchable, we consider them controllable within their available output range to facilitate real-time coordination. Following the modeling framework of [36], the cost function of each RG agent is modeled as a TV quadratic function, as follows:
where denotes the forecasted available output, and is the scheduled value from the previous time step. , , and are TV coefficients.
3.3. Energy Storage Agents
Energy storage agents (e.g., BESSs, supercapacitors) act as controllable and dispatchable units that provide temporal balancing by charging during periods of low marginal cost and discharging during peak demand or high-cost intervals. Inspired by the modeling approaches in [3], to comprehensively reflect the operational characteristics of batteries—including energy conversion losses, degradation costs, and dynamic control effort—we adopt the following TV cost function:
where is the charging/discharging power of storage agent i, with for discharging and for charging; is the state of charge; is the reference or scheduled value; and are continuously TV coefficients. The marginal cost is given by the following:
The operational constraints of the battery are as follows:
where and denote the minimum and maximum charging/discharging power, respectively, and and represent the lower and upper bounds of the state of charge.
3.4. Load Agents
Load agents represent controllable or shiftable loads, such as HVAC systems, industrial machinery, or smart appliances, whose power consumption can be adjusted to support grid stability and economic dispatch. However, such flexibility typically incurs user discomfort or performance degradation. To model this trade-off, and motivated by the formulation in [11], we adopt the following TV cost function:
where is power consumption of load agent i; denotes the desired or baseline load level at time t; and are TV weights reflecting sensitivity to deviation and response effort. The marginal cost is given by the following:
The allowable range of adjustable load is defined by the following:
where and represent the minimum and maximum allowable power consumption of load agent i, respectively.
3.5. Utility Agents
MG operation typically alternates between two modes—islanded and grid-connected. The utility agent becomes active during grid-connected operation, representing the interaction with the external utility grid. It monitors the net power exchange between the MG and the main grid and applies corresponding charges or credits. To account for the asymmetry between purchase and sale electricity prices, we adopt a smooth TV cost function as follows [37]:
where and denote the TV purchase and sale electricity rates, and is a smoothing parameter. In the grid-connected mode, the optimality condition requires that the marginal cost of each dispatchable agent equals the electricity rate imposed by the utility grid.
3.6. Formulation of the TV RMP
In an MG consisting of CDGs, RGs, BESSs, controllable loads (flexible or shiftable loads), and a utility interface, the objective is to minimize the aggregate operation cost of all agents while maintaining supply–demand balance.
To accommodate both islanded and grid-connected operating modes within a unified formulation, we introduce a binary mode indicator , where denotes the grid-connected mode, and corresponds to an islanded operation. Accordingly, the convex optimization problem is formulated as follows:
where , , , and represent the power output or consumption of the CDGs, RGs, BESSs, and load agents, respectively. denotes the power exchanged with the utility grid, and is the associated cost function. The switching variable allows the model to seamlessly adapt to both operational modes.
To simplify the notation, and following the modeling approach described in [37], we define the total number of agents as , where the last agent represents the utility grid. Let denote the output power of agent i, and be its upper and lower bounds, respectively. Accordingly, the optimization problem can be reformulated as follows:
Remark 1.
The growing use of RDGs, flexible loads, and energy storage units has introduced more uncertainty and variability into modern MG operations. As a result, static or single-period optimization models are often inadequate for capturing the real-time dynamics of such systems. To address this challenge, we formulate the MG RMP as a constrained TV convex optimization problem. This modeling approach offers the following advantages: (i) Real-time adaptability: Enables continuous response to renewable fluctuations, load shifts, and market signals; (ii) Theoretical tractability: Convexity and smoothness guarantee solution uniqueness and support gradient-based methods; (iii) Distributed readiness: Fits well with distributed control methods based on local communication. Overall, this TV optimization model provides a rigorous and flexible foundation for a real-time RMP in complex MG environments.
4. Main Results
4.1. Design of the FXT Distributed Algorithm
To incorporate this mechanism, the following TV penalty function is adopted:
where is an exponentially decaying function with and . By using this penalty function, the RMP (8) is subsequently reformulated as follows:
where , and is a positive penalty parameter. Define and as the optimal solution for the TV optimal RMP (8) and (10) at time t, respectively.
In our case, the penalty parameter is not fixed but varies with time as , where is strictly positive and monotonically decreasing over time. According to the designed TV penalty function (9), and inspired by [38], setting , for each t, the relationship between (8) and (10) can be expressed as follows:
Furthermore, as , we have , which implies the following:
where , represents the vector of Lagrange multipliers that satisfy the Karush–Kuhn–Tucker (KKT) conditions as referenced in [38]. Moreover, as stated in [39], the upper bound of is determined by the following:
where denotes the gradient of with regard to , and and .
Remark 2.
Unlike traditional fixed-penalty methods [3,38] that yield only ϵ-suboptimal solutions, the proposed TV penalty scheme with ensures asymptotic convergence to the exact solution of the original constrained problem. As , the optimality gap vanishes, guaranteeing exact optimality in the limit. This adaptive design also avoids the manual tuning of a small static ϵ, which is often challenging in practice. Instead, it achieves a balance between early-stage numerical stability and late-stage accuracy. The theoretical guarantee follows by extending the penalty-based convergence results in [38].
Before proceeding with the main analysis, we introduce the following standard assumptions commonly adopted in the literature on distributed optimization and control [14,21,25,26,40,41].
Assumption 1.
The switching graph is undirected and connected. The duration between any two consecutive switching instances exceeds a positive threshold . Furthermore, within each time interval, the communication graph remains fixed τ.
Assumption 2.
Slater’s condition holds for the TV optimization problem (8), i.e., there exists a feasible allocation such that and .
Assumption 3.
For all , each is -strongly convex and twice continuously differentiable with respect to , and continuously differentiable in t.
The FXT distributed optimization algorithm refers to a class of distributed control strategies that solve optimization problems over MASs with the guarantee that convergence to the optimal solution is achieved within a uniform and bounded time, regardless of the initial conditions. In the FXT framework, each agent relies solely on local objective information and communication with neighbors, making the algorithm fully distributed.
To address the TV RMP, we develop a fully distributed FXT optimization algorithm based on the -penalty function. The core idea is to ensure that all agents reach consensus on the penalized gradients within a fixed time, despite the switching nature of the communication topology. To this end, we incorporate a nonlinear consensus protocol that includes a discontinuous term and a power function , which together guarantee FXT convergence in the presence of network dynamics. Beyond enforcing agreement, each agent updates its state along a direction determined by the local Hessian and gradient of its penalized cost function. In addition, a time derivative compensation term is also introduced to account for the explicit temporal evolution of the objective. This combination enables each agent to optimize its decision variable based on both dynamic local objectives and network-wide coordination.
Utilizing this structure, the FXT distributed optimization algorithm is constructed as follows. The MAS dynamics for agent i are characterized by the following:
where denotes the local gradient, is the corresponding Hessian of the penalized cost function. The functions and (with ) are discontinuous or non-smooth, so the system dynamics are understood in the Filippov sense. The positive parameter is a control gain to be designed. Note that the update rule in (12) is fully distributed, allowing each agent to compute its state using only local gradients and information from neighboring agents under a switching communication topology.
Remark 3.
Compared to [26], our method explicitly addresses the global equality constraint and guarantees FXT convergence without relying on a global time variable t, which enhances its practical applicability. In contrast to [41], our controller features a simpler structure and lower implementation complexity, while still ensuring strong convergence guarantees. It is worth noting that the satisfaction of the equality constraint relies on the initialization condition . From an engineering perspective, setting the initial outputs to sum to a prescribed constant is straightforward to achieve through centralized initialization or lightweight coordination, and doing so avoids the need for explicit constraint enforcement during the evolution, thereby reducing the overall control cost.
Remark 4.
Additionally, although the use of the discontinuous sign function may lead to chattering effects in physical implementations, this issue can be effectively mitigated by employing smooth approximations such as the hyperbolic tangent , logistic sigmoid , or saturation-type functions like . These approximations preserve convergence behavior while improving robustness and continuity, making them more suitable for real-world deployment.
Lemma 6
Proof.
Let denote the optimal solution of problem (10), where is the corresponding Lagrange multiplier. The Lagrangian function is given by the following:
From the KKT conditions, we obtain the following:
- (1)
- , which implies ;
- (2)
- Primal feasibility: .In addition, the strong convexity of each ensures that the optimal solution is unique.
Conversely, suppose there exists a feasible allocation such that
where is a common gradient value shared by all agents under . By convexity of each , we have the following:
Summing the above inequality over all i, and using the fact that the gradients are equal to , along with the observation that both and satisfy the equality constraint in (13), we can deduce the following:
Since is the optimal solution, equality must hold. By strong convexity of the objective function, this implies . □
4.2. Convergence Analysis
In the following section, we establish two theorems addressing the cases where the Hessians of the TV cost functions are either identical or heterogeneous. The corresponding convergence properties are rigorously analyzed.
4.2.1. Identical Hessian Case
This subsection focuses on the case where the Hessians of the cost functions in (10) are identical across agents, that is, , for and .
Assumption 4.
For all and , there exist positive constants τ and κ that satisfy and .
Theorem 1.
Proof.
Since by definition, and is strongly convex, its Hessian is positive definite and hence invertible. Applying the chain rule yields the following:
Substituting the Filippov differential inclusion from the system dynamics (12) into the expression of , we obtain the following:
Summing over all agents , and since the interaction graph is undirected, we achieve the following: . Therefore, the total power allocation remains invariant, as follows:
Define the error . It is easy to verify that the relative error satisfies . We consider the following Lyapunov candidate:
Since the interaction graph is undirected and connected, it follows that the errors are zero-mean, i.e., . Taking the time derivative of , and using the identity , we obtain the following:
We now consider the first term in (16). Since all the Hessians are identical, i.e., , and the graph is undirected (i.e., ), we have the following:
Using the fact that , and that the Hessian is uniformly lower bounded as , we obtain the following:
Next, we consider the second term in (16). Following the same lines with the above analysis, we obtain the following:
Now, we bound the last term in (16) involving TV gradients. Rewriting the term using the definition of yields the following:
Applying the triangle inequality and Assumption 4, we achieve the following:
Integrating the bounds derived in (17)–(20) and applying Lemmas 3 and 4, we obtain the following from (16) under the condition :
Since the graph is undirected and connected, the edge-wise disagreement can be bounded as follows, using the second smallest eigenvalue of the Laplacian:
Substituting this into the previous bound yields the following:
where , and . Applying Lemma 2 and the comparison principle, it follows that the system state achieves consensus in fixed time , with the settling time estimated by the following:
Finally, by invoking Lemma 6, it can be concluded that the TV regularized RMP (10) is solved within FXT , i.e., for all . □
Remark 5.
Although the proposed FXT algorithm guarantees convergence within a fixed time independent of the initial conditions, the convergence trajectory follows a nonlinear power law decay profile. Specifically, the evolution of the state error typically satisfies a relation of the form with , indicating a slower convergence rate as the trajectory approaches the fixed settling time .
Moreover, according to (22), the result implies that increases polynomially with the number of agents N and decreases with the algebraic connectivity of the switching graph over the dwell interval . Therefore, while the FXT consensus is theoretically ensured, the practical convergence speed may degrade in large-scale or weakly connected networks.
4.2.2. Nonidentical Hessian Case
While the previous analysis relied on the assumption of identical Hessians, real-world systems often involve heterogeneity across agents. In the following section, we extend our results to a case where the Hessian matrices are allowed to differ.
Assumption 5.
For all and , the partial time derivative is uniformly Lipschitz continuous with respect to . That is, there exists a constant such that ,
Theorem 2.
Proof.
Similar to the proof for global equality satisfaction in Theorem 1, the structure of the system dynamics in (12) guarantees that the supply–demand balance is preserved at all times.
According to Assumption 3, the total cost function is strongly convex. Therefore, we define the following Lyapunov candidate:
which is positive definite with respect to the optimal point , i.e., , and if and only if .
Taking the time derivative of , we obtain the following:
where , and .
By virtue of Lemma 5, the following can be concluded:
Substituting this into the inequality above yields the following:
with , .
For the remaining terms in (23), and invoking Assumption 5, we have the following:
Since each is -strongly convex, one has , with . Therefore, it follows that
Combine with (23) and (24), one can further obtain the following:
where . Provided that the gain condition holds, we have and the FXT convergence follows. Applying Lemma 2 and the comparison principle, the state reaches the optimal trajectory of the TV RMP (10) in the fixed time , with the settling time bounded by the following:
Finally, by invoking Lemma 6, it follows that the TV regularized RMP (10) is solved in fixed time , i.e., for all . □
Remark 6.
The validity of Theorems 1 and 2 relies on several structural and regularity assumptions. Specifically, both theorems require that Assumptions 1–3 hold; the communication graph must be connected within every switching interval, the TV optimization problem must satisfy Slater’s condition, and the initial state of the agents must satisfy the global equality constraint . In addition, each local cost function is assumed to be -strongly convex, twice continuously differentiable with respect to , and continuously differentiable in time t. To further guarantee FXT convergence, Theorem 1 assumes that the time derivative of the gradient, , is uniformly bounded, while Theorem 2 requires that the partial time derivative is uniformly Lipschitz continuous in .
While these conditions are commonly adopted in the literature on distributed optimization [14,21,25,26,40,41], some of them may not always be easy to satisfy in real-world applications, especially in systems with nonconvex objectives, fast-varying dynamics, or intermittent communication.
Remark 7.
This work considers both identical and nonidentical Hessian cases in the TV RMP. When the Hessians are identical across agents, the analysis is more straightforward, requiring milder conditions to ensure FXT convergence and yielding tighter bounds on the settling time. This setting is suitable for systems with homogeneous or coordinated devices. In contrast, the nonidentical Hessian case captures more realistic scenarios where agents have diverse dynamic behaviors and cost structures. Although it introduces stricter convergence requirements, it significantly broadens the model’s applicability to practical, heterogeneous MGs. The inclusion of both cases demonstrates the flexibility and generality of the proposed framework.
Remark 8.
Lemma 6, and Theorem 1 jointly demonstrate that the proposed distributed FXT algorithm is capable of solving the TV RMP (10), which involves both local inequality constraints and a global equality constraint, within a guaranteed fixed settling time . Moreover, as , the algorithm asymptotically converges to the exact solution to the original problem (8) without regularization. At the settling time , the solution trajectory remains -close to the optimal solution of problem (8), where defines the vanishing regularization parameter. This allows the optimality gap to be explicitly tuned via the parameters and α, making it arbitrarily small and within acceptable bounds in practice. Such a trade-off is particularly beneficial in engineering applications, as it enables a significantly simpler algorithmic structure while ensuring high-quality near-optimal performance.
Remark 9.
The switching topology is considered in this paper, because it is essential due to the dynamic nature of communication links in MAS, where changes in distance, environmental interference, or operational factors can cause link failures or new connections. Research in this area is crucial for designing the optimization algorithms that adapt to these dynamics, ensuring system performance and stability even with topology changes. This facilitates robust, efficient operations across diverse applications such as drone swarms, automated vehicle coordination, and mobile sensor networks [42,43,44], where consistent communication is vital for coordinated action and resource management.
5. Simulation Results
To validate the effectiveness of the proposed distributed FXT optimization strategy, two illustrative case studies are conducted based on the IEEE 14-bus test system. As shown in Figure 3, the system includes one utility grid connection, two RGs, two conventional dispatchable generators, two BESSs, and three loads.
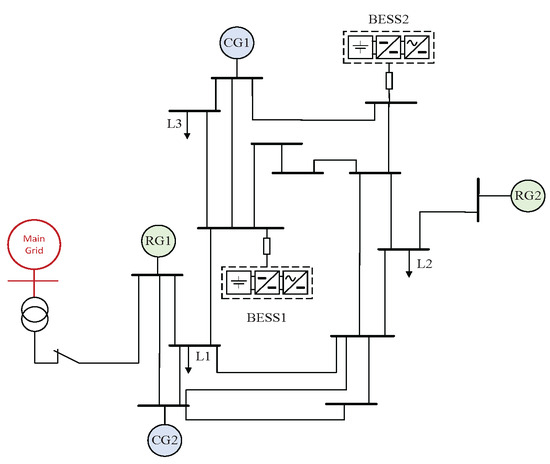
Figure 3.
IEEE 14-bus test system.
5.1. Effectiveness Test
In this case study, we evaluate the accuracy of the proposed control algorithm. The communication graphs switch cyclically from (1) to (4) as depicted in Figure 4. In particular, nodes 1 to 10 correspond to the MG components RG1, RG2, CG1, CG2, BESS1, BESS2, L1–L3, and PCC, respectively. The detailed parameters associated with each component are listed in Table 1. The total power demand is quantified at 200 MW. The TV cost function of each device of MG is selected as . In addition, the lower and upper bounds of are set to MW and MW.
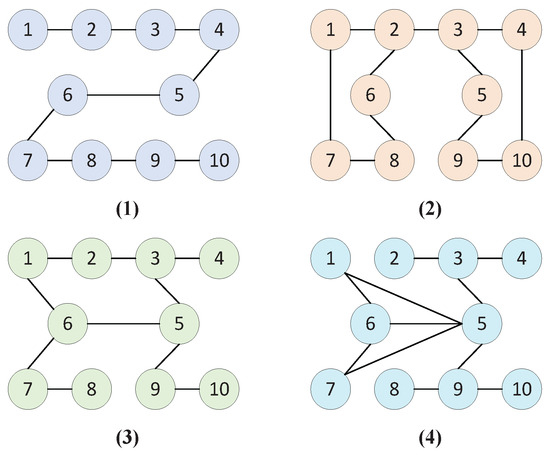
Figure 4.
Agent communication graphs.

Table 1.
TV cost parameters and inequality constraints.
Figure 5a shows that the curves of marginal cost of each agent reach a consensus after about 0.32 s. From Figure 5b, it can be observed that the trajectories for power generation/consumption stabilize at MW.
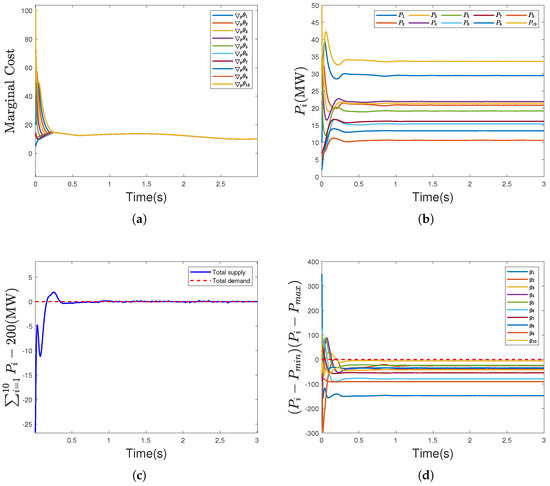
Figure 5.
(a) Marginal utility trajectories; (b) power evolution of –; (c) demand–supply synchronization; (d) curves of inequality constraint functions.
Figure 5c displays the total generated power curve, demonstrating that it converges to the total demand of 200 MW within approximately 0.36 s. The simulation results for the inequality constraint functions is shown in Figure 5d. Clearly, all curves, regardless of whether they started inside or outside the designated area, converge to the feasible region.
5.2. Plug-and-Play Capability Test
This case evaluates the plug-and-play capability of the proposed FXT distributed optimization algorithm. The communication topology, cost parameters, and load demand are maintained as identical to those in the precedent studied case.
Initially, the system reaches an optimal operating point, with all the devices active. Subsequently, PCC and RG1 are disconnected from the system at and , respectively, and their associated control variables are reset to zero. As shown in Figure 6a–d, it can be observed that the output of the remaining generators and energy storage devices and loads have increased/decreased, and re-balance at a very fast speed. Additionally, the total output supply of each device meets the total demand.
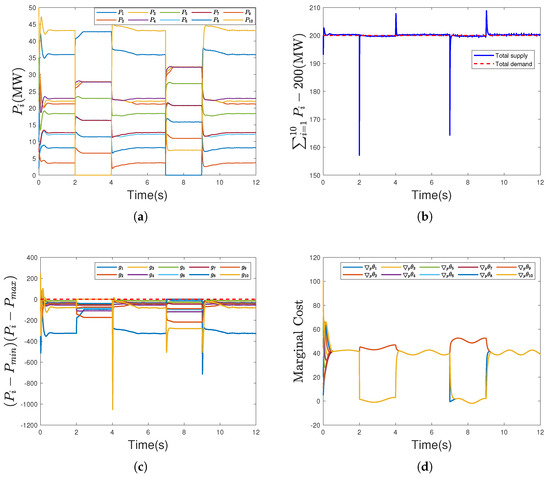
Figure 6.
(a) Actual output power ; (b) power demand and supply; (c) curves of inequality constraint functions; (d) marginal cost of MG.
At and , DG1 and RG1 are reconnected to the system. The system quickly returns to the pre-disconnection operational state, with all devices resuming their original optimal values.
These results demonstrate the plug-and-play capability of the proposed algorithm, enabling fast reconfiguration and re-optimization in response to dynamic changes in system components.
Remark 10.
In real-world applications, the plug-and-play capability is crucial for maintaining the adaptability and scalability of MGs. It allows for the seamless addition or upgrading of components to respond to new technologies and changing energy needs, ensuring that MGs remain robust and efficient in the face of dynamic energy landscapes. Furthermore, the proposed algorithm also supports the dynamic connection and disconnection of the utility grid, enhancing system-level flexibility and enabling hierarchical energy management.
5.3. Comparative Experiment
To verify that the distributed FXT optimization algorithm proposed in this paper has a faster convergence rate, a comparative study is conducted in this section. The proposed distributed FXT optimization algorithm is evaluated against the algorithms presented in [26,28]. Under this test, uniform TV communication network settings, load demand, and initial conditions were employed across all algorithms. The test system and switching communication graph used here remain the same as in the previous section. The load demand is set as 100 MW, and the cost parameters of each devices are listed in Table 1.
As depicted in Figure 7a–c, all marginal costs converge to the similar dynamic optimal value. While the competing algorithms referenced in [26,28] exhibit fluctuations and a slower approach towards the equilibrium state, the algorithm from this study achieves a rapid and steady convergence to the optimal marginal cost within just 2 s.
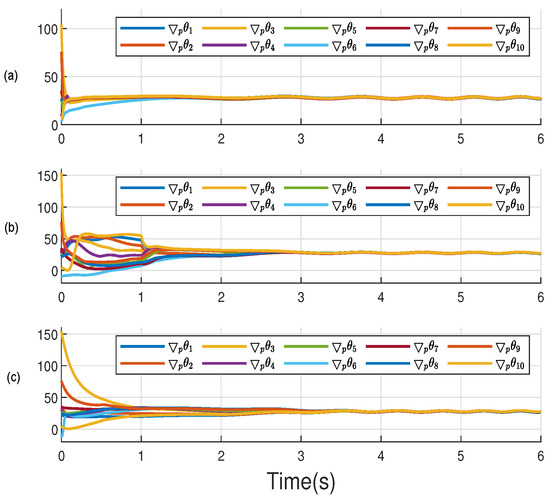
Figure 7.
Comparison of marginal cost curves: (a) proposed in this paper; (b) adopted from [26]; (c) adopted from [28].
This performance gap highlights not only the efficiency but also the robustness of the proposed method. This enhanced performance underscores improvements in computational efficiency, making it a compelling choice for real-time applications in dynamic environments.
5.4. Effectiveness of Smooth Approximations to the Sign Function
To reduce chattering, the simulations in this section adopt a smooth approximation to replace the discontinuous sign function in the controller.
As shown in Figure 5c and Figure 6c, using the sign function in the controller leads to noticeable chattering in the total supply curves. To reduce this effect, we replace the sign function with a smooth approximation, specifically the hyperbolic tangent function , . As illustrated in Figure 8a,b, this change effectively reduces the chattering and results in smoother system behavior and better demand–supply matching.
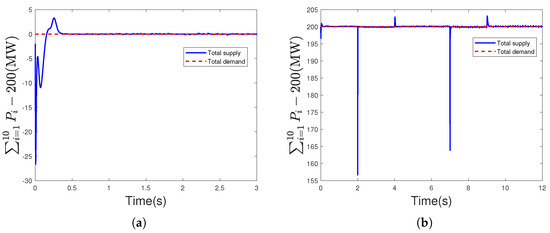
Remark 11.
The theoretical guarantees in this paper are established under several technical assumptions, including persistent connectivity of the switching communication graph and strong convexity of local cost functions (Assumption 1 and 3). These conditions ensure rigorous FXT convergence but may be restrictive in practice. If the communication graph becomes temporarily disconnected, information flow among agents is interrupted, which can prevent marginal cost consensus and lead to coordination failure. Similarly, if some local cost functions lose strong convexity, the gradient dynamics may become ill-conditioned, potentially causing oscillations or divergence from the optimal trajectory. Nevertheless, once connectivity and strong convexity conditions are restored, the system is expected to re-enter the convergence regime and recover stable coordination. These observations highlight the conservative nature of the current theoretical framework. Future work will aim to relax these assumptions by considering jointly connected graphs and general convex (not necessarily strongly convex) objectives, thereby improving the robustness and applicability of the algorithm in practical settings.
6. Conclusions
This paper proposed a novel FXT distributed optimization algorithm to solve the constrained TV RMP in MGs under an MAS framework. By integrating a time-decaying regularized penalty function, the algorithm simultaneously addressed both local inequality and global equality constraints, ensuring that the regularized problem was solved within a provable FXT. Meanwhile, the original constrained TV RMP was asymptotically solved as the regularization diminished over time, yielding a tunable and vanishing optimality gap. Theoretical analysis rigorously established FXT convergence under both identical and heterogeneous Hessian scenarios. Numerical experiments on the IEEE 14-bus MG further verified the algorithm’s effectiveness in terms of convergence speed, distributed adaptability, and robustness to dynamic switching topologies.
While the present study focused on undirected communication graphs, future work will extend the FXT framework to directed or unbalanced communication topologies, further enhancing its applicability in more complex and realistic distributed energy systems.
Author Contributions
Conceptualization T.Z. and Y.A.-A.; methodology T.Z., S.L. and Y.A.-A.; software T.Z.; validation S.L. and Y.A.-A.; writing—original draft preparation T.Z.; writing—review and editing S.L. and Y.A.-A.; supervision S.L. and Y.A.-A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
The following symbols are used in this manuscript:
| Symbol | Meaning |
| Switching signal mapping time to graph index | |
| Laplacian matrix under the current switching graph | |
| Second smallest eigenvalue of L | |
| Neighbor set of agent i | |
| Binary mode indicator: 1 for grid-connected, 0 for islanded | |
| Time-varying penalty parameter, | |
| Smooth penalty function for agent i | |
| Hessian of penalized cost for agent i | |
| Gradient of the penalized local cost: | |
| Lagrange multiplier | |
| Auxiliary scalar representing a shared gradient value across agents | |
| Optimal solution of the constrained RMP | |
| Optimal solution of the penalized RMP | |
| Error variable of agent i | |
| Fixed-time settling time | |
| Upper bound estimate of the fixed-time |
References
- De Azevedo, R.; Cintuglu, M.; Ma, T.; Mohammed, O. Multiagent-Based Optimal Microgrid Control Using Fully Distributed Diffusion Strategy. IEEE Trans. Smart Grid 2017, 8, 1997–2008. [Google Scholar] [CrossRef]
- Wu, J.; Ji, Y.; Sun, X.; Fu, W.; Zhao, S. Anonymous Flocking With Obstacle Avoidance via the Position of Obstacle Boundary Point. IEEE Internet Things J. 2025, 12, 2002–2013. [Google Scholar] [CrossRef]
- Zhao, T.; Ding, Z. Distributed Finite-Time Optimal Resource Management for Microgrids Based on Multi-Agent Framework. IEEE Trans. Ind. Electron. 2018, 65, 6571–6580. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Z. Distributed optimal resource management based on the consensus algorithm in a microgrid. IEEE Trans. Ind. Electron. 2015, 62, 2584–2592. [Google Scholar] [CrossRef]
- Duan, Y.; Zhao, Y.; Hu, J. An initialization-free distributed algorithm for dynamic economic dispatch problems in microgrid: Modeling, optimization and analysis. Sustain. Energy Grids Netw. 2023, 34, 101004. [Google Scholar] [CrossRef]
- Wu, K.; Li, Q.; Chen, Z.; Lin, J.; Yi, Y.; Chen, M. Distributed optimization method with weighted gradients for economic dispatch problem of multi-microgrid systems. Energy 2021, 222, 119898. [Google Scholar] [CrossRef]
- Li, Q.; Liao, Y.; Wu, K.; Zhang, L.; Lin, J.; Chen, M.; Guerrero, J.; Abbott, D. Parallel and distributed optimization method with constraint decomposition for energy management of microgrids. IEEE Trans. Smart Grid 2021, 12, 4627–4640. [Google Scholar] [CrossRef]
- Wang, A.; Liu, W. Distributed incremental cost consensus-based optimization algorithms for economic dispatch in a microgrid. IEEE Access 2020, 8, 12933–12941. [Google Scholar] [CrossRef]
- Mao, S.; Dong, Z.; Schultz, P.; Tang, Y.; Meng, K.; Dong, Z.; Qian, F. A finite-time distributed optimization algorithm for economic dispatch in smart grids. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 2068–2079. [Google Scholar] [CrossRef]
- Cao, Q.; Xie, W. Optimal Frequency Control for Inverter-Based Micro-Grids Using Distributed Finite-Time Consensus Algorithms. IEEE Access 2020, 8, 185243–185252. [Google Scholar] [CrossRef]
- Liu, L.; Yang, G. Distributed fixed-time optimal resource management for microgrids. IEEE Trans. Autom. Sci. Eng. 2023, 20, 404–412. [Google Scholar] [CrossRef]
- Li, Y.; Dong, P.; Liu, M.; Yang, G. A distributed coordination control based on finite-time consensus algorithm for a cluster of DC microgrids. IEEE Trans. Power Syst. 2019, 34, 2205–2215. [Google Scholar] [CrossRef]
- Zaery, M.; Wang, P.; Huang, R.; Wang, W.; Xu, D. Distributed economic dispatch for islanded DC microgrids based on finite-time consensus protocol. IEEE Access 2020, 8, 192457–192468. [Google Scholar] [CrossRef]
- Wang, B.; Fei, Q.; Wu, Q. Distributed time-varying resource allocation optimization based on finite-time consensus approach. IEEE Control Syst. Lett. 2021, 5, 599–604. [Google Scholar] [CrossRef]
- Liu, R.; Wang, D.; Han, Y.; Fan, X.; Luo, Z. Adaptive low-rank subspace learning with online optimization for robust visual tracking. Neural Netw. 2017, 88, 90–104. [Google Scholar] [CrossRef]
- Sun, C.; Feng, Z.; Hu, G. Distributed time-varying formation and optimization with inequality constraints of a multi-robot system. In Proceedings of the 2019 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Hong Kong, 8–12 July 2019; pp. 629–634. [Google Scholar]
- Xiao, Y.; Krunz, M. AdaptiveFog: A modelling and optimization framework for fog computing in intelligent transportation systems. IEEE Trans. Mob. Comput. 2022, 21, 4187–4200. [Google Scholar] [CrossRef]
- Jafarzadeh, S.; Mirheidari, R.; Motlagh, M.J.; Barkhordari, M. Designing PID and BELBIC controllers in path tracking and collision problem in automated highway systems. Int. J. Comput. Commun. Control 2009, 3, 343–348. [Google Scholar]
- Liao, S.; Li, S.; Liu, J.; Huang, H.; Xiao, X. A zeroing neural dynamics based acceleration optimization approach for optimizers in deep neural networks. Neural Netw. 2022, 150, 440–461. [Google Scholar] [CrossRef]
- Lee, S.G.; Egerstedt, M. Controlled coverage using time-varying density functions. IFAC Proc. Vol. 2013, 46, 220–226. [Google Scholar] [CrossRef]
- Huang, B.; Zou, Y.; Meng, Z.; Ren, W. Distributed time-varying convex optimization for a class of nonlinear multiagent systems. IEEE Trans. Autom. Control 2020, 65, 801–808. [Google Scholar] [CrossRef]
- Ning, B.; Han, Q.; Zuo, Z. Distributed optimization for multiagent systems: An edge-based fixed-time consensus approach. IEEE Trans. Cybern. 2019, 49, 122–132. [Google Scholar] [CrossRef] [PubMed]
- Huang, B.; Zou, Y.; Chen, F.; Meng, Z. Distributed time-varying economic dispatch via a prediction-correction method. IEEE Trans. Circuits Syst. I Regul. Pap. 2022, 69, 4215–4224. [Google Scholar] [CrossRef]
- Wang, B.; Sun, S.; Ren, W. Distributed time-varying quadratic optimal resource allocation subject to nonidentical time-varying hessians with application to multiquadrotor hose transportation. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 6109–6119. [Google Scholar] [CrossRef]
- Sun, C.; Ye, M.; Hu, G. Distributed time-varying quadratic optimization for multiple agents under undirected graphs. IEEE Trans. Autom. Control 2017, 62, 3687–3694. [Google Scholar] [CrossRef]
- Li, H.; Yue, X.; Qin, S. Distributed time-varying optimization control protocol for multi-agent systems via finite-time consensus approach. Neural Netw. 2024, 171, 73–84. [Google Scholar] [CrossRef]
- Liu, H.; Zheng, W.; Yu, W. Continuous-time algorithm based on finite-time consensus for distributed constrained convex optimization. IEEE Trans. Autom. Control 2022, 67, 2552–2559. [Google Scholar] [CrossRef]
- Zhu, W.; Wang, Q. Distributed finite-time optimization of multi-agent systems with time-varying cost functions under digraphs. IEEE Trans. Netw. Sci. Eng. 2024, 11, 556–565. [Google Scholar] [CrossRef]
- Huang, Y.; Werner, S.; Huang, J.; Kashyap, N.; Gupta, V. State estimation in electric power grids: Meeting new challenges presented by the requirements of the future grid. IEEE Signal Process. Mag. 2012, 29, 33–43. [Google Scholar] [CrossRef]
- Kantamneni, A.; Brown, L.E.; Parker, G.; Weaver, W.W. Survey of multi-agent systems for microgrid control. Eng. Appl. Artif. Intell. 2015, 45, 192–203. [Google Scholar] [CrossRef]
- Molzahn, D.K.; Dörfler, F.; Sandberg, H.; Low, S.H.; Chakrabarti, S.; Baldick, R.; Lavael, J. A survey of distributed optimization and control algorithms for electric power systems. IEEE Trans. Smart Grid 2017, 8, 2941–2962. [Google Scholar] [CrossRef]
- Bhat, S.; Bernstein, D.S. Finite-time stability of continuous autonomous systems. Siam J. Control Optim. 2000, 38, 751–766. [Google Scholar] [CrossRef]
- Hu, C.; He, H.; Jiang, H. Fixed/Preassigned-time synchronization of complex network via improving fixed-time stability. IEEE Trans. Cybern. 2020, 51, 2882–2892. [Google Scholar] [CrossRef]
- Filippov, A.F. Differential Equations with Discontinuous Righthand Sides; Kluwer Academic: Boston, MA, USA, 1988. [Google Scholar]
- Firouzbahrami, M.; Nobakhti, A. Cooperative fixed-time/finite-time distributed robust optimization of multi-agent systems. Automatica 2022, 142, 110358. [Google Scholar] [CrossRef]
- Rodriguez, S.; AI-Sumaiti, A.; Alsumaiti, T. Quantification of Uncertainty Cost Functions for Controllable Solar Power Modeling. Wseas Trans. Power Syst. 2024, 19, 88–95. [Google Scholar] [CrossRef]
- Liu, L.; Yang, G.; Wasly, S. Distributed predefined-time dual-mode energy management for a microgrid over event-triggered communication. IEEE Trans. Ind. Inform. 2024, 20, 3295–3305. [Google Scholar] [CrossRef]
- Pinar, M.; Zenios, S. On smoothing exact penalty functions for convex constrained optimization. Siam J. Optim. 1994, 4, 486–511. [Google Scholar] [CrossRef]
- Kia, S. Distributed optimal resource allocation over networked systems and use of an e-exact penalty function. IFAC—PapersOnLine 2016, 49, 13–18. [Google Scholar] [CrossRef]
- Liu, L.; Yang, G. Distributed optimal economic environmental dispatch for microgrids over time-varying directed communication graph. IEEE Trans. Netw. Sci. Eng. 2021, 8, 1913–1924. [Google Scholar] [CrossRef]
- Zhou, Z.; Guo, G.; Zhang, R. A fixed-time convergent distributed algorithm for time-varying optimal resource allocation problem. IEEE Trans. Signal Inf. Process. Over Netw. 2025, 11, 48–58. [Google Scholar] [CrossRef]
- Jin, L.; Qi, Y.; Luo, X.; Li, S.; Shang, M. Distributed competition of multi-robot coordination under variable and switching topologies. IEEE Trans. Autom. Sci. Eng. 2022, 19, 3575–3586. [Google Scholar] [CrossRef]
- Zhao, Y.; Guo, G.; Ding, L. Guaranteed cost control of mobile sensor networks with Markov switching topologies. ISA Trans. 2015, 58, 206–213. [Google Scholar] [CrossRef] [PubMed]
- Xiao, S.; Ge, X.; Han, Q.; Zhang, Y. Dynamic event-triggered platooning control of automated vehicles under random communication topologies and various spacing policies. IEEE Trans. Cybern. 2022, 52, 11477–11490. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).