A Power Decoupling Control Strategy for Multi-Port Bidirectional Grid-Connected IPT Systems
Abstract
1. Introduction
2. Multi-Port BDIPT System Modeling and Analysis
2.1. Model of the Multi-Port BDIPT System
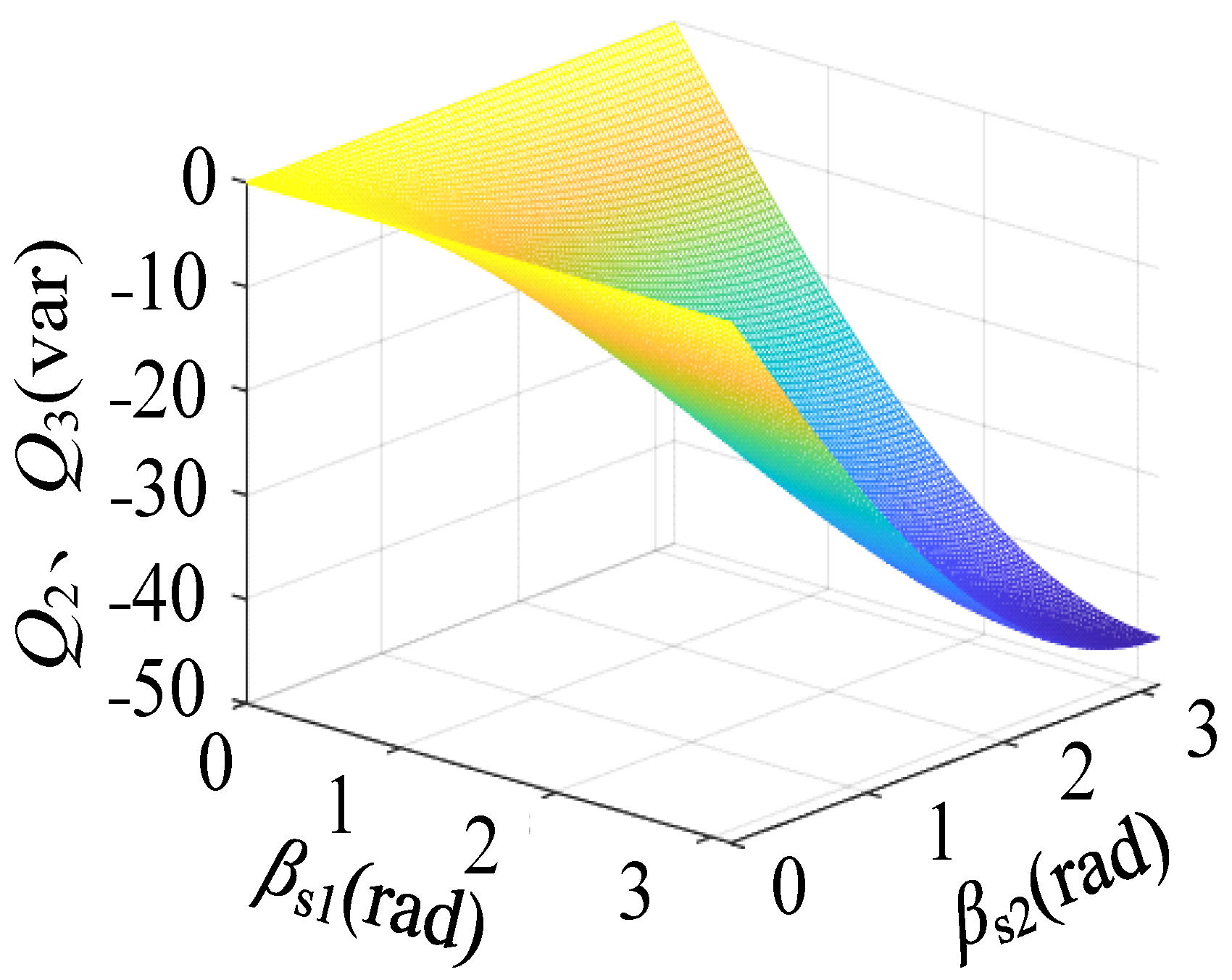
2.2. Analysis of the System Transmission Power Characteristics
3. Proposed Power Decoupling and Power Control Strategy
3.1. Power Decoupling
3.2. Analysis of System Transmission Power Regulation
4. Experimental Verification
4.1. The Experimental Verification of Power Decoupling
4.2. The Experimental Verification of the System Power Transmission Characteristics
4.3. The Experimental Verification of Closed-Loop Power Control Strategy
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, Q.; Wong, S.C.; Tse, C.K.; Ruan, X. Analysis, design, and control of a transcutaneous power regulator for artificial hearts. IEEE Trans. Biomed. Circuits Syst. 2009, 3, 23–31. [Google Scholar] [CrossRef] [PubMed]
- Bosshard, R.; Kolar, J.W. All-SiC 9.5 kW/dm3 on-board power electronics for 50 kW/85 kHz automotive IPT system. IEEE Trans. Emerg. Sel. Top. Power Electron. 2017, 5, 419–431. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, L.; Zhu, Q.; Liao, C.; Li, F. Switch-on modeling and analysis of dynamic wireless charging system used for electric vehicles. IEEE Trans. Ind. Electron. 2016, 63, 6568–6579. [Google Scholar] [CrossRef]
- Feng, H.; Cai, T.; Duan, S.; Zhao, J.; Zhang, X.; Chen, C. An LCC compensated resonant converter optimized for robust reaction to large coupling variation in dynamic wireless power transfer. IEEE Trans. Ind. Electron. 2016, 63, 6591–6601. [Google Scholar] [CrossRef]
- Dai, J.; Ludois, D.C. A survey of wireless power transfer and a critical comparison of inductive and capacitive coupling for small gap applications. IEEE Trans. Power Electron. 2015, 30, 6017–6029. [Google Scholar] [CrossRef]
- Rozario, D.; Azeez, N.A.; Williamson, S.S. Comprehensive review and comparative analysis of compensation networks for capacitive power transfer systems. In Proceedings of the 2016 IEEE 25th International Symposium on Industrial Electronics (ISIE), Santa Clara, CA, USA, 8–10 June 2016; pp. 823–829. [Google Scholar]
- Tavakoli, R.; Pantic, Z. Analysis, design and demonstration of a 25-kW dynamic wireless charging system for roadway electric vehicles. IEEE Trans. Emerg. Sel. Top. Power Electron. 2018, 6, 1378–1393. [Google Scholar] [CrossRef]
- Dai, X.; Li, X.; Li, Y.; Hu, A.P. Impedance-matching range extension method for maximum power transfer tracking in IPT system. IEEE Trans. Power Electron. 2018, 33, 4419–4428. [Google Scholar] [CrossRef]
- Madawala, U.K.; Thrimawithana, D.J. A bidirectional inductive power interface for electric vehicles in V2G systems. IEEE Trans. Ind. Electron. 2011, 58, 4789–4796. [Google Scholar] [CrossRef]
- Zhang, X.; Cai, T.; Duan, S.; Feng, H.; Hu, H.; Niu, J.; Chen, C. A Control Strategy for Efficiency Optimization and Wide ZVS Operation Range in Bidirectional Inductive Power Transfer System. IEEE Trans. Ind. Electron. 2019, 66, 5958–5969. [Google Scholar] [CrossRef]
- Cao, L.; Bao, J.; Loo, K.-H.; Pan, X.; Zhang, R. A hybrid control strategy for dynamic compensation of cross-coupling effect in two-load IPT system. IET Power Electron. 2023, 16, 1943–1957. [Google Scholar] [CrossRef]
- Li, G.; Pan, X.; Bao, D.; Cai, Z.; Kumar, A. A novel noncommunication-based inductive power transfer control technique for battery charging application. IET Power Electron. 2025, 18, e12837. [Google Scholar] [CrossRef]
- Mohamed, A.A.S.; Berzoy, A.; de Almeida, F.G.N.; Mohammed, O. Modeling and Assessment Analysis of Various Compensation Topologies in Bidirectional IWPT System for EV Applications. IEEE Trans. Ind. Appl. 2017, 53, 4973–4984. [Google Scholar] [CrossRef]
- Li, G.; Cai, Z.; Feng, C.; Sun, Z.; Pan, X. DAB-Based Bidirectional Wireless Power Transfer System with LCC-S Compensation Network under Grid-Connected Application. Energies 2024, 17, 4519. [Google Scholar] [CrossRef]
- Jiang, Y.; Wang, L.; Fang, J.; Zhao, C.; Wang, K.; Wang, Y. A Joint Control with Variable ZVS Angles for Dynamic Efficiency Optimization in Wireless Power Transfer System. IEEE Trans. Power Electron. 2020, 35, 11064–11081. [Google Scholar] [CrossRef]
- Tang, Y.; Chen, Y.; Madawala, U.K.; Thrimawithana, D.J.; Ma, H. A New Controller for Bidirectional Wireless Power Transfer Systems. IEEE Trans. Power Electron. 2018, 33, 9076–9087. [Google Scholar] [CrossRef]
- Liu, C.; Ge, S.; Guo, Y.; Li, H.; Cai, G. Double-LCL resonant compensation network for electric vehicles wireless power transfer: Experimental study and analysis. IET Power Electron. 2016, 9, 2262–2270. [Google Scholar] [CrossRef]
- Li, W.; Zhao, H.; Deng, J.; Li, S.; Mi, C.C. Comparison Study on SS and Double-Sided LCC Compensation Topologies for EV/PHEV Wireless Chargers. IEEE Trans. Veh. Technol. 2016, 65, 4429–4439. [Google Scholar] [CrossRef]
- Li, J.; Zhang, X.; Tong, X. Research and Design of Misalignment-Tolerant LCC–LCC Compensated IPT System with Constant-Current and Constant-Voltage Output. IEEE Trans. Power Electron. 2023, 38, 1301–1313. [Google Scholar] [CrossRef]
- Peng, J.; Zhang, B.; Su, W. A Hybrid Control Strategy of LCC–LCC Compensated Electric Vehicles Wireless Charging System with Wide ZVS Range. IEEE Trans. Power Electron. 2025, 40, 6282–6295. [Google Scholar] [CrossRef]
- Deng, J.; Mao, Q.; Wang, W.; Li, L.; Wang, Z.; Wang, S.; Guidi, G. Frequency and Parameter Combined Tuning Method of LCC–LCC Compensated Resonant Converter with Wide Coupling Variation for EV Wireless Charger. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 956–968. [Google Scholar] [CrossRef]
- Fu, M.; Ma, C.; Zhu, X. A Cascaded Boost–Buck Converter for High-Efficiency Wireless Power Transfer Systems. IEEE Trans. Ind. Inform. 2014, 10, 1972–1980. [Google Scholar] [CrossRef]
- Zhang, K.; Ye, T.; Yan, Z.; Song, B.; Hu, A.P. Obtaining Maximum Efficiency of Inductive Power-Transfer System by Impedance Matching Based on Boost Converter. IEEE Trans. Transp. Electrif. 2020, 6, 488–496. [Google Scholar] [CrossRef]
- Vu, V.-B.; Tran, D.-H.; Choi, W. Implementation of the Constant Current and Constant Voltage Charge of Inductive Power Transfer Systems with the Double-Sided LCC Compensation Topology for Electric Vehicle Battery Charge Applications. IEEE Trans. Power Electron. 2018, 33, 7398–7410. [Google Scholar] [CrossRef]
- Liu, X.; Yuan, X.; Xia, C.; Wu, X. Analysis and Utilization of the Frequency Splitting Phenomenon in Wireless Power Transfer Systems. IEEE Trans. Power Electron. 2021, 36, 3840–3851. [Google Scholar] [CrossRef]
- Fu, N.; Deng, J.; Wang, Z.; Wang, W.; Wang, S. A hybrid mode control strategy for LCC–LCC-compensated WPT system with wide ZVS operation. IEEE Trans. Power Electron. 2022, 37, 2449–2460. [Google Scholar] [CrossRef]

















| Symbol | Parameters | Value |
|---|---|---|
| f | Switching frequency | 85 kHz |
| Lp | Port 1 coil inductance | 122 μH |
| L1 | Port 1 compensation inductance | 14.6 μH |
| C1 | Port 1 parallel compensation capacitor | 233.4 nF |
| Cp | Port 1 series compensation capacitor | 34.01 nF |
| Ls1 | Port 2 coil inductance | 50 μH |
| L2 | Port 2 compensation inductance | 15 μH |
| C2 | Port 2 parallel compensation capacitor | 233.1 nF |
| Cs1 | Port 2 series compensation capacitor | 100.3 nF |
| Ls2 | Port 3 coil inductance | 50 μH |
| L3 | Port 3 compensation inductance | 15.2 μH |
| C3 | Port 3 parallel compensation capacitor | 233.3 nF |
| Cs2 | Port 3 series compensation capacitor | 100.5 nF |
| M12 | Mutual inductance between port 1&2 | 11.72 μH |
| M13 | Mutual inductance between port 1&3 | 11.72 μH |
| M23 | Mutual inductance between port 2&3 | 7.5 μH |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, X.; Ma, P.; Cai, Z.; Bao, D. A Power Decoupling Control Strategy for Multi-Port Bidirectional Grid-Connected IPT Systems. Energies 2025, 18, 2589. https://doi.org/10.3390/en18102589
Pan X, Ma P, Cai Z, Bao D. A Power Decoupling Control Strategy for Multi-Port Bidirectional Grid-Connected IPT Systems. Energies. 2025; 18(10):2589. https://doi.org/10.3390/en18102589
Chicago/Turabian StylePan, Xuewei, Peiwen Ma, Zhouchi Cai, and Danyang Bao. 2025. "A Power Decoupling Control Strategy for Multi-Port Bidirectional Grid-Connected IPT Systems" Energies 18, no. 10: 2589. https://doi.org/10.3390/en18102589
APA StylePan, X., Ma, P., Cai, Z., & Bao, D. (2025). A Power Decoupling Control Strategy for Multi-Port Bidirectional Grid-Connected IPT Systems. Energies, 18(10), 2589. https://doi.org/10.3390/en18102589






