Effect of Combined Wave and Current Loading on the Hydrodynamic Characteristics of Double-Pile Structures in Offshore Wind Turbine Foundations
Abstract
1. Introduction
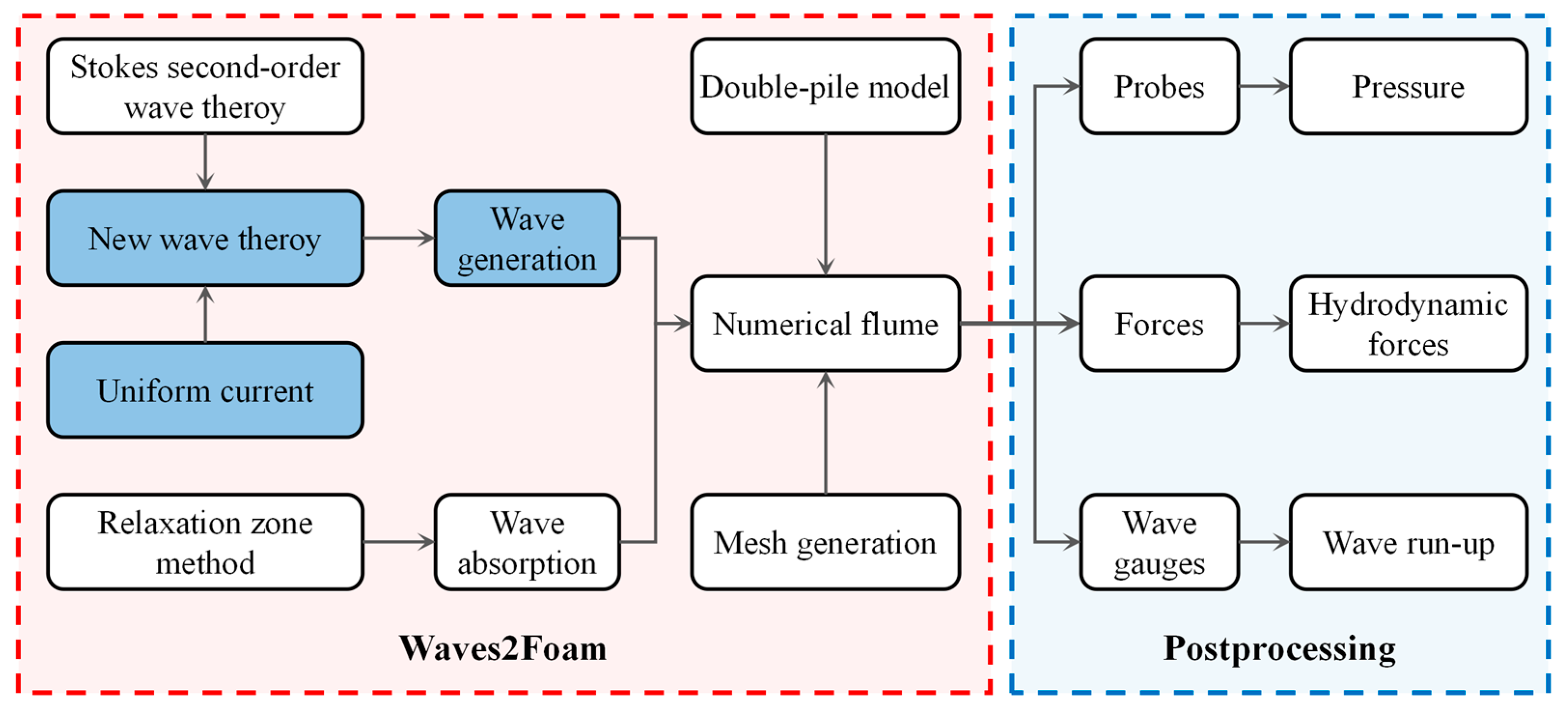
2. Theoretical Method
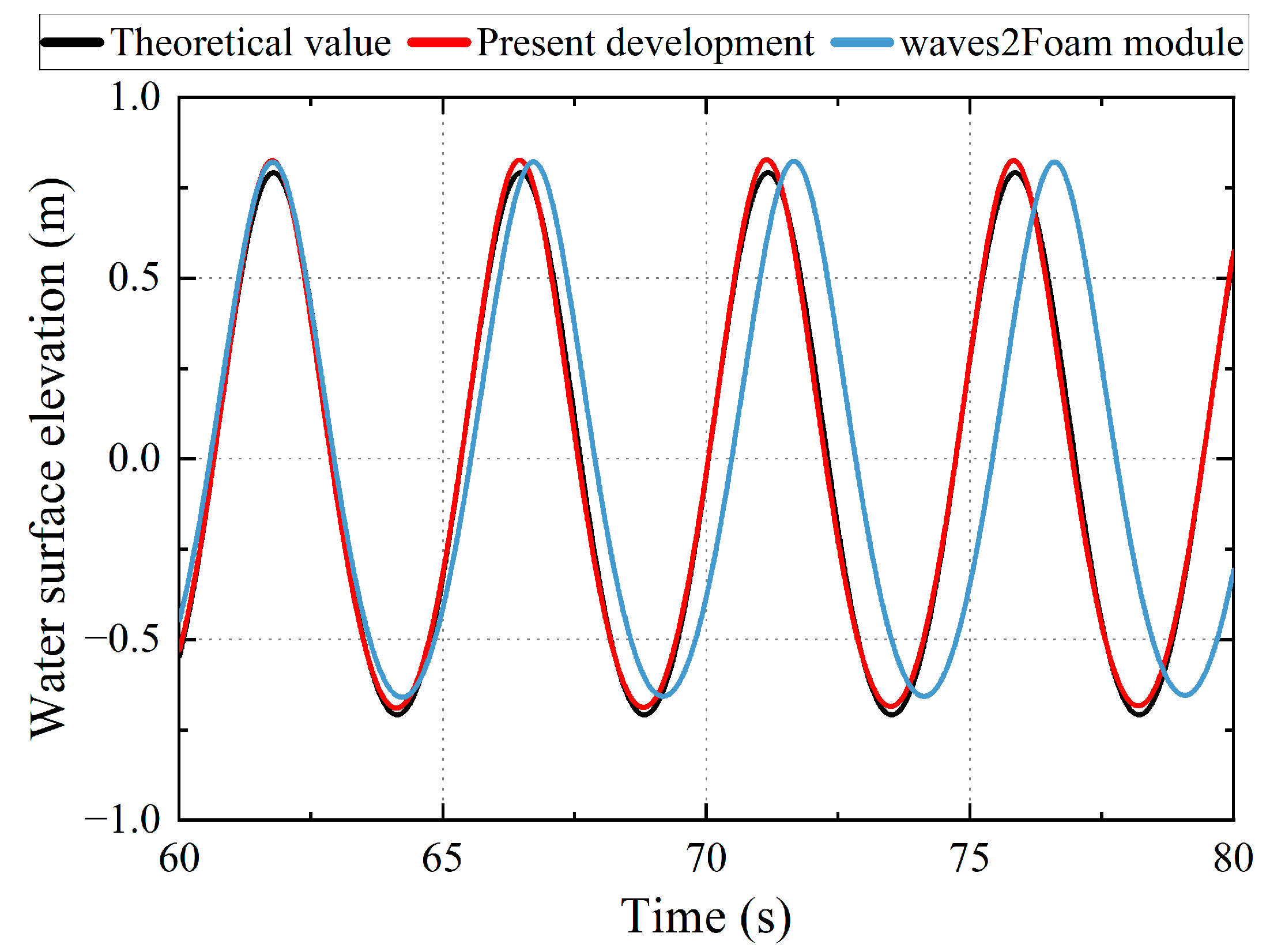
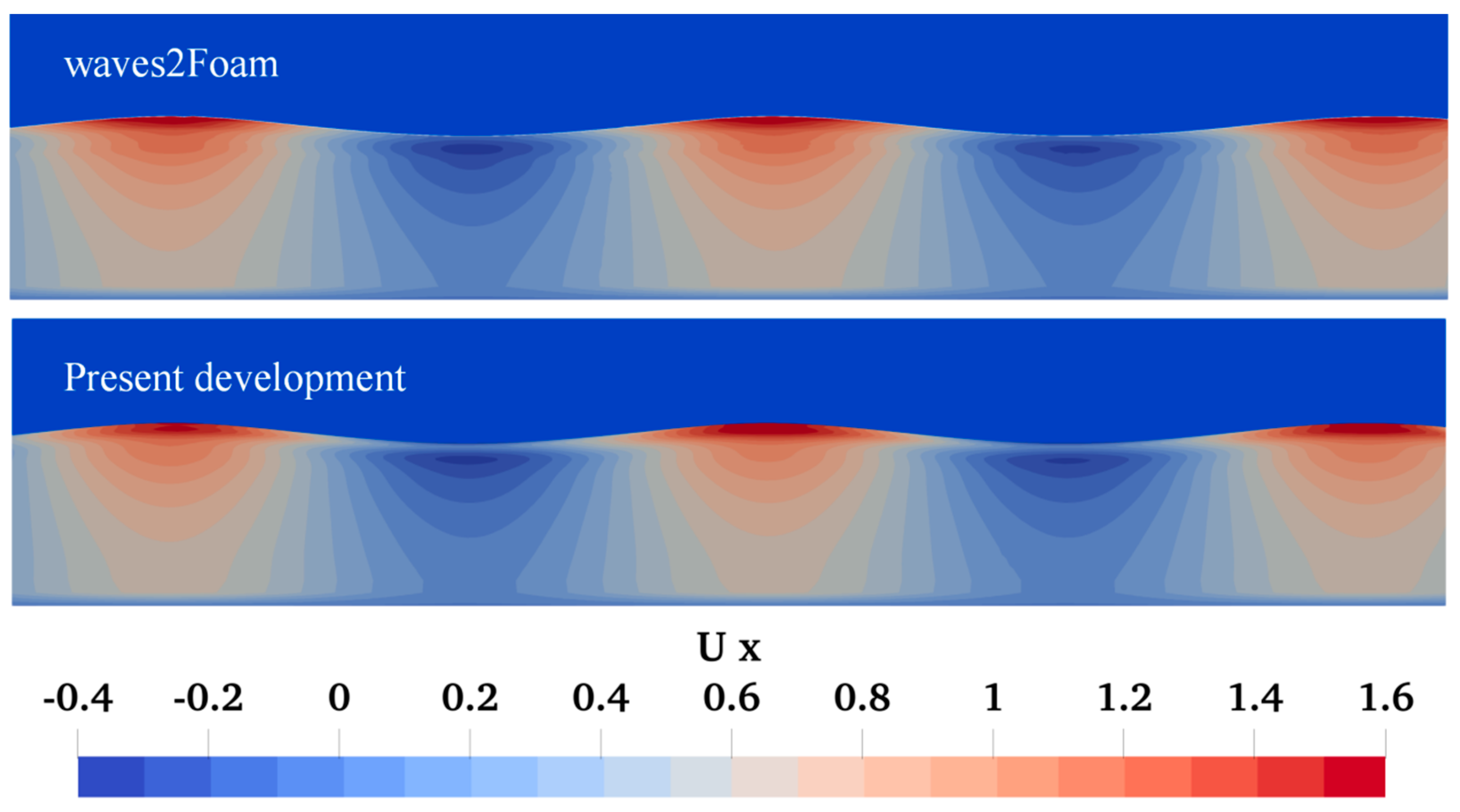
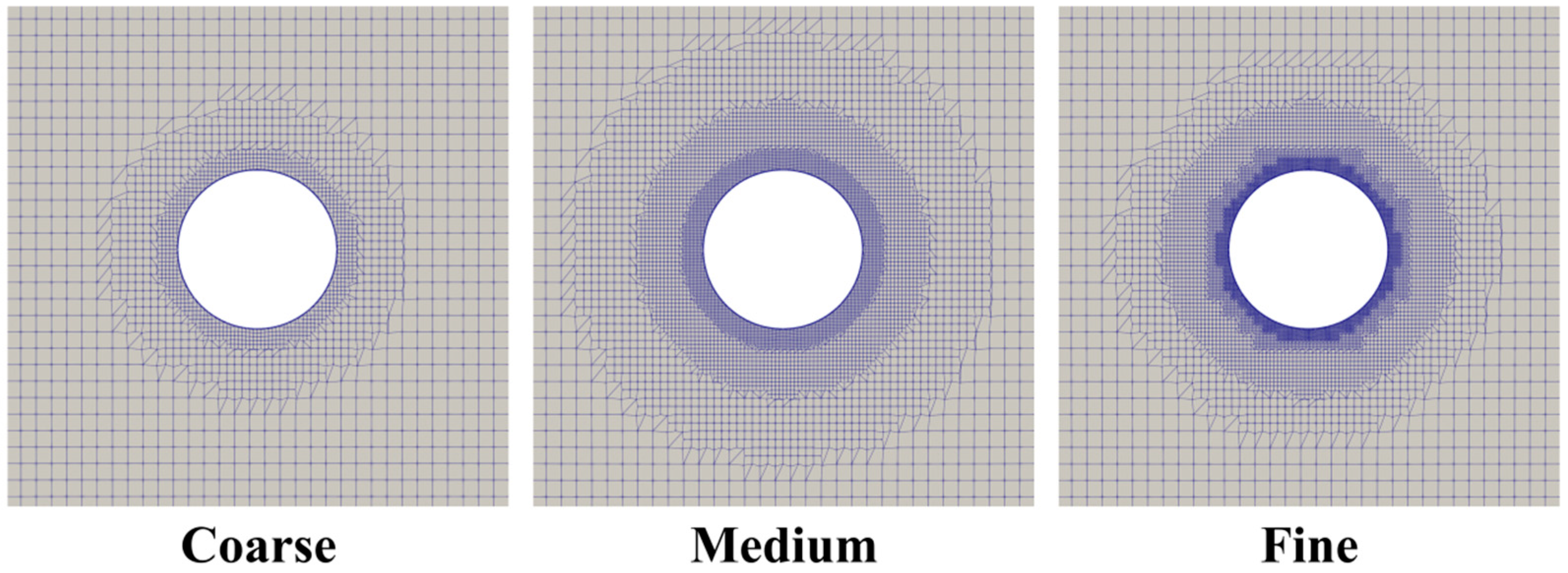
3. Establishment and Verification of the Numerical Model
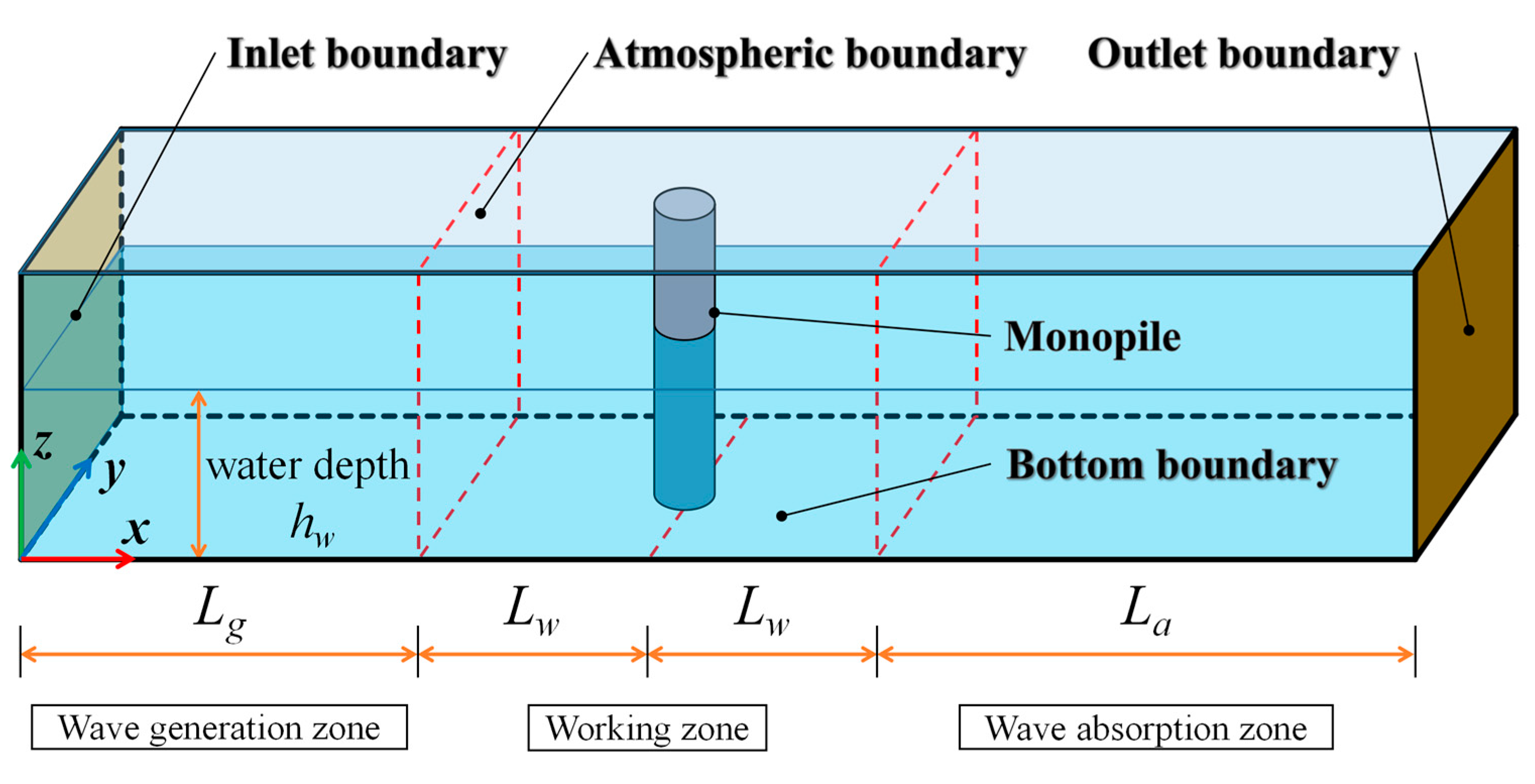
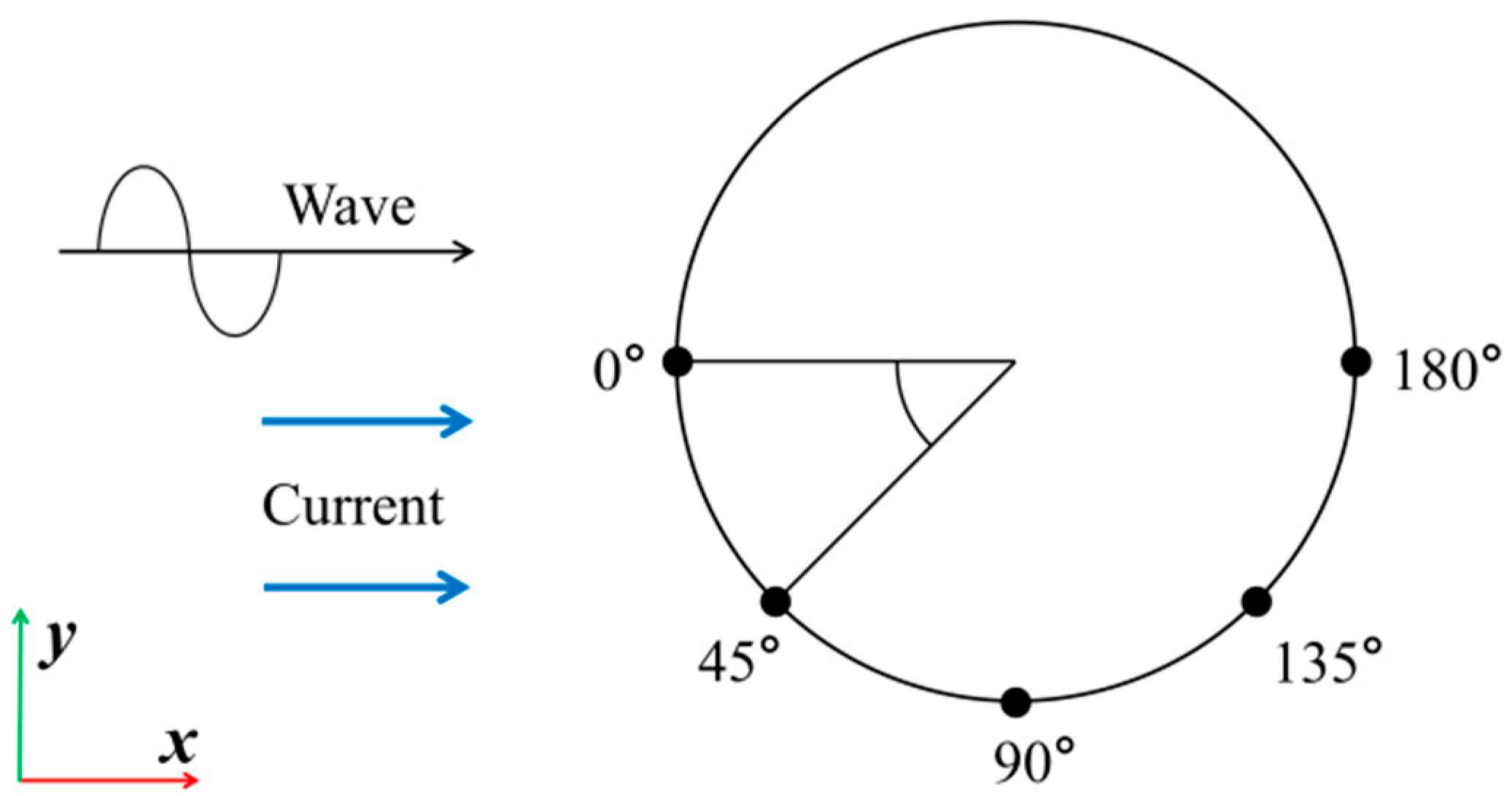
4. Computational Domain and Boundary Conditions
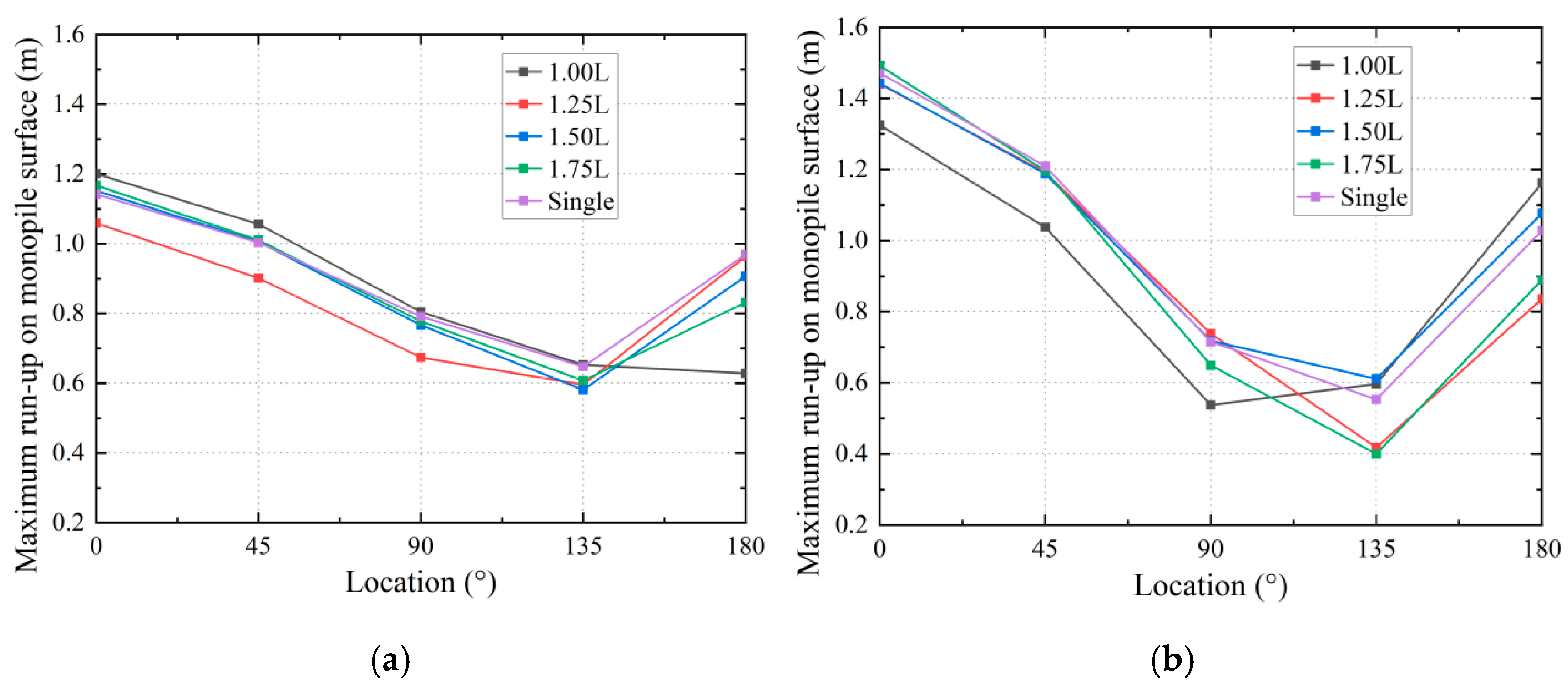
4.1. Wave Run-Up on the Monopile Surface
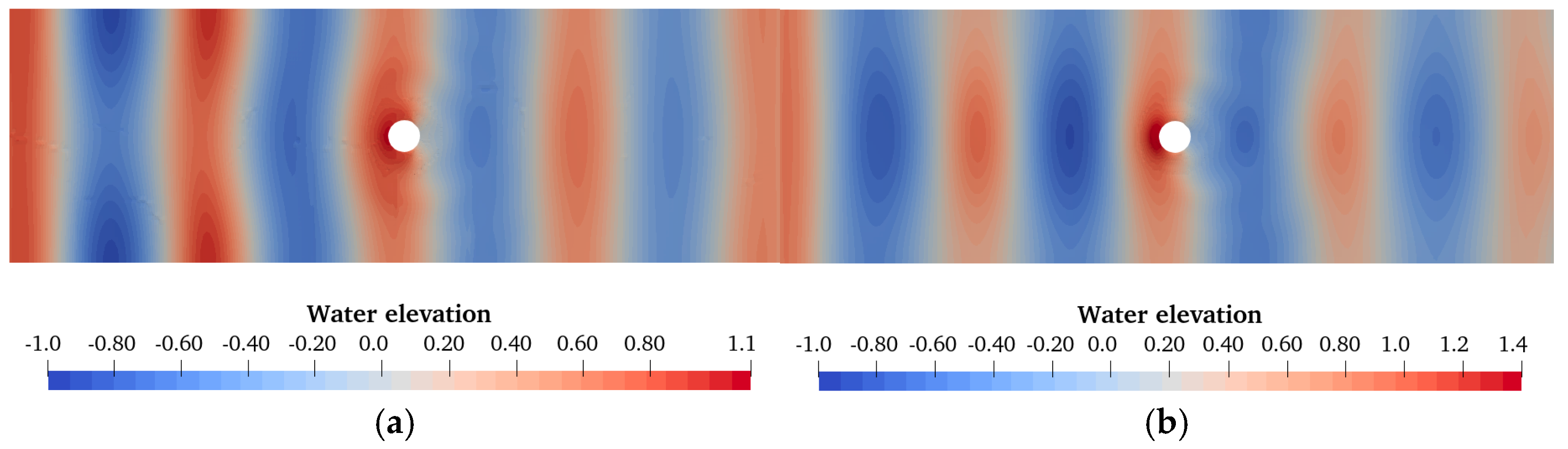
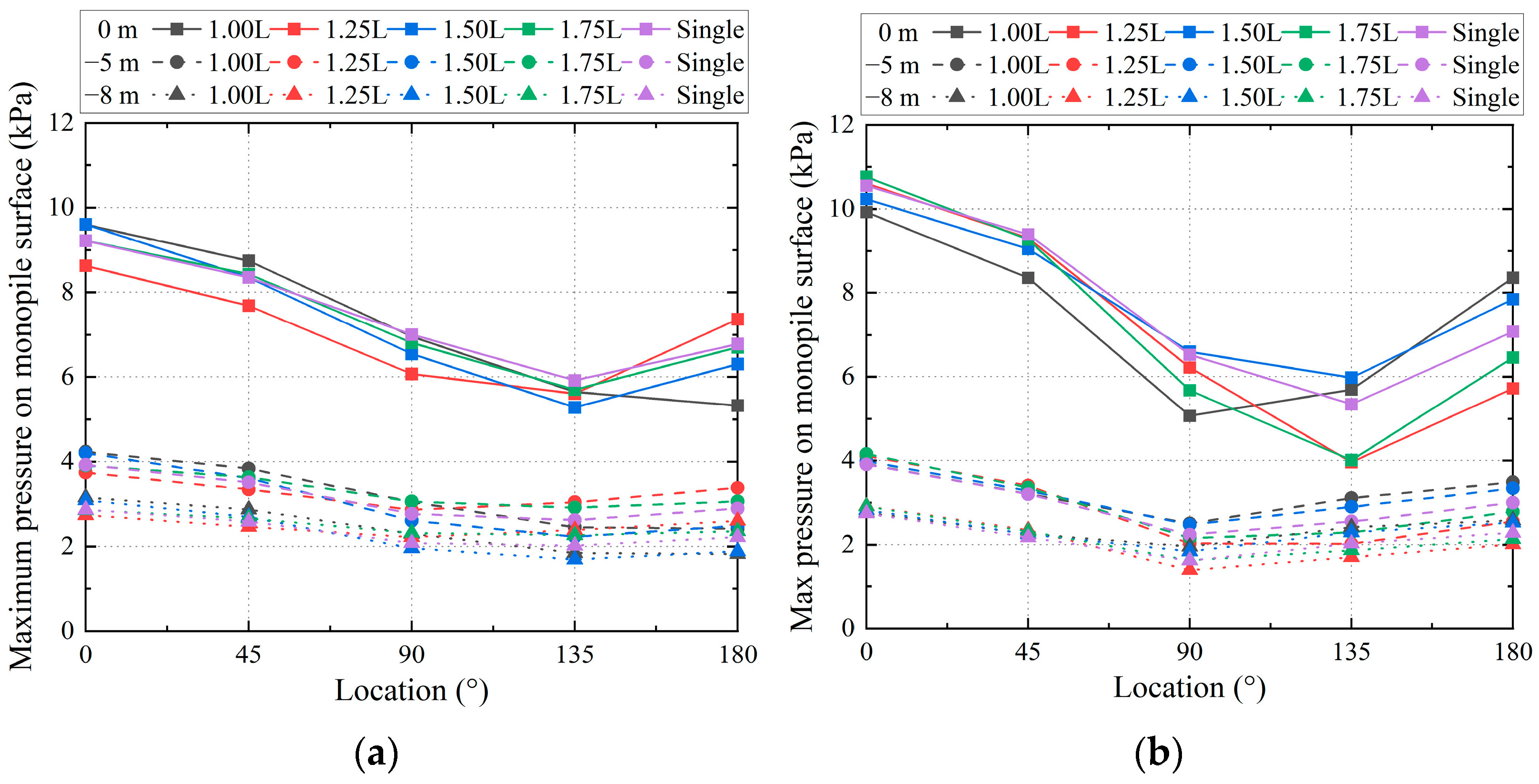
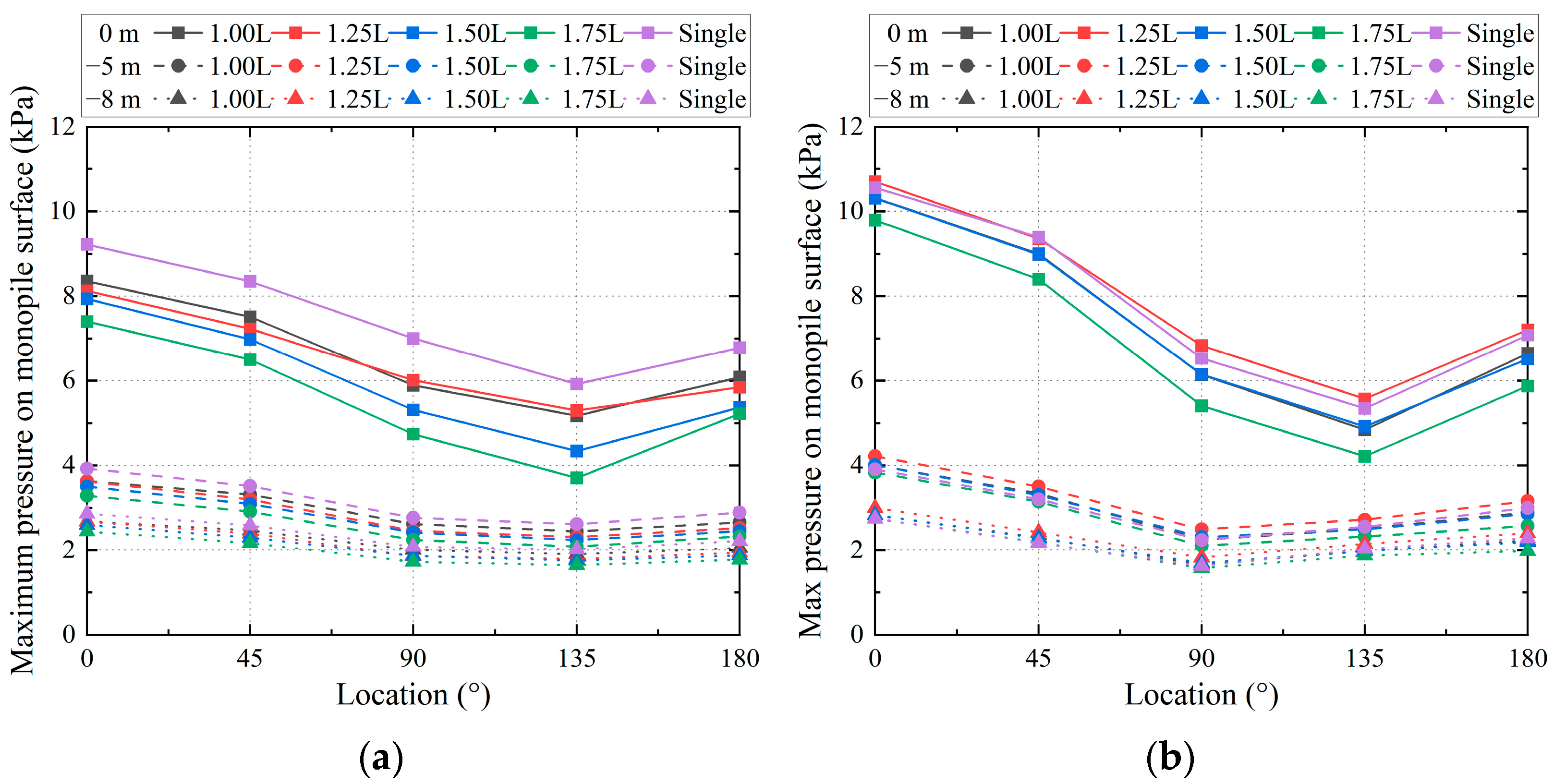
4.2. Pressure Distribution on Double Monopile Surface
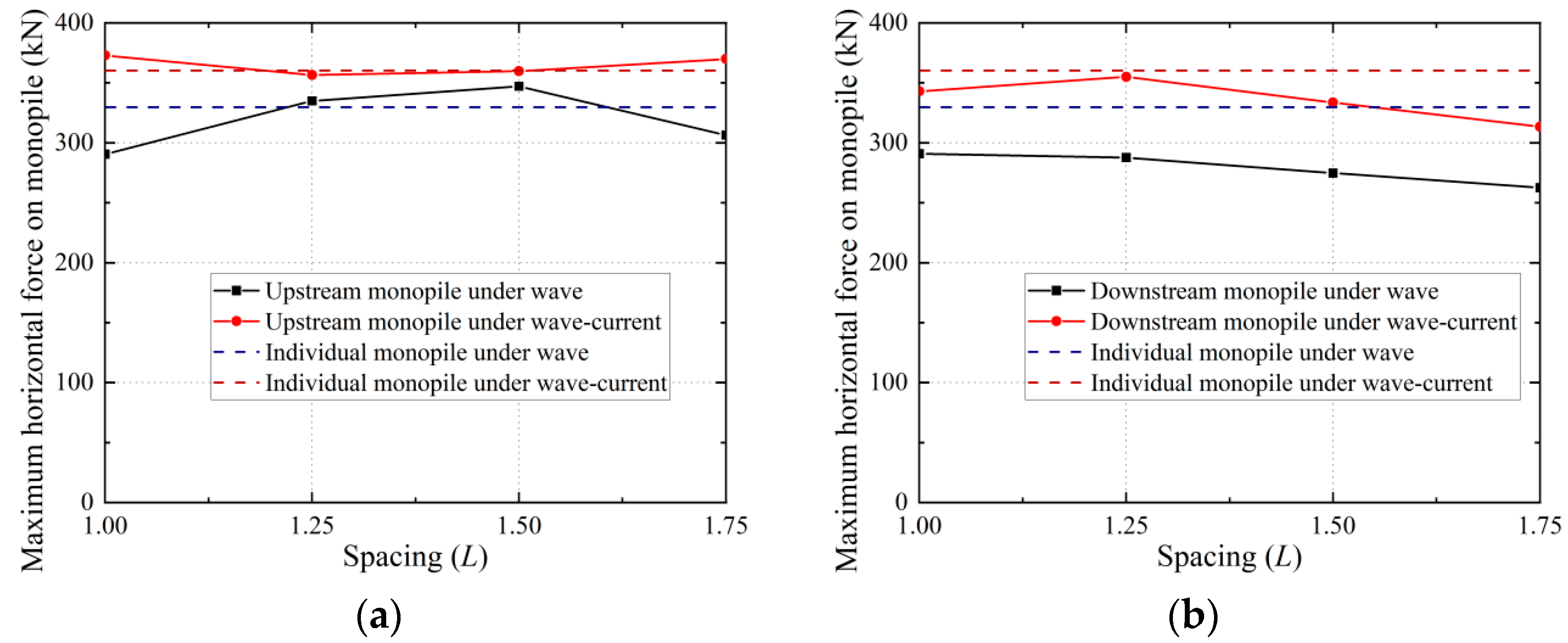
4.3. Horizontal Force on Double Monopile
5. Conclusions
- (1)
- Compared to the results of the individual monopile under wave loading, due to the wave trough induced by reflected waves and the fluid shedding phenomenon caused by current loading, the maximum wave run-up at the leeward side of the upstream monopile for the case of combined wave–current loading is significantly reduced by about 24% compared with that of the individual monopile when the spacing is 1.25 and 1.75 times the wave length. Under the combined wave–current loading, the maximum wave run-up discrepancy between the downstream monopile and the individual monopile is about 29% on average, which is lower than the approximately 41% discrepancy observed under wave-only loading. Moreover, it is found that the combined wave–current loading attenuates the effect of spacing on the maximum wave run-up on the downstream monopile surface.
- (2)
- When the loading conditions and spacing are changed, the maximum surface pressure at the free water surface changes similarly to that of the maximum wave run-up. At heights of –5 m and –8 m, the combined wave–current loading does not significantly change the maximum pressure distribution on the leeward side of both the upstream and downstream monopiles compared to the wave loading conditions. Furthermore, the maximum pressure distribution on the surface of the upstream monopile is significantly reduced by the influence of the downstream monopile as the location gets closer to the water bottom.
- (3)
- Under the wave loading, the maximum horizontal force of the upstream monopile increases first and then decreases with the increase in spacing; however, after applying the combined wave–current loading, it shows an opposite trend. Conversely, for the downstream monopile, the maximum horizontal force decreases with increasing spacing no matter whether the wave load or the combined wave–current load is applied. For the overall double-pile structure, compared with the case under wave loading, combined wave–current loading significantly reduces the influence of spacing on the maximum horizontal force of the upstream/downstream monopile and reduces the discrepancy in maximum horizontal force between the double-pile structure and individual monopile.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sarkar, N.; Konar, T.; Ghosh, A.D. Passive vibration control techniques for offshore structures under different environmental loading: A review. Ocean Eng. 2025, 320, 120296. [Google Scholar] [CrossRef]
- Li, C.; Jin, T.; Chen, Z.; Wei, G. A De-Nesting Hybrid Reliability Analysis Method and Its Application in Marine Structure. J. Mar. Sci. Eng. 2024, 12, 2221. [Google Scholar] [CrossRef]
- Wang, S.; Xing, Y.; Balakrishna, R.; Shi, W.; Xu, X. Design, local structural stress, and global dynamic response analysis of a steel semi-submersible hull for a 10-MW floating wind turbine. Eng. Struct. 2025, 291, 116474. [Google Scholar] [CrossRef]
- Konispoliatis, D.N.; Mavrakos, S.A. Hydrodynamic research of marine structures. J. Mar. Sci. Eng. 2024, 12, 2049. [Google Scholar] [CrossRef]
- Ali, A.; Shi, W.; Wang, S.; Zhai, H.; Haider, R.; Leng, S.; Li, X.; Han, X. Dynamic analysis of a TetraSpar floating offshore wind turbine with different tendons failure scenario. Ocean Eng. 2025, 323, 120607. [Google Scholar] [CrossRef]
- Cai, Y.; Zhao, H.; Li, X.; Shi, W.; Xiao, Q. Developing an OpenFOAM solver for coupled aero-hydrodynamic analysis of integrated structure with floating offshore wind turbine and aquaculture net cage. Coast. Eng. 2025, 198, 104720. [Google Scholar] [CrossRef]
- Arshad, M.; O’Kelly, B.C. Piled-cruciform attachment to monopile head reduces deflection. Proc. Inst. Civil Eng.-Geotech. Eng. 2016, 169, 321–335. [Google Scholar] [CrossRef]
- Chen, H.; Ni, Y. Numerical analysis of wave run-up characteristics on dual non-submerged vertical cylinders system. Hydro-Sci. Eng. 2020, 6, 42–47. [Google Scholar]
- Guo, J.; Han, B.; Ma, Z.; Zhang, B.; Guo, M.; He, B. Research on the strain response of offshore wind turbine monopile foundation through integrated fluid-structure-seabed model test. Ocean Eng. 2024, 314, 119729. [Google Scholar] [CrossRef]
- Xie, W.; Zhang, Q.; Cai, H.; Fu, M. Numerical Investigation on the Interaction between a Tsunami-like Solitary Wave and a Monopile on a Sloping Sandy Seabed. J. Mar. Sci. Eng. 2024, 12, 1421. [Google Scholar] [CrossRef]
- Schløer, S.; Bredmose, H.; Bingham, B.H. The influence of fully nonlinear wave forces on aero-hydro-elastic calculations of monopile wind turbines. Mar. Struct. 2016, 50, 162–188. [Google Scholar] [CrossRef]
- Zeng, X.; Shi, W.; Michailides, C.; Zhang, S.; Li, X. Numerical and experimental investigation of breaking wave forces on a monopile-type offshore wind turbine. Renew. Energy 2021, 175, 501–519. [Google Scholar] [CrossRef]
- Zhu, J.; Gao, Y.; Wang, L.; Li, W. Experimental investigation of breaking regular and irregular waves slamming on an offshore monopile wind turbine. Mar. Struct. 2022, 86, 103270. [Google Scholar] [CrossRef]
- Shi, W.; Zhang, S.; Michailides, C.; Zhang, L.; Zhang, P.; Li, X. Experimental investigation of the hydrodynamic effects of breaking waves on monopiles in model scale. J. Mar. Sci. Technol. 2023, 28, 314–325. [Google Scholar] [CrossRef]
- Xu, P.; Li, Q.; Wang, C.; Li, L.; Tan, D.; Wu, H. Interlayer healing mechanism of multipath deposition 3D printing models and interlayer strength regulation method. J. Manuf. Process. 2025, 141, 1031–1047. [Google Scholar] [CrossRef]
- Tan, Y.; Ni, Y.; Xu, W.; Xie, Y.; Li, L.; Tan, D. Key technologies and development trends of the soft abrasive flow finishing method. J. Zhejiang Univ.-SCI A 2023, 24, 1043–1064. [Google Scholar] [CrossRef]
- Tang, Y.; Shi, W.; You, J.; Michailides, C. Effects of nonlinear wave loads on large monopile offshore wind turbines with and without ice-breaking cone configuration. J. Mar. Sci. Technol. 2021, 26, 37–53. [Google Scholar] [CrossRef]
- Li, M.; Zhang, H.; Guan, H. Study of offshore monopile behaviour due to ocean waves. Ocean Eng. 2011, 38, 1946–1956. [Google Scholar] [CrossRef]
- Lin, Y.H.; Chen, J.F.; Lu, P.Y. A CFD model for simulating wave run-ups and wave loads in case of different wind turbine foundations influenced by nonlinear waves. Ocean Eng. 2017, 129, 428–440. [Google Scholar] [CrossRef]
- Wang, M.; Si, W.; Gao, Y.; Cui, L.; Jeng, D.S.; Sun, K.; Chen, B.; Zhao, H. Experimental Study of the Random Wave-Induced Hydrodynamics and Soil Response in a Porous Seabed Around Double Piles. J. Mar. Sci. Eng. 2024, 12, 1715. [Google Scholar] [CrossRef]
- Yao, Y.; Tang, Z.; He, F.; Yuan, W.C. Numerical investigation of solitary wave interaction with double row of vertical slotted piles. J. Eng. Mech. 2018, 144, 04017147. [Google Scholar] [CrossRef]
- Koraim, A.S.; Iskander, M.M.; Elsayed, W.R. Hydrodynamic performance of double rows of piles suspending horizontal c shaped bars. Coast. Eng. 2014, 84, 81–96. [Google Scholar] [CrossRef]
- Chen, L.; Zhai, H.; Wang, P.; Jeng, D.S.; Zhang, Q.; Wang, S.; Duan, L.; Liu, Y. Physical modeling of combined waves and current propagating around a partially embedded monopile in a porous seabed. Ocean Eng. 2020, 205, 107307. [Google Scholar] [CrossRef]
- Cheng, H.; Cheng, Y.; Wang, X.; Xia, B.; Lyu, X.; Zheng, Y.; Zhang, J. Experimental study of local scour around inclined piles in combined waves and current. Ocean Eng. 2022, 266, 112511. [Google Scholar] [CrossRef]
- Chen, L.; Yang, X.; Li, L.; Wu, W.; EI Naggar, M.H.; Wang, K.; Chen, J. Numerical analysis of the deformation performance of monopile under wave and current load. Energies 2020, 13, 6431. [Google Scholar] [CrossRef]
- Shi, L.; Cheng, Y.; Zheng, Y.; Xia, B.; Huang, X. Experimental study on local scour at the monopile foundation of an offshore wind turbine under the combined action of wave–current–vibration. J. Mar. Sci. Eng. 2024, 12, 963. [Google Scholar] [CrossRef]
- Qi, W.G.; Gao, F.P. Equilibrium scour depth at offshore monopile foundation in combined waves and current. Sci. China: Technol. Sci. 2014, 57, 1030–1039. [Google Scholar] [CrossRef]
- Büchmann, B.; Skourup, J.; Cheung, K.F. Run-up on a structure due to second-order waves and a current in a numerical wave tank. Appl. Ocean Res. 1998, 20, 297–308. [Google Scholar] [CrossRef]
- Hong, C.; Lyu, Z.; Wang, F.; Zhao, Z.; Wang, L. Wave-Current Loads on a Super-Large-Diameter Pile in Deep Water: An Experimental Study. Appl. Sci. 2023, 13, 8859. [Google Scholar] [CrossRef]
- Shi, Q.; Hu, Y.; Zhao, H.; Jiang, C.; Zou, C.; Nian, J.; Li, X. Hydrodynamic analysis of the monopile-supported offshore wind turbine integrated with the UHMWPE cage under wave-current loading. In Proceedings of the International Offshore and Polar Engineering Conference, International Society of Offshore and Polar Engineers, Rhodes, Greece, 16–21 June 2024; pp. 1013–1020. [Google Scholar]
- Jacobsen, N.G. Waves2foam Manual. 2017. Available online: https://www.researchgate.net/publication/319160515_waves2Foam_Manual (accessed on 16 April 2025).
- Robertson, A.N.; Wendt, F.; Jonkman, J.M.; Popko, W.; Borg, M.; Bredmose, H.; Schlutter, F.; Qvist, J.; Bergua, R.; Harries, R.; et al. OC5 Project Phase Ib: Validation of Hydrodynamic Loading on a Fixed, Flexible Cylinder for Offshore Wind Applications. Energy Procedia 2016, 94, 82–101. [Google Scholar] [CrossRef]

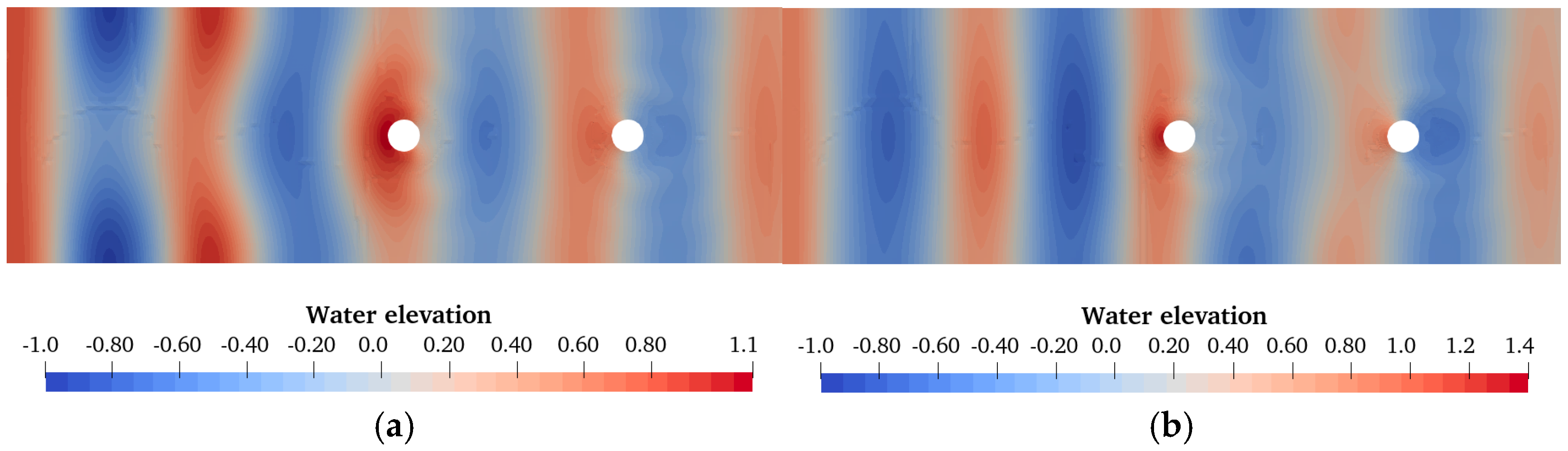
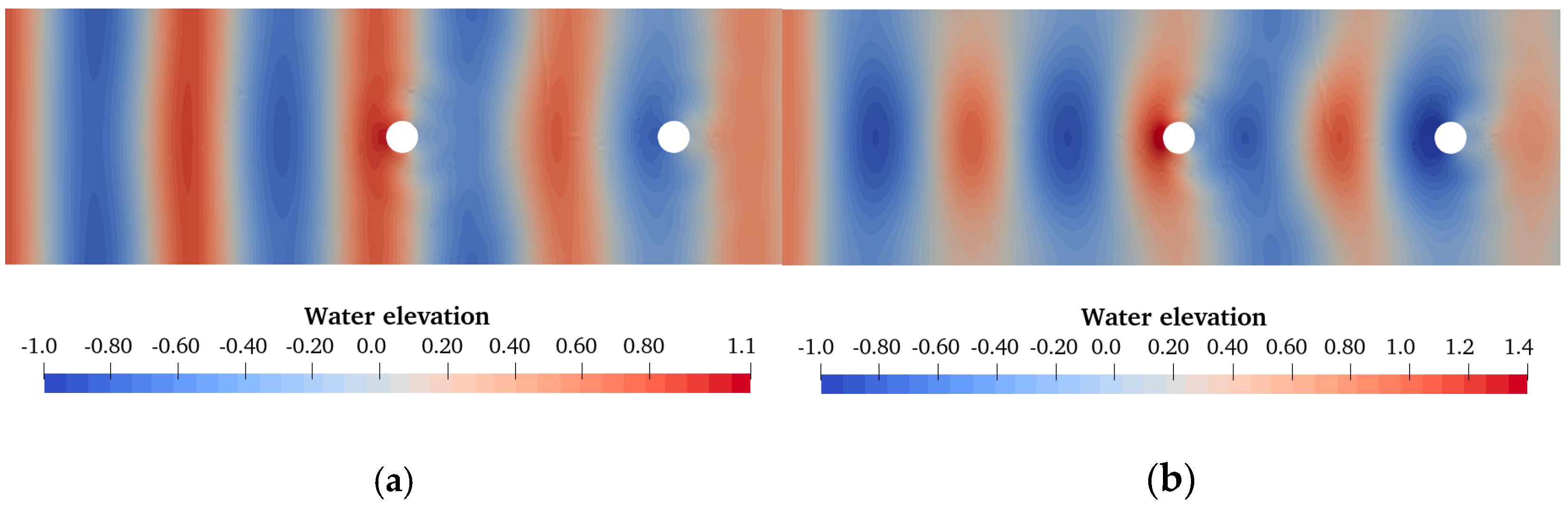
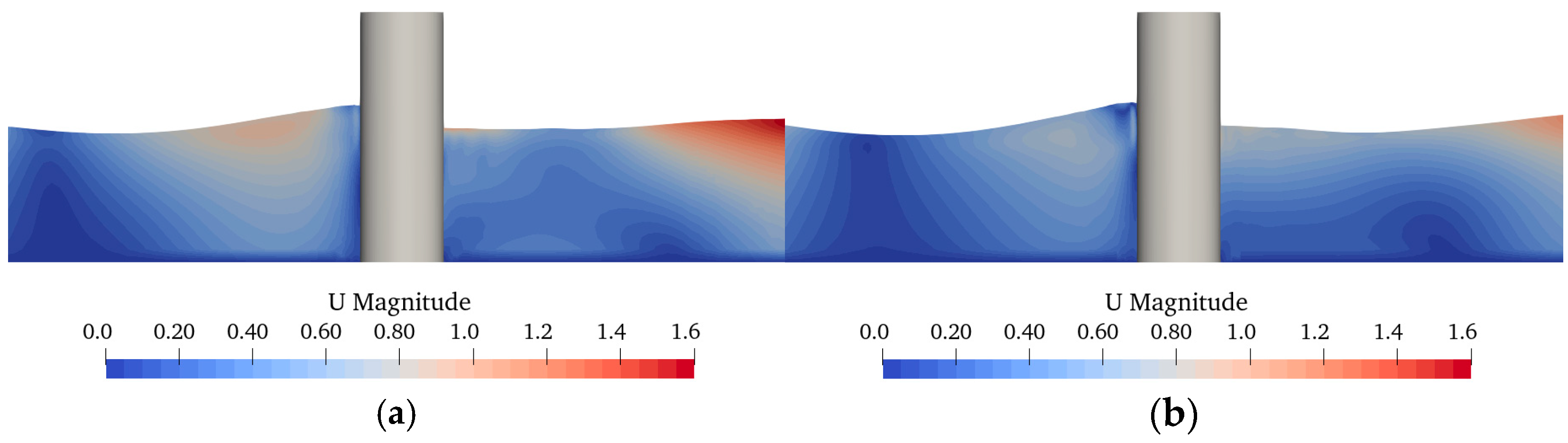

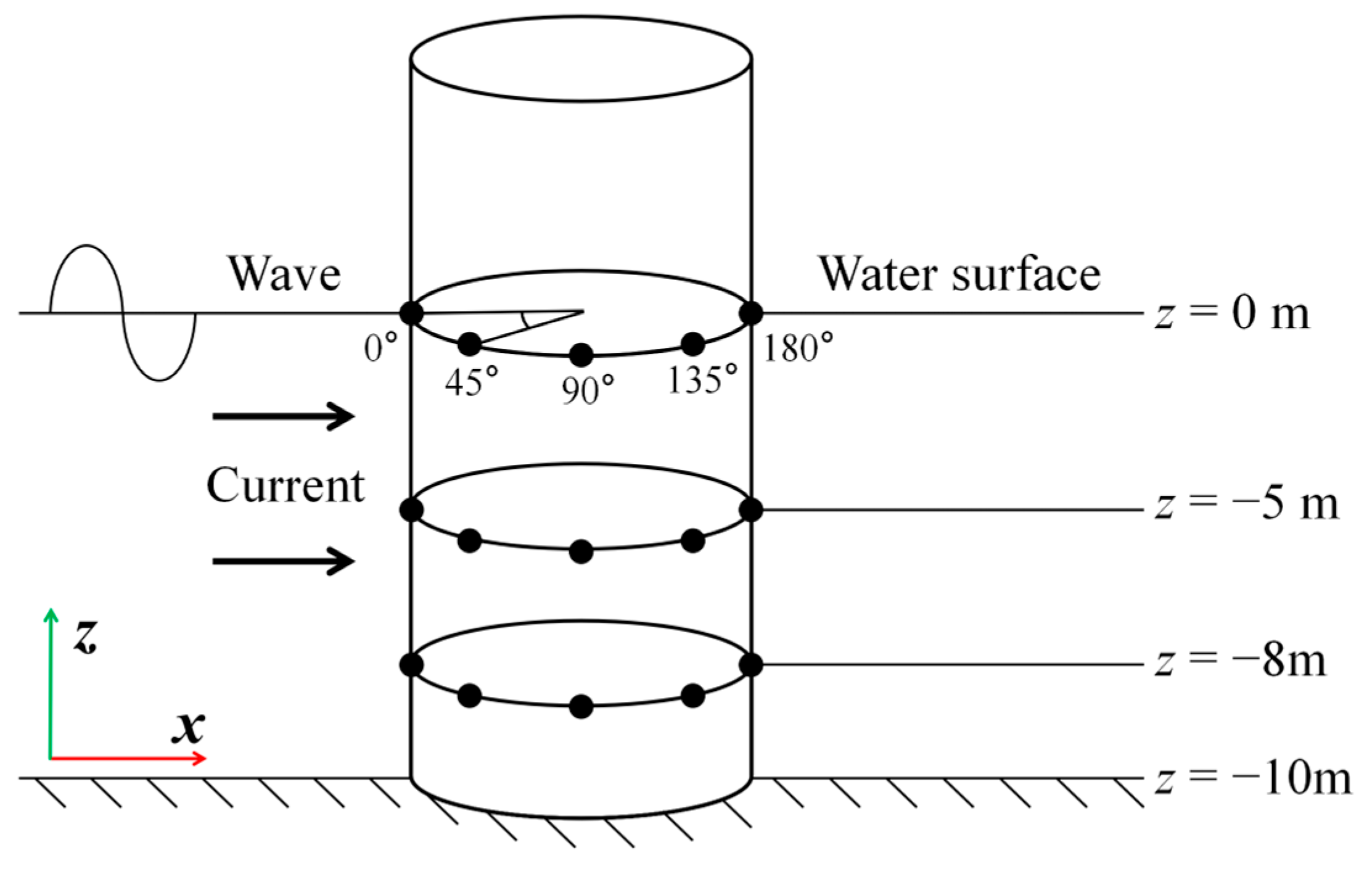
| Wave Height | Wave Cycle | Water Depth | Water Velocity |
|---|---|---|---|
| 1.50 m | 4.95 s | 10 m | 0.4 m/s |
| Monopile Diameter | Wave Height | Wave Period | Water Depth | Flume Length | Flume Width | Flume Height |
|---|---|---|---|---|---|---|
| 0.075 m | 0.09 m | 1.5655 s | 0.78 m | 16 m | 0.8 m | 1.18 m |
| No. | Double-Pile Spacing | Current Velocity (m/s) | ||||
|---|---|---|---|---|---|---|
| LC 1 | 1.5 | 4.95 | 36 | 10 | 1.00 | 0 |
| LC 2 | 1.5 | 4.95 | 36 | 10 | 1.25 | 0 |
| LC 3 | 1.5 | 4.95 | 36 | 10 | 1.50 | 0 |
| LC 4 | 1.5 | 4.95 | 36 | 10 | 1.75 | 0 |
| LC 5 | 1.5 | 4.95 | 36 | 10 | 1.00 | 0.4 |
| LC 6 | 1.5 | 4.95 | 36 | 10 | 1.25 | 0.4 |
| LC 7 | 1.5 | 4.95 | 36 | 10 | 1.50 | 0.4 |
| LC 8 | 1.5 | 4.95 | 36 | 10 | 1.75 | 0.4 |
| Monopile Position | Loading Condition | The Largest Differences Compared to Individual Monopile Results |
|---|---|---|
| Upstream | Wave | 7.1% |
| Upstream | Wave–current | 3.5% |
| Downstream | Wave | 20% |
| Downstream | Wave–current | 13% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lai, Y.; Cai, L.; Wu, X.; Wang, B.; Hu, Y.; Liang, Y.; Zhao, H.; Shi, W. Effect of Combined Wave and Current Loading on the Hydrodynamic Characteristics of Double-Pile Structures in Offshore Wind Turbine Foundations. Energies 2025, 18, 2573. https://doi.org/10.3390/en18102573
Lai Y, Cai L, Wu X, Wang B, Hu Y, Liang Y, Zhao H, Shi W. Effect of Combined Wave and Current Loading on the Hydrodynamic Characteristics of Double-Pile Structures in Offshore Wind Turbine Foundations. Energies. 2025; 18(10):2573. https://doi.org/10.3390/en18102573
Chicago/Turabian StyleLai, Yongqing, Li Cai, Xinyun Wu, Bin Wang, Yiyang Hu, Yuwei Liang, Haisheng Zhao, and Wei Shi. 2025. "Effect of Combined Wave and Current Loading on the Hydrodynamic Characteristics of Double-Pile Structures in Offshore Wind Turbine Foundations" Energies 18, no. 10: 2573. https://doi.org/10.3390/en18102573
APA StyleLai, Y., Cai, L., Wu, X., Wang, B., Hu, Y., Liang, Y., Zhao, H., & Shi, W. (2025). Effect of Combined Wave and Current Loading on the Hydrodynamic Characteristics of Double-Pile Structures in Offshore Wind Turbine Foundations. Energies, 18(10), 2573. https://doi.org/10.3390/en18102573








