Position Sensorless Control of Permanent Magnet Synchronous Motor Based on Improved Model Reference Adaptive Systems

Abstract

To address the issues of poor stability and susceptibility to external disturbances in traditional model reference adaptive systems (MRASs) for permanent magnet synchronous motors (PMSMs), this paper proposes a sliding mode control strategy based on an improved model reference adaptive observer. First, the dynamic equations of the PMSM are used as the reference model, while the stator current equations incorporating speed variables are constructed as the adjustable model. Subsequently, a novel adaptive law is designed using Popov’s hyperstability theory to enhance the estimation accuracy of rotor position. A fractional-order system was introduced to construct both a fractional-order sliding surface and reaching law. Subsequently, a comparative study was conducted between the conventional integral terminal sliding surface and the proposed novel sliding mode reaching law. The results demonstrate that the new reaching law can adaptively adjust the switching gain based on system state variables. Under sudden load increases, the improved system achieves a 25% reduction in settling time compared to conventional sliding mode control (SMC), along with a 44% decrease in maximum speed fluctuation and a 42% reduction in maximum torque ripple, significantly enhancing dynamic response performance. Furthermore, a variable-gain terminal sliding mode controller is derived, and the stability of the closed-loop control system is rigorously proven using Lyapunov theory. Finally, simulations verify the effectiveness and feasibility of the proposed control strategy in improving system robustness and disturbance rejection capability.

1. Introduction

Permanent magnet synchronous motors (PMSMs) have been widely applied in domains such as electric drives, aerospace, and industrial applications owing to their simple structure, high operational efficiency, elegant control performance, strong reliability, and compact size [1,2]. In these applications, the control performance of PMSMs highly depends on the accurate acquisition of the rotor position angle. However, in high-speed permanent magnet synchronous motors, the sampling frequency and processing delay of position sensors can lead to estimation lag, affecting the system’s control accuracy [3]. Moreover, in HSPMSMs, the position sensors must endure significant mechanical stress and centrifugal force due to high-speed rotation, reducing system reliability. Hence, sensorless control has become a prominent research direction in motor control [4].

Current sensorless control strategies for PMSMs primarily encompass high-frequency injection methods [5,6] typically applied in low-speed scenarios, along with back-EMF-based approaches including sliding mode observer algorithms [7,8], extended Kalman filtering [9,10,11], and model reference adaptive methods [12,13]. An optimized sliding mode observer structure was proposed in [14] for estimating motor speed and rotor angle information, demonstrating strong anti-interference capability while suffering from high-frequency chattering due to its variable structure control nature. Reference [15] introduced an EKF-based state observation method for real-time rotor position and speed estimation, achieving excellent prediction accuracy at the cost of computationally intensive matrix operations. The model reference adaptive control strategy presented in [16] enabled sensorless vector control of a PMSM with satisfactory estimation precision, though its performance remains constrained by modeling accuracy limitations and exhibits inadequate dynamic stability and disturbance rejection. A novel adaptive full-order observer developed in [17] integrates model reference adaptive strategy with state estimation equations and error compensation mechanisms through feedback correction terms for closed-loop observation, while employing sliding mode control instead of conventional PI regulators for speed loop control to enhance external disturbance suppression capability.

A key feature of sliding mode variable structure control is its fast response and strong disturbance rejection capability, making it widely used in PMSM control systems [18]. A terminal composite sliding mode control strategy was developed in [19], which integrates hybrid-reaching-law-based sliding mode control with an extended sliding mode disturbance observer, combining both terminal and proportional reaching terms in the variable speed component to effectively suppress chattering and reduce reaching time compared with conventional approaches. Reference [20] proposed an improved SMVSC-based model reference adaptive sensorless method that replaces traditional PI control with a sliding mode algorithm, thereby simplifying system structure while employing a saturation-function-based speed switching estimation algorithm to address chattering phenomena, which not only enhances estimation accuracy but also eliminates the need for low-pass filters. To further mitigate system chattering, [21] introduced a novel exponential reaching law combined with an adaptive extended Kalman filter incorporating fading factors for rotor position and speed prediction, demonstrating improved estimation precision and enhanced system stability and robustness under high-dynamic conditions. These studies collectively indicate that incorporating advanced sliding mode reaching laws can significantly boost the performance of sensorless PMSM control systems, particularly in high-speed operational scenarios.

This paper introduces a vector control strategy based on a model reference adaptive system (MRAS) incorporating a sliding mode controller. The proposed method integrates the sliding mode control strategy into the traditional MRAS approach by replacing the conventional PI speed controller with a sliding mode speed controller. Moreover, a fractional-order sliding mode surface is selected that effectively suppresses chattering compared to traditional sliding mode surfaces, thereby enhancing control accuracy and system stability. Additionally, a novel-reaching law addresses the issue of imprecise parameter tuning in traditional PI regulators across a wide speed range. A simulation model of the PMSM sensorless vector control validates the effectiveness of the proposed control strategy, demonstrating that the improved control strategy exhibits superior control and observation performance compared to traditional sliding mode control. The developed method provides more stable control across a wide speed range and performs well under external disturbances and parameter variations.

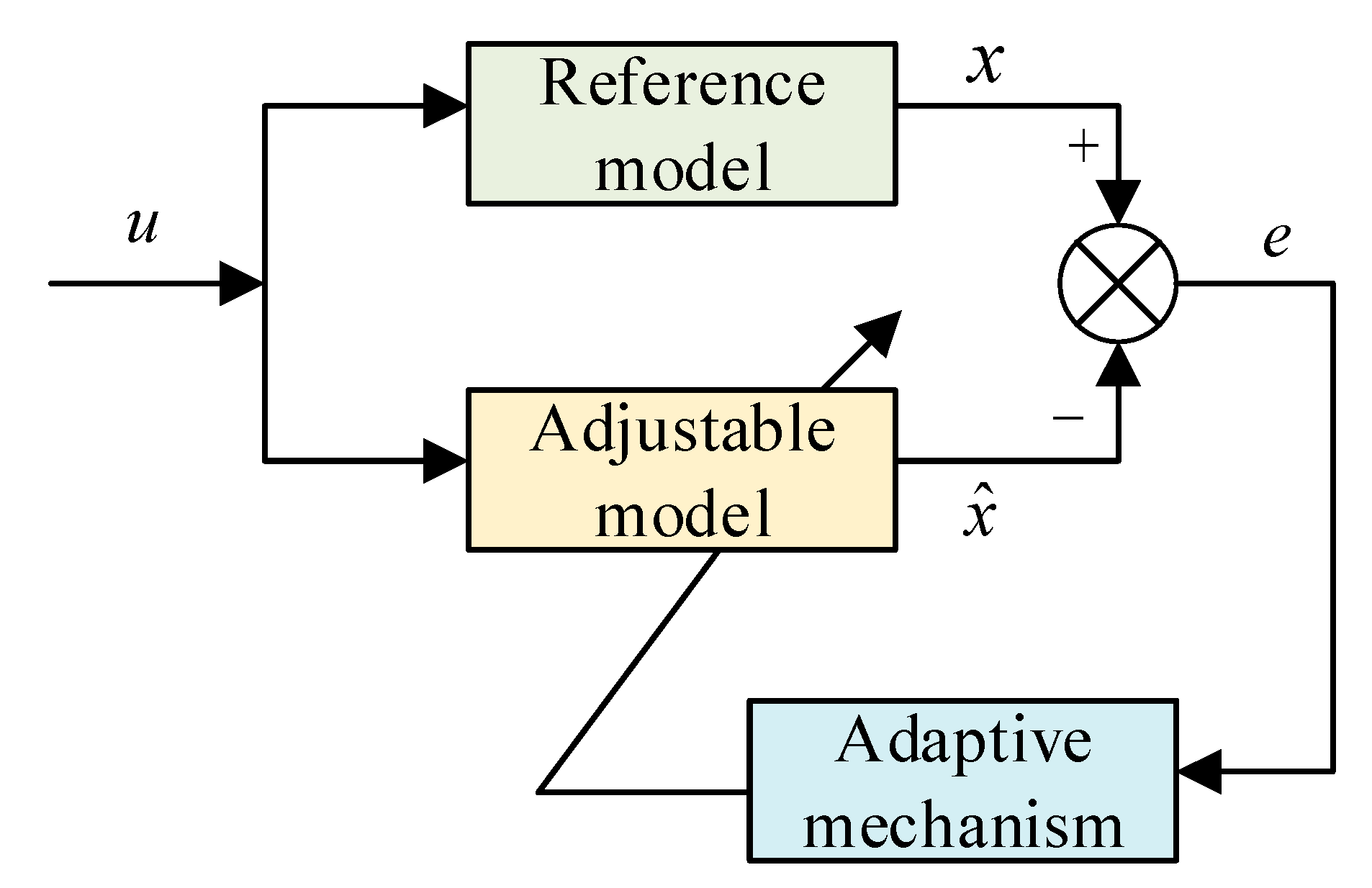
2. PMSM Model Reference Adaptive System

There are various types of adaptive systems, among which the model-reference adaptive system studied in this paper represents one category. Structurally, the MRAS can be divided into three components: the adjustable model, the reference model, and the adaptation mechanism. An MRAS aims to measure the difference between the reference model and the adjustable model’s indices to adjust this error using an adaptive law. The estimated parameters are input back into the adjustable model until the index error is reduced to zero [22]. This study adopts the widely used parallel structure, with its basic structure illustrated in Figure 1.

2.1. Selection of Reference Model and Adjustable Model

To establish an adaptive identification model for permanent magnet synchronous motors (PMSMs), the stator current equations from the PMSM mathematical model in the d-q synchronous rotating reference frame are selected as the reference model. To derive the adjustable model of the identification system, the stator currents of the PMSM can undergo Clarke and Park transformations, yielding the stator current equations in the synchronous rotating reference frame. Based on the obtained stator current equations, the adjustable model of the identification system can be established. The stator voltage equation of PMSM in the two-phase rotating coordinate system is expressed as

$$\left\{\begin{array}{l}{u}_d=R_s{i}_d+L_d{\displaystyle \frac{d{i}_d}{dt}}-{\omega }_r{\psi }_q\hfill \\ u_q=R_s{i}_q+L_q{\displaystyle \frac{d{i}_q}{dt}}+{\omega }_r{\psi }_d+{\omega }_r{\psi }_f\hfill \end{array}\right.$$

(1)

The electromagnetic torque equation is given by

$$T_e={\displaystyle \frac{3}{2}}{p}_n{i}_q\left[{\psi }_f{i}_q+\left(L_d-L_q\right)i_d\right]$$

(2)

where $L_d=L_q$.

For the surface-mounted PMSM used in this study, the electromagnetic torque equation can be simplified as follows:

$$T_e={\displaystyle \frac{3}{2}}{p}_n{i}_q{\psi }_f$$

(3)

The mechanical motion equation is

$$J{\displaystyle \frac{d{\omega }_r}{dt}}=T_e-T_L$$

(4)

where ${\omega }_r$ is the rotor speed, $R_s$ represents the stator resistance, and $i_d$ and $i_q$ denote the d-axis and q-axis currents, respectively. $L_d$ and $L_q$ are the d-axis and q-axis inductances, respectively; ${\psi }_d$ and ${\psi }_q$ represent the flux linkages in the d-axis and q-axis of the rotor; and $u_d$ and $u_q$ are the voltages along the d-axis and q-axis, respectively. Moreover, $p_n$ is the number of pole pairs of the motor, $T_e$ represents the electromagnetic torque, $T_L$ is the load torque, $J$ is the moment of inertia [23].

Rewriting Equation (1) as a state equation with stator currents $i_d$ and $i_q$ as state variables provides

$$\left\{\begin{array}{l}{\displaystyle \frac{d{i}_d}{dt}}=-{\displaystyle \frac{R_s}{L_s}}{i}_d+{\displaystyle \frac{u_d}{L_s}}+{\omega }_r{i}_q\\ {\displaystyle \frac{d{i}_q}{dt}}=-{\displaystyle \frac{R_s}{L_s}}{i}_q-{\omega }_r{i}_q-{\omega }_r{\displaystyle \frac{{\psi }_f}{L_s}}+{\displaystyle \frac{u_d}{L_s}}\end{array}\right.$$

(5)

Let ${i_d}^{\prime }=i_d+{\displaystyle \frac{{\psi }_f}{L_s}}$, ${i_q}^{\prime }=i_q$, ${u_d}^{\prime }=u_d+{\displaystyle \frac{R_s}{L_s}}{\psi }_f$, and ${u_q}^{\prime }=u_q$; then, Equation (5) can be rewritten as

$$\left\{\begin{array}{l}{\displaystyle \frac{d{i^{\prime }}_d}{dt}}=-{\displaystyle \frac{R_s}{L_s}}{i^{\prime }}_d+{\omega }_r{i^{\prime }}_q+{\displaystyle \frac{{u^{\prime }}_d}{L_s}}\\ {\displaystyle \frac{d{i^{\prime }}_q}{dt}}=-{\displaystyle \frac{R_s}{L_s}}{i^{\prime }}_q-{\omega }_r{i^{\prime }}_d+{\displaystyle \frac{{u^{\prime }}_q}{L_s}}\end{array}\right.$$

(6)

By expressing the parameters to be identified and the state variables in Equation (6) using their estimated values and taking the difference with Equation (6), the current error state equation is obtained:

$${\displaystyle \frac{d}{dt}}\left[\begin{array}{l}{i_d}^{\prime }-{\widehat{i^{\prime }}}_d\hfill \\ {i_q}^{\prime }-{\widehat{i^{\prime }}}_q\hfill \end{array}\right]=\left[\begin{array}{cc}-{\displaystyle \frac{R}{L_s}}& {\omega }_r\\ -{\omega }_r& -{\displaystyle \frac{R}{L_s}}\end{array}\right]\left[\begin{array}{c}{i_d}^{\prime }-{\widehat{i^{\prime }}}_d\\ {i_q}^{\prime }-{\widehat{i^{\prime }}}_q\end{array}\right]-J\left({\omega }_r-{\widehat{\omega }}_r\right)\left[\begin{array}{c}{\widehat{i^{\prime }}}_d\\ {\widehat{i^{\prime }}}_q\end{array}\right]$$

(7)

where $e=\left[\begin{array}{l}{i_d}^{\prime }-{\widehat{i}}_d^{\prime }\hfill \\ {i_q}^{\prime }-{\widehat{i}}_q^{\prime }\hfill \end{array}\right]$, $A=\left[\begin{array}{cc}-{\displaystyle \frac{R}{L_s}}& {\omega }_r\\ -{\omega }_r& -{\displaystyle \frac{R}{L_s}}\end{array}\right]$, $W=J\left({\omega }_r-{\widehat{\omega }}_r\right)\left[\begin{array}{c}{\widehat{i^{\prime }}}_d\\ {\widehat{i^{\prime }}}_q\end{array}\right]$, $J=\left[\begin{array}{cc}0& -1\\ 1& 0\end{array}\right]$.

2.2. Selection of the Adaptive Law

The above equations can be rewritten in the state space form as

$${\displaystyle \frac{de}{dt}}=Ae-W$$

(8)

According to Popov’s hyperstability theory, the stability of the system must be satisfied:

(1) The transfer matrix $H\left(s\right)={\left(sI-A_e\right)}^{-1}$ is strictly positive definite.

(2) $\eta \left(0,t_1\right)={\displaystyle {\int }_0^{t_1}{V}^{T}Wd\tau \gg -}{\mathsf{\gamma }}_0^2,\forall t_1\ge 0$, ${\mathsf{\gamma }}_0$ is any finite positive number. In this case, $\underset{t\to \infty }{\lim }e\left(t\right)=0$, such that MRAS is progressively stable.

The adaptive law can be derived based on the Popov integral inequality as follows:

$${\widehat{\omega }}_r(s)=K_p\left({i_d}^{\prime }{\widehat{i}}_q^{\prime }-{i_q}^{\prime }{\widehat{i}}_d^{\prime }\right)+{\displaystyle {\int }_0^t{K}_i\left({i_d}^{\prime }{\widehat{i}}_q^{\prime }-{i_q}^{\prime }{\widehat{i}}_d^{\prime }\right)}d\tau$$

(9)

Equation (8) can be rewritten as

$${\widehat{\omega }}_r(s)=\left(K_p+{\displaystyle \frac{K_i}{s}}\right)e_{\omega }$$

(10)

where $e_{\omega }=\left({i_d}^{\prime }{\widehat{i}}_q^{\prime }-{i_q}^{\prime }{\widehat{i}}_d^{\prime }\right)$.

The simplified rotor speed estimation equation can be expressed as

$${\widehat{\omega }}_r(s)=\left(K_p+{\displaystyle \frac{K_i}{s}}\right)\left[{i_d}^{\prime }{\widehat{i}}_q^{\prime }-{i_q}^{\prime }{\widehat{i}}_d^{\prime }-{\displaystyle \frac{{\psi }_f}{L_s}}\left(i_q-{\widehat{i}}_q\right)\right]$$

(11)

The rotor position angle can be obtained by integrating speed:

$$\widehat{\theta }={\displaystyle {\int }_0^t{\widehat{\omega }}_{r}dt}$$

(12)

3. Design of the Sliding Mode Controller

3.1. Construction of the Fractional-Order Sliding Mode Surface

Let the system state variables be

$$\left\{\begin{array}{l}{x}_1={\omega }_{ref}-{\omega }_r\\ x_2={\dot{x}}_1=-{\dot{\omega }}_r\end{array}\right.$$

(13)

Let $D=3p_n{\psi }_f/2J$, and $u=d{i}_q/dt$. Then, Equation (13) can be transformed into

$$\left[\begin{array}{c}{\dot{x}}_1\\ {\dot{x}}_2\end{array}\right]=\left[\begin{array}{cc}0& 1\\ 0& 0\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]+\left[\begin{array}{c}0\\ -D\end{array}\right]u$$

(14)

The Caputo type is one of the fractional-order calculus types widely used due to its simple definition and computational convenience [24].

Let the $\alpha$-th order Caputo-type derivative of $f\left(t\right)$ be

$${}_a{}^{C}D{}_t{}^{\alpha }f\left(t\right)={\displaystyle \frac{1}{\Gamma \left(\sigma \right)}}{\displaystyle {\int }_a^t{\left(t-\tau \right)}^{\sigma -1}}{f}^{\left(\left[\alpha \right]+1\right)}\left(\tau \right)d\tau$$

(15)

where C represents the type of calculus, a is the initial condition, and $\alpha$ is the fractional order. $\Gamma \left(\sigma \right)$ denotes the Gamma function, where $\sigma =\left[n\right]+1-n$, $\left[n\right]$ represents the largest integer less than n.

Let the speed error e be

$$e={\omega }_{ref}-{\omega }_r$$

(16)

where ${\omega }_{ref}$ is the reference speed of the PMSM, which is typically a constant.

Let $sig{\left(e\right)}^{\mathsf{\gamma }}$ be defined as follows:

$$sig{\left(e\right)}^{\mathsf{\gamma }}={\left|e\right|}^{\mathsf{\gamma }}\mathrm{sgn}\left(e\right)$$

(17)

where $\mathrm{sgn}\left(e\right)$ is the sign function, expressed as

$$\mathrm{sgn}\left(e\right)=\left\{\begin{array}{c}e/\left|e\right|,e\ne 0;\\ 0,e=0.\end{array}\right.$$

(18)

The term $sig{\left(e\right)}^{\mathsf{\gamma }}$ represents a lower-order term of the error, ensuring that the state variable converges to zero in finite time.

The fractional-order sliding mode surface is defined as:

$$s={\lambda }_a^C{D}_t^{\alpha +1}e+b_{0}e+c_0{\displaystyle {\int }_0^{t}sig{\left(e\right)}^{\mathsf{\gamma }}dt}$$

(19)

The parameters a represent initial conditions, while $\lambda ,c_0,b_0$ are positive constants. In addition, $0<\alpha$, $\mathsf{\gamma }<1$.

3.2. Design of the Reaching Law

The traditional reaching law is improved based on the super-twisting sliding mode algorithm to enhance the system’s dynamic performance. The improved reaching law is given by

$$\left\{\begin{array}{l}\dot{s}=-k_{1}f\left(s\right){\left|s\right|}^{{\displaystyle \frac{1}{2}}}sgn\left(s\right)-k_{2}sat\left(s\right)\\ f\left(s\right)={\displaystyle \frac{1}{e^{-\left|s\right|}+\frac{1}{\left|s\right|}}}\end{array}\right.$$

(20)

where $k_1>0$, $k_2>0$, and $sat\left(s\right)$ represents the saturation function.

Compared with the traditional exponential reaching law, the improved reaching law demonstrates better overshoot suppression, reduces chattering, and enhances the system’s adaptive capability.

3.3. Design of the Fractional-Order Sliding Mode Controller

Considering the time t derivative on both sides of Equation (19) and applying the Caputo fractional derivative properties provides

$$\dot{s}=\lambda {}_a{}^{C}D_t^{\alpha +2}e+b_0\dot{e}+c_{0}sig{\left(e\right)}^{\mathsf{\gamma }}$$

(21)

By combining Equations (19) and (20), we derive

$$\begin{array}{cc}\lambda {}_a{}^{C}D_t^{\alpha +2}e+b_0\dot{e}+c_{0}sig{\left(e\right)}^{\mathsf{\gamma }}& =-k_{1}f\left(s\right){\left|s\right|}^{{\displaystyle \frac{1}{2}}}sgn\left(s\right)\hfill \\ & -k_{2}sat\left(s\right)\hfill \end{array}$$

(22)

Substituting Equation (16) into Equation (22) yields

$$\begin{array}{cc}u& ={\displaystyle \frac{D}{\lambda }}{}_a{}^{C}D_t^{-\alpha }\{b_0\dot{e}+c_{0}sig{\left(e\right)}^{\mathsf{\gamma }}+k_{1}f\left(s\right){\left|s\right|}^{{\displaystyle \frac{1}{2}}}sgn\left(s\right)\hfill \\ & +k_{2}sat(s)\}\hfill \end{array}$$

(23)

To analyze the stability of the controller, we consider the Lyapunov function:

$$V={\displaystyle \frac{1}{2}}{s}^2$$

(24)

Taking the derivative of V provides

$$\begin{array}{cc}\dot{V}& =s\left(-k_{1}f\left(s\right){\left|s\right|}^{{\displaystyle \frac{1}{2}}}sign\left(s\right)-k_{2}sat\left(s\right)\right)\hfill \\ & \le -k_{1}f\left(s\right){\left|s\right|}^{{\displaystyle \frac{3}{2}}}-k_2\left|s\right|\hfill \end{array}$$

(25)

According to the Lyapunov stability criterion, the system is stable if $k_1>0$, $f\left(s\right)\ge 0$, and $k_2>0$, ensuring that $\dot{V}<0$. Thus, the system is proven to be stable.

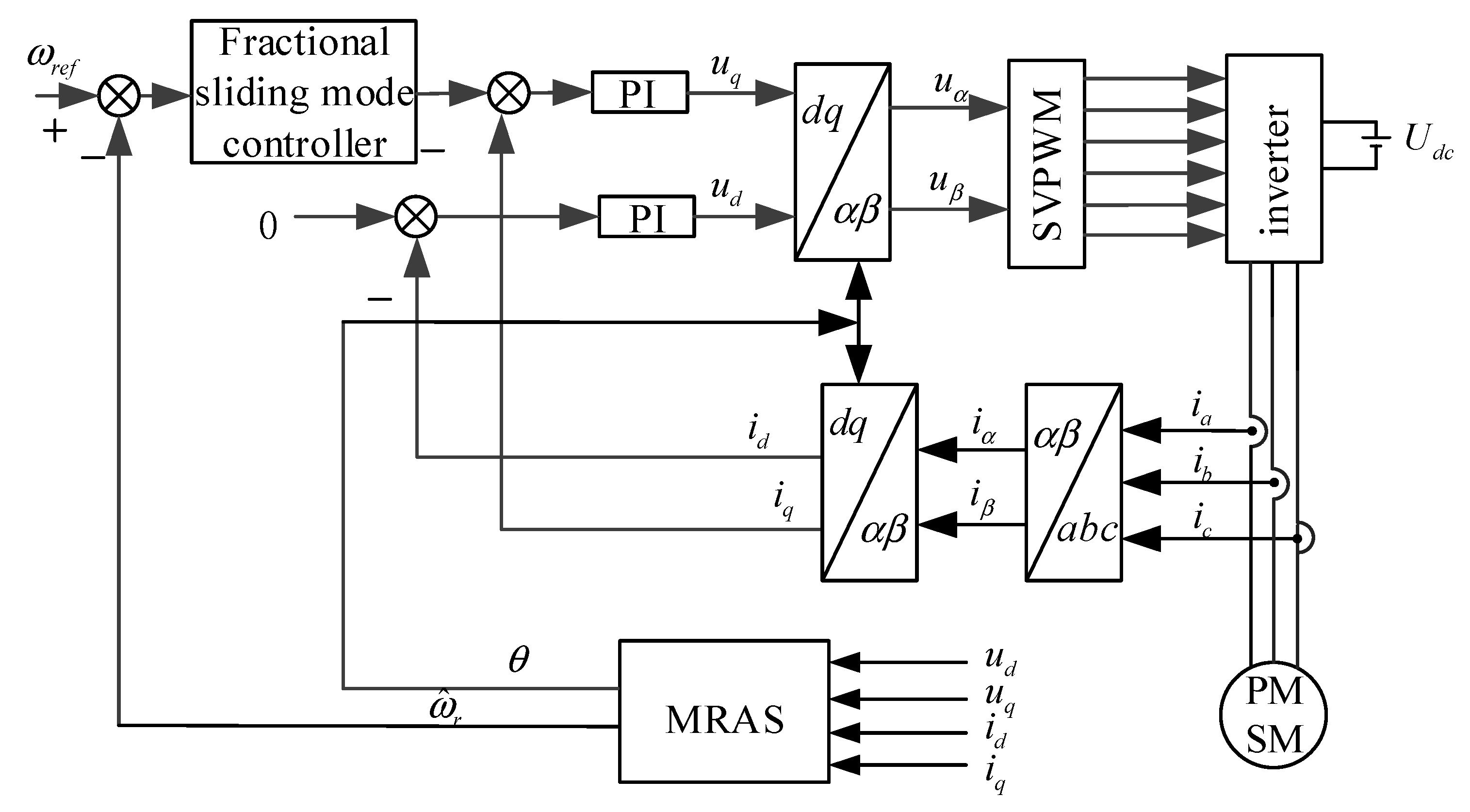
4. Simulation and Experimental Results Analysis

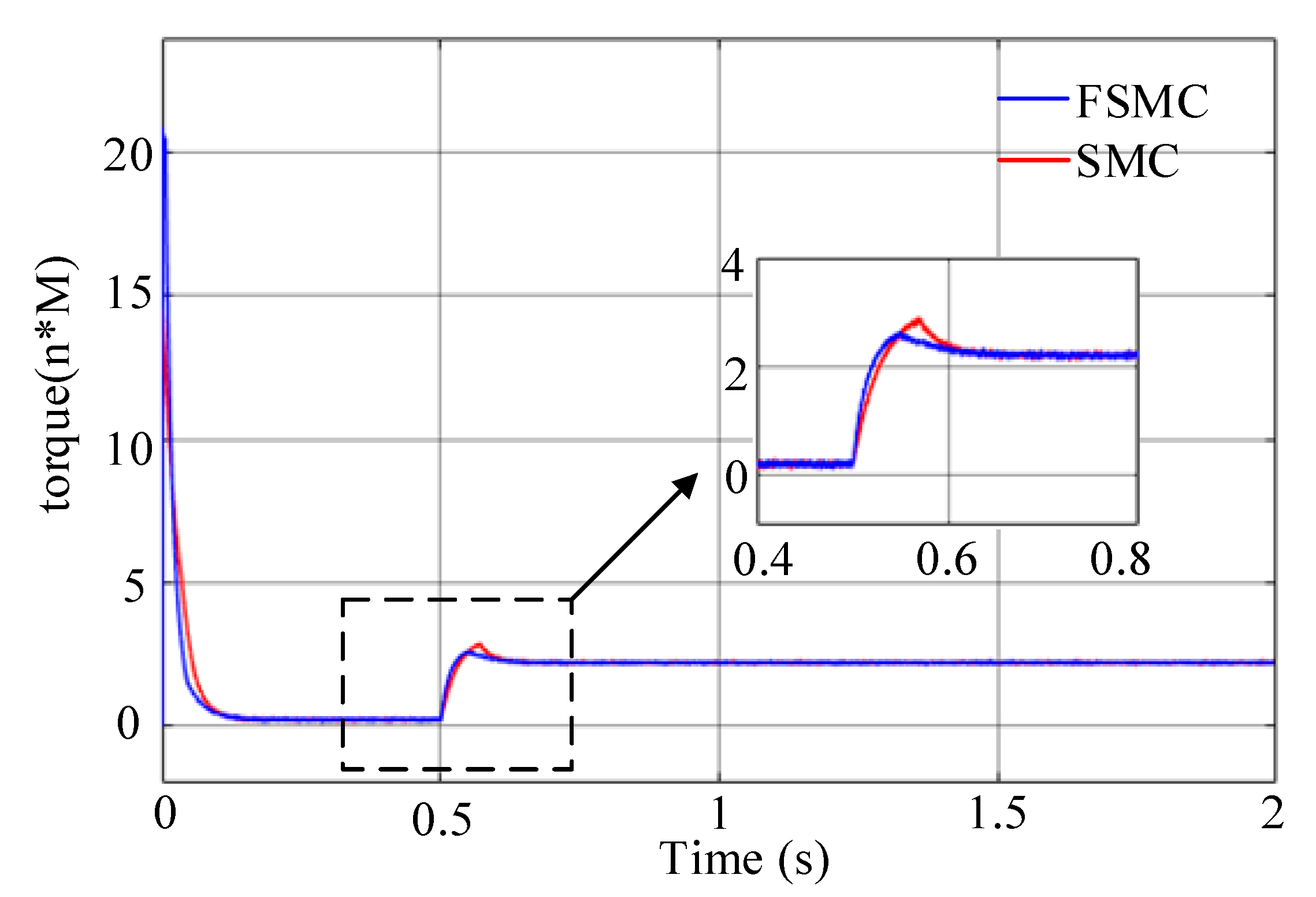
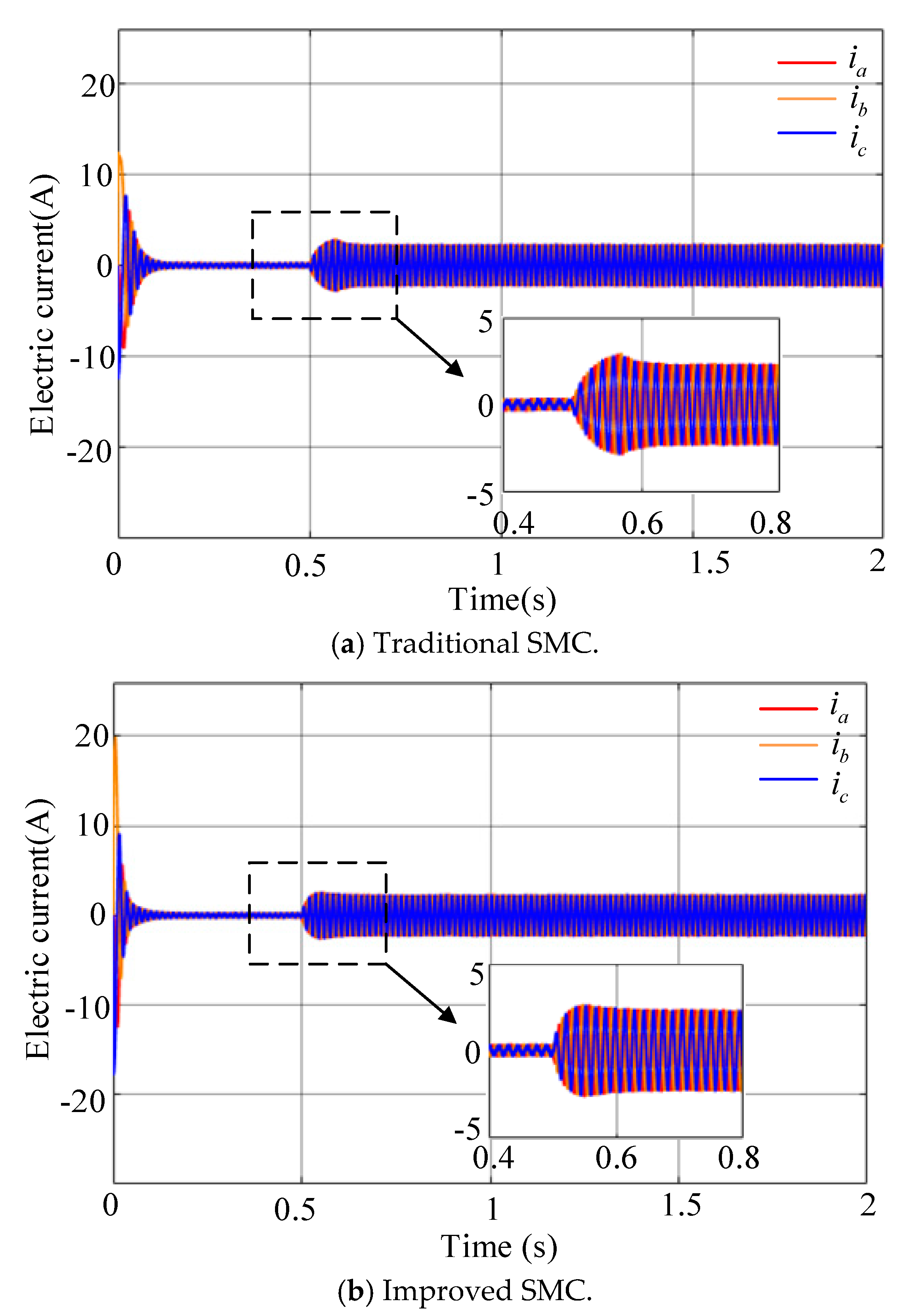
4.1. Simulation Analysis

A three-phase PMSM is selected as the control object, which combines a vector control strategy $i_d=0$ and space vector pulse width modulation (SVPWM). The proposed PMSM vector control simulation model is based on the MRAS and was developed in MATLAB/Simulink. The proposed improved fractional-order sliding mode control (FSMC) was compared with the traditional integral-type sliding mode control (SMC). Figure 2 depicts the schematic diagram of the PMSM speed control system, and

Table 1. Motor parameters.

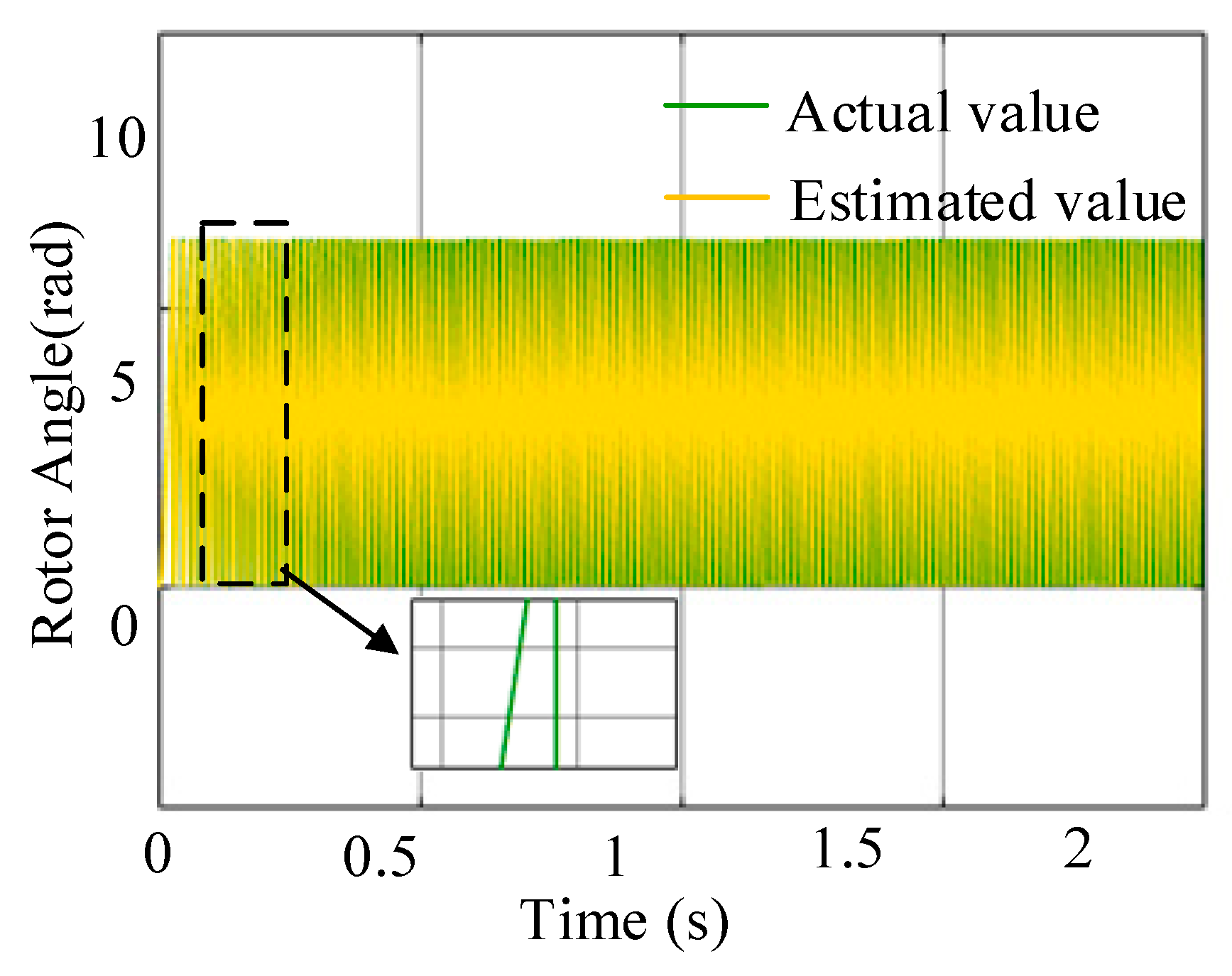
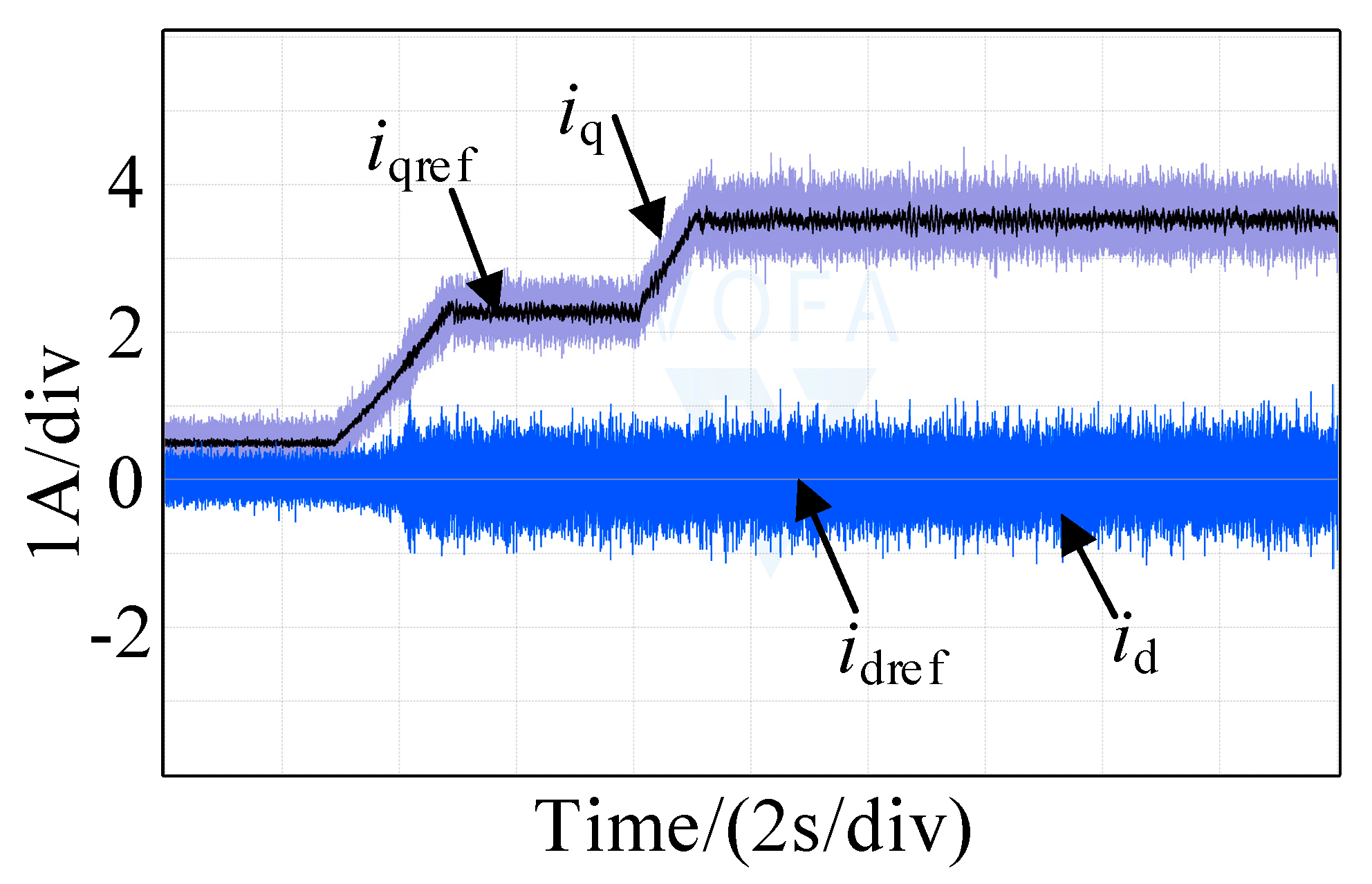
Parameter	Value
Stator resistance Rs/Ω	0.117
Stator inductance Ls/mH	0.63
Flux linkage Ψf/Wb	0.041
Moment of inertia J/(kg ∗ mg2)	1.75 × 10−5
Number of pole pairs pn	1
Reference speed ωref	10000
Damping coefficient B	0.002

reports the motor parameters.

The SMC replaces the traditional PI controller in the system, and an improved fractional-order sliding mode speed controller is designed based on the novel reaching law. Traditional SMCs and FSMCs are simulated under identical conditions, with a $2\mathrm{N}\cdot \mathrm{m}$ load torque applied at $t=0.5 \mathrm{s}$. Figure 3, Figure 4 and Figure 5 illustrate the rotor speed response, torque response, and current curves under load disturbances, respectively. The results highlight that the traditional SMC suffers significant speed fluctuations during startup. It presents a maximum speed fluctuation of approximately 69 r/min and requires about 200 ms to restore speed stability. In contrast, the FSMC achieves faster regulation with reduced speed fluctuation, where the maximum speed fluctuation is around 48 r/min, and speed stabilization occurs at approximately 160 ms.

Figure 4 suggests that the FSMC reduces torque fluctuation during motor startup compared to the traditional SMC method. The maximum torque fluctuation under FSMC is about 14.6 N·m, which is lower than the 20.8 N·m observed in SMC. When the load torque changes, the FSMC exhibits smaller torque fluctuations, faster torque recovery, and lower overshoot, enhancing dynamic response performance.

Figure 5 reveals that the traditional SMC has more significant current fluctuations and longer stabilization times under load variations. In contrast, the FSMC reduces current fluctuations and achieves faster stabilization. Moreover, Figure 6 infers that the rotor position estimation under FSMC has a smaller deviation from the actual value, reducing rotor angle error and improving system tracking performance.

These findings demonstrate that the improved vector control system with the fractional-order sliding mode controller achieves faster steady-state convergence and reduced speed fluctuations during motor startup. Under load disturbances, the proposed system effectively suppresses speed fluctuations, reduces rotor angle errors, and enhances system control performance and disturbance rejection capabilities.

4.2. Experimental Analysis

The proposed algorithm was experimentally validated under motor speed variations, i.e., 9800 r/min, to verify its feasibility further. The experimental platform primarily consists of the following hardware components: a DC power supply, digital and analog signal processing circuits, position sampling circuits, power drive circuits, overvoltage and overcurrent protection circuits, and a DC-AC inverter module. The core processor of the system is the TMS320F28335 DSP chip from Texas Instruments (TI) (Changsha, China), which operates at a clock frequency of 150 MHz and features a 32-bit floating-point unit. This processor provides dedicated peripherals for motor drive control, including six channels of high-resolution pulse width modulation (PWM) outputs, an enhanced quadrature encoder pulse (QEP) processing unit, and an SPI interface, all of which are utilized in the hardware design of the experimental platform. An oscilloscope (Yokogawa DLM4058, Beijing Zhianjian Technology Co., Ltd., Beijing, China) and a current probe (Tektronix A622, Zibo Best Experimental Equipment Co., Ltd., Zibo, China) are employed to measure and analyze the motor phase current signals. Figure 7 illustrates the experimental setup. Figure 8 and Figure 9 present the current speed and dq-axis response under FSMC, and Figure 10, Figure 11 and Figure 12 display the current response waveforms at different speeds.

Figure 7 and Figure 8 demonstrate that the improved control system achieves accurate speed estimation and tracking under speed variations, with minimal estimation errors between the estimated and actual speeds. The FSMC provides excellent tracking control. Additionally, Figure 9, Figure 10 and Figure 11 indicate that as speed increases, the harmonic content of the current waveform decreases, approaching a near-sinusoidal shape. This demonstrates higher estimation accuracy, reduced torque ripple during motor operation, and superior control performance at high speeds.

5. Conclusions

This study proposes a novel model reference adaptive speed control strategy for permanent magnet synchronous motors (PMSMs) based on an advanced sliding mode controller (SMC) for vector control applications. To enhance system dynamic response and mitigate chattering issues inherent in conventional SMC approaches, a fractional-order sliding surface is implemented along with an innovative adaptive law incorporating an exponential reaching law. The research involves establishing a PMSM vector speed regulation system model that modifies the traditional model reference adaptive system (MRAS) by replacing its PI controller with the proposed enhanced SMC scheme, with theoretical validation provided through Lyapunov stability analysis. Mathematical analysis and experimental results collectively demonstrate the method’s effectiveness, with simulation data revealing significant performance improvements: the fractional-order SMC (FSMC) achieves 25% shorter settling time, a 44% reduction in maximum speed fluctuation, and a 42% decrease in maximum torque ripple compared to a conventional SMC during load step changes, while exhibiting superior disturbance rejection capability, rapid response characteristics, and excellent dynamic performance. Experimental verification confirms that the improved MRAS control system delivers accurate speed tracking and stable operation across the entire speed range. Furthermore, comparative analysis with References [20,21] highlights the advantages of the proposed super-twisting reaching law-based SMC implementation combined with an MRAS for simultaneous speed and position estimation, showing enhanced estimation accuracy and improved stability under high-dynamic conditions. However, the proposed control strategy exhibits certain limitations, as parameter variations induced by external factors may adversely affect the adaptation mechanism of the MRAS.