Data-Driven Proactive Early Warning of Grid Congestion Probability Based on Multiple Time Scales
Abstract
1. Introduction
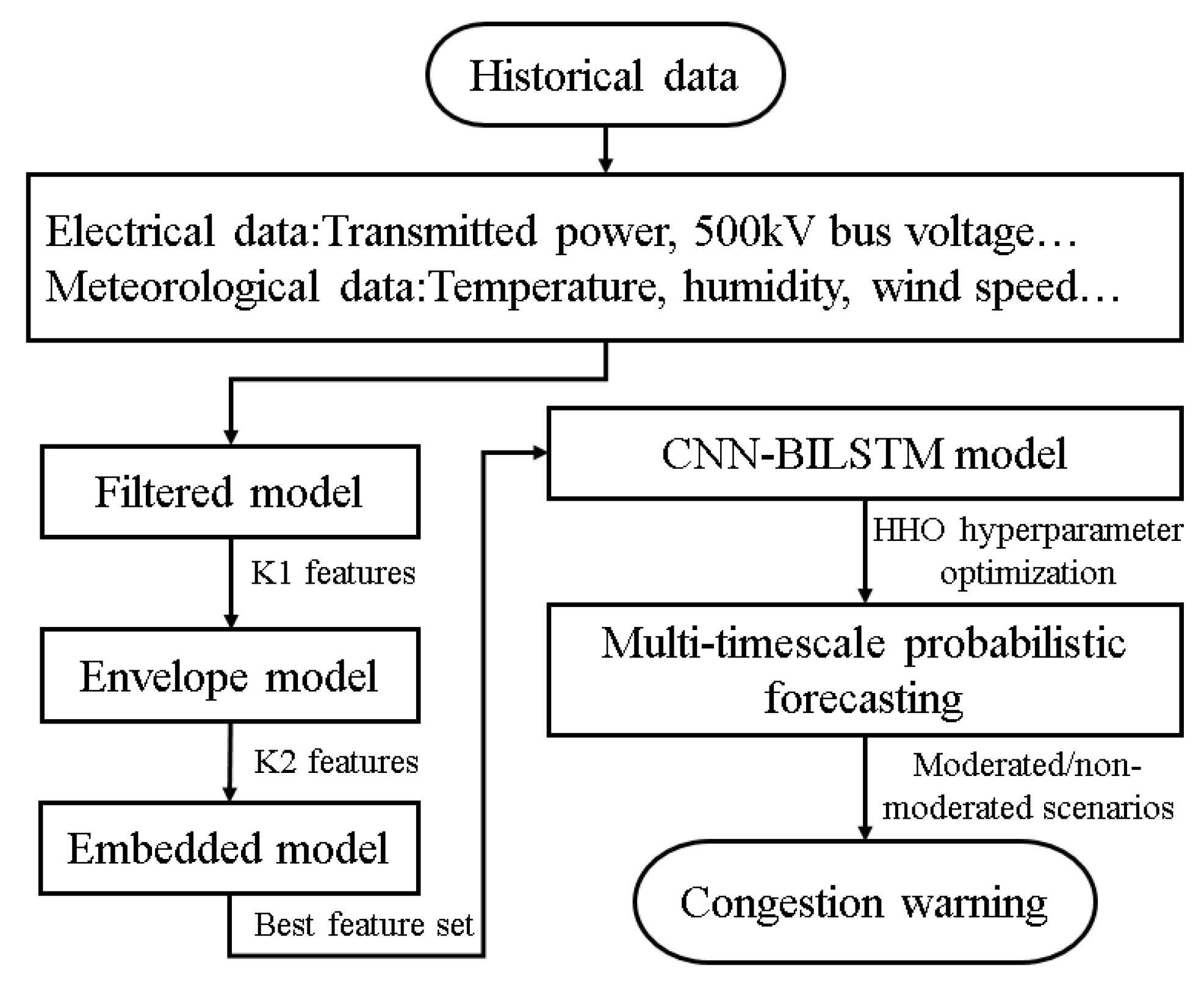
2. Joint Optimization Feature Selection Model
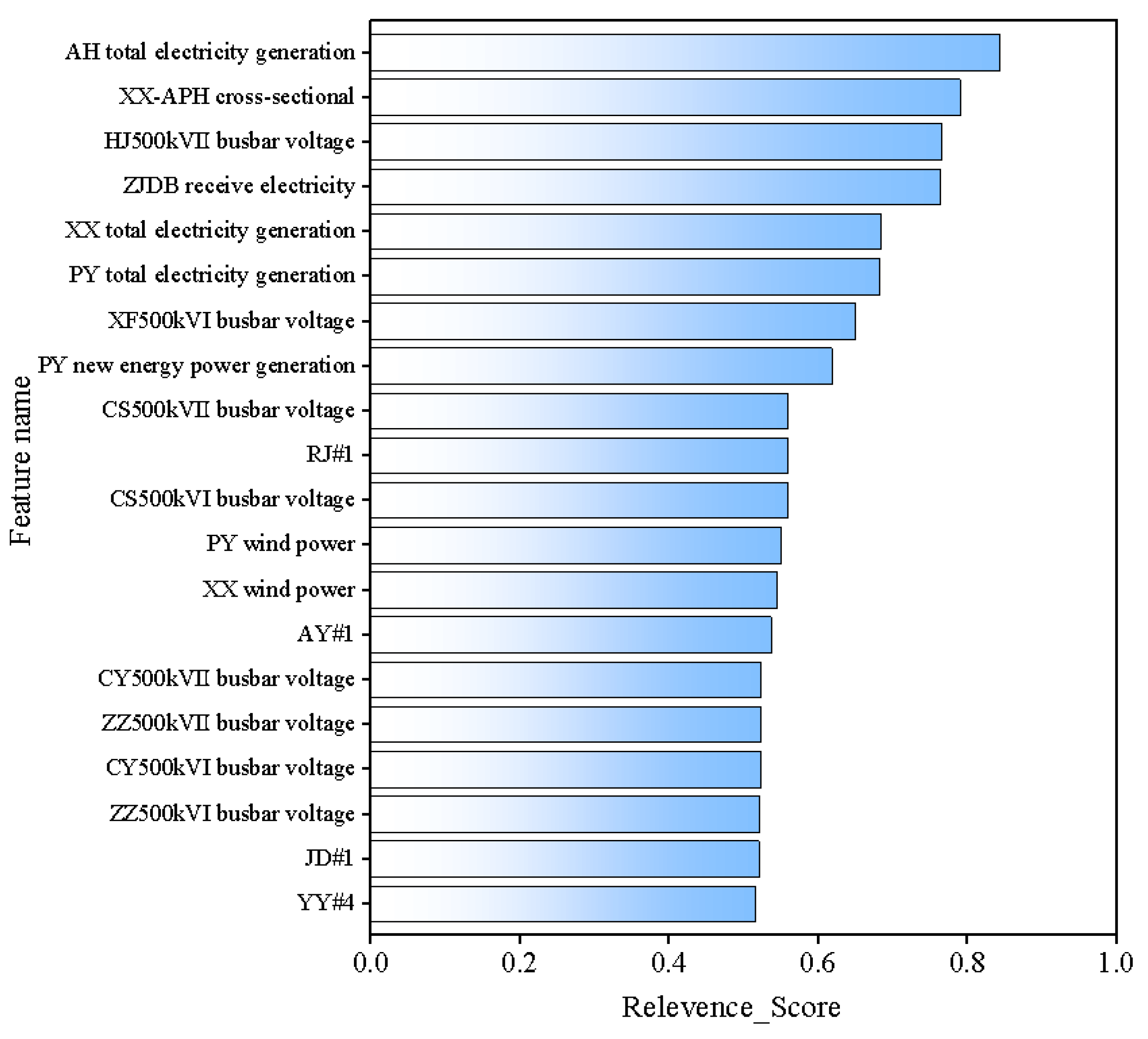
2.1. Initial Screening Phase
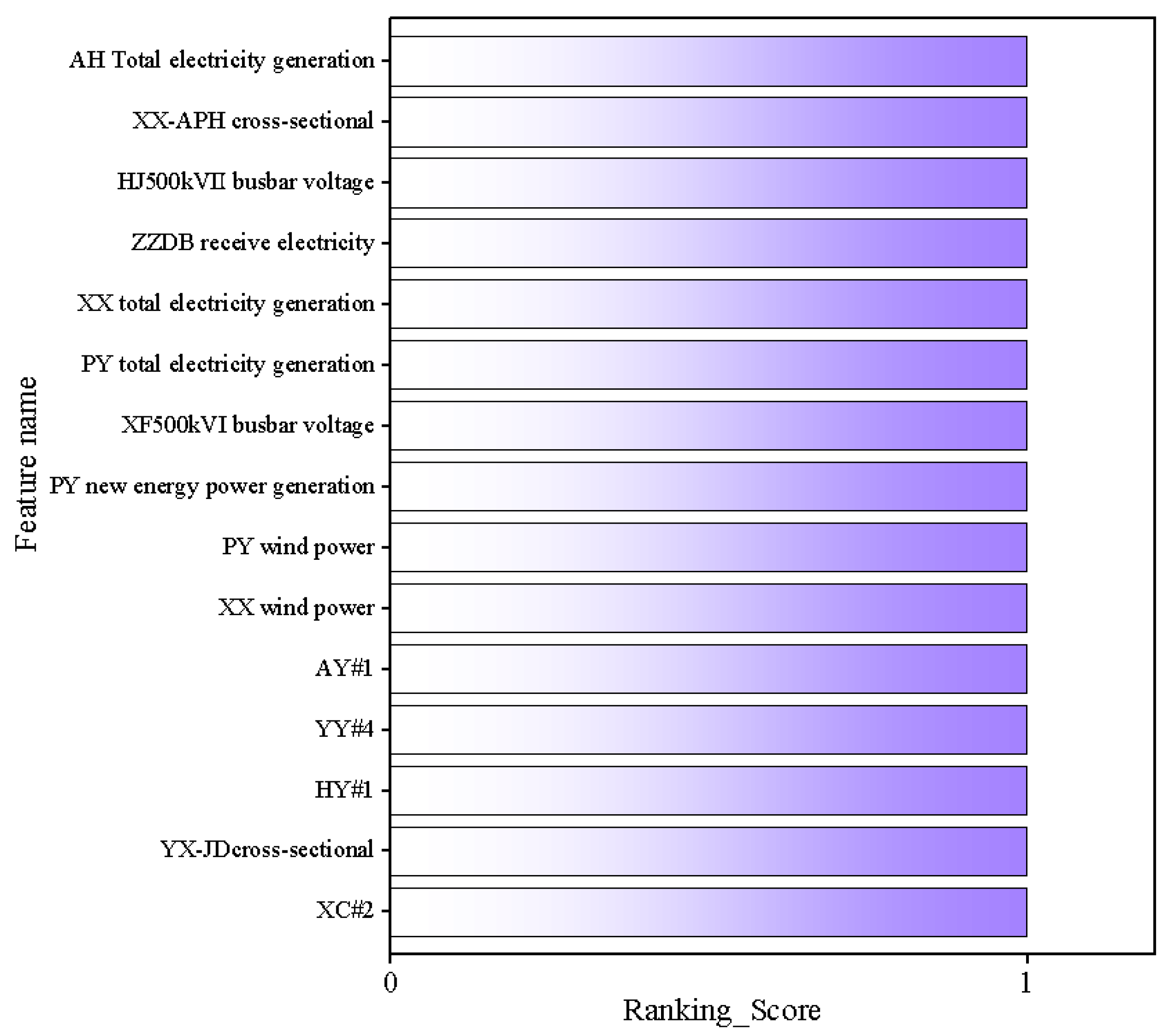
2.2. Fine Screening Phase
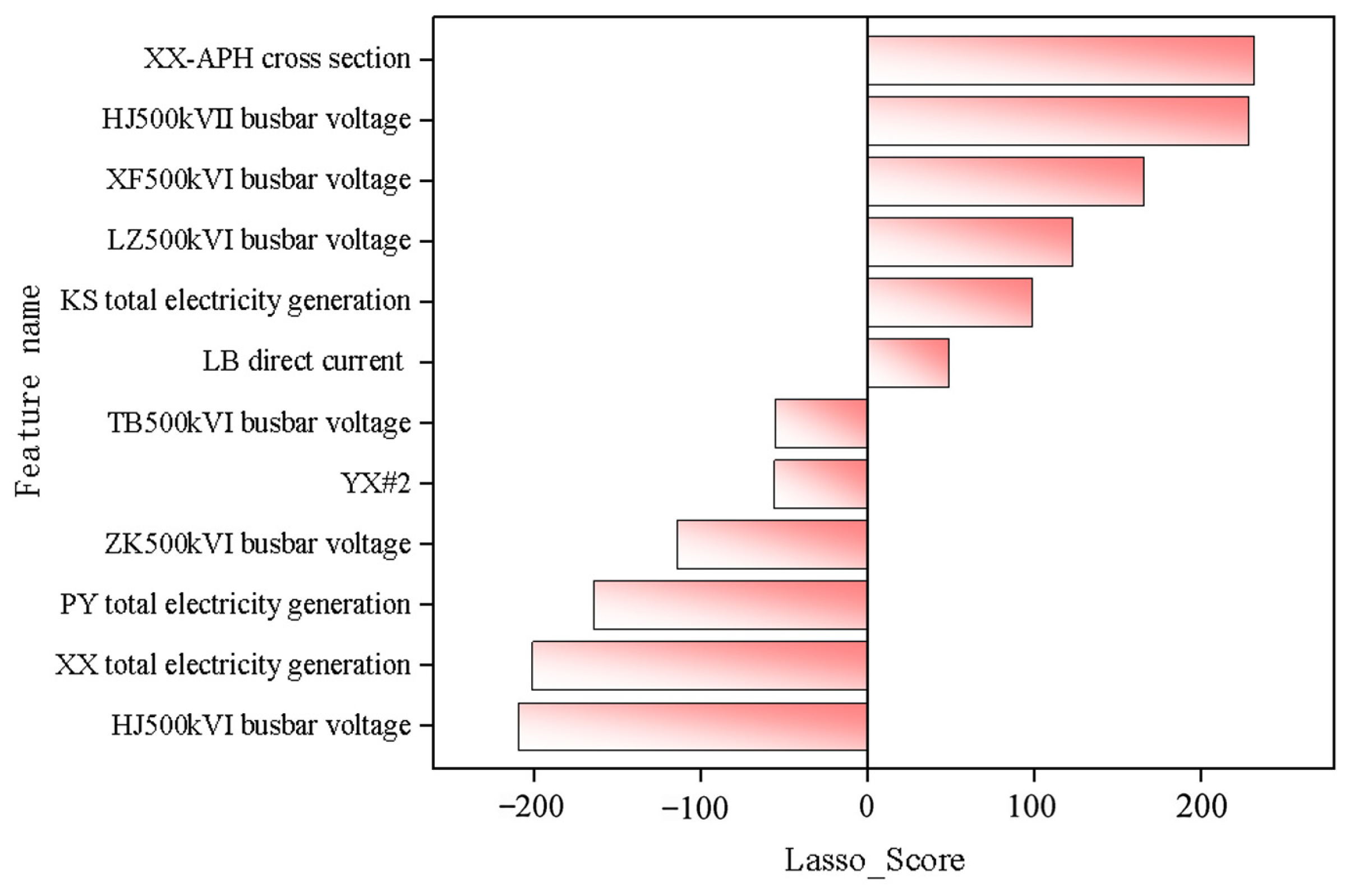
2.3. Iterative Optimization Phase
3. Active Early Warning Model for Grid Congestion Based on Optimization Algorithm
3.1. Multi-Time-Scale Warning Model Based on CNN-BILSTM
3.2. Introduction to the HHO Principle
4. Example Analysis
4.1. Definition of Grid Congestion Events
4.2. Multi-Stage Feature Selection Model Construction
4.3. Probabilistic Prediction Model Construction
4.4. Active Warning Results Based on Multiple Time Scales
5. Conclusions and Prospectives
- (1).
- The model is able to filter out the optimal feature set based on historical data, thus improving the prediction efficiency and accuracy of the prediction model. At the same time, the data-driven approach avoids the drawbacks of the traditional parametric model that is affected by the system operation mode and enhances the robustness of the prediction model.
- (2).
- While providing probabilistic outputs and early warning results, the model adopts a multi-time-scale prediction approach, thus providing more valuable information for dispatchers to make auxiliary decisions and help the operational safety of the power system.
- (3).
- In this paper, during the feature selection process, only the correlation between the feature set and the requested features is considered, and the interactions within the feature set are not taken into account, which may weaken the potential impact of certain features. Therefore, subsequent attempts will be made to explore the synergistic or antagonistic effects between features to further improve the representativeness of the selected features.
- (4).
- This paper focuses on the early warning of the future grid congestion probability of the power system, thus guiding active regulation, and in the subsequent work, the specific regulation strategy can be further considered to improve grid congestion early warning and active regulation so as to carry out a more comprehensive active regulation strategy development.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sun, Y.Z.; Wu, J.; Li, G.J.; He, J. Development models and key technologies of future grid in China. Proc. CSEE 2014, 34, 4999–5008. [Google Scholar]
- Sun, Y.Z.; Wu, J.; Li, G.J.; He, J. Dynamic economic dispatch considering wind power penetration based on wind speed forecasting and stochastic programming. Proc. CSEE 2009, 29, 41–47. [Google Scholar]
- Sha, Y.; Qiu, X.; Ning, X.; Han, X. Multi-objective optimization of active distribution network by coordinating energy storage system and flexible load. Power Syst. Technol. 2016, 40, 1394–1399. [Google Scholar]
- Lu, W.; Du, H.; Ding, Q.; Tu, M.; Li, W.; Ji, W. Design and key technologies of optimal dispatch for smart distribution network. Autom. Electr. Power Syst. 2017, 41, 1–6. [Google Scholar]
- Liu, Q.; Li, J.; Ni, M. Situation awareness of grid cyber-physical system; current status and research ideas. Autom. Electr. Power Syst. 2019, 43, 9–21. [Google Scholar]
- Wang, C.; Luo, F.; Zhang, T. Review on key technologies of smart urban power network. High Volt. Eng. 2016, 42, 2017–2027. [Google Scholar]
- Huang, M.; Wei, Z.; Sun, G.; Zang, H.; Huang, Q. A novel situation awareness approach based on historical data mining model in distribution networks. Power Syst. Technol. 2017, 41, 1139–1145. [Google Scholar]
- Li, B.Q.; Liu, D.W.; Qin, X.H.; Yan, J.F. Concept and theory framework of panoramic security defense for bulk power system driven by information. Proc. CSEE 2016, 36, 5796–5805. [Google Scholar]
- Xu, C.; Liang, R.; Cheng, Z.; Xu, D. Security situation awareness of smart distribution grid for future energy internet. Electr. Power Autom. Equip. 2016, 36, 13–18. [Google Scholar]
- Zhu, Q.; Dang, J.; Chen, J.; Xu, Y.; Li, Y.; Duan, X. A method forpower system transient stability assessment based on deep belief networks. Proc. CSEE 2018, 38, 735–743. [Google Scholar]
- Dai, Y.; Chen, L.; Zhang, W.; Min, Y.; Li, W. Power system transient stability assessment based on multi-support vector machines. Proc. CSEE 2016, 36, 1173–1180. [Google Scholar]
- Hu, W.; Zheng, L.; Min, Y.; Dong, Y.; Yu, R.; Wang, L. Research on power system transient stability assessment based on deep learning of big data technique. Power Syst. Technol. 2017, 41, 3140–3146. [Google Scholar]
- Duan, B.; Chen, M.; Li, H.; Lai, J. Decision method of proactive operation for distributed generation based on power quality situation awareness. Autom. Electr. Power Syst. 2016, 40, 176–181. [Google Scholar]
- Mccalley, J.D.; Vitta, L.V. An overview of risk based security assessment. In Proceedings of the IEEE Power Engineering Society Summer Meeting, Edmonton, AB, Canada, 18–22 July 1999. [Google Scholar]
- Kirschen, D.S.; Jayaweera, D. Comparison of risk based and deterministic security assessments. IET Gener. Transm. Distrib. 2007, 1, 527–533. [Google Scholar] [CrossRef]
- McCalley, J.; Fouad, A.; Vittal, V.; Irizarry-Rivera, A.; Agrawal, B.; Farmer, R. A risk based security index for determining operating limits in stability limited electric power systems. IEEE Trans. Power Syst. 1997, 12, 1210–1219. [Google Scholar] [CrossRef]
- Ni, M.; McCalley, J.D.; Vittal, V.; Tayyib, T. Online risk based security assessment. IEEE Trans. Power Syst. 2003, 18, 258–265. [Google Scholar] [CrossRef]
- Hu, S.; Chao, Z.; Zhong, H. Modeling and application of power grid dispatching operation risk consequences. Autom. Electr. Power Syst. 2016, 40, 54–60. [Google Scholar] [CrossRef]
- Chen, W.H.; Jiang, Q.Y.; Cao, Y.J.; Han, Z.X. Risk assessment of voltage collapse in power system. Power Syst. Technol. 2005, 29, 6–11. [Google Scholar]
- Shi, H.J.; Ge, F.; Ding, M.; Zhang, R.L.; Huang, D.; Xu, T.; Lin, H. Research on online assessment of transmission network operation risk. Power Syst. Technol. 2005, 29, 43–48. [Google Scholar]
- Qiu, W.; Zhang, J.; Liu, N.; Zhu, X.; Liu, L. Multi-objective optimal generation dispatch with consideration of operation risk. Proc. CSEE 2012, 32, 64–72. [Google Scholar]
- Yu, Y.; Wang, D. Dynamic security risk assessment and optimization of transmission systems. Sci. China 2009, 39, 286–292. [Google Scholar] [CrossRef]
- Chen, W.H. Risk-Based Security Analysis and Preventive Control in Power System. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2007. [Google Scholar]
- Jiang, Y.; Mccalley, J.D.; Voorhis, T.V. Risk-based resource optimization for transmission system maintenance. IEEE Trans. Power Syst. 2006, 21, 1191–1200. [Google Scholar] [CrossRef]
- Veeramsetty, V.; Reddy, K.R.; Santhosh, M.; Mohnot, A.; Singal, G. Short-term electric power load forecasting using random forest and gated recurrent unit. Electr. Eng. 2022, 104, 307–329. [Google Scholar] [CrossRef]
- Ahmad, T.; Manzoor, S.; Zhang, D. Forecasting high penetration of solar and wind power in the smart grid environment using robust ensemble learning approach for large-dimensional data. Sustain. Cities Soc. 2021, 75, 103269. [Google Scholar] [CrossRef]
- Eseye, A.T.; Zhang, J.; Zheng, D. Short-term photovoltaic solar power forecasting using a hybrid Wavelet-PSO-SVM model based on SCADA and Meteorological information. Renew. Energy 2018, 118, 357–367. [Google Scholar] [CrossRef]
- Nam, S.; Hur, J. Probabilistic forecasting model of solar power outputs based on the naive Bayes classifier and kriging models. Energies 2018, 11, 2982. [Google Scholar] [CrossRef]
- Wang, J.; Li, P.; Ran, R.; Che, Y.; Zhou, Y. A short-term photovoltaic power prediction model based on the gradient boost decision tree. Appl. Sci. 2018, 8, 689. [Google Scholar] [CrossRef]
- Xu, J.; Jiang, X.; Liao, S.; Ke, D.; Sun, Y.; Yao, L.; Mao, B. Probabilistic prognosis of wind turbine faults with feature selection and confidence calibration. IEEE Trans. Sustain. Energy 2023, 15, 52–67. [Google Scholar] [CrossRef]
- Memmel, E.; Steens, T.; Schlüters, S.; Völker, R.; Schuldt, F.; Von Maydell, K. Predicting renewable curtailment in distribution grids using neural networks. IEEE Access 2023, 11, 20319–20336. [Google Scholar] [CrossRef]
- Sharma, S.; Srivastava, L. Prediction of transmission line overloading using intelligent technique. Appl. Soft Comput. 2008, 8, 626–633. [Google Scholar] [CrossRef]
- Balaraman, S.; Kamaraj, N. Cascade BPN based transmission line overload prediction and preventive action by generation rescheduling. Neurocomputing 2012, 94, 1–12. [Google Scholar] [CrossRef]
- Almassalkhi, M.R.; Hiskens, I.A. Model-predictive cascade mitigation in electric power systems with storage and renewables—Part I: Theory and implementation. IEEE Trans. Power Syst. 2014, 30, 67–77. [Google Scholar] [CrossRef]
- Kalogeropoulos, I.; Sarimveis, H. Predictive control algorithms for congestion management in electric power distribution grids. Appl. Math. Model. 2020, 77, 635–651. [Google Scholar] [CrossRef]
- Jibran, M.; Nasir, H.A.; Qureshi, F.A.; Ali, U.; Jones, C.; Mahmood, I. A demand response-based solution to overloading in underdeveloped distribution networks. IEEE Trans. Smart Grid 2021, 12, 4059–4067. [Google Scholar] [CrossRef]
- Liao, S.; Liu, Y.; Xu, J.; Jia, L.; Ke, D.; Jiang, X. Data-Driven Real-Time Congestion Forecasting and Relief with High Renewable Energy Penetration. IEEE Trans. Ind. Inform. 2024, 21, 12–29. [Google Scholar] [CrossRef]
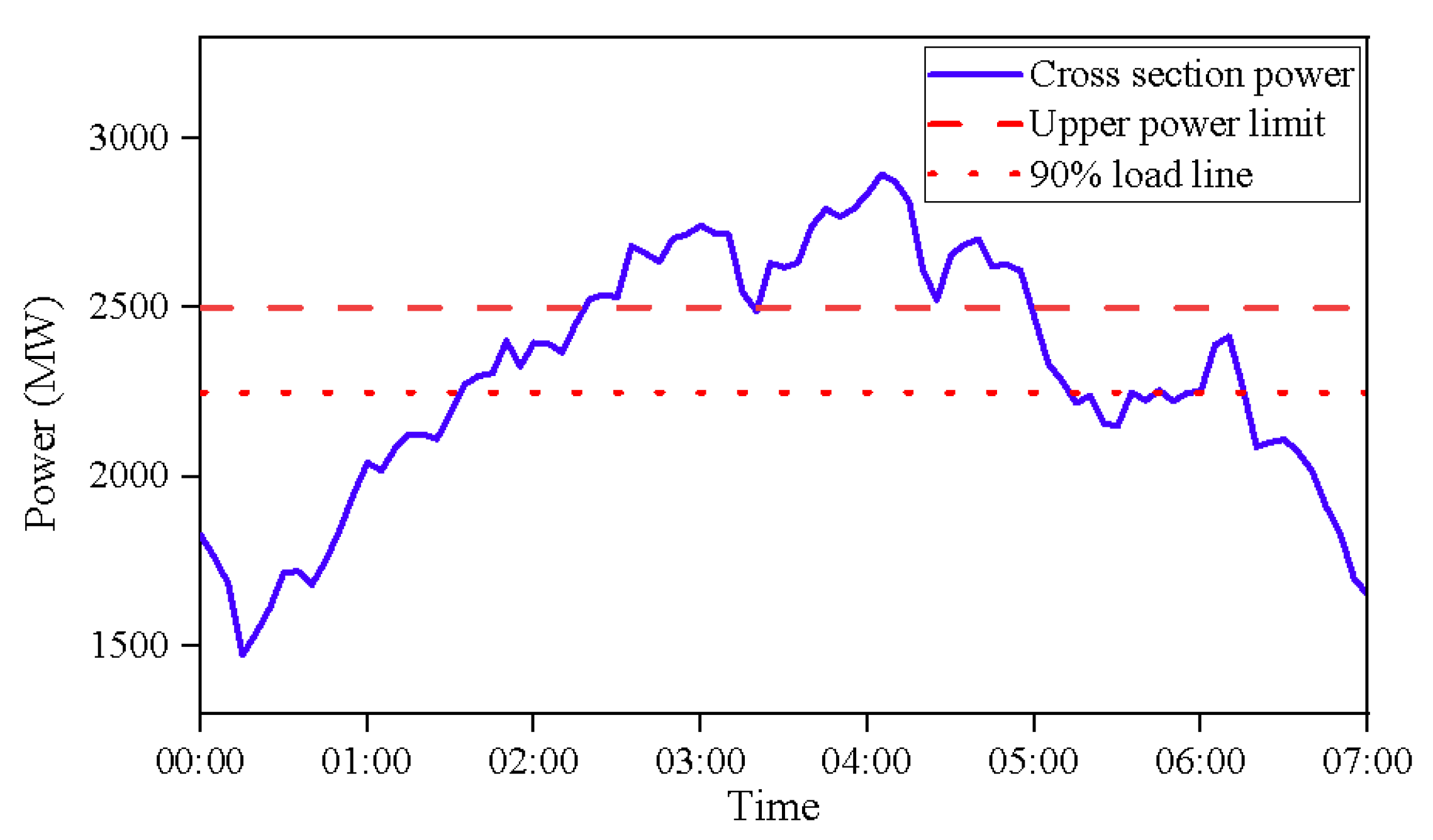
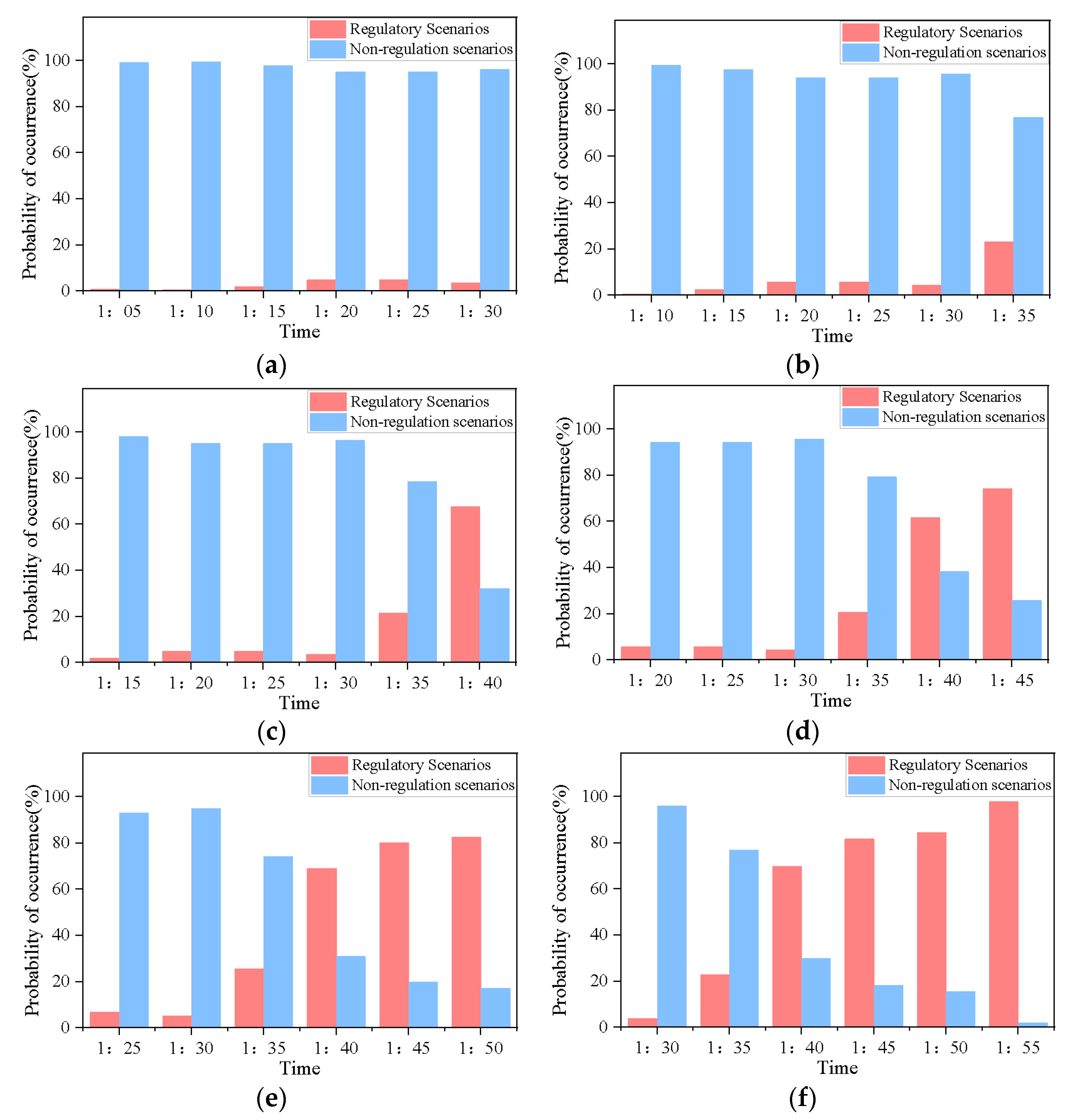
| LLF | ≤90% | >90% |
|---|---|---|
| categories | Non-regulatory Scenarios | Regulation scenarios |
| tab | 0 | 1 |
| Algorithm | Accuracy | Training Time/s | Prediction Time/s |
|---|---|---|---|
| SVM | 0.83 | 78.24 | 2.76 |
| LR | 0.74 | 29.20 | 0.92 |
| KN | 0.71 | 2.46 | 2.33 |
| RF | 0.84 | 30.55 | 0.79 |
| CNN-BILSTM | 0.88 | 15.81 | 0.81 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, H.; Wang, R.; Zhai, B.; Li, Y.; Li, P.; Zhang, R.; He, H.; Liao, S. Data-Driven Proactive Early Warning of Grid Congestion Probability Based on Multiple Time Scales. Energies 2025, 18, 2530. https://doi.org/10.3390/en18102530
Fu H, Wang R, Zhai B, Li Y, Li P, Zhang R, He H, Liao S. Data-Driven Proactive Early Warning of Grid Congestion Probability Based on Multiple Time Scales. Energies. 2025; 18(10):2530. https://doi.org/10.3390/en18102530
Chicago/Turabian StyleFu, Haobo, Ruizhuo Wang, Bingxu Zhai, Yuanzhuo Li, Pengyuan Li, Rui Zhang, Haoyuan He, and Siyang Liao. 2025. "Data-Driven Proactive Early Warning of Grid Congestion Probability Based on Multiple Time Scales" Energies 18, no. 10: 2530. https://doi.org/10.3390/en18102530
APA StyleFu, H., Wang, R., Zhai, B., Li, Y., Li, P., Zhang, R., He, H., & Liao, S. (2025). Data-Driven Proactive Early Warning of Grid Congestion Probability Based on Multiple Time Scales. Energies, 18(10), 2530. https://doi.org/10.3390/en18102530






