Optimization Scheduling of Integrated Energy Systems Considering Power Flow Constraints
Abstract
1. Introduction
- (1)
- This paper investigates a data-driven two-stage distributionally robust optimization method based on the Hausdorff distance. Unlike traditional methods for constructing uncertainty ambiguity sets, this approach captures the overall difference between ambiguity sets more comprehensively, better approximates the true distribution of uncertain variables, and achieves a more effective balance between economic efficiency and robustness.
- (2)
- The data-driven electricity–heat–gas integrated energy system built in this study incorporates a two-stage distributionally robust optimization model that accounts for the effects of various coupling components and energy storage devices. The system’s economy and capacity to absorb wind power are both enhanced compared to the two-grid integrated energy system concept.
- (3)
- In this paper, the AC power flow model is integrated into the system framework, and the nonlinear components are handled using the second-order cone programming method. Furthermore, the influence of wind power on the system’s reactive voltage is analyzed. Simulation results demonstrate that the proposed electricity–heat–gas integrated energy system effectively reduces voltage fluctuations in the power grid and improves the overall voltage quality.
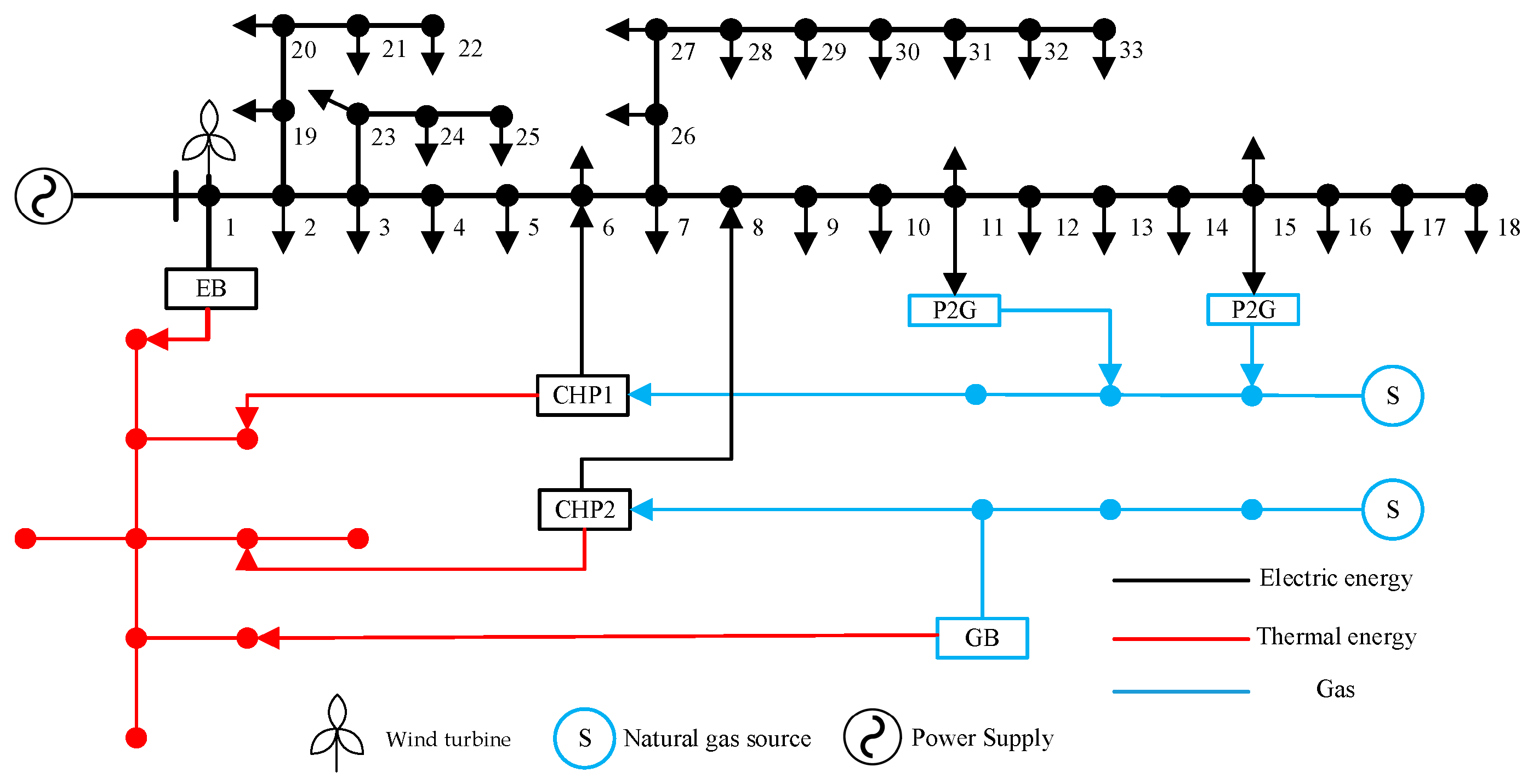
2. System Model
2.1. Objective Function
- Generation cost of CHP:
- 2.
- Natural gas cost:
- 3.
- Cost of wind abandonment:
2.2. Grid Constraints
- Electric power balance constraints:
- 2.
- CHP operation constraints:
- 3.
- Power storage device constraints:
- 4.
- Electric power restriction of electric boiler:
- 5.
- Wind power output constraints:
- 6.
- AC power flow constraints:
- 7.
- Voltage and line power constraints:
2.3. Heat Network Constraints
- Thermal power balance constraints:
- 2.
- Thermal power constraints of a gas-fired boiler:
2.4. Gas Network Constraints
- Natural gas source flow constraints:
- 2.
- Node pressure constraints:
- 3.
- Flow equation of natural gas pipeline:
- 4.
- Compressor station constraints:
- 5.
- P2G device constraints:
- 6.
- Network node flow balance constraints:
2.5. Coupling Constraints
- Electric boiler electrothermal coupling constraints:
- 2.
- Coupling constraints of CHP:
- 3.
- Gas–thermal coupling constraint of a gas-fired boiler:
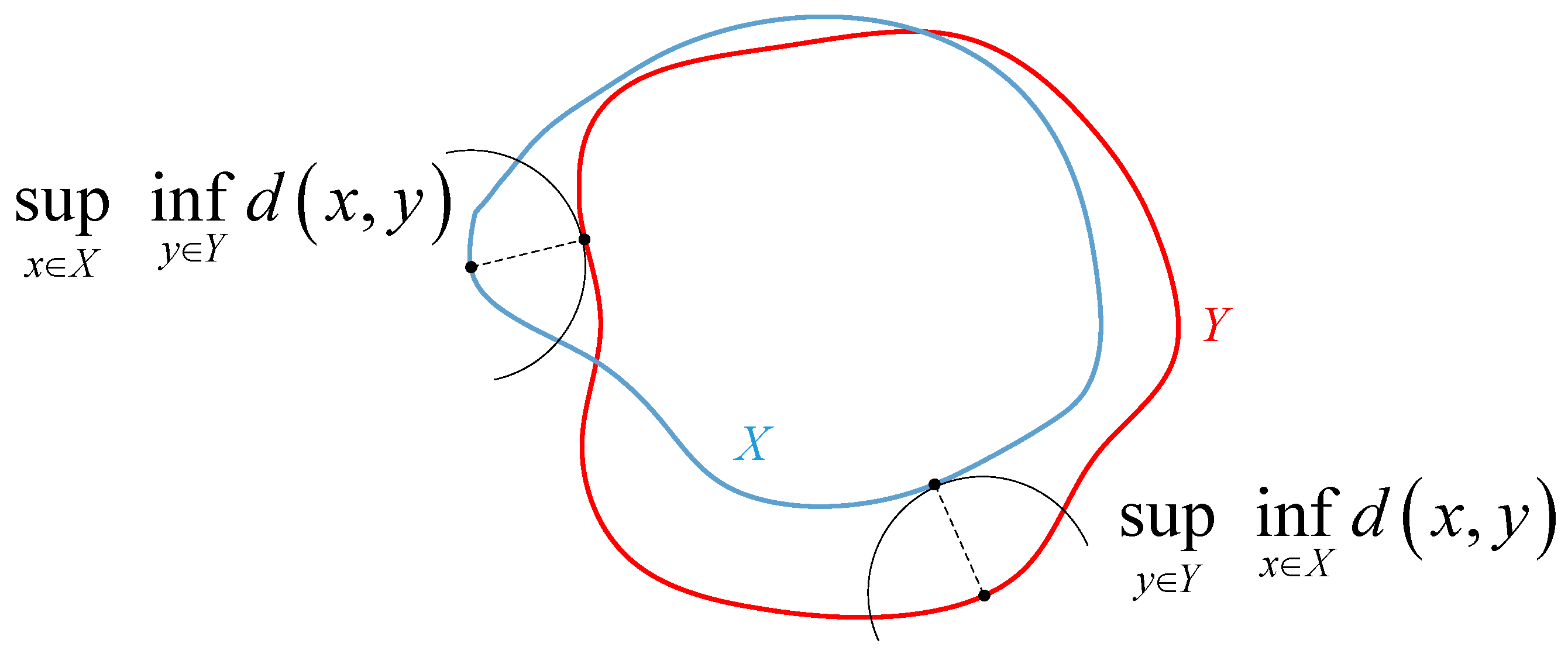
3. Data-Driven Robust Optimization Modeling Based on Hausdorff Distance
3.1. Robust Optimization Mathematical Model
3.2. Ambiguity Set Based on Hausdorff Distance
4. Case Study
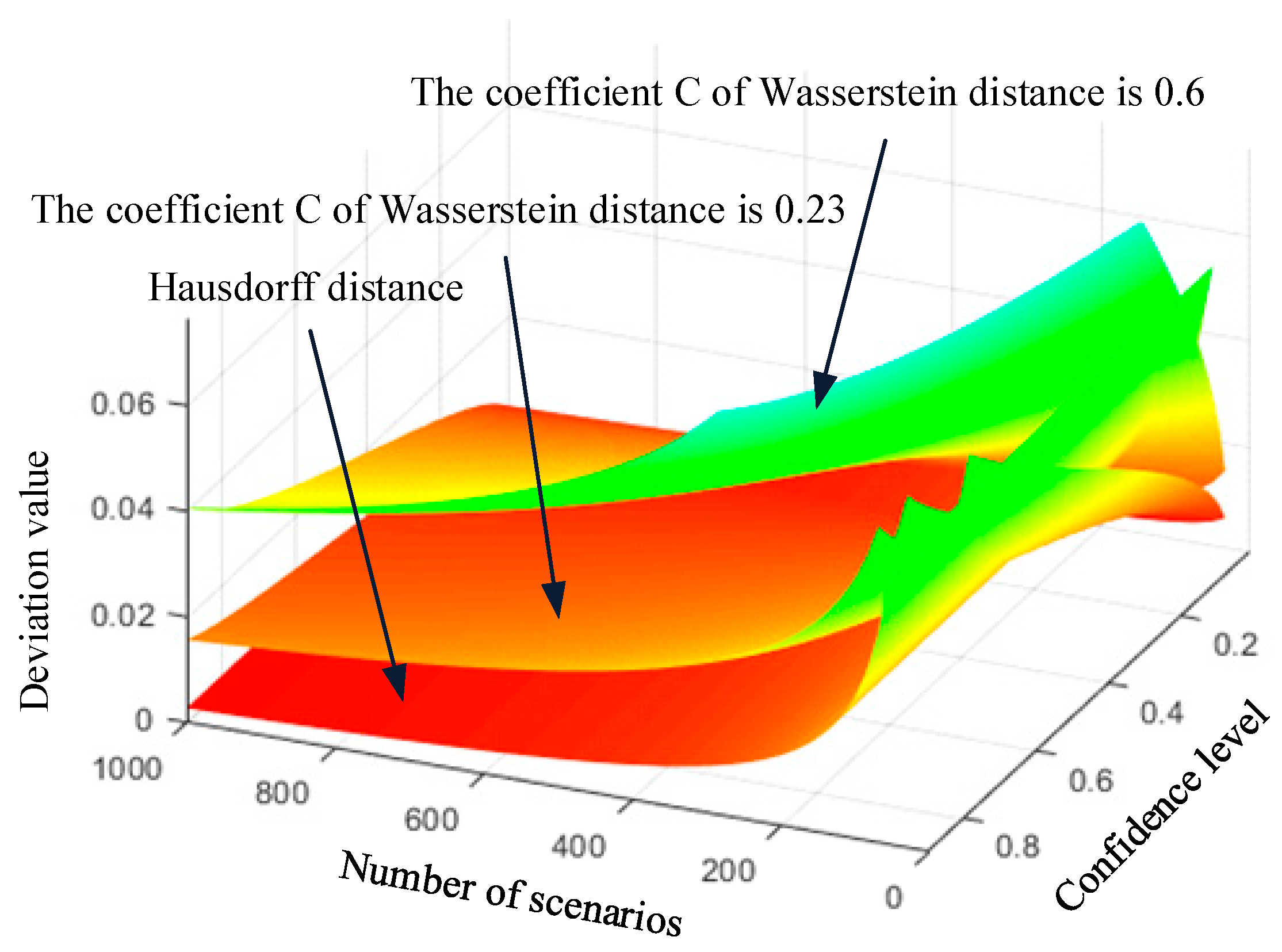
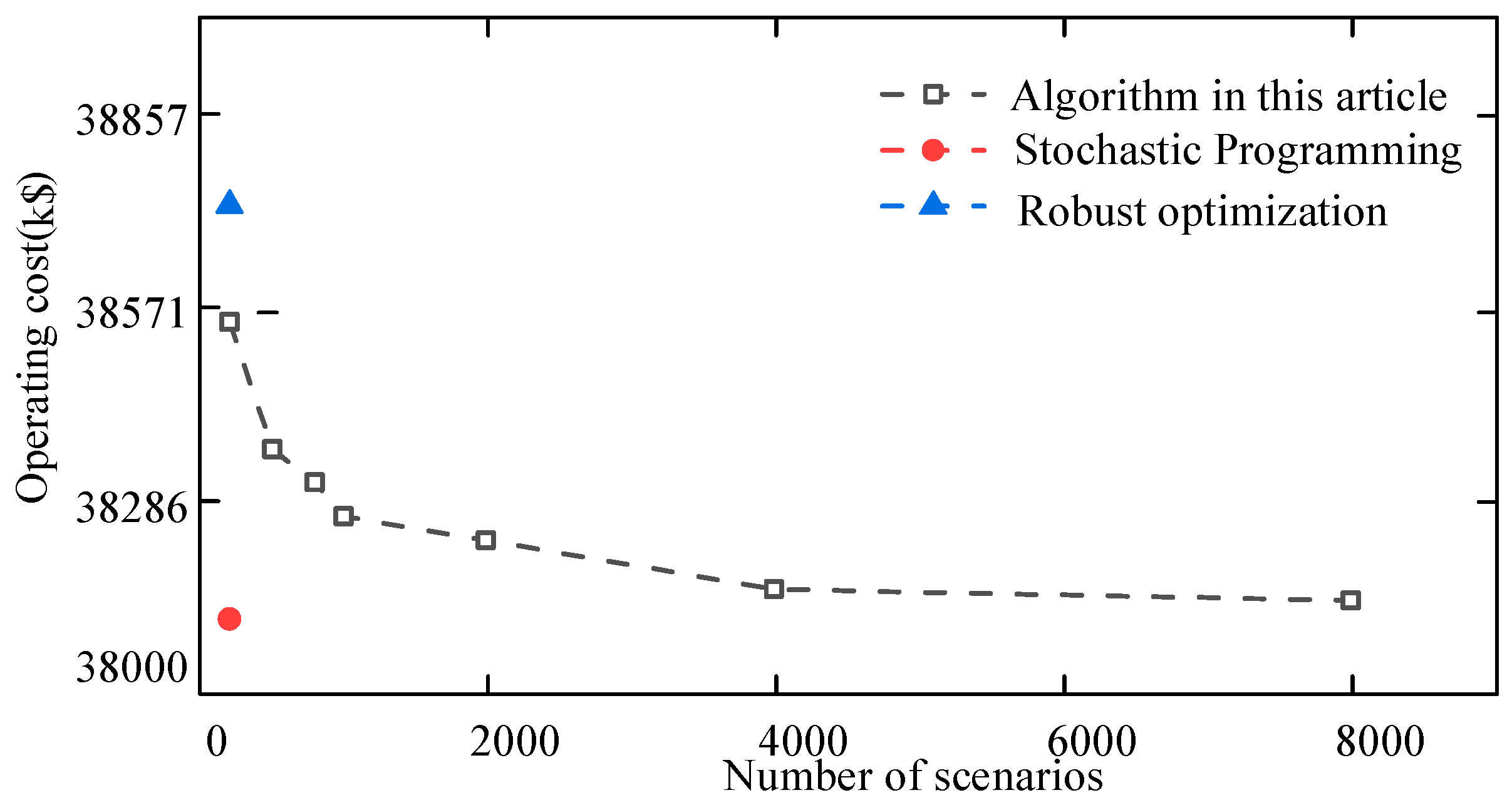
4.1. Analysis of Data-Driven Results Based on Hausdorff Distance
- Economic operation cost analysis
- 2.
- Analysis of results at various confidence levels
- 3.
- Analysis of Hausdorff Distance and Norm Results
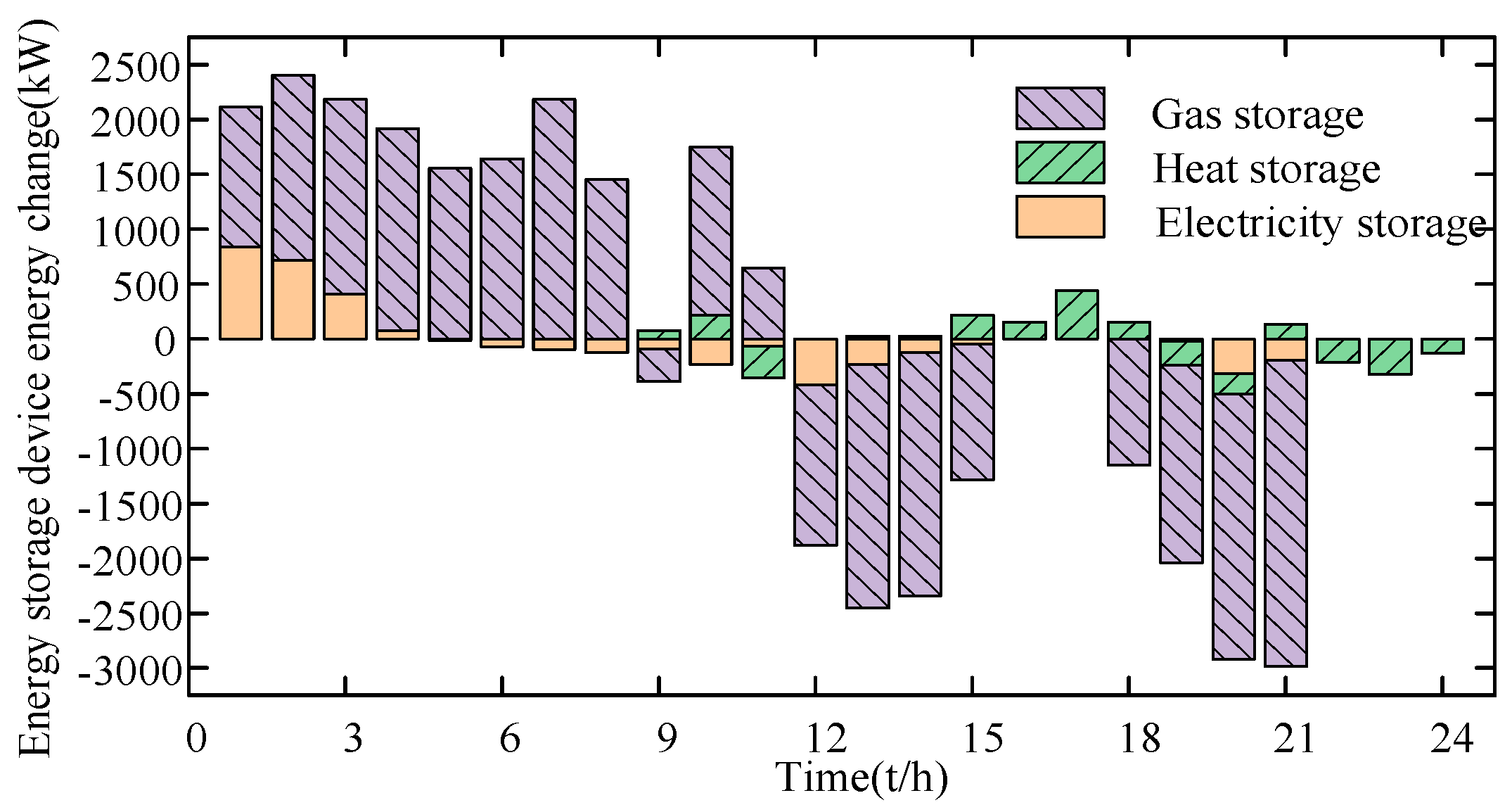
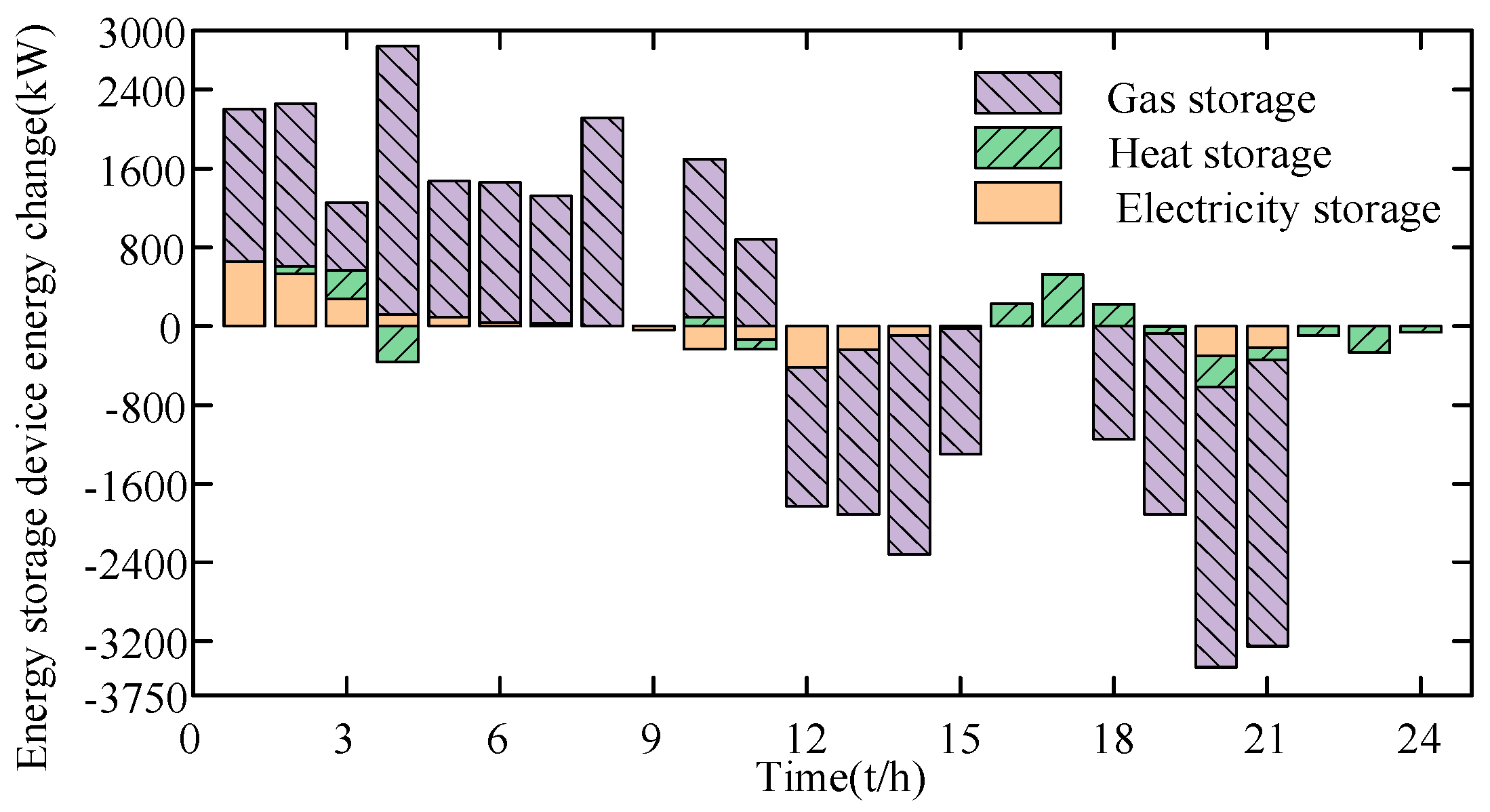
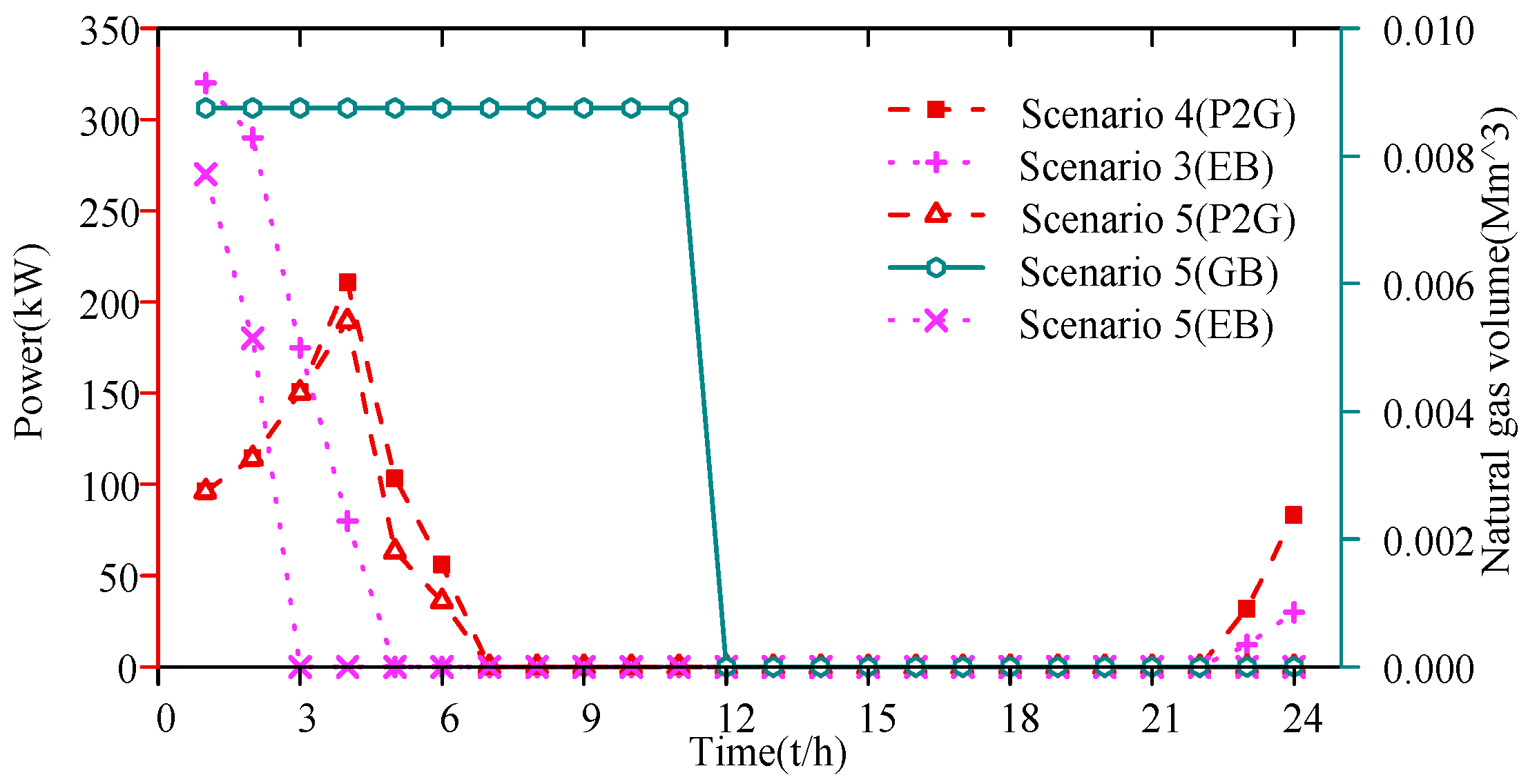
4.2. Comparative Analysis of Different Operation Scenarios of CEGHS
- Comparative analysis of Scenario 2 and Scenario 3
- 2.
- Comparative analysis of wind power output in different scenarios
- 3.
- Analysis of iteration results
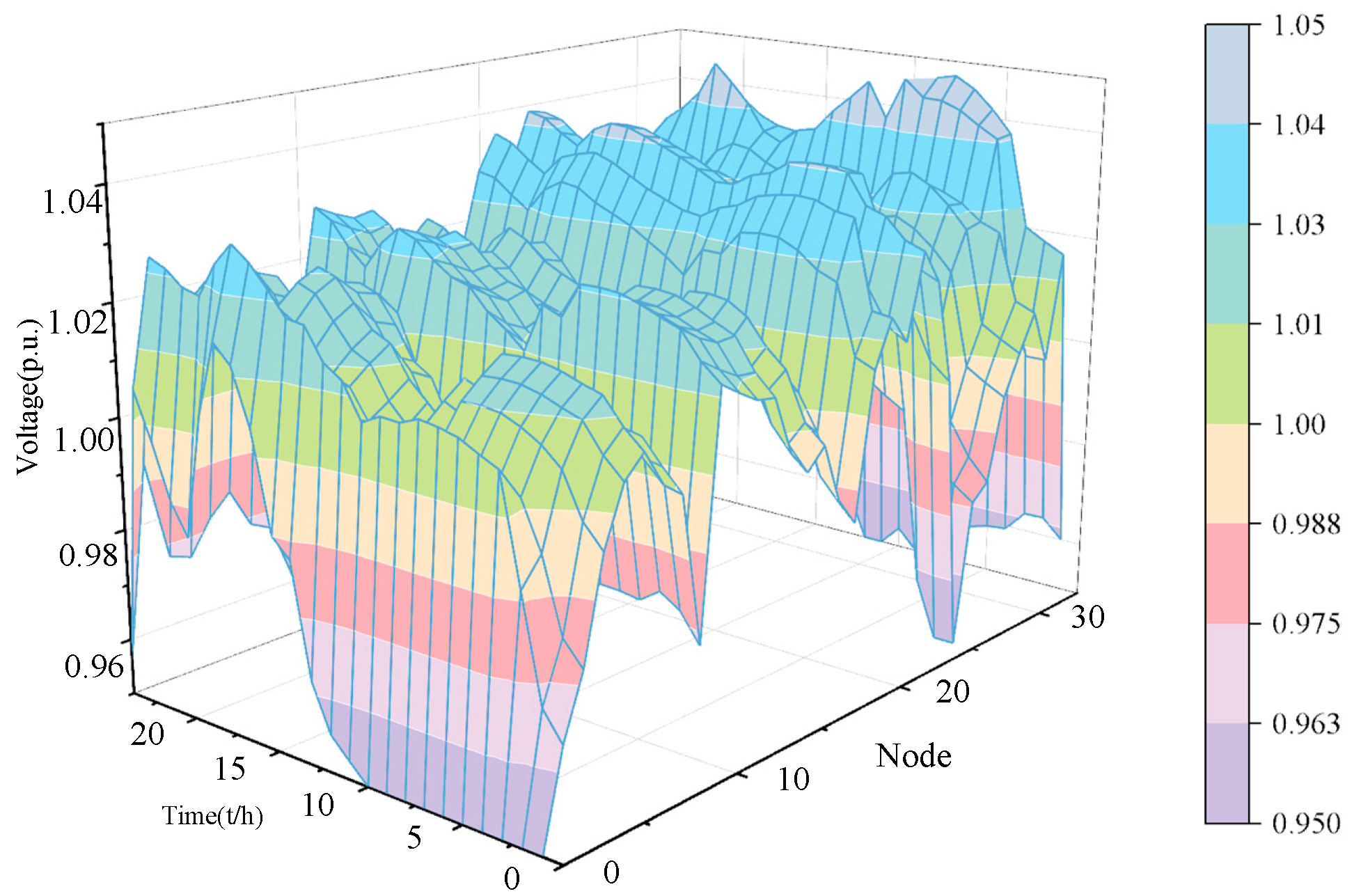
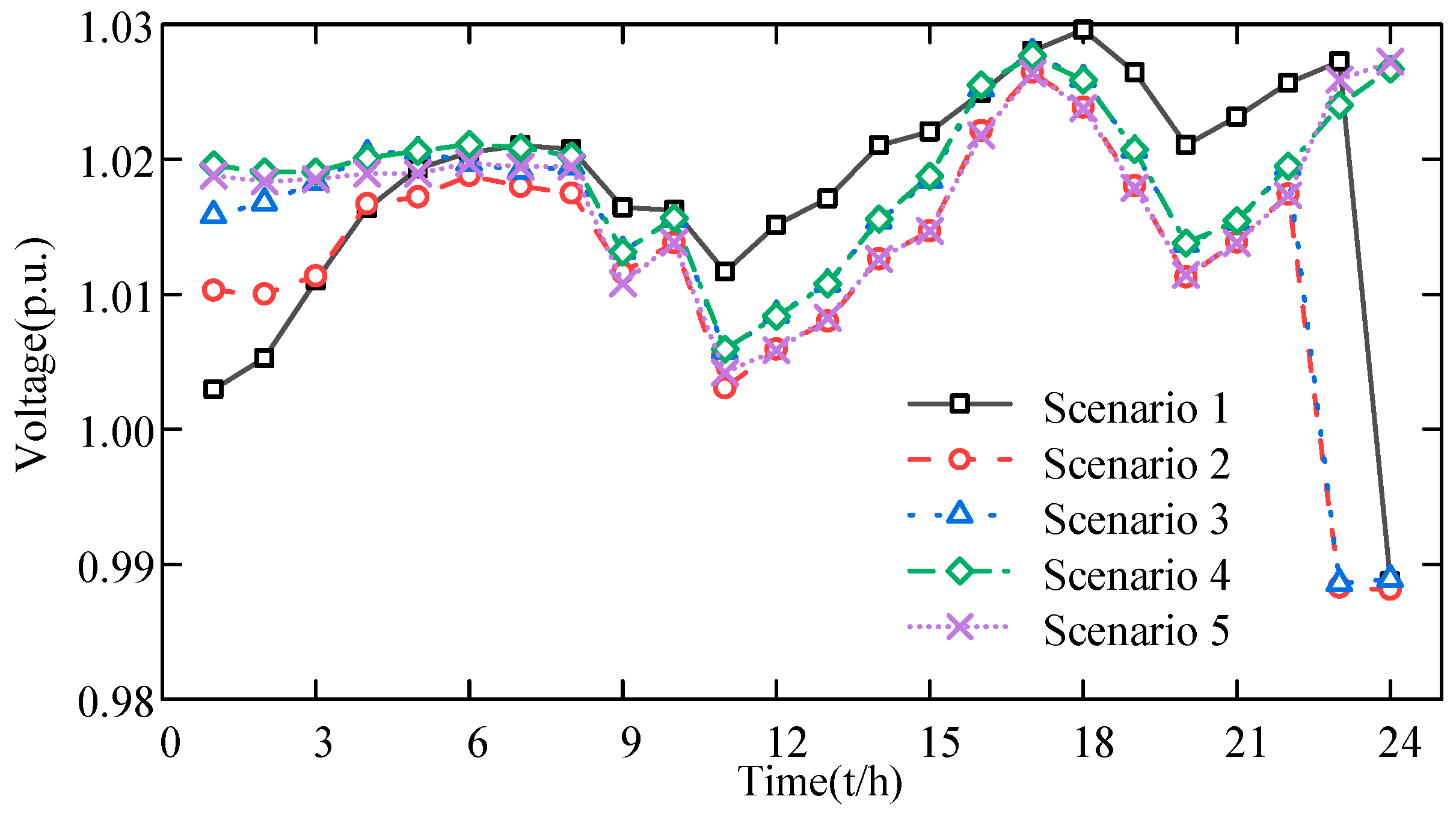
4.3. Analysis of Reactive Power and Voltage Characteristics of Electric–Heat–Gas Integrated Energy System
5. Conclusions
- (1)
- It introduces a data-driven distributionally robust optimization method based on Hausdorff distance. This method comprehensively considers the difference between ambiguity sets and, compared with norm constraints, better simulates the true distribution of uncertainty variables. The model introduces AC power flow constraints and utilizes the second-order cone method to handle the nonlinear component. Additionally, it analyzes the impact of wind power access on system voltage quality, demonstrating that the model can reduce voltage fluctuations and enhance voltage quality.
- (2)
- The distributionally robust algorithm proposed in this paper strikes a better balance between economic efficiency and robustness compared to stochastic optimization and robust optimization methods. Compared to robust optimization, the proposed algorithm reduces robustness but improves economic performance. In summary, the proposed comprehensive energy system scheduling strategy outperforms traditional models in terms of economy and wind power utilization efficiency. Compared with the benchmark scenario, the operating cost of Scenario 5 has decreased by 6.65%, and the cost of wind power curtailment has decreased by 34.3%.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Second-Order Taper of AC Power Flow
Appendix A.2. Linearization of Flow Equation of Natural Gas Pipeline
Appendix A.3. Linearization of Heat Network Power Flow Equation
Appendix B
CCG Solving Algorithms Second-Order Taper of AC Power Flow
| CCG solving algorithm |
| The main problem of the two-stage model is as follows: |
| Initialize probability distribution Find the optimal solution ,returns the lower bound of the model Given the first stage variables , solve the sub problem: |
| The model for each scenario k in the sub problem is as follows: |
| After substituting K optimal solutions , the subproblem becomes: |
| The upper bound of the model obtained by solving subproblems |
References
- Cai, Y.; Cai, J.; Xu, L.; Tan, Q.; Xu, Q. Integrated risk analysis of water-energy nexus systems based on systems dynamics, orthogonal design, and copula analysis. Renew. Sustain. Energy Rev. 2019, 99, 125–137. [Google Scholar] [CrossRef]
- Hu, J.; Liu, X.; Shahidehpour, M.; Xia, S. Optimal Operation of Energy Hubs with Large-Scale Distributed Energy Resources for Distribution Network Congestion Management. IEEE Trans. Sustain. Energy 2021, 12, 1755–1765. [Google Scholar] [CrossRef]
- Wang, D.; Liu, L.; Jia, H.; Wang, W.; Zhi, Y.; Meng, Z.; Zhou, B. Review of key problems related to integrated energy distribution systems. CSEE J. Power Energy Syst. 2018, 4, 130–145. [Google Scholar] [CrossRef]
- Chen, X.; Kang, C.; O’Malley, M.; Xia, Q.; Bai, J.; Liu, C.; Sun, R.; Wang, W.; Li, H. Increasing the Flexibility of Combined Heat and Power for Wind Power Integration in China: Modeling and Implications. IEEE Trans. Power Syst. 2015, 30, 1848–1857. [Google Scholar] [CrossRef]
- Li, J.; Fang, J.; Zeng, Q.; Chen, Z. Optimal operation of the integrated electrical and heating systems to accommodate the intermittent renewable sources. Appl. Energy 2016, 167, 244–254. [Google Scholar] [CrossRef]
- Li, Z.; Wu, W.; Wang, J.; Zhang, B.; Zheng, T. Transmission-Constrained Unit Commitment Considering Combined Electricity and District Heating Networks. IEEE Trans. Sustain. Energy 2016, 7, 480–492. [Google Scholar] [CrossRef]
- Vandewalle, J.; Bruninx, K.; D’Haeseleer, W. Effects of large-scale power to gas conversion on the power, gas and carbon sectors and their interactions. Energy Convers. Manag. 2015, 94, 28–39. [Google Scholar] [CrossRef]
- Zhang, X.; Shahidehpour, M.; Alabdulwahab, A.; Abusorrah, A. Optimal Expansion Planning of Energy Hub with Multiple Energy Infrastructures. IEEE Trans. Smart Grid 2015, 6, 2302–2311. [Google Scholar] [CrossRef]
- Götz, M.; Lefebvre, J.; Mörs, F.; Koch, A.M.; Graf, F.; Bajohr, S.; Reimert, R.; Kolb, T. Renewable power-to-gas: A technological and economic review. Renew. Energy 2016, 85, 1371–1390. [Google Scholar] [CrossRef]
- Salimi, M.; Ghasemi, H.; Adelpour, M.; Vaez-Zadeh, S. Optimal planning of energy hubs in interconnected energy systems: A case study for natural gas and electricity. Gener. Transm. Distrib. Iet 2015, 9, 695–707. [Google Scholar] [CrossRef]
- Qadrdan, M.; Wu, J.; Jenkins, N.; Ekanayake, J. Operating Strategies for a GB Integrated Gas and Electricity Network Considering the Uncertainty in Wind Power Forecasts. IEEE Trans. Sustain. Energy 2014, 5, 128–138. [Google Scholar] [CrossRef]
- Alabdulwahab, A.; Abusorrah, A.; Zhang, X.; Shahidehpour, M. Coordination of Interdependent Natural Gas and Electricity Infrastructures for firming the Variability of Wind Energy in Stochastic Day-Ahead Scheduling. IEEE Trans. Sustain. Energy 2015, 6, 606–615. [Google Scholar] [CrossRef]
- Li, Y.; Zou, Y.; Tan, Y.; Cao, Y.; Liu, X.; Shahidehpour, M.; Tian, S.; Bu, F. Optimal Stochastic Operation of Integrated Low-Carbon Electric Power, Natural Gas, and Heat Delivery System. IEEE Trans. Sustain. Energy 2018, 9, 273–283. [Google Scholar] [CrossRef]
- He, C.; Wu, L.; Liu, T.; Shahidehpour, M. Robust Co-Optimization Scheduling of Electricity and Natural Gas Systems via ADMM. IEEE Trans. Sustain. Energy 2017, 8, 658–670. [Google Scholar] [CrossRef]
- Zhang, Y.; Ai, X.; Wen, J.; Fang, J.; He, H. Data-Adaptive Robust Optimization Method for the Economic Dispatch of Active Distribution Networks. IEEE Trans. Smart Grid 2019, 10, 3791–3800. [Google Scholar] [CrossRef]
- Duan, C.; Fang, W.; Jiang, L.; Yao, L.; Liu, J. Distributionally Robust Chance-Constrained Approximate AC-OPF with Wasserstein Metric. IEEE Trans. Power Syst. 2018, 33, 4924–4936. [Google Scholar] [CrossRef]
- Lu, X.; Chan, K.W.; Xia, S.; Zhou, B.; Luo, X. Security-Constrained Multiperiod Economic Dispatch with Renewable Energy Utilizing Distributionally Robust Optimization. IEEE Trans. Sustain. Energy 2019, 10, 768–779. [Google Scholar] [CrossRef]
- Shi, Z.; Liang, H.; Huang, S.; Dinavahi, V. Distributionally Robust Chance-Constrained Energy Management for Islanded Microgrids. IEEE Trans. Smart Grid 2019, 10, 2234–2244. [Google Scholar] [CrossRef]
- Ding, Y.; Morstyn, T.; McCulloch, M.D. Distributionally Robust Joint Chance-Constrained Optimization for Networked Microgrids Considering Contingencies and Renewable Uncertainty. IEEE Trans. Smart Grid 2022, 13, 2467–2478. [Google Scholar] [CrossRef]
- Duan, C.; Jiang, L.; Fang, W.; Liu, J.; Liu, S. Data-Driven Distributionally Robust Energy-Reserve-Storage Dispatch. IEEE Trans. Ind. Inform. 2018, 14, 2826–2836. [Google Scholar] [CrossRef]
- Xiong, P.; Jirutitijaroen, P.; Singh, C. A Distributionally Robust Optimization Model for Unit Commitment Considering Uncertain Wind Power Generation. IEEE Trans. Power Syst. 2017, 32, 39–49. [Google Scholar] [CrossRef]
- Alismail, F.; Xiong, P.; Singh, C. Optimal Wind Farm Allocation in Multi-Area Power Systems Using Distributionally Robust Optimization Approach. IEEE Trans. Power Syst. 2018, 33, 536–544. [Google Scholar] [CrossRef]
- Chen, Y.; Guo, Q.; Sun, H.; Li, Z.; Wu, W.; Li, Z. A Distributionally Robust Optimization Model for Unit Commitment Based on Kullback–Leibler Divergence. IEEE Trans. Power Syst. 2018, 33, 5147–5160. [Google Scholar] [CrossRef]
- Hu, Z.; Hong, J.L. Kullback–Leibler Divergence Constrained Distributionally Robust Optimization. 2012. Available online: http://www.optimization-online.org/DB_FILE/2012/11/3677.pdf (accessed on 15 March 2024).
- Wang, C.; Gao, R.; Wei, W.; Shafie-khah, M.; Bi, T.; Catalão, J.P.S. Risk-Based Distributionally Robust Optimal Gas-Power Flow with Wasserstein Distance. IEEE Trans. Power Syst. 2019, 34, 2190–2204. [Google Scholar] [CrossRef]
- Zhao, P.; Gu, C.; Cao, Z.; Hu, Z.; Zhang, X.; Chen, X.; Hernando-Gil, I.; Ding, Y. Economic-Effective Multi-Energy Management Considering Voltage Regulation Networked with Energy Hubs. IEEE Trans. Power Syst. 2021, 36, 2503–2515. [Google Scholar] [CrossRef]
- Ding, T.; Yang, Q.; Yang, Y.; Li, C.; Bie, Z.; Blaabjerg, F. A Data-Driven Stochastic Reactive Power Optimization Considering Uncertainties in Active Distribution Networks and Decomposition Method. IEEE Trans. Smart Grid 2018, 9, 4994–5004. [Google Scholar] [CrossRef]
- Zhao, C.; Guan, Y. Data-Driven Stochastic Unit Commitment for Integrating Wind Generation. IEEE Trans. Power Syst. 2016, 31, 2587–2596. [Google Scholar] [CrossRef]
- Zeng, B.; Zhao, L. Solving two-stage robust optimization problems using a column-and-constraint generation method. Oper. Res. Lett. 2013, 41, 457–461. [Google Scholar] [CrossRef]
- Taha, A.; Allan, H. An efficient algorithm for calculating the exact Hausdorff distance. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 2153–2163. [Google Scholar] [CrossRef]
- Schutze, O.; Esquivel, X.; Lara, A.; Coello, C.A.C. Using the averaged Hausdorff distance as a performance measure in evolutionary multiobjective optimization. IEEE Trans. Evol. Comput. 2012, 16, 504–522. [Google Scholar] [CrossRef]
- Farivar, M.; Low, S.H. Branch Flow Model: Relaxations and Convexification—Part II. IEEE Trans. Power Syst. 2013, 28, 2565–2572. [Google Scholar] [CrossRef]
- He, Y.; Yan, M.; Shahidehpour, M.; Li, Z.; Guo, C.; Wu, L.; Ding, Y. Decentralized Optimization of Multi-Area Electricity-Natural Gas Flows Based on Cone Reformulation. IEEE Trans. Power Syst. 2018, 33, 4531–4542. [Google Scholar] [CrossRef]




| Confidence Level | Model Economic Operating Cost (kUSD) |
|---|---|
| 0.2 | 37,913 |
| 0.5 | 38,261 |
| 0.7 | 38,289 |
| 0.9 | 38,309 |
| Confidence Level | Model Economic Operating Cost (kUSD) | ||
|---|---|---|---|
| Hausdorff Distance | 1-Norm | -Norm | |
| 0.2 | 37,913 | 38,309 | 38,299 |
| 0.5 | 38,261 | 38,309 | 38,299 |
| 0.7 | 38,289 | 38,309 | 38,299 |
| 0.9 | 38,310 | 38,309 | 38,299 |
| Scenario | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Operating Cost (kUSD) | 40,987 | 40,220 | 38,799 | 38,866 | 38,261 |
| Cost of wind abandonment (kUSD) | 548.4 | 438.1 | 395.1 | 401.1 | 360.6 |
| Iterations | Upper Bound Value (kUSD) | Lower Bound Value (kUSD) |
|---|---|---|
| 1 | 62,664 | 22,399 |
| 2 | 38669 | 37,847 |
| 3 | 38,261 | 38,261 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, S.; Zong, X.; Chen, Q.; Zhang, W.; Zhou, H. Optimization Scheduling of Integrated Energy Systems Considering Power Flow Constraints. Energies 2025, 18, 2442. https://doi.org/10.3390/en18102442
Zou S, Zong X, Chen Q, Zhang W, Zhou H. Optimization Scheduling of Integrated Energy Systems Considering Power Flow Constraints. Energies. 2025; 18(10):2442. https://doi.org/10.3390/en18102442
Chicago/Turabian StyleZou, Sheng, Xuanjun Zong, Quan Chen, Wang Zhang, and Hongwei Zhou. 2025. "Optimization Scheduling of Integrated Energy Systems Considering Power Flow Constraints" Energies 18, no. 10: 2442. https://doi.org/10.3390/en18102442
APA StyleZou, S., Zong, X., Chen, Q., Zhang, W., & Zhou, H. (2025). Optimization Scheduling of Integrated Energy Systems Considering Power Flow Constraints. Energies, 18(10), 2442. https://doi.org/10.3390/en18102442





