Hybrid Approach for Detection and Diagnosis of Short-Circuit Faults in Power Transmission Lines
Abstract
1. Introduction
2. State of the Art
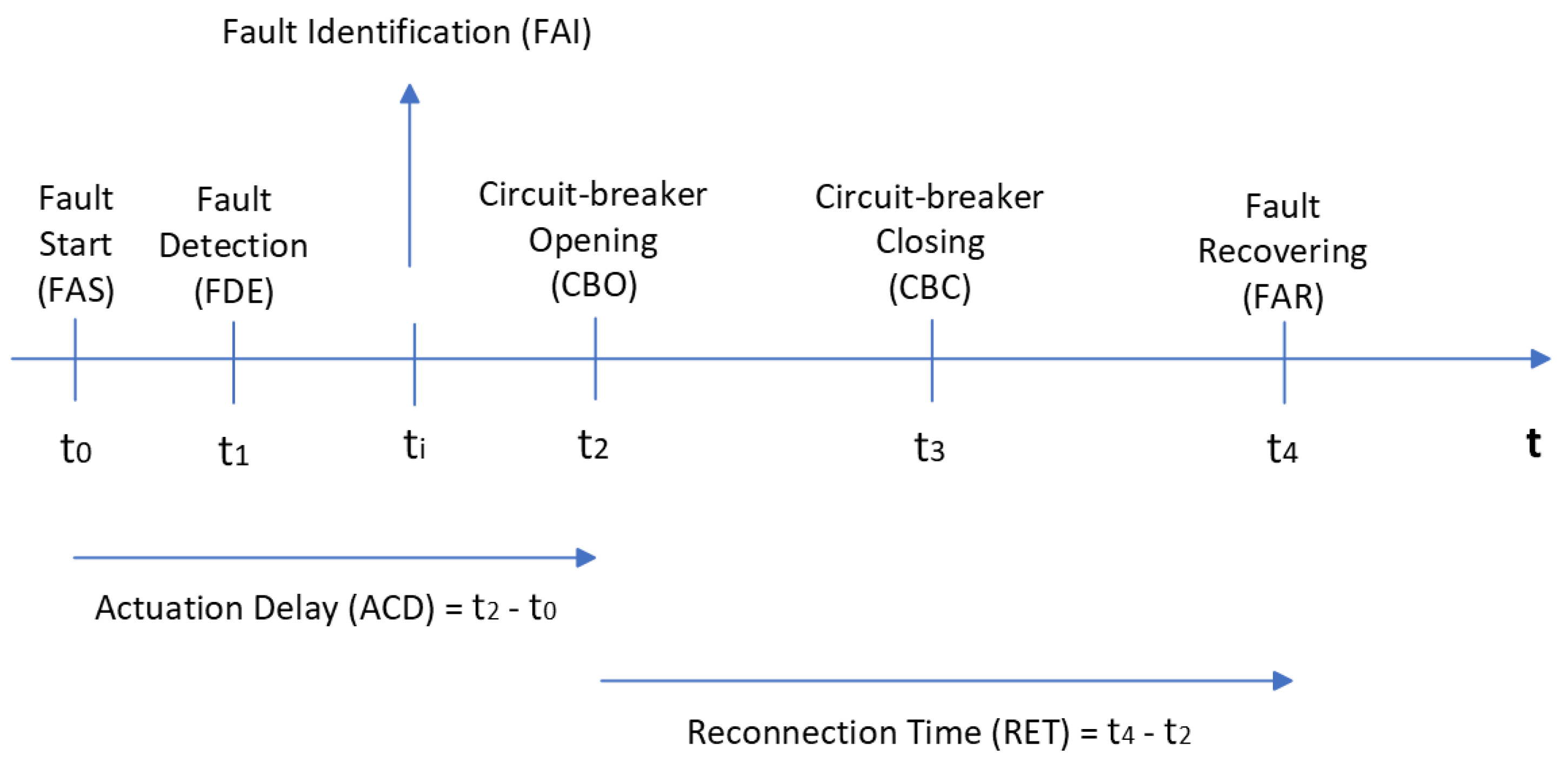
2.1. Terminology and Notation
2.2. Three-Phase Power Systems and Typical Faults
2.3. Circuit Breakers and Protective Relays
2.4. Fault Detection and Diagnosis Approaches
- Rule-based signal processing approaches. Relevant studies include (a) phasor-based algorithms, time-domain analysis, time–frequency analysis (Fourier transform and wavelet transform) [28]; (b) approach based on positive sequence voltage and current measurement from phasor measurement units (PMUs) [35]; (c) harmonic analysis and use of discrete Fourier transform (DFT) [36]; (d) fault classification based on group sparse representation [37].
- Data-driven machine learning/artificial intelligence approaches. Relevant studies include (a) fault detection and classification based on neural ELM networks [43]; (b) fault detection using the Pruned Exact Linear Time (PELT) algorithm in large datasets, and classification using wavelet transform [44]; (c) performance evaluation of different machine learning algorithms [45]; (d) different machine learning algorithms [28]; (e) automatic oscillography analysis with neural networks [46]; (f) variational autoencoders (VAEs) in conjunction with ML algorithms [47]; (g) empirical wavelet transform (EWT), local energy (LE), and support vector machine (SVM) [48]; (h) data-based Cauchy distribution weighting M-estimate RVFLNs neural method [30]; (i) review on artificial intelligence-based fault location methods in power distribution networks [18]; (j) fault location in power distribution systems via deep graph convolutional networks [49]; (k) fault identification based on deep reinforcement learning, using deep Q-network [50].
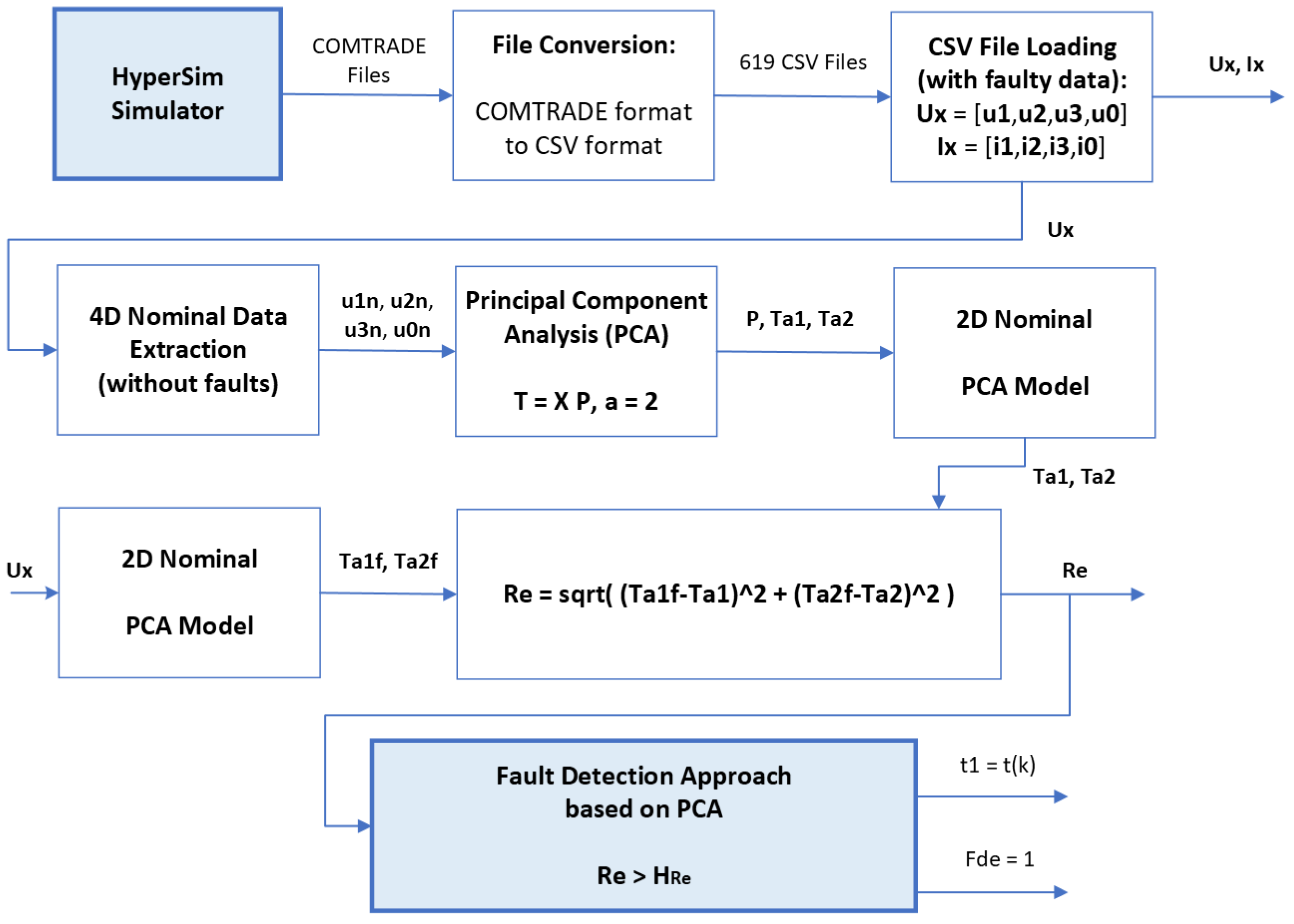
3. Proposed Fault Detection and Diagnosis Approach
3.1. HyperSim Simulator and COMTRADE Files
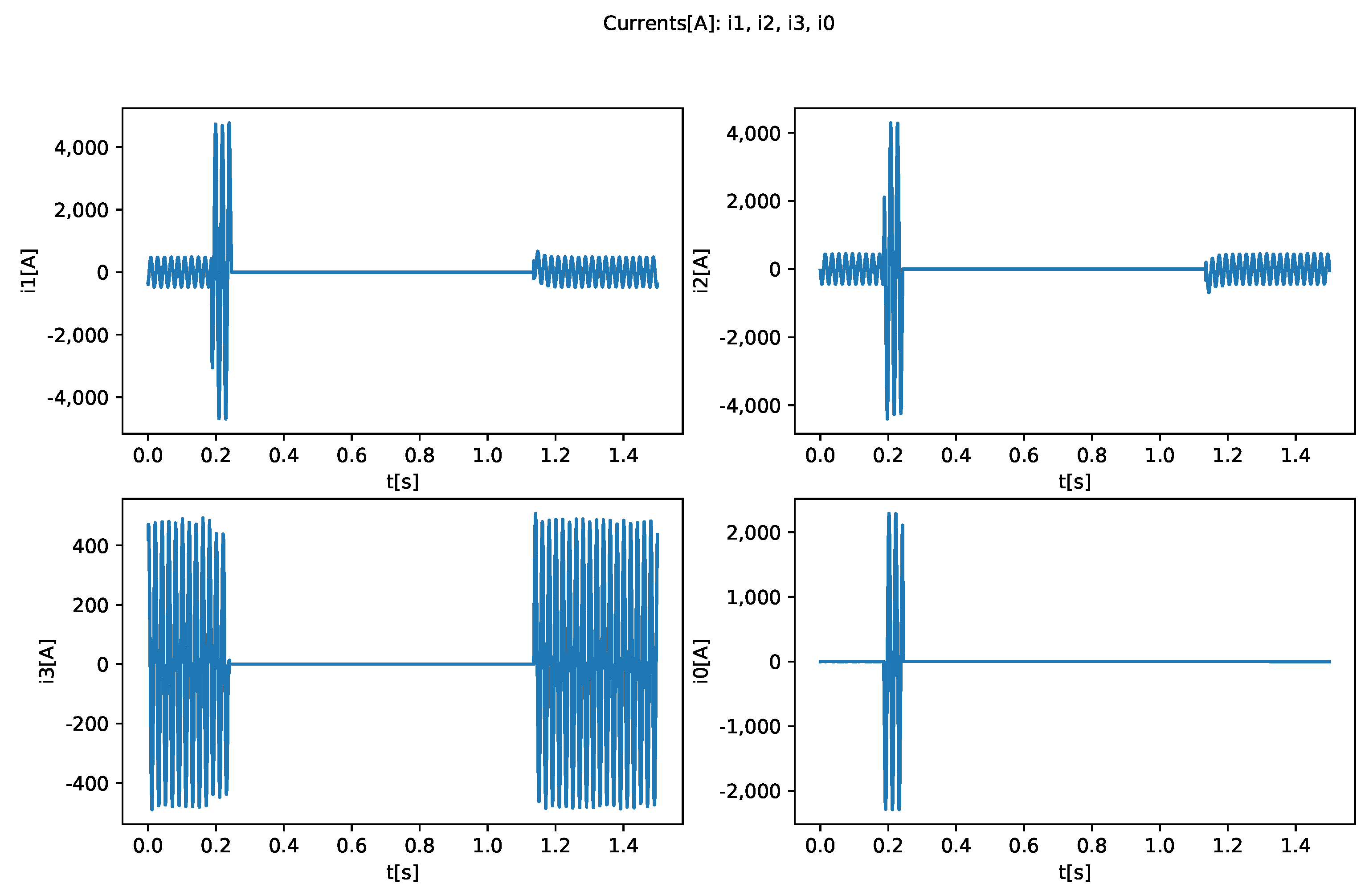
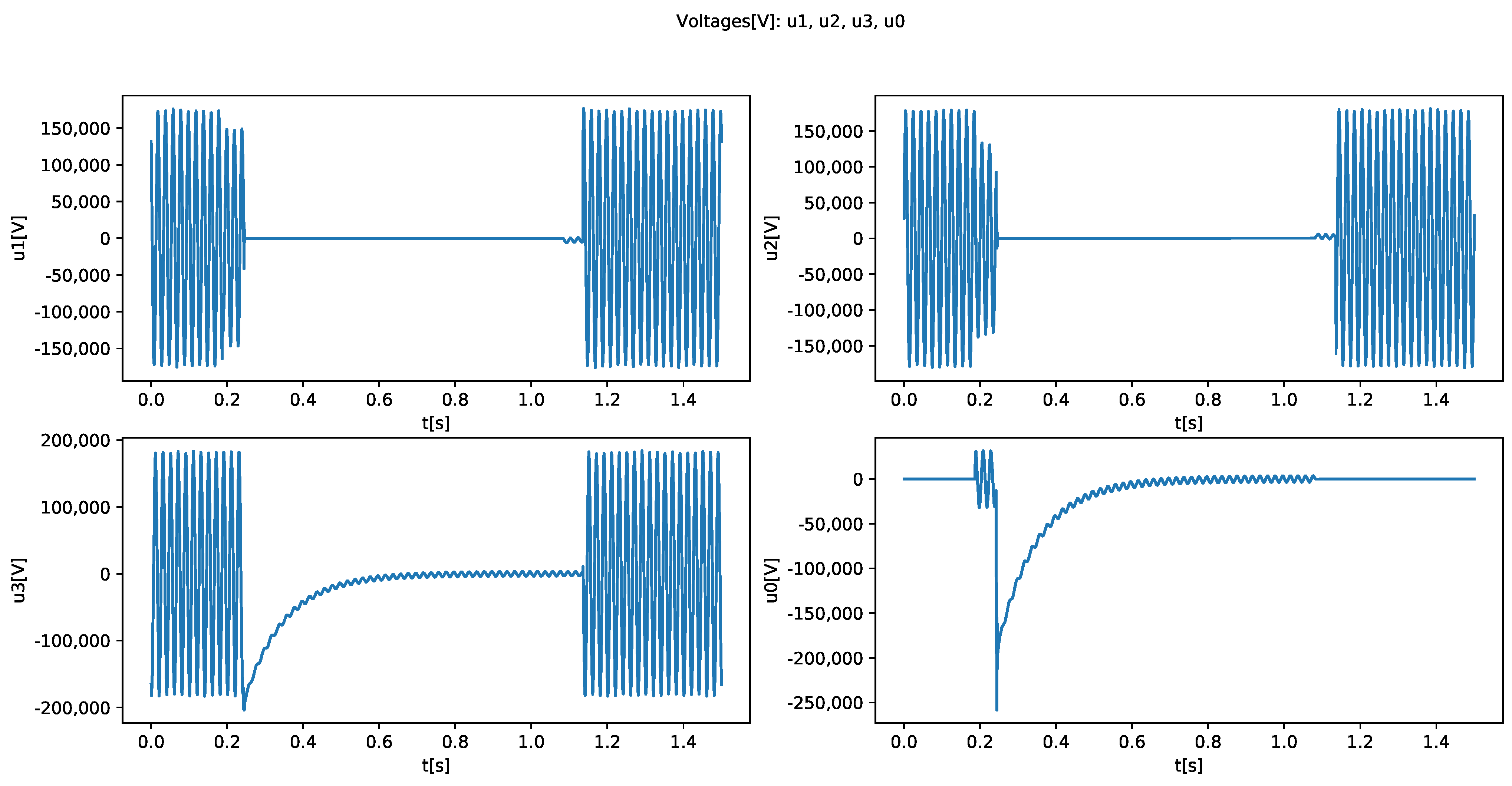
3.2. Nominal Operation, SNR, Short-Circuit Faults, and Main Symptoms
3.3. High-Level Architecture of the Proposed Fault Detection and Diagnosis Approach
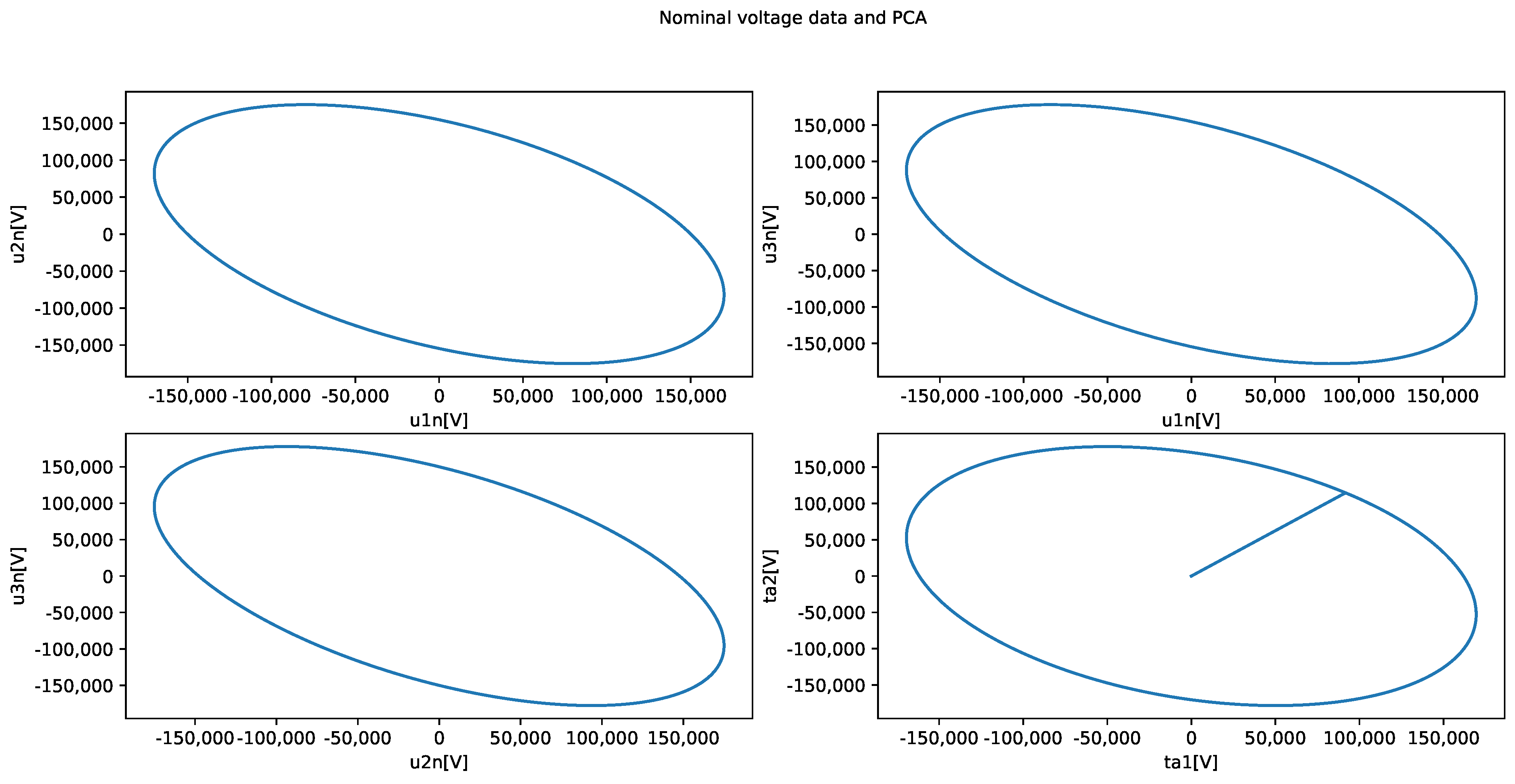
3.4. Fault Detection Approach
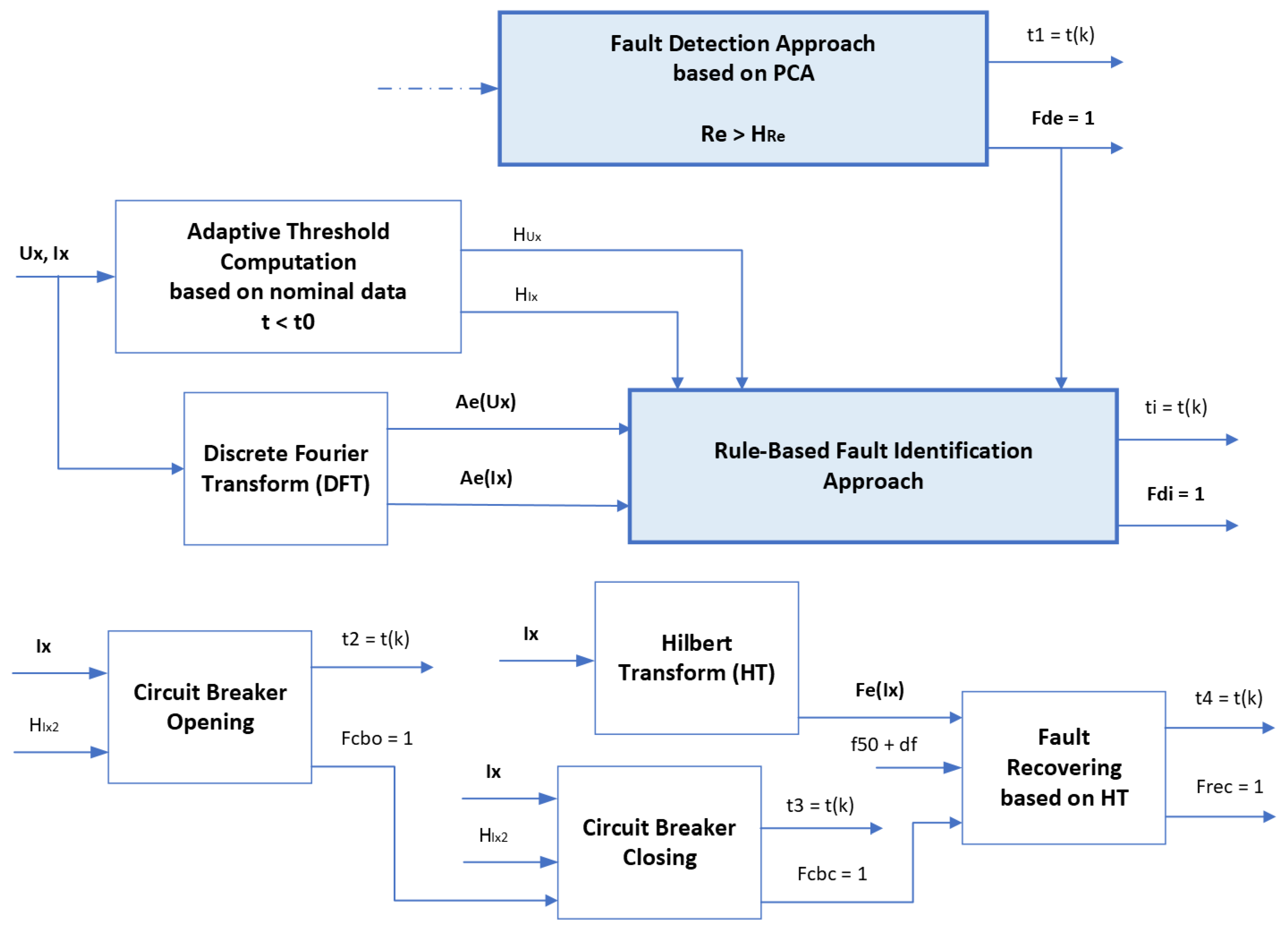
3.5. Fault Diagnosis Approach
3.5.1. Rule-Based Fault Identification
3.5.2. Circuit Breaker Opening
3.5.3. Circuit Breaker Closing
3.5.4. Fault Recovery
3.6. Thresholds and Robustness to Noise
3.7. Pseudo-Code of the Hybrid FDD Algorithm
| Algorithm 1 Hybrid Fault Detection and Diagnosis |
|
4. Simulation Results and Discussion
4.1. Dataset, HyperSim, and Programming Language
4.2. Simulation Parameters
4.3. Fault Detection Results
4.4. Fault Diagnosis Results
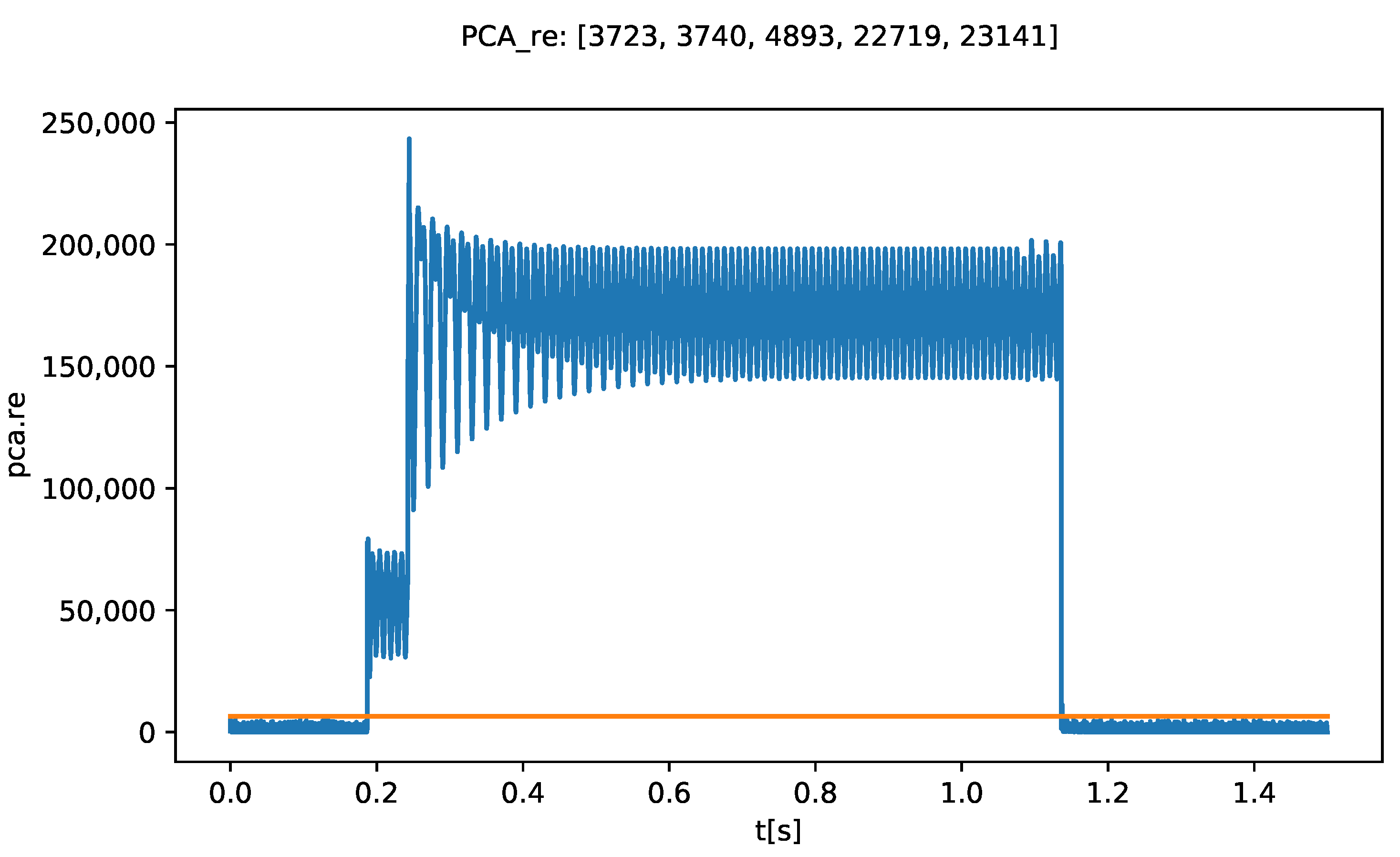
- (a) the fault detection signal “Re” (blue signal), and the respective adaptive threshold (orange signal);
- (b) the signal “fde01”, which corresponds to the moments in which the fault is active;
- (c) the “fde” signal, that records the various time instants, ; In the figure title, the vector associated with the fault times , in samples , is presented.
- (d) the “fdi01” signal, that allows evaluating, in the identification window, the short-circuit faults identified; in this case, two faults were identified: first, the fault F4 (AG) for a short time (in magenta color); and second, the correct fault F6 (ABG) for most of the time (in pink color);
- (e) the signal “fdi”, which indicates which fault was well identified based on the rules and on the probabilistic decision system: in this case, fault F6 (ABG) and the respective instant ; the colored dots define the beginning and end of the fault identification window;
- (f) the relevant FDD times are s, and s;
- (g) the title of the figure also mentions the number of the processed file (0, in this case), the identified fault "ABG" and the real fault "ABG*" (marked with the symbol "*").
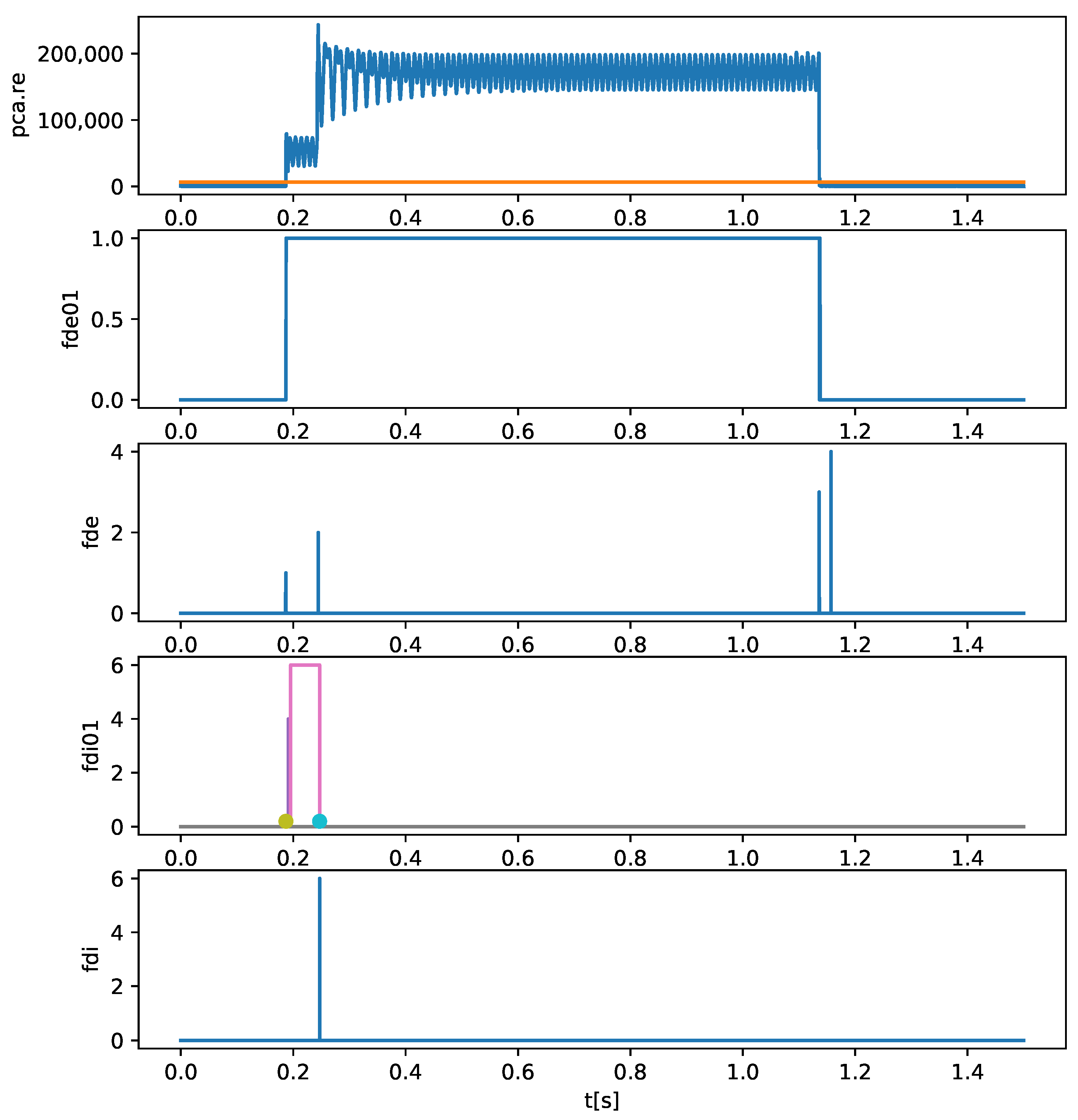
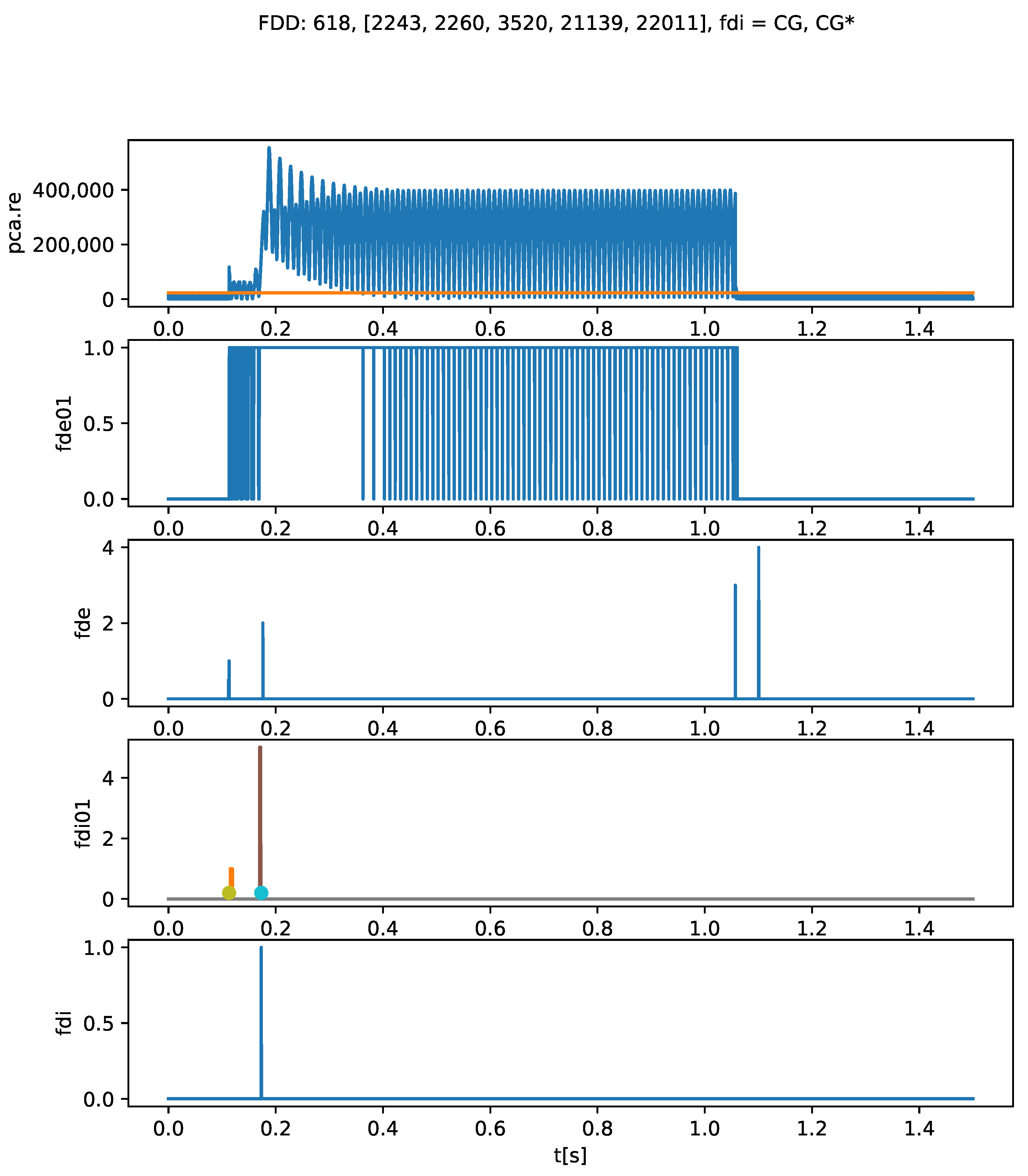
- (a) the fault detection signal “Re” (blue signal), and the respective adaptive threshold (orange signal);
- (b) the signal “fde01”, which corresponds to the moments in which the fault is active;
- (c) the “fde” signal, that records the various time instants, ; In the figure title, the vector associated with the fault times , in samples is presented.
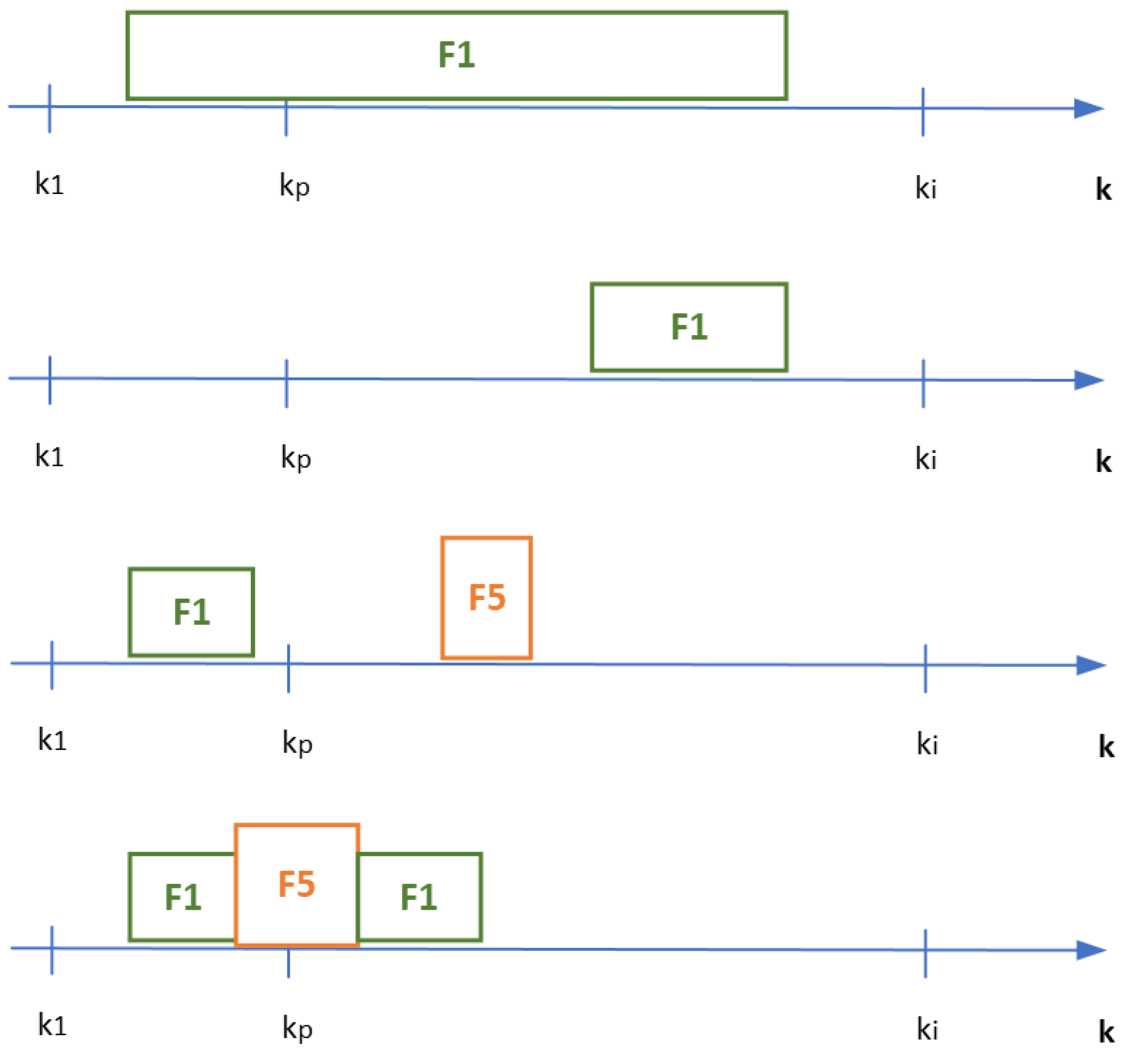
- (d) the “fdi01” signal, that allows evaluation of, in the identification window, the short-circuit faults identified; in this case, two faults were identified: first, the correct fault F1 (CG) at the beginning of the identification window (in orange color); and second, the fault F5 (ACG) at the end of the identification window (in brown color);
- (e) the signal “fdi”, which indicates which fault was well identified based on the rules and on the probabilistic decision system: in this case fault F1 (CG) and the respective instant ; the colored dots define the beginning and end of the fault identification window;
- (f) the relevant FDD times are s, and s;
- (g) the title of the figure also mentions the number of the processed file (618, in this case), the identified fault "CG" and the real fault "CG*" (marked with the symbol "*").
4.5. Main Results and Discussion
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ACD | Actuation delay of circuit breaker, |
| AI | Artificial intelligence |
| CB | Circuit breaker |
| CBC | Circuit breaker closing, |
| CBO | Circuit breaker opening, |
| DFT | Discrete Fourier transform |
| DHT | Discrete Hilbert transform |
| EWT | Empirical wavelet transform |
| FAI | Fault identification, |
| FAR | Fault recovery, |
| FAS | Fault start, |
| FDD | Fault detection and diagnosis |
| FDE | Fault detection, |
| HIF | High-impedance faults |
| ML | Machine learning |
| PCA | Principal component analysis |
| RET | Reconnection time of circuit breaker, |
| SNR | Signal-to-noise ratio |
| SVD | Singular value decomposition |
| SVM | Support vector machine |
References
- Kiessling, F.; Nefzger, P.; Nolasco, J.; Kaintzyk, U. Overhead Power Lines: Planning, Design, Construction; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Conejo, A.; Baringo, L. Power System Operations; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Kothari, D.; Nagrath, I. Modern Power System Analysis; Tata McGraw-Hill: New Delhi, India, 2011. [Google Scholar]
- Das, J. Short-Circuits in AC and DC Systems: ANSI, IEEE, and IEC Standards (Power Systems Handbook); CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Flurscheim, C. Power Circuit Breaker Theory and Design; IEE Power Engineering Series 1; Peter Peregrinus Ltd.: London, UK, 1982. [Google Scholar]
- Ciufo, J.; Cooperberg, A. Power System Protection—Fundamentals and Applications; Wiley: Hoboken, NJ, USA; IEEE Press: Piscataway, NJ, USA, 2021. [Google Scholar]
- Anderson, P.; Henville, C.; Rifaat, R.; Johnson, B.; Meliopoulos, S. Power System Protection; Wiley: Hoboken, NJ, USA; IEEE Press: Piscataway, NJ, USA, 2021. [Google Scholar]
- Papailiou, K. (Ed.) Springer Handbook of Power Systems; Springer: Gateway East, Singapore, 2021. [Google Scholar]
- Abood, S.; Fuller, J. Power System Protection and Relaying—Computer-Aided Design Using SCADA Technology; CRC Press: Boca Raton, FL, USA, 2023. [Google Scholar]
- Brito Palma, L. Fault Detection, Diagnosis and Fault Tolerance Approaches in Dynamic Systems based on Black-Box Models. Ph.D. Thesis, NOVA University Lisbon, Lisbon, Portugal, 2007. Available online: https://run.unl.pt/handle/10362/66049 (accessed on 8 February 2024).
- Blanke, M.; Kinnaert, M.; Lunze, J.; Staroswiecki, M. Diagnosis and Fault-Tolerant Control; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Ding, S. Advanced Methods for Fault Diagnosis and Fault-Tolerant Control; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Bindi, M.; Piccirilli, M.; Luchetta, A.; Grasso, F. A Comprehensive Review of Fault Diagnosis and Prognosis Techniques in High Voltage and Medium Voltage Electrical Power Lines. Energies 2023, 16, 7317. [Google Scholar] [CrossRef]
- Raza, A.; Benrabah, A.; Alquthami, T.; Akmal, M. A Review of Fault Diagnosing Methods in Power Transmission Systems. Appl. Sci. 2020, 10, 1312. [Google Scholar] [CrossRef]
- Furse, C.; Kafal, M.; Razzaghi, R.; Shin, Y. Fault Diagnosis for Electrical Systems and Power Networks: A Review. IEEE Sens. J. 2021, 21, 888–906. [Google Scholar] [CrossRef]
- Nandhini, K.; Prajith, C. Review on Fault Detection and Classification in Transmission Line using Machine Learning Methods. In Proceedings of the 5th International Conference on Control, Communication and Computing (ICCC), Kerala, India, 19–21 May 2023. [Google Scholar]
- Park, Y.; Fan, S.; Hsu, C. A Review on Fault Detection and Process Diagnostics in Industrial Processes. Processes 2020, 8, 1123. [Google Scholar] [CrossRef]
- Rezapour, H.; Jamali, S.; Bahmanyar, A. Review on Artificial Intelligence-Based Fault Location Methods in Power Distribution Networks. Energies 2023, 16, 4636. [Google Scholar] [CrossRef]
- Shakiba, F.; Azizi, S.; Zhou, M.; Abusorrah, A. Application of Machine Learning Methods in Fault Detection and Classification of Power Transmission Lines: A Survey. Artif. Intell. Rev. 2023, 56, 5799–5836. [Google Scholar] [CrossRef]
- Isermann, R.; Ballé, P. Trends in the Application of Model-Based Fault Detection and Diagnosis of Technical Processes. Control Eng. Pract. 1997, 5, 709–719. [Google Scholar] [CrossRef]
- Isermann, R. Fault Diagnosis Systems; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Fleckenstein, J. Three-Phase Electrical Power; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Grigsby, L. Electric Power Generation, Transmission, and Distribution; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Chattopadhyay, S.; Das, A. Overhead Electric Power Lines: Theory and Practice; The Institution of Engineering and Technology (IET): Stevenage, UK, 2021. [Google Scholar]
- Wang, X.; Hu, H.; Liang, Z.; Guo, L.; Gao, J.; Kheshti, M.; Liu, W. Single Phase to Ground Fault Location Method of Overhead Line based on Magnetic Field Detection and Multi-Criteria Fusion. Int. J. Electr. Power Energy Syst. 2023, 145, 108699. [Google Scholar] [CrossRef]
- Gonen, T. Modern Power System Analysis; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Ibrahim, M. Disturbance Analysis for Power Systems; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Saha, M.; Izykowski, J.; Rosolowski, E. Fault Location on Power Networks; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Dashtdar, M.; Hussain, A.; Al Garni, H.Z.; Mas’ud, A.A.; Haider, W.; AboRas, K.M.; Kotb, H. Fault Location in Distribution Network by Solving the Optimization Problem Based on Power System Status Estimation Using the PMU. Machines 2023, 11, 109. [Google Scholar] [CrossRef]
- Haydaroglu, C.; Gumus, B. Fault Detection in Distribution Network with the Cauchy-M Estimate—RVFLN Method. Energies 2023, 16, 252. [Google Scholar] [CrossRef]
- Short, T. Electric Power Distribution Equipment and Systems; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Das, J. Power Systems Protective Relaying (Power Systems Handbook); CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Gertler, J. Fault Detection and Diagnosis in Engineering Systems; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Chiang, L.; Russell, E.; Braatz, R. Fault Detection and Diagnosis in Industrial Systems; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Khan, A.; Ullah, Q.; Sarwar, M.; Gul, S.; Iqbal, N. Transmission Line Fault Detection and Identification in an Interconnected Power Network using Phasor Measurement Units. IFAC-PapersOnLine 2018, 51, 1356–1363. [Google Scholar] [CrossRef]
- Wilson, A.; Reising, D.; Hay, R.; Johnson, R.; Karrar, A.; Loveless, T. Automated Identification of Electrical Disturbance Waveforms Within an Operational Smart Power Grid. IEEE Trans. Smart Grid 2020, 11, 4380–4389. [Google Scholar] [CrossRef]
- Shi, S.; Zhu, B.; Mirsaeidi, S.; Dong, X. Fault Classification for Transmission Lines Based on Group Sparse Representation. IEEE Trans. Smart Grid 2019, 10, 4673–4682. [Google Scholar] [CrossRef]
- Kaffashbashi, A.; Damchi, Y. Statistical Approach for Detection of Fault and Stable and Unstable Power Swings based on Signal Energy. Int. J. Electr. Power Energy Syst. 2023, 145, 108638. [Google Scholar] [CrossRef]
- Alsafasfeh, Q.; Abdel-Qader, I.; Harb, A. Symmetrical Pattern and PCA based Framework for Fault Detection and Classification in Power Systems. In Proceedings of the IEEE International Conference on Electro Information Technology, Normal, IL, USA, 20–22 May 2010. [Google Scholar]
- Petrovic, I.; Nikolovski, S.; Glavas, H.; Relic, F. Power System Fault Detection Automation Based on Fuzzy Logic. In Proceedings of the International Conference on Smart Systems and Technologies (SST), Osijek, Croatia, 14–16 October 2020. [Google Scholar]
- Zhang, Y.; He, G.; Li, G. Automatic Electrical System Fault Diagnosis Using a Fuzzy Inference System and Wavelet Transform. Processes 2023, 11, 2231. [Google Scholar] [CrossRef]
- Santos, A.; Faria, L.; Lopes, M.; Lotufo, A.; Minussi, C. Efficient Methodology for Detection and Classification of Short-Circuit Faults in Distribution Systems with Distributed Generation. Sensors 2022, 22, 9418. [Google Scholar] [CrossRef] [PubMed]
- Goni, O.; Nahiduzzaman; Anower, S.; Rahman, M.; Islam, R.; Ahsan, M.; Haider, J.; Shahjalal, M. Fast and Accurate Fault Detection and Classification in Transmission Lines using Extreme Learning Machine. Elsevier Prime-Adv. Electr. Eng. Electron. Energy 2023, 3, 100107. [Google Scholar] [CrossRef]
- Silva, F.; Amaro, N. Circuit Breaker Condition Based Maintenance Using Advanced Fault Detection and Analysis on COMTRADE Event Data. In CONTROLO 2022. Lecture Notes in Electrical Engineering, Volume 930; Brito Palma, L., Neves-Silva, R., Gomes, L., Eds.; Springer: Cham, Switzerland, 2022; pp. 542–553. [Google Scholar]
- Gutierrez-Rojas, D.; Christou, I.; Dantas, D.; Narayanan, A.; Nardelli, P.; Yang, Y. Performance Evaluation of Machine Learning for Fault Selection in Power Transmission Lines. Knowl. Inf. Syst. 2022, 64, 859–883. [Google Scholar] [CrossRef]
- Atela, P. Automatic Oscillography Analysis Associated with Short Circuits in Electrical Power Transmission Lines (in Portuguese). Master’s Thesis, NOVA University, Lisbon, Portugal, 2022. Available online: https://run.unl.pt/handle/10362/155373 (accessed on 8 February 2024).
- Khan, M.A.; Asad, B.; Vaimann, T.; Kallaste, A.; Pomarnacki, R.; Hyunh, V.K. Improved Fault Classification and Localization in Power Transmission Networks Using VAE-Generated Synthetic Data and Machine Learning Algorithms. Machines 2023, 11, 963. [Google Scholar] [CrossRef]
- Huang, N.; Qi, J.; Li, F.; Yang, D.; Cai, G.; Huang, G.; Zheng, J.; Li, Z. Short-Circuit Fault Detection and Classification Using Empirical Wavelet Transform and Local Energy for Electric Transmission Line. Sensors 2017, 17, 2133. [Google Scholar] [CrossRef]
- Chen, K.; Hu, J.; Zhang, Y.; Yu, Z.; He, J. Fault Location in Power Distribution Systems via Deep Graph Convolutional Networks. IEEE J. Sel. Areas Commun. 2020, 38, 119–131. [Google Scholar] [CrossRef]
- Li, M.; Zhang, H.; Ji, T.; Wu, Q. Fault Identification in Power Network Based on Deep Reinforcement Learning. CSEE J. Power Energy Syst. 2022, 8, 721–731. [Google Scholar] [CrossRef]
- Jolliffe, I. Principal Component Analysis; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Jackson, J. A User’s Guide To Principal Components; Wiley: Hoboken, NJ, USA, 2003. [Google Scholar]
- Kong, X.; Hu, C.; Duan, Z. Principal Component Analysis Networks and Algorithms; Springer: Gateway East, Singapore, 2017. [Google Scholar]
- Naik, G. Advances in Principal Component Analysis: Research and Development; Springer: Gateway East, Singapore, 2018. [Google Scholar]
- Brito Palma, L.; Vieira Coito, F.; Sousa Gil, P.; Neves-Silva, R. Process Control based on PCA Models. In Proceedings of the 2010 IEEE 15th Conference on Emerging Technologies and Factory Automation (ETFA 2010), University of the Basque Country, Bilbao, Spain, 13–16 September 2010. [Google Scholar]
- Brito Palma, L.; Vieira Coito, F.; Sousa Gil, P. PI Controller for SISO Linear Systems based on Neural Linear PCA. In Proceedings of the 2014 European Control Conference (ECC), Strasbourg, France, 24–27 June 2014. [Google Scholar]
- Brito Palma, L.; Vieira Coito, F.; Sousa Gil, P. Neural PCA Controller Based on Multi-Models. In Proceedings of the 11th Portuguese Conference on Automatic Control (Controlo 2014), University of Porto, Porto, Portugal, 21–23 July 2014. [Google Scholar]
- Jacobsen, E.; Lyons, R. The Sliding DFT. IEEE Signal Process. Mag. 2003, 20, 74–80. [Google Scholar] [CrossRef]
- King, F. Hilbert Transforms—Vols. 1 & 2; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Halvorsen, H. Python for Science and Engineering. 2019. Available online: https://www.halvorsen.blog/documents/programming/python/ (accessed on 23 January 2024).
- McKinney, W. Python for Data Analysis—Data Wrangling with Pandas, NumPy, and Jupyter; O’Reilly Media, Inc.: Sevastopol, CA, USA, 2022. [Google Scholar]
- Wu, Y.; Liu, X.; Wang, Y.; Li, Q.; Guo, Z.; Jiang, Y. Improved deep PCA and Kullback–Leibler divergence based incipient fault detection and isolation of high-speed railway traction devices. Sustain. Energy Technol. Assess. 2023, 57, 103208. [Google Scholar] [CrossRef]



| Symbol | Meaning |
|---|---|
| t | Continuous time |
| k | Discrete time |
| Voltage signals | |
| , , | Voltage signals in phases A, B, C |
| Voltage signal in grounded (earthed) neutral wire | |
| Current signals | |
| , , | Current signals in phases A, B, C |
| Current signal in grounded (earthed) neutral wire | |
| Amplitude of a signal | |
| T | Period of a signal |
| f | Frequency of a signal |
| w | Angular frequency of a signal: w = 2 π / T = 2 π f |
| Phase of a signal | |
| Threshold for the signal | |
| Simulation time in HyperSim: s | |
| Sampling time in HyperSim: 50 µs | |
| Number of CSV files processed for each experiment: 619 | |
| n | Number of samples in each signal per experiment in HyperSim: 30,001 |
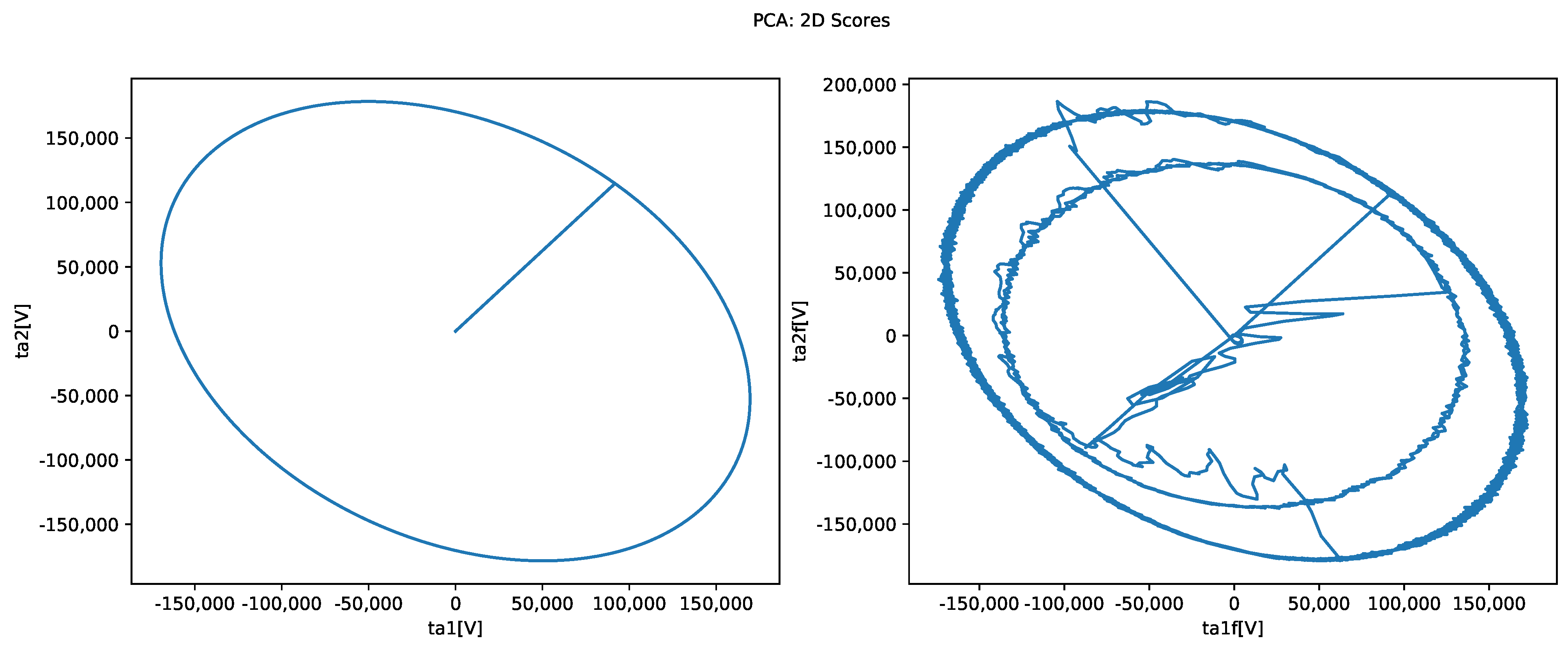
| a | Number of relevant principal components in the PCA model: |
| && | Logical AND |
| || | Logical OR |
| max() | Maximum function |
| min() | Minimum function |
| Approach | Diagnostics Technique | Reference | Year |
|---|---|---|---|
| PCA, DFT, and DHT | Rule-based | This article | 2024 |
| Data-based RVFLNs neural method | ML/AI | [30] | 2023 |
| Machine learning and variational autoencoders | ML/AI | [47] | 2023 |
| Wavelets and fuzzy decision system | Rule-based | [42] | 2022 |
| PELT and wavelet transform | ML/AI | [44] | 2022 |
| Machine learning with neural networks | ML/AI | [45] | 2022 |
| Wavelet transform and neural networks | ML/AI | [46] | 2022 |
| Deep reinforcement learning | ML/AI | [50] | 2022 |
| Power quality events | ML/AI | [36] | 2020 |
| Deep graph convolutional networks | ML/AI | [49] | 2020 |
| Group sparse representation | Rule-based | [37] | 2019 |
| Wavelets, local energy, and SVM | ML/AI | [48] | 2017 |
| [dB] | [dB] | || [A] |
|---|---|---|
| 85 | 80 | <1 |
| 55 | 50 | <1 |
| 35 | 30 | <1 |
| 30 | 25 | <1 |
| 25 | 20 | <1 |
| Fault | ID | Type | |||||||
|---|---|---|---|---|---|---|---|---|---|
| F7 | 3P | Three-Phase to Ground | +1 | +1 | +1 | +1 | −1 | −1 | −1 |
| F6 | ABG | Two-Phase to Ground | +1 | +1 | +1 | 0 | −1 | −1 | 0 |
| F5 | ACG | Two-Phase to Ground | +1 | +1 | 0 | +1 | −1 | 0 | −1 |
| F4 | AG | Phase–Ground | +1 | +1 | 0 | 0 | −1 | 0 | 0 |
| F3 | BCG | Two-Phase to Ground | +1 | 0 | +1 | +1 | 0 | −1 | −1 |
| F2 | BG | Phase–Ground | +1 | 0 | +1 | 0 | 0 | −1 | 0 |
| F1 | CG | Phase–Ground | +1 | 0 | 0 | +1 | 0 | 0 | −1 |
| F0 | F0 | No Fault | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| a | Choice | |
|---|---|---|
| 1 | 51.3249% | |
| 2 | 99.9989% | |
| 3 | 99.9999% | |
| 4 | 100% |
| Fault | ID | Type | |||||||
|---|---|---|---|---|---|---|---|---|---|
| F5 | ACG | Two-Phase to Ground | +1 | +1 | 0 | +1 | −1 | 0 | −1 |
| F1 | CG | Phase–Ground | +1 | 0 | 0 | +1 | 0 | 0 | −1 |
| F0 | F0 | No Fault | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Case | Fault | ||
|---|---|---|---|
| C1 | F1 | F1 | F1 |
| C2 | F0 | F1 | F1 |
| C3 | F1 | F5 | F1 |
| C4 | F1 | F1 | F1 |
| Task | Thresholds | Expression | Value | SNR Dependence |
|---|---|---|---|---|
| Fault Detection | = 1.2 | Equation (21) | ||
| Fault Identification | = 1.2 | Equation (24) | ||
| Fault Identification | = 0.95 | Equation (25) | ||
| Circuit Breaker Opening | 1.0 A | |||
| Circuit Breaker Closing | 1.0 A | |||
| Fault Recovery | 15 Hz |
| Parameter | Minimum Value | Maximum Value | Variation |
|---|---|---|---|
| Start of fault | 0.1 s | 0.3 s | 0.01 s |
| Circuit breaker opening | Start of fault + 0.04 s | Start of fault + 0.06 s | 0.001 s |
| End of fault | Circuit breaker closing − 0.06 s | Circuit breaker closing − 0.04 s | 0.001 s |
| Circuit breaker closing | Circuit breaker opening + 0.9 s | Circuit breaker opening + 0.9 s | 0 s |
| Fault location | 40% of the line length | 60% of the line length | 10% of the line length |
| Fault resistance (ohm) | 2 | 20 | 1 |
| Fault | ID | Type | File |
|---|---|---|---|
| F7 | 3P | Three-Phase to Ground | “LCGRM1_4_15_30_43.csv” |
| F6 | ABG | Two-Phase to Ground | “LCGRM1_1_11_15_54.csv” |
| F5 | ACG | Two-Phase to Ground | “LCGRM1_2_12_36_39.csv” |
| F4 | AG | Phase–Ground | “LCGRM1_5_17_16_58.csv” |
| F3 | BCG | Two-Phase to Ground | “LCGRM1_3_14_18_05.csv” |
| F2 | BG | Phase–Ground | “LCGRM1_6_18_21_34.csv” |
| F1 | CG | Phase–Ground | “LCGRM1_7_20_24_10.csv” |
| F0 | F0 | No Fault |
| Parameters/Times | Value |
|---|---|
| HyperSim simulation parameters | See Table 9 |
| Simulation time in HyperSim, | s |
| Sampling time in HyperSim, | 50 µs |
| Number of samples in each signal generated by HyperSim, n | |
| Number of CSV files processed in Python | 619 |
| CPU processing time for each CSV file | s |
| Number of Portuguese overhead power lines simulated | 12 |
| Voltages on power lines [kV] | |
| [dB] in current signals | 20, 25, 30, 50, 80 |
| [dB] in voltage signals | 25, 30, 35, 55, 85 |
| Load variations on power lines | Yes |
| Low-, medium-, and high-impedance short-circuit faults | Yes |
| Fault start estimation, | || > 1 A |
| Fault detection parameters | = 1.2 |
| Fault identification parameters | = 1.2, = 0.95 |
| Fault identification window size | 60 or 80 ms |
| Fault | ID | Sim | FDD | FDD-Sim |
|---|---|---|---|---|
| F7 | 3P | 90 | 90 | 0 |
| F6 | ABG | 87 | 82 | −5 |
| F5 | ACG | 89 | 83 | −6 |
| F4 | AG | 90 | 91 | +1 |
| F3 | BCG | 86 | 86 | 0 |
| F2 | BG | 87 | 90 | +3 |
| F1 | CG | 90 | 95 | +5 |
| Fx | xyz | 0 | 2 | +2 |
| 619 | 619 | 0 |
| Fault | ID | Sim | 20 dB | 25 dB | 30 dB | 50 dB | 80 dB |
|---|---|---|---|---|---|---|---|
| F7 | 3P | 90 | 90 | 90 | 90 | 90 | 90 |
| F6 | ABG | 87 | 84 | 83 | 82 | 82 | 82 |
| F5 | ACG | 89 | 86 | 87 | 85 | 84 | 83 |
| F4 | AG | 90 | 87 | 89 | 92 | 91 | 91 |
| F3 | BCG | 86 | 84 | 84 | 84 | 86 | 86 |
| F2 | BG | 87 | 89 | 91 | 91 | 90 | 90 |
| F1 | CG | 90 | 97 | 94 | 95 | 96 | 95 |
| Fx | xyz | 0 | 2 | 1 | 0 | 0 | 2 |
| 619 | 619 | 619 | 619 | 619 | 619 |
| Task | ID | 20 dB | 25 dB | 30 dB | 50 dB | 80 dB |
|---|---|---|---|---|---|---|
| Fault Detection [%] | FDE | 100 | 100 | 100 | 100 | 100 |
| Fault Identification [%] | FDI | 97.09 | 97.90 | 98.22 | 98.06 | 97.58 |
| Times and Delays [ms] | 20 dB | 25 dB | 30 dB | 50 dB | 80 dB |
|---|---|---|---|---|---|
| Fault Detection Delay: | 4.83 | 1.64 | 0.91 | 0.80 | 0.81 |
| Fault Identification Delay: | 60.19 | 60.19 | 60.26 | 60.77 | 61.00 |
| CB Actuation Delay: | 58.94 | 59.10 | 59.22 | 59.41 | 59.81 |
| CB Reconnection Time: | 929.62 | 929.62 | 929.62 | 929.62 | 929.62 |
| Approach | Reference | Dataset/SW | Noise | Accuracy [%] |
|---|---|---|---|---|
| Rule-Based: PCA, DFT and DHT | This Article | REN: HyperSim | Yes | 98.22 |
| Deep reinforcement learning | [50] | IEEE 14-bus | Yes | 100.00 |
| Wavelets, local energy and SVM | [48] | PSCAD | Yes | 99.77 |
| Deep graph convolutional networks | [49] | IEEE 123-bus | Yes | 99.38 |
| Group sparse representation | [37] | PSCAD | Yes | 99.09 |
| Machine learning and variational autoencoders | [47] | Aspen | No | 99.00 |
| Wavelet transform and neural networks | [46] | REN: HyperSim | No | 98.50 |
| Machine learning with neural networks | [45] | Matlab/Simulink | Yes | 98.47 |
| Wavelets and fuzzy decision system | [42] | IEEE 34-bus | No | 94.90 |
| Power quality events | [36] | Real Smart Grid | No | 92.90 |
| PELT and wavelet transform | [44] | REN: Real Data | No | 91.56 |
| Data-based RVFLNs neural method | [30] | RTDS-RTS | Yes | 89.94 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brito Palma, L. Hybrid Approach for Detection and Diagnosis of Short-Circuit Faults in Power Transmission Lines. Energies 2024, 17, 2169. https://doi.org/10.3390/en17092169
Brito Palma L. Hybrid Approach for Detection and Diagnosis of Short-Circuit Faults in Power Transmission Lines. Energies. 2024; 17(9):2169. https://doi.org/10.3390/en17092169
Chicago/Turabian StyleBrito Palma, Luís. 2024. "Hybrid Approach for Detection and Diagnosis of Short-Circuit Faults in Power Transmission Lines" Energies 17, no. 9: 2169. https://doi.org/10.3390/en17092169
APA StyleBrito Palma, L. (2024). Hybrid Approach for Detection and Diagnosis of Short-Circuit Faults in Power Transmission Lines. Energies, 17(9), 2169. https://doi.org/10.3390/en17092169






