Design and Implementation of Robust H∞ Control for Improving Disturbance Rejection of Grid-Connected Three-Phase PWM Rectifiers
Abstract
1. Introduction
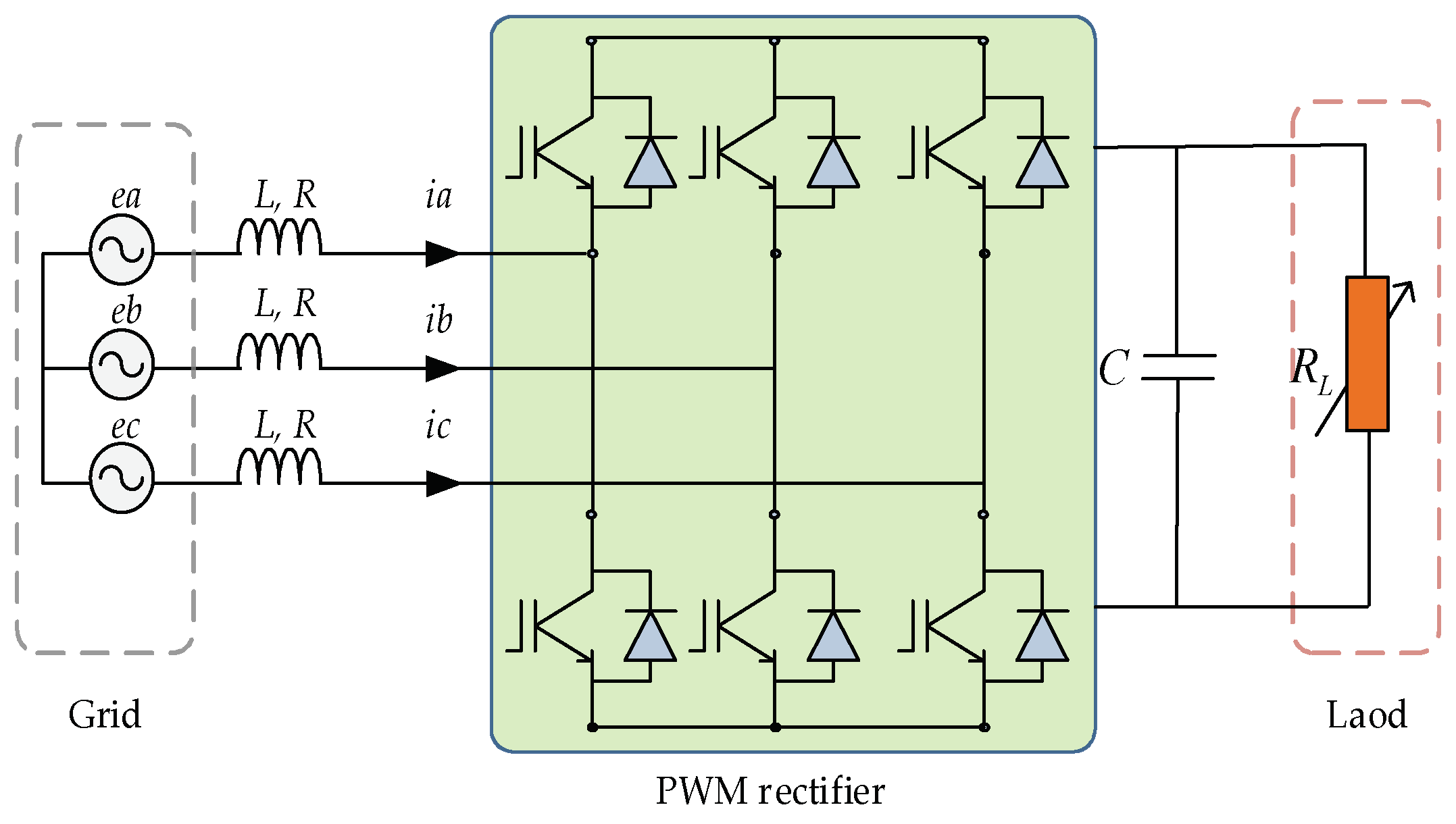
2. System Description and Modeling
3. H∞ Control Principle
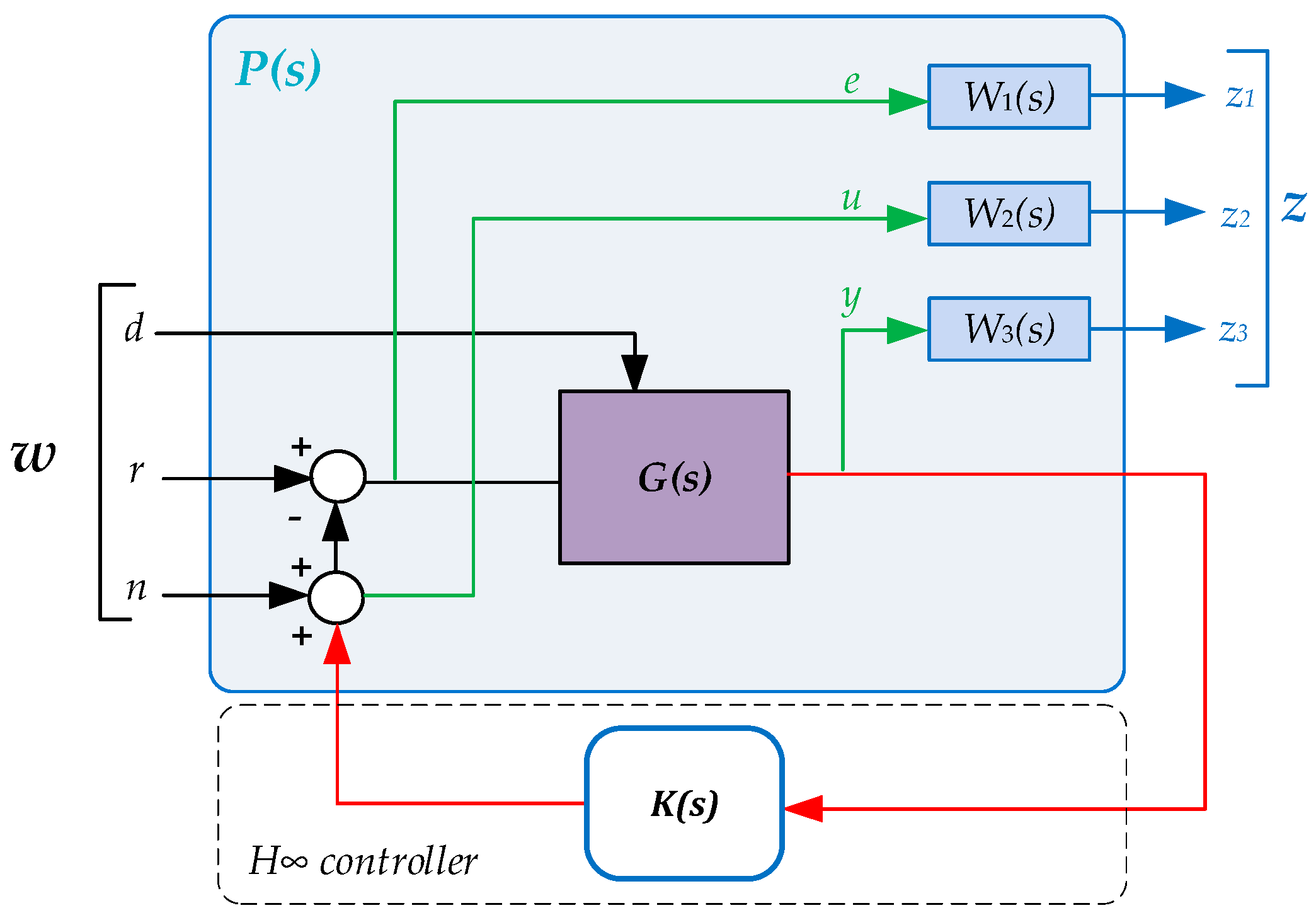
3.1. Control Problem Formulation
3.2. Mixed Sensitivity Formulation
- (, ) is stabilizable and () is detectable;
- ;
- has a full column rank for ;
- has a full row rank for .
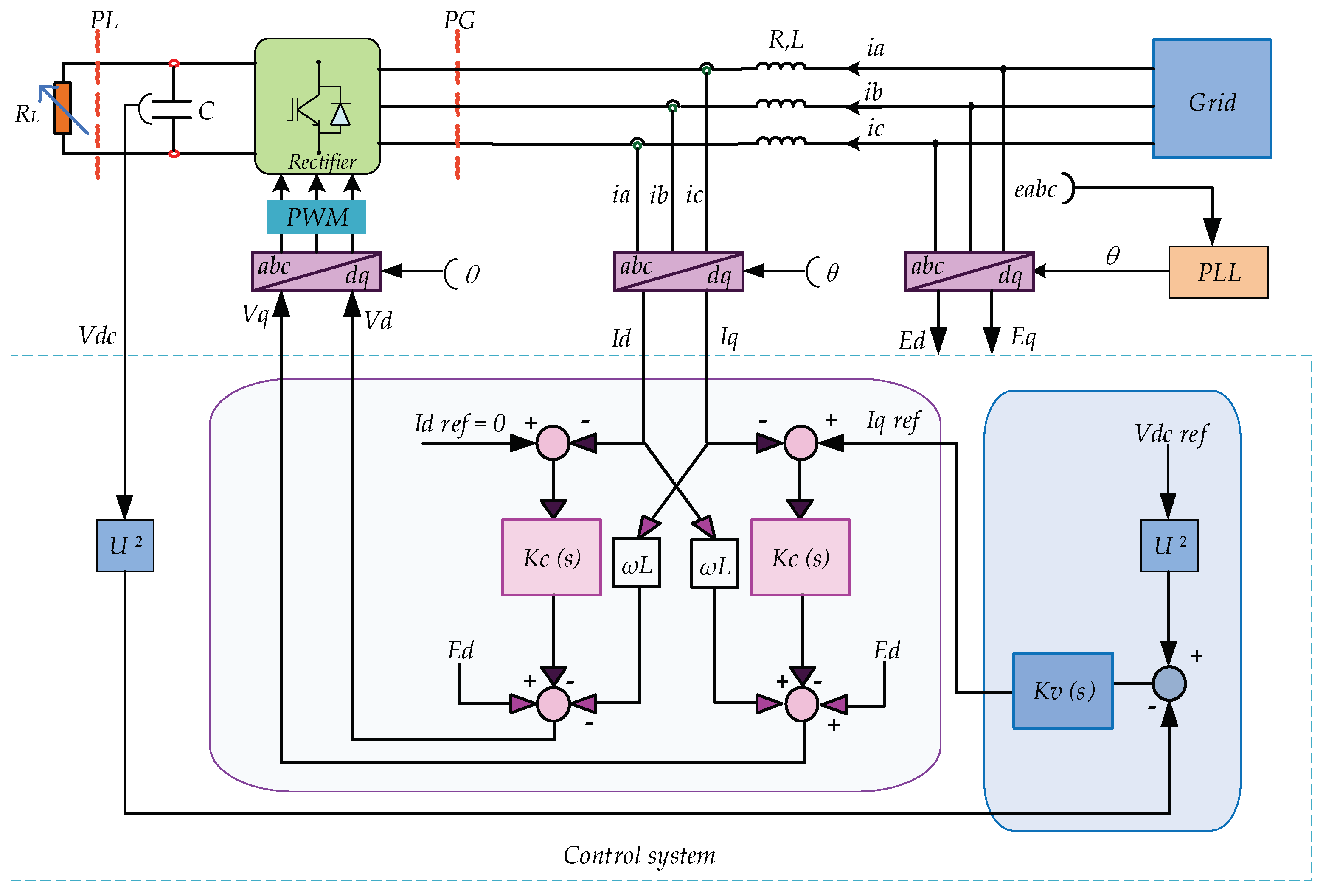
4. Proposed H∞ Cascaded Control Loops Design
4.1. State Space Realization Models of Control Loops
4.2. Weight Functions Selection for H∞ Controllers
4.3. Stability and Robustness Performance Analysis
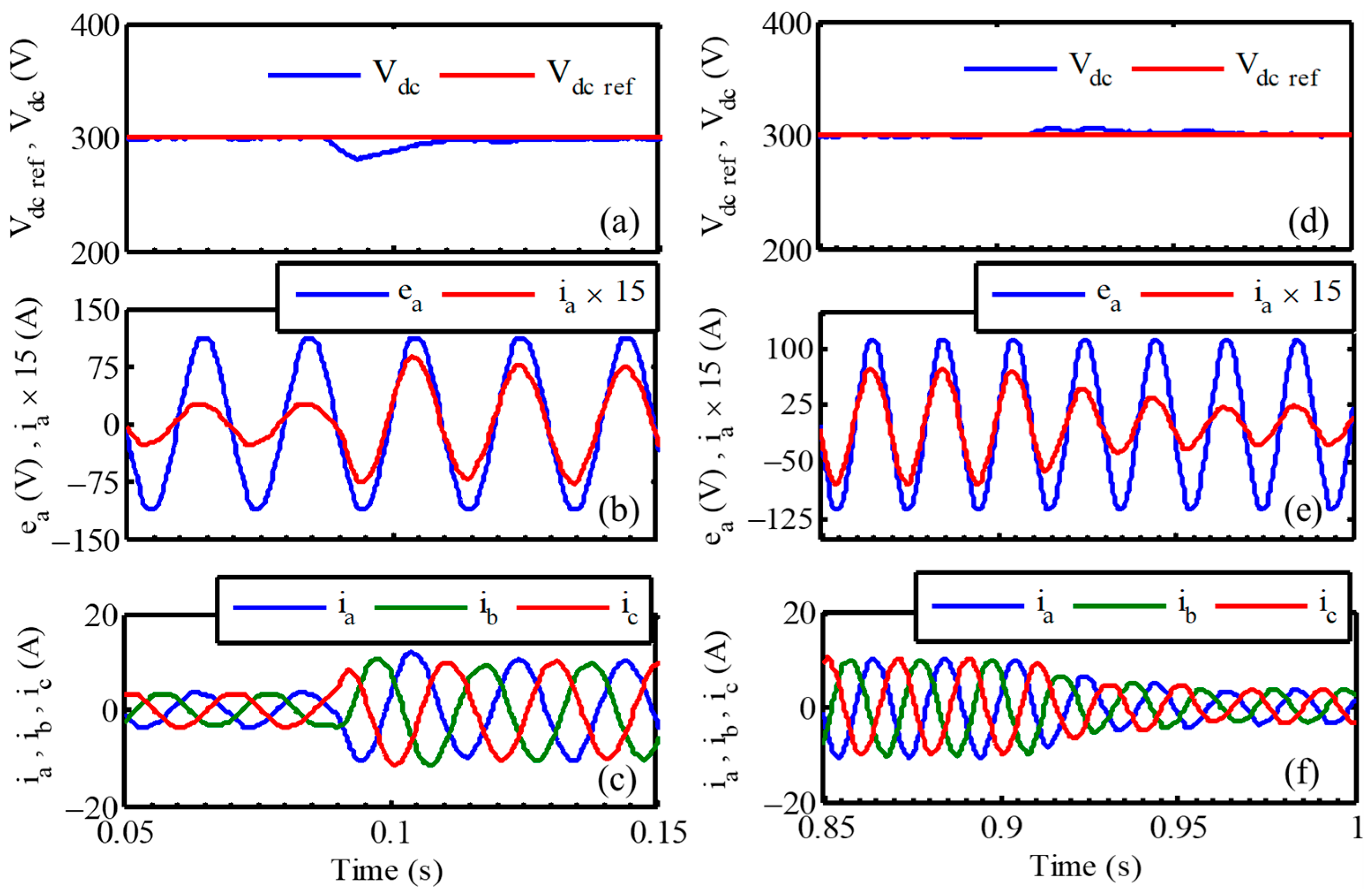
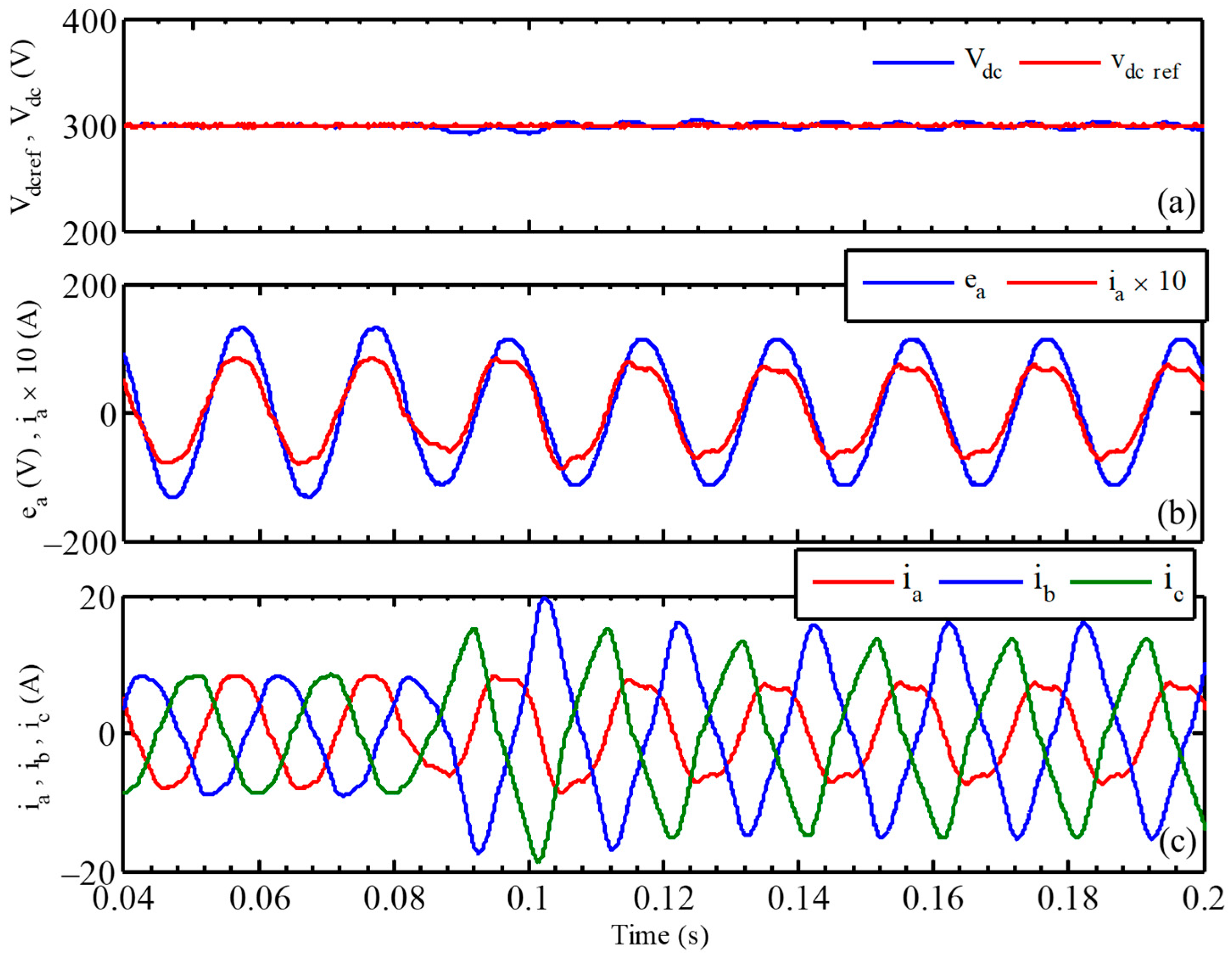
5. Experimental Results
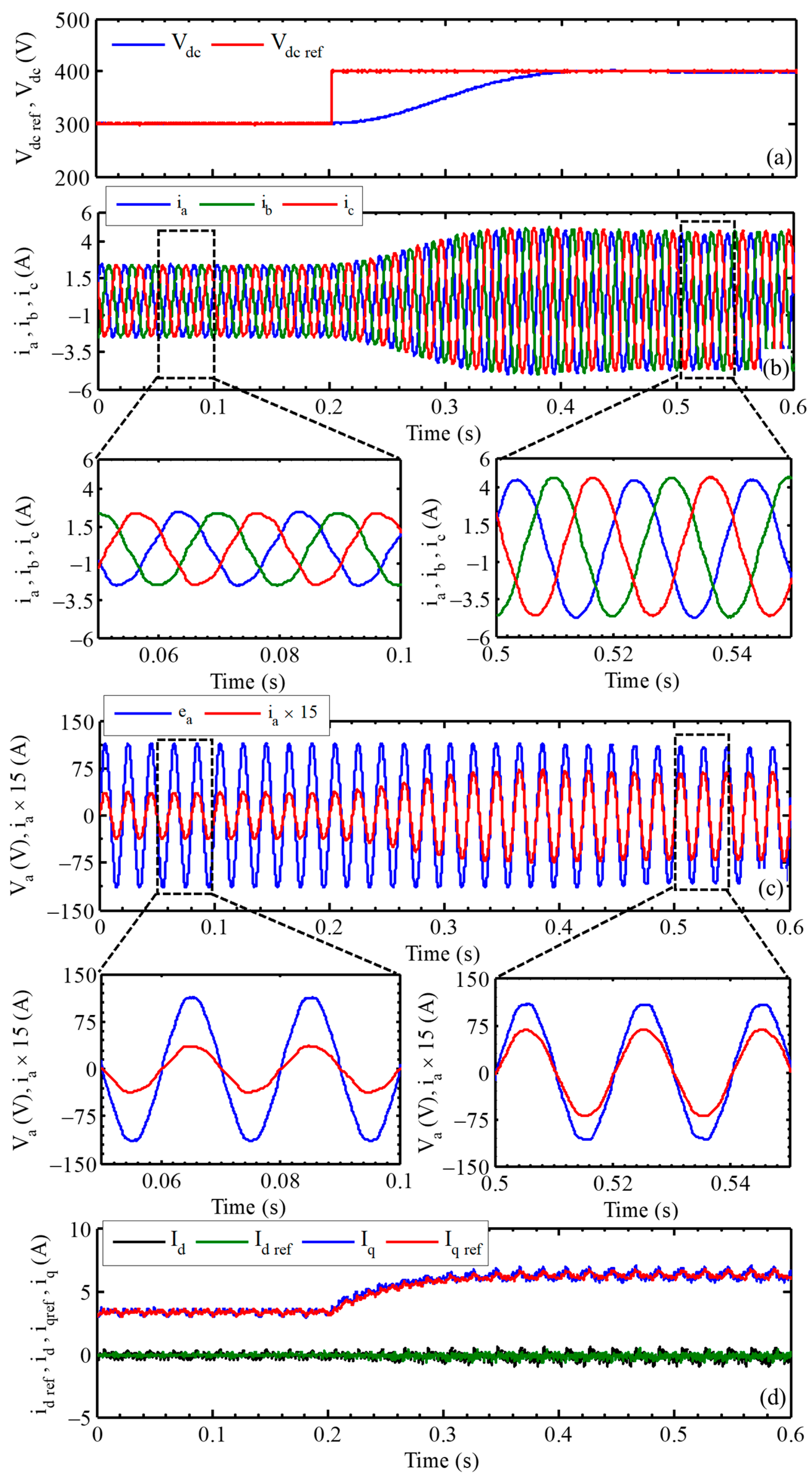
5.1. Tracking Performance
5.2. Performances under Transient Loading Conditions
5.3. Performance under Unbalanced Grid Voltage
5.4. Control Performance Comparison
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ryndzionek, R.; Sienkiewicz, Ł. Evolution of the HVDC Link Connecting Offshore Wind Farms to Onshore Power Systems. Energies 2020, 13, 1914. [Google Scholar] [CrossRef]
- Mesbah, K.; Rahoui, A.; Boukais, B. Neural Network Quadrature Signal Generator-Based Virtual Flux Estimation for Predictive Control of PWM Converters. IEEE Trans. Ind. Electron. 2024, 71, 4785–4794. [Google Scholar] [CrossRef]
- Cittanti, D.; Gregorio, M.; Bossotto, E.; Mandrile, F.; Bojoi, R. Three-Level Unidirectional Rectifiers under Non-Unity Power Factor Operation and Unbalanced Split DC-Link Loading: Analytical and Experimental Assessment. Energies 2021, 14, 5280. [Google Scholar] [CrossRef]
- Rahoui, A.; Mesbah, K.; Boukais, B.; Otmane-Cherif, T. Frequency-Adaptive Neural Network Based Virtual Flux Estimation for Sensorless Control of PWM Converters under Unbalanced Conditions. In Proceedings of the 2020 International Conference on Electrical Engineering (ICEE), Istanbul, Turkey, 25–27 September 2020; pp. 1–6. [Google Scholar]
- Kakkar, S.; Maity, T.; Ahuja, R.K.; Walde, P.; Saket, R.K.; Khan, B.; Padmanaban, S. Design and Control of Grid-Connected PWM Rectifiers by Optimizing Fractional Order PI Controller Using Water Cycle Algorithm. IEEE Access 2021, 9, 125941–125954. [Google Scholar] [CrossRef]
- Song, T.; Wang, P.; Zhang, Y.; Gao, F.; Tang, Y.; Pholboon, S. Suppression Method of Current Harmonic for Three-Phase PWM Rectifier in EV Charging System. IEEE Trans. Veh. Technol. 2020, 69, 9634–9642. [Google Scholar] [CrossRef]
- Wang, H.; Wang, S.; Ding, H.; Shi, C.; Jia, D.; Chen, C.; Guerrero, J.M. An Novel Six-Segment Modulation Strategy for Three-Phase Isolated PFC Converter. Energies 2022, 15, 2598. [Google Scholar] [CrossRef]
- Saidi, Y.; Mezouar, A.; Miloud, Y.; Benmahdjoub, M.A. A Robust Control Strategy for Three Phase Voltage t Source PWM Rectifier Connected to a PMSG Wind Energy Conversion System. In Proceedings of the 2018 International Conference on Electrical Sciences and Technologies in Maghreb (CISTEM), Algiers, Algeria, 29–31 October 2018; pp. 1–6. [Google Scholar]
- Song, Y.; Jeon, T.; Paek, I.; Dugarjav, B. Design and Validation of Pitch H-Infinity Controller for a Large Wind Turbine. Energies 2022, 15, 8763. [Google Scholar] [CrossRef]
- Djerioui, A.; Houari, A.; Ait-Ahmed, M.; Benkhoris, M.-F.; Chouder, A.; Machmoum, M. Grey Wolf Based Control for Speed Ripple Reduction at Low Speed Operation of PMSM Drives. ISA Trans. 2018, 74, 111–119. [Google Scholar] [CrossRef] [PubMed]
- Viera Díaz, R.I.; Nuñez, C.; Visairo Cruz, N.; Segundo Ramírez, J. A Polynomial Synthesis Approach to Design and Control an LCL-Filter-Based PWM Rectifier with Extended Functions Validated by SIL Simulations. Energies 2023, 16, 7382. [Google Scholar] [CrossRef]
- Suul, J.A.; D’Arco, S.; Rodríguez, P.; Molinas, M. Impedance-compensated Grid Synchronisation for Extending the Stability Range of Weak Grids with Voltage Source Converters. IET Gener. Transm. Distrib. 2016, 10, 1315–1326. [Google Scholar] [CrossRef]
- Wang, J.-H.; Li, H.-D.; Wang, L.-M. Direct Power Control System of Three Phase Boost Type PWM Rectifiers. Proc. CSEE 2006, 26, 54–60. [Google Scholar]
- Yang, D.; Lu, Z.; Hang, N.; Li, G. Novel Quasi Direct Power Control for Three-Phase Voltage-Source PWM Rectifiers with a Fixed Switching Frequency. Soc. Electr. Eng. 2011, 31, 66–73. [Google Scholar]
- Ge, J.; Zhao, Z.; Yuan, L.; Lu, T.; He, F. Direct Power Control Based on Natural Switching Surface for Three-Phase PWM Rectifiers. IEEE Trans. Power Electron. 2015, 30, 2918–2922. [Google Scholar] [CrossRef]
- Zhang, Y.; Qu, C. Direct Power Control of a Pulse Width Modulation Rectifier Using Space Vector Modulation under Unbalanced Grid Voltage. IEEE Trans. Power Electron. 2015, 30, 5892–5901. [Google Scholar] [CrossRef]
- Cho, Y.; Lee, K.-B. Virtual-Flux-Based Predictive Direct Power Control of Three-Phase PWM Rectifiers with Fast Dynamic Response. IEEE Trans. Power Electron. 2015, 31, 3348–3359. [Google Scholar] [CrossRef]
- Kwak, S.; Mun, S. Model Predictive Control Methods to Reduce Common-Mode Voltage for Three-Phase Voltage Source Inverters. IEEE Trans. Power Electron. 2015, 30, 5019–5035. [Google Scholar] [CrossRef]
- Dannehl, J.; Wessels, C.; Fuchs, F. Limitations of Voltage-Oriented PI Current Control of Grid-Connected PWM Rectifiers With Filters. IEEE Trans. Ind. Electron. 2009, 56, 380–388. [Google Scholar] [CrossRef]
- Zeng, Z.; Zheng, W.; Zhao, R.; Zhu, C.; Yuan, Q. Modeling, Modulation, and Control of the Three-Phase Four-Switch PWM Rectifier Under Balanced Voltage. IEEE Trans. Power Electron. 2015, 31, 4892–4905. [Google Scholar] [CrossRef]
- Galecki, A.; Kaszewski, A.; Ufnalski, B.; Grzesiak, L. State Current Controller with Oscillatory Terms for Three-Level Grid-Connected PWM Rectifiers under Distorted Grid Voltage Conditions. In Proceedings of the 2015 17th European Conference on Power Electronics and Applications (EPE’15 ECCE-Europe), Geneva, Switzerland, 8–10 September 2015; p. 10. [Google Scholar]
- Campos-Gaona, D.; Peña-Alzola, R.; Ordonez, M. Nonminimum Phase Compensation in VSC-HVDC Systems for Fast Direct Voltage Control. IEEE Trans. Power Deliv. 2015, 30, 2535–2543. [Google Scholar] [CrossRef]
- Jamma, M.; Barara, M.; Akherraz, M.; Enache, B.A. Voltage Oriented Control of Three-Phase PWM Rectifier Using Space Vector Modulation and Input Output Feedback Linearization Theory. In Proceedings of the 2016 8th International Conference on Electronics, Computers and Artificial Intelligence (ECAI), Ploiesti, Romania, 30 June–2 July 2016; pp. 1–8. [Google Scholar]
- Akagi, H.; Watanabe, E.H.; Aredes, M. Instantaneous Power Theory and Applications to Power Conditioning; Wiley: Hoboken, NJ, USA, 2006; ISBN 978-0-470-10761-4. [Google Scholar]
- Trivedi, T.A.; Jadeja, R.; Bhatt, P. A Review on Direct Power Control for Applications to Grid Connected PWM Converters. Eng. Technol. Appl. Sci. Res. 2015, 5, 841–849. [Google Scholar] [CrossRef]
- Longyue, Y.; Jianhua, L.; Chonglin, W. Quasi-Sliding Mode Control of Active Power Filters Based on Exact Feedback Linearization. Proc. CSEE 2014, 34, 5868–5875. [Google Scholar]
- Wang, E.; Huang, S. A Novel Double Closed Loops Control of the Three-Phase Voltage-Sourced PWM Rectifier. Chin. Soc. Electr. Eng. 2012, 32, 24–30. [Google Scholar]
- Si, G.; Zhao, W.; Guo, Z.; Shi, J. A Novel Double Closed Loops Control Strategy of Three-Phase Voltage Source PWM Rectifier with Disturbances. In Proceedings of the 33rd Chinese Control Conference, Nanjing, China, 28–30 July 2014; IEEE: Piscataway, NJ, USA, 2014. [Google Scholar]
- Wang, H.; Zhu, C.; Zhang, J.; Zhu, M.; Cai, X. Improved Control for Three-Phase PWM Rectifier Based on Power-Current Model. In Proceedings of the IECON 2020 the 46th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 18–21 October 2020; pp. 3773–3778. [Google Scholar]
- Chen, J.; Yao, W.; Zhang, C.-K.; Ren, Y.; Jiang, L. Design of Robust MPPT Controller for Grid-Connected PMSG-Based Wind Turbine via Perturbation Observation Based Nonlinear Adaptive Control. Renew. Energy 2019, 134, 478–495. [Google Scholar] [CrossRef]
- Haneesh, K.M.; Raghunathan, T. Robust Control of DFIG Based Wind Energy System Using an H∞ Controller. J. Electr. Eng. Technol. 2021, 16, 1693–1707. [Google Scholar] [CrossRef]
- Azza, A.; Kherfane, H. Robust Control of Doubly Fed Induction Generator Using Fractional Order Control. Int. J. Power Electron. Drive Syst. IJPEDS 2018, 9, 1072. [Google Scholar] [CrossRef]
- Zhao, K. PWM Rectifier with Fuzzy Sliding Mode Variable Structure Control. Diangong Jishu Xuebao Trans. China Electrotech. Soc. 2006, 21, 49–53. [Google Scholar]
- Lei, T.; Tan, W.; Chen, G.; Kong, D. A Novel Robust Model Predictive Controller for Aerospace Three-Phase PWM Rectifiers. Energies 2018, 11, 2490. [Google Scholar] [CrossRef]
- Johnson, B.B.; Lundstrom, B.R.; Salapaka, S.; Salapaka, M. Optimal Structures for Voltage Controllers in Inverters; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2018. [Google Scholar]
- Yang, S.; Lei, Q.; Peng, F.Z.; Qian, Z. A Robust Control Scheme for Grid-Connected Voltage-Source Inverters. IEEE Trans. Ind. Electron. 2010, 58, 202–212. [Google Scholar] [CrossRef]
- Weiss, G.; Zhong, Q.-C.; Green, T.C.; Liang, J. H∞ Repetitive Control of DC-AC Converters in Microgrids. IEEE Trans. Power Electron. 2004, 19, 219–230. [Google Scholar] [CrossRef]
- Steenis, J.; Tsakalis, K.; Ayyanar, R. Robust Control of an Islanded Microgrid. In Proceedings of the IECON 2012—38th Annual Conference on IEEE Industrial Electronics Society, Montreal, QC, Canada, 25–28 October 2012; pp. 2447–2451. [Google Scholar]
- Steenis, J.; Breazeale, L.; Tsakalis, K.; Ayyanar, R. H∞ and Gain Scheduled H∞ Control for Islanded Microgrids. In Proceedings of the 2013 IEEE Energy Conversion Congress and Exposition, Denver, CO, USA, 15–19 September 2013; pp. 4603–4608. [Google Scholar]
- Ibrahim, M.; Ma, L.; Zhao, Y.; Liu, H.; Bo, T. Reliable Current Control for Single-phase Pulse Width Modulation Rectifiers Based on H∞ Loop Shaping Controller. IET Power Electron. 2023, 16, 2504–2514. [Google Scholar] [CrossRef]
- Koch, G.G.; Pinheiro, H.; Maccari, L.A.; Oliveira, R.C.L.F.; Ferreira, A.A.; Montagner, V.F. Robust H∞ control for rejection of voltage disturbances in grid-connected converters. In Proceedings of the 12th IEEE International Conference on Industry Applications, Curitiba, PR, Brazil, 20–23 November 2016; pp. 1–6. [Google Scholar]
- Tahami, F.; Ahmadian, H.M.; Moallem, A. Robust H∞ control design for PFC rectifiers. In Proceedings of the 7th International Conference on Power Electronics and Drive Systems, Bangkok, Thailand, 27–30 November 2007; pp. 948–952. [Google Scholar]
- Ibrahim, M.M.; Ma, L.; Zhao, Y.; Liu, H. Robust Direct Current Control of Single-Phase PWM Rectifiers Based on a Mixed H. Stud. Inform. Control 2023, 32, 81–90. [Google Scholar] [CrossRef]
- Rahoui, A.; Boukais, B.; Mesbah, K.; Otmane-Cherif, T. Neural Networks Based Frequency Locked Loop for Grid Synchronization under Unbalanced and Distorted Conditions. In Proceedings of the 2020 International Conference on Electrical Engineering (ICEE), Istanbul, Turkey, 25–27 September 2020; pp. 1–5. [Google Scholar]
- Doyle, J.; Glover, K.; Khargonekar, P.; Francis, B. State-space solutions to standard h2 and h-infinity control problems. IEEE Trans. Autom. Control 1989, 34, 831–847. [Google Scholar] [CrossRef]
- Zhao, Y.; Ma, L.; Liu, H.; Peng, L. A dual-loop model predictive power control scheme for single-phase PWM rectifiers. In Proceedings of the 42nd IEEE Chinese Control Conference (CCC), Tianjin, China, 24–26 July 2023; pp. 2670–2675. [Google Scholar]
- Pérez, J.; Cobreces, S.; Griñó, R.; Sánchez, F.J.R. H∞ current controller for input admittance shaping of VSC-based grid applications. IEEE Trans. Power Electron. 2017, 32, 3180–3191. [Google Scholar] [CrossRef]




| Loop | Weight Functions Wi(s) | |
|---|---|---|
| Inner loop | γ = 0.707038 | |
| Outer loop | γ = 0.858063 |
| Parameters Description | Value |
|---|---|
| Grid frequency | 50 Hz |
| Grid rms voltage | 80 V |
| Filter resistance R | 0.1 Ω |
| Filter inductance L | 10 mH |
| DC-link capacitor C | 1100 µF |
| Sampling time Ts | 100 µs |
| Switching frequency fw | 5 kHz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ait Ramdane, N.; Rahoui, A.; Boukais, B.; Benkhoris, M.F.; Ait-Ahmed, M.; Djerioui, A. Design and Implementation of Robust H∞ Control for Improving Disturbance Rejection of Grid-Connected Three-Phase PWM Rectifiers. Energies 2024, 17, 2166. https://doi.org/10.3390/en17092166
Ait Ramdane N, Rahoui A, Boukais B, Benkhoris MF, Ait-Ahmed M, Djerioui A. Design and Implementation of Robust H∞ Control for Improving Disturbance Rejection of Grid-Connected Three-Phase PWM Rectifiers. Energies. 2024; 17(9):2166. https://doi.org/10.3390/en17092166
Chicago/Turabian StyleAit Ramdane, Naima, Adel Rahoui, Boussad Boukais, Mohamed Fouad Benkhoris, Mourad Ait-Ahmed, and Ali Djerioui. 2024. "Design and Implementation of Robust H∞ Control for Improving Disturbance Rejection of Grid-Connected Three-Phase PWM Rectifiers" Energies 17, no. 9: 2166. https://doi.org/10.3390/en17092166
APA StyleAit Ramdane, N., Rahoui, A., Boukais, B., Benkhoris, M. F., Ait-Ahmed, M., & Djerioui, A. (2024). Design and Implementation of Robust H∞ Control for Improving Disturbance Rejection of Grid-Connected Three-Phase PWM Rectifiers. Energies, 17(9), 2166. https://doi.org/10.3390/en17092166









