Definition of Regulatory Targets for Electricity Default Rate in Brazil: Proposition of a Fuzzy Inference-Based Model
Abstract
1. Introduction
- RQ1: What are the main challenges faced by ANEEL in defining regulatory targets to limit or reduce electricity default rates for electricity distribution utilities in Brazil?
- RQ2: What are the essential premises that must be considered when developing a conceptual model to define regulatory targets to limit or reduce electricity default rates that meet the fundamental requirements of incentive-based regulation?
- RQ3: To what extent can an alternative model based on fuzzy inference methodology better assist ANEEL in defining regulatory targets for limiting or reducing electricity default rates in Brazil?
- RQ4: Is it feasible to demonstrate the applicability of the proposed model by focusing on the residential class of electricity consumption in Brazil?
2. Literature Review
2.1. Electricity Defaults
2.2. Incentive-Based Regulatory Approaches
2.3. Fuzzy Inference-Based Models
3. Research Design and Methodology
4. Proposition of a Fuzzy Inference-Based Model to Establish Regulatory Targets for Electricity Default
4.1. Phase 1: Definition and Classification of Input Variables
- Maintain the principles of incentive regulation, which can be considered a gain from the evolution of methodologies adopted by ANEEL;
- Capture the heterogeneity of the concession areas of distribution utilities;
- Provide equal treatment to all distribution utilities;
- Robust and proven effective methodology;
- Use the default rates’ database of distribution utilities to extract learning and observed patterns;
- Be easy to implement.
- Vulnerability of the concession area: Consists of variables indicating the socioeconomic conditions of each distribution utility concession area.
- Size of the distribution utility: Consists of variables associated with the size of distribution utilities, such as kilometers of the transmission line network of a given electricity distribution utility.
4.2. Phase 2: Database Preparation and Inputs for Fuzzy Inference
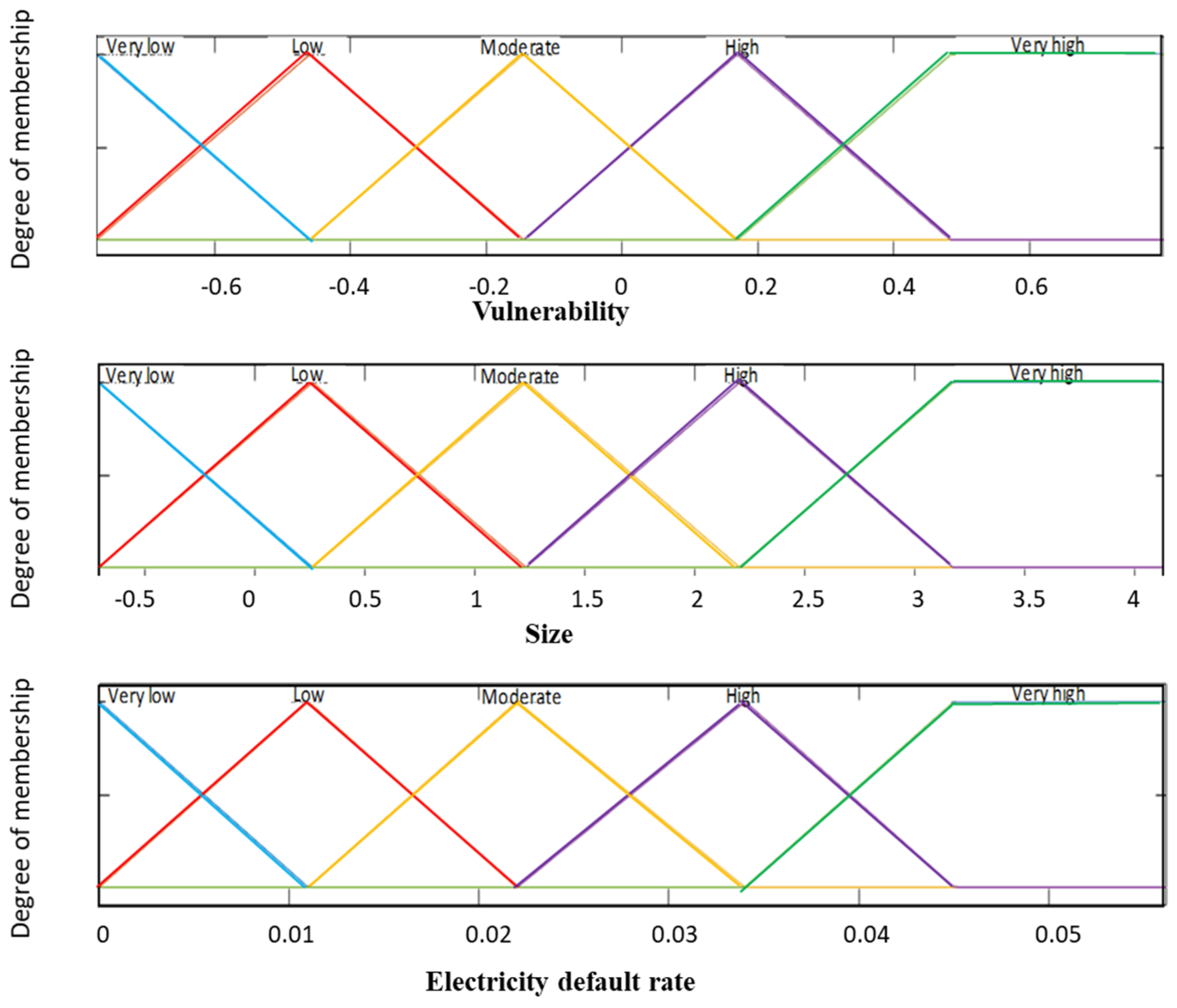
- Step 1: Determination of the range of each variable in the model, obtaining equal class intervals for the fuzzy groups, represented by N1, N2, N3, N4, N5, N6;
- Step 2: Once the ranges are defined, the vertices of the membership functions can be determined as follows:
- VL fuzzy group—Triangular with vertices at: N1; N1; N2;
- L fuzzy group—Triangular with vertices at: N1; N2; N3;
- M fuzzy group—Triangular with vertices at: N2; N3; N4;
- H fuzzy group—Triangular with vertices at: N3; N4; N5;
- VH fuzzy group—Trapezoidal with vertices at: N4; N5; N6; N6.
4.3. Phase 3: Fuzzy Inference, Defuzzification, and Definition of Regulatory Targets
5. Demonstration of the Applicability of the Proposed Model Focusing on the Residential Class of Electricity Consumption in Brazil
- Can we effectively demonstrate the applicability of the proposed model by focusing on the residential electricity consumption class in Brazil?
- Can the empirical results evidence the benefits of using a fuzzy inference-based model to establish regulatory targets to limit or reduce electricity default rates?
5.1. Phase 1: Definition and Classification of Input Variables
5.2. Phase 2: Database Preparation and Inputs for Fuzzy Inference
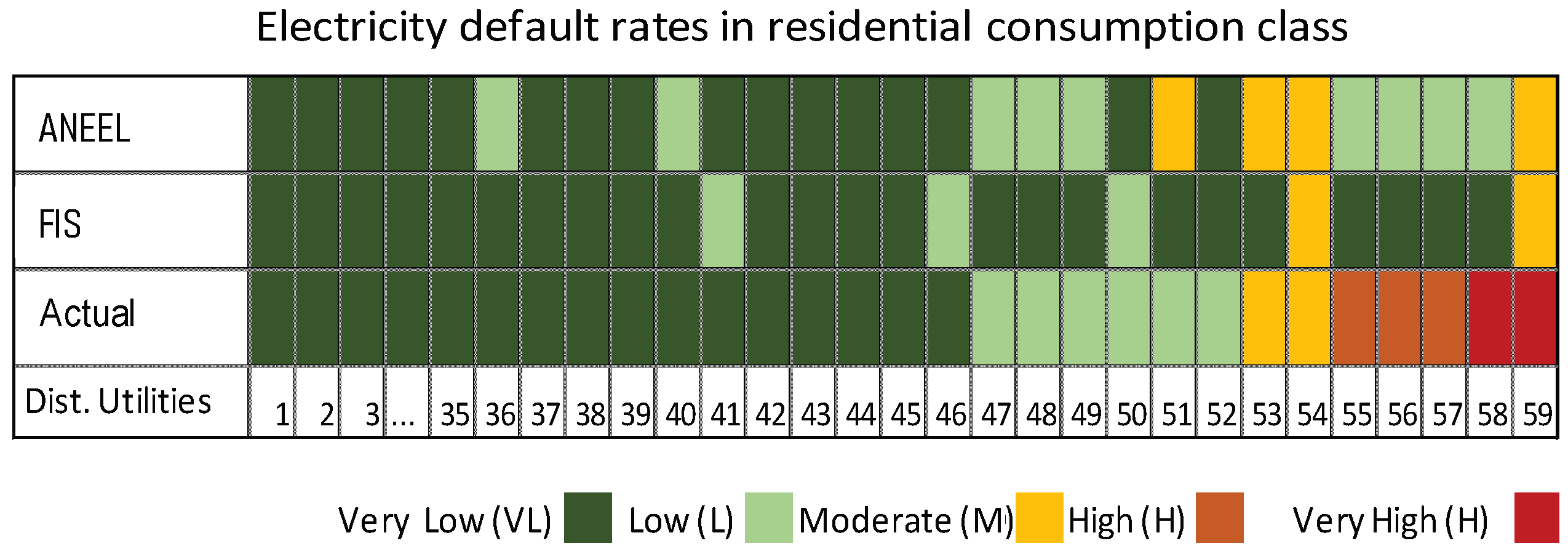
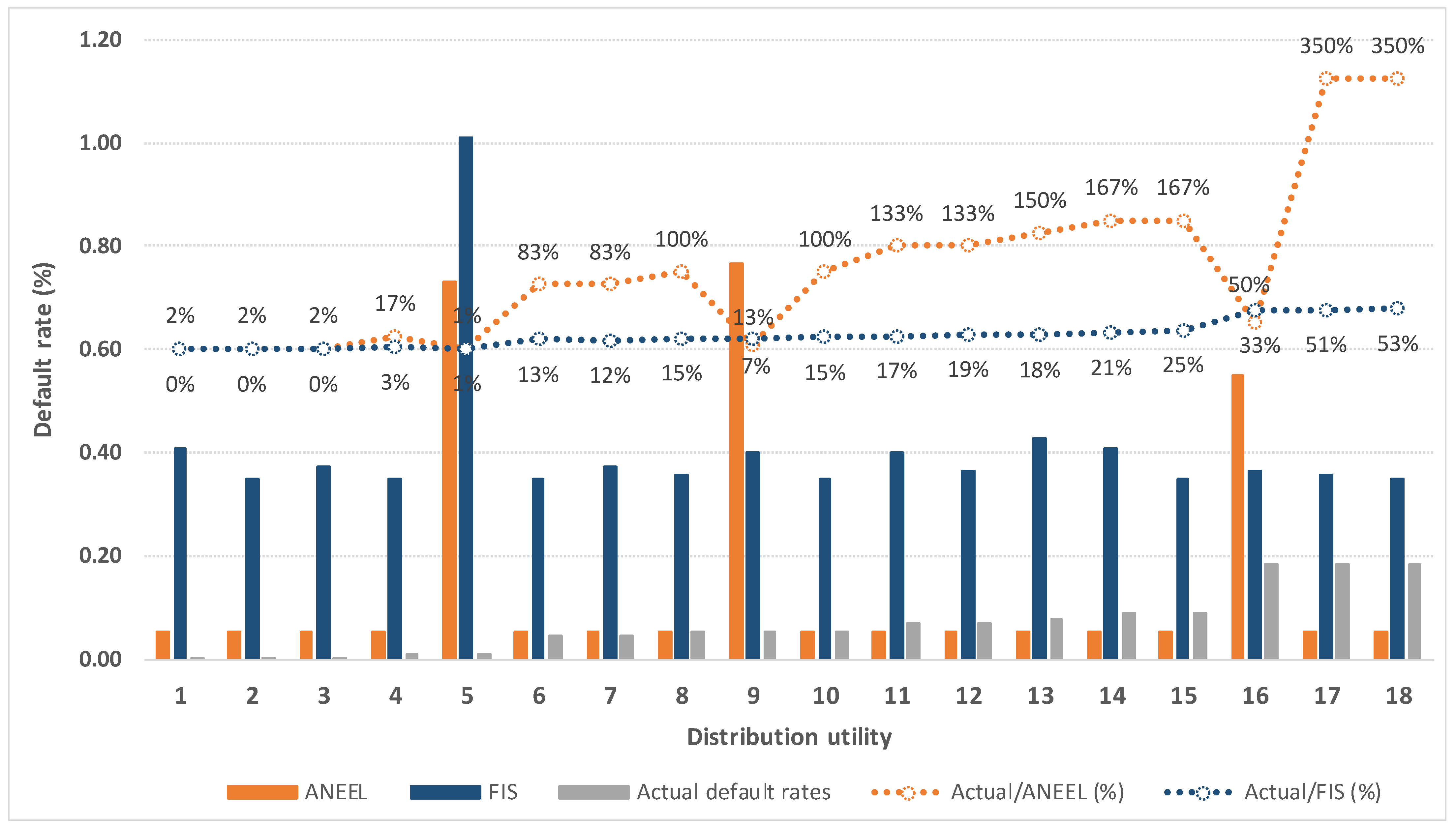
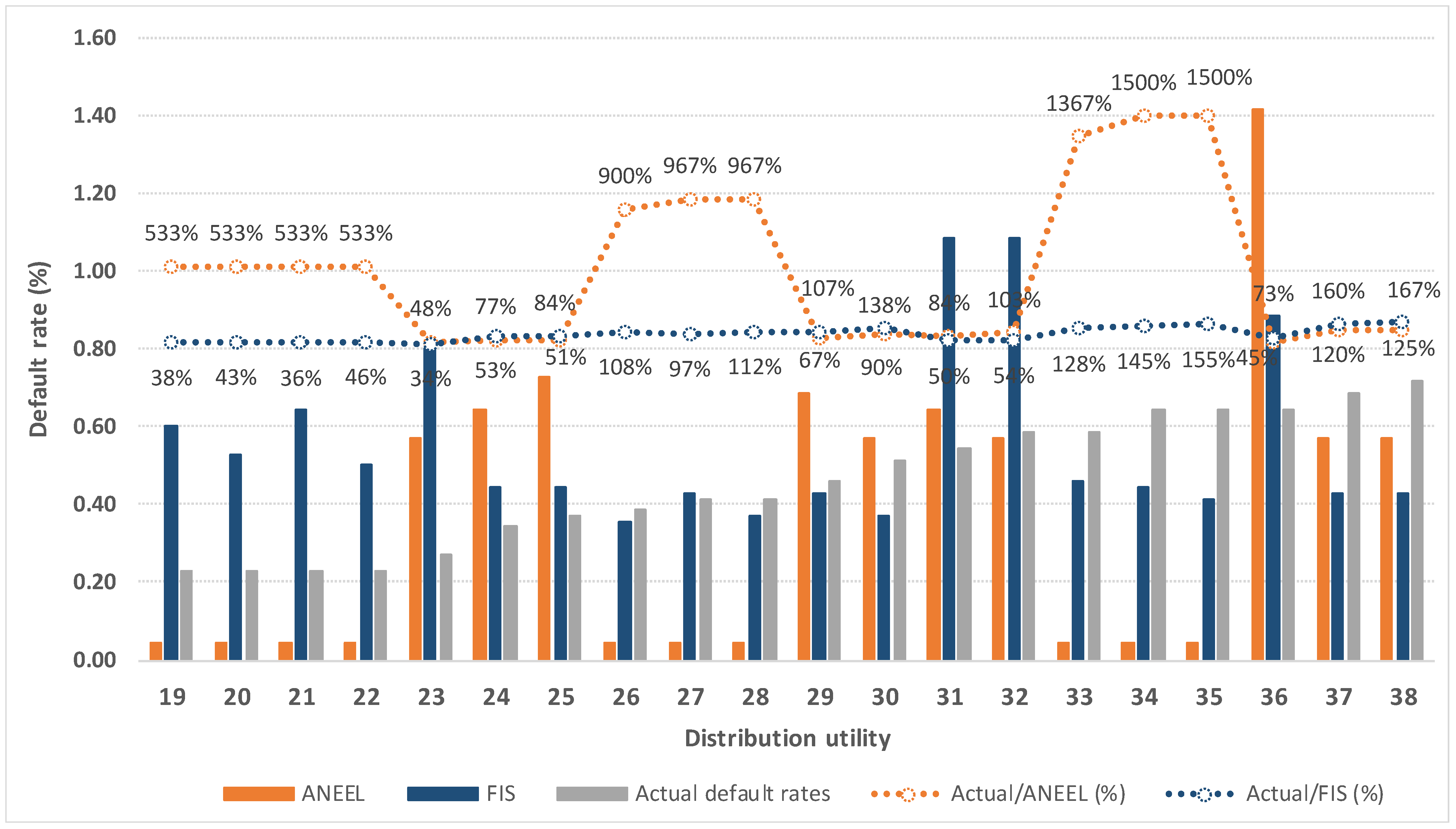
5.3. Phase 3: Fuzzy Inference, Defuzzification, and Definition of Regulatory Targets
6. Discussion
7. Conclusions
- The proposed fuzzy inference-based model offers a promising approach for defining regulatory targets to limit or reduce default electricity rates in Brazil. The model demonstrates superior capabilities compared with the current methodology employed by ANEEL;
- This study contributes significantly to the research on electricity defaults from a regulatory perspective by introducing a novel and effective method for addressing non-payment issues in the electricity distribution sector. The model aligns with the principles of incentive regulation and provides a comprehensive solution to incentivize distribution utilities to mitigate their default rates;
- The exploration of fuzzy inference systems (FIS) in the context of incentive regulation, particularly within the yardstick competition modality, showcases the adaptability and effectiveness of fuzzy logic in regulatory decision-making processes. This study expands the application of the FIS and highlights its potential to enhance regulatory frameworks in the electricity distribution sector;
- The empirical results obtained by applying the fuzzy inference-based model to the residential class of electricity consumption in Brazil demonstrated the feasibility and efficacy of the model in setting regulatory targets. The ability of the model to align with the reality of each electricity distribution utility underscores its practical relevance and applicability across different categories of electricity consumption.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Search Histories in the Web of Science and Scopus Databases
| Ref. | Keyword Search | Documents |
|---|---|---|
| #1 | TS (default* OR “non-payment” OR “nonpayment”) | 67,390 |
| #2 | TS (electricity OR “electrical power” OR “electric energy”) | 40,434 |
| #3 | TS (regulation) | 1,569,243 |
| #4 | TS (“fuzzy inference system” OR “fuzzy inference model*”) | 15,446 |
| #5 | #1 AND #2 | 45 |
| #6 | #2 AND #3 | 1409 |
| #7 | #5 AND #6 | 0 |
| #8 | #4 AND #7 | 0 |
| Ref. | Keyword Search | Documents |
|---|---|---|
| #1 | TITLE-ABS-KEY (default* OR “non-payment” OR “nonpayment”) | 80,938 |
| #2 | TITLE-ABS-KEY (“electricity” OR “electrical power” OR “electric energy”) | 86,004 |
| #3 | TITLE-ABS-KEY (regulation) | 2,737,797 |
| #4 | TITLE-ABS-KEY (“fuzzy inference system” OR “fuzzy inference model*”) | 22,703 |
| #5 | #1 AND #2 | 73 |
| #6 | #2 AND #3 | 3035 |
| #7 | #5 AND #6 | 0 |
| #8 | #4 AND #7 | 0 |
References
- Price Water House Coopers. Best Practices and Strategies for Distribution Loss Reduction; Final Report Forum of Regulators; Price Water House Coopers (PWC): London, UK, 2016. [Google Scholar]
- Miranda, M.; Ruffin, C.; Dantas, G.; Pedreira, N.; Guerra, M.; Zamboni, L.; Mendes, P.; Alvares, J. International review of regulatory aspects related to electricity loss in distribution sector. In Proceedings of the International Conference on Applied Energy 2019, Västerås, Sweden, 12–15 August 2019. [Google Scholar]
- Carr, D.; Thomson, M. Non-technical electricity losses. Energies 2022, 15, 2218. [Google Scholar] [CrossRef]
- Savian, F.S.; Siluk, J.C.M.; Garlet, T.B.; Nascimento, F.M.; Pinheiro, J.R.; Vale, Z. Non-technical losses in Brazil: Overview, challenges, and directions for identification and mitigation. Int. J. Energy Econ. Policy 2022, 12, 93. [Google Scholar] [CrossRef]
- Araújo, A.C.M. Perdas e inadimplência na atividade de distribuição de energia elétrica no Brasil. In Tese (doutorado)-Coordenação dos Programas de Pós-Graduação de Engenharia-COPPE; Universidade Federal do Rio de Janeiro: Rio de Janeiro, Brazil, 2007; 116p. [Google Scholar]
- Zhou, H.; Wang, Y.; Wang, W.; Li, T.; Yang, H. Prediction of default probability of clients’ electricity charge arrears. IEEE Int. Conf. Serv. Operat. Logist. Inform. 2008, 2, 2582–2586. [Google Scholar]
- Szabó, A.; Ujhelyi, G. Reducing non-payment for public utilities: Experimental evidence from South Africa. J. Dev. Econ. 2015, 117, 20–31. [Google Scholar] [CrossRef]
- Khanna, S.; Rowe, K. Should regulators make electric utilities pay customers for poor reliability? India’s Power Outage Compensation Policies Policy Brief, 9 June 2020. [Google Scholar]
- Fowlie, M.; Wolfram, C.; Baylis, P.; Spurlock, A.; Todd-Blick, A.; Cappers, P. Default effects and follow-on behaviour: Evidence from an electricity pricing program. Rev. Econ. Stud. 2021, 88, 2886–2934. [Google Scholar] [CrossRef]
- Murwirapachena, G.; Kabange, M.M.; Ifeacho, C. Non-payment culture and the financial performance of urban electricity utilities in South Africa. Dev. S. Afr. 2022, 40, 615–631. [Google Scholar] [CrossRef]
- Moita, R.; Rodrigues, H.; Rodrigues, T.; Lucinda, C.; Lopes, R.; Stefanello, C.; Chaves, T. Household Electricity Default in Brazil: Evidence from Billing Data; Working Papers, Department of Economics 2024_05; University of São Paulo (FEA-USP): São Paulo, Brazil, 2024. [Google Scholar]
- Joskow, P.L. Incentive Regulation in Theory and Practice: Electricity Distribution and Transmission Networks. In Economic Regulation and Its Reform: What Have We Learned? 2005. Available online: http://www.nber.org/chapters/c12566 (accessed on 1 March 2024).
- Vogelsang, I. Incentive regulation and competition in public utility markets: A 20-year perspective. J. Regul. Econ. 2011, 39, 159–176. [Google Scholar]
- Armah, B.K.; Mensah, E.J.; Dieli, D.A. Incentive regulation and utility benchmarking for electricity network security. Electr. Power Syst. Res. 2014, 106, 237–244. [Google Scholar]
- Heine, K. Inside the black box: Incentive regulation and incentive channeling on energy markets. J. Manag. Gov. 2013, 17, 157–186. [Google Scholar] [CrossRef][Green Version]
- Shleifer, A. A theory of yardstick competition. RAND J. Econ. 1985, 16, 319–327. [Google Scholar] [CrossRef]
- Resende, M. Relative efficiency measurement and prospects for yardstick competition in Brazilian electricity distribution. Energy Policy 2002, 30, 637–647. [Google Scholar] [CrossRef]
- Kumbhakar, S.C.; Lien, G. Yardstick Regulation of Electricity Distribution—Disentangling Short-run and Long-run Inefficiencies. Energy J. 2017, 38, 17–38. [Google Scholar] [CrossRef]
- Agência Nacional de Energia Elétrica. Nota Técnica No. 106/2015–Metodologia de Tratamento Regulatório para Perdas Não Técnicas de Energia Elétrica; SGT/SRM/ANEEL: Brasília, Brazil, 2015.
- Souza, R.C.; Calili, R.F.; Simões, P.F.M. Termo Aditivo ao Contrato de Concessão de Distribuição de Energia Elétrica da Enel Distribuição Rio Energia e Serviços, S.A-Contribuições e Críticas à Metodologia de Perdas não Técnicas; Audiência N° 095/2017; Rio de Janeiro, Brasil, 2017.
- Castro, N.D.; Chaves, A.C.; Ferreira, D.V.; Tommaso, F.; Ozorio, L.; Maestrini, M.; Mendes, P. Análise das Propostas de Alterações Metodológicas para Determinação das Metas Regulatórias das Perdas Não Técnicas, na Distribuição de Energia Elétrica; NT46/2020 TDSE Texto de Discussão do Setor Elétrico N° 94 outubro de 2020; UFRJ–Grupo de Estudos do Setor Elétrico: Rio de Janeiro, Brasil, 2020. [Google Scholar]
- Agência Nacional de Energia Elétrica. Nota Técnica No. 46/2020–Proposta de Consulta Pública para Revisão da Metodologia e Atualização dos Parâmetros dos Submódulos 2.2/2.2A (Receitas Irrecuperáveis) e 2.6 (Perdas de Energia) dos Procedimentos de Revisão Tarifária-PRORET; Agência Nacional de Energia Elétrica (ANEEL), SRM/SGT: Brasília, Brasil, 2020.
- Leite, D.; Pessanha, J.; Simões, P.; Calili, R.; Souza, R. A stochastic frontier model for definition of non-technical loss targets. Energies 2020, 13, 3227. [Google Scholar] [CrossRef]
- Simões, P.F.M.; Souza, R.C.; Calili, R.F.; Pessanha, J.F.M. Analysis and short-term predictions of non-technical loss of electric power based on mixed effects models. Socio-Econ. Plan. Sci. 2020, 71, 100804. [Google Scholar] [CrossRef]
- Correia, E.; Calili, R.; Pessanha, J.; Almeida, M.F. Definition of regulatory targets for electricity non-technical losses: Proposition of na automatic model-selection technique for panel-data regressions. Energies 2023, 16, 2519. [Google Scholar] [CrossRef]
- Guillaume, S. Designing fuzzy inference systems from data: An interpretability-oriented review. IEEE Trans. Fuzzy Syst. 2001, 9, 426–443. [Google Scholar] [CrossRef]
- Zadeh, L.A. Outline of a new approach to the analysis of complex systems and decision processes. IEEE Trans. Syst. Man Cybern. 1973, 3, 28–44. [Google Scholar] [CrossRef]
- Zadeh, L.A.; Klir, G.J.; Yuan, B. Fuzzy Sets, Fuzzy Logic, and Fuzzy Systems: Selected Papers by Lotfi a Zadeh, 1st ed.; World Scientific Publishing Company: Hackensack, NJ, USA, 1996. [Google Scholar]
- Kalogirou, S.A. Solar Energy Engineering: Processes and Systems, 2nd ed.; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Velázquez, D.R.T.; Louzada, D.R.; Monteiro, E.C.; Fortaleza, L.G.S.; Barbosa, C.R.H.; Silva, E.C.; Gusmão, L.A.P. Multiparameter fuzzy design space for QbD approach applied in the development of biomedical devices. J. Phys. Conf. Ser. 2018, 1044, 12051. [Google Scholar] [CrossRef]
- Mamdani, E.H.; Assilian, S. An experiment in linguistic synthesis with a fuzzy logic controller. Int. J. Man-Mach. Stud. 1975, 7, 1–13. [Google Scholar] [CrossRef]
- Sugeno, M. Industrial Applications of Fuzzy Control; Elsevier Science Inc.: New York, NY, USA, 1985. [Google Scholar]
- Martins, F.; Almeida, M.F.; Calili, R.; Oliveira, A. Design Thinking applied to smart home projects: A user-centric and sustainable perspective. Sustainability 2020, 12, 10031. [Google Scholar] [CrossRef]
- Aeyels, D.; Smet, F. A mathematical model for the dynamics of clustering. Phys. D Nonlinear Phenomena 2008, 237, 2517–2530. [Google Scholar] [CrossRef]
- Saxena, A.; Prasad, M.; Gupta, A.; Bharill, N.; Patel, O.; Tiwari, A.; Er, M.; Ding, W.; Lin, C. A review of clustering techniques and developments. Neurocomputing 2017, 267, 664–681. [Google Scholar] [CrossRef]
- Engquist, B.; Souganidis, P. Asymptotic and numerical homogenization. Acta Numerica 2008, 17, 147–190. [Google Scholar] [CrossRef]
- Salmon, W. Objectively homogeneous reference classes. Synthese 1977, 36, 399–414. [Google Scholar] [CrossRef]
- Liu, T.; Liu, S.; Shi, L. Regression Analysis of Panel Data. In Time Series Analysis Using SAS Enterprise Guide; Springer: Singapore, 2020; pp. 101–123. [Google Scholar]
- He, X.; Tong, X.; Sun, J.; Cook, R. Regression analysis of multivariate panel count data. Biostatistics 2007, 9, 234–248. [Google Scholar] [CrossRef]
- MatWorks. MATLAB® Documentation. 2023. Available online: https://www.mathworks.com/help/matlab/ (accessed on 1 March 2024).
- Maraj, A.; Shatri, B.; Rugova, S. Selection of defuzzification method for outing metrics in MPLS network to obtain better crisp values for link optimization. In Proceedings of the 7th WSEAS International Conference on System Science and Simulation in Engineering, Venice, Italy, 21–23 November 2008; World Scientific and Engineering Academy and Society (WSEAS): Stevens Point, WI, USA, 2008. [Google Scholar]
- Energy Research Company. 2023 Statistical Yearbook of Electricity. 2022 Baseline Year; EPE: Rio de Janeiro, Brazil, 2023. Available online: https://dashboard.epe.gov.br/apps/anuario-livro-eng/ (accessed on 1 March 2024).







| Phase | Stage | Research Questions [Sections] |
|---|---|---|
| Motivation (Why?) |
| Why should we propose a fuzzy inference-based model to assist ANEEL in defining regulatory targets to limit or reduce electricity default rates in Brazil? (Section 1). |
| Conceptualisation and development (What and how?) |
| What is the state of research on regulatory models and instruments to limit or reduce electricity default rates in distribution utilities, with special attention paid to those works aligned with incentive-based regulation? (Section 2). What are the main limitations of the current methodologial approach adopted by ANEEL to define regulatory targets for limiting or reducing electricity default rates? (Section 1 and Section 2). |
| From a regulatory perspective, how can a fuzzy inference-based model be developed and validated in the context of Brazil’s electricity distribution sector to limit or reduce electricity default rates? [Section 3]. | |
| What are the essential premises that must be considered when developing a conceptual model to define regulatory targets for limiting or reducing electricity default rates that meet the fundamental requirements of incentive-based regulation? (Section 4). To what extent can a fuzzy inference-based model better assist ANEEL in defining regulatory targets for limiting or reducing electricity default rates in Brazil? (Section 4). | |
| Validation (How to demonstrate the applicability of the proposed technique?) |
| Is it feasible to demonstrate the applicability of the proposed model by focusing on the residential electricity consumption class in Brazil? (Section 5). Can the empirical results evidentiate the benefits of using a fuzzy inference-based model to establish regulatory targets to limit or reduce electricity default rates? (Section 5 and Section 6). |
| What are the differentials of the proposed methodological approach over the current econometric models used by ANEEL to define regulatory targets for limiting or reducing electricity default rates in Brazil? (Section 5 and Section 6). |
| Categories of Input Variables | Input Variables | Definition | Sources |
|---|---|---|---|
| Vulnerability of the concession area | Pob | Percentage of people with per capita income less than half the minimum wage | Brazilian Institute of Geography and Statistics (IBGE) and Institute of Applied Economic Research (IPEA) |
| Vio | Deaths due to assault | Department of Informatics of the Unified Health System (DATASUS/Ministry of Health) | |
| Sub2 | Percentage of people in subnormal households | Brazilian Institute of Geography and Statistics (IBGE) | |
| Gini | Gini Index | Brazilian Institute of Geography and Statistics (IBGE) | |
| Inadpf | Percentage of default rate among individuals in the credit sector | Central Bank of Brazil (BACEN) | |
| Rendtotal | Average income from formal and informal work | Brazilian Institute of Geography and Statistics (IBGE) | |
| Ocupform | Percentage of individuals aged 16 and over, formally employed during the reference week | Brazilian Institute of Geography and Statistics (IBGE) | |
| RGA | Percentage of households with piped water supply in at least one room (estimates based on growth rates from similar tables of PNAD/IBGE at the state level). | National Household Sample Survey (PNAD/IBGE) | |
| ADMD | Percentage of households with more than three residents per bedroom (high density of residents per household). Estimates based on growth rates from similar tables of PNAD/IBGE at the state level. | National Household Sample Survey (PNAD/IBGE) | |
| EEM | Percentage of individuals over 25 years old who dropped out of high school (estimates based on growth rates from similar tables of PNAD/IBGE at the state level). | National Household Sample Survey (PNAD/IBGE) | |
| Size of the distribution utility | Market (GWh) | Billed consumption of electricity distribution utilities | Market Information Monitoring System for Economic Regulation (SAMP/ANEEL). |
| Number of consumers | Total number of consumers of electricity distribution utilities | Market Information Monitoring System for Economic Regulation (SAMP/ANEEL). | |
| Transmission network length | Kilometers of transmission line network of electricity distribution utilities | Market Information Monitoring System for Economic Regulation (SAMP/ANEEL). |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Celestino, N.M.; Calili, R.; Louzada, D.; Almeida, M.F. Definition of Regulatory Targets for Electricity Default Rate in Brazil: Proposition of a Fuzzy Inference-Based Model. Energies 2024, 17, 2147. https://doi.org/10.3390/en17092147
Celestino NM, Calili R, Louzada D, Almeida MF. Definition of Regulatory Targets for Electricity Default Rate in Brazil: Proposition of a Fuzzy Inference-Based Model. Energies. 2024; 17(9):2147. https://doi.org/10.3390/en17092147
Chicago/Turabian StyleCelestino, Nivia Maria, Rodrigo Calili, Daniel Louzada, and Maria Fatima Almeida. 2024. "Definition of Regulatory Targets for Electricity Default Rate in Brazil: Proposition of a Fuzzy Inference-Based Model" Energies 17, no. 9: 2147. https://doi.org/10.3390/en17092147
APA StyleCelestino, N. M., Calili, R., Louzada, D., & Almeida, M. F. (2024). Definition of Regulatory Targets for Electricity Default Rate in Brazil: Proposition of a Fuzzy Inference-Based Model. Energies, 17(9), 2147. https://doi.org/10.3390/en17092147





