Mean Field Game-Based Algorithms for Charging in Solar-Powered Parking Lots and Discharging into Homes a Large Population of Heterogeneous Electric Vehicles

Abstract

An optimal daily scheme is presented to coordinate a large population of heterogeneous battery electric vehicles when charging in daytime work solar-powered parking lots and discharging into homes during evening peak-demand hours. First, we develop a grid-to-vehicle strategy to share the solar energy available in a parking lot between vehicles where the statistics of their arrival states of charge are dictated by an aggregator. Then, we develop a vehicle-to-grid strategy so that vehicle owners with a satisfactory level of energy in their batteries could help to decongest the grid when they return by providing backup power to their homes at an aggregate level per vehicle based on a duration proposed by an aggregator. Both strategies, with concepts from Mean Field Games, would be implemented to reduce the standard deviation in the states of charge of batteries at the end of charging/discharging vehicles while maintaining some fairness and decentralization criteria. Realistic numerical results, based on deterministic data while considering the physical constraints of vehicle batteries, show, first, in the case of charging in a parking lot, a strong to slight decrease in the standard deviation in the states of charge at the end, respectively, for the sunniest day, an average day, and the cloudiest day; then, in the case of discharging into the grid, over three days, we observe at the end the same strong decrease in the standard deviation in the states of charge.

1. Introduction

The use of electric vehicles worldwide has exponentially increased, thanks to technological advances and climate change policies. There were 18 million battery electric vehicles (BEVs) in 2022, and 28 million in 2023 [1]. Incentives are put in place to achieve sales of BEVs in 2030 representing $30\%$ of the overall vehicle sales market [2]. At the end of 2023, there were $3.2$ million public charging stations (including $1.8$ million slow chargers, i.e., with a charging rate up to 22 kW, and $1.4$ million fast chargers, i.e., with a charging rate of more than 22 kW and up to 350 kW) and almost ten times more home charging stations than public ones [1]. However, the use of millions of BEVs will inevitably have significant impacts on the grid [3]. When too many BEVs are charged at the same time, that may create both local transformer and eventually system-wide overloads [4]. Furthermore, the adequate management of battery storage associated with an aggregate of BEVs can transform such an aggregate into a virtual power plant. Thus, in the context of integration with renewable energy sources, such as photovoltaics, BEVs’ batteries could store the solar energy available during the day when BEVs are parked [5,6,7] and then restore part of the energy in their batteries into the grid during evening peak-demand hours. Multiple studies worldwide (from Canada, the United States, Brazil, Europe, Asia, and Africa) on the feasibility of these new attributes of BEVs have been discussed in the literature [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26].

Our objective in this paper is to develop control strategies for the charging and discharging of BEVs, with the aim being to offer tools that will possibly lead to the implementation of a viable economic model exploiting BEVs [27,28]. Our envisioned business scheme, but by no means the only one, is the daily operation of daytime solar-powered parking lots. A parking lot operator would share everyday solar energy amongst the present BEVs in a parking lot. BEVs would be owned by customers working near the parking lot who could charge their batteries at least partially depending on the available daily solar energy. The parking lot operator would charge each customer a monthly parking subscription fee proportional to their battery capacity for the use of a parking space and the associated charging station. If the customers then decided to recover part of their parking subscription costs, they could choose to participate in a grid support operation coordinated by the parking lot operator. More precisely, upon returning to their homes, the customers would commit to supplying the grid using their batteries during evening peak-demand hours at an aggregated power level per vehicle based on a duration proposed by the parking lot operator. The daily amount of energy supplied to the grid, based on grid demand and participating BEVs, would be negotiated at a reasonable price between the parking lot operator and the grid operator. An agreed fraction of the resulting income would then be redistributed to the customers based on their contribution to the grid, allowing everyone to benefit accordingly.

On the other hand, the parking lot operator should guarantee a competitive monthly parking subscription fee for each customer. Knowing that the sun shines during the day in the parking lot, and in the absence of large batteries dedicated to solar energy storage, which can be costly, the solar energy acquired must be shared instantly and as fairly as possible between BEVs. An adequate control system for charging BEVs must be developed by the parking lot operator to maximize the chances that customers can return to their homes without needing to charge at an arbitrary station. The necessary daily solar energy forecast should be carried out based on the weather. To avoid having to connect the parking lot to an external supply grid, the parking lot operator should then announce a daily expected sunshine level to the customers. Consequently, a daily average state-of-charge (SOC) level can be expected for the entire aggregate of BEVs upon their arrival in the parking lot. This expected average SOC level will be dictated by the parking lot operator so that the expected daily solar energy in the parking lot will be less than the energy that the entire aggregate of BEVs will need to charge their batteries at a maximum level that day. Therefore, we shall assume that the solar parking lot supply–demand ratio (SDR) for charging all BEVs is less than one. Otherwise, any excess energy in the parking lot at the end of the day could be stored in a battery and restored into the grid during peak evening hours.

To maximize customer participation in our business scheme, coordinated by the parking lot operator, so that everyone benefits, the proposed control strategies must be the following:

(i)

As fair as possible: We want, at the end of charging or discharging, for each customer to have the state of charge of their battery to always be close to the average of the states of charge of the batteries of all customers, regardless of their state of charge upon arrival. We are therefore leaning towards a charging or discharging algorithm a priori favoring BEVs which are the emptiest compared to those that are more full when they arrive. The justification for this bias in favor of emptier vehicles is the potential urgency of charging them in the parking lot in the case of early departures, but also, by the appropriate equalization of vehicle states of charge, we maximize a priori the chances of participation of a given vehicle in grid support operations during peak evening hours. However, the emptiest BEVs upon arrival must in no way exceed those arriving fuller when charging in the parking lot or discharging into the grid.

(ii)

As decentralized as possible: From the aggregator’s point of view, decentralized control strategies are quite desirable because they minimize the information exchange and the need to observe the individual batteries, which could be complex and invasive. Additionally, a local policy allows a customer to interrupt their charging or discharging process at any time (emergency departure, battery life cycle health, etc.).

The coordination of charging or discharging electric vehicles is obtained in most cases from centralized control strategies in the literature [29,30,31,32,33,34], or it is a decentralized control strategy that will allow a customer to determine their own charging pattern depending on the time of the day, the electricity cost, or the health of their battery. Therefore, decentralized control strategies provide more guarantee of a viable economic model [35,36] but are often achievable by more sophisticated approaches (multi-agent system optimization, optimization by particle swarms, artificial intelligence, etc.) requiring a lot of simulation time, which sometimes might not be feasible [7,35,36,37].

In this paper, we rely on Mean Field Game (MFG) theory [38,39,40,41,42], which, when we use adequate cost functions [43,44,45], allows us to provide decentralized vehicle charging and discharging algorithms by favoring the lowest states of charge, which fits perfectly with our research framework. The problem is therefore formulated as a game with a large number of agents (here, BEVs). The stochastic model of the state of charge of the battery of a BEV is linear, and when we consider quadratic costs, the MFG algorithms result in analytically calculable charging laws that are linear and varying over time.

The MFG concept, in the recent literature, has been successfully applied in the general context of energy management systems. A Nash equilibrium solution, for the management of a large population of space heaters, was presented with an integral control approach in 2019 [44], and with a reverse engineering (or inverse Nash) approach in 2021 [45]. It is this last avenue that we consider in this paper for the charging and discharging of BEVs.

The first formulation of game theory in vehicle charging or discharging problems associated with the coordination of energy restitution from electric vehicles into the grid came up in 2011 [46]. In that formulation, each group of hybrid electric vehicles could decide on the maximum amount of surplus energy they were willing to sell to the grid to maximize a utility function based on the economic benefits of selling energy and the associated costs. The trading price governing the energy market between vehicles and the grid was determined using a double strategic auction defined by the authors. To solve the game, an algorithm based on the best response dynamics was proposed, thanks to which the groups of vehicles could reach a Nash equilibrium. Then, in 2012 [47], the authors, in the same economic context of energy trade-off, presented a formulation of Mean Field Games theory associated with the coordination of non-hybrid electric vehicles (also known BEVs).

The first rigorous formulations using Mean Field Games theory in the vehicle charging or discharging problem came up in 2013 and 2015 [35,48]. The authors framed the problem as a game with a large population of hybrid electric vehicles over a finite charging interval. They studied the existence, uniqueness, and optimality of the Nash equilibrium of the problem to minimize the costs of local electricity and also to fully charge vehicles. In a decentralized mechanism, they showed under deterministic consideration that the solution converges to a unique Nash equilibrium: it is globally optimal for a homogeneous population, and almost globally optimal for a heterogeneous population. The problem was presented in the economic context of the penetration of electric vehicles into the grid, from which energy was directly drawn. The authors (in 2014 [49], 2015 [50], 2016 [51], and 2019 [52], respectively) also conducted their research based on economic contexts, where refs. [49,50] studied the heterogeneous case with constraints in the charging times by adding an iterative algorithm so that the solution converged towards a Nash equilibrium, ref. [51] considered simultaneous charging during a flexible period, and ref. [52] added battery degradation constraints.

The first applications of Mean Field Games theory in the charging of BEVs in solar parking lots were presented in 2021 [27,28]. In May 2021 [27], the authors solved the problem when all BEVs were present at the start of charging. The heterogeneous case was solved by considering homogeneous classes of BEVs resulting in a control policy per homogeneous class. In this case, the formulation remained the same and therefore did not require an iterative algorithm, as in [35] for the solution to converge to a Nash equilibrium. However, the algorithm in the heterogeneous case became more complex as the number of different classes of homogeneous BEVs increased. And it was in December 2021 [28] that the problem when BEVs arrive and leave the parking lot randomly was solved, but considering the MFG classic formulation where the number of agents is assumed to be fixed. In both [27,28], a rigorous justification was not given to guarantee that a solution will exist in the Nash equilibrium problem. More recently, the authors, in 2021 and 2023 [53,54], added constraints for battery charging and discharging in their mathematical formalism, and the authors in 2023 [55] they added behavioral considerations of the owners of electric vehicles (availability, planning, etc.) in their analysis.

The main contribution of this paper’s conclusions as follows:

(i)

A novel MFG inverse Nash algorithm for charging heterogeneous BEVs in a solar-powered parking lot or discharging their energy into the grid.

(ii)

A rigorous justification of the existence of the solution to the MFG inverse Nash problem for deterministic data aimed at achieving a fair and decentralized charging or discharging algorithm.

(iii)

Testing and validation of the MFG inverse Nash algorithm for charging and discharging a large population of heterogeneous BEVs, based on realistic data while considering the physical constraints of vehicle batteries, on three days in a year (the sunniest, an average, and the cloudiest).

The rest of this paper is organized as follows. In Section 2, we present the Mean Field Game-based algorithm for charging or discharging a large population of heterogeneous BEVs. The theoretical underpinnings and mathematical details are presented in Appendix A. We also present a simpler version of the Mean Field Game-based algorithm in Appendix B. In Section 3, we present the numerical results in the case of charging in the parking lot. In Section 4, we present the numerical results in the case of discharging into the grid. The numerical results in Section 3 and Section 4 are reported in the case of the sunniest day, an average day, and the cloudiest day. Other detailed numerical results are presented in Appendix C (see

Table A1. Detailed numerical results per battery capacity when charging and discharging heterogeneous BEVs.

Charging Heterogeneous BEVs	$\beta$ [kWh]	16	22	31	40	54	62	70	80	93	100
	$N_{\beta }$	44	38	42	36	27	55	35	42	40	41
	${\overline{x}}_{0,\beta }$	$0.125$	$0.193$	$0.166$	$0.140$	$0.126$	$0.152$	$0.134$	$0.143$	$0.170$	$0.156$
	${\sigma }_{x_{i,0,\beta }}$	$0.102$	$0.115$	$0.095$	$0.104$	$0.095$	$0.114$	$0.073$	$0.082$	$0.112$	$0.107$
	$W_{0,\beta }$ [kWh]	88	161	216	202	183	520	327	479	632	641
	$f_{W_{0,\beta }}$	$2.5\%$	$4.7\%$	$6.3\%$	$5.8\%$	$5.3\%$	$15.1\%$	$9.5\%$	$13.9\%$	$18.3\%$	$18.6\%$
Sunniest day	${\overline{x}}_{0-T,\beta }$	$\uparrow 623\%$	$\uparrow 372\%$	$\uparrow 445\%$	$\uparrow 544\%$	$\uparrow 617\%$	$\uparrow 493\%$	$\uparrow 575\%$	$\uparrow 533\%$	$\uparrow 433\%$	$\uparrow 478\%$
	${\sigma }_{x_{i,0-T,\beta }}$	$\downarrow 88.60\%$	–	–	–	–	–	–	–	–	–
	$W_{T,\beta }$ [kWh]	634	760	1179	1300	1314	3083	2210	3034	3371	3709
	$f_{W_{0-T,\beta }}$	$\uparrow 21.2\%$	$\downarrow 20.9\%$	$\downarrow 8.7\%$	$\uparrow 7.8\%$	$\uparrow 20.1\%$	$\downarrow 0.6\%$	$\uparrow 13.1\%$	$\uparrow 6.1\%$	$\downarrow 10.7\%$	$\downarrow 3.1\%$
	$U_{max,\beta }^{\ast }$ [kW]	$3.2$	$4.4$	$5.6$	$7.8$	$9.8$	$12.0$	$12.7$	$15.1$	$17.4$	$20.0$
Average day	${\overline{x}}_{0-T,\beta }$	$\uparrow 288\%$	$\uparrow 172\%$	$\uparrow 205\%$	$\uparrow 251\%$	$\uparrow 285\%$	$\uparrow 228\%$	$\uparrow 266\%$	$\uparrow 246\%$	$\uparrow 200\%$	$\uparrow 221\%$
	${\sigma }_{x_{i,0-T,\beta }}$	$\downarrow 40.96\%$	–	–	–	–	–	–	–	–	–
	$W_{T,\beta }$ [kWh]	340	437	661	709	705	1703	1196	1659	1896	2057
	$f_{W_{0-T,\beta }}$	$\uparrow 17.7\%$	$\downarrow 17.5\%$	$\downarrow 7.3\%$	$\uparrow 6.6\%$	$\uparrow 16.8\%$	$\downarrow 0.5\%$	$\uparrow 11.0\%$	$\uparrow 5.1\%$	$\downarrow 9.0\%$	$\downarrow 2.6\%$
	$U_{max,\beta }^{\ast }$ [kW]	$2.9$	$3.9$	$5.6$	$7.2$	$9.4$	$11.0$	$12.6$	$14.6$	$17.0$	$17.8$
Cloudiest day	${\overline{x}}_{0-T,\beta }$	$\uparrow 24.0\%$	$\uparrow 14.1\%$	$\uparrow 17.1\%$	$\uparrow 20.9\%$	$\uparrow 23.7\%$	$\uparrow 18.9\%$	$\uparrow 22.3\%$	$\uparrow 20.6\%$	$\uparrow 16.8\%$	$\uparrow 18.4\%$
	${\sigma }_{x_{i,0-T,\beta }}$	$\downarrow 3.28\%$	$\downarrow 3.20\%$	$\downarrow 3.07\%$	$\downarrow 3.42\%$	$\downarrow 2.91\%$	$\downarrow 3.16\%$	$\downarrow 3.24\%$	$\downarrow 3.20\%$	$\downarrow 3.39\%$	$\downarrow 3.10\%$
	$W_{T,\beta }$ [kWh]	109	184	253	244	227	618	400	578	740	759
	$f_{W_{0-T,\beta }}$	$\uparrow 4.1\%$	$\downarrow 4.2\%$	$\downarrow 1.7\%$	$\uparrow 1.5\%$	$\uparrow 3.9\%$	$\downarrow 0.2\%$	$\uparrow 2.7\%$	$\uparrow 1.2\%$	$\downarrow 2.0\%$	$\downarrow 0.6\%$
	$U_{max,\beta }^{\ast }$ [kW]	$1.6$	$1.8$	$2.9$	$3.2$	$4.4$	$5.6$	$6.1$	$7.2$	$7.8$	$9.3$
Discharging Heterogeneous BEVs	$\beta$ [kWh]	16	22	31	40	54	62	70	80	93	100
	${\overline{x}}_{0-T,\beta }$	$\downarrow 81.50\%$	–	–	–	–	–	–	–	–	–
	${\sigma }_{x_{i,0-T,\beta }}$	$\downarrow 81.50\%$	–	–	–	–	–	–	–	–	–
	$f_{W_{0-T,\beta }}$	$\downarrow 0\%$	–	–	–	–	–	–	–	–	–
Sunniest day	$N_{\beta }$	44	38	42	36	27	55	35	42	40	41
	${\overline{x}}_{0,\beta }$	$0.785$	$0.829$	$0.850$	$0.862$	$0.869$	$0.877$	$0.878$	$0.881$	$0.891$	$0.886$
	${\sigma }_{x_{i,0,\beta }}$	$0.072$	$0.045$	$0.039$	$0.031$	$0.022$	$0.022$	$0.013$	$0.019$	$0.015$	$0.015$
	$W_{0,\beta }$ [kWh]	553	693	1106	1242	1267	2992	2151	2959	3313	3633
	$f_{W_{0,\beta }}$	$2.8\%$	$3.5\%$	$5.6\%$	$6.2\%$	$6.4\%$	$15\%$	$10.8\%$	$14.9\%$	$16.6\%$	$18.2\%$
	$W_{T,\beta }$ [kWh]	102	128	205	230	235	554	398	548	614	673
	$U_{max,\beta }^{\ast }$ [kW]	$13.5$	$18.5$	$25.9$	$34.1$	$45.5$	$53.2$	$58.6$	$67.5$	$79.1$	$85.8$
Average day	$N_{\beta }$	44	37	41	36	27	55	35	42	40	41
	${\overline{x}}_{0,\beta }$	$0.382$	$0.439$	$0.454$	$0.452$	$0.451$	$0.473$	$0.464$	$0.471$	$0.494$	$0.483$
	${\sigma }_{x_{i,0,\beta }}$	$0.080$	$0.080$	$0.066$	$0.071$	$0.060$	$0.071$	$0.041$	$0.055$	$0.066$	$0.065$
	$W_{0,\beta }$ [kWh]	269	357	577	651	658	1611	1137	1583	1839	1981
	$f_{W_{0,\beta }}$	$2.6\%$	$3.4\%$	$5.4\%$	$6.1\%$	$6.2\%$	$15.1\%$	$10.7\%$	$14.8\%$	$17.2\%$	$18.6\%$
	$W_{T,\beta }$ [kWh]	50	66	107	120	122	298	211	293	340	367
	$U_{max,\beta }^{\ast }$ [kW]	$11.7$	12	17	$22.4$	$29.7$	$35.7$	$35.1$	$43.6$	$56.3$	$61.2$
Cloudiest day	$N_{\beta }$	38	31	34	27	19	43	27	35	34	32
	${\overline{x}}_{0,\beta }$	$0.173$	$0.195$	$0.166$	$0.172$	$0.198$	$0.150$	$0.141$	$0.202$	$0.139$	$0.188$
	${\sigma }_{x_{i,0,\beta }}$	$0.086$	$0.075$	$0.089$	$0.095$	$0.102$	$0.073$	$0.063$	$0.098$	$0.093$	$0.103$
	$W_{0,\beta }$ [kWh]	105	133	175	185	203	401	267	565	439	603
	$f_{W_{0,\beta }}$	$3.9\%$	$5.2\%$	$6.7\%$	$7.8\%$	$6.8\%$	$12.6\%$	$8.6\%$	$17.8\%$	$13.0\%$	$17.6\%$
	$W_{T,\beta }$ [kWh]	20	25	32	34	38	74	49	105	81	112
	$U_{max,\beta }^{\ast }$ [kW]	$7.4$	$10.1$	$13.2$	$22.1$	$22.7$	$20.4$	$18.1$	$37.9$	$30.9$	$42.1$

). Finally, in Section 5, we conclude and give an outlook on future research.

2. Mean Field Game-Based Control for Charging or Discharging a Large Population of Heterogeneous BEVs

2.1. Battery Model

2.1.1. Heterogeneous Batteries

We consider a population of N heterogeneous BEVs in a parking lot. The assumption of a large population is needed only if, as we do in (1) below, we assume randomness in the dynamics of battery charging, and later on in our analysis we will assimilate the empirical mean of states of charge (SOCs) with its mathematical expectation (a predictable deterministic quantity) by virtue of the law of large numbers. Because of the linearity of the model, the analysis will be perfectly exact for arbitrarily small numbers of BEVs if the battery charging processes remain deterministic. Each BEV, i, $i=1,\dots ,N$, has a state of charge (SOC) $x_{i,0}$ upon arrival which is the result of a daily traffic pattern from home to the parking lot. We can then write the SOC stochastic dynamics for BEV i as follows [28,35]:

$$\begin{array}{c}\hfill d{x}_{i,t}=\frac{\alpha }{{\beta }_i}{U}_{i,t}dt+\nu d{\omega }_i,\end{array}$$

(1)

where $t\in [t_0,T]$ is the time in h, $x_{i,t}$ is the SOC in pu (per unit) of capacity, $\alpha \in [-1,1]$ is the charger efficiency in pu/h (where $\alpha >0$ when charging and $\alpha <0$ when discharging), ${\beta }_i\in {\mathbb{N}}^{\ast }$ is the battery capacity in kWh, $U_{i,t}\in {\mathbb{R}}^{+}$ is the charging or discharging rate in kW (note that $U_{i,t}$ is maximally bounded by $P_{max}$, a physical maximum charging or discharging rate), ${\omega }_i$ is a normalized Brownian process, $\nu$ is the intensity of that Brownian noise, and ${\omega }_i$ is assumed to be independent of ${\omega }_j$ for $i\ne j$. The term $\nu d{\omega }_i$ defines the stochasticity of the battery model, which can result physically from fluctuations when charging or discharging.

2.1.2. Homogeneous Batteries

We consider an elementary battery model to replace the N heterogeneous BEVs with capacities ${\beta }_i$ with n elementary homogeneous batteries with a capacity of 1 kWh, i.e.,

$$\begin{array}{c}\hfill n=\sum _{i=1}^N{\beta }_i.\end{array}$$

(2)

We can then rewrite (1) as follows:

$$\begin{array}{cc}\hfill d{x}_{i,t}& =\alpha \frac{U_{i,t}}{{\beta }_i}dt+\nu d{\omega }_i\hfill \\ \hfill & =\alpha u_{i,t}dt+\nu d{\omega }_i.\hfill \end{array}$$

(3)

In conclusion, we use heterogeneous batteries as integer multiples of the elemental building block batteries of 1 kWh. In effect, once the charging or discharging rate policy $u_{i,t}^{\ast }$ for the elemental battery building block is determined, the real charging or discharging rate policy $U_{i,t}^{\ast }$ will be a multiple of that associated with the building block, i.e.,

$$\begin{array}{c}\hfill U_{i,t}^{\ast }={\beta }_i{u}_{i,t}^{\ast }.\end{array}$$

(4)

This results in one simple control policy $U_{i,t}^{\ast }$, in contrast to [27], for the N heterogeneous BEVs.

2.2. Establishment of Individual Battery Cost Function

In a game theory context [27,28,44,45], the local cost function of charging or discharging a BEV, i, $i=1,\dots ,N$, to be minimized is given by

$$\begin{array}{c}\hfill J_i(x_{i,0},u_{i,t})=\mathbb{E}\left[{\int }_{t_0}^T{e}^{-\delta t}\left[\frac{r}{2}{u}_{i,t}^2+\frac{q_t^y}{2}{(x_{i,t}-y)}^2+\frac{q_{x_0}}{2}{(x_{i,t}-x_{i,0})}^2\right]dt|x_{i,0}\right],\end{array}$$

(5)

where the variables are as follows:

(i)

$[t_0,T]$ is the control horizon.

(ii)

$\delta >0$ is a discount coefficient to guarantee the convergence of the cost J in a context of extension to an infinite horizon ($T\to \infty$). Then, $\delta =0$ for a finite horizon $[t_0,T]$.

(iii)

r is a coefficient common to all BEVs which penalizes charging or discharging intensity. Therefore, we would like it to be as small as possible.

(iv)

$x_{i,t}$ is the state of charge of BEV i at time t. Note that at $t_0$, the states of charge $x_{i,0},i=1,\dots ,N$ of BEVs are assumed to be known, with a finite mean ${\overline{x}}_0$ and a finite standard deviation (STD) ${\sigma }_{x_{i,0}}$.

(v)

y is a state-of-charge value serving as a possible final destination for $x_{i,t}$ Therefore, $y=1$ in the vehicle charging problem and $y=0$ in the vehicle discharging problem.

(vi)

$q_t^y$ is a coefficient, at time t, common to all BEVs which penalizes any distance from y. Then, $q_t^y$ is the pressure field that would give priority to the less-full BEVs upon arrival. It would be calculated in the reverse engineering mechanism (called inverse Nash) [27,28,45] detailed in Appendix A, the aim of which is to reduce the standard deviation in the states of charge of BEVs at the end of charging or discharging. It is $q_t^y$ that creates the link between agents (here, BEVs) in the game (i.e., as the mean field).

(vii)

$q_{x_0}$ is a coefficient common to all BEVs which penalizes any distance from $x_{i,0}$. Then, $q_{x_0}$ would preserve the order of the states of charge upon arrival and so, added with the effect of $q_t^y$, the emptiest BEVs upon arrival must in no way exceed those arriving fuller. We consequently obtain a fair and decentralized algorithm.

2.3. Implementation of the MFG Inverse Nash Algorithm

The MFG inverse Nash algorithm, with mathematical details in Appendix A, is developed in this paper to charge BEVs in a solar-powered parking lot and discharge BEVs into the grid under the following assumptions:

(i)

The MFG inverse Nash algorithm is implemented under deterministic consideration, i.e., the data on solar acquisition in the parking lot, the duration of the evening peak, and the numbers of arriving and departing BEVs are assumed to be known in advance, such that all BEVs start and finish charging or discharging at the same time.

(ii)

There exists a two-way communication infrastructure to coordinate BEVs charging in the parking lot or discharging into the grid.

(iii)

BEV owners use chargers that are equipped with microprocessors allowing them to compute and implement a local feedback-based algorithm for charging or discharging their batteries.

(iv)

BEV owners communicate their battery energy on their usable capacity upon arrival (for example, 25 kWh/100 kWh 0.25 of SOC) and then the aggregator provides them with the common pressure field trajectory $q_t^y$ that each BEV owner uses to locally compute their optimal feedback-based charging or discharging policy $U_{i,t}^{\ast }$.

2.4. MFG Inverse Nash Algorithm for Charging or Discharging Heterogeneous BEVs

Figure 1 shows the outline of the operation of the MFG inverse Nash algorithm (Algorithm 1) for charging or discharging heterogeneous BEVs. Note that we propose also a simpler version of the Algorithm in Appendix B.

Algorithm 1 MFG Inverse Nash algorithm for Charging or Discharging Heterogeneous BEVs

Require: [DATA] time $t\in [t_0,T]$ (control horizon), $dt>0$ (step time), $u_{W_t}\in {\mathbb{R}}^{+}$ (power generation at time t for charging BEVs), $N>0$ (number of heterogeneous BEVs upon arrival, i.e., at $t_0$), $x_{i,0}\in [0,1],i=1,2,3,\dots ,N,$ (N BEVs’ SOCs at $t_0$), ${\beta }_i\in {\mathbb{N}}^{\ast }$ (N BEVs’ capacities), $n,n={\sum }_{i=1}^N{\beta }_i$, (elementary homogeneous batteries of 1 kWh), ${\overline{x}}_0$ (average of N BEVs’ SOCs at $t_0$), $\alpha \in [-1,1],y\in [0,1],\nu >0,q_{x_0}>0,r>0,\delta \ge 0$. Part I—The aggregator computes the pressure field ($q_t^y$) of N heterogeneous BEVs using the steps: 1. Compute the average target SOC trajectory ${\overline{x}}_t^{target}$ by using (7) in the case of charging or (8) in the case of discharging, and then the corresponding $\frac{d{\overline{x}}_t^{target}}{dt}$. 2. Calculate the steady-state values $q_T^y=q_{x_0}\left(\frac{{\overline{x}}_T^{target}-{\overline{x}}_0}{y-{\overline{x}}_T^{target}}\right),{\pi }_T=\frac{-\delta +\sqrt{{\delta }^2+4\left[\frac{{\alpha }^2}{r}(q_{x_0}+q_T^y)\right]}}{2\left(\frac{{\alpha }^2}{r}\right)}$ and ${\overline{s}}_T={\pi }_T(y-{\overline{x}}_T^{target})$. 3. Solve $\frac{d{\overline{s}}_t}{dt}=\frac{{\overline{s}}_t^2{\alpha }^2}{r(y-{\overline{x}}_t^{target})}+{\overline{s}}_t\left[\delta +\frac{\frac{d{\overline{x}}_t^{target}}{dt}}{y-{\overline{x}}_t^{target}}\right]+q_{x_0}({\overline{x}}_0-y)$ backwards, knowing ${\overline{s}}_T$. 4. Compute ${\pi }_t=\frac{1}{y-{\overline{x}}_t^{target}}\left({\overline{s}}_t+\frac{r}{{\alpha }^2}\frac{d{\overline{x}}_t^{target}}{dt}\right)$, and then $\frac{d{\pi }_t}{dt}$ by using mean value theorem. 5. Compute $q_t^y=\frac{{\alpha }^2}{r}{\pi }_t^2+\delta {\pi }_t-\frac{d{\pi }_t}{dt}-q_{x_0}$. Part II—Each BEV $i,i=1,\dots ,N$, computes its local optimal feedback strategy using the steps: 1. Solve $\frac{d{s}_{i,t}}{dt}=\frac{{\alpha }^2}{r}{\pi }_t{s}_{i,t}+\delta s_{i,t}+q_{x_0}(x_{i,0}-y)$ backwards, knowing $s_{i,T}=\frac{{\pi }_T{q}_{x_0}(y-x_{i,0})}{q_{x_0}+q_T^y}$. 2. Compute $U_{i,t}^{\ast }=-\frac{\alpha }{r}\left[{\pi }_t(x_{i,t}-y)+s_{i,t}\right]{\beta }_i$, and then solve $d{x}_{i,t}^{\ast }=\frac{\alpha }{{\beta }_i}{U}_{i,t}^{\ast }dt+\nu d{\omega }_i$.

3. Charging a Large Population of Heterogeneous BEVs in a Parking Lot

3.1. Experimental Platform and Data Sources in the Case of Charging

(i)

Population of BEVs based on realistic data [56,57]: We consider BEVs with 10 different capacities $\beta$, and a charger efficiency $\alpha =0.85$. Each BEV could use at most a charger which can deliver up to $P_{max}=20$ kW of charging rate (i.e., $max\left(U_{i,t}^{\ast }\right)\le 20$ kW).

(ii)

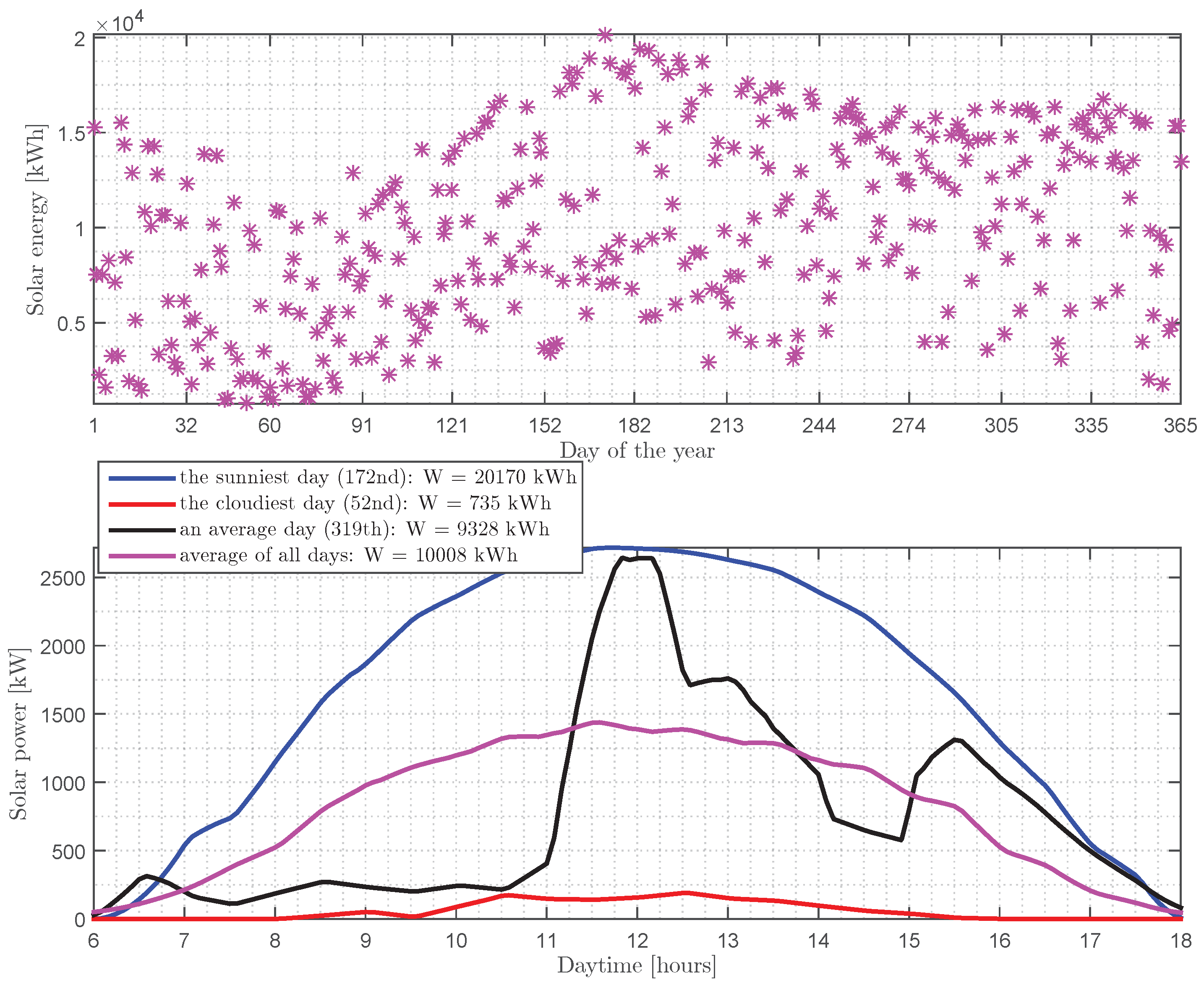
Simulation prerequisites: We consider charging $N=400$ heterogeneous BEVs between $t_0=6$ and $T=18$ (i.e., the charging of all BEVs in the parking lot starts at 6 a.m. and stops at 6 p.m.) with a random normal distribution of SOCs upon arrival (with an average of $0.15$ and a standard deviation of $0.10$), which is the result of a daily traffic pattern from home to the parking lot, and $dt=0.01$ h, $\delta =0,\nu =r=0.001,q_{x_0}=1,$ and $y=1$. The MFG inverse Nash algorithm and numerical results are carried out in Matlab 2021b software.

The number n of elementary batteries of 1 kWh, as in (2), and the average ${\overline{x}}_0$ of 400 heterogeneous BEVs’ SOCs upon arrival, illustrated in Figure 2, are given by

$$\begin{array}{c}\hfill n=\sum _{k=1}^{10}{\beta }_k{N}_{{\beta }_k},{\overline{x}}_0=\frac{1}{n}\sum _{k=1}^{10}{\beta }_k{N}_{{\beta }_k}{\overline{x}}_{0,{\beta }_k}.\end{array}$$

(6)

(iii)

Solar generation based on realistic data [28]: we consider installing 250 solar panels in a parking lot ($45.50$ North, $73.58$ West) in the city of Montréal (Québec, Canada) to obtain, in a year, daily solar power curves $u_{W_t}$ and daily solar energies $W={\int }_{t_0}^T{u}_{W_t}dt$ between 6 a.m. and 6 p.m., by using data from the Photovoltaic Geographical Information System (PVGIS) website and the Transient System Simulation (TRNSYS) tool.

We determined three different realistic solar power curves to compare the differences in solar generation on the behavior of the MFG inverse Nash charging algorithm. Note that the aggregator broadcasts the weather forecast the day before so that a majority of customers arrive in the parking lot with a state of charge with which they will not need to recharge their vehicle at another station at the end of the day. However, in this paper, for comparison purposes, we work with the same distribution of SOCs upon arrival, in Figure 2, as for the three days (the sunniest, an average, and the cloudiest), in Figure 3.

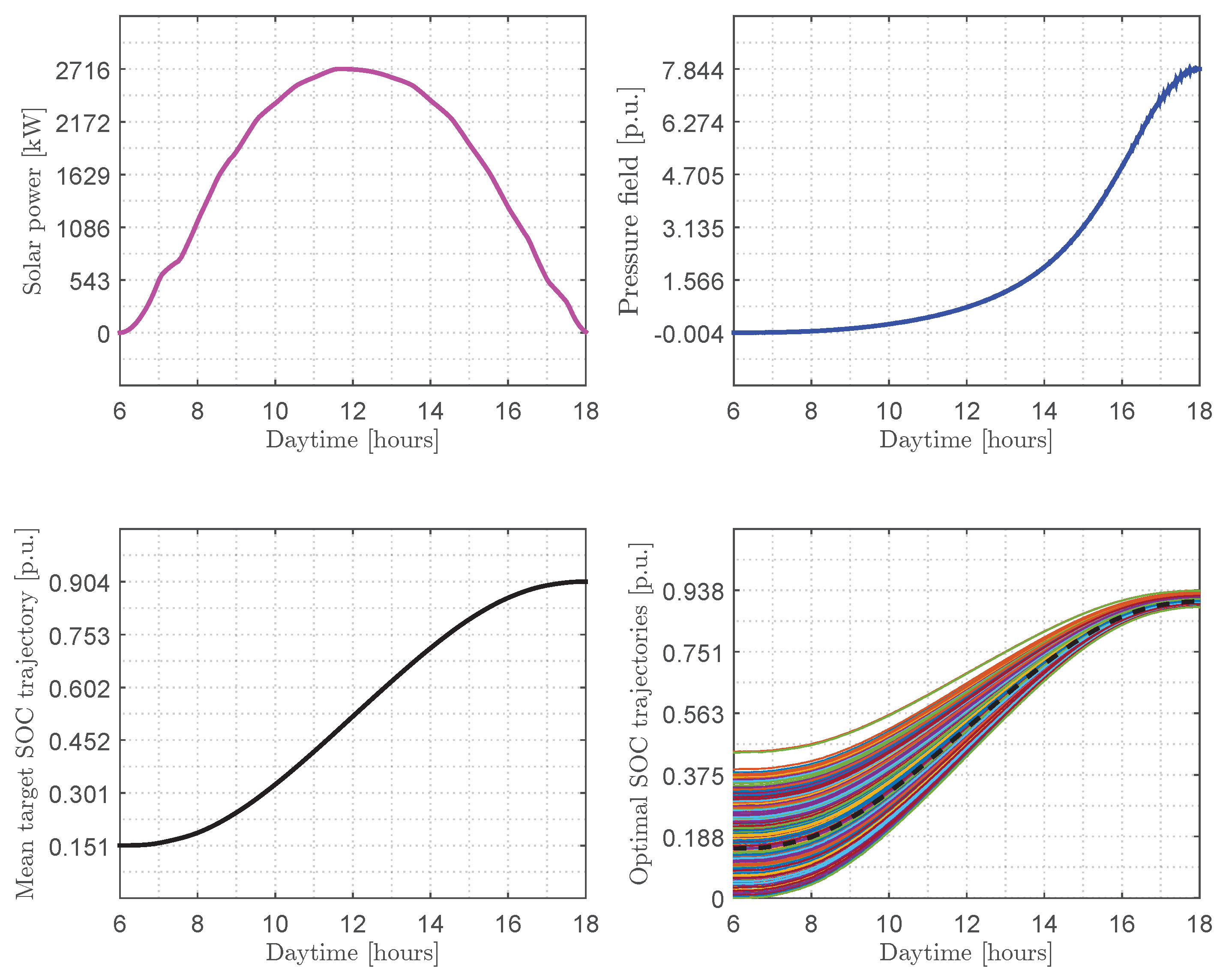
3.2. Calculation of the Average Target SOC Trajectory in the Case of Charging

In a reverse engineering mechanism for obtaining their optimal SOC trajectories $x_{i,t}^{\ast }$, which we explain in detail in Appendix A, all N heterogeneous BEVs use the average target SOC trajectory ${\overline{x}}_t^{target}$ (such that the empirical average SOC per BEV, ${\overline{x}}_t^{\ast }=\frac{1}{N}{\sum }_{i=1}^N{x}_{i,t}^{\ast }$, is equivalent to ${\overline{x}}_t^{target},\forall t\in [t_0,T]$), calculated as follows:

$$\begin{array}{cc}\hfill \frac{d{\overline{x}}_t^{target}}{dt}& =\frac{1}{n}\alpha u_{W_t},{\overline{x}}_{t_0}^{target}={\overline{x}}_0.\hfill \\ \hfill \Rightarrow {\overline{x}}_t^{target}& ={\overline{x}}_0+\frac{\alpha }{n}{\int }_t^T{u}_{W_t}d\tau ,\alpha >0,\hfill \end{array}$$

(7)

where $u_{W_t}$ is the assumed deterministic power curve such that, with the known quantities of n and ${\overline{x}}_0$ in (6) and $\alpha$, ${\overline{x}}_t^{target}$ will stabilize at a steady state ${\overline{x}}_T^{target}<1$.

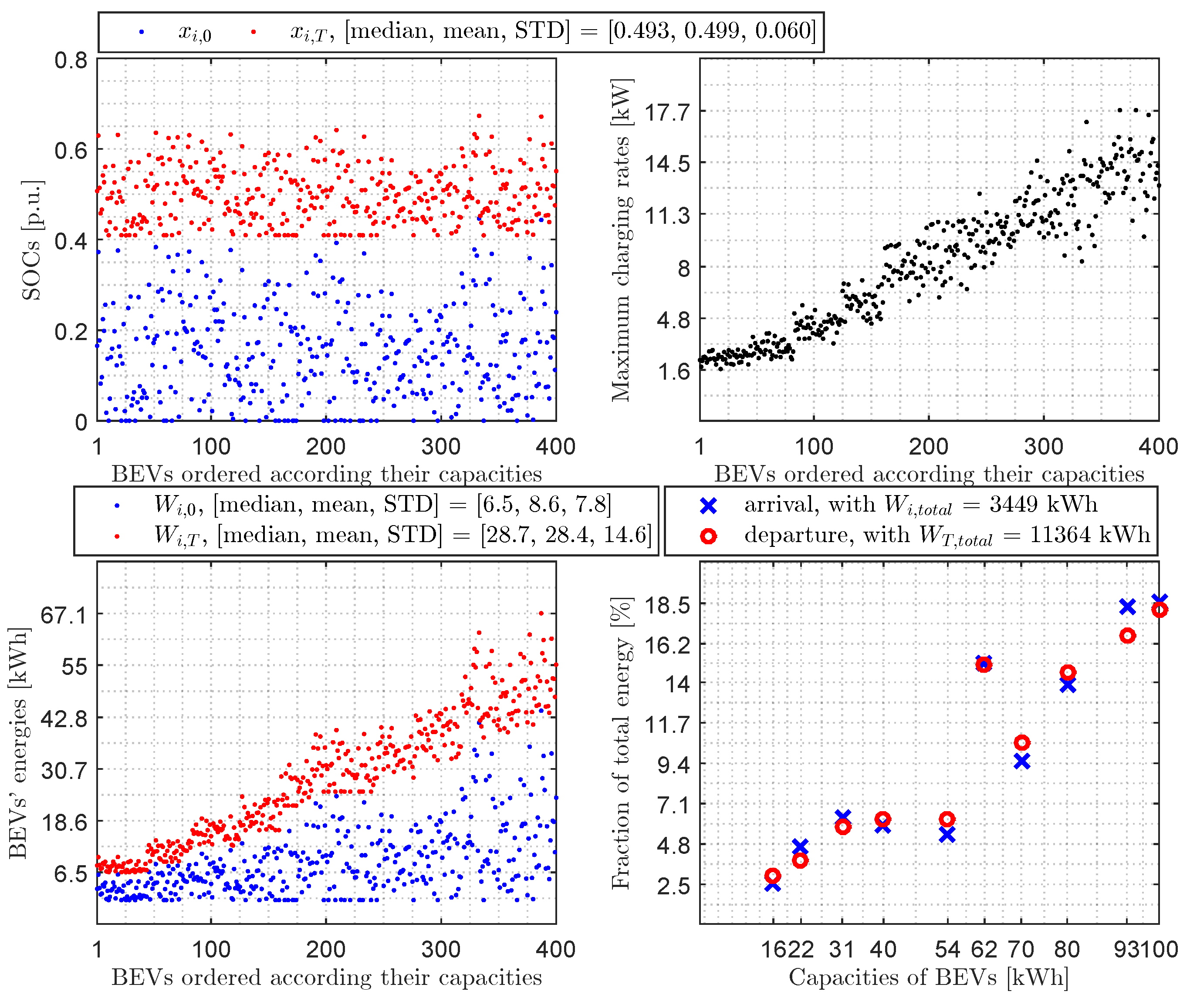
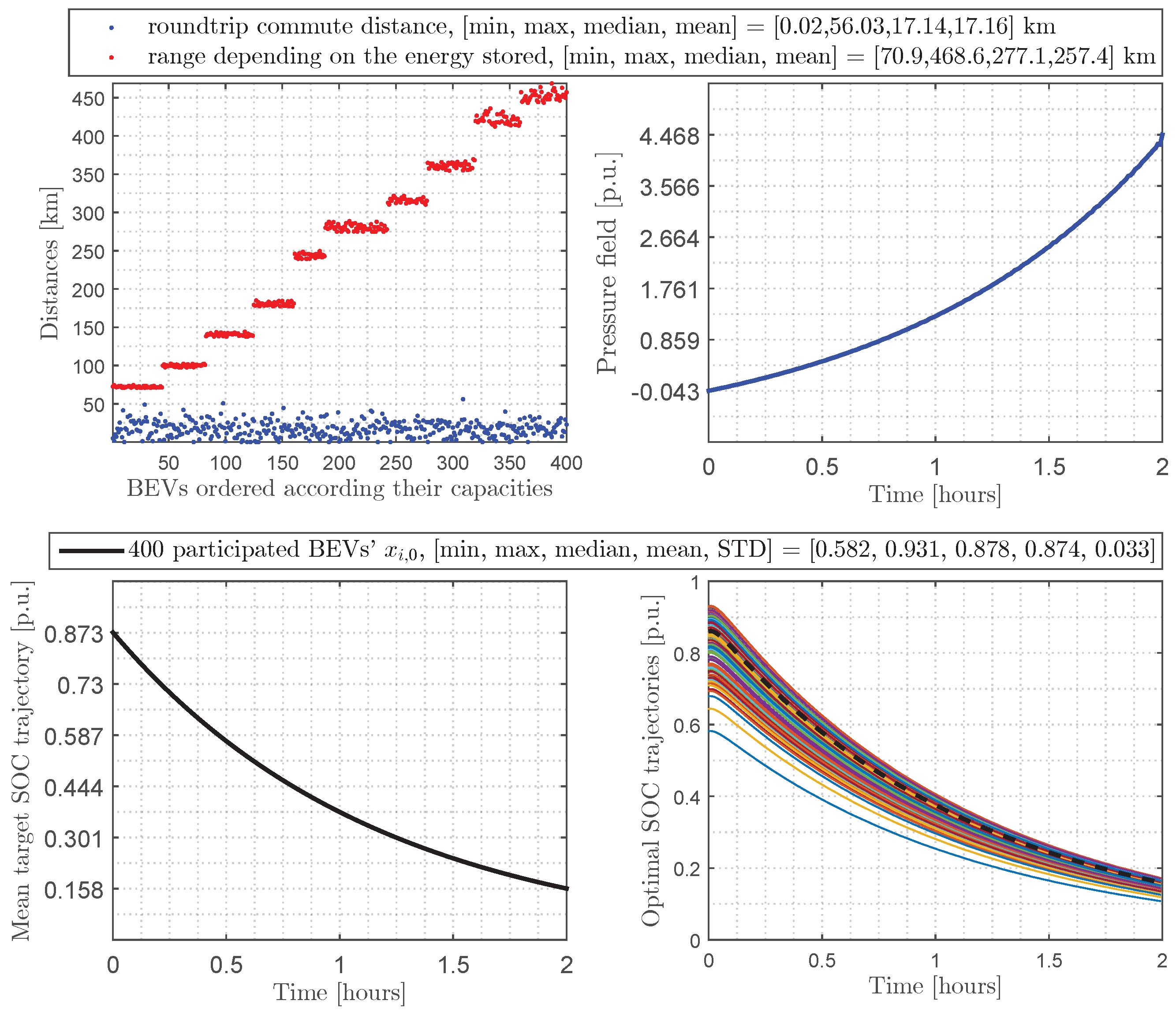
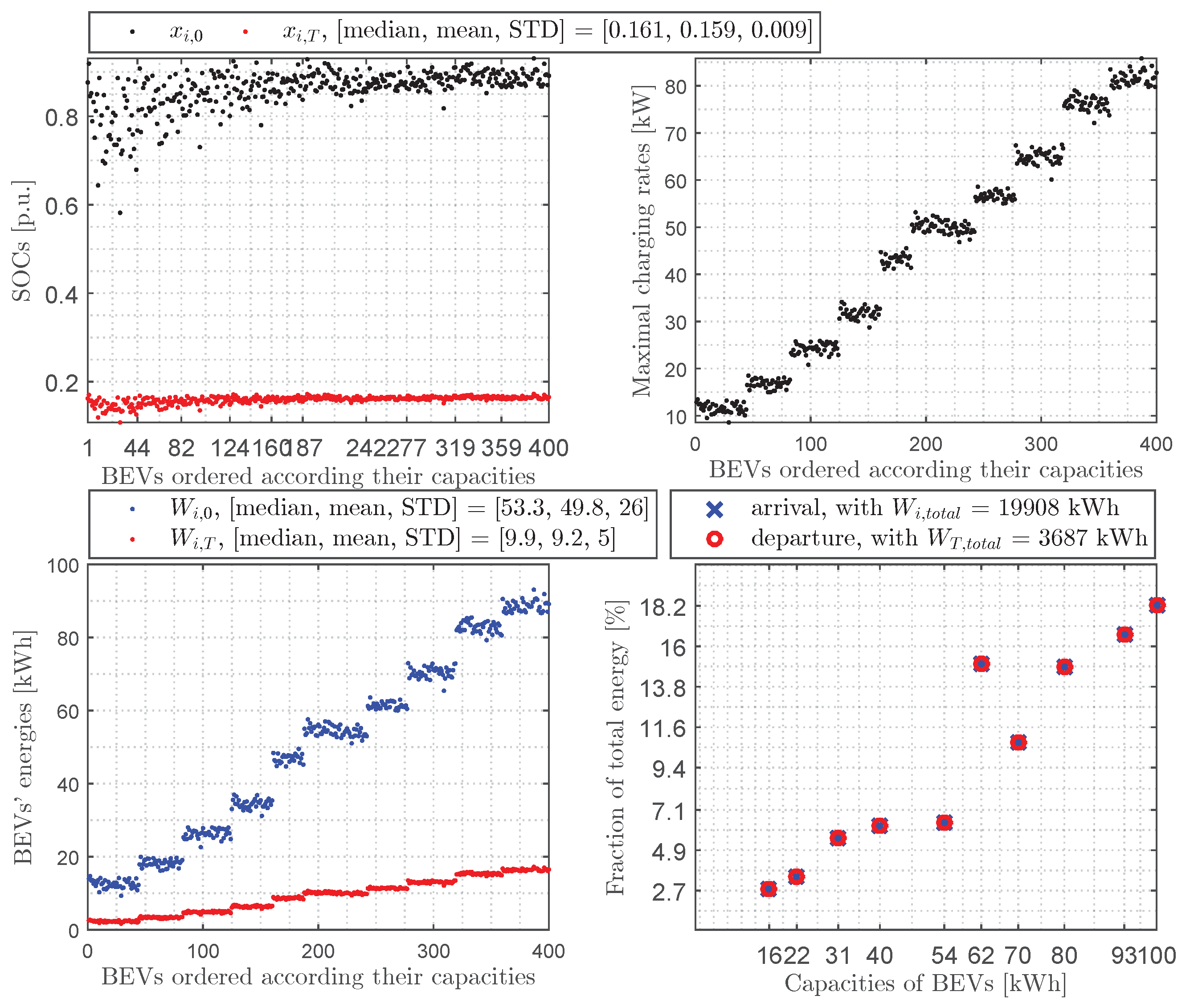
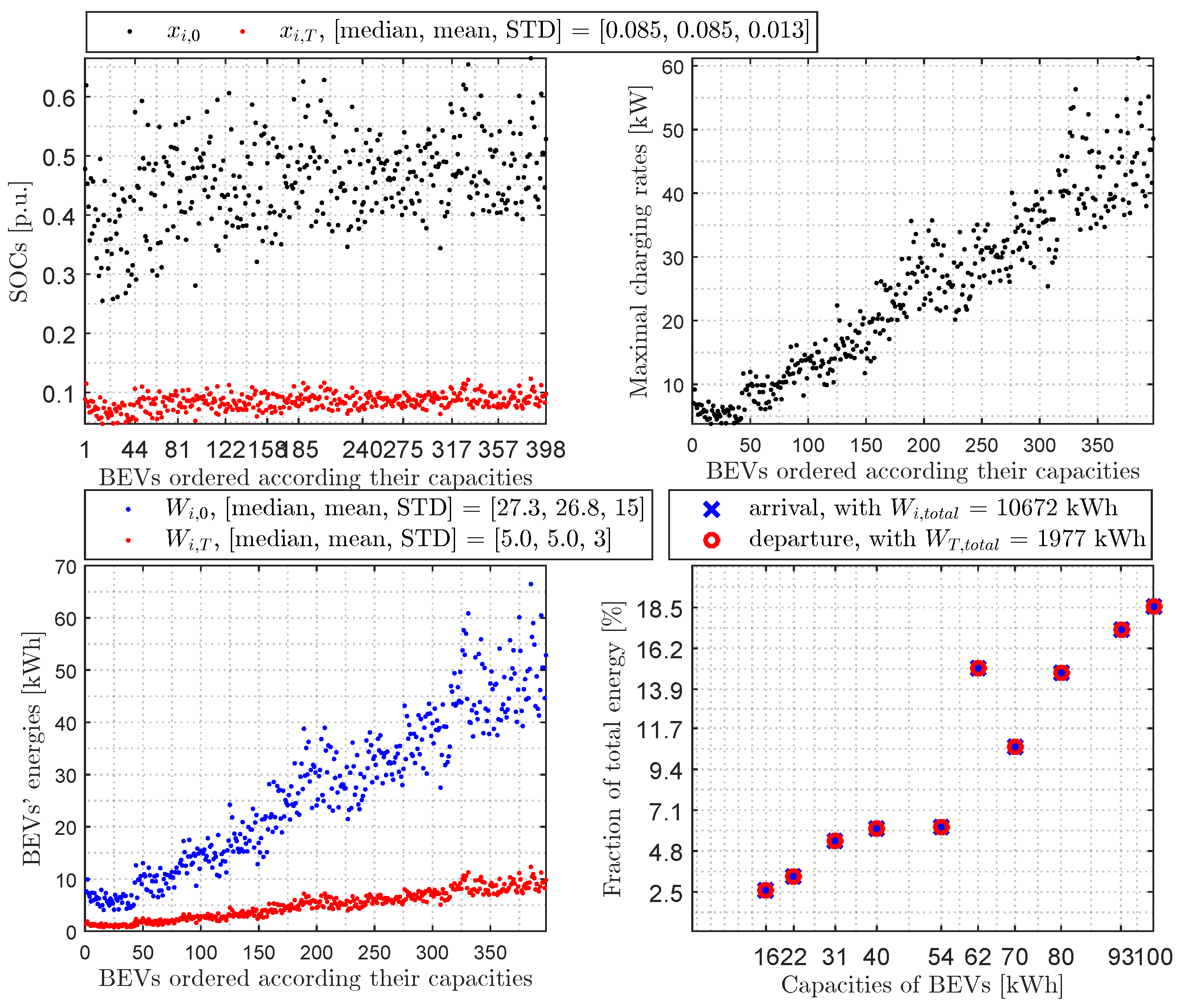
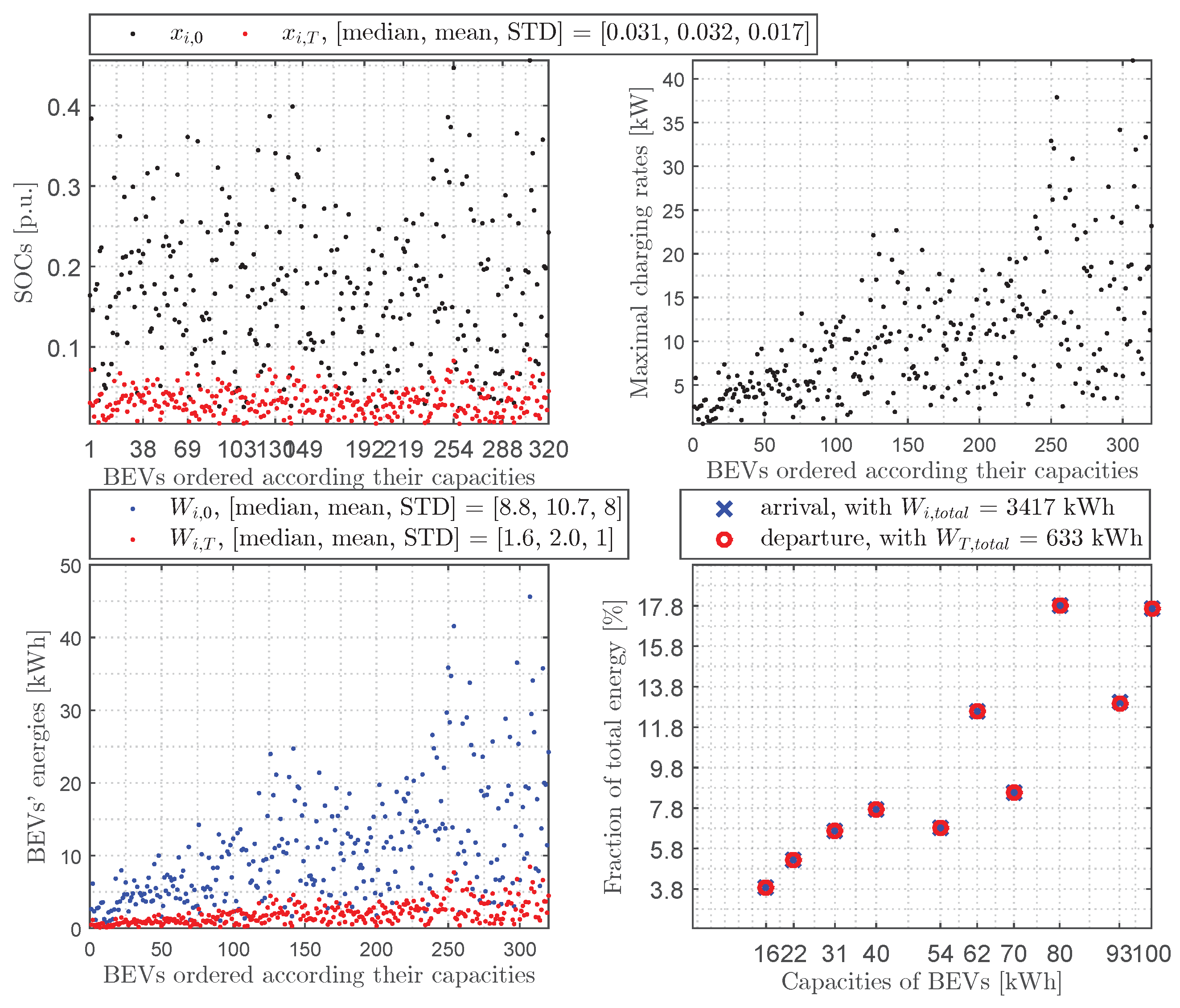
3.3. Numerical Results in the Case of Charging

In Figure 4, Figure 5 and Figure 6, we first notice that the trajectories, ${\overline{x}}_t^{target}$, obtained in (7) by integrating the solar power curve $u_{W_t}$, then $q_t^y$, obtained in (A15) by inverse Nash while using ${\overline{x}}_t^{target}$, finally $x_{i,t}^{\ast }$, obtained in (1) when BEVs locally apply their optimal control laws while using $q_t^y$, respectively, follow the fluctuations in the solar power curves for the three days (sunniest, average, and cloudiest). Then, we see that the reduction in the standard deviation in the optimal SOC trajectories $x_{i,t}^{\ast }$ is proportional to $q_t^y$, where its steady state $q_T^y$ is proportional to $q_{x_0}$ and ${\overline{x}}_T^{target}$, with the latter proportional to the available solar energy W.

In Figure 7, Figure 8 and Figure 9, as expected, we first see a reduction in the standard deviation, proportional to $q_T^y$, in the SOCs upon departure $x_{i,T}$ for the three days ($89\%$ for the sunniest case, $41\%$ for an average case, and $3\%$ for the cloudiest case) regardless of their SOCs upon arrival $x_{i,0}$ and their battery capacities ${\beta }_i$ (as confirmed in Table A1). Then, we notice that the maximum charging rates $U_{i,max}^{\ast }$ of BEVs at a given time depend on the quantity of energy available W, their SOCs upon arrival $x_{i,0}$, and their battery capacities ${\beta }_i$. We also confirm that the condition of the maximum charging rate of 20 kW, for a BEV charger, is well respected (i.e., $U_{i,max}^{\ast }\le 20$ kW). Note that we chose an adequate value of $q_{x_0}$, with respect to Appendix A in (A18), to satisfy the latter condition. Finally, the results upon departure of the BEVs’ energies $W_{i,T}$ and the fractions of total energy $f_{W_{T,\beta }}$ depend on the available solar energy W, their energies upon arrival $W_{i,0}$, and their battery capacities ${\beta }_i$. More detailed numerical results in Appendix C in the case of charging confirm all these tendencies.

4. Discharging a Large Population of Heterogeneous BEVs into the Grid

4.1. Experimental Platform and Data Sources in the Case of Discharging

(i)

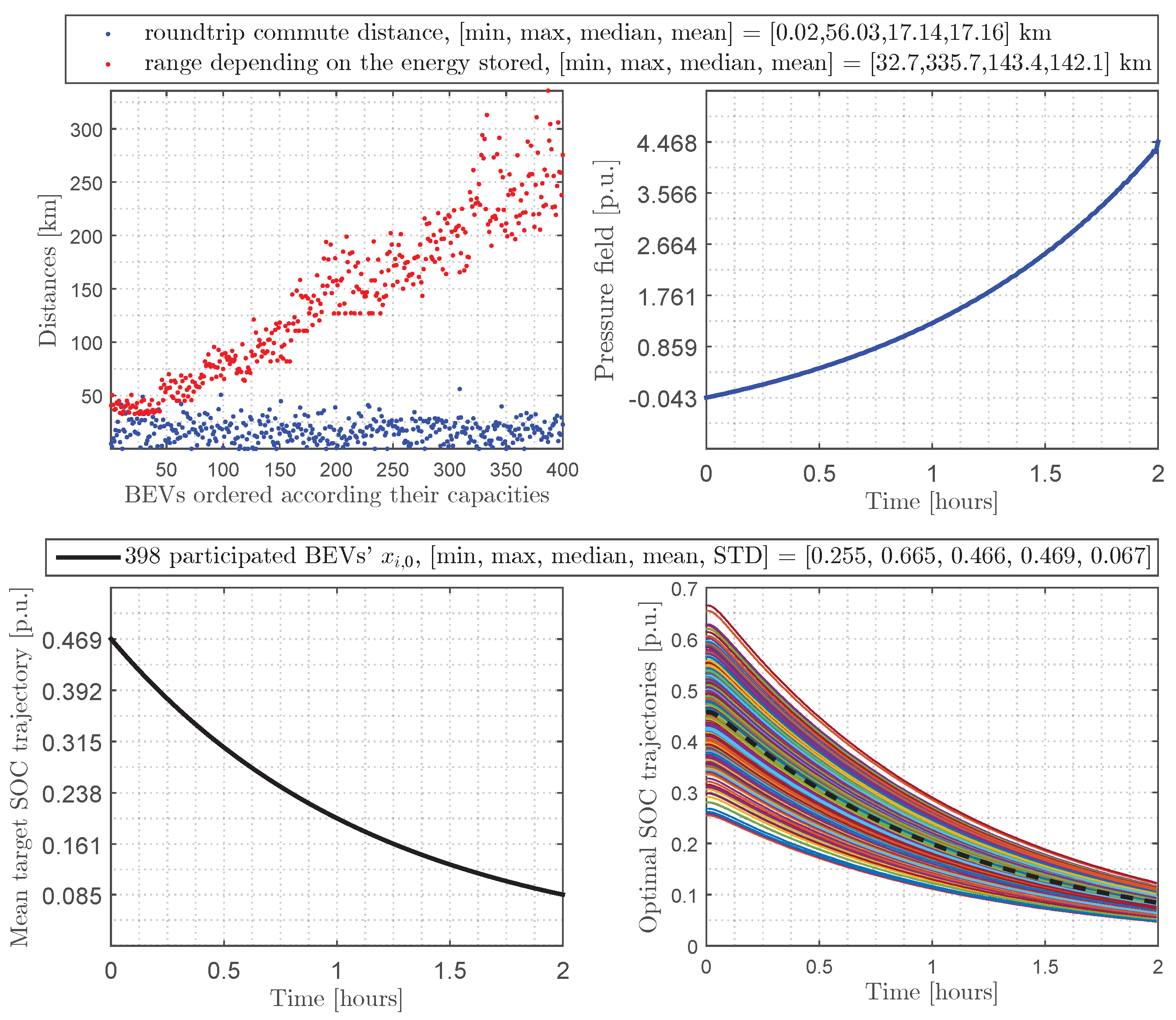
Population of BEVs based on realistic data [56,57,58]: We consider BEVs with a charger efficiency $\alpha =-0.85$ and an average consumption of $0.2$ kWh/km. Each BEV could use at most a charger which can deliver up to $P_{max}=100$ kW of discharging rate (i.e., $max\left(U_{i,t}^{\ast }\right)\le 100$ kW). Also, the commute distances are a random normal distribution with an average of 9 km and a standard deviation of 5 km. Therefore, a BEV with a roundtrip commute distance superior to its range according to its energy stored would not participate in the discharging operation into the grid during peak evening hours.

(ii)

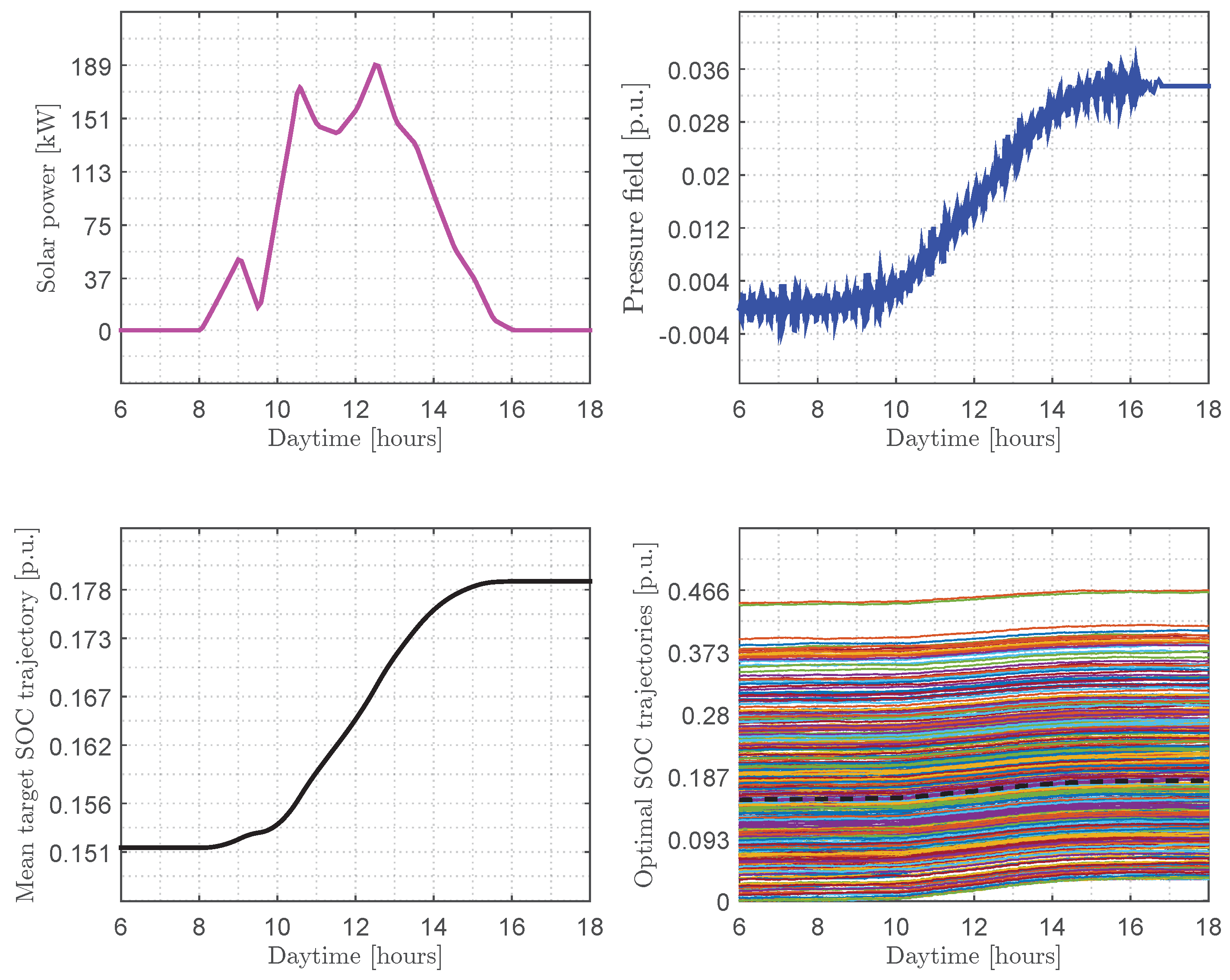
Simulation prerequisites: We consider discharging all participating BEVs into their homes during the evening peak of 2 h (i.e., $t_0=0$, $T=2$), and $dt=0.01$ h, $\delta =0,\nu =r=0.001,q_{x_0}=1,$ and $y=0$. Finally, the MFG inverse Nash algorithm and numerical results are carried out in Matlab 2021b software.

4.2. Calculation of the Average Target SOC Trajectory in the Case of Discharging

The vehicle discharging problem presents a particular difficulty if it is not correctly formulated. Indeed, the energy demand of the grid corresponds to a constant power over a finite horizon $[t_0,T]$. So, we need to remove the energy at a constant power over a finite horizon, $[t_0,T]$, by dropping the power exponentially to compute the average target SOC trajectory ${\overline{x}}_t^{target},\forall t\in [t_0,T]$, which will stabilize at a steady state ${\overline{x}}_T^{target}>0$.

$$\begin{array}{cc}\hfill \frac{d{\overline{x}}_t^{target}}{dt}& =\alpha {\overline{x}}_t^{target},{\overline{x}}_{t_0}^{target}={\overline{x}}_0.\hfill \\ \hfill \Rightarrow {\overline{x}}_t^{target}& =e^{\alpha t+ln{\overline{x}}_0},\alpha <0,t_0=0.\hfill \end{array}$$

(8)

The resulting average target SOC trajectory ${\overline{x}}_t^{target}$ in (8), with the known quantities of $\alpha$ and ${\overline{x}}_0$ (as calculated in (6) with only the participating BEVs), is then used by all participating heterogeneous BEVs to obtain their optimal SOC trajectories $x_{i,t}^{\ast }$ in a reverse engineering mechanism, as in the case of charging, which we explain in Appendix A.

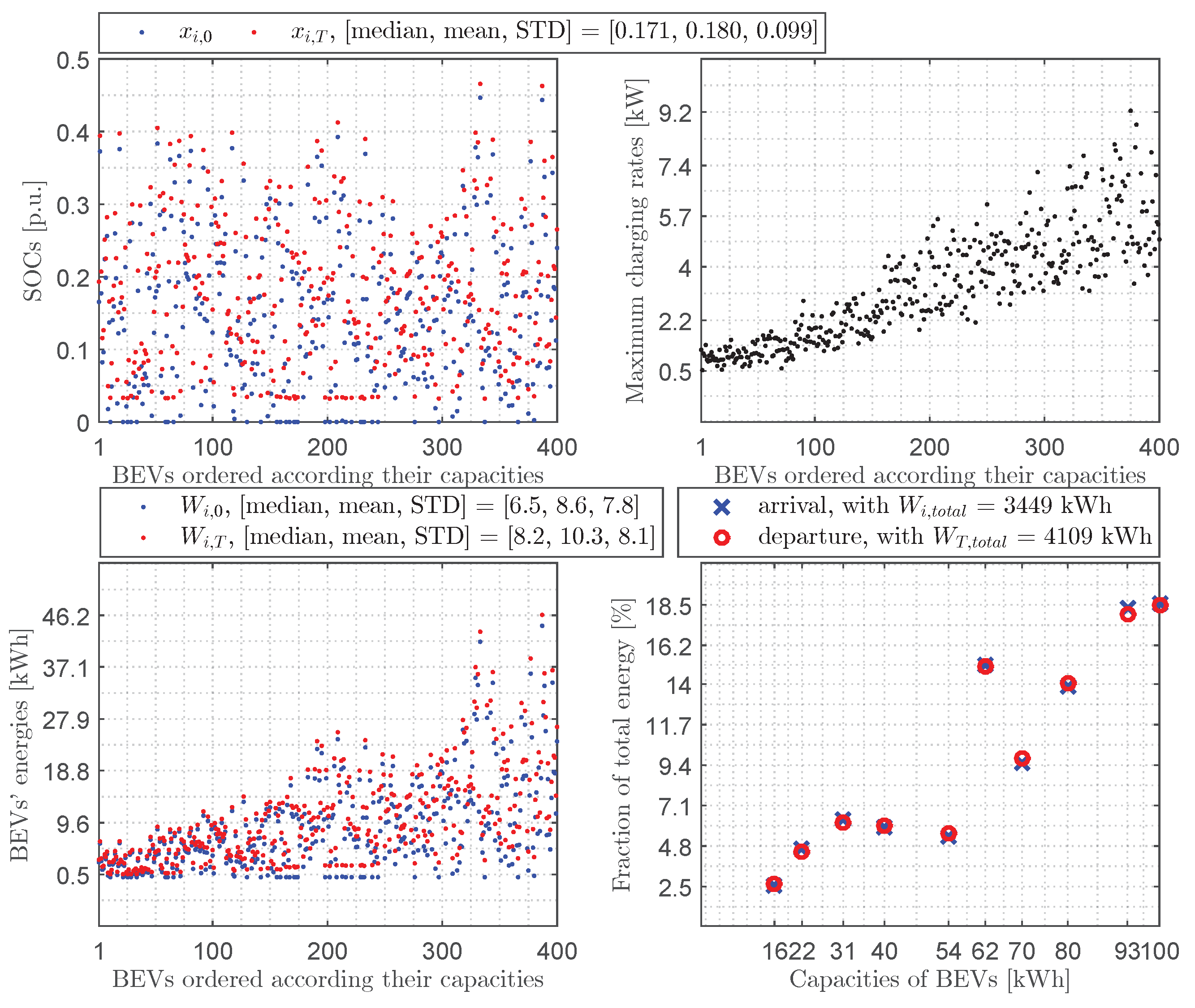
4.3. Numerical Results in the Case of Discharging

In Figure 10, Figure 11 and Figure 12, we first notice that the trajectories ${\overline{x}}_t^{target}$, obtained in (8) by exponentially dropping the energy in the participating BEVs (as observed in top left of these figures) for two straight hours during the evening peak, then $q_t^y$, obtained in (A15) by inverse Nash while using ${\overline{x}}_t^{target}$, finally $x_{i,t}^{\ast }$, obtained in (1) when BEVs locally apply their optimal control laws while using $q_t^y$, are, respectively, smooth exponential functions for the three days (sunniest, average, and cloudiest). From the trajectories ${\overline{x}}_t^{target}$, we expect for the three days that all BEVs restore into the grid approximately $82\%\left(\frac{{\overline{x}}_0-{\overline{x}}_T^{target}}{{\overline{x}}_0}\right)$ of their total energy upon arrival $W_{i,total}$. Therefore, for the three days, we have the same trajectory $q_t^y$ and the same reduction in standard deviation in the optimal SOC trajectories $x_{i,t}^{\ast }$.

In Figure 13, Figure 14 and Figure 15, as expected, we first see the same reduction of $82\%$ in the standard deviation in the SOCs at the end of discharging $x_{i,T}$ for the three days regardless of their SOCs upon arrival $x_{i,0}$ and their battery capacities ${\beta }_i$ (as confirmed in Table A1). Then, we notice that the maximum discharging rates $U_{i,max}^{\ast }$ of BEVs at a given time depend on the quantity of available energy $W_{i,total}$, their SOCs upon arrival $x_{i,0}$ and their battery capacities ${\beta }_i$. We also confirm that the condition of the maximum discharging rate of 100 kW, for a BEV charger, is well respected (i.e., $U_{i,max}^{\ast }\le 100$ kW). Note that we chose an adequate value of $q_{x_0}$, with respect to Appendix A in (A19), to satisfy the latter condition. Finally the results at the end of discharging of the BEVs’ energies $W_{i,T}$ and the fractions of total energy $f_{W_{T,\beta }}$ depend on the available energy $W_{i,total}$, their energies upon arrival $W_{i,0}$, and their battery capacities ${\beta }_i$. The more detailed numerical results in Appendix C in the case of discharging confirm all these tendencies.

5. Conclusions

In this paper, we have considered a large daytime work solar-powered parking lot with heterogeneous BEVs. We first developed a Mean Field Game-based algorithm to charge heterogeneous BEVs under deterministic consideration, i.e., the data of the parking lot for the number of BEVs upon arrival and the solar power generation are supposed to be known in advance. Then, we considered a large amount of energy restitution to the grid during peak evening hours using heterogeneous BEVs with a satisfactory level of energy in their batteries. We then developed a Mean Field Game-based algorithm to discharge heterogeneous BEVs also under deterministic consideration, i.e., the data for the number of participating BEVs in their residences and the duration of the evening peak are also supposed to be known in advance.

Both algorithms, fair and decentralized, were developed based on realistic data while considering the physical constraints of vehicle batteries for the sunniest day, an average day, and the cloudiest day of the year, where the goal was to reduce the BEVs’ SOC standard deviation at the end of charging and discharging. This resulted in the following:

(i)

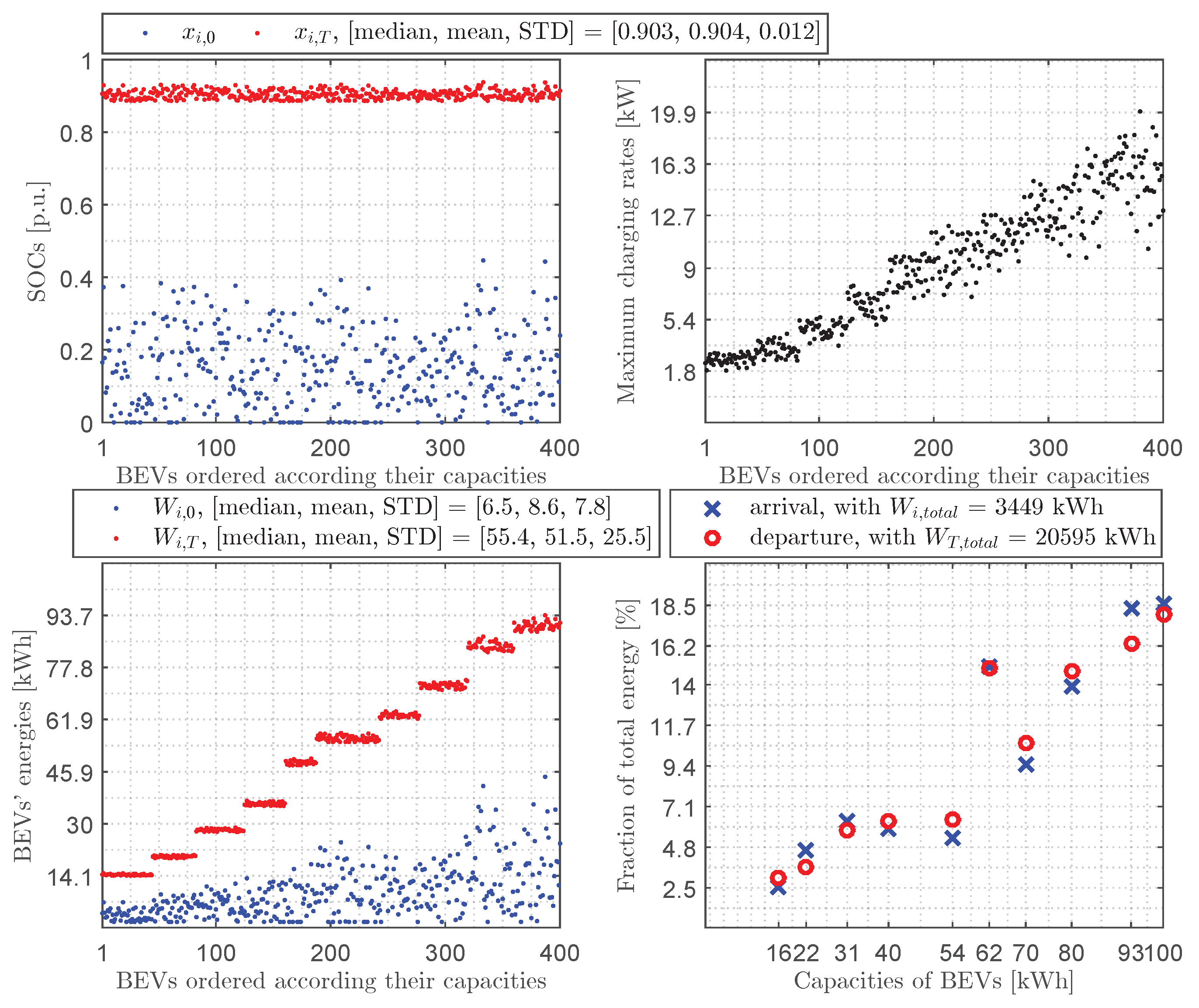
In the case of charging: we elevated the BEVs’ SOCs upon departure , by using all the solar energy in the parking lot, to a satisfactory level (on average, an increase of $500\%$ for the sunniest day, $230\%$ for an average day, and $20\%$ for the cloudiest day) while reducing their standard deviation regardless of their SOC upon arrival to maximize the number of participating BEVs, which would help to decongest the grid during peak evening hours.

(ii)

In the case of discharging: we restored into the grid the same fraction of $82\%$ of the total energy of BEVs upon arrival for the three days.

A comparison was carried out with the results for the three days and, as expected, showed the following:

(i)

In the case of charging: we achieved a strong to slight reduction in the standard deviation in the states of charge at the end, respectively, for the sunniest day ($89\%$), an average day ($41\%$), and the cloudiest day ($3\%$).

(ii)

In the case of discharging: for the three days, we achieved the same reduction of $82\%$ in the standard deviation in the states of charge at the end and the same fractions of energies at the beginning and the end of discharging BEVs with the same battery capacity.

In future research, we shall extend this work by considering stochastic solar acquisition in the parking lot and explore Mean Field Game-based algorithms when the number of BEVs arriving at the parking lot and their homes and when departing from the parking lot fluctuates.