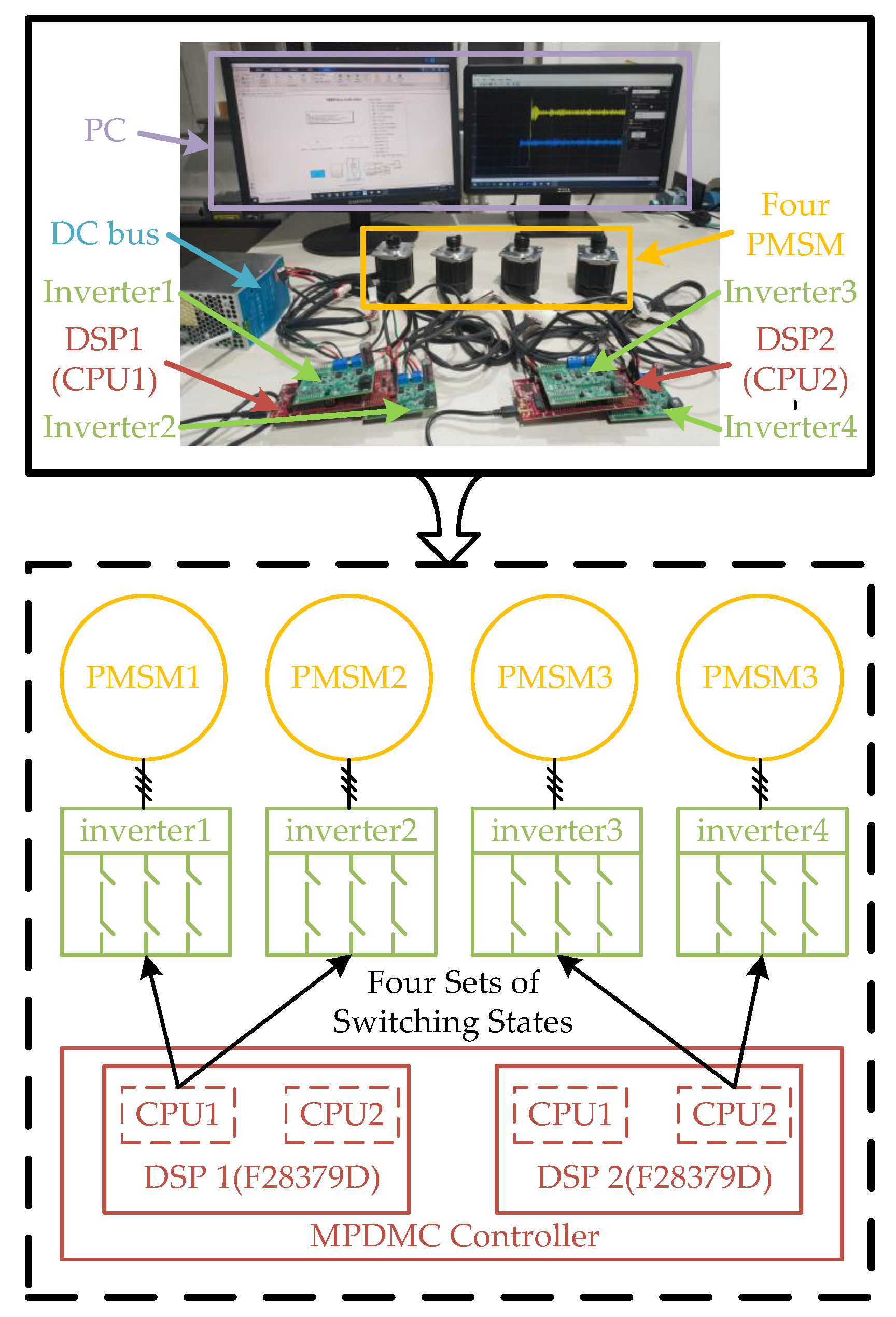
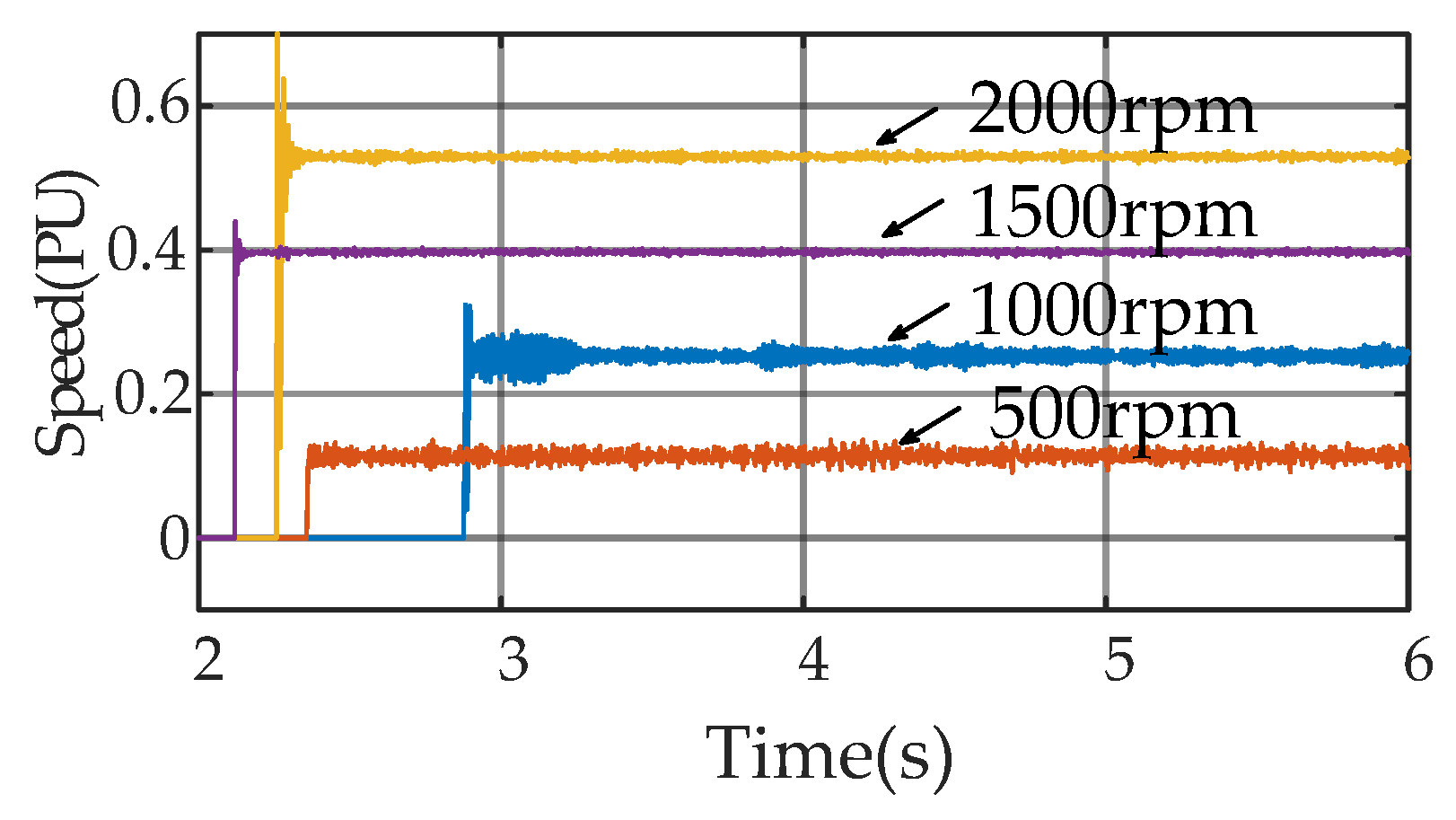
1. Introduction
Distributed drive electric vehicles (DDEVs) are garnering significant attention in vehicle research owing to their numerous benefits, including rapid dynamic response, streamlined chassis structure, and adaptable control systems. Unlike centralized drive setups, DDEVs provide greater controllability with additional degrees of freedom. However, their vehicle models display nonlinear characteristics, posing challenges for effective control. As a result, optimizing driving conditions has emerged as a pivotal focus in DDEV research endeavors.
Unlike centralized drive systems, DDEVs offer more controllable degrees of freedom, and their vehicle models exhibit nonlinear characteristics. Traditional control systems for DDEVs typically adopt a series-connected structure consisting of a vehicle controller and four wheel hub motor controllers. The vehicle controller, which takes the vehicle body state as the control object, designs overall control strategies to calculate torque expectations for the four wheel hub motors. Then, the wheel hub motor controllers utilize appropriate motor control strategies to calculate the input control signals for the inverters based on these torque expectations, thereby achieving vehicle state tracking. The vehicle controller used for driving and stability design often fully utilizes the independent controllability of each wheel of distributed drive electric vehicles to achieve motion control in longitudinal, lateral, and yaw directions. Firstly, reference [
1] presents a lateral dynamic control system tailored for electric vehicles, focusing on customized objectives to improve performance. Then, reference [
2] introduces a coordinated torque distribution method aimed at enhancing vehicle lateral stability and ride comfort by merging balanced torque vectoring distribution and differential braking methods. Moreover, reference [
3] proposes a coordinated control strategy specifically designed for DDEVs integrating adaptive model predictive control and direct yaw moment control to ensure yaw stability. Additionally, reference [
4] presents a hierarchical coordinated control strategy to address challenges in maintaining speed and desired distance within vehicle platoons, particularly under difficult conditions such as low adhesion or curves. Furthermore, reference [
5] introduces a robust framework merging active front-wheel steering with direct yaw moment control to bolster maneuverability and stability in DDEVs. Subsequently, reference [
6] devises a supervisory control strategy for DDEVs, amalgamating various controllers to enhance vehicle handling, lateral stability, and energy efficiency. Lastly, reference [
7] introduces an innovative motion control strategy utilizing model predictive control to handle longitudinal and lateral motion concurrently in DDEVs, resulting in cost reduction and improved handling performance through more efficient control mechanisms. Due to the advantages of the model predictive direct motion control strategy presented in reference [
7], such as its simple structure, high integration, and fast dynamic response, this paper chooses this control strategy as the foundational control strategy for DDEVs. Based on this strategy, the paper conducts research on centralized disturbance suppression in vehicles.
Model predictive control (MPC) offers simplicity in structure, excellent dynamic performance, and ease in handling nonlinear systems, making it highly promising for DDEVs. However, its efficacy in DDEVs hinges on the accuracy of the vehicle’s mathematical model for predicting future states. Variations in inertia parameters, nonlinear tire forces, and external disturbances can introduce inaccuracies. As a result, scholars globally have explored various disturbance suppression strategies for DDEVs, including centralized compensation methods, parameter identification techniques, and robust control strategies.
Implementing MPC in DDEVs presents several challenges. Firstly, the nonlinear characteristics of DDEVs escalate the complexity of required models for effective control. Secondly, the distributed drive system introduces additional control degrees of freedom, complicating predictive control design and execution. Moreover, DDEVs’ rapid dynamic response may strain computational resources as MPC optimizes across multiple future time steps, potentially impeding real-time performance. Additionally, real-time acquisition of vehicle state and environmental data poses a challenge, given their critical role in MPC control. Thus, effectively applying MPC in DDEVs remains a pertinent technical hurdle requiring resolution.
- (1)
Centralized Disturbance Compensation Methods
Firstly, some researchers aim to suppress the impact of disturbances on vehicle motion control by observing and compensating for these disturbances. In the context of lateral motion disturbance suppression, reference [
8] utilizes a second-order lateral dynamics model to consolidate parameter uncertainties and external disturbances into a disturbance term. They design an extended observer to estimate this disturbance and employ a robust nonlinear control strategy based on obstacle Lyapunov functions to compensate for the observed disturbance while achieving lateral vehicle control. In reference [
9], a sliding mode control strategy based on obstacle Lyapunov functions is employed to address unknown lateral tire forces, road curvature angles, and parameter uncertainties, achieving robust lateral vehicle control. Addressing disturbances caused by lateral wind, reference [
10] uses a combination of feedforward and feedback control strategies to achieve lateral vehicle control. They also use a disturbance observer to mitigate the effects of disturbances caused by lateral wind. To tackle the centralized disturbance issue resulting from model errors and complex driving environments, reference [
11] employs a nonlinear disturbance observer for estimation and compensation, resolving the sliding mode control oscillation problem caused by centralized disturbances. Reference [
12] adopts model predictive control as a vehicle stability control strategy, utilizing a disturbance observer based on extended Kalman filtering to estimate the equivalent additional yaw moment generated by external disturbances. This estimated moment is then incorporated into the linear vehicle model for compensation, but the article only considers model errors in the yaw direction. Reference [
13] uses a disturbance observer based on sliding mode theory to address uncertainties and unknown relationships between tire–road friction coefficients and vehicle slip ratio. They propose a nonlinear sliding mode surface. Reference [
14] employs an extended state observer to provide real-time estimation and compensation for unmodeled dynamics and unknown external disturbances.
- (2)
Parameter Identification Methods
Parameter identification methods are the primary approach for predicting and suppressing certain external disturbances in distributed drive electric vehicles, such as tire load, tire stiffness, vehicle mass, and center of gravity position. In reference [
15], intelligent tires with built-in sensors and vehicle states are employed to rapidly and stably estimate tire load and vehicle parameters (total mass, center of gravity position). Reference [
16] uses nonlinear particle filtering to estimate vehicle mass. Reference [
17] employs the method of least squares with dual forgetting factors and an extended Kalman particle filter to perform real-time estimation of vehicle mass and road incline. Reference [
18] utilizes a dual Kalman filter for real-time estimation of vehicle inertia parameters. In reference [
19], a sliding mode observer is designed to predict longitudinal and lateral tire forces separately. Reference [
20] adopts a cascaded observer approach to predict longitudinal and lateral tire forces. Reference [
21] utilizes existing vehicle sensors and a dual Kalman filter to design a state parameter observer, enabling real-time estimation of vehicle mass. The article also discusses the impact of mass changes on the vehicle. Reference [
22] employs Bayesian methods to predict tire stiffness.
- (3)
Disturbance-Resistant Robust Control Strategies
In addition to the aforementioned methods, some scholars have focused on enhancing the disturbance resistance capabilities of the strategies themselves. Reference [
23] proposes a robust controller with adaptive gain scheduling for stability control incorporating linear parameter-varying systems and H
∞-optimized control. This controller utilizes linear matrix inequalities to suppress system uncertainties and sensor noise. Reference [
24] designs a robust loop-shaping method and engineers weight functions according to engineering specifications. Through this control structure, the strategy can overcome issues related to model uncertainty, lateral wind disturbances, and parameter variations. Reference [
25] establishes a time-varying vehicle model considering changes in the center of gravity position and uses sliding mode control to achieve lateral stability control. Reference [
26] develops a vehicle lateral dynamics model incorporating combined slip tire forces considering tire force nonlinearity and combined slip friction effects. The authors use this model to design a model predictive controller that maintains the lateral response of the vehicle within a constrained stable region. To address uncertainties in parameters such as vehicle mass and longitudinal velocity, reference [
27] employs a polytope uncertainty approach to construct a linear parameter-varying lateral model. This leads to the design of an H
∞ feedback control algorithm based on linear matrix inequalities. Given the presence of many uncertain disturbances during vehicle operation, expressed as a random additional yaw moment, reference [
28] designs a state feedback elastic controller to ensure that yaw angle and yaw angular velocity meet performance criteria for H
∞ and L2-L
∞. Reference [
29] uses global sliding mode control theory to derive the discontinuous part of the control law, addressing issues related to changing vehicle parameters and model uncertainty. In response to external disturbances caused by lateral wind, reference [
30] designs a disturbance suppression strategy based on Lyapunov theory, restricting control objectives to a reasonable range. The article presents a complex model, capturing the effects of lateral wind, with disturbance terms in both the yaw and lateral directions. Reference [
31] uses a nonlinear model predictive control strategy to achieve stable control of vehicle lateral dynamics. To enhance controller performance, the authors propose a high-order neural network modeling method, enabling iterative optimization of the vehicle’s yaw angular velocity and steady-state response of the center of gravity lateral deviation.
DDEVs are electric vehicles where each wheel is powered independently by its own motor. This design offers several advantages, including improved traction, enhanced maneuverability, and more efficient energy usage. Here are some examples of DDEVs and their preferred fields of use: In reference [
32], Rivian’s electric pickup truck (R1T) and SUV (R1S) are equipped with four electric motors, one for each wheel. These vehicles are designed for off-road adventures and outdoor enthusiasts who require ruggedness, versatility, and all-terrain capabilities. In reference [
33], the Lordstown Endurance is an all-electric pickup truck designed for commercial fleets. It features four in-wheel hub motors, providing power to each wheel individually. This configuration enhances traction and stability, making it suitable for utility companies, delivery services, and other fleet operators. These examples demonstrate how DDEVs are utilized across various sectors, including off-road exploration, high-performance driving, commercial fleet operations, and luxury transportation. The distributed drive system offers benefits such as improved control, efficiency, and performance, making DDEVs versatile options for a range of applications.
Scholars have conducted in-depth research on electric vehicles. In reference [
34], a bilayer coordinated operation strategy is introduced for a multi-energy building microgrid (MEBM) to manage various uncertainties. This strategy involves a two-layer approach: first, employing a stochastic-weighted robust optimization-based day-ahead operation to dispatch energy storage assets and demand response followed by a second layer determining the operation of power-to-thermal conversion units, CCHP plants, and electricity transactions with the utility grid considering uncertainty realizations. In reference [
35], researchers address challenges in vehicle-to-grid (V2G) technology, aiming to improve load peak shaving, valley filling, and PV self-consumption. They introduce FedPT-V2G, a federated transformer learning method, to handle data distribution disparities among charging stations, facilitating real-time decision-making while preserving local privacy. This approach integrates deep learning models trained on past and present data, incorporating the Proximal algorithm and Transformer model to synchronize local models and leverage feature diversity, enhancing V2G scheduling predictions. Unlike these existing studies, the paper focuses on the control problem under the complex disturbances of distributed drive electric vehicles and proposes a centralized disturbance suppression strategy for disturbance mitigation.
In summary, vehicles experience the influence of multiple disturbance factors during operation. In the case of distributed drive electric vehicles, the research on disturbance suppression methods is more flexible and complex due to their multiple power sources. Implementing multiple-disturbance suppression through a multi-motor drive system for distributed drive electric vehicles is expected to significantly enhance the vehicles’ maneuvering performance under complex operating conditions.
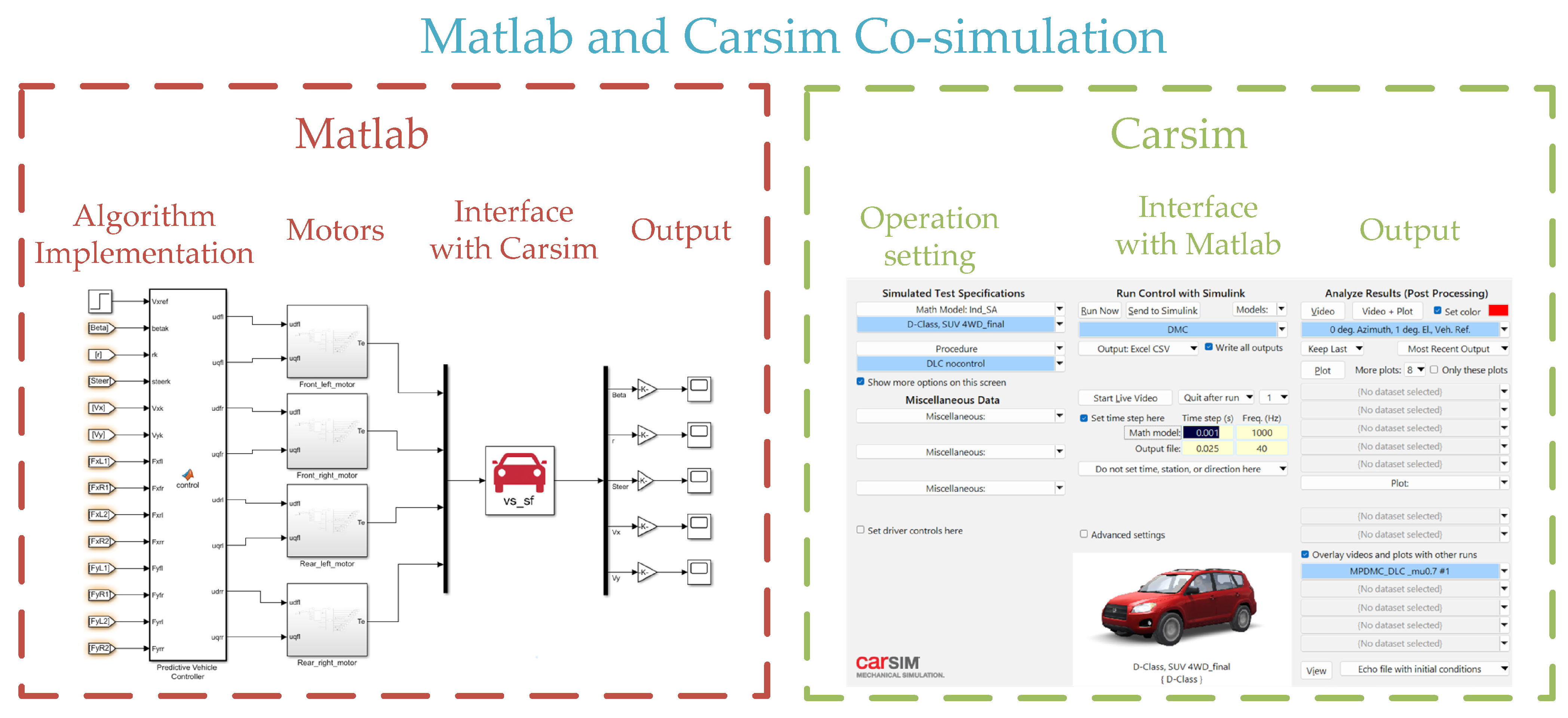
2. Model Predictive Direct Motion Control
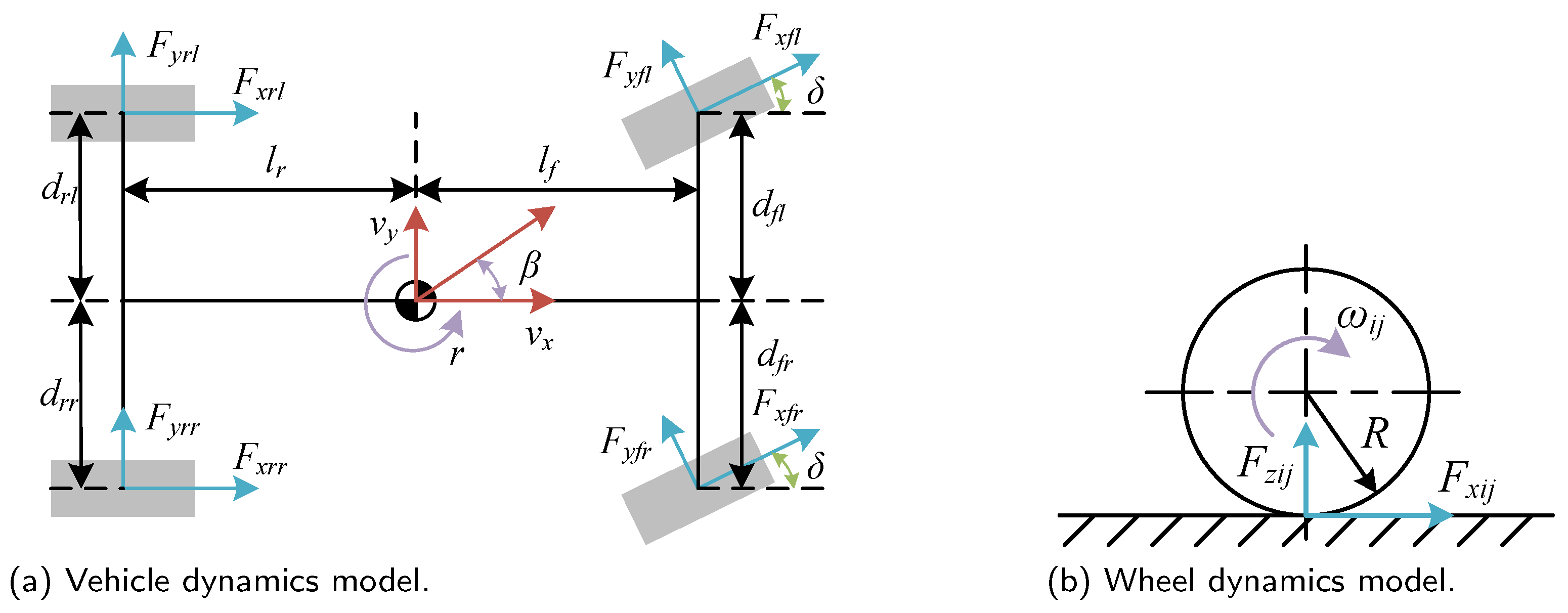
The mathematical model of a distributed drive electric vehicle is primarily divided into two parts: the vehicle mathematical model and the wheel hub motor mathematical model. The vehicle mathematics is depicted in
Figure 1, and its dynamic equation is as follows:
In the equations,
,
, and
r represent the longitudinal velocity, lateral velocity, and yaw angular velocity of the vehicle, respectively.
,
,
, and
denote the longitudinal forces experienced by the front left, front right, rear left, and rear right wheels, respectively.
,
,
, and
represent the lateral forces on the front left, front right, rear left, and rear right wheels, respectively.
is the steering angle of the front wheels,
m is the total vehicle mass,
and
represent the longitudinal distances from the vehicle’s center of gravity to the front and rear axles, respectively.
is the vehicle’s rotational inertia,
and
are the front and rear axle distances, respectively. Additionally, the dynamic equation for the wheels is as follows:
In the equations, represents the front or rear wheels, represents the left or right wheels, is the electromagnetic torque of the wheel hub motor, is the rotational inertia of the wheel, R is the wheel radius, and is the wheel rotational speed.
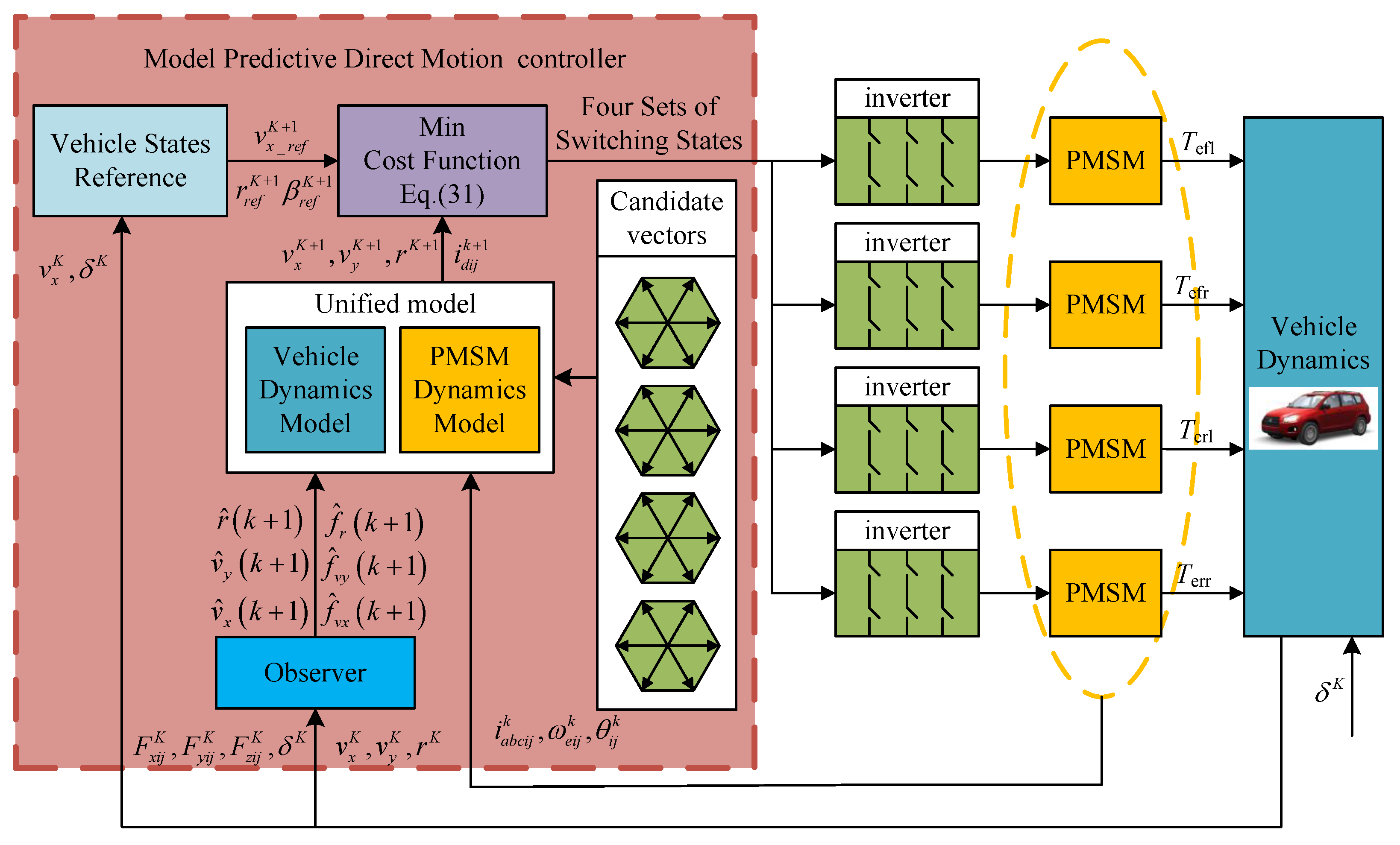
The proposed model predictive direct motion control strategy can directly obtain the optimal voltage vector combination applied to the wheel hub motors within a finite time. As illustrated in
Figure 2, the model predictive control used in this paper for DDEVs can efficiently determine the optimal combination of voltage vectors applied to the motors within a finite time frame. Essentially, the control strategy operates by considering the discrete nature of motor inverters, resulting in a finite set of potential voltage vector combinations for the four motor systems. By utilizing a unified mathematical model, predicted values for a finite number of future vehicle states are obtained, followed by the design of an evaluation function to assess these predictions while considering constraints. The selected voltage vector combination that minimizes the evaluation function is then outputted to the motor inverter, and this process is iteratively repeated for rolling optimization of the entire system. The control objectives of the four motors are unified to represent core variables of the vehicle state, encompassing longitudinal velocity, centroid lateral deviation angle, and yaw angular velocity. By aligning motor control objectives with these core state variables, a cohesive description of vehicle motion is achieved, thereby preventing inconsistencies in objectives among the motors. This unified design ensures that all four motors work towards the same overarching objective throughout the control process, thereby improving system stability and coordination.
To achieve precise and stable operation of a DDEV, the vehicle control objectives are primarily divided into two aspects: maintaining longitudinal speed for vehicle movement along the longitudinal axis and controlling yaw rate and sideslip angle to ensure vehicle stability. The calculation of specific setpoints can be found in reference [
7].
3. Vehicle Disturbance Analysis
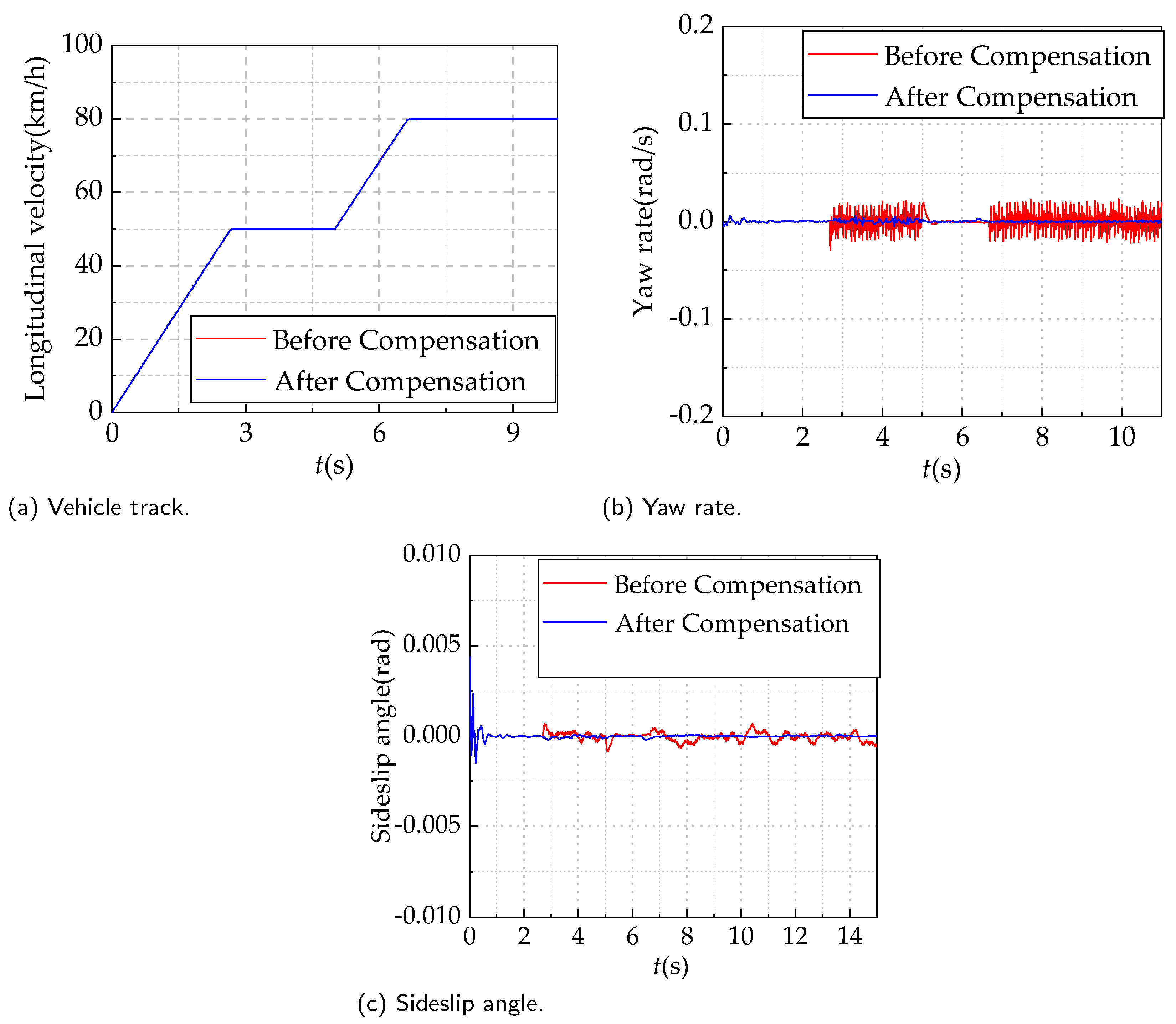
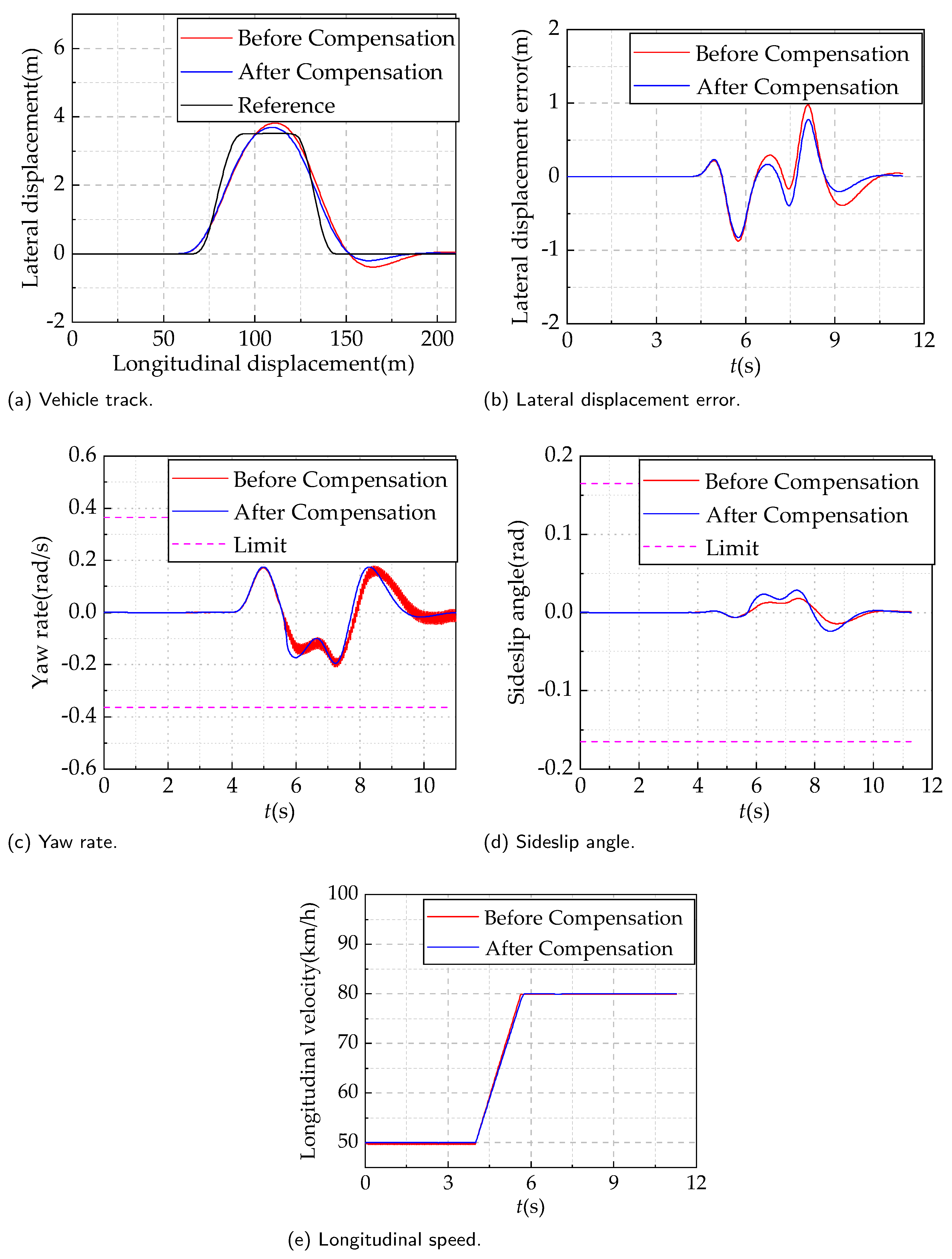
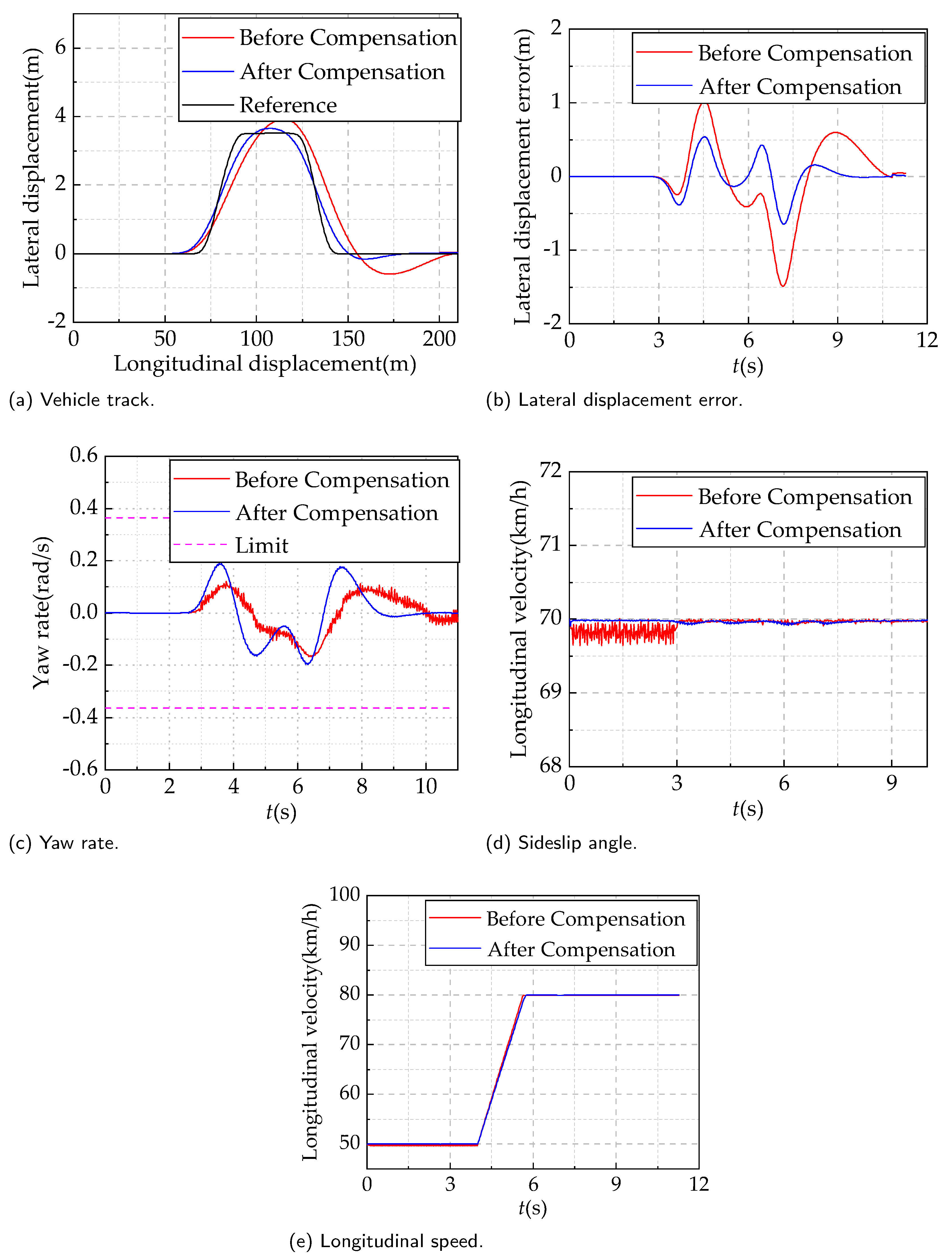
The cooperative model predictive control (MPC) strategy for a multi-motor vehicle system utilizes the dynamic model of the vehicle and the mathematical model of the permanent-magnet synchronous motor (PMSM) to predict and control the states of both the vehicle and the motors. The accuracy of the mathematical models for both the vehicle and the motors is crucial for the control performance of this strategy. The design and effectiveness of the control system directly depend on the accuracy of the models. If there are errors or uncertainties in the mathematical models, it will directly impact the performance and stability of the control strategy. However, vehicles face even more complex and variable disturbance factors during actual operation, which are challenging to precisely estimate. Examples include variations in vehicle parameters, external disturbances, and the nonlinear characteristics of the tires. Therefore, for the composite disturbances that a vehicle may encounter during operation, adopting traditional methods of precise modeling and estimation may be impractical or not accurate enough. This paper establishes a vehicle dynamics model that incorporates disturbance factors. To effectively address these disturbances, the paper represents them as a composite disturbance term in the dynamic model and designs a sliding mode observer to estimate them.
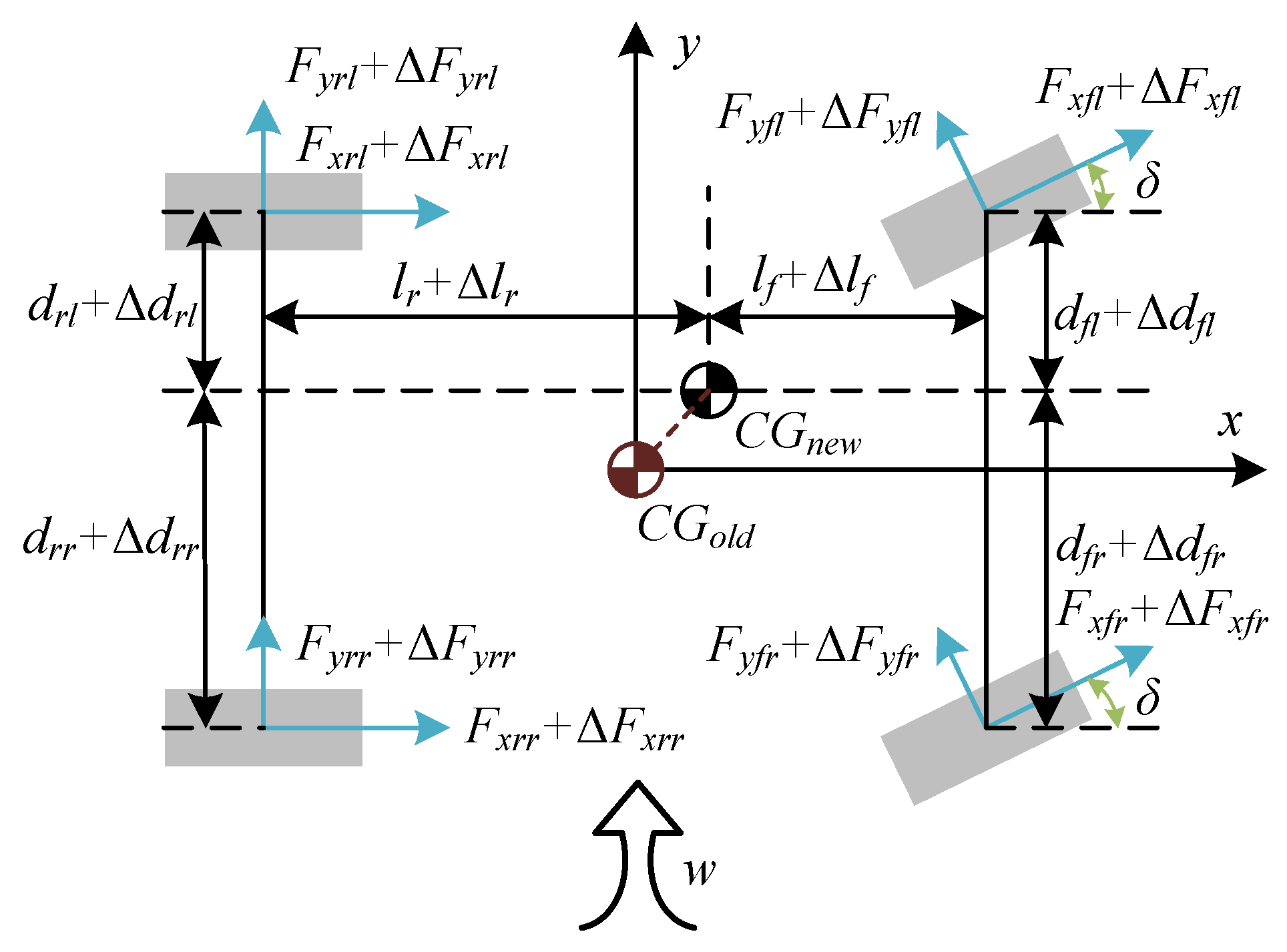
In the motion of distributed drive electric vehicles, disturbance factors mainly include variations in vehicle parameters, external disturbances, and the nonlinear characteristics of the tire model, as illustrated in
Figure 3.
During the operation of the vehicle, it may encounter different operating conditions, such as changes in the load of goods or the number of passengers. These factors can cause variations in the vehicle’s center of gravity position and total mass, leading to changes in vehicle parameters. In
Figure 3, the center of gravity position changes from CG
old to CG
new, resulting in errors
,
,
,
,
, and
in the distances from the center of gravity to the front and rear axles and the front and rear wheelbase. The vehicle’s total mass error is
. Additionally, the vehicle may face external disturbances,
w, such as crosswinds or lateral forces on the center of gravity, which cause the vehicle to deviate from the intended trajectory. Furthermore, the mechanical characteristics of the tire pose a complex nonlinear problem. Under different conditions, the tire’s mechanical properties can change, leading to variations in the vehicle’s longitudinal forces, i.e.,
,
,
, and
. These changes in parameters introduce uncertainty into the mathematical model of the vehicle, affecting the accuracy of the control system.
Therefore, incorporating these disturbance errors into Equations (
5)–(
7) yields the actual mathematical model of the vehicle dynamics as follows:
From the above description, it can be concluded that the disturbance factors affecting the vehicle are highly complex, including variations in vehicle parameters, external disturbances, and the nonlinearities of the tire model. Unlike motor parameter errors, it is challenging to individually identify and compensate for these vehicle disturbance factors. Therefore, to effectively address the disturbance errors in the vehicle, all disturbance factors are comprehensively considered and consolidated into a composite disturbance term. By aggregating all disturbance errors into a composite disturbance term, it becomes more efficient to observe and compensate for the disturbance errors in the vehicle. This integrated approach is better equipped to handle various vehicle disturbance factors, thereby enhancing the robustness of the control system against complex disturbances.
In the centralized disturbance suppression strategy designed in this paper, only centralized disturbances in three directions exist. By employing a sliding mode observer to observe and compensate for these three centralized disturbances, different disturbances to the vehicle can be suppressed. The nonlinearity of the tire model is only a small part of these three centralized disturbances and can indeed be ignored.
4. Observation and Suppression of Composite Disturbances Based on Sliding Mode Observer
The composite disturbance suppression strategy based on the sliding mode observer is employed to address the impact of parameter variations, external disturbances, and nonlinearities in the tire model on the operation of distributed drive electric vehicles. This strategy involves designing a sliding mode observer to centrally observe the composite disturbance errors in the vehicle and achieve their suppression through online compensation. The goal is to enhance the stability and control performance of the vehicle.
By consolidating the disturbance errors caused by parameter variations, external disturbances, and the nonlinearity of the tire model into a composite disturbance term, the actual dynamics model of the vehicle can be rewritten as:
In the equation,
,
, and
represent the concentrated disturbances caused by parameter variations, external disturbances, and the nonlinearity of the tire model. Additionally,
,
, and
denote the disturbance rates of
,
, and
, respectively. The composite disturbance terms
,
, and
encapsulate the disturbance errors caused by parameter variations, external disturbances, and the nonlinearity of the tire model. Their specific expressions are as follows:
To design the corresponding sliding mode observers, consider the following:
In the equation, , , and are the predicted values of the longitudinal velocity, lateral velocity, and yaw rate, respectively. Similarly, , , and are the predicted values of the rates of change for , , and . The parameters , , and are sliding mode parameters, and , , and are sliding mode functions.
In this paper, the estimation errors of longitudinal velocity, lateral velocity, and yaw rate are chosen as the linear sliding mode surface as follows:
To suppress the chattering issue, the following sliding mode reaching law is chosen, where
is the sliding mode reaching law parameter:
Reference [
36] examines the observation effects of different sliding mode surfaces, which could be referenced in future research to further optimize the sliding mode observer proposed in this paper.
The discrete equation for the sliding mode reaching law is:
The error equation for the sliding mode observer is:
In the equations,
is the predicted error for longitudinal disturbance,
is the predicted error for lateral disturbance, and
is the predicted error for yaw disturbance. Thus, the sliding mode control functions are given by:
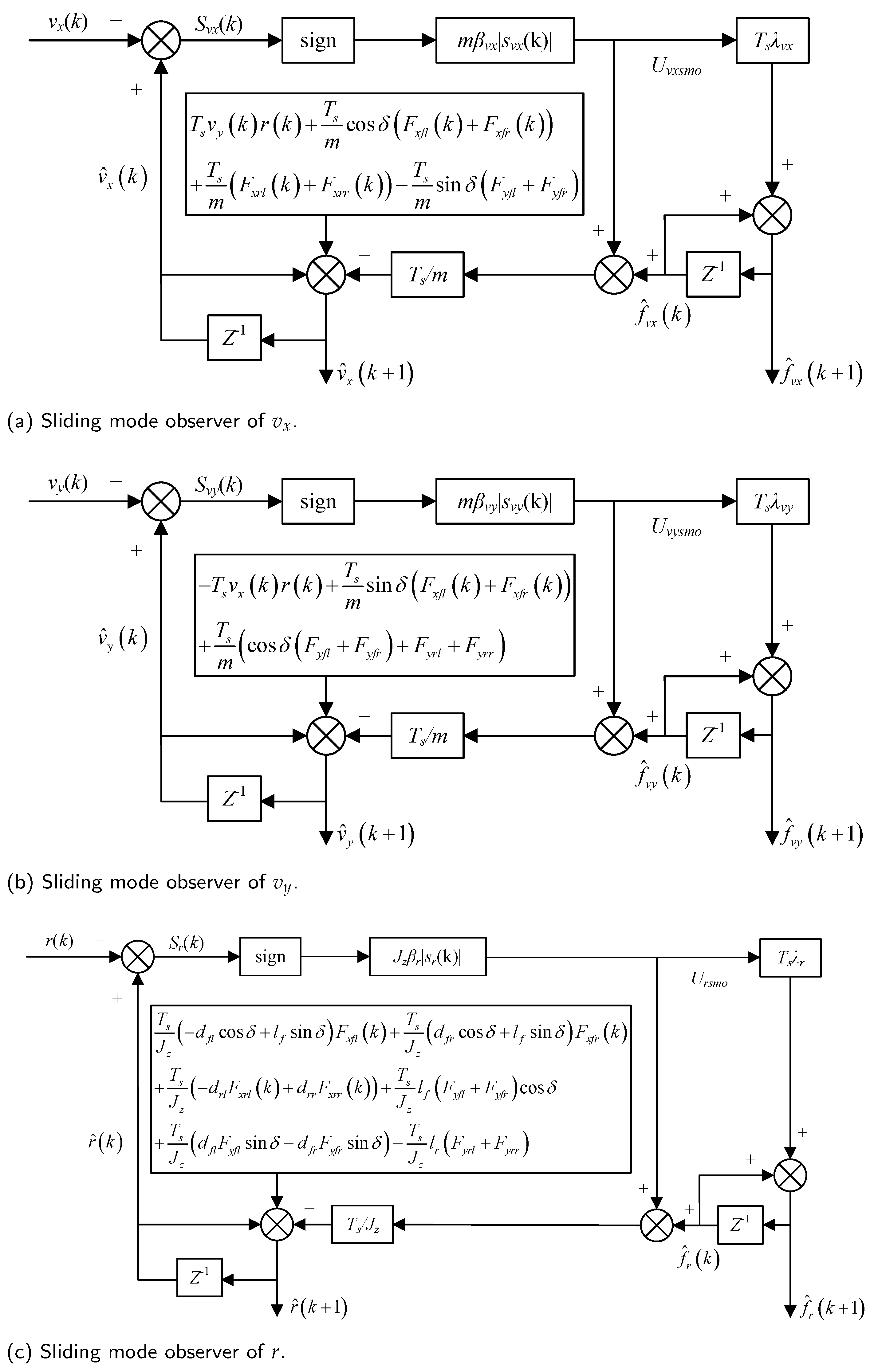
Finally, the sliding mode observer can be written in the following discrete form:
The block diagram of the proposed FPLO is shown in
Figure 4.
To ensure the stability of the sliding mode observer, it is necessary to reasonably select the sliding mode parameters for the longitudinal, lateral, and yaw directions. According to the sliding mode stability condition, the derivative of the Lyapunov function
needs to be negative, i.e.,
. Therefore, the following inequality must be satisfied:
Therefore, the admissible ranges for the reaching law parameters
,
, and
are:
When the sliding mode observer converges, the sliding mode surface and its derivative satisfy
. Equation (
17) can be simplified to:
The solutions for the predicted errors of the compound disturbances in the longitudinal, lateral, and yaw directions are as follows:
Here, , , and are constants. According to the above equations, the sliding mode parameters , , and need to be positive to ensure that the disturbance prediction errors , , and converge to zero.