Combined Effects of Thermal Buoyancy, Wind Action, and State of the First-Floor Lobby Entrance on the Pressure Difference in a High-Rise Building
Abstract
1. Introduction
2. Description of the Building and Simulation Settings
Overview of the High-Rise Building
3. Simulation Settings
3.1. The COMIS Model
3.2. Simulation Parameters
3.2.1. Wind Pressure
3.2.2. Temperature and Airtightness of Structural Components
4. Simulation Results
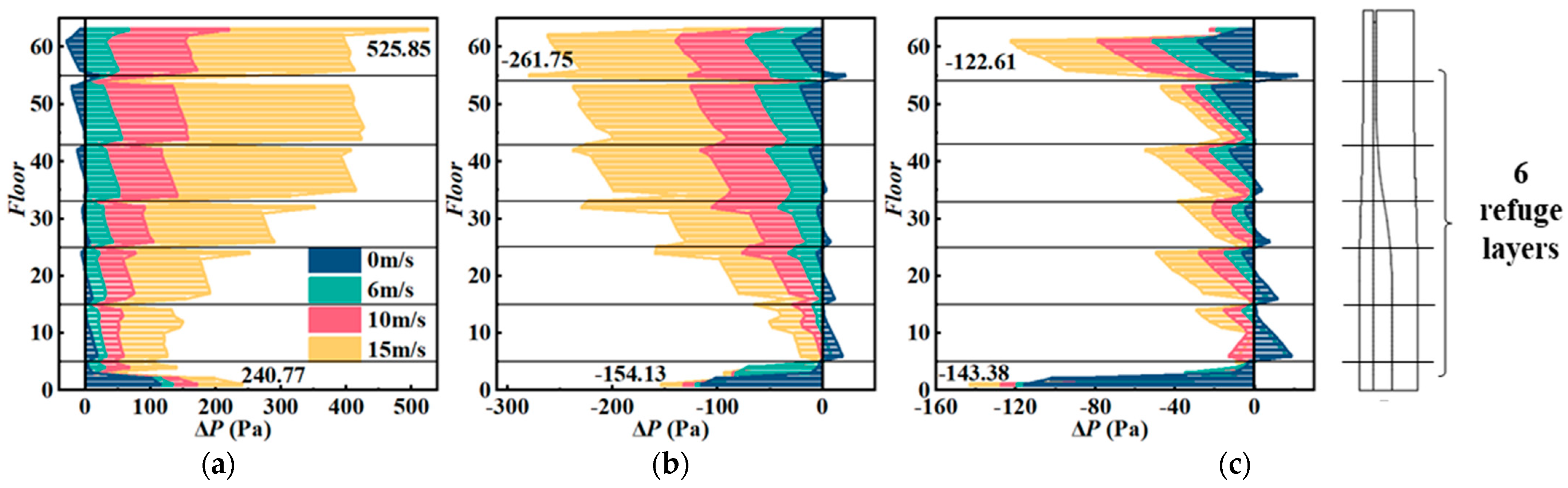
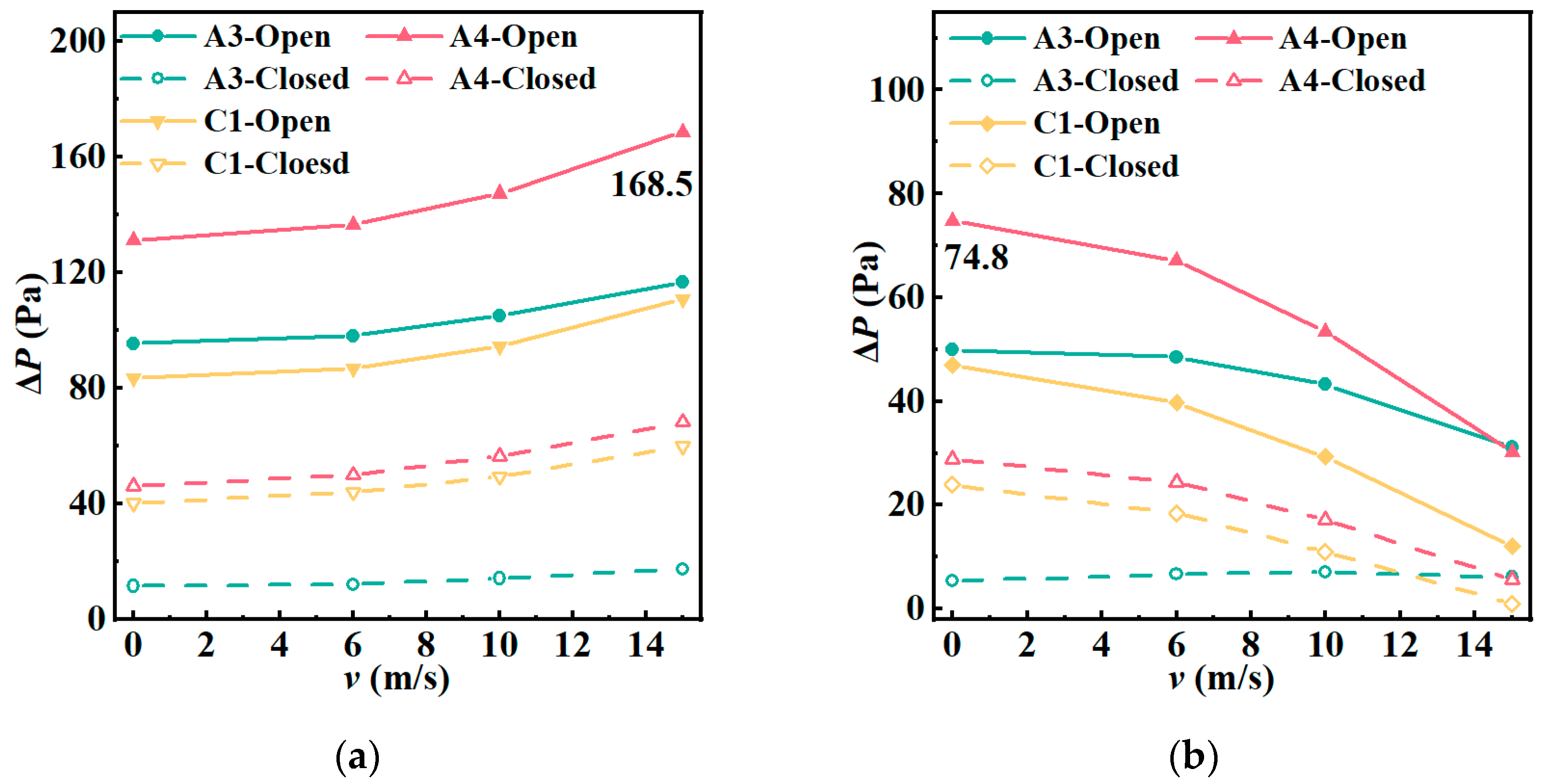
4.1. The Effect of Wind Speed (Cases 1–4)
4.2. The Effect of Wind Attack Angle (Cases 3, 5–11)
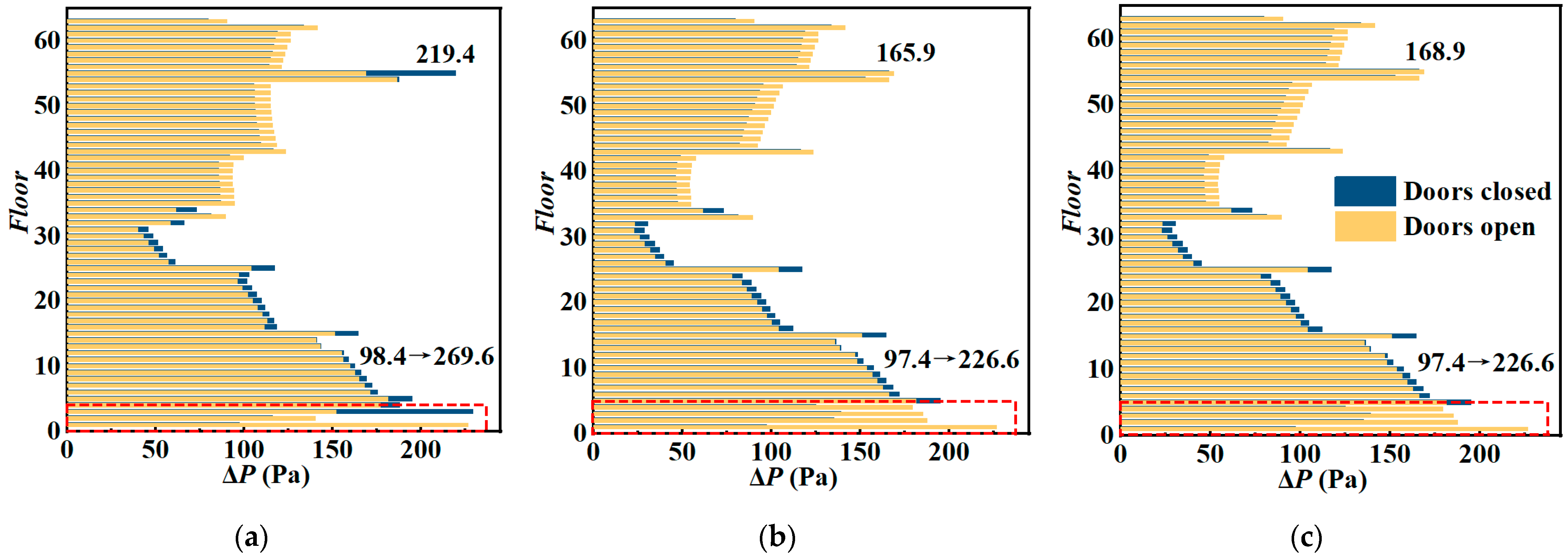
4.3. The Effect of Open/Closed States of the First-Floor Entrance (Case 12)
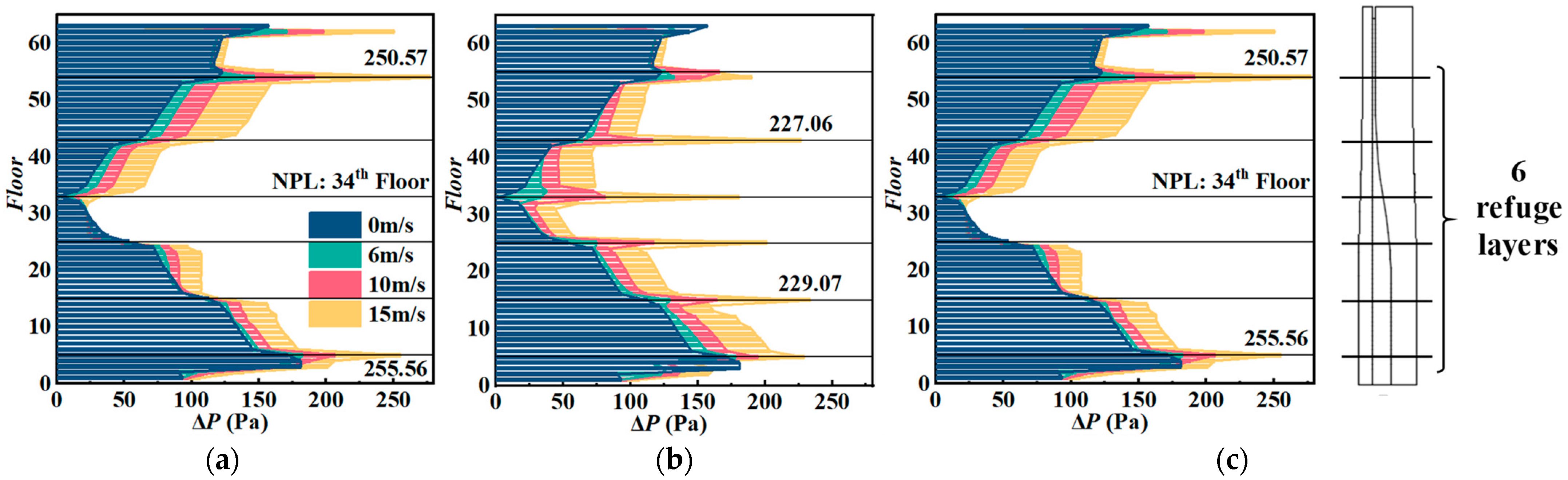
4.4. The Combined Effect of Wind Speed and the Opening of the First-Floor Lobby Entrance under Different Temperature Environments (Cases 3, 12–14)
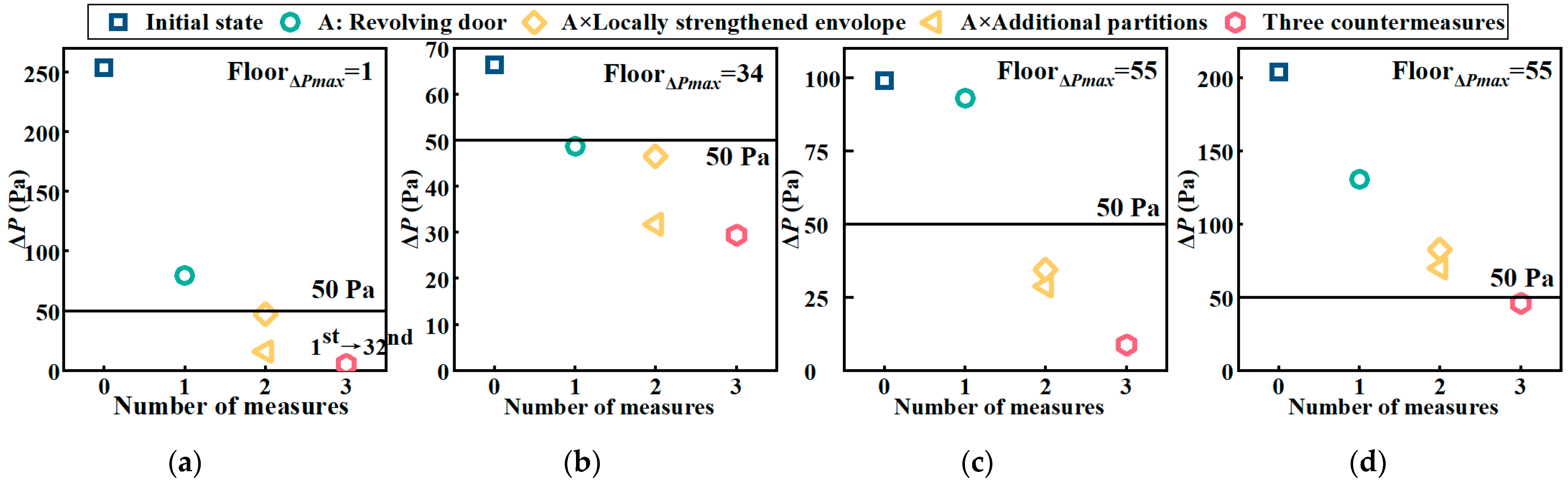
5. Countermeasures for Excessive Pressure Difference
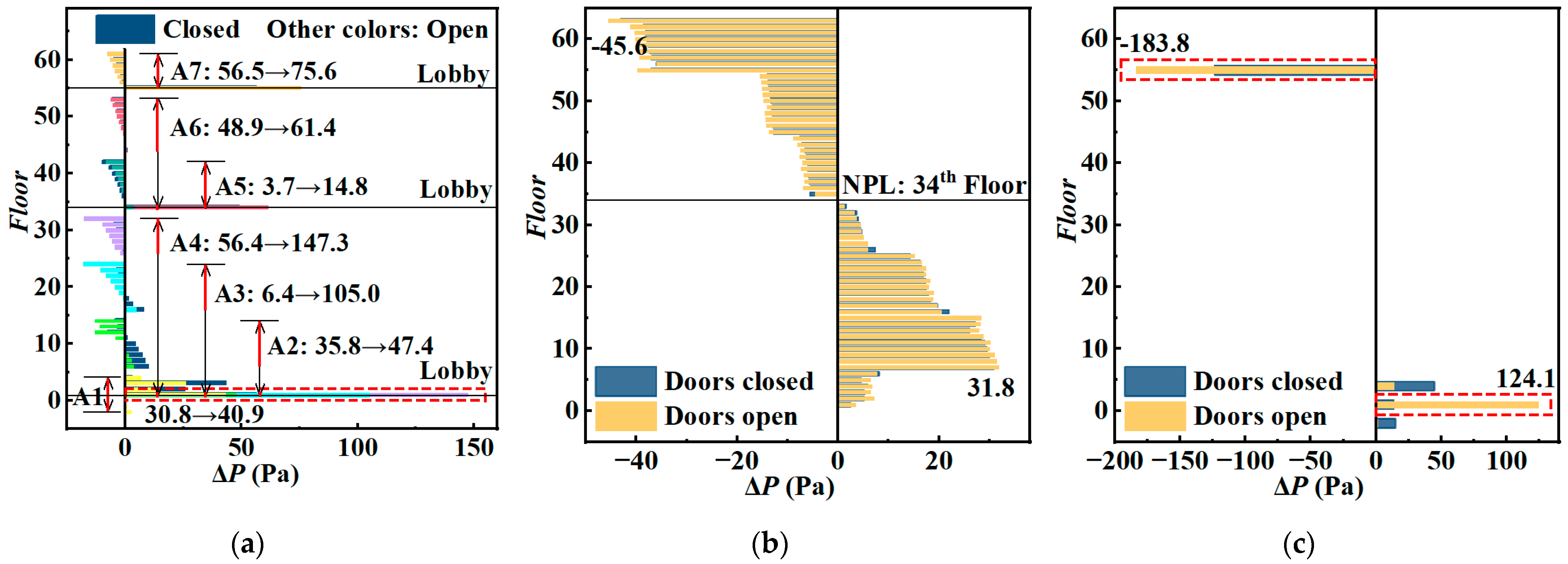
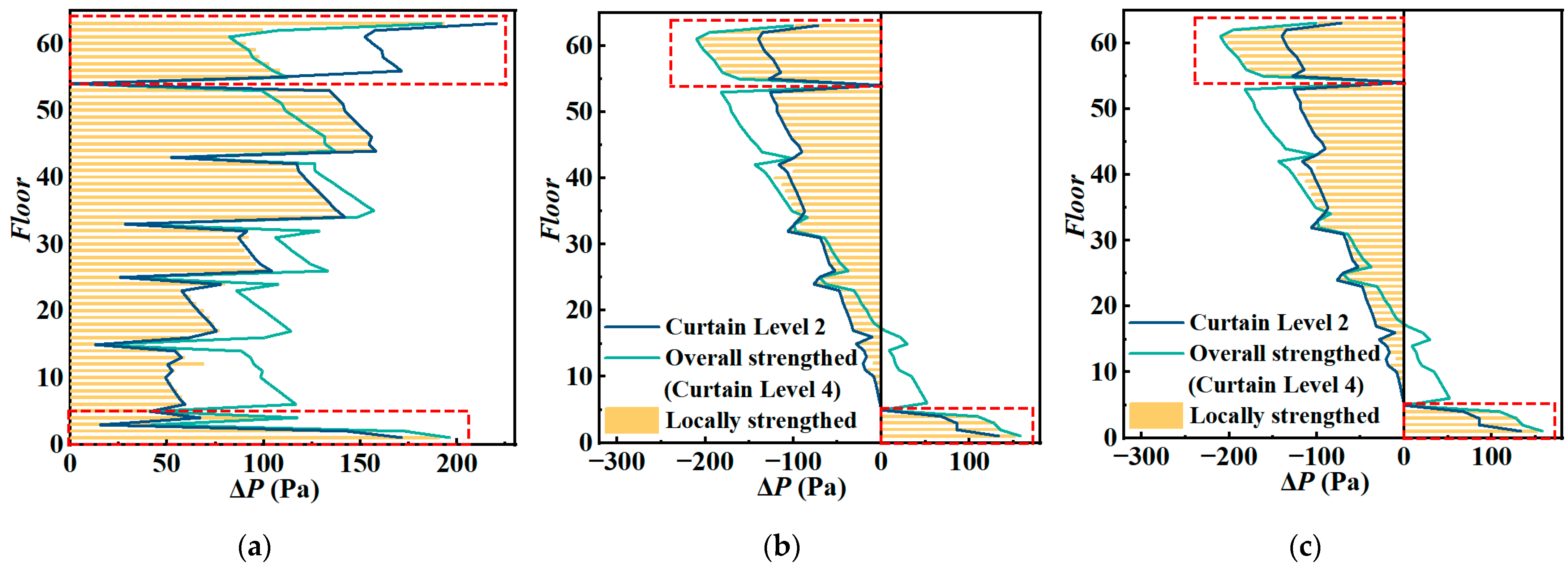
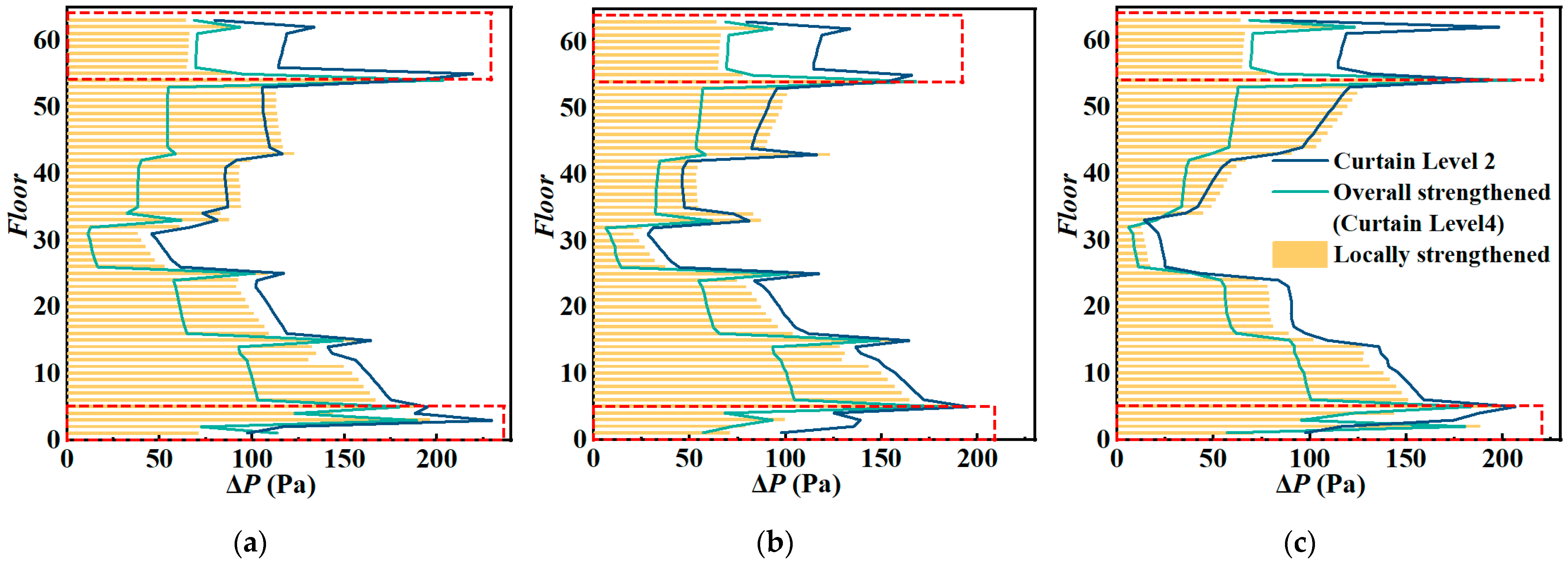
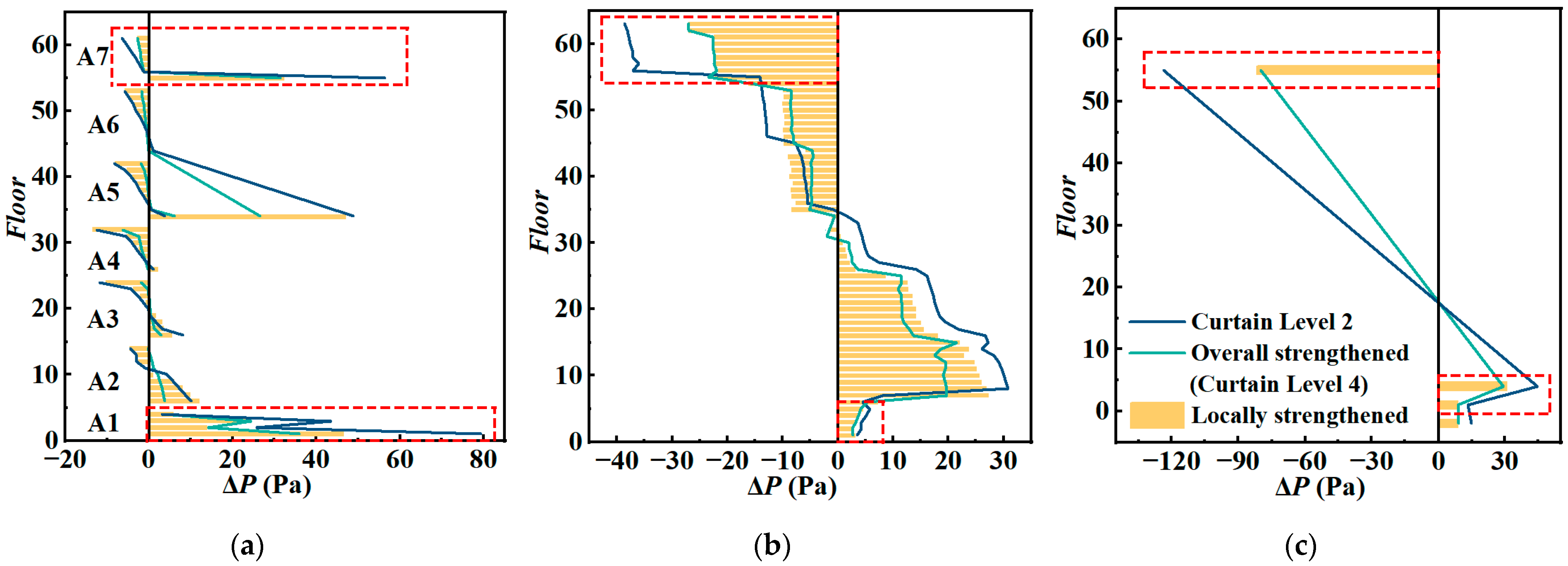
5.1. A New Method: Locally Strengthened Airtightness of Envelope
5.2. The Synergistic Effect of a Comprehensive Countermeasure Scheme
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Doosam, S.; Sungmin, Y.; Chanwoul, J.; Joowook, K.; Hyunwoo, L. Heat, vapor, and CO2 transportation caused by airflow in high-rise residential buildings. Build. Environ. 2019, 160, 106176. [Google Scholar]
- Sowoo, P.; Yun, C.; Hyunwoo, L.; Doosam, S. Analysis of vertical movement of particulate matter due to the stack effect in high-rise buildings. Atmos. Environ. 2022, 279, 119113. [Google Scholar]
- Tamura, G.T. Smoke Movement and Control in High-Rise Buildings; National Fire Protection Association: Boston, MA, USA, 1994. [Google Scholar]
- Khoukhi, M.; Asma, A.M. Stack Pressure and Airflow Movement in High and Medium Rise buildings. Energy Procedia 2011, 6, 422–431. [Google Scholar] [CrossRef]
- Doosam, S.; Hyunwoo, L.; Joonghoon, L.; Jungmin, S. Application of the mechanical ventilation in elevator shaft space to mitigate stack effect under operation stage in high-rise buildings. Indoor Built Environ. 2014, 23, 81–91. [Google Scholar]
- Antony, W.; Ruba, S. Guide to Natural Ventilation in High Rise Office Buildings, 1st ed.; Routledge: London, UK, 2012; p. 184. [Google Scholar]
- Ai, Z.T.; Mak, C.M.; Cui, D.J. On-site measurements of ventilation performance and indoor air quality in naturally ventilated high-rise residential buildings in Hong Kong. Indoor Built Environ. 2015, 24, 214–224. [Google Scholar] [CrossRef]
- Hyesoo, S.; Byungseon Sean, K.; Taeyeon, K.; Jeonghee, L. Influence analysis of stack effect on odor dispersion from unit to core in the high-rise residential buildings. Proc. Build. Simul. 2007, 1062–1068. [Google Scholar]
- Taesub, L.; Jinkyun, C.; Byungseon, S.K. Predictions and measurements of the stack effect on indoor airborne virus transmission in a high-rise hospital building. Build. Environ. 2011, 46, 2413–2424. [Google Scholar]
- Sergey, M.; Stefano, C. Stack effect in high-rise buildings: A review. Int. J. High-Rise Build. 2016, 5, 327–338. [Google Scholar]
- Jung-yeon, Y.; Kyoo-dong, S.; Dong-woo, C. Resolving stack effect problems in a high-rise office building by mechanical pressurization. Sustainability 2017, 9, 1731. [Google Scholar]
- Yoon, S.; Song, D.; Kim, J.; Lim, H. Stack-driven infiltration and heating load differences by floor in high-rise residential buildings. Build. Environ. 2019, 157, 366–379. [Google Scholar] [CrossRef]
- Jing, J.; Lee, D.S.; Joe, J.; Kim, E.J.; Cho, Y.H.; Jo, J.H. A sensing-based visualization method for representing pressure distribution in a multi-zone building by floor. Sensors 2023, 23, 4116. [Google Scholar] [CrossRef] [PubMed]
- Tamura, G.T.; Wilson, A.G. Pressure differences caused by chimney effect in three high buildings. ASHRAE Trans. 1967, 73, 1–10. [Google Scholar]
- Park, S.-Y.; Lee, D.-S.; Ji, K.-H.; Jo, J.-H. Simplified model for estimating the neutral pressure level in the elevator shaft of a building. Build Engine 2023, 79, 107850. [Google Scholar] [CrossRef]
- Xie, M.X.; Wang, J. Determination of Pressure Difference Coefficient of Shuttle Elevator Doors in Super High-Rise Buildings under Stack Effect. Build. Environ. 2023, 232, 110076. [Google Scholar] [CrossRef]
- Shin, H.K. A Calculation Method for Determining Air Infiltration of High-Rise Buildings Based on Airtightness and Stack Effect Pressure. Ph.D. Thesis, Inha University, Incheon, Republic of Korea, 2018. [Google Scholar]
- Walker, I.S.; Wilson, D.J. Evaluating models for superposition of wind and stack effect in air infiltration. Build. Environ. 1993, 28, 201–210. [Google Scholar] [CrossRef]
- Jae-Hun, J.; Jae-Han, L.; Seung-Yeong, S.; Myoung-Souk, Y.; Kwang-Woo, K. Characteristics of pressure distribution and solution to the problems caused by stack effect in high-rise residential buildings. Build. Environ. 2007, 42, 263–277. [Google Scholar]
- Hyunwoo, L.; Jungmin, S.; Doosam, S.; Sungmin, Y.; Joowook, K. Interaction analysis of countermeasures for the stack effect in a high-rise office building. Build. Environ. 2020, 168, 106530. [Google Scholar]
- Khoukhi, M.; Hiroshi, Y.; Jing, L. The effect of the wind speed velocity on the stack pressure in medium-rise buildings in cold region of China. Build. Environ. 2007, 42, 1081–1088. [Google Scholar] [CrossRef]
- Gang, T.; Leon, R.G. Application of integrating multi-zone model with CFD simulation to natural ventilation prediction. Energy. Build. 2005, 37, 1049–1057. [Google Scholar]
- Marcello, C.; Pascal, S.; Dominique, M. Full scale experimental study of single-sided ventilation: Analysis of stack and wind effects. Ener. Build. 2011, 43, 1765–1773. [Google Scholar]
- Joonghoon, L.; Taeyon, H.; Doosam, S.; Jeong, T.K. Quantitative reduction method of draft in high-rise buildings, using revolving doors. Indoor Built Environ. 2012, 21, 79–91. [Google Scholar]
- Joonghoon, L.; Beomseok, G.; Taeyon, H. Characteristics of revolving door use as a countermeasure to the stack effect in buildings. J. Asian Architect. Build. Eng. 2018, 16, 417–424. [Google Scholar]
- Sung-Han, K.; Jae-Hun, J.; Hoi-Soo, S.; Myong-Souk, Y.; Kwang-Woo, K. Influence of architectural elements on stack effects in tall residential building. In Proceedings of the CTBUH 2004 Seoul Confernce, Seoul, Republic of Korea, 10–13 October 2004. [Google Scholar]
- Jungyeon, Y.; Angie, K.; Sanghwan, B.; Dongwoo, C.; Kee, H.K. HVAC operation schemes and commissioning process resolving stack effect problem and adjusting according to changes in the environment: A case study in high-rise building in South Korea. Energies 2021, 14, 2299. [Google Scholar]
- Mengxiao, X.; Jian, W.; Jing, Z.; Jun, G.; Chengwei, P.; Chenyu, L. Field measurement and coupled simulation for the shuttle elevator shaft cooling system in super high-rise buildings. Build. Environ. 2021, 187, 107387. [Google Scholar]
- Feustel, H.E. COMIS—An international multizone air-flow and contaminant transport model. Energy Build. 1999, 30, 3–18. [Google Scholar]
- Khoukhi, M. A simplified procedure to investigate airflow patterns inside tall buildings using COMIS. Archit. Sci. Rev. 2007, 50, 365–369. [Google Scholar]
- Wang, L.Z.; Chen, Q.Y. Evaluation of some assumptions used in multizone airflow network models. Build. Environ. 2008, 43, 1671–1677. [Google Scholar] [CrossRef]
- Yoon, S.M.; Seo, J.M.; Cho, W.H.; Song, D.S. A calibration method for whole-building airflow simulation in high-rise residential buildings. Build. Environ. 2015, 85, 253–262. [Google Scholar] [CrossRef]
- GB50009-2012; Load Code for the Design of Building Structures. Ministry of Housing and Urban-Rural Development of the People’s Republic of China (MOHURD): Beijing, China, 2012.
- GB 50736-2012; Design Code for Heating Ventilation and Air Conditioning of Civil Buildings. Ministry of Housing and Urban-Rural Development of the People’s Republic of China (MOHURD): Beijing, China, 2012.
- GB/T7106-2019; Test Methods of Air Permeability, Watertightness, Wind Load Resistance Performance for Building External Windows and Doors. Ministry of Housing and Urban-Rural Development of the People’s Republic of China (MOHURD): Beijing, China, 2019.
- Tamblyn, R.T. Coping with air pressure problems in tall buildings. ASHRAE Trans. 1991, 97, 824–827. [Google Scholar]
- Saroglou, T.; Theodosiou, T.; Givoni, B.; Meir, I.A. Studies on the optimum double-skin curtain wall design for high-rise buildings in the Mediterranean climate. Ener. Build. 2020, 208, 109641. [Google Scholar] [CrossRef]
- Becker, R. Air Leakage of Curtain Walls—Diagnostics and Remediation. Build. Phys. 2010, 34, 57–75. [Google Scholar] [CrossRef]
- Tamblyn, R.T. HVAC system effects for tall buildings. ASHRAE Trans. 1993, 99, 789–792. [Google Scholar]
- Lovatt, J.E.; Wilson, A.G. Stack effect in tall buildings. ASHRAE Trans. 1994, 100, 420–431. [Google Scholar]


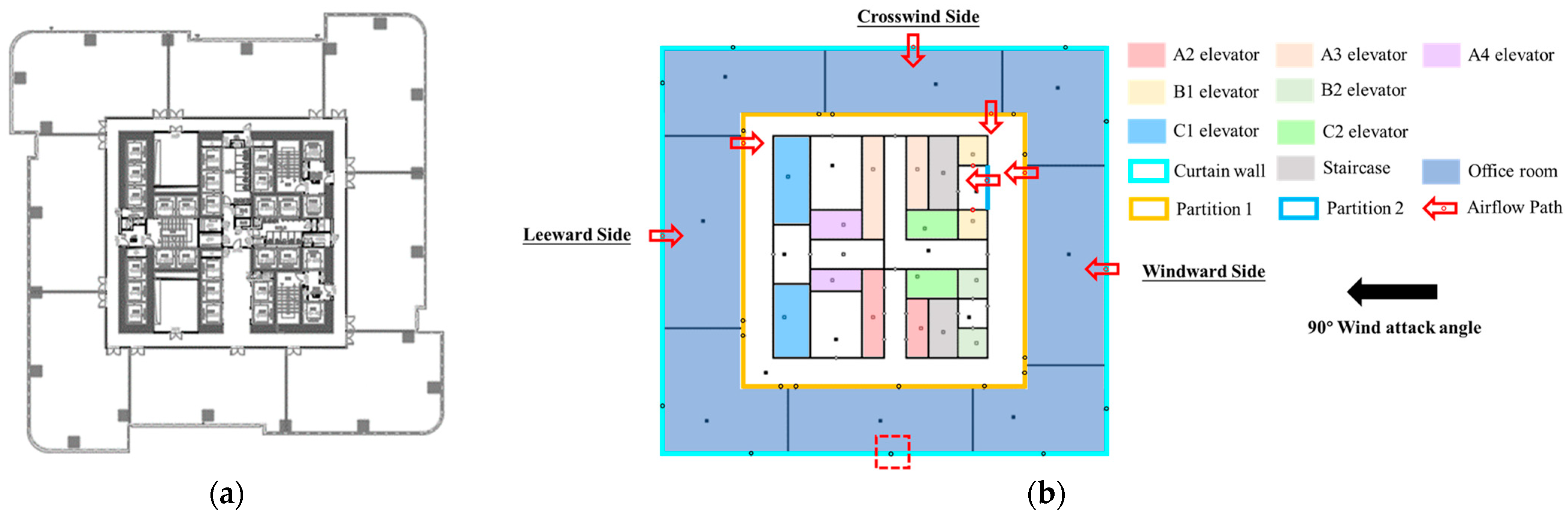
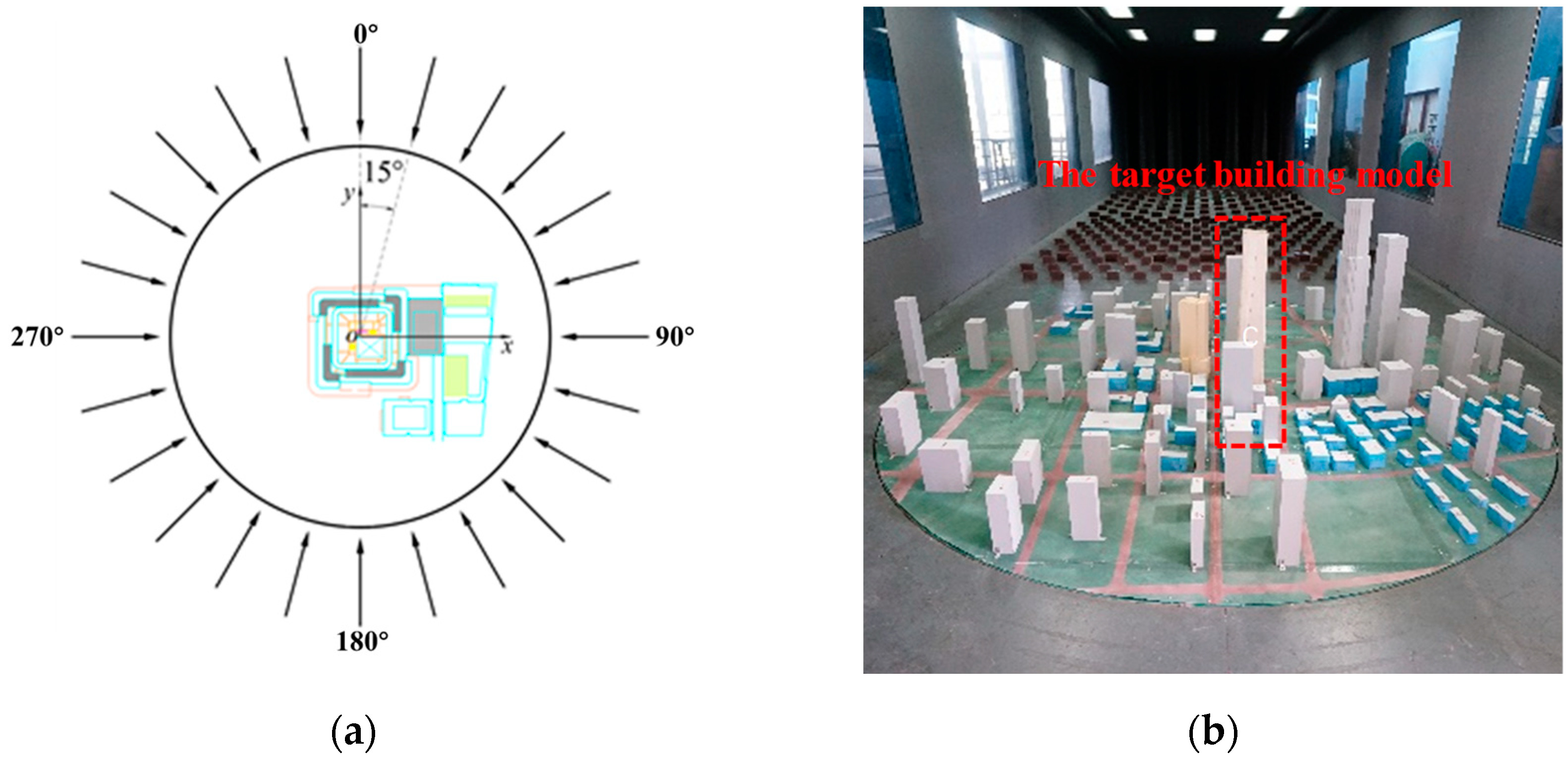

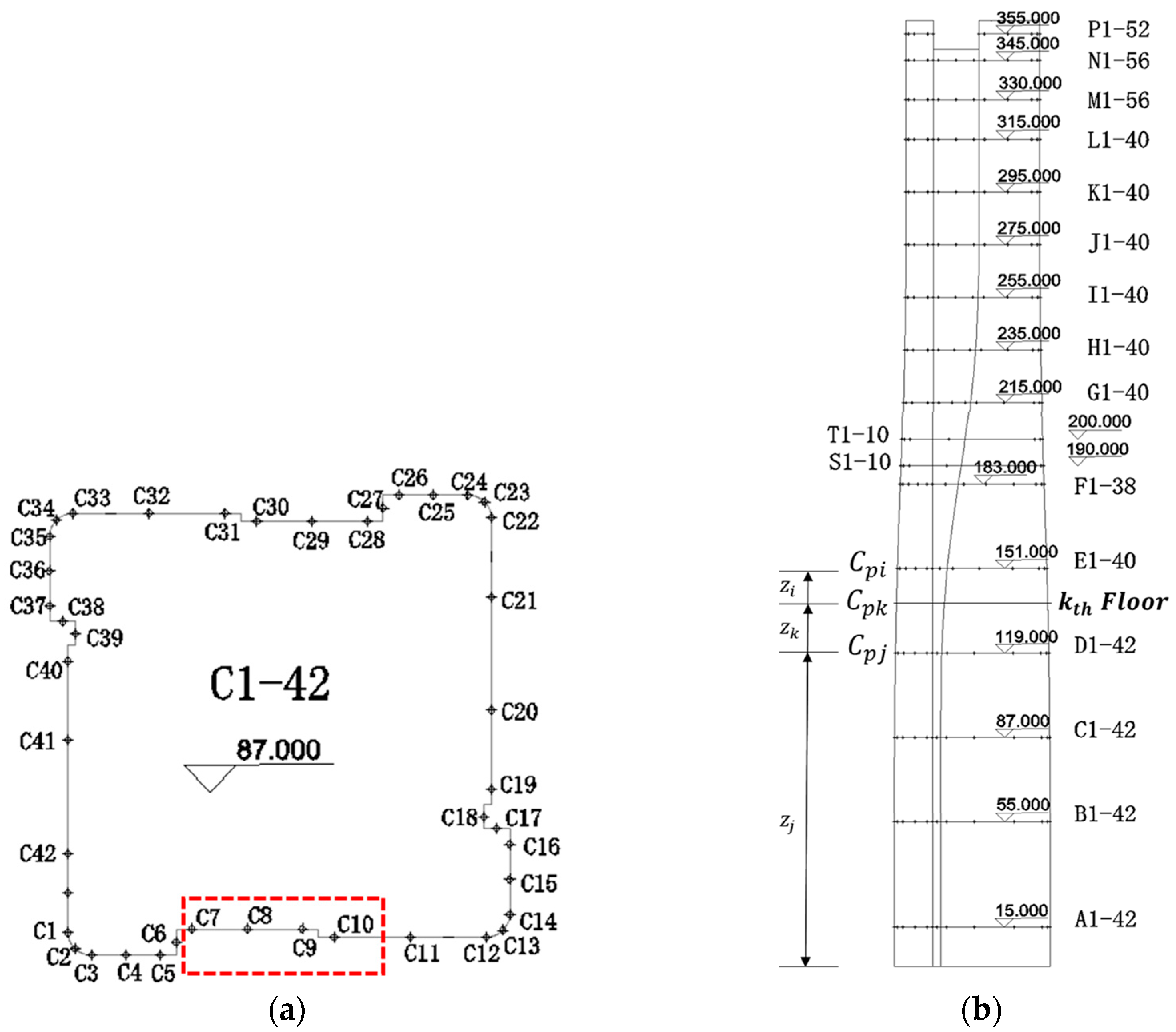
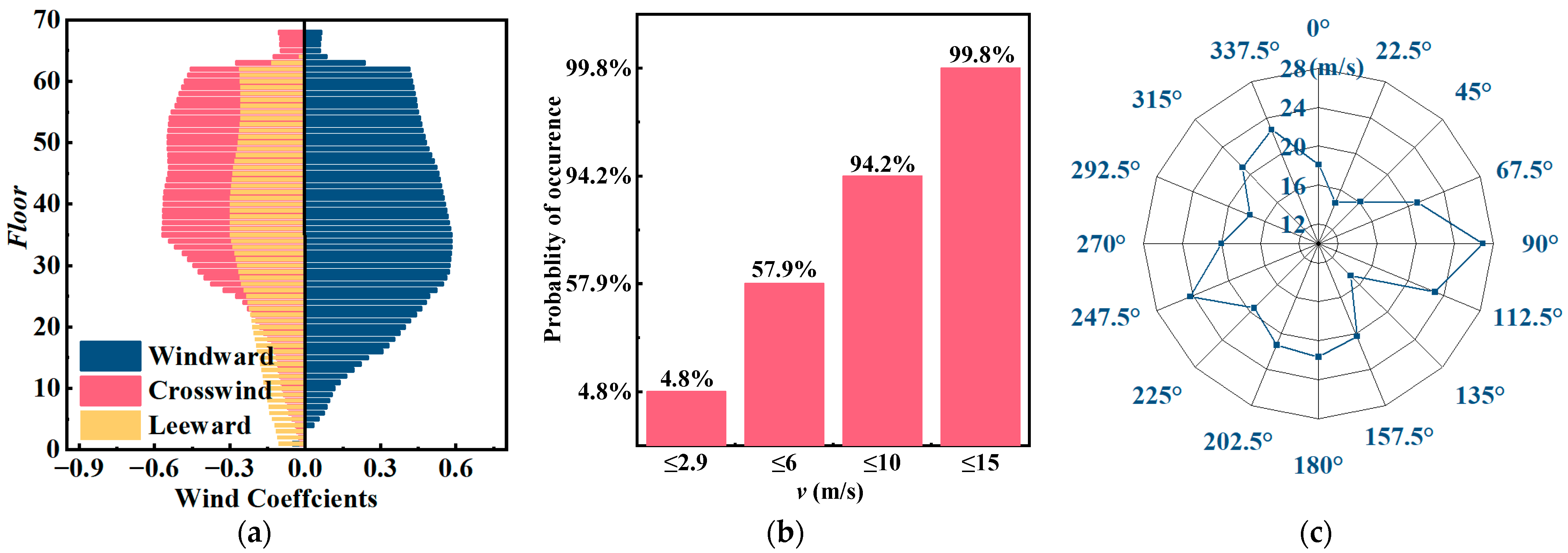





| Building Components | Air Leakage Data | Sourse |
|---|---|---|
| Curtain wall | Level 4: 0.5 m3/(m2·h) Level 2: 2 m3/(m2·h) | Chinese code [36] |
| Elevator door | *EqLA10: 325 cm2/item | Ref. [19] |
| Stairwell door | *EqLA75: 120 cm2/item | |
| Office door | *EqLA10: 200 cm2/item | Ref. [25] |
| Revolving door on lobby floor | *EqLA10: 10.88 cm2/item | Ref. [24] |
| Swing door on lobby floor | *EqLA10: 21 cm2/item | Ref. [37] |
| Effects | Case Number | Outdoor Temperature (°C) | Indoor Temperature (°C) | Wind Speed (m/s) | Wind Attack Angle | State of the First-Floor Entrance |
|---|---|---|---|---|---|---|
| Wind speed | 1 | −7.7 | 20 | 0 | 90° | Closed |
| 2 | −7.7 | 20 | 6 | 90° | Closed | |
| 3 | −7.7 | 20 | 10 | 90° | Closed | |
| 4 | −7.7 | 20 | 15 | 90° | Closed | |
| Wind attack angle | 5 | −7.7 | 20 | 10 | 0° | Closed |
| 6 | −7.7 | 20 | 10 | 45° | Closed | |
| 7 | −7.7 | 20 | 10 | 135° | Closed | |
| 8 | −7.7 | 20 | 10 | 180° | Closed | |
| 9 | −7.7 | 20 | 10 | 225° | Closed | |
| 10 | −7.7 | 20 | 10 | 270° | Closed | |
| 11 | −7.7 | 20 | 10 | 315° | Closed | |
| First-floor entrance state | 12 | −7.7 | 20 | 10 | 90° | Open |
| Thermal buoyancy | 13 | 34.7 | 24 | 10 | 90° | Closed |
| 14 | 34.7 | 24 | 10 | 90° | Open |
| Type | Short-Distance Elevator | Long-Distance Elevator | Shuttle Elevator | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Number | A1 | A2 | A3 | A4 | A5 | A6 | A7 | B1 | B2 | C1 | C2 |
| ΔPmax (Pa) | 70.0 | 47.4 | 105.0 | 147.3 | 14.8 | 61.4 | 75.6 | −53.8 | −53.1 | −123.5 | −183.8 |
| Exceed 50 Pa | Yes | No | Yes | Yes | No | Yes | Yes | Yes | Yes | Yes | Yes |
| Floor of ΔPmax | 1st | 1st | 1st | 1st | 34th | 34th | 55th | 63rd, 54th | 1st | 1st | 55th |
| Main reasons | Thermal buoyancy | Thermal buoyancy Wind attack angle | Thermal buoyancy Opening first-floor lobby entrance | ||||||||
| Opening first-floor lobby entrance | / | Wind action | |||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, H.; Su, L.; Lou, W.; Shan, H. Combined Effects of Thermal Buoyancy, Wind Action, and State of the First-Floor Lobby Entrance on the Pressure Difference in a High-Rise Building. Energies 2024, 17, 2117. https://doi.org/10.3390/en17092117
Xu H, Su L, Lou W, Shan H. Combined Effects of Thermal Buoyancy, Wind Action, and State of the First-Floor Lobby Entrance on the Pressure Difference in a High-Rise Building. Energies. 2024; 17(9):2117. https://doi.org/10.3390/en17092117
Chicago/Turabian StyleXu, Haiwei, Lingfeng Su, Wenjuan Lou, and Hongyang Shan. 2024. "Combined Effects of Thermal Buoyancy, Wind Action, and State of the First-Floor Lobby Entrance on the Pressure Difference in a High-Rise Building" Energies 17, no. 9: 2117. https://doi.org/10.3390/en17092117
APA StyleXu, H., Su, L., Lou, W., & Shan, H. (2024). Combined Effects of Thermal Buoyancy, Wind Action, and State of the First-Floor Lobby Entrance on the Pressure Difference in a High-Rise Building. Energies, 17(9), 2117. https://doi.org/10.3390/en17092117






