Research on the Measurement Method of the Prompt Neutron Decay Constant Based on LHS-DMD-Rossi-Alpha
Abstract
1. Introduction
2. Theory of the LHS-DMD-Rossi-Alpha Method
2.1. The Rossi-Alpha Method
2.2. Dynamic Mode Decomposition Method
2.3. Latin Hypercube Sampling
- Determine the number of samples: First, determine the number of samplings D and the characteristic dimensions M, where D represents the number of pulse signal intervals detected by a detector within the measurement time. Then, establish an M-dimensional space based on M random variables X1, X2, …, XM.
- Stratification: Divide each dimensional datum into D equal subintervals based on a uniform distribution.
- Random sampling: Randomly select one sampling point from each dimensional subinterval, repeating this process D times to generate M × D sample points.
- Mapping to the target distribution: Each element in the M × D sampling matrix represents an index of a sampling point, indicating the coordinates of the sampling point in the original sample set.
- Validation of sample distribution: The Rossi-alpha method was used to compare the original data samples with the sampling data after using the LHS method to ensure the applicability of the LHS method.
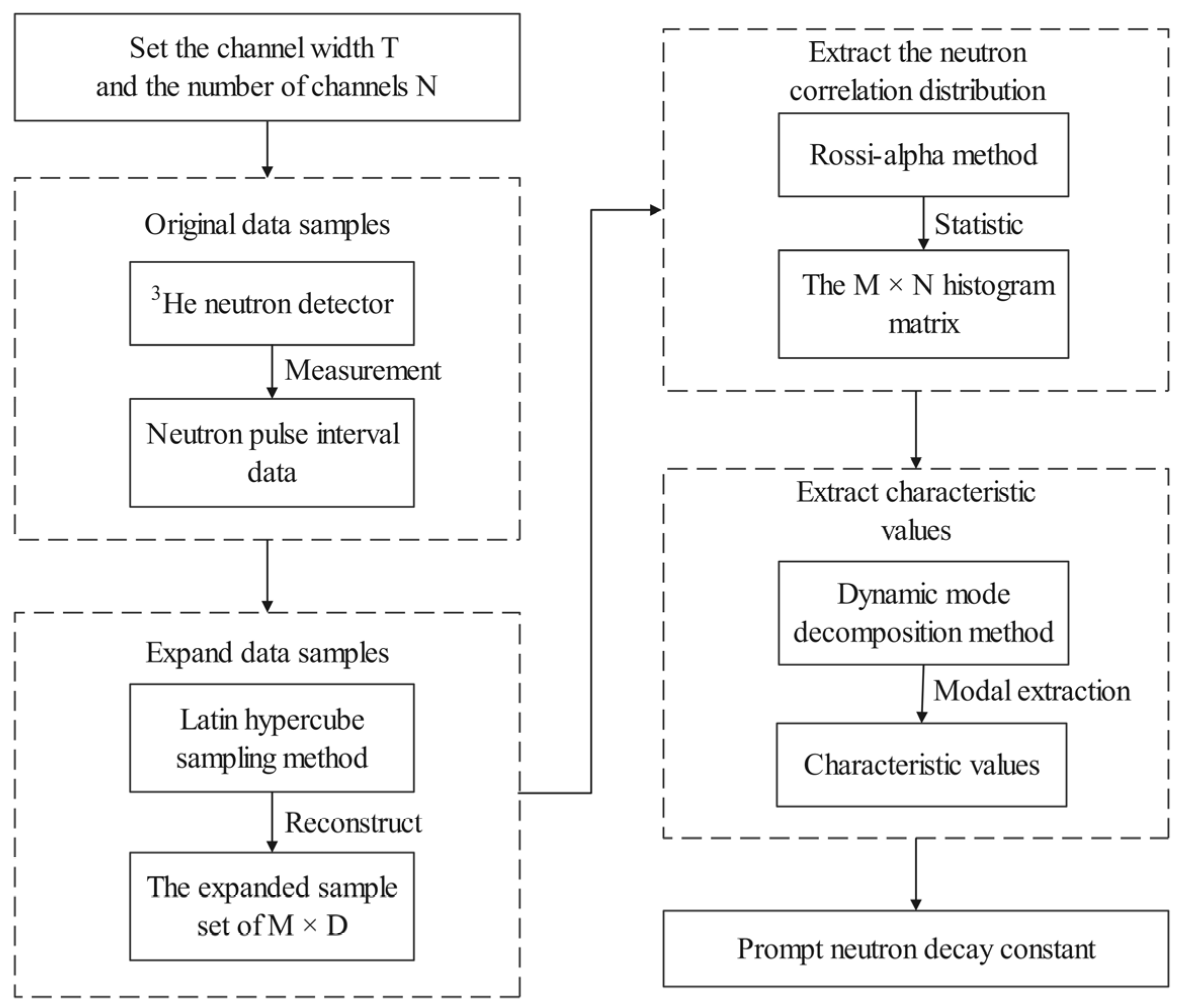
2.4. Construction of the LHS-DMD-Rossi-Alpha Method
- Set the channel width T and the number of channels N in the Rossi-alpha method parameters.
- Capture neutron pulse interval data with a single 3He neutron detector using the Rossi-alpha measurement method as the original data sample.
- Employ the LHS to reconstruct the original data sample, generating an expanded sample set of M × D, thus optimizing the DMD-Rossi-alpha method, which originally required M detectors for measurement, to be measured with a single detector.
- Use the Rossi-alpha method to extract the neutron correlation distribution from the expanded sample set of M × D, generating an M × N histogram matrix.
- Extract characteristic values representing the prompt neutron decay constant from the Rossi-alpha histogram distribution matrix using the DMD method.
3. Research on the LHS-DMD-Rossi-Alpha Method
3.1. Numerical Simulation of the KUCA Facility Based on RMC3.5
3.2. Performance Analysis of the LHS-DMD-Rossi-Alpha Method
4. Conclusions
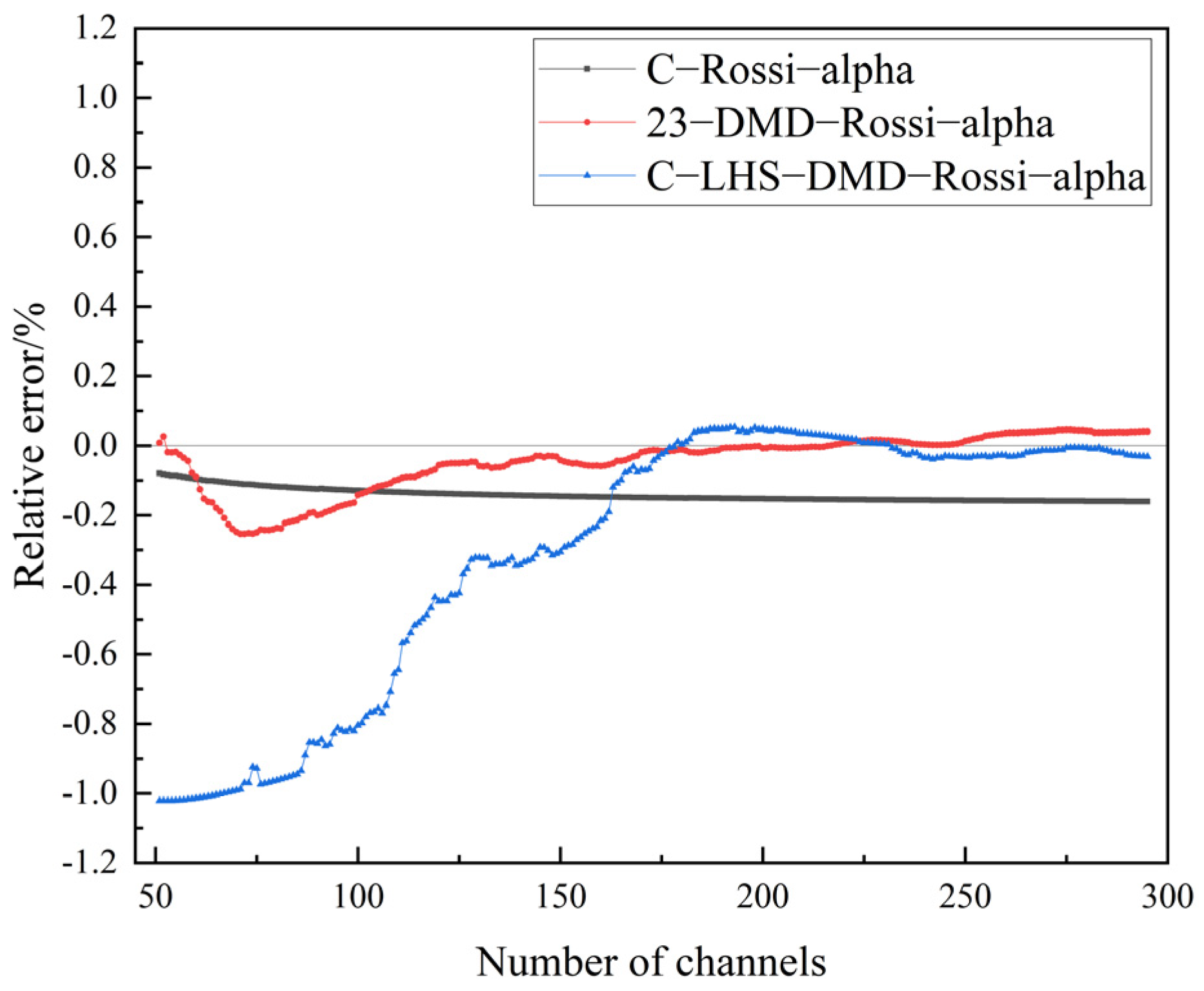
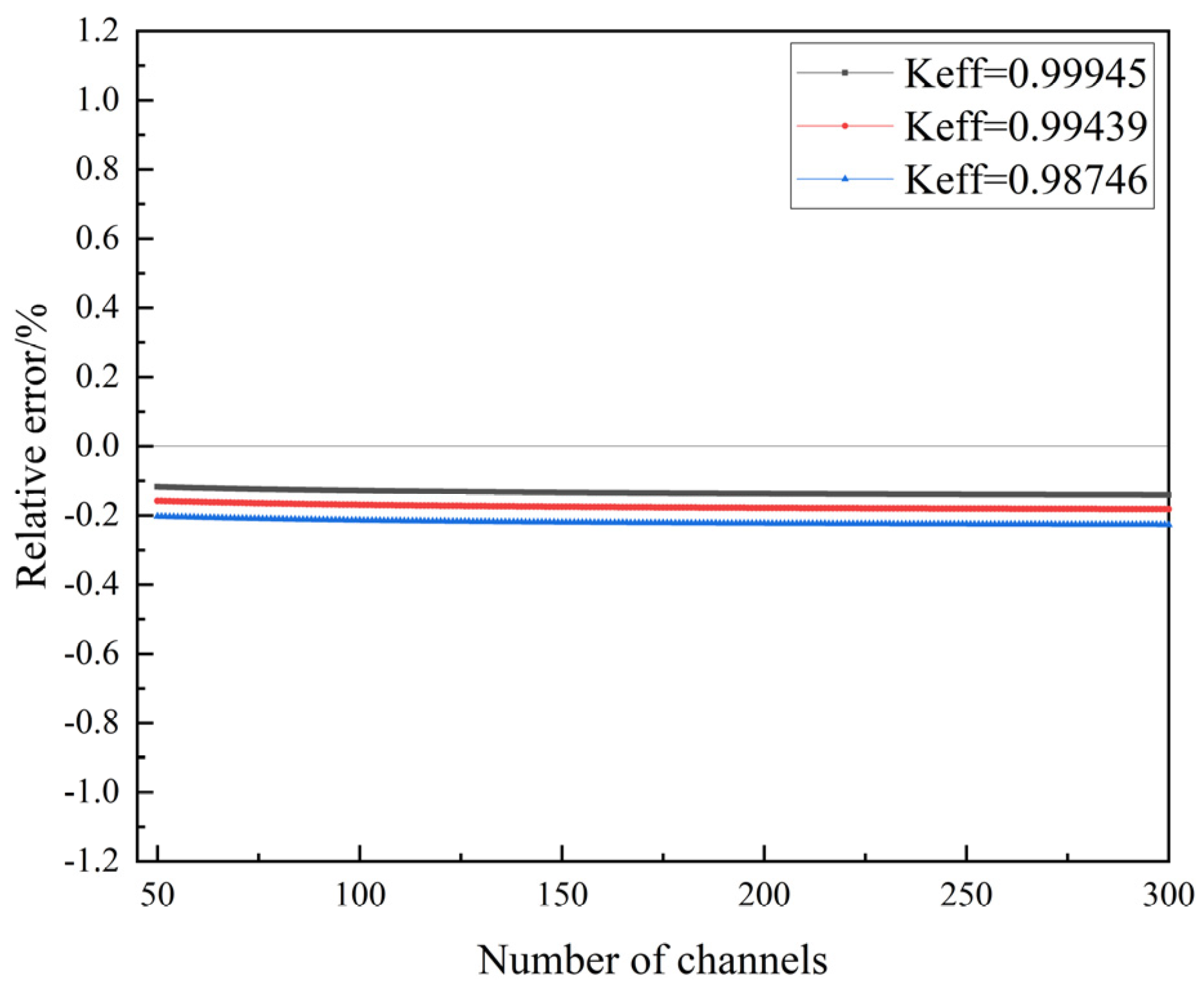
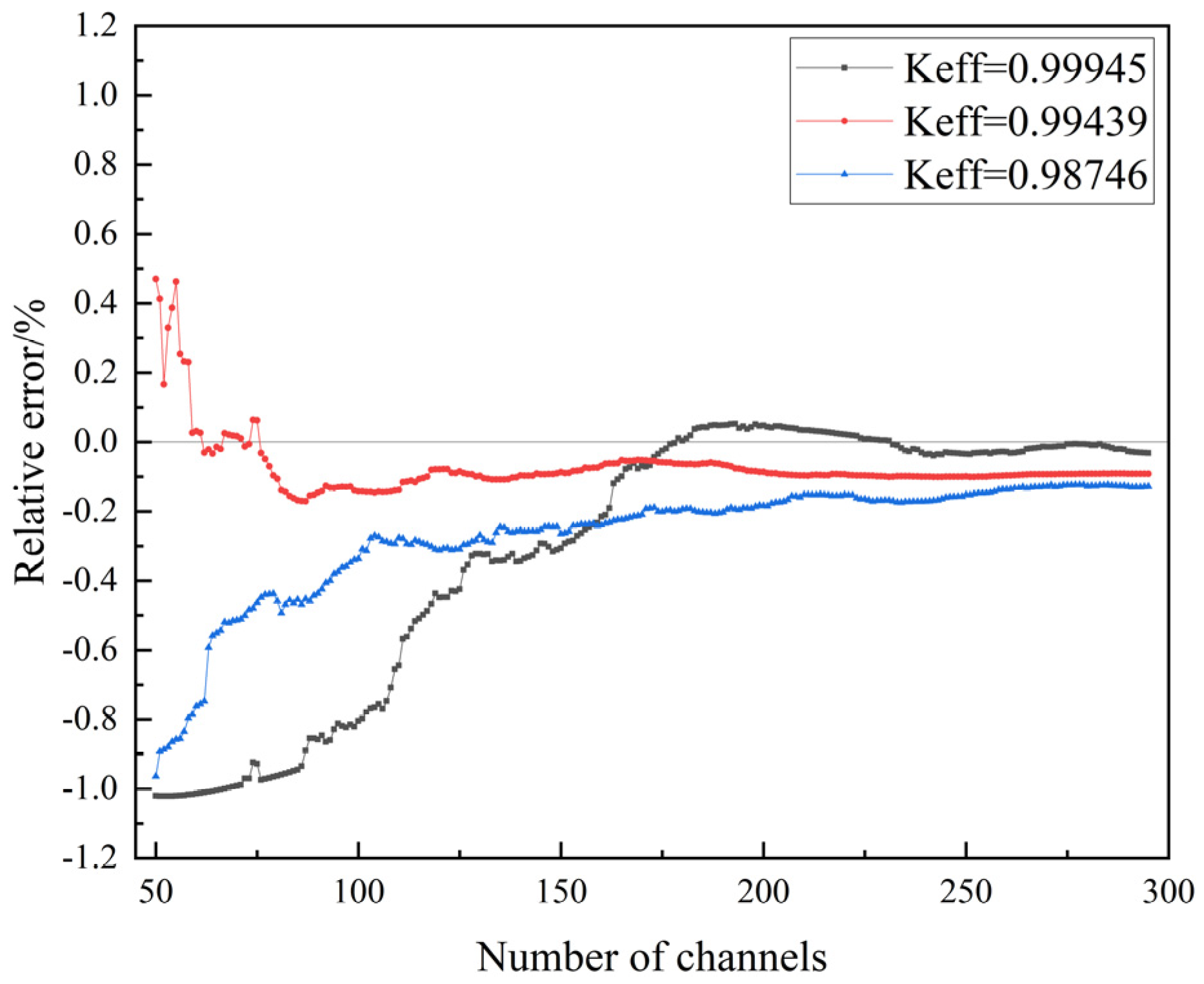
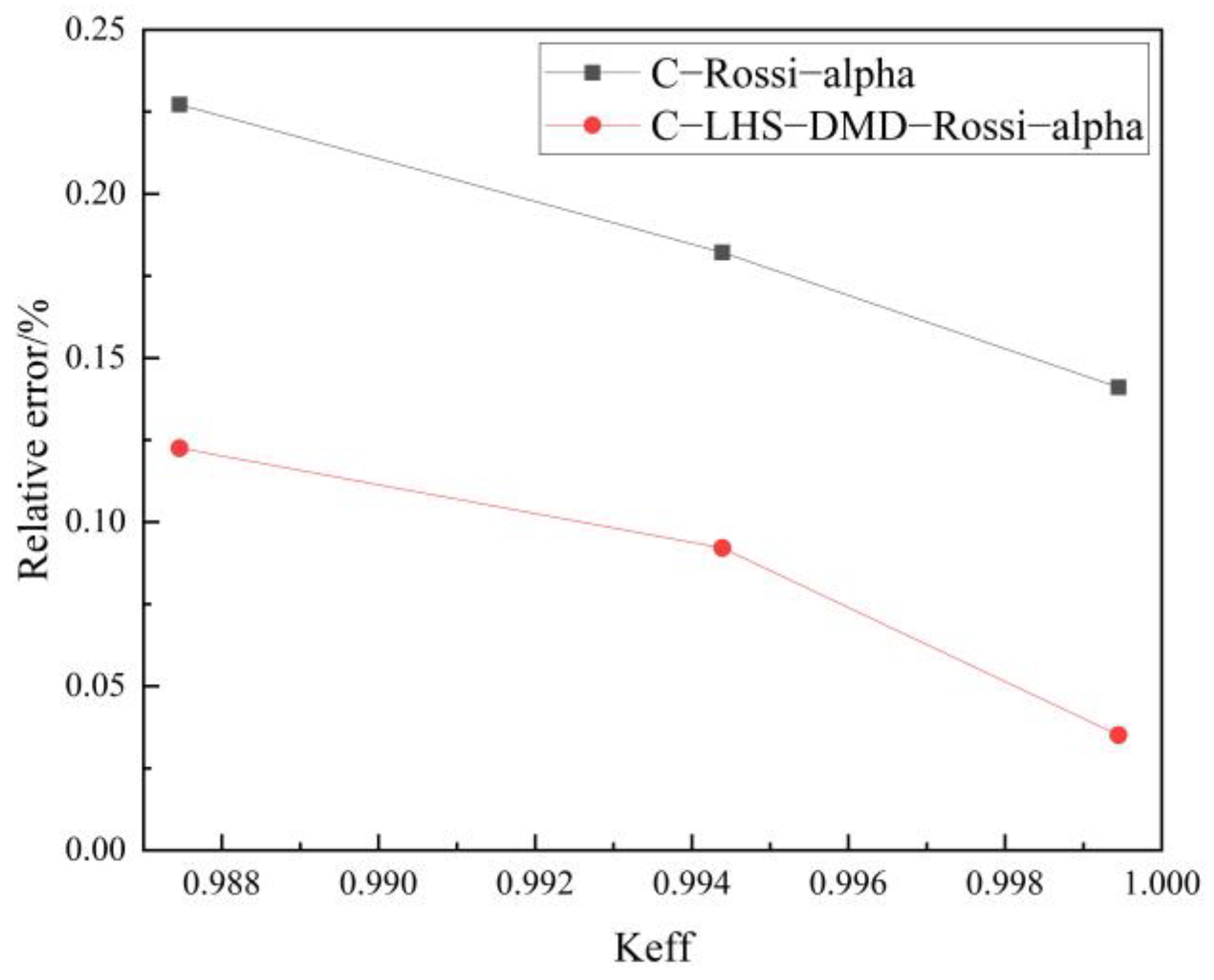
- In the critical state, compared with the DMD-Rossi-alpha method and the Rossi-alpha method, the results of the LHS-DMD-Rossi-alpha method for measuring the prompt neutron decay constant are less deviated from the calculation of the benchmark experimental values. The research shows that the LHS-DMD-Rossi-alpha method reduces the 23 detector data required by the DMD-Rossi-alpha method to one, and reduces the relative error of the calculation of the prompt neutron decay constant by 0.75%.
- As the subcriticality deepens, both the Rossi-alpha method and the LHS-DMD-Rossi-alpha method show an increase in the relative error in calculating the prompt neutron decay constant. However, the relative error of the prompt neutron decay constant calculated by the LHS-DMD-Rossi-alpha method is still smaller than that calculated by the Rossi-alpha method, and the relative error is reduced by 9%.
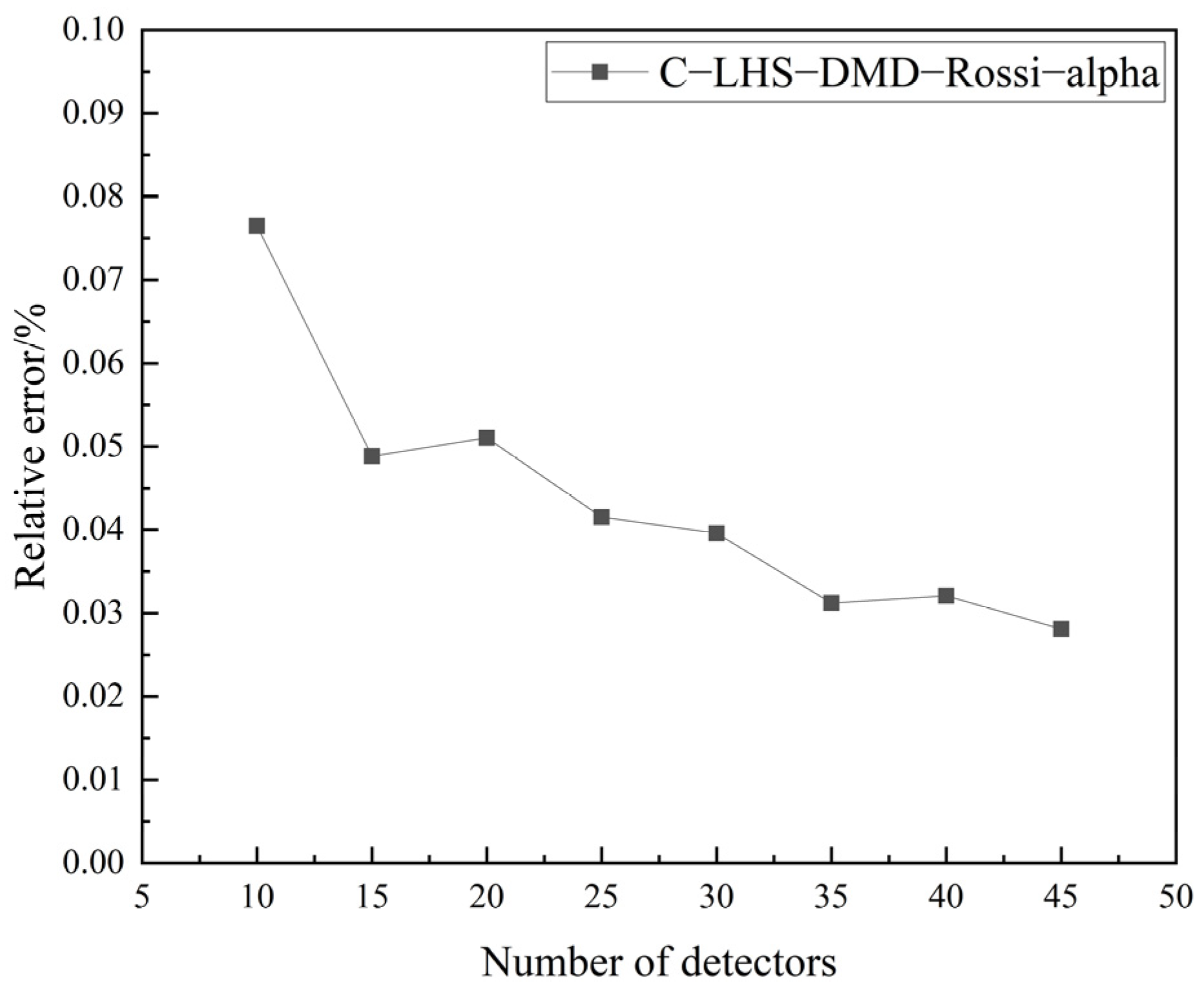
- By investigating the relative error of measuring the prompt neutron decay constant using datasets generated by varying the number of detectors (M) in the LHS-DMD-Rossi-alpha method through sampling, it was found that increasing the number of detectors can reduce the error of the LHS-DMD-Rossi-alpha method. However, the margin of error reduction gradually diminishes when the number of detectors increases to 35.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Talamo, A.; Gohar, Y.; Gabrielli, F.; Rineiski, A.; Pyeon, C. Advances in the computation of the Sjöstrand, Rossi, and Feynman distributions. Prog. Nucl. Energy 2017, 101, 299–311. [Google Scholar] [CrossRef]
- Muñoz-Cobo, J.-L.; Berglöf, C.; Peña, J.; Villamarín, D.; Bournos, V. Feynman-α and Rossi-α formulas with spatial and modal effects. Ann. Nucl. Energy 2011, 38, 590–600. [Google Scholar] [CrossRef]
- Hua, M.Y.; Darby, F.B.; Hutchinson, J.D.; McKenzie, G.E.; Clarke, S.D.; Pozzi, S.A. Validation of the two-region Rossi-alpha model for reflected assemblies. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2020, 981, 164535. [Google Scholar] [CrossRef]
- Kong, C.; Lee, D. Sensitivity analysis of source intensity and time bin size for the Rossi-alpha method in a numerical reactor model. Ann. Nucl. Energy 2019, 130, 157–163. [Google Scholar] [CrossRef]
- Yamamoto, T.; Sakamoto, H. Higher harmonic analyses of the Rossi-α method and application of dynamic mode decomposition for time decay constant determination in a 1D subcritical system. Ann. Nucl. Energy 2022, 168, 108886. [Google Scholar] [CrossRef]
- Albugami, A.O.; Alomari, A.S.; Almarshad, A.I. Modeling and simulation of VERA core physics benchmark using OpenMC code. Nucl. Eng. Technol. 2023, 55, 3388–3400. [Google Scholar] [CrossRef]
- Wang, K.; Li, Z.; She, D.; Liang, J.; Xu, Q.; Qiu, Y.; Yu, J.; Sun, J.; Fan, X.; Yu, G. RMC–A Monte Carlo code for reactor core analysis. Ann. Nucl. Energy 2014, 82, 121–129. [Google Scholar] [CrossRef]
- Pyeon, C.H.; Yamanaka, M.; Endo, T.; Chiba, G.; Van Rooijen, W.F.G.; Watanabe, K. Neutron Generation Time in Highly-Enriched Uranium Core at Kyoto University Critical Assembly. Nucl. Sci. Eng. 2020, 194, 1116–1127. [Google Scholar] [CrossRef]
- Talamo, A.; Gohar, Y.; Yamanaka, M.; Pyeon, C.H. Paralyzable and non-paralyzable dead-time corrections for the neutron detectors of the KUCA facility driven by external neutron sources. J. Nucl. Sci. Technol. 2020, 57, 157–168. [Google Scholar] [CrossRef]
- Szieberth, M.; Klujber, G.; Kloosterman, J.L.; de Haas, D. Measurement of multiple α -modes at the Delphi subcritical assembly by neutron noise techniques. Ann. Nucl. Energy 2015, 75, 146–157. [Google Scholar] [CrossRef]
- Yamanaka, M.; Pyeon, C.H.; Kim, S.H.; Shiga, H.; Kitamura, Y.; Misawa, T. Effective delayed neutron fraction by Rossi-α method in accelerator-driven system experiments with 100 MeV protons at kyoto university critical assembly. J. Nucl. Sci. Technol. 2017, 54, 293–300. [Google Scholar] [CrossRef]
- Jiang, H.; Dong, W.; Li, P.; Zhang, H. Based on Wavelet and Windowed Multi-Resolution Dynamic Mode Decomposition, Transient Axial Force Analysis of a Centrifugal Pump under Variable Operating Conditions. Energies 2023, 16, 7176. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, X.; Zhang, Z. Analysis of V-Gutter Reacting Flow Dynamics Using Proper Orthogonal and Dynamic Mode Decompositions. Energies 2020, 13, 4886. [Google Scholar] [CrossRef]
- Guan, W.; Dong, L.; Zhang, A.; Cai, Y. Output-only modal identification with recursive dynamic mode decomposition for time-varying systems. Measurement 2023, 224, 113852. [Google Scholar] [CrossRef]
- Hardy, Z.K.; Morel, J.E.; Ahrens, C. Dynamic Mode Decomposition for Subcritical Metal Systems. Nucl. Sci. Eng. 2019, 193, 1173–1185. [Google Scholar] [CrossRef]
- Schmid, P.J. Application of the dynamic mode decomposition to experimental data. Exp. Fluids 2011, 50, 1123–1130. [Google Scholar] [CrossRef]
- Yang, W.; Zhang, Y.; Wang, Y.; Liang, K.; Zhao, H.; Yang, A. Multi-Angle Reliability Evaluation of Grid-Connected Wind Farms with Energy Storage Based on Latin Hypercube Important Sampling. Energies 2023, 16, 6427. [Google Scholar] [CrossRef]
- Pyeon, C.H.; Talamo, A.; Fukushima, M. Special issue on accelerator-driven system benchmarks at Kyoto University Critical Assembly. J. Nucl. Sci. Technol. 2020, 57, 133–135. [Google Scholar] [CrossRef]
- Peplowski, P.N.; Yokley, Z.W.; Liebel, M.; Cheng, S.; Elphic, R.C.; Hoogerheide, S.F.; Lawrence, D.J.; Nico, J.S. Position-dependent neutron detection efficiency loss in 3He gas proportional counters. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2020, 982, 164574. [Google Scholar] [CrossRef]
- Talamo, A.; Gohar, Y.; Yamanaka, M.; Pyeon, C.H. Calculation of the prompt neutron decay constant for the KUCA facility driven by a stationary or pulsed external neutron source. J. Nucl. Sci. Technol. 2020, 57, 145–156. [Google Scholar] [CrossRef]
- Hursin, M.; Zoia, A.; Rouchon, A.; Brighenti, A.; Zmijarevic, I.; Santandrea, S.; Vinai, P.; Mylonakis, A.; Yi, H.; Demazière, C.; et al. Modeling noise experiments performed at AKR-2 and CROCUS zero-power reactors. Ann. Nucl. Energy 2023, 194, 110066. [Google Scholar] [CrossRef]
- Yamamoto, T.; Sakamoto, H. Application of dynamic mode decomposition to exponential experiment for spatial decay constant determination. Ann. Nucl. Energy 2021, 162, 108506. [Google Scholar] [CrossRef]
- Oettingen, M. Criticality analysis of the Louis Slotin accident. Nucl. Eng. Des. 2018, 338, 92–101. [Google Scholar] [CrossRef]
- Oettingen, M. A criticality study on the LA-1 accident using Monte Carlo methods. Nucl. Eng. Des. 2020, 359, 110467. [Google Scholar] [CrossRef]

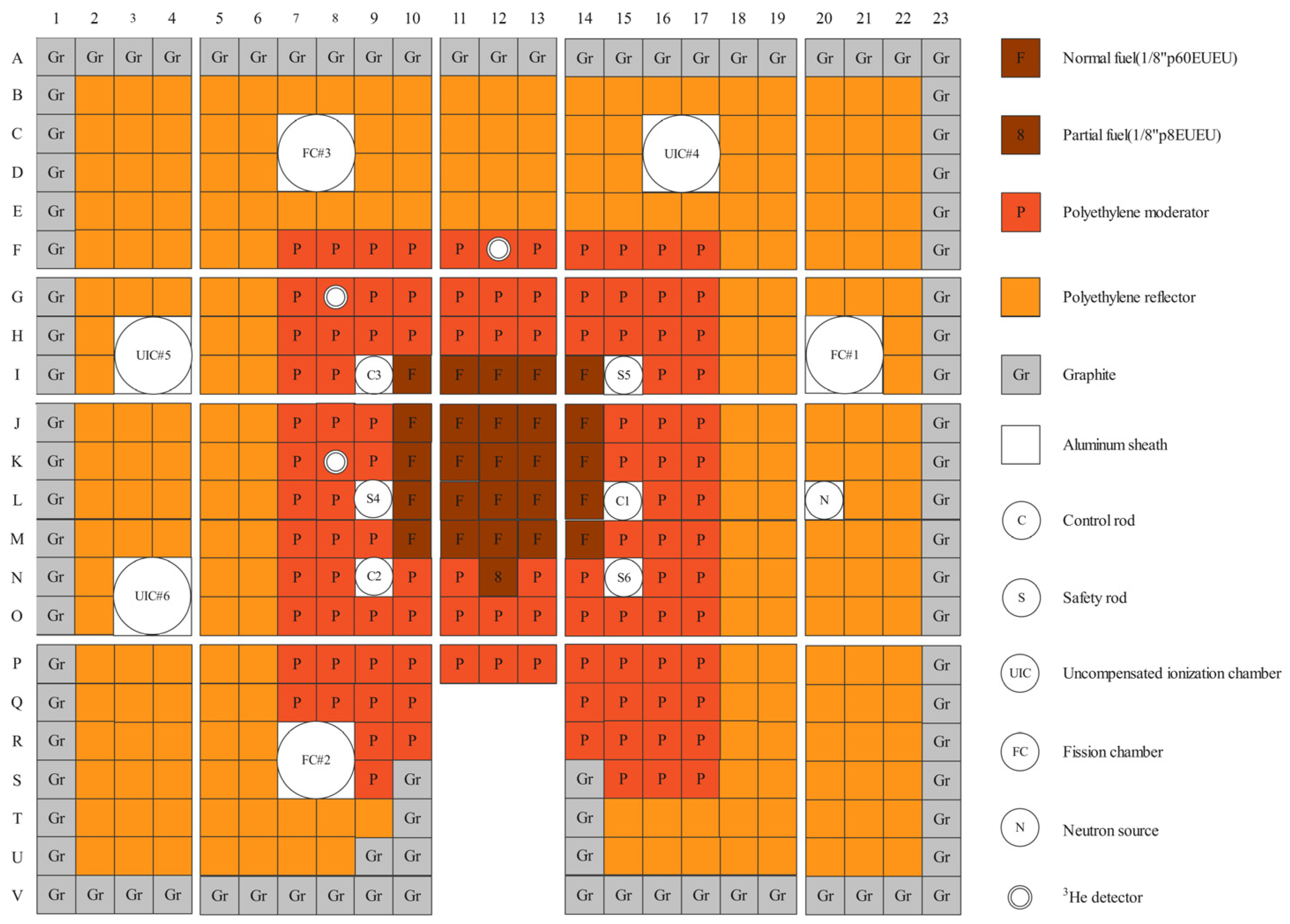
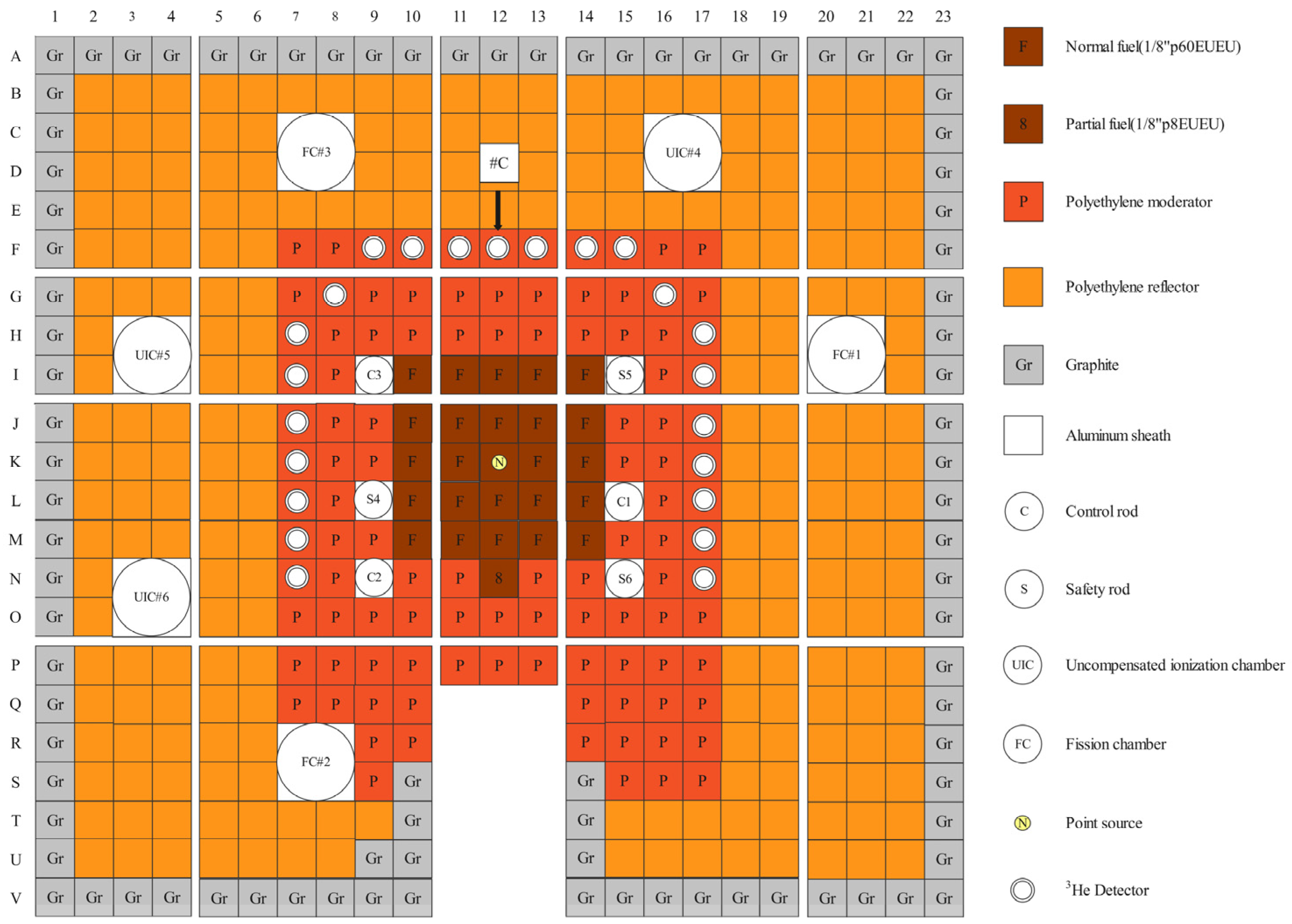
| Control Rods | Safety Rods | ||||
|---|---|---|---|---|---|
| C1 | C2 | C3 | S4 | S5 | S6 |
| 1200.00 mm | 1200.00 mm | 630.01 mm | 1200.00 mm | 1200.00 mm | 1200.00 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Xie, J.; Deng, N.; Zhang, E.; Wu, Z.; Tong, J.; Yu, T. Research on the Measurement Method of the Prompt Neutron Decay Constant Based on LHS-DMD-Rossi-Alpha. Energies 2024, 17, 2034. https://doi.org/10.3390/en17092034
Li J, Xie J, Deng N, Zhang E, Wu Z, Tong J, Yu T. Research on the Measurement Method of the Prompt Neutron Decay Constant Based on LHS-DMD-Rossi-Alpha. Energies. 2024; 17(9):2034. https://doi.org/10.3390/en17092034
Chicago/Turabian StyleLi, Junguang, Jinsen Xie, Nianbiao Deng, Erpin Zhang, Zhiqiang Wu, Ji Tong, and Tao Yu. 2024. "Research on the Measurement Method of the Prompt Neutron Decay Constant Based on LHS-DMD-Rossi-Alpha" Energies 17, no. 9: 2034. https://doi.org/10.3390/en17092034
APA StyleLi, J., Xie, J., Deng, N., Zhang, E., Wu, Z., Tong, J., & Yu, T. (2024). Research on the Measurement Method of the Prompt Neutron Decay Constant Based on LHS-DMD-Rossi-Alpha. Energies, 17(9), 2034. https://doi.org/10.3390/en17092034






