Harmonic Distortion Study of a Photovoltaic Generator in a Microgrid under Disturbances

Abstract

This paper describes research on the harmonic-distortion capacity of a single-stage photovoltaic (PV) 3.68 kWp generator in a microgrid configuration. An overview of various harmonic compensator methods used in PV generators is presented to evaluate their advantages and disadvantages. Proportional-resonant (PR) structures with harmonic compensators (HCs) are designed, modeled, and validated through real-time tests. The modeling of harmonic compensation structures for a photovoltaic inverter using MATLAB/SIMULINK R2022a is explained in detail. The harmonic compensation capacity of a PV generator inverter is studied under voltage harmonics, grid frequency variation, and voltage unbalance. The contributions of this work are, firstly a bibliographic analysis of various strategies currently used for harmonic compensation in grid-connected inverters and secondly, a detailed explanation of the modeling of harmonic compensation structures using MATLAB/SIMULINK. Finally, a demonstration of the improvement in energy quality that results from using harmonic compensation techniques in photovoltaic generators in microgrid configurations affected by grid disturbances is performed. The obtained results show that harmonic compensation strategies based on resonant filters are a good alternative for the reduction of harmonic voltage distortion in the presence of grid disturbances such as frequency variation and voltage unbalance.

1. Introduction

As part of compliance with the regulations governing good practices related to the use of energy in electrical systems, power quality is an aspect of great importance that is used when determining the characteristics of electrical energy. In recent decades, there has been increasing interest in the study and development of techniques aimed at improving power quality, motivated by the increasingly stringent quality requirements derived from new grid codes and standards [1]. It should be noted that non-compliance with power-quality regulations can result in a penalty and even force a generator to be disconnected from the utility grid.

As shown in [2], alterations in the sinusoidal voltage and current waveforms may occur in the production, transport, and distribution processes, as well as in energy use by certain types of loads. Therefore, they are unavoidable. However, only in recent years have they become a cause for concern. In the utility grid, among the different disturbances that can be found, one of the most predominant is harmonic distortion, which is mainly due to the existence of non-linear loads, which are defined by a pure non-sinusoidal demand current and, therefore, by a distorted wave [3,4,5]. This harmonic pollution can introduce current distortions in the utility grid [6].

Grid tie (grid-connected) inverters have played an extremely interesting role in the incorporation of renewable energy sources (RES) into the utility grid. Power electronics converters (PEC) and control interfaces are critical for the power conditioning required for the integration of RES-based distributed generation (DG). Nevertheless, important challenges are associated with the increasing number of PE interfaces in the electrical utility: stability under weak grid conditions, limited short-circuit current, and nonlinear dynamics [7,8]. The nonlinear nature of switching devices and their high-frequency operation are important contributors to the increased presence of harmonics in utility grids with high penetration of RES and PEC [9]; thus, the study of harmonic compensation techniques as auxiliary services of PEC interfaces is an important issue for enabling large-scale integration of RES and DG. Due to the above factors, various studies focused on the use of techniques to improve power quality in relation to current harmonic distortion have been presented in the scientific literature [10,11,12,13,14,15,16,17,18,19].

Microgrids are defined as a collection of DG and loads (critical and non-critical) with the capability for either islanded or grid-tied operation [20]. As discussed in [21], the presence of current harmonics may present important challenges in the operation of microgrid systems. These harmonics can affect internal PEC measurements, causing voltage distortion at the point of common coupling (PCC) and, in case of large harmonic presence, lead to the activation of the PEC’s internal protection. From this perspective, the study of auxiliary services related to harmonic compensation inside of microgrids is of importance.

As harmonics reduce electrical power quality, this paper will focus on the mitigation of harmonics in inverters used in PV generators in a microgrid configuration connected to the utility grid. The methodology will be based on the creation of a model in MATLAB/SIMULINK R2022a of a PV generator belonging to a microgrid affected by grid disturbances such as harmonic distortion, fundamental frequency variation and voltage unbalance. A study of the grid currents with and without a HC strategy will be conducted on the PV generator of the microgrid using MATLAB’s Fast Fourier Transform (FFT) analyzer [22]. The FFT represents a calculation algorithm that provides the content of the different pure sine waves that make up the deformed wave. A final validation of the HC structures is carried out through real-time simulations using an OP5707XG simulator from OPAL-RT [23]. As shown in [24], these types of validation are of relevance for the implementation of advanced control techniques focused on harmonics mitigation. Nevertheless, hardware constraints limit the number of harmonic compensation structures that can be implemented. Thus, it is of importance to test how this new generation of digital simulators may enable the simulation of more complex harmonic compensation structures.

The contributions of this research can be summarized in three main points: firstly, a bibliographic analysis of different strategies used for current harmonic compensation in grid-connected inverters; secondly, a detailed explanation of the modeling of a HC structure using MATLAB/SIMULINK; and finally, the real-time validation of a harmonic compensation structure up to the 17th harmonic, taking advantage of the new simulation capacities presented by the OP5707XG simulator from Opal RT. This approach allows the demonstration of the improvement in energy quality realized by using harmonic compensation techniques in inverters of photovoltaic generators connected to utility grid affected by harmonic pollution and other grid disturbances.

Different methodologies used for harmonic compensation and improved power quality in PV generators in microgrid configurations are discussed in Section 2. In Section 3, a case study of a microgrid is explained. The methodology used in this paper is shown in Section 4. To study the harmonic behavior of the case studies, various simulations using MATLAB/SIMULINK are described in Section 5. Several real-time tests performed using a digital simulator are described in Section 6. The discussion of the results obtained is shown in Section 7. Finally, some conclusions are presented in Section 8.

2. Review of Grid Tie Inverter Control Techniques for Harmonic Compensation

Below, some works from the scientific literature aimed at improving quality, in terms of harmonic mitigation, in microgrids and distributed generation systems are discussed. These works were selected by searching for keywords such as “harmonic compensation”, “microgrids”, and “distributed generation”. The journals where they were published and their impact were also taken into consideration.

In the review presented in [10], the authors comment on the versatility of operation offered by PEC-based microgrids (MG), which can be used in either an islanded or a grid-tie operation. This versatility creates an array of opportunities for providing auxiliary services to the electrical utility with the goal of improving power quality indicators. Typically, the control structure of microgrids has been separated into three hierarchical levels. The primary level oversees internal voltage/frequency regulation; the secondary level monitors and compensate for deviations in the primary-level control variables; and finally, the tertiary control level ensures correct energy management under grid-tie or grid-forming operation. Nevertheless, harmonic presence due to nonlinear loads, switching, and resonance is an important problem for the implementation of hierarchical control. As mentioned by the authors, numerous investigations have been carried out on harmonic compensation using the PEC of the MG systems. These studies have focused on one of the following objectives: harmonic mitigation at the common connection point (PCC), harmonic cancellation in local loads, and mitigation of line current harmonics. The first step in the harmonic compensation process is detection, wherein spectral-analysis methods like the discrete Fourier transform (DFT) and the sliding DFT (SDFT) have been applied. In the first compensation strategies, authors elaborated on primary-level compensation methods, among them modified droop control (MDC), adaptive virtual impedance (VIA), and proportional-resonance regulator (PR). Harmonic compensation at the secondary level can be separated in two principal approaches: centralized and distributed. In both, the main objective is the online monitoring of harmonic presence for each MG with the purpose of adjusting the harmonic compensation at the individual level. Finally, compensation at the tertiary level focuses on the optimization process, in which optimal set points are selected to minimize the harmonic presence of each MG. In their conclusion, the authors comment on the directions future research must take in order to develop inverter-based harmonic compensation, highlighting the importance of improved and more powerful control methods based on predictive control or artificial intelligence approaches. Additionally, it is important to note that the harmonic compensation structures reviewed by the authors were directed to the 11th harmonic and bellow, making a case for the evaluation of the design of higher-order harmonic compensation structures, as proposed by this work.

Classical proportional resonant methods for harmonic compensation are shown in [11]. The presented frequency-adaptive architecture can be tuned by using the information provided by the harmonic detection strategy. This detection procedure is carried out using a modified second-order generalized integrator (SOGI) together with a synchronous reference frame phase-locked loop (SRF-PLL). The authors study the bandwidth of the SOGI and the capacity of the SRF-PLL to compensate for harmonics outside its central frequency, adding an adaptive parameter for the detection of the harmonic with the higher amplitude without losing stability. The validation is done by means of harmonic injection-induced variation. In their results, the authors comment on the adaptability of the proposed strategy, which is capable of reducing the harmonic with the greatest amplitude and of adding more SRF-PLL stages for further harmonic compensation. Nevertheless, the considerations for the evaluation of the system account for only the 3rd and the 5th harmonics.

In [12], a strategy for harmonic compensation using grid-tie converters and considering capacity limitations is presented. The authors note that previous works do not consider constraints related to the capacity of the inverter; that is, the rated apparent power of the inverter should not exceed the active and the apparent power rating of the inverter during the harmonic compensation process. To achieve the above aim, the proposed control strategy calculates the maximum allowable current for harmonic compensation. The harmonics are detected using the d-q current reference frame, where the current waveforms are low-pass filtered and subtracted to determine the harmonic content. A regulation factor is calculated for the maximum allowable harmonic compensation current. Two harmonic compensation strategies are compared: quasi-proportional resonant (QPR) and vector resonant (VR) controller; both strategies provide better robustness compared to traditional proportional resonant (PR) control. These controllers are coupled with a traditional proportional-integral (PI) control for the internal DC loops in the d-q reference frame for the operation of the inverter. In their results, the authors show the harmonic suppression of the PI + QPR strategy under capacity limitation, validating their proposed strategy. A point is made concerning the inter-harmonic coupling, which affects the compensation strategy in both controllers. Nevertheless, the best results are obtained with the PI + VR strategy due to its better performance in harmonic tracking, with a reduction of THD from 7.69% to 3.78%. This paper concludes by noting the good performance of the proposed strategies and the need for future research regarding the inter-harmonic coupling effect to improve performance with regard to harmonic suppression. This inter-harmonic coupling effect recognized by the authors is an important motivator in studies of the design of higher-order HC structures like the one proposed in this work.

The development of resonant converters for harmonic compensation is also studied in [13]; the authors comment on the computational burden imposed by multiple resonant controllers (MRSCs) if compensation is required for various harmonic frequencies. Furthermore, there are stability issues related to RSC in cases of utility frequency deviation. Such issues require the adaptive online tuning of these types of controllers. The authors proposed a novel downsampling method to reduce the computational burden imposed by multiple MRSCs that uses a multi-rate resonant controller implementation. The developed methodology creates a multirate RSC combining the 6th, 12th, and 18th harmonics and uses power-hardware-in-the-loop (PHIL) simulations for validation. The results show that the computational burden is reduced by a factor of two with the proposed strategy and that the obtained THD is below 6% for each of the studied cases. The article concludes by recommending this type of strategy for the deployment of embedded inverter control systems and the reduction of total system costs. This work is a good reference regarding enhanced performance in higher-order HC compensation structures; in this paper, this type of strategy will be incremented to include the 3rd, 5th, 7th, 11th, 13th, 15th, and 17th harmonics, taking advantage of the increased hardware performance of the latest generation of digital simulators.

The deployment of advanced optimization techniques to improve the harmonic characteristics of PEC is presented in [14]. A modified grey wolf optimization algorithm (MGWO) is proposed to solve the nonlinear problematic of selective harmonic elimination pulse width modulation (SHE-PWM) and offers better harmonic suppression performance compared to other modulation strategies. The improved exploration and exploitation capabilities of the proposed MGWO algorithm offer advantages over other types of optimization strategies such as particle swarm optimization (PSO), traditional grey wolf optimization (GWO), or genetic algorithms (GA). The proposed MGWO introduces a chaotic variable to enhance the exploration and exploitation capabilities of traditional GWO. In the methodology, nonlinear switching equations that account for harmonics up to the 13th harmonic are presented. They are used with the purpose of solving the system of equations to reduce the presence of harmonics. Various tests are conducted under different modulation indices to validate the proposed strategy. The proposed MGWO could produce a THD of 5.54% with a modulation index of 0.6 and a THD of 6.03% with a modulation index of 1.1, offering a lower THD when compared to the GWO solution. Validations were conducted in simulated and physical environments; in their conclusions, the authors comment on the rapidity with which the MGWO was able to obtain the solutions required for the harmonic reduction strategies.

As several PEC interfaces may operate in parallel under MG islanded operation, the evaluation of harmonic suppression at the PCC is of interest. The authors of [15] studied the implementation of coordinated control strategies for harmonic compensation involving several DG agents. For this purpose, an adaptive virtual impedance controller (VIC) is used to compensate for THD at the PCC. The VIC is a modification of the classical droop controller, where a virtual impedance is applied to enhance reactive power sharing. This approach can be extended to provide harmonic compensation at the PCC, as demonstrated by the authors using a negative virtual impedance value. Additionally, the authors formulated a strategy for the regulation of PCC voltage and harmonic levels that involved dividing the virtual impedance into two components. A microgrid central controller (MGCC) manages the operation of each individual VIC and provides the necessary reference points to achieve the desired harmonic compensation level based on each measurement of the PCC harmonic distortion. Robustness against communication delays was tested for the centralized control system, and it was found that a communication delay of 10 ms can be tolerated. The results show a harmonic reduction with the proposed strategy, where the initial 7.55% THD was reduced to 2.76%. The simulation was conducted using four DG units, and a physical implementation of the system was constructed using three inverters. In the physical implementation, the initial harmonic presence was 6.20%, and after the activation of the VIC strategy, a reduction to 3.07% was obtained. In their conclusions, the authors comment on the viability of the proposed strategy, which is due to its simple implementation.

As can be seen from [15], the dependency on a centralized controller is an important limitation in the implementation of multiagent harmonic compensation strategies.

In [16], a distributed event-triggered approach for the multiagent compensation of harmonics by means of PEC is described. Stability conditions for the proposed control system were studied using Lyapunov formulations. In this approach, events are triggered by the deviation error from the desired total harmonic value. After this step, each internal harmonic compensation network of the agents is adjusted by the consensus rule proposed by the authors. The stability of the consensus criterium is tested, and experimental results are produced. The testing involves a nonlinear load producing 3.5% THD, which is reduced to levels below 1%. Various cases are studied, with changes in the information shared between each agent and maintenance of the correct harmonic compensation. The authors conclude by discussing the robustness of the proposed strategy and the possibility of discretizing event monitoring to reduce the communication burden.

Due to increasing use of hybrid AC/DC MG, the authors of [17] present a harmonic compensation strategy for the DC bus in a hybrid MG based on the use of GA. In the case of DC sub grids inside a MG, the even-numbered harmonics are presented. This paper focuses on mitigating the 2nd harmonic by means of introducing a compensation current that acts like a virtual impedance. The GA algorithm calculates the set point for this current, executing an online evaluation of its fitting function. Results from both simulated and physical implementations show a reduction in voltage ripple on the DC bus, from 16.2 V to less than 2.5 V in both scenarios. The presented conclusions comment on the viability of using the GA algorithm for online optimization; furthermore, the proposed methodology was validated by the obtained results.

In the research presented in [25], the authors use a harmonic compensation strategy based on the use of parallel resonant filters. Each resonant filter corresponds to the harmonic that will be compensated for within the control current loop used in the inverter of a grid-connected photovoltaic generator. This harmonic compensation strategy allows for frequency-adaptive harmonic compensation, since the frequency estimated by the synchronization algorithm is relayed to the harmonic compensation block. This ability of this harmonic compensation technique to adapt to frequency variations makes it attractive for use in settings in which photovoltaic generators are connected to a weak electrical grid susceptible to electrical disturbances. The biggest drawback of this technique is that a high PWM switching frequency is necessary to compensate for harmonics exceeding the 13th order.

The work presented in [26] introduces a new procedure aimed at optimally designing harmonic control and compensation strategies for three-phase inverters with grid support in AC microgrids. The strategy is based on a three-level cascade control developed in the stationary system ab, using PI and PR regulators. The authors note that the proposed strategy can reduce the THD and the individual harmonic distortion of the voltages in the microgrid. In the presence of nonlinear loads, the voltage THD could be decreased to 0.19%. The design of the optimized harmonic compensation strategy and the inverter controller utilized an optimization algorithm called H-HHOPSO. This optimization algorithm was developed through a hybridization between a particle swarm optimization algorithm and a Harris Hawks optimization algorithm. The validation of the proposed strategy was carried out using models created in MATLAB/SIMULINK. The design of the controller and the optimized HC strategy was divided into two stages. The purpose of the first stage was the calculation and selection of the parameters corresponding to the voltage and current control of the inverter through PR regulators and the harmonic compensation strategy. In the second stage, the coefficients of the droop control controllers, the secondary control level and the synchronization control were designed.

The proposed strategy was compared with other harmonic compensation techniques when non-linear loads were connected, and the THD of voltage in the microgrid was reduced from 5.23% to 4.18% when a traditional control based on a PI regulator was used. When the H-HHOPSO strategy presented by the authors was used, the voltage THD was reduced to 0.16%. It should be noted that other types of grid disturbances such as voltage unbalance and voltage flickers were not considered in the study. Furthermore, it should be noted that the evaluation of the proposed technique was validated through simulations.

Table 1. Summary of the harmonic compensation methods addressed in the review.

Reference	Harmonic Detection Method	Compensation Method	Harmonic Reduction Level	Observations	Validation Method
[11]	SRF-PLL	Adaptive PR control	25%	Only one harmonic is compensated	Numerical simulation and experimental setup
[12]	FFT	PI + VR	49%	Interharmonics coupling	Numerical simulations
[13]	FFT	MRSC	108%	Lower performance with reduced sampling frequency	Numerical simulations and PHIL
[14]	FFT	MGWO with current compensation	55%	Only tested for compensation up to the 13th harmonic	Numerical simulations and experimental setup
[15]	FFT	Centralized multiagent VIC	50%	Reduced performance under communication channel delays	Numerical simulations and experimental setup
[16]	Low Pass Filtering in DQ Frame	Distributed event-triggered	33%	Study limited to only three DG agents	Numerical simulations and PHIL
[17]	FFT	GA for the calculation of compensation current	93%	Mitigation strategy focuses only on the 2nd harmonic	Numerical simulations and experimental setup
[25]	MSOGI-FLL	Adaptive PR control	-	Only the 5th and 7th harmonics were compensated during the tests	Numerical simulations and CHIL
[26]	-	PR+ optimized HC	0.16%	No experiments were performed.Different grid disturbances were not included when the proposed methodology was validated.	Numerical simulations

summarizes the harmonic compensation strategies described above, classifying them by the technique used to detect harmonics, the compensation method, the harmonic reduction, the limitations of the studies carried out, and finally, the validation method. As can be seen from the limitations of the reviewed works, the higher-order HC structure designed in this paper is significant because it enables the study of compensating a broader range of harmonics in the proposed MG real-time test case.

3. Proposed Study Case

3.1. PUCMM Microgrid Laboratory

A microgrid laboratory located at the PUCMM aims to provide a testing ground for the evaluation of control techniques related to resiliency enhancement by means of the implementation of microgrid architectures within the utility grid. This laboratory was designed with the objective of providing a real-time simulation environment for testing various control strategies for microgrid systems and their interconnection with the utility grid. The central equipment of this laboratory is a Real-Time Control Unit implemented using OPAL-RT hardware and RT-LAB software version v2023.2.1578, which provides real-time simulation capabilities on a nanosecond scale. Furthermore, the selected inverter modules can operate in PHIL, in Controller Hardware-in-the-Loop (CHIL), and as standalone converters with their own internal controllers (see Figure 1). The laboratory is equipped with a total of 3.68 KWp of solar photovoltaic modules and a 5 kWh lithium battery. The photovoltaic modules are described in

Table 2. Parameters of a Q. PEAK DUO XL-G9.3 460 kW photovoltaic module.

Parameters	Value
Maximum power	460 W
Maximum power voltage	44.89 V
Maximum power current	10.25 A
Open-circuit voltage	53.25 V
Short-circuit current	10.70 A
Cell numbers per module	156
Temperature coefficient of short-circuit current	0.04%/deg. °C
Temperature coefficient of open-circuit voltage	−0.27%/deg. °C

, and the photovoltaic array is described in

Table 3. Parameters of the 3.68 kWp array.

Parameters	Value
Number of strings	1
Number of series modules	8
Maximum power current	10.25 A
Maximum power voltage	359.12 V
DC output power	3.68 kW
Open-circuit voltage	426 V
Short-circuit current	10.7 A

. All components are connected in a load center capable of grid-connected operations, supervised by a feeder protection relay system.

3.2. Photovoltaic Single-Stage Grid-Connected Generator

With the objective of evaluating the importance of using harmonic compensation strategies in grid-connected inverters of PV generators, the PV generator shown in Figure 1 is described below.

Figure 2 is a diagram of the 3.68 kWp photovoltaic generator at the microgrid laboratory depicted in Figure 1. The photovoltaic generator has been divided into two subsystems. The top section shows the power subsystem, which is made up of photovoltaic modules whose function is to transform energy from the sun into electrical energy [27]. The PV modules are model DUO XL-G9.3 from QCELL, each with a power of 460 Watts [28]. Parameters of the PV modules used in this case are shown in Table 2. The capacitor link with the DC bus is also shown. The voltage source inverter (VSI) has the function of converting the electrical energy from photovoltaic panels into alternating current (AC) energy. An LC filter is responsible for mitigating ripples produced by switching in the inverter. A transformer located between the PV generator and the utility grid provides galvanic isolation.

The control subsystem of the PV generator can be seen at the bottom of Figure 2. It incorporates a maximum power point tracker (MPPT) algorithm whose purpose is to obtain the greatest amount of power from the photovoltaic modules under the available solar irradiance. A cascade control approach is used in the inverter, where an external loop is controlled by a PI regulator that manages the power flow. An internal control loop regulates the power factor (PF) of the generator.

To determine the frequency and the phase angle of the utility grid, a block labeled as the synchronization algorithm is used. In this work, a Multiple Second-Order Generalized Integrator-Frequency Locked Loop (MSOGI-FLL) synchronization algorithm is used due to its ability to maintain accuracy when disturbances occur [29].

As shown in Figure 2, the DC component of the VSI can be established, as shown in Equation (1):

$$\begin{gathered} i_p=i_{clink}+i_{DC} \\ {i}_{DC}=S_u.i_u+S_v.i_v+S_w.i_w \\ {i}_{clink}=C_{link}\frac{d{v}_{DC}}{dt} \\ {P}_{PV}=i_p{v}_p \end{gathered}$$

(1)

where $ip$ is the output PV current, $vp$ is the output PV voltage, $P_{PV}$ is the power available as a function of the cell temperature and a specific irradiance, $v_{DC}$ is the voltage on the DC bus, $i_{clink}$ is the current through the link capacitor $C_{link}$, and $i_{DC}$ is the current sent to the VSI (being dependent of the states of the power-poles $S_u,S_v,S_w$ and the line currents $i_u,i_v,i_w$).

It is assumed that the voltages of the filter capacitors correspond to the grid voltage values. If the instantaneous values of the variables of the three-phase utility grid are expressed as vectors, generic space vectors can be obtained and the dynamics of the ac side can be expressed as follows [30]:

$${\mathbf{u}-\mathbf{u}}_{\mathbf{A}\mathbf{C}}=R\mathbf{i}+L\frac{d\mathbf{i}}{dt}={{\mathbf{u}}_{\mathbf{R}}+\mathbf{u}}_{\mathbf{L}}$$

(2)

where u is the inverter voltage space vector, i is the inverter line current space vector, u_AC is the utility grid voltage space vector, and L is the line inductance and its cupper resistance R.

Based on the Akagi theory of instantaneous active power ($p$) and instantaneous reactive power ($q$) [31], the power flow the between the PV generator and the utility grid is expressed as follows:

$$p=va{c}_{\alpha }{i}_{\alpha }+va{c}_{\beta }{i}_{\beta }$$

(3)

$$q=va{c}_{\beta }{i}_{\alpha }-va{c}_{\alpha }{i}_{\beta }$$

(4)

where $va{c}_{\alpha }$, $va{c}_{\beta }$, $i_{\alpha },$ and $i_{\beta }$ are the αβ components of three-phase voltages and currents, respectively.

The utility-grid voltage (see Figure 2) with a harmonic can be expressed as a sum of voltages with frequencies that are multiples of the fundamental frequency (in this study, 60 Hz). Equation (5) shows a mathematical expression representing the three-phase voltages of the fundamental frequency plus the distortion of the 5th-, 7th-, 11th-, 13th-, and 17th-order harmonics.

$$\begin{gathered} U_{gr\left(t\right)}=U_{1r}\cos \left(\omega t+{\theta }_{U1r}\right)+U_{h5r}\cos \left(5\omega t+{\theta }_{Uh5r}\right)+U_{h7r}\cos \left(7\omega t+{\theta }_{Uh7r}\right)+U_{h11r}\cos (11\omega t+{\theta }_{Uh11r}) \\ +U_{h13r}\cos (13\omega t+{\theta }_{Uh13r})+U_{h17r}\cos (17\omega t+{\theta }_{Uh17r}) \\ {U}_{gs\left(t\right)}=U_{1s}\cos (\omega t+{\theta }_{U1s})+U_{h5s}\cos \left(5\omega t+{\theta }_{Uh5s}\right)+U_{h7s}\cos (7\omega t+{\theta }_{Uh7s})+U_{h11s}\cos (11\omega t+{\theta }_{Uh11s}) \\ +U_{h13s}\cos (13\omega t+{\theta }_{Uh13s})+U_{h17s}\cos (17\omega t+{\theta }_{Uh17s}) \\ {U}_{gt\left(t\right)}=U_{1t}\cos (\omega t+{\theta }_{U1t})+U_{h5t}\cos \left(5\omega t+{\theta }_{Uh5t}\right)+U_{h7t}\cos (7\omega t+{\theta }_{Uh7t})+U_{h11t}\cos (11\omega t+{\theta }_{Uh11t}) \\ +U_{h13t}\cos (13\omega t+{\theta }_{Uh13t})+U_{h17t}\cos (17\omega t+{\theta }_{Uh17t}) \end{gathered}$$

(5)

where $h$ is the harmonic order, $\omega$ is the angular fundamental frequency, $U$ is the voltage magnitude, $\theta$ is the voltage phase angle of the fundamental frequency, and ${\theta }_{Uh}$ is the voltage phase angle of the harmonic $h$.

3.3. Photovoltaic Array

Various works have established a mathematical model for the PV module [32,33], based mainly on equivalent circuit models. The methodology and equations used to obtain the equivalent circuit parameters are detailed in [34,35]. From the data sheet of a Q.PEAK DUO XL-G9.3 460 kW monocrystalline PV module produced by QCELLS [28], the parameters of the PV modules used in this work are obtained (see Table 2).

The maximum power of the PV model used for this work is 3.68 kW, with parameters at standard test conditions (STC) listed in Table 3.

The upper part of Figure 3a shows the voltage and current curves of the PV array for several temperatures. The bottom part of Figure 3a shows the power and voltage values for different temperatures. Note that for a temperature of 25 degrees Celsius and an irradiance of 1 kW/m² (STC), the power of the photovoltaic array is 3.68 kW. The upper part of Figure 3b shows different values of voltages and currents for various irradiance conditions. Analysis of these data resulted in the various PV power curves shown at the bottom of Figure 3b.

4. Methodology

4.1. Cascade Control

The inverter control strategy is based on cascade control. Two control loops are detailed below.

4.1.1. DC Voltage Control Loop

According to Figure 2, in the external control loop, the DC bus voltage is compared with the reference DC voltage coming from the MPPT block using a PI regulator [36,37,38]. The aim of this setup is to maintain a constant DC voltage at the input of the inverter and guarantee the flow of power from the PV generator to the utility grid. At the output of the PI regulator, which handles the DC voltage control, the reference for the d component of the three-phase currents of the VSI (i*_d) is generated (see Figure 2). For the calculation of the proportional and integral constants ($K_P$ and $K_I$), the methodology presented in [39] is used.

4.1.2. Inverter Current Control Loop

Because the harmonic compensation method based on resonant filters is used, proportional-resonant (PR) regulators [40] are used in the internal control loop of the inverter. PR regulators are replacing the PI regulators in the internal current loops of photovoltaic inverters. If PI regulators are compared to PR regulators, the advantage of the PR tends to be infinite at the frequency for which they have been designed, in this case, 376.99 rad/s. If the inverse Park transform is applied to the component references I_d and I_q shown in Figure 2, the reference currents i*_α, i*_β are obtained. Then, by applying the Clarke transformation to the line currents, the iα, i_β components are obtained. These quantities are then compared with the reference components i*_α, i*_β [41]. The error obtained from this comparison is sent to two PR regulators in a stationary reference frame, and the outputs are the inverter voltage references, which are then inputted into a space vector modulation (SVM) [42] block. The SVM block determines the state of the inverter power poles (see the bottom part of Figure 2).

The two types of PR regulators shown in [9] are the ideal PR and the so-called non-ideal PR. The non-ideal PR has the advantage of being more stable than the ideal PR. The above result is achieved by adding a term called cut-off frequency ${\omega }_c$ to the ideal PR regulator.

Given these advantages, the non-ideal PR is used in this article. In Equation (6), the transfer function of the non-ideal PR is shown. The proportional gain $K_P$ is determined in a manner similar to that used with PI regulators, while the integral gain $K_I$ is set at a relatively high value but one that maintains stability limits [43]. The cut-off frequency ${\omega }_c$ is adjusted based on empirical observations [43]. The parameters used to determine the constant $K_P$, the selected $K_I$ constant ${\omega }_c,$ and the fundamental resonance angular frequency ${\omega }_0$ are shown in Table 4 and Table 5.

$$GPR(s)=K_P+\frac{2K_I{\omega }_{c}s}{s^2+2{\omega }_{c}s+{{\omega }_0}^2}$$

(6)

4.2. Harmonic Compensation Method

Harmonics produced by non-linear loads are common disturbances in the utility. They are defined by a pure non-sinusoidal demand current and, therefore, a distorted wave [3,4,5]. This harmonic pollution can influence the quality of currents in the utility grid [6]. Due to its simplicity of design and implementation, the harmonic compensation strategy used in this work relies on resonant filters and is discussed in [25,40]. In future work, other harmonic compensation methods will be evaluated.

If multiple generalized integrators (GI) are placed in the PR regulator shown in Equation (6) in a cascade, each GI can be turned to a specific frequency corresponding to the angular frequency of the harmonic targeted for compensation. The transfer function of the HC structure is shown in Equation (7), where $h$ corresponds to the order of the harmonic that will be compensated. $K_{Ih}$ and ${\omega }_{ch}$ can be set similarly, as in the non-ideal PR regulator [44], as follows:

$$Gh\left(s\right)={\sum }_{h=\mathrm{5,7},\mathrm{11,13,17}}\frac{2KIh{\omega }_{ch}s}{s^2+2{\omega }_{ch}s+(h\omega 0{)}^2}$$

(7)

The PR regulator (6) and the HC structure (7) can be seen in Figure 4 for the 5th, 7th, 11th, 13th, and 17th harmonics. Figure 4 shows how the angular frequency ω of the utility grid voltages is fed back to the PR regulator and the HC structure, allowing for frequency-adaptive control. This structure requires the use of a synchronization method capable of estimating the frequency and the phase angle of the voltages of the three-phase utility grid in the presence of disturbances. One challenge worth mentioning involves tuning this parallel configuration of PR regulators within the HC structure. For this purpose, a frequency-based design for the stability margins of the regulators will be described in the next section. This design uses the MATLAB/SIMULINK control toolbox functions.

The result of the discretization process of (7) using the Tustin method [45] is shown in Equation (8), as follows:

$$Gh(z)=\frac{Y\left(z\right)}{X\left(z\right)}=\frac{KihTs{\omega }_{ch}(1-z^{-2})}{1-2z^{-1}+z^{-2}+{\omega }_{ch}Ts(1-z^{-2})+{\left(\frac{h\omega Ts}{2}\right)}^2\left(1+2z^{-1}+z^{-2}\right)}$$

(8)

Operating the inverse Z transform and assuming zero initial conditions, the following expression will be obtained [45]:

$$y\left(n\right)=K1y\left(n-1\right)-K2y\left(n-2\right)+K3x\left(n\right)-K3x\left(n-2\right)$$

(9)

where

$$K1=\frac{2\left[1-{\left(\frac{h\omega Ts}{2}\right)}^2\right]}{1+Ts{\omega }_{ch}+{\left(\frac{h\omega Ts}{2}\right)}^2},K2=\frac{1-Ts{\omega }_{ch}+{\left(\frac{h\omega Ts}{2}\right)}^2}{1+Ts{\omega }_{ch}+{\left(\frac{h\omega Ts}{2}\right)}^2}\mathrm{and}K3=\frac{KihTs{\omega }_{ch}}{1+Ts{\omega }_{ch}+{\left(\frac{h\omega Ts}{2}\right)}^2}$$

Equation (9) shows that K1, K2, and K3 depend on the sampling period Ts, the cutoff frequency ${\omega }_{ch}$, and the integral gain $Kih$ of the specific angular frequency of the utility grid and its harmonics ($h\omega$) [45].

5. MATLAB/SIMULINK Simulations

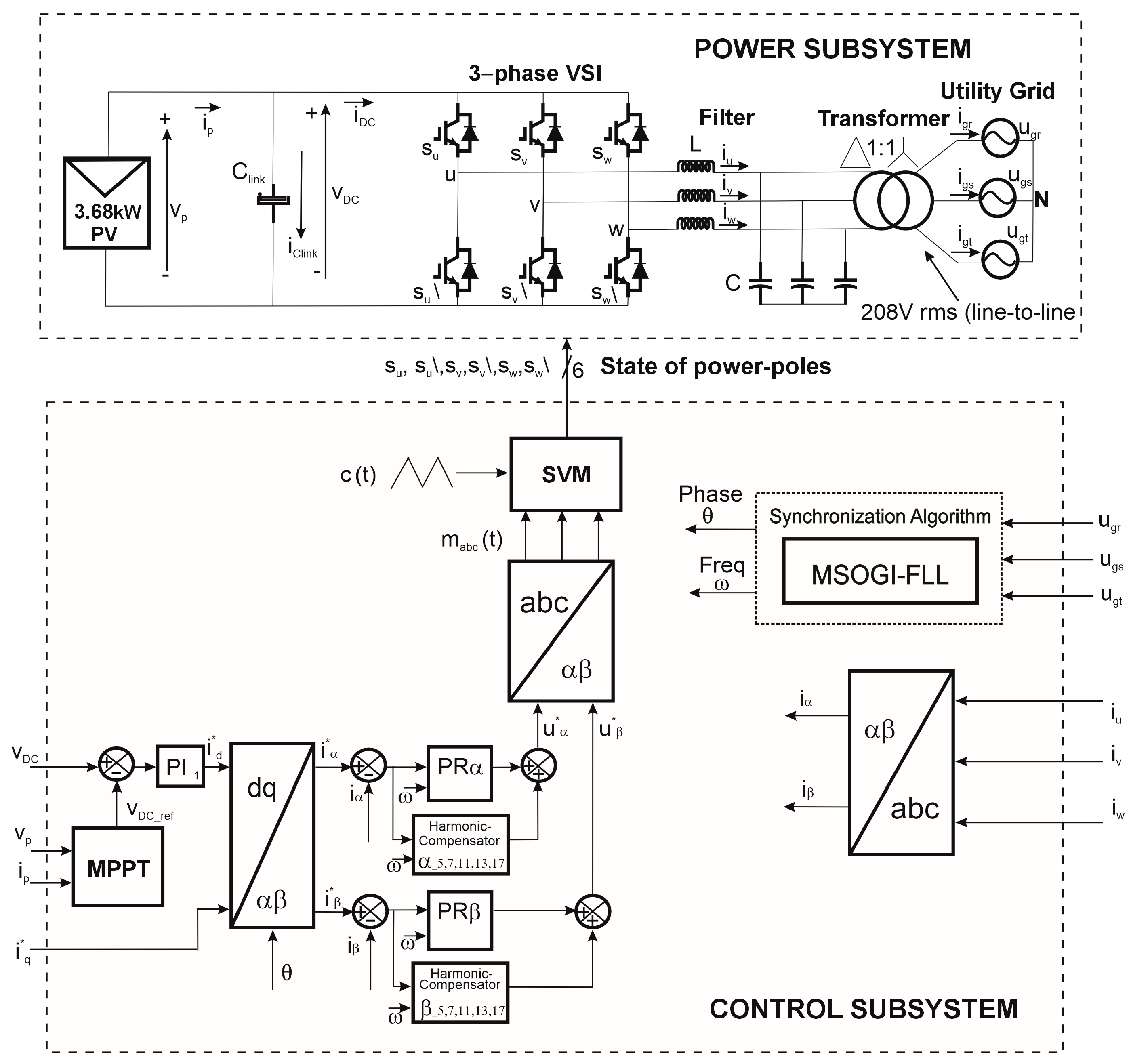
In this section, a MATLAB/SIMULINK model of a 3.68 kWp single-stage PV generator in a microgrid schema is presented. The power subsystem includes a PELab-6PH-SiC-8A-2LC25-4.7uF-16CH-INT Dual 3-phase Voltage Source Inverter 8 A Leg, 800 V DC-Link Max from Taraz Technologies. This system uses semiconductors [46] and is configured to operate at a PWM switching frequency of 35 kHz. It includes six 2.5 mH inductors and two EMC filters, each with a capacity of 4.7 uF. The parameters for this inverter are detailed in this work, as can be seen in Table 4, which outlines the parameters of the power subsystem.

To guarantee accurate detection of the phase angle of the grid voltages, as well as precise estimation of the grid frequency to be relayed to the control subsystem, an MSOGI-FLL is used as a synchronization algorithm [29]. In various works, this algorithm has been implemented due to its effectiveness in handling disturbances in the three-phase utility grid [25,45,47]. In Table 5, the parameters of the control subsystem are summarized.

Table 4. Parameters of the power subsystem.

Parameters	Value
Link capacitor (Clink)	15,000 μF
Switching frequency (fsw)	35 kHz
Line inductance (L)	2.5 mH
AC system (ugrst)	120 V(rms) phase-to-neutral Frequency: 60 Hz and 65 Hz
Transformer resistance (RT)	0.0231 Ω
Transformer inductance (LT)	2400 µH

Table 4. Parameters of the power subsystem.

Parameters	Value
Link capacitor (Clink)	15,000 μF
Switching frequency (fsw)	35 kHz
Line inductance (L)	2.5 mH
AC system (ugrst)	120 V(rms) phase-to-neutral Frequency: 60 Hz and 65 Hz
Transformer resistance (RT)	0.0231 Ω
Transformer inductance (LT)	2400 µH

Table 5. Parameters of the control subsystem.

Parameters	Value
Proportional constant of the PR regulator (KPαβ)	0.15
Integral constant of the PR regulator (KIαβ)	10
Resonant angular frequency of the PR regulator (ωo′)	377/408.408 rad/s
Cut-off frequency of the PR regulator (ωc)	1 rad/s
Proportional constant of the DC voltage regulator (KPVDC)	0.2813
Integral constant of the DC voltage regulator (KIVDC)	8.81
Phase margin of the inner current loop (PMI)	83°
Phase margin of the outer voltage loop (PMV)	63.5°
Sample time of the power subsystem (TS)	1.0417 μs
Sample time of the control subsystem (Treg)	33.3 μs
Time constant ($\tau$)	$L/R$
Full-scale range of the ADC (FSR)	1
Gain of the current transducer GTI	1
Inverter gain (KINV)	$\frac{2}{3}{\mathrm{v}}_{\mathrm{D}\mathrm{C}}$

Table 5. Parameters of the control subsystem.

Parameters	Value
Proportional constant of the PR regulator (KPαβ)	0.15
Integral constant of the PR regulator (KIαβ)	10
Resonant angular frequency of the PR regulator (ωo′)	377/408.408 rad/s
Cut-off frequency of the PR regulator (ωc)	1 rad/s
Proportional constant of the DC voltage regulator (KPVDC)	0.2813
Integral constant of the DC voltage regulator (KIVDC)	8.81
Phase margin of the inner current loop (PMI)	83°
Phase margin of the outer voltage loop (PMV)	63.5°
Sample time of the power subsystem (TS)	1.0417 μs
Sample time of the control subsystem (Treg)	33.3 μs
Time constant ($\tau$)	$L/R$
Full-scale range of the ADC (FSR)	1
Gain of the current transducer GTI	1
Inverter gain (KINV)	$\frac{2}{3}{\mathrm{v}}_{\mathrm{D}\mathrm{C}}$

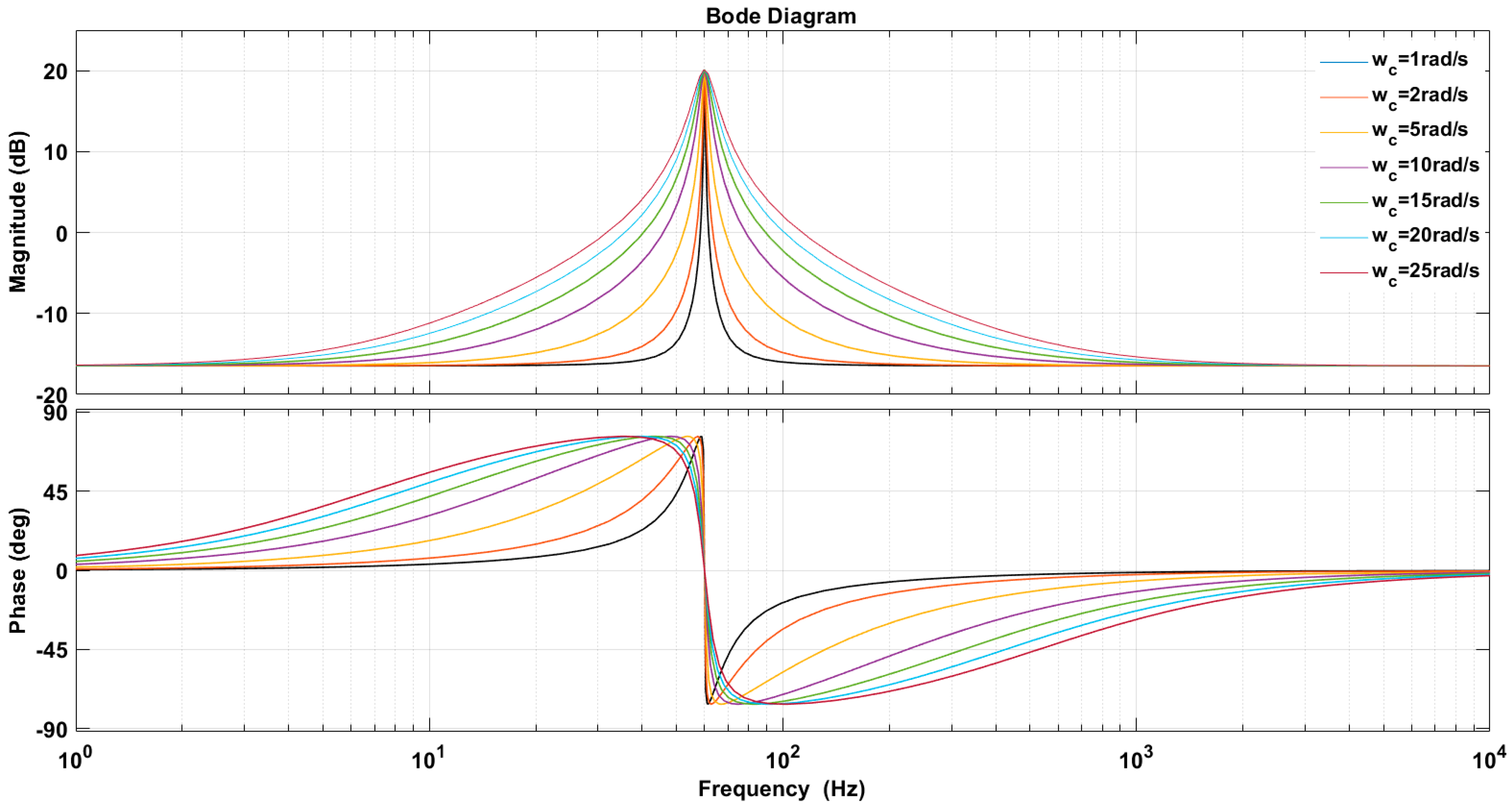
The dynamics of the current control loop can be evaluated using a Bode plot. Using the parameters given in Table 4 and Table 5, the open-loop Bode diagram shown in Figure 5 was created for the fundamental grid frequency and for the 5th, 7th, 11th, 13th, and 17th harmonics. There is a phase margin of 83 degrees for a frequency of 60 Hz and for a frequency increase of 5 Hz (65 Hz). The above finding suggests that the internal current control will remain stable during variations in the grid frequency. This characteristic is useful in a microgrid affected by harmonic pollution and simultaneous frequency variations.

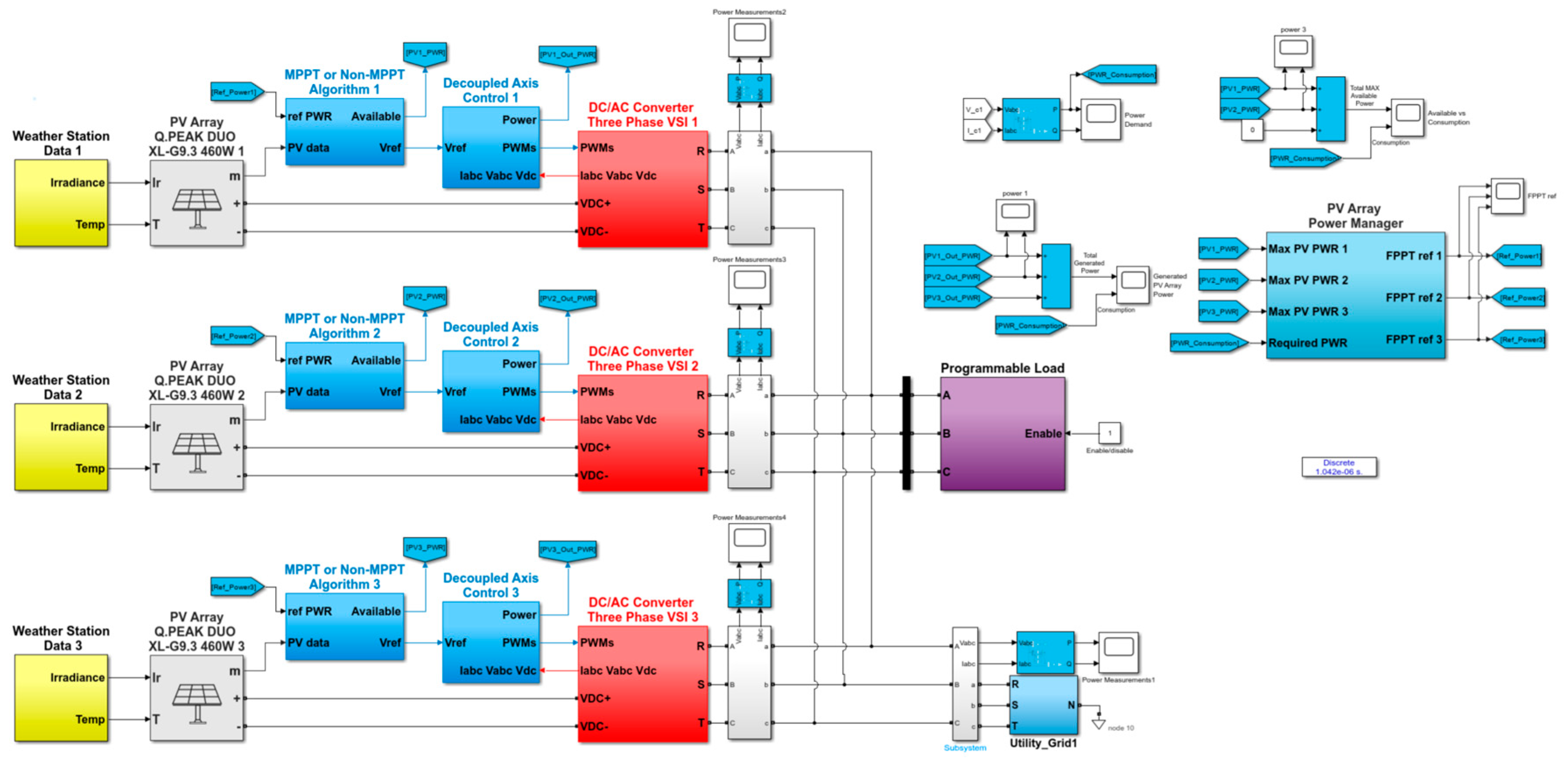
To investigate the harmonic compensation method selected for this work, a SIMULINK model of a microgrid has been developed, taking as reference some of the elements shown in Figure 1. The SIMULINK model shown in Figure 6 includes a comprehensive 11 kWp grid-connected photovoltaic (PV) system comprising three PV generators, each rated at 3.68 kW, and real weather station data. Additionally, the system includes a resistive programmable load, one power-management subsystem, and a variety of different measurement scopes throughout the system. The color of each block represents the group to which it belongs: yellow represents weather data, red represents power systems, blue represents control subsystems, purple represents grid loads, and white represents measurement points. In the section below, a detailed explanation of each block is provided.

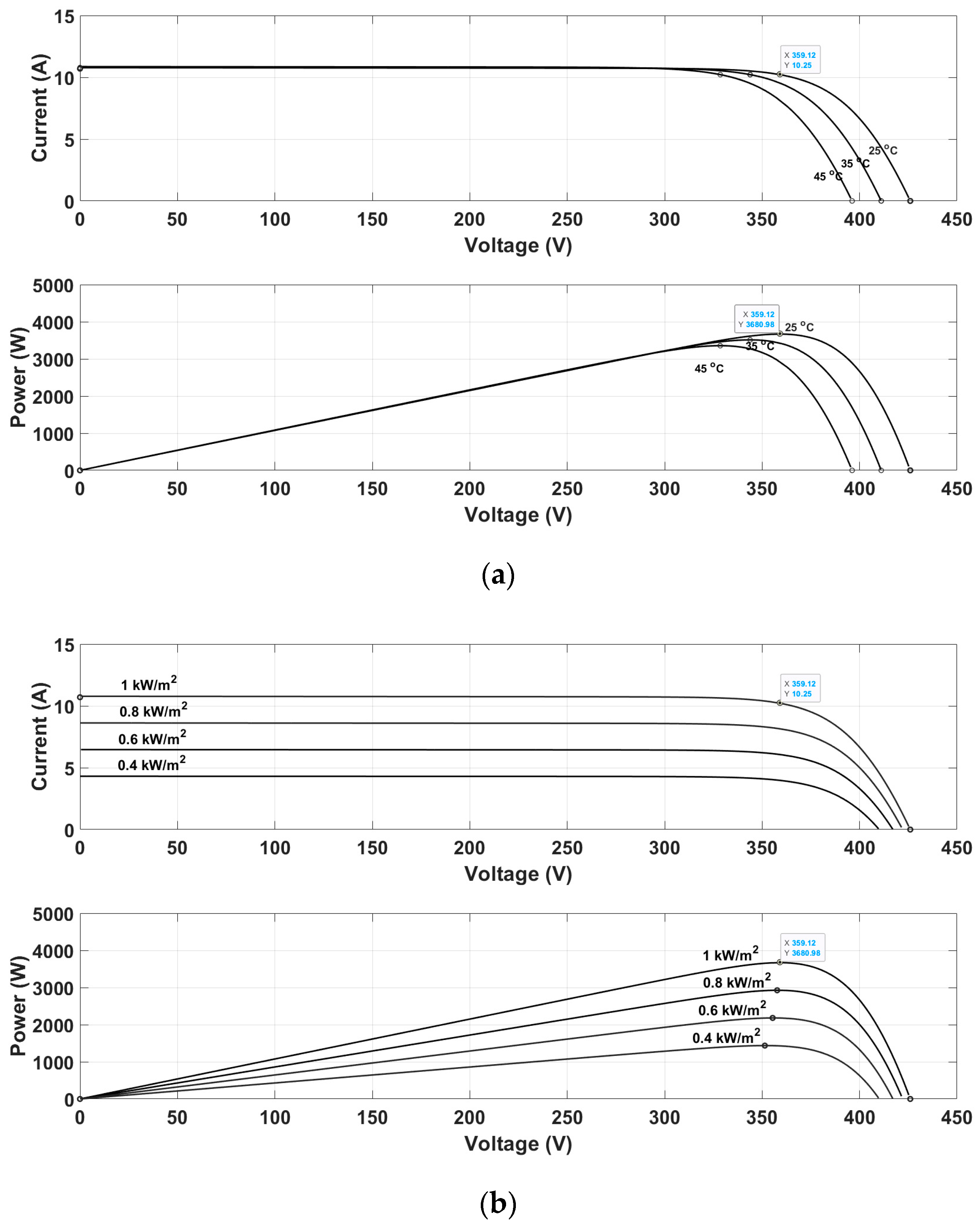
The weather station data block includes an extensive 6-month real-world database that stores irradiance and temperature measurements taken from a Vantage Pro 2 integrated sensor suite, then outputs the information for a preselected day found in that time frame. Afterward, weather data is directly supplied to a PV array SIMULINK block featuring an array of eight series-connected 460 W Q.PEAK DUO XL-G9.3 solar panels.

The MPPT or non-MPPT algorithm controls the quantity of power produced by the PV array by providing a reference voltage point to the decoupled axis control block for the inverter to follow. It works in two operational modes based on the implemented algorithm: either it extracts the maximum available power thought a MPPT algorithm or it limits power by a constant or flexible power factor (FP) provided from the reference power port. Systems employing what are typically known as flexible power point tracker (FPPT) algorithms allow for more complete synergy with the electrical grid. They actively control the total generated power to match that expressly required by the power at a given moment. Aside from the reference voltage out port, this block also features an output port for a maximum power tracker (MPT) algorithm that calculates the maximum available power of the PV generator.

Decoupled axis control, as the names implies, contains a decoupled axis control strategy for the inverter. In this strategy, real and reactive power are extracted from the time-domain components of the three-phase electrical grid system and operated independently of one another to obtain the target specified by the MPPT or FPPT algorithm.

The DC/AC converter (VSI) encompasses all the power elements of a single-stage PV generator. It includes a PELab-6PH three-phase voltage source inverter, one DC-link 1500 uF capacitor, an LC filter, and a 208Δ/208Y three-phase transformer.

The PV array power management subsystem focuses on appropriate independent power distribution among all the PV generators. Based on the absolute error formula, this block proportionally divides the required grid power among all three generators, such that, regardless of the maximum available power of each PV plant, the load is always fairly distributed across all generators.

The programmable load consists of five constant time-triggered three-phase resistive loads in a Y connection, which can be instructed to connect or disconnect from the power grid at any given moment.

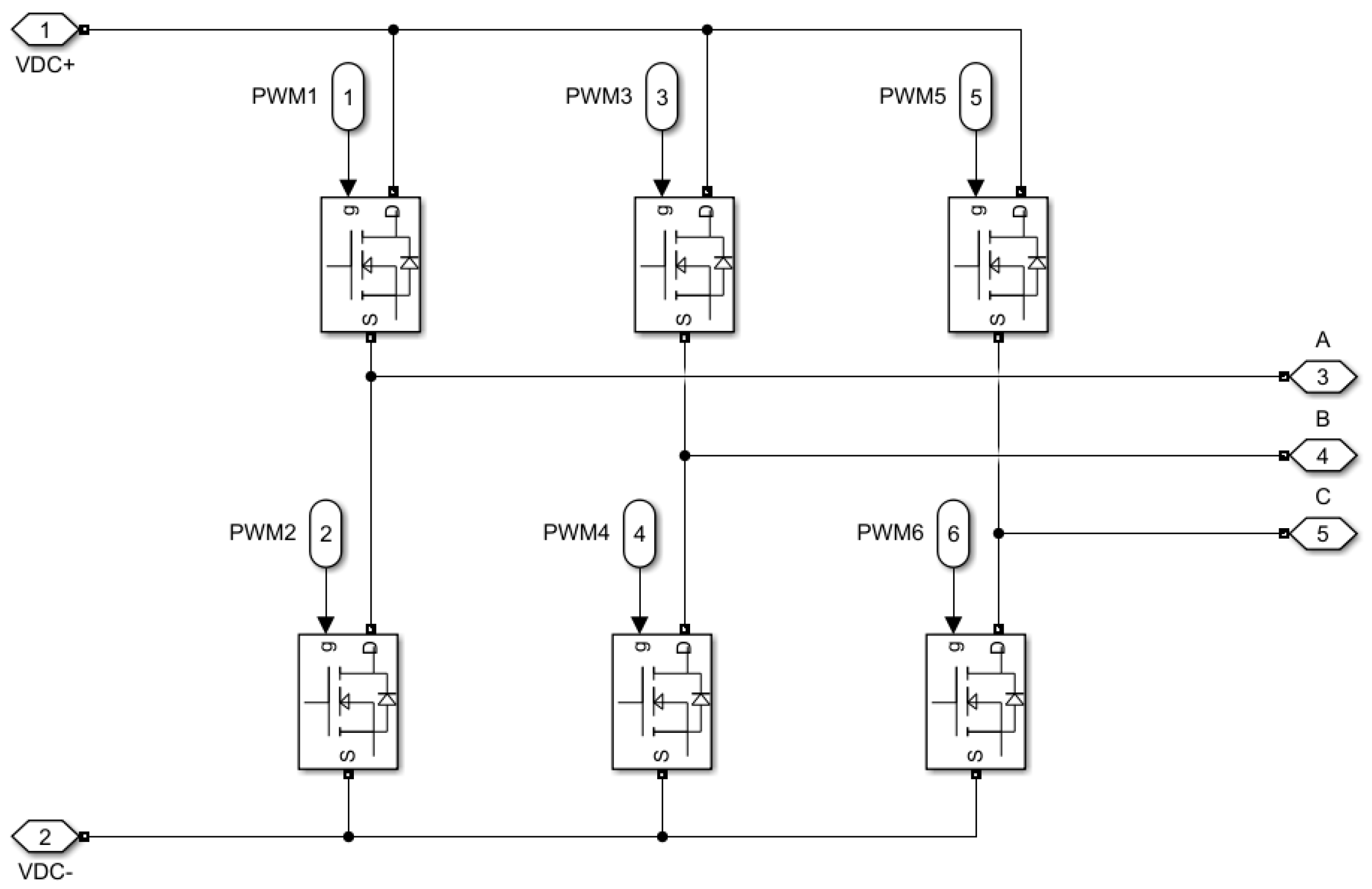
Figure 7 shows a three-phase inverter model corresponding to one of the photovoltaic generators of the microgrid depicted in Figure 6. This model was developed using parameters corresponding to the technical specifications of a PELab-6PH-SiC-8A-2LC25-4.7uF-16CH-INT Dual 3-phase VSI 8 A Leg, 800 V DC-Link Max from Taraz Technologies [46]. The PWM switching frequency is set at 35 kHz (FPWM = 35 kHz).

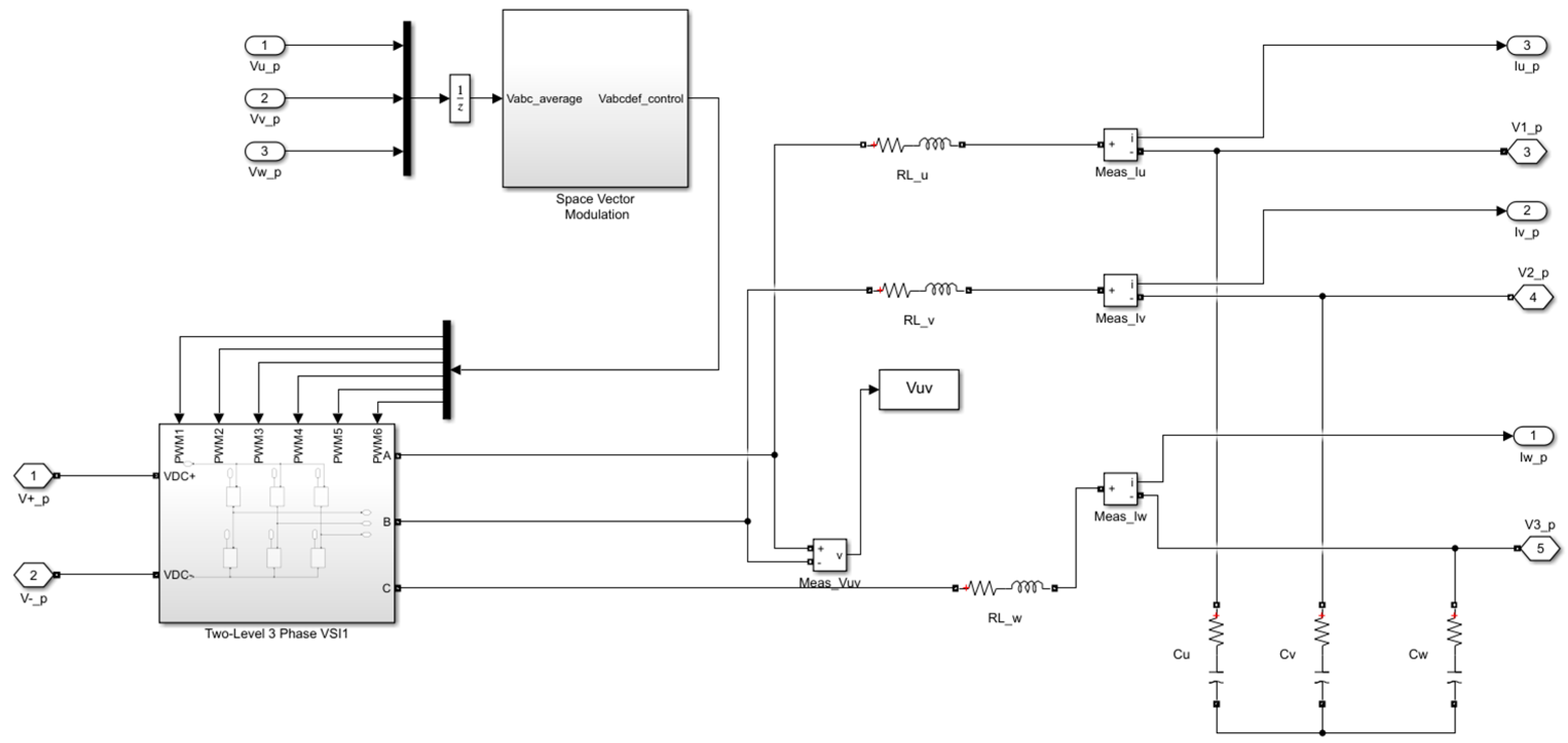
A MATLAB/SIMULINK model of the LC inverter-filter assembly with inductance and capacitance values of 2.5 mH and 4.7 uF, respectively, is shown in Figure 8.

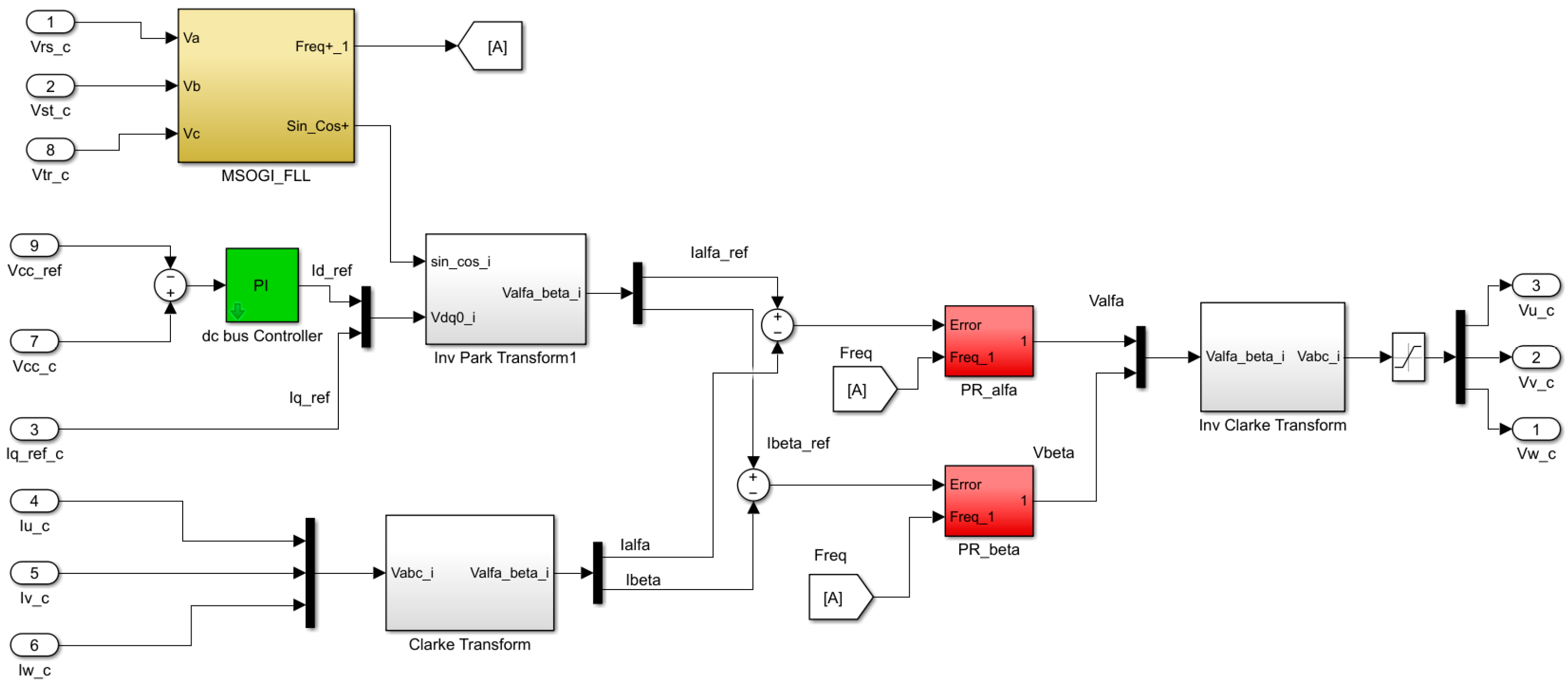
Figure 9 shows the implementation in MATLAB/SIMULINK of the control used in the PV inverter. At the top, in yellow, is the block with the MSOGI-FLL algorithm. The PI regulator of the external voltage loop is shown in green. In red, the PR regulators for the internal loop are shown.

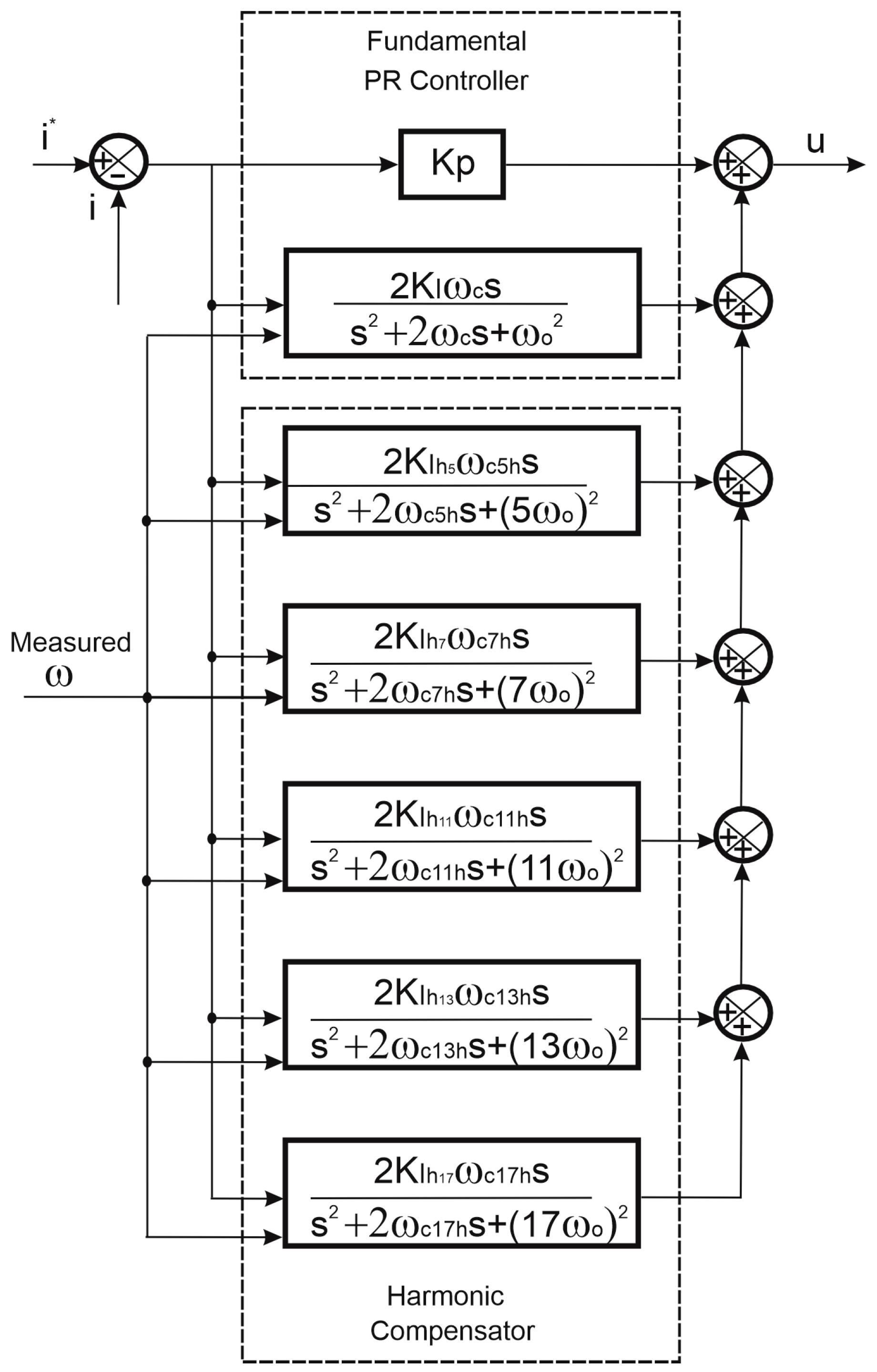
Figure 10 shows the implementation in MATLAB/SIMULINK of the HC structure corresponding to Equation (7). Note at the top, in red, the proportional constant $K_P$ of the PR regulator. Placed in cascade are the resonant filters corresponding to the fundamental frequency and each of the harmonics to be compensated for. The fundamental frequency is sent to each of the resonant filters with the purpose of achieving control capable of adapting to variations in the grid frequency.

Simulation Results

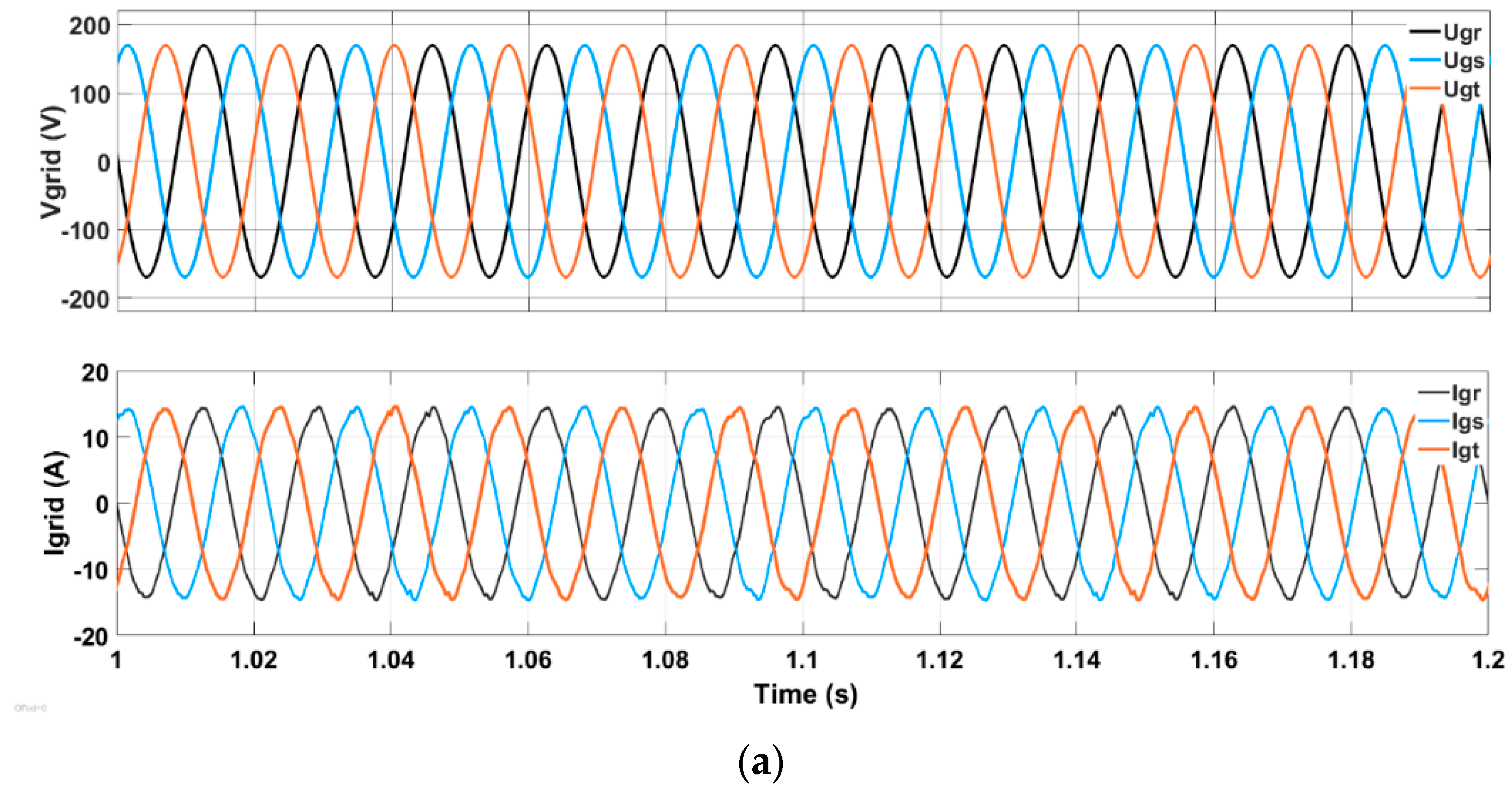
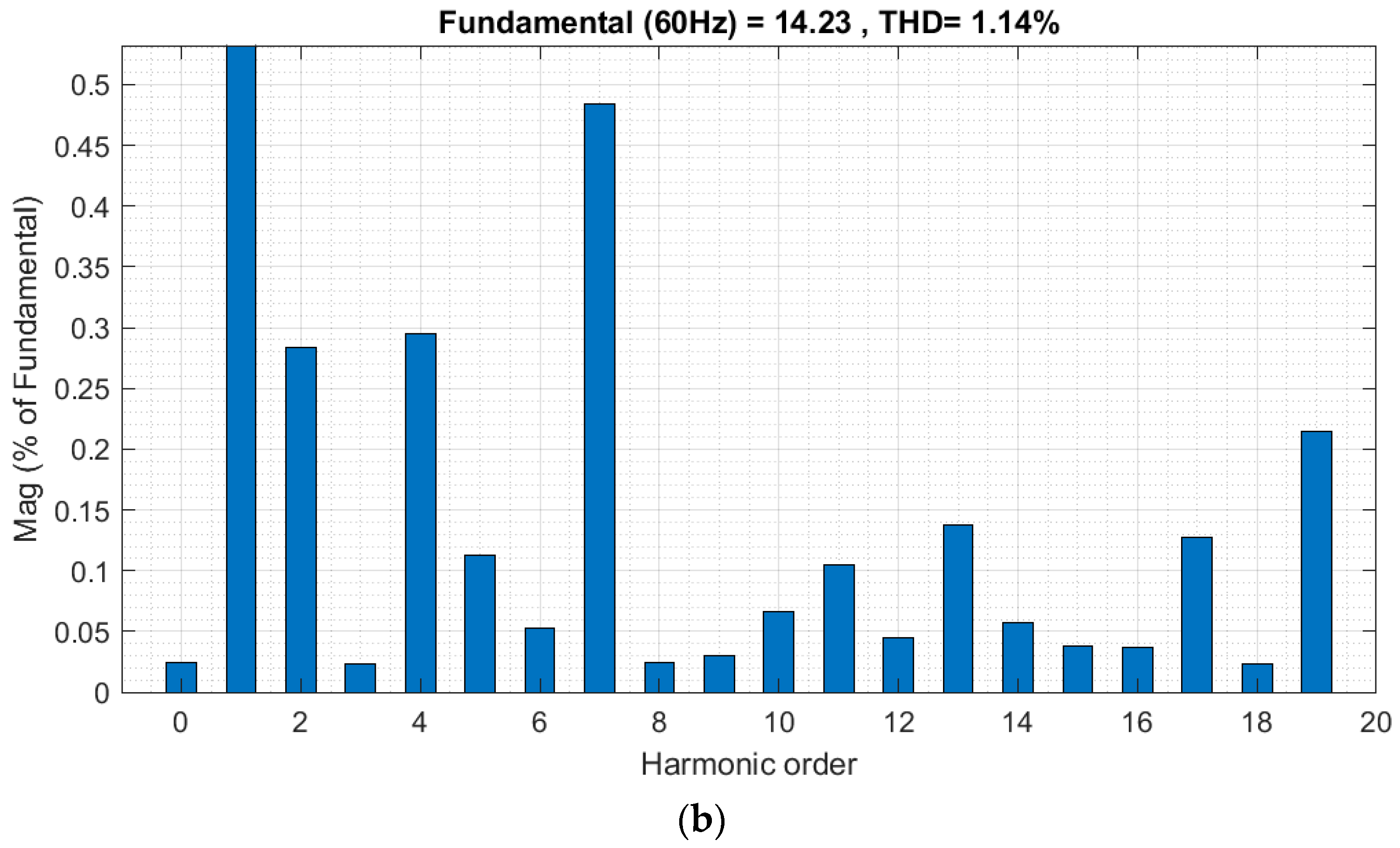
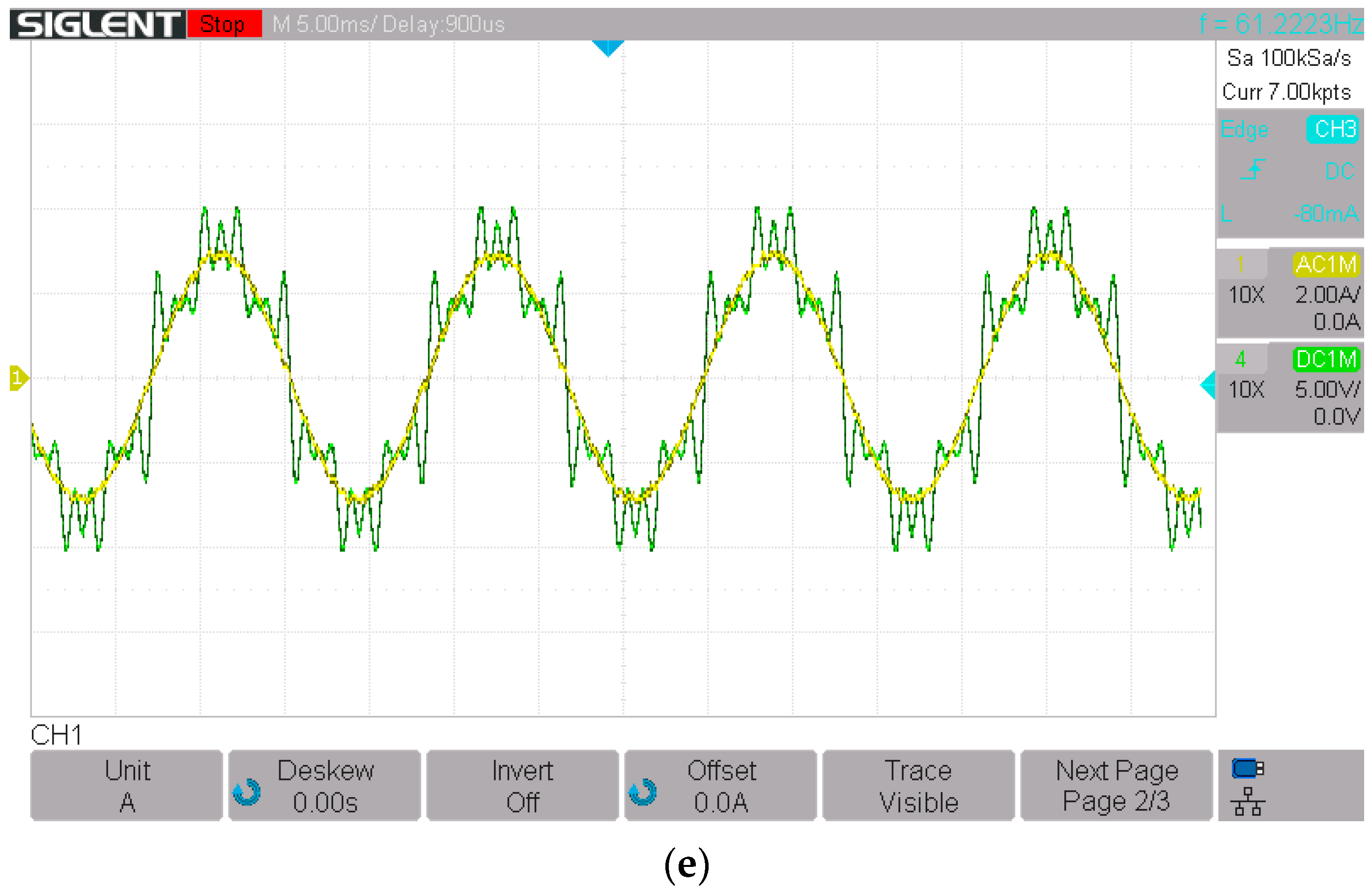
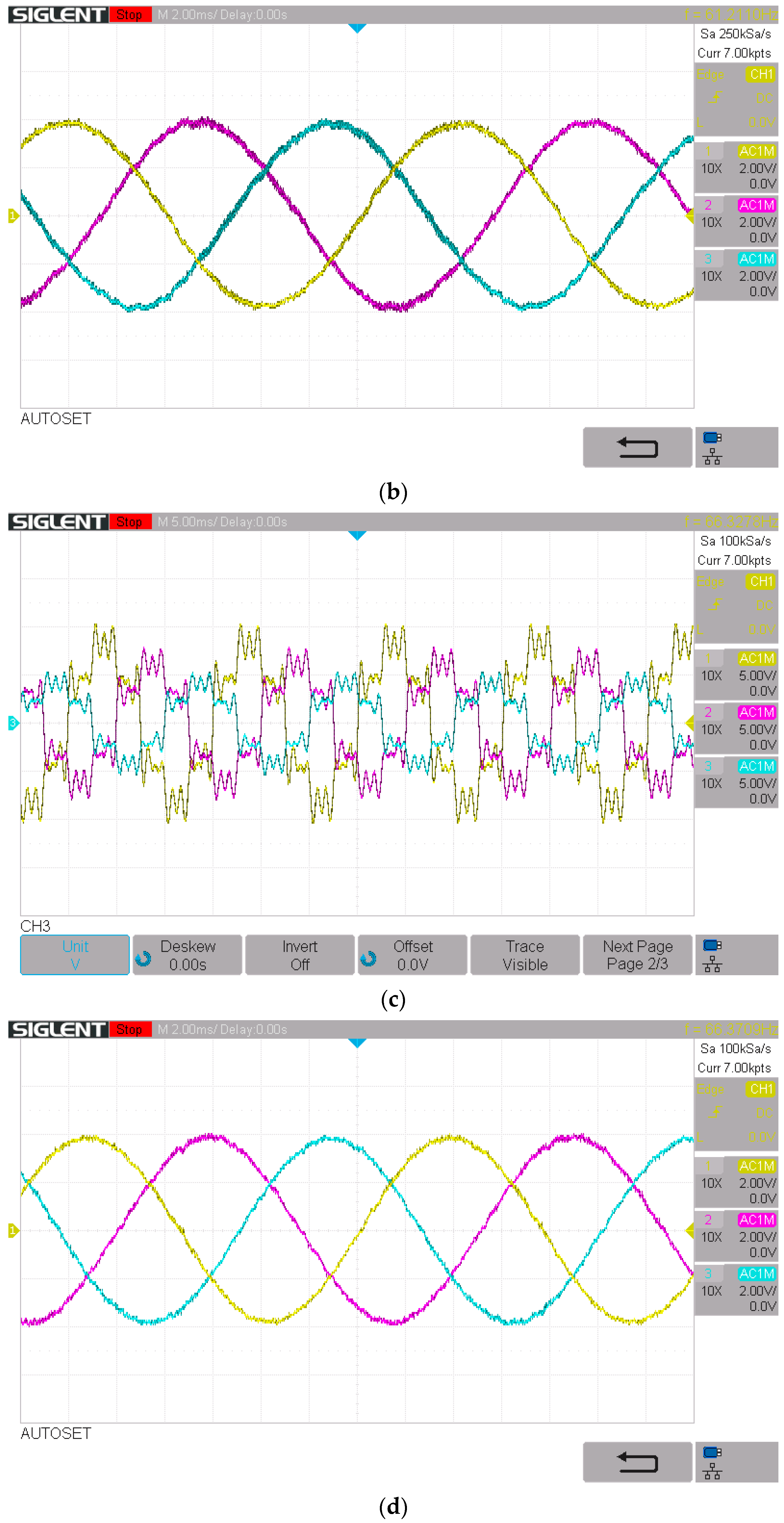
The upper part of Figure 11a shows the evolution over time of the voltages of the utility grid. No harmonics have been introduced into the grid voltages to evaluate the grid currents of the PV generator, which has a power of 3.68 kW. The bottom part of Figure 11a shows the evolution over time of the grid currents from the simulation when no voltage harmonics are introduced. The grid currents exhibit a low amount of harmonics distortion, leading to a total harmonic distortion (THD) of 1.14% at phase 1 (see Figure 11b). The Fast Fourier Transform (FFT) analysis tool from MATLAB/SIMULINK [22] was used to determine the THD of the acurrent (THD_I).

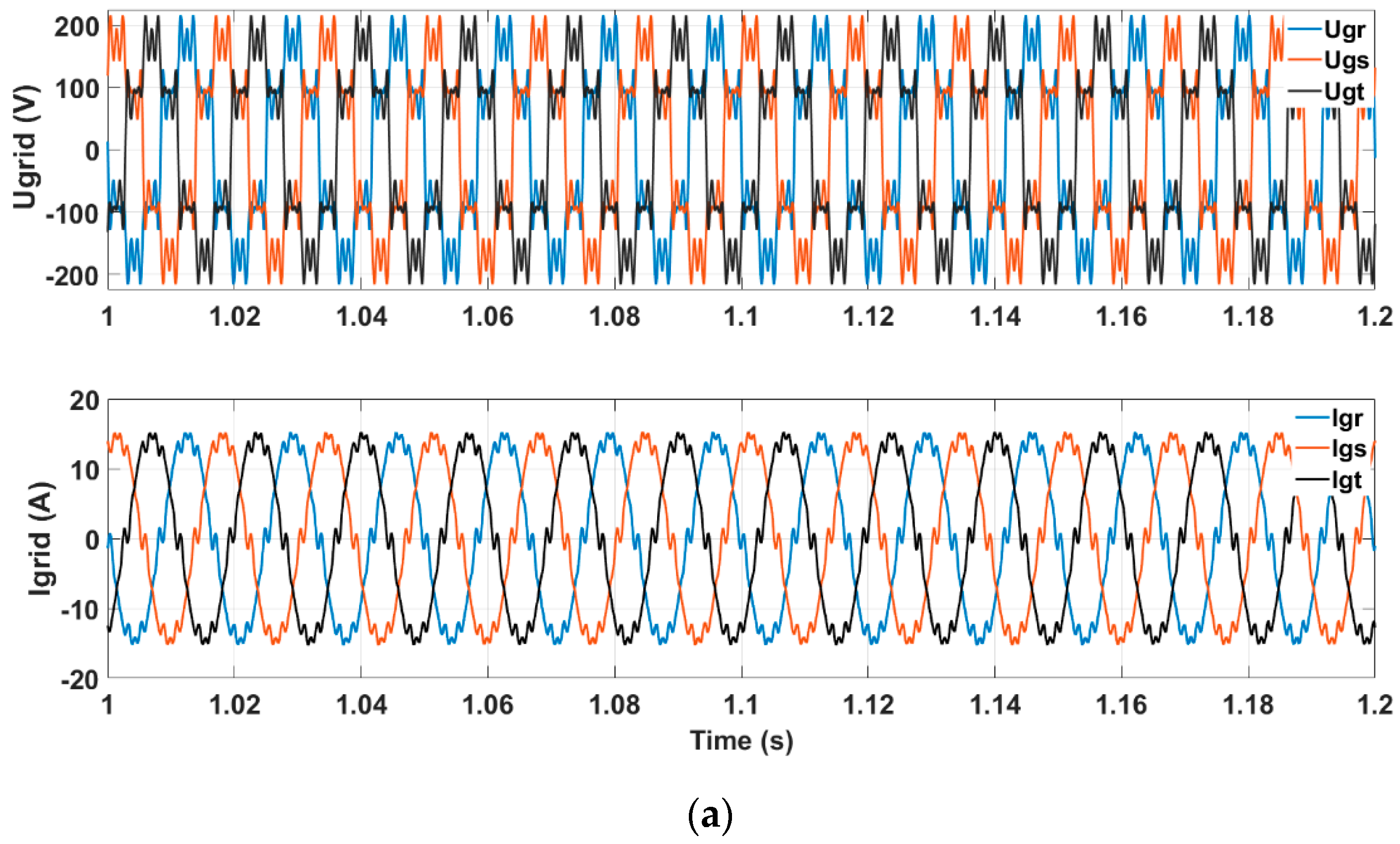
In the simulation shown below, a 15% harmonic contamination of the 5th, 7th, 11th, 13th, and 17th harmonics in the grid voltages is applied to the grid voltages (see upper part of Figure 12a), resulting in a TDH of voltage (THD_V) of 33.54%, as can be observed in Figure 12b. Note that the bottom part of Figure 12a shows the distortion in the grid currents caused by the effect of voltage harmonics, leading to a current THD of 7.27% at phase 1, as can be seen in Figure 12c. In this scenario, no harmonic compensation strategy is used in the control of the inverter, leading to non-compliance with the harmonic distortion limits established by the IEEE Std. 519-2022 standard [1].

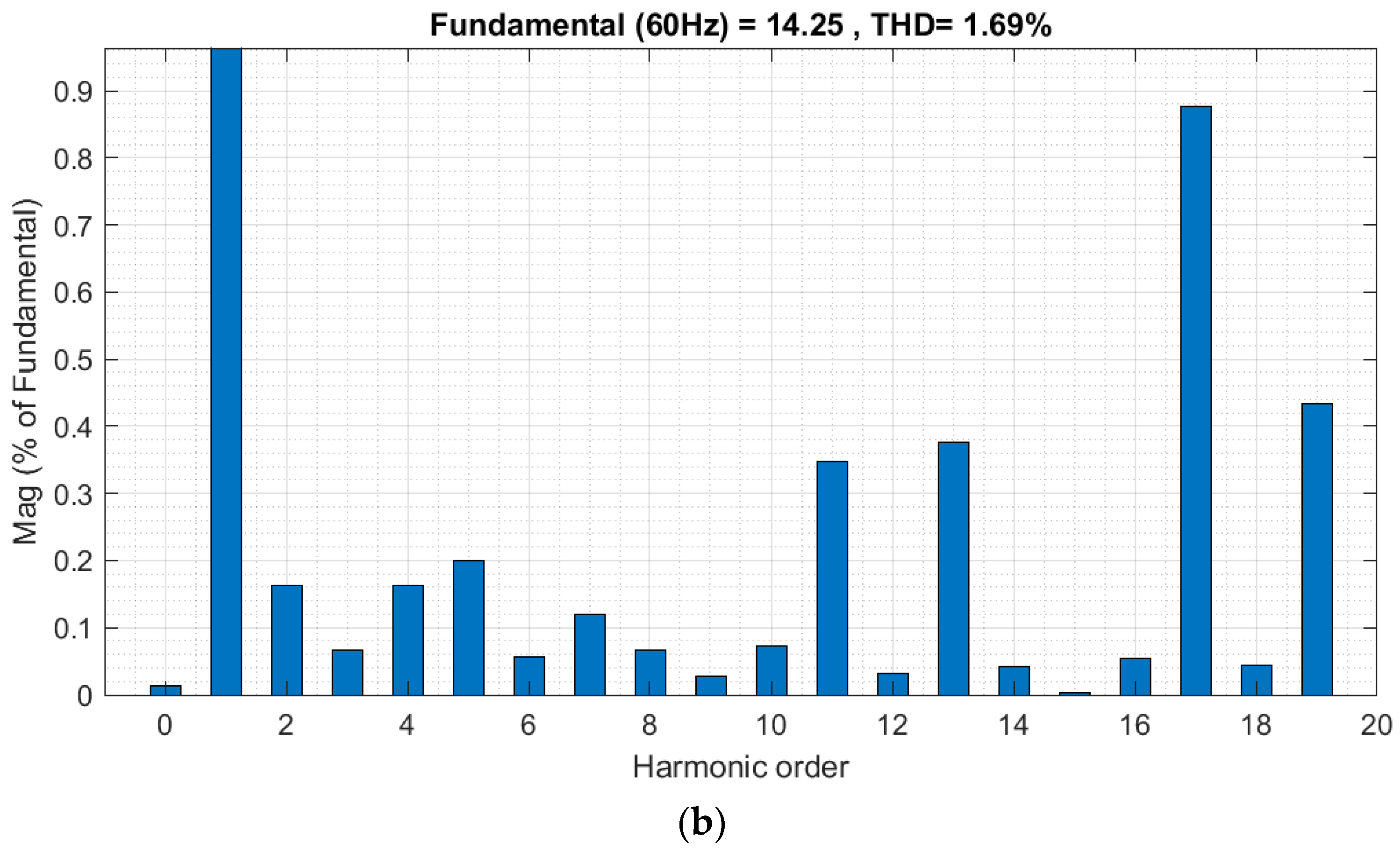
In the upper part of Figure 13a, the grid voltages are illustrated with a THD_V of 33.55%. In the bottom part of Figure 13a, the grid currents are shown with a low amount of harmonic distortion, obtaining a THD_I of 1.69% (see Figure 13b). The above results indicate the importance of using harmonic compensation strategies to improve the quality of electrical energy in microgrids.

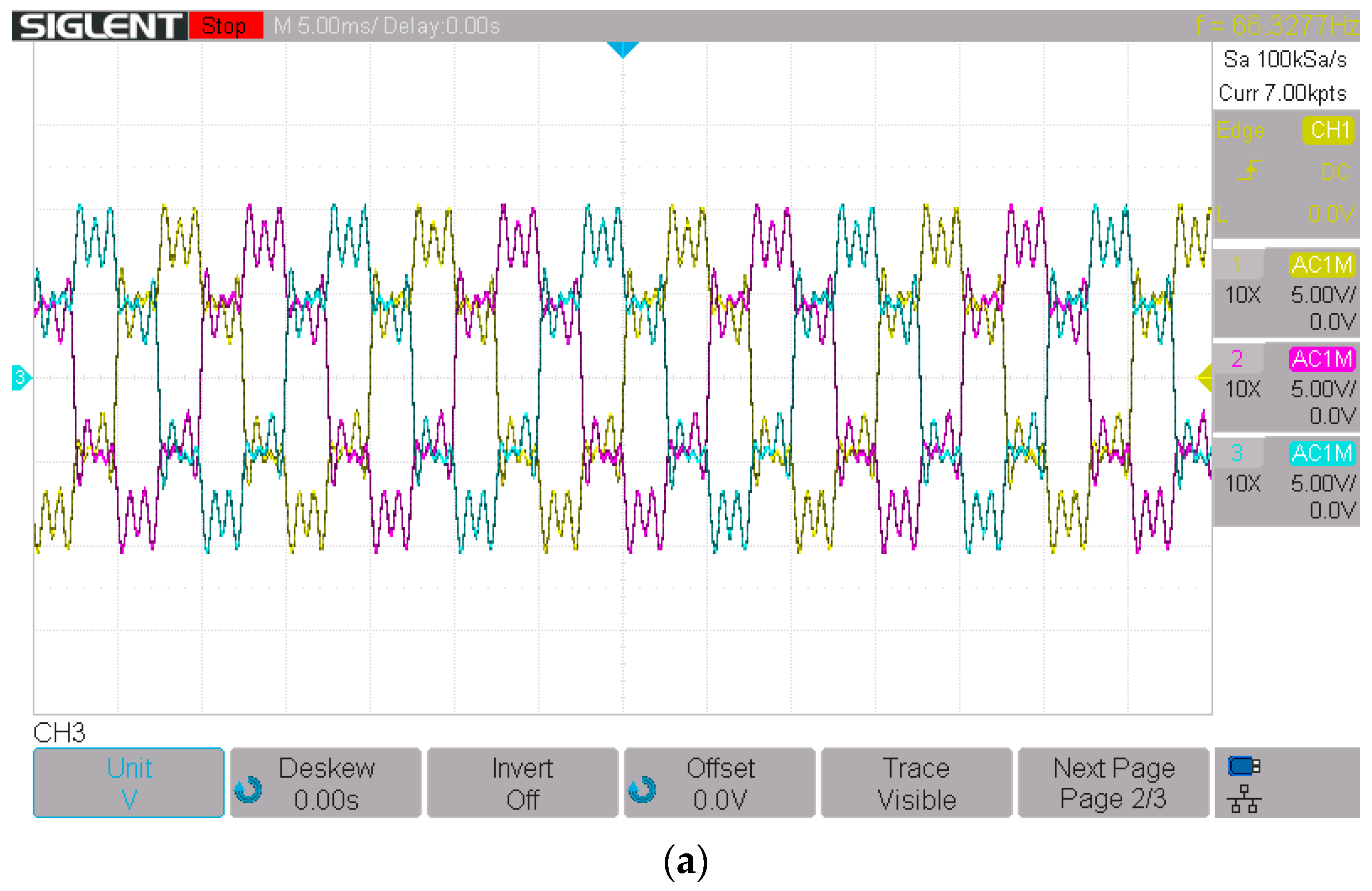
In the simulations shown below, a THD_V of 33.54% is applied. In addition, a frequency step from 60 Hz to 65 Hz is applied to evaluate the harmonic behavior of the PV generator under conditions of both harmonic distortion and variations in the grid frequency.

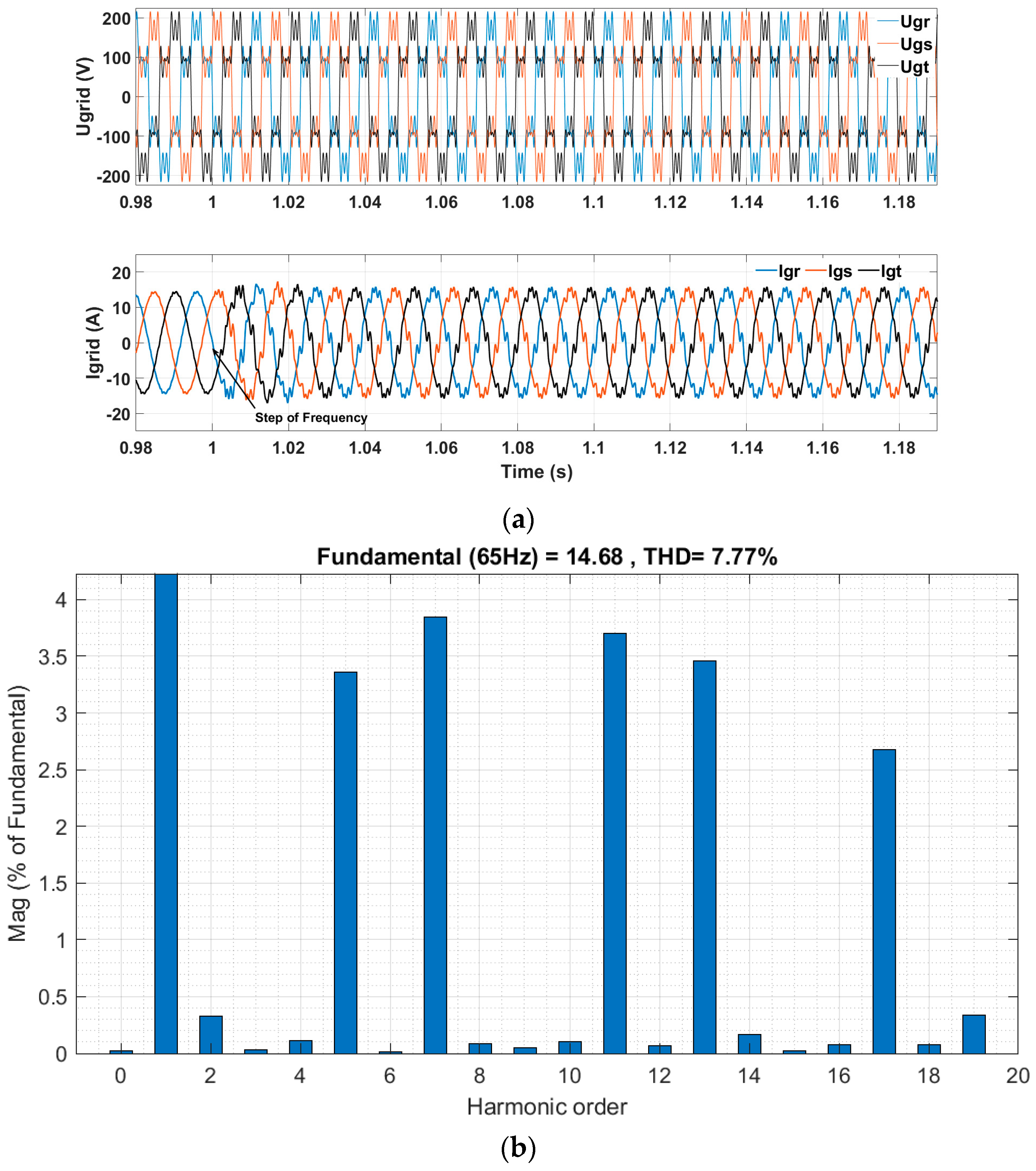
Figure 14 shows the distorted grid voltages during a frequency step from 60 Hz to 65 Hz. As shown in the bottom part of Figure 14a, before the frequency step, the grid currents had a low amount of harmonic distortion due to the use of a harmonic compensation strategy. However, following the frequency shift, the grid currents become distorted, reaching a THD_I of 7.77%, as can be observed in Figure 14b. 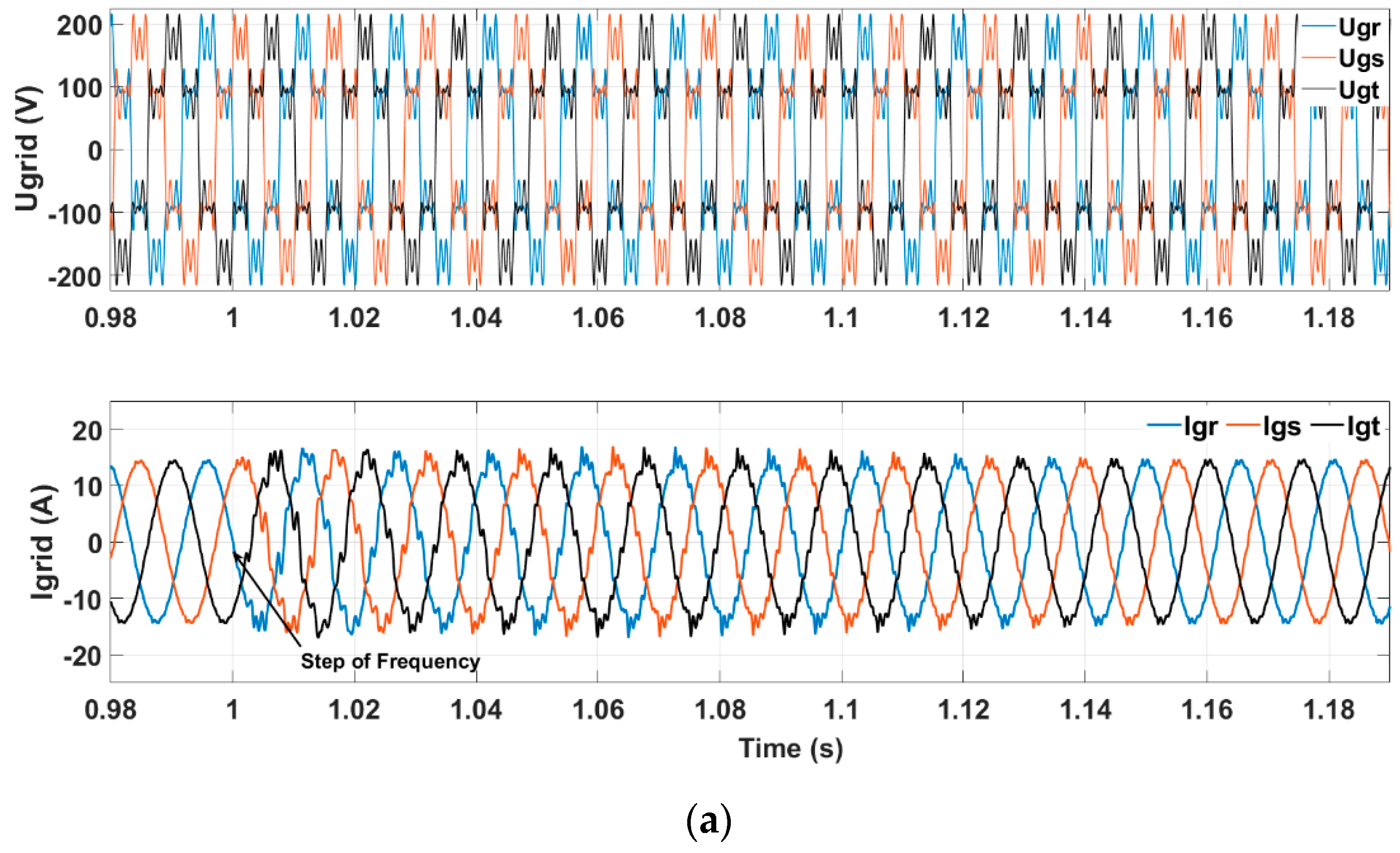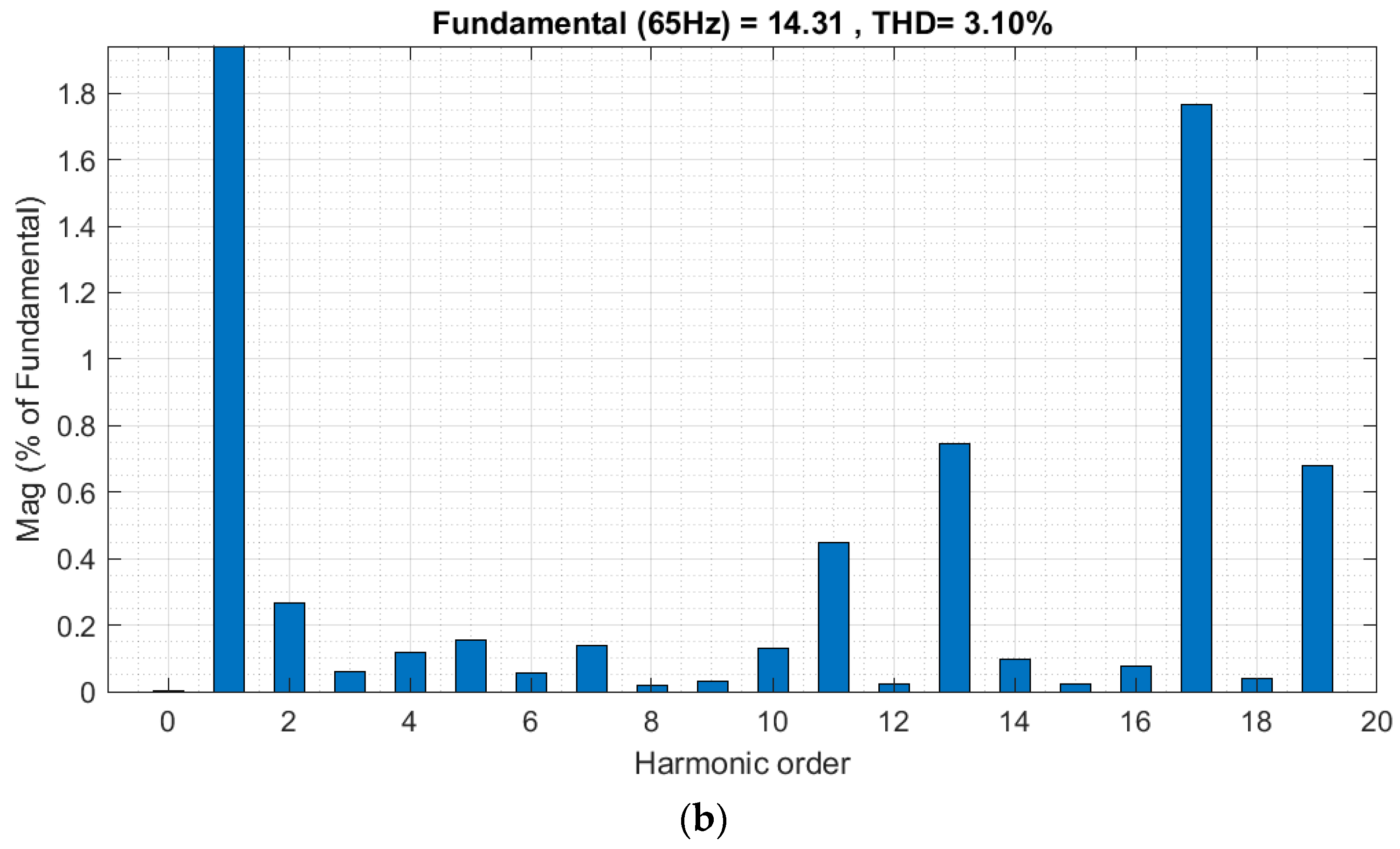In Figure 15, the grid conditions of Figure 14 have been replicated; however, harmonic compensation technique with frequency adaptation of Equation (9) has been used, resulting in a THD_I of 3.10% at phase 1. The above observations suggest that in microgrids with frequency variations, employing a frequency-adaptive HC strategy is advisable.

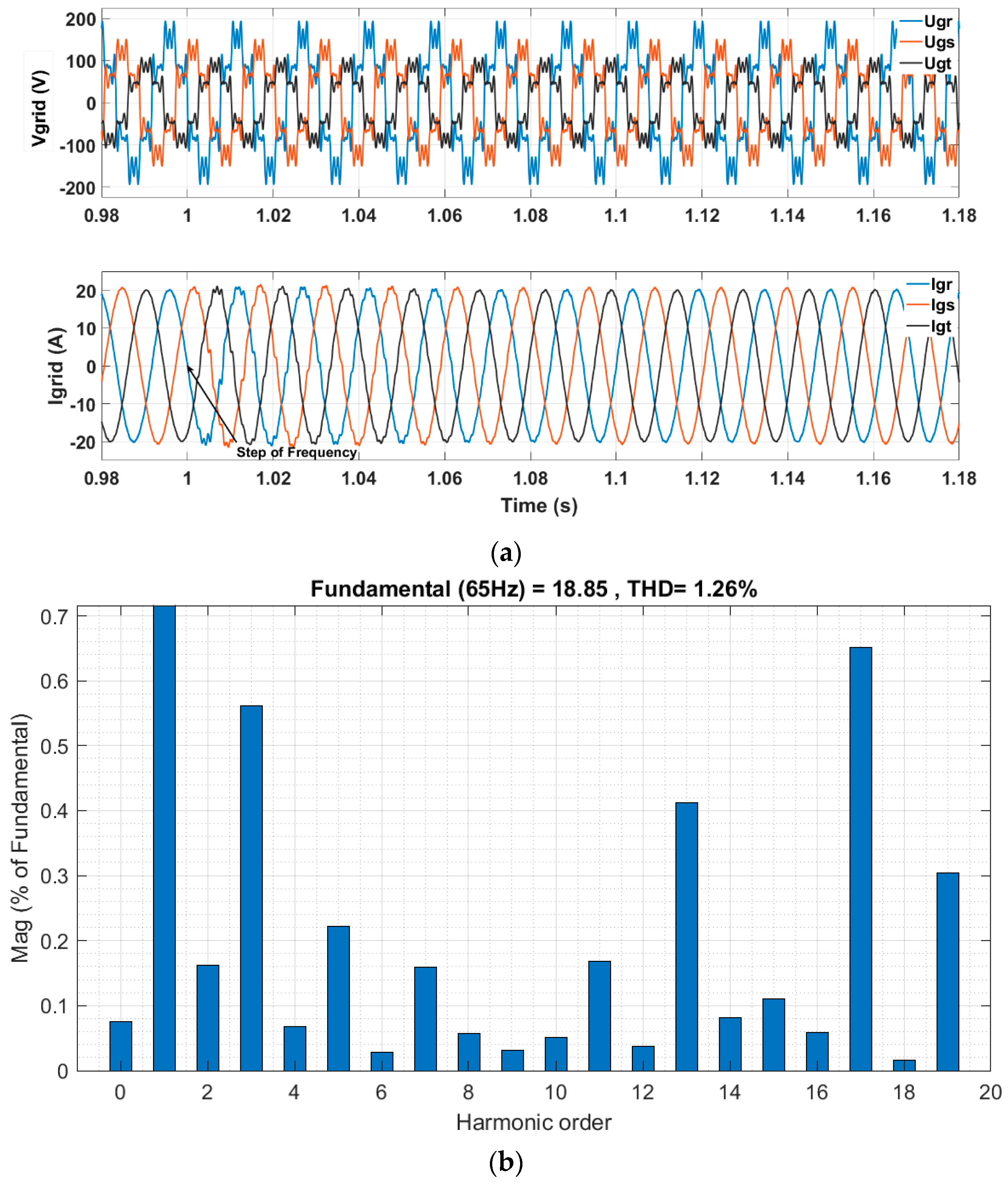
In the fourth and final scenario, the ability of the PV generator to compensate for harmonics under various grid disturbances is tested by adding harmonic distortion (THD_V = 33.54%), frequency variation (step from 60 Hz to 65 Hz), and voltage unbalance ($U_{gr}$, $U_{gs}$, $U_{gt}$ = 169.8 V, 127.14 V, and 84.9 V, respectively). Figure 16 shows the three-phase utility grid affected by the three types of disturbances: voltage unbalance, frequency variation, and harmonic pollution (see top of Figure 16a). Despite the presence of the grid disturbances, the use of an adaptive-frequency HC strategy resulted in a THD_I of 1.26% at phase 1 (see Figure 16b). Due to the voltage unbalance, an increase in the grid currents can be noted.

6. Real-Time Tests

With the aim of carrying out tests that closely mimic real photovoltaic systems, several real-time simulations were carried out using an OP5707XG real-time simulator from OPAL-RT [23].

Real-Time Digital Simulation Setup

Figure 17 shows a photo of the setup for carrying out the tests in real time. An OP5707XG real-time simulator is shown in the center, a server is used as a host PC, and finally, an oscilloscope is used to capture voltage and current waveforms.

To perform real-time digital simulations, certain changes in the MATLAB/SIMULINK model configuration are needed. As seen in Figure 18, adjustments include changes from solver to tasking and sample time options, as well as the establishment of a fixed-step size of 1/(4f_sw) in the model settings option for proper system deployment [48]. These changes ensure the model runs synchronously with actual time, thus providing accurate per-clock results when complied by RT-Lab. RT-Lab serves as a bridge application between the MATLAB/SIMULNK model and the real-time platform from Opal-RT Technologies. RT-Lab is also used to configure various execution parameters of the target platform, as detailed in [49,50].

In addition to a custom model settings configuration, a custom model layout is needed. For this layout, the previously designed model must be moved inside a subsystem called a master subsystem. The name of this subsystem always begins with ‘SM’, as seen in Figure 19 [51,52]. For the case study, the master subsystem was named SM_CONTROL_PLANT, and it contains both the plant and the controller for the real-time simulation. Also, a specialized communication block is used to connect the digital signals from the model that will run in real time. These signals, termed ‘Group1A_CHx_AOUT’, facilitate the interaction between the CPU and the FPGA, using the latter’s analog outputs for measurements. Because the maximum range of the output ports of the FPGA is limited to ±10, all measured variables require special scaling before they can be transmitted to the output ports, as per Equation (10) [49].

$$Aout=digitalvalue\frac{Chanelrangepk-pk}{digitalmeasurementrangepk-pk·Overshooting\%}+offset$$

(10)

The voltage and current measurements are obtained after scaling in Equations (11) and (12), respectively.

$$Aout=digitalvalue\frac{20\mathrm{V}}{{Vrms}_{pk-pk}linevoltage·102\%}$$

(11)

$$Aout=digitalvalue\frac{20\mathrm{V}}{Maximumpowercurrent·487.7\%}$$

(12)

Figure 19 depicts a diagram of the test system and the interconnections between each component. As seen, the OP5707XG features a Virtex 7 FAPG (VC707) with the capacity for up to eight modules, seven of which are enabled, and one analog output module (Aout) to which a Siglent SDS1204X-E oscilloscope is connected to carry out the case study. Note that for this study, the model will execute only in the CPU and not in the FPGA, the latter being used only to relay the digital signals. Aside from the target real-time platform, a host PowerEdge R230 server computer was used to compile the project file and communicate with the platform, running MATLAB version R2022a and RT-LAB v2023.2.1.578.

The scenarios shown in the simulations in MATLAB/SIMULINK are replicated in the following tests. Figure 20a shows the grid voltages affected by harmonic distortion at 15% for the 5th, 7th, 11th, 13th, and 17th harmonics. As a result of the harmonic distortion of the grid voltages, distorted grid currents are observed in Figure 20b. In this scenario, no harmonic compensation structure was used in the inverter of the photovoltaic generator. Figure 20c shows the grid voltage and current at phase 1, which shows the effect that voltage harmonics have on the grid currents of the photovoltaic inverter. Note that a gain was applied to align the visualization of the grid current with the grid voltage. A difference in the behavior of the grid currents is seen when the resonant HC structure is used. Figure 20d shows the grid currents that result when HC structures are used. It can be observed that there is a significant reduction in the harmonic pollution of grid currents. Figure 20e shows the distorted grid voltage and the current without harmonics at phase 1 when HC is used.

In the tests shown below, a frequency step of 5 Hz is applied to the grid frequency. Figure 21a shows a screenshot from the oscilloscope of the grid voltages affected by harmonic pollution. In addition, a frequency increase of 5 Hz has been applied. Figure 21b shows the grid voltage and the grid current when the frequency-adaptive harmonic compensation structure is used. A grid current with minimal harmonic distortion can be observed due to the use of the adaptative HC structure.

Next, harmonic distortions of 15% for the 5th, 7th, 11th, 13th, and 17th harmonics are introduced into the grid voltages. A frequency step of 5 Hz is applied to the grid frequency, and an unbalance is introduced in the grid voltages. Figure 22a shows the unbalanced grid voltages affected by harmonic distortion. Figure 22b shows the grid currents obtained using the HC structure; in that figure, currents without harmonic distortion can be seen. In addition to harmonic distortion and voltage unbalances, a 5 Hz increase in the grid frequency is shown in Figure 22c. Grid currents without harmonic distortion can be observed in Figure 22d. The above results show the importance of using harmonic compensation structures in microgrids affected by different types of disturbances to ensure compliance with power quality standards.

7. Discussion

A summary of the THD_I obtained under the different scenarios and using harmonic compensation technique configurations with resonant filters is shown. In the first scenario, the THD_I of phase 1 of the grid current was measured when there were no disturbances in the utility grid. Only PR regulators were used to control the inverter currents, resulting in a THD of 1.14% on the grid current at phase 1. In the second scenario, a 15% harmonic pollution was applied to the 5th, 7th, 11th, 13th, and 17th harmonics in the three-phase voltages of the utility grid were applied, leading to a TDH of voltage (THD_V) of 33.54%. First, the current harmonic distortion was determined at phase 1 when only PR regulators were employed for control; second, the THD was determined when the resonant compensation strategy was used, resulting in THD_I = 7.27% and THD_I = 1.69%, respectively.

A THD_V of 33.54% in the utility voltages combined with a variation in the grid frequency constitute the third scenario used in the study of the harmonics of the PV generator. In the first simulation for this scenario, the harmonic compensation strategy was used without frequency feedback from the mains, resulting in a THD_I of 7.77%, a value fails to comply with international standards on harmonic distortion [1]. In the second simulation of this scenario, the grid frequency estimated by the synchronization algorithm was incorporated into the PR + HC strategy, resulting in a THD_I of 3.10% in phase 1.

In the fourth scenario, the three-phase utility grid is affected by three types of disturbances: voltage unbalance, frequency variation, and harmonic pollution. As can be seen in

Table 6. Summary of THD_I at phase 1 under different scenarios.

Scenery	PR Regulator THDI	PR + HC THDI	PR + Adaptive-Freq. HC THDI	THDI Limit
No grid disturbances.	1.14%	-	-	<5.0%
Harmonic pollution in grid voltages.	7.27%	1.69%.	-	<5.0%
Harmonic pollution + grid frequency variation.	-	7.77%.	3.10	<5.0%
Harmonic pollution + grid frequency variation + voltage unbalance.	-	-	1.26	<5.0%

, despite the presence of grid disturbances, the use of a harmonic compensation strategy resulted in a THD_I of 1.26% at phase 1, ensuring compliance with the established harmonic limits.

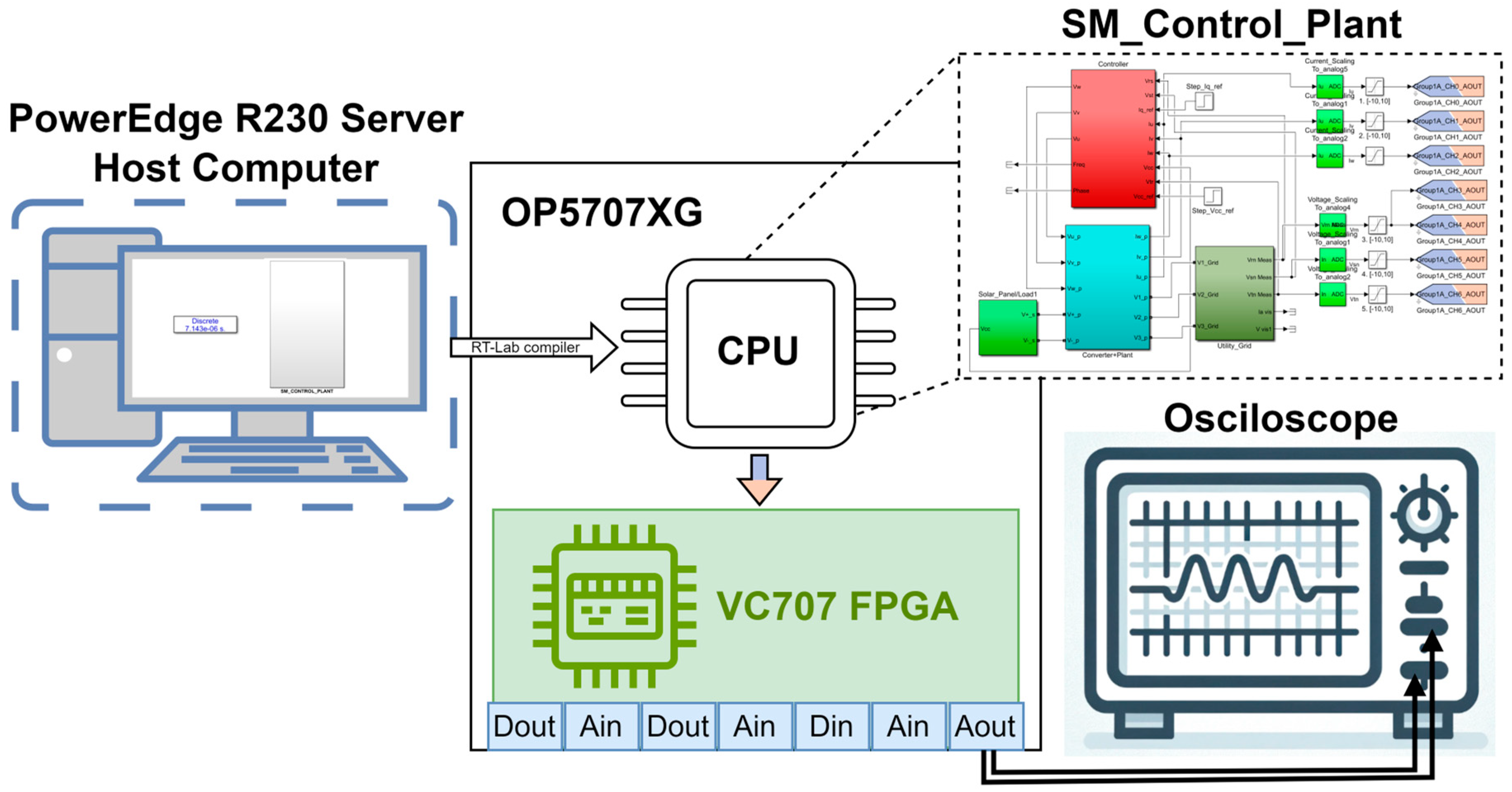
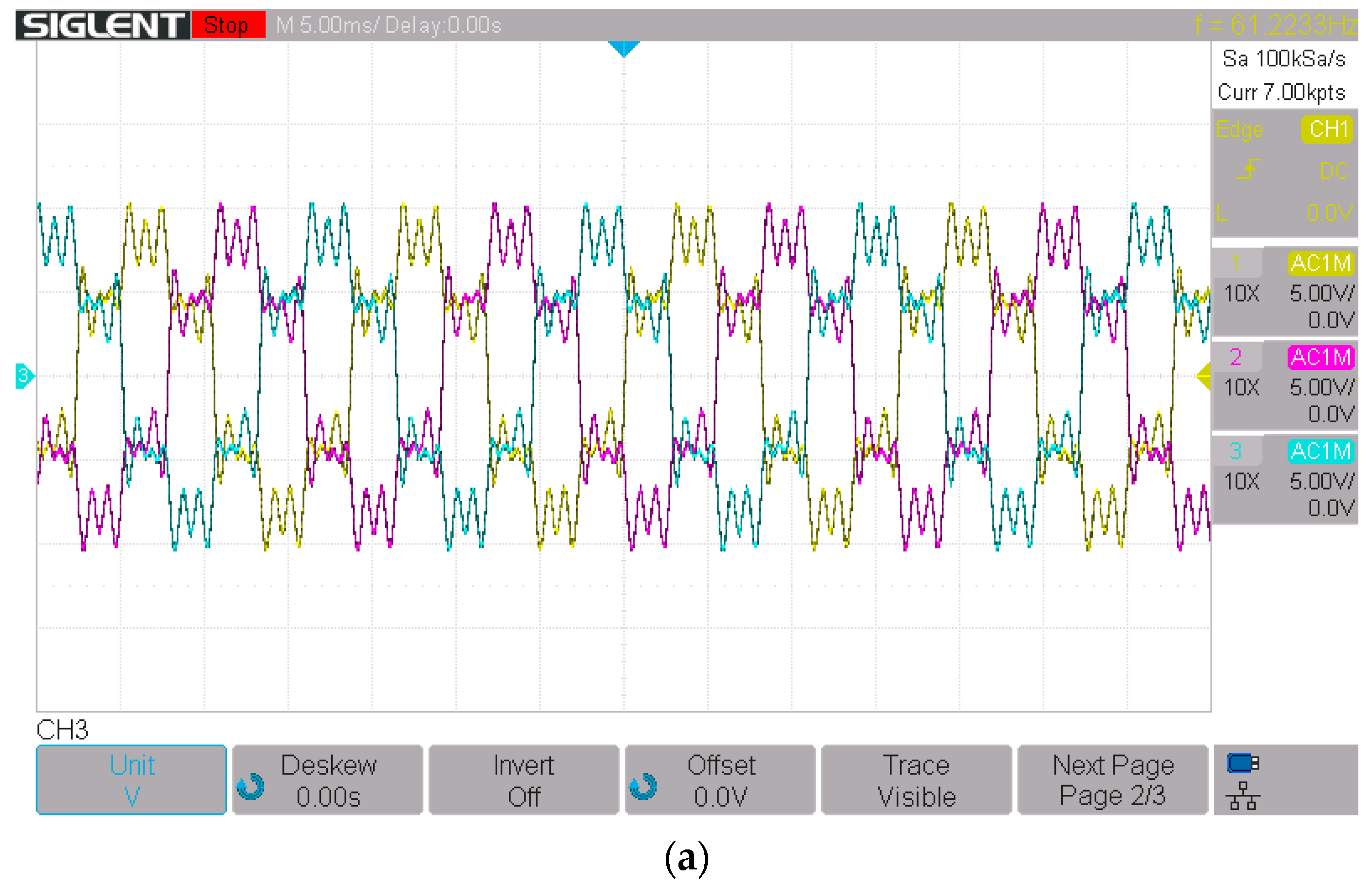
The results obtained in the real-time simulations mirror those obtained during the MATLAB/SIMULINK model simulations. The importance of using the digital simulator is that the tests are carried out in an environment that more closely resembles a real photovoltaic generator.

8. Conclusions

In this paper, a review of several methods used to compensate for harmonics in photovoltaic systems was carried out with the objective of showing the advantages that these methods offer in relation to improving power quality and complying with international standards on harmonic distortion. A MATLAB/SIMULINK model of an electrical microgrid was developed. A harmonic compensation strategy based on resonant filters was modeled. Model development involved explaining in detail each of the blocks necessary for its implementation in MATLAB/SIMULINK. The intention of carrying out and explaining this modeling is to serve as a guide to implementing this harmonic compensation strategy within a photovoltaic generator model. The behavior, in terms of harmonics, of a photovoltaic generator with a peak power of 3.68 kW within the microgrid was studied under different utility-grid conditions. Real-time simulations facilitated the debugging and validation of control algorithms, which later may be implemented on inverter controllers for real photovoltaic generators. Several tests with different scenarios were carried out using a real-time simulator.

The results of the harmonic compensation strategy demonstrated that it is a good alternative when the utility grid is affected by different types of disturbances.

In future work, new methods to compensate for harmonics in photovoltaic generators will be evaluated and designed, as well as implemented in physical photovoltaic generators.