Uncertainty Quantification of Engineering Parameters for a Nuclear Reactor Loaded with Dispersed Fuel Particles
Abstract
1. Introduction
2. Uncertainty Quantification
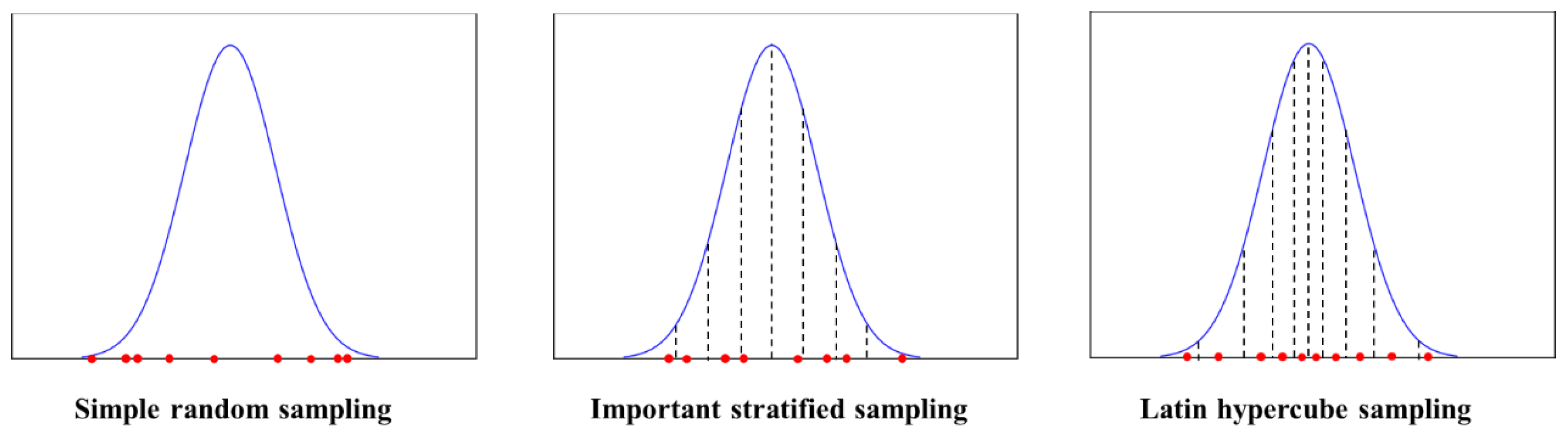
2.1. Statistical Sampling Method
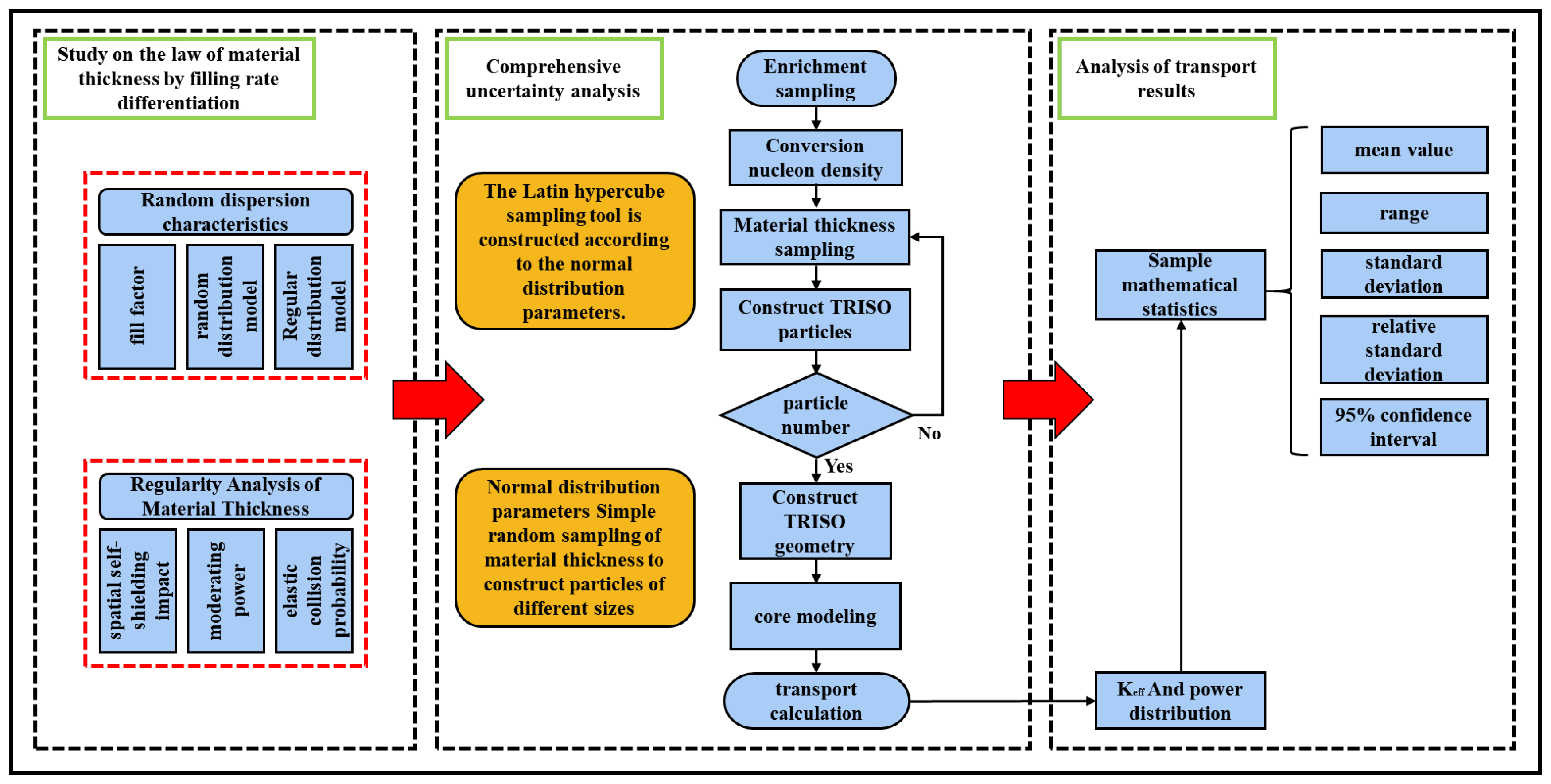
2.2. Development of an Uncertainty Analysis Tool
3. Quantitative Analysis of Uncertainty
3.1. Transport Calculation Model
3.2. Analysis of Variances under Different Packing Fractions
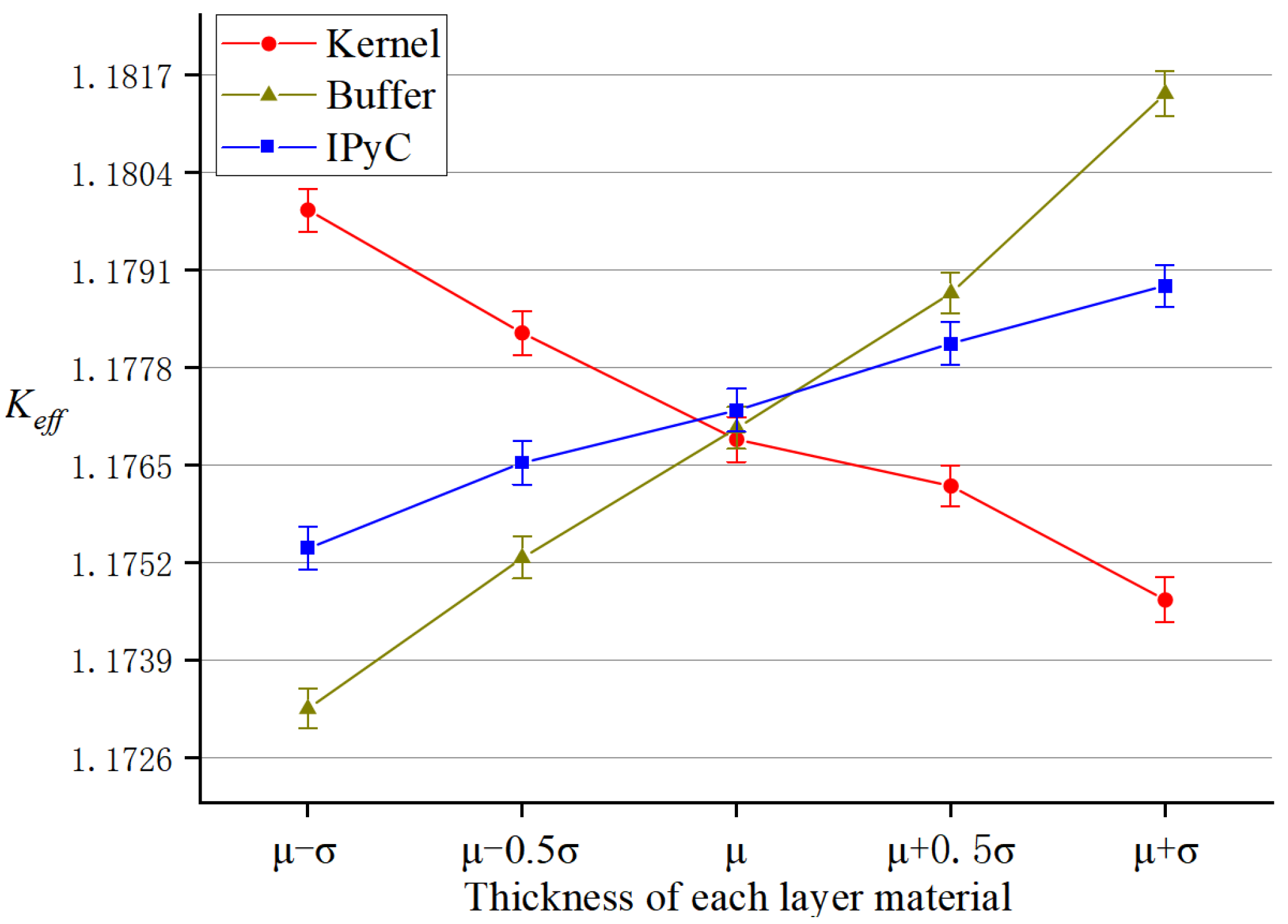
3.3. Regularity Analysis of Material Thickness
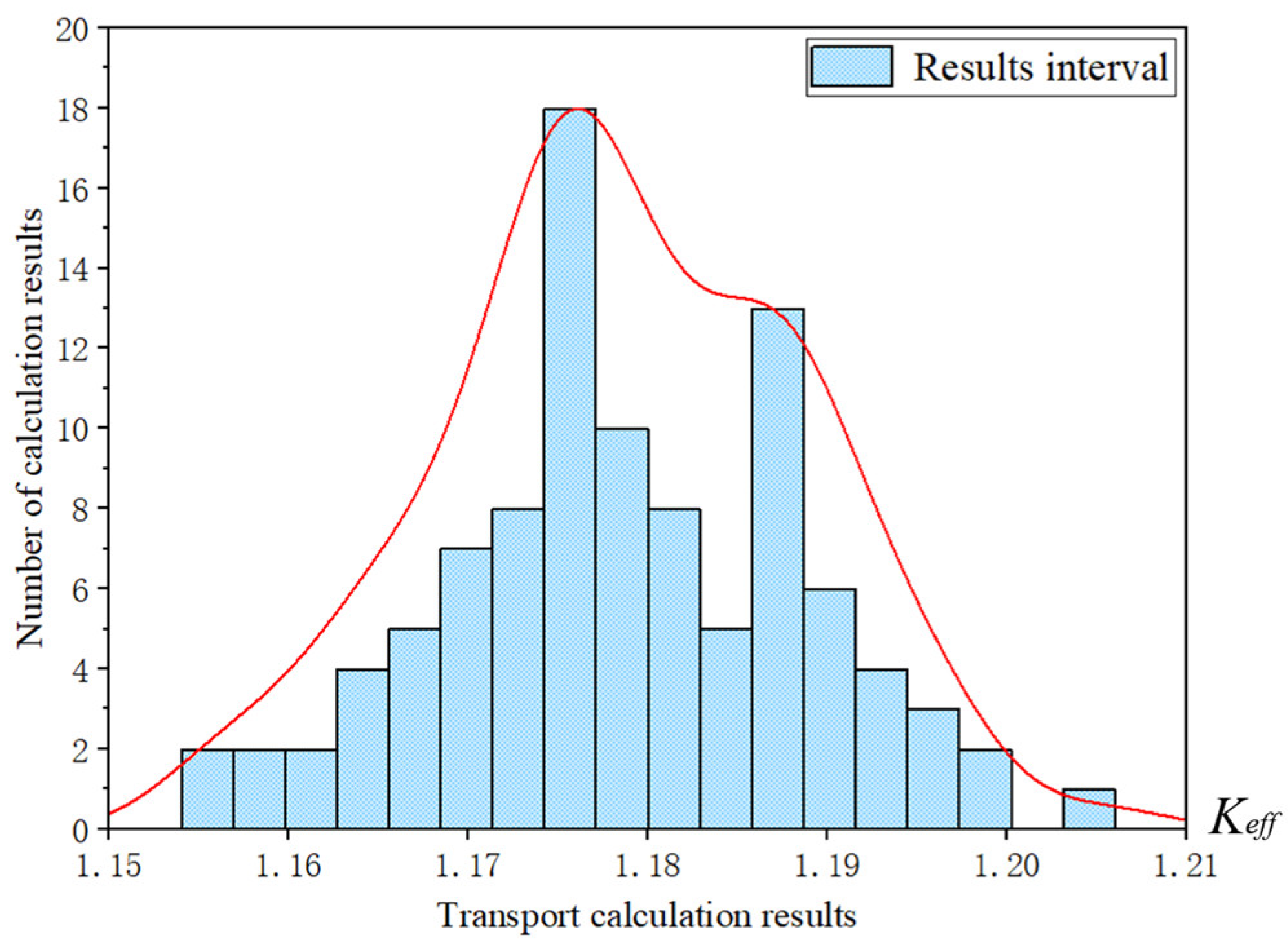
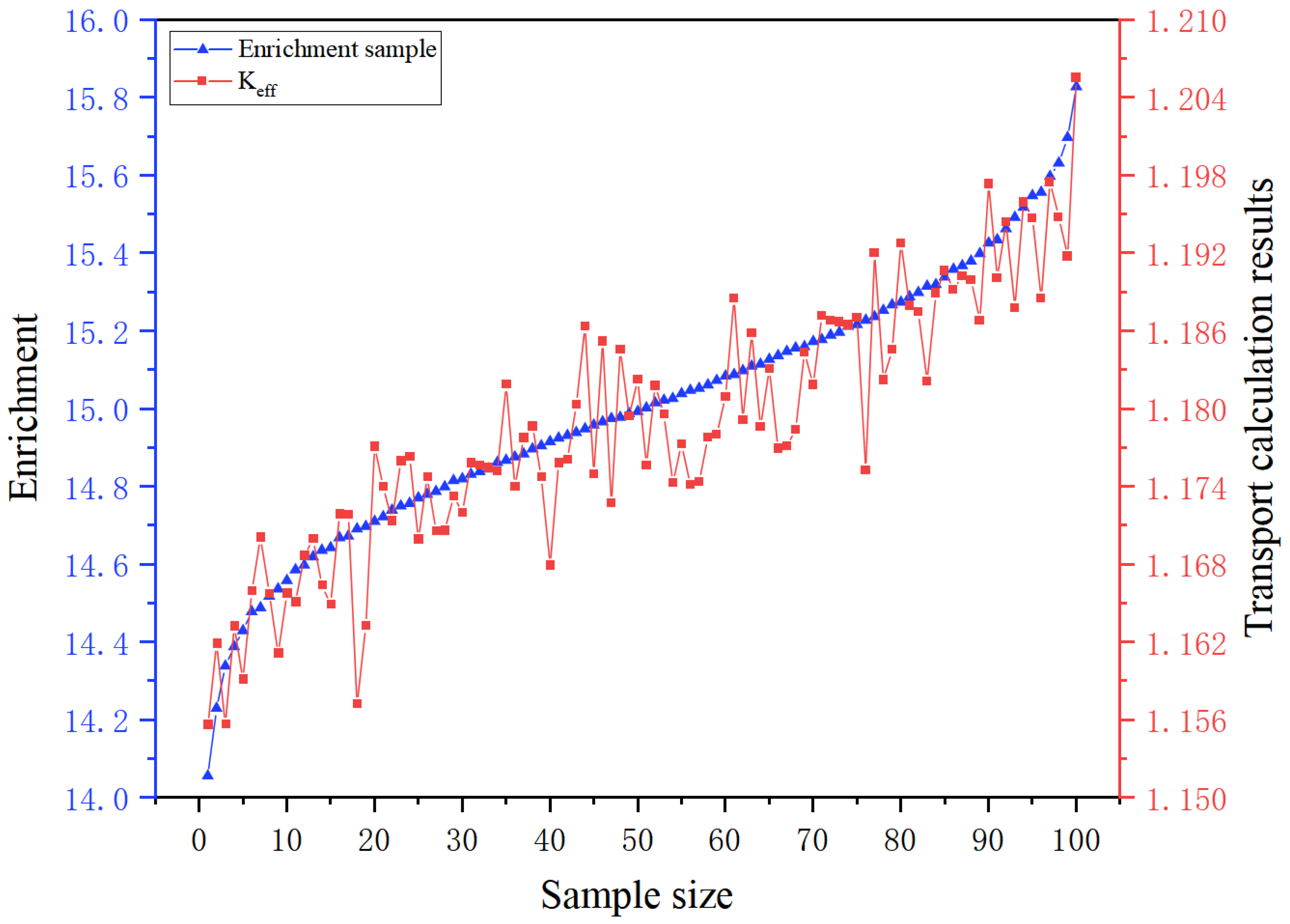
3.4. Multi-Engineering Parameter Quantitative Analysis of Overall Uncertainty
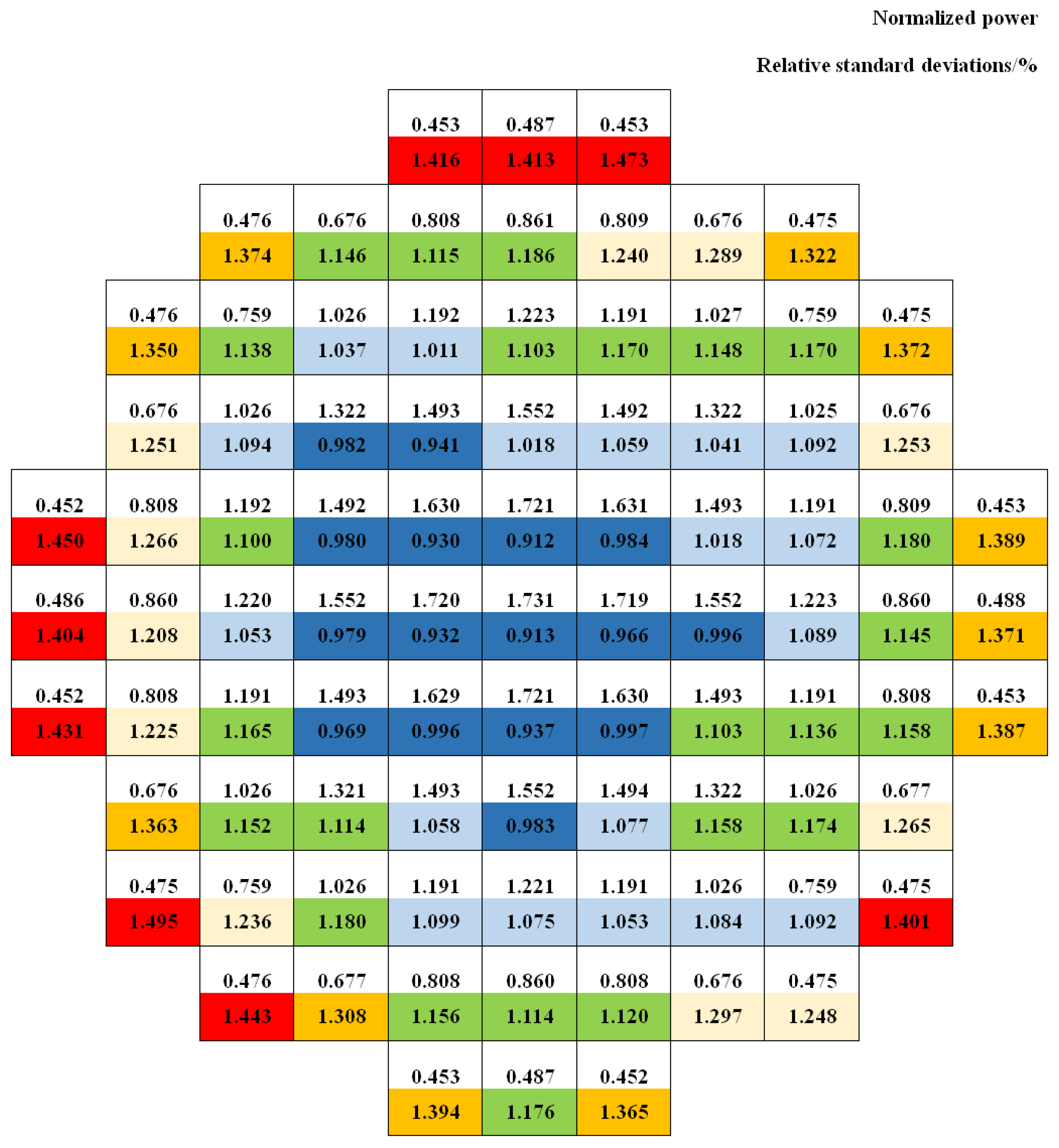
3.5. Multi-Engineering Parameter Quantitative Analysis of Uncertainty in the Power Distribution
- (1)
- Neutron transport behaviors in the edge region of the reactor core are affected by boundary effects, and geometric and material boundaries increase uncertainty induced by engineering parameters.
- (2)
- The flow paths of neutrons in the edge region of the reactor core are more complex, thus increasing the uncertainty induced by engineering parameters.
- (3)
- The magnitude of the neutron flux in the core region is large, and uncertainty induced by engineering parameters has a small effect on it. In contrast, the magnitude of the deposition energy in the edge region is small, and uncertainty induced by engineering parameters has a large effect on it.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sadekin, S.; Zaman, S.; Mahfuz, M.; Sarkar, R. Nuclear power as foundation of a clean energy future: A review. Energy Procedia 2019, 160, 513–518. [Google Scholar] [CrossRef]
- Deng, N.; Xie, C.; Hou, C.; Li, Z.; Xie, J.; Yu, T. The Influence Mechanism of Neutron Kinetics of the Accelerator-Driven Subcritical Reactor Based on the Fast/Thermal Neutron Spectra by Monte Carlo Homogenization Method. Energies 2023, 16, 3545. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, P.; Jiang, F.; Xie, J.; Yu, T. Fault Diagnosis of Nuclear Power Plant Based on Sparrow Search Algorithm Optimized CNN-LSTM Neural Network. Energies 2023, 16, 2934. [Google Scholar] [CrossRef]
- Ni, Z.; Chen, X.; Xie, J.; Wasaye, M.A.; Yu, T. Quantitative Analysis Study of Effects of Nuclide Concentration Uncertainties on Biases and Bias Uncertainties in Criticality Calculation Method. Energies 2023, 16, 7378. [Google Scholar] [CrossRef]
- Mu, R.; Zuo, J.; Yuan, X. China’s approach to nuclear safety—From the perspective of policy and institutional system. Energy Policy 2015, 76, 161–172. [Google Scholar] [CrossRef]
- Mo, K.; Lee, S.J.; Seong, P.H. A dynamic neural network aggregation model for transient diagnosis in nuclear power plants. Prog. Nucl. Energy 2007, 49, 262–272. [Google Scholar] [CrossRef]
- Lee, U.; Lee, C.; Kim, M.; Kim, H.R. Analysis of the influence of nuclear facilities on environmental radiation by monitoring the highest nuclear power plant density region. Nucl. Eng. Technol. 2019, 51, 1626–1632. [Google Scholar] [CrossRef]
- Jiao, Y.; Yu, J.; Zhou, Y.; Li, Y.; Chen, P.; Duan, Z. Development progress and application prospects of commercial pressurized water reactor nuclear fuel. Nucl. Power Eng. 2022, 43, 1–7. [Google Scholar] [CrossRef]
- Dai, X. Physical Design of SiC Matrix TRISO Fuel Small PWR Core; Harbin Engineering University: Harbin, China, 2014. [Google Scholar]
- Hao, C.; Li, F. Uncertainty Analysis of Nuclear Reactor Physics Calculations; Tsinghua University Press: Beijing, China, 2022; pp. 34–38. [Google Scholar]
- Cheng, Y.; Hao, C.; Li, F. Uncertainty quantification of fuel pebble model and its effect on the uncertainty propagation of nuclear data in pebble bed HTR. Ann. Nucl. Energy 2020, 139, 107286. [Google Scholar] [CrossRef]
- Cheng, Y. Research on Physical Calculation Uncertainty of Ball Bed High Temperature Gas Cooled Reactor; Harbin Engineering University: Harbin, China, 2020. [Google Scholar] [CrossRef]
- Lou, L.; Chai, X.; Yao, D.; Li, M.; Chen, L.; Liu, X.; Zhang, H.; Li, S.; Tang, X.; Zhou, N. A Study on the Dual Inhomogeneity Physical Boundary of Dispersive Particle Systems. Nucl. Power Eng. 2021, 42, 82–88. [Google Scholar] [CrossRef]
- Zhang, Y.; Lin, J.; Zhang, H.; Zhu, Z. Influence of particle size and its standard deviation on failure probability of coated fuel particles. Nucl. Tech. 2016, 39, 73–78. [Google Scholar]
- Fan, K.; Wei, C.; Li, F. Effect of Random Distribution of Coated Particle Fuel. At. Energy Sci. Technol. 2013, 47, 220–223. [Google Scholar]
- Kępisty, G.; Oettingen, M.; Stanisz, P.; Cetnar, J. Statistical error propagation in HTR burnup model. Ann. Nucl. Energy 2017, 105, 355–360. [Google Scholar] [CrossRef]
- Zhuang, C.; He, C. Basics of Applied Mathematical Statistics; South China University of Technology Press: Guangzhou, China, 2006. [Google Scholar]
- Wu, J. Quantitative Research on Uncertainty of Activation Calculation Based on Nuclear Data; University of South China: Hengyang, China, 2022. [Google Scholar]
- Zhang, Y.; Yang, J. Stratified Latin Hypercube Sampling Method and Application. Stat. Decis. 2023, 39, 48–51. [Google Scholar] [CrossRef]
- Rosales, J.; Francois, J.L.; Garcia, C. Neutronic assessment of a PWR-type SMR core with TRISO particles using mixed-oxide fuel strategies. Prog. Nucl. Energy 2022, 154, 104470. [Google Scholar] [CrossRef]
- Zhang, Y. Research on the Structure and Failure Behavior of TRISO Coated Fuel Particles; Graduate School of Chinese Academy of Sciences (Shanghai Institute of Applied Physics): Shanghai, China, 2016. [Google Scholar]
- Xie, X. Research on Hydrothermal Corrosion Behavior of Nuclear Silicon Carbide Materials; Shanghai Jiao Tong University: Shanghai, China, 2020. [Google Scholar] [CrossRef]
- Hussain, A.; Cao, X. Small PWR core design with coated particle-based fuel with a novel composition. Prog. Nucl. Energy 2010, 52, 531–535. [Google Scholar] [CrossRef]
- Huang, Z. Fundamentals of Nuclear Reactor Dynamics; Atomic Energy Press: Vienna, Austria, 1983. [Google Scholar]
- Zhao, B.; Li, Q.; Li, H.; Huang, Y.; Ma, Q.; Li, M.; Liu, Z.; Qi, H.; Ma, C.; Chen, H. Performance Analysis and Optimization Study of Prism Dispersive Microencapsulated Fuel for Gas Cooled Reactors. Nucl. Power Eng. 2022, 43, 89–95. [Google Scholar] [CrossRef]
- Lou, L.; Chai, X.; Yao, D.; Chen, L.; Liu, X.; Li, S.; Tang, X.; Zhang, C. Primary Research of Double Heterogeneity on Particle-dispersed Fuel and Burnable Poisons. China Nucl. Power 2022, 15, 610–617. [Google Scholar]
- Er, Y. Safety Thermodynamics of Water-Cooled Reactors; Atomic Energy Press: Vienna, Austria, 1982. [Google Scholar]
- Yang, L.; Zou, D. Project Management Practice of Qinshan Nuclear Power Phase II Expansion Project; Engineering Chapter; Atomic Energy Press: Vienna, Austria, 2012. [Google Scholar]

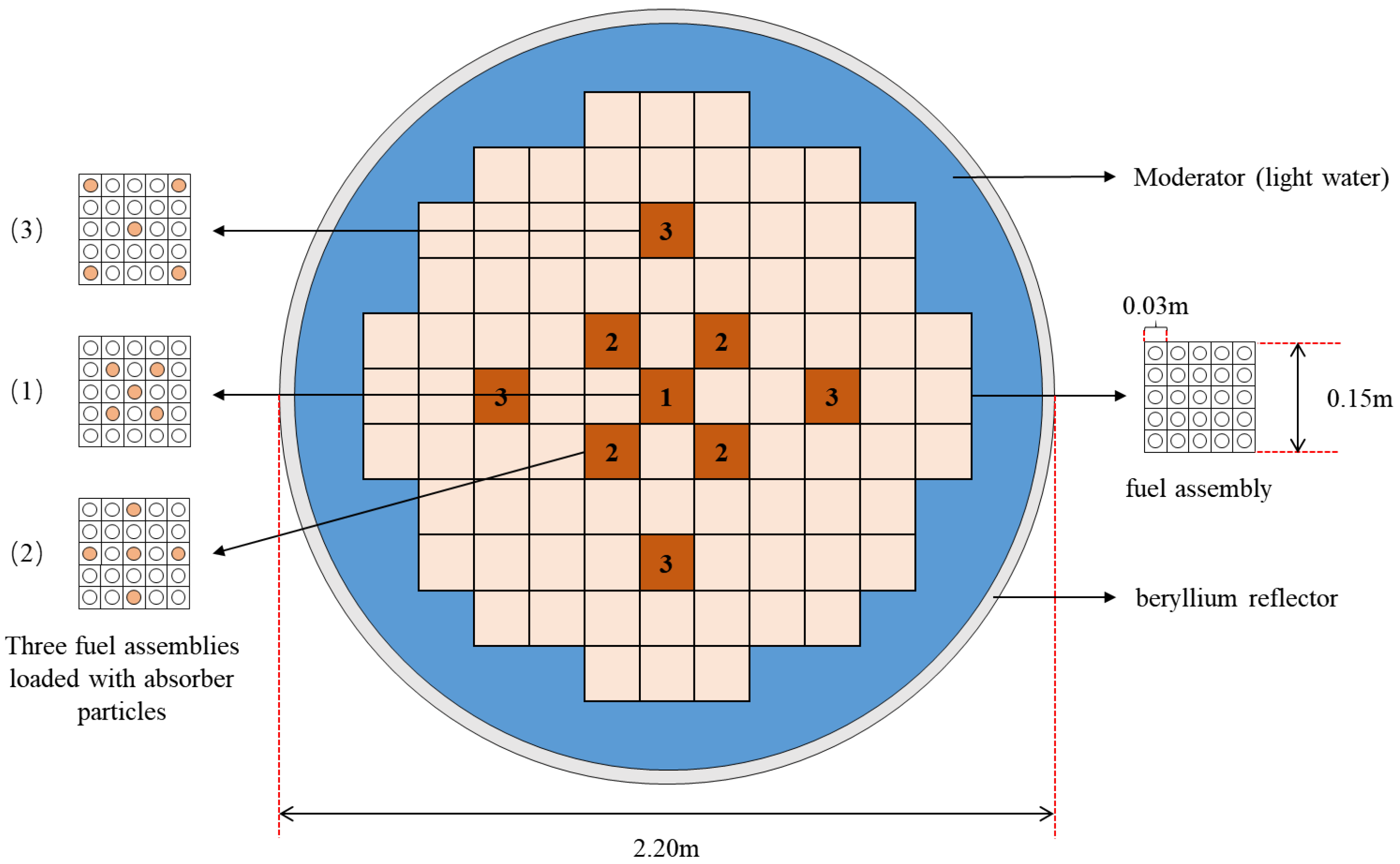
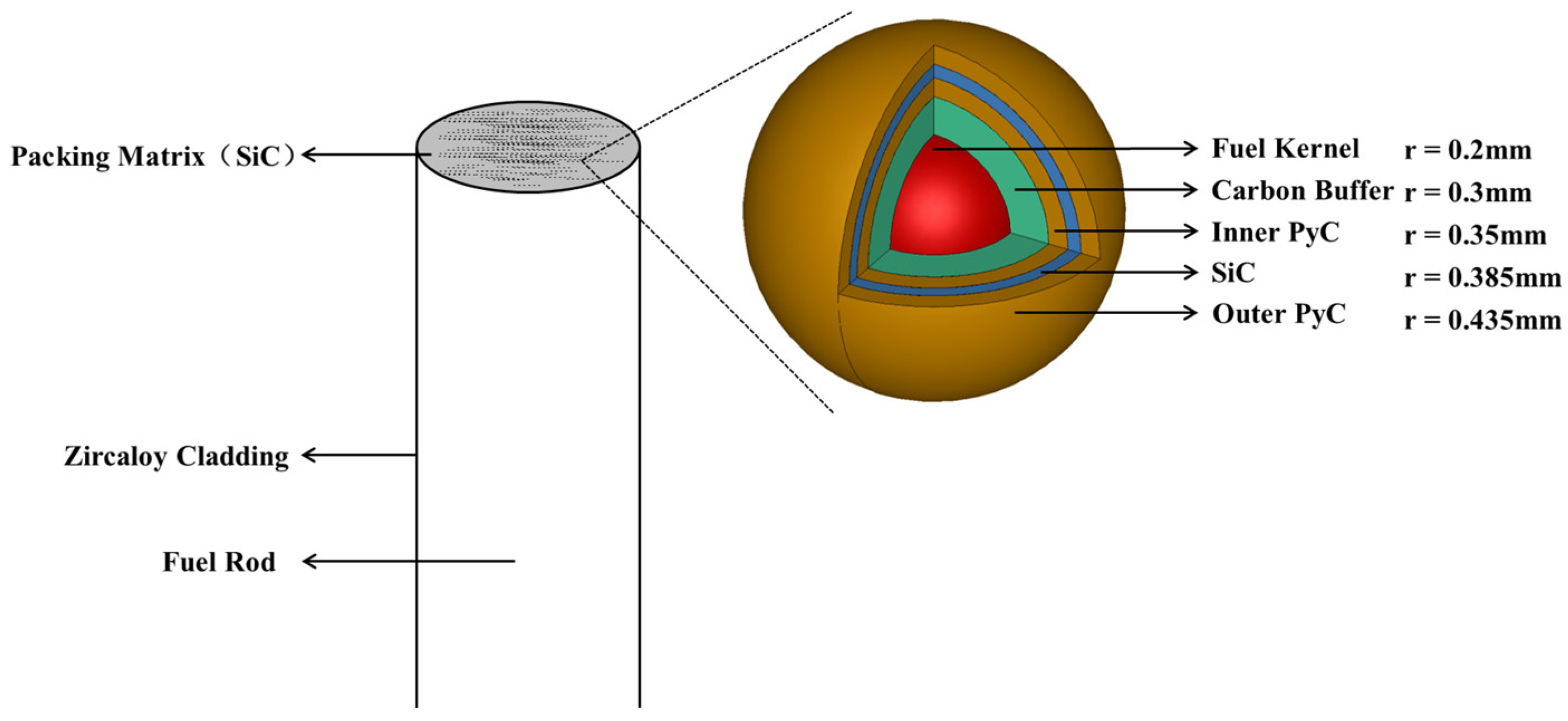



| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Power | 25 MWth | Fuel type | TRISO |
| Height of reactor core | 170 cm | 235U enrichment | 15% |
| Reactor core equivalent diameter | 220 cm | Number of assemblies | 89 |
| Height of active zone | 150 cm | Number of assembly cells | 5 × 5 |
| Grid spacing | 3 cm | Assembly without control rod | 80 |
| Diameter of fuel rod | 2 cm | Assembly with control rods | 9 |
| Thickness of the cladding layer | 0.15 cm | Number of control rods | 45 |
| Packing fraction | 30% | Packing matrix | SiC |
| Moderator/coolant | Light water | Fuel | UO2 |
| Packing Fraction | Keff of Regular Model | Keff Mean of Random Model | Standard Deviation of Random Model (pcm) | Relative Difference of Model (pcm) |
|---|---|---|---|---|
| 1% | 0.11842 | 0.12029 | 4.2 | 1554.6 |
| 5% | 0.43368 | 0.44283 | 22.2 | 2066.3 |
| 10% | 0.69283 | 0.70579 | 23.7 | 1836.2 |
| 15% | 0.86609 | 0.87906 | 24.3 | 1475.4 |
| 20% | 0.99748 | 1.00910 | 26.1 | 1151.5 |
| 25% | 1.09436 | 1.10332 | 29.5 | 812.1 |
| 30% | 1.16899 | 1.17629 | 29.0 | 620.5 |
| 35% | 1.22304 | 1.22864 | 22.2 | 455.7 |
| 40% | 1.27725 | 1.28052 | 28.6 | 255.3 |
| 45% | 1.31643 | 1.31869 | 21.6 | 171.3 |
| Material Layer | Designed Thickness (mm) | Standard Deviation of Thickness (μm) |
|---|---|---|
| Kernel radius | 0.200 | 12.76 |
| Buffer cladding layer | 0.100 | 22.96 |
| IPyC cladding layer | 0.050 | 10.20 |
| SiC cladding layer | 0.035 | 5.10 |
| OPyC cladding layer | 0.050 | 10.20 |
| Designed Thickness (mm) | Number of Fuel Particles | Transport Calculation Results (Keff) | |
|---|---|---|---|
| Kernel | 0.018724 | 60,993 | 1.17990 ± 0.00029 |
| 0.019362 | 55,160 | 1.17826 ± 0.00029 | |
| 0.02 | 50,048 | 1.17684 ± 0.00030 | |
| 0.020638 | 45,548 | 1.17622 ± 0.00027 | |
| 0.021276 | 41,573 | 1.17470 ± 0.00030 | |
| Buffer cladding layer | 0.007704 | 50,048 | 1.17325 ± 0.00027 |
| 0.008852 | 50,048 | 1.17526 ± 0.00028 | |
| 0.01 | 50,048 | 1.17699 ± 0.00028 | |
| 0.011148 | 50,048 | 1.17879 ± 0.00027 | |
| 0.012296 | 50,048 | 1.18145 ± 0.00030 | |
| IPyC cladding layer | 0.00398 | 50,048 | 1.17539 ± 0.00029 |
| 0.00449 | 50,048 | 1.17653 ± 0.00029 | |
| 0.005 | 50,048 | 1.17723 ± 0.00029 | |
| 0.00551 | 50,048 | 1.17812 ± 0.00029 | |
| 0.00602 | 50,048 | 1.17889 ± 0.00028 |
| Regression Analysis Parameters | Kernel | Buffer Cladding Layer | IPyC Cladding Layer |
|---|---|---|---|
| Slope | −1.94984 | 1.73606 | 1.68431 |
| Intercept | 1.21618 | 1.15979 | 1.16881 |
| Coefficient of determination (R2) | 0.98241 | 0.99333 | 0.99400 |
| p value | 0.00010 | 0.00023 | 0.00019 |
| Standard error | 0.15060 | 0.08215 | 0.07549 |
| Calculation Data | Mean | Extreme Difference | Significance Level (p-Value) | ||
|---|---|---|---|---|---|
| Uniform Distribution | Normal Distribution | Triangular Distribution | |||
| Enrichment sample | 14.998% | 1.7728% | 5.9257 × 10−4 | 1.00000 | 0 |
| Transport calculation results | 1.17862 | 0.04996 | 6.4101 × 10−4 | 0.85763 | 0 |
| Parameter | Calculation Result |
|---|---|
| Mean | 1.17862 ± 0.00028 |
| Extreme difference | 0.04996 |
| Standard deviation | 0.01003 |
| Relative standard deviation | 0.851% |
| 95% confidence interval of mean | 1.15896/1.19828 |
| Pearson correlation coefficient | 0.91443 |
| Spearman’s rank correlation coefficient | 0.90890 |
| Kendall’s rank correlation coefficient | 0.74088 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Chen, Z.; Yang, C.; Huang, G.; Gao, K.; Sun, A.; Liu, C.; Wu, Z. Uncertainty Quantification of Engineering Parameters for a Nuclear Reactor Loaded with Dispersed Fuel Particles. Energies 2024, 17, 2245. https://doi.org/10.3390/en17102245
Li Y, Chen Z, Yang C, Huang G, Gao K, Sun A, Liu C, Wu Z. Uncertainty Quantification of Engineering Parameters for a Nuclear Reactor Loaded with Dispersed Fuel Particles. Energies. 2024; 17(10):2245. https://doi.org/10.3390/en17102245
Chicago/Turabian StyleLi, Yukun, Zhenping Chen, Chao Yang, Guocai Huang, Kekun Gao, Aikou Sun, Chengwei Liu, and Zhiqiang Wu. 2024. "Uncertainty Quantification of Engineering Parameters for a Nuclear Reactor Loaded with Dispersed Fuel Particles" Energies 17, no. 10: 2245. https://doi.org/10.3390/en17102245
APA StyleLi, Y., Chen, Z., Yang, C., Huang, G., Gao, K., Sun, A., Liu, C., & Wu, Z. (2024). Uncertainty Quantification of Engineering Parameters for a Nuclear Reactor Loaded with Dispersed Fuel Particles. Energies, 17(10), 2245. https://doi.org/10.3390/en17102245






