Local DER Control with Reduced Loop Interactions in Active Distribution Networks
Abstract
1. Introduction
- new market agents are being introduced that aggregate DERs to provide ASs at transmission system level [11], in particular by mitigating the negative effects of RES power fluctuations [12], as well as new entities, such as energy communities [13], to promote the power balance and the AS provision at distribution system level.
- The AS of voltage regulation provided by DERs locally varying, primarily, their reactive power injection according to an integral law, and, in the case of reactive current saturation, their active power injection according to a given droop law.
- A two-step-based sequential design using only local measurements.
- Reduction in the internal and external interaction level.
- Robust stability in the presence of parameter uncertainty in the matrix model plant.
- Simplicity of the controller’s structure easily implementable in real ADNs.
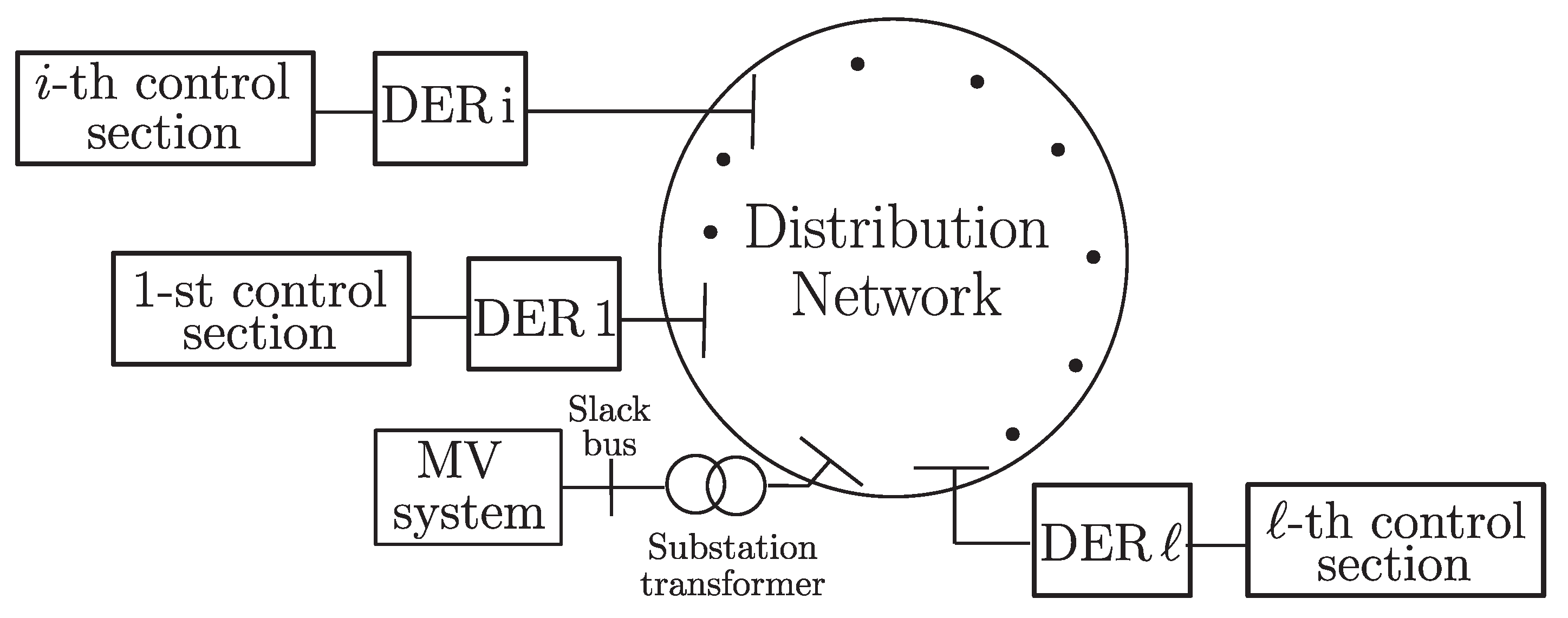
2. ADN Model
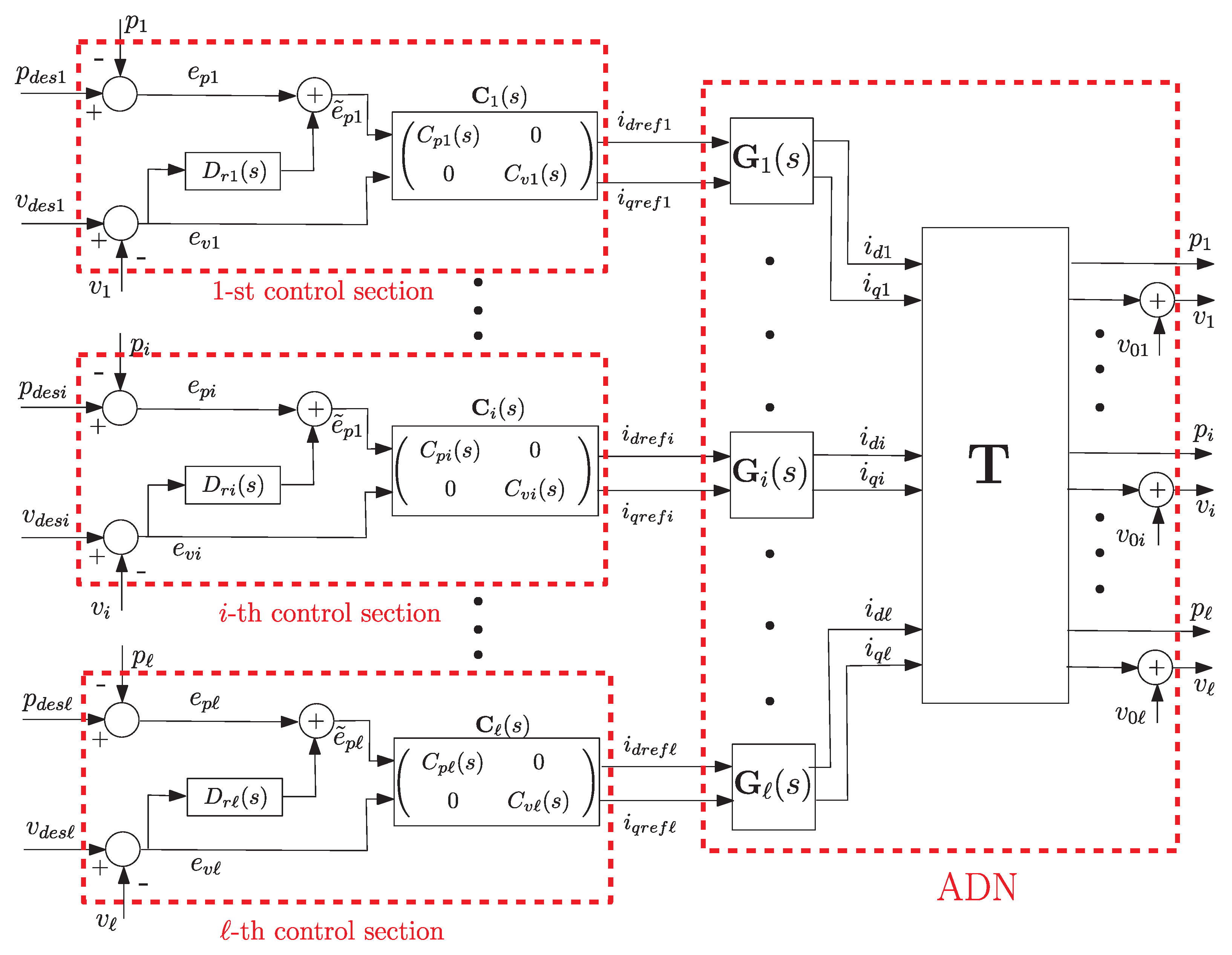
3. The Proposed Control Design
3.1. DER Interaction Analysis
3.2. First Step in the Design Procedure
3.3. Second Step in the Design Procedure
- The EOTF obtained by (8) may present a complicated dynamic form; in this case, it can be easily reduced by using the Hankel-norm approximation with balanced realization available in the Control Toolbox of Matlab.
- A single parameter to design any IMC-PI controller.
- The adopted IMC technique guarantees robustness against model parameter uncertainty in model and .
- In the case of installation of a new DER or structural changes in the network topology, it is necessary to develop a new design. The updated gains are sent by the DSO to the local PI controllers by a low-capacity low-cost one-way communication, f.i. based on standard wireless mobile telecommunications technology. However, these circumstances are rare and known in advance since they require a planning activity by the DSO. On the contrary, during operation, if a DER is switched off, no action is required.
- Step 1:
- Given , extract the sub-matrix using (7).
- Step 2:
- For any DER, calculate the EOTF according to Equation (8) and, eventually, reduce its order.
- Step 3:
- Form the diagonal control matrix as in Equation (9).
- Step 4:
- Find the free parameters that solve problem (10).
- Step 5:
- Verify the fulfillment of condition (12) for any DER.
- Step 6:
- Using , determine (s) as in Equation (13).
- Step 7:
- Find the free parameter and that solve problem (16).
- Step 8:
- Repeat step 6 and step 7 for all DERs.
4. Cases Study and Simulation Results
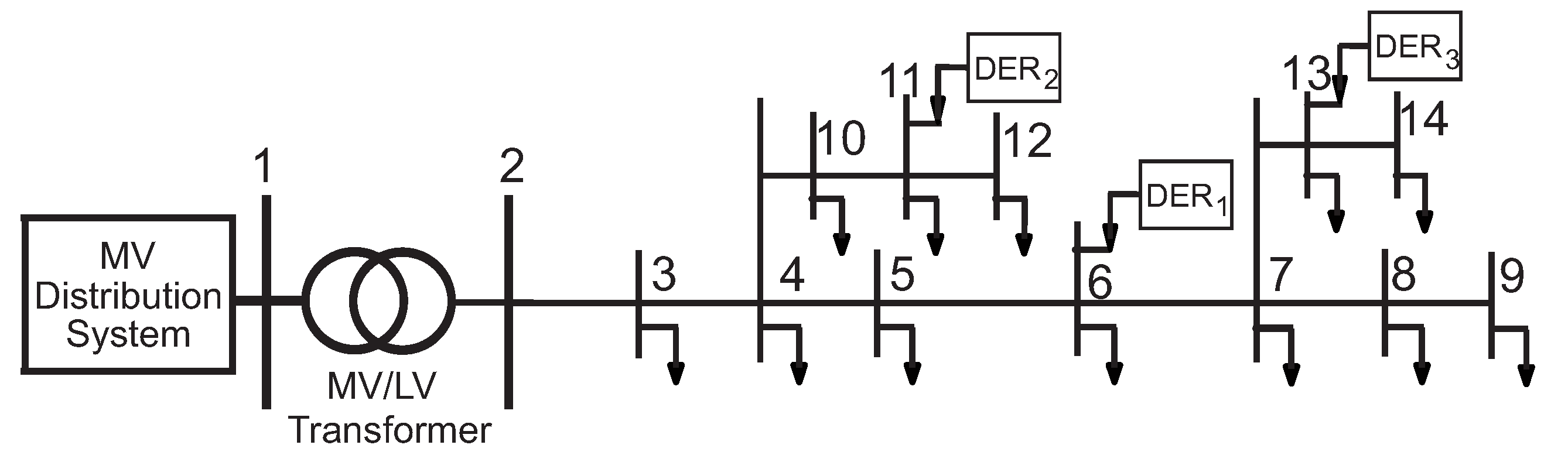
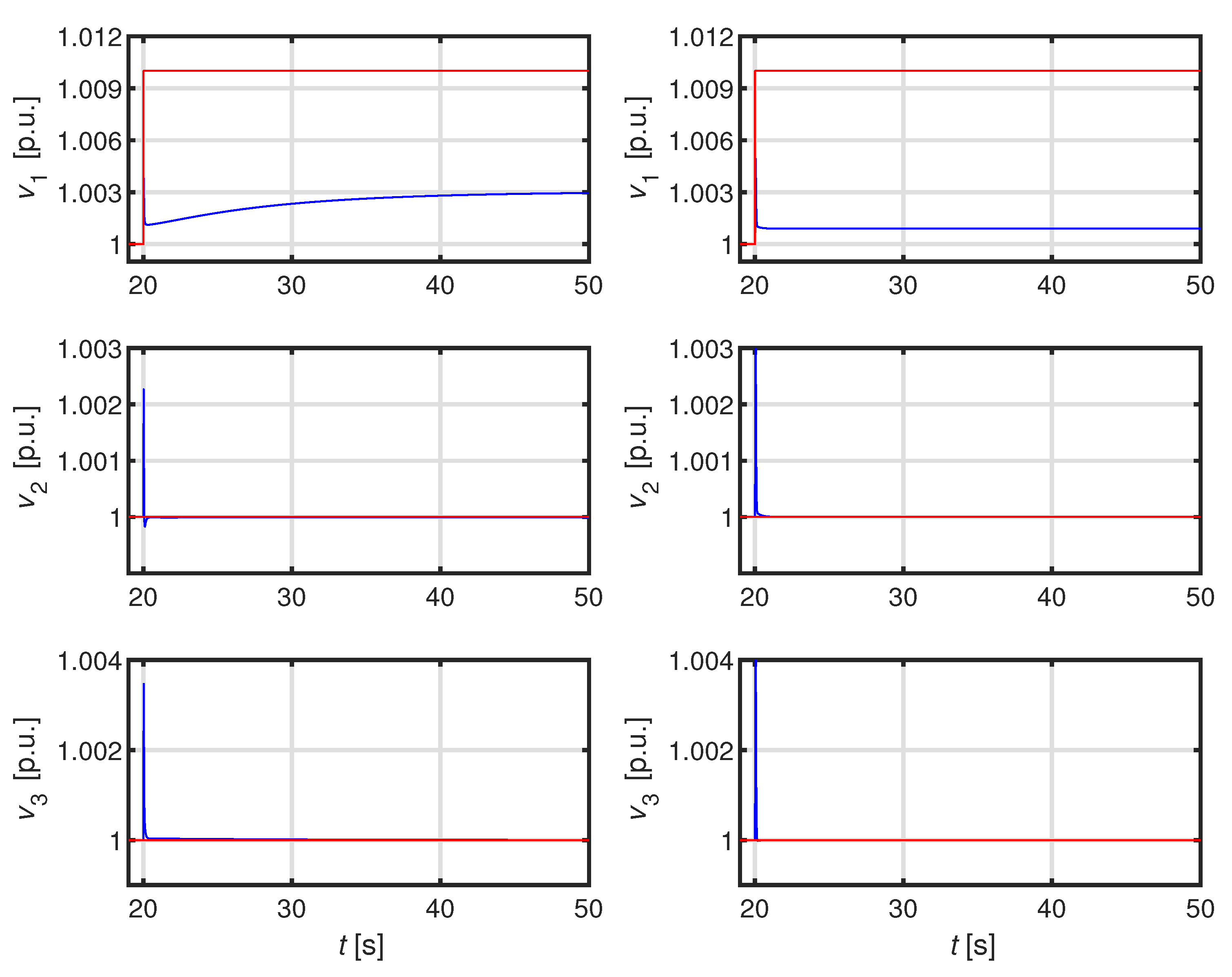
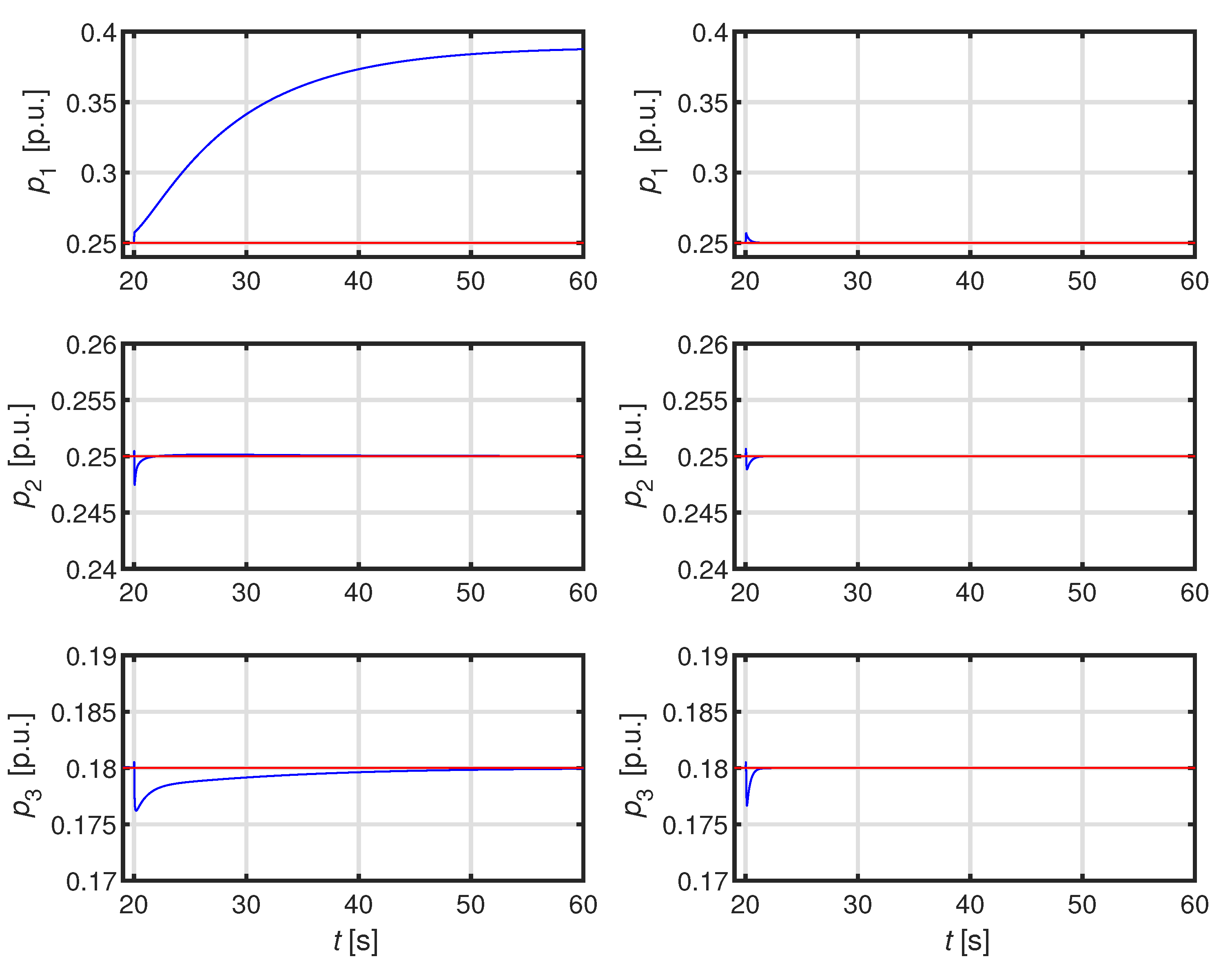
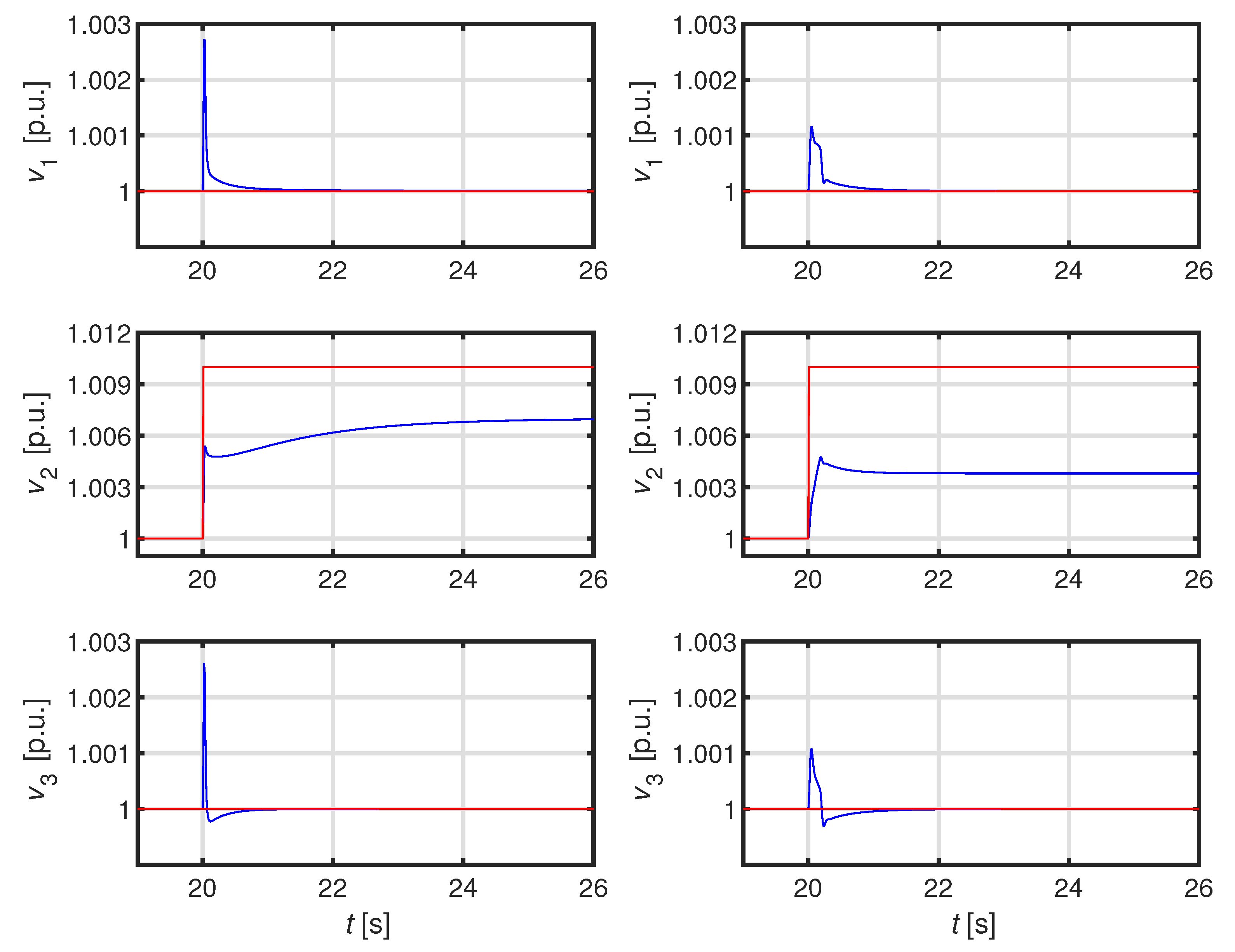
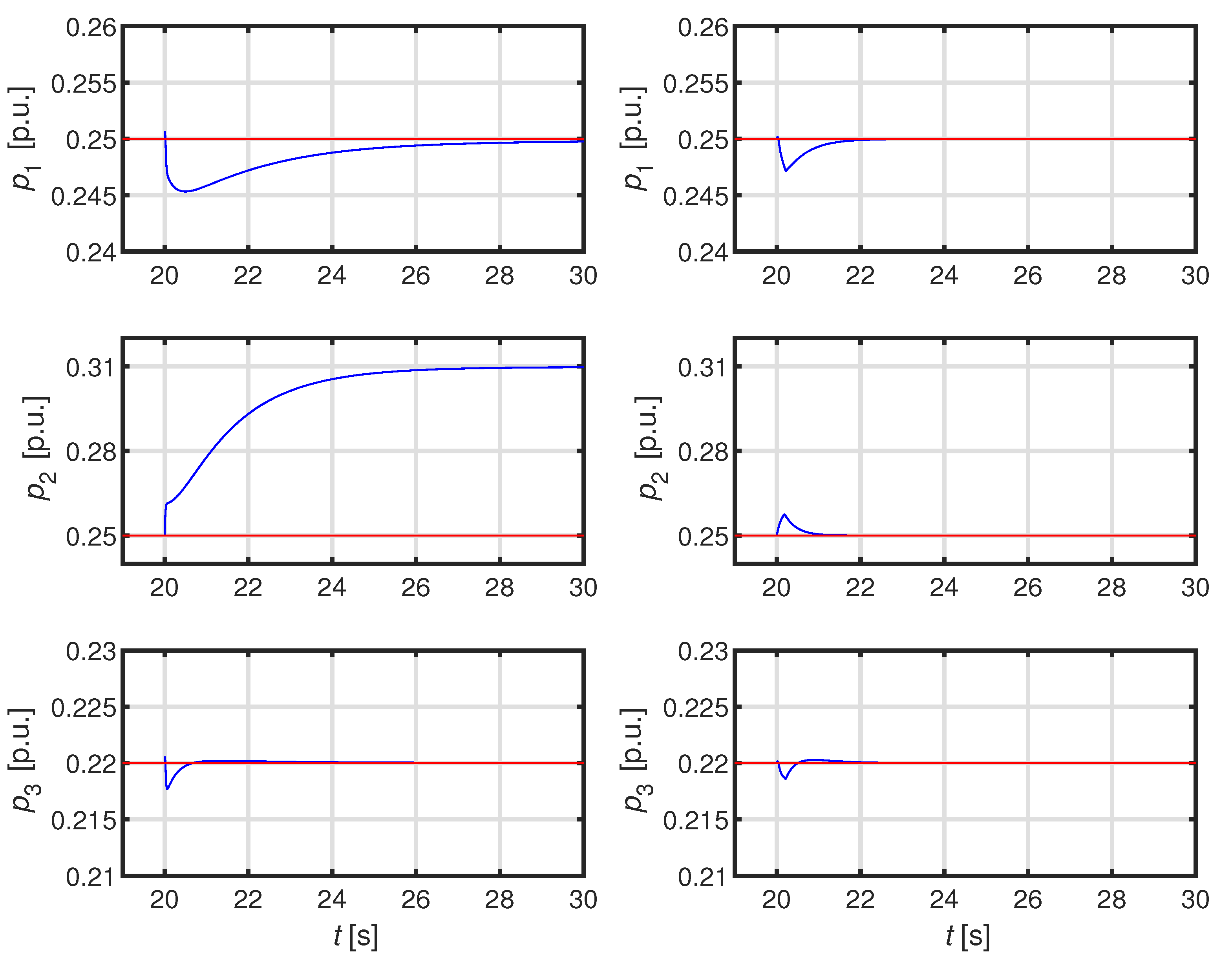
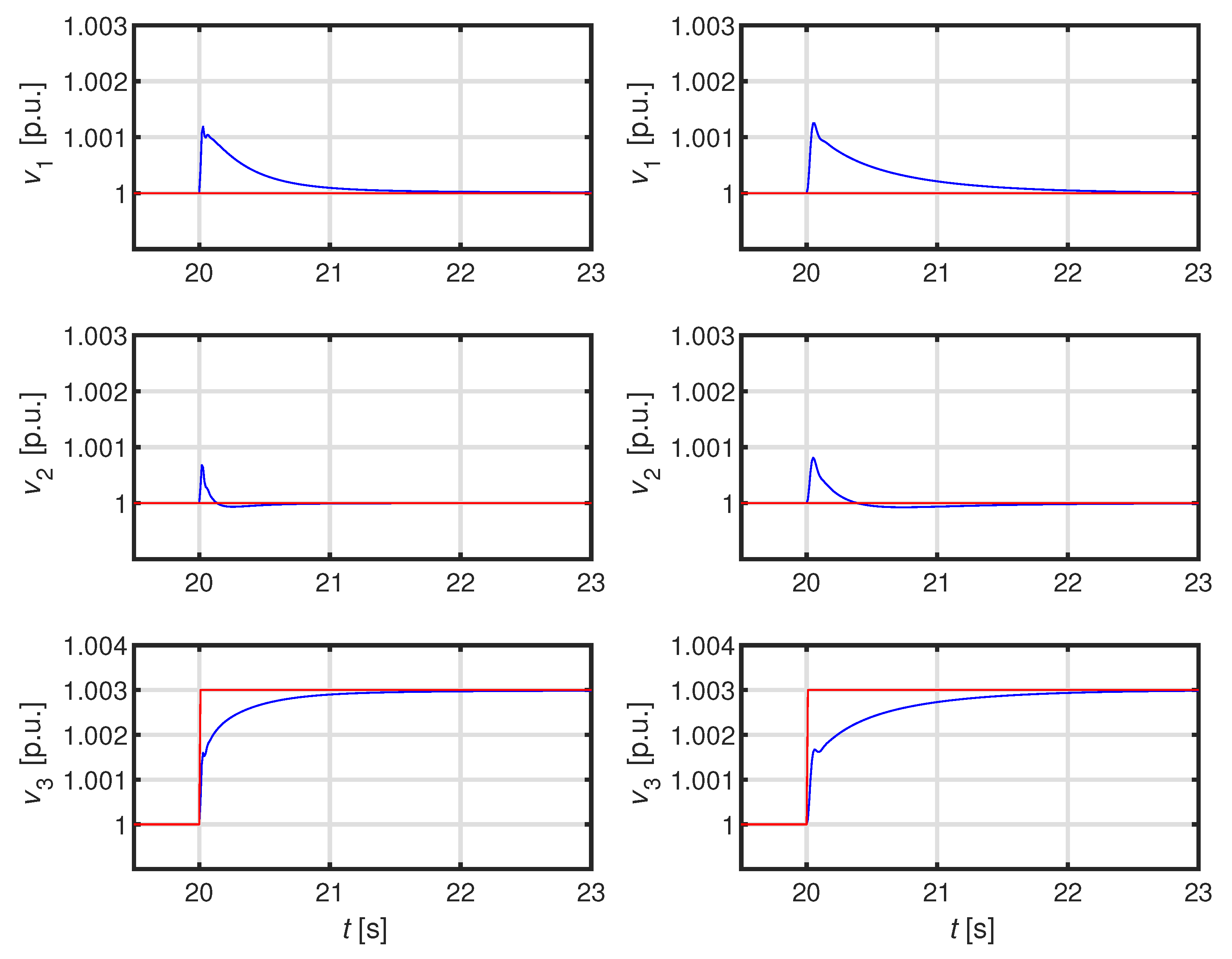
4.1. First Test System: ADN with One Feeder and Three DERs
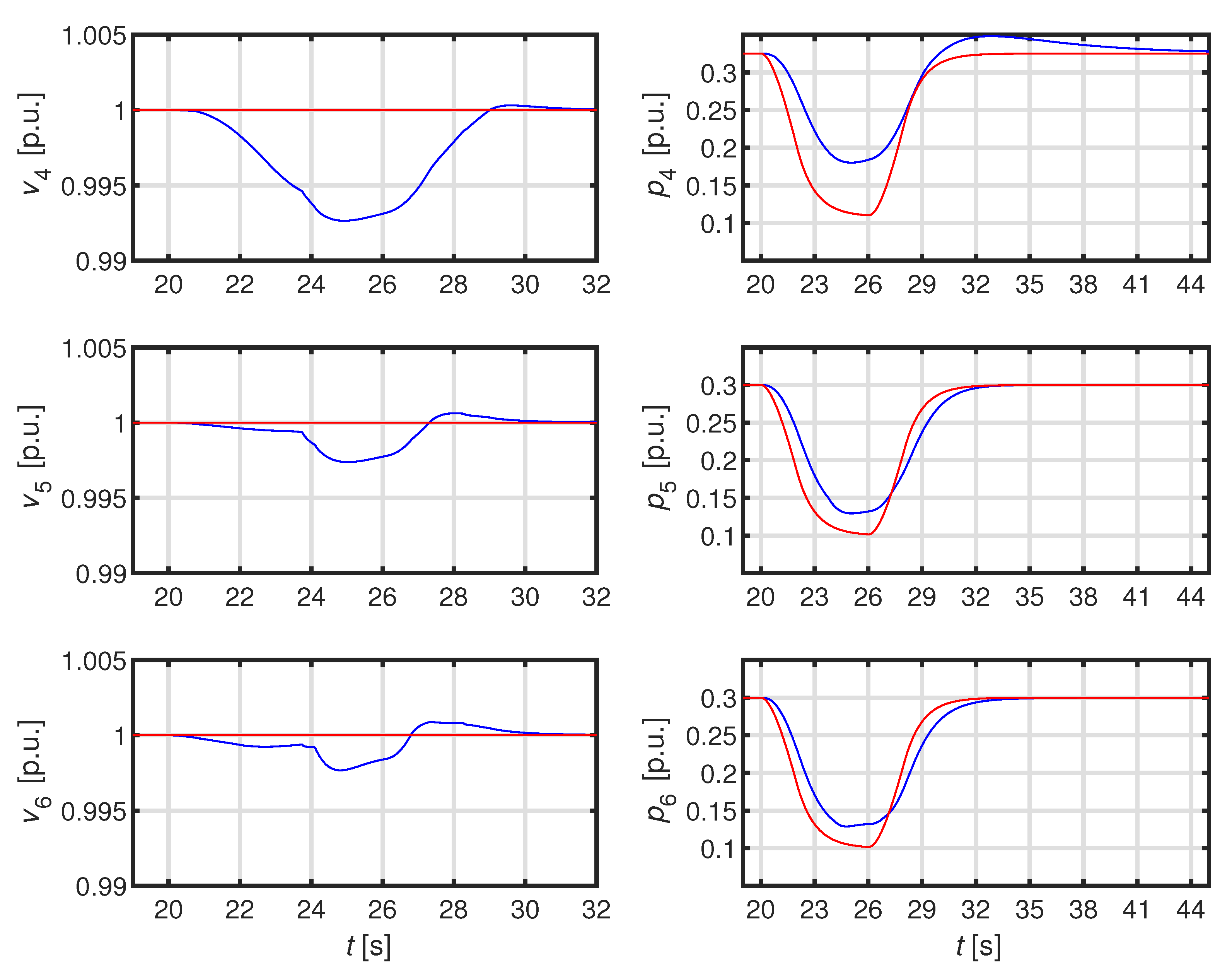
4.2. Second Test System: ADN with Three Feeders and Nine DERs
4.2.1. Simulation 1: Large Load Connection
4.2.2. Simulation 2: Time-Varying Irradiation
4.2.3. Simulation 3: Variation in the Substation Transformer Ratio
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ADN | Active Distribution Network |
| APC | Active Power Curtailment |
| AS | Ancillary Service |
| BESS | Battery Energy Storage System |
| DER | Distributed Energy Resource |
| DG | Distributed Generation |
| DSO | Distribution System Operator |
| EOTF | Effective Open-Loop Transfer Function |
| EV | Electric Vehicle |
| IMC | Internal Model Control |
| MIMO | Multi-Input Multi-Output |
| PI | Proportional Integral |
| RES | Renewable Energy Source |
| RGA | Relative Gain Matrix |
| TITO | Two-Input Two-Output |
| VSC | Voltage Source Converter |
References
- Olivier, F.; Aristidou, P.; Ernst, D.; Cutsem, T.V. Active Management of Low-Voltage Networks for Mitigating Overvoltages Due to Photovoltaic Units. IEEE Trans. Smart Grid 2016, 7, 926–936. [Google Scholar] [CrossRef]
- Ceylan, O.; Paudyal, S.; Pisica, I. Nodal Sensitivity-Based Smart Inverter Control for Voltage Regulation in Distribution Feeder. IEEE J. Photovolt. 2021, 11, 1105–1113. [Google Scholar] [CrossRef]
- Almasalma, H.; Deconinck, G. Robust Policy-Based Distributed Voltage Control Provided by PV-Battery Inverters. IEEE Access 2020, 8, 124939–124948. [Google Scholar] [CrossRef]
- Zhang, Z.; Dou, C.; Yue, D.; Zhang, Y.; Zhang, B.; Li, B. Regional Coordinated Voltage Regulation in Active Distribution Networks with PV-BESS. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 596–600. [Google Scholar] [CrossRef]
- Gorbachev, S.; Mani, A.; Li, L.; Li, L.; Zhang, Y. Distributed Energy Resources Based Two-Layer Delay-Independent Voltage Coordinated Control in Active Distribution Network. IEEE Trans. Ind. Inform. 2024, 20, 1220–1230. [Google Scholar] [CrossRef]
- Gush, T.; Kim, C.H.; Admasie, S.; Kim, J.S.; Song, J.S. Optimal Smart Inverter Control for PV and BESS to Improve PV Hosting Capacity of Distribution Networks Using Slime Mould Algorithm. IEEE Access 2021, 9, 52164–52176. [Google Scholar] [CrossRef]
- Cheng, Z.; Wang, L.; Zeng, S.; Su, C.; Zhang, R.; Zhou, W. Partition-Global Dual-Layer Collaborative Voltage Control Strategy for Active Distribution Network with High Proportion of Renewable Energy. IEEE Access 2024, 12, 22546–22556. [Google Scholar] [CrossRef]
- Zhang, Z.; Mishra, Y.; Dou, C.; Yue, D.; Zhang, B.; Tian, Y.C. Steady-State Voltage Regulation with Reduced Photovoltaic Power Curtailment. IEEE J. Photovolt. 2020, 10, 1853–1863. [Google Scholar] [CrossRef]
- Xu, S.; Xue, Y.; Chang, L. Review of Power System Support Functions for Inverter-Based Distributed Energy Resources- Standards, Control Algorithms, and Trends. IEEE Open J. Power Electron. 2021, 2, 88–105. [Google Scholar] [CrossRef]
- Oureilidis, K.; Malamaki, K.N.; Gallos, K.; Tsitsimelis, A.; Dikaiakos, C.; Gkavanoudis, S.; Cvetkovic, M.; Mauricio, J.M.; Maza Ortega, J.M.; Ramos, J.L.M.; et al. Ancillary Services Market Design in Distribution Networks: Review and Identification of Barriers. Energies 2020, 13, 917. [Google Scholar] [CrossRef]
- do Prado, J.C.; Qiao, W.; Qu, L.; Agüero, J.R. The Next-Generation Retail Electricity Market in the Context of Distributed Energy Resources: Vision and Integrating Framework. Energies 2019, 12, 491. [Google Scholar] [CrossRef]
- Sun, Y.; Zhao, Z.; Yang, M.; Jia, D.; Pei, W.; Xu, B. Overview of energy storage in renewable energy power fluctuation mitigation. CSEE J. Power Energy Syst. 2020, 6, 160–173. [Google Scholar] [CrossRef]
- Gui, E.M.; MacGill, I. Typology of future clean energy communities: An exploratory structure, opportunities, and challenges. Energy Res. Soc. Sci. 2018, 35, 94–107. [Google Scholar] [CrossRef]
- Barr, J.; Majumder, R. Integration of Distributed Generation in the Volt/VAR Management System for Active Distribution Networks. IEEE Trans. Smart Grids 2015, 6, 576–586. [Google Scholar] [CrossRef]
- Eggli, A.; Karagiannopoulos, S.; Bolognani, S.; Hug, G. Stability analysis and design of local control schemes in active distribution grids. IEEE Trans. Power Syst. 2020, 36, 1900–1909. [Google Scholar] [CrossRef]
- Kazeminejad, M.; Banejad, M.; Annakkage, U.; Hosseinzadeh, N. The effect of high penetration level of distributed generation sources on voltage stability analysis in unbalanced distribution systems considering load model. J. Oper. Autom. Power Eng. 2019, 7, 196–205. [Google Scholar]
- Ranamuka, D.; Agalgaonkar, A.; Muttaqu, K. Online Voltage Control in Distribution Systems with Multiple Voltage Regulating Devices. IEEE Trans. Sustain. Energy 2014, 5, 617–628. [Google Scholar] [CrossRef]
- Cavraro, G.; Carli, R. Local and distributed voltage control algorithms in distribution networks. IEEE Trans. Power Syst. 2017, 33, 1420–1430. [Google Scholar] [CrossRef]
- Nawaz, F.; Pashajavid, E.; Fan, Y.; Batool, M. A Comprehensive Review of the State-of-the-Art of Secondary Control Strategies for Microgrids. IEEE Access 2023, 11, 102444–102459. [Google Scholar] [CrossRef]
- Bedawy, A.; Yorino, N.; Mahmoud, K.; Lehtonen, M. An Effective Coordination Strategy for Voltage Regulation in Distribution System Containing High Intermittent Photovoltaic Penetrations. IEEE Access 2021, 9, 117404–117414. [Google Scholar] [CrossRef]
- Duan, J.; Wang, C.; Xu, H.; Liu, W.; Xue, Y.; Peng, J.C.; Jiang, H. Distributed control of inverter-interfaced microgrids based on consensus algorithm with improved transient performance. IEEE Trans. Smart Grid 2019, 10, 1303–1312. [Google Scholar] [CrossRef]
- Fu, A.; Cvetković, M.; Palensky, P. Distributed Cooperation for Voltage Regulation in Future Distribution Networks. IEEE Trans. Smart Grid 2022, 13, 4483–4493. [Google Scholar] [CrossRef]
- Kryonidis, G.; Kontis, E. A Coordinated Droop Control Strategy for Overvoltage Mitigation in Active Distribution Networks. IEEE Trans. Smart Grid 2018, 9, 5260–5270. [Google Scholar] [CrossRef]
- Bolognani, S.; Carli, R.; Cavraro, G.; Zampieri, S. On the need for communication for voltage regulation of power distribution grids. IEEE Trans. Control Netw. Syst. 2019, 6, 1111–1123. [Google Scholar] [CrossRef]
- Reno, M.J.; Quiroz, J.E.; Lavrova, O.; Byrne, R.H. Evaluation of communication requirements for voltage regulation control with advanced inverters. In Proceedings of the 2016 North American Power Symposium (NAPS), Denver, CO, USA, 18–20 September 2016; pp. 1–6. [Google Scholar]
- Wu, X.; Deng, S.; Yuan, W.; Mei, S. A Robust Distributed Secondary Control of Microgrids Considering Communication Failures. In Proceedings of the 2022 4th International Conference on Power and Energy Technology (ICPET), Xining, China, 28–31 July 2022; pp. 395–400. [Google Scholar]
- Sadnan, R.; Dubey, A. Distributed optimization using reduced network equivalents for radial power distribution systems. IEEE Trans. Power Syst. 2021, 36, 3645–3656. [Google Scholar] [CrossRef]
- Antoniadu-Plytaria, K.; Kouveliotis-Lysikatos, I.; Georgilakis, P.; Hatziargyriou, N. Distributed and Decentralized Voltage Control of smart Distribution Networks: Models, Methods, and Future Research. IEEE Trans. Smart Grid 2017, 8, 2999–3008. [Google Scholar] [CrossRef]
- Vu, T.; Lee, M. Independent design of multi-loop PI/PID controllers for interacting multivariable processes. J. Process Control 2010, 20, 922–933. [Google Scholar] [CrossRef]
- Vu, T.N.L.; Lee, J.; Lee, M. Design of multi-loop PID controllers based on the generalized IMC-PID method with Mp criterion. Int. J. Control Autom. Syst. 2007, 5, 212. [Google Scholar]
- Fusco, G.; Russo, M.; Casolino, G.M. Voltage and active power local PI control of distributed energy resources based on the effective transfer function method. Int. J. Electr. Power Energy Syst. 2023, 152, 1–15. [Google Scholar] [CrossRef]
- Fusco, G.; Russo, M. A Decentralized Approach for Voltage Control by Multiple Distributed Energy Resources. IEEE Trans. Smart Grid 2021, 12, 3115–3127. [Google Scholar] [CrossRef]
- Albertos, P.; Antonio, S. Multivariable Control Systems: An Engineering Approach; Springer: London, UK, 2004. [Google Scholar]
- Manitoba HVDC Research Centre. PSCAD User’s Guide; Manitoba Hydro International Ltd.: Winnipeg, MB, Canada, 2018. [Google Scholar]



| From Node | To Node | R (p.u.) | X (p.u.) | Load (kW–kVAr) |
|---|---|---|---|---|
| 2 | 3 | 0.0105 | 0.0025 | 3.11–1.56 |
| 3 | 4 | 0.0059 | 0.0014 | 2.05–1.02 |
| 4 | 5 | 0.0114 | 0.0027 | 2.05–1.02 |
| 5 | 6 | 0.0079 | 0.0011 | 7.97–3.96 |
| 6 | 7 | 0.0095 | 0.0014 | 2.05–1.02 |
| 7 | 8 | 0.0053 | 0.0007 | 3.11–1.56 |
| 8 | 9 | 0.0040 | 0.0006 | 3.11–1.56 |
| 4 | 10 | 0.0106 | 0.0015 | 3.11–1.56 |
| 10 | 11 | 0.0121 | 0.0017 | 3.11–1.56 |
| 11 | 12 | 0.0040 | 0.0006 | 3.11–1.56 |
| 7 | 13 | 0.0089 | 0.0011 | 3.11–1.56 |
| 13 | 14 | 0.0037 | 0.0002 | 3.11–1.56 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fusco, G.; Russo, M. Local DER Control with Reduced Loop Interactions in Active Distribution Networks. Energies 2024, 17, 1991. https://doi.org/10.3390/en17091991
Fusco G, Russo M. Local DER Control with Reduced Loop Interactions in Active Distribution Networks. Energies. 2024; 17(9):1991. https://doi.org/10.3390/en17091991
Chicago/Turabian StyleFusco, Giuseppe, and Mario Russo. 2024. "Local DER Control with Reduced Loop Interactions in Active Distribution Networks" Energies 17, no. 9: 1991. https://doi.org/10.3390/en17091991
APA StyleFusco, G., & Russo, M. (2024). Local DER Control with Reduced Loop Interactions in Active Distribution Networks. Energies, 17(9), 1991. https://doi.org/10.3390/en17091991







