Abstract
Modern low-voltage distribution lines, especially those linked with renewable energy sources, face technical hurdles like unaccounted and illegal electricity use, increased power losses, voltage control issues, and overheating. Tackling these challenges effectively requires continuously monitoring power flows and identifying problematic network spots. This study introduces a method involving ongoing energy flow monitoring from distribution transformers and other sources to end-users through auxiliary facilities. The algorithm seamlessly integrates with consumers’ existing smart power meters and supporting infrastructure, eliminating the need for extra equipment or data. Deployed in several distribution networks totaling about 40 GWh/year over two years, this diagnostic system showed promising results. It notably cut total power consumption by around 6% by detecting and mitigating illegal energy waste and addressing technical issues. Additionally, it reduced technical personnel involvement in operational tasks by approximately twentyfold, significantly enhancing network profitability overall.
1. Introduction
The expansion of modern smart grid networks comes with a host of technical challenges, such as asymmetrical phase loads, voltage control issues, and weak connections between infrastructure elements like distribution transformers, auxiliary facilities, and end-users. Additionally, unauthorized and illegal energy consumption poses a significant hurdle to the widespread adoption of smart grids [1,2,3,4]. This problem includes issues like electricity theft, technical errors, and the improper use of network equipment and facilities, as highlighted in previous studies [5,6,7,8,9,10,11,12,13,14,15,16]. Addressing these challenges requires estimating line currents and node voltages, as well as developing mathematical models for the distribution network [5,6,7].
One idea from [5] proposes adding more sensors to every network node and using data from individual consumers’ meters. While this could improve monitoring accuracy, the added cost of these sensors makes this approach less practical.
Another approach discussed in [6,7,8] involves monitoring current and voltage, considering how cable resistance changes with temperature due to factors like current flow and environmental conditions. This method shows promise in boosting diagnostic accuracy.
Original methods using Artificial Intelligence (AI) applications have been documented in [9,10,11,12,13,14,15,16,17,18]. It is worth noting that these methods seem to be some of the most reliable diagnostic approaches, capable of providing more accurate and dependable results. A representative sample of existing AI methods applicable for detecting electricity theft in smart grids can be found in [9,10,11,12]. Presently, all the AI-based methods mentioned can be grouped into two main categories. The methods and algorithms in the first category directly incorporate data from individual consumers [13,14,15,16]. There are several notable advantages to using these AI-based algorithms. Firstly, they offer the flexibility to assess non-standard situations using information from only a subset of consumers. In this case, the methods [13,14] use a special neural recurrent network. The gradient boosting approach and wide deep convolutional neural networks are represented in [15,16], with both providing more accurate identification of illegal consumption locations.
The methods from the second category of AI methods conversely analyze energy profile data from distribution transformers alongside individual consumer data [17,18]. They provide the functional capability to determine the network state without needing precise topology knowledge. However, AI methods do have drawbacks, such as extended adaptation times where the control system needs to accumulate consumer information, potentially leading to erroneous conclusions. Additionally, AI systems can be used to monitor for illegal energy consumption at nodes where power meters are installed.
Another crucial aspect of the monitoring system is its role in providing recommendations to balance individual consumer connections for distributing transformer load evenly. Various solutions addressing this phase identification (PI) challenge are discussed in [19,20,21,22,23,24]. All methods mentioned for monitoring the PI problem rely on statistical analysis of electricity consumption alongside voltage monitoring in network nodes equipped with power meters. However, some systems only utilize information from individual power consumers [19,20,21], while others combine power metering with instantaneous voltage magnitude measurements at energy users’ nodes [22,23,24]. These latter systems require frequent voltage and power metering measurements, leading to increased system memory usage, broader communication line bandwidth requirements, and more complex calculations.
Another important aspect of monitoring involves continuously estimating the state of the grid, which includes measuring and assessing various technical parameters (such as voltages, currents, power flows, and temperatures) at all network nodes and segments. These data are crucial for ensuring the network functions properly and for distinguishing between technical issues beyond human control and problems related to unaccounted or illegal electricity usage. The studies referenced in [25,26,27,28,29] focus on addressing this task.
The existing approaches proposed so far require ongoing and instant monitoring of power consumption and RMS voltages at each metering node, including users and local low-voltage transformers. This requirement poses a significant challenge to widespread adoption due to the complexities involved in the measurement and communication equipment.
In recent years, the control of power flows has been introduced in low-voltage smart-grids as well [30,31]. Monitoring the network for these novel control approaches represents an important task. The principles of monitoring developed in the present work can also be useful for this mission. Novel methods like the electricity market clearing model [32], which incorporates networks with renewable energy facilities, show promising potential in modern and future networks that require monitoring systems. This is similarly applicable to developing energy systems reliant on renewable electricity sources and peer-to-peer energy trading markets, as outlined in [33,34]. The energy monitoring approach proposed in our current work has the potential to enhance the efficiency, quality, and reliability of these networks in both the near and distant future.
In this study, we aim to enhance the accuracy and efficiency of monitoring systems for detecting unaccounted and illegal electricity consumption while also simplifying the supervising equipment. Our goal is to make such systems compatible with existing networks that have specific infrastructure equipped with automatic reading and measurement capabilities.
To achieve this, we propose a method that involves:
- (a)
- Improving the circuitry model of a network based on the predominantly provided approximate grid topology and continuously collecting measurement data using numerical optimization of a specific objective function.
- (b)
- Employing statistical modelling to develop a correlation matrix that describes the correlation coefficients between all power flows within the network.
By implementing these approaches, we anticipate improved precision in identifying unaccounted and illegal electricity consumption while streamlining the monitoring process. This will make the system more accessible and applicable to a wider range of network infrastructures.
The primary contributions of the current paper are as follows:
- The algorithm for the adaptation of the initial grid topology model during network exploitation ensuring a permanent improvement in the exactness of the system parameters evaluation.
- The developed approach for the exact localization of unaccounted and illegal electricity consumption.
- The improved method for the PI determination of all participating grid consumers.
This article is organized as follows: Section 2 represents the method for the estimation of network techno-electrical parameters (currents, voltages in different nodes, resistances, and temperatures of connecting wires) based on power metering only, as well as the localization of illegal users and PI. Section 3 describes the design of the monitoring system. Results of the system exploitation in a real network grid are accumulated and represented in Section 4. Section 4 provides conclusions and a discussion of the proposed monitoring system.
2. Method
In our study, we were looking into spotting irregularities within a network where energy provided by the electrical company was being wasted, either due to technical issues or unauthorized usage. Our main goal was to pinpoint and track down the end-users responsible for this improper usage. Our method mainly involved:
- Estimating various techno-electrical parameters across the network, such as currents, voltages at different nodes, resistances, and wire temperatures.
- Identifying phases for all network loads.
- Locating users who are illegally consuming energy in case of any abnormal situations in the grid.
By focusing on these aspects, we aimed to improve the efficiency of identifying and addressing energy wastage and unauthorized consumption, ultimately benefiting the overall functioning of the network.
The main reason behind developing this approach was the need to depend solely on data from the existing metering infrastructure. This included regular power meters installed in local transformers and at the end loads, along with automatic meter-reading systems (AMRs). It was crucial that all data from these meters be synchronized in time to ensure accurate analytical results. These data were collected through existing telecommunication equipment and then processed using the algorithms we had developed.
2.1. The Detection and Localization of Illegal Energy Consumption
The primary objective of the presented study was to localize unaccounted energy consumption and identify illegal end-users. Detection of unaccounted energy consumption was based on the verification of a balance between what was coming from a local transformer and the sum of all end-users’ currents.
where is the RMS current from a local transformer, is all consumer currents (n = 1, 2, …, N), and t is the number of sequential intervals of a current examination. All currents are considered as average RMS values.
When the value of provided by the current balance (1) is noticeably greater than the total measurement error, it is illegal consumption. As soon as this anomalous state of the energy supply is acknowledged, the location of the unreported electricity use is unavoidably necessary. The localization of such illegal end-users is based on the equation of power balance where the sum of all end-users’ powers and technical losses in connecting infrastructure is subtracted from the energy supplied by the local transformer. If the accuracy of metering equipment ensures the correctness of consumed power, then the estimation of technical losses encounters several challenges.
Firstly, accurate calculation of power losses in the infrastructure is hindered by the difficulties of defining resistances of wires and cables. This circumstance is owing to the uncertainty of the knowledge of the exact topology of end-consumer connections to specific network phases. Typically, grid specifications do not provide this accurate information, adding to the difficulty of the problem. However, certain fundamental topological aspects must be confirmed. In targeted grid operations, verification can be achieved through the implementation of Artificial Intelligence (AI) methods such as neural networks or through the expertise of qualified personnel. An additional hurdle relates to the low resistances of wires and cables, leading to the restricted accuracy of their definitions. But on the other hand, the low resistance of wires causes relatively low losses, many times smaller than illegal losses. As a result, this circumstance simplifies the exact estimation of illegal losses. Both challenges are addressed by representing the entire grid topology using a single-phase equivalent circuit as represented in Figure 1. The topology scheme comprises local transformer T, n number of end-users, power meters, and connecting wires and cables defined by their impedances. End-users are denoted by the letter L, followed by symbols indicating their branching degree from the main line. For instance, loads connected to the main line before the first offshoot are designated by the letter L, followed by an underscore and the number 1, with all subsequent loads in this line ordered sequentially after the minus sign. End-users situated after the first offshoot are identified by two underscore symbols after the minus sign, followed by their sequential order. This principle applies to all users situated at any offshoots.
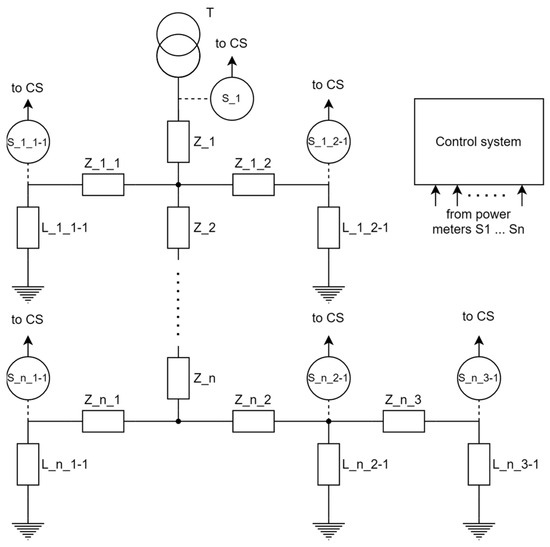
Figure 1.
A typical example of a single-phase simplified network topology.
The same principle of denotation applies to the power meters connected to the corresponding users, with their designation starting with the letter S. Similarly, impedances of connecting wires and cables follow a similar naming convention, commencing with the letter Z.
Given that the simplified scheme may not precisely reflect a network’s topology, inaccuracies can arise when estimating technical losses and unaccounted energy use. To address this, a specialized approach was proposed to mitigate such discrepancies. Any errors stemming from this simplification are alleviated through statistical methods, which involve aggregating multiple energy consumption measurements from all individual end-users.
Expanding on the aforementioned, the described approach can be outlined as reliant on sequential evaluations of the average power consumed by all end-users, with values aggregated by the control system for subsequent decisions. Each observation interval should ideally range from several to tens of minutes. The imbalance, denoted as signifies the residual energy remaining after deducting the total consumed power determined by the metering infrastructure from the average power supplied by the local transformer. This imbalance is calculated as follows:
where represent the average supplied and consumed power, respectively.
It is important to emphasize that every consumer, whether legal or not, contributes to power losses resulting from the current flowing through connecting wires. Regarding legal consumers, the average power losses () within each observation time interval (t) can be calculated using information gathered from all power meters:
where is the sequential number of each grid network segment; L is the number of segments, where each of them represents the line connecting two neighbor nodes; is the average current in the observation time interval t; and is the thermally dependent resistance of the l-network section during time interval t.
Since the control system solely gathers information from power meters, losses (3) can only be estimated for lawful consumption. Currents associated with illicit consumption, not captured by individual power meters, thus do not affect the magnitude of expression (3).
To define power imbalance, indicating unaccounted electricity, we should represent and analyze the average power supplied from the local transformer to the grid (Equation (4)).
The expression (4) includes summarized legal energy use estimated from all power meters, losses of energy in connecting wires, cables, and electrical connections caused both by legal and illegal electricity usage , is average current of the illegal consuming) plus illegal energy consumption . As the result of Equation (4) cannot be obtained at this stage of the calculations, we recommend first estimating the residual imbalance associated with the entire grid network after the transformer. This can be calculated as:
where is the illegal consumption in the t-interval of observation.
The final expression of the residual imbalance (Equation (5)) incorporates both illegal energy use and its corresponding energy losses . Due to the relatively minor magnitude of energy losses , the residual imbalance closely aligns with the unaccounted electricity. Given this consideration, the identification of problematic users can be assessed as follows. Initially, it is crucial to emphasize that all calculations are performed within each observation interval t.
It is assumed that within each observation interval, illegal consumption occurs in only one location. The scenario where two or more unaccounted illegal users are present in the network simultaneously will be examined later. As previously mentioned, the estimated residual imbalance () (5) indicates unaccounted energy usage if it exceeds zero or a minimal value defined by the accuracy of the estimation. To pinpoint the precise location of this unaccounted energy usage, we add the sequentially calculated residual imbalance to the average power of the network nodes, including those related to individual consumers.
After this adjustment, we recalculate the network’s residual imbalance, which will inevitably yield a new value. If the unaccounted energy usage indeed occurs at the selected node, this newly calculated residual imbalance should become zero, as the surplus energy compensates for the waste power. However, practical considerations such as inherent errors in technical measurements may cause deviations in the residual imbalance at problematic points. Hence, the node with the minimal absolute value of residual imbalance appears suspicious and warrants further investigation. The process of identifying these problematic nodes is illustrated in Figure 2a,b.
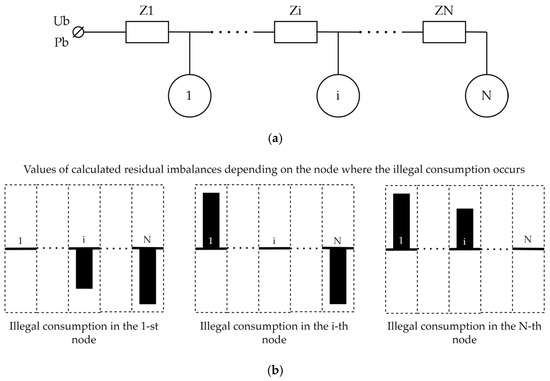
Figure 2.
The identification procedure for the verification of a problem user: (a) An example of a branch connected to one of the network nodes with n serially connected end-users; (b) The results of residual imbalance calculation for the illegal consumption related to the different nodes.
Any technical system implemented for monitoring and identification within the grid is subject to limitations in measurement accuracy, which can potentially lead to erroneous conclusions. To mitigate such instances, we propose employing statistical methods, which involve accumulating calculations and conclusions obtained over multiple observation intervals. Only after multiple repetitive results consistently identify a specific node or end-user should a final solution be reached. Building on the aforementioned approach, the following expression outlines the process for obtaining the final decision:
where T is the number of observation intervals; and n, N are the sequential and total numbers of nodes in the grid.
Based on experimental trials with pilot systems, it was shown that for statistical analysis to be effective, we need a minimum of 30–40 observation intervals. However, to achieve even better accuracy, a larger dataset of around 100 intervals proved to be more reliable. With this larger data set, we managed to pinpoint problematic points with accuracy levels reaching an impressive 92–95%.
When the grid incorporates multiple illegal users, the same algorithm can be applied with modifications to accommodate the broader statistical data. These modifications stem from the realization that there is a non-zero probability that not all illegal loads will consume unaccounted energy simultaneously. It is conceivable that during certain observation intervals, only one of the illegal users engages in electricity theft. Therefore, the solution in this scenario is to expand the statistical data gathered during grid monitoring. As demonstrated by experimental exploitation, this expanded dataset should consist of no fewer than 400–500 observations if there are not more than two or three illegal users.
The next challenge in the task involves assessing network parameters such as voltage, current, and resistance, and estimating wire temperatures.
2.2. Estimation of Network Parameters
It is worth highlighting that when evaluating network parameters, we should focus solely on power metering. A key initial step in understanding the grid involves calculating current magnitudes. As discussed earlier, an important signal of an abnormal situation is the imbalance between supplied and consumed currents in the grid.
Estimating current poses a significant challenge because power meters offer real-time data on active–reactive power but do not measure voltage magnitudes. We can only access network input voltage after the local transformer for these estimations. Hence, we opted for a special artificial procedure to assess current. This method employs a search algorithm to estimate the resistances of all connecting wires and currents. The goal is to find a combination of these parameters that minimizes the deviation between the calculated total network power and its measured counterpart.
The challenge in calculating a summarized network power arises from the need to evaluate all currents flowing through connecting wires and cables, along with their resistances. These resistances vary with alternating temperatures, influenced by the magnitudes of the currents themselves, and are not initially known to the algorithm. Consequently, the conventional approach to solving N non-linear algebraic equations is not feasible.
To address this challenge, a new method for estimating currents and resistances was proposed. This method revolves around the formulation of equations, each incorporating individual load voltages and forming loops extending to the local transformer through connecting resistances. The additional generating facilities presented in the grid are accounted for in the loop equations as consumers with negative powers. In essence, these equations represent N current loops that are combined to derive a solution. Importantly, all circuit currents are inevitably accounted for at least once in these equations.
Given the impracticality of finding a conventional solution, an initial set of probing currents and resistances is repeatedly defined, encompassing those associated with consumers and flowing through connecting wires. The initial resistances of connecting cables and wires are evaluated based on their specifications and the approximate network topology. The initial currents of consumers are estimated using their nominal voltages and powers. Kirchhoff’s current law is applied to calculate identical initial currents for all connecting cables. Subsequently, all actual resistances (obviously different from their initial values) are computed using a specialized algorithm based on a set of network Equation (7) corresponding to a selected grid topology, as represented in Figure 1.
where j is a sequential number and ki is the total quantity of lines segments connecting i-load to the transformer.
In the subsequent step, the obtained resistance values undergo modification based on previously determined currents, considering the temperature of the wires as a function of power losses and environmental temperature. Subsequently, these modified resistances are integrated into Equation (7), and new current values are computed. This iterative process, involving the successive modification of resistances and subsequent estimation of new circuit currents, represents a sequential convergence process culminating in the numeric result providing the required accuracy.
The necessity to incorporate temperature arises from its significant impact on resistances and, consequently, on the accuracy of parameter estimation, which is crucial for the success of the proposed method. Indeed, temperature fluctuations in wires are observable in many Western countries within the range of −40 °C to +90 °C. Under these operating conditions, the resulting resistance deviation (∆R) can vary significantly, up to:
where:
α is the average coefficient of thermal resistance (0.0043 1/°C for aluminum);
is a range of operating temperatures of the wire (−40°…+90°).
The temperature of connecting wires and cables is estimated in accordance with wire specifications, flowing current, and ambient temperature:
where θ0 is the ambient temperature, °C; I is the RMS of a wire’s current; and K is the integral coefficient considering specifications and conditions for wire usage.
Once the set of calculated circuit parameters (currents, resistances) is obtained, it ensures the summarized power. Utilizing this data, the decision algorithm compares the calculated summarized network power with the measured one. Based on this comparison, the algorithm systematically adjusts a set of new initial probing currents in a specialized manner, aiming to minimize the criterion (10). Upon reaching the global minimum deviation, it becomes possible to declare that the set of resistances and currents associated with this minimum accurately represents the real parameters of the network.
This described procedure essentially constitutes a specialized optimization problem employing the Hooke–Jeeves approach [35]. The foundation of this approach lies in the Hooke–Jeeves algorithm, which involves formulating an objective Function (10) and iteratively refining the solution space to converge towards the optimal solution.
where D is the summarized deviation representing the criterion of parameters estimation; and , are the estimated and real measured power of a load number i.
Expression (11) symbolizes the disparities between the estimated and actual power output from the local transformer. Essentially, it quantifies the cumulative differences between measured and calculated power grid flows, with the objective of minimizing these variations throughout the estimation process. The procedural framework for determining current magnitudes is depicted in Figure 3.
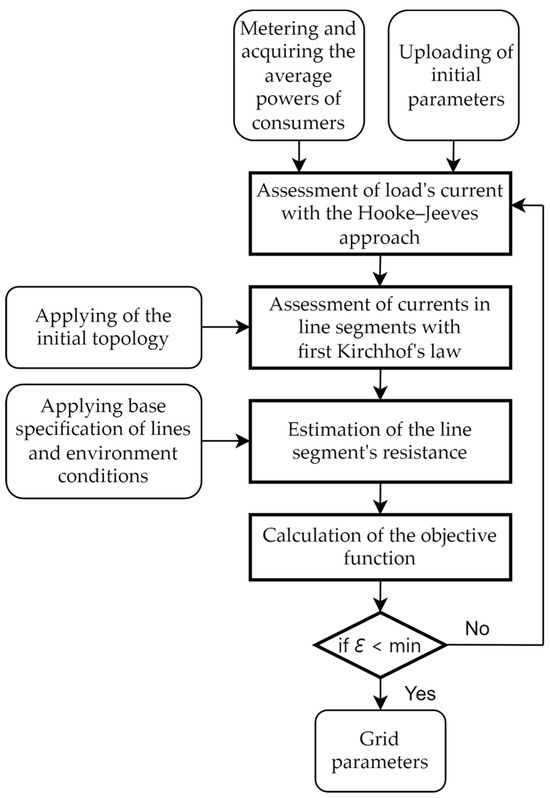
Figure 3.
Block scheme for grid parameters estimation.
The localization of unaccounted users can be significantly enhanced by conducting phase identification for all consumers during network operation. Knowing which phase of the grid a specific load is connected to ensures improved specification of network topology, thereby enabling more accurate estimation of network parameters.
2.3. Phase Identification
Ensuring a balanced distribution of loads across grid phases is crucial for keeping the three-phase network symmetrical. This balance not only helps regulate consumer voltages but also cuts down losses in the neutral conductor. Yet, figuring out which phase of the line (referred to as L1, L2, and L3) each subscriber is linked to poses a challenge because of the absence of prior information.
To address this challenge, the main idea of phase identification involves establishing a correlation between the power consumption of each load phase and those supplied by a local transformer. This correlation can be determined through prolonged monitoring of each load profile (consumed power, energy) and that of the transformer in sequential time intervals. This process generates a series of numerical arrays of instantaneous and synchronized power for every consumer and local transformer phase, which are then analyzed.
Subsequently, matrices of Pearson correlation coefficients [36] between the power of the corresponding transformer phases and the load lines are calculated for each consumer. Separate matrices are calculated for three-phase and single-phase loads. In the case of a three-phase load, a matrix consisting of nine (3 × 3) coefficients is generated, illustrating the dependence between the power of specific load phases and transformer phases. Each row of the matrix represents the correlation coefficient of a load phase with the three transformer phases, allowing for accurate phase identification.
The matrix representing a one-phase load is characterized by three coefficients, highlighting the stochastic relationship between the load and the transformer phases.
Phase identification can initially rely on the highest Pearson correlation coefficient within each row of the matrix. However, this determination should prioritize the most heavily loaded consumer line, considering its highest correlation coefficient as the primary indicator. Subsequently, the phase determination of the remaining terminals of consumer’s lines is carried out by each power meter alone based on the information of phase rotation direction.
Phase verification based on Pearson coefficients offers quick and relatively accurate results. However, the stochastic relationship between transformer and consumer power can lead to false outcomes, and the likelihood of this occurrence cannot be disregarded. To ensure final phase identification reliability, additional verification steps are necessary.
An additional verification method involves confirming energy imbalances in each transformer phase. Phase identification can be deemed correct if the discrepancy ( between the total energy over an extended period in each transformer phase and the combined energies of all consumers connected to the same line is either zero (neglecting power losses in the network) or minimized in practical scenarios.
The mathematical formulation below (Equation (11)) outlines how to assess this discrepancy for each phase (A, B, and C):
where is the total power of the grid phase during time intervals t; n is the N sequential and total load numbers; T is the total number of observation intervals; is the consumer power at input n, in the current arrangement assigned to phase (phase); and n = 1, 2, 3.
It is crucial to note that the number T of observation intervals should be no less than three times the number of consumers (3N).
It is essential to emphasize that phase identification should occur only after excluding all uncontrolled consumption from the grid. The elimination of illegal loads should be conducted using the method detailed in Section 2.1 above.
3. Results
3.1. Confirmation of System Functionality
We created a software solution for the control algorithm, which can be used in both real networks and simulations, using the GOLANG programming language [37]. The goal of this software was to test the approaches we have outlined and simulate real network scenarios, showing the key benefits of the systems we developed. The algorithm and software are part of a cloud-based platform. You can see how it all works in Figure 4, which illustrates the functionality of the software with a block scheme diagram.
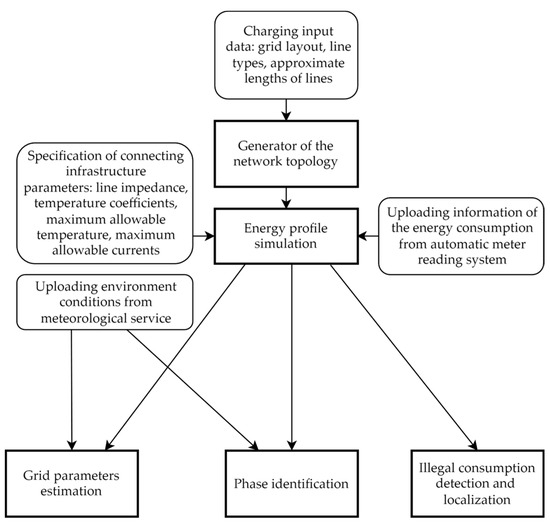
Figure 4.
Block scheme of the monitoring system.
The block scheme encompasses a simulation of a grid topology with the capability for grid modifications. The emulator is tasked with imitating energy flows and the stochastic behavior of consumers within the system.
3.2. Verification on Grid Emulator
As a vital part of the monitoring system, we developed a specialized three-phase grid emulator. Its purpose is to mimic real operations in electrical networks, including AC electrical sources, loads, and connecting infrastructure. Just like the main monitoring system, this emulator runs on GOLANG software and operates in a cloud-based internet environment. You can see how the emulator works in Figure 5, which illustrates its block scheme.
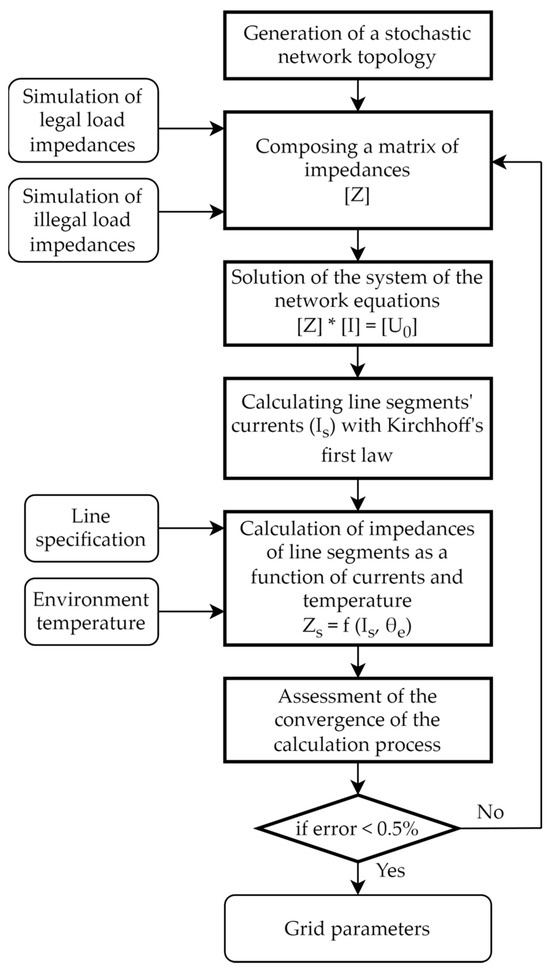
Figure 5.
Block scheme of the grid emulator. Note: the sign “*” in the block scheme designates the matrix multiplication.
The emulator functions based on the principles of AC electrical circuitry and considers the impedance of connecting wires and cables, taking into account their temperature-dependent characteristics.
The main benefits of the emulator are as follows:
- (a)
- Modeling and calculation of network parameters for different situations occurring in a grid.
- (b)
- Confirming the system’s functionality and estimating the quality of its monitoring.
- (c)
- Diagnostic of a metering infrastructure.
The developed emulator was applied for the assessment of the functionality of the developed monitoring approach.
3.3. Results of the Verification on the Emulator
The main goal of verifying the emulator was to check how well our algorithm holds up under different conditions. We wanted to make sure it can achieve accurate results even when there are random energy flows and some measurement errors.
To test this, we had the emulator simulate all sorts of scenarios: temperature changes, different loads, and random measurement errors in electric meters, with a variance of around ±1% introduced by white noise. Temperature fluctuations were modeled to follow a normal distribution, with a variation of ±5%. We also made sure to consider any differences that might occur due to our estimation scheme not being a perfect match for the real grid.
The monitoring system algorithm was tasked with verifying such scenarios and, despite these challenges, providing accurate diagnostic solutions. Approximately one million attempts were generated for virtual networks ranging from 10 to 200 consumers. The distances between adjacent loads varied from around 1 m to 100 m. Various load profiles were considered, encompassing private homes and industrial consumption during winter, spring, summer, and autumn seasons, with average power ranging from approximately 0.1 to 100 kW. Additional generating facilities within the network, such as solar plants and wind turbines, were simulated as negative stochastic consumers. Stochastic illegal loads were introduced at different grid nodes, ranging from one to eight locations.
The results of the monitoring confirmation provided by the emulator are shown in Table 1, Table 2, Table 3 and Table 4.

Table 1.
The estimation error for parameters assessment.

Table 2.
The average number of computing iterations required for phase identification.

Table 3.
The minimum relative consumption power possible for phase identification.

Table 4.
The probability of detecting illegal consumption.
Table 1 illustrates the average grid parameter estimation error relative to the total number of network consumers. The estimation error ranges from 0.5% to 1.5%, gradually decreasing as the number of consumers increases from 10 to 200.
Table 2 demonstrates the growing average number of calculation iterations needed for phase identification of all participating loads as the number of consumers varies from 10 to 200.
Table 3 presents the minimum identifiable load power (related to the nominal local transformer power). It appears that the minimum identifiable load should have increased power as the number of grid consumers increases.
Table 4 illustrates the primary outcome of the monitoring system—the probability of detecting illegal users among other consumers in a grid as the number of consumers in a network increase from 10 to 200. The system’s effectiveness in identifying unaccounted users remains quite substantial across a wide range of network complexities, achieving 88–90%, 87–89%, 82–84%, and 80–82% for grids with 10, 50, 100, and 200 end-consumers, respectively.
3.4. Results of Full-Scale Tests
The real-world testing (certification) of the proposed monitoring system occurred across five networks in various geographic areas. These networks included a total of thirty-seven local transformers, serving around 1600 end-users. Each network was equipped with automatic meter reading systems, allowing for communication and data transfer with a central monitoring facility. The certification process unfolded in the following stages:
- Installation of the monitoring system in a selected network and verification of the measuring and communication infrastructure.
- Preliminary identification of grid topology and measurement equipment to ensure compatibility between elements of the automatic meter reading system and the grid topology.
- Analysis of the network to identify unaccounted consumption, including phase identification of all grid loads, recognition of network technical issues such as overload and overheating of connecting wires and cables, and detection of network nodes with over- and under-voltages.
- Identification of nodes with unaccounted consumption followed by physical and visual verification, with subsequent documentation.
- Implementation of the suggested algorithm: after eliminating unaccounted consumption, instrumental clarification of network parameters and load phase identification, in alignment with the monitoring system’s estimations.
- Evaluation of system efficiency by comparing power losses before and after the implementation of monitoring.
The outcomes of the full-scale deployment of the developed approach are detailed in Table 5. The deployment was executed across various regions:
- Northeastern Europe mid-latitude.
- Eastern Europe mid-latitude.
- Baltic region.
- North Caucasus region.
- Western Siberia region.

Table 5.
The results of monitoring system’s exploitation in different geographic areas.
Table 5.
The results of monitoring system’s exploitation in different geographic areas.
| Region | A | B | C | D | E |
|---|---|---|---|---|---|
| Exploitation period | November 2019 April 2022 | March 2022 June 2022 | November 2022 November 2022 | January 2023 March 2023 | February 2022 February 2022 |
| Duration of observation interval | 24 h | 24 h | 1 h | 24 h | 1 h |
| Total number of transformers in a grid | 9 | 7 | 3 | 16 | 2 |
| Total number of end-users | 408 | 189 | 160 | 356 | 46 |
| Power losses before system monitoring installation | 12% | 7% | 10% | 42% | 13% |
| Power losses due to technical issues | 4% | 2.5% | 3% | 5% | 4% |
| Illegal consumers found and eliminated | 12 | 3 | 1 | 27 | 1 |
| Power loss decrease | 6% | 4.5% | 7% | 37% | 9% |
The results of the full-scale deployment demonstrated promising outcomes for the algorithm and monitoring system developed in the present work.
4. Conclusions
This article presents the utilization of the developed algorithm and monitoring system in low-voltage smart-grid networks to address technical challenges, particularly unaccounted and illegal electricity usage, heightened power losses, inadequate voltage control, and thermal overheating of connecting infrastructure.
Smart-grid networks, especially those integrated with renewable generating facilities, encounter issues such as unaccounted electrical consumption and grid voltage instability, along with various other technical challenges.
An effective solution for the aforementioned issues involves specialized monitoring of consumers with metering infrastructure, employing algorithms designed to pinpoint problematic network nodes. These algorithms focus on identifying abnormal power losses, heating of connecting wires and cables, faulty electrical contacts and terminals, and other potential issues within the grid. The work presented encompasses the following:
- A monitoring algorithm and diagnostic system developed using specialized software, operating within a cloud-based internet environment.
- The method for the estimation of network parameters with only a metering infrastructure.
- A method for localization of the illegal consumption.
- An approach for detecting phase connections of individual consumers.
- A network emulator designed using GOLANG 1.21.9 (Google) software to test monitoring algorithms and systems.
The advantages of the proposed work compared with other approaches are as follows:
- The use of solely the existing metering infrastructure in every consumer installation without the need to provide additional voltage measurements in all network nodes.
- Decreased time for the algorithm’s adaptation to a specific network and simplified requirements for the database regarding consumer energy profiles and for the computing equipment.
- Significant efficiency and accuracy in identifying network electrical parameters and unaccounted consumption, even in grids comprising up to 200 individual consumers.
- Potential hurdles in implementing the proposed monitoring system include the challenge of identifying illegal consumers whose metering devices do not transmit data to the infrastructure or are situated far from measuring nodes. Furthermore, accurately estimating network parameters necessitates continuous access to local transformer voltage information. However, these difficulties will be eliminated in future versions of the monitoring diagnostic systems.
The full-scale deployment of multiple monitoring systems over more than three years in diverse geographic locations has confirmed the high proficiency of the developed diagnostic method. The reduction in power losses amounts to no less than 4.5%, reaching up to 37% in certain locations. Verification of unaccounted electricity consumption can achieve success rates of 90–95%. Additionally, prolonged grid monitoring has the potential to substantially reduce illegal energy use to negligible levels.
It is recommended to continue the development and refinement of monitoring algorithms to further enhance the efficiency of electrical networks, reduce power losses, and eliminate unaccounted energy usage.
Despite being proposed for low-voltage networks exclusively, the algorithms can be adapted to high-voltage distribution and transmission lines as well. Considering the increasing utilization of optimal power flow control and energy market clearing in modern smart grids, it seems important to extend the applicability of the results to these areas. However, for the successful implementation of the suggested monitoring methods, several technical challenges need to be addressed. These include the necessity to account for the absence of a neutral conductor in transmission lines and the requirement to estimate the sources of subsidiary losses.
Author Contributions
Conceptualization, I.A. and M.A.; methodology, I.A.; formal analysis and investigation, I.A.; resources, M.A.; data curation, I.A.; writing—original draft preparation, M.A.; writing—review and editing, I.A. and M.A.; supervision, M.A.; project administration, M.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Xu, Z.; Salehi Shahraki, A.; Rudolph, C. Blockchain-Based Malicious Behaviour Management Scheme for Smart Grids. Smart Cities 2023, 6, 3005–3031. [Google Scholar] [CrossRef]
- Wood, A.J.; Wollenberg, B.F.; Sheblé, G.B. Power Generation, Operation, and Control; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Farmanbar, M.; Parham, K.; Arild, Ø.; Rong, C. A widespread review of smart grids towards smart cities. Energies 2019, 12, 4484. [Google Scholar] [CrossRef]
- Lamnatou, C.; Chemisana, D.; Cristofari, C. Smart grids and smart technologies in relation to photovoltaics, storage systems, buildings and the environment. Renew. Energy 2022, 185, 1376–1391. [Google Scholar] [CrossRef]
- Wabukala, B.M.; Mukisa, N.; Watundu, S.; Bergland, O.; Rudaheranwa, N.; Adaramola, M.S. Impact of household electricity theft and unaffordability on electricity security: A case of Uganda. Energy Policy 2023, 173, 113411. [Google Scholar] [CrossRef]
- McLaughlin, S.; Holbert, B.; Fawaz, A.; Berthier, R.; Zonouz, S. A multi-sensor energy theft detection framework for advanced metering infrastructures. IEEE J. Sel. Areas Commun. 2013, 31, 1319–1330. [Google Scholar] [CrossRef]
- Tariq, M.; Poor, H.V. Electricity theft detection and localization in grid-tied microgrids. IEEE Trans. Smart Grid 2016, 9, 1920–1929. [Google Scholar] [CrossRef]
- Sahoo, S.; Nikovski, D.; Muso, T.; Tsuru, K. Electricity theft detection using smart meter data. In Proceedings of the 2015 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 18–20 February 2015; pp. 1–5. [Google Scholar]
- Jiang, R.; Lu, R.; Wang, Y.; Luo, J.; Shen, C.; Shen, X. Energy-theft detection issues for advanced metering infrastructure in smart grid. Tsinghua Sci. Technol. 2014, 19, 105–120. [Google Scholar] [CrossRef]
- Yan, Z.; Wen, H. Performance analysis of electricity theft detection for the smart grid: An overview. IEEE Trans. Instrum. Meas. 2021, 71, 2502928. [Google Scholar] [CrossRef]
- Villar-Rodriguez, E.; Del Ser, J.; Oregi, I.; Bilbao, M.N.; Gil-Lopez, S. Detection of non-technical losses in smart meter data based on load curve profiling and time series analysis. Energy 2017, 137, 118–128. [Google Scholar] [CrossRef]
- Firoozi, H.; Mashhadi, H.R. Non-technical loss detection in limited-data low-voltage distribution feeders. Int. J. Electr. Power Energy Syst. 2022, 135, 107523. [Google Scholar] [CrossRef]
- Adil, M.; Javaid, N.; Qasim, U.; Ullah, I.; Shafiq, M.; Choi, J.G. LSTM and bat-based RUSBoost approach for electricity theft detection. Appl. Sci. 2020, 10, 4378. [Google Scholar] [CrossRef]
- Hasan, M.N.; Toma, R.N.; Nahid, A.A.; Islam, M.M.; Kim, J.M. Electricity theft detection in smart grid systems: A CNN-LSTM based approach. Energies 2019, 12, 3310. [Google Scholar] [CrossRef]
- Punmiya, R.; Choe, S. Energy theft detection using gradient boosting theft detector with feature engineering-based preprocessing. IEEE Trans. Smart Grid 2019, 10, 2326–2329. [Google Scholar] [CrossRef]
- Zheng, Z.; Yang, Y.; Niu, X.; Dai, H.N.; Zhou, Y. Wide and deep convolutional neural networks for electricity-theft detection to secure smart grids. IEEE Trans. Ind. Inform. 2017, 14, 1606–1615. [Google Scholar] [CrossRef]
- Jindal, A.; Dua, A.; Kaur, K.; Singh, M.; Kumar, N.; Mishra, S. Decision tree and SVM-based data analytics for theft detection in smart grid. IEEE Trans. Ind. Inform. 2016, 12, 1005–1016. [Google Scholar] [CrossRef]
- Jokar, P.; Arianpoo, N.; Leung, V.C. Electricity theft detection in AMI using customers’ consumption patterns. IEEE Trans. Smart Grid 2015, 7, 216–226. [Google Scholar] [CrossRef]
- Jayadev, S.P.; Rajeswaran, A.; Bhatt, N.P.; Pasumarthy, R. A novel approach for phase identification in smart grids using Graph Theory and Principal Component Analysis. In Proceedings of the 2016 American Control Conference (ACC), Boston, MA, USA, 6–8 July 2016; pp. 5026–5031. [Google Scholar]
- Arya, V.; Seetharam, D.; Kalyanaraman, S.; Dontas, K.; Pavlovski, C.; Hoy, S.; Kalagnanam, J.R. Phase identification in smart grids. In Proceedings of the 2011 IEEE International Conference on Smart Grid Communications (SmartGridComm), Brussels, Belgium, 17–20 October 2011; pp. 25–30. [Google Scholar]
- Tang, X.; Milanovic, J.V. Phase identification of LV distribution network with smart meter data. In Proceedings of the 2018 IEEE Power & Energy Society General Meeting (PESGM), Portland, OR, USA, 5–10 August 2018; pp. 1–5. [Google Scholar]
- Wang, W.; Yu, N.; Foggo, B.; Davis, J.; Li, J. Phase identification in electric power distribution systems by clustering of smart meter data. In Proceedings of the 2016 15th IEEE International Conference on Machine Learning and Applications (ICMLA), Anaheim, CA, USA, 18–20 December 2016; pp. 259–265. [Google Scholar]
- Heidari-Akhijahani, A.; Safdarian, A.; Aminifar, F. Phase identification of single-phase customers and pv panels via smart meter data. IEEE Trans. Smart Grid 2021, 12, 4543–4552. [Google Scholar] [CrossRef]
- Hoogsteyn, A.; Vanin, M.; Koirala, A.; Van Hertem, D. Low voltage customer phase identification methods based on smart meter data. Electr. Power Syst. Res. 2022, 212, 108524. [Google Scholar] [CrossRef]
- Grigoras, G.; Neagu, B.C. Smart Meter Data-based three-stage algorithm to calculate power and energy losses in low voltage distribution networks. Energies 2019, 12, 3008. [Google Scholar] [CrossRef]
- Nainar, K.; Iov, F. Smart meter measurement-based state estimation for monitoring of low-voltage distribution grids. Energies 2020, 13, 5367. [Google Scholar] [CrossRef]
- Wellssow, W.H.; Waeresch, D. Identification of topology faults by smart meter data in meshed low voltage grids. In Proceedings of the 2014 Power Systems Computation Conference, Wroclaw, Poland, 18–22 August 2014; pp. 1–7. [Google Scholar]
- Waeresch, D.; Brandalik, R.; Wellssow, W.H.; Jordan, J.; Bischler, R.; Schneider, N. Linear state estimation in low voltage grids based on smart meter data. In Proceedings of the 2015 IEEE Eindhoven PowerTech, Eindhoven, The Netherlands, 29 June–2 July 2015; pp. 1–6. [Google Scholar]
- Abdel-Majeed, A.; Braun, M. Low voltage system state estimation using smart meters. In Proceedings of the 2012 47th International Universities Power Engineering Conference (UPEC), London, UK, 4–7 September 2012; pp. 1–6. [Google Scholar]
- Chen, Z.; Amani, A.M.; Yu, X.; Jalili, M. Control and optimization of power grids using smart meter data: A review. Sensors 2023, 23, 2118. [Google Scholar] [CrossRef] [PubMed]
- Kaur, M.; Narang, N. An integrated optimization technique for optimal power flow solution. Soft Comput. 2020, 24, 10865–10882. [Google Scholar] [CrossRef]
- Xu, G.; Wang, X. Research on the Electricity Market Clearing Model for Renewable Energy. Energies 2022, 15, 9124. [Google Scholar] [CrossRef]
- Xia, Y.; Xu, Q.; Huang, Y.; Du, P. Peer-to-peer energy trading market considering renewable energy uncertainty and participants’ individual preferences. Int. J. Electr. Power Energy Syst. 2023, 148, 108931. [Google Scholar] [CrossRef]
- Feng, C.; Liang, B.; Li, Z.; Liu, W.; Wen, F. Peer-to-peer energy trading under network constraints based on generalized fast dual ascent. IEEE Trans. Smart Grid 2022, 14, 1441–1453. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, J.; Zhou, W.; Peng, X. Hooke-jeeves bat algorithm for systems of nonlinear equations. In Proceedings of the 2017 13th International Conference on Natural Computation, Fuzzy Systems and Knowledge Discovery (ICNC-FSKD), Guilin, China, 29–31 July 2017; pp. 542–547. [Google Scholar]
- Liu, Y.; Mu, Y.; Chen, K.; Li, Y.; Guo, J. Daily activity feature selection in smart homes based on pearson correlation coefficient. Neural Process. Lett. 2020, 51, 1771–1787. [Google Scholar] [CrossRef]
- GOLANG. Open-Source Programming Language. Available online: https://go.dev/ (accessed on 10 January 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).