Solution for Post-Mining Sites: Thermo-Economic Analysis of a Large-Scale Integrated Energy Storage System
Abstract
1. Introduction
2. Materials and Methods
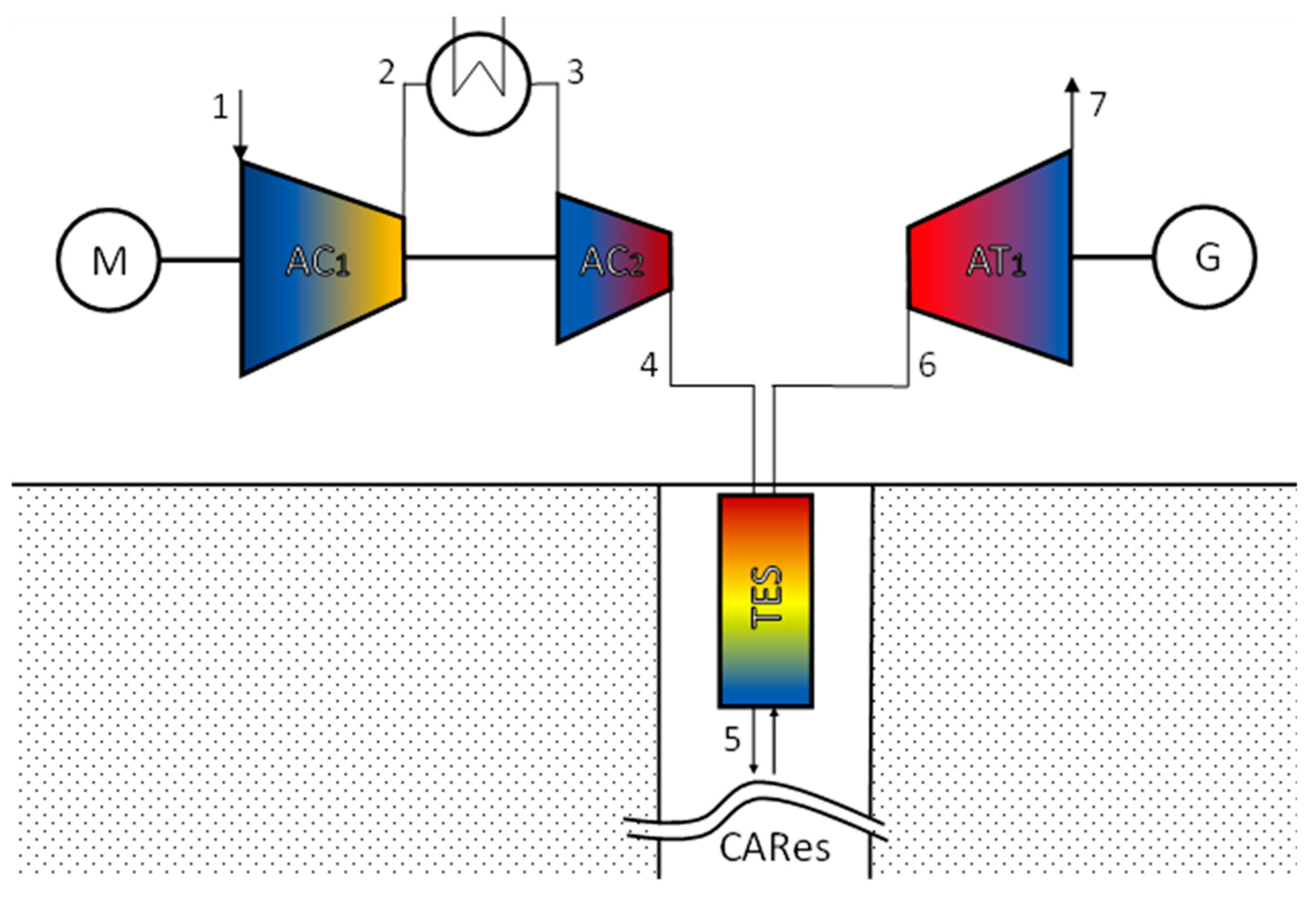
2.1. Adiabatic Compressed Air Energy Storage System Description
2.2. Thermodynamic Model
- A mechanical model that, based on technical standards and preliminary assumptions of system pressure limits, as well as maximum allowable air temperatures, allows determining the minimum recommended parameters of the TES tank [23].
- A thermodynamic model of the compression and expansion system, which uses the dynamic characteristics of these devices that depend on the ratio of pressures and temperatures to nominal parameters [24]. The characteristics allow the determination of instantaneous internal efficiencies. The thermodynamic model, along with the main relationships, is discussed in detail in Bartela et al. [25].
- A dynamic model of the charging, heat storage, and discharge stages of the TES tank, which operates in parallel with the thermodynamic model of the compression and expansion system, allows calculation of air pressure drop, as well as dynamic calculation of air and rock material temperatures inside the heat storage tank. The numerical model also includes calculations of heat loss to the environment, as well as heat accumulation in the tank wall and insulation [26].
- An economic model that allows the selected system operating scenario to be adjusted to the accepted data in the range of time-varying energy prices.
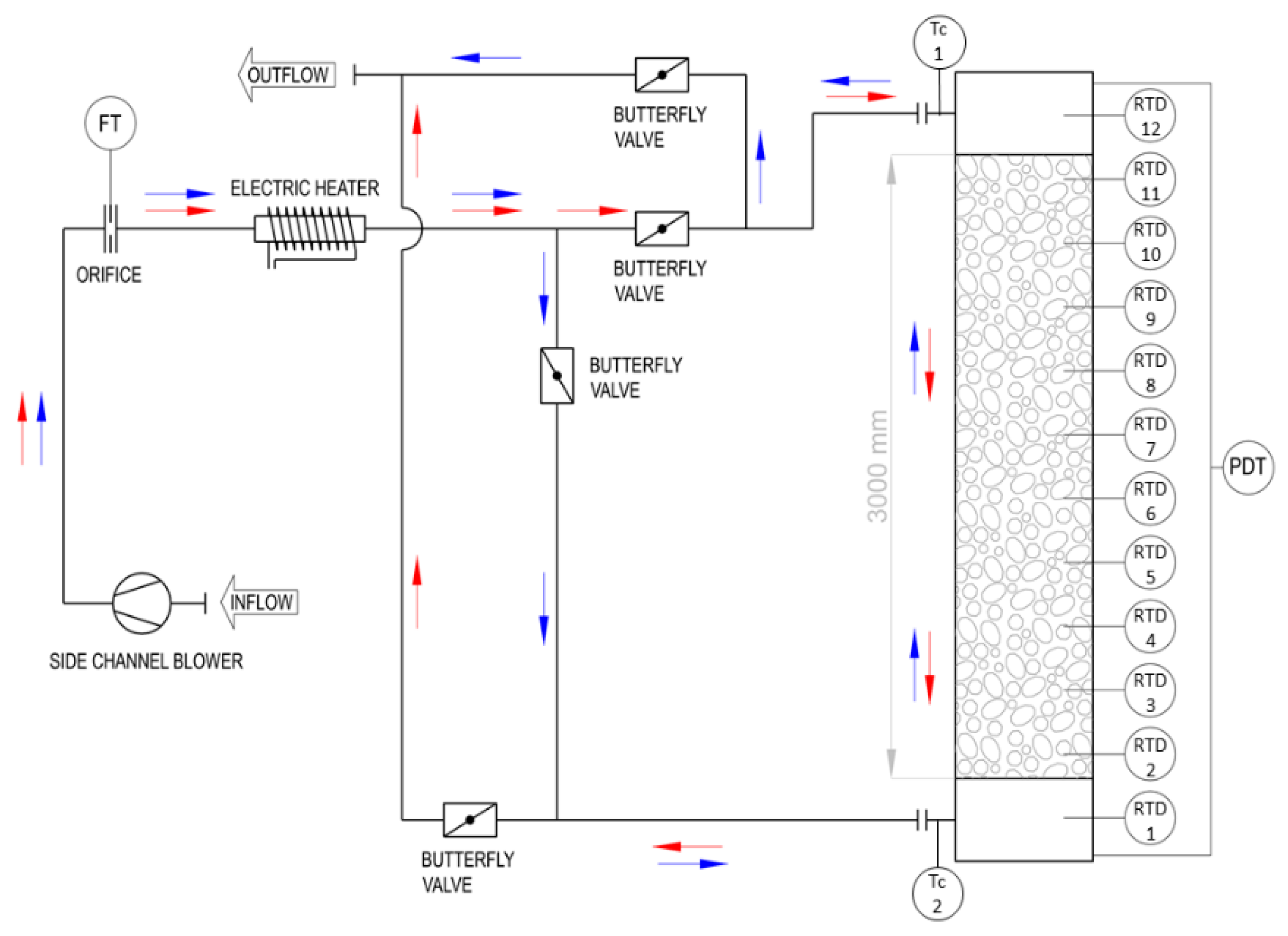
2.3. Laboratory Stand and Thermal Energy Storage Investigation
2.4. Assumption for Analysis
3. Results
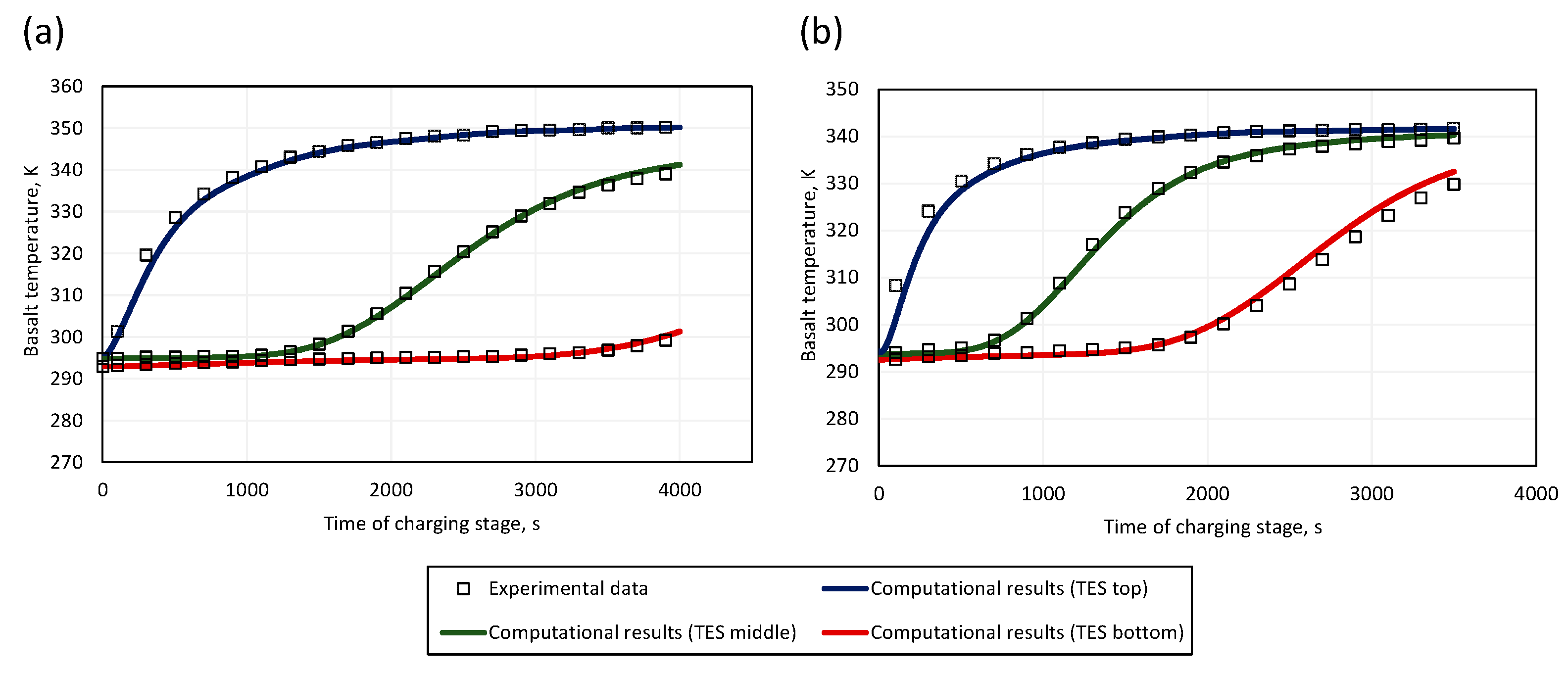
3.1. Numerical Model Validation
3.2. Results of Thermodynamic Analysis
3.3. Economic Assessment of the A-CAES System Using Post-Mine Shaft
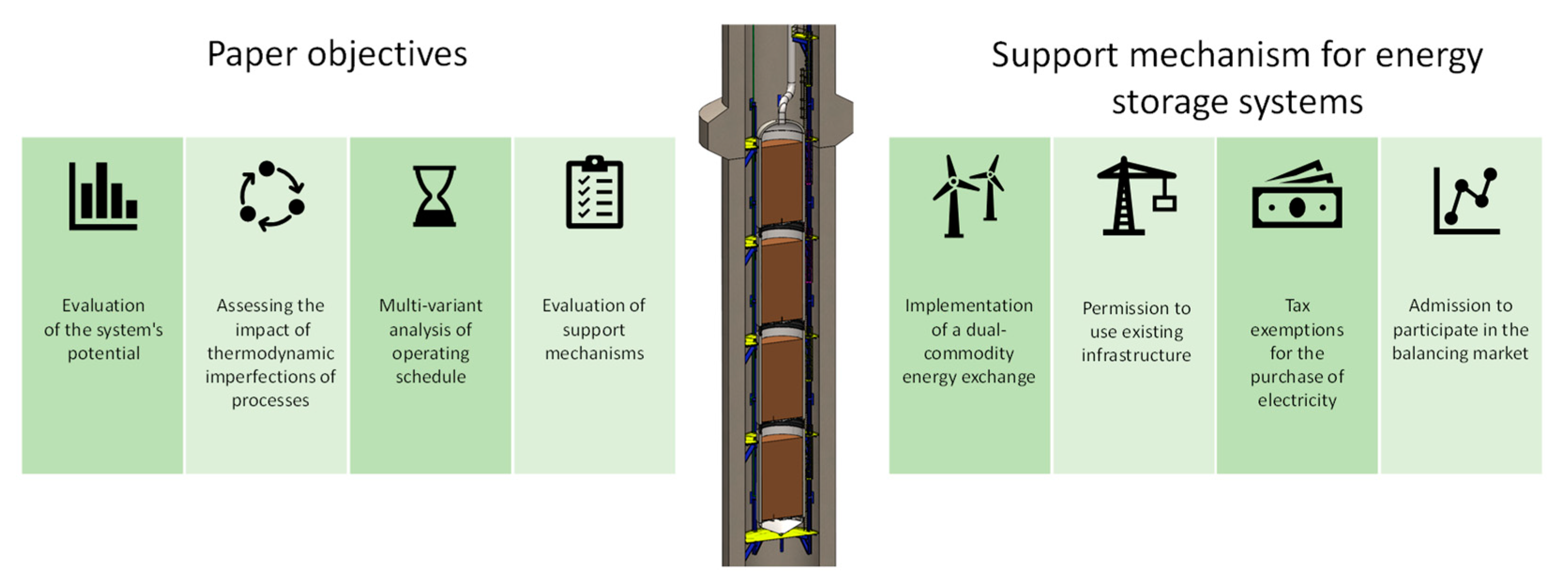
- Permission to use existing infrastructure—regulations are needed to transfer post-mining infrastructure or salt caverns used as fuel storage to implement energy storage systems. There is a need to develop a methodology for determining the safety and operation of these structures. In addition, it is also possible to convert existing conventional systems to increase their flexibility. Such a conversion can include the installation of a TES tank [44,45].
- Admission to participate in the balancing market—allowing energy storage systems into the balancing market for power grid parameters will increase the viability of these systems. In some European countries, storage systems are already allowed to participate in this market. The grid operator determines the time and period of activation of the system (both generation and consumption of energy) thanks to which the differences between demand and generation are reduced.
- Tax exemptions for the purchase of electricity—allow to increase the profitability of investments in energy storage systems and faster payback time. The discount covers the period of energy purchase while the system is charging.
- Implementation of dual-commodity energy exchange—a mechanism that involves rewarding the energy storage system operator both when energy is produced according to grid demand and when the system is ready to energy production. The fact that the energy storage system remains in the system operator’s reserve resources makes it possible to protect the grid during periods of high load variability, planned shutdowns of other systems or failures.
- Implementation of a virtual power plant—a system that allows the optimization and interaction of interconnected energy systems. This enables more efficient planning of operating schedules, as well as optimal management of surplus energy.
4. Conclusions
- The in-house numerical model demonstrates very high accuracy in both the modeling of the Thermal Energy Storage reservoir and the adiabatic Compressed Air Energy Storage system, which has been proven experimentally and comparatively with the analytical results of other studies.
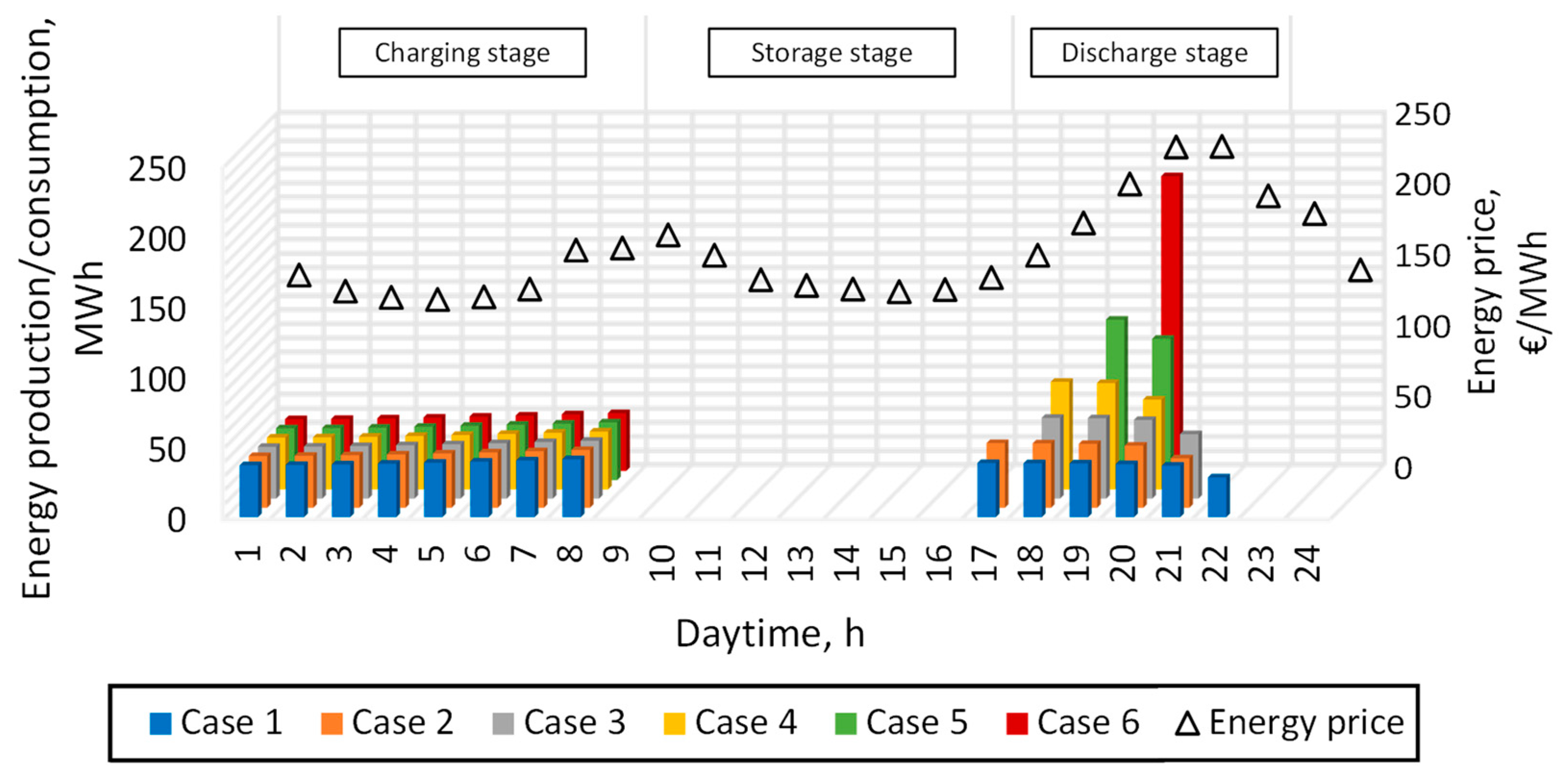
- The maximum round-trip efficiency was 70.32% for the system, whose discharge stage length was the longest among those tested, lasting 6 h. The lowest efficiency was achieved for the shortest discharge stage lasting 1 h and was 67.91%. The length of the energy storage stage was also shown to affect the system’s cycle efficiency. The efficiency of the system is affected not only by heat loss to the environment from the TES tank, but also by internal heat dispersion in the rock material and tank walls.
- Reducing the time of the discharge stage results in an increase in the value of the air pressure drop on the heat storage tank. For the case of a discharge stage lasting 6 h, the value did not exceed 45 kPa. For a one-hour discharge stage, the maximum value of the pressure drop was 1468 kPa. During the discharge stage, a continuous decrease in the temperature of the regenerated air is observed.
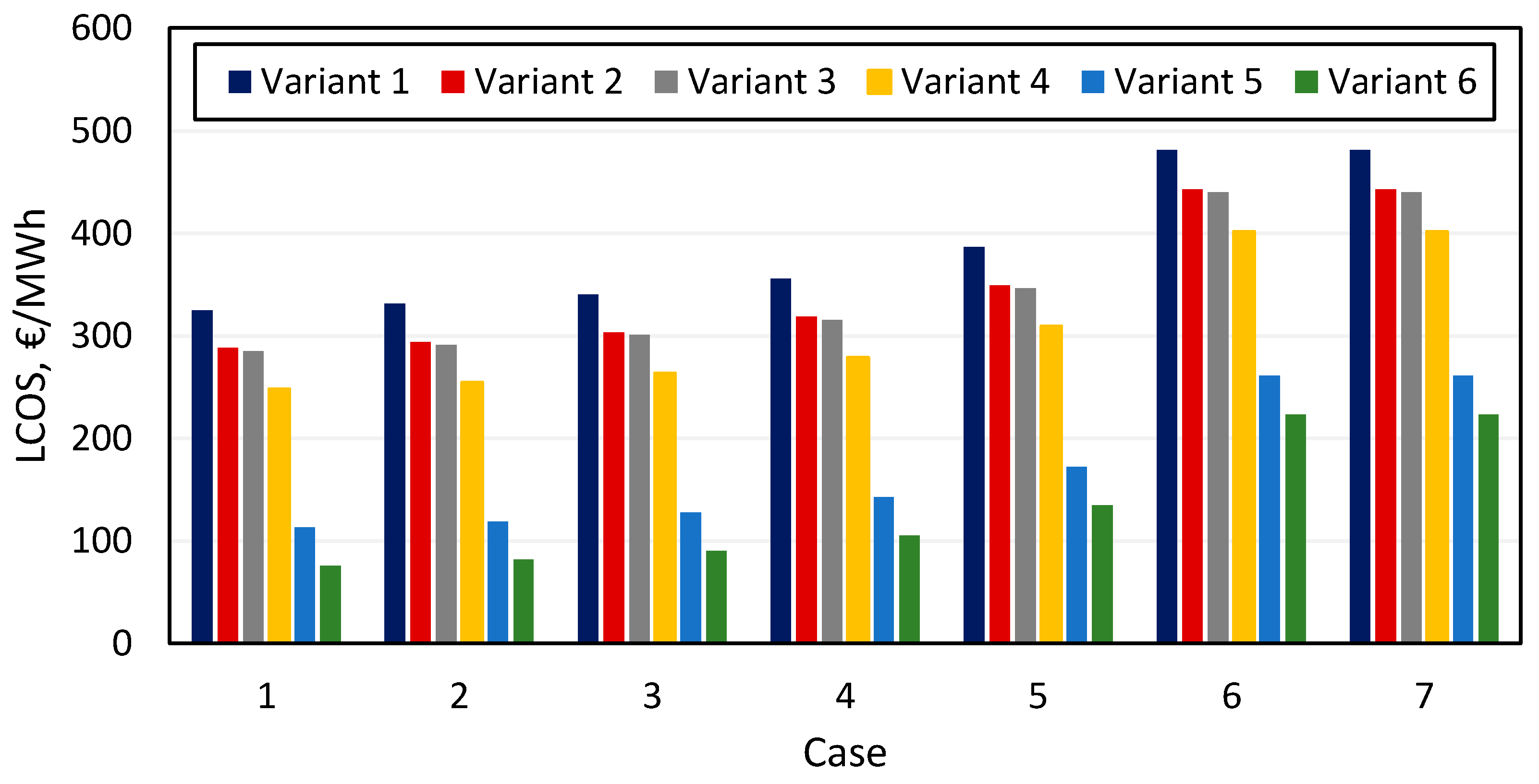
- The economic analysis performed for the least favorable variant of adiabatic CAES system shows the LCOS value equal to 223.24 EUR/MWh. The LCOS value varies significantly depending on the assumptions made for economic calculations. The most favorable LCOS equaled 75.86 EUR/MWh. It was achieved for the case with the smallest investment outlay, which was the result of the longest discharge phase and thus the smallest capacities of the tested expander. In addition, in this case, the electricity was free, reflecting the case of operating the system as an integrating RES with the power grid.
- Legislative support has been shown to be strongly relevant to the viability of an energy storage system. The difference in LCOS for the option without the energy purchase tax was in each case approximately 15 EUR/MWh lower than in the case where the system operator is forced to purchase energy at the full market amount.
- Future studies should focus on setting a roadmap for implementation of large-scale systems to determine the scopes of legislative support. In addition, the presented numerical model can be used to determine the optimal parameters of the TES tank in terms of dimensions, type of storage material, as well as type of walls and thermal insulation.
- Future research should focus on the development of a consistent methodology to determine the potential for large-scale energy storage at a given location of post-mining infrastructure. The methodology should cover not only the local energy storage needs of the grid, but also infrastructure strength aspects such as rocks stability and composition, the condition of the shaft casing and other infrastructure, as well as locally occurring water and gas leaks.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviations | |
| A-CAES | Adiabatic compressed air energy storage |
| CAES | Compressed Air Energy Storage |
| CAPEX | Capital Expenditure |
| EASE | The European Association for Storage of Energy |
| LCOS | Levelized cost of storage |
| MARI | Manually Activated Reserves Initiative |
| mFRR | manual Frequency Restoration Reserve |
| NPV | Net Present Value |
| NPVR | Net Present Value ratio |
| PHS | Pumped Hydro Storage |
| RES | Renewable Energy Sources |
| RMSE | Root mean square error |
| TERRE | Trans European Replacement Reserves Exchange |
| TES | Thermal Energy Storage |
| UDEC | Universal Distinct Element Code |
| Symbols | |
| A | area, m2 |
| AC | air compressor |
| Ac | avoided costs, EUR |
| AT | air expander |
| b | range of measuring device |
| CARes | compressed air reservoir |
| CF | cash flow |
| cp | heat capacity at constant pressure, J/kgK |
| D | diameter, m |
| E | energy, J |
| e | energy price. EUR/MWh |
| h | heat transfer coefficient, W/m2K |
| h | enthalpy, J/kg |
| J | investment cost, EUR |
| k | heat conductivity coefficient, W/mK |
| K | Operating and maintenance costs, EUR |
| L | length, m |
| L | liquidation value, EUR |
| M | motor |
| m | mass flow, kg/s |
| N | TES diameter to particle diameter ratio, - |
| n | number of TES segments, - |
| Nu | Nusselt number, - |
| p | pressure, Pa |
| Pr | Prandtl number, - |
| Re | Reynolds number, - |
| S | Income, EUR |
| t | time, s |
| T | temperature, K |
| v | velocity, m/s |
| V | volume, m3 |
| Greek symbols | |
| ɛ | porosity, - |
| ϴ | uncertainty |
| μ | dynamic viscosity, Pa·s |
| ρ | density, kg/m3 |
| σ | experimental standard deviation |
| Subscript | |
| a | air |
| A | type A uncertainty |
| av | average |
| b | basalt |
| B | type B uncertainty |
| f | fluid |
| fs | fluid-solid |
| fw | fluid-wall |
| i_c | energy consumption/energy price |
| i_p | energy production/energy price |
| max | maximum |
| min | minimum |
| O&M_F | fixed operation and maintenance costs |
| O&Mf | fixed part of operating costs |
| O&Mv | variable part of operating costs |
| p | particle |
| s | solid |
| TES_n | nominal TES volume |
References
- Thomas, M.; DeCillia, B.; Santos, J.B.; Thorlakson, L. Great expectations: Public opinion about energy transition. Energy Policy 2022, 162, 112777. [Google Scholar] [CrossRef]
- Statistics Poland. Available online: https://stat.gov.pl/ (accessed on 1 July 2022).
- Global Economic Data. Available online: https://www.ceicdata.com (accessed on 1 July 2022).
- Renewable Energy Market Update—May 2022. Outlook for 2022 and 2023. Iea Full Raport, May 2022. Available online: https://www.iea.org/reports/renewable-energy-market-update-may-2022 (accessed on 2 September 2022).
- Power Installed and Achievable in National Power Plants. Available online: https://www.pse.pl/dane-systemowe/funkcjonowanie-kse/raporty-roczne-z-funkcjonowania-kse-za-rok/raporty-za-rok-2021 (accessed on 9 September 2022).
- European Association for Storage of Energy. Available online: https://ease-storage.eu/ (accessed on 17 February 2023).
- European Association for the Cooperation of Transmission System Operators for Electricity. Available online: https://www.entsoe.eu/ (accessed on 17 February 2023).
- Courtois, N.; Najafiyazdi, M.; Lotfalian, R.; Boudreault, R.; Picard, M. Analytical expression for the evaluation of multi-stage adiabatic-compressed air energy storage (A-CAES) systems cycle efficiency. Appl. Energy 2021, 288, 116592. [Google Scholar] [CrossRef]
- Malka, L.; Daci, A.; Kuriqi, A.; Bartocci, P.; Rrapaj, E. Energy Storage Benefits Assessment Using Multiple-Choice Criteria: The Case of Drini River Cascade, Albania. Energies 2022, 15, 4032. [Google Scholar] [CrossRef]
- Klaas, A.-K.; Beck, H.-P. A MILP Model for Revenue Optimization of a Compressed Air Energy Storage Plant with Electrolysis. Energies 2021, 14, 6803. [Google Scholar] [CrossRef]
- Polański, K. Influence of the Variability of Compressed Air Temperature on Selected Parameters of the Deformation-Stress State of the Rock Mass Around a CAES Salt Cavern. Energies 2021, 14, 6197. [Google Scholar] [CrossRef]
- Yu, Q.; Tian, L.; Li, X.; Tan, X. Compressed Air Energy Storage Capacity Configuration and Economic Evaluation Considering the Uncertainty of Wind Energy. Energies 2022, 15, 4637. [Google Scholar] [CrossRef]
- Lv, H.; Chen, Y.; Wu, J.; Zhu, Z. Performance of isobaric adiabatic compressed humid air energy storage system with shared equipment and road-return scheme. Appl. Therm. Eng. 2022, 211, 118440. [Google Scholar] [CrossRef]
- Deng, K.; Zhang, K.; Xue, X.; Zhou, H. Design of a New Compressed Air Energy Storage System with Constant Gas Pressure and Temperature for Application in Coal Mine Roadways. Energies 2019, 12, 4188. [Google Scholar] [CrossRef]
- Wojcik, J.; Wang, J. Feasibility study of Combined Cycle Gas Turbine (CCGT) power plant integration with Adiabatic Compressed Air Energy Storage (ACAES). Appl. Energy 2018, 221, 477–489. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, Y.; Zhou, X.; Guo, H.; Zhang, X.; Chen, H. Compressed air energy storage system with variable configuration for accommodating large-amplitude wind power fluctuation. Appl. Energy 2019, 239, 957–968. [Google Scholar] [CrossRef]
- Zunft, S.; Dreissigacker, V.; Bieber, M.; Banach, A.; Klabunde, C.; Warweg, O. Electricity storage with adiabatic compressed air energy storage: Results of the BMWi-project ADELE-ING. In Proceedings of the International ETG Congress, Bonn, Germany, 28–29 November 2017; pp. 28–29. [Google Scholar]
- Bartela, Ł.; Lutyński, M.; Smolnik, G.; Waniczek, S. Underground Compressed Air Storage Installation. European Patent No. 3792467, 8 March 2023. [Google Scholar]
- Ochmann, J.; Bartela, Ł.; Rusin, K.; Jurczyk, M.; Stanek, B.; Rulik, S.; Waniczek, S. Experimental studies of packed-bed Thermal Energy Storage system performance. J. Power Technol. 2022, 102, 37–44. [Google Scholar]
- Waniczek, S.; Ochmann, J.; Bartela, Ł.; Rulik, S.; Lutyński, M.; Brzuszkiewicz, M.; Kołodziej, K.; Smolnik, G.; Jurczyk, M.; Lipka, M. Design and Construction Challenges for a Hybrid Air and Thermal Energy Storage System Built in the Post-Mining Shaft. J. Therm. Sci. 2022, 31, 1302–1317. [Google Scholar] [CrossRef]
- Waniczek, S. System Magazynowania Energii w Sprężonym Powietrzu Sprofilowany na Potrzeby Dużych Jednostek Wytwórczych (Compressed Air Energy Storage System Profiled For The Needs Of Large Generating Units). Ph.D. Thesis, Silesian University of Technology, Gliwice, Poland, 2023. Available online: https://bip.polsl.pl/nadania_dr/sebastian-waniczek/ (accessed on 15 April 2024). (In Polish).
- Lemmon, E.W.; Jacobsen, R.T.; Penoncello, S.G.; Friend, D.G. Thermodynamic Properties of Air and Mixtures of Nitrogen, Argon, and Oxygen from 60 to 2000 K at Pressures to 2000 MPa. J. Phys. Chem. Ref. Data 2000, 29, 331–385. [Google Scholar] [CrossRef]
- PN-EN 1991-4:2008; Oddziaływania na Konstrukcje—Część 4: Silosy i Zbiorniki (Actions on Structures—Part 4: Silos and Tanks). SBD, Sektor Budownictwa i Konstrukcji Budowlanych: Warsaw, Poland, 2008.
- Bloch, H.P.; Soares, C. Turboexpanders and Process Applications; Elsevier Science & Technology: Amsterdam, The Netherlands, 2001. [Google Scholar] [CrossRef]
- Bartela, Ł.; Ochmann, J.; Waniczek, S.; Lutyński, M.; Smolnik, G.; Rulik, S. Evaluation of the energy potential of an adiabatic compressed air energy storage system based on a novel thermal energy storage system in a post mining shaft. J. Energy Storage 2022, 54, 105282. [Google Scholar] [CrossRef]
- Ochmann, J.; Rusin, K.; Bartela, Ł. Comprehensive analytical model of energy and exergy performance of the thermal energy storage. Energy 2023, 283, 128783. [Google Scholar] [CrossRef]
- Ochmann, J.; Rusin, K.; Rulik, S.; Waniczek, S.; Bartela, Ł. Experimental and computational analysis of packed-bed thermal energy storage tank designed for adiabatic compressed air energy storage system. Appl. Therm. Eng. 2022, 213, 118750. [Google Scholar] [CrossRef]
- Wakao, N.; Kaguei, S. Heat and Mass Transfer in Packed Beds; Gordon and Breach Science: Philadelphia, PA, USA, 1982. [Google Scholar]
- Kaviany, M. Principles of Heat Transfer in Porous Media; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Rao, G.S.; Sharma, K.V.; Chary, S.P.; Bakar, R.A.; Rahman, M.M.; Kadirgama, K.; Noor, M.M. Experimental study on heat transfer coefficient and friction factor of Al2O3 nanofluid in a packed bed column. J. Mech. Eng. Sci. 2011, 1, 1–15. [Google Scholar] [CrossRef]
- Specchia, V.; Baldi, G.; Sicardi, S. Heat transfer in backed bed reactors with one phase flow. Chem. Eng. Commun. 1980, 4, 361–380. [Google Scholar] [CrossRef]
- Wehinger, G.D.; Sharf, F. Thermal radiation effects on heat transfer in slender packed-bed reactors: Particle-resolved CFD simulations and 2D modeling. Chem. Eng. Res. Des. 2022, 184, 24–38. [Google Scholar] [CrossRef]
- Ergun, S. Fluid Flow through Packed Column. Chem. Eng. Prog. 1952, 48, 89. [Google Scholar]
- Rusin, K.; Ochmann, J.; Bartela, Ł.; Rulik, S.; Stanek, B.; Jurczyk, M.; Waniczek, S. Influence of geometrical dimensions and particle diameter on exergy performance of packed-bed thermal energy storage. Energy 2022, 260, 125204. [Google Scholar] [CrossRef]
- Bonk, A.; Knoblauch, N.; Braun, M.; Bauer, T.; Schmücker, M. An inexpensive storage material for molten salt based thermocline concepts: Stability of AlferRock in solar salt. Sol. Energy Mater. Sol. Cells 2020, 212, 110578. [Google Scholar] [CrossRef]
- Zunft, S. Adiabatic CAES: The ADELE-ING Project, German Aerospace Center (DLR) SCCER Heat & Electricity Storage Symposium; PSI: Villigen, Switzerland, 2015. [Google Scholar]
- Martin, C.; Bonk, A.; Braun, M.; Odenthal, C.; Bauer, T. Investigation of the long-term stability of quartzite and basalt for a potential use as filler materials for a molten-salt based thermocline storage concept. Sol. Energy 2018, 171, 827–840. [Google Scholar] [CrossRef]
- Roos, P.; Hadelbacher, A. Analytical modeling of advanced adiabatic compressed air energy storage: Literature review and new models. Renew. Sustain. Energy Rev. 2022, 163, 112464. [Google Scholar] [CrossRef]
- Energy Prices in Poland in 2022. Available online: https://tge.pl/ (accessed on 20 February 2023).
- Peters, M.; Timmerhaus, K.; West, R. Plant Design and Economics for Chemical Engineers; Springer Science & Business Media: Basel, Switzerland, 2003. [Google Scholar]
- Bartela, Ł.; Skorek-Osikowska, A.; Dykas, S.; Stanek, B. Thermodynamic and economic assessment of compressed carbon dioxide energy storage systems using a post-mining underground infrastructure. Energy Convers. Manag. 2021, 241, 114297. [Google Scholar] [CrossRef]
- Schmidt, O.; Melchior, S.; Hawkes, A.; Staffell, I. Projecting the Future Levelized Cost of Electricity Storage Technologies. Joule 2019, 3, 81–100. [Google Scholar] [CrossRef]
- The European Commission Recommendation for the Implementation of Support Mechanisms for Energy Storage Systems to Improve Energy Security. Available online: https://energy.ec.europa.eu/topics/research-and-technology/energy-storage/recommendations-energy-storage_en (accessed on 5 May 2023).
- Kosman, W.; Rusin, A. The Application of Molten Salt Energy Storage to Advance the Transition from Coal to Green Energy Power Systems. Energies 2020, 13, 2222. [Google Scholar] [CrossRef]
- Bartela, Ł.; Gładysz, P.; Ochmann, J.; Qvist, S.; Sancho, L.M. Repowering a Coal Power Unit with Small Modular Reactors and Thermal Energy Storage. Energies 2022, 15, 5830. [Google Scholar] [CrossRef]
- Jarosz, J. Prawne i Ekonomiczne Aspekty Procesu likwidacji Kopalń Węgla Kamiennego w Polsce (Legal and Economic Aspects of the Mine Liquidation Process Hard Coal in Poland); Zeszyty Naukowe Instytutu Gospodarki Surowcami Mineralnymi i Energią Polskiej Akademii Nauk 75: Kraków, Poland, 2009. (In Polish) [Google Scholar]
- Mongird, K.; Viswanathan, V.; Alam, J.; Vartanian, C.; Baxter, R. 2020 Grid Energy Storage Technology Cost and Performance Assessment; U.S Department of Energy: Washington, DC, USA, 2020. [Google Scholar]
- Black & Veatch. Cost and Performance Data for Power Generation Technologies; Prepared for the National Renewable Energy Laboratory; Black & Veatch: Overland Park, KS, USA, 2012. [Google Scholar]
- HDR Inc. Update to Energy Storage Screening Study for Integrating Variable Energy Resources within the PacifiCorp System; HDR Inc.: Salt Lake City, UT, USA, 2014. [Google Scholar]
- Jülch, V. Comparison of electricity storage options using levelized cost of storage (LCOS) method. Appl. Energy 2016, 183, 1594–1606. [Google Scholar] [CrossRef]
- The 10-Year Network Development Plan. Available online: https://tyndp.entsoe.eu/ (accessed on 5 May 2023).


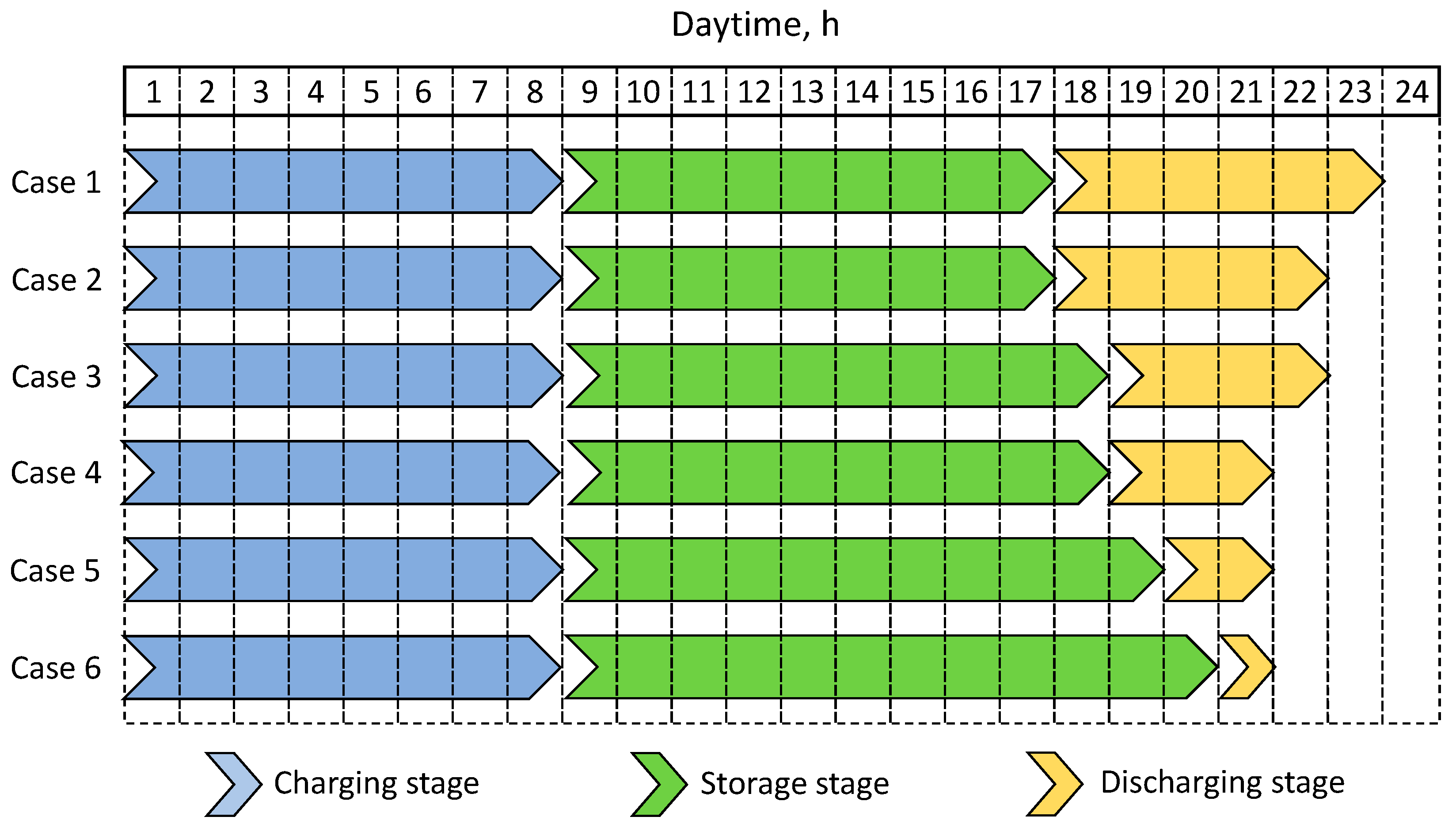
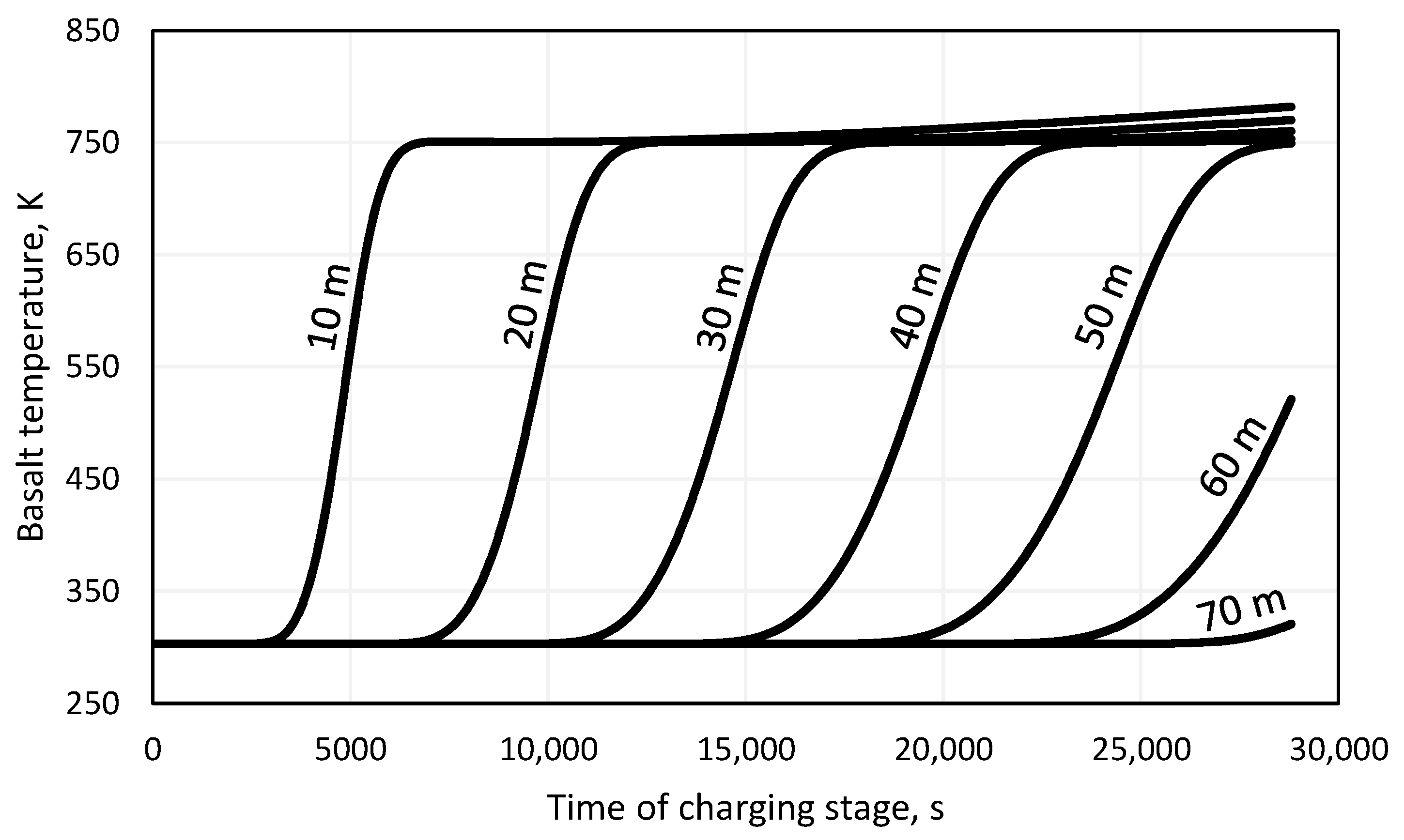
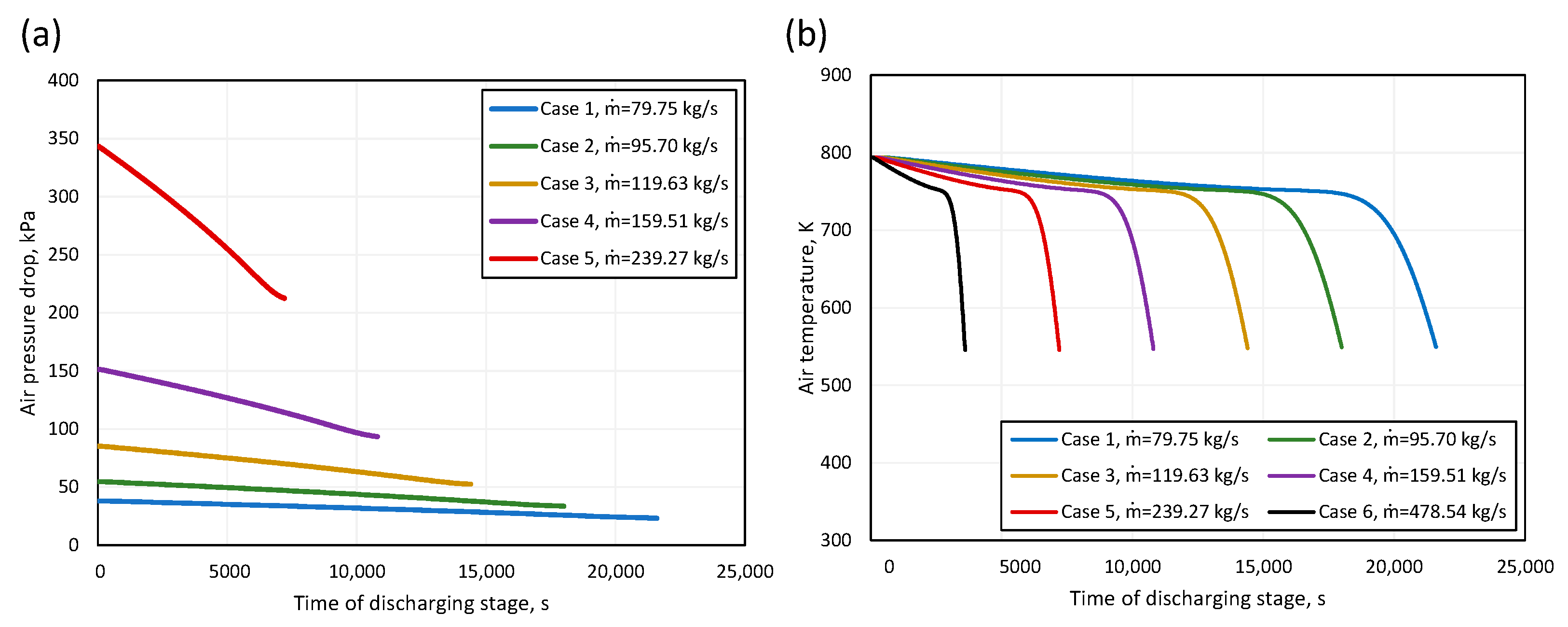
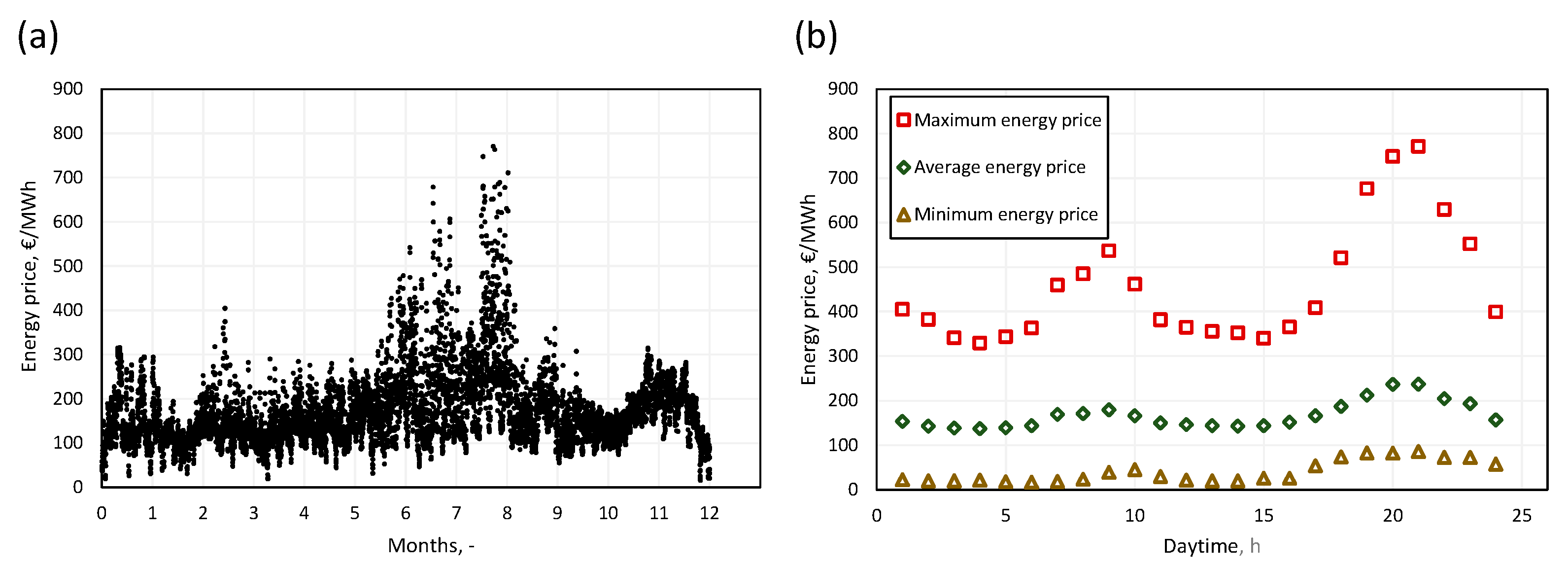
| Item | Value | Unit |
|---|---|---|
| Volume of mine shaft | 63,000 | m3 |
| Ambient temperature | 20 | °C |
| Ambient pressure | 101.325 | kPa |
| Minimum pressure in reservoir | 5600 | kPa |
| Maximum pressure in reservoir | 8000 | kPa |
| Air temperature in reservoir | 30 | °C |
| Maximum temperature of compressed air | 530 | °C |
| Efficiency of compressor sections (nominal) | 0.85 | - |
| Efficiency of turbine sections (nominal) | 0.88 | - |
| Electromechanical efficiency of compressor/turbine | 0.98 | - |
| Compressor time operation (charging stage) | 8 | h |
| TES segment height | 10 | m |
| TES segment diameter | 5 | m |
| Packed bed material | Basalt grit | - |
| Material heat capacity (average) | 920 | J/kgK |
| Material density | 2660 | kg/m3 |
| Packed bed porosity | 0.38 | - |
| Basalt particles diameter | 16 | mm |
| Item | Zunft [33] | Present Paper |
|---|---|---|
| Expander power | ~260 MW | 260.9 MW |
| Compressor power | ~200 MW | 191.8 MW |
| Storage capacity | ~1 GWh | 1.04 GWh |
| Round trip efficiency | ~70% | 70.5% |
| Storage Stage Duration, h | Average Basalt Temperature, K | Maximum Basalt Temperature, K | Minimum Basalt Temperature, K |
|---|---|---|---|
| 0 | 701.10 | 794.91 | 320.89 |
| 9 | 700.72 | 794.18 | 322.23 |
| 10 | 700.68 | 794.12 | 322.31 |
| 11 | 700.64 | 794.05 | 322.38 |
| 12 | 700.58 | 793.97 | 322.45 |
| Energy Consumption, MWh | Energy Production, MWh | Energy Efficiency, % | |
|---|---|---|---|
| Case 1 | 308.19 | 216.73 | 70.32 |
| Case 2 | 308.19 | 216.48 | 70.24 |
| Case 3 | 308.19 | 216.11 | 70.12 |
| Case 4 | 308.19 | 215.55 | 69.94 |
| Case 5 | 308.19 | 214.38 | 69.56 |
| Case 6 | 308.19 | 209.32 | 67.91 |
| Item | Value | Unit |
|---|---|---|
| Installation lifetime | 50 | years |
| Construction time | 3 | years |
| Distribution of capital expenditures | 10/30/60 | % |
| Discount rate | 10 | % |
| Unit indicator of fixed operation and maintenance costs | 18 | Euro/kW per year |
| Unit indicator of variable operation and maintenance costs | 2 | Euro/MWh |
| Mine liquidation cost (2009) | 19.98 | mln Euro |
| Inflation rate | 20 | % |
| Liquidation value | 11.54 | mln Euro |
| Euro to PLN exchange rate | 4.81 | PLN/Euro |
| Dollar to PLN exchange rate | 4.5 | PLN/Dollar |
| Tax | 23 | % |
| Energy Purchase Tax | Shaft Decommissioning Avoidance Cost | Free Electricity Cost | |
|---|---|---|---|
| Variant 1 | ✓ | ✕ | ✕ |
| Variant 2 | ✕ | ✕ | ✕ |
| Variant 3 | ✓ | ✓ | ✕ |
| Variant 4 | ✕ | ✓ | ✕ |
| Variant 5 | - | ✕ | ✓ |
| Variant 6 | - | ✓ | ✓ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ochmann, J.; Jurczyk, M.; Rusin, K.; Rulik, S.; Bartela, Ł.; Uchman, W. Solution for Post-Mining Sites: Thermo-Economic Analysis of a Large-Scale Integrated Energy Storage System. Energies 2024, 17, 1970. https://doi.org/10.3390/en17081970
Ochmann J, Jurczyk M, Rusin K, Rulik S, Bartela Ł, Uchman W. Solution for Post-Mining Sites: Thermo-Economic Analysis of a Large-Scale Integrated Energy Storage System. Energies. 2024; 17(8):1970. https://doi.org/10.3390/en17081970
Chicago/Turabian StyleOchmann, Jakub, Michał Jurczyk, Krzysztof Rusin, Sebastian Rulik, Łukasz Bartela, and Wojciech Uchman. 2024. "Solution for Post-Mining Sites: Thermo-Economic Analysis of a Large-Scale Integrated Energy Storage System" Energies 17, no. 8: 1970. https://doi.org/10.3390/en17081970
APA StyleOchmann, J., Jurczyk, M., Rusin, K., Rulik, S., Bartela, Ł., & Uchman, W. (2024). Solution for Post-Mining Sites: Thermo-Economic Analysis of a Large-Scale Integrated Energy Storage System. Energies, 17(8), 1970. https://doi.org/10.3390/en17081970







