Comparison of Single-Phase Mathematical Models for Solid-State Packed Beds for Thermal Energy Storage
Abstract
1. Introduction
2. Materials and Methods
2.1. Base Model
2.2. Numerical Approach
- Porosity (ε): 0.4.
- Permeability (η): 2.596 × 10−5.
2.3. Mathematical Model
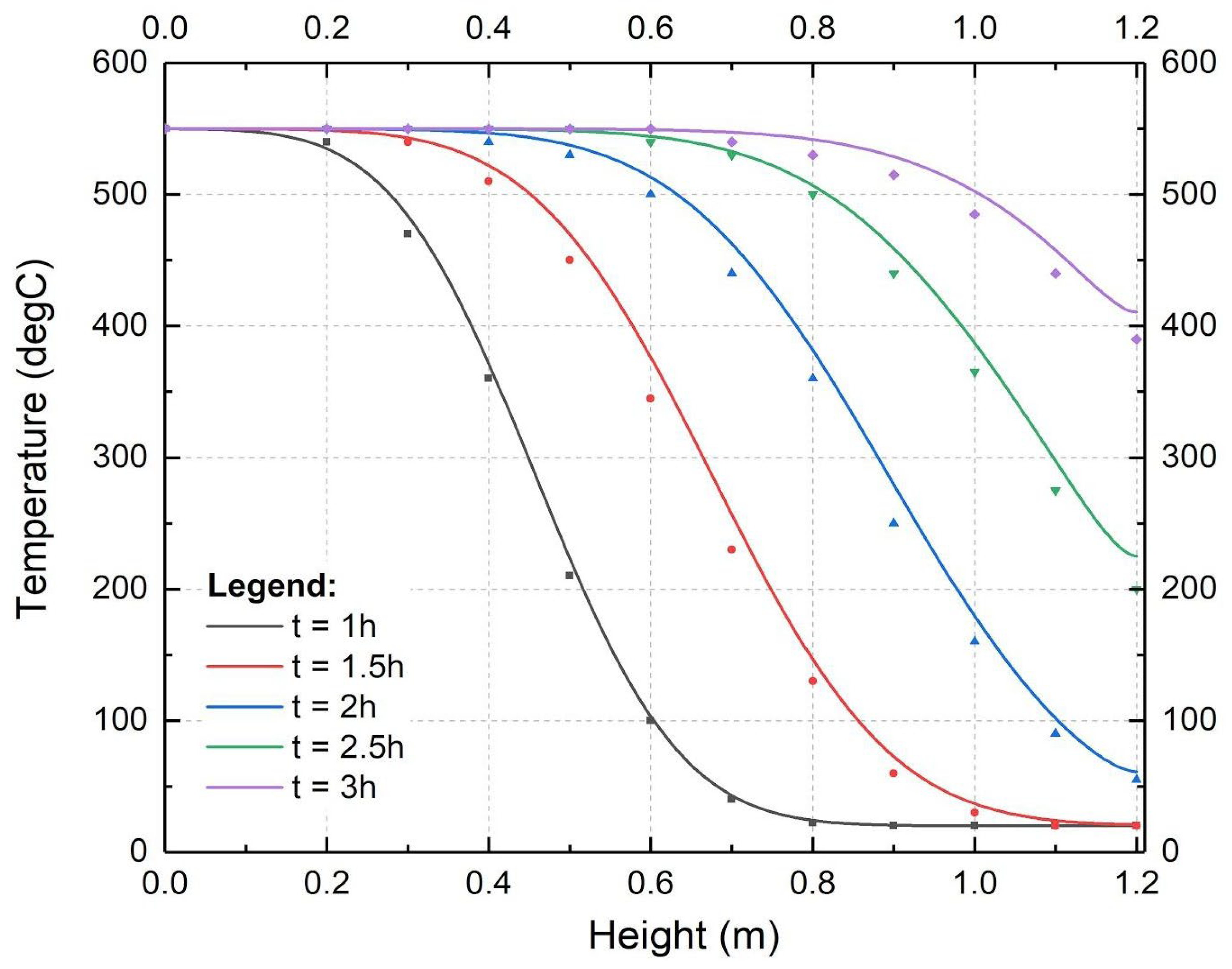
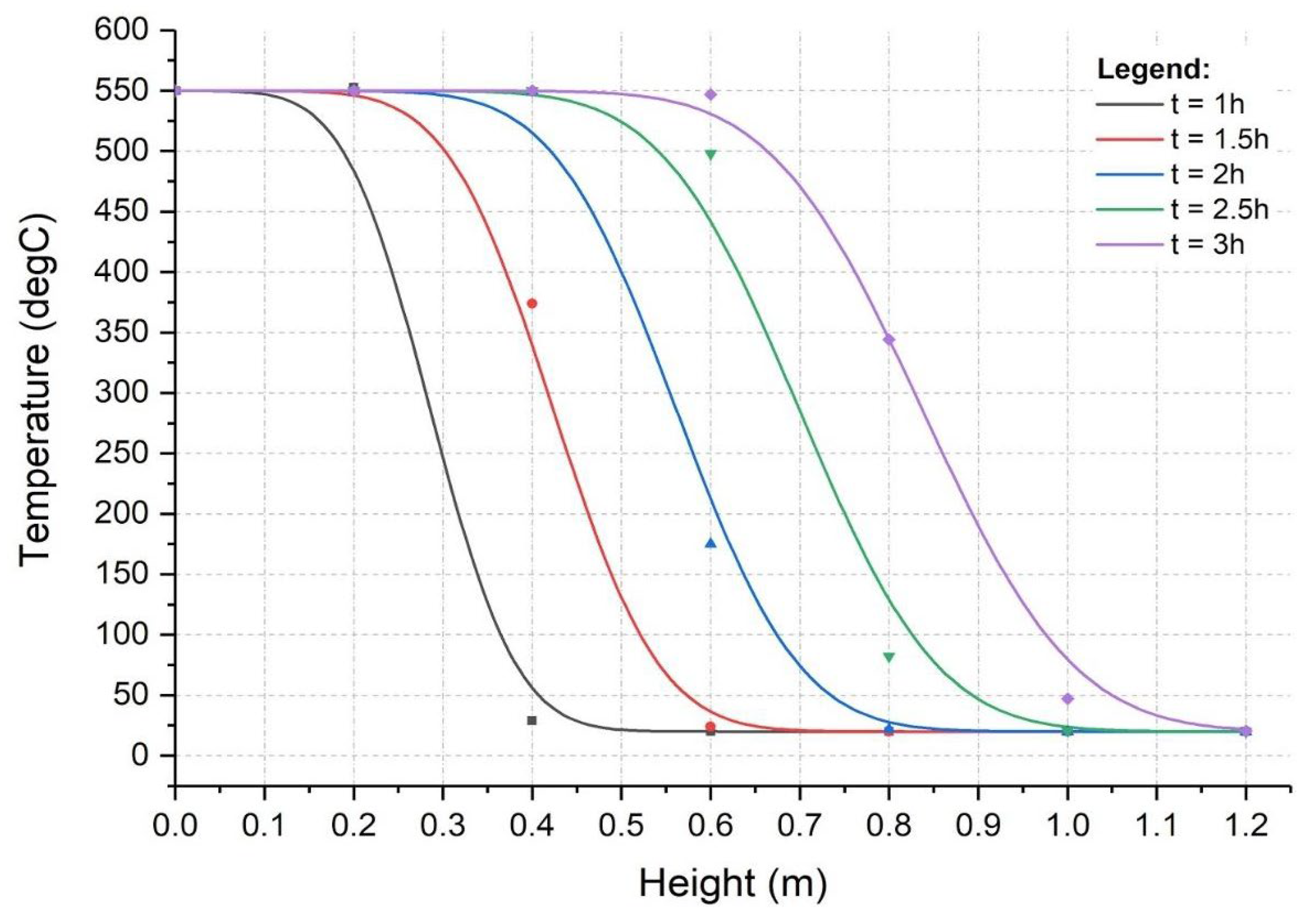
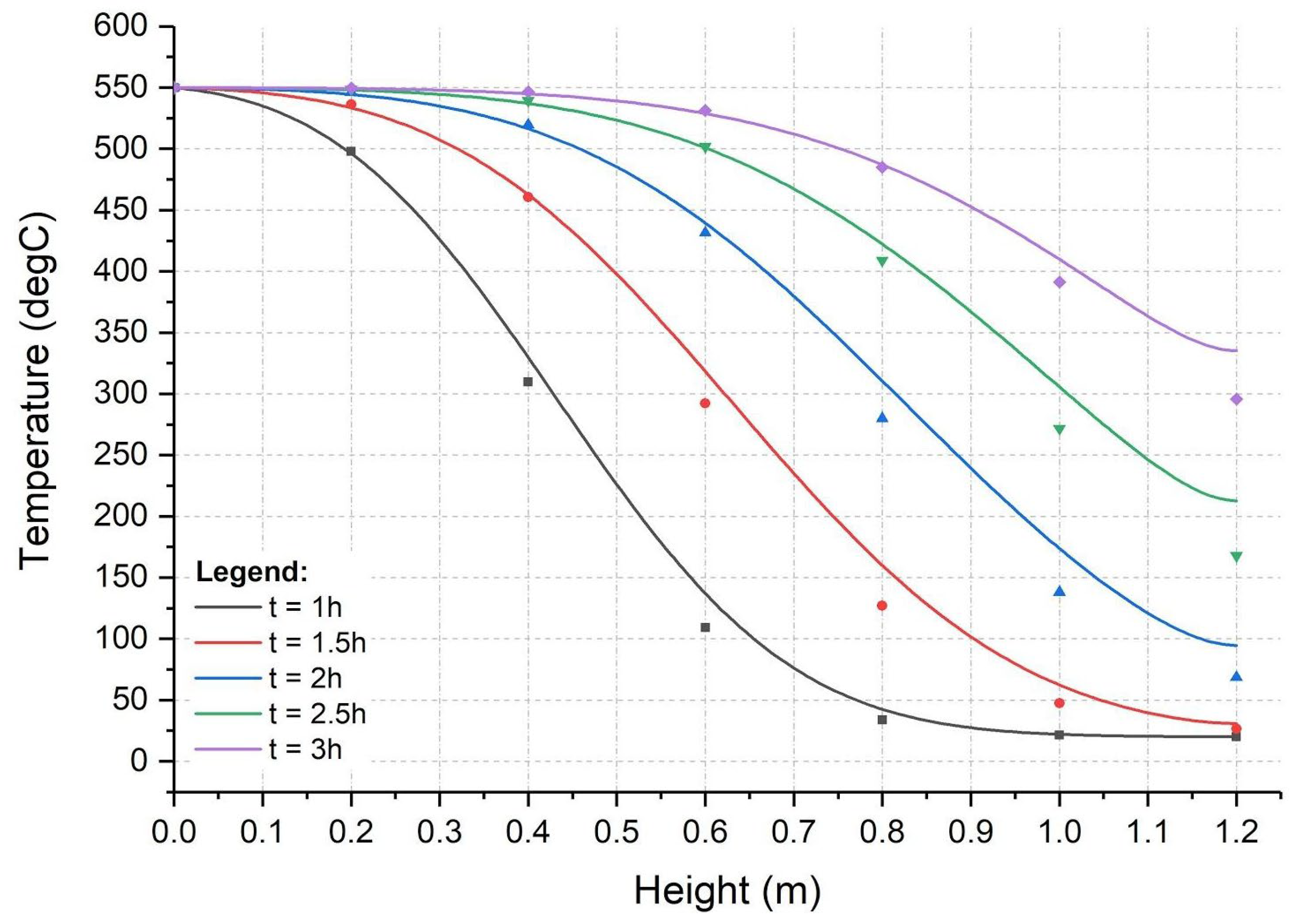
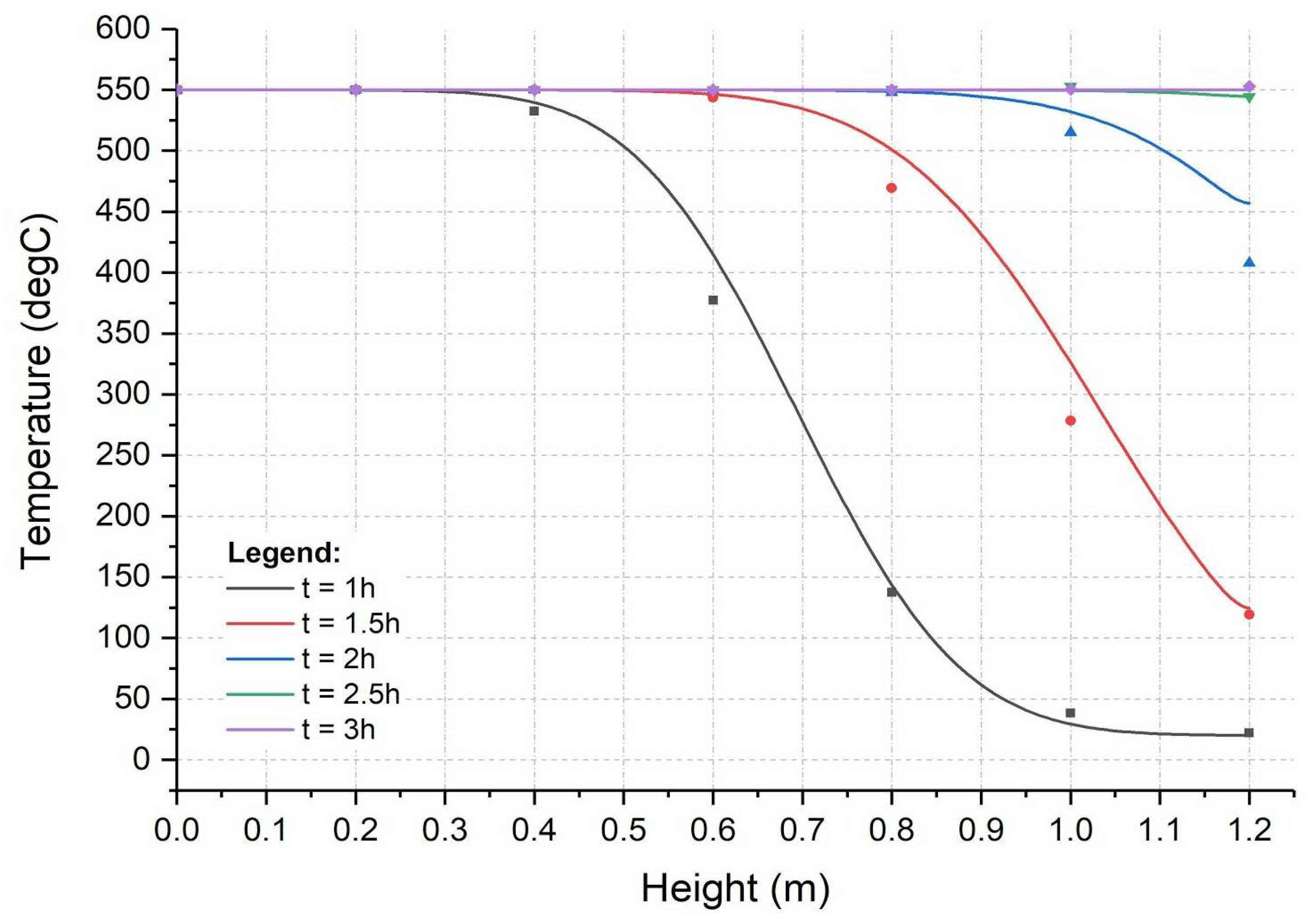
3. Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| ρ | density (kg/m3) |
| cp | specific heat capacity (kJ/kgK) |
| μ | viscosity (Pa∙s) |
| ε | porosity (void fraction) |
| η | permeability |
| ks | thermal conductivity of the solid material (kW/mK) |
| effective thermal conductivity of the HTF (kW/mK) | |
| km | effective thermal conductivity of the packed bed (kW/mK) |
| s | solid medium |
| f | heat transfer fluid |
| m | packed bed |
Appendix A
References
- Elouali, A.; Kousksou, T.; El Rhafiki, T.; Hamdaoui, S.; Mahdaoui, M.; Allouhi, A.; Zeraouli, Y. Physical models for packed bed: Sensible heat storage systems. J. Energy Storage 2019, 23, 69–78. [Google Scholar] [CrossRef]
- Sarbu, I.; Sebarchievici, C. A Comprehensive Review of Thermal Energy Storage. Sustainability 2018, 10, 191. [Google Scholar] [CrossRef]
- Lou, W.; Fan, Y.; Luo, L. Single-tank thermal energy storage systems for concentrated solar power: Flow distribution optimization for thermocline evolution management. J. Energy Storage 2020, 32, 101749. [Google Scholar] [CrossRef]
- Cascetta, M.; Petrollese, M.; Oyekale, J.; Cau, G. Thermocline vs. two-tank direct thermal storage system for concentrating solar power plants: A comparative techno-economic assessment. Int. J. Energy Res. 2021, 45, 17721–17737. [Google Scholar] [CrossRef]
- Al-Azawii, M.M.S.; Theade, C.; Bueno, P.; Anderson, R. Experimental study of layered thermal energy storage in an air-alumina packed bed using axial pipe injections. Appl. Energy 2019, 249, 409–422. [Google Scholar] [CrossRef]
- Brosseau, D.; Kelton, J.W.; Ray, D.; Edgar, M.; Chisman, K.; Emms, B. Testing of Thermocline Filler Materials and Molten-Salt Heat Transfer Fluids for Thermal Energy Storage Systems in Parabolic Trough Power Plants. J. Sol. Energy Eng. 2005, 127, 109–116. [Google Scholar] [CrossRef]
- Mawire, A.; McPherson, M.; van den Heetkamp, R.R.J.; Mlatho, S.J.P. Simulated performance of storage materials for pebble bed thermal energy storage (TES) systems. Appl. Energy 2009, 86, 1246–1252. [Google Scholar] [CrossRef]
- Contestabile, F.; Cornolti, L.; Zavattoni, S.; Barbato, M.C. An advanced wall treatment for a 1D model of packed bed thermal energy storage systems. J. Energy Storage 2019, 26, 100918. [Google Scholar] [CrossRef]
- Yang, X.; Cai, Z. An analysis of a packed bed thermal energy storage system using sensible heat and phase change materials. Int. J. Heat Mass Transf. 2019, 144, 118651. [Google Scholar] [CrossRef]
- Adine, H.A.; El Qarnia, H. Numerical analysis of the thermal behaviour of a shell-and-tube heat storage unit using phase change materials. Appl. Math. Model. 2009, 33, 2132–2144. [Google Scholar] [CrossRef]
- Lamberg, P.; Siren, K. Approximate analytical model for solidification in a finite PCM storage with internal fins. Appl. Math. Model. 2003, 27, 491–513. [Google Scholar] [CrossRef]
- Hilton, J.E.; Cleary, P.W. Comparison of non-cohesive resolved and coarse grain DEM models for gas flow through particle beds. Appl. Math. Model. 2014, 38, 4197–4214. [Google Scholar] [CrossRef]
- Burlayenko, V.N.; Altenbach, H.; Sadowski, T.; Dimitrova, S.D.; Bhaskar, A. Modelling functionally graded materials in the heat transfer and thermal stress analysis by means of graded finite elements. Appl. Math. Model. 2017, 45, 422–438. [Google Scholar] [CrossRef]
- Bhattacharya, M.C. Technical Note: A new improved finite difference equation for heat transfer during transient change. Appl. Math. Model. 1986, 10, 68–70. [Google Scholar] [CrossRef]
- Díaz-Heras, M.; Belmonte, J.F.; Almendros-Ibáñez, J.A. Effective thermal conductivities in packed beds: Review of correlations and its influence on system performance. Appl. Therm. Eng. 2020, 171, 115048. [Google Scholar] [CrossRef]
- Gerstle, W.H.; Schroeder, N.R.; McLaughlin, L.P.; Ho, C.K.; Laubscher, H.F.; Kao, S. Experimental testing and computational modeling of a radial packed bed for thermal energy storage. Sol. Energy 2023, 264, 111993. [Google Scholar] [CrossRef]
- Available online: https://www.comsol.com/release/6.0/porous-media-flow-module (accessed on 1 April 2024).
- Meier, A.; Winkler, C.; Wuillemin, D. Experiment for modelling high temperature rock bed storage. Sol. Energy Mater. 1991, 24, 255–264. [Google Scholar] [CrossRef]
- Calderón-Vásquez, I.; Cortés, E.; García, J.; Segovia, V.; Caroca, A.; Sarmiento, C.; Barraza, R.; Cardemil, J.M. Review on modeling approaches for packed-bed thermal storage systems. Renew. Sustain. Energy Rev. 2021, 143, 110902. [Google Scholar] [CrossRef]
- Díaz-Alonso, S.; Sánchez-González, A.; Hernández-Jiménez, F.; Soria-Verdugo, A. Modeling sensible thermal energy storage in solid blocks for concentrating solar power. Results Eng. 2023, 18, 101051. [Google Scholar] [CrossRef]
- Sathishkumar, A.; Sundaram, P.; Cheralathan, M.; Ganesh Kumar, P. Effect of nano-enhanced phase change materials on performance of cool thermal energy storage system: A review. J. Energy Storage 2024, 78, 110079. [Google Scholar] [CrossRef]
- Prabakaran, R.; Dhamodharan, P.; Sathishkumar AGullo, P.; Vikram, M.P.; Pandiaraj, S.; Alodhayb, A.; Khouqeer, G.A.; Kim, S.-C. An Overview of the State of the Art and Challenges in the Use of Gelling and Thickening Agents to Create Stable Thermal Energy Storage Materials. Energies 2023, 16, 3306. [Google Scholar] [CrossRef]
- Vrbanc, F.; Vašak, M.; Lešić, V. Simple and Accurate Model of Thermal Storage with Phase Change Material Tailored for Model Predictive Control. Energies 2023, 16, 6849. [Google Scholar] [CrossRef]

| Storage Medium | Melting Temperature (°C) | Density (kg/m3) | Thermal Conductivity (W/mK) | Specific Heat Capacity (J/kg°C) | Capsule Diameter (m) | Thermal Conductivity Ratio with HTF (-) |
|---|---|---|---|---|---|---|
| Salt (NaCl) | 802 | 2160 | 7.0 | 850 | 0.0002 | 160.66 |
| Cordierite | 1435 | 2300 | 2.5 | 900 | 0.02 | 57.38 |
| Aluminum Oxide 1 | 2072 | 3550 | 17.5 | 902 | 0.008 | 401.65 |
| Magnetite | 1538 | 5175 | 1.0 | 874.2 | 0.02 | 22.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Coates, T.; Torres Sevilla, L.; Saeed, B.; Radulovic, J. Comparison of Single-Phase Mathematical Models for Solid-State Packed Beds for Thermal Energy Storage. Energies 2024, 17, 1842. https://doi.org/10.3390/en17081842
Coates T, Torres Sevilla L, Saeed B, Radulovic J. Comparison of Single-Phase Mathematical Models for Solid-State Packed Beds for Thermal Energy Storage. Energies. 2024; 17(8):1842. https://doi.org/10.3390/en17081842
Chicago/Turabian StyleCoates, Thomas, Law Torres Sevilla, Burhan Saeed, and Jovana Radulovic. 2024. "Comparison of Single-Phase Mathematical Models for Solid-State Packed Beds for Thermal Energy Storage" Energies 17, no. 8: 1842. https://doi.org/10.3390/en17081842
APA StyleCoates, T., Torres Sevilla, L., Saeed, B., & Radulovic, J. (2024). Comparison of Single-Phase Mathematical Models for Solid-State Packed Beds for Thermal Energy Storage. Energies, 17(8), 1842. https://doi.org/10.3390/en17081842






