Application of Machine Learning for Productivity Prediction in Tight Gas Reservoirs
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Sources
2.2. Correlation Analysis
2.3. Machine Learning Model
2.3.1. Support Vector Regression
2.3.2. Back Propagation Neural Network
2.3.3. Random Forest Regression
2.3.4. Grid Search Method
2.3.5. K-Fold Cross-Validation
2.3.6. Confidence Interval
2.3.7. Summary of This Section
3. Productivity Prediction of Tight Gas Wells
3.1. Correlation Analysis Results
3.2. Model Building and Hyper-Parameter Optimization
3.3. K-Fold Cross-Validation
3.4. Evaluation of Test Results
3.4.1. Comparative Analysis of Models
3.4.2. Confidence Interval Validation
3.4.3. RF Model Validation
3.5. Sensitivity Analysis
- (1)
- Reservoir thickness
- (2)
- Gas saturation
- (3)
- Stratigraphic coefficient
- (4)
- Porosity
- (5)
- Liquid nitrogen volume
- (6)
- Rock density
- (7)
- Permeability
- (8)
- Resistivity
- (9)
- Gamma-ray
4. Model Application
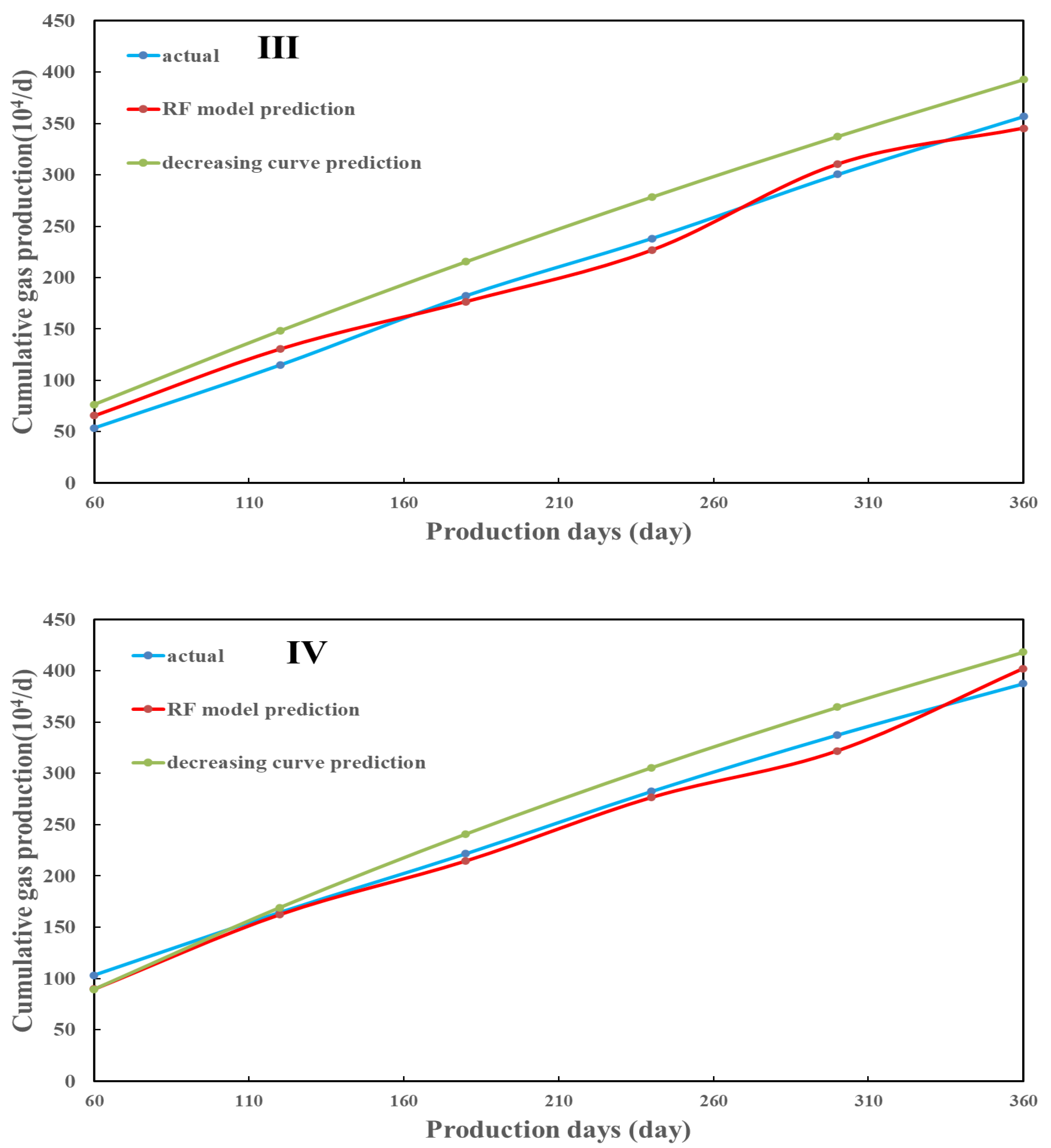
4.1. Decreasing Curve Prediction
4.2. RF Model Prediction
4.3. EUR Prediction
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| EUR | Estimated Ultimate Recovery |
| SVR | Support Vector Regression |
| RF | Random Forest |
| BP | Back Propagation |
| Pearson | Pearson’s correlation coefficient method |
| Spearman | Spearman’s correlation coefficient method |
| Kendall | Kendall’s correlation coefficient method |
| Spearman coefficient value | |
| Pearson coefficient value | |
| Kendall coefficient value | |
| C | The penalty coefficient |
| Linear | Linear Kernel |
| poly | Polynomial Kernel |
| rbf | Radial Basis Function |
| RMSE | Root Mean Square Error |
| R2 | Coefficient of Determination |
| OFM | Oil Field Management |
References
- Motiur Rahman, M. Productivity Prediction for Fractured Wells in Tight Sand Gas Reservoirs Accounting for Non-Darcy Effects. In Proceedings of the SPE Russian Oil and Gas Technical Conference and Exhibition, Moscow, Russia, 28 October 2008. [Google Scholar]
- Wu, Y.; Cheng, L.; Huang, S.; Fang, S.; Killough, J.E.; Jia, P.; Wang, S. A Transient Two-Phase Flow Model for Production Prediction of Tight Gas Wells with Fracturing Fluid-Induced Formation Damage. In Proceedings of the SPE Western Regional Meeting, San Jose, CA, USA, 22 April 2019. [Google Scholar]
- Aranguren, C.; Fragoso, A.; Aguilera, R. Sequence-to-Sequence (Seq2Seq) Long Short-Term Memory (LSTM) for Oil Production Forecast of Shale Reservoirs. In Proceedings of the SPE/AAPG/SEG Unconventional Resources Technology Conference, Houston, TX, USA, 20–22 June 2022. [Google Scholar]
- Biswas, D. Adapting Shallow and Deep Learning Algorithms to Examine Production Performance—Data Analytics and Forecasting. In Proceedings of the SPE/IATMI Asia Pacific Oil & Gas Conference and Exhibition, Bali, Indonesia, 25 October 2019. [Google Scholar]
- Kocoglu, Y.; Gorell, S.; McElroy, P. Application of Bayesian Optimized Deep Bi-LSTM Neural Networks for Production Forecasting of Gas Wells in Unconventional Shale Gas Reservoirs. In Proceedings of the SPE/AAPG/SEG Unconventional Resources Technology Conference, Houston, TX, USA, 26–28 July 2021. [Google Scholar]
- Le, N.T.; Shor, R.J.; Chen, Z. Physics-Constrained Deep Learning for Production Forecast in Tight Reservoirs. In Proceedings of the SPE/AAPG/SEG Asia Pacific Unconventional Resources Technology Conference, Virtual, 16–18 November 2021. [Google Scholar]
- Wu, T.; Fang, H.; Sun, H.; Zhang, F.; Wang, X.; Wang, Y.; Li, S. A Data-Driven Approach to Evaluate Fracturing Practice in Tight Sandstone in Changqing Field. In Proceedings of the International Petroleum Technology Conference, Virtual, 16 March 2021. [Google Scholar]
- Chunxin, W.; Shaopeng, W.; Jianwei, Y.; Chao, L.; Qi, Z. A prediction model of specific productivity index using least square support vector machine method. Adv. Geo-Energy Res. 2020, 4, 460–467. [Google Scholar]
- Vyas, A.; Datta-Gupta, A.; Mishra, S. Modeling Early Time Rate Decline in Unconventional Reservoirs Using Machine Learning Techniques. In Proceedings of the Abu Dhabi International Petroleum Exhibition & Conference, Abu Dhabi, UAE, 13 November 2017. [Google Scholar]
- Liao, L.; Zeng, Y.; Liang, Y.; Zhang, H. Data Mining: A Novel Strategy for Production Forecast in Tight Hydrocarbon Resource in Canada by Random Forest Analysis. In Proceedings of the International Petroleum Technology Conference, Dhahran, Kingdom of Saudi Arabia, 13 January 2020. [Google Scholar]
- Han, D.; Kwon, S.; Kim, J.; Jin, W.; Son, H. Comprehensive Analysis for Production Prediction of Hydraulic Fractured Shale Reservoirs Using Proxy Model Based on Deep Neural Network. In Proceedings of the SPE Annual Technical Conference and Exhibition, Virtual, 19 October 2020. [Google Scholar]
- Xianmu, H.; Fuyong, W.; Yun, Z. Prediction of Porosity and Permeability of Carbonate Reservoirs Based on Machine Learning and Logging Data. J. Jilin Univ. (Earth Sci. Ed.) 2022, 52, 644–653. [Google Scholar]
- Li, Y.; Han, Y. Decline Curve Analysis for Production Forecasting Based on Machine Learning. In Proceedings of the SPE Symposium: Production Enhancement and Cost Optimisation, Kuala Lumpur, Malaysia, 7 November 2017. [Google Scholar]
- Amr, S.; El Ashhab, H.; El-Saban, M.; Schietinger, P.; Caile, C.; Kaheel, A.; Rodriguez, L. A Large-Scale Study for a Multi-Basin Machine Learning Model Predicting Horizontal Well Production. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 23 September 2018. [Google Scholar]
- Alimohammadi, H.; Rahmanifard, H.; Chen, N. Multivariate Time Series Modelling Approach for Production Forecasting in Unconventional Resources. In Proceedings of the SPE Annual Technical Conference and Exhibition, Virtual, 19 October 2020. [Google Scholar]
- Wang, J.; Sajeev, S.K.; Ozbayoglu, E.; Baldino, S.; Liu, Y.; Jing, H. Reducing NPT Using a Novel Approach to Real-Time Drilling Data Analysis. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 9 October 2023; SPE: Houston, TX, USA, 2023; p. D021S012R005. [Google Scholar]
- Wang, J.; Ozbayoglu, E.; Baldino, S.; Liu, Y.; Zheng, D. Time Series Data Analysis with Recurrent Neural Network for Early Kick Detection. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 24 May 2023; OTC: Houston, TX, USA, 2023; p. D021S020R002. [Google Scholar]
- Odi, U.; Ayeni, K.; Alsulaiman, N.; Reddy, K.; Ball, K.; Basri, M.; Temizel, C. Applied Transfer Learning for Production Forecasting in Shale Reservoirs. In Proceedings of the SPE Middle East Oil & Gas Show and Conference, Event Canceled, 15 November 2021. [Google Scholar]
- Sun, J.; Ma, X.; Kazi, M. In Comparison of Decline Curve Analysis DCA with Recursive Neural Networks RNN for Production Forecast of Multiple Wells. In Proceedings of the SPE Western Regional Meeting, Garden Grove, CA, USA, 22 April 2018. [Google Scholar]
- Temizel, C.; Canbaz, C.H.; Alsaheib, H.; Yanidis, K.; Balaji, K.; Alsulaiman, N.; Basri, M.; Jama, N. Geology-Driven EUR Forecasting in Unconventional Fields. In Proceedings of the SPE Middle East Oil & Gas Show and Conference, Event Canceled, 15 November 2021. [Google Scholar]
- Li, B.; Nie, X.; Cai, J.; Zhou, X.; Wang, C.; Han, D. U-Net model for multi-component digital rock modeling of shales based on CT and QEMSCAN images. J. Pet. Sci. Eng. 2022, 216, 110734. [Google Scholar] [CrossRef]
- Al Selaiti, I.; Mata, C.; Saputelli, L.; Badmaev, D.; Alatrach, Y.; Rubio, E.; Mohan, R.; Quijada, D. Robust Data Driven Well Performance Optimization Assisted by Machine Learning Techniques for Natural Flowing and Gas-Lift Wells in Abu Dhabi. In Proceedings of the SPE Annual Technical Conference and Exhibition, Virtual, 19 October 2020. [Google Scholar]
- Noshi, C.I.; Eissa, M.R.; Abdalla, R.M. An Intelligent Data Driven Approach for Production Prediction. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 26 May 2019. [Google Scholar]
- Li, B.; Billiter, T.C.; Tokar, T. Rescaling Method for Improved Machine-Learning Decline Curve Analysis for Unconventional Reservoirs. SPE J. 2021, 26, 1759–1772. [Google Scholar] [CrossRef]
- Adesina, E.; Olusola, B. Application of Machine Learning Algorithm for Predicting Produced Water Under Various Operating Conditions in an Oilwell. In Proceedings of the SPE Nigeria Annual International Conference and Exhibition, Lagos, Nigeria, 1 August 2022. [Google Scholar]
- Trafalis, T.B.; Ince, H. Support vector machine for regression and applications to financial forecasting. In Proceedings of the IEEE-INNS-ENNS International Joint Conference on Neural Networks. IJCNN 2000. Neural Computing: New Challenges and Perspectives for the New Millennium, Como, Italy, 27–27 July 2000; IEEE: Piscataway, NJ, USA, 2000; pp. 348–353. [Google Scholar]
- Zheng, D.; Ozbayoglu, E.M.; Miska, S.Z.; Liu, Y. Cement sheath fatigue failure prediction by support vector machine based model. In Proceedings of the SPE Eastern Regional Meeting, Wheeling, WV, USA, 18 October 2022; OnePetro: Houston, TX, USA, 2022. [Google Scholar]
- Taylor, C.; Vasco, D. Inversion of gravity gradiometry data using a neural network. In SEG Technical Program Expanded Abstracts 1990; Society of Exploration Geophysicists: Houston, TX, USA, 1990; pp. 591–593. [Google Scholar]
- Madan, T.; Sagar, S.; Virmani, D. Air quality prediction using machine learning algorithms—A review. In Proceedings of the 2020 2nd International Conference on Advances in Computing, Communication Control and Networking (ICACCCN), Greater Noida, India, 18–19 December 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 140–145. [Google Scholar]
- Cutler, A. Random Forests for Regression and Classification; Utah State University: Ovronnaz, Switzerland, 2010. [Google Scholar]
- Zheng, D.; Ozbayoglu, E.; Miska, S.Z.; Liu, Y.; Li, Y. Cement sheath fatigue failure prediction by ANN-based model. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 25 May 2022; OTC: Houston, TX, USA, 2022; p. D011S013R009. [Google Scholar]
- Temizel, C.; Canbaz, C.H.; Palabiyik, Y.; Aydin, H.; Tran, M.; Ozyurtkan, M.H.; Yurukcu, M.; Johnson, P. A Thorough Review of Machine Learning Applications in Oil and Gas Industry. In Proceedings of the SPE/IATMI Asia Pacific Oil & Gas Conference and Exhibition, Virtual, 4 October 2021. [Google Scholar]
- Wang, L.; Yao, Y.; Wang, K.; Adenutsi, C.D.; Zhao, G. Combined Application of Unsupervised and Deep Learning in Absolute Open Flow Potential Prediction: A Case Study of the Weiyuan Shale Gas Reservoir. In Proceedings of the SPE/AAPG/SEG Asia Pacific Unconventional Resources Technology Conference, Virtual, 15 November 2021. [Google Scholar]
- Yang, R.; Liu, W.; Qin, X.; Huang, Z.; Shi, Y.; Pang, Z.; Zhang, Y.; Li, J.; Wang, T. A Physics-Constrained Data-Driven Workflow for Predicting Coalbed Methane Well Production Using A Combined Gated Recurrent Unit and Multi-Layer Perception Neural Network Model. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dubai, UAE, 15 September 2021. [Google Scholar]


























| Well Type | Absolute Open Flow (104 m3/d) |
|---|---|
| Low-producing well | ≤1 |
| Medium-producing well | 1~5 |
| High-producing well | >5 |
| Parameter | Correlation Ranking of Different Algorithms | Comprehensive Rank | ||
|---|---|---|---|---|
| Spearman | Pearson | Kendall | ||
| Gas saturation | 1 | 1 | 1 | 1 |
| Stratigraphic coefficient | 2 | 2 | 2 | 2 |
| Flowback fluid volume | 3 | 5 | 3 | 3 |
| Reservoir thickness | 4 | 7 | 4 | 4 |
| Permeability | 5 | 4 | 5 | 5 |
| Porosity | 7 | 3 | 7 | 6 |
| Gamma-ray | 8 | 6 | 8 | 7 |
| Rock density | 6 | 9 | 6 | 8 |
| Resistivity | 10 | 10 | 10 | 9 |
| Reservoir depth | 12 | 8 | 12 | 10 |
| Liquid nitrogen volume | 9 | 11 | 9 | 11 |
| Sand ratio | 11 | 12 | 11 | 12 |
| Fracturing fluid volume | 13 | 14 | 13 | 13 |
| Sand filling amount | 14 | 13 | 14 | 14 |
| Model Name | Parameter Name | Parameter Range | Parameter Step |
|---|---|---|---|
| RF | n_estimators | (40, 500) | 10 |
| max_depth | (3, 13) | 1 | |
| max_features | (0.1, 1) | 0.1 | |
| SVR | kernel function | (linear, poly, rbf) | - |
| C | (10, 100) | 10 | |
| gamma | (0.01, 0.1) | 0.01 | |
| BP | hidden layer | (1, 10) | 1 |
| hidden layer size | (20, 120) | 10 | |
| batch_size | (20, 100) | 10 | |
| epochs | (100, 1000) | 100 |
| Prediction Model | RMSE | R2 |
|---|---|---|
| RF | 3.98 | 0.91 |
| SVR | 12.83 | 0.72 |
| BP | 5.90 | 0.87 |
| Model | Average Value | Standard Deviation | Confidence Interval |
|---|---|---|---|
| RF | 87 | 4.5 | [82.5, 91.5] |
| SVR | 63 | 6.7 | [56.3, 69.7] |
| BP | 83 | 4.9 | [78.1, 87.9] |
| Well Category | Absolute Open Flow (104 m3/d) | Ratio of Initial Production and Absolute Open Flow | Annual Decline Rate (%) | b Value of Decline Curve |
|---|---|---|---|---|
| I | ≤1 | 0.71 | 37.4 | 0.36 |
| II | 1~3 | 0.36 | 25 | 0.76 |
| III | 3~5 | 0.31 | 32.7 | 0.68 |
| IV | >5 | 0.16 | 51.4 | 0.52 |
| Well Name | Well−1 (104 m3/d) | Well−3 (104 m3/d) | Well−5 (104 m3/d) | |
|---|---|---|---|---|
| Prediction Results | ||||
| RF prediction results | 1.58 | 3.68 | 25.56 | |
| True value | 1.96 | 4.41 | 30.94 | |
| Initial Production (104 m3/d) | 0.48 | 1.14 | 4.09 | |
| EUR prediction | 958.8 | 1819.9 | 4109.8 | |
| EUR predicted by OFM | 872.5 | 2106.6 | 4394.4 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, M.; Shi, H.; Li, H.; Liu, T. Application of Machine Learning for Productivity Prediction in Tight Gas Reservoirs. Energies 2024, 17, 1916. https://doi.org/10.3390/en17081916
Fang M, Shi H, Li H, Liu T. Application of Machine Learning for Productivity Prediction in Tight Gas Reservoirs. Energies. 2024; 17(8):1916. https://doi.org/10.3390/en17081916
Chicago/Turabian StyleFang, Maojun, Hengyu Shi, Hao Li, and Tongjing Liu. 2024. "Application of Machine Learning for Productivity Prediction in Tight Gas Reservoirs" Energies 17, no. 8: 1916. https://doi.org/10.3390/en17081916
APA StyleFang, M., Shi, H., Li, H., & Liu, T. (2024). Application of Machine Learning for Productivity Prediction in Tight Gas Reservoirs. Energies, 17(8), 1916. https://doi.org/10.3390/en17081916





