Integrated Black Oil Modeling for Efficient Simulation and Optimization of Carbon Storage in Saline Aquifers
Abstract
1. Introduction
2. Thermodynamic Model
2.1. Equilibrium Definition
2.2. The Solubility Model: Mole Fractions of H2O in the Gas Phase and CO2 in the Liquid Phase
2.3. Extended Solubility Model Considering Salinity
2.4. Fugacity and Activity Coefficient Models
2.4.1. Fugacity Model and Equilibrium Constant
2.4.2. Activity Coefficient Model
2.5. Extended Solubility Model Considering Wider T (up to 300 °C)
2.6. Numerical Implementation
3. CO2–Brine Phase Behavior in Black Oil Simulation: Representation and Application
3.1. The Representation of PVT CO2–Brine Equations in a Black Oil Simulator
- Phases encountered underground
- Thermodynamic mechanisms at play
- Dissolution of CO2 into the brine. Under isothermal reservoir conditions, the dissolution is a function of a pressure change in the reservoir from the initial pressure to maximum pressure (typically 90% of fracture pressure).
- Change in volume of the brine solution (swelling or shrinking) due to dissolution or the release of CO2 from the aqueous phase. Under isothermal condition, this mechanism is also a function of pressure.
- Compression and expansion of the CO2 free phase, which is also a function of pressure changes.
- Vaporization of brine into the gas phase which is ignored in this context due to its negligible effect.
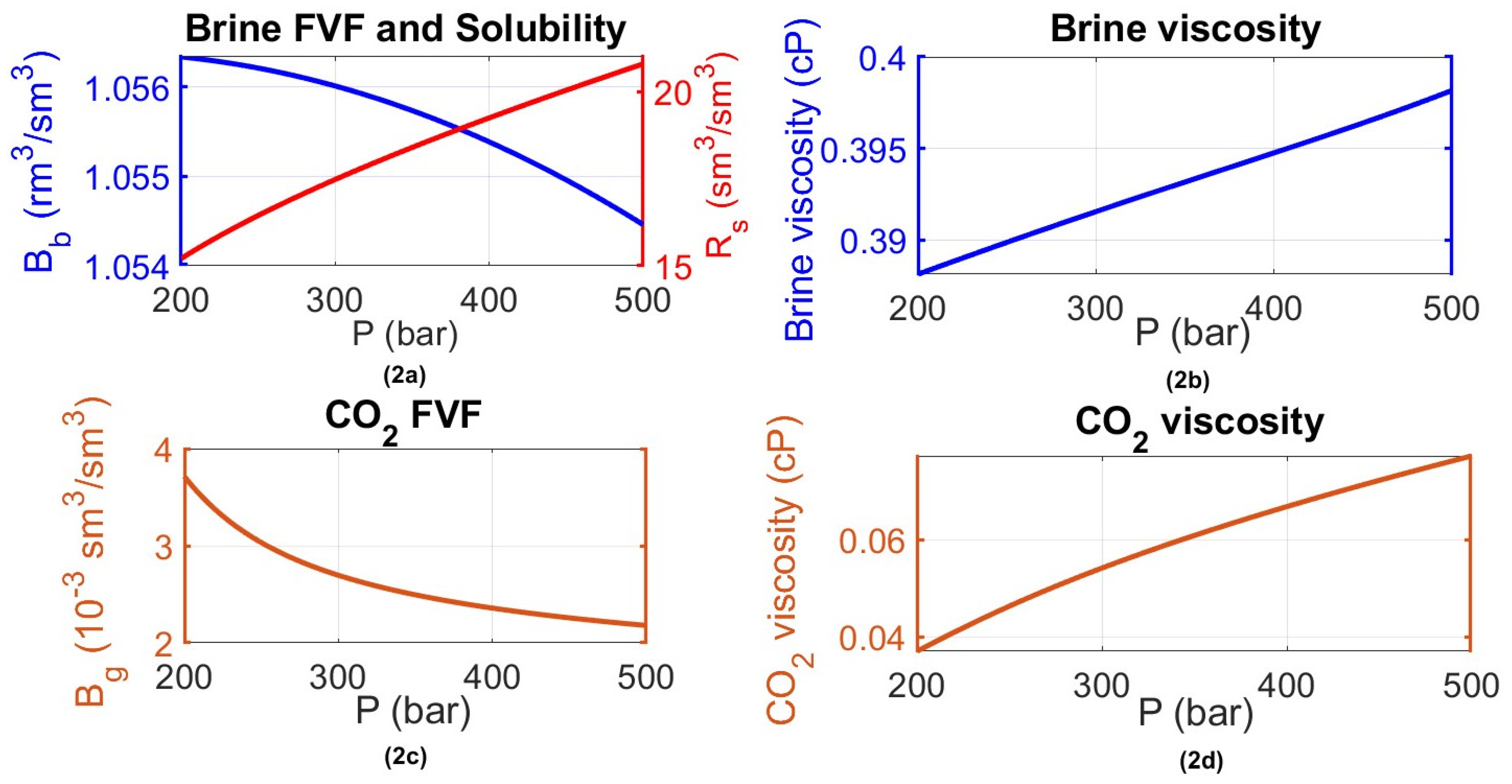
- (solution gas–oil ratio or CO2–brine ratio) as a function of pressure, assessing the dissolution effect of CO2 into brine while covering pressure levels anticipated in the reservoir ( to ).
- Brine formation volume factor () to account for the change in the volume of the brine solution due to CO2 solubility and therefore swelling and/or shrinking in the case of CO2 release from the solution as a function of the reservoir pressure state.
- CO2 formation volume factor () to describe the compression and expansion of the free CO2 phase volume with a pressure change at different stages of the CCS project (injection/closure/post-closure monitoring).
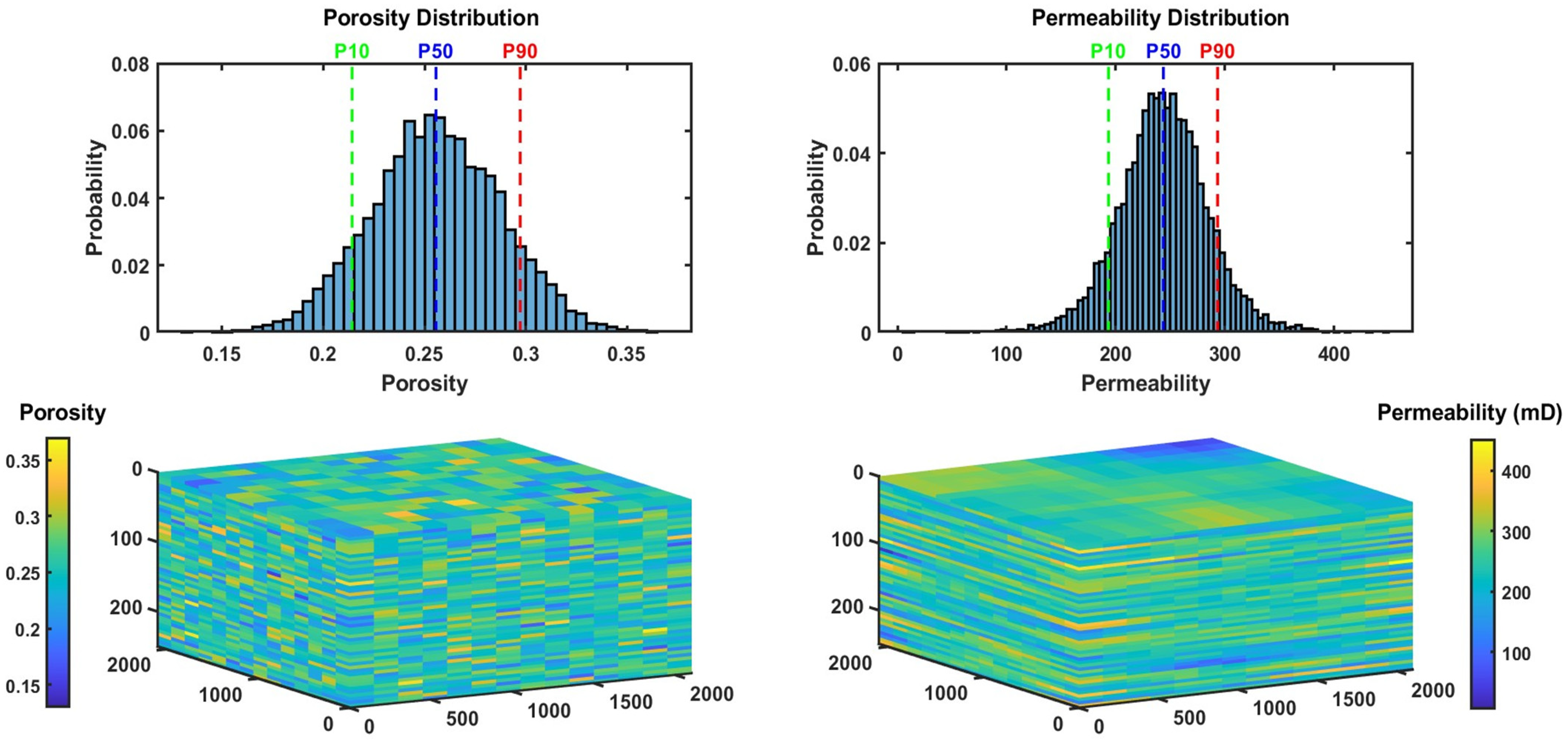
3.2. Black Oil Simulation and Generation of PVT CO2–Brine Data: A Case Study of Typical Saline Aquifer Conditions
3.2.1. Black Oil Simulation: Characteristics and PVT Data
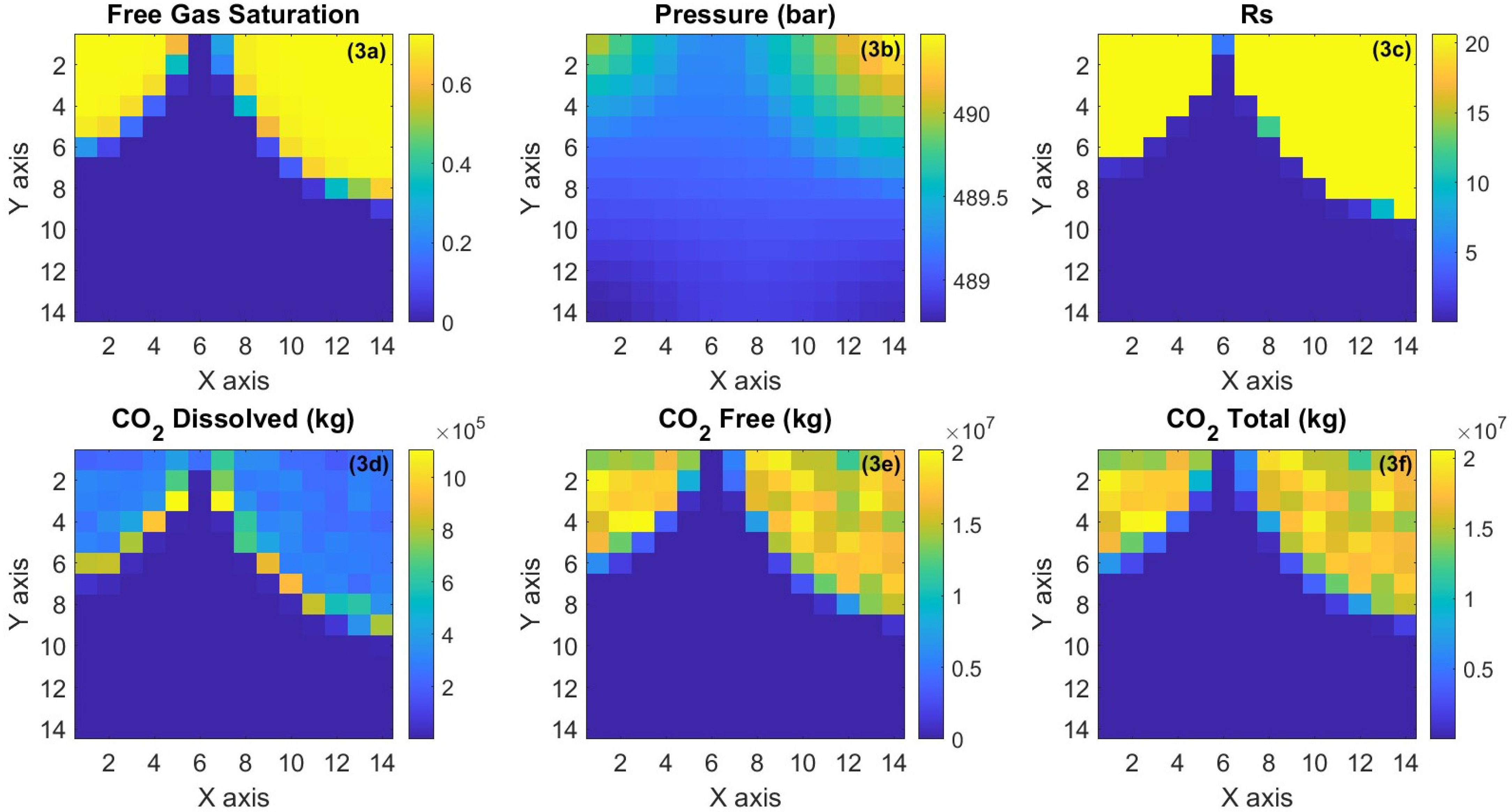
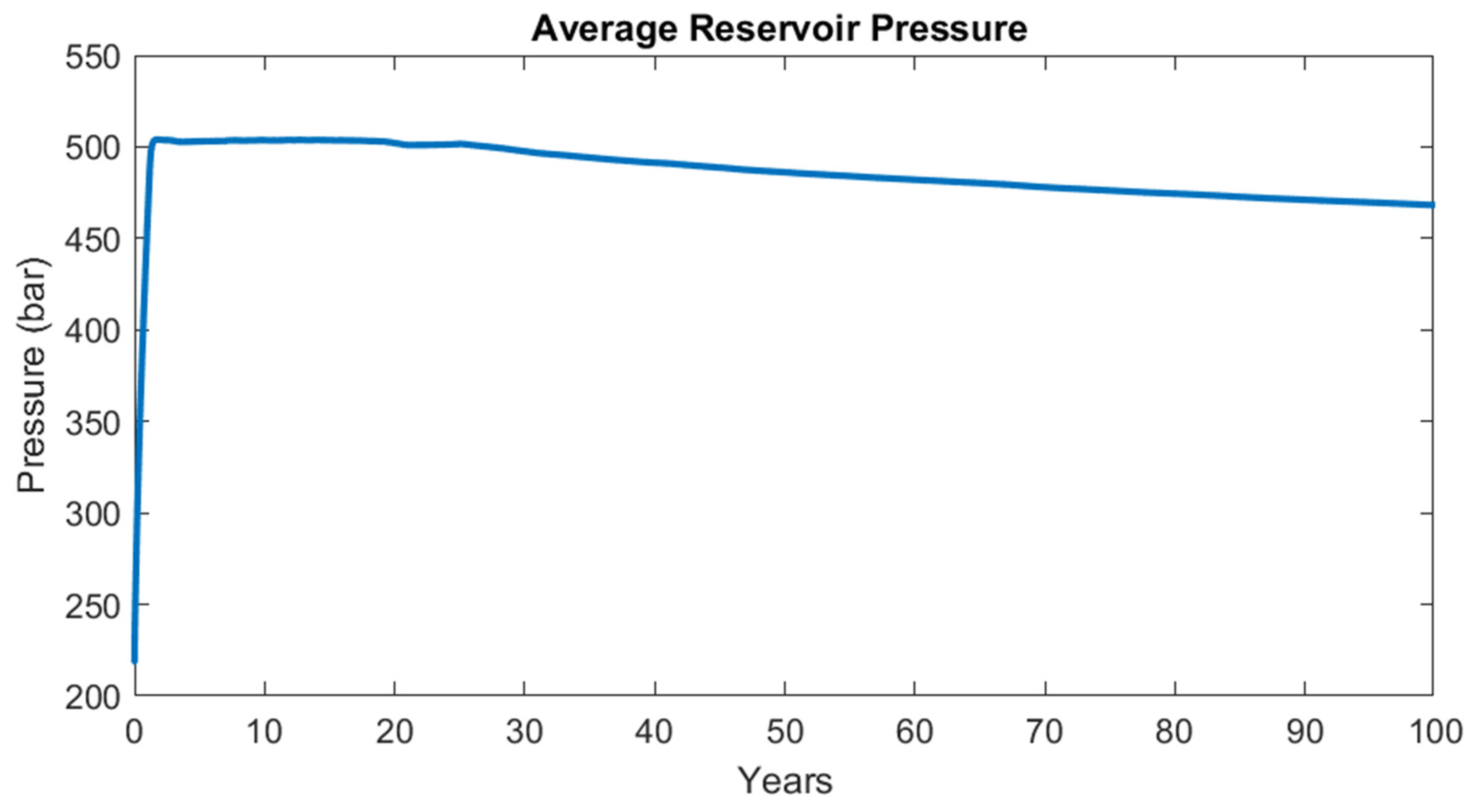
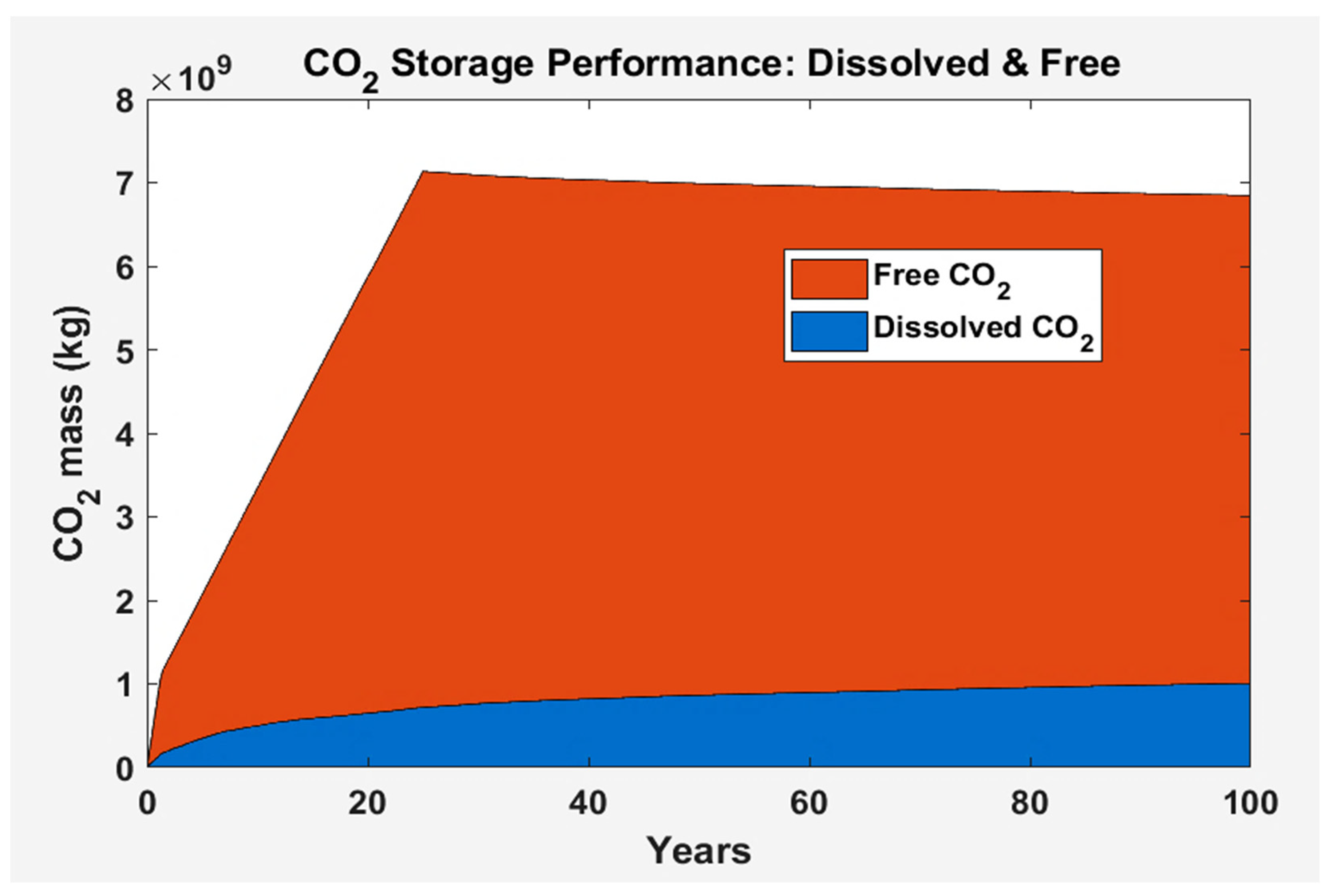
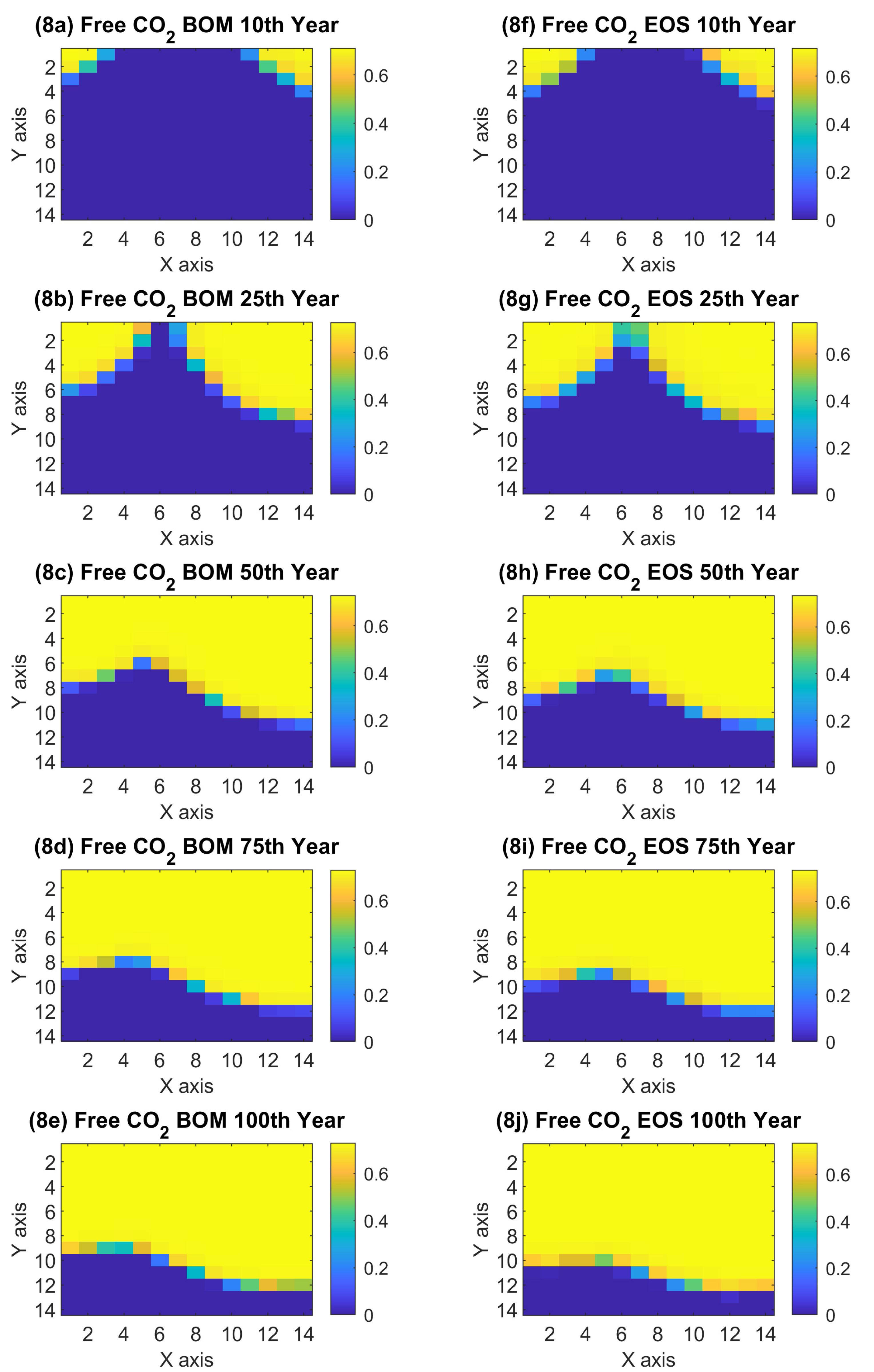
3.2.2. Black Oil Simulation: Results
4. Performance Comparison between Black Oil Model and Compositional Model
5. Discussion
Author Contributions
Funding

Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Low-temperature parameters: 12–109 °C, 1–600 bar (Spycher et al., 2003) [21] | ||||||
| Parameter | Parameter units | Regression coefficients | ||||
| a | b | c | d | e | ||
| bar cm6 K0.5 mol−2 | 7.54 × 107 | −4.13 × 104 | ||||
| a | bar cm6 K0.5 mol−2 | 0.0 | 0.0 | |||
| bar cm6 K0.5 mol−2 | 7.89 × 107 | 0.0 | ||||
| cm3 mol−1 | 27.80 | |||||
| cm3 mol−1 | 18.18 | |||||
| log ( ) | bar | −2.209 | 3.097 × 10−2 | −1.089 × 10−4 | 2.048 × 10−7 | 0.0 |
| log ( ) (L) b | bar mol−1 | 1.169 | 1.368 × 10−2 | −5.380 × 10−5 | 0.0 | 0.0 |
| log ( ) | bar mol−1 | 1.189 | 1.304 × 10−2 | −5.446 × 10−5 | 0.0 | 0.0 |
| CO2 | cm3 mol−1 | 32.6 | 0.0 | |||
| H2O | cm3 mol−1 | 18.1 | 0.0 | |||
| N/A | 0.0 | 0.0 | ||||
| bar | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| High-temperature parameters: 99–300 °C, 1–600 bar (Spycher et al., 2010) [23] | ||||||
| bar cm6 K0.5 mol−2 | 8.008 × 107 | −4.984 × 104 | 0.0 | 0.0 | 0.0 | |
| bar cm6 K0.5 mol−2 | 1.337 × 108 | −1.4 × 104 | 0.0 | 0.0 | 0.0 | |
| bar cm6 K0.5 mol−2 | and below | |||||
| NA | 1.427 × 10−2 | −4.037 × 10−4 | ||||
| NA | 0.4228 | −7.422 × 10−4 | ||||
| cm3 mol−1 | 28.25 | |||||
| cm3 mol−1 | 15.70 | |||||
| log ( ) | bar | −2.1077 | 2.8127 × 10−2 | −8.4298 × 10−5 | −1.4969 × 10−7 | −1.1812 × 10−10 |
| log ( ) | bar mol−1 | 1.668 | 3.992 × 10−3 | −1.156 × 10−5 | 1.593 × 10−9 | 0.0 |
| CO2 | cm3 mol−1 | 32.6 | 3.413 × 10−2 | |||
| H2O | cm3 mol−1 | 18.1 | 3.137 × 10−2 | |||
| NA | −3.0840 × 10−2 | 1.927 × 10−5 | ||||
| (T ≤ 100 °C) | bar | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| (T > 100 °C) c | bar | 1.9906 × 10−1 | 2.0471 × 10−3 | 1.0152 × 10−4 | −1.4234 × 10−6 | 1.4168 × 10−8 |
| CO2 activity coefficient for salt effects: ~20–305 °C | ||||||
| λ | ΝA | 2.217 × 10−4 | 1.074 | 2648 | ||
| ξ | ΝA | 1.30 × 10−5 | −20.12 | 5259 | ||
Appendix B
Appendix B.1. Brine Density and Compressibility
Appendix B.2. Brine Viscosity
| Constant | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| 3.324 × 10−2 | 3.624 × 10−2 | −1.879 × 10−4 | ||||
| −3.96 × 10−2 | 1.02 × 10−2 | 7.02 × 10−4 | ||||
| 1.2378 | −1.303 × 10−3 | 3.06 × 10−6 | 2.55 × 10−8 | |||
| 6.044 | 2.8 × 10−3 | 3.6 × 10−5 | ||||
| −1.279 | 5.74 × 10−2 | −6.97 × 10−4 | 4.47 × 10−6 | −1.05 × 10−8 | ||
| 2.5 | −2.0 | 0.5 |
References
- Jarvis, S.M.; Samsatli, S. Technologies and Infrastructures Underpinning Future CO2 Value Chains: A Comprehensive Review and Comparative Analysis. Renew. Sustain. Energy Rev. 2018, 85, 46–68. [Google Scholar] [CrossRef]
- Gabrielli, P.; Gazzani, M.; Mazzotti, M. The Role of Carbon Capture and Utilization, Carbon Capture and Storage, and Biomass to Enable a Net-Zero-CO2 Emissions Chemical Industry. Ind. Eng. Chem. Res. 2020, 59, 7033–7045. [Google Scholar] [CrossRef]
- Bui, M.; Gazzani, M.; Pozo, C.; Puxty, G.D.; Soltani, S.M. Editorial: The Role of Carbon Capture and Storage Technologies in a Net-Zero Carbon Future. Front. Energy Res. 2021, 9, 733968. [Google Scholar] [CrossRef]
- Martin-Roberts, E.; Scott, V.; Flude, S.; Johnson, G.; Haszeldine, R.S.; Gilfillan, S. Carbon Capture and Storage at the End of a Lost Decade. One Earth 2021, 4, 1569–1584. [Google Scholar] [CrossRef]
- Peres, C.B.; Resende, P.M.R.; Nunes, L.J.R.; Morais, L.C.D. Advances in Carbon Capture and Use (CCU) Technologies: A Comprehensive Review and CO2 Mitigation Potential Analysis. Clean Technol. 2022, 4, 1193–1207. [Google Scholar] [CrossRef]
- Li, Q.; Liu, J.; Wang, S.; Guo, Y.; Han, X.; Li, Q.; Cheng, Y.; Dong, Z.; Li, X.; Zhang, X. Numerical Insights into Factors Affecting Collapse Behavior of Horizontal Wellbore in Clayey Silt Hydrate-Bearing Sediments and the Accompanying Control Strategy. Ocean. Eng. 2024, 297, 117029. [Google Scholar] [CrossRef]
- International Energy Agency. Putting CO2 to Use; International Energy Agency: Paris, France, 2019. [Google Scholar]
- Ji, X.; Zhu, C. Aquifers. In Novel Materials for Carbon Dioxide Mitigation Technology; Elsevier: Amsterdam, The Netherlands, 2015; pp. 299–332. [Google Scholar] [CrossRef]
- Hannis, S.; Lu, J.; Chadwick, A.; Hovorka, S.; Kirk, K.; Romanak, K.; Pearce, J. CO2 Storage in Depleted or Depleting Oil and Gas Fields: What Can We Learn from Existing Projects? Energy Procedia 2017, 114, 5680–5690. [Google Scholar] [CrossRef]
- Gassara, O.; Estublier, A.; Garcia, B.; Noirez, S.; Cerepi, A.; Loisy, C.; Le Roux, O.; Petit, A.; Rossi, L.; Kennedy, S.; et al. The Aquifer-CO2Leak Project: Numerical Modeling for the Design of a CO2 Injection Experiment in the Saturated Zone of the Saint-Emilion (France) Site. Int. J. Greenh. Gas. Control 2021, 104, 103196. [Google Scholar] [CrossRef]
- Michael, K.; Allinson, G.; Golab, A.; Sharma, S.; Shulakova, V. CO2 Storage in Saline Aquifers II–Experience from Existing Storage Operations. Energy Procedia 2009, 1, 1973–1980. [Google Scholar] [CrossRef]
- Pruess, K.; García, J.; Kovscek, T.; Oldenburg, C.; Rutqvist, J.; Steefel, C.; Xu, T. Code Intercomparison Builds Confidence in Numerical Simulation Models for Geologic Disposal of CO2. Energy 2004, 29, 1431–1444. [Google Scholar] [CrossRef]
- Class, H.; Ebigbo, A.; Helmig, R.; Dahle, H.K.; Nordbotten, J.M.; Celia, M.A.; Audigane, P.; Darcis, M.; Ennis-King, J.; Fan, Y.; et al. A Benchmark Study on Problems Related to CO2 Storage in Geologic Formations. Comput. Geosci. 2009, 13, 409–434. [Google Scholar] [CrossRef]
- Ismail, I.; Gaganis, V. Carbon Capture, Utilization, and Storage in Saline Aquifers: Subsurface Policies, Development Plans, Well Control Strategies and Optimization Approaches—A Review. Clean Technol. 2023, 5, 609–637. [Google Scholar] [CrossRef]
- Blair, L.M.; Quinn, J.A. Measurement of Small Density Differences: Solutions of Slightly Soluble Gases. Rev. Sci. Instrum. 1968, 39, 75–77. [Google Scholar] [CrossRef]
- Sayegh, S.G.; Najman, J. Phase Behavior Measurements of CO2 -SO2 -brine Mixtures. Can. J. Chem. Eng. 1987, 65, 314–320. [Google Scholar] [CrossRef]
- Lindeberg, E.; Wessel-Berg, D. Vertical Convection in an Aquifer Column under a Gas Cap of CO2. Energy Convers. Manag. 1997, 38, S229–S234. [Google Scholar] [CrossRef]
- Ennis-King, J.; Paterson, L. Role of Convective Mixing in the Long-Term Storage of Carbon Dioxide in Deep Saline Formations. SPE J. 2005, 10, 349–356. [Google Scholar] [CrossRef]
- Hassanzadeh, H.; Pooladi-Darvish, M.; Keith, D.W. Modelling of Convective Mixing in CO2 Storage. In Canadian International Petroleum Conference; Petroleum Society of Canada: Calgary, AB, Canada, 2004. [Google Scholar] [CrossRef]
- Yang, Z.-L.; Yu, H.-Y.; Chen, Z.-W.; Cheng, S.-Q.; Su, J.-Z. A Compositional Model for CO2 Flooding Including CO2 Equilibria between Water and Oil Using the Peng–Robinson Equation of State with the Wong–Sandler Mixing Rule. Pet. Sci. 2019, 16, 874–889. [Google Scholar] [CrossRef]
- Spycher, N.; Pruess, K.; Ennis-King, J. CO2-H2O Mixtures in the Geological Sequestration of CO2. I. Assessment and Calculation of Mutual Solubilities from 12 to 100 °C and up to 600 Bar. Geochim. Cosmochim. Acta 2003, 67, 3015–3031. [Google Scholar] [CrossRef]
- Spycher, N.; Pruess, K. CO2-H2O Mixtures in the Geological Sequestration of CO2. II. Partitioning in Chloride Brines at 12–100 °C and up to 600 Bar. Geochim. Cosmochim. Acta 2005, 69, 3309–3320. [Google Scholar] [CrossRef]
- Spycher, N.; Pruess, K. A Phase-Partitioning Model for CO2–Brine Mixtures at Elevated Temperatures and Pressures: Application to CO2-Enhanced Geothermal Systems. Transp. Porous Media 2010, 82, 173–196. [Google Scholar] [CrossRef]
- Duan, Z.; Sun, R. An Improved Model Calculating CO2 Solubility in Pure Water and Aqueous NaCl Solutions from 273 to 533 K and from 0 to 2000 Bar. Chem. Geol. 2003, 193, 257–271. [Google Scholar] [CrossRef]
- Duan, Z.; Sun, R.; Zhu, C.; Chou, I.-M. An Improved Model for the Calculation of CO2 Solubility in Aqueous Solutions Containing Na+, K+, Ca2+, Mg2+, Cl−, and SO42−. Mar. Chem. 2006, 98, 131–139. [Google Scholar] [CrossRef]
- Tödheide, K.; Franck, E.U. Das Zweiphasengebiet Und Die Kritische Kurve Im System Kohlendioxid–Wasser Bis Zu Drucken von 3500 Bar. Z. Für Phys. Chem. 1963, 37, 387–401. [Google Scholar] [CrossRef]
- Takenouchi, S.; Kennedy, G.C. The Binary System H2O-CO2 at High Temperatures and Pressures. Am. J. Sci. 1964, 262, 1055–1074. [Google Scholar] [CrossRef]
- Blencoe, J.G.; Naney, M.T.; Anovitz, L.M. The CO2–H2O System: III. A New Experimental Method for Determining Liquid-Vapor Equilibria at High Supercritical Temperatures. Am. Mineral. 2001, 86, 1100–1111. [Google Scholar] [CrossRef]
- Hu, J.; Duan, Z.; Zhu, C.; Chou, I.-M. PVTx Properties of the CO2–H2O and CO2–H2O–NaCl Systems below 647 K: Assessment of Experimental Data and Thermodynamic Models. Chem. Geol. 2007, 238, 249–267. [Google Scholar] [CrossRef]
- Fotias, S.P.; Bellas, S.; Gaganis, V. Optimizing Geothermal Energy Extraction in CO2 Plume Geothermal Systems. Mater. Proc. 2023, 15, 52. [Google Scholar] [CrossRef]
- Mathias, P.M.; Klotz, H.C.; Prausnitz, J.M. Equation-of-State Mixing Rules for Multicomponent Mixtures: The Problem of Invariance. Fluid. Phase Equilib. 1991, 67, 31–44. [Google Scholar] [CrossRef]
- King, M.B.; Mubarak, A.; Kim, J.D.; Bott, T.R. The Mutual Solubilities of Water with Supercritical and Liquid Carbon Dioxides. J. Supercrit. Fluids 1992, 5, 296–302. [Google Scholar] [CrossRef]
- Carlson, H.C.; Colburn, A.P. Vapor-Liquid Equilibria of Nonideal Solutions. Ind. Eng. Chem. 1942, 34, 581–589. [Google Scholar] [CrossRef]
- Hassanzadeh, H.; Pooladi-Darvish, M.; Elsharkawy, A.M.; Keith, D.W.; Leonenko, Y. Predicting PVT Data for CO2–Brine Mixtures for Black-Oil Simulation of CO2 Geological Storage. Int. J. Greenh. Gas. Control 2008, 2, 65–77. [Google Scholar] [CrossRef]
- Lie, K.-A. An Introduction to Reservoir Simulation Using MATLAB/GNU Octave; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar] [CrossRef]
- Advanced Modeling with the MATLAB Reservoir Simulation Toolbox; Lie, K.-A., Møyner, O., Eds.; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar] [CrossRef]
- Rowe, A.M.; Chou, J.C.S. Pressure-Volume-Temperature-Concentration Relation of Aqueous Sodium Chloride Solutions. J. Chem. Eng. Data 1970, 15, 61–66. [Google Scholar] [CrossRef]
- Kestin, J.; Khalifa, H.E.; Correia, R.J. Tables of the Dynamic and Kinematic Viscosity of Aqueous NaCl Solutions in the Temperature Range 20–150 °C and the Pressure Range 0.1–35 MPa. J. Phys. Chem. Ref. Data 1981, 10, 71–88. [Google Scholar] [CrossRef]
- Advanced Resources International, Inc. Geologic Storage Capacity for CO2 of The Lower Tuscaloosa Group and Woodbine Formations; Advanced Resources International, Inc.: Arlington, VA, USA, 2009. [Google Scholar]
- Schlumberger. Eclipse Reservoir Simulation Software—Reference Manual; Schlumberger: Houston, TX, USA, 2024. [Google Scholar]



| Parameter | Value | Units |
|---|---|---|
| 7.54 × 4.02 × × T (in °K) Fitted T range: 280–380 °K | bar | |
| 27.86 | ||
| 18.10 | ||
| 7.89 × | bar |
| Regression Function (T in °C) | ||||||
|---|---|---|---|---|---|---|
| Regression Coefficient | ||||||
| Species | a | b | c | d | e | |
| H2O | −2.215 | 3.162 × | −1.294 × | 4.187 × | −7.331 × | 18.5 |
| CO2 (g) | 1.188 | 1.307 × | −5.445 × | 0.0 | 0.0 | 32.1 |
| CO2 (l) | 1.168 | 1.361 × | −5.135 × | 0.0 | 0.0 | 32.1 |
| Coefficient | ||
|---|---|---|
| −0.411370585 | 3.36389723 × | |
| 6.07632013 × | −1.98298980 × | |
| 97.5347708 | 0 | |
| −0.0237622469 | 2.12220830 × | |
| 0.0170656236 | −5.24873303 × | |
| 1.41335834 × | 0 |
| Project Name | Location | Inj. Start | Aquifer Unit (Lithology) | Average Porosity | Average Permeability | Depth | Thickness (m) | Temperature (ICI) | Pressure (MPa) |
|---|---|---|---|---|---|---|---|---|---|
| Snohvit | Barents Sea, Norway | 2008 | Tubasen Formation (Sandstone) | 13 | 450 | 2550 | 60 | 95 | 28.5 |
| Sleipner | North Sea, Norway | 1996 | Utsira Formation (Sandstone) | 37 | 5000 | 1000 | 250 | 37 | 10.3 |
| In Salah | Krechba, Algeria | 2004 | Krechba Formation (Sandstone) | 17 | 5 | 1850 | 29 | 90 | 17.9 |
| Gorgon | Barrow Island, WA, Australia | 2014 | Dupuy Formation (Sandstone) | 20 | 25 | 2300 | N/A | 100 | 22 |
| Parameter | Value |
|---|---|
| Standard brine density | 1092 kg/m3 |
| Standard CO2 density | 1.8 kg/m3 |
| Average brine viscosity | 0.393 cp |
| Average CO2 viscosity | 0.06 cp |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ismail, I.; Fotias, S.P.; Avgoulas, D.; Gaganis, V. Integrated Black Oil Modeling for Efficient Simulation and Optimization of Carbon Storage in Saline Aquifers. Energies 2024, 17, 1914. https://doi.org/10.3390/en17081914
Ismail I, Fotias SP, Avgoulas D, Gaganis V. Integrated Black Oil Modeling for Efficient Simulation and Optimization of Carbon Storage in Saline Aquifers. Energies. 2024; 17(8):1914. https://doi.org/10.3390/en17081914
Chicago/Turabian StyleIsmail, Ismail, Sofianos Panagiotis Fotias, Dimitris Avgoulas, and Vassilis Gaganis. 2024. "Integrated Black Oil Modeling for Efficient Simulation and Optimization of Carbon Storage in Saline Aquifers" Energies 17, no. 8: 1914. https://doi.org/10.3390/en17081914
APA StyleIsmail, I., Fotias, S. P., Avgoulas, D., & Gaganis, V. (2024). Integrated Black Oil Modeling for Efficient Simulation and Optimization of Carbon Storage in Saline Aquifers. Energies, 17(8), 1914. https://doi.org/10.3390/en17081914





