Thermodynamic Analysis of an Increasing-Pressure Endothermic Power Cycle Integrated with Closed-Loop Geothermal Energy Extraction
Abstract
1. Introduction
2. Geothermal Power Generation Systems
2.1. Description of the IPEPC
2.2. Description of the Trans-Critical Carbon Dioxide (t-CO2) System
2.3. Description of the Organic Rankine Cycle (ORC) System
2.4. Description of the Single-Flash (SF) System
3. Methodology and Models
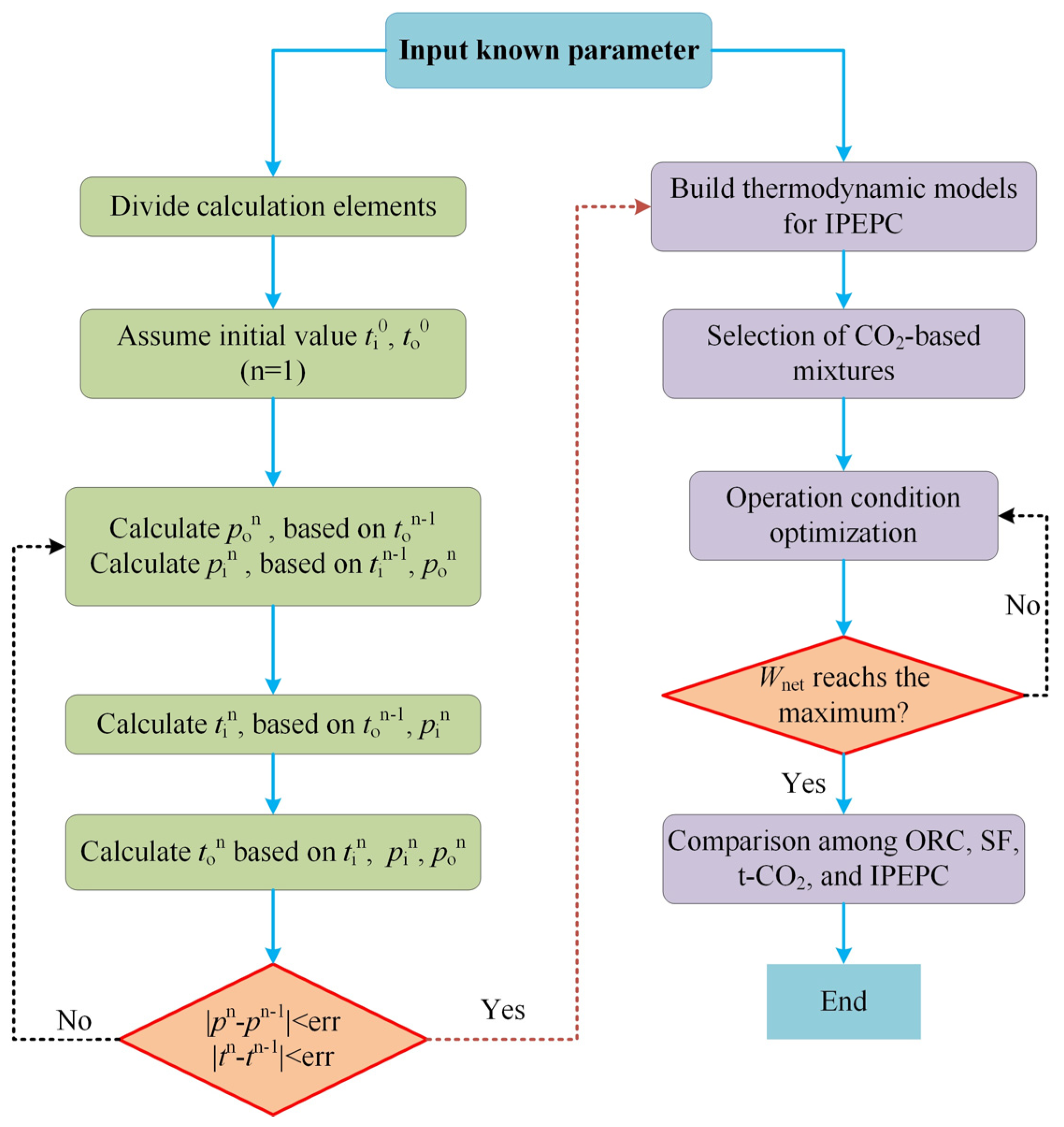
3.1. Solution Procedure and Assumptions
- The four systems are all operating in a stable state;
- The flow friction and heat losses in pipes are disregarded in the ground power generation equipment;
- The CO2-based mixture is in a saturated liquid state at the condenser outlet;
- The geothermal gradient of the geo-formation remains constant, the temperature increases linearly with depth;
- The turbine and pump efficiencies, as well as the temperature of the cooling water, remain consistent across all four systems;
- A 20% increase in net power generation is the criterion by which IPEPC, ORC, and SF systems are superior to t-CO2, which aligns with the requirements of our ongoing sponsored project.
3.2. Power Generation Model
3.2.1. Turbine
3.2.2. Condenser
3.2.3. Working Fluid Pump
3.3. Downhole Heat Exchanger (DHE) Model
3.3.1. DHE Flow Pressure Model
3.3.2. DHE Flow Temperature Model
3.3.3. DHE Heat Transfer Model
- (a)
- Heat transfer between the inner and outer pipe
- (b)
- Heat transfer between the geological formation and outer pipe
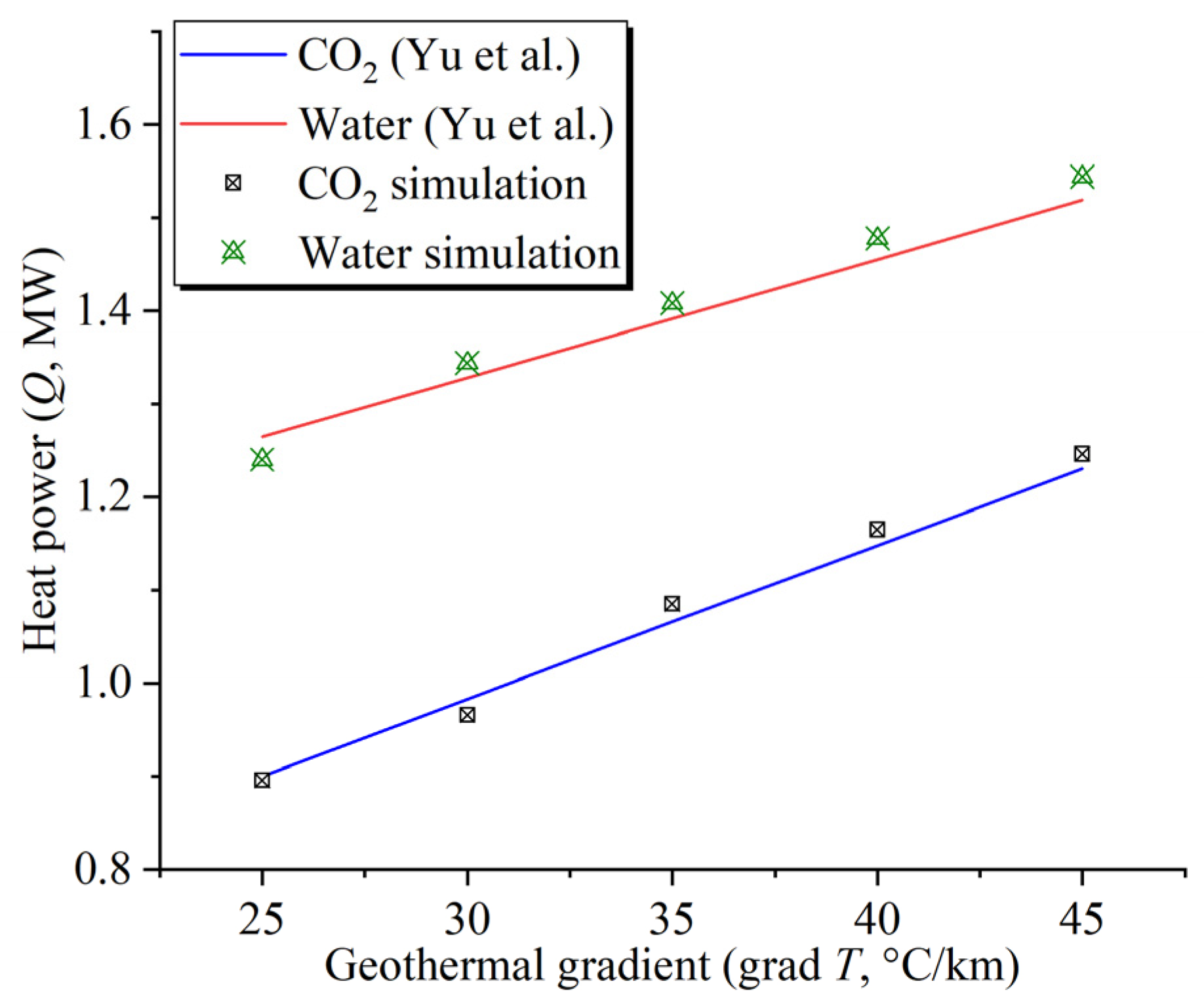
3.4. Model Verification
4. Results and Discussion
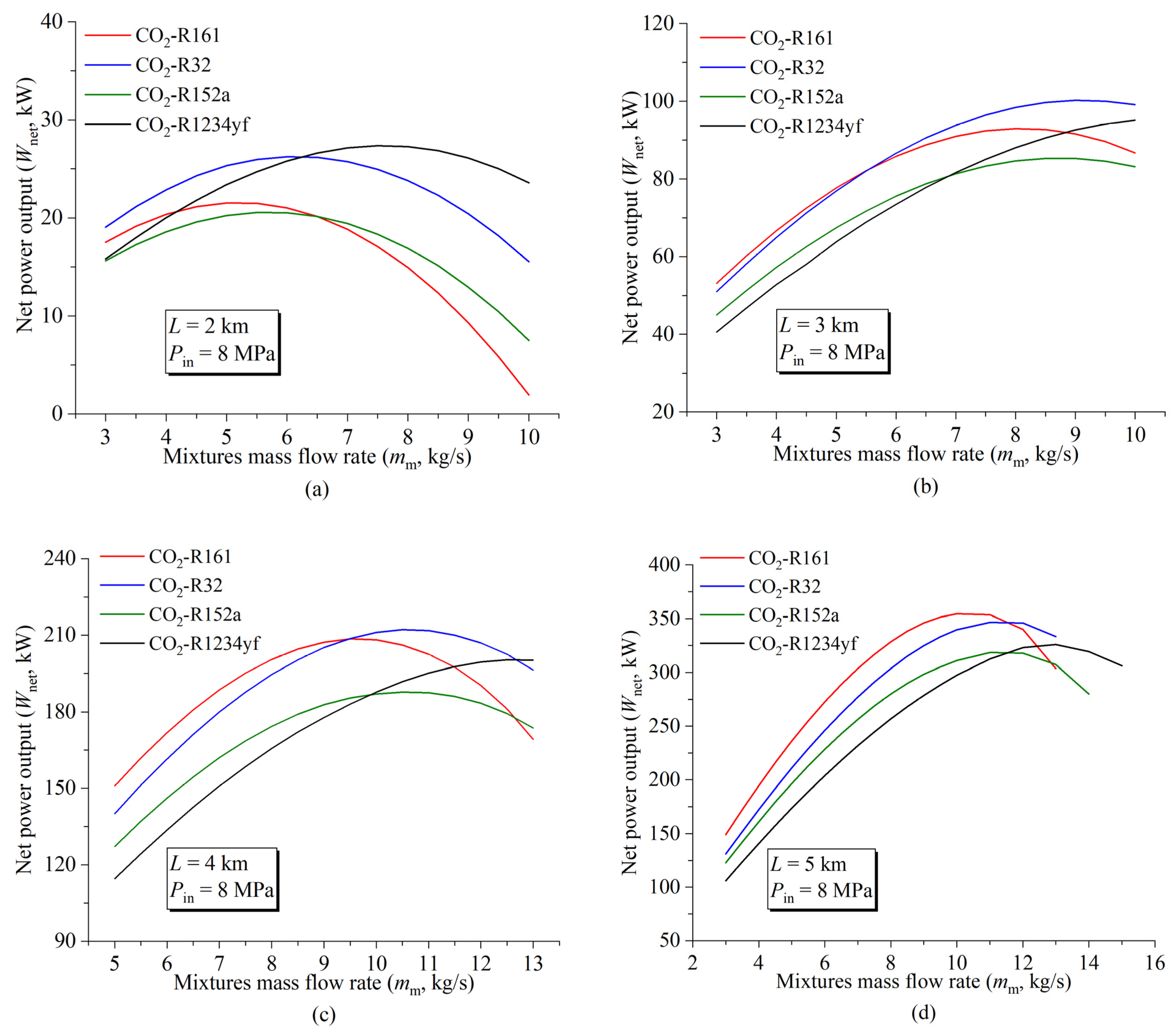
4.1. CO2-Based Mixture Selection
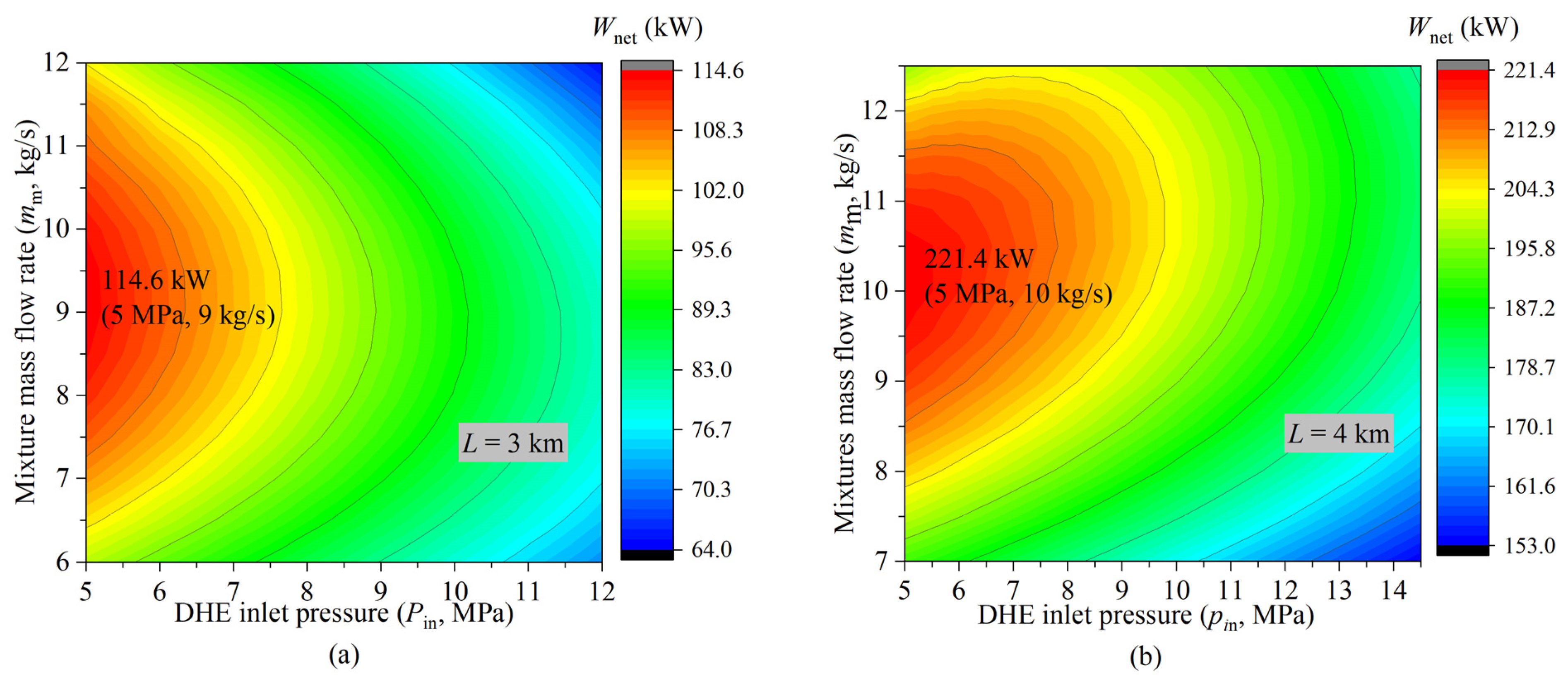
4.2. Effect of the DHE Inlet Pressure and Mixture Mass Flow Rate
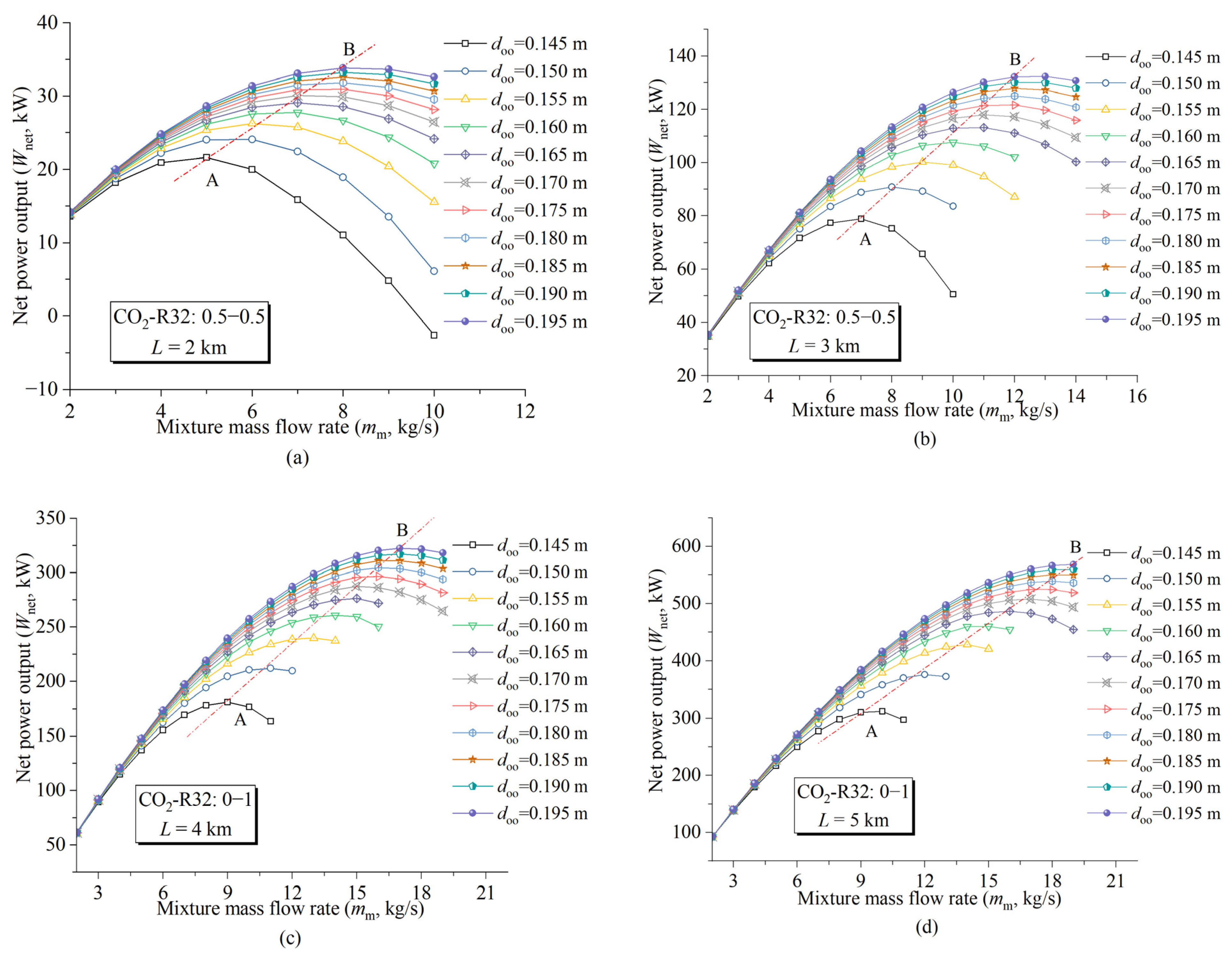
4.3. Matching Relationship between the Mass Flow Rate and Pipe Diameter
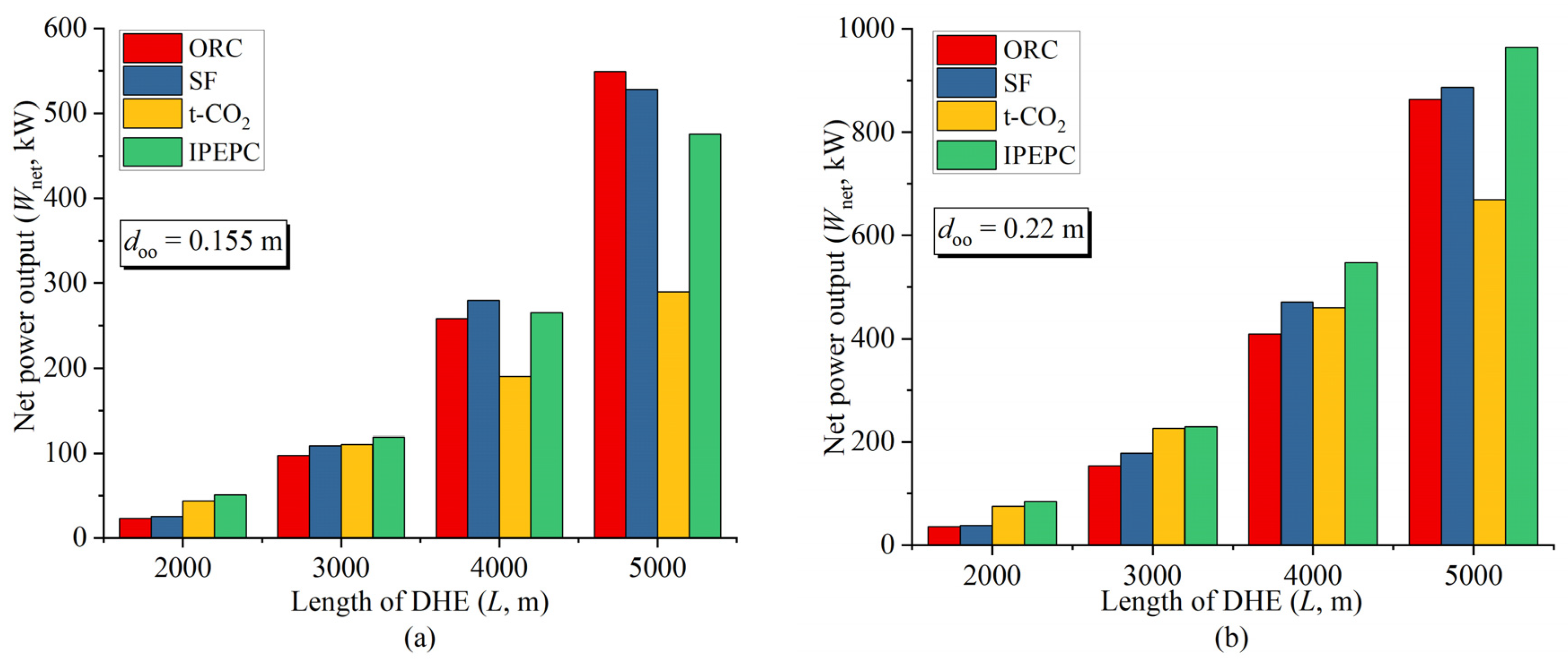
4.4. Comparison among ORC, SF, t-CO2, and IPEPC
5. Further Study
6. Conclusions
- (1)
- The IPEPC model using a CO2-based mixture as the working fluid has been developed, which can utilize a wide range of geothermal resources, including hot dry rock geothermal energy. The IPEPC, with a CO2-R32 mixture as its working fluid, demonstrates an advantage over the other three power generation systems (t-CO2, SF, and ORC).
- (2)
- It is shown that the power generation performance of the IPEPC can be enhanced by choosing a DHE inlet pressure slightly higher than the condensation pressure. The analysis of the thermosiphon effect indicates that the IPEPC system can achieve energy savings of 43.3% and 53.8% in pump power consumption corresponding to a DHE length of 3 km and 4 km, respectively.
- (3)
- There is an approximately linear matching relationship between the outer pipe’s outside wall diameter and the optimal mass flow rate of the working fluid.
- (4)
- An IPEPC with a smaller outer pipe outside diameter (doo = 0.155 m) shows an advantage over the other three systems (t-CO2, SF, and ORC) in terms of net power outputs only when the DHE length (L) is less than or equal to 3 km. In the case that the DHE length is 2 km, the net power output of IPEPC surpasses that of the t-CO2, SF, and ORC by 17.5%, 98.4%, and 120%, respectively.
- (5)
- An IPEPC with a larger outer pipe outside diameter (doo = 0.22 m) shows an advantage in power generation over the other three systems (t-CO2, SF, and ORC) for a wider range of the DHE length (ranging from 2 km to 5 km). In the case that the DHE length is 5 km, the net power output of IPEPC surpasses that of the t-CO2, SF, and ORC by 44.2%, 8.7%, and 11.7%, respectively.
- (6)
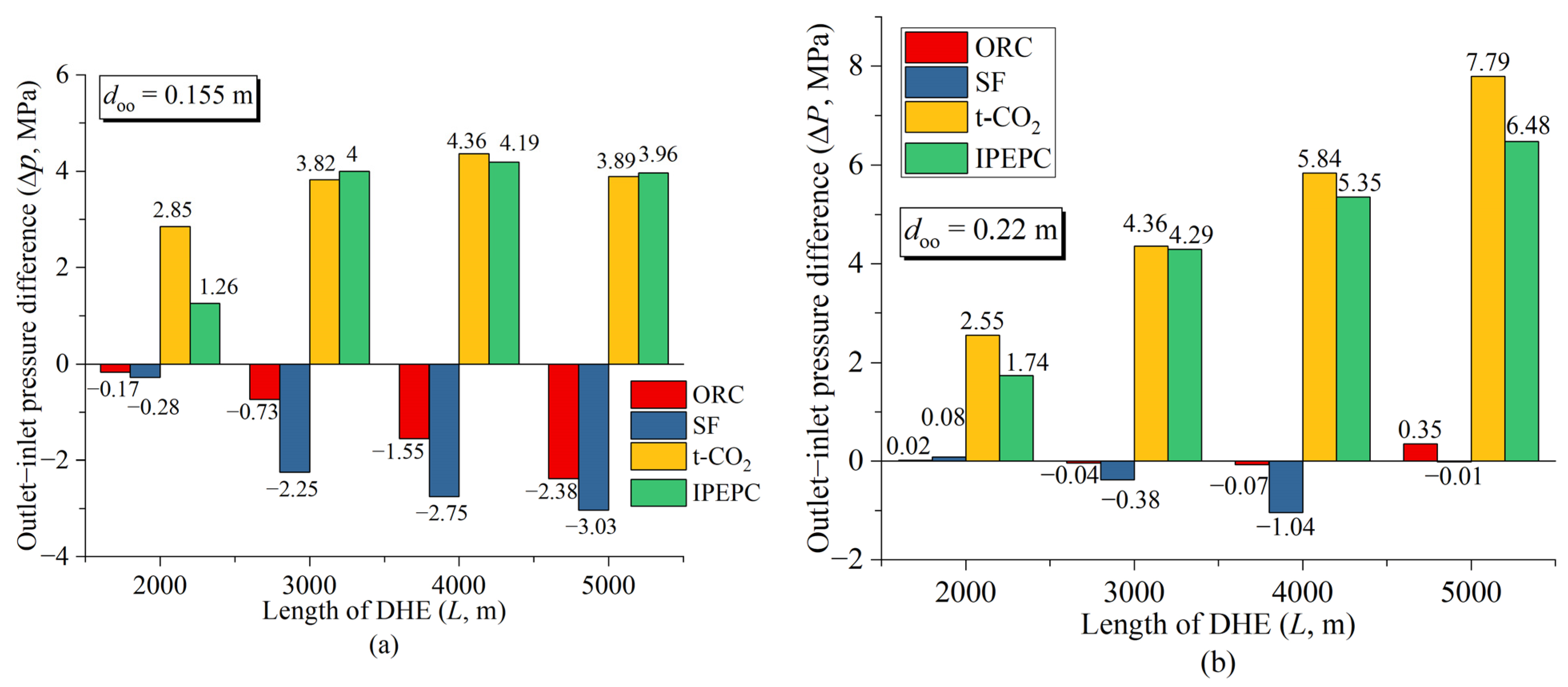
- The DHE outlet–inlet pressure difference (ΔP) of either IPEPC or t-CO2 system is positive for any given DHE length ranging from 2 km to 5 km, indicating that the DHE outlet pressure is greater than the inlet pressure if the IPEPC or t-CO2 system is applied. This thermosiphon effect increases with the increase in DHE length for the system with a larger diameter (doo = 0.22 m). In contrast, the DHE outlet pressure is less than the inlet pressure in most cases if the ORC or SF system is applied.
- (7)
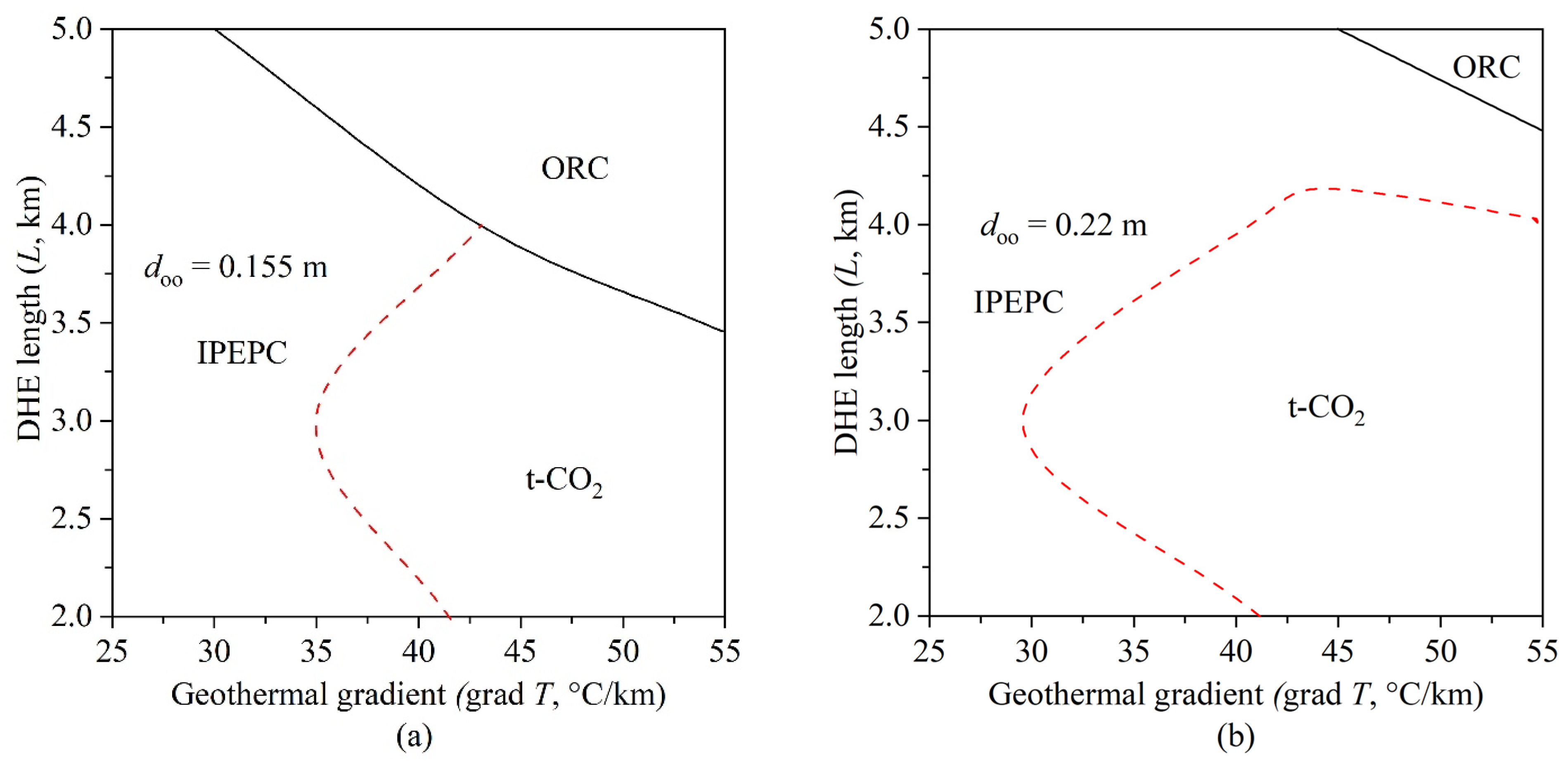
- The generated application scopes for the three investigated systems (IPEPC, t-CO2, and ORC) show that the IPEPC always has an advantage over the t-CO2 and ORC systems when the geothermal gradient is 30 °C/km or less. The greater the geothermal gradient and the longer the DHE, the more tendency is to use the ORC; however, a larger geothermal gradient alone can increase the tendency of using the t-CO2 system. Increasing the outer pipe’s outside diameter (doo) from 0.155 m to 0.22 m results in a larger application scope of the t-CO2 system but a smaller scope of the ORC system.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| h | Specific enthalpy, kJ/kg | Rio | Total thermal resistance in DHE, K/W |
| L | DHE length, m | Uio | Overall heat transfer coefficient in DHE, W/m2·K |
| mm | CO2 mixture mass flow rate, kg/s | Row | Thermal resistance between wellbore and outer pipe, K/W |
| Wg | Turbine-generated power output, kW | Uow | Overall heat transfer coefficient between wellbore and outer pipe, W/m2·K |
| Wp | Pump consumed power, kW | z | Vertical coordinate, m |
| Wnet | Net power output, kW | f | Friction factor |
| Q | Heat transfer rate, kW | d | Diameter, m |
| Pin | DHE inlet pressure, MPa | q | Heat flux per unit length, W/m |
| Pout | DHE outlet pressure, MPa | Cp | Heat capacity at constant, J/kg∙K |
| Pc | Critical pressure, MPa | µJ-T | Joule–Thomson coefficient, K/MPa |
| Tin | DHE inlet temperature, °C | Ap | Flow area, m2 |
| Tout | DHE outlet temperature, °C | λi | Inner pipe conductivity, W/m∙K |
| Tc | Critical temperature, °C | λc | Well casing thermal conductivity, W/m∙K |
| Te | Formation temperature, °C | λins | Insulated pipe thermal conductivity, W/m∙K |
| Tw | Wellbore outside wall temperature, °C | λo | Outer pipe conductivity, W/m∙K |
| ηt | Turbine isentropic efficiency, % | Abbreviations | |
| ηp | Pump isentropic efficiency, % | DHE | Downhole heat exchanger |
| dii | Inner pipe inside wall diameter, m | IPEC | Increasing-pressure endothermic cycle |
| dio | Inner pipe outside wall diameter, m | ORC | Organic Rankine cycle |
| doi | Outer pipe inside wall diameter, m | SF | Single-flash system |
| doo | Outer pipe outside wall diameter, m | t-CO2 | Trans-critical CO2 cycle |
| dc | Well casing diameter, m | OWF | Organic working fluid |
| ρe | Density of rock, kg/m3 | HDR | Hot dry rock |
| Shear stress, MPa | EGS | Enhanced geothermal system | |
| v | Fluid velocity, m/s | ODP | Ozone depletion potential |
| g | Gravitational acceleration, m/s2 | GWP | Global warming potential |
| CLGEE | Closed-loop geothermal energy extraction | ||
References
- Budiono, A.; Suyitno, S.; Rosyadi, I.; Faishal, A.; Ilyas, A.X. A Systematic Review of the Design and Heat Transfer Performance of Enhanced Closed-Loop Geothermal Systems. Energies 2022, 15, 742. [Google Scholar] [CrossRef]
- Sharmin, T.; Khan, N.R.; Akram, M.S.; Ehsan, M.M. A State-of-the-Art Review on Geothermal Energy Extraction, Utilization, and Improvement Strategies: Conventional, Hybridized, and Enhanced Geothermal Systems. Int. J. Thermofluids 2023, 18, 100323. [Google Scholar] [CrossRef]
- Goldemberg, J. World Energy Assessment Report: Energy and the Challenge of Sustainability; United Nations Pubns: New York, NY, USA, 2000. [Google Scholar]
- Yu, H.; Lu, X.; Ma, F.; Zhang, W.; Liu, J.; Li, C. A study on geothermal electricity systems for Tibet geothermal fields considering thermal performance, economic analysis, and CaCO3 scaling. J. Renew. Sustain. Energy 2023, 15, 013901. [Google Scholar] [CrossRef]
- Xu, C.; Dowd, P.A.; Tian, Z.F. A simplified coupled hydro-thermal model for enhanced geothermal systems. Appl. Energy 2015, 140, 135–145. [Google Scholar] [CrossRef]
- Huang, W.; Cao, W.; Jiang, F. A novel single-well geothermal system for hot dry rock geothermal energy exploitation. Energy 2018, 162, 630–644. [Google Scholar] [CrossRef]
- Breede, K.; Dzebisashvili, K.; Liu, X.; Falcone, G. A systematic review of enhanced (or engineered) geothermal systems: Past, present and future. Geotherm. Energy 2013, 1, 4. [Google Scholar] [CrossRef]
- Baek, H.; Chung, J.B.; Yun, G.W. Differences in public perceptions of geothermal energy based on EGS technology in Korea after the Pohang earthquake: National vs. local. Technol. Forecast. Soc. Chang. 2021, 172, 121027. [Google Scholar] [CrossRef]
- Beckers, K.F.; Rangel-Jurado, N.; Chandrasekar, H.; Hawkins, A.J.; Fulton, P.M.; Tester, J.W. Techno-Economic Performance of Closed-loop Geothermal Systems for Heat Production and Electricity Generation. Geothermics 2022, 100, 102381. [Google Scholar] [CrossRef]
- Hodgson, J.L. Examination of the problem of utilizing the Earth’s internal heat. In Proceedings of the Section G of the British Association for the Advancement of Science at Its Leeds Meeting, Nottingham, UK, 2 September 1927. [Google Scholar]
- Kohl, T.; Brenni, R.; Eugster, W. System performance of a deep borehole heat exchanger. Geothermics 2002, 31, 687–708. [Google Scholar] [CrossRef]
- Yuan, W.; Chen, Z.; Grasby, S.E.; Little, E. Closed-loop geothermal energy recovery from deep high enthalpy systems. Renew. Energy 2021, 177, 976–991. [Google Scholar] [CrossRef]
- Fox, D.; Higgins, B.; Energy, G.; Emeryville, C.A. The effect of well density on resource depletion for a vertical closed-loop sCO2 Geothermal Well System. Geotherm. Resour. Counc. Trans. 2016, 40. Available online: https://www.greenfireenergy.com/ (accessed on 4 April 2024).
- Yildirim, N.; Parmanto, S.; Akkurt, G.G. Thermodynamic assessment of downhole heat exchangers for geothermal power generation. Renew. Energy 2019, 141, 1080–1091. [Google Scholar] [CrossRef]
- Amaya, A.; Scherer, J.; Muir, J.; Patel, M.; Higgins, B. GreenFire Energy Closed-Loop Geothermal Demonstration using Supercritical Carbon Dioxide as Working Fluid. In Proceedings of the 45th Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 10–12 February 2020. [Google Scholar]
- Wang, G.; Ma, H.; Liu, S.; Yang, D.; Xu, X.; Fu, M.; Jia, H. Thermal power extraction from a deep, closed-loop, multi-level, multi-branch, U-shape borehole heat exchanger geothermal system. Renew. Energy 2022, 198, 894–906. [Google Scholar] [CrossRef]
- Pokhrel, S.; Sasmito, A.P.; Sainoki, A.; Tosha, T.; Tanaka, T.; Nagai, C.; Ghoreishi-Madiseh, S.A. Field-scale experimental and numerical analysis of a downhole coaxial heat exchanger for geothermal energy production. Renew. Energy 2022, 182, 521–535. [Google Scholar] [CrossRef]
- Yu, Y.; Cheng, F.; Cheng, J.; Yang, G.; Ma, X. Comparative thermo-economic analysis of co-axial closed-loop geothermal systems using CO2 and water as working fluids. Appl. Therm. Eng. 2023, 230, 120710. [Google Scholar] [CrossRef]
- Dai, J.; Li, J.; Wang, T.; Zhu, L.; Tian, K.; Chen, Z. Thermal performance analysis of coaxial borehole heat exchanger using liquid ammonia. Energy 2023, 263, 125986. [Google Scholar] [CrossRef]
- Liu, S.; Taleghani, A.D. Factors affecting the efficiency of closed-loop geothermal wells. Appl. Therm. Eng. 2023, 222, 119947. [Google Scholar] [CrossRef]
- Guo, T.; Wang, H.; Zhang, S. Comparative analysis of CO2-based transcritical Rankine cycle and HFC245fa-based subcritical organic Rankine cycle using low-temperature geothermal source. Sci. China 2010, 53, 1638–1646. [Google Scholar] [CrossRef]
- Garg, G.; Kumar, P.; Srinivasan, K.; Dutta, P. Evaluation of carbon dioxide blends with isopentane and propane as working fluids for organic Rankine cycles. Appl. Therm. Eng. 2013, 52, 439–448. [Google Scholar] [CrossRef]
- Dai, B.; Li, M.; Ma, Y. Thermodynamic analysis of carbon dioxide blends with low GWP (global warming potential) working fluids-based trans-critical Rankine cycles for low-grade heat energy recovery. Energy 2014, 64, 942–952. [Google Scholar] [CrossRef]
- Pan, L.; Wei, X.; Shi, W. Performance analysis of a zeotropic mixture (R290/CO2) for trans-critical power cycle. Chin. J. Chem. Eng. 2015, 23, 572–577. [Google Scholar] [CrossRef]
- Sánchez, C.J.N.; Da Silva, A.K. Technical and environmental analysis of trans-critical Rankine cycles operating with numerous CO2 mixtures. Energy 2018, 142, 180–190. [Google Scholar] [CrossRef]
- Xia, J.; Wang, J.; Zhang, G.; Lou, J.; Zhao, P.; Dai, Y. Thermo-economic analysis and comparative study of trans-critical power cycles using CO2-based mixtures as working fluids. Appl. Therm. Eng. 2018, 144, 31–44. [Google Scholar] [CrossRef]
- Guo, J.; Li, M.; He, Y.; Xu, J. A study of new method and comprehensive evaluation on the improved performance of solar power tower plant with the CO2-based mixture cycles. Appl. Energy 2019, 256, 113837. [Google Scholar] [CrossRef]
- Pan, L.; Ma, Y.; Li, T.; Li, H.; Li, B.; Wei, X. Investigation on the cycle performance and the combustion characteristic of two CO2-based binary mixtures for the trans-critical power cycle. Energy 2019, 179, 454–463. [Google Scholar] [CrossRef]
- Yu, H.; Lu, X.; Zhang, W.; Liu, J. A Theoretical Study on the Thermal Performance of an Increasing Pressure Endothermic Cycle for Geothermal Power Generation. Energies 2024, 17, 1031. [Google Scholar] [CrossRef]
- Lemmon, E.W.; Bell, I.H.; Huber, M.L.; McLinden, M.O. NIST Standard Reference Database 23: Reference Fluid Thermodynamic and Transport Properties-REFPROP; Version 10.0; National Institute of Standards and Technology; Standard Reference Data Program: Gaithersburg, MD, USA, 2018. [CrossRef]
- Wu, C.; Wang, S.; Jiang, X.; Li, J. Thermodynamic analysis and performance optimization of transcritical power cycles using CO2-based binary zeotropic mixtures as working fluids for geothermal power plants. Appl. Therm. Eng. 2017, 115, 292–304. [Google Scholar] [CrossRef]
- Wang, Z.; Hu, Y.; Xia, X.; Zuo, Q.; Zhao, B.; Li, Z. Thermo-economic selection criteria of working fluid used in dual-loop ORC for engine waste heat recovery by multi-objective optimization. Energy 2020, 197, 117053. [Google Scholar] [CrossRef]
- Abas, N.; Kalair, A.R.; Khan, N. Natural and synthetic refrigerants, global warning: A review. Renew. Sustain. Energy Rev. 2018, 90, 557–569. [Google Scholar] [CrossRef]
- Hasan, A.R.; Kabir, C.S.; Sarica, C. Fluid Flow and Heat Transfer in Wellbores; Society of Petroleum Engineers: Richardson, TX, USA, 2002. [Google Scholar]
- Wang, Z.; Sun, B.; Wang, J.; Hou, L. Experimental study on the friction coefficient of supercritical carbon dioxide in pipes. Int. J. Greenh. Gas Control 2014, 25, 151–161. [Google Scholar] [CrossRef]
- Hasan, A.R.; Kabir, C.S. A mechanistic model for computing fluid temperature profiles in gas-lift wells. SPE Prod. Facil. 1996, 11, 179–185. [Google Scholar] [CrossRef]





| Source | DHE Type | DHE Depth | Bottom Temperature | Working Fluid | Findings |
|---|---|---|---|---|---|
| Fox et al. (2016) [13] | Co-axial case | 5.5 km | 680 °C | sCO2 | 1 MW of power generation over 25 years of operation. A 100 m well spacing should be selected to avoid thermal interference. |
| Yildirim et al. (2019) [14] | Co-axial case; Multi-tube; U-type | 2500 m | 160 °C | R134a | The optimal mass flow rate for R134a is determined to be 64 kg/s with a net power output of 2511 kW; annual electricity generation is calculated as 20.89 GWh. |
| Amaya et al. (2020) [15] | Vertical tube-in-tube | 330 m | 180 °C | Water and sCO2 | GreenFire Energy installed a demonstration closed-loop geothermal power generation system; tests show that the power output is up to 1.2 MW. |
| Yuan et al. (2021) [12] | U-type | 1828.8 m | 150 °C | Water | The heat exchange in vertical injection and production well is minimal compared with the 10-multilateral tube; the CLGEE can provide 9 to 11 MW of stable heat production over 30 years. |
| Beckers et al. (2022) [9] | Co-axial case; U-type | 2–4 km | 500 °C | Water and sCO2 | The thermal output range for 2 km vertical co-axial is 0.4 to 0.9 MW, and that of 2 km U-type is 1.3 to 4.5 MW; Utilizing sCO2 as the working fluid to drive a turbine for electricity generation is more effective than using a water-driving turbine. |
| Wang et al. (2022) [16] | U-type with multi-level or multi-branch | 3 km | 200 °C | Water | The maximum heat transfer efficiency can be achieved at a mass flow rate of 40 kg/s under the condition of 3 branches and a horizontal tube length of 2000 m; The lowest power generation price is obtained under the condition of 4 branches and a 3000 m horizontal tube when the temperature is between 180 to 240 °C. |
| Pokhrel et al. (2022) [17] | Co-axial case | 500 m | 190 °C | Water | The average output thermal power for 456 h from the geothermal system ranges from 172 kW to 262 kW based on the operating condition chosen, and the total thermal energy generated changes between 82 MWh and 194 MWh from a single borehole. |
| Yu et al. (2023) [18] | Co-axial case in abandoned wells | 3 km | 146 °C | Water and sCO2 | CO2-based CLGEE produces two times more heating power than water-based CLGS when the working fluid is entirely driven by the thermosiphon effect. |
| Dai et al. (2023) [19] | Co-axial case | 1.8 km | 57 °C | Ammonia, water, CO2, R32 et al. | Ammonia, water, CO2, isobutane, R41, R152a, R245fa, R32, and R134a were compared; The ammonia has a relatively low inlet pressure (5 MPa) and pressure loss (2.7 MPa), which means ammonia has a lower circulation pump. |
| Liu et al. (2023) [20] | Co-axial case | 2.6 km | 175 °C | Water | A higher fluid capacity yields lower production temperature but higher thermal power; The tube’s outer diameter has a limited effect on the thermal power efficiency. |
| Substance | Critical Temperature (Tc, °C) | Critical Pressure (Pc, MPa) | ODP | GWP | Atmospheric Life (Years) | ASHRAE Class |
|---|---|---|---|---|---|---|
| CO2 | 30.98 | 7.38 | 0 | 1 | 200 | A1 |
| R32 | 78.1 | 5.78 | 0 | 675 | 4.9 | A2 |
| R1234yf | 94.7 | 3.38 | 0 | 4.4 | 0.029 | A2L |
| R161 | 102.2 | 5.09 | 0 | 12 | 0.21 | A3 |
| R152a | 113.3 | 4.52 | 0 | 124 | 1.4 | A2 |
| Items | Parameters |
|---|---|
| Isentropic efficiency of turbine, ηt | 0.85 |
| Isentropic efficiency of pump, ηp | 0.8 |
| Condenser outlet temperature, Tco (°C) | 25 |
| Cooling water temperature, Tci (°C) | 20 |
| Inner pipe inside diameter, dii (m) | 0.083 |
| Inner pipe outside diameter, dio (m) | 0.10 |
| Annulus pipe inside diameter, doi (m) | 0.135 |
| Annulus pipe outside diameter, doo (m) | 0.155 |
| Well casing diameter, dc (m) | 0.178 |
| Rock formation density, ρe (kg/m3) | 2650 |
| Rock heat capacity, ce (J/kg·k) | 837 |
| Rock formation thermal conductivity, λe (W/m·k) | 2.5 |
| Well casing thermal conductivity, λca (W/m·k) | 30 |
| Insulated tube thermal conductivity, λins (W/m·k) | 0.02 |
| Cement thermal conductivity, λce (W/m·k) | 0.72 |
| Geothermal gradient, grad T (°C/km) | 40 |
| Items | Parameters |
|---|---|
| Well depth, km | 3 |
| Rock density, kg/m3 | 2570 |
| Heat conductivity, W/m·K | 1.8 |
| Surface temperature, °C | 12 |
| Rock permeability, m2 | 1.5 × 10−15 |
| DHE inner radius, mm | 65 |
| DHE outer radius, mm | 100 |
| Wellbore wall heat conductivity, W/m·K | 2.5 |
| Insulation layer heat conductivity, W/m·K | 0.02 |
| Working fluid inlet temperature, °C | 10 |
| CO2 wellhead pressure, MPa | 7.5 |
| Water wellhead pressure, MPa | 0.1013 |
| Equipment | Items | DHE: 3 km CO2-R32 = 0.5–0.5, 9 kg/s | DHE: 4 km CO2-R32 = 0.5–0.5, 10 kg/s | ||
|---|---|---|---|---|---|
| Inlet | Outlet | Inlet | Outlet | ||
| Pump working Scenario 1 | T, °C | 25 | 29.79 | 25 | 29.79 |
| P, MPa | 4 | 8 | 4 | 8 | |
| h, kJ/kg | 253.9 | 260.02 | 253.9 | 260.02 | |
| Wp1, kW | 55.1 | 61.2 | |||
| DHE | P, MPa | 8 | 11.16 | 8 | 12.78 |
| Pump working Scenario 2 | P, MPa | As Pump 1 | 11.16 | As Pump 1 | 12.78 |
| h, kJ/kg | As Pump 1 | 264.7 | As Pump 1 | 267.16 | |
| Wp2, kW | 97.2 | 132.6 | |||
| Pump power consumption difference | Wp2 − Wp1 | 42.1 | 71.4 | ||
| (Wp2 − Wp1)/Wp2 × % | 43.3% | 53.8% | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, H.; Lu, X.; Zhang, W.; Liu, J. Thermodynamic Analysis of an Increasing-Pressure Endothermic Power Cycle Integrated with Closed-Loop Geothermal Energy Extraction. Energies 2024, 17, 1756. https://doi.org/10.3390/en17071756
Yu H, Lu X, Zhang W, Liu J. Thermodynamic Analysis of an Increasing-Pressure Endothermic Power Cycle Integrated with Closed-Loop Geothermal Energy Extraction. Energies. 2024; 17(7):1756. https://doi.org/10.3390/en17071756
Chicago/Turabian StyleYu, Hao, Xinli Lu, Wei Zhang, and Jiali Liu. 2024. "Thermodynamic Analysis of an Increasing-Pressure Endothermic Power Cycle Integrated with Closed-Loop Geothermal Energy Extraction" Energies 17, no. 7: 1756. https://doi.org/10.3390/en17071756
APA StyleYu, H., Lu, X., Zhang, W., & Liu, J. (2024). Thermodynamic Analysis of an Increasing-Pressure Endothermic Power Cycle Integrated with Closed-Loop Geothermal Energy Extraction. Energies, 17(7), 1756. https://doi.org/10.3390/en17071756







