Numerical Simulation of the Transport and Sealing Law of Temporary Plugging Particles in Complex Fractures of Carbonate-Type Thermal Storage
Abstract
1. Introduction
2. Mathematical Model
2.1. Basic Assumption
2.2. Governing Equation of Fluid
2.3. Governing Equation of Particle
2.4. Governing Equation of Heat Transfer
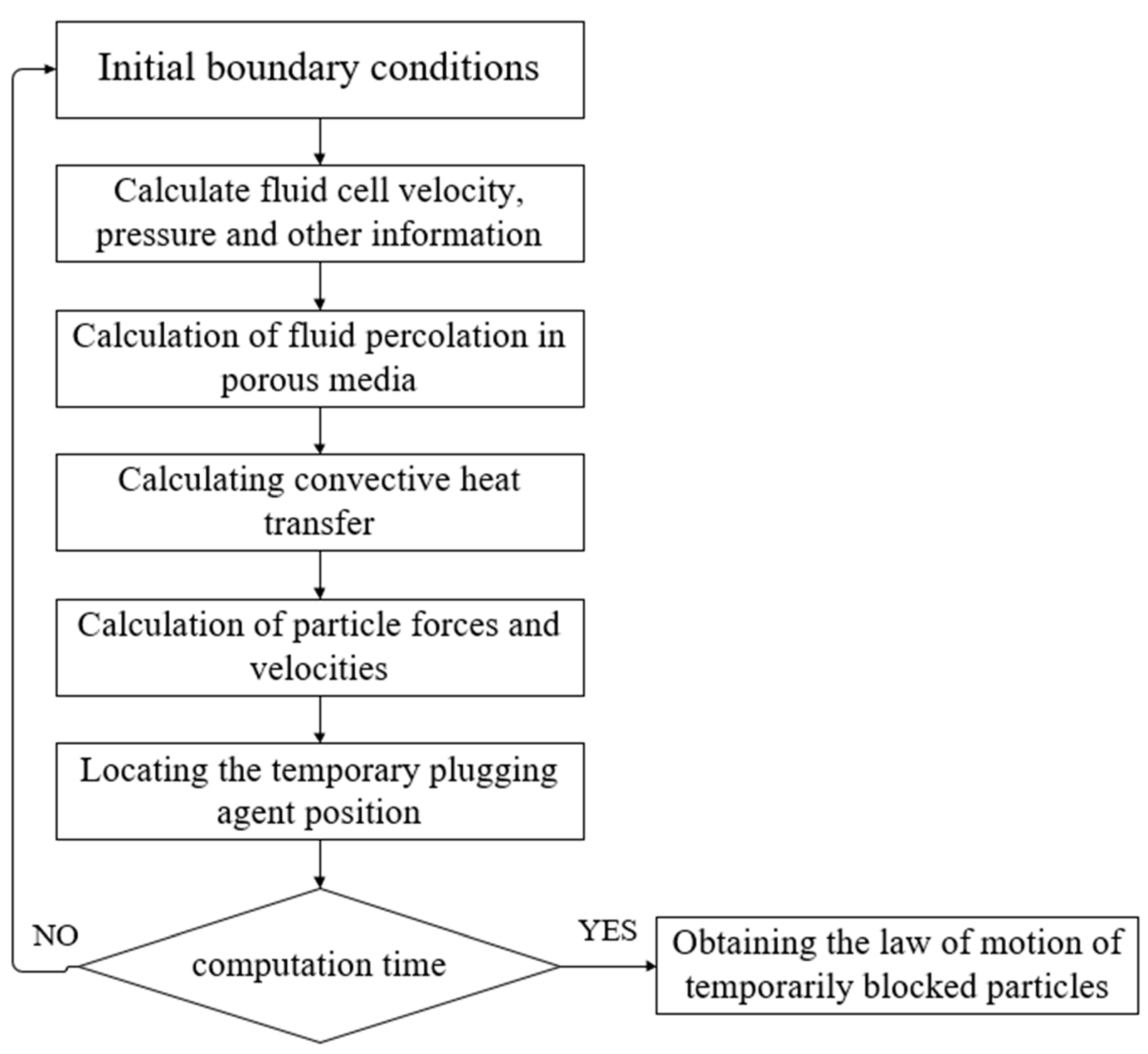
2.5. CFD-DEM Coupling Calculation
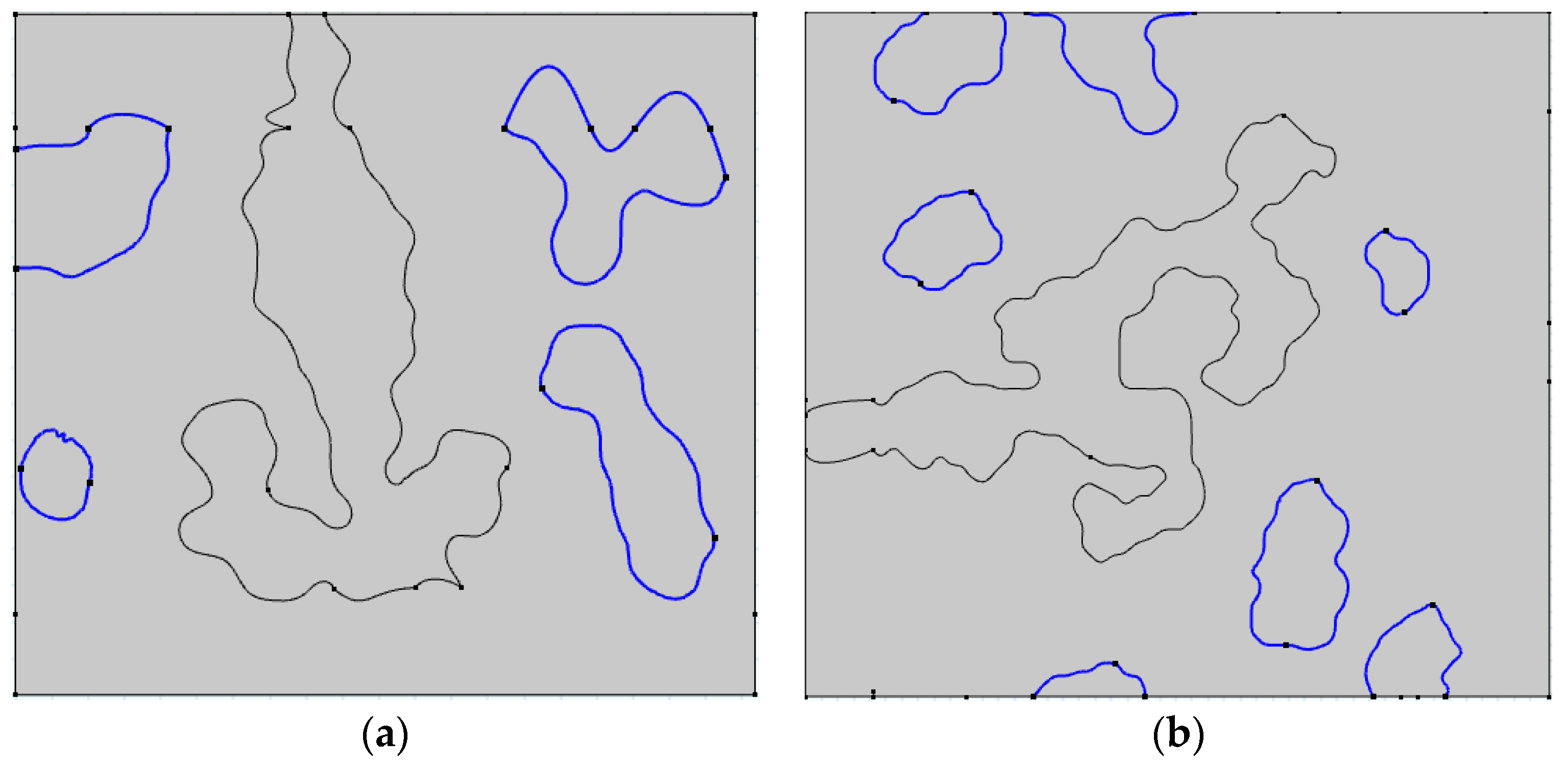
3. Construction of Numerical Model
3.1. Construction of Numerical Model
3.2. Initial and Boundary Conditions
3.3. Grid Independence Verification
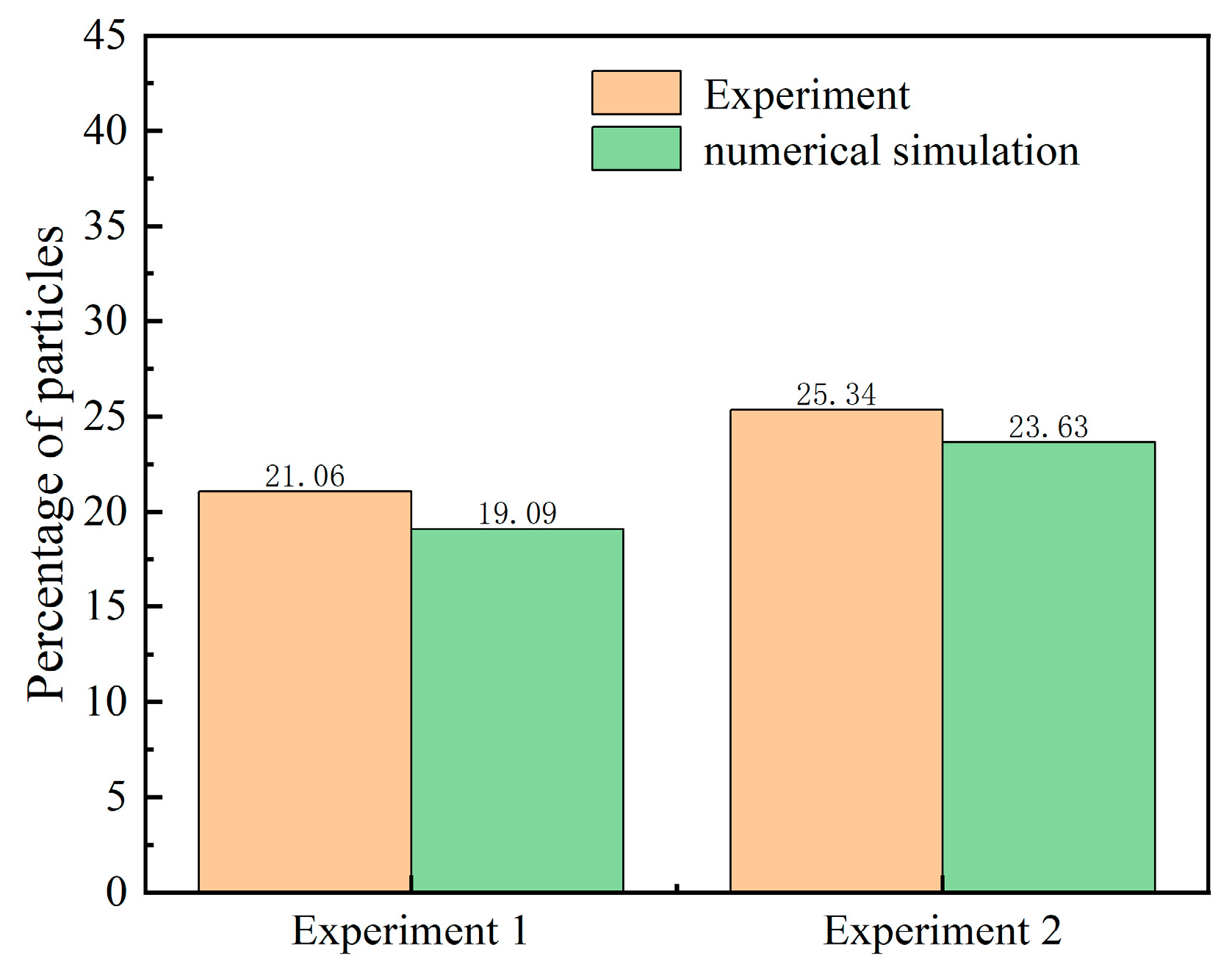
3.4. Model Validation
4. Results and Discussion
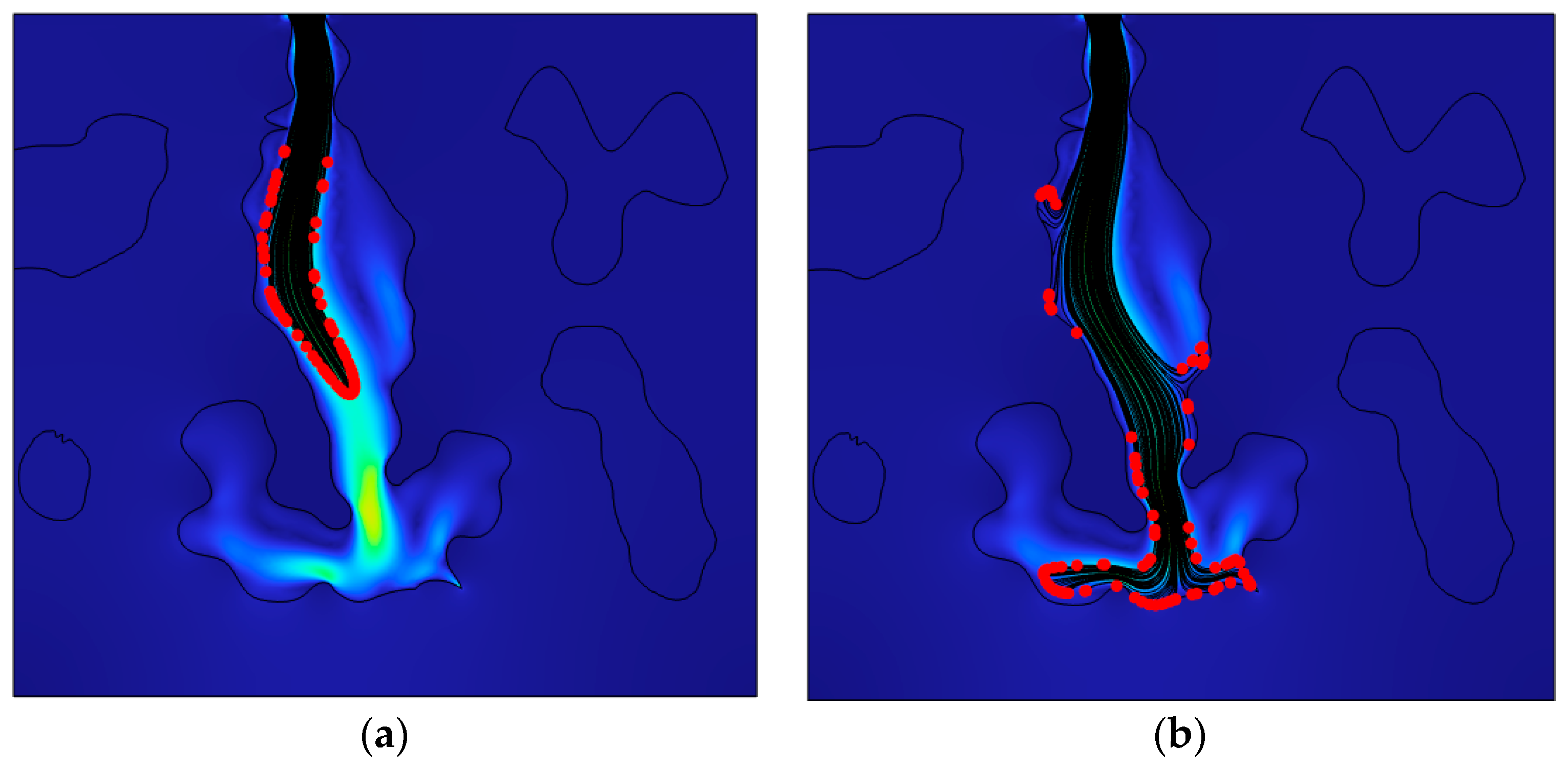
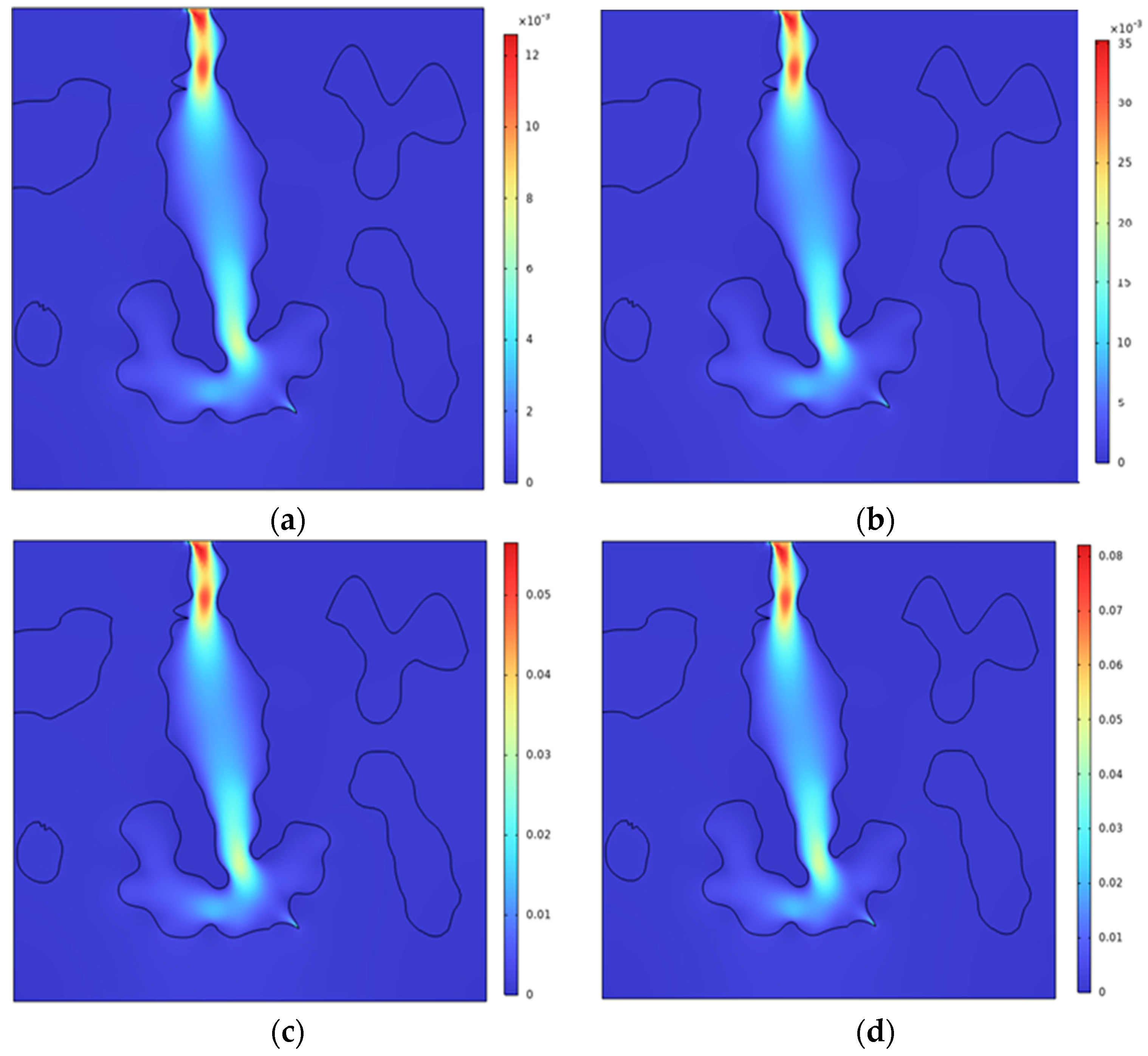
4.1. Particle Migration and Plugging Simulation
4.2. Simulation of Temporary Plugging of Fracture Slit
4.2.1. Effects of Different Injected Displacements
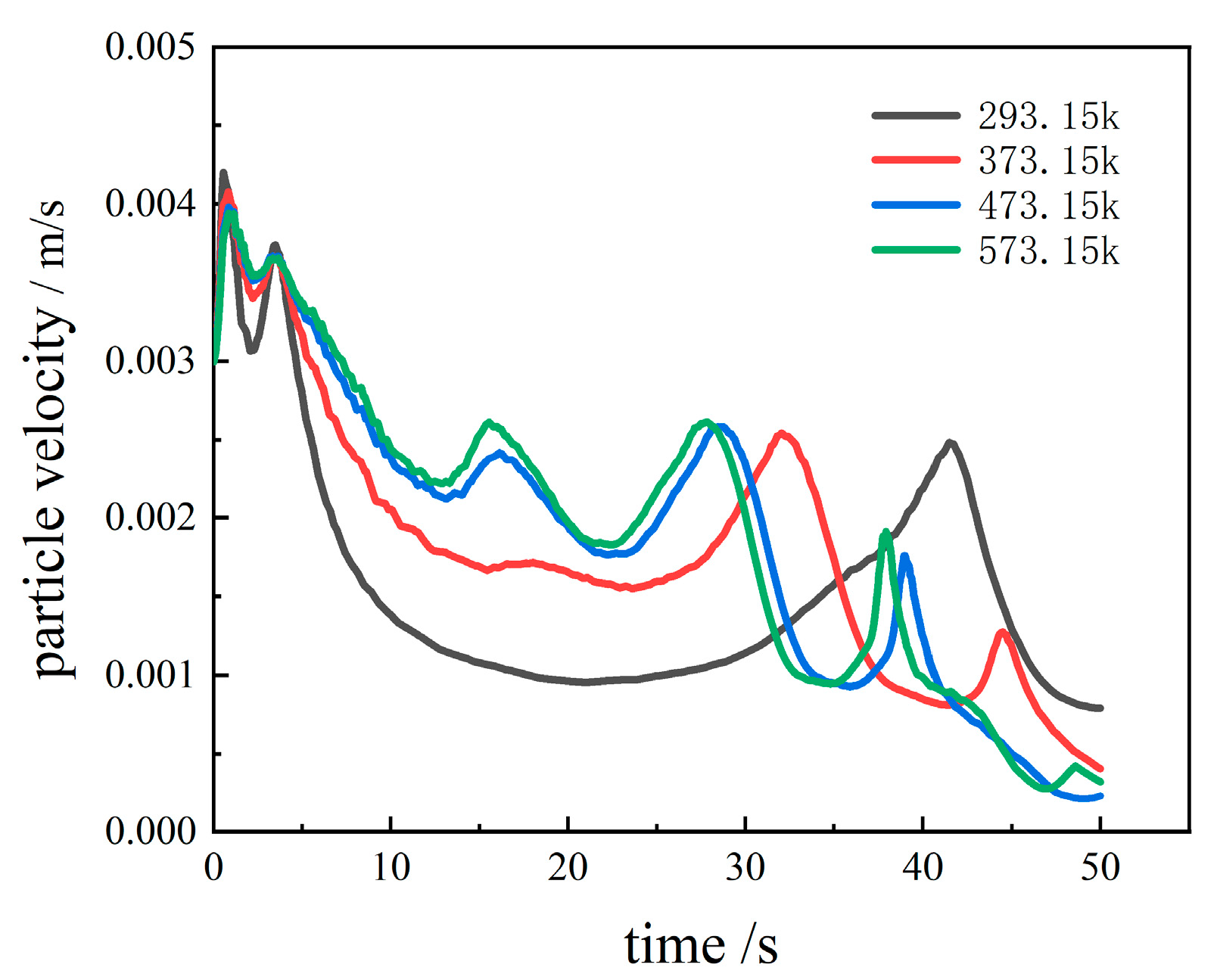
4.2.2. Effect of Different Temperatures
4.3. Simulation of the Temporary Plugging of Complex Fractures
4.3.1. Effect of Different Fracturing Fluid Viscosities
4.3.2. Effect of Different Temperatures
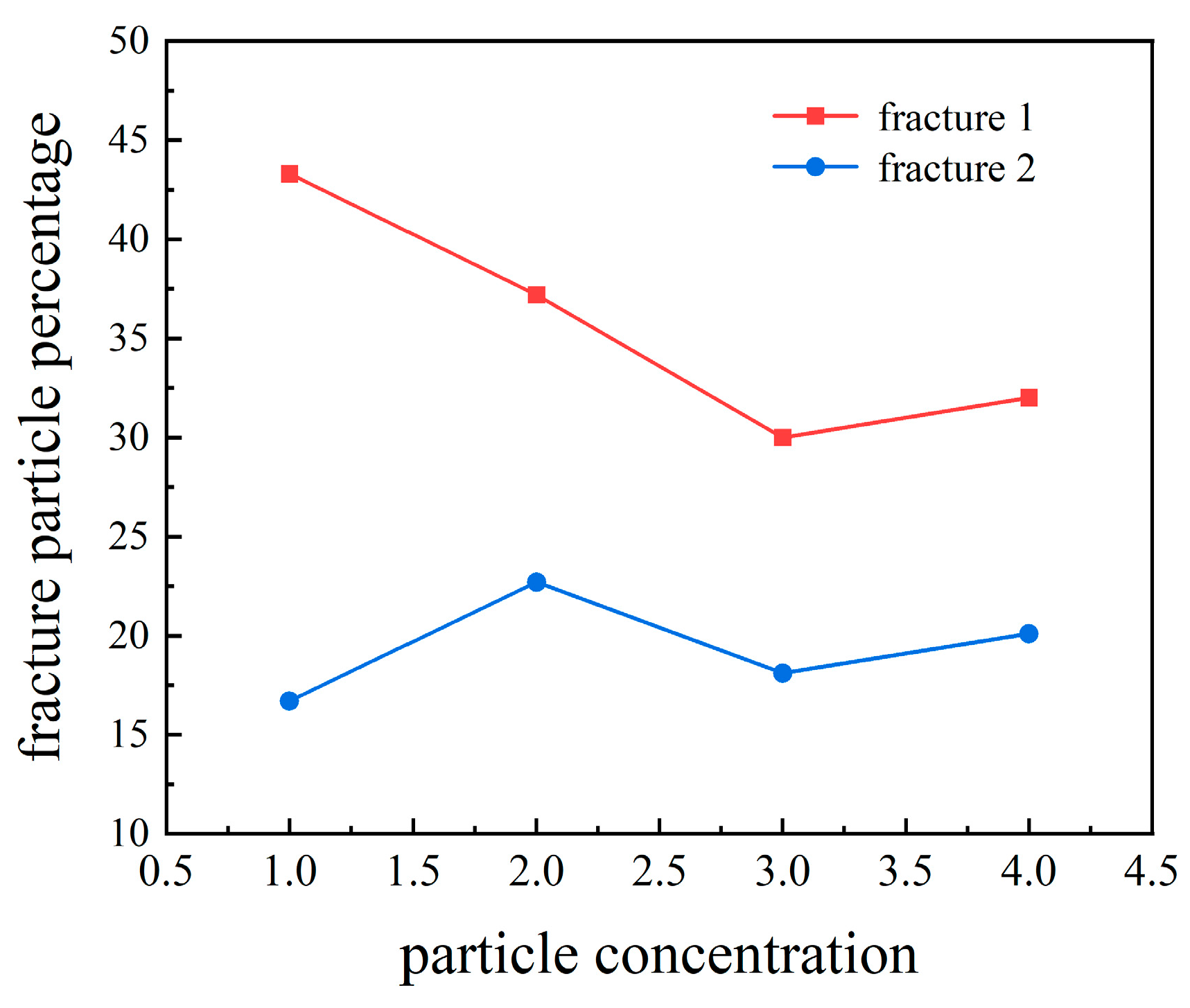
4.3.3. Effect of the Concentration of Temporary Plugging Particles
4.3.4. Effect of Different Particle Size Combinations
5. Conclusions
- Transient plugging particle transport in thermal storage fractures can be simulated using CFD-DEM methods
- High-viscosity fracking fluids can cause the dispersion of temporary plugging particles during transport
- Different combinations of particle sizes give better results for temporary plugging particles
- High temperatures increase particle velocity
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, G.; Wu, X.; Song, X.; Zhou, S.; Li, M.; Zhu, H.; Kong, Y.; Huang, Z. Status and Challenges of Dry hot Rock Geothermal Resource Extraction Technology. Pet. Sci. Bull. 2022, 7, 343–364. [Google Scholar]
- Wang, J.; Hu, S.; Pang, Z.; He, L.; Zhao, P.; Zhu, C.; Rao, S.; Tang, X.; Kong, Y.; Luo, L.; et al. Assessment of Geothermal Resource Potential of Dry Hot Rocks in Mainland China. Sci. Technol. Her. (Newsp.) 2012, 30, 25–31. [Google Scholar]
- Xu, T.; Wang, Y.; Feng, G. Research Progress and Development Prospects of Deep Supercritical Geothermal Resources. Gas Ind. 2021, 41, 155–167. [Google Scholar] [CrossRef]
- Yang, Y.; Fu, G.; Zhao, J.; Gu, L. Heat Production Capacity Simulation and Parameter Sensitivity Analysis in the Process of Thermal Reservoir Development. Energies 2023, 16, 7258. [Google Scholar] [CrossRef]
- Guo, T.; Gong, F.; Wang, X.; Lin, Q.; Qu, Z.; Zhang, W. Performance of enhanced geothermal system (EGS) in fractured geothermal reservoirs with CO2 as working fluid. Appl. Therm. Eng. 2019, 152, 215–230. [Google Scholar] [CrossRef]
- Song, G.; Song, X.; Xu, F.; Li, G.; Shi, Y.; Ji, J. Contributions of Thermo-Poroelastic and Chemical Effects to the Production of Enhanced Geothermal System Based on Thermo-Hydro-Mechanical-Chemical Modeling. J. Clean. Prod. 2022, 377, 134471. [Google Scholar] [CrossRef]
- Li, M.; Zhou, F.; Sun, Z.; Dong, E.; Zhuang, X.; Yuan, L.; Wang, B. Experimental Study on Plugging Performance and Diverted Fracture Geometry during Different Temporary Plugging and Diverting Fracturing in Jimusar Shale. J. Pet. Sci. Eng. 2022, 215, 110580. [Google Scholar] [CrossRef]
- Wang, D.B.; Zhou, F.J.; Li, Y.P.; Yu, B.; Martyushev, D.; Liu, X.F.; Wang, M.; He, C.M.; Han, D.X.; Sun, D.L. Numerical Simulation of Fracture Propagation in Russia Carbonate Reservoirs during Refracturing. Pet. Sci. Engl. Ed. 2022, 19, 2781–2795. [Google Scholar] [CrossRef]
- Trumble, M.; Sinkey, M.; Meehleib, J. Got Diversion? Real Time Analysis to Identify Success or Failure. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, The Woodlands, TX, USA, 5–7 February 2019. [Google Scholar] [CrossRef]
- Wang, B.; Zhou, F.; Liang, T.; Wang, D.; Gao, L.; Hu, J. Evaluations of Fracture Injection Pressure and Fracture Mouth Width during Separate-Layer Fracturing with Temporary Plugging. Math. Probl. Eng. 2018, 2018, 3489656. [Google Scholar] [CrossRef]
- Zhou, F.; Liu, Y.; Yang, X.; Zhang, F.; Xiong, C.; Liu, X. Case Study: YM204 Obtained High Petroleum Production by Acid Fracture Treatment Combining Fluid Diversion and Fracture Reorientation. In Proceedings of the 8th European Formation Damage Conference, Scheveningen, The Netherlands, 27–29 May 2009; Society of Petroleum Engineers: Kuala Lumpur, Malaysia, 2019. [Google Scholar] [CrossRef]
- Allison, D.; Curry, S.; Todd, B. Restimulation of Wells Using Biodegradable Particulates as Temporary Diverting Agents. In Proceedings of the Canadian Unconventional Resources Conference, Calgary, AB, Canada, 15–17 November 2011; OnePetro: Richardson, TX, USA, 2011. [Google Scholar] [CrossRef]
- Yang, B. Study on the Formation Mechanism of Hydraulic Fracturing with Multi-Branch Seams. Master’s Thesis, Northeast Petroleum University, Da Qing, China, 2017. [Google Scholar]
- Li, B.; Zhou, F.; Yuan, L.; Li, H.; Cheng, J.; Tan, Y.; Zhang, Y.; Xian, B.; Fan, W. Experimental Investigation on the Fracture Diverting Mechanism and Plugging Efficiency Using 3D Printing Fractures. In Proceedings of the 53rd U.S. Rock Mechanics/Geomechanics Symposium, New York, NY, USA, 23–26 June 2019; OnePetro: Richardson, TX, USA, 2019. [Google Scholar]
- Zhang, R.; Hou, B.; Tan, P.; Muhadasi, Y.; Fu, W.; Dong, X.; Chen, M. Hydraulic Fracture Propagation Behavior and Diversion Characteristic in Shale Formation by Temporary Plugging Fracturing. J. Pet. Sci. Eng. 2020, 190, 107063. [Google Scholar] [CrossRef]
- Li, M.-H.; Zhou, F.-J.; Liu, J.-J.; Yuan, L.-S.; Huang, G.-P.; Wang, B. Quantitative Investigation of Multi-Fracture Morphology during TPDF through True Tri-Axial Fracturing Experiments and CT Scanning. Pet. Sci. 2022, 19, 1700–1717. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Q.; Zou, Y. Experimental Investigation of the Growth Law of Multi-Fracture during Temporary Plugging Fracturing within a Stage of Multi-Cluster in a Horizontal Well. Processes 2022, 10, 637. [Google Scholar] [CrossRef]
- Chen, X.; Zhao, L.; Liu, P.; Du, J.; Wang, Q.; An, Q.; Chang, B.; Luo, Z.; Zhang, N. Experimental Study and Field Verification of Fracturing Technique Using a Thermo-Responsive Diverting Agent. J. Nat. Gas Sci. Eng. 2021, 92, 103993. [Google Scholar] [CrossRef]
- McCartney, E.S.; Kennedy, R.L. A Family of Unique Diverting Technologies Increases Unconventional Production and Recovery in Multiple Applications—Initial Fracturing, Refracturing, and Acidizing. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 9–11 February 2016; OnePetro: Richardson, TX, USA, 2016. [Google Scholar] [CrossRef]
- Arnold, D.; Fragachan, F. Eco-Friendly Degradable Mechanical Diverting Agents for Combining Multiple-Staged Vertical Wells: Case History from Wasatch Formation. In Proceedings of the Abu Dhabi International Petroleum Exhibition and Conference, Abu Dhabi, United Arab Emirates, 10–13 November 2014; OnePetro: Richardson, TX, USA, 2014. [Google Scholar] [CrossRef]
- Vidma, K.; Abivin, P.; Dunaeva, A.; Panga, M.; Nikolaev, M.; Usoltsev, D.; Mayo, J.T. Far-Field Diversion Technology to Prevent Fracture Hits in Tightly Spaced Horizontal Wells. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 24–26 September 2018; OnePetro: Richardson, TX, USA, 2018. [Google Scholar] [CrossRef]
- Shahri, M.P.; Huang, J.; Smith, C.S.; Fragachán, F.E. An Engineered Approach to Design Biodegradables Solid Particulate Diverters: Jamming and Plugging. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 9–11 October 2017; OnePetro: Richardson, TX, USA, 2017. [Google Scholar] [CrossRef]
- Hu, X.; Wu, K.; Song, X.; Yu, W.; Tang, J.; Li, G.; Shen, Z. A New Model for Simulating Particle Transport in a Low-Viscosity Fluid for Fluid-Driven Fracturing. AIChE J. 2018, 64, 3542–3552. [Google Scholar] [CrossRef]
- Zhao, J.; Zhao, X.; Zhao, J.; Cao, L.; Hu, Y.; Liu, X. Coupled Model for Simulating Proppant Distribution in Extending Fracture. Eng. Fract. Mech. 2021, 253, 107865. [Google Scholar] [CrossRef]
- Yuan, L.; Zhou, F.; Li, M.; Wang, B.; Bai, J. Experimental and Numerical Investigation on Particle Diverters Transport during Hydraulic Fracturing. J. Nat. Gas Sci. Eng. 2021, 96, 104290. [Google Scholar] [CrossRef]
- Gong, Y.; Mehana, M.; El-Monier, I.; Viswanathan, H. Proppant placement in complex fracture geometries: A computational fluid dynamics study. J. Nat. Gas Sci. Eng. 2020, 79, 103295. [Google Scholar] [CrossRef]
- Han, K.; Feng, Y.T.; Owen, D.R.J. Coupled lattice Boltzmann and discrete element modelling of fluid–particle interaction problems. Comput. Struct. 2007, 85, 1080–1088. [Google Scholar] [CrossRef]
- Wu, C.-H.; Yi, S.; Sharma, M.M. Proppant Distribution Among Multiple Perforation Clusters in a Horizontal Wellbore. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, The Woodlands, TX, USA, 24–26 January 2017; OnePetro: Richardson, TX, USA, 2017. [Google Scholar] [CrossRef]
- Ren, L.; Lin, C.; Zhao, J.; Lin, R.; Wu, J.; Wu, J.; Hu, Z. Numerical Simulation of Coated Proppant Transport and Placement in Hydraulic Fractures Based on CFD-DEM. In Petroleum Science and Technology; Taylor and Francis: Abingdon, UK, 2023; pp. 1–21. [Google Scholar] [CrossRef]
- Sui, W.; Tian, Y.; Zheng, Y.; Dong, K. Modeling Temporary Plugging Agent Transport in the Wellbore and Fracture with a Coupled Computational Fluid Dynamics–Discrete Element Method Approach. Energy Fuels 2021, 35, 1422–1432. [Google Scholar] [CrossRef]
- Wang, D.; Qin, H.; Zheng, C.; Sun, D.; Yu, B. Transport Mechanism of Temporary Plugging Agent in Complex Fractures of Hot Dry Rock: A Numerical Study. Geothermics 2023, 111, 102714. [Google Scholar] [CrossRef]
- Zheng, C.; Wang, D.; Wang, Q.; Sun, S.; Sun, D.; Yu, B. The Migration Mechanism of Temporary Plugging Agents in Rough Fractures of Hot Dry Rock: A Numerical Study. Phys. Fluids 2024, 36, 023323. [Google Scholar] [CrossRef]
- Anderson, T.B.; Jackson, R. Fluid Mechanical Description of Fluidized Beds. Equ. Motion. Ind. Eng. Chem. Fund. 1967, 6, 527–539. [Google Scholar] [CrossRef]
- Guo, T.; Tang, S.; Liu, S.; Liu, X.; Zhang, W.; Qu, G. Numerical Simulation of Hydraulic Fracturing of Hot Dry Rock under Thermal Stress. Eng. Fract. Mech. 2020, 240, 107350. [Google Scholar] [CrossRef]
- Li, Z. Mechanisms of Proppant Transport and Pressure Embedding in Fractured Coal Seams. Ph.D. Thesis, China University of Mining and Technology, Xuzhou, China, 2024. [Google Scholar]















| Parameters | Units | Values |
|---|---|---|
| Fracturing fluid density | kg/m3 | 1200 |
| Fracturing fluid viscosity | Pa s | 0.03 |
| Initial fluid temperature | k | 293.15 |
| Initial fluid displacement | mL/min | 15 |
| Density of plugged particles | kg/m3 | 2200 |
| Plugging particle size | cm | 0.05 |
| Matrix porosity | - | 0.05 |
| Matrix penetration rate | m2 | 5 × 10−18 |
| Matrix density | kg/m3 | 2800 |
| Matrix thermal conductivity | W/(m k) | 2 |
| Matrix heat capacity | J/(kg k) | 920 |
| Number | Particle Size Combination | Particle Diameter | Particle Number Ratio |
|---|---|---|---|
| 1 | Single particle size | 0.05 | 1 |
| 2 | Two particle sizes | 0.05, 0.03 | 1:4 |
| 3 | Three particle sizes | 0.05, 0.03, 0.01 | 1:1:3 |
| 4 | Three particle sizes | 0.05, 0.03, 0.01 | 1:1:4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, A.; Fu, G.; Tang, J.; Wang, D. Numerical Simulation of the Transport and Sealing Law of Temporary Plugging Particles in Complex Fractures of Carbonate-Type Thermal Storage. Energies 2024, 17, 3283. https://doi.org/10.3390/en17133283
Tian A, Fu G, Tang J, Wang D. Numerical Simulation of the Transport and Sealing Law of Temporary Plugging Particles in Complex Fractures of Carbonate-Type Thermal Storage. Energies. 2024; 17(13):3283. https://doi.org/10.3390/en17133283
Chicago/Turabian StyleTian, Anle, Guoqiang Fu, Jinyu Tang, and Dezhao Wang. 2024. "Numerical Simulation of the Transport and Sealing Law of Temporary Plugging Particles in Complex Fractures of Carbonate-Type Thermal Storage" Energies 17, no. 13: 3283. https://doi.org/10.3390/en17133283
APA StyleTian, A., Fu, G., Tang, J., & Wang, D. (2024). Numerical Simulation of the Transport and Sealing Law of Temporary Plugging Particles in Complex Fractures of Carbonate-Type Thermal Storage. Energies, 17(13), 3283. https://doi.org/10.3390/en17133283






