Abstract
In this study, a power cycle (IPEC), with an increasing pressure endothermic process in a downhole heat exchanger (DHE) and a CO2-based working fluid mixture, was developed for geothermal power generation. The increasing pressure endothermic process, which cannot be achieved in a conventional evaporator on the ground, was realized using the gravitational potential energy in the DHE. The parameters of the power cycle and the structural size of the DHE were optimized simultaneously. Using CO2-R32 as the working fluid of the IPEC provides the highest net power output. The net power generated with the IPEC was compared with a single-flash (SF) system, a trans-critical CO2 (t-CO2) system, and an organic Rankine cycle (ORC) under the same heat source and sink conditions. Six selection maps were generated for choosing the optimum power cycle for electricity production, in which four power generation systems (ORC, t-CO2, IPEC, and SF) were included, and two DHE diameters (0.155 m and 0.22 m) were investigated. It was found that the IPEC system had more net power output than the other three systems (ORC, t-CO2, and SF) under the conditions that the geofluid’s mass flow rate was less than 10 kg/s and its temperature was lower than 180 °C.
1. Introduction
Geothermal energy is a type of renewable energy resource that can help to alleviate the current global energy crisis; it literally means Earth’s heat and is estimated to measure more than 6000 °C at the Earth’s core. On average, the crust of the Earth has a temperature gradient of 30 °C/km [1]. Different utilization schemes can be designed according to the characteristics of various geothermal resource types, such as hot, dry rock (HDR), wet steam, hydrothermal, geo-pressure, and magma [2]. Indirect and direct applications of geothermal energy, like power generation, food drying, aquaculture, vegetable cultivation, heating, cooling, etc., are possible through the extraction of hot water/steam [3]. Geothermal power generation mainly involves the selection of the system, the optimization of the operation parameters, the screening of the working fluid, the analysis of underground heat exchangers, etc. A review of the literature was also carried out according to these aspects.
In terms of geothermal power generation systems, there are two types: the direct cycle and the indirect cycle. The direct cycle usually refers to feeding the geo-fluid into the steam turbine for the direct generation of electricity. In contrast, in the so-called indirect cycle, the geo-fluid is sent into the heat exchanger, where a second fluid (clean water, organic matter, ammonia, or CO2) is heated up to a certain temperature, which is then used for electricity generation [4]. The single-flash or multi-flash system is the main form of direct-cycle geothermal power generation. Luo et al. [5] and Zhao et al. [6] analyzed the performance of a single-flash system in Fengshun (China) and compared it with a binary cycle; in low-geothermal-temperature conditions (91 °C), the SF system exhibited better economic benefits than the ORC. Zhu et al. [7] and Lu et al. [8] assessed the thermodynamic performance and performed techno-economic analyses of single-flash and compound systems (double-flash, flash–ORC, and double-flash–ORC) at different geo-fluid temperatures and dryness levels; maps containing the application scope of each flash system were also generated.
The organic Rankine cycle (ORC) is a common geothermal power generation technology, which is usually divided into sub-critical and trans-critical types. A comparison of the working fluid in sub- and trans-critical ORCs, as well as an investigation of the system’s optimal operation conditions, were conducted by Zhang et al. [9]; the trans-critical ORC with R125 as the working fluid was the most economical and effective method for low-temperature geo-fluid conditions. Lecompte et al. [10] found that the trans-critical ORC (TCORC) has 31.5% more net power output than the sub-critical ORC. Walraven et al. [11] conducted a comparison study on various types of ORCs (simple ORC, ORC with recuperation, ORC with turbine bleeding, and triple-pressure ORC) under different geo-fluid conditions (100–150 °C); the trans-critical and multi-pressure ORCs were the most highly performing thermodynamic cycles in most cases.
Another major research focus is how to choose an appropriate working fluid to reduce the entropy increase during endothermic and exothermic processes and improve the performance of power generation systems. In the study of Chys et al. [12], the selection method of mixtures and their optimal concentration are discussed; the results of the study showed that the ORC with binary mixtures has 15.7% more efficiency and produces 12.3% more electricity at low temperatures (150 °C). Similar results have been found in other studies [13,14]. Collings et al. [15] proposed a dynamic ORC using a zeotropic mixture to match the ambient air temperature and improve the thermodynamic performance; this system may have better applications for geothermal energy. An ORC system designed for diesel engine waste heat utilization, with R141b–cyclohexane (0.5–0.5) as the working fluid, can produce an 88.7 kW net power output and has a 13.3% greater net power output compared to that of pure cyclohexane [16].
In addition to organic compounds, CO2 and its mixtures are also being paid more and more attention in the field of geothermal power generation. A novel EGS model with CO2 as the working fluid was first proposed by Brown, who demonstrated that CO2 geological sequestration can be achieved while heat is extracted from the formation [17]. Pruess et al. [18] identified that CO2 has advantages over water in extracting heat from geothermal reservoirs. CO2 also has a great advantage in the flow of wellbores, which may reduce the power consumption required for circulation. Wang et al. [19] designed and analyzed a trans-critical CO2 cycle and a super-critical CO2 cycle used for waste heat recovery; the thermodynamic optimization study revealed that the second-law efficiency of the sCO2-tCO2 cycle was higher than that of the sCO2-ORC cycle. Ayachi et al. [20] proposed a new concept of thermo-electric energy storage based on geothermal reservoirs and the CO2 trans-critical cycle. The system has two thermodynamic cycles: a charging process and a discharging process. Their results showed that the regenerative system with a two-stage discharging cycle had a roundtrip efficiency of 49% (thermal efficiency: 13.7%) for a 10 MW power output.
Although the thermodynamic performance of the CO2 cycle is better than the ORC, it is difficult to condense CO2 into liquid at ambient temperatures, which hinders its popularization and application. One novel t-CO2 with an ejector can solve the condensation problem of CO2; hence, the novel t-CO2 cycle is applicable at higher ambient temperatures [21]. However, the most common and practical approach is to add a second organic compound with a higher critical temperature to CO2 to form a mixture. A thermodynamic and economic analysis of a trans-critical cycle using CO2-based mixtures for low-temperature geothermal power generation was carried out by Wu et al. [22]; they found that CO2-R161 is the best working fluid under the geo-fluid condition (temperatures lower than 150 °C), and the CO2-based mixtures can decrease the operational pressure and enlarge the range of the condensation temperature compared with pure CO2. Sanchez et al. [23] analyzed the influence of the composition of mixtures and mass fraction, heat source temperature, and turbine inlet pressure on the net power generation performance of a trans-critical Rankine cycle, confirming that the addition of refrigerants to the CO2 has a beneficial effect on net power production. Compared with the sCO2 cycle, the super-critical Brayton cycle with a CO2-based mixture as the working fluid shows thermodynamic advantages under a higher ambient temperature [24]. In the study of Rodríguez et al. [25], the power generation performances of pure CO2 and three mixtures (CO2-C6F6, CO2-TiCl4, and CO2-SO2) in transcritical power cycles were analyzed and compared under two different turbine inlet temperatures (550 and 700 °C). Under the low turbine inlet temperature (550 °C), the power cycle of the CO2-based mixtures had 2.7% more second law efficiency than the steam Rankine cycle; at 700 °C, the CO2-based mixtures outperformed the pure CO2 cycle and steam Rankine cycle and had a thermal efficiency as high as 51.6%.
Optimization of the underground heat exchanger structure and heat transfer process is also the main way to improve the utilization of geothermal energy. Bu et al. [26] developed a mathematical model to demonstrate the feasibility of utilizing geothermal energy from a retrofitted well, and the economic earnings of electricity can reach USD 36,833.26/year. A combined reservoir and heat pipe system using CO2 as the working fluid was designed by Huang et al. [27]; the heat extraction rate was twice as high as that of water and a conventional DHE system. The influences of reservoir permeability, the thermal conductivity coefficient of rocks, the inlet temperature, and different working fluids on the heat extraction performance of a downhole exchanger have been studied [28,29]. Li et al. [30] proposed a direct-expansion DHE using supercritical CO2 as the working fluid; the novel exchanger can increase the heat flux by 18.6%, but the short-circuit coefficient is about three times compared to the conventional DHE.
According to a review of the literature, the following aspects of generating a trans-critical power cycle, coupled with a downhole heat exchanger (DHE) in an artesian geothermal well, need to be investigated in detail:
- (1)
- CO2-based working fluid mixtures used in a power cycle integrated with a DHE should be fully studied, based on which the optimal working fluid mixture can be determined;
- (2)
- The thermal siphon effect that occurred in a large-scale DHE when a CO2-based working fluid mixture was used should be quantitatively analyzed, although it has been described in our previous study [31];
- (3)
- An integrated research study of power generation and heat extraction in the DHE should be carried out to obtain the optimum parameters of the whole system.
The aim of this study is to analyze the thermal performance of a “novel” power cycle with an increasing pressure endothermic process that cannot be achieved in an evaporator on the ground, as is commonly used in a conventional organic Rankine cycle. In contrast to the Brayton power cycle and the working fluid (CO2) that was used by Amaya et al. [32], a CO2-based mixture of working fluids are thoroughly investigated in this study. A phase-change condensing process can be recognized since the critical point of each CO2-based mixture investigated in this study is greater than that of pure CO2. Therefore, it is thermodynamically possible to recognize a trans-critical power cycle, which may result in a higher thermal efficiency in power generation. In previous studies, detailed thermal-performance comparisons between the IPEC and other power cycles (in particular, ORC, t-CO2, and SF) have not been investigated; hence, it is necessary to carry out detailed research to fill this gap and, furthermore, to generate useful maps for selecting an optimum power cycle under different geothermal conditions.
The underground and above-ground sections were treated as a whole to build the increasing pressure endothermic cycle (IPEC), the effects of CO2-based mixtures composition and mass fraction, the inlet pressure of DHE, the geometrical size of DHE, and the match of geo-fluid and working fluid mass flow rate are investigated. The application scopes of IPEC are also carried out in this study under different geo-fluid conditions (Tg = 90–200 °C, mg = 3–40 kg/s).
2. Description of the Power Generation System
The schematic diagram of the increasing pressure endothermic cycle (IPEC) is shown in Figure 1a, and the temperature-entropy (T-s) diagram of the power generation system is shown in Figure 1b. The IPEC consists of an underground downhole heat exchanger (DHE) and an above-ground power generation system. The coaxial DHE is installed in a production well, and the power generation system operates in a trans-critical mode.
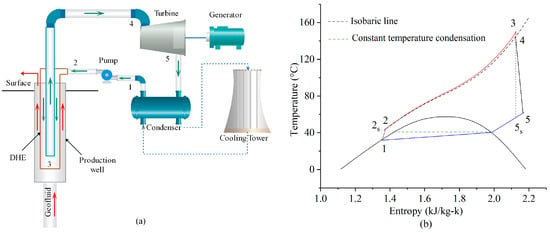
Figure 1.
Schematic diagram (a) and temperature-entropy diagram (b) of the increasing pressure endothermic power generation system.
The CO2-based working fluid mixture (in liquid state) from the condenser is pressurized into the supercritical state (processes 1–2) and is then injected into the DHE annular conduit between the inner tube and outer tube. The downward annulus flow of the working fluid absorbs heat from the upward-flowing geo-water outside the DHE, as illustrated with processes 2–3 in Figure 1b. Due to the gravity field, the working fluid absorbs heat with an increasing pressure endothermic process. The inner and outer pipes are connected at the bottom of the DHE, where the working fluid that extracted heat passes upward from the bottom to the top (processes 3–4) in the inner pipe. The working fluid from the DHE enters the turbine to drive the generator for electricity generation (processes 4–5). The turbine exhaust (state 5) flows into the condenser, where it discharges heat to the cooling water until it is condensed into a complete liquid phase (state 1), which is a non-isothermal condensation progress due to the temperature slide of the CO2 mixture. Then, another cycle starts.
The downward working fluid (CO2-based mixture) and the upward geo-water form a counter-flow mode in the production well, which enhances the heat transfer process. Since the increasing pressure endothermic process (processes 2–3) is the most important feature of this cycle, this power cycle is called the increasing pressure endothermic cycle (IPEC). Only in a large enough vertical scale DHE can the gravitational potential energy that works on the working fluid become significant, resulting in an obvious thermosiphon effect. The red line (processes 2–3) in Figure 1b shows the increasing pressure endothermic process, which is different from the constant-pressure evaporation process in an on-the-ground traditional ORC system (shown by the isobaric processes 2–4), where the effect of the gravitational potential energy does not exist. In the IPEC, due to the difference in the working fluid density between the upward and downward pipes, the DHE outlet working fluid pressure can be boosted by the buoyancy-driven thermosiphon effect. Hence, the power generation performance of the IPEC can be improved under certain conditions.
Due to the existence of temperature glide, the zeotropic working fluid mixture can better match not only the hot source but also the cold source in the condensation process [22,23]. CO2-based mixtures are selected as working fluids in this study. Thermal properties, toxicity, flammability, and environmental friendliness have been considered in the selection of an organic working fluid (OWF). Based on a review of the literature [33], seven organic working fluids (R161, R32, R134a, R152a, R600a, R1234yf, and R601a) commonly used in power generation units were investigated in this study. Their thermal and physical properties are shown in Table 1.

Table 1.
Thermal–physical properties of the organic working fluids (OWF) were investigated [33,34].
According to the ASHRAE standard 34, the safety of refrigerants mainly refers to their toxicity, flammability, and explosibility. The safety of refrigerants is classified by A, B, and C, followed by 1, 2, and 3. A1 denotes the highest level of safety, whereas C3 denotes the lowest level [34,35]. All the organic working fluids adopted in this study have a safety of class A. Based on the thermodynamic analysis and comparison among the seven mixtures, selecting the optimal CO2-based working fluid mixture was the first and foremost task in this study.
Figure 2 shows the temperature glide of the CO2-based mixtures with respect to the mass fraction of the OWF. The red line represents the dew point temperature, and the blue line represents the bubble point temperature. The difference between the dew point and bubble point is the glide (green dashed line). Each CO2-based mixture has an optimal mass fraction that maximizes the temperature glide.
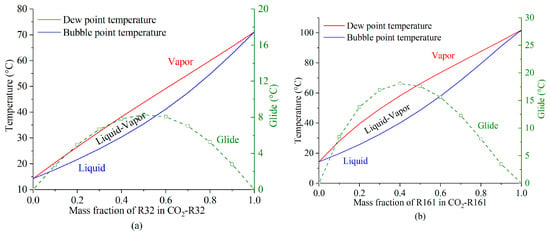
Figure 2.
Temperature glide of CO2-based mixtures with changes in the mass fraction of the OWF: (a) working fluid: CO2-R32; (b) working fluid: CO2-R161.
3. Methodology
Figure 3 shows the flow chart of the IPEC model solution procedure. As the ORC, t-CO2, and SF systems have been extensively studied and can be found in many existing references, it is considered that the thermodynamic models of ORC, t-CO2, and SF are well known, and so are not elaborated here. In our previous study [36], the models of ORC and SF were extensively reviewed and elucidated. The t-CO2 model was introduced in detail by Guo et al. [37].
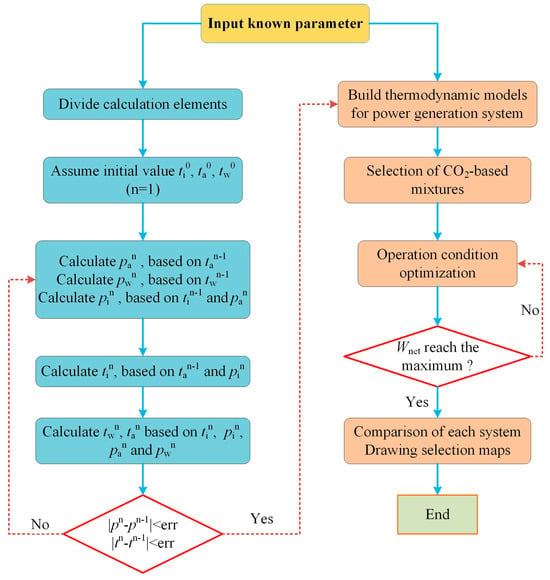
Figure 3.
Flow chart of the IPEC model solution procedure.
3.1. Thermodynamic Model
Thermodynamic modeling of the IPEC, ORC, t-CO2, and SF was carried out based on the following assumptions:
- (1)
- The IPEC, ORC, t-CO2, and SF systems are operating in steady state;
- (2)
- In the above-ground equipment, heat losses and flow friction losses in pipes are ignored;
- (3)
- The injection pressure of the CO2-based mixture is higher than its critical pressure;
- (4)
- The pump inlet state of the CO2-based mixture is saturated liquid;
- (5)
- In the SF system, the pressure and heat loss in the flasher and separator are 10% and 3%, respectively;
- (6)
- The cooling water temperature is the same for each of the four systems;
- (7)
- The turbine and pump efficiencies of the four systems are assumed to be the same.
In this study, all of the thermal–physical properties of the working fluids were calculated following consultation with the National Institute of Standards and Technology (NIST) Reference Fluid Thermodynamic and Transport Properties Database (REFPROP 10) [38]. The accuracy of each calculated property depends on the binary interaction parameter, which is obtained from experimental data, and the error is less than 5% [39]. The simulation studies were carried out using the Engineering Equation Solver (EES. Version 10).
According to Figure 1, the turbine-generator power output can be determined as follows:
where W represents the power output (kW), and m represents the mass flow rate (kg/s).
Due to the temperature glide in the condensation process of the CO2-based mixture, there is a better match of the temperature changes between the working fluid and the cooling water, resulting in less heat transfer irreversibility. The heat and mass balances in the condenser are provided below:
where Q is the heat exchange in the condenser (kW).
The power consumption of the injection pump is determined as follows:
The net power output of the system is equal to the power generated minus the power consumption of the pump, which is provided as follows:
The parameters used in the simulation are shown in Table 2.

Table 2.
Parameters used in the model [31,36].
The selection maps of the four investigated systems (ORC, t-CO2, IPEC, and SF) were obtained based on the following procedures:
- (1)
- The choice of the maximum Wnet as the objective function when conducting the thermodynamic analysis of each system;
- (2)
- The determination of the optimal operation parameters of each system for a given Tg and mg;
- (3)
- Through the comparison of the Wnet of the three systems (ORC, IPEC, and SF) with that of the reference system (t-CO2), the determination of which geo-fluid conditions permitted each of the three systems to generate 20% more net power output;
- (4)
- The generation of the selection map based on the comparison results;
- (5)
- The implementation of additional investigations through changing the working fluid and the annulus-pipe outside wall diameter (dao) and repeating steps (1) to (4).
The selection criteria was chosen as 20% mainly because of the requirements of our current sponsored research project, as well as maintaining consistency with our previous studies (Zhu et al. [7] and Lu et al. [8]).
3.2. DHE Model
As the DHE and the production well are concentric, the heat transfer model was simplified to a radially symmetric model. The DHE model includes the following aspects: heat transfer between the DHE outer and inner pipes, heat transfer between the DHE and the geo-fluid, heat transfer between the geo-fluid and geological formation, and heat conduction in the geological formation.
3.2.1. Pressure-Field Model
The flow model, coupled with the heat transfer model, is calculated using the finite difference method. The geo-fluid and the working fluid temperature distributions, as well as their pressure distributions, are coupled and solved at the same time. The mass and momentum conservation equations were simplified as follows [40]:
Upon combining Equations (6) and (7), the pressure expression can be written as follows:
where ρ is the fluid density; v is the velocity of the fluid; z is the flow direction coordinate; g is the gravitational acceleration; P is the pressure; is the cross-sectional area; d is the equivalent diameter; is the shear stress; and “+” and “−” represent the same or opposite direction of the gravitational acceleration. In this study, the Darcy friction factor, f, was determined based on the study of Wang et al. [41].
3.2.2. Temperature Field Model
The working fluid energy conservation equation is provided as follows:
Upon combining Equations (6) and (9), the energy conservation equation is as follows:
where q is the heat transferred per unit length.
According to the definition of the specific enthalpy, the “h” has another expression as follows [42]:
where is the specific heat capacity at constant pressure and is the Joule–Thomson coefficient [43].
Upon combining Equations (10) and (11), the temperature expression is as follows:
3.2.3. DHE Heat Transfer Model
Figure 4 shows the schematic diagram of the DHE and the production well, in which the inner pipe’s thermal insulation layer between the outside and inside walls is filled with adiabatic material. The DHE heat transfer model includes the following aspects: heat transfer between the DHE outer and inner pipes, heat transfer between the DHE and geological formation, and heat conduction in the geological formation. The heat transferred per unit length is as provided in [44]:
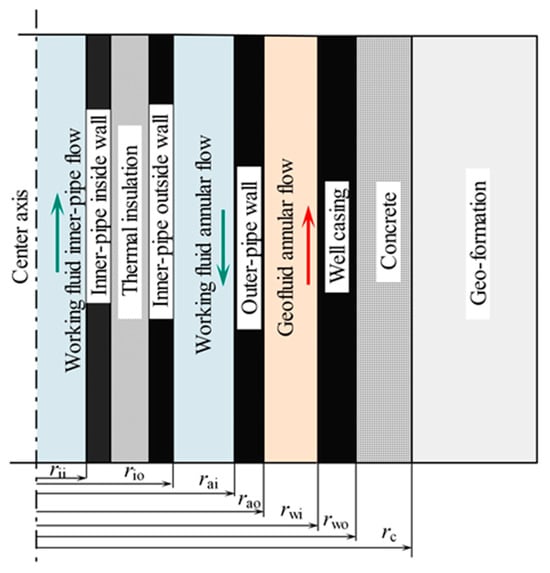
Figure 4.
Schematic diagram of the DHE model.
- (a)
- Heat transfer between the outer pipe and inner pipe
In this study, the inner pipe consists of three parts: the inside wall, the insulation layer, and the outside wall. The heat transfer can be described as follows:
where is the overall thermal resistance between the outer and inner pipes; and are the inner and outer radius of the inner-pipe inside wall; and are the inner and outer radius of the inner-pipe outside wall; and are the thermal conductivity coefficient of the outside and inside walls; is the thermal conductivity coefficient of the insulation layer; is the convective heat transfer coefficient between the inner wall of the inner pipe and working fluid; is the convective heat transfer coefficient between the inner wall of the outer pipe and working fluid; and is the overall coefficient of heat transfer between the outer and inner pipes.
- (b)
- Heat transfer between the geofluid and annulus
- (c)
- Heat transfer between the geological formation and geofluid
The heat transfer between the wellbore and geological formation is as provided in [45]:
where is the thermal conductivity coefficient of the geological formation; is the temperature of the geological formation; is the wellbore outside wall temperature; and is the dimensionless transient thermal conduction function.
Taking into account the importance of wellbore heat capacity, Cheng et al. [46] suggested a simplified transient thermal conduction function, which is used in this study, as follows:
where is a production time which is dimensionless, ; a is the thermal diffusivity(λ/ρc), m2/s; t is the production time, s; rwi is the wellbore radius, m; and m is the geo-fluid mass flow rate, kg/s. In this study, t is 10,000 h. It is assumed that after 10,000 h, the heat capacity of the wellbore has no effect on the heat transfer between the geofluid and geo-formation, and the heat transfer is then in a steady state.
Since the is relatively large in this study, the can be neglected, and the following simplified formula is used:
The heat transfer between the geological formation and the wellbore is as follows:
where is the total thermal resistance between the geological formation and geofluid; is the overall coefficient of heat transfer between the geological formation and geofluid; and is the outer and inner radius of the wellbore, respectively.
4. Optimization Results and Discussion
In this section, optimization of the IPEC is carried out, including a comparison of the working fluids, the optimization of the system parameters, and an analysis of the effect of the DHE structure on the system’s power generation performance. The net power output of IPEC was compared with that of the ORC, the trans-critical CO2 (t-CO2) cycle, and the single-flash (SF) system under the condition that each system operates within its optimal parameters.
4.1. Comparison of IPEC Using Different CO2-Based Mixtures
Figure 5 shows the effects of different CO2-based working fluid mixtures and mass flow rates (mm) on the DHE working fluid outlet pressure (Pout). The geo-fluid temperatures (Tg) investigated were 100 °C, 125 °C, 150 °C, and 175 °C. The geo-fluid mass flow rate (mg) and the DHE inlet pressure (Pin) were maintained at 5 kg/s and 12 MPa, respectively.
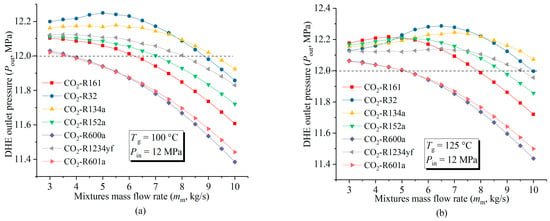
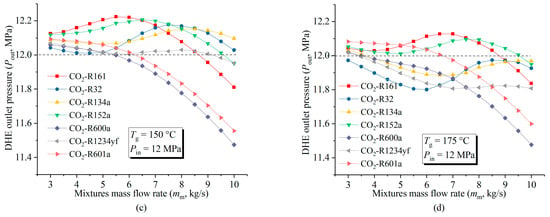
Figure 5.
Effect of the working fluid flow rates on DHE outlet pressures with changes in different CO2-based working fluid mixtures (mass fraction: OWF/CO2 = 0.5/0.5): (a) Tg = 100 °C; (b) Tg = 125 °C; (c) Tg = 150 °C; and (d) Tg = 175 °C.
When the geo-fluid temperature (Tg) is 100 °C (Figure 5a), the general trend is that the DHE working fluid outlet pressure (Pout) of each working fluid decreases with an increase in its mass flow rate mm, except for CO2-R32 (there is a maximum pressure when mm = 5 kg/s). The horizontal black-dash-dotted line denotes the working fluid inlet pressure (Pin). Pressure variations in the Pout above this line indicate a thermal siphon effect, which means that when using gravitational potential energy, the Pout of the DHE can be greater than the corresponding Pin of the DHE for a certain range of mass flow rate mm. Since the thermal siphon effect can compensate for the pump power consumption (Pout > Pin), the inlet pressure of the turbine becomes higher and hence results in a better power-cycle performance.
It can be seen that when geo-fluid temperatures are relatively low (corresponding to 100 °C and 125 °C), as shown in Figure 5a,b, using CO2-R32 and CO2-R134a as working fluids can generate greater thermal siphon effects than other working fluids over a wide range of mm. When the geo-fluid temperature is 150 °C (Figure 5c), four working fluids, CO2-R161, CO2-R152a, CO2-R32, and CO2-R134a, show obvious thermal siphon effects, with the former two having outlet pressure peak values corresponding to relative lower mass flow rates (ranging from 6 to 7 kg/s) and the latter two corresponding to higher mass flow rates (ranging from 8 to 9 kg/s). When the geo-fluid temperature is relatively high (175 °C), CO2-R161 and CO2-R152a show dominant thermal siphon effects over a wide range of mm, as shown in Figure 5d.
The IPEC net power output (Wnet) variations with respect to different CO2-based mixtures and mass flow rates (mm) are shown in Figure 6. Each CO2-based mixture has an optimal mass flow rate that maximizes the net power output. When the geo-fluid temperature (Tg) is 100 °C (Figure 6a), using CO2-R32 as working fluid has the highest Wnet (61 kW), much higher than using other working fluids. CO2-R601a and CO2-R600a are the two mixtures showing the worst power generation performance. When the geofluid temperature is 125 °C (Figure 6b), the Wnet curve of CO2-R161 moves towards that of CO2-R32, almost becoming the second-highest one in net power output. When the geofluid temperatures are 150 °C and 175 °C (Figure 6c,d), the net power outputs of CO2-R161 become higher than that of CO2-R32 under the conditions that mass flow rates are relatively low (less than 5.5 kg/s for 150 °C and less than 7 kg/s for 175 °C). However, CO2-R32 is still the best working fluid of the IPEC for relatively high mass flow rate conditions (greater than 5.5 kg/s for 150 °C and greater than 7 kg/s for 175 °C).
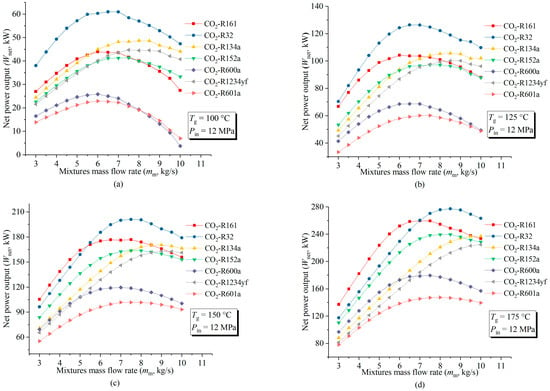
Figure 6.
Effect of the working fluid flow rates on net power outputs with changes in different CO2-based working fluid mixtures (mass fraction: OWF/CO2 = 0.5/0.5): (a) Tg = 100 °C; (b) Tg = 125 °C; (c) Tg = 150 °C; and (d) Tg = 175 °C.
Figure 7 shows the effect of the mass fraction on the DHE working fluid outlet pressure (Pout) for four geo-fluid temperature conditions (100 °C, 125 °C, 150 °C, and 175 °C), with the DHE inlet pressure (Pin) maintained at 12 Mpa.
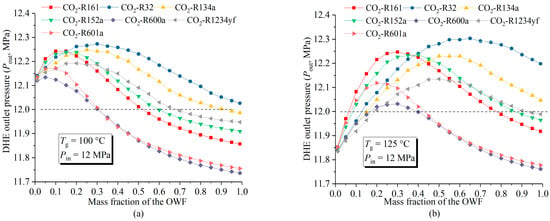
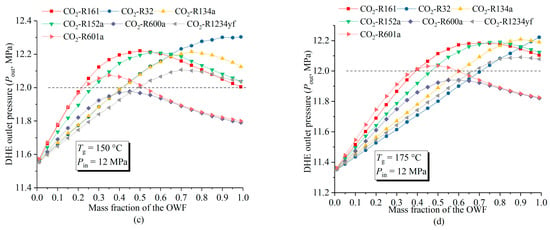
Figure 7.
Variations in DHE outlet pressure with changes in the working fluid mass fraction (OWF/CO2) for different CO2-based working fluid mixtures (DHE inlet pressure (Pin) = 12 Mpa): (a) Tg = 100 °C; (b) Tg = 125 °C; (c) Tg = 150 °C; and (d) Tg = 175 °C.
When the geo-fluid temperature is 100 °C (Figure 7a), the DHE outlet pressure first increases and then decreases with the increase in the mass fraction of the OWF in all the CO2-based mixtures. There is an optimal mass fraction of the mixtures for a given geo-fluid temperature (Tg) corresponding to the maximum value of the Pout. At some mass fraction, the Pout is greater than the Pin (horizontal black-dash-dotted line), which means that the CO2-based mixture can make full use of the thermal siphon effect to compensate for the pump power consumption. The Pout curve of CO2-R32 is higher than the Pin (dash-dotted line) for all mass fraction conditions and, in most cases (except when the mass fraction < 0.2), is higher than that of the other mixtures.
When the geo-fluid temperature is 125 °C (Figure 7b), the optimal mass fraction corresponding to the maximum Pout shifts to the right. The same trend is seen in Figure 6d and Figure 7c (Tg =150 °C and 175 °C, respectively). It is worth noting that the higher the geo-fluid temperature, the smaller the mass fraction range in which the DHE outlet pressure (Pout) is greater than the inlet pressure (Pin). It is also noted that when the geo-fluid temperature is 175 °C (Figure 7d), the outlet pressure of CO2-R32 increases almost linearly with the increase in its mass fraction.
The IPEC net power output (Wnet) variations with respect to working fluid mass fractions for different CO2-based mixtures are shown in Figure 8. When the geo-fluid temperature is low (100 °C, Figure 8a), the maximum net power output of each mixture of working fluid corresponds to a mass fraction value of 0, which means that, under this temperature condition, pure CO2 should be used for better power generation performance.
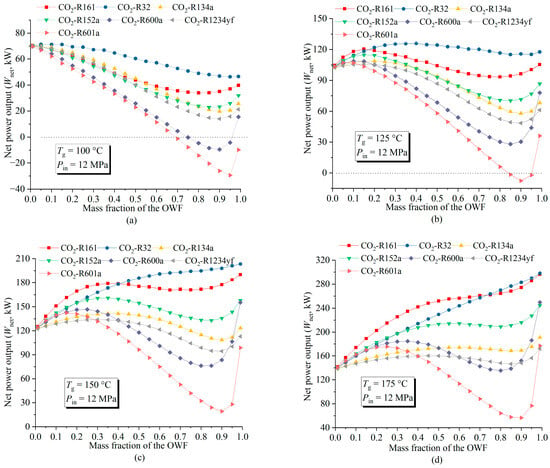
Figure 8.
Variations in the IPEC net power output with changes in the working fluid mass fraction (OWF/CO2) for different CO2-based working fluid mixtures: (a) Tg = 100 °C; (b) Tg = 125 °C; (c) Tg = 150 °C; and (d) Tg = 175 °C.
As the geo-fluid temperature increases, the optimal mass fraction corresponding to the maximum Wnet shifts to the right. Taking CO2-R32 as an example, the optimal values of the mass fractions of R32/CO2 are 0.35/0.65 and 1/0 for the geo-fluid temperatures of 125 °C (Figure 8b) and 150 °C (Figure 8c), respectively. It is worth pointing out that when the geo-fluid temperature is 150 °C, the increase in Wnet is almost negligible after the mass fraction of R32 continues to increase from 0.6 to 1. Under the condition that the geo-fluid temperature is high (175 °C, Figure 8d), a pure organic working fluid could be a better choice in each case, as can be seen in Figure 8d, where each curve has the highest point corresponding to the mass fraction equal to 1.
It is also noticed that using CO2-R600a or CO2-R601a as the working fluids results in the poorest performances in power generation, especially when the OWF mass fraction is around 0.9, and the geo-fluid temperature is lower than 150 °C. A negative net power output means the power generated by the turbine is less than the power consumption of the pump.
It can be seen from Figure 6 and Figure 8 that using CO2-R32 as the working fluid of the IPEC has the highest net power output. In the following parts of this study, CO2-R32 has been selected for performance analyses of the IPEC.
The influence of the thermal siphon effect on pump power consumption is illustrated in Table 3. Using CO2-R32 as the working fluid, we have illustrated the effect of the thermosiphon under two different geo-fluid conditions (100 °C and 130 °C). When the geo-fluid temperature is 100 °C, the optimal DHE inlet pressure is 11 mPa, and the DHE outlet pressure is 11.3 mPa (due to the thermal siphon effect). In a conventional ORC with an on-the-ground evaporator, the evaporator’s outlet pressure of the working fluid can not be greater than the inlet pressure, with its maximum outlet pressure being the same as the inlet value. Thus, when comparing Scenario 1 and Scenario 2, as set out in Table 3, the thermal siphon’s effect on the pump power consumption can be determined. In Scenario 1, when the working fluid was pressurized to 11 mPa, the pump work consumption was 55.2 kW. In Scenario 2, when the working fluid was pressurized to 11.3 mPa, the pump work consumption was 58.2 kW. The thermal siphon effect can compensate for the 3 kW pump work consumption, which is 5.4% of the pump work. When the geo-fluid temperature is 130 °C, the thermal siphon effect can compensate for the 2.6 kW pump work consumption, which is 3.3% of the pump work.

Table 3.
Influence of thermal siphon effect on pump power consumption (working fluid: CO2-R32).
4.2. Optimization of Parameters
The effect of the IPEC operation parameters (the inlet pressure of DHE (Pin) and outlet temperature of the condenser (Tco)) on net power output (Wnet) is shown in Figure 9. Reducing the Tco can effectively increase the Wnet of the IPEC, indicating that the lower DHE injection temperature does not reduce the power output of the system. There is an optimal DHE inlet pressure that maximizes the Wnet; the higher the geo-fluid temperature, the higher the optimal DHE inlet pressure. As can be seen in Figure 9, when the outlet temperatures of the condenser are 15 °C and 40 °C, the optimal inlet pressures are shown by points A and B, respectively; the optimal inlet pressure corresponding to each Tg investigated is approximately the intersection between its net power output curve and the line A-B. When the geo-fluid temperature is low (100 °C), the optimal Pin corresponding to each condensation temperature is basically around 9 mPa (see Figure 9a). When the Tg rises to 125 °C (Figure 9b), the optimal Pin corresponding to each condensing temperature varies from 9 mPa (Tco = 15 °C) to 11 mPa (Tco = 40 °C). The optimal Pin corresponding to each condensing temperature ranges from 11 mPa to 13 mPa when Tg is 150 °C, as shown in Figure 9c. Under the condition that the geo-fluid temperature is high (175 °C), the optimal Pin values become greater, ranging from 13 mPa to 16 mPa.
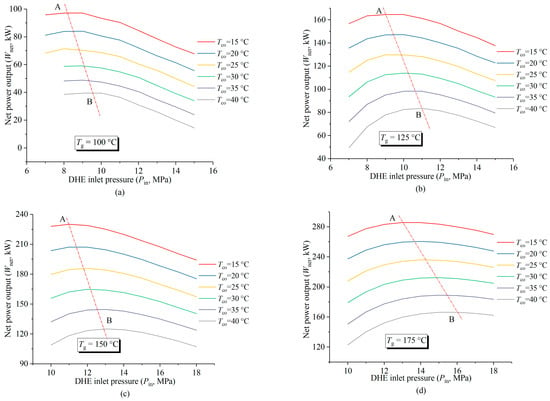
Figure 9.
Variations in IPEC net power output with changes in the different DHE inlet pressures and condensation temperatures (mg = 5 kg/s, mm = 6 kg/s, mass fraction of R32/CO2 = 0.5/0.5): (a) Tg = 100 °C; (b) Tg = 125 °C; (c) Tg = 150 °C; and (d) Tg = 175 °C. Points A and B are the optimal DHE inlet pressure when the outlet temperatures of the condenser are 15 °C and 40 °C, respectively.
4.3. Effect of the DHE Structure Size
Figure 10 shows the IPEC net power output variations with respect to the DHE length L and the outer-pipe wall diameter dao (refer to Figure 4). Increasing the dao and L increases the heat exchange area of the DHE, which creates an increased heat transfer between the CO2-based mixture and the geo-fluid and, hence, increases the working fluid’s temperature at the DHE outlet, resulting in more power generation. As can be seen in Figure 10, for a certain DHE length L, the Wnet increases with the increase in the dao (in most cases when dao < 0.14 m); it then levels off when the dao becomes larger.
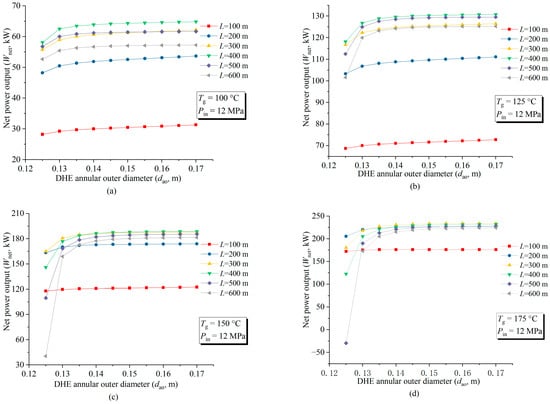
Figure 10.
Variations in IPEC net power output with changes in L and dao (mg = 5 kg/s, mass fraction of R32/CO2 = 0.5/0.5): (a) Tg = 100 °C; (b) Tg = 125 °C; (c) Tg = 150 °C; and (d) Tg = 175 °C.
In Figure 10, it is also found that when the L is 100 m, the net power output is much less than that when the DHE length (L) is greater than 200 m. Under conditions when the geo-fluid temperatures are relatively low (Tg = 100 °C and 125 °C), as shown in Figure 10a,b, the optimal DHE length is 400 m (see the green curve in each case). If the geo-fluid temperatures are high (Tg = 150 °C and 175 °C), as shown in Figure 10c,d, respectively, the optimal DHE length is 300 m (see the yellow curve in each case) under the condition that dao is not less than 0.13 m.
4.4. Optimization of Mass Flow Rates
Figure 11 shows the IPEC net power output tendency with respect to different geo-fluid (mg) and CO2-R32 mass flow rates (mm) for mg ranging from 4 kg/s to 40 kg/s. In Figure 11a (Tg = 100 °C), for each given mg, there is an optimal mm corresponding to the maximum net power output.
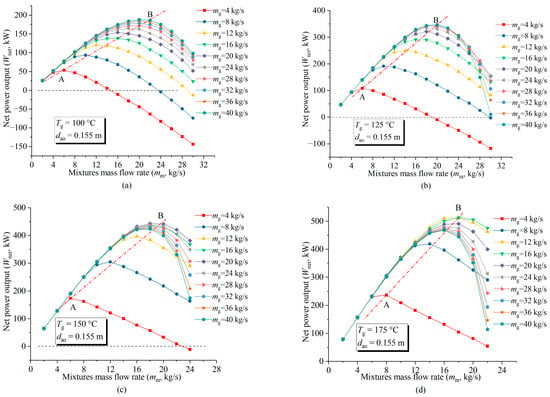
Figure 11.
Variations in IPEC net power output with changes in mg and mm (L = 300 m, Pin = 12 MPa, mass fraction of R32/CO2 = 0.5/0.5, dao = 0.155 m): (a) Tg = 100 °C; (b) Tg = 125 °C; (c) Tg = 150 °C; and (d) Tg = 175 °C.
Under the low geo-fluid temperature condition (Figure 11a), the optimal mm increases with the increase in mg (when mg ≤ 28 kg/s). When mg is higher than 28 kg/s (see the top three curves), the increase in Wnet with the change in mg is not obvious, and the optimal mm is about constant (mm = 22 kg/s).
Under the condition that the geo-fluid temperature is 125 °C (Figure 11b), once the mg is greater than 24 kg/s (see the top four curves), there is no significant increase in Wnet with a change in the mm. Instead, when the mm is greater than 24 kg/s, the net power output decreases even under a much higher mg condition (mg > 24 kg/s).
When the geo-fluid temperature (Tg) is 150 °C (Figure 11c), for a higher geo-fluid mass flow rate condition (mg= 20, 24, 28, 32, 36, or 40 kg/s), the net power output (Wnet) decreases as the mg increases when the working fluid mass flow rate (mm) is greater than 18 kg/s. In other words, the optimal mm decreases with an increase in geo-fluid temperature (Tg), as can be seen by comparing Figure 11a,c; a similar trend is also shown in Figure 11d.
It is noticed that the reversal value of mg (corresponding to the maximum net power output Wnet) decreases with the increase in the geo-fluid temperature Tg. As can be seen in Figure 11c,d, the reversal values of mg are 20 kg/s and 16 kg/s, respectively, corresponding to the geo-fluid temperatures Tg = 150 °C and 175 °C.
4.5. Comparison among ORC, t-CO2, SF and IPEC
Comparisons of the net power outputs (Wnet) among four systems (ORC, t-CO2, SF, and IPEC) in terms of different geo-fluid temperatures (Tg) and mass flow rates (mg) are shown in Figure 12. Comparisons were carried out based on each of the four systems having attained its optimum operation condition. Here, R245fa is used as the working fluid for ORC, and the working fluid mixture CO2-R32 is chosen for IPEC. The red line represents the ORC system, the blue dashed line represents the t-CO2 system, the black line represents the SF system, and the green line represents the IPEC system.
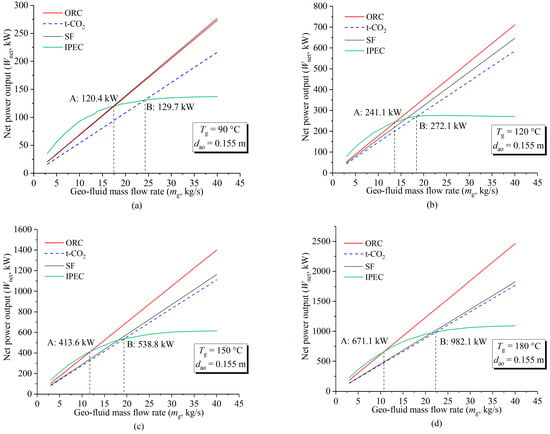
Figure 12.
Comparisons of net power output (Wnet) among various geothermal power generation systems with changes in different geo-fluid temperatures (Tg) and mass flow rates (mg): (a) Tg = 90 °C; (b) Tg = 120 °C; (c) Tg = 150 °C; and (d) Tg = 180 °C.
When the geo-fluid temperature is 90 °C (Figure 12a), it is found that the net power outputs of the ORC and SF are about the same but always higher than that of the t-CO2. With the increase in geo-fluid mass flow rate (mg), the net power output of the IPEC system increases first (for an mg ranging from 3 kg/s to 24 kg/s) and then levels off when mg is greater than 24 kg/s. The IPEC uses a DHE, which is limited by the wellbore size and structure, so the heat exchange area is limited, which flattens out the heat exchanged in the DHE as the geo-fluid mass flow rate increases. Therefore, the net power output of the IPEC flattens out. In contrast, since the relevant equipment of the ORC, SF, and t-CO2 are all installed on the ground, their thermal performances are not limited by the increasing geo-fluid mass flow rate. Hence, the net power outputs of the other three systems still increase linearly with an increase in the geo-fluid mass flow rate. It is also found that the net power outputs of ORC, SF, and IPEC are equal when mg is 17.5 kg/s (point A); the net power outputs of t-CO2 and IPEC are also equal when mg is 24 kg/s (point B).
When the geo-fluid temperature is 120 °C (Figure 12b), the net power output of SF is between that of the ORC and t-CO2. Under the condition that the geo-fluid temperature is 150 °C (see Figure 12c), the net power output curve of the SF is closer to that of the t-CO2. When the geo-fluid temperature is 180 °C (Figure 12d), the net power outputs of t-CO2 and SF are about the same and much less than that of the ORC. It is worth noticing that the higher the geofluid temperature, the smaller the range of the mg in which the IPEC system can generate more net power than other systems.
Taking the geo-fluid condition (130 °C, 5 kg/s) in the Qiabuqia geothermal field as an example, the IPEC system can generate 149.5 kW of net power output. In contrast, a conventional ORC with the working fluid of R245fa can only generate 113.6 kW of net power output. Therefore, the IPEC can generate 35.9 kW (31.6%) more net power than ORC, which is shown in Table 4.

Table 4.
Net power output comparison between an IPEC and a conventional ORC.
In order to show the application scope of each system under different geo-fluid temperature (Tg) and mass flow rate (mg) conditions, selection maps of the IPEC, ORC, and SF (in comparison with t-CO2) were generated (see Figure 13). Figure 13a–c illustrate a scenario when a smaller annulus-pipe outside wall diameter (dao = 0.155 m) is used, while Figure 13d–f illustrate a scenario when a larger annulus-pipe outside wall diameter (dao = 0.22 m) is used. Three ORC working fluids (R245fa, R600a, and R32) were considered for each of the scenarios. Selection maps were generated based on comparisons among the four systems with the goal of increasing the net power output by 20% under the condition that the t-CO2 system is replaced with one of the three systems (IPEC, ORC, or SF).
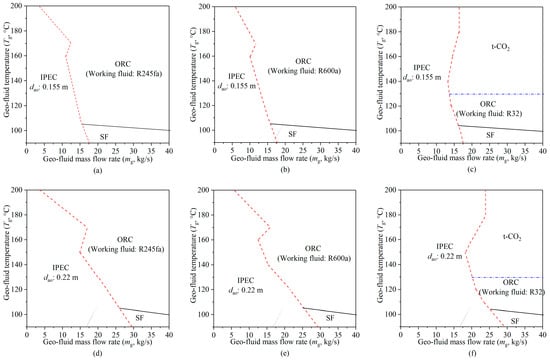
Figure 13.
Selection maps of the IPEC, ORC, and SF (in comparison with t-CO2) under different geo-fluid temperature and flow rate conditions: (a) dao = 0.155 m, ORC working fluid: R245fa; (b) dao = 0.155 m, ORC working fluid: R600a; (c) dao = 0.155 m, ORC working fluid: R32; (d) dao = 0.22 m, ORC working fluid: R245fa; (e) dao = 0.22 m, ORC working fluid: R600a; and (f) dao = 0.22 m, ORC working fluid: R32.
When R245fa is used as the ORC working fluid and the annulus-pipe outside wall diameter is relatively small (dao = 0.155 m), the selection map (Figure 13a) was divided into three regions (scopes) by the black solid line and the red dash line. The area to the left of the red dashed line is the IPEC application scope, in which the IPEC generates more net power than the ORC and SF systems. When the geo-fluid temperature (Tg) is 90 °C, the upper limit of the geo-fluid mass flow rate for using IPEC is 17.5 kg/s. When the geo-fluid temperature becomes 130 °C, the upper limit of the geo-fluid mass flow rate decreases to 15 kg/s. When the geo-fluid temperature is 200 °C, the upper limit of the geo-fluid mass flow rate is only about 5 kg/s, showing that the lower the geo-fluid temperature, the wider the IPEC application scope (with respect to its geo-fluid flow rate range). Figure 13a also shows that, under the condition that the geo-fluid mass flow rate is relatively high (to the right of the red dash line), the ORC system is the best choice when the geo-fluid temperature is relatively high (above the black solid line); if the geo-fluid temperature is low (below the black solid line), the SF system should be selected.
The selection map (Figure 13b) was also obtained when R600a was used as the ORC working fluid. It is noticed that the application scope of the ORC in Figure 13b has a narrower mg range than that in Figure 13a when the geofluid temperature is higher than 180 °C.
When R32 is chosen as the ORC working fluid, the selection map becomes obviously different, as shown in Figure 13c. The map is divided into four regions. The t-CO2 system appears on the top right of the map, which indicates that when the geo-fluid temperature is higher than 130 °C and its mass flow rate mg is also high (to the right of the red dash line); none of the three systems (IPEC, ORC, and SF) can generate 20% more net power than the t-CO2 system. The ORC application scope moves down for a geo-fluid temperature below 130 °C and becomes narrower because the SF scope remains about the same as in Figure 13a,b. The IPEC application scope (with respect to the geo-fluid mass flow rate) becomes narrower in the middle (around Tg = 140 °C) but is wider at high and low-temperature ends.
When the annulus-pipe outside wall diameter is larger (dao = 0.22 m), corresponding selection maps were also generated, as shown in Figure 13d–f. It is worth noting that, for a given geo-fluid temperature, the IPEC application scope in each map becomes wider with respect to the upper limit of the geo-fluid mass flow rate, compared with the case when a smaller dao (0.155 m) is used.
5. Conclusions
In this study, an increasing pressure endothermic cycle (IPEC) using geo-fluid in an artesian geothermal well to generate electricity was investigated. The power generation performances of the IPEC were investigated through analyses of the impacts of the following key parameters: mass fraction and varieties of the CO2-based mixtures, condenser working fluid outlet temperatures and DHE working fluid inlet pressures, and the DHE length and its annulus-pipe outside wall diameter. Furthermore, the net power output was compared between the IPEC, conventional organic Rankine cycle (ORC), trans-critical CO2 (t-CO2) system, and the single-flash (SF) system. Six selection maps were generated under different geo-fluid conditions considering the use of three different ORC working fluids (R245fa, R600a, and R32). Two annulus-pipe outside wall diameters (0.155 m and 0.22 m) were investigated in this study. The main conclusions are as follows:
- (1)
- An increasing pressure endothermic cycle combining on-the-ground and downhole components was developed using large-scale DHE and CO2-based mixtures. The non-isothermal condensation process is achieved with the use of a zeotropic mixture of working fluids. The temperature variation between the working fluid and cooling water can be better matched;
- (2)
- Comparisons of net power outputs among seven different CO2-based mixtures with respect to different geo-fluid temperatures show that using the working fluid mixture of CO2-R32 has a better thermodynamic performance. Under the geo-fluid conditions (130 °C, 5 kg/s) in the Qiabuqia geothermal field, the CO2-R32 mixture is found to be the best in terms of obtaining the maximum net power output. The optimal working fluid mass flow rate, mass fraction, and inlet pressure are 6.5 kg/s, 0.5/0.5, and 11 MPa, respectively;
- (3)
- This numerical study shows that an optimum length and an optimum diameter of the DHE exist, corresponding to the best IPEC power production performance. Under the geo-fluid conditions in the Qiabuqia geothermal field, the optimum length and diameter of the DHE are found to be 400 m and 0.14 m, respectively;
- (4)
- Compared with conventional power stations, large-scale DHE using CO2-based mixtures as the working fluid can make full use of gravitational potential energy that results in a thermal siphon effect that is useful for increasing the DHE outlet pressure and improving the power generation performance. It is found that the thermal siphon effect is affected by the varieties of the mixture, mass flow rate, geo-fluid conditions, and DHE size;
- (5)
- For a given geo-fluid temperature and mass flow rate, an optimal working fluid mass flow rate exists, corresponding to the maximum value of the IPEC net power output;
- (6)
- In terms of the net power output, the IPEC shows advantages over the other three systems (ORC, t-CO2, and SF) under the condition that the geo-fluid flow rate is less than 10 kg/s.
Author Contributions
Conceptualization, H.Y. and X.L.; methodology, H.Y.; software, H.Y.; validation, H.Y., X.L. and J.L.; formal analysis, W.Z.; investigation, J.L.; resources, X.L.; data curation, W.Z.; writing—original draft preparation, H.Y.; writing—review and editing, X.L.; visualization, H.Y.; supervision, X.L.; project administration, X.L.; funding acquisition, X.L. and W.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Ministry of Science and Technology of China (Grant No. 2018YFB1501805).
Data Availability Statement
Data is contained within the article.
Acknowledgments
We thank the anonymous reviewers and editors for their comments and suggestions.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Nomenclature
| h | Specific enthalpy, kJ/kg | Rio | Total thermal resistance in DHE |
| mg | Geo-fluid mass flow rate, kJ/kg | Uio | Overall heat transfer coefficient in DHE |
| mm | CO2 mixture mass flow rate, kJ/kg | Raw | Thermal resistance between the geofluid and annulus |
| Wg | Turbine-generated power output, kW | Uaw | Overall heat transfer coefficient between the geofluid and annulus |
| Wp | Pump consumed power, kW | tD | Dimensionless time (at/rwi2) |
| Wnet | Net power output, kW | t | Production time, s |
| Q | Heat transfer rate, kW | a | Thermal diffusivity (λ/ρc), m2/s |
| Pin | DHE inlet pressure, MPa | v | Fluid velocity, m/s |
| Pout | DHE outlet pressure, MPa | g | Gravitational acceleration, m/s2 |
| Pc | Critical pressure, MPa | z | Vertical coordinate, m |
| Tin | DHE inlet temperature, °C | f | Friction factor |
| Tout | DHE outlet temperature, °C | d | Diameter, m |
| Tc | Critical temperature, °C | q | Heat flux per unit length, w/m |
| Tg | Geo-fluid temperature, °C | Cp | Heat capacity at constant, J/kg∙K |
| Tci | Cooling water inlet temperature, °C | j | Joule-Thomson coefficient, K/MPa |
| Tco | Outlet temperature of condenser, °C | Ap | Flow area, m2 |
| Te | Formation temperature, °C | λe | Rock thermal conductivity, W/m∙K |
| Two | Wellbore outside wall temperature, °C | λc | Casing thermal conductivity, W/m∙K |
| ηt | Turbine isentropic efficiency, % | λi | Insulated pipe thermal conductivity, W/m∙K |
| ηp | Pump isentropic efficiency, % | λce | Cement thermal conductivity, W/m∙K |
| ηg | Generator efficiency, % | Abbreviations | |
| ηm | Turbine mechanical efficiency, % | DHE | Downhole heat exchanger |
| dii | Inner-pipe inside wall diameter, m | IPEC | Increasing pressure endothermic cycle |
| dio | Inner-pipe outside wall diameter, m | ORC | Organic Rankine cycle |
| dai | Annulus-pipe inside wall diameter, m | SF | Single flash system |
| dao | Annulus-pipe outside wall diameter, m | t-CO2 | Trans-critical CO2 cycle |
| dwi | Wellbore inside diameter, m | OWF | Organic working fluid |
| dwo | Wellbore outside diameter, m | HDR | Hot Dry Rock |
| ρe | Density of rock, kg/m3 | EGS | Enhanced geothermal system |
| Shear stress, MPa | ODP | Ozone depletion potential | |
| GWP | Global warming potential | ||
References
- Xu, R.; Zhang, L.; Zhang, F.; Jiang, P. A review on heat transfer and energy conversion in the enhanced geothermal systems with water/CO2 as working fluid. Int. J. Energy Res. 2015, 39, 1722–1741. [Google Scholar] [CrossRef]
- Esmaeilpour, M.; Gholami, K.M.; Kohl, T. Impact of thermos siphoning on long-term behavior of closed-loop deep geothermal systems for sustainable energy exploitation. Renew. Energy 2022, 194, 1247–1260. [Google Scholar] [CrossRef]
- Sircar, A.; Solanki, K.; Bist, N.; Yadav, K. Enhanced Geothermal Systems—Promises and Challenges. Int. J. Renew. Energy Dev. 2022, 11, 333–346. [Google Scholar] [CrossRef]
- DiPippo, R. Geothermal Power Plants: Principles, Applications, Case Studies and Environmental Impact, 4th ed.; Chapter 11 in Larderello Dry-Steam Power Plants, Tuscany, Italy; Butterworth-Heinemann: Oxford, UK, 2016; p. 329. [Google Scholar]
- Luo, C.; Huang, L.; Gong, Y.; Ma, W. Thermodynamic comparison of different types of geothermal power plant systems and case studies in China. Renew. Energy 2012, 48, 155–160. [Google Scholar] [CrossRef]
- Zhao, Y.; Du, B.; Chen, S.; Zhao, J.; Gong, Y.; Bu, X.; Li, H.; Wang, L. Thermo-Economic Comparison Between Organic Rankine Cycle and Binary-Flashing Cycle for Geothermal Energy. Front. Earth Sci. 2021, 9, 759872. [Google Scholar] [CrossRef]
- Zhu, J.; Hu, K.; Zhang, W.; Lu, X. A study on generating a map for selection of optimum power generation cycles used for Enhanced Geothermal Systems. Energy 2017, 133, 502–512. [Google Scholar] [CrossRef]
- Lu, X.; Zhao, Y.; Zhu, J.; Zhang, W. Optimization and applicability of compound power cycles for enhanced geothermal systems. Appl. Energy 2018, 229, 128–141. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, H.; Guo, T. Performance comparison and parametric optimization of subcritical Organic Rankine Cycle (ORC) and transcritical power cycle system for low-temperature geothermal power generation. Appl. Energy 2011, 88, 2740–2754. [Google Scholar] [CrossRef]
- Lecompte, S.; Lemmens, S.; Huisseune, H.; Van den Broek, M.; De Paepe, M. Multi-Objective Thermo-Economic Optimization Strategy for ORCs Applied to Subcritical and Transcritical Cycles for Waste Heat Recovery. Energies 2015, 8, 2714–2741. [Google Scholar] [CrossRef]
- Walraven, D.; Laenen, B.D.; Haeseleer, W. Comparison of thermodynamic cycles for power production from low-temperature geothermal heat sources. Energy Convers. Manag. 2013, 66, 220–233. [Google Scholar] [CrossRef]
- Chys, M.; van den Broek, M.; Vanslambrouck, B. Potential of zeotropic mixtures as working fluids in organic Rankine cycles. Energy 2012, 44, 623–632. [Google Scholar] [CrossRef]
- Lecompte, S.; Ameel, B.; Ziviani, D.; van den Broek, M.; De Paepe, M. Exergy analysis of zeotropic mixtures as working fluids in Organic Rankine Cycles. Energy Convers. Manag. 2014, 85, 727–739. [Google Scholar] [CrossRef]
- Dong, B.; Xu, G.; Cai, Y.; Li, H. Analysis of zeotropic mixtures used in high-temperature Organic Rankine cycle. Energy Convers. Manag. 2014, 84, 253–260. [Google Scholar] [CrossRef]
- Collings, P.; Yu, Z.; Wang, E. A dynamic organic Rankine cycle using a zeotropic mixture as the working fluid with composition tuning to match changing ambient conditions. Appl. Energy 2016, 171, 581–591. [Google Scholar] [CrossRef]
- Song, J.; Gu, C. Analysis of ORC (Organic Rankine Cycle) systems with pure hydrocarbons and mixtures of hydrocarbon and retardant for engine waste heat recovery. Appl. Therm. Eng. 2015, 89, 693–702. [Google Scholar] [CrossRef]
- Brown, D. A Hot Dry Rock geothermal energy concept utilizing supercritical CO2 instead of water. In Proceedings of the Twenty-Fifth Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 24–26 January 2000; pp. 233–238. [Google Scholar]
- Pruess, K. Enhanced geothermal systems (EGS) using CO2 as working fluid—A novel approach for generating renewable energy with simultaneous sequestration of carbon. Geothermics 2006, 35, 351–367. [Google Scholar] [CrossRef]
- Wang, X.; Dai, Y. Exergoeconomic analysis of utilizing the transcritical CO2 cycle and the ORC for a recompression supercritical CO2 cycle waste heat recovery: A comparative study. Appl. Energy 2016, 170, 193–207. [Google Scholar] [CrossRef]
- Ayachi, F.; Tauveron, N.; Tartière, T.; Colasson, S.; Nguyen, D. Thermo-Electric Energy Storage involving CO2 transceitical cycles and ground heat storage. Appl. Therm. Eng. 2016, 108, 1418–1428. [Google Scholar] [CrossRef]
- Xia, J.; Wang, J.; Zhou, K.; Zhao, P.; Dai, Y. Thermodynamic and economic analysis and multi-objective optimization of a novel transcritical CO2 Rankine cycle with an ejector driven by low grade heat source. Energy 2018, 161, 337–351. [Google Scholar] [CrossRef]
- Wu, C.; Wang, S.; Jiang, X.; Li, J. Thermodynamic analysis and performance optimization of transcritical power cycles using CO2-based binary zeotropic mixtures as working fluids for geothermal power plants. Appl. Therm. Eng. 2017, 115, 292–304. [Google Scholar] [CrossRef]
- Sánchez, C.J.N.; Da Silva, A.K. Technical and environmental analysis of transcritical Rankine cycles operating with numerous CO2 mixtures. Energy 2018, 142, 180–190. [Google Scholar] [CrossRef]
- Liu, X.; Xu, Z.; Xie, Y.; Yang, H. CO2-based mixture working fluids used for the dry-cooling supercritical Brayton cycle: Thermodynamic evaluation. Appl. Therm. Eng. 2019, 162, 114226. [Google Scholar] [CrossRef]
- Rodríguez, P.; Grespi, F.; Sánchez, D.; Muñoz, A.; Sánchez, T. The potential of transcritical cycles based on CO2 mixtures: An exergy-based analysis. Renew. Energy 2022, 199, 1606–1628. [Google Scholar] [CrossRef]
- Bu, X.; Ma, W.; Li, H. Geothermal energy production utilizing abandoned oil and gas wells. Renew. Energy 2012, 41, 80–85. [Google Scholar] [CrossRef]
- Huang, W.; Cao, W.; Jiang, F. A novel single-well geothermal system for hot dry rock geothermal energy exploitation. Energy 2018, 162, 630–644. [Google Scholar] [CrossRef]
- Shi, Y.; Song, X.; Li, G.; Yang, R.; Shen, Z.; Lyu, Z. Numerical investigation on the reservoir heat production capacity of a downhole heat exchanger geothermal system. Geothermics 2018, 72, 163–169. [Google Scholar] [CrossRef]
- Zhang, Y.; Yu, C.; Li, G.; Guo, X.; Wang, G.; Shi, Y.; Peng, C.; Tan, Y. Performance analysis of a downhole coaxial heat exchanger geothermal system with various working fluids. Appl. Therm. Eng. 2019, 163, 114317. [Google Scholar] [CrossRef]
- Li, Y.; Xu, W.; Ma, L.; Zhao, J.; Li, W.; Wang, S.; Liu, J. Dynamic heat transfer analysis of a direct-expansion CO2 downhole heat exchanger. Appl. Therm. Eng. 2021, 189, 116733. [Google Scholar] [CrossRef]
- Geng, C.; Lu, X.; Yu, H. Theoretical Study of a Novel Power Cycle for Enhanced Geothermal Systems. Processes 2022, 10, 516. [Google Scholar] [CrossRef]
- Amaya, A.; Scherer, J.; Muir, J. GreenFire Energy Closed-Loop Geothermal Demonstration using Supercritical Carbon Dioxide as Working Fluid. In Proceedings of the 45th Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 10–12 February 2020. [Google Scholar]
- Wang, Z.; Hu, Y.; Xia, X.; Zuo, Q.; Zhao, B.; Li, Z. Thermo-economic selection criteria of working fluid used in dual-loop ORC for engine waste heat recovery by multi-objective optimization. Energy 2020, 197, 117053. [Google Scholar] [CrossRef]
- Abas, N.; Kalair, A.R.; Khan, N. Natural and synthetic refrigerants, global warning: A review. Renew. Sustain. Energy Rev. 2018, 90, 557–569. [Google Scholar] [CrossRef]
- Devecioglu, A.G.; Oruc, V. An analysis on the comparison of low-GWP refrigerants to alternatively use in mobile air-conditioning systems. Therm. Sci. Eng. Prog. 2017, 1, 1–5. [Google Scholar] [CrossRef]
- Yu, H.; Lu, X.; Ma, F.; Zhang, W.; Liu, J.; Li, C. A study on geothermal electricity systems for Tibet geothermal fields considering thermal performance, economic analysis, and CaCO3 scaling. J. Renew. Sustain. Energy 2023, 15, 013901. [Google Scholar] [CrossRef]
- Guo, T.; Wang, H.; Zhang, S. Comparative analysis of CO2-based transcritical Rankine cycle and HFC245fa-based subcritical organic Rankine cycle using low-temperature geothermal source. Sci. China Tech. Sci. 2010, 53, 1638–1646. [Google Scholar] [CrossRef]
- Lemmon, E.W.; Bell, I.H.; Huber, M.L.; McLinden, M.O. NIST Standard Reference Database 23: Reference Fluid Thermodynamic and Transport Properties-REFPROP, Version 10.0; Standard Reference Data Program; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2018. [CrossRef]
- Bell, I.H.; Lemmon, E.W. Automatic Fitting of Binary Interaction Parameters for Multi-fluid Helmholtz-Energy-Explicit Mixture Models. J. Chem. Eng. Data 2016, 61, 3752–3760. [Google Scholar] [CrossRef]
- Hasan, A.R.; Kabir, C.S.; Sarica, C. Fluid Flow and Heat Transfer in Wellbores; Society of Petroleum Engineers: Richardson, TX, USA, 2002. [Google Scholar]
- Wang, Z.; Sun, B.; Wang, T.; Hou, L. Experimental study on the friction coefficient of supercritical carbon dioxide in pipes. Int. J. Greenh. Gas Control. 2014, 25, 151–161. [Google Scholar] [CrossRef]
- Hasan, A.R.; Kabir, C.S. A mechanistic model for computing fluid temperature profiles in gas-lift wells. SPE Prod. Facil. 1996, 11, 179–185. [Google Scholar] [CrossRef]
- Li, X.; Li, G.; Wang, H.; Tian, S.; Song, X.; Lu, P.; Wang, M. A unified model for wellbore flow and heat transfer in pure CO2 injection for geological sequestration, EOR and fracturing operations. Int. J. Greenh. Gas Control. 2017, 57, 102–115. [Google Scholar] [CrossRef]
- Hasan, A.R.; Kabir, C.S. Wellbore heat-transfer modeling and applications. J. Pet. Sci. Eng. 2012, 86, 127–136. [Google Scholar] [CrossRef]
- Hasan, A.R.; Kabir, C.S. Heat transfer during two-Phase flow in Wellbores; Part I—Formation temperature. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 6–9 October 1991. [Google Scholar] [CrossRef]
- Cheng, W.; Huang, Y.; Lu, D. A novel analytical transient heat-conduction time function for heat transfer in steam injection wells considering the wellbore heat capacity. Energy 2011, 36, 4080–4088. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).